Electro-chemo-mechanics of solid state batteries with lithium plating and stripping

This note is about a novel, thermodynamically consistent formulation for small strains continuum electro-chemo-mechanics applied to all solid state batteries, which are claimed to be the next-generation battery system in view of their safety accompanied by high energy densities. The response of a cell, made of a lithium metal foil, a solid electrolyte, and a porous LiCoO₂ cathode, has been investigated in terms of quantities of interest such as the electric potential, the lithium concentrations profiles, displacements, and stresses. The plating and stripping of the lithium has been considered together with the volumetric evolution of the porous cathode. Together they contribute to the outbreak of mechanical stresses, which may influence the life cycle of a battery.

1 Introduction

All solid state batteries (ASSBs) are claimed to be the next-generation battery system, since they combine superior thermal and electrochemical stability and avoid hazardous liquid electrolyte leakage Schnell et al. (2018); Zheng et al. (2018); Boz et al. (2021). In spite of these promising features, ASSBs still present a number of chemo-mechanical issues, pointed out extensively in Bistri et al. (2021). Accurate and rigorous models may contribute to understanding the physics behind those pitfalls, incorporating several processes that are interconnected at different scales during batteries operations Li and Monroe (2020). Numerical simulations may provide insights into battery degradation, by reproducing capacity fade in charge/discharge cycles.

Here, we focus on the effect of plating and stripping Carter et al. (2019); Zhang et al. (2022) in the state of stress of a battery. An approach to describe the evolution of such processes at the anode/electrolyte interface was presented, for small strain theory, in Liu and Lu (2017) using the meshing capabilities of Matlab. The detrimental effects of plating and stripping at the lithium metal/solid electrolyte interface in ASSB have been modeled in Narayan and Anand (2020), mimicking the process of addition of new layers of Li at the anode interface with a conforming interphase layer, avoiding the fact that physical quantities evolve and hence there is no fixed reference configuration. In this note, we describe the thickening of the lithium foil during galvanostatic charge and determine the state of stress in the cell, together with fundamental quantities of interest such as the electric potential and the lithium concentrations profiles. Internal stresses arise after imposing that the battery case is extremely stiff, hence preventing the expansion of the cell at the two current collectors.

The modeling of a solid, Lithium phosphorus oxynitride (LiPON henceforth) electrolyte, stems from a previous paper Cabras et al. (2022), where the authors proposed a two-mechanisms and multiscale compatible approach. The paper is organized as follows. The fundamental statements for the electrochemical modeling of the solid electrolyte and plating evolution are described in Section 2, while the balance equations and the thermodynamics prescriptions have been derived in Section 3. Governing equations include the deposition and extraction of lithium from the anode, which have been considered together with the expansion and shrinkage of the porous cathode. Eventually, the simulation of charge and discharge of a whole cell has been carried out via the finite element method in Section 4. Although we approximated numerically the solution of a one-dimensional problem, the governing equations have been stated in a general form. Outcomes are profoundly discussed in Section 4.3, before drawing conclusions and further developments.

2 Electrochemical modeling of the solid electrolyte and plating evolution

2.1 Electrochemical modeling

A multiphysics, two-mechanisms model of ionic conduction in LIPON has been recently formulated in Cabras et al. (2022). The developed continuum theory for coupled electro-chemistry advances Raijmakers et al. (2020) in modeling the replenishment of vacancies and is thermodynamically consistent as well as multi-scale-compatible.

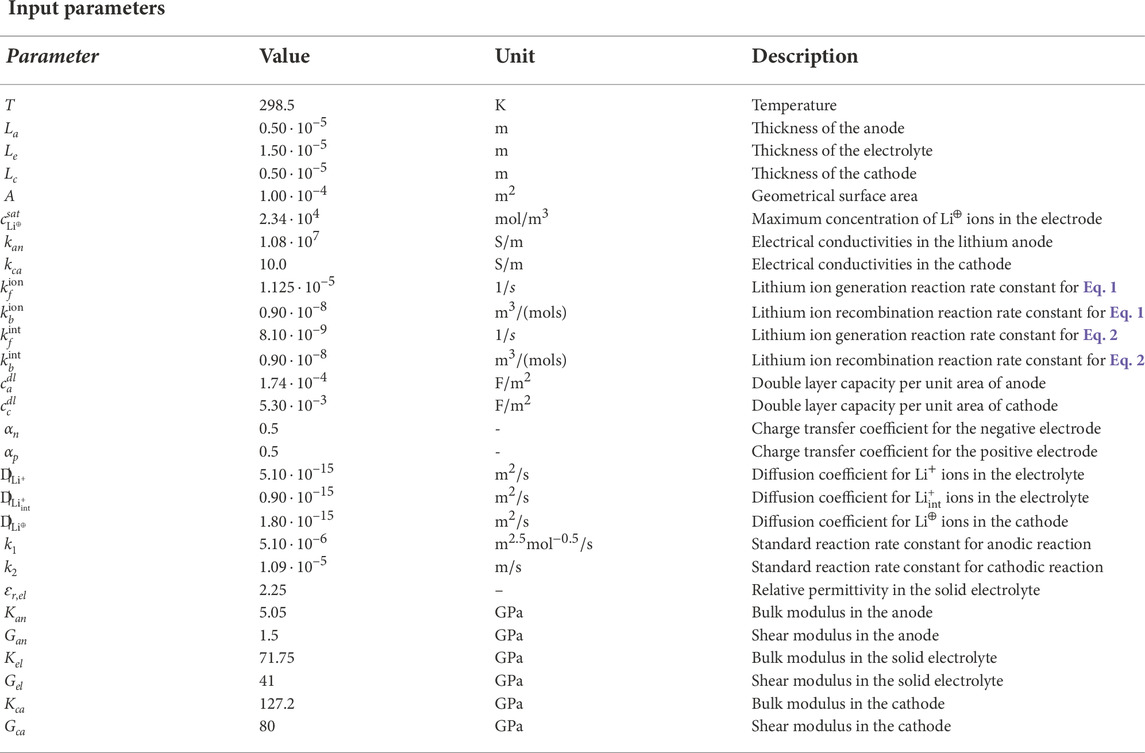
The amorphous structure of the LiPON electrolyte is schematically shown in Figure 1. It highlights two types of nitrogen bonds, either triply- or doubly coordinated. Li₀ denotes the (ionic) lithium bound to the non-bridging oxygen atoms, Li⁺ is a lithium ion and n⁻ is the uncompensated negative charge associated with a vacancy formed in the LiPON matrix at the place where Li⁺ was originally bound. The maximal concentration of host-sites, denoted with c₀, is established by the stoichiometric composition of the electrolyte material and it is reached in the ideal case of absolute zero temperature, when all available host sites are fully filled with lithium ions and the ionic conductivity vanishes because all ions are immobile. In standard conditions some of the Li-ions are thermally excited and the chemical ionization reaction

$\mathrm{L}{\mathrm{i}}_{\mathrm{0}}\underset{k_b^{\text{ion}}}{\stackrel{k_f^{\text{ion}}}{\rightleftarrows }}\mathrm{L}{\mathrm{i}}^{+}+{\mathrm{n}}^{-}(1)$

occurs, $k_f^{\text{ion}}$ and $k_b^{\text{ion}}$ being the forward and backward rate constants for the ionization (or recombination) reaction, respectively. The ratio

$K_{\text{eq}}^{\text{ion}}=k_f^{\text{ion}}/k_b^{\text{ion}}$

is the equilibrium constant of the ionization Eq. 1. Some ions, denoted henceforth with${\mathrm{L}\mathrm{i}}_{\text{int}}^{+}$, move in a meta-stable interstitial state, whereas the remaining Li⁺ ions hop and fill neighboring vacancies. This ionic interplay is described through a further reaction that splits the amount of ions made available by Eq. 1 into hopping (the reactants) and interstitial (the products)

$\mathrm{L}{\mathrm{i}}^{+}\underset{k_b^{\text{int}}}{\stackrel{k_f^{\text{int}}}{\rightleftarrows }}{\mathrm{L}\mathrm{i}}_{\text{int}}^{+},(2)$

where $k_f^{\text{int}}$ and $k_b^{\text{int}}$ are the rate constants for Eq. 2 and their ratio $K_{\text{eq}}^{\text{int}}=k_f^{\text{int}}/k_b^{\text{int}}$ is the equilibrium constant of Eq. 2. The chemical kinetics of Eqs. 1, 2 are modeled via the law of mass action, which writes:

$w=k_f^{\text{ion}}{c}_{{\text{Li}}_0}-k_b^{\text{ion}}{c}_{{\text{Li}}^{+}}{c}_{{\text{n}}^{-}},\mathrm{a}\mathrm{n}\mathrm{d}y=k_f^{\text{int}}{c}_{{\text{Li}}^{+}}-k_b^{\text{int}}{c}_{{\text{Li}}_{\text{int}}^{+}}.(3)$

FIGURE 1

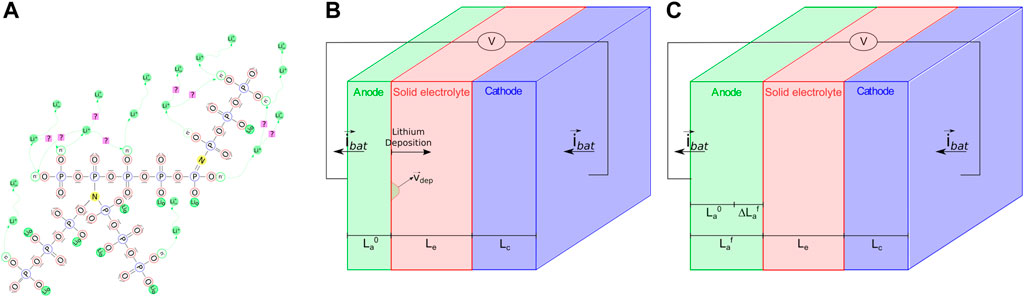
FIGURE 1. (A) Representation of the LiPON matrix with triply- and doubly coordinated nitrogen and with lithium ions Li⁺. (B) Initial configuration of the cell made of three different domains: a metal lithium anode, a solid electrolyte and a porous cathode. (C) Configuration of the cell during a process of charging with visible the lithium deposition on the anode surface at the interface with the solid electrolyte.

2.2 Mechanical modeling

The lithium plating is modeled in accordance with Liu and Lu (2017), where the normal velocity of lithium deposition at the anode interface with the solid electrolyte,${\vec{v}}_{\mathit{dep}}$, is given as a function of the current density

${\vec{v}}_{\mathit{dep}}=\frac{{\mathrm{\Omega }}_{\text{Li}}}{F}{\vec{i}}_{\mathit{bat}}.(4)$

Ω_Li is the molar volume of the lithium, F the Faraday constant and ${\vec{i}}_{\mathit{bat}}$ is the current density flowing through the interface between anode and solid electrolyte.

Figure 2 depicts the behaviour of the cell during the lithium deposition. If we focus on Figure 2B, which depicts a stress-free, intermediate configuration in which the cell is free to expand, at a generic instant t_f an increment of the initial thickness of the anode $L_a^0$ is visible. It amounts at

$\mathrm{\Delta }{L}_a^{\mathit{dep}}={\int }_0^{t_f}{v}_{\mathit{dep}}\mathrm{d}t.(5)$

In operative conditions the cell is confined by a stiff case. The displacements of the two ends of the cell are therefore fixed and the thickening of the anode due to deposition is influenced by the mechanical response, as illustrated in Figure 2C. The swelling–shrinking response of the cathode also plays a role in the definition of the stresses in a confined cell, depending on the material response upon intercalation/extraction.

FIGURE 2

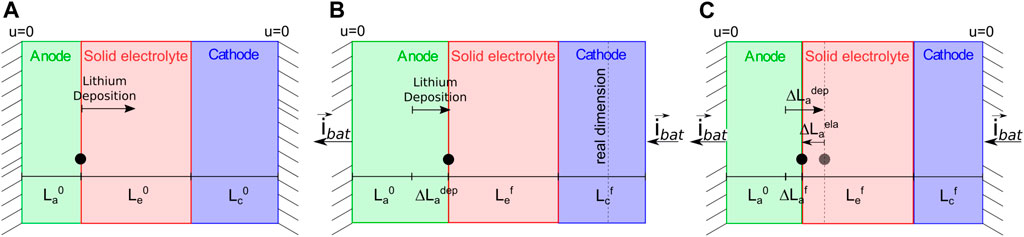
FIGURE 2. (A) A pictorial view of the cell in its initial state, before current is applied. (B) Free expansion of the cell induced by the lithium deposition $\mathrm{\Delta }{L}_a^f=\mathrm{\Delta }{L}_a^{\mathit{dep}}$. (C) A confined cell in operative conditions, the motion of the interface is given by the contributions of deposition and of the mechanical response.

3 Governing equations

3.1 Balance equations

3.1.1 Solid electrolyte

In the multiphysics picture illustrated in Section 2.1, positive ions are the only moving species, and the relocation of vacancies is the outcome of the ionic transport1. Denote with c_α the concentration (i.e. the number of moles per unit volume) of a generic species α and with ${\vec{h}}_{\alpha }$ the mass flux in terms of moles, i.e. the number of moles of species α measured per unit area per unit time. The mass balance equations characterize the chemo-diffusive transport of four different species within the solid electrolyte. They read:

$\frac{\partial c_{{\text{Li}}_0}}{\partial t}=-w,(\mathrm{6a})$

$\frac{\partial c_{n^{-}}}{\partial t}=w,(\mathrm{6b})$

$\frac{\partial c_{{\text{Li}}^{+}}}{\partial t}+\mathrm{d}\mathrm{i}\mathrm{v}\left[{\vec{h}}_{{\text{Li}}^{+}}\right]=w-y,(\mathrm{6c})$

$\frac{\partial c_{{\text{Li}}_{\text{int}}^{+}}}{\partial t}+\mathrm{d}\mathrm{i}\mathrm{v}\left[{\vec{h}}_{{\text{Li}}_{\text{int}}^{+}}\right]=y,(\mathrm{6d})$

where the overall rate of the charge carrier generation is given by the mass action laws (3). The set of 4 mass balance Eqs 6a, 6b, 6c, 6d, contains five unknowns, the concentrations c_Li0, c_n⁻, $c_{{\text{Li}}^{+}}$, and $c_{{\text{Li}}_{\text{int}}^{+}}$ plus the electric potential ϕ, which is constitutively related to the mass fluxes ${\vec{h}}_{\alpha }$. In the present paper, the additional required equation is Ampère’s law (with Maxwell’s correction), which reads:

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\frac{\partial \vec{D}}{\partial t}+F\left({\vec{h}}_{{\text{Li}}^{+}}+{\vec{h}}_{{\text{Li}}_{\text{int}}^{+}}\right)\right]=0.(7)$

To conclude the set of balance equations, we introduce the usual balance of forces in small strains:

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\mathit{\sigma }\right]+\vec{b}=\vec{0}.(8)$

3.1.2 Electrodes

The anode is a foil of pure metal lithium, a continuous reservoir of ions. Balance equations depict the conservation of charge and linear momentum, in the two unknowns electric potential ϕ and displacements $\vec{u}$:

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\vec{i}\right]=0,(\mathrm{9a})$

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\mathit{\sigma }\right]+\vec{b}=\vec{0}.(\mathrm{9b})$

During intercalation in the cathode, the lithium keeps its ionic nature “shielded” by its own electron. Such a species will be denoted with Li^⊕ to distinguish it from mobile charges Li⁺ in the electrolyte. Balance equations characterize the chemo-diffusive migration transport of Li^⊕, the electronic motion, and mechanical stress:

$\frac{\partial c_{{\text{Li}}^{\oplus }}}{\partial t}-\mathrm{d}\mathrm{i}\mathrm{v}\left[{\vec{h}}_{{\text{Li}}^{\oplus }}\right]=0,(\mathrm{10a})$

$\mathrm{d}\mathrm{i}\mathrm{v}\left[{\vec{i}}_{ca}\right]=0,(\mathrm{10b})$

$\mathrm{d}\mathrm{i}\mathrm{v}\left[\mathit{\sigma }\right]+\vec{b}=\vec{0}.(\mathrm{10c})$

3.2 Constitutive theory

Governing equations emanate from balance equations, provided that appropriate constitutive laws are given. For the sake of limiting the length of this note, we do not indulge in details on the thermodynamic analysis, which can be derived from Salvadori et al. (2015a,b, 2018).

3.2.1 Electrolyte

The constitutive laws for the electric displacement $\vec{D}$, the fluxes of the species ${\vec{h}}_{\alpha }$ and the stress tensor σ shall be defined. The electric displacement field is related to the electric potential ϕ constitutively by:

$\vec{D}=-{\epsilon |}_{el}\nabla \left[\varphi \right],(11)$

where ɛ |_el = ɛ |_r ɛ |₀ is the electric permittivity and its value is ɛ |_r times the electric permittivity in vacuum, denoted with ɛ |₀ = 8.85 × 10^–12 C/(V m). A linear dependence on the gradient of the electrochemical potential ${\bar{\mu }}_{\alpha }$ is taken for the mass flux ${\vec{h}}_{\alpha }$ of positive ions $\alpha =\mathrm{L}{\mathrm{i}}^{+},{\mathrm{L}\mathrm{i}}_{\text{int}}^{+}$ in the absence of convection:

${\vec{h}}_{\alpha }=-\frac{{\mathrm{D}|}_{\alpha }{c}_{\alpha }}{RT}\nabla \left[{\bar{\mu }}_{\alpha }\right],(\mathrm{12a})$

equipped with the thermodynamic specification

${\bar{\mu }}_{\alpha }={\mu }_{\alpha }^0+RT\left(1+\text{ln}\left[c_{\alpha }\right]\right)+z_{\alpha }F\varphi ,(\mathrm{12b})$

where R is the universal gas constant, D |_α is the diffusivity of species α,${\mu }_{\alpha }^0$ is a reference value of the chemical potential, and T is the absolute temperature. Fick’s law (12a) takes the Nernst-Planck form

${\vec{h}}_{\alpha }=-{\mathrm{D}|}_{\alpha }\nabla \left[c_{\alpha }\right]-\frac{{\mathrm{D}|}_{\alpha }F}{RT}{c}_{\alpha }\nabla \left[\varphi \right].(\mathrm{12c})$

LiPON is an inorganic solid electrolyte, a glass ceramic which assumes an amorphous state instead of a regular crystalline structure. Its brittle, mechanical response is here described as for an homogeneous and isotropic material in small strains:

$\mathit{\sigma }=K_{el}\mathrm{t}\mathrm{r}\left[\mathit{\epsilon }\right]\mathbb{1}+2G_{el}\mathrm{d}\mathrm{e}\mathrm{v}\left[\mathit{\epsilon }\right],(13)$

where K_el, G_el are the bulk and shear modulus respectively. The governing equations for the solid electrolyte at all points $\vec{x}$ and times t come out incorporating constitutive Eqs 11–13 into the balance Eqs 6–8.

3.2.2 Electrodes

For the anode, an Ohmic behaviour models the electron flow

${\vec{i}}_{an}=-k_{an}\nabla \left[\varphi \right],(14)$

where k_an represents the electric conductivity. Although we are well aware that complex visco-plastic models exist for the lithium metal, see Anand and Narayan (2019); Sedlatschek et al. (2021) among others, in this note we limit ourselves to investigate the elastic response of the foil, i.e.

$\mathit{\sigma }=K_{an}\mathrm{t}\mathrm{r}\left[\mathit{\epsilon }\right]\mathbb{1}+2G_{an}\mathrm{d}\mathrm{e}\mathrm{v}\left[\mathit{\epsilon }\right],(15)$

with K_an, G_an the bulk and shear modulus respectively.

The constitutive equations result more involved for the cathode, since swelling-shrinking upon intercalation are accounted for in the definition of the small strain tensor ɛ and of the chemical potential ${\mu }_{{\text{Li}}^{\oplus }}$. Intercalation in the cathode active material entails an interaction between electro-chemistry and mechanics, bringing coupling terms in the chemical potential

$\begin{array}{c}{\mu }_{{\text{Li}}^{\oplus }}={\mu }_{{\text{Li}}^{\oplus }}^0+RT\left(1+\text{ln}\left[c_{{\text{Li}}^{\oplus }}\right]\right)-p{\mathrm{\Omega }}_{{\text{Li}}^{\oplus }},\end{array}(16)$

and in the De Saint Venant–Kirchhoff constitutive model of the stress

$\mathit{\sigma }=K_{ca}\mathrm{t}\mathrm{r}\left[\mathit{\epsilon }-{\mathit{\epsilon }}^{\mathit{s}}\right]\mathbb{1}+2G_{ca}\mathrm{d}\mathrm{e}\mathrm{v}\left[\mathit{\epsilon }-{\mathit{\epsilon }}^{\mathit{s}}\right],(17)$

with the pressure

$p=\mathrm{t}\mathrm{r}\left[\mathit{\sigma }\right]/3(18)$

and

${\mathit{\epsilon }}^s=\frac{{\mathrm{\Omega }}_{{\text{Li}}^{\oplus }}}{3}\left(c_{\text{Li}}^{\oplus }-c_{{\text{Li}}^{\oplus }}^0\right)\mathbb{1}.$

The Fickian flux of lithium Li^⊕ is defined as usual:

${\vec{h}}_{{\text{Li}}^{\oplus }}=-\frac{{\mathrm{D}|}_{{\text{Li}}^{\oplus }}{c}_{{\text{Li}}^{\oplus }}}{RT}\nabla \left[{\mu }_{{\text{Li}}^{\oplus }}\right].(19)$

The electron flow in the active and conductive material obeys Ohm’s law (14) with parameters that refer to the cathode. The governing equations for the electrodes incorporate Eqs 14, 15 into Eqs 9a, 9b for the anode and Eqs 14, 17, 19 into Eqs 10a, 10b, 10c for the cathode.

4 Simulations

The problem formulated above is applied to a planar, thin film all-solid-state battery with LiPON electrolyte. A one-dimensional geometry is suitable for this problem, since the ratio between the lateral dimension and the thickness is large enough for the former to be considered as infinite. Figure 3 depicts the battery as consisting in a positive LiCoO₂ electrode with thickness L_c = 0.50 μm, a metallic lithium Li foil with thickness L_a = 0.50 μm and a layer of LiPON with thickness L_e = 1.50 μm.

FIGURE 3

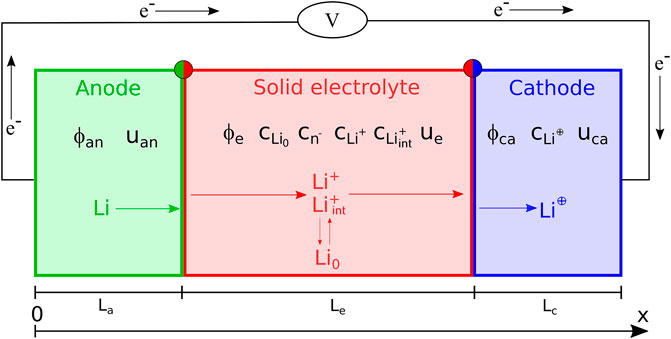
FIGURE 3. A pictorial view of the all-solid-state electrochemical cell used to validate the solid electrolyte model proposed, together with the unknown fields.

Li-ions are extracted from the positive electrode during charge, when the Li ions move across the solid electrolyte and are reduced into metallic Li at the lithium foil surface; vice versa during discharge. Charge-transfer kinetics at both electrode/electrolyte interfaces, diffusion, and migration of mobile lithium ions in the electrolyte (Li⁺) have been accounted for. Double layers at both electrode/electrolyte interfaces have been considered, too. The process is isothermal, invoking thermal equilibrium; volume changes of the solid electrolyte during cycling are neglected, whereas the swelling and shrinking of the cathode are modeled. Furthermore the model encompasses the evolution of the lithium deposition/remotion on the anode/electrolyte surface.

The surface area of the electrodes is A = 10⁻⁴ m² and the theoretical storage capacity of the battery amounts at 1.53 ⋅ 10⁻⁵Ah. A galvanostatic process of charge followed by discharge, under a temperature-controlled condition of 25°C, is applied with current density i_bat = 0.035 A/m². The equilibrium constants for the two reactions have been assumed as follows: $K_{\text{eq}}^{\text{ion}}=1250$ and $K_{\text{eq}}^{\text{int}}=0.9$. Table 1 reports all the values of material and geometrical parameters.

TABLE 1

TABLE 1. Model parameters for the numerical simulations of a all-solid-state electrochemical cell.

4.1 Initial and boundary conditions

Concentrations of species are uniform and satisfy thermodynamic equilibrium at time t = 0. They hold:

$c_{{\text{Li}}_0}\left(x,0\right)=4.93\cdot 10^4\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{m}}^{\mathrm{3}}{L}_a\le x\le L_a+L_e,(\mathrm{20a})$

$c_{{\text{n}}^{-}}\left(x,0\right)=1.08\cdot 10^4\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{m}}^{\mathrm{3}}{L}_a\le x\le L_a+L_e,(\mathrm{20b})$

$c_{{\text{Li}}^{+}}\left(x,0\right)=5.68\cdot 10^3\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{m}}^{\mathrm{3}}{L}_a\le x\le L_a+L_e,(\mathrm{20c})$

$c_{{\text{Li}}_{\text{int}}^{+}}\left(x,0\right)=5.12\cdot 10^3\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{m}}^{\mathrm{3}}{L}_a\le x\le L_a+L_e,(\mathrm{20d})$

$c_{{\text{Li}}^{\oplus }}\left(x,0\right)=c_{{\text{Li}}^{\oplus }}^{\mathit{sat}}\mathrm{m}\mathrm{o}\mathrm{l}/{\mathrm{m}}^{\mathrm{3}}{L}_a+L_e\le x\le L_a+L_e+L_c.(20e)$

The electric potential of the lithium foil at the interface between the anode and the solid electrolyte is fixed as:

$\varphi \left(0,t\right)=0\left[V\right]\forall t.(21)$

To simulate the presence of a stiff, protective case, which confines the displacements at the two ends of the cell, two Dirichlet boundary conditions are imposed:

$u\left(0,t\right)=0\text{\hspace{0.17em}and}L\left(t\right)=L^0\forall t,(22)$

where L⁰ is the total length of the cell in the reference configuration at the initial time and L(t) is the total length of the cell in the current configuration at time t.

Boundary conditions for the galvanostatic process are imposed as:

$\vec{i}\left(0,t\right)\cdot \vec{n}=i_{\mathit{bat}}\left(t\right)\vec{i}\left(L,t\right)\cdot \vec{n}=-i_{\mathit{bat}}\left(t\right),(\mathrm{23a})$

Where $\vec{n}$ is the outward normal to a surface. At the electrolyte interfaces with the electrodes, the total lithium flux $({\vec{h}}_{{\text{Li}}_{\text{tot}}^{+}}={\vec{h}}_{{\text{Li}}^{+}}+{\vec{h}}_{{\text{Li}}_{\text{int}}^{+}})$ is split into two terms, corresponding to the fluxes generated by the two mechanisms.

$\begin{array}{ll}\hfill {\vec{h}}_{{\text{Li}}^{+}}\left(L_a,t\right)\cdot \vec{n}& =-h_{{\text{Li}}^{+}}^{BV,an}\left(t\right),\hfill \\ \hfill {\vec{h}}_{{\text{Li}}_{\text{int}}^{+}}\left(L_a,t\right)\cdot \vec{n}& =-h_{{\text{Li}}_{\text{int}}^{+}}^{BV,an}\left(t\right),\hfill \end{array}(\mathrm{24a})$

$\begin{array}{ll}\hfill {\vec{h}}_{{\text{Li}}^{+}}\left(L_a+L_e,t\right)\cdot \vec{n}& =-h_{{\text{Li}}^{+}}^{BV,ca}\left(t\right),\hfill \\ \hfill {\vec{h}}_{{\text{Li}}_{\text{int}}^{+}}\left(L_a+L_e,t\right)\cdot \vec{n}& =-h_{{\text{Li}}_{\text{int}}^{+}}^{BV,ca}\left(t\right),\hfill \end{array}(\mathrm{24b})$

Where the mass fluxes $h_{{\text{Li}}^{+}}^{BV,\alpha }$ and $h_{{\text{Li}}_{\text{int}}^{+}}^{BV,\alpha }$, with α identifying the anode (an) and the cathode (ca) interfaces, must descend from a proper interface equation, generally of Butler-Volmer type, as in Cabras et al. (2022).

The traction continuity is imposed:

$\begin{array}{ll}\hfill {\mathit{\sigma }}_{an}\left(L_a,t\right)\cdot \vec{n}& =-{\mathit{\sigma }}_{el}\left(L_a,t\right)\cdot \vec{n}\hfill \\ \hfill {\mathit{\sigma }}_{el}\left(L_a+L_e,t\right)\cdot \vec{n}& =-{\mathit{\sigma }}_{ca}\left(L_a+L_e,t\right)\cdot \vec{n}.\hfill \end{array}(\mathrm{25a})$

4.2 Solution schemes

The governing equations are numerically solved with the finite element method, with an in house implementation of weak forms in the commercial numerical software Matlab. The geometry and the unknown fields are discretized with 80 linear elements, 40 of them covering the electrolyte and 20 tessellating each electrode. The time marching is dealt with the backward Euler method, with fixed time increments of Δt = 1.0 s. Since we are dealing with a problem of deposition, the reference configuration of the system is not established in time. Rather, it is updated at each time step. The evolution of the reference configuration is driven by the (one-dimensional) increment of the thickness, which is defined in Eq. 5. If the cell is not confined, no mechanical stresses are generated (see Figure 4B). When the cell is confined, as in the proposed case-study, to restore compatibility a displacement is imposed in the intermediate configuration at the right end of the cell,

$u\left(L\left(t\right),t\right)=-\mathrm{\Delta }{L}_a^{\mathit{dep}}\left(t\right).$

FIGURE 4

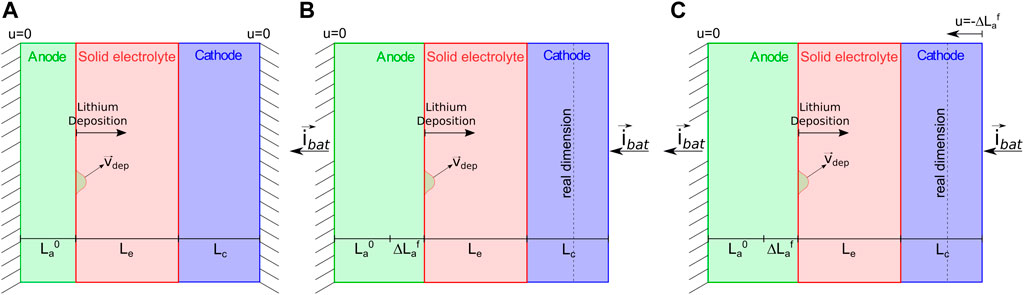
FIGURE 4. (A) A pictorial view of the cell in the reference configuration, when no current is applied. (B) The cell in the intermediate configuration, after the current is applied. The configuration corresponds to a cell free to expand, where the elongation of the cell is induced by the deposition $\mathrm{\Delta }{L}_a^f=\mathrm{\Delta }{L}_a^{\mathit{dep}}$. (C) The current configuration of the cell. Compatibility is recovered applying on the right end of the cell a displacement opposite to the deposition $u(L(t),t)=-\mathrm{\Delta }{L}_a^{\mathit{dep}}$. The actual displacement field inside the cell is due to the lithium deposition, of the elastic deformation, and of the volume change of the cathode.

During the numerical simulation the reference configuration of the system has been updated at each time step, increasing or reducing the thickness of the anode because of the deposition or extraction of the lithium from its surface.

4.3 Numerical results

4.3.1 Discharge curves

Initial and boundary conditions are made compatible with thermodynamic equilibrium at t = 0, tuning the current density i_bat(t) in time. Figure 5A shows the applied current density i_bat(t), modeled via a logistic curve, as a function of time. After a short steep transient, the current reaches a plateau, which corresponds to a steady current density |i_bat| = 0.035 [A/m²]. It is kept fixed for about 40 h. The cell is discharged afterwards. In Figure 5B, the charge/discharge curves are plotted against the extracted charge: the voltage of the cell increases up to its maximum value 4.2 [V] while charging. The discharge process starts afterwards, the voltage reduces and a voltage drop becomes evident when the saturation concentration of the lithium in the cathode (the limiting factor) is approached.

FIGURE 5

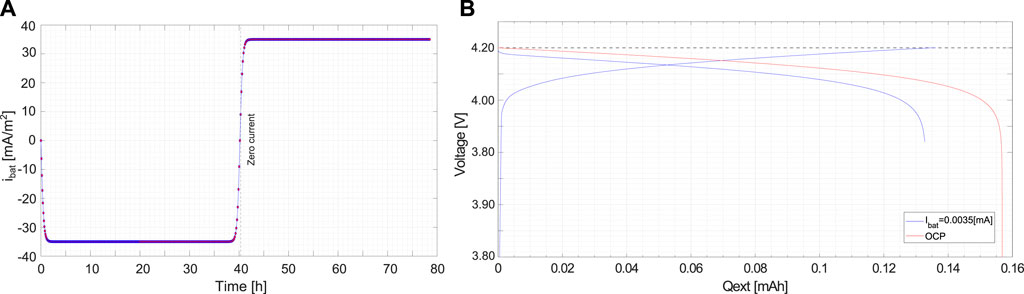
FIGURE 5. (A) Applied current density as a function of time i_bat(t). (B) Charge/Discharge curves as a function of the extracted charge.

Charging and discharging cause the deposition and remotion of lithium at the anode surface in contact with the solid electrolyte. No degradation models are introduced, hence the hysteresis diagram of Figure 5B is replicated during further cycles. The open circuit potential (OCP) used in the simulations has been calculated analytically, following the approach proposed in Purkayastha and McMeeking (2012).

4.3.2 Electric potential profiles

The electric potential profile ϕ(x) in the battery at different times is depicted in Figure 6A, in the current configuration. The blue curve corresponds to the initial condition, when no current is applied. The black one to the maximum value after charging. At full charge, the electric potential discontinuities at the interfaces make Butler-Volmer currents vanishing. Based on the measured battery OCP, at full charge state

$\varphi \left(L,t^f\right)-\varphi \left(0,t^f\right)=4.2\left[V\right].$

FIGURE 6

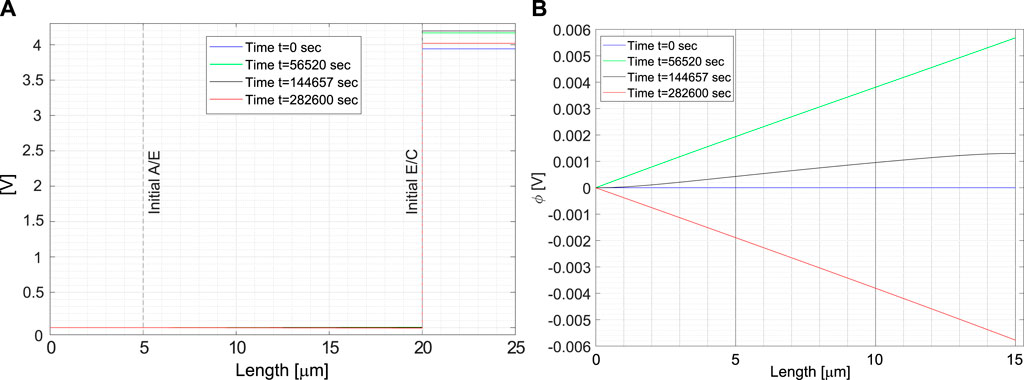
FIGURE 6. (A) Electric potential profile in the cell at different time steps. (B) Electric potential in the electrolyte at different time steps.

Complete discharging, when the concentration of lithium Li^⊕ inside the cathode is close to the saturation limit of the cathode $c_{{\text{Li}}^{\oplus }}^{\text{sat}}$, is captured by the red line. Cathodic saturation is the limit factor for the battery operation (see also Magri et al. (2022) for an extensive discussion on limiting factors in electrochemical cells, induced by materials and architectures).

4.3.3 Lithium concentrations profiles

The evolution of lithium concentration in the current configuration of the cell at different time steps is given in Figure 7A. Note the interface motion due to deposition. The anode is an unlimited reservoir of lithium. The concentration of lithium (i.e. its density) does not change while the thickness does. The blue curve corresponds to the initial condition, at thermodynamic equilibrium, with the concentration of lithium inside the cathode equal to the saturation limit $c_{{\text{Li}}^{\oplus }}^{\text{sat}}$. The black curve reports the concentration of lithium during charge, when the potential reaches the limit value of 4.2 [V], corresponding to the end of the charge phase; the red curve depicts the final state at discharging, when the saturation limit at the interface between the electrolyte and the cathode is reached. Both black and red plots refer to states out of equilibrium. Although the C-rate is small, it is evident how lithium intercalates inside the cathode and accumulates near the electrolyte/cathode interface in the discharge process. Vice versa, the removal of lithium from the anodic foil is visible in charge.

FIGURE 7

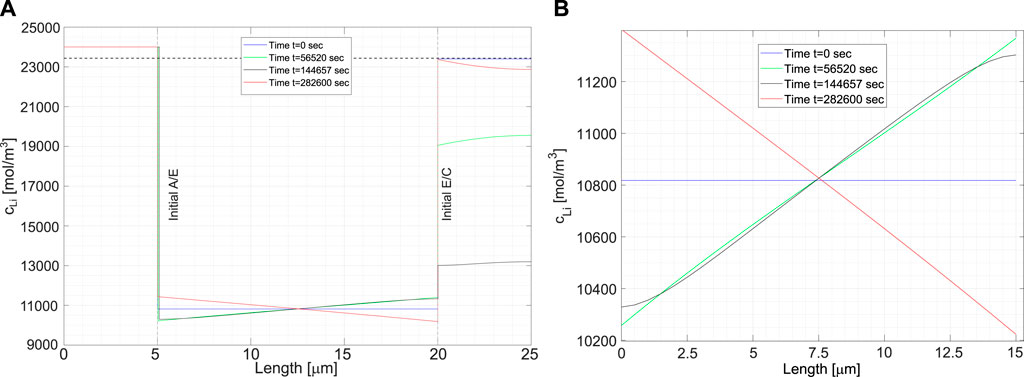
FIGURE 7. (A) Lithium concentration profiles at different time steps. The blue line corresponds to the initial time step, at thermodynamic equilibrium. Cathode is fully saturated. The black line corresponds to full charge, while the red line to the final values of the concentrations after the discharge. (B) The lithium concentration in the solid electrolyte: the sum $(c_{{\text{Li}}^{+}}+c_{{\text{Li}}_{\text{int}}^{+}})$ is reported.

Figure 7B magnifies Figure 7A and highlights the evolution of the lithium concentration in the electrolyte. Since two ionic concentrations are concurrently present, only their sum $(c_{\text{Liˆ}+}+c_{{\text{Li}}_{\text{int}}^{+}})$ has been plotted. Before the current is inverted, lithium concentration decreases in the left half of the electrolyte and increases by the cathode. During discharging, the opposite is seen.

The concentrations of species c_{Li_{0}},${\mathrm{c}}_{n^{-}}$,${\mathrm{c}}_{L{i}^{+}}$ and ${\mathrm{c}}_{L{i}_{\mathit{int}}^{+}}$ are plotted separately in Figure 8A. The concentration profiles, after a transition period, tend to linearize. Notice the reciprocal exchange between the Li⁺ and ${\mathrm{L}\mathrm{i}}_{\mathit{int}}^{+}$, ruled by reaction 2, and how the (negative) uncompensated charges are filled by hopping lithium. Finally, the lithium concentrations in the solid electrolyte of Li⁺, ${\mathrm{L}\mathrm{i}}_{\mathit{int}}^{+}$ and their sum at the interfaces with the electrodes as a function of time are reported in Figure 8B. The continuous lines correspond to the values estimated at the anodic interface, while the dashed curves correspond to the values at the cathode interface. The concentrations show an increment at the anode interface and a decrement at the cathode interface during discharging; before the current is inverted, the trend of the concentration was the opposite.

FIGURE 8

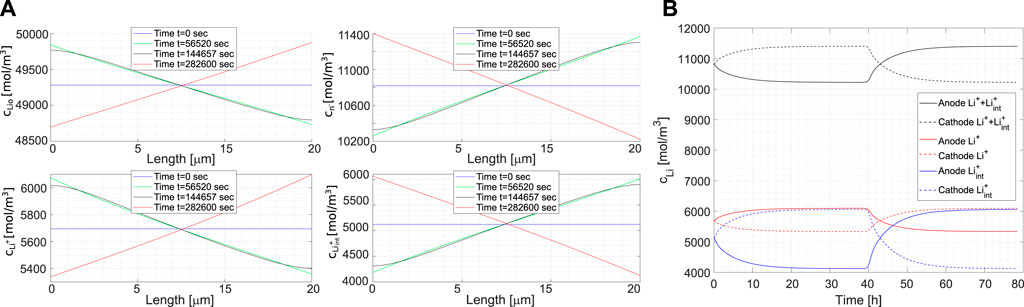
FIGURE 8. (A) Lithium concentration profiles of the different species c_Li0,${\mathrm{c}}_{n^{-}}$,${\mathrm{c}}_{L{i}^{+}}$ and ${\mathrm{c}}_{L{i}_{\mathit{int}}^{+}}$ inside the solid electrolyte at different time steps. (B) Lithium concentrations for Li⁺,${\mathrm{L}\mathrm{i}}_{\mathit{int}}^{+}$ and their sum at the interfaces with the electrodes. The continuous lines correspond to the values measured at the interface anode/electrolyte and the dashed line corresponds to the values in the interface electrolyte/cathode.

4.3.4 Mechanical response

Figure 9A depicts the displacement of the anode/electrolyte and electrolyte/cathode interfaces as a function of time. They are induced by the thickening of the anode during charge (and vice versa during discharge), by the elastic deformation due to the lateral constraints, and by the swelling/shrinking of the cathode upon extraction/intercalation. Since the adopted model is one dimensional and no bulk forces are applied along the cell, the Cauchy stress is uniform. It is plotted in Figure 9B as a function of time.

FIGURE 9

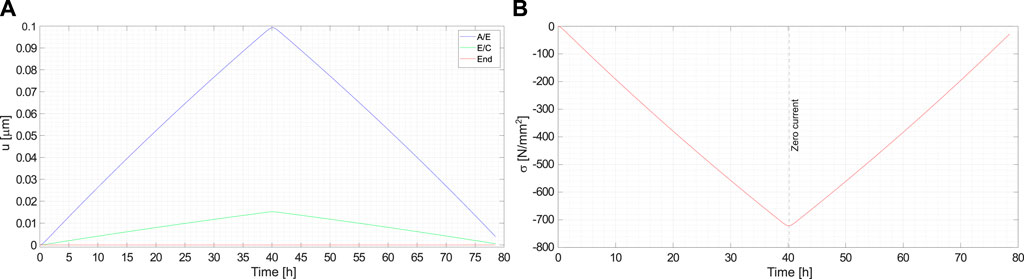
FIGURE 9. (A) Displacements of the interfaces anode/electrolyte, electrolyte/cathode and of the right end of the cell are shown as a function of time. (B) Mechanical stress in the cell as a function of time.

The swelling-shrinking of the cathode upon intercalation/extraction can sharpen or reduce the stress in the cell, depending upon the cathodic change in volume with the lithium ions concentration. For LiCoO₂, a loss of lithium causes a volumetric expansion, as reported by Mendoza et al. (2016) and Reimers and Dahn (1992). Delithiation induced swelling during battery charge is governed by the molar volume (three times the chemical expansion coefficient) ${\mathrm{\Omega }}_{L{i}^{\oplus }}=-2.4\cdot 10^{-7}{\mathrm{m}}^{\mathrm{3}}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-\mathrm{1}}$ Mendoza et al. (2016), where the negative value indicates expansion during delithiation.

Define as usual displacement as the difference between the location in the current configuration and the point position in the reference, i.e.

$\vec{u}\left(\vec{X}\right)=\vec{x}-\vec{X}.(26)$

Such a field is shown in Figure 10 at different time steps, in the current configuration. The initial configuration (t = 0), assumed at thermodynamic equilibrium, is taken to be displacement and stress free (blue curve). To better figure out the motion scenario within the cell, consider the reference and the intermediate configuration. All points that belong to the anode in the initial (referential) state do no undergo any configurational change, i.e. their position is unchanged in the intermediate configuration. Consider a point $\vec{P}$ in the LIPON electrolyte in the reference configuration. At a given time, the lithium plating causes a positive (rightward) displacement of the electrolyte/lithium foil interface, which corresponds to a rigid displacement at the point $\vec{P}$ for the intermediate configuration. The current configuration is a competition between the configurational change of the anode and the mechanical response due to the compressive state of the cell induced by the boundary conditions. In view of the lithium plating during charge, the anode thickens and fixing the two ends of the cell generates a compressive state of stress. The intermediate configuration deforms (shortening) into the current configuration, inducing a leftward (negative) displacement to all points in the anode that existed at the beginning of the charging process. The displacements within the electrolyte turned out to be still rightward, i.e. positive. A similar outcome holds for the cathodic displacement field. They are depicted in Figure 10. The definition (26) cannot apply to the material that has been generated because of plating, since new volume has been created. For them, we can adopt a different definition of displacements, i.e. the difference between the location in the current configuration and the point position in the intermediate configuration, i.e.

${\vec{u}}^{*}\left(\overrightarrow{X^{*}}\right)=\vec{x}-\overrightarrow{X^{*}}(27)$

FIGURE 10

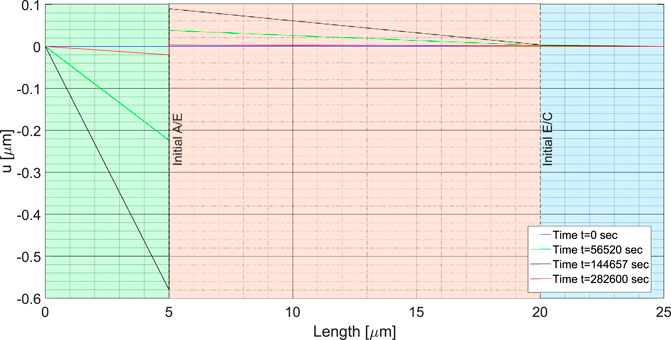
FIGURE 10. Displacements of the pre-existing lithium foil, electrolyte and cathode at different time steps. The blue line corresponds to the initial time step, when no external forces and currents are applied. The black line corresponds to the end of the charge phase, and the red line to the end of the discharge, when the saturation limit of the lithium concentration in the electrolyte-cathode interface is reached.

The definitions (26) and (27) are identical for the anode, but different for electrolyte and cathode. We will thus base the notion of strain from definition (26) for the latter, and from definition (27) for the anode. It is trivial to show that the definition of all strain measures is consistent with the classical ones within each material. The same conclusion can therefore be inferred for the constitutive laws. Since we assumed that the response of all materials in the cell is linear elastic, a straight line depicts the displacement field in Figure 10. The displacement jump at the electrolyte/lithium foil interface corresponds to the effect of thickening due to plating, followed by the elastic deformation of the freshly deposited lithium. The blue line refers to the initial time step: since no external force is applied, no displacement is observed. Once the charging process takes place, an elastic displacement arises concurrently with deposition and cathode swelling. At the full charge, identified by the black line in Figure 10, the displacement (26) discontinuity ΔL_a = ΔL^ela + ΔL^dep at the electrolyte/lithium foil interface is clearly visible. Being constrained by $\vec{u}(L_a+L_e+L_c)=\vec{0}$, the right end of the cell results motionless. After the current is inverted, lithium starts to be stripped from the anode surface, and the displacements decrease. Since the plated lithium cannot be fully extracted (unless the C-rate tends to zero) a residual displacement field, with its related stress, is seen at full discharge.

To emphasize the role of plating, the mechanics of charging/descharging has been plotted in Figure 11 neglecting the effects of deposition, as per anodic intercalation without swelling. The consequences on the electro-chemical response are small, but from a mechanical prospective, outcomes largely differ. Displacements are plotted in Figure 11A, to be compared with Figure 10. The extraction of lithium from the cathode causes an expansion of the latter, which induces compressive stresses due to the fully restrained boundary conditions at the two ends of the battery. The maximum displacements are reached on full charge, depicted with a black curve in Figure 11A, which is one order of magnitude smaller than the one with plating–see Figure 10. The stress arising from the mere cathodic expansion is very small compared to the one due to plating.

FIGURE 11

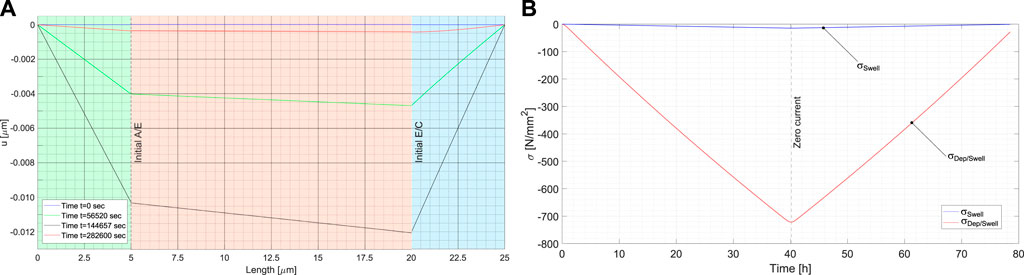
FIGURE 11. (A) Displacement inside the cell at different time steps, neglecting the lithium deposition at the anode surface. The blue line corresponds to the initial time step, when no external forces and currents are applied. The black line corresponds to the end of the charge phase, and the red line to the end of the discharge, when the saturation limit of the lithium concentration in the electrolyte-cathode interface is reached. (B) Mechanical stress inside the cell as a function of time. In black the stress induced by the mere cathode swelling, compared to the stresses in Figure 9, here reprinted in red.

5 Conclusion

In this note we thoroughly investigated battery cells made of a metal lithium foil, a solid electrolyte, and a porous cathode. The overall response of a cell is evaluated in terms of quantities of interest, such as the electric potential, the lithium concentrations profiles, displacements, and stresses. A thermodynamically consistent formulation for coupled continuum electro-chemo-mechanics has been developed. The plating and stripping of the lithium has been considered, together with the expansion and shrinking of the porous cathode. Together, these two processes contribute to the outbreak of mechanical stresses inside the cell, which can lead to fracturing the components and delaminating the interfaces.

The formulation has been applied to a thin film battery with LIPON electrolyte. This easy yet real geometrical configuration is amenable of a one-dimensional modeling, which greatly simplifies the numerical simulations. The fully coupled problem has been solved numerically via the finite element method, using a monolithic scheme Grazioli et al. (2016); Fang et al. (2019). Major outcomes of the simulations have been discussed in section 4.3.

In being one-dimensional, though, the surface area of the lithium anode, where extraction/deposition of lithium occurs, remained unaltered over cycling. After each cycle of charging/discharging, degradation phenomena occur. Accordingly, lithium is not deposited and extracted in the same amounts, in-homogeneity in the interface surface arises together with accumulation of material. Furthermore, stresses are reduced by lithium plasticity. We recognize these events, which will be removed in future works, as the most severe limitations of the present scientific effort.

Author contributions

Conceptualization, LC and AS; methodology, MS, LC, and AS; resources, MS and AS; data curation, writing—original draft preparation, LC and AS; writing—review and editing, MS, LC, and AS; supervision, AS; project administration, AS; funding acquisition, AS and LC All authors have read and agreed to the published version of the manuscript.

Funding

MS expresses his gratitude to the Ferriera Valsabbia company for the liberal donation given in order to fund studies in the field of Mechanobiology. AS and LC acknowledge the funding from BMW Group through the project “Modelling and Simulation of 2-Way Interactions between Mechanics and Electro-Chemistry for Lithium Plating in ASSB” (TIMECLiP).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anand, L., and Narayan, S. (2019). An elastic-viscoplastic model for lithium. J. Electrochem. Soc. 166, A1092–A1095. doi:10.1149/2.0861906jes

CrossRef Full Text | Google Scholar

Bistri, D., Afshar, A., and Di Leo, C. (2021). Modeling the chemo-mechanical behavior of all-solid-state batteries: A review. MECCANICA 56, 1523–1554. doi:10.1007/s11012-020-01209-y

CrossRef Full Text | Google Scholar

Boz, B., Dev, T., Salvadori, A., and Schaefer, J. (2021). Review—electrolyte and electrode designs for enhanced ion transport properties to enable high performance lithium batteries. J. Electrochem. Soc. 168, 090501. doi:10.1149/1945-7111/ac1cc3

CrossRef Full Text | Google Scholar

Cabras, L., Danilov, D., Subber, W., Oancea, V., and Salvadori, A. (2022). A two-mechanism and multiscale compatible approach for solid state electrolytes of (li-ion) batteries. J. Energy Storage 48, 103842. doi:10.1016/j.est.2021.103842

CrossRef Full Text | Google Scholar

Carter, R., Klein, E., Kingston, T., and Love, C. (2019). Detection of lithium plating during thermally transient charging of li-ion batteries. Front. Energy Res. 7, 144. doi:10.3389/fenrg.2019.00144

CrossRef Full Text | Google Scholar

Fang, R., Kronbichler, M., Wurzer, M., and Wall, W. A. (2019). Parallel, physics-oriented, monolithic solvers for three-dimensional, coupled finite element models of lithium-ion cells. Comput. Methods Appl. Mech. Eng. 350, 803–835. doi:10.1016/j.cma.2019.03.017

CrossRef Full Text | Google Scholar

Grazioli, D., Magri, M., and Salvadori, A. (2016). Computational modeling of Li-ion batteries. Comput. Mech. 58, 889–909. doi:10.1007/s00466-016-1325-8

CrossRef Full Text | Google Scholar

Li, G., and Monroe, C. W. (2020). Multiscale lithium-battery modeling from materials to cells. Annu. Rev. Chem. Biomol. Eng. 11, 277–310. doi:10.1146/annurev-chembioeng-012120-083016

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, G., and Lu, W. (2017). A model of concurrent lithium dendrite growth, SEI growth, SEI penetration and regrowth. J. Electrochem. Soc. 164, A1826–A1833. doi:10.1149/2.0381709jes

CrossRef Full Text | Google Scholar

Magri, M., Boz, B., Cabras, L., and Salvadori, A. (2022). Quantitative investigation of the influence of electrode morphology in the electro-chemo-mechanical response of li-ion batteries. Electrochimica Acta 405, 139778. doi:10.1016/j.electacta.2021.139778

CrossRef Full Text | Google Scholar

Mendoza, H., Roberts, S. A., Brunini, V. E., and Grillet, A. M. (2016). Mechanical and electrochemical response of a licoo2 cathode using reconstructed microstructures. Electrochimica Acta 190, 1–15. doi:10.1016/j.electacta.2015.12.224

CrossRef Full Text | Google Scholar

Narayan, S., and Anand, L. (2020). On modeling the detrimental effects of inhomogeneous plating-and-stripping at a lithium-metal/solid-electrolyte interface in a solid-state-battery. J. Electrochem. Soc. 167, 040525. doi:10.1149/1945-7111/ab75c1

CrossRef Full Text | Google Scholar

Purkayastha, R., and McMeeking, R. (2012). An integrated 2-D model of a lithium ion battery: The effect of material parameters and morphology on storage particle stress. Comput. Mech. 50, 209–227. doi:10.1007/s00466-012-0724-8

CrossRef Full Text | Google Scholar

Raijmakers, L., Danilov, D., Eichel, R., and Notten, P. (2020). An advanced all-solid-state li-ion battery model. Electrochim. Acta 330, 135147. doi:10.1016/j.electacta.2019.135147

CrossRef Full Text | Google Scholar

Reimers, J. N., and Dahn, J. R. (1992). Electrochemical and in situ x-ray diffraction studies of lithium intercalation in li x coo2. J. Electrochem. Soc. 139, 2091–2097. doi:10.1149/1.2221184

CrossRef Full Text | Google Scholar

Salvadori, A., Grazioli, D., Geers, M., Danilov, D., and Notten, P. (2015a). A multiscale-compatible approach in modeling ionic transport in the electrolyte of (lithium ion) batteries. J. Power Sources 293, 892–911. doi:10.1016/j.jpowsour.2015.05.114

CrossRef Full Text | Google Scholar

Salvadori, A., Grazioli, D., Magri, M., Geers, M., Danilov, D., and Notten, P. (2015b). On the role of saturation in modeling ionic transport in the electrolyte of (Lithium ion) batteries. J. Power Sources 294, 696–710. doi:10.1016/j.jpowsour.2015.06.061

CrossRef Full Text | Google Scholar

Salvadori, A., McMeeking, R., Grazioli, D., and Magri, M. (2018). A coupled model of transport-reaction-mechanics with trapping. Part I - small strain analysis. J. Mech. Phys. Solids 114, 1–30. doi:10.1016/j.jmps.2018.02.006

CrossRef Full Text | Google Scholar

Schnell, J., Günther, T., Knoche, T., Vieider, C., Köhler, L., Just, A., et al. (2018). All-solid-state lithium-ion and lithium metal batteries – paving the way to large-scale production. J. Power Sources 382, 160–175. doi:10.1016/j.jpowsour.2018.02.062

CrossRef Full Text | Google Scholar

Sedlatschek, T., Lian, J., Li, W., Jiang, M., Wierzbicki, T., Bazant, M. Z., et al. (2021). Large-deformation plasticity and fracture behavior of pure lithium under various stress states. Acta Mater. 208, 116730. doi:10.1016/j.actamat.2021.116730

CrossRef Full Text | Google Scholar

Zhang, S., Yang, G., Li, X., Li, Y., Wang, Z., and Chen, L. (2022). Controlled lithium deposition. Front. Energy Res. 10, 837071. doi:10.3389/fenrg.2022.837071

CrossRef Full Text | Google Scholar

Zheng, F., Kotobuki, M., Song, S., Lai, M., and Lu, L. (2018). Review on solid electrolytes for all-solid-state lithium-ion batteries. J. Power Sources 389, 198–213. doi:10.1016/j.jpowsour.2018.04.022

CrossRef Full Text | Google Scholar