This study deals with numerical solution of momentum and heat transfer of fractional ordered Maxwell fluids within a coaxial cylinder. It is well known that the complex dynamics of flow regime can be well-described by the fractional approach. In this paper, a fractional differentiation operator $D_t^{\alpha }$ of Caputo was applied for fractional modeling of magneto-hydro-dynamic (MHD) fluid. A set of appropriate transformations was applied to make the governing equations dimensionless. The finite differences were calculated by the discretization of momentum profile $u\left(r,t\right)$ and heat profile $T\left(r,t\right)$. The results obtained for $u\left(r,t\right)$ and $T\left(r,t\right)$ were plotted against different physical parameters, such as Prandtl number $\mathit{Pr}$, the square of Hartmann number $H_a$, thermal Grashof number $Gr,$ thermal radiation parameter $Nr$, and heat source/sink parameter $Q_0$. The results were verified by comparing data from the proposed method with MAPLE built-in command results. Subjecting the system to a strong magnetic field led to increasing $T\left(r,t\right)$ and decreasing $u\left(r,t\right)$. It was found that increasing $Gr\mathrm{a}\mathrm{n}\mathrm{d}\mathit{Pr}$ increased the velocity and temperature profiles. Addition of $Cu$ nanoparticles to a base fluid of $H_{2}O$ enhanced its heat transfer capability. Also, increasing the angular frequency of inner cylinder velocity resulted in a high velocity profile of fractional Maxell nano-fluids within a coaxial region (cylinder).

Introduction

The viscoelastic flow of Maxwell fluids within a circular cylinder requires more attention in many areas, such as the chemical, food, and petroleum industries. Nguyen et al. (1983), Nieckele and Patankar (1985), Hayase et al. (1992), Haldar (1998), and Chung (1999) have studied viscoelastic flow between two concentric cylinders. Dependent flow of second-grade fluid in cylindrical geometry has been investigated by Ting (1963). In a similar trend, Maxwell fluids have been examined in a cylindrical coordinate system (Srivastava, 1966). Also, Waters and King (1971) studied Oldroyd-B fluid focused in a cylindrical domain. All results were analytically driven. Considerable work has been carried out by Fetecau et al. in investigating one-dimensional viscoelastic flow between circular regions under different conditions, such as a rotating axis. In Fetecau et al. (2008), an exact solution of Oldroyd-B fluid was examined. A solution was offered as the sum of steady-state and transient-state solution. M Jamil et al., studied helical flow Maxwell fluids by using the analytical approach of Hankel transformation (Jamil and Fetecau, 2010). Wood investigated an exact solution of Oldroyd-B fluids in a straight pipe of circular cross sections (Wood, 2001). However, the study of coaxial cylindrical geometry of an oscillating inner cylinder has been infrequent. An important geometry and motion problem is that of cylindrical geometry. Finite or infinite lengths of annular geometry play vital roles in fluid dynamics. Cylindrical flow has various applications in different fields of the food industry, medicine, chemistry, bio-engineering, and oil exploitation (Hartnett and Kostic, 1989).

In research already discussed, a classical approach of constitutive relations for Maxwell fluids had been applied for mathematical modeling. Recently, the fractional approach of constitutive equations of viscoelastic fluid has been the focus of researchers as the fractional approach can provide a better interpretation of viscoelastic fluids than the classical integer-order derivative approach (Bagley and Torvik, 1983; Friedrich, 1991; Haitao and Mingyu, 2009; Magin, 2010; Ming et al., 2016; Sun et al., 2018).

Fractional calculus has been a hot topic among researchers in the recent era of basic science as it provides a new direction in describing dynamics such as time relaxation, time retardation, viscoelastic behavior, and flow regime. Fractional-order (non-integer) partial differential equations (PDEs) are well-suited to address the physical phenomena related to transportation of heat and mass as well. The fractional mathematical model was initially one of classical integer order, which has been modified by replacing integer-order with non-integer order (Sheikh et al., 2017; Saqib et al., 2018; Saqib et al., 2020). For the purpose fractional differentiation, some operators that have been used include Riemann, Riemann–Liouville, Caputo, Caputo–Fabrizio, and Anatangna Beleanu fractional operators (Shah et al., 2018a; Shah et al., 2018b). Using Laplace and Hankel transformation, the analytical solution of a generalized Maxwell model was solved by Mahmood et al. (2009). Subsequently, exact solutions of fractional Maxwell fluids were investigated using Laplace and Hankel transformation (Fetecau et al., 2010; Fetecau et al., 2011).

For the last few decades, nanotechnology has been a research focus due to its broad range of applications, including those in solar energy, weapons, vehicles, and electronics, stemming from strong thermal properties. Nano-fluids are prepared by mixing up nano-sized (1 nm–100 nm) particles in base fluids (water, blood, engine oil, kerosene oil, etc.). The idea of nano-fluids was first developed by Choi and Eastman (1995), and considerable work has since been by carried out by Tiwari and Das on the effectiveness of different shapes and sizes of nanoparticles in a flow regime (Tiwari and Das, 2007). Using Laplace Transform, a study of a nano-fluid model has been done, while considering the flow passing through an accelerating infinite vertical plate situated in porous medium. Activation energy of Maxwell nano-fluids and binary chemical reaction of carbon nanotubes (CNTs) have been investigated using Runge–Kutta on MAPLE (Subbarayudu et al., 2019). Non-Newtonian nano-fluids have been examined numerically by Rashad et al. (2013) using finite difference methods (FDMs). In Rashad and Nabwey (2019), FDM was applied to investigate the gyrotactic mixed bioconvection flow of a nano-fluid passing through a circular region.

Considering the literature discussed previously, research gaps exist. These include the following:

• Lack of study of the problems involving non-linearity and cylindrical geometry.

• Assumptions made to simplify systems governing equations to obtain analytical solutions.

• Application of analytical techniques to calculate results.

In order to address these gaps, we focused on unsteady flow fractional Maxwell nano-fluids between coaxial cylinders. Flow through an annular region was assumed due to oscillation of the inner cylinder under the effects of thermal radiation and strong magnetic field. Due to its flexibility and efficiency in addressing problems with initial and boundary conditions, the Caputo time fractional operator was used as the mathematical model. Cylindrical geometry is complex to solve numerically, therefore, the numerical approach of the finite difference method was applied to obtain the results. We compared the results obtained using the built-in command in MAPLE with those obtained using our model.

Mathematical formulation

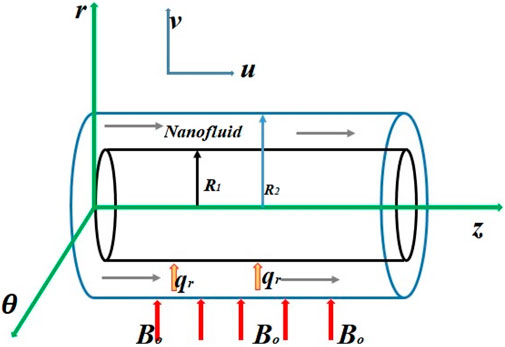
Suppose that an incompressible, unsteady, and one-dimensional flow of viscoelastic nano-fluid is at rest at time $t=0$ within the annular region of two infinite coaxial cylinders having radii $R_1\mathrm{a}\mathrm{n}\mathrm{d}{R}_2$ such that $R_1<R_2$. The inner cylinder oscillates with angular velocity $\omega$ along $z-\mathrm{d}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}$, whereas the outer cylinder remains stationary. These cylinders are subjected to the strong magnetic field $B_0$ and thermal radiation. With the passage of time, the fractional Maxwell nano-fluid moves with velocity $\mathit{V}\left(r,\theta ,z,t\right)=u\left(r,t\right)$. The flow diagram of the physical problem is given in Figure 1, as referenced in Fetecau et al. (2011).

FIGURE 1

FIGURE 1. Problem geometry and coordinate system.

The following assumptions were made for the aforementioned problem.

• The flow is one-dimensional, unsteady, and incompressible.

• Body forces are considered.

• Viscous dissipation and pressure gradients are neglected.

• Fluid is magnetic-hydro-dynamic (MHD), but induced magnetic field is ignored.

• Thermal radiation is applied.

Then, the equation of continuity in cylindrical form (Zhang et al., 2019) is as follows:

$\frac{1}{r}\frac{\partial \left[ru\left(r,t\right)\right]}{\partial r}=0.(1)$

The stress tensor for fractional Maxwell nano-fluid (Anwar et al., 2020) is as follows:

$\mathit{T}=-p\mathit{I}+\mathit{S}(2)$

and

$\mathit{S}+\lambda \frac{\delta \mathit{S}}{\delta t}=\mu {\mathit{A}}_{\mathbf{1}},(3)$

in which $-p\mathit{I}$ is the intermediate spherical stress tensor of order $3\times 3$. $\mathit{S}$ is the extra stress tensor, which is defined by Eq. 3, and $\frac{\delta \mathit{S}}{\delta t}$ is further expressed as (Salah, 2013)

$\frac{\delta \mathit{S}}{\delta t}=\frac{D\mathit{S}}{Dt}-\mathit{L}\mathit{S}-\mathit{S}{\mathit{L}}^t.(4)$

Also, ${\mathit{A}}_{\mathbf{1}}$ is first Rivline Ericksen tensor (Salah, 2013):

${\mathit{A}}_{\mathbf{1}}=\mathit{L}+{\mathit{L}}^t.(5)$

In the expression, $\mathit{L}=\nabla \mathit{V}$ is the velocity gradient and superscript $t$ is transpose notation.

Accounting for significant body forces and the strong magnetic field (neglecting induced magnetic field) to which the cylinders are subjected, then the Navier Stokes equation in cylindrical form (Zhao et al., 2022) is as follows:

${\rho }_{nf}\frac{\partial u\left(r,t\right)}{\partial t}=-\frac{\partial p}{\partial z}+\frac{\mathit{S}\left(r,t\right)}{r}+\frac{\partial \mathit{S}\left(r,t\right)}{\partial r}+g{\left(\rho {\beta }_T\right)}_{nf}\left(T-T_0\right)+{\left(\mathit{J}\times \mathit{B}\right)}_r.(6)$

With rotational symmetry $\frac{\partial p}{\partial \theta }=0$ and ignoring pressure gradient, then $\frac{\partial p}{\partial z}=0$ (Awan et al., 2020) is as follows:

${\rho }_{nf}\frac{\partial u\left(r,t\right)}{\partial t}=\frac{\mathit{S}\left(r,t\right)}{r}+\frac{\partial \mathit{S}\left(r,t\right)}{\partial r}+g{\left(\rho {\beta }_T\right)}_{nf}\left(T-T_0\right)+{\left(\mathit{J}\times \mathit{B}\right)}_r.(7)$

In the aforementioned expression, $\mathit{S}\left(r,t\right)$ is the extra stress tensor and its non-zero component based on the aforementioned assumptions is ${\mathit{S}}_{rz}\left(r,t\right)$. The balance of the aforementioned equation in the absence of the both pressure gradient and viscous dissipation in the flow direction leads to $S_{rr}=S_{\theta \theta }=S_{zz}=S_{r\theta }=S_{\theta z}=0$, and the constitutive equation for fractional Maxwell nano-fluid is then defined as follows (Jamil and Fetecau, 2010):

$\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right){\mathit{S}}_{rz}\left(r,t\right)={\mu }_{nf}\frac{u\left(r,t\right)}{\partial r}.(8)$

Also,

${\left(\mathit{J}\times \mathit{B}\right)}_r=-\left({\sigma }_{nf}{B}_0^{2}u\left(r,t\right),\mathrm{0,0}\right).(9)$

Taking into the account that $\mathit{B}=B_0+b_0$, where $B_0$ is applied and $b_0$ is the induced magnetic field, respectively, Eq. 7 then takes the form

${\rho }_{nf}\frac{\partial u\left(r,t\right)}{\partial t}=\frac{\mathit{S}\left(r,t\right)}{r}+\frac{\partial \mathit{S}\left(r,t\right)}{\partial r}+g{\left(\rho {\beta }_T\right)}_{nf}\left(T-T_0\right)+{\left(\mathit{J}\times \mathit{B}\right)}_r.(10)$

Multiplying both sides of the aforementioned equation by $\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)$ and using Eqs 8, 9 in Eq. 10:

${\rho }_{nf}\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{\partial u\left(r,t\right)}{\partial t}=\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{{\mathit{S}}_{rz}\left(r,t\right)}{r}+\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{\partial {\mathit{S}}_{rz}\left(r,t\right)}{\partial r}+g{\left(\rho {\beta }_T\right)}_{nf}\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\left(T-T_0\right)-{\sigma }_{nf}{B}_0^2\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)u\left(r,t\right).(11)$

In this expression, ${\lambda }_1^{\alpha }$ is the time relaxation and $D_t^{\alpha }$ is the Caputo fractional derivative as defined by (Asjad et al., 2017):

$D_t^{\alpha }u\left(r,t\right)=\frac{1}{\mathrm{\Gamma }\left(1-\alpha \right)}{\int }_0^t{\left(t-\tau \right)}^{-\alpha }\frac{\partial u\left(r,\tau \right)}{\partial \tau }d\tau .(12)$

In Askey and Roy (2010), $\Gamma \left(.\right)$ is the gamma function and may be expressed as follows:

$\mathrm{\Gamma }\left(x\right)=\int {\eta }^{x-1}{e}^{-\eta }d\eta ,xϵ\mathbb{C},\mathbb{R}e\left(x\right)>0,(13)$

${\rho }_{nf}\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{\partial u\left(r,t\right)}{\partial t}={\mu }_{nf}\frac{1}{r}\frac{u\left(r,t\right)}{\partial r}+{\mu }_{nf}\frac{{\partial }^{2}u\left(r,t\right)}{\partial r^2}.+g{\left(\rho {\beta }_T\right)}_{nf}\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\left(T-T_0\right)-{\sigma }_{nf}{B}_0^2\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)u\left(r,t\right).(14)$

By following a similar trend for heat transfer analysis, the governing equation for temperature profile is expressed as (Khan and Mustafa, 2018)

${\left(\rho C_p\right)}_{nf}\frac{\partial T}{\partial t}=K_{nf}\left(\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial r^2}\right)-\nabla .q_r+Q\left(T-T_0\right).(15)$

In the aforementioned expression, $\rho$ is viscosity, $C_p$ is the specific heat, $T$ is temperature, $T_0$ is ambient temperature at time $t=0$, $K_{nf}$ is the thermal conductivity, $Q$ is the heat absorption/source, and $q_r$ is radiative heat flux of the fractional Maxwell nano-fluid, where $q_r$ is defined by (Rosseland, 2013)

$q_r=-\left(\frac{4}{3k^{*}}\right)\nabla .e_b,(16)$

where $k^{*}$ is the mean absorption coefficient and $e_b$ denotes the black body emissive power of the mathematical form $e_b={\sigma }^{*}{T}^4$, with ${\sigma }^{*}=5.7\times {10}^{-8}{W/m^{2}K}^4$ as the Stefan–Boltzmann constant (Khan and Mustafa, 2018). Then, Eq. 16 can be written as follows:

$q_r=-\left(\frac{4}{3k^{*}}\right)\frac{\partial T^4}{\partial r}.(17)$

Using Taylor series expansion, approximation of $T^4$ has been made near $T_0$; therefore, with $T^4=4T_0^{3}T-3T_0^4$ and neglecting higher power (Taitel and Hartnett, 1968),

$q_r=-\frac{16{\sigma }^{*}{T}_0^3}{3k^{*}}\frac{\partial T}{\partial r}.(18)$

Eq. 17 takes the following form;

Then, multiplying both sides of Eq. 15 by $\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)$,

${\left(\rho C_p\right)}_{nf}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T}{\partial t}=K_{nf}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\left(\frac{1}{r}\frac{\partial T}{\partial r}+\frac{{\partial }^{2}T}{\partial r^2}\right)-\nabla .q_r+Q\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\left(T-T_0\right).(19)$

Using Eq. 18, the resulting expression is as follows:

${\left(\rho C_p\right)}_{nf}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T}{\partial t}=K_{nf}\frac{1}{r}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T}{\partial r}+K_{nf}\left[1+\frac{16{\sigma }^{*}{T}_0^3}{3k^{*}{K}_{nf}}\right]\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{{\partial }^{2}T}{\partial r^2}+Q\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\left(T-T_0\right).(20)$

The proposed initial and boundary conditions for momentum and heat of this physical phenomenon are given as follows:

$u\left(r,0\right)=\frac{\partial u\left(r,0\right)}{\partial t}=0,R_1\le r\le R_2,(21)$

$u\left(R_1,t\right)=E\left(1-\mathit{cos}\omega t\right),u\left(R_2,t\right)=0,t>0.(22)$

For temperature,

$T\left(r,0\right)=T_0,\frac{\partial T\left(r,0\right)}{\partial t}=0,R_1\le r\le R_2,(23)$

$T\left(R_1,t\right)=T_0,\frac{\partial T\left(R_2,t\right)}{\partial r}=0,\mathrm{f}\mathrm{o}\mathrm{r}t>0.(24)$

Under the aforementioned initial and boundary conditions, $\omega$ is the frequency of inner cylinder velocity and $R_1,R_2$ are radii of the inner and outer cylinders such that $R_2{>R}_1$, and $E$ is the maximum velocity term.

Introducing the transformation for proposed geometry in Eqs 14, 20,

$x^{*}=\frac{x}{R_2},r^{*}=\frac{r}{R_2},u^{*}=u\frac{R_2}{v_f},t^{*}=t\frac{{\nu }_f}{R_2^2},{\lambda }_1^{*}={\lambda }_1\frac{{\nu }_f}{R_2^2},{\lambda }_2^{*}={\lambda }_2\frac{{\nu }_f}{R_2^2},T^{*}=\frac{T-T_0}{T_0},{\omega }^{*}=\omega \frac{R_2^2}{{\nu }_f},$

and with the usage of thermo-physical properties of nanoparticles,

$\left.\begin{array}{c}\frac{{\rho }_{nf}}{{\rho }_f}=a_1=\left[\left(1-\varphi \right)+\varphi \frac{{\rho }_s}{{\rho }_f}\right],\frac{{\left(\rho {\beta }_{\theta }\right)}_{nf}}{{\left(\rho {\beta }_{\theta }\right)}_f}=a_2=\left[\left(1-\varphi \right)+\varphi \left(\frac{{\left(\rho {\beta }_T\right)}_s}{{\left(\rho {\beta }_T\right)}_f}\right)\right],\\ \frac{{\mu }_{nf}}{{\mu }_f}=a_3=\frac{1}{{\left(1-\varphi \right)}^{2.5}},\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f}=a_4=\left[\left(1-\varphi \right)+\varphi \left(\frac{{\left(\rho C_p\right)}_s}{{\left(\rho C_p\right)}_f}\right)\right],\\ \frac{k_{nf}}{k_f}=a_5=\frac{k_s+2k_f-2\varphi \left(k_f-k_s\right)}{k_s+2k_f+\varphi \left(k_f-k_s\right)},\frac{{\left(\sigma \right)}_{nf}}{{\left(\sigma \right)}_f}=a_6=1+\frac{3\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_s}{{\sigma }_f}-2\right)-\left(\frac{{\sigma }_s}{{\sigma }_f}-1\right)\varphi }.\end{array}\right\}(25)$

The non-dimensional form of velocity profile along a circular cylinder is as follows:

$\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{\partial u^{*}}{\partial t^{*}}=b_1\left[\frac{{\partial }^2{u}^{*}}{\partial {r^{*}}^2}+\frac{1}{r^{*}}\frac{\partial u^{*}}{\partial r^{*}}\right]-b_2{H}_a^2\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)u^{*}+b_{3}Gr{\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)T}^{*}.(26)$

The heat equation takes the following dimensionless form:

$\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T^{*}}{\partial t^{*}}=\frac{b_1}{r^{*}\mathit{Pr}}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T^{*}}{\partial r^{*}}+\frac{b_1}{\mathit{Pr}}\left[1+N_r\right]\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{{\partial }^2{T}_0}{\partial {r^{*}}^2}+\frac{Q_0}{a_4}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)T^{*}.(27)$

The dimensionless initial and boundary conditions are as follows:

$u^{*}\left(r,0\right)=0,\frac{\partial u^{*}\left(r,0\right)}{\partial r}=0,R_1\le r\le R_2,(28)$

$u^{*}\left(r,t\right)=E^{*}\left[1-\mathit{cos}{\omega }^{*}{t}^{*}\right],u^{*}\left(R_2,t\right)=0,t>0.(29)$

For temperature profile,

$T^{*}\left(r,0\right)=0,\frac{\partial T^{*}\left(r,0\right)}{\partial t^{*}}=0,R_1\le r\le R_2,(30)$

$T^{*}\left(R_2,t\right)=0,t>0.(31)$

The dimensionless velocity and temperature profiles of the problem are given, and after eliminating $\left(*\right)$ representation, for the sake of simplicity, is as follows:

$\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)\frac{\partial u}{\partial t}=b_1\left[\frac{{\partial }^{2}u\left(r,t\right)}{\partial r^2}+\frac{1}{r}\frac{\partial u\left(r,t\right)}{\partial r}\right]-b_2{H}_a^2\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)u\left(r,t\right)+b_{3}Gr\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)T\left(r,t\right)(32)$

and

$\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T}{\partial t}=\frac{b_4}{r.\mathit{Pr}}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{\partial T}{\partial r}+b_4\frac{1+N_r}{\mathit{Pr}}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)\frac{{\partial }^{2}T}{\partial r^2}+\frac{Q_0}{a_4}\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)T.(33)$

Also, initial and boundary conditions are as follows:

$u\left(r,0\right)=0,\frac{\partial u\left(r,0\right)}{\partial r}=0,R_1\le r\le R_2,(34)$

$u\left(r,t\right)=E\left[1-\mathit{cos}\omega t\right],u\left(R_2,t\right)=0,t>0.(35)$

For temperature profile,

$T\left(r,0\right)=0,\frac{\partial T\left(r,0\right)}{\partial t}=0,R_1\le r\le R_2,(36)$

$T\left(R_2,t\right)=0,t>0,(37)$

where

$b_1=\frac{a_3}{a_1},b_2=\frac{a_6}{a_1},b_3=\frac{a_2}{a_1},b_4=\frac{a_5}{a_4},H_a^2=\frac{{\sigma }_f{B}_0^2{R}_2^2}{{\mu }_f},Gr=\frac{g{\left({\beta }_T\right)}_f{T_{0}R}_2^3}{{\nu }_f^2},{\mathit{Pr}=\frac{{\mu }_f{\left(C_p\right)}_f}{K_f},N}_r=\frac{16{\sigma }^{*}{T}_0^3}{3{a_{5}k}^{*}{K}_f},Q_0=\frac{{QR}_2^2}{{\mu }_f{\left(C_p\right)}_f}.$

The dimensionless governing equations for velocity and temperature profiles in Eqs 32, 33 and non-dimensional initial and boundary conditions in Eqs 34–37 express the physical phenomenon of flow of fractional Maxwell nano-fluid within a coaxial cylinder under the influence of magnetic field and heat source/sink, in which $b_1,b_2,b_3,\mathrm{a}\mathrm{n}\mathrm{d}{b}_4$ are constants and ratios of thermo-physical properties of nanoparticle and base fluid, and where $H_a^2,Gr,\mathit{Pr},N_r,\mathrm{a}\mathrm{n}\mathrm{d}{\mathrm{Q}}_0$ are the square of Hartmann number, and the Grashof number, Prandtl number, thermal radiation parameter, and constant of heat source/sink, respectively. Table 1 contains the numerical values of nanoparticles and different base fluids at room temperature (25 $C^0$) (Usman et al., 2018).

TABLE 1

TABLE 1. Contains the numerical values of nanoparticles and different base fluids at room temperature 25° presented in (Usman et al., 2018).

Skin friction and Nusselt number

The significant physical quantities of skin friction and local Nusselt number for prescribed geometry are described as follows (Khan and Mustafa, 2018):

$C_f=\frac{{\mu }_{nf}}{\rho u_0^2}{\left(\frac{\partial u}{\partial r}\right)}_{r=R_2}.(38)$

The instantaneous Nusselt number near the wall for a cylindrical region is given as follows (Zhao et al., 2022):

$Nu=-k_{nf}\left(1+\frac{16{\sigma }^{*}{T}_0^3}{3k^{*}{K}_{nf}}\right){\left(\frac{\partial T}{\partial y}\right)}_{r=R_2}.(39)$

After applying the fractional Maxwell operator to both sides of Eqs 38, 39, we have

$C_f\left(1+{\lambda }_1^{\alpha }{D}_t^{\alpha }\right)=\frac{{\mu }_{nf}}{\rho u_0^2}{\left(\frac{\partial u}{\partial r}\right)}_{r=R_2}(40)$

and

$Nu\left(1+{\lambda }_2^{\beta }{D}_t^{\beta }\right)=-k_{nf}\left(1+\frac{16{\sigma }^{*}{T}_0^3}{3k^{*}{K}_{nf}}\right){\left(\frac{\partial T}{\partial y}\right)}_{r=R_2}.(41)$

Using transformations and the thermo-physical properties of nano-fluids expressed in Eq. 25,

$\left(C_f+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }{C}_f}{\partial t^{\alpha }}\right)=\frac{a_3}{R{e}^2}{\left(\frac{\partial u^{*}}{\partial r^{*}}\right)}_{r=R_2}.(42)$

The dimensionless expression for the Nusselt number is obtained (after ignoring the star notation) as follows:

$\left(Nu+{\lambda }_1^{\alpha }\frac{{\partial }^{\alpha }Nu}{\partial t^{\alpha }}\right)=-{a_{5}k}_f\left(1+Nr\right){\left(\frac{\partial T}{\partial y}\right)}_{r=R_2}(43)$

in which $a_3,a_5$ are constants, and $N_r,Re$ are the thermal radiation parameter and the Reynold number, respectively, and defined as follows:

$N_r=\frac{16{\sigma }^{*}{T}_0^3}{3k^{*}{K}_f},Re=\frac{u_0^2{R}_2^2}{{\nu }_f^2}.$

Numerical procedure

The numerical technique of the finite difference method is a strong and accurate tool used for solving the partial difference equation, even of non-linear order. The proposed model is a non-linear coupled model of PDEs that express the momentum and temperature equations. The discretization of governing equations are expressed as. It is well-known that the discretization of ${{}_0{}^{C}D}_t^{\alpha }u,{{}_0{}^{C}D}_t^{1+\alpha }u$ for $0<\alpha \le 1,u_t$ and $u_{rr}$ is defined as follows (Liu et al., 2004):

${{}_0{}^{C}D}_{t_{j+1}}^{\alpha }u\left(r_i,t_{j+1}\right)=\frac{{\mathit{\Delta t}}^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left[u_i^{j+1}-u_i^j\right]+\frac{{\mathit{\Delta t}}^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-u_i^{j-l}\right)b_l^{\alpha },(44)$

${{}_0{}^{C}D}_{t_{j+1}}^{1+\alpha }u\left(r_i,t_{j+1}\right)=\frac{\mathit{\Delta }{t}^{-\left(1+\alpha \right)}}{\Gamma \left(2-\alpha \right)}\left[u_i^{j+1}-2u_i^j+u_i^{j-1}\right]+\frac{\mathit{\Delta }{t}^{-\left(1+\alpha \right)}}{\Gamma \left(2-\alpha \right)}\times {\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-2u_i^{j-l}+u_i^{j-l-1}\right)b_l^{\alpha },(45)$

${\left.\frac{\partial }{\partial t}u\left(r_i,t_{j+1}\right)\right|}_{t=t_{j+1}}=\frac{1}{\mathit{\Delta }t}\left[u_i^{j+1}-u_i^j\right],(46)$

${\left.\frac{{\partial }^2}{\partial r^2}u\left(r_{i+1},t_j\right)\right|}_{r=r_{i+1}}=\frac{1}{\mathit{\Delta }{r}^2}\left[u_{i+1}^{j+1}-2u_i^{j+1}+u_{i-1}^{j+1}\right].(47)$

In Eq. 44, $b_l^{\alpha }={\left(l+1\right)}^{1-\alpha }-l^{1-\alpha },l=\mathrm{1,2,3},\dots ,j.$ Rectilinear grids are pondered for the numerical solution, with grid spacing $\mathrm{\Delta }t>0,\mathrm{\Delta }r>0$, where $\mathrm{\Delta }r=\left(R_2-R_1\right)/M,\mathrm{\Delta }t=T/N$ with $\mathrm{\Delta }r,\mathrm{\Delta }t$ from ${\mathbb{Z}}^{+}$. Points $\left(r_i,t_j\right)$ in $\Omega =\left[0,T\right]\times \left[0,L\right]$ are defined as $r_i=i\mathrm{\Delta }r$ and $t_j=j\mathrm{\Delta }t$. Considering the aforementioned assumptions, the discussed model of Eqs 32, 33 at $\left(i,j\right)$ is defined as follows:

$\frac{1}{\mathrm{\Delta }t}\left(u_i^{j+1}-u_i^j\right)+\frac{{\lambda }_1^{\alpha }\mathrm{\Delta r}{t}^{-1-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\left(u_i^{j+1}-2u_i^j+u_i^{j-1}+{\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-2u_i^{j-l}+u_i^{j-l-1}\right)b_l^{\alpha }\right)$

$=b_1\left(\frac{u_{i+1}^{j+1}-2u_i^{j+1}+u_{i-1}^{j+1}}{{\mathrm{\Delta r}}^2}+\frac{1}{2i\mathrm{\Delta }{r}^2}\left(u_{i+1}^{j+1}-u_{i-1}^{j+1}\right)\right)+b_{2}Gr\left(T_i^{j+1}+\frac{{\lambda }_1^{\alpha }\mathrm{\Delta }r{t}^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\right.\left(T_i^{j+1}-T_i^j\right.\times \left.+{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha }\right)$

$-b_{3}H{a}^2\left(u_i^{j+1}+\frac{{\lambda }_1^{\alpha }\mathrm{\Delta r}{t}^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\left(u_i^{j+1}-u_i^j+{\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-u_i^{j-l}\right)b_l^{\alpha }\right)\right),$

$\frac{1}{\mathrm{\Delta r}t}\left(T_i^{j+1}-T_i^j\right)+\frac{{\lambda }_2^{\beta }\mathrm{\Delta r}{t}^{-1-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\left(T_i^{j+1}-2T_i^j+T_i^{j-1}+{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-2T_i^{j-l}+T_i^{j-l-1}\right)b_l^{\alpha }\right)$

$=\frac{b_4}{2\mathrm{Pr}i\mathrm{\Delta }{r}^2}\left(T_{i+1}^{j+1}-T_{i-1}^{j+1}+\frac{{\lambda }_2^{\beta }\mathrm{\Delta r}{t}^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\left(T_{i+1}^{j+1}-T_{i+1}^j+{\displaystyle \sum }_{l=1}^j\left(T_{i+1}^{j-l+1}-T_{i+1}^{j-l}\right)b_l^{\alpha }-T_{i-1}^{j+1}+T_{i-1}^j\right.\right.$

$-\left.\left.{\displaystyle \sum }_{l=1}^j\left(T_{i-1}^{j-l+1}-T_{i-1}^{j-l}\right)b_l^{\alpha }\right)\right)+\frac{b_4\left(1+Nr\right)}{\mathrm{\Delta }{r}^2\mathrm{Pr}}\left(T_{i+1}^{j+1}-2T_i^{j+1}+T_{i-1}^{j+1}+\frac{{\lambda }_2^{\beta }\mathrm{\Delta }{t}^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}\right.$

$\times \left(T_{i+1}^{j+1}-T_{i+1}^j+{\displaystyle \sum }_{l=1}^j\left(T_{i+1}^{j-l+1}-T_{i+1}^{j-l}\right)b_l^{\alpha }-2T_i^{j+1}+2T_i^j-2{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha }+T_{i-1}^{j+1}-T_{i-1}^j\right.+\left.\left.{\displaystyle \sum }_{l=1}^j\left(T_{i-1}^{j-l+1}-T_{i-1}^{j-l}\right)b_l^{\alpha }\right)\right)$

$+\frac{Q_0}{a_4}\left(T_i^{j+1}+\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left(T_i^{j+1}-T_i^j+{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha }\right)\right)$

$+\frac{Q_0}{a_4}\left(T_i^{j+1}+\frac{{\lambda }_2^{\beta }{t}^{-\alpha }}{\Gamma \left(2-\alpha \right)}\left(T_i^{j+1}-T_i^j+{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha }\right)\right).$

$\left(-\frac{b_1}{\Delta r^2}+\frac{b_1}{2i\Delta r^2}\right)u_{i-1}^{j+1}+\left(\frac{1}{\Delta t}+{\lambda }_1^{\alpha }\frac{\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}+\frac{{2b}_1}{\Delta r^2}+b_{3}H{a}^2+b_{3}H{a}^2{\lambda }_1^{\alpha }\frac{t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)u_i^{j+1}$

$+\left(-\frac{b_1}{\Delta r^2}-\frac{b_1}{2i\Delta r^2}\right)u_{i+1}^{j+1}+\left(-b_{2}Gr-b_{2}Gr{\lambda }_1^{\alpha }\frac{t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_i^{j+1}={\lambda }_1^{\alpha }\frac{t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}{u}_i^{j-1}$

$+\left(\frac{1}{\Delta t}+2{\lambda }_1^{\alpha }\frac{\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}-b_{3}H{a}^2{\lambda }_1^{\alpha }\frac{t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)u_i^j-b_{2}Gr{\lambda }_1^{\alpha }\frac{\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{T}_i^j+f_{i,j}^1+f_{i,j}^2+f_{i,j}^3.$

$\left(\frac{b_4}{2\mathrm{Pr}i\Delta r^2}+\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_{i-1}^{j+1}$

$+\left(\frac{1}{\Delta t}+{\lambda }_2^{\beta }\frac{\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}+2\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}+2\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}-\frac{Q_0}{a_4}-\frac{Q_0}{a_4}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_i^{j+1}$

$+\left(-\frac{b_4}{2\mathrm{Pr}i\Delta r^2}-\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_{i+1}^{j+1}$

$=\left(-\frac{{\lambda }_2^{\beta }\Delta t^{-1-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}+\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_{i-1}^j$

$+\left(\frac{1}{\Delta t}+2\frac{{\lambda }_2^{\beta }\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}+2\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}-\frac{Q_0}{a_4}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_i^j$

$+\left(-\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}-\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}\right)T_{i+1}^j+g_{i,j}^1+g_{i,j}^2+g_{i,j}^3+g_{i,j}^4+g_{i,j}^5+g_{i,j}^6+g_{i,j}^7.$

$f_{i,j}^1=-{\lambda }_1^{\alpha }\frac{\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-2u_i^{j-l}+u_i^{j-l-1}\right)b_l^{\alpha },f_{i,j}^2=b_{2}Gr\frac{{\lambda }_1^{\alpha }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha },$

$f_{i,j}^3=-b_{3}H{a}^2{\lambda }_1^{\alpha }\frac{\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(u_i^{j-l+1}-u_i^{j-l}\right)b_l^{\alpha },$

$g_{i,j}^1=\frac{{\lambda }_2^{\beta }\Delta t^{-1-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-2T_i^{j-l}+T_i^{j-l-1}\right)b_l^{\alpha },g_{i,j}^2=\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_{i+1}^{j-l+1}-T_{i+1}^{j-l}\right)b_l^{\alpha },$

$g_{i,j}^3=\frac{b_4}{2\mathrm{Pr}i\Delta r^2}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_{i-1}^{j-l+1}-T_{i-1}^{j-l}\right)b_l^{\alpha },g_{i,j}^4=\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}$

$\times {\displaystyle \sum }_{l=1}^j\left(T_{i+1}^{j-l+1}-T_{i+1}^{j-l}\right)b_l^{\alpha },g_{i,j}^5=-2\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\Gamma \left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha },$

$g_{i,j}^6=\frac{b_4\left(1+Nr\right)}{\Delta r^2\mathrm{Pr}}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_{i-1}^{j-l+1}-T_{i-1}^{j-l}\right)b_l^{\alpha },g_{i,j}^7=\frac{Q_0}{a_4}\frac{{\lambda }_2^{\beta }\Delta t^{-\alpha }}{\mathrm{\Gamma }\left(2-\alpha \right)}{\displaystyle \sum }_{l=1}^j\left(T_i^{j-l+1}-T_i^{j-l}\right)b_l^{\alpha }.$

For $j=\mathrm{1,2,3},\dots ,N-1,i=\mathrm{1,2,3},\dots ,N-1$, with the following initial and boundary conditions,

$u_i^0=0,u_i^1=u_i^{-1},T_i^0=0,T_i^1=T_i^{-1},\mathrm{f}\mathrm{o}\mathrm{r}i=\mathrm{0,1,2,3},\dots ,M,$

$u_0^j=E_M\left(1-\cos w\Delta t\right),u_M^j=0,T_0^j=1,T_M^j=0,\mathrm{f}\mathrm{o}\mathrm{r}j=\mathrm{1,2,3},\dots ,N-1.$

Results and discussion

We have developed a fractional model of Maxwell nano-fluids under the effects of magnetic field, thermal radiation, and heat source/sink. The physical properties of nano-fluids were utilized to model the physical phenomenon. The focus of the problem was the cylindrical coordinate system in which coaxial geometry was assumed to formulate the problem. Using the Caputo fractional order operator in the model, the finite difference scheme was applied to obtain numerical results using mathematical software MAPLE. In this section, we report our results and discuss the plots and comparison, of important physical properties such as $H_a,\mathit{Pr},Nr,Gr,\varphi ,\alpha ,\beta ,Re,\mathrm{a}\mathrm{n}\mathrm{d}{Q}_0$, demonstrating the square of the Hartmann number (magnetic field parameter), non-dimensional Prandlt number, thermal radiation parameter, non-dimensional Grashof number, volumetric fraction of nanoparticle, non-integral-order parameters, non-dimensional Reynolds number, and heat source/sink parameter. The trends of the aforementioned parameters were observed for momentum and temperature profiles of the system in the annular region. The results were obtained by developing MAPLE code and then used to produce graphical plots.

The results were obtained through discretization of the governing equations (Eqs 32, 33), with initial and boundary conditions expressed in Eqs 34–37. The graphical results for the velocity profile $u\left(r,t\right)$ and temperature profile $T\left(r,t\right)$ were plotted against $H_a,\mathit{Pr},Nr,Gr,\varphi ,$

$\alpha ,\beta ,Re,\mathrm{a}\mathrm{n}\mathrm{d}{Q}_0$. For validation, results obtained using our model were compared with those from the built-in model using MAPLE .

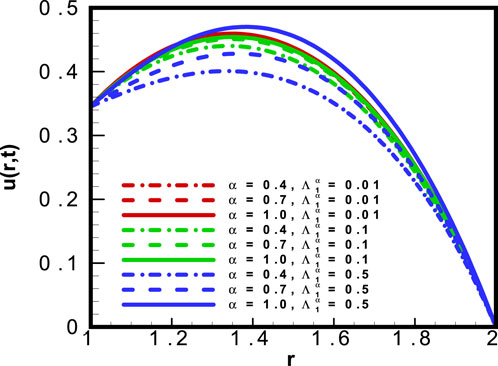
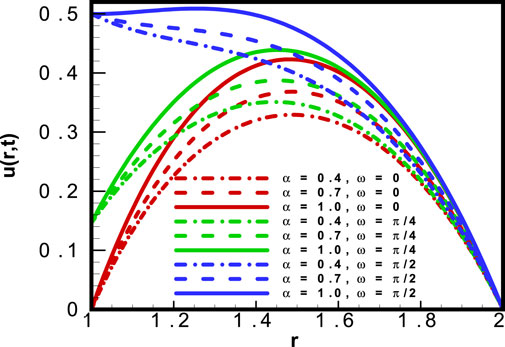
Figure 2 shows the results obtained for velocity profile $u\left(r,t\right)$ with respect to the time relaxation parameter ${\lambda }_1$ for a range of values $\left({\lambda }_1=0.01,0.1,0.5\right)$, with varying fractional-order parameters $\left(\alpha =0.4,0.7,1.0\right)$. The data demonstrate that an increase in the time relaxation parameter led to a direct increase in the velocity profile. Time relaxation is a material’s characteristic capacity to be relaxed for a certain period of time. With the passage of time, fluid flow becomes laminar and internal resistance decreases, which increases the velocity profile of the fractional Maxwell nano-fluid within an annular region of a coaxial cylinder.

FIGURE 2

FIGURE 2. Impact of ${\lambda }_1$ on $u\left(r,t\right)$.

In Figure 3, the results for velocity profile $u\left(r,t\right)$ are plotted against the magnetic field parameter $H_a$ (the square of the Hartmann number) for a range of values $\left(H_a=0,1,2\right)$, with a range of fractional-order parametric values $\left(\alpha =0.4,0.7,1.0\right)$. The plots demonstrate that by increasing the value of the magnetic field parameter, the velocity profile $u\left(r,t\right)$ is reduced. The increased value of $H_a$ gives rise to Lorentz force that increases the intermolecular force and the internal resistance between fluid particles. Consequently, a reducing trend in the velocity profile $u\left(r,t\right)$ is apparent; the value is high near the boundary of the inner cylinder, and the velocity profile $u\left(r,t\right)$ gains its maximum at the mid-point between the inner and outer cylinder.

FIGURE 3

FIGURE 3. Impact of $Ha$ on $u\left(r,t\right)$.

The plot for velocity $u\left(r,t\right)$ against the Grashof number $Gr$ is presented in Figure 4 for a range of values $\left(Gr=5,10,15\right)$. Since the Grashof number is the ratio of two different forces related to the fluid properties of buoyancy and viscosity, an increase in $Gr$ is observed when viscous forces decrease. Therefore, the value of $Gr$ increases only when there is a reduction in viscous force and, consequently, the velocity profile $u\left(r,t\right)$ within the cylindrical region increases and gains its maximum value at the middle of the two radii due to decreasing viscous behavior of the MHD fractional Maxwell nano-fluid.

FIGURE 4

FIGURE 4. Impact of $Gr$ on $u\left(r,t\right)$.

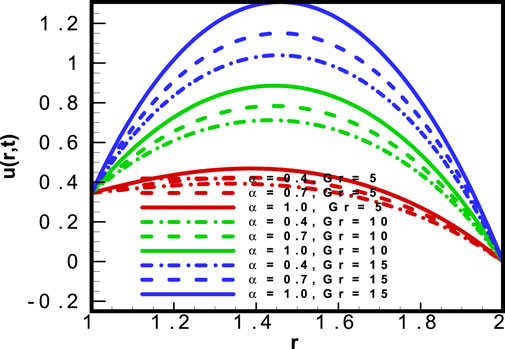
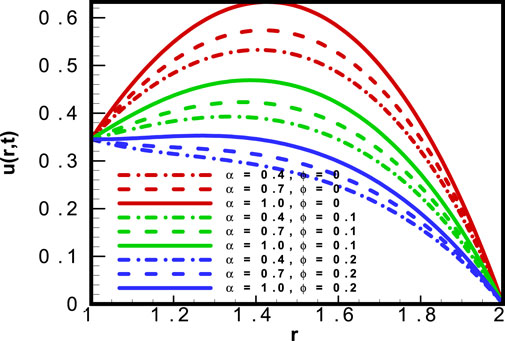
Figure 5 depicts the results for the most important physical parameter: the volumetric fraction $\varphi$ of nanoparticles in base fluid. The addition of nanoparticles to base fluid reduces the velocity profile $u\left(r,t\right)$ within the coaxial cylinder. Therefore, the results were plotted for a range of values $\left(\varphi =0,\mathrm{0.1,0.2}\right)$, considering different values of the fractional-order parameter $\alpha$. Addition of nanoparticles to base fluid increases intermolecular forces and collision of molecules increase, thereby decreasing the velocity profile $u\left(r,t\right)$.

FIGURE 5

FIGURE 5. Impact of $\varphi$ on $u\left(r,t\right)$.

Figure 6 is a graphical representation of the maximum velocity term $E,$ indicating that velocity reaches its maximum value of $E$ near the boundary of the inner cylinder; on the other hand, it is at its lowest degree at the boundary of the outer cylinder. This graph indicates that, for the lowest value of $r$ and maximum of value of $E$, $u\left(r,t\right)$ increases in value.

FIGURE 6

FIGURE 6. Impact of $E$ on $u\left(r,t\right)$

The term $\omega$ is the frequency of inner cylinder velocity, and Figure 7 depicts the graphical results for a range of values, such as $\left(\omega =0,\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right.,\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$. For the interval $\left[0,\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right.\right],$ due to the cosine function, increasing the value of $\omega$ results in an increased velocity profile $u\left(r,t\right)$. The reverse trend occurred for the closed interval $\left[\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$4$}\right.,\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right].$

FIGURE 7

FIGURE 7. Impact of $\omega$ on $u\left(r,t\right)$.

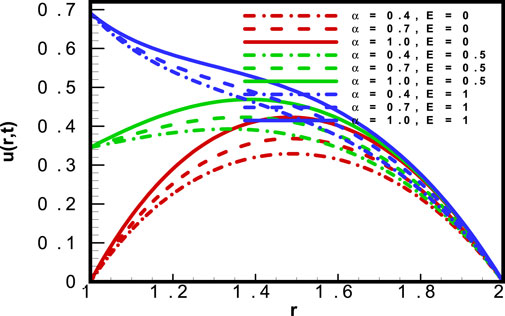
The impact of the time relaxation parameter ${\lambda }_2^{\beta }$ on temperature profile $T\left(r,t\right)$ is plotted in Figure 8 The range of values for ${\lambda }_2^{\beta }$ (${\lambda }_2^{\beta }=0.01,0.1,0.5$) was assessed for impact on $T\left(r,t\right)$. It was noted that increasing the value of ${\lambda }_2^{\beta }$ reduced the temperature. This effect is based on the characteristics of the material and the time in which the system relaxes under specific conditions. Therefore, as collision between particles in a fluid decreases, the heat transfer process of system is reduced. The graph shows that the temperature profile attained its high value near the wall of the outer cylinder for different fractional parametric values of $\beta$.

FIGURE 8

FIGURE 8. Impact of ${\lambda }_2^{\beta }$ on $T\left(r,t\right)$.

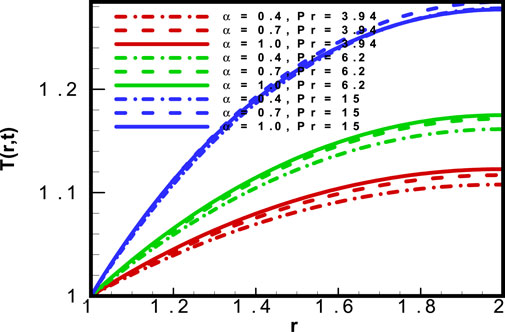
The impact of the Prandlt number ($\mathit{Pr}$) on heat transfer capability of a coupled non-linear fractional model is illustrated in Figure 9 for a range of values $\left(\mathit{Pr}=3.94,6.2,15\right)$. $\mathit{Pr}$ is the basic fluid property used to calculate heat transfer capability. It is the ratio of kinematic viscosity to thermal diffusivity. $\mathit{Pr}$ is inversely related to thermal diffusivity, which is directly related to heat capability. Increasing heat capacity increases the thermal diffusivity of a material. Therefore, increasing $\mathit{Pr}$ increases the temperature profile $T\left(r,t\right)$ of the system.

FIGURE 9

FIGURE 9. Impact of $\mathit{Pr}$ on $T\left(r,t\right)$.

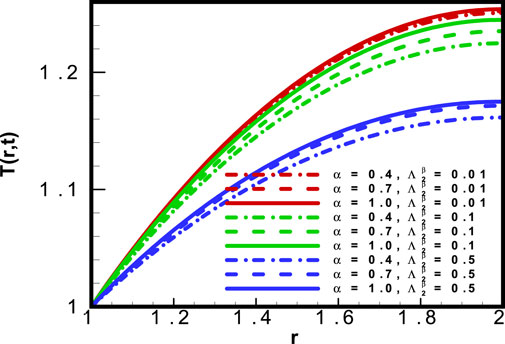
In Figure 10, the temperature profile $T\left(r,t\right)$ of the fractional Maxwell nano-fluid is quantified for a range of thermal radiation parameters $\left(Nr=0,2,5\right)$. It has been observed that an increase in the thermal radiation parameter $Nr$ increases the heat transfer capability of a system for a specific range of fractional-order parameters ($\alpha =0.4,0.7,1.0$), thereby reducing the temperature profile of the system, which is very low near the inner cylinder surface.

FIGURE 10

FIGURE 10. Impact of $Nr$ on $T\left(r,t\right)$.

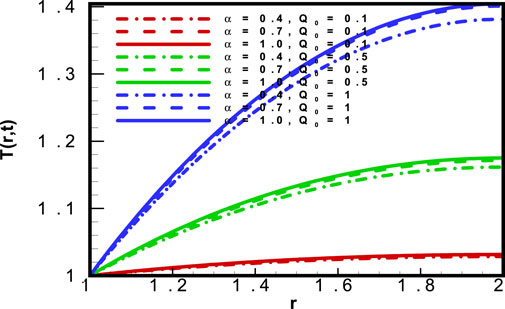
Figure 11 describes the conduct of the heat profile $T\left(r,t\right)$ for the flow of fractional Maxwell nano-fluid within a coaxial cylinder under the effects of the heat source/sink parameter $Q_0$. Subjecting the system to a heat source directly affected the heat capability, with the temperature profile $T\left(r,t\right)$ increasing with increasing heat source/sink values $\left(Q_0=0.1,0.5,1.0\right)$ and achieving its maximum value at the outer boundary of the cylinders. Within the cylindrical region, the temperature profile attained its minimum value near the boundary of the inner cylinder and gained its maximum value near the boundary of outer cylinder.

FIGURE 11

FIGURE 11. Impact of $Q_0$ on $T\left(r,t\right)$.

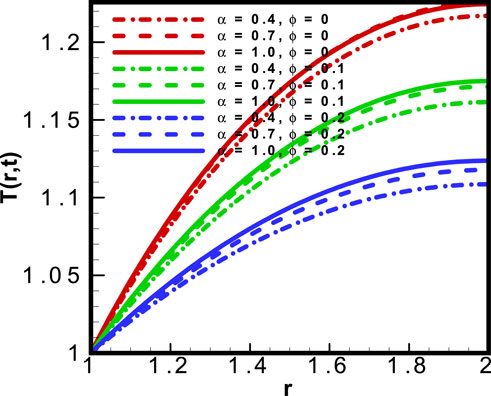
The addition of nanoparticles to base fluids enhances entropy generation, and there is reduced loss of useful energy. This expected result was obtained over a range of values of volumetric fraction of nanoparticles $\left(\varphi =0,0.1,0.2\right)$ and is depicted in Figure 12. Heat transfer was reduced by the addition of nanoparticles to base fluids.

FIGURE 12

FIGURE 12. Impact of $\varphi$ on $T\left(r,t\right)$.

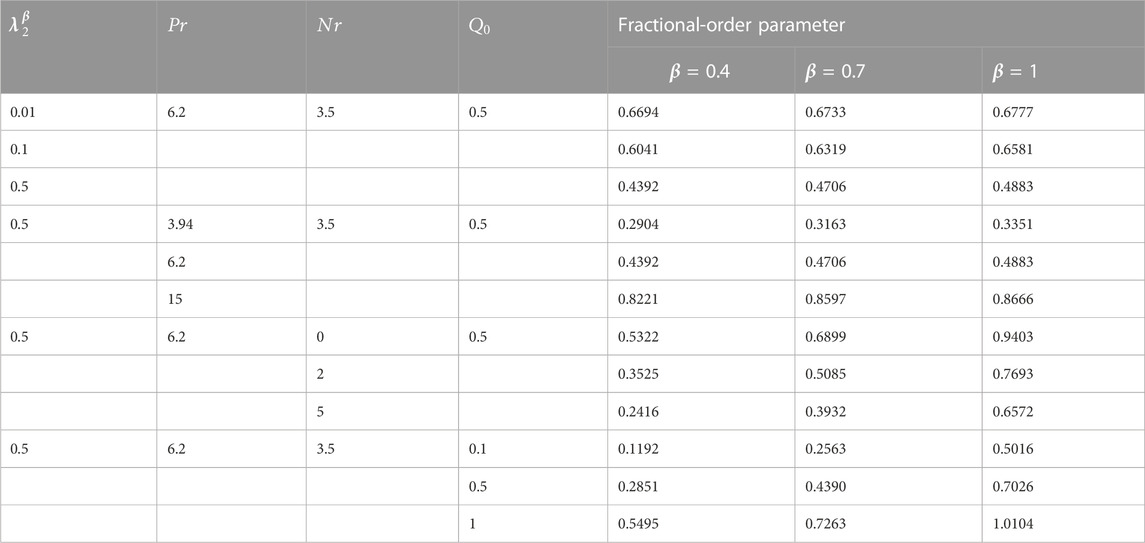
The important physical quantities of skin friction($C_f$) and local Nusselt number ($Nu$) have been quantified against different physical parameters mentioned in the previous sections. The results are arranged in Table 2 and Table 3 respectively.

TABLE 2

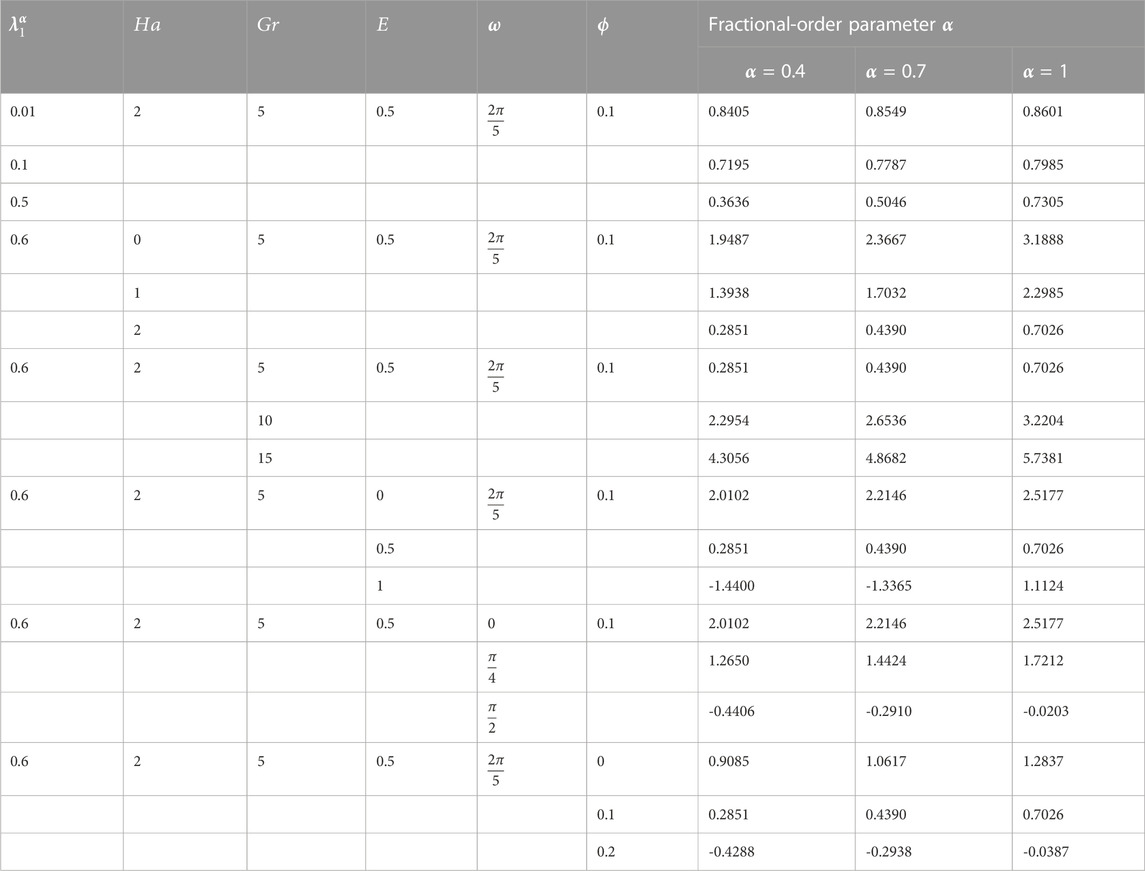
TABLE 2. Variation in the skin friction coefficient with respect to varying physical parameters and $\alpha$.

TABLE 3

TABLE 3. Variation in the local Nusselt number with respect to varying physical parameters and $\alpha$.

Table 2 shows an ascending trend in $C_f$ for increasing values of fractional-order parameter $\alpha =0.4,0.7,1.0$ and varying ${\lambda }_1^{\alpha },Ha,Gr,E,\omega ,\mathrm{a}\mathrm{n}\mathrm{d}\varphi$.

Similar behavior of $Nu$ was observed, as shown in Table 3, in that increasing values of fractional-order parameter $\beta =0.4,0.7,1.0$ resulted in increased $Nu$ for different values of ${\lambda }_2^{\beta },\mathit{Pr},Nr,\mathrm{a}\mathrm{n}\mathrm{d}$ $Q_0$.

Validation of scheme

This section of the study focused on validation of the proposed scheme. The graphical results were obtained by using mathematical software MAPLE. Figures 13A, B depict the effectiveness and accuracy of the proposed scheme for the velocity profile $u\left(r,t\right)$ and temperature profile $T\left(r,t\right)$ against an important physical parameter, the thermal radiation parameter $Nr$. MAPLE built-in command results and results obtained via our model were compared.

FIGURE 13

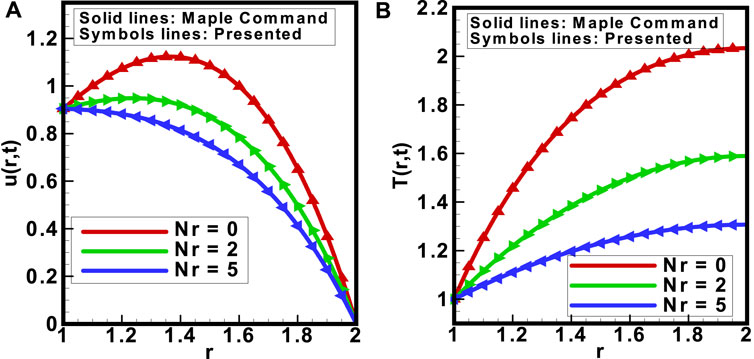
FIGURE 13. Comparison between the MAPLE built-in command results and results obtained from the model for (A) velocity and (B) temperature profiles in respect to the variation in $Nr$.

Figures 14A, B illustrate the comparison between results obtained using the built-in command in MAPLE and results obtained using the proposed scheme. The investigation assessed the velocity profile $u\left(r,t\right)$ and temperature profile $T\left(r,t\right)$ with respect to the non-dimensional Prandlt number $\mathit{Pr}.$

FIGURE 14

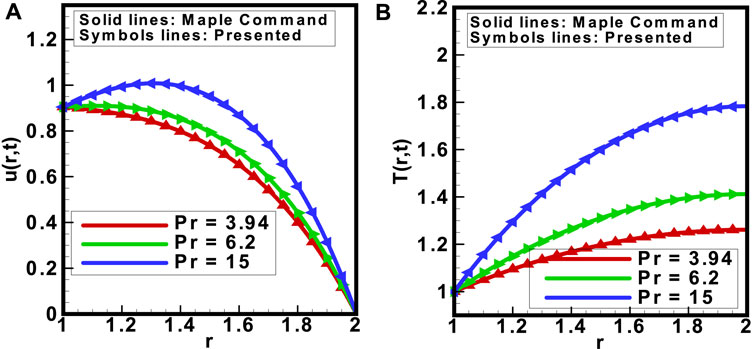
FIGURE 14. Comparison between the MAPLE built-in command results and results obtained from the model for (A) velocity and (B) temperature profiles in respect to the variation in $\mathit{Pr}$.

Conclusion

In this study, we numerically investigated the MHD flow of fractional Maxwell nano-fluid and heat transfer. The flow was measured within a cylindrical coordinate system in which coaxial geometry was considered. Thermal radiation was applied across the circular region. Water ($H_{2}O$) was adopted as the base fluid, whereas $Cu$ was considered in preparation of the nano-fluid. The problem was modeled fractionally using the Caputo time fractional differentiation operator. For discretization, the finite difference method was applied to the governing equations for the velocity and temperature profiles. The results were organized graphically using MAPLE mathematical software. For validation, the results obtained via the proposed scheme versus the built-in analysis via MAPLE were compared. Some of our key findings are as follows:

• By increasing the angular frequency of inner cylinder velocity, the velocity profile of fractional Maxwell nano-fluids is increased.

• The addition of $Cu$ nanoparticles to a base fluid of water enhances its heat transfer capability.

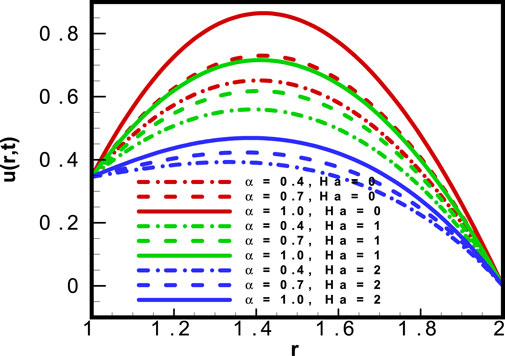
• Subjecting the system to a strong magnetic field increases heat transfer and lowers the velocity profile of the system.

• The thermal radiation parameter $Nr$ has a direct impact on the temperature profile $T\left(r,t\right)$ of fractional Maxwell nano-fluids.

• The non-dimensional parameters $\mathit{Pr},Gr$ are directly related to the temperature and velocity profiles, respectively.

• The finite difference scheme is a strong technique that can be used to solve fractional-order mathematical models.

• The result validation section shows that the scheme applied is strong and effective for the proposed problem in cylindrical geometry.

• These findings lead further toward the numerical investigation of fractional Maxwell bio-nano fluids within blood arteries.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, MIA; methodology, MU; validation, ATA; investigation, MIA; writ draft preparation, AA and MU; write and editing, TEM; visualization, MU and AA; supervision, MIA; project administration, ATA; funding acquisition, TEM. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors are grateful to HEC Pakistan for facilitating this research underresearch project No 15911 (NRPU).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aleem, M., Asjad, M. I., Shaheen, A., and Khan, I. (2020). MHD Influence on different water based nanofluids (TiO2, Al2O3, CuO) in porous medium with chemical reaction and Newtonian heating. Chaos, Solit. Fractals 130, 109437. doi:10.1016/j.chaos.2019.109437

CrossRef Full Text | Google Scholar

Anwar, T., Kumam, P., Khan, I., and Watthayu, W. (2020). Heat transfer enhancement in unsteady MHD natural convective flow of CNTs Oldroyd-B nanofluid under ramped wall velocity and ramped wall temperature. Entropy 22 (4), 401. doi:10.3390/e22040401

PubMed Abstract | CrossRef Full Text | Google Scholar

Asjad, M. I., Shah, N. A., Aleem, M., and Khan, I. (2017). Heat transfer analysis of fractional second-grade fluid subject to Newtonian heating with caputo and caputo-fabrizio fractional derivatives: A comparison. Eur. Phys. J. plus 132 (8), 340–358. doi:10.1140/epjp/i2017-11606-6

CrossRef Full Text | Google Scholar

Askey, R. A., and Roy, R., Gamma function. Available at: https://en.wikipedia.org/wiki/Gamma_function, 2010.

Google Scholar

Awan, A. U., Imran, M., Athar, M., Kamran, M., et al. (2020). Exact analytical solutions for a longitudinal flow of a fractional Maxwell fluid between two coaxial cylinders. Punjab Univ. J. Math. 45 (1).

Google Scholar

Bagley, R. L., and Torvik, P. (1983). A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheology 27 (3), 201–210. doi:10.1122/1.549724

CrossRef Full Text | Google Scholar

Choi, S. U., and Eastman, J. A. (1995). “Enhancing thermal conductivity of fluids with nanoparticles,” in Conference: 1995 International mechanical engineering congress and exhibition, Argonne, IL (United States) (Lemont, IL: Argonne National Lab.ANL).

Google Scholar

Chung, J. (1999). Numerical investigation on the bifurcative natural convection in a horizontal concentric annulus. Numer. Heat. Transf. Part A Appl. 36 (3), 291–307. doi:10.1080/104077899274778

CrossRef Full Text | Google Scholar

Fetecau, C., Hayat, T., and Fetecau, C. (2008). Starting solutions for oscillating motions of Oldroyd-B fluids in cylindrical domains. J. Newt. fluid Mech. 153 (2-3), 191–201. doi:10.1016/j.jnnfm.2008.02.005

CrossRef Full Text | Google Scholar

Fetecau, C., Mahmood, A., and Jamil, M. (2010). Exact solutions for the flow of a viscoelastic fluid induced by a circular cylinder subject to a time dependent shear stress. Commun. Nonlinear Sci. Numer. Simul. 15 (12), 3931–3938. doi:10.1016/j.cnsns.2010.01.012

CrossRef Full Text | Google Scholar

Fetecau, C., Retracted, A. R. T. I. C. L. E., Jamil, M., and Mahmood, A. (2011). Retracted article: Flow of fractional Maxwell fluid between coaxial cylinders. Archive Appl. Mech. 81 (8), 1153–1163. doi:10.1007/s00419-011-0536-x

CrossRef Full Text | Google Scholar

Friedrich, C. (1991). Relaxation and retardation functions of the Maxwell model with fractional derivatives. Rheol. Acta 30 (2), 151–158. doi:10.1007/bf01134604

CrossRef Full Text | Google Scholar

Haitao, Q., and Mingyu, X. (2009). Some unsteady unidirectional flows of a generalized Oldroyd-B fluid with fractional derivative. Appl. Math. Model. 33 (11), 4184–4191. doi:10.1016/j.apm.2009.03.002

CrossRef Full Text | Google Scholar

Haldar, S. (1998). Combined convection in developing flow through a horizontal concentric annulus. Numer. Heat. Transf. Part A Appl. 34 (6), 673–685. doi:10.1080/10407789808914009

CrossRef Full Text | Google Scholar

Hartnett, J. P., and Kostic, M. (1989). Heat transfer to Newtonian and non-Newtonian fluids in rectangular ducts. Adv. heat Transf. 19, 247–356. Elsevier. doi:10.1016/S0065-2717(08)70214-4

CrossRef Full Text | Google Scholar

Hayase, T., Humphrey, J., and Greif, R. (1992). Numerical calculation of convective heat transfer between rotating coaxial cylinders with periodically embedded cavities. J. Heat. Transf. 114 (3), 589–597. doi:10.1115/1.2911322

CrossRef Full Text | Google Scholar

Jamil, M., and Fetecau, C. (2010). Helical flows of Maxwell fluid between coaxial cylinders with given shear stresses on the boundary. Nonlinear Anal. Real World Appl. 11 (5), 4302–4311. doi:10.1016/j.nonrwa.2010.05.016

CrossRef Full Text | Google Scholar

Khan, J. A., and Mustafa, M. (2018). A numerical analysis for non-linear radiation in MHD flow around a cylindrical surface with chemically reactive species. Results Phys. 8, 963–970. doi:10.1016/j.rinp.2017.12.067

CrossRef Full Text | Google Scholar

Liu, F., Anh, V., and Turner, I. (2004). Numerical solution of the space fractional Fokker–Planck equation. J. Comput. Appl. Math. 166 (1), 209–219. doi:10.1016/j.cam.2003.09.028

CrossRef Full Text | Google Scholar

Magin, R. L. (2010). Fractional calculus models of complex dynamics in biological tissues. Comput. Math. Appl. 59 (5), 1586–1593. doi:10.1016/j.camwa.2009.08.039

CrossRef Full Text | Google Scholar

Mahmood, A., Parveen, S., Ara, A., and Khan, N. (2009). Exact analytic solutions for the unsteady flow of a non-Newtonian fluid between two cylinders with fractional derivative model. Commun. Nonlinear Sci. Numer. Simul. 14 (8), 3309–3319. doi:10.1016/j.cnsns.2009.01.017

CrossRef Full Text | Google Scholar

Ming, C., Liu, F., Zheng, L., Turner, I., and Anh, V. (2016). Analytical solutions of multi-term time fractional differential equations and application to unsteady flows of generalized viscoelastic fluid. Comput. Math. Appl. 72 (9), 2084–2097. doi:10.1016/j.camwa.2016.08.012

CrossRef Full Text | Google Scholar

Nguyen, T. H., Vasseur, P., Robillard, L., and Chandra Shekar, B. (1983). Combined free and forced convection of water between horizontal concentric cylinders. J. Heat. Transf. 105 (3), 498–504. doi:10.1115/1.3245613

CrossRef Full Text | Google Scholar

Nieckele, A., and Patankar, S. (1985). Laminar mixed convection in a concentric annulus with horizontal axis. J. Heat. Transf. 107 (4), 902–909. doi:10.1115/1.3247519

CrossRef Full Text | Google Scholar

Rashad, A., Chamkha, A. J., and Abdou, M. (2013). Mixed convection flow of non-Newtonian fluid from vertical surface saturated in a porous medium filled with a nanofluid. J. Appl. Fluid Mech. 6 (2), 301–309.

Google Scholar

Rashad, A., and Nabwey, H. A. (2019). Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. J. Taiwan Inst. Chem. Eng. 99, 9–17. doi:10.1016/j.jtice.2019.02.035

CrossRef Full Text | Google Scholar

Rosseland, S. (2013). Astrophysik: Auf atomtheoretischer grundlage, 11. Berlin, Germany: Springer-Verlag.

Google Scholar

Salah, F., (2013). MHD accelerated flow of Maxwell fluid in a porous medium and rotating frame. Int. Sch. Res. Notices.

CrossRef Full Text | Google Scholar

Saqib, M., Ali, F., Khan, I., Sheikh, N. A., Jan, S. A. A., and Samiulhaq, (2018). Exact solutions for free convection flow of generalized jeffrey fluid: A caputo-fabrizio fractional model. Alexandria Eng. J. 57 (3), 1849–1858. doi:10.1016/j.aej.2017.03.017

CrossRef Full Text | Google Scholar

Saqib, M., Hanif, H., Abdeljawad, T., Khan, I., Shafie, S., and Sooppy Nisar, K. (2020). Heat transfer in mhd flow of Maxwell fluid via fractional cattaneo-friedrich model: A finite difference approach. Comput. Mat. Contin. 65 (3), 1959–1973. doi:10.32604/cmc.2020.011339

CrossRef Full Text | Google Scholar

Shah, N. A., Elnaqeeb, T., Animasaun, I. L., and Mahsud, Y. (2018). Insight into the natural convection flow through a vertical cylinder using caputo time-fractional derivatives. Int. J. Appl. Comput. Math. 4 (3), 80–18. doi:10.1007/s40819-018-0512-z

CrossRef Full Text | Google Scholar

Shah, N., Hajizadeh, A., Zeb, M., Ahmad, S., and Mahsud, Y. (2018). Effect of magnetic field on double convection flow of viscous fluid over a moving vertical plate with constant temperature and general concentration by using new trend of fractional derivative. Open J. Math. Sci. 2 (1), 253–265. doi:10.30538/oms2018.0033

CrossRef Full Text | Google Scholar

Sheikh, N. A., Ali, F., Saqib, M., Khan, I., Jan, S. A. A., Alshomrani, A. S., et al. (2017). Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 7, 789–800. doi:10.1016/j.rinp.2017.01.025

CrossRef Full Text | Google Scholar

Srivastava, P. (1966). Non-steady helical flow of a visco-elastic liquid(Nonsteady helical flow of viscoelastic liquid contained in circular cylinder, noting occurrence of oscillations in fluid decaying exponentially with time). Arch. Mech. Stosow. 18 (2), 145–150.

Google Scholar

Subbarayudu, K., Suneetha, S., Bala Anki Reddy, P., and Rashad, A. M. (2019). Framing the activation energy and binary chemical reaction on CNT’s with Cattaneo–Christov heat diffusion on Maxwell nanofluid in the presence of nonlinear thermal radiation. Arabian J. Sci. Eng. 44 (12), 10313–10325. doi:10.1007/s13369-019-04173-2

CrossRef Full Text | Google Scholar

Sun, H., Zhang, Y., Wei, S., Zhu, J., and Chen, W. (2018). A space fractional constitutive equation model for non-Newtonian fluid flow. Commun. Nonlinear Sci. Numer. Simul. 62, 409–417. doi:10.1016/j.cnsns.2018.02.007

CrossRef Full Text | Google Scholar

Taitel, Y., and Hartnett, J. (1968). Application of Rosseland approximation and solution based on series expansion of the emission power to radiation problems. AIAA J. 6 (1), 80–89. doi:10.2514/3.4444

CrossRef Full Text | Google Scholar

Ting, T. W. (1963). Certain non-steady flows of second-order fluids. Archive Ration. Mech. Analysis 14 (1), 1–26. doi:10.1007/bf00250690

CrossRef Full Text | Google Scholar

Tiwari, R. K., and Das, M. K. (2007). Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. heat Mass Transf. 50 (9-10), 2002–2018. doi:10.1016/j.ijheatmasstransfer.2006.09.034

CrossRef Full Text | Google Scholar

Usman, M., Hamid, M., Zubair, T., Ul Haq, R., and Wang, W. (2018). Cu-AlO/Water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via LSM. Int. J. Heat Mass Transf. 126, 1347–1356. doi:10.1016/j.ijheatmasstransfer.2018.06.005

CrossRef Full Text | Google Scholar

Waters, N., and King, M. (1971). The unsteady flow of an elastico-viscous liquid in a straight pipe of circular cross section. J. Phys. D Appl. Phys. 4 (2), 304–211. doi:10.1088/0022-3727/4/2/304

CrossRef Full Text | Google Scholar

Wood, W. (2001). Transient viscoelastic helical flows in pipes of circular and annular cross-section. J. Newt. fluid Mech. 100 (1-3), 115–126. doi:10.1016/s0377-0257(01)00130-6

CrossRef Full Text | Google Scholar

Zhang, Y., Jiang, J., and Bai, Y. (2019). MHD flow and heat transfer analysis of fractional Oldroyd-B nanofluid between two coaxial cylinders. Comput. Math. Appl. 78 (10), 3408–3421. doi:10.1016/j.camwa.2019.05.013

CrossRef Full Text | Google Scholar

Zhao, Q., Mao, B., Bai, X., Chen, C., and Wang, Z. (2022). Heat transfer suppression mechanism of magnetogasdynamic flow in a circular tube subjected to transverse magnetic field regulation. Int. Commun. Heat Mass Transf. 134, 105990. doi:10.1016/j.icheatmasstransfer.2022.105990

CrossRef Full Text | Google Scholar

Nomenclature

velocity $u\left(r,t\right)\left(m/s\right)$

temperature $T\left(r,t\right)\left(K\right)$

density of nano-fluid ${\rho }_{nf}\left(kg/m^3\right)$

dynamic viscosity of nano-fluid ${\mu }_{nf}\left(kg/ms\right)$

thermal conductivity of nano-fluid $K_{nf}\left(W/mK\right)$

volumetric thermal expansion coefficient ${\beta }_{\theta }\left(K^{-1}\right)$

gravitational acceleration $g\left(m/s^2\right)$

heat capacity of nanoparticles ${\left(C_p\right)}_{nf}$

electrical conductivity of nanoparticles ${\sigma }_{nf}\left(S/m\right)$

kinematic viscosity of nanoparticles ${\nu }_{nf}\left(m^2/s\right)$

volume fraction of nanoparticles $\varphi$

radius of the inner cylinder $R_1$

radius of the outer cylinder $R_2$