- 1Department of Mechanical Engineering, University of Rochester, Rochester, NY, United States
- 2Department of Physics and Astronomy, West Virginia University, Morgantown, WV, United States
The stability of the stored information in magnetic recording media depends on the anisotropy energy Ea (=Keff V) of nanoparticles (NPs) of volume V or diameter D. Therefore, it is important to know how the effective anisotropy constant Keff varies with size D of the NPs. In a recent paper [Appl. Phys. Lett. 110, 222409 (2017)], the observed Keff versus D variation in NPs of maghemite (γ-Fe2O3) was explained on the basis of the core-shell-surface layer (CSSL) model given by Eq.: Keff = Kb + (6KS/D) +Ksh{[1-(2d/D)]−3–1}, where Kb, KS, and Ksh are the anisotropy constants of spins in the core, surface layer, and a shell of thickness d, respectively. This CSSL model is an extension of an earlier core-surface layer (CSL) model described by Keff = Kb + (6KS/D) [Phys. Rev. Lett. 72, 282 (1994)] proposed to explain the Keff versus D variation in Fe NPs. For the NPs of γ-Fe2O3, the additional term of the CSSL model involving Ksh was found to be necessary to fit the data for sizes D < 5 nm. In this paper, we report the validity of the CSSL model for NPs of several other systems viz. Co, Ni, NiO, and Fe3O4 using the available data from literature. In selecting the data, care was taken to consider data only for non-interacting NPs since the interparticle interactions generally overshadow the actual value of Keff in NPs. It is shown that the new CSSL model describes very well the Keff vs. D variation for all particle sizes whereas the CSL model fails for smaller particles with the notable exception of Fe NPs. This validation of the CSSL model for the NPs of Co, Ni, NiO, Fe3O4, and γ-Fe2O3 suggests its general validity for magnetic NPs. Discussion is also presented on the comparative magnitudes of the parameters Kb, KS, and Ksh obtained from the fits to the CSSL model.
Introduction
The increasing demand of magnetic nanoparticles (NPs) for applications in compact magnetic storage media, catalysis, ferrofluids, sensors, magnetic drug delivery, and biomedicine have secured a unique place for nanoparticle research in the scientific community (Fiorani, 2005; Gubin, 2009; Thanh, 2012; Fuxi and Yang, 2015; Seehra, 2017). A particularly interesting feature of magnetic NPs is their size-dependent magnetic properties, both due to finite-size effects and the increasing role of surface spins with decreasing particle size. With decreasing particle size (D), the concentration of unsaturated surface spins increases as 1/D causing reduction in the net magnetization and enhancement in the effective magnetic anisotropy (Keff) of NPs. Details of the size-dependence of Keff is of primary interest for applications in magnetic data storage technology since the stability of the stored information in recording media depends on the anisotropy energy Ea = KeffV of NPs of volume V. Large anisotropy energy is desired to keep the stored information robust against the thermal activation of spins. Generally, a ratio (KeffV)/(kBT) > 40 is required for reliable storage of data for ∼10 years, kBT being the average thermal energy (Fuxi and Yang, 2015).
The spins on the surface of the NPs experience a different anisotropy compared to those in the bulk (core) of the NPs due to the broken exchange bonds and reduced crystalline symmetry of the surface. Taking this fact into consideration, Bodker et al. (1994) proposed a core-surface layer (CSL) model to describe the linear trend of Keff versus 1/D data for Fe NPs and to separate the contributions of the surface and bulk spins in the total effective anisotropy energy of magnetic NPs. Although this CSL model has been often used to describe the Keff versus 1/D data for magnetic NP systems, deviations from this model have been reported for ultra-fine magnetic NPs (Chen et al., 1995; Yanes et al., 2007; Shim et al., 2008; Laha et al., 2014; Singh et al., 2017a; Singh et al., 2017b; Pisane et al., 2017). The main reason for the limitation of the CSL model for ultra-fine magnetic NPs is that the model does not account for the spins in the shell layer. Recent experimental, theoretical, and computational studies have shown that the surface spin disorder in NPs is not localized at the surface layer only, but it tends to gradually propagate towards the core forming a shell of finite thickness d (Kachkachi et al., 2000; Millan et al., 2007; Dutta et al., 2009; Krycka et al., 2010; Krycka et al., 2014). This makes the ordering of spins and hence the magnetic anisotropy in the shell layer quite different from that of in the core or at the surface. Here we show that the effects of the shell layer become prominent only for very small particle sizes D < 5 nm.
In a recent work, Pisane et al. (2017) reported an extension of the CSL model to account the effect of shell layer in the total effective magnetic anisotropy data of maghemite (γ-Fe2O3) NPs. The new model considers the core-shell-surface layer (CSSL) geometry of NPs, and it has been proven successful to adequately describe the Keff versus 1/D data in NPs of Ni and NiO systems (Singh et al., 2017b) in addition to NPs of γ-Fe2O3 (Pisane et al., 2017). In this paper, we test the validity of the CSSL model for additional NP systems of Co, Fe, and magnetite (Fe3O4) since it is important to test the validity of the CSSL model for all magnetic NPs. The Keff vs. D data used here for testing the model was taken from the published papers in literature (Mørup et al., 1982; Bødker et al., 1992; Bodker et al., 1994; Bødker and Mørup, 1994; Chen et al., 1995; Petit et al., 1998; Sun and Murray, 1999; Kumar et al., 2001; Fonseca et al., 2002; Goya et al., 2003a; Goya et al., 2003b; Petit et al., 2005; Lima et al., 2006; Guardia et al., 2007; Wu et al., 2007; Dutta et al., 2009; Masunaga et al., 2009; Singh et al., 2009; Parker et al., 2010; Díaz et al., 2011; Fonseca et al., 2011; Lisiecki, 2012; Ruano et al., 2013; Chesnel et al., 2014; Yang et al., 2014), selecting data only for the non-interacting NPs since the interparticle interactions generally overshadow the actual value of Keff in NPs and often lead to various emergent magnetic phases such as superparamagnetism, superspin glass, and superferromagnetism (Majetich and Jin, 1999; Majetich and Sachan, 2006; Bedanta and Kleemann, 2009). This analysis shows that the CSL model only captures the size-variation of Keff for larger size Ni, Co, and magnetite NPs, whereas the CSSL model adequately describes the Keff versus 1/D data for all particle sizes of Ni, Co, and magnetite (Fe3O4) NPs. The only exception appears to be the NPs of Fe for which the linear behavior of Keff vs. 1/D data as predicted by the CSL model is valid (Bodker et al., 1994). Details of these results and discussion are presented below.
Interparticle interactions and effective magnetic anisotropy
It is important to first discuss the role of interparticle interactions (IPI) and its effect on the measured blocking temperature TB which is often used to determine Keff. The dipolar interactions between the magnetic moments of the NPs yield an additional enhancement in the magnetic anisotropy of NPs (Bedanta et al., 2005; Chen et al., 2005; Majetich and Sachan, 2006; Petracic et al., 2006; Bedanta et al., 2007), causing a noticeable increase in TB, as schematically demonstrated in Figure 1A. To reduce IPI due to dipole-dipole interactions, experimentalists often use following two methods: 1) proper coating of NPs by surfactants, and 2) dispersion/separation of NPs on a non-magnetic matrix or in suitable solvent. The strength of the IPI in blocking temperature (TB) measurements can be characterized by an effective T0 leading to (Seehra and Pisane, 2016)
Here kB is the Boltzmann constant, f0 ∼ 1010–1012 Hz is the system-dependent attempt frequency varying only weakly with temperature, fm is the experimental measurement frequency, and T0 is an effective temperature representing the strength of the IPI. To determine T0, one can measure TB at two different measurement frequencies and evaluate the following quantities (Seehra and Pisane, 2016)
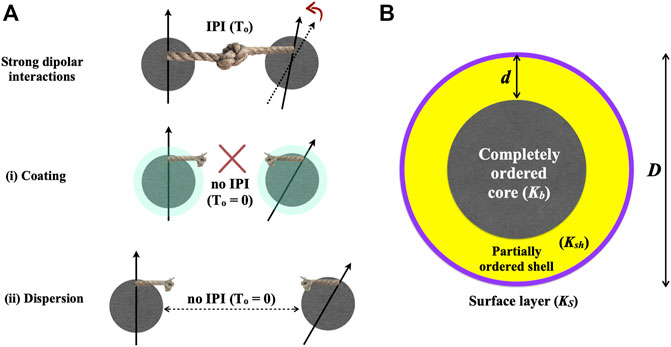
FIGURE 1. (A) Schematic representation of the effect of IPI on the effective magnetic anistropy (Keff) of NPs. The black arrow represents the magnetization easy axis and rope depicts the effect of IPI on Keff. (B) Core-shell-surface layer (CSSL) geometry of a spherical magnetic NP of diameter D and shell thickness d. T0 represents temperature corresponding to the strength of IPI.
and
Here TB (1) and TB (2) are the blocking temperature measured at two sufficiently different frequencies fm (1) and fm (2), respectively. For no IPI (T0 = 0),
The core-shell-surface layer model
Figure 1B shows a pictorial representation of the CSSL model. The spins in core (shell) are well-ordered (partially ordered), whereas the ordering of spins is disrupted at the surface layer due to the broken crystalline symmetry and presence of dangling bonds. The formation of shell layer is preferred because it reduces the total energy of the magnetic NPs (Krycka et al., 2014). Neutron diffraction measurements have confirmed the existence of shell layer in magnetite NPs (Krycka et al., 2010). Furthermore, by means of Monte-Carlo simulations, Kachkachi et al. (2000) have demonstrated the formation of a shell layer of finite thickness in maghemite NPs. Since the magnetic anisotropy constants Kb, KS, and Ksh corresponding to the spins in the core, at surface layer, and in a shell of thickness d, respectively, are expected to be different, it is essential to separate the contributions of Ksh from Kb and KS in the Keff versus D data of magnetic NPs. According to the core-surface layer (CSL) model (Bodker et al., 1994)
The factor 6/D in Eq. 5 represents the surface/volume ratio of spherical NPs with diameter D. The CSSL model represents an extension of the CSL model of Eq. 5 in which we include an extra term addressing the contribution of magnetic anisotropy from the spin in the spherical shell of thickness d (Pisane et al., 2017)
The term {[1-(2d/D)]−3–1}in Eq. 6 represents the ratio of the shell volume to the core volume, and it represents the contribution of a fraction of the spins in a shell with effective anisotropy Ksh different from Kb and KS. The Ksh contribution particularly dominates the Kb and KS contributions in ultra-fine magnetic NPs. For example, it was found that for maghemite NPs, the total contribution of the Ksh term to Keff is about 38% for D = 3 nm NPs but it rapidly decreases to ∼13% for D = 4 nm, to ∼3.7% for D = 8 nm and to ∼2% for D = 15 nm (Pisane et al., 2017). However, the contribution of the KS term remains significant even for D = 20 nm (Pisane et al., 2017). The validity of the CSSL model is limited to D > 2d since only in this limit the NPs have a core of nonzero diameter (D-2d > 0). For morphologies different from a sphere, the factor 6 in Eqs 5, 6 should be replaced by a proper factor representing the non-spherical morphology of NPs.
Here, it is important to comment on the size dependence of shell thickness, i.e., d(D). In the semi-empirical CSSL model, the shell thickness is assumed to be same for all particle sizes for simplicity and to avoid any additional fitting parameters in Eq. 6. Although this assumption is not very accurate, it can be justified by reported experimental observations (Chen et al., 1996; Goya et al., 2003b; Caruntu et al., 2007; Millan et al., 2007; Dutta et al., 2009; Krycka et al., 2010). Magnetic measurements on magnetic NPs with a wide range of particle sizes yield almost similar shell thickness for a given magnetic NP system (Chen et al., 1996; Goya et al., 2003b; Caruntu et al., 2007; Dutta et al., 2009; Krycka et al., 2010). For instance, Millan et al. reported a shell (magnetic dead layer) of ∼1 nm constant thickness for maghemite NPs in size range 1.6–15 nm with 10% size dispersion (Millan et al., 2007). Also, a maximum deviation of 0.2 nm was observed for the shell thickness of Fe3O4 NPs in 4–12 nm size range (Dutta et al., 2009). Motivated from these studies, a constant d, independent of D, can be justified at the simplest level in the CSSL model.
Validation of the CSSL model
Now we test the validity of the CSSL model for four different magnetic NP systems, namely–Ni, Co, Fe, and magnetite (Fe3O4). Figures 2, 3 show variation in Keff vs. 1/D data for these four NPs. The data was collected from available reports in the literature, where the effects due to IPI were taken into account, with the relevant references listed in the figures. Deviations from the linear trend of the Keff vs. 1/D variations predicted by the CSL model (Eq. 5) are for smaller sizes of the Ni, Co and magnetite NPs, the exception being the Fe NPs which follow a linear trend. The red line shows the best fit of the data to Eq. 6 and green line shows the best fit to Eq. 5. Although, all the data points do not exactly fall on the fitted curve, the overall trend of Keff vs. 1/D variation is well-captured by Eq. 6 within the experimental uncertainties.
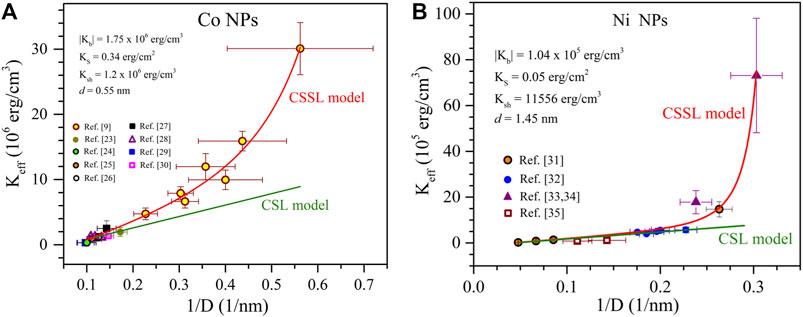
FIGURE 2. The Keff vs. 1/D variation of (A) Co, and (B) Ni NPs. The red (green) line shows the best fit to the CSSL (CSL) model. The best fitting parameters along with the sources of the data (Chen et al., 1995; Petit et al., 1998; Sun and Murray, 1999; Fonseca et al., 2002; Goya et al., 2003a; Petit et al., 2005; Masunaga et al., 2009; Singh et al., 2009; Parker et al., 2010; Díaz et al., 2011; Fonseca et al., 2011; Lisiecki, 2012; Ruano et al., 2013; Yang et al., 2014) are given in the inset.
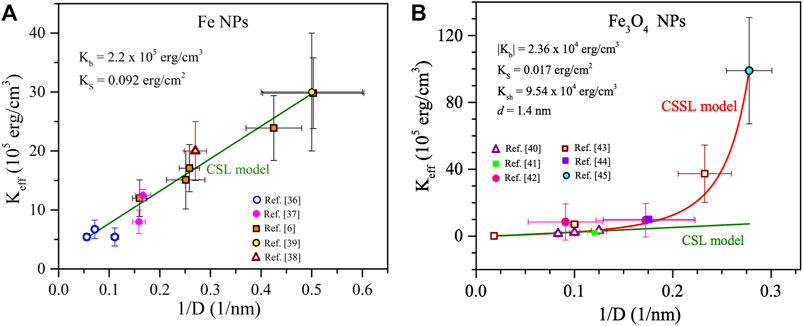
FIGURE 3. The Keff vs. 1/D variation of (A) Fe, and (B) magnetite (Fe3O4) NPs. The red (green) line shows the best fit of the data to the CSSL (CSL) model. The best fitting parameters along with the sources of the data (Mørup et al., 1982; Bødker et al., 1992; Bodker et al., 1994; Bødker and Mørup, 1994; Kumar et al., 2001; Goya et al., 2003b; Lima et al., 2006; Guardia et al., 2007; Wu et al., 2007; Dutta et al., 2009; Chesnel et al., 2014) are given in the inset.
It is important to describe the procedure used for fitting the data to the CSSL model since there are four fitting parameters (Kb, KS, Ksh, and d). To gain confidence in the procedure, this 4-parameter problem was split into two 2-parameters problems. First, we fitted the linear part of Keff vs. 1/D data for larger NPs (D > 5 nm) using Eq. 5 and determined the magnitudes of Kb and KS from the linear fitting. Next, we used the obtained values of Kb and KS as guidelines to determine the magnitudes of Ksh and d by fitting the overall data for all size ranges. The magnitudes of the best fitting parameters along with the references of the sources of the data are listed in the inset of figures. Note that these parameters obtained from the fits give important physical insights into magnetic ordering of the spins in the NPs. The magnitudes of the obtained magnetic anisotropy constants and the shell thickness are in excellent agreement with the reported experimental data on Ni, Co, and Fe3O4 NPs (Amighian and Corner, 1976; Birss et al., 1977; Wohlfarth, 1980; Kachkachi et al., 2000; Dutta et al., 2009; Krycka et al., 2010).
A comparison of the magnitudes of the fitted parameters Kb, KS, Ksh, and d on the six systems of NPs (γ-Fe2O3, NiO, Fe3O4, Ni, Co, and Fe) on which the CSSL system has been tested so far is given in Table 1. Among these systems, NPs of two systems stand out: Fe for zero values of d and Ksh, and Co for the largest magnitudes of Kb, KS, and Ksh and smallest value of non-zero d. For Co, the large magnitude of KS, and Ksh are likely related to its large Kb which is due to its hexagonal structure. Bare Fe is easily oxidized to one of its oxides (α-Fe2O3, Fe3O4, γ-Fe2O3, etc.) depending on the experimental conditions and this may be the reason for the absence of the formation of a shell in this case (d = 0). Our efforts to find sufficient published data of Keff vs. D for NPs of other magnetic systems for testing the CSSL model in which IPI has been adequately addressed have not yet been successful.
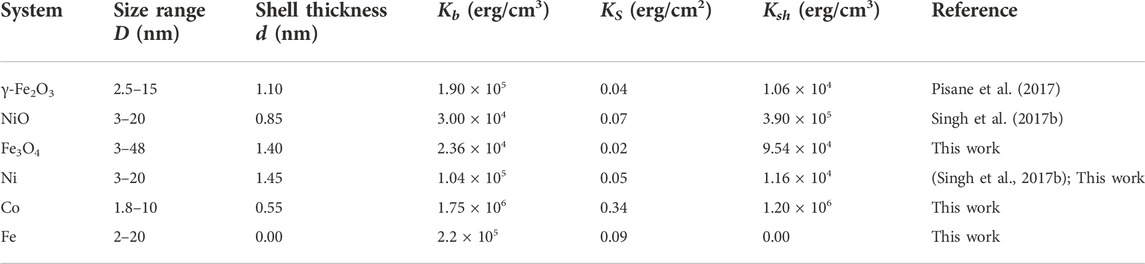
TABLE 1. The effective bulk (Kb), surface (KS), and shell (Ksh) magnetic anisotropies along with the shell thickness (d) obtained from fitting the CSSL model for maghemite (γ-Fe2O3), NiO, Fe3O4, Ni, Co, and Fe nanoparticles.
Conclusion
In this paper, we have tested the validity of the CSSL model on the variation of Keff vs. D for NPs of six systems of γ-Fe2O3, NiO, Fe3O4, Ni, Co, and Fe, the results presented here for Fe3O4, Co, and Fe being the new contributions. For the NPs of Ni, Co, and Fe3O4 discussed here and those of NiO (Pisane et al., 2017) and maghemite (Singh et al., 2017b) reported recently, the variation of Keff vs. 1/D is best described by the CSSL model. For the NPs of Fe, the CSL model appears to be quite adequate as if the Fe NPs do not have a shell. These differences for the Fe NPs might be related to how the Fe NPs were prepared, or perhaps, peculiar and yet un-understood physics of the Fe nanoparticles. The analysis presented here also shows that the CSSL model and hence contributions of the spins in the shell to Keff become important only for sizes D < ∼5 nm and that for larger NPs, the CSL model appears to be quite adequate to describe the linear variation of Keff vs. 1/D. It is likely that the CSSL may also be applicable for other magnetic NP systems where Keff vs. D data becomes available over a large enough size range without the interference of the interparticle interactions. An improved model considering the particle size dependent shell thickness d (D) and core-shell mixing terms of magnetic anisotropy would be desired in future. Results reported here may be particularly important for computational modelling of the studied magnetic nanoparticles (Reeves and Weaver, 2014; Winkler, 2017; Mahmood and Yingling, 2022).
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Amighian, J., and Corner, W. D. (1976). Measurement of the anisotropy constants K3and K1for nickel and a dilute nickel-vanadium alloy. J. Phys. F. Met. Phys. 6 (11), L309–L312. doi:10.1088/0305-4608/6/11/004
Bedanta, S., Eimüller, T., Kleemann, W., Rhensius, J., Stromberg, F., Amaladass, E., et al. (2007). Overcoming the Dipolar Disorder in Dense CoFe nanoparticle Ensembles: Superferromagnetism. Phys. Rev. Lett. 98, 176601. doi:10.1103/physrevlett.98.176601
Bedanta, S., and Kleemann, W. (2009). Supermagnetism. J. Phys. D. Appl. Phys. 42, 013001. doi:10.1088/0022-3727/42/1/013001
Bedanta, S., Sahoo, S., Chen, X., Kleemann, W., Sudfeld, D., Wojczykowski, K., et al. (2005). Intra- and interparticle interaction in a dense frozen ferrofluid. Phase Transitions 78, 121–129. doi:10.1080/01411590412331316654
Birss, R. R., Keeler, G. J., and Shepherd, C. H. (1977). Measurements of the anisotropy energy of nickel in the (100) plane. Phys. B+C 86, 257–258. doi:10.1016/0378-4363(77)90304-7
Bodker, F., Morup, S., and Linderoth, S. (1994). Surface effects in metallic iron nanoparticles. Phys. Rev. Lett. 72, 282–285. doi:10.1103/physrevlett.72.282
Bødker, F., and Mørup, S. (1994). Magnetic properties of 2 nm α-Fe particles. Hyperfine Interact. 93 (1), 1421–1425. doi:10.1007/bf02072887
Bødker, F., Mørup, S., Oxborrow, C. A., Linderoth, S., Madsen, M. B., and Niemansverdriet, J. W. (1992). Mossbauer studies of ultrafine iron-containing particles on a carbon support. J. Phys. Condens. Matter 4, 6555–6568. doi:10.1088/0953-8984/4/31/008
Caruntu, D., Caruntu, G., and J O’Connor, C. (2007). Magnetic properties of variable-sized Fe3O4nanoparticles synthesized from non-aqueous homogeneous solutions of polyols. J. Phys. D. Appl. Phys. 40, 5801–5809. doi:10.1088/0022-3727/40/19/001
Chen, J. P., Sorensen, C. M., Klabunde, K. J., Hadjipanayis, G. C., Devlin, E., and Kostikas, A. (1996). Size-dependent magnetic properties ofMnFe2O4fine particles synthesized by coprecipitation. Phys. Rev. B 54, 9288–9296. doi:10.1103/physrevb.54.9288
Chen, J. P., Sorensen, C. M., Klabunde, K. J., and Hadjipanayis, G. C. (1995). Enhanced magnetization of nanoscale colloidal cobalt particles. Phys. Rev. B 51, 11527–11532. doi:10.1103/physrevb.51.11527
Chen, X., Bedanta, S., Petracic, O., Kleemann, W., Sahoo, S., Cardoso, S., et al. (2005). Superparamagnetism versus superspin glass behavior in dilute magnetic nanoparticle systems. Phys. Rev. B 72, 214436. doi:10.1103/physrevb.72.214436
Chesnel, K., Trevino, M., Cai, Y., Hancock, J. M., Smith, S. J., and Harrison, R. G. (2014). Particle size effects on the magnetic behaviour of 5 to 11 nm Fe3O4nanoparticles coated with oleic acid. J. Phys. Conf. Ser. 521 (1), 012004. doi:10.1088/1742-6596/521/1/012004
Díaz, M., Martínez, L., Ruano, M. M., Llamosa, P. D., Román, E., García-Hernandez, M., et al. (2011). Morphological, structural, and magnetic properties of Co nanoparticles in a silicon oxide matrix. J. Nanoparticle Res. 13 (10), 5321.
Dutta, P., Pal, S., Seehra, M. S., Shah, N., and Huffman, G. P. (2009). Size dependence of magnetic parameters and surface disorder in magnetite nanoparticles. J. Appl. Phys. 105, 07B501. doi:10.1063/1.3055272
Fonseca, F. C., Goya, G. F., Jardim, R. F., Muccillo, R., Carreno, N. L., Longo, E., et al. (2002). Superparamagnetism and magnetic properties of Ni nanoparticles embedded inSiO2. Phys. Rev. B 66, 104406. doi:10.1103/physrevb.66.104406
Fonseca, F. C., Jardim, R. F., Escote, M. T., Gouveia, P. S., Leite, E. R., and Longo, E. (2011). Superparamagnetic Ni:SiO2–C nanocomposites films synthesized by a polymeric precursor method. J. Nanopart. Res. 13 (2), 703–710. doi:10.1007/s11051-010-0068-2
Fuxi G., and Yang W. (Editors) (2015). Data storage at the Nanoscale: Advances and applications (Singapore: CRC Press).
Goya, G. F., Berquo, T. S., Fonseca, F. C., and Morales, M. P. (2003). Static and dynamic magnetic properties of spherical magnetite nanoparticles. J. Appl. Phys. 94 (5), 3520–3528. doi:10.1063/1.1599959
Goya, G. F., Fonseca, F. C., Jardim, R. F., Muccillo, R., Carreno, N. L. V., Longo, E., et al. (2003). Magnetic dynamics of single-domain Ni nanoparticles. J. Appl. Phys. 93 (10), 6531–6533. doi:10.1063/1.1540032
Guardia, P., Batlle-Brugal, B., Roca, A. G., Iglesias, O., Morales, M. P., Serna, C. J., et al. (2007). J. Magn. Magn. Mater. 316 (2), e756–e759.
Kachkachi, H., Nogues, M., Tronc, E., and Garanin, D. A. (2000). Finite-size versus surface effects in nanoparticles. J. Magn. Magn. Mater. 221, 158–163. doi:10.1016/s0304-8853(00)00390-5
Krycka, K. L., Booth, R. A., Hogg, C. R., Ijiri, Y., Borchers, J. A., Chen, W. C., et al. (2010). Core-shell magnetic morphology of Structurally Uniform magnetite nanoparticles. Phys. Rev. Lett. 104, 207203. doi:10.1103/physrevlett.104.207203
Krycka, K. L., Borchers, J. A., Booth, R. A., Ijiri, Y., Hasz, K., Rhyne, J. J., et al. (2014). Kryckaet al.Reply:. Phys. Rev. Lett. 113, 149702. doi:10.1103/physrevlett.114.149702
Kumar, D., Narayan, J., Kvit, A. V., Sharma, A. K., and Sankar, J. (2001). High coercivity and superparamagnetic behavior of nanocrystalline iron particles in alumina matrix. J. Magn. Magn. Mater. 232 (3), 161–167. doi:10.1016/s0304-8853(01)00191-3
Laha, S. S., J Tackett, R., and Lawes, G. (2014). Interactions in γ-Fe2O3 and Fe3O4 nanoparticle systems. Phys. B Condens. Matter 448, 69–72. doi:10.1016/j.physb.2014.03.036
Lisiecki, I. (2012). From the Co nanocrystals to their Self-organizations: Towards Ferromagnetism at Room temperature. Acta Phys. Pol. A 121 (2), 426–433. doi:10.12693/aphyspola.121.426
Mahmood, A. U., and Yingling, Y. G. (2022). All-atom simulation method for Zeeman Alignment and Dipolar assembly of magnetic nanoparticles. J. Chem. Theory Comput. 18 (5), 3122–3135. doi:10.1021/acs.jctc.1c01253
Majetich, S. A., and Jin, Y. (1999). Magnetization Directions of Individual nanoparticles. Science 284 (5413), 470–473. doi:10.1126/science.284.5413.470
Majetich, S. A., and Sachan, M. (2006). Magnetostatic interactions in magnetic nanoparticle assemblies: Energy, time and length scales. J. Phys. D. Appl. Phys. 39, R407–R422. doi:10.1088/0022-3727/39/21/r02
Masunaga, S. H., Jardim, R. F., Fichtner, P. F. P., and Rivas, J. (2009). Role of dipolar interactions in a system of Ni nanoparticles studied by magnetic susceptibility measurements. Phys. Rev. B 80, 184428. doi:10.1103/physrevb.80.184428
Millan, A., Urtizberea, A., Silva, N. J., Palacio, F., Amaral, V. S., Snoeck, E., et al. (2007). Surface effects in maghemite nanoparticles. J. Magn. Magn. Mater. 312, L5.
Mørup, S., Topsøe, H., and Clausen, B. S. (1982). Magnetic properties of Microcrystals studied by Mössbauer Spectroscopy. Phys. Scr. 25 (6A), 713–719. doi:10.1088/0031-8949/25/6a/015
Parker, D., Lisiecki, I., and Pileni, M. P. (2010). Do 8 nm Co nanocrystals in Long-range-ordered Face-Centered Cubic (fcc) supracrystals show superspin glass behavior? J. Phys. Chem. Lett. 1, 1139–1142. doi:10.1021/jz1001874
Petit, C., Taleb, A., and Pileni, M. P. (1998). Self-organization of magnetic Nanosized cobalt particles. Adv. Mater. 10 (3), 259–261. doi:10.1002/(sici)1521-4095(199802)10:3<259:aid-adma259>3.0.co;2-r
Petit, C., Wang, Z. L., and Pileni, M. P. (2005). Seven-nanometer hexagonal Close Packed cobalt nanocrystals for High-temperature magnetic applications through a Novel Annealing process. J. Phys. Chem. B 109 (32), 15309–15316. doi:10.1021/jp052487+
Petracic, O., Chen, X., Bedanta, S., Kleemann, W., Sahoo, S., Cardoso, S., et al. (2006). Collective states of interacting ferromagnetic nanoparticles. J. Magn. Magn. Mater. 300, 192–197. doi:10.1016/j.jmmm.2005.10.061
Pisane, K. L., Singh, S., and Seehra, M. S. (2015). Synthesis, structural characterization and magnetic properties of Fe/Pt core-shell nanoparticles. J. Appl. Phys. 117, 17D708. doi:10.1063/1.4908304
Pisane, K. L., Singh, S., and Seehra, M. S. (2017). Unusual enhancement of effective magnetic anisotropy with decreasing particle size in maghemite nanoparticles. Appl. Phys. Lett. 110, 222409. doi:10.1063/1.4984903
Pramanik, P., Thota, S., Singh, S., Joshi, D. C., Weise, B., Waske, A., et al. (2017). Effects of Cu doping on the electronic structure and magnetic properties of MnCo2O4nanostructures. J. Phys. Condens. Matter 29, 425803. doi:10.1088/1361-648x/aa839d
Reeves, D. B., and Weaver, J. B. (2014). Approaches for modeling magnetic nanoparticle Dynamics. Crit. Rev. Biomed. Eng. 421, 85–93. doi:10.1615/critrevbiomedeng.2014010845
Ruano, M., Diaz, M., Martinez, L., Navarro, E., Roman, E., Garcia-Hernandez, M., et al. (2013). Matrix and interaction effects on the magnetic properties of Co nanoparticles embedded in gold and vanadium. Phys. Chem. Chem. Phys. 15, 316–329. doi:10.1039/c2cp42769a
Seehra M. S. (Editor) (2017). Nanostructured materials - Fabrication to application (London: InTech).
Seehra, M. S., and Pisane, K. L. (2016). Relationship between blocking temperature and strength of interparticle interaction in magnetic nanoparticle systems. J. Phys. Chem. Solids 93, 79–81. doi:10.1016/j.jpcs.2016.02.009
Seehra, M. S., Singh, V., Dutta, P., Neeleshwar, S., Chen, Y. Y., Chen, C. L., et al. (2010). Size-dependent magnetic parameters of fcc FePt nanoparticles: Applications to magnetic hyperthermia. J. Phys. D. Appl. Phys. 43 (14), 145002. doi:10.1088/0022-3727/43/14/145002
Shim, H., Dutta, P., Seehra, M. S., and Bonevich, J. (2008). Size dependence of the blocking temperatures and electron magnetic resonance spectra in NiO nanoparticles. Solid State Commun. 145, 192–196. doi:10.1016/j.ssc.2007.10.026
Singh, S., Pisane, K. L., and Seehra, M. S. (2017). “A core-shell-surface layer model to explain the size dependence of effective magnetic anisotropy in magnetic nanoparticles,” in 2017 IEEE 17th International Conference on Nanotechnology (IEEE-NANO), Pittsburgh, PA, July 2017 (IEEE), 1014–1018.
Singh, S., Pramanik, P., Sangaraju, S., Mallick, A., Giebeler, L., and Thota, S. (2017). Size-dependent structural, magnetic, and optical properties of MnCo2O4nanocrystallites. J. Appl. Phys. 121 (19), 194303. doi:10.1063/1.4983360
Singh, V., Seehra, M. S., and Bonevich, J. (2009). Ac susceptibility studies of magnetic relaxation in nanoparticles of Ni dispersed in silica. J. Appl. Phys. 105, 07B518. doi:10.1063/1.3073949
Sun, S., and Murray, C. B. (1999). Synthesis of monodisperse cobalt nanocrystals and their assembly into magnetic superlattices (invited). J. Appl. Phys. 85, 4325–4330. doi:10.1063/1.370357
Thanh N. T. K. (Editor) (2012). Magnetic nanoparticles: From Fabrication to Clinical applications (Boca Raton, FL: CRC Press).
Wu, Jun-Hua, Ko, S. P., Liu, H.-L., Kim, S., Ju, J.-S., and Kim, Y. K. (2007). Sub 5 nm magnetite nanoparticles: Synthesis, microstructure, and magnetic properties. Mater. Lett. 61 (14), 3124.
Yanes, R., Chubykalo-Fesenko, O., Kachkachi, H., Garanin, D. A., Evans, R., and Chantrell, R. W. (2007). Effective anisotropies and energy barriers of magnetic nanoparticles with Néel surface anisotropy. Phys. Rev. B 76, 064416. doi:10.1103/physrevb.76.064416
Keywords: magnetic nanoparticles, interparticle interactions, blocking temperature, effective magnetic anisotropy, size dependence, core-shell
Citation: Singh S and Seehra MS (2022) Testing the validity of the core-shell-surface layer model on the size dependence of effective magnetic anisotropy in magnetic nanoparticles. Front. Mater. 9:1050600. doi: 10.3389/fmats.2022.1050600
Received: 21 September 2022; Accepted: 14 November 2022;
Published: 25 November 2022.
Edited by:
Dhiren Kumar Pradhan, The University of Tennessee, Knoxville, United StatesReviewed by:
Proloy Taran Das, Postdoctoral Researcher, Vienna, AustriaSubhankar Bedanta, National Institute of Science Education and Research (NISER), India
Copyright © 2022 Singh and Seehra. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sobhit Singh, cy5zaW5naEByb2NoZXN0ZXIuZWR1; Mohindar S. Seehra, bXNlZWhyYUBtYWlsLnd2dS5lZHU=
 Sobhit Singh
Sobhit Singh Mohindar S. Seehra2*
Mohindar S. Seehra2*