A unified non-empirical strength model

Strength, as an important indicator of structural materials, has always been an important research topic in materials science. Theoretically, building a strength model is a rewarding method to understand the relationship between the mechanical properties and microstructure of materials. Although many strength models can reduplicate experimental values very well, they are empirical models, and their applicability is limited to materials for which empirical parameters have been obtained. Here, a non-empirical strength model is proposed based on the two-dimensional (2D) displacement potential of dislocation slipping, which can be applied to different chemically bonded crystals. Owing to the large electron localization function (ELF), covalent and ionic crystals have a high 2D displacement potential of dislocation slipping, and their dislocation slip mode prefers the kink-pair mode, further exhibiting a high critical resolved shear stress (CRSS). In contrast, metallic crystals with a small ELF have a low 2D displacement potential of dislocation slipping, and their dislocation slip mode is more inclined to the string mode, showing a low CRSS. This work provides new insights into dislocation-slipping configurations that will be useful for the development of new high-performance structural materials.

1 Introduction

With the rapid development of science and technology, the service environment of structural materials has become increasingly harsh (Williams and Starke, 2003). To ensure the reliability and durability of engineering components, structural materials with very high performance are needed, and a very deep understanding of their strengthening mechanism is necessary. Since the strength is closely related to the microstructure, understanding and constructing the correlation between the strength and microstructure has always been an important research topic in materials science (Caillard, 2007; Wen et al., 2019; Xiao et al., 2020; Sun et al., 2022).

As early as 1926, a theoretical strength model was proposed by Frenkel (1926). However, the strength calculated by this model is several orders of magnitude higher than the experimental observation. Therefore, this model is inadequate for calculating and understanding the strength of materials.

To date, according to the principle on which strength models are based, they have been categorized into two categories, which can be used to obtain strengths similar to experimental values. One category is based on dislocation theory, and these models are usually used to study the yield strength of metallic materials. The other category is based on valence bond theory, and these models are usually used to study the hardness of covalent and ionic materials.

For the yield strength models based on dislocation theory, the original model is the Peierls-Nabarro (P-N) model (Peierls, 1940; Nabarro, 1947). In the P-N model, a one-dimensional (1D) displacement potential (P-N barrier) is used, and a non-empirical expression of the force required for dislocation motion (P-N force) is given. Although the predicted P-N force is consistent with the experimental results in terms of the order of magnitude, the temperature and stain rate effects on the strength cannot be considered in this model (Hull and Bacon, 2001). To overcome this drawback, two empirical models have been built on the basis of transmission electron microscopy (TEM) observations and the 1D P-N barrier. One is the Seeger model (kink-pair model) (Seeger, 1955; Seeger et al., 1957), which is applicable to some covalent materials (Xiao et al., 2018) or body-centred-cubic (BCC) metallic materials (Seeger and Wüthrich, 1976). The other model is the string model, which was built by Freudenthal. (1959) and is applicable to some metallic materials (Oh et al., 2009). Although thermal activation for dislocation movement has been considered and the predicted strength is consistent with the experimental results (Seeger et al., 1957; Haasen, 1958; Conrad, 1964; Seeger and Wüthrich, 1976), their application scope is questioned owing to the empirical dislocation slipping mode used. Hence, the use of these models in the design of mechanical properties for new materials is unreliable.

The strength (hardness) models based on valence bond theory are mainly for covalent and ionic materials (Gao et al., 2003; Šimůnek and Vackář, 2006; Li et al., 2008; Lyakhov and Oganov, 2011; Mazhnik and Oganov, 2019; Mazhnik and Oganov, 2020). Currently, only the properties of chemical bonds are considered in all these models. According to these models, single-crystal diamond should obviously be the hardest material because the sp³ (Xiao et al., 2020) hybridized C−C bond in diamond is the strongest bond in the three-dimensional network (Chaudhri and Lim, 2005). However, recently synthesized nanotwinned diamond is more than twice as hard as single-crystal diamond (Huang et al., 2014). Obviously, explaining the hardening mechanism of covalent materials based only on these hardness models is unreasonable, and a more profound theory is urgently needed to investigate the hardness of covalent and ionic crystals.

For the mechanical response of metallic, ionic and covalent materials under complex loading conditions, the microscopic deformation mechanisms all involve in dislocation slip (Xiao et al., 2018; Xiao et al., 2019; Zhai et al., 2020). Also, previous studies have proven that metallic materials are weakly directional, similar to covalent bonds (Ogata et al., 2002). For covalent crystals, such as diamond and silicon, the room temperature dislocation plasticity is observed directly (Šimůnek and Vackář, 2006; Li et al., 2008; Nie et al., 2020). Therefore, dislocation theory is utilized to understand the origin of the hardness of covalent materials (Xiao et al., 2018; Nie et al., 2020; Feng et al., 2021). These cases offer a feasible means: a unified strength model based on dislocation theory can be used to deal with metallic, covalent, and ionic materials. The displacement potential of dislocation slipping has been found to be dominated by the two adjacent atomic planes in a crystal lattice, and the dislocation bends and kinks when moving on its slip plane (Hirth et al., 1983a); therefore, the displacement potential of dislocation slipping should be considered a two-dimensional (2D) potential. Naturally, the joint influence of the directionality and strength of the chemical bonds on a dislocation can be included. Based on this idea, a unified strength (yield strength/hardness) model for different chemically bonded crystals is proposed in this work. In contrast to previous empirical strength (yield strength/hardness) models based on empirical observations or data fitting, our model is derived from the fundamentals of strength based on dislocations. This will provide insight into the physical mechanism of the dislocation slipping mode and strength, which will be helpful for designing and studying structural materials.

2 Origin of different dislocation slipping modes in the 2D displacement potential

A dislocation is a line defect on a slip plane, and its motion is limited to its slip plane. At finite temperatures, thermal activity is essential; hence, the dislocation slipping mode is dominated not only by mechanical activation but also by thermal activation. Therefore, a dislocation slipping by keeping a straight line mode (P-N model) with invalid thermal activation is infeasible, and an actual dislocation slipping mode should be partially protruding (Seeger et al., 1957). In this situation, the displacement potential of dislocation slipping includes not only the 1D P-N barrier (E_PN) but also the migration barrier (E_M) of sideways movement of the protruding parts. These two barriers distribute in mutual angle directions and constitute a 2D barrier surface, which not only restricts the expansion of dislocation lines but also restricts the shape of dislocation motion and affects its slipping mode (Caillard and Martin, 2003).

The 2D barrier obstructing dislocation motion is related to the crystal structure and dislocation properties (Peierls, 1940; Nabarro, 1947), such as shear modulus G, Poisson’s ratio ν, and Burgers vector b. Thus, the 2D barrier is an intrinsic property of a material. Under finite temperature T and applied shear stress τ conditions, both temperature and shear stress contribute to overcoming this 2D barrier, and the slipping mode varies with temperature and applied shear stress (Long et al., 2013). According to the relative energies of the thermal activation energy mk_BT [k_B is the Boltzmann constant, and m is a coefficient (George and Rabier, 1987)] and E_M as well as E_PN, the slipping mode can be divided into four categories (as shown in Figure 1):

FIGURE 1

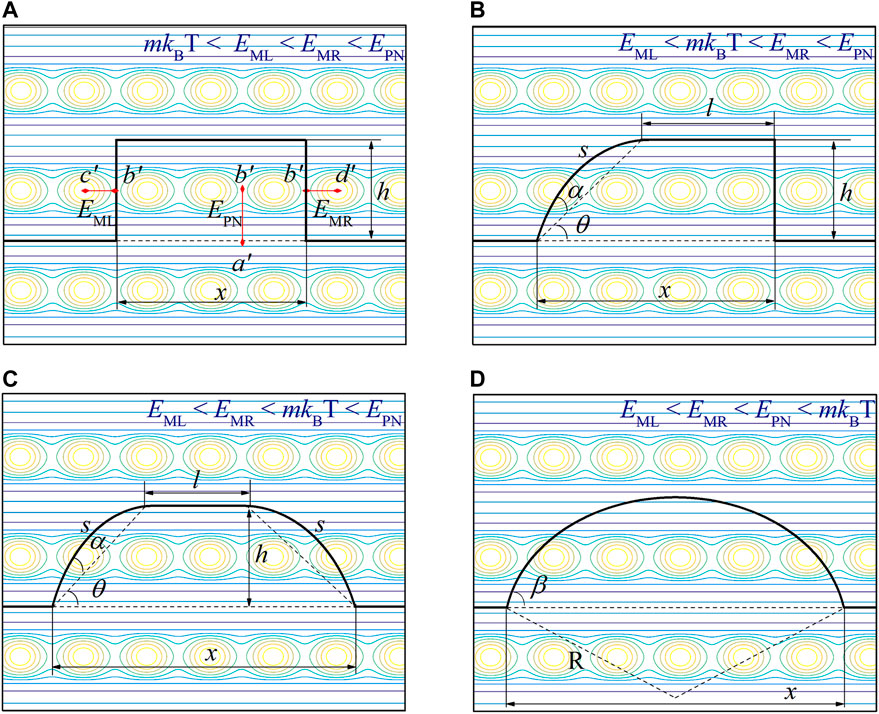
FIGURE 1. 2D displacement potential of dislocation slipping and origin of dislocation slipping modes. (A) Hard kink-pair mode. The black line represents the dislocation line configuration, and the background represents the projection of the 2D displacement potential, where the energy difference from the Peierls valley (a′) to the saddle point (b′) represents the P-N barrier (E_PN); the energy difference from the saddle point (b′) to the left barrier peak (c′) represents the left migration barrier (E_ML); and the energy difference from the saddle point (b′) to the right barrier peak (d′) represents the right migration barrier (E_MR). Furthermore, according to the restrictions from the 2D displacement potential on the dislocation, the dislocation slipping modes can be divided into mixed kink-pair mode (B), soft kink-pair mode (C), and string mode (D).

1. Hard kink-pair mode When the temperature is low, thermal activation cannot overcome barriers in any direction. At this time, all protruding dislocation segments are straight in three directions due to the restrictions from E_ML, E_MR, and E_PN, as shown in Figure 1A.

2. Mixed kink-pair mode When the thermal activation energy is higher than E_ML but lower than E_MR (E_ML < mk_BT < E_MR < E_PN), the thermal activation overcomes the left migration barrier. Accordingly, the left dislocation segment transforms into the string mode, which is bounded only by its line tension. However, the dislocation in such a temperature range is still constrained by E_MR and E_PN, and the other two dislocation segments are straight, as shown in Figure 1B.

3. Soft kink-pair mode When the thermal activation energy is higher than E_ML and E_MR but smaller than E_PN, i.e., E_ML < E_MR < mk_BT < E_PN, the thermal activation overcomes the left and right migration barriers. Therefore, the left and right dislocation segments transform into the string mode, but the dislocation segment perpendicular to E_PN remains straight, as shown in Figure 1C.

4. String mode With increasing temperature, thermal activation overcomes barriers in any direction, and all protruding dislocation segments enter the string mode, which is only bounded by the line tension, as shown in Figure 1D.

3 Mathematical model of material strength

3.1 Critical resolved shear stress (CRSS) of dislocation slip

To obtain the CRSS of dislocation slip, the energy of the dislocation system is mathematically modelled for nucleation and expansion in different slipping modes. In this work, the energy of the dislocation system includes four parts: elastic energy, interaction energy, work done by the applied shear stress, and stacking fault energy. Because the dislocation core energy is approximately 1/10–1/15 of the elastic energy (Hull and Bacon, 2001), it is ignored.

For the hard kink-pair mode, as shown in Figure 1A, a dislocation line in its initial state is located in the Peierls valley, it moves to the nearest equivalent Peierls valley under the effect of the applied shear stress τ (Peierls, 1940; Nabarro, 1947). When the critical configuration is formed, the length of this dislocation line increases by 2h compared with the initial state, so the elastic energy of the dislocation line increases (Hirth et al., 1983b).

$W_{elas}=\frac{A_{1}G{b}^{2}h}{2\pi }\ln \left(\frac{R_{\mathrm{i}}}{r}\right),(1)$

where $A_1={\cos }^2\beta +\frac{{\sin }^2\beta }{1-v}$, $\beta$ is the angle between the dislocation line and Burger′s vector $b$, G is the shear modulus of the material, $h$ is the kink height, $R_{\mathrm{i}}$ is the integral range of linear elasticity theory, $r$ is the dislocation core radius.

The interaction energy between two parallel kinks with length h can be obtained according to literature (EshelbyDouglas, 1962) and can be written as

$W_{\mathrm{int}}=-\frac{A_{2}G{b}^2{h}^2}{8\pi x},(2)$

where $A_2=\frac{\left(1+v\right){\cos }^2\beta +\left(1-2v\right){\sin }^2\beta }{1-v}$, x is nucleus size.

The work done by the applied stress τ can be expressed as

$W_{\tau }=-hbx\tau .(3)$

The stacking fault energy can be expressed as

$W_{\gamma }=hx{\gamma }_{SEF},(4)$

where ${\gamma }_{SEF}$ is the stacking fault energy of unit area.

As a result, the energy of the dislocation system is the sum of the four parts (Eqs 1–4) and can be expressed as a function of the applied shear stress τ and nucleus size x:

$E\left(x,\tau \right)=\frac{A_{1}G{b}^{2}h}{2\pi }\ln \left(\frac{R_{\mathrm{i}}}{r}\right)-\frac{A_{2}G{b}^2{h}^2}{8\pi x}-hbx\tau +hx{\gamma }_{SEF}.(5)$

Similarly, for the mixed kink-pair mode, as shown in Figure 1B, the energy of the dislocation system can also be expressed as a function of τ and x:

$\begin{array}{l}E\left(x,\tau \right)=\frac{\mathrm{s}{E}_0}{\cos \left(\theta +\alpha \right)}+\frac{l{E}_0\cos \left(\theta -\alpha \right)}{\cos \left(\theta +\alpha \right)}+\frac{A_{1}Gh{b}^2}{4\pi }\ln \left(\frac{R_{\mathrm{i}}}{r}\right)-x{E}_0-\frac{A_{2}G{b}^2{h}^2}{8\pi x}\\ -\left[\frac{1}{2}\left(l+x\right)h+R^2\left(\alpha -\frac{1}{2}\sin 2\alpha \right)\right]b\tau +\left[\frac{1}{2}\left(l+x\right)h+R^2\left(\alpha -\frac{1}{2}\sin 2\alpha \right)\right]{\gamma }_{SEF}\end{array},(6)$

where s is the length of the arc (R is the radius), l is the length of the partial protrusion, $2\alpha$ is the central angle of the arc, and $E_0=\frac{1}{2}G{b}^2$ is the energy per unit length of the straight dislocation.

For the soft kink-pair mode, as shown in Figure 1C, the energy of the dislocation system can also be expressed as a function of τ and x:

$\begin{array}{l}E\left(x,\tau \right)=\frac{2\mathrm{s}{E}_0}{\cos \left(\theta +\alpha \right)}+\frac{l{E}_0\cos \left(\theta -\alpha \right)}{\cos \left(\theta +\alpha \right)}-x{E}_0-\frac{A_{2}G{b}^2{h}^2}{8\pi x}\\ -\left[\frac{1}{2}\left(l+x\right)h+2R^2\left(\alpha -\frac{1}{2}\sin 2\alpha \right)\right]b\tau +\left[\frac{1}{2}\left(l+x\right)h+2R^2\left(\alpha -\frac{1}{2}\sin 2\alpha \right)\right]{\gamma }_{SEF}\end{array}.(7)$

For the string mode, as shown in Figure 1D, the energy of the dislocation system can be expressed as a function of τ and nucleus size R:

$E\left(R,\tau \right)=2R\beta \frac{E_0}{\cos \beta }-2R\sin \beta E_0-b\tau R^2\left(\beta -\frac{1}{2}\sin 2\beta \right)+R^2\left(\beta -\frac{1}{2}\sin 2\beta \right){\gamma }_{SEF},(8)$

where $2\beta$ is the central angle of the string.

When τ is given, the energy of the dislocation system, E, is a function of the nucleus size x or R. As schematically shown in Figure 2A, the energy of the dislocation system initially increases, followed by a decrease as the nucleus size keeps increasing. There exists a maximum of the energy, which is called the thermal activation energy barrier Q(τ) for dislocation motion at a given applied shear stress τ. Mathematically, Q(τ) can be determined by calculating the first derivative of E with respect to x or R. Therefore, Q(τ) as a function of τ can be obtained, as schematically shown in Figure 2B. For all four slipping modes, Q(τ) monotonically decreases with increasing τ. Under the same applied shear stress, the dislocation slipping mode with a low activation energy barrier is priority activated. E_PN, E_ML, and E_MR equivalently decrease with increasing τ. The final dislocation slipping mode is determined by two factors: one is the relative energies of the thermal activation energy mk_BT and E_M as well as E_PN, as mentioned in Section 2, and the second factor is the competition between different slipping modes to ensure a lower energy barrier.

FIGURE 2

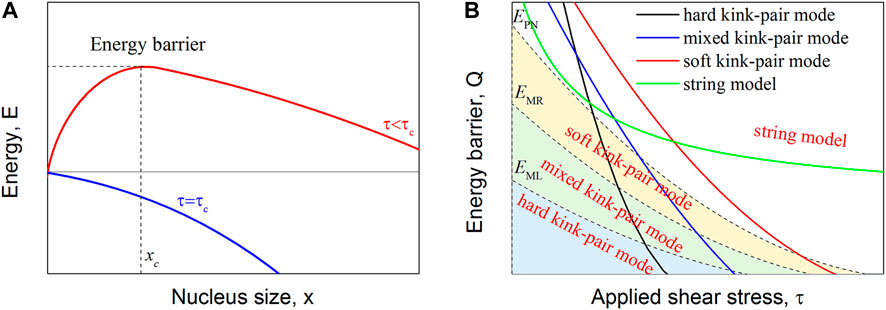
FIGURE 2. Competition of dislocation slipping modes under a given applied shear stress. (A) Dislocation system energy as a function of nucleus size under certainly applied shear stress. When the first derivative of the system energy reaches zero, the maximum value of the system energy can be defined as the thermal activation energy barrier, and x_c can be called the critical nucleus size. (B) Thermal activation energy barrier of the four dislocation slip modes as well as the E_ML, E_MR, and E_PN energy barriers.

By combining the Orowan equation (Orowan, 1934; Schoeck, 1965; Hirth and Nix, 1969) and Arrhenius’s dislocation velocity expressions (Laidler, 1984), the following relationship can be obtained:

$Q\left(\tau \right)=k_{B}T\ln \left(\frac{{\rho }_{m}b{\lambda }_b{v}_D}{\dot{\epsilon }}\right),(9)$

where ρ_m is the density of movable dislocations; λ_b is the average free path of dislocations; v_D is the Debye frequency of the material; and $\dot{\epsilon }$ is the strain rate.

By solving Eq. 9, the CRSS can be obtained for given temperature, dislocation density, and strain rate.

3.2 Non-empirical strength model for polycrystalline materials

A polycrystalline material is composed of many single-crystal grains with different orientations, and a single crystal grain with high symmetry, such as face-centred-cubic (FCC) and BCC crystals, exhibits a multiple slip system. Although the CRSS can characterize the critical shear strength of dislocation motion on a single slip plane and dominate the strength of a polycrystalline material, the CRSS cannot be directly used as the strength of a polycrystalline material, and there exists a geometric transformation between them. Usually, the yield strength of polycrystalline materials can be calculated from the CRSS by using the Sachs model (Barnett et al., 2006), the Taylor model (Taylor, 1938), and the self-consistent (SC) model (Hutchinson, 1970). In this work, the yield strength of polycrystalline materials is calculated from the CRSS by using the Sachs model as an example.

According to Schmid’s law, the uniaxial yield stress of a single crystal is equal to the CRSS divided by the corresponding Schmid factor. Figure 3A shows the distribution of the Schmid factor of a single slip system for an FCC crystal. For a high symmetry single crystal, e.g., an FCC crystal, there are multiple slip systems and 48 patches of the Schmid factor, and the distribution is shown in Figures 3B, C. However, the uniaxial yield stress of a single crystal can also be calculated by Schmid’s law, as shown in Figure 3D. In polycrystalline materials, there are many single-crystal grains with different orientations, as shown in Figure 3E. Under the action of uniaxial stress, grains with different orientations have different yield stresses. With increasing uniaxial stress, the number of yielded grains increases. When the number of yielded grains reaches a specific proportion (e.g., 90%), the corresponding uniaxial stress is treated as the yield strength of the polycrystalline material by using the Sachs model, as shown in Figure 3F. Furthermore, the Vickers hardness of polycrystalline materials can be calculated by using Tabor’s law (Tabor, 2000); that is, the Vickers hardness is approximately 2.74 times the yield strength of the polycrystalline material.

FIGURE 3

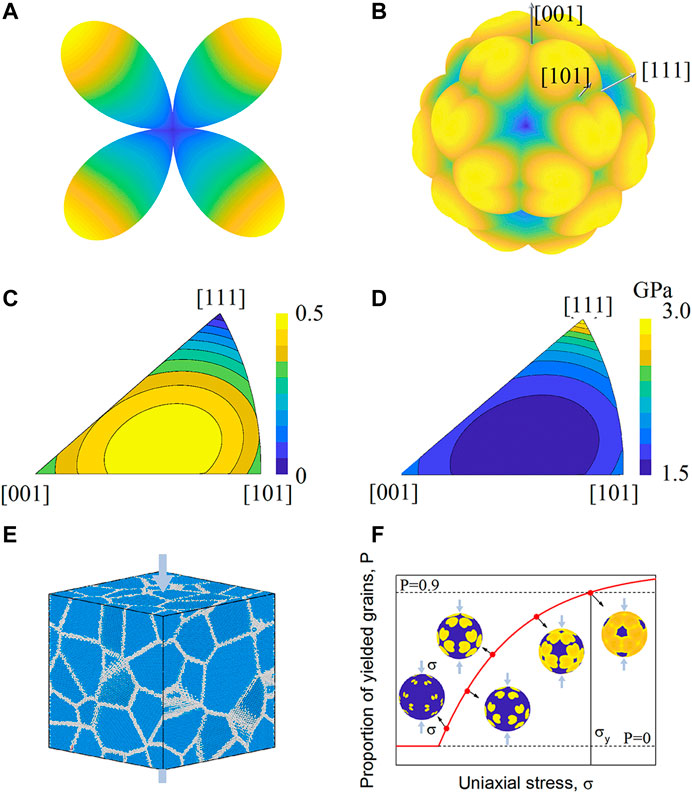
FIGURE 3. Polycrystalline material strength calculation from the CRSS. (A) Three-dimensional plot of the Schmid factor distribution for a single slip system under different external force orientations. (B) Outer envelope of Schmid factors for 12 slip systems under different external force orientations. The grooves coincide with the edges of the characteristic triangle, where two slip systems are equally favoured. (C) Schmid factor of grains with different orientations under uniaxial stress conditions. (D) Yield strength of grains with different orientations. (E) Polycrystalline structure. (F) Population of yielded grains as a function of uniaxial stress.

In Section 3.1, the CRSS of dislocation slip was calculated by using Eqs 1–9 (as shown in Supplementary Figures S5–S6). The physical meaning of all parameters used in Eqs 1–9 is clear, and no empirical parameters are used in these equations. Furthermore, the yield strength and Vickers hardness for a polycrystalline material are completely dependent on the CRSS and orientations of different grains. Therefore, our strength model for polycrystalline materials is totally non-empirical, and its application scope is not constrained by sources of empirical parameters.

4 Universality and reliability of the strength model

To verify the universality and reliability of our non-empirical strength model, the strengths (yield strength/hardness) of six multicrystals with different chemical bond types (i.e., diamond and cubic BN with covalent bonds, NaCl and MgO with ionic bonds, and Cu and Al with metallic bonds) are calculated. Here, the material properties and dislocation type parameters used in the strength model are obtained by the first-principles method, which is described in Supplementary Part I and II. The calculated material property parameters, generalized stacking fault energy (GSFE) surface, and dislocation types are listed and plotted in Supplementary Tables S1, S2; Supplementary Figures S1–S3, respectively.

By using the method described in Section 3, the strengths for the above-mentioned six multicrystals are calculated, and they are plotted in Figure 4 and Supplementary Figure S4. All calculated strengths agree well with the experimental observations spanning a certain range of temperatures and strain rates (Atkins and Tabor, 1967; Gridneva et al., 1972; Davis, 1993; Novikov et al., 1993; Weidner et al., 1994; Cáceres et al., 2002; Almasri and Voyiadjis, 2007; Voyiadjis and Almasri, 2008; Bhakhri et al., 2012; Li and Zinkle, 2012; Pradeep Kumar, 2018), which implies the universality and reliability of our non-empirical strength model. For covalent crystals and ionic crystals, their Vickers hardness continuously decreases with increasing temperature under a given dislocation density. There exist two distinct regimes with different temperature-softening rates, which is consistent with our previous result from the kink-pair model (Feng et al., 2021), and the reason is that the dominant dislocation type changes with increasing temperature. For metallic crystals Cu and Al, there also exist two distinct regimes with different temperature-softening rates, but this change is contributed by the change in the dislocation mode from the hard kink-pair mode to the string mode with increasing temperature. Recently, Lunev’s molecular dynamic simulation results for UO₂ (Lunev et al., 2018) indicated that its dislocation slipping mode changes with applied shear stress and temperature. This consistency shows the rationality of our model to some extent.

FIGURE 4

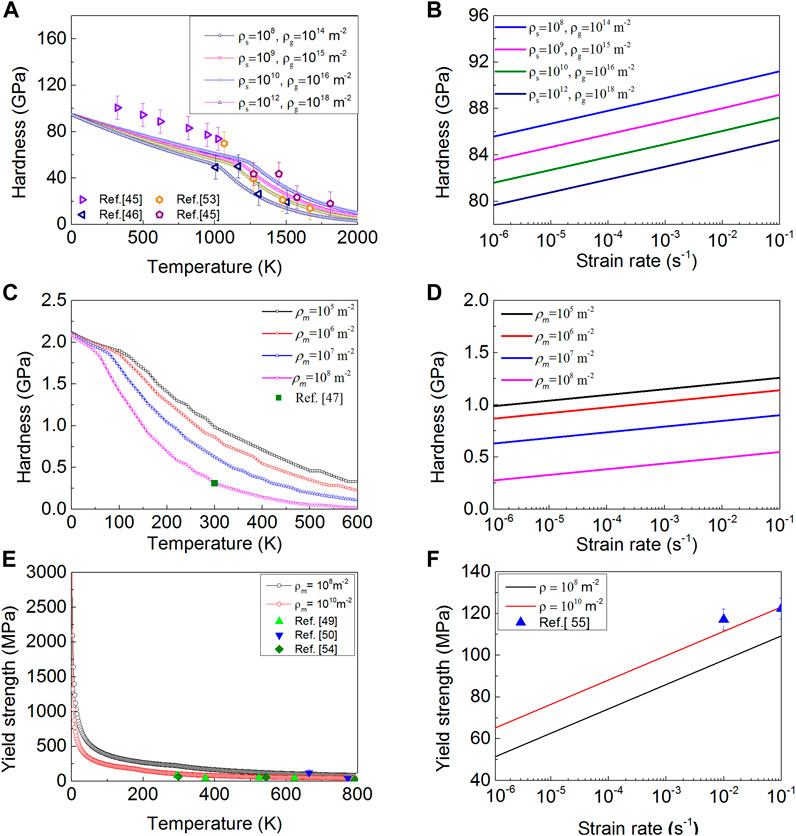
FIGURE 4. Universality and reliability of our strength model. (A,B) The hardness of diamond varies as a function of temperature and strain rate. (C,D) The hardness of NaCl varies as a function of temperature and strain rate. (E,F) The yield strength of Cu varies as a function of temperature and strain rate.

For all studied crystals, one can note that the strength increases with increasing strain rate (Figure 4 and Supplementary Figure S4), which indicates a strain rate hardening behaviour (Ayres and Wenner, 1979). In addition, their strength increases with decreasing dislocation density due to the work-hardening mechanism that can be ignored under low dislocation density.

In addition, the activated dislocation types under various temperatures are counted (Figure 5 and Supplementary Figures S7–S10). The types of activated slip systems of the six multicrystal materials agree with experimental observations (Riviere et al., 1981; Hull and Bacon, 2001; Jo et al., 2014; Xiao et al., 2018; Feng et al., 2021). This further confirms the universality of our non-empirical strength model, which can be adopted not only for covalent crystal research but also for ionic and metallic crystals. Moreover, its calculated results agree very well with the experimental values, showing its reliability.

FIGURE 5

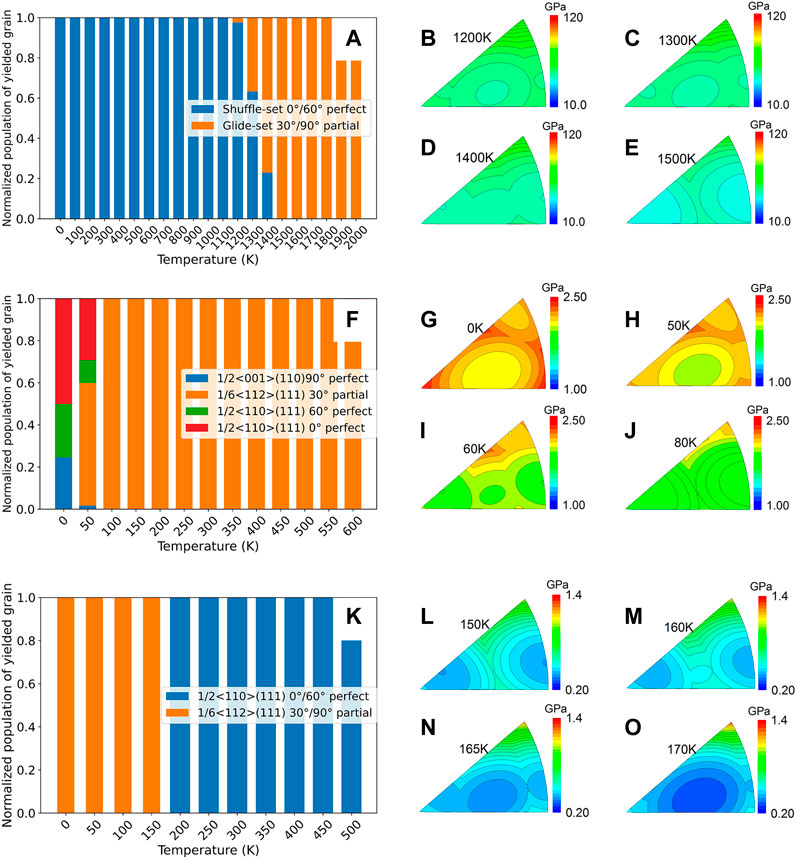
FIGURE 5. Types of slipping dislocation in crystals, as well as their influence on strength. (A) Count of slipping dislocations at various temperatures in diamond, and orientation-dependent hardness under different temperature scopes (B–E). (F,K) Count of slipping dislocations in NaCl and Cu, and orientation-dependent hardness (G)–(J), (L–O).

5 Reconciling chemical bonds and dislocations in the unified strength model

For a crystal material, its strength is directly related to its plastic deformation (Haines et al., 2001) and is related to its dislocation motion. From a microscopic point of view, dislocation motion is a chemical bond breaking and rebonding process; therefore, bond properties have an important effect on dislocation motion. For the strength model based on dislocation theory (Hirth, 1985), only dislocation defects are considered, and no bond properties are considered; therefore, this model can only be adopted for some metallic materials with less electron localization. For the hardness model based of valence bond theory (Gao et al., 2003; Šimůnek and Vackář, 2006; Li et al., 2008; Lyakhov and Oganov, 2011; Mazhnik and Oganov, 2019; Mazhnik and Oganov, 2020), only bond properties are considered, and no dislocation defects are considered; therefore, this model can only be adopted for some covalent materials with high electron localization. The effect factor on strength is not fully considered in the previous two types of strength models. Even though some empirical parameters are used in these models, their results consistent with experimental values. However, this leads to these models being empirical, and their applicability is limited to the materials for which they were obtained.

The motion of dislocations is controlled by the combination of mechanical and thermal action (as schematically shown in Figure 6A) (Caillard and Martin, 2003). Mechanical action leads to a change in crystal cell shape and further affects bond properties. This leads to the energy for chemical bond breaking being lower (Figure 6B). In our model, with increasing applied shear stress, the 2D displacement potential (including the P-N barrier and the migration barrier) monotonically decreases (in Figure 2B), which is the result of mechanical action. A previous study revealed that the barrier for chemical bond breaking is quantitatively correlated with the difference in the degree of electron localization (Zhang et al., 2017). To quantitatively discuss the effect of mechanical action on the 2D displacement potential, the electron localization function (ELF) (Becke and Edgecombe, 1990) for crystals under shear conditions is calculated, and the results are shown in Supplementary Figure S11. Under the same strain conditions, the difference in the ELF (∆ELF) for covalent or ionic crystals is usually larger than that for metallic crystals. This means that there are higher energy barriers for covalent or ionic crystal deformation than for metallic crystal deformation. The calculated ∆ELF between a perfect bond and dislocation core (Supplementary Figures S12, S13) also illustrates this point.

FIGURE 6

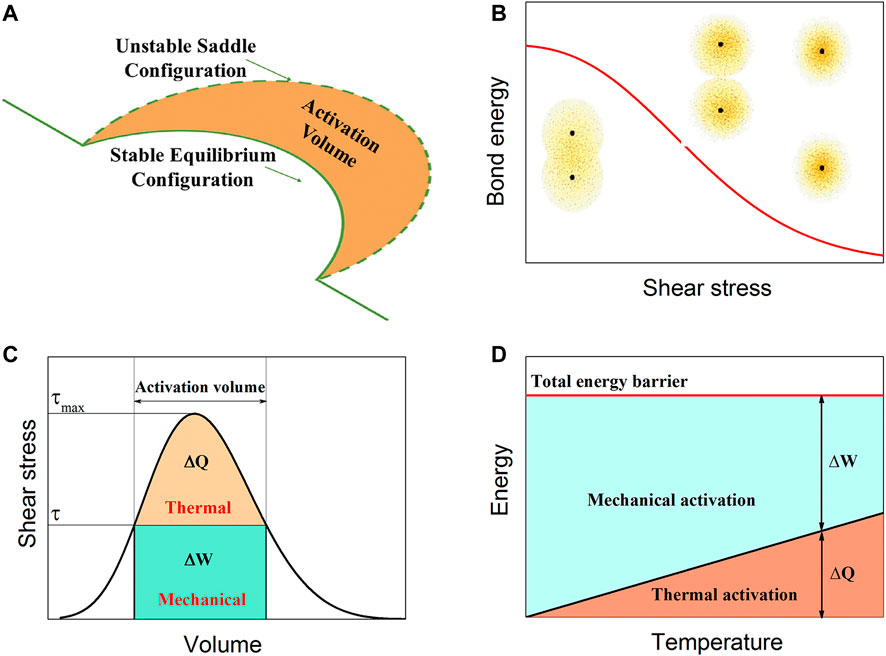
FIGURE 6. Reconciling of chemical bonds and dislocations. (A) Schematic illustrating that the motion of a dislocation is controlled by the combination of mechanical and thermal actions. (B) Mechanical action leads to the energy for chemical bond breaking being lower. (C) Relationship between the mechanical and thermal activations. (D) Temperature-dependent mechanical and thermal activations.

With increasing applied shear stress, the system energy increases through mechanical action, and the thermal activation barrier decreases (in Figure 6C). Furthermore, the total energy barrier can be overcome by both mechanical and thermal actions. As schematically shown in Figure 6D, because thermal activation energy ∆G is proportional to temperature, at given movable dislocation density and strain rate, ∆G linearly increases with temperature. Therefore, the thermal activation energy ∆G is permanent for any crystal. For covalent and ionic crystals with high 2D displacement potential, a high mechanical action is needed to overcome the barrier of dislocation slipping, which leads to a high strength for these crystals. For metallic crystals with low 2D displacement potential, thermal activation has an important contribution to overcoming the barrier of dislocation slipping, which leads to a low strength for these crystals and a high temperature-softening rate.

Another function of mechanical action is to decrease the energy of the dislocation system by the work done by the applied shear stress. Therefore, the larger the activation volume is, the larger the effect of mechanical action. For different dislocation slipping modes, the activation volume is different, and the slope of energy with respect to the applied shear stress can directly reflect the activation volume (in Figure 2B). For the string mode, line tension shortens the length of the dislocation line as much as possible, and the activation volume is larger than that of the hard kink-pair mode. The energy of the dislocation system is sensitive to the applied shear stress, and the slope of the energy with respect to the applied shear stress is larger than that for the hard kink-pair mode. This is a partial reason why the strength of a crystal with the string mode is usually lower than that with the hard kink-pair mode.

In our model, the bond property effect on dislocation motion has been considered by establishing a 2D displacement potential of dislocation slipping, and this is the root of the universality of our non-empirical strength model. The reconciling of chemical bonds and dislocations makes our strength model applicable to different chemically bonded crystals.

6 Conclusion

By establishing a 2D displacement potential of dislocation slipping, a unified non-empirical strength model is proposed. In this strength model, both chemical bond and dislocation effects on strength can be considered, and it can be used to predict the strength of different chemically bonded crystals. For covalent crystals and ionic crystals that have large electron localization, the dislocation prefers to slip in the kink-pair mode, exhibiting high CRSS and high strength. In contrast, metallic crystals with low electron localization prefer the string mode since the 2D displacement potential can be easily overcome by thermal activation; thus, metallic materials usually have low CRSS and low strength. All parameters used in our model are meaningful and non-empirical, and its application scope is unlimited; hence, our model is helpful for revealing the physical mechanism of strength and provides a direct tool for the design of new structural materials.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

BW conceived the project. XF, GS, and SZ performed the calculations. BW, XF, and GS analyzed the data and co-wrote the paper. All authors discussed the results and commented on the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos 51925105 and 51771165) and the National Key R&D Program of China (YS2018YFA070119).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.1049956/full#supplementary-material

References

Almasri, A. H., and Voyiadjis, G. Z. (2007). Effect of strain rate on the dynamic hardness in metals. J. Eng. Mat. Technol. 129, 505. doi:10.1115/1.2744430

CrossRef Full Text | Google Scholar

Atkins, A., and Tabor, D. (1967). Mutual indentation hardness of single-crystal magnesium oxide at high temperatures. J. Am. Ceram. Soc. 50, 195–198. doi:10.1111/j.1151-2916.1967.tb15079.x

CrossRef Full Text | Google Scholar

Ayres, R. A., and Wenner, M. L. (1979). Strain and strain-rate hardening effects in punch stretching of 5182-0 aluminum at elevated temperatures. Metall. Trans. A 10, 41–46. doi:10.1007/bf02686404

CrossRef Full Text | Google Scholar

Barnett, M. R., Keshavarz, Z., and Ma, X. (2006). A semianalytical sachs model for the flow stress of a magnesium alloy. Metall. Mat. Trans. A 37A, 2283–2293. doi:10.1007/bf02586147

CrossRef Full Text | Google Scholar

Becke, A. D., and Edgecombe, K. E. (1990). A simple measure of electron localization in atomic and molecular systems. J. Phys. Chem. 92, 5397–5403. doi:10.1063/1.458517

CrossRef Full Text | Google Scholar

Bhakhri, V., Wang, J., Ur-rehman, N., Ciurea, C., Giuliani, F., and Vandeperre, L. J. (2012). Instrumented nanoindentation investigation into the mechanical behavior of ceramics at moderately elevated temperatures. J. Mater. Res. 27, 65–75. doi:10.1557/jmr.2011.246

CrossRef Full Text | Google Scholar

Cáceres, D., Vergara, I., González, R., and Chen, Y. (2002). Hardness and elastic modulus from nanoindentations in nominally pure and doped MgO single crystals. Philos. Mag. A 82, 1159–1171. doi:10.1080/01418610208240022

CrossRef Full Text | Google Scholar

Caillard, D., and Martin, J.-L. (2003). Thermally activated mechanisms in crystal plasticity. Netherland: Elsevier.

Google Scholar

Caillard, D. (2007). Dislocations and mechanical properties. New Jersey: John Wiley and Sons.

Google Scholar

Chaudhri, M. M., and Lim, Y. Y. (2005). Harder than diamond? Just fiction. Nat. Mat. 4, 4. doi:10.1038/nmat1288

CrossRef Full Text | Google Scholar

Conrad, H. (1964). Thermally activated deformation of metals. Jom 16, 582–588. doi:10.1007/bf03378292

CrossRef Full Text | Google Scholar

Davis, J. R. (1993). Aluminum and aluminum alloys. Ohio: ASM international, 152–156.

Google Scholar

Eshelby, J. D. (1962). The interaction of kinks and elastic waves. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 266, 222–246.

Google Scholar

Feng, X., Xiao, J., Wen, B., Zhao, J., Xu, B., Wang, Y., et al. (2021). Temperature-dependent hardness of zinc-blende structured covalent materials. Sci. China Mat. 16, 2280–2288. doi:10.1007/s40843-020-1620-4

CrossRef Full Text | Google Scholar

Frenkel, J. (1926). Zur theorie der elastizitätsgrenze und der festigkeit kristallinischer körper. Z. Phys. 37, 572–609. doi:10.1007/bf01397292

CrossRef Full Text | Google Scholar

Freudenthal, and A., M. (1959). Internal stresses and fatigue in metals. Phys. Today 12, 16–19. doi:10.1063/1.3060669

CrossRef Full Text | Google Scholar

Gao, F., He, J., Wu, E., Liu, S., Yu, D., Li, D., et al. (2003). Hardness of covalent crystals. Phys. Rev. Lett. 91, 015502. doi:10.1103/physrevlett.91.015502

PubMed Abstract | CrossRef Full Text | Google Scholar

George, A., and Rabier, J. (1987). Dislocations and plasticity in semiconductors. I—dislocation structures and dynamics. Rev. Phys. Appl. 22, 941–966. doi:10.1051/rphysap:01987002209094100

CrossRef Full Text | Google Scholar

Gridneva, I., Milman, Y. V., and Trefilov, V. (1972). Phase transition in diamond-structure crystals during hardness measurements. Phys. status solidi (a) 14, 177–182. doi:10.1002/pssa.2210140121

CrossRef Full Text | Google Scholar

Haasen, P. (1958). Plastic deformation of nickel single crystals at low temperatures. Philos. Mag. 3, 384–418. doi:10.1080/14786435808236826

CrossRef Full Text | Google Scholar

Haines, J., Leger, J., and Bocquillon, G. (2001). Synthesis and design of superhard materials. Annu. Rev. Mat. Res. 31, 1–23. doi:10.1146/annurev.matsci.31.1.1

CrossRef Full Text | Google Scholar

Hirth, J., and Nix, W. (1969). An analysis of the thermodynamics of dislocation glide. Phys. Status Solidi B 35, 177–188. doi:10.1002/pssb.19690350116

CrossRef Full Text | Google Scholar

Hirth, J. P., Lothe, J., and Anderson, P. M. (1983a). Theory of dislocations. 2nd ed.50. Florida: Wiley, 476.

Google Scholar

Hirth, J. P., Lothe, J., and Anderson, P. M. (1983b). Theory of dislocations. J. Appl. Mech., 476.50

Google Scholar

Hirth, J. (1985). A brief history of dislocation theory. Metall. Mat. Trans. A 16, 2085–2090. doi:10.1007/bf02670413

CrossRef Full Text | Google Scholar

Huang, Q., Yu, D., Xu, B., Ma, Y., Wang, Y., Wen, B., et al. (2014). Nanotwinned diamond with unprecedented hardness and stability. Nature 510, 250–253. doi:10.1038/nature13381

PubMed Abstract | CrossRef Full Text | Google Scholar

Hull, D., and Bacon, D. J. (2001). Introduction to dislocations. Oxford: Butterworth-Heinemann.

Google Scholar

Hutchinson, J. (1970). Elastic-plastic behaviour of polycrystalline metals and composites. Proc. R. Soc. Lond. Ser. A 319, 247–272.

Google Scholar

Jo, M., Koo, Y. M., Lee, B. J., Johansson, B., Vitos, L., and Kwon, S. K. (2014). Theory for plasticity of face-centered cubic metals. P Natl. Acad. Sci. U. S. A. 111, 6560–6565. doi:10.1073/pnas.1400786111

PubMed Abstract | CrossRef Full Text | Google Scholar

Laidler, K. J. (1984). The development of the Arrhenius equation. J. Chem. Educ. 61, 494. doi:10.1021/ed061p494

CrossRef Full Text | Google Scholar

Li, M., and Zinkle, S. (2012). 4.20-physical and mechanical properties of copper and copper alloys. Comprehensive nuclear materials 4. Netherland: Elsevier, 667–690.

CrossRef Full Text | Google Scholar

Li, K., Wang, X., Zhang, F., and Xue, D. (2008). Electronegativity identification of novel superhard materials. Phys. Rev. Lett. 100, 235504. doi:10.1103/physrevlett.100.235504

PubMed Abstract | CrossRef Full Text | Google Scholar

Long, F., Xu, F., and Daymond, M. R. (2013). Temperature dependence of the activity of deformation modes in an HCP zirconium alloy. Metall. Mat. Trans. A 44, 4183–4193. doi:10.1007/s11661-013-1758-z

CrossRef Full Text | Google Scholar

Lunev, A., Starikov, S., Aliev, T., and Tseplyaev, V. (2018). Understanding thermally-activated glide of 1/2⟨110⟩{110} screw dislocations in UO2 – a molecular dynamics analysis. Int. J. Plast. 110, 294–305. doi:10.1016/j.ijplas.2018.07.003

CrossRef Full Text | Google Scholar

Lyakhov, A. O., and Oganov, A. R. (2011). Evolutionary search for superhard materials: Methodology and applications to forms of carbon and TiO2. Phys. Rev. B 84, 092103. doi:10.1103/PhysRevB.84.092103

CrossRef Full Text | Google Scholar

Mazhnik, E., and Oganov, A. R. (2019). A model of hardness and fracture toughness of solids. J. Appl. Phys. 126, 125109. doi:10.1063/1.5113622

CrossRef Full Text | Google Scholar

Mazhnik, E., and Oganov, A. R. (2020). Application of machine learning methods for predicting new superhard materials. J. Appl. Phys. 128, 075102. doi:10.1063/5.0012055

CrossRef Full Text | Google Scholar

Nabarro, F. (1947). Dislocations in a simple cubic lattice. Proc. Phys. Soc. 59, 256–272. doi:10.1088/0959-5309/59/2/309

CrossRef Full Text | Google Scholar

Nie, A., Bu, Y., Huang, J., Shao, Y., Zhang, Y., Hu, W., et al. (2020). Direct observation of room-temperature dislocation plasticity in diamond. Matter 2, 1222–1232. doi:10.1016/j.matt.2020.02.011

CrossRef Full Text | Google Scholar

Novikov, N. V., Sirota, Y. V., Mal'Nev, V. I., and Petrusha, I. A. (1993). Mechanical properties of diamond and cubic BN at different temperatures and deformation rates Diamond Relat. Mater 2, 1253–1256.

CrossRef Full Text | Google Scholar

Ogata, S., Li, J., and Yip, S. (2002). Ideal pure shear strength of aluminum and copper. Science 298, 807–811. doi:10.1126/science.1076652

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, S. H., Legros, M., Kiener, D., and Dehm, G. (2009). In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mat. 8, 95–100. doi:10.1038/nmat2370

PubMed Abstract | CrossRef Full Text | Google Scholar

Orowan, E. (1934). Plasticity of crystals. Z. Phys. 89, 634–659. doi:10.1007/bf01341480

CrossRef Full Text | Google Scholar

Peierls, R. (1940). The size of a dislocation. Proc. Phys. Soc. 52, 34–37. doi:10.1088/0959-5309/52/1/305

CrossRef Full Text | Google Scholar

Pradeep Kumar, J. (2018). Effect of temperature distribution in ultrasonically welded joints of copper wire and sheet used for electrical contacts. Materials 11, 1010. doi:10.3390/ma11061010

PubMed Abstract | CrossRef Full Text | Google Scholar

Riviere, A., Amirault, J., and Woirgard, J. (1981). High temperature internal friction and dislocation motion in poly and single crystals of fcc metals. J. Phys. Colloq. 42, C5-439–C5-444. doi:10.1051/jphyscol:1981565

CrossRef Full Text | Google Scholar

Schoeck, G. (1965). The activation energy of dislocation movement. Phys. Status Solidi B 8, 499–507. doi:10.1002/pssb.19650080209

CrossRef Full Text | Google Scholar

Seeger, A., and Wüthrich, C. (1976). Dislocation relaxation processes in body-centred cubic metals. Il Nuovo Cimento B 33, 38–75. doi:10.1007/bf02722472

CrossRef Full Text | Google Scholar

Seeger, A., Donth, H., and Pfaff, F. (1957). The mechanism of low temperature mechanical relaxation in deformed crystals. Discuss. Faraday Soc. 23, 19–30. doi:10.1039/df9572300019

CrossRef Full Text | Google Scholar

Seeger, A. (1955). CXXXII. The generation of lattice defects by moving dislocations, and its application to the temperature dependence of the flow-stress of F.C.C. crystals. Philos. Mag. 46, 1194–1217. doi:10.1080/14786441108520632

CrossRef Full Text | Google Scholar

Šimůnek, A., and Vackář, J. (2006). Hardness of covalent and ionic crystals: First-principle calculations. Phys. Rev. Lett. 96, 085501. doi:10.1103/physrevlett.96.085501

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, G., Feng, X., Wu, X., Zhang, S., and Wen, B. (2022). Is hardness constant in covalent materials? J. Mat. Sci. Technol. 114, 215–221. doi:10.1016/j.jmst.2021.10.032

CrossRef Full Text | Google Scholar

Tabor, D. (2000). The hardness of metals, 553. Oxford: Oxford University Press.

Google Scholar

Taylor, G. I. (1938). Plastic strain in metals. J. Inst. Met. 62, 307–324.

Google Scholar

Voyiadjis, G. Z., and Almasri, A. H. (2008). A physically based constitutive model for fcc metals with applications to dynamic hardness. Mech. Mater. 40, 549–563. doi:10.1016/j.mechmat.2007.11.008

CrossRef Full Text | Google Scholar

Weidner, D. J., Wang, Y., and Vaughan, M. T. (1994). Strength of diamond. Science 266, 419–422. doi:10.1126/science.266.5184.419

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, B., Xu, B., Wang, Y., Gao, G., Zhou, X. F., Zhao, Z., et al. (2019). Continuous strengthening in nanotwinned diamond. npj Comput. Mater 5, 117. doi:10.1038/s41524-019-0256-2

CrossRef Full Text | Google Scholar

Williams, J. C., and Starke, E. A. (2003). Progress in structural materials for aerospace systems11The golden jubilee issue—selected topics in materials science and engineering: Past, present and future, edited by S. Suresh. Acta Mater 51, 5775–5799. doi:10.1016/j.actamat.2003.08.023

CrossRef Full Text | Google Scholar

Xiao, J., Yang, H., Wu, X., Younus, F., Tian, Y., Wen, B., et al. (2018). Dislocation behaviors in nanotwinned diamond. Sci. Adv. 4, eaat8195. doi:10.1126/sciadv.aat8195

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiao, J., Yang, H., Liu, H., Younus, F., Xu, B., Zhang, X., et al. (2019). Strengthening-softening transition in yield strength of nanotwinned Cu. Scr. Mater. 162, 372–376. doi:10.1016/j.scriptamat.2018.11.049

CrossRef Full Text | Google Scholar

Xiao, J., Wen, B., Xu, B., Zhang, X., Wang, Y., and Tian, Y. (2020). Intersectional nanotwinned diamond-the hardest polycrystalline diamond by design. npj Comput. Mater 6, 119–127. doi:10.1038/s41524-020-00387-3

CrossRef Full Text | Google Scholar

Zhai, J.-H., Hirel, P., and Carrez, P. (2020). Atomic-scale properties of jogs along 1/2⟨110⟩{1¯10} edge dislocations in MgO. Scr. Mater. 181, 66–69. doi:10.1016/j.scriptamat.2020.02.013

CrossRef Full Text | Google Scholar

Zhang, Y. H., Zhuang, Y., Hu, A., Kai, J. J., and Liu, C. T. (2017). The origin of negative stacking fault energies and nano-twin formation in face-centered cubic high entropy alloys. Scr. Mat. 130, 96–99. doi:10.1016/j.scriptamat.2016.11.014

CrossRef Full Text | Google Scholar