A low-power magnetorheological fluid clutch utilizing electropermanent magnet arrays

In this work, we develop a compact, low-power and partially 3D-printed magnetorheological fluid clutch that operates by variably and reversibly altering the shear stress of the fluid through the local activation of an array of electropermanent magnets (EPMs). By toggling the magnetization of each EPM independently on the order of a few milliseconds, we allow for rapid response times and variable torque transmission without further power input. Selectively polarizing the EPMs for different lengths of time results in repeatable and variable magnetic flux, in turn enabling further control precision. We present the design, modeling, and measured performance of this clutch with various control strategies, and demonstrate its utility as a low-power alternative to more traditional clutch designs.

1 Introduction

In robotics, there is widespread interest in expanding physical cooperation between people and robots, a field commonly referred to as physical human robot interaction (pHRI). This interest extends to diverse domains where people may physically wear the robot (e.g., exoskeletons, rehabilitative devices) or work with/around the robot in collaborative spaces (e.g., warehouses, shipping facilities, health care settings). For applications including pHRI, it is critical that the robot’s design requirements consider safety of the human user. One popular approach for enabling safe and effective pHRI is to add compliance to the robot’s actuators. Soft robotics, series elastic actuators, and variable stiffness actuators Wolf et al. (2016) are some of the methods that can be used to provide compliant actuation for pHRI.

Common implementations of soft robotics and compliant mechanisms utilize deformable materials, such as silicone or other elastomers, in their designs. Flexibility and elasticity improve overall compliance, but constructing robots from these materials often limits the overall strength and speed of a robot. Another method to implement pHRI is with smart materials that respond to specific stimuli to variably change their physical properties. This controllable property enables many control strategies, such as variable stiffness joints in actuated linkages, variable grip strength Bira et al. (2022), and conformal grasping.

In this paper, we focus on the use of magnetorheological fluid (MRF), a smart material that variably alters its shear behaviour in the presence of an externally applied magnetic field (see Figure 1A). A MRF contains small ferromagnetic particles, usually iron, that create the magnetic response. Without an external field, the MRF is a liquid and flows with little resistance; with an applied field, the MRF behaves like a Bingham plastic Bingham (1922), flowing with greater resistance after an initial yield stress defined by the magnetic field intensity. Since MRF requires magnetic fields of magnitudes considered safe for human exposure and demonstrates rapid response times, it is an appealing candidate for pHRI applications Shafer and Kermani (2009).

FIGURE 1

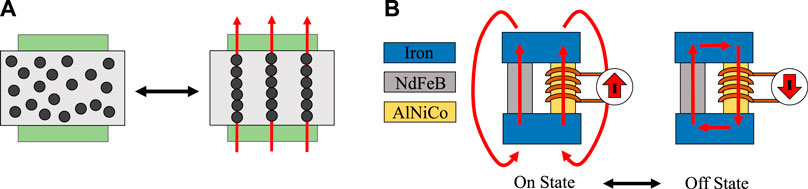
FIGURE 1. (A) The principle of MRF, where an applied magnetic field causes the ferromagnetic particles in suspension to align and form polymer-like chains, affecting the fluid’s shear behavior. (B) The principle of an EPM, where two states can be toggled by the direction of the magnetization of the AlNiCo magnet.

MRF reacts to an applied magnetic field rapidly and reversibly, and since the intensity of magnetic fields can be selectively controlled by electromagnets, this fluid has been deployed in the development of MRF-based actuators, brakes, clutches, dampers, and valves Phu and Choi (2019). A suction-based flexible gripper was developed using MRF and a controllable magnetic field, achieving improved grip strength while the magnetic field is active Koivikko et al. (2021). Another study designed a laparoscopic actuator with MRF and electromagnets to control the joint stiffness between each link and alter its curvature Kitano et al. (2020). Another recent article developed a hybrid MRF and shape-memory alloy (SMA) linkage Yang et al. (2022). The SMAs are deployed along the length of the linkage, while each joint of the linkage consisted of a MRF-filled bearing which responds to an electromagnet coil adjacent to it to increase local joint stiffness.

There is also substantial prior work on the use of MRF-based clutch mechanisms for transmitting torque between robotic linkages. One paper characterized an MRF clutch and modeled how the input magnetic field maps to an output torque, highlighting how MRF clutches can control the amount of transmitted torque through the intensity of the applied field Yadmellat and Kermani (2013). Other researchers developed a small-scale MRF clutch and compared it to that of a traditional DC motor for potential use in haptic feedback systems Najmaei et al. (2014). Another publication developed and characterized a five degree-of-freedom robotic arm with MRF clutches in each joint; electromagnets in conjunction with a permanent magnet were used to control a specific range of magnetic field to variably control the joint stiffness at each joint Pisetskiy and Kermani (2021). A recent article developed an upper leg prosthesis, combining a MRF clutch with an MRF brake to provide improved energy efficiency compared to a motor-reducer for walking de Andrade et al. (2021). Later work by the same authors focused on the backdrivability of the MRF clutch in a leg exoskeleton, demonstrating its useful properties compared to traditional designs Andrade et al. (2022). Some desirable properties for all clutches are: small physical size, reduced complexity where possible, low power consumption, and high accuracy in the desired torque being transmitted to allow for reliable and predictable behavior. While an industrial manufacturing robot is less constrained by size and power concerns than a small, mobile robot, these design considerations apply in most circumstances.

One significant drawback of MRF devices utilizing conventional electromagnets is substantial power consumption—continuous use of relatively large currents is required to maintain the magnetic fields needed to keep the fluid in an active state. This constraint limits the potential for untethered, remote operation, and suggests that innovations in how the magnetic field is created and controlled can improve the utility of MRF devices. Electropermanent magnets (EPMs) are an alternative mechanism for magnetic field generation. EPMs are assemblies of both an electromagnet with a magnetic core (usually AlNiCo) and a hard permanent magnet nearby (usually NdFeB). These two elements are connected with soft magnetic material such as ferromagnetic iron or steel, and this connection enables the shaping of magnetic flux in the magnetic circuit. The electromagnet can be supplied with a pulse of current in a positive or negative direction to magnetize the AlNiCo in either direction. The resulting assembly of magnets and iron components has two states, on or off, which represent the net magnetic flux present in the desired region when the magnetic circuit is at rest after polarization of the AlNiCo (see Figure 1B). When no current is being applied and the EPM is a rest, it retains its magnetization state and has a constant magnetic flux. This control method is possible due to the coercivity of AlNiCo being much smaller than that of NdFeB (H_{c_AlNiCo} ≪ H_{c_NdFeB}). Toggling the magnetization of the AlNiCo still requires power, but it can be done on the order of milliseconds and then holding in a latched state, as opposed to needing continuous current delivery like a traditional iron-core electromagnet. This lends itself towards untethered operation, as the overall power consumption is reduced compared to always-on devices.

Prior work has demonstrated that EPMs are viable control tools for MRF-related actuation strategies, such as the work presented by (Leps et al., 2020). This work developed a MRF valve for low-power, distributed control of flowing MRF in soft robotic systems. Similarly, recent research with MRF valves demonstrated control over the flow of MRF through a series of soft robotic actuators using EPMs, generating bending in the actuators by building pressure behind an EPM-based valve McDonald et al. (2022). These works highlight the importance of EPMs as latching, low-power devices, and their capacity to be used with MRF for controlling actuators. Another research group developed a soft robotic gripper which uses electropermanent magnets as the control input, combined with magnetic elastomers which deform in the presence of a magnetic field to create actuation Zhang et al. (2021). Other researchers developed a MRF clutch that uses a single permanent magnet in conjunction with an electromagnet, to modulate the overall field within the clutch and the resulting transmitted torque Moghani and Kermani (2019). This is not an EPM, since it does not represent latching on or off-states, but instead requires active input to raise or lower the effective output of the permanent magnet. This strategy is utilized in the robotic arm described in the previous paragraph Pisetskiy and Kermani (2021).

With these recent developments in mind, in this paper we propose and demonstrate an MRF-filled clutch surrounded by an EPM array (abbreviated here as MEC). Our primary contribution is the use of this EPM array as a low-power density method for variably adjusting output torque in a repeatable and programmable manner with a compact form factor. We start by fabricating the EPM array from available materials and size constraints, then characterize the typical magnetic field generation at the manufactured scale. Next, we simulate the performance of the EPMs in Ansys Maxwell and compare it to the observed behavior. We then develop an analytical model of torque transmission to examine the contribution of physical parameters on MEC performance, and we use this model alongside further simulation to inform our physical design and construction of the MEC. Lastly, we assemble and characterize the MEC prototype in a bench-top study, finishing with a discussion of its performance, control methods for torque transmission, and low-power requirements. Our prototype MEC and EPM designs are visible in Figure 2.

FIGURE 2

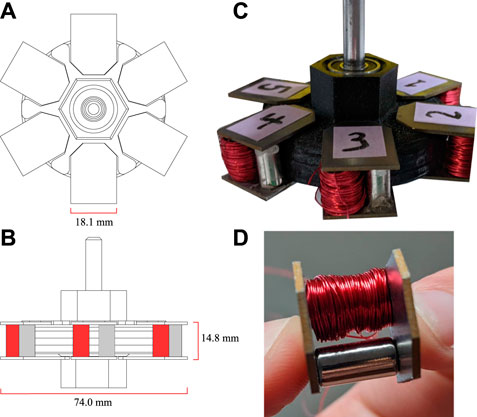
FIGURE 2. An assembled MRF Clutch with six EPMs. (A) Top-view and (B) Side-view. The coils are not depicted in the 3D rendering, but their locations are highlighted in red, while the NdFeB magnet is shown in gray. (C) A photo of the final MEC, shown from the isometric view (D) A single EPM, viewed head-on to see the two magnets and coil.

2 Methodology

Here we describe the process for developing and fabricating the MEC. We begin by creating several EPMs, testing their performance, and comparing this to simulations performed in Ansys Maxwell. Next we developed an analytical model for the potential MEC device to describe the transmitted torque. We also examined the field intensity within a 3D model in Ansys Maxwell using these same parameters. From these models, we chose physical design parameters for the MEC, and then created a prototype. We placed the prototype into a experimental setup to measure its performance, allowing us to compare our model with the real-world behavior.

2.1 EPM fabrication

First, we wanted to validate that the scale and design of an EPM array would perform within the boundaries of what is required to generate the MR effect in a fluid-based clutch. Physical parameters for a modular EPM were selected based on available materials, size, and power considerations. Each EPM consists of a NdFeB grade 42 hard permanent magnet (12.7 mm length and 6.35 mm diameter), an AlNiCo grade 5 magnet of the same dimensions, two thin steel rectangular plates (1008 cold rolled steel, 1.07 mm thickness) cut into a rectangular shape with the corners removed to accommodate closer positioning (see Figure 2A), and a copper magnet wire (AWG 28, 0.32 mm diameter) coil around the AlNiCo five magnet (120 windings each, evenly spaced along the length of the coil, approximately 3.3 m in length). Each magnet was positioned and glued in place with cyanoacrylate glue to the plates (see Figure 2D). After fabricating all six EPMs, each was tested for its polarizing and depolarizing ability, using a teslameter with resolution up to 10 μT (TES11A model, Qingdao Tlead International Co., Qingdao China) to validate the amount of flux with more precision. The initially observed values for each EPM were between 45 and 55 mT in magnetic flux density in the centerline between the plates when on and approximately 0–5 mT when off. Each EPM was polarized by applying a current first in the positive direction to polarize the EPM, and later in the opposite direction to depolarize it. The EPMs were then wired into three motor controllers with high current ratings and H-bridge functionality (15A Dual Motor Drive Module, NYBG Electronics, Wuhan, China), each with the capacity to supply current in either direction with the control signal provided by an Arduino Mega running a custom program. Each EPM was polarized with increasing lengths of polarization time (on the order of 0–3,000 μs). While this more precise characterization revealed differences between each EPM regarding the maximum amount of flux produced at the center point between each of the plates, the general variation was within standard deviation and therefore acceptable for the prototype design. The MRF will be flowing between the plates, so this first pass was sufficient for estimating the general capabilities of the EPMs. These variations are directly attributable to the irregularities introduced from hand-assembling each EPM, cutting the steel sheets and magnets to size, and hand-winding the coils. Furthermore, misalignments of the teslameter probe used when measuring the generated B field could account for discrepancies. The results of this characterization can be seen in Section 3; Figure 9.

2.2 Ansys EPM simulation

We also modeled the EPM array in Ansys Maxwell Magnetostatic Simulation software to predict the magnetic field formation characteristics. The cylinder representing the AlNiCo five magnet was given properties corresponding to a magnetization in the positive or negative z-direction for a given simulation and at values appropriate for that grade of magnet (magnitude of magnetization provided by the existing material libraries in Ansys). The N42 magnet was given a constant magnetization of a set value using the built-in magnetic properties library for Maxwell. The results of this simulation are shown in Figure 3, and demonstrate that each EPM can be expected to generate up to ≈55 mT in ideal conditions when in the on state. It also demonstrated that the EPMs produce ≈0 mT between the plates when they are in the off state. These validation steps show good agreement between the observed behavior for a single EPM (maximum polarization of 49.264 ± 2.01 mT) and the theoretical ideal behavior (55 mT). These simulation results provide a baseline for further modeling and construction of the MRF clutch, as described in the next section.

FIGURE 3

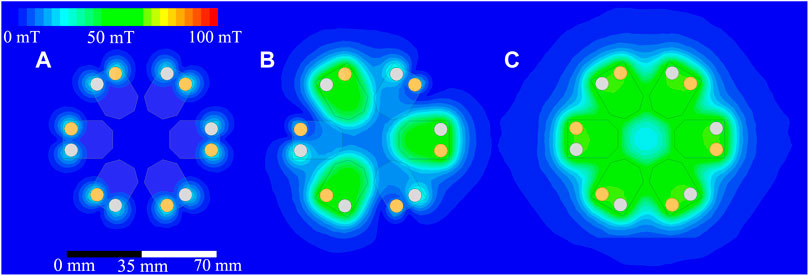
FIGURE 3. Depicted are three simulations completed in Ansys Maxwell of the EPM array from the top-down perspective. The AlNiCo magnet is orange, while the NdFeB magnet is white. (A) All EPMs are in the OFF configuration. (B) Three of the EPMs are ON, while the other three remain OFF. (C) All six EPMs are active, demonstrating fields of approximately 55 mT in the regions of interest, at the midpoint between the plates of the EPM and where the MRF will reside.

2.3 Analytical modeling

To predict the torque transmission behavior of the clutch design, the MR effect was modeled in MATLAB (Mathworks, Natick, MA, United States) for various physical parameters of the MEC. Unlike with electric fields, magnetic fields are generally non-linear unless shaped by magnetic circuits. Since our EPMs, along with the steel fins of the MEC, present a region of high permeability for the magnetic flux, we approximated the magnetic field within the MEC as a constant scalar value for modeling simplicity. The majority of the volume of the MRF will be between the parallel plates of the EPM and the internal fins of the MEC, where the magnetic field is primarily linear (directed between the plates of the EPM). We utilized the Bingham model Bingham (1922) for a viscoplastic fluid with a finite yield stress to represent the MRF’s yield behavior as well as the characterization data from the manufacturer of the MRF fluid (LORD Corp, Cary, NC, United States). The first step towards modeling the torque is to approximate the magnetic field intensity within the active region of the MRF clutch design, denoted by a single value for H (units of kA/m). While the field does vary within the total active region, it does so only a few mT between the plates as shown in Figure 3C). This initial approximation is accomplished from the Ansys Maxwell simulations of our EPM characterization to estimate a typical magnetic flux density value provided by the EPMs, in this case, ≈ 50 mT. From the relationship between magnetic flux density (B) and magnetic field strength (H) in the B-H magnetization curves from the MRF materials datasheet, we estimated a H-value of ≈5 kA/m. This approximation is for the magnetic field strength inside an EPM filled with MRF.

Having established a given static H value, we now approximate the effect of the magnetized MRF on the rotating steel fins of the MEC. The torque transferred from the input shaft of the motor is the summation of shear stresses developed between multiple stacked discs (See Figure 4). The active region (shown in orange) is where the analysis will be focusing on, since the other regions are much smaller and at the edges of the active region, experiencing less magnetic flux density. The Bingham model for a viscoplastic fluid with a finite yield stress is shown in Eq. 1, where $\dot{\gamma }$ is the shear rate (sec⁻¹), τ_y is the yield stress (Pa), and μ_p (Pa⋅ s) is the plastic viscosity. From the datasheet for the MRF, μ_p is estimated to be 0.28.

$\begin{array}{c}\dot{\gamma }=0\text{if\hspace{0.17em}}\tau <{\tau }_y\hfill \\ \tau ={\tau }_y+{\mu }_p\dot{\gamma }\text{if\hspace{0.17em}}\tau >{\tau }_y\hfill \end{array}(1)$

FIGURE 4

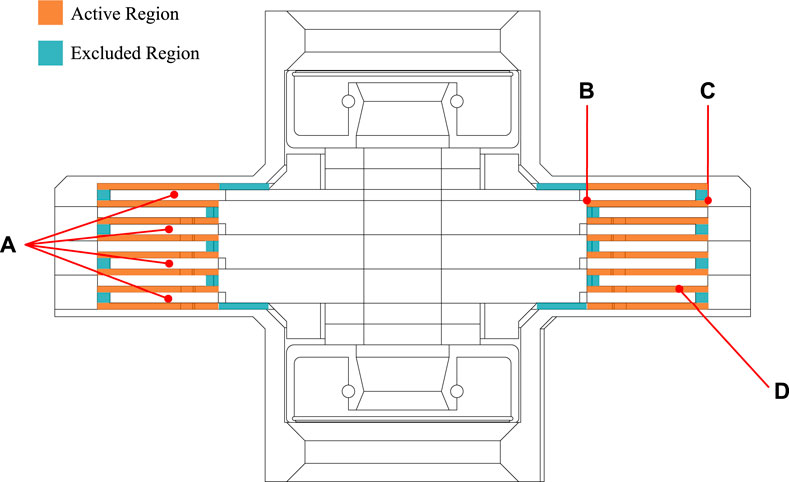
FIGURE 4. The cross-section of the active region of the MRF clutch design. The horizontal regions highlighted in orange are described with the total torque from Eq. 8, while the regions in blue are excluded from the model. The MRF fills the empty space (both blue and orange) inside the MEC, between each of the interdigitated fins inside all available internal space not taken up by the fins or the inner and outer walls of the device. (A) The number of fins (here, there are four), (B) The inner radius (C) The outer radius, and (D) the gap size.

The calculation for τ_y is fit to the characterization data for the MRF from LORD Corp as a third order polynomial:

${\tau }_y\left\{H\right\}=-0.0000011503H^3-0.00098714H^2+0.52701H+1.43(2)$

From our earlier choice of 5 kA/m for H, this approximates the τ_y to be 20.9 kPa. The gap between the parallel steel fins is small (0.5 mm), so the flow can be approximated as a Couette flow during operation at a given rotational velocity $\dot{\theta }$. The significance of the Couette flow solution is that the viscous stress tensor is constant everywhere in the flow field Davidson and Krebs (2018), Bingham (1922). The shear rate along the surface of one of the fins of the MEC is a function of the radius along the width of the fin, its rotational velocity, and the gap (g, shown in Figure 4D) between fins:

$\dot{\gamma }=\frac{r\dot{\theta }}{g}(3)$

The differential torque dT generated by an element dA is:

$dT=r\left(\tau \left\{H\right\}dA\right)=r\left(\tau \left\{H\right\}2\pi rdr\right)(4)$

Inserting the Bingham model from Eqs 1–3 (which assumes we operate in the post-yield region) for shear stress yields the following equation for the differential torque:

$dT=2\pi \left({\tau }_y\left\{H\right\}+{\mu }_p\left(\frac{r\dot{\theta }}{g}\right)\right)r^{2}dr(5)$

The total torque from the surface of one fin is found by integrating the differential torque over the boundaries of the fin (between the inner and outer radius of the fin, shown in Figure 4B and 4C):

$T_{\mathit{fin}}=2\pi {\tau }_y\left\{H\right\}{\int }_{r_i}^{r_o}{r}^{2}dr+\frac{2\pi {\mu }_p\dot{\theta }}{g}{\int }_{r_i}^{r_o}{r}^{3}dr(6)$

Performing integration yields the following equation for the torque transferred to the surface of a single fin:

$T_{\mathit{fin}}=\frac{2\pi }{3}{\tau }_y\left\{H\right\}\left(r_o^3-r_i^3\right)+\frac{\pi {\mu }_p\dot{\theta }}{2g}\left(r_o^4-r_i^4\right)(7)$

Since each fin attached to the central shaft has two surfaces, and there are a total of four fins used in the final design, we calculate the net torque transferred to the MEC to be equal to the sum of each of the individual fin surfaces’ torques.

$T_{\mathit{total}}=2*\left(4*\left(T_{\mathit{fin}}\right)\right)(8)$

By varying the applied field H to approximate the τ_y using Eq. 2, we can plot the anticipated total torque from Eq. 8 as the result of various modifications to the geometric constraints of the MEC. The resultant effects on torque transmission are calculated using Eq. 8 and are depicted in Figure 5. In that plot, we see that making the fins wider, as well as increasing the number of stacked discs, has a strong impact on the resultant torque transmitted. Increasing the gap size between fins decreases the transmitted torque, but the effect of gap size is much smaller than the effects from disc radius or number of discs (0.12% decrease at 48 kA/m from 0.5 mm to 1.0 mm gap size). In reality, altering the gap spacing would likely impact the assumed homogeneity of the applied magnetic field, and would contribute larger changes for different gap sizes. As expected, the conclusions from this modeling demonstrated generally that for larger surface areas, greater torque will be transmitted.

FIGURE 5

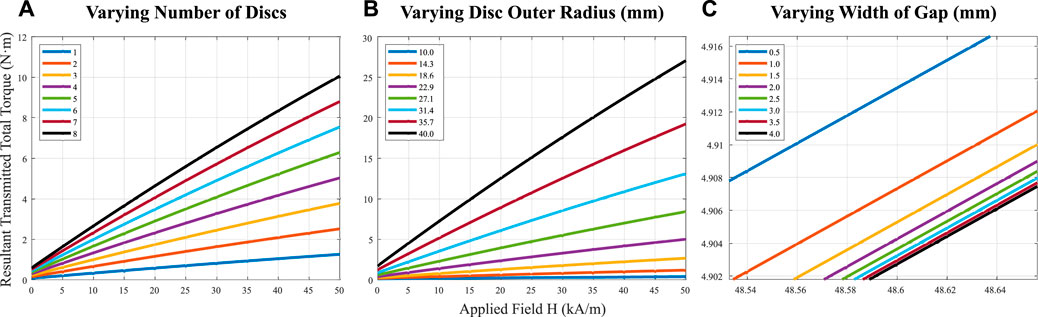
FIGURE 5. Three simulations of the effect of varying physical parameters of the MEC on transmitted torques. Transmitted torque increases with (A) adding additional fins, and (B) larger radii of the fins. Transmitted torque decreases with (C) larger gap sizes, but by a relatively small amount (0.12% decrease at 48 kA/m from 0.5 mm to 1.0 mm gap size).

Taking these considerations in mind, and basing design choices on the physical constraints of the EPMs and the thickness of the steel stock material (0.9 mm thickness), we chose the parameters of four discs (see Figure 4A), 0.5 mm gap thickness, and a disc with an inner radius of 15.5 mm and an outer radius of 25 mm. The rest of the physical dimensions are described in Table 1 below.

TABLE 1

TABLE 1. A bill of materials for the interior MEC assembly.

2.4 Ansys MEC simulation

Returning to magnetostatic simulations, we created a 3D model that best represents a balance between the takeaways from the previous section concerning gap and fin size. While more surface area is important for increasing transmitted torque, it also creates regions that are farther from the central active zone between the two plates of an EPM. Considering the physical constraints of the array of EPMs along with the design goal of increasing surface area, we chose dimensions for the steel fins that would ideally attract the flux and present a balance between more surface area and higher magnetic field intensity between the fins. We then simulated the magnetic fields for the design in Ansys Maxwell, retaining the settings from the previous simulations for only an array of EPMs (Figure 3). We also created B-H curve characterization data for the MRF from the provided manufacturer materials datasheet using curve fitting and input that into the simulation to model the effect of MRF in the spaces between the fins. The results of this simulation can be see in Figure 6A. In conclusion, the resulting MEC design will produce sufficiently high magnetic fields in the active regions, necessary for the operation of a MRF clutch (around 150 mT within the MRF between the fins, or a value of about 8 kA/m). With this value of H field, we anticipate the design to be capable of transmitting over 1.1 N⋅m of torque in ideal conditions (see Figure 6B), with a minimum value of 0.3 N⋅m without any applied field (this nominal value comes from the baseline yield stress of the MRF in the absence of an applied magnetic field).

FIGURE 6

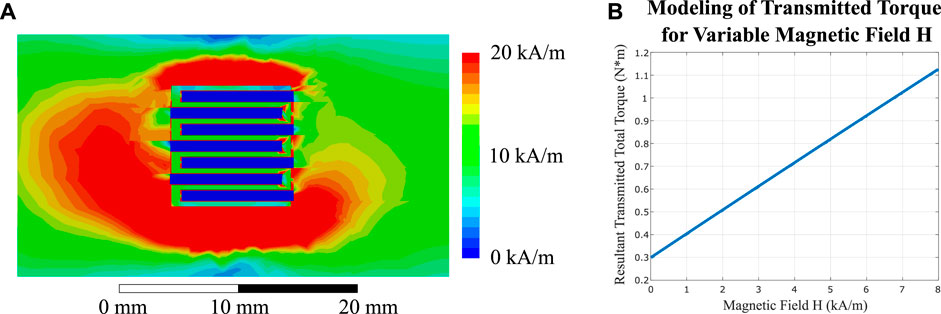
FIGURE 6. (A) A cross-section (left half, right half not shown) of the MEC fins with MRF between them, simulated in Ansys Maxwell with EPMs actively generating their maximum magnetic field. This image indicates the magnetic field intensity (H-field) present within the MRF in the regions of interest is between 8 and 10 kA/m. (B) A simulation using the previously derived equations of ideal-case torque transmission, for H-field values between 0 and 8 kA/m, showing a maximum transmitted torque of over 1.1 N⋅m. The blue regions of low H-field are the steel fins of the MEC. The center of the MEC shaft is not shown, and to the right of the active region.

2.5 MRF EPM clutch assembly

To fabricate the MEC, multiple fabrication and assembly steps are required. For the final design, multiple sub components 3D modeled using SolidWorks 2022 (Dassault Systems, Paris, France) and were 3D-printed (Prusa MK3S, Prusa Research, Prague, Czech Republic) at 0.1 mm vertical resolution and 20% infill with standard PLA filament. For the metal fins, each was cut into discs from sheet metal (1008 grade cold-rolled steel, 0.3 mm thickness) using a water-jet (ProtoMAX Water Jet, OMAX Corp, Kent, Washington, United States). A 6.35 mm diameter aluminum rod was cut to a length of 150 mm for the central shaft. After all the individual pieces were fabricated, the layered fins consisting of metal rings and plastic hoops or discs were aligned and glued together using CA glue. All of the sub-elements of the MEC assembly are shown in Figure 7 and described in Table 1. The design files are available on GitHub Bira (2022) The final design parameters for the miscellaneous elements of the clutch are as follows in this table:

FIGURE 7

FIGURE 7. All of the sub-elements included within the final MEC interior assembly, described in Table 1. The completed assembly without EPMs or the cap (D), from the side view.

After all sub-components were fabricated, the MEC was assembled layer by layer, from bottom to top. The shaft seals (Table 1E) were press-fit into position on either side of the top (Table 1H) and bottom (Table 1I) 3D printed components, followed by a ball bearing (Table 1G) for shaft alignment and rotation. The aluminum rod (Table 1A) was placed and aligned in the bottom component, and PTFE washers (Table 1J) and 3D-printed spacers (Table 1F) were placed on top of the shaft seal to ensure proper spacing of the fins. Then, successive layers of inner (Table 1C) and outer (Table 1B) fins were positioned and glued to either the central rod or the outer housing. The top component was assembled the same way as the bottom, but in reverse order (PTFE washers, 3D-printed spacers, top sub-assembly with shaft seal and bearing). After all layers were positioned and glued, with time to allow the glue to dry, the assembled MEC was visually inspected and tested for free, low friction rotation.

The MEC needs MRF to be filled into all of its void spaces, and the authors decided upon filling the MEC using a non-magnetic metal syringe through an opening in the outer housing that allows access to all of the internal spaces (see the right of Figure 7). After all internal voids were filled with the MRF (MRF-140CG, Lord Corp), the shaft was rotated to ensure no bubbles remained. Then, the opening was capped and glued shut with a 3D-printed cap (Table 1D) and CA glue.

Having assembled all the internal elements of the MEC, six EPMs were then positioned radially around the perimeter of the completed sub-assembly of the MEC, such that each EPM has its active region targeting about 1/6th of the overall volume. The 3D-printed top and bottom elements provide alignment features for even spacing. All these components were assembled by hand and aligned visually, but minor imperfections present in the tolerances of the 3D printed and hand-cut elements likely contribute to some of the variability and noise present in the recorded data in the next section. The complete MEC was ready for testing and performance analysis, and was placed into a custom-designed testing apparatus to evaluate its performance (see Figure 8). This apparatus utilizes a stepper motor spinning at a constant RPM controlled by a power supply, an Arduino Uno, and a stepper driver. The output shaft of the stepper motor was coupled to the input shaft of the MEC with a shaft collar and set screw, and the outer housing of the MEC was fixed at the bottom to a 6-axis force/torque sensor (Figure 8D) (Mini40 Six-Axis Force/Torque Sensor, ATI, Apex, NC, United States) rigidly attached between the base of the test-bed and the clutch. This sensor collected force and torque data at 10,000 Hz, to observe changes on the same timescale of our EPM pulse lengths (100s of μs).

FIGURE 8

FIGURE 8. The full test-bed for measuring the torque transmission of the MEC, consisting of (A) an Arduino Uno with power supply and stepper driver to control a stepper motor for the input torque to the MEC, (B) an Arduino Mega to control three H-bridge Motor Driver connected to a bench-top power supply for current supply to the MEC (not shown), and (C) the mounting frame allowing the stepper motor to slide linearly into place and be coupled to the MEC input shaft (see Figure 7A) with a set screw collar (i), and (D) the force-torque sensor on the bottom, with a collar for holding the bottom component of the MEC.

3 Results

In this section, we describe the characterizations performed for both the EPM array (shown below in Figure 9) as well as the completed prototype MEC. We report on the torque transmission capabilities of the MEC, and we utilize a control strategy developed from curve-fitting functions to observed data at different EPM pulse lengths. The resulting set-point control method is demonstrated in Figure 12, and this is followed by an examination of the MEC response to variable pulse lengths applied rapidly, as well as different rotational velocities.

FIGURE 9

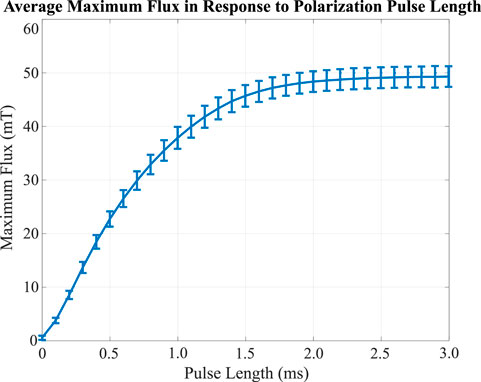
FIGURE 9. The characterization of all six EPMs, showing the magnetic flux density generated between the steel plates at the midpoint between each plate as a result of the current pulse length applied to each EPM. Data was collected with a teslameter, as described in Section 2.1.

For the characterization of the final MEC, the stepper motor was driven at 50 RPM, a medium speed for the stepper motor. A number of tests were performed to highlight the overall performance of the MEC, as well as possibilities from different low-power control strategies. First, we completed two tests that examined the immediate response of the MEC to an input sequence where multiple EPMs are activated in sequence. This sequence of turning on sequential EPMs one by one, or two at a time, resulted in rapid changes in transmitted torque from the input shaft and was repeatable in both the rising and falling directions. These control patterns are shown in Figure 10, where each plot represents the average of three separate data series following the same control input. All torque values were normalized to the baseline torque of the MEC with all EPMs off (0.10 N⋅m without MRF added, from friction, and 0.16 N⋅m with MRF). A typical rise time from EPM activation until the MEC has reached its next target transmitted torque is 3.97 ms for the single-step modality (see Figure 10A), where each EPM activates individually. (this value was averaged from nine separate activation trials, with a standard deviation of 1.98 ms), while the rise time for the two-step modality (see Figure 10B) was 23.14 ms on average (with a standard deviation of 0.98 ms). These values coincide with the length of polarization for each individual EPM, which was set to 5.0 ms for these tests to ensure complete polarization and activation of each EPM. The two-step mode would take 11.0 ms to polarize two EPMs fully, with programmed delays in the arduino script. The two-step mode took longer than the single-step mode for its rise time, but it was also rising a greater amount. As shown in Figure 10C, all trials were observed to begin changing in response to the EPM polarizing on the order of a couple ms, which agrees with many other MRF-based clutches (often with response times on the order of $<$10 ms Phu and Choi (2019)). These results demonstrate the rapid, repeatable, and reversible nature of the MEC design.

FIGURE 10

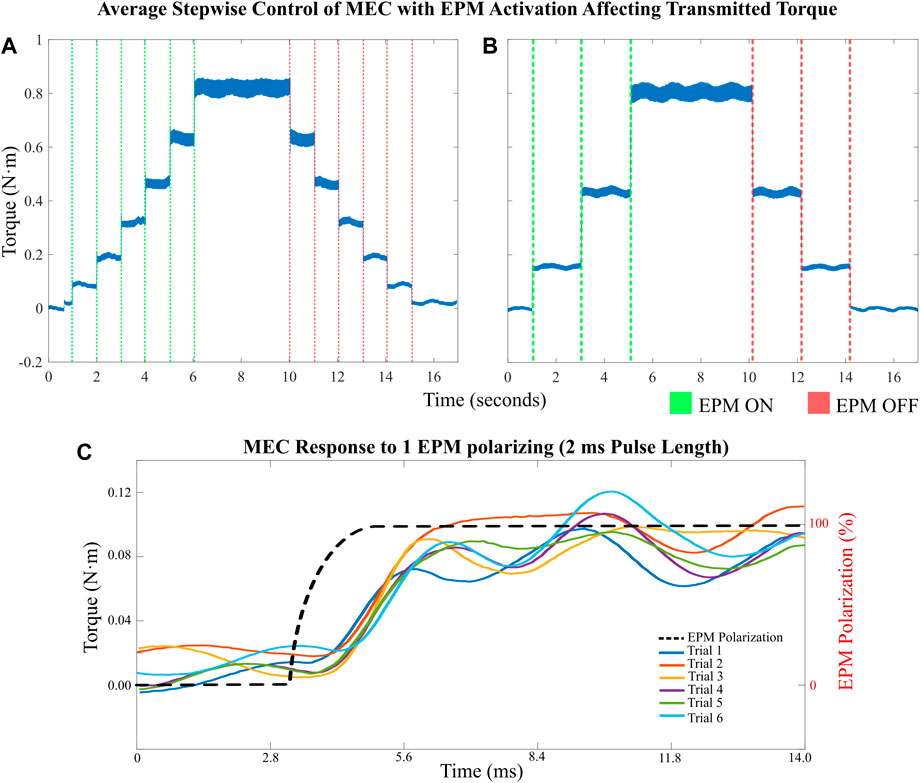
FIGURE 10. Demonstrating step-wise control of the MEC. (A) Each EPM is activated sequentially, resulting in six steps up until being held at the maximum value, before stepping back down to zero. (B) Two EPMs (on opposite sides of the MEC) are activated at once, resulting in larger jumps between each step, but behaving similarly to when single steps are made. (C) Six trials are shown where a single EPM is activated, resulting in a jump in the transmitted torque. The EPM polarization length was 2 ms, and the response of the MEC closely adheres to the EPM magnetization with a delay of about 1 ms.

Next, we studied how the length of polarization affected the overall transmitted torque in the MEC. Data was recorded for both polarization and depolarization of the MEC at different pulse lengths. For polarization, the pulse length was applied after all EPMs were depolarized completely with a pulse of 5 ms. For depolarization, all EPMs were fully polarized at 5 ms before applying the depolarizing pulse. The transmitted torque was measured 9 times, and the average changes in transmitted torque as a function of pulse length are shown in Figure 11. This plot demonstrates significant hysteresis between polarization and depolarization for the length of pulse required to affect a change in the total torque transmission. This aligns with the general principles of the magnetization behavior of a permanent magnet such as AlNiCo; these outcomes are discussed in Section 4.

FIGURE 11

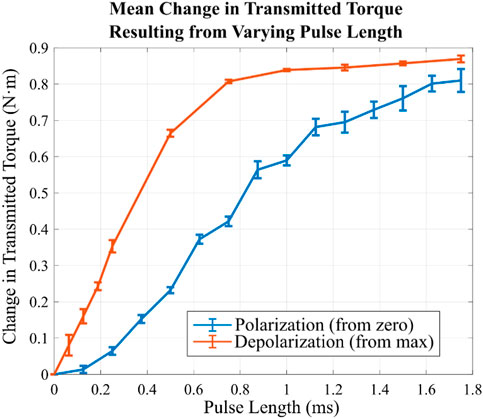
FIGURE 11. The change in average transmitted torque as a function of pulse length for the MEC. Polarization requires greater pulse lengths to achieve the largest possible transmitted torque, while depolarization can have larger changes with shorter pulse lengths.

After collecting this data, we fit two functions to the polarizing and depolarizing data, utilizing the MATLAB curve-fitting toolbox. The resulting two inverse-tangent equations can then be used to choose an arbitrary set point within the range of possible torque values for the MEC. The inverse-tangent was chosen as it provided the greatest fit for polarization while keeping calculations simple (adjusted R²-value was 0.97). These equations calculate the length of a pulse required to then magnetize or demagnetize all six EPMs from zero or saturation by the desired amount to reach the set point. Solving for the pulse length (x, in seconds) and calculating the change in target torque from the current torque (δ), the two equations take the form of:

$\begin{array}{c}{x}_{\mathit{polarize}}=\left(\tan \left(\delta /0.9\right)/759.0\right)\hfill \\ x_{\mathit{depolarize}}=\left(\tan \left(-\delta /0.9\right)/1713.0\right)\hfill \end{array}(9)$

Utilizing this control strategy, we defined a series of arbitrary set points in sequence, and applied Eq. 9 to adjust the transmitted torque by activating the EPMs for a set pulse length determined by the new set point. The results of this experiment are shown in Figure 12. It can be seen that the initial increase in torque overshoots the control signal by ≈ 0.03 Nm, and this initial offset propagates throughout the rest of the test. While the direction and magnitude of the corrections are close to the control signal, these errors compound over time, leading to overshooting or undershooting the targeted torque. These results are discussed further in Section 4.

FIGURE 12

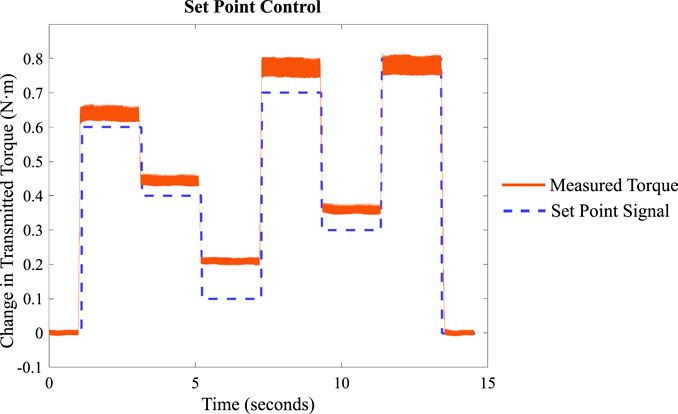
FIGURE 12. Demonstrating the set-point control strategy using the equations derived from the data in Figure 11.

After observing the differences between the targeted torque and the actual behavior of the MEC while following the control signal, we sought to observe more closely how the pulse length affects the torque transmission, focusing on small pulse lengths applied in rapid succession (30 times total) to slowly increase the overall magnetization of the EPMs. This was measured for two pulse lengths (0.1 and 0.2 ms respectively), each being applied to all six EPMs sequentially (taking about 30 ms total) with a short pause (300 ms) in between each application. The result is shown in Figure 13A, and demonstrates that a pulse length of only 100 μs raised the transmitted torque to about 0.2 N⋅m before stopping, while doubling the pulse length to 200 μs was sufficient to raise the transmitted torque a maximum value of about 0.65 N⋅m. The significance of this behavior is discussed in Section 4 alongside the previous figures. Lastly, the input motor RPM was considered for its effect on the results of the tests. Shown in Figure 13B, there was a slight increase in total transmitted torque as the RPM increased, but the effect was within standard deviation for each speed, and therefore negligible.

FIGURE 13

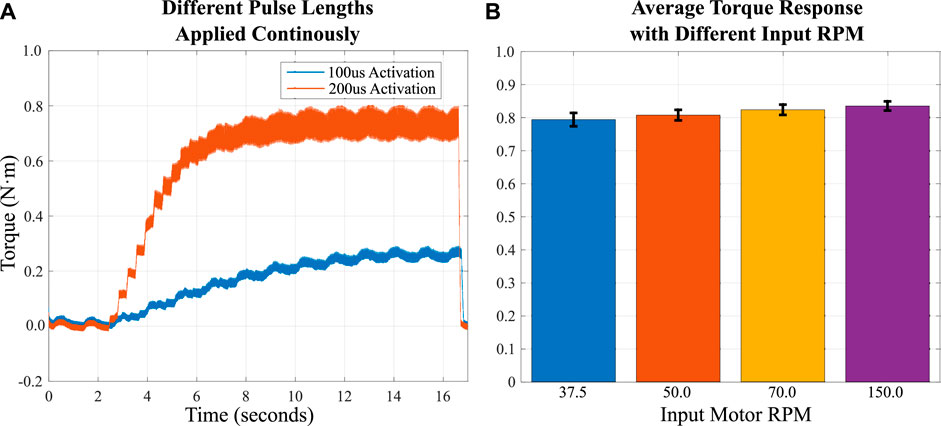
FIGURE 13. (A) This plot demonstrates how cumulative pulses (5 ms to each EPM until all have been activated, with 300 ms in between each step) can gradually bring the torque up to a set maximum, which is determined by the pulse length. (B) This bar plot compares how RPM affects maximum transmitted torque, with all EPMs being full saturated/active.

4 Discussion

In this section, we discuss the results of our experiments and consider shortcomings and advantages of the chosen design. We consider possible reasons for the discrepancies between our tested control strategy and the actual performance of the MEC. We also highlight the potential power-consumption advantages of the MEC and its place within the broader research topic of MRF-based transmission devices.

We completed various experiments to demonstrate the torque-transmitting capabilities of the MEC and to characterize its behavior. While the MEC was highly repeatable for the individually addressed EPM tests shown in Figure 10, there was greater variability introduced when attempting to utilize the magnetization properties of the AlNiCo (not full saturation) in the EPM array to control a specific torque. Controlling pulse length did demonstrate that each EPM could be controlled in the amount of magnetic flux density it would generate (Figure 9), but the developed equations fit to observational data in Figure 11 were less accurate at producing an arbitrarily targeted torque. This is likely the result of the hysteresis present during the magnetization of the AlNiCo core magnet. This phenomenon can be seen in the data in Figure 11; when starting from zero (demagnetized) magnetization, greater pulse lengths are required to create a change in torque; or, more accurately, to create a change in the magnetization of the AlNiCo magnet that then results in the net magnetic field generated by the EPM. When the AlNiCo magnet is fully magnetized and saturated, much shorter pulse lengths rapidly cause a decrease in transmitted torque (more directly, a decrease in the magnetization of the AlNiCo magnet). This phenomenon is seen in other MRF-based clutch designs, and adaptive control strategies were deployed to compensate Yadmellat and Kermani (2016). Additionally, with short pulse lengths (0.1–0.2 ms) there is the ability to slowly build the transmitted torque incrementally, as opposed to larger jumps (as shown in Figure 13A). Using only a 0.1 ms pulse length was limited by the amount of torque it was able to transmit when starting from 0 polarization, and this brief polarization is likely unable to enact a magnetization of the AlNiCo beyond the plateau value. Larger pulse lengths quickly overcome this shortcoming, with 0.2 ms pulse length reaching much closer to the overall intended maximum transmitted torque. Future work may benefit in further analyzing the granularity of small pulse lengths (between 0.05 and 0.5 ms), and characterizing the resistance to magnetization present in the EPMs at all magnetization levels to better inform a control strategy for slower torque transmission responses. These small adjustments would also allow for more gradual set-point following, with smoother transitions similar to that of PID controllers.

The magnetic hysteresis of AlNiCo is visible in characterization B− H curves Yu et al. (2014), but differs from our design due to the shape-dependent demagnetization field. Our control strategy (shown in Figure 12), which considered only the magnitude of difference between the current torque value and the projected torque value, fails to incorporate this hysteresis into its calculation, assuming the magnitude of change is relative to either fully magnetized or fully demagnetized. This is an important consideration for future control implementations, and existing characterization curves for AlNiCo can be utilized to realise more sophisticated strategy that tracks the current magnetization of the EPM. Additionally, some sensing feedback of the current transmitted torque could be incorporated, allowing for control strategies such as PID to fine tune transmitted torque with small pulse lengths to adjust the current torque to the target torque on short time scales (tens of milliseconds).

Other control strategies can combine both the individual EPM control shown in Figure 10 with the pulse-length control in Figure 11 to realize unique patterns of EPM activation to realize more complex torque transmission modalities, such as linearly or exponentially ramping the torque as opposed to jumping from one set point to another. Combinations of both pulse length and individually addressing each EPM allow for granular control of transmitted torque across the entire spectrum of possible torques. Additionally, the significant manufacturing differences between each EPM and the overall construction of the MEC are the source of much of the variability present in the characterization data. Improvements to manufacturing methodology, better precision machining, and better tolerances will contribute greatly to minimize variability between each EPM and the overall MEC behavior. This reduction in variability, while unlikely to account for all the discrepancies previously described, would give greater confidence to all control strategies developed for accurate torque transmission.

In the modeling performed in Section 2, we predicted a possible maximum transmitted torque of about 1.1 N⋅m. As shown by the maximum holding torque in Figure 10 of ≈0.8 N⋅m, the difference between the two is a delta of about 0.3 N⋅m. In Figure 14, the simulation from Figure 6 is plotted along with a theoretical ideal-case behavior, where each EPM contributes 1/6th of the total torque as it is added in sequence. By the time all six have been added, it reaches the maximum torque. Plotted in yellow is the average behavior of the MEC with all six EPMs activating in sequence, drawn from Figure 10A. The measured data looks quite similar to the theoretical data, and, if it were shifted up 0.2 N⋅m, would be in excellent agreement. This demonstrates that our modeling approach captures the overall scale and slope of the MEC’s behavior, but overestimates the initial holding torque of the MEC without any applied field. The yield stress contribution from friction and the MRF was observed to translate into only 0.1 N⋅m of torque. This error likely comes from estimations and approximations made from the provided manufacturer data, since estimates of the yield stress at low fields may be inaccurate. Other sources of error could arise from differences between the MRF’s physical properties once shaken and poured into the MEC, and the ideal conditions assumed by the manufacturer.

FIGURE 14

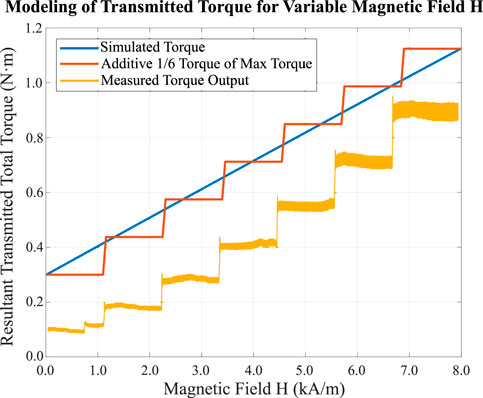
FIGURE 14. A simulation plotted alongside averaged data for torque transmission, where each EPM is activated in sequence, adding 1/6th of the total possible torque until the average H field applied from the EPMs reaches 8 kA/m around the perimeter of the entire MEC when all are active. The observed maximum for the observed data is about 0.3 N⋅m less (27%) than the model predicted.

The MEC consumes several orders of magnitude less power than a traditional MRF-based clutch utilizing electromagnets for its control. For consideration, some simple calculations begin to demonstrate the significance of being able to set any torque within the operational range without any additional power input, once set. One EPM has a wattage of about 75 W (15 V at 3 Ω, drawing about 5 Amps), and can achieve maximum torque output with a pulse of 5 ms. This translates to a power consumption of 0.104 mWh, or 0.626 mWh for all six EPMs in the array. Turning the MEC into the on state and then back to the off state requires pulsing both directions, so to transmit maximum torque with the MEC for 1 hour and then turn it back off, the total power consumption would be about 1.25 mWh. Other relevant MRF-based clutch designs that utilize active electromagnets to transmit torque require being on for the entirety of maximum (or minimum) torque transmission for 1 hour. One sample design using this modality requires about about 3.5 W Pisetskiy and Kermani (2021), which translates to 3,500 mWh of power consumption for maximum torque transmission. The MEC consumes several orders of magnitude less energy than comparable devices for the same function (in this calculation, only 0.036% of the electromagnet-based design). While the MEC and the compared devices are not equivalent, and this calculation does not represent a real-world power-consumption scenario, it still serves to highlight how low-power the MEC can be. Additional optimizations in manufacturing tolerances, parameter optimization and EPM design will reduce the power and power consumption further.

In essence, the MEC only needs to be supplied current for the time it takes to fully magnetize the EPMs (tens of milliseconds), whereas an electromagnet must be supplied power for the entire length of operation. These differences are inconsequential on the timescale of tens of milliseconds, but the power draw becomes significant the longer active operation is required. This decrease in power consumption opens the door for many desirable applications, since this could significantly extend the time of remote operation and reduce energy costs. Electric vehicles or robots that currently utilize MRF clutches could significantly reduce their power consumption by adopting a similar design, improving battery life and range.

5 Conclusion

In this work, the authors designed and fabricated a prototype MRF-based device utilizing an array of EPMs for low-power, variable control of torque transmission. The authors designed and simulated the performance of EPMs for the purpose of controlling the behavior of MRF in a clutch design, and then fabricated and characterized the EPMs, seeing good agreement between real-world performance and simulation. The MEC was then designed and analytically modeled, demonstrating that potential torque transmission would be significant enough to be possible. After picking design parameters for the application that considered the physical constraints of the system and modeling insights, the authors fabricated the full MEC and a testing apparatus.

In conclusion, the various experiments to characterize the real-world performance of the MEC demonstrate that can transmit between 0.16 and 0.96 N⋅m of torque, with rapid response times (≈5–20 ms) and low-power consumption (1.25 mWh). Future work to optimize the MEC will explore different form factors, increase the torque transmission capabilities, and further lower power consumption. The EPM arrangement approach is scalable, and can be modified to a wide range of possible clutch form factors. For applications requiring greater torque, redesigning the physical parameters to incorporate more EPMs or larger, more powerful EPMs would enable greater larger MEC devices. With greater volume and surface area, it is possible to generate a greater range of transmittable torque for a given application. The MEC represents a new control strategy for MRF-based torque transmission devices, and has many applications in varied robotic and automotive research areas.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

NB wrote the paper, edited the paper, designed experiments, analyzed experimental data, and created the figures. JD edited the paper, contributed to modeling, helped design experiments, and was the adviser for the project. PD provided editing and advising.

Funding

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1840998.

Acknowledgments

The authors would like to thank the members of the OSU robotics and electrical engineering departments for their assistance in investigating current research in this field and relating to this topic. Additionally, the authors thank Maren Gingerich for their contributions during their REU in the summer of 2021, as well as the insight from Rafhael M. Andrade into the magnetic properties of plastic.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Andrade, R. M., Ulhoa, P. H. F., and Vimieiro, C. B. S. (2022). “Designing a highly backdrivable and kinematic compatible magneto-rheological knee exoskeleton,” in 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23-27 May 2022, 5724–5730. doi:10.1109/ICRA46639.2022.9812308

CrossRef Full Text | Google Scholar

Bingham, E. C. (1922). Fluidity and plasticity. New York, United States: McGraw-Hill.

Google Scholar

Bira, N., Dhagat, P., and Davidson, J. R. (2022). Tuning the grasping strength of soft actuators with magnetic elastomer fingertips. Smart Mat. Struct. 31, 045013. doi:10.1088/1361-665x/ac57b1

CrossRef Full Text | Google Scholar

Bira, N. (2022). Mec design files. Philadelphia: IEEE Available at: https://github.com/BiraN2019/MEC.

Google Scholar

Davidson, J. R., and Krebs, H. I. (2018). An electrorheological fluid actuator for rehabilitation robotics. Ieee. ASME. Trans. Mechatron. 23, 2156–2167. doi:10.1109/tmech.2018.2869126

CrossRef Full Text | Google Scholar

de Andrade, R. M., Martins, J. S. R., Pinotti, M., Filho, A. B., and Vimieiro, C. B. S. (2021). Novel active magnetorheological knee prosthesis presents low energy consumption during ground walking. J. Intelligent Material Syst. Struct. 32, 1591–1603. doi:10.1177/1045389X20983923

CrossRef Full Text | Google Scholar

Kitano, S., Komatsuzaki, T., Suzuki, I., Nogawa, M., Naito, H., and Tanaka, S. (2020). Development of a rigidity tunable flexible joint using magneto-rheological compounds—Toward a multijoint manipulator for laparoscopic surgery. Front. Robot. AI 7, 59. doi:10.3389/frobt.2020.00059

PubMed Abstract | CrossRef Full Text | Google Scholar

Koivikko, A., Drotlef, D.-M., Sitti, M., and Sariola, V. (2021). Magnetically switchable soft suction grippers. Extreme Mech. Lett. 44, 101263. doi:10.1016/j.eml.2021.101263

PubMed Abstract | CrossRef Full Text | Google Scholar

Leps, T., Glick, P., Ruffatto, D., Parness, A., Tolley, M., and Hartzell, C. (2020). A low-power, jamming, magnetorheological valve using electropermanent magnets suitable for distributed control in soft robots. Smart Mat. Struct. 29, 105025. doi:10.1088/1361-665x/abadd4

CrossRef Full Text | Google Scholar

McDonald, K. J., Kinnicutt, L., Moran, A. M., and Ranzani, T. (2022). Modulation of magnetorheological fluid flow in soft robots using electropermanent magnets. IEEE Robot. Autom. Lett. 7, 3914–3921. doi:10.1109/LRA.2022.3147873

CrossRef Full Text | Google Scholar

Moghani, M., and Kermani, M. R. (2019). A lightweight magnetorheological actuator using hybrid magnetization. Ieee. ASME. Trans. Mechatron. 25, 76–83. doi:10.1109/tmech.2019.2951340

CrossRef Full Text | Google Scholar

Najmaei, N., Kermani, M. R., and Patel, R. V. (2014). Suitability of small-scale magnetorheological fluid-based clutches in haptic interfaces for improved performance. Ieee. ASME. Trans. Mechatron. 20, 1863–1874. doi:10.1109/tmech.2014.2357447

CrossRef Full Text | Google Scholar

Phu, D. X., and Choi, S.-B. (2019). Magnetorheological fluid based devices reported in 2013–2018: Mini-review and comment on structural configurations. Front. Mat. 6, 19. doi:10.3389/fmats.2019.00019

CrossRef Full Text | Google Scholar

Pisetskiy, S., and Kermani, M. (2021). High-performance magneto-rheological clutches for direct-drive actuation: Design and development. J. Intelligent Material Syst. Struct. 32, 2582–2600. doi:10.1177/1045389x211006902

CrossRef Full Text | Google Scholar

Shafer, A. S., and Kermani, M. R. (2009). “On the feasibility and suitability of mr and er based actuators in human friendly manipulators,” in Proceedings of the 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems (IEEE), St. Louis, MO, USA, 10-15 Oct. 2009, 2904–2909.

CrossRef Full Text | Google Scholar

Wolf, S., Grioli, G., Eiberger, O., Friedl, W., Grebenstein, M., Höppner, H., et al. (2016). Variable stiffness actuators: Review on design and components. Ieee. ASME. Trans. Mechatron. 21, 2418–2430. doi:10.1109/TMECH.2015.2501019

CrossRef Full Text | Google Scholar

Yadmellat, P., and Kermani, M. R. (2016). Adaptive control of a hysteretic magnetorheological robot actuator. Ieee. ASME. Trans. Mechatron. 21, 1336–1344. doi:10.1109/tmech.2016.2524673

CrossRef Full Text | Google Scholar

Yadmellat, P., and Kermani, M. R. (2013). Adaptive modeling of a magnetorheological clutch. Ieee. ASME. Trans. Mechatron. 19, 1716–1723. doi:10.1109/tmech.2013.2292594

CrossRef Full Text | Google Scholar

Yang, J., Sun, S., Yang, X., Ma, Y., Yun, G., Chang, R., et al. (2022). Equipping new sma artificial muscles with controllable mrf exoskeletons for robotic manipulators and grippers. Ieee. ASME. Trans. Mechatron., 1–12. doi:10.1109/TMECH.2022.3157329

CrossRef Full Text | Google Scholar

Yu, C., Niu, S., Ho, S. L., Fu, W., and Li, L. (2014). Imbalanced force in permanent magnet brushless motors with magnetic and/or electric asymmetries. IEEE Trans. Magn. 51, 1–4. doi:10.1109/tmag.2014.2329951

CrossRef Full Text | Google Scholar

Zhang, P., Kamezaki, M., He, Z., Sakamoto, H., and Sugano, S. (2021). Epm–mre: Electropermanent magnet–magnetorheological elastomer for soft actuation system and its application to robotic grasping. IEEE Robot. Autom. Lett. 6, 8181–8188. doi:10.1109/LRA.2021.3100939

CrossRef Full Text | Google Scholar