
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 01 December 2022
Sec. Colloidal Materials and Interfaces
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.1037201
This article is part of the Research Topic New Frontiers in Hybrid Nanofluids for Heat Transfer Process and Applications View all 14 articles
 Zahoor Iqbal1*
Zahoor Iqbal1* S. Yashodha2
S. Yashodha2 A. K. Abdul Hakeem2
A. K. Abdul Hakeem2 Abdulrahman Alsawi3
Abdulrahman Alsawi3 Maryam Ahmed Alyami4
Maryam Ahmed Alyami4 El. Sayed Yousef5,6
El. Sayed Yousef5,6 Ali H. Amin7,8
Ali H. Amin7,8 Sayed M. Eldin9
Sayed M. Eldin9The influence of the magnetic field on
In this industrialized world, the heat transfer process plays a significant role in upgrading the efficiency of industrial applications. To accomplish this global industrialization, in 1995 Choi devised a new progressive class of heat transfer fluids, known as nanofluids (Choi and Eastman, 1995), in which the characteristics of both nanoparticles and base fluid become efficient. Heat transfer in nanofluid is more proficient than in common fluids. Preparation of nanofluids is not simply the mixture of solids and liquids but requires beneficial methods, as elaborated in Xuan and Li (2000), which presents the procedure for nanofluid preparation. Choosing the nanoparticle and base fluid wisely leads to excellent results depending on the need, as discussed in Usri et al. (2015). Recent research works have been implemented using a novel category of fluids known as nanofluids, which have brought changes widely, including in the industrial, engineering, and medical fields (Vishnu Ganesh et al., 2014; Abdul Hakeem et al., 2017). Different geometrical shapes give different results, including cone and wedge (Anantha Kumar et al. (2018), rotating disk (Gholinia et al. (2019), and vertical cone geometric shapes (CemEce, 2005; Raju and Sandeep, 2016). Nanofluids are the best solutions for heat transfer fluids since they have good thermal performance. Therefore, researchers are proposing suitable models. In this regard, three methods are employed for improving thermal performance (Maleki et al., 2020). To adopt nanofluid applications in daily life, and to increase nanofluid’s performance in several applications, nanofluid stability is a critical factor discussed in (Chakraborty and Kumar Panigrahi, 2020). To enhance heat transfer, comparison among different nanofluids for different parameters has been conducted (Dinarvand and Pop, 2017; Aghamajidi et al., 2018). Nanofluid applications have been used in multidisciplinary research. There is a broad range of utilizations in the areas of microalgal cultivation, friction reduction, magnetic sealing, reactor–heat exchange, optical and biomedical applications, nanofluid detergent, electronics cooling, and heating buildings (Vargas-Estrada et al., 2020; Rafiq et al., 2021). With progress in nuclear energy, nanoparticles are also used as coolants in nuclear power plants (Hamidreza Arab BafraniNoori-kalkhoran et al., 2020), in enhancing oil recovery, nano-refrigerants, and nano-lubricants (de Carvalho et al., 2020; SahbanAlnarabiji and Husein, 2020; Salari and Seid Mahdi Jafari, 2020; Mallikarjuna et al., 2021), and in turning and grinding processes (SaswatKhatai et al., 2020). In addition to nanofluid, the flow of hybrid nanofluid across a stretched surface has recently been studied (Aly and Pop, 2019; Aly and Pop, 2020a; Aly and Ebaid, 2020; Aly and Pop, 2020b; Aly et al., 2021; Ahmad et al., 2022; Aly et al., 2022; Arafat et al., 2022; Reddy et al., 2022; Usafzai et al., 2022).
Using a water–ethylene glycol (50:50) combination as the base fluid and
The aspect of the present work is listed below.
➢ Water–ethylene glycol (50:50) mixture is considered a base fluid with Pr = 29.86.
➢
➢ The geometric cone is used for fluid flow as shown in Figure 1.
➢ The effect of viscous dissipation, the resistance heating effect of the fluid, and the slip effect are regarded as negligible.
A continuous two-dimensional flow of a combination of
The
The models that govern the phenomena are given below (Aghamajidi et al., 2018).
Here,
The boundary conditions for the above governing equations are given below.
Prescribed surface temperature case:
The thermophysical properties are given in Table 1. The nanofluid properties are given by (Saranya et al., 2022)

TABLE 1. Thermophysical properties of
Nanofluid’s thermal conductivity and electrical conductivity are given by
Here,
For the current analysis, the following variables are utilized (Aghamajidi et al., 2018):
where u, v, and w represent the velocity components x direction, y direction, and θ direction, respectively, and
The Prandtl number (Pr), reference velocity (U), and Grashof number (Gr) are defined as
where
The governing equations from Eq. 1 to Eq. 4 take the following non-dimensional form after substituting the dimensionless variables, as defined in Eqs 14–16:
The boundary conditions are given below.
Prescribed surface temperature case:
The rotational Reynolds number, the magnetic field function Λ, and the magnetic parameter are
The function
where ψ is stream function and the boundary layer variables can be presented as
Applying the boundary layer variables as written in Eq. 26, the non-dimensional governing Eqs 17–20 are converted into the system of Ordinary differential equations (ODEs).
Here F(y), G(y), and H(y) represent the tangential velocity profile, swirl velocity profile, and temperature profile, respectively.
where
The boundary conditions from Eqs 21 to 23 are reduced to
The skin friction coefficient
where
Using the non-dimensional transformations, we obtain
Eqs 27–29 with boundary conditions (Eqs 30, 31) specify nonlinear ordinary differential equations. By using a fourth-order Runge–Kutta finite difference scheme and shooting approach, this model is solved numerically to examine the effects of M,
We represent
To authenticate our work, the outcomes were compared with the results of Ece (2006), Dinarvand (2011), and Aghamajidi et al. (2018), which are shown in Table 2. It is worth mentioning that the present outcomes have excellent compatibility with the solutions obtained by Ece (2006), Dinarvand (2011), and Aghamajidi et al. (2018) for the case ϕ = 0.
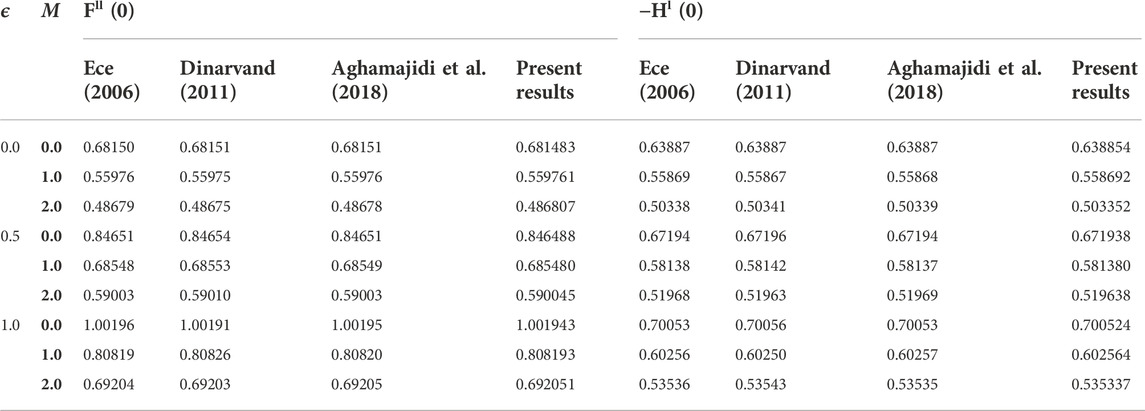
TABLE 2. Comparison with the results of Ece (2006), Dinarvand (2011), and Aghamajidi et al. (2018) for regular fluid (
The effects of spin parameter
The tangential velocity profile decreases as the range of magnetic parameters increases. This is because a magnetic field creates a drag force, known as the Lorentz force, in an electrically conducting fluid. There is a dip in the velocity profile due to this significant resistive force acting counter to the direction of fluid flow. As a result, as M becomes stronger, the hydrodynamic boundary layer thickness becomes thinner.
To overcome drag force, the fluid must do some additional work, which is transformed into thermal energy and leads to an increase in the temperature of the fluid.
As the spin parameter appears in the momentum equation, the effect of spin parameter is more in this equation, and increased values of the spin parameter dynamically promote tangential velocity.
Temperature is reduced as spin parameter increases. Therefore, there is reduction in the thickness of the thermal boundary layer for varying magnitudes of spin parameter. Fe3O4 nanoparticles are compressed more toward the surface than are the Al2O3 nanoparticles as the spin parameter rises, as indicated in Figure 5.
The influence of nanoparticle volume fraction on tangential and swirl velocity profile is depicted in Figure 6. As the value of ϕ rises, the tangential velocity of the flow increases. The opposite behavior is examined in the case of swirl velocity profile.
In Figure 7, the influence of the Al2O3 and Fe3O4 nanoparticle volume fraction for thermal distribution is plotted. Analysis of this plot showed that the temperature distribution builds up by enhancing the volume fraction of Al2O3.
Table 3 shows the variation of skin friction coefficient and nusselt number for different values of solid volume fraction, spin parameter and magnetic parameter. It is found that magnetic nanoparticles have high skin friction and nusselt number values.
The numerical solution was achieved using the fourth-order Runge–Kutta method combined with boundary conditions and shooting methods to the non-dimensional ODEs. The following graph-related points are noteworthy:
➢ Intensification of the extent of spin parameter dynamically promotes the tangential velocity, and
➢ Higher magnetic parameters decrease the momentum transport of hydrodynamic flow and accelerate thermal transport in the presence of
➢ Higher spin parameter reduces the thermal profile of nanofluid.
➢ The tangential velocity of Fe3O4 is shown to be greater than for the Al2O3 nanoparticle.
➢ It is worth mentioning that the present outcomes are highly compatible with solutions obtained in previous research for the special case.
The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors express their appreciation to “The Research Center for Advanced Materials Science (RCAMS)” at King Khalid University, Saudi Arabia, for funding this work under the grant number RCAMS/KKU/002-22. The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code (22UQU4331100DSR18).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abdul Hakeem, A. K., Saranya, S., and Ganga, B. (2017). Comparative study on Newtonian/non-Newtonian base fluids with magnetic/non-magnetic nanoparticles over a flat plate with uniform heat flux. J. Mol. Liq. 230, 445–452. doi:10.1016/j.molliq.2016.12.087
Aghamajidi, Mohammad, EftekhariYazdi, Mohammad, Dinarvand, Saeed, and Pop, Ioan (2018). Tiwari-Das nanofluid model for magnetohydrodynamics (MHD) naturalconvective flow of a nanofluid adjacent to a spinning down-pointing vertical cone. Propuls. Power Res. 7 (1), 78–90. doi:10.1016/j.jppr.2018.02.002
Ahmad, N. P., Indumathi, N., Ganga, B., Charles, S., Hakeem, A. K. A., Iqbal, Z., et al. (2022). Forced convection of non-Darcy flow of ethylene glycol conveying copper (II) oxide and titanium dioxide nanoparticles subject to lorentz force on wedges: Non-Newtonian Casson model. Front. Chem. 10, 1010591. doi:10.3389/fchem.2022.1010591
Aly, E. H., and Ebaid, A. (2020). MHD Marangoni boundary layerproblem for hybrid nanofluidswith thermal radiation. Int. J. Num. Meth. Heat Fluid Flow.31.
Aly, E. H., Mahabaleshwar, U. S., Anusha, T., Usafzai, W. K., and Pop, I. (2022). Wall jet flow and heat transfer of a hybrid nanofluid subject to suction/injection with thermal radiation. Therm. Sci. Eng. Prog. 32 (1), 101294. doi:10.1016/j.tsep.2022.101294
Aly, E. H., and Pop, I. (2020). Merkin and Needham wall jet problem for hybrid nanofluids withthermal energy. Eur. J. Mech. - B/Fluids 83, 195–204. doi:10.1016/j.euromechflu.2020.05.004
Aly, E. H., and Pop, I. (2020). MHD flow and heat transfer near stagnation point over a stretching/shrinking surface with partial slip and viscous dissipation: Hybrid nanofluid versus nanofluid. Powder Technol. 367, 192–205. doi:10.1016/j.powtec.2020.03.030
Aly, E. H., and Pop, I. (2019). MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat. Fluid Flow. 29 (9), 3012–3038. doi:10.1108/hff-12-2018-0794
Aly, E. H., Rosca, A. V., Rosca, N. C., and Pop, I. (2021). Convective heat transfer of a hybrid nanofluid over a nonlinearly stretching surface with radiation effect. Mathematics 9, 2220. doi:10.3390/math9182220
Anantha Kumar, K., Ramana Reddy, J. V., Sugunamma, V., and Sandeep, N. (2018). Magnetohydrodynamic Cattaneo-Christov flow past a cone and a wedge with variable heat source/sink. Alexandria Eng. J. 57, 435–443. doi:10.1016/j.aej.2016.11.013
Arafat, H., Iqbal, Z., T-Eldin, E., Almohiemn, M., Yassin, M. F., Guedri, K., et al. (2022). Energy transport features of Oldroyd-B nanofluid flow over bidirectional stretching surface subject to Cattaneo-Christov heat and mass fluxes. Front. Energy Res. 10, 1361. doi:10.3389/fenrg.2022.985146
CemEce, Mehmet (2005). Free convection flow about a cone under mixed thermal boundary conditions and a magnetic field. Appl. Math. Model. 29, 1121–1134. doi:10.1016/j.apm.2005.02.009
Chakraborty, Samarshi, and Kumar Panigrahi, Pradipta (2020). Stability of nanofluid: A review. Appl. Therm. Eng. 174, 115259. doi:10.1016/j.applthermaleng.2020.115259
Choi, S. U. S., and Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. ASME International Mechanical Engineering Congress & Exposition, San Francisco, CA, November 12–17, 1995.
De Carvalho, J. E. S. P., Sotomayor, P. O., Parise, J. A. R., and Florian, P. (2020). Numerical assessment of critical properties of nanofluids: Applications to nanorefrigerants and nanolubricants. Journal of Molecular Liquids, , 318, doi:10.1016/j.molliq.2020.113938
Dinarvand, Saeed, and Pop, Ioan (2017). Free-convective flow of copper/water nanofluid about a rotating down-pointing cone using Tiwari-Das nanofluid scheme. Advanced Powder Technology, 28, doi:10.1016/j.apt.2016.12.016
Dinarvand, S. (2011). The laminar free-convection boundary-layer flow about a heated and rotating down-pointing vertical cone in the presence of a transverse magnetic field. Int. J. Numer. Meth. Fluids 67 (12), 2141–2156. doi:10.1002/fld.2489
Ece, M. C. (2006). Free convection flow about a vertical spinning cone under a magnetic field. Appl. Math. Comput. 179, 231–242. doi:10.1016/j.amc.2005.11.099
Gholinia, M., Hosseinzadeh, Kh., Mehrzadi, H., Ganji, D. D., and Ranjbar, A. A. (2019). Investigation of MHD Eyring–Powell fluid flow over a rotating disk under effect of homogeneous–heterogeneous reactions. Case Stud. Therm. Eng. 13, 100356. doi:10.1016/j.csite.2018.11.007
Hamidreza, A. B., Omid, N.-K., Massimiliano, G., Rohollah, A., and Mohammad, M. M. (2020). On the use of boundary conditions and thermophysical properties of nanoparticles for application of nanofluids as coolant in nuclear power plants; a numerical study. Prog. Nucl. Energy 126, 103417. doi:10.1016/j.pnucene.2020.103417
Maleki, Akbar, Elahi, Milad, Mamdouh El Haj Assad, , Alhuyi Nazari, Mohammad, Mostafa Safdari Shadloo, , and Nabipour, Narjes (2020). Thermal conductivity modeling of nanofluids with ZnO particles by using approaches based on artificial neural network and MARS. J. Therm. Anal. Calorim. 143, 4261–4272. doi:10.1007/s10973-020-09373-9
Mallikarjuna, K., Santhoshkumar Reddy, Y., Hemachandra Reddy, K., and Sanjeeva Kumar, P. V. (2021). A nanofluids and nanocoatings used for solar energy harvesting and heat transfer applications: A retrospective review analysis. Mater. Today Proc. 37, 823–834. doi:10.1016/j.matpr.2020.05.833
Rafiq, Muhammad, Shafique, Muhammad, Azam, Anam, and Ateeq, Muhammad (2021). Transformer oil-based nanofluid: The application of nanomaterials on thermal, electrical and physicochemical properties of liquid insulation-A review. Ain Shams Eng. J. 12, 555–576. doi:10.1016/j.asej.2020.08.010
Raju, C. S. K., and Sandeep, N. (2016). Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate with cross diffusion. J. Mol. Liq. 215, 115–126. doi:10.1016/j.molliq.2015.12.058
Reddy, S. C., Asogwa, K. K., Yassen, M. F., Adnan, , Iqbal, Z., M-Eldin, S., et al. (2022). Dynamics of MHD second-grade nanofluid flow with activation energy across a curved stretching surface. Front. Energy Res. 10, 1007159. doi:10.3389/fenrg.2022.1007159
SahbanAlnarabiji, Mohamad, and Husein, Maen M. (2020). Application of bare nanoparticle-based nanofluids in enhanced oil recovery. Fuel 267, 117262. doi:10.1016/j.fuel.2020.117262
Salari, Saeed, and Seid Mahdi Jafari, (2020). Application of nanofluids for thermal processing of food products. Trends Food Sci. Technol. 97, 100–113. doi:10.1016/j.tifs.2020.01.004
Saranya, Shekar, Baranyi, László, and Qasem, M. (2022). Al- Free convection flow of hybrid ferrofluid past a heated spinning cone. Therm. Sci. Eng. Prog.
Saranya, S., Ragupathi, P., Ganga, B., Sharma, R. P., and Abdul Hakeem, A. K. (2018). Non-linear radiation effects on magnetic/non-magnetic nanoparticles with different base fluids over a flat plate. Advanced Powder Technology, 29, doi:10.1016/j.apt.2018.05.002
SaswatKhatai, Ramanuj Kumar, Ashok Kumar Sahoo, , Panda, Amlana, and Das, Diptikanta (2020). Metal-oxide based nanofluid application in turning and grinding processes: A comprehensive review. Mater. Today Proc.
Usafzai, W. K., Aly, E. H., Alshomrani, A. S., and Ullah, M. Z. (2022). Multiple solutions for nanofluids flow and heat transfer in porous medium with velocity slip and temperature jump. Int. Commun. Heat Mass Transf. 131, 105831. doi:10.1016/j.icheatmasstransfer.2021.105831
Usri, N. A., Azmi, W. H., Rizalman, M., Abdul Hamid, K., and Najafi, G. (2015). Thermal conductivity enhancement of Al2O3 nanofluid in ethylene glycol and water mixture, 2015 international conference on alternative energy in developing countries and emerging economies. Energy Procedia 79, 397–402. doi:10.1016/j.egypro.2015.11.509
Vargas-Estrada, Laura, Torres-Arellano, S., Longoria, Adriana, Dulce, M., Arias, Patrick U., and Sebastian, P. J. (2020). Role of nanoparticles on microalgal cultivation: A review. Fuel 280, 118598. doi:10.1016/j.fuel.2020.118598
Vishnu Ganesh, N., Ganga, B., and Abdul Hakeem, A. K. (2014). Lie symmetry group analysis of magnetic field effects on free convective flow of a nanofluid over a semi-infinite stretching sheet. J. Egypt. Math. Soc. 22, 304–310. doi:10.1016/j.joems.2013.08.003
Xuan, Yimin, and Li, Qiang (2000). Heat transfer enhancement of nanofluids, school of power EngineeringP. Nanjing: Nanjing University of Science and Technology. eople's Republic of China.
k thermal conductivity, Wm−1K−1
H dimensionless fluid temperature
G dimensionless swirl velocity
Cp specific heat, Jkg−1K−1
M magnetic parameter
F dimensionless tangential velocity
g acceleration due to gravity, ms−2
L reference length, m
Nux local Nusselt number
Cf skin friction coefficient
B magnetic field intensity, kgs−2A−1
r dimensionless radius
Tr reference temperature, K
Gr Grashof number
To temperature of the cone surface, K
Pr Prandtl number
u,v,w velocity component in the x,y,z direction respectively
T temperature, K
Re local Reynolds number
y dimensionless coordinate normal to the surface
U reference velocity, ms−1
x dimensionless coordinate measured along the surface
β thermal expansion coefficient, K−1
ϕ nanoparticle volume fraction
ε spin parameter
γ half of vertex angle
Ω angular velocity of the cone
Θ dimensionless temperature ratio
Keywords: spinning down-pointing vertical cone, water–ethylene glycol, nanofluid, transverse magnetic field, heat transport
Citation: Iqbal Z, Yashodha S, Hakeem AKA, Alsawi A, Alyami MA, Yousef ES, Amin AH and Eldin SM (2022) Energy transport analysis in natural convective flow of water:Ethylene glycol (50:50)-based nanofluid around a spinning down-pointing vertical cone. Front. Mater. 9:1037201. doi: 10.3389/fmats.2022.1037201
Received: 05 September 2022; Accepted: 04 November 2022;
Published: 01 December 2022.
Edited by:
Safia Akram, National University of Sciences and Technology, PakistanReviewed by:
Aurang Zaib, Federal Urdu University of Arts, Sciences and Technology Islamabad, PakistanCopyright © 2022 Iqbal, Yashodha, Hakeem, Alsawi, Alyami, Yousef, Amin and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahoor Iqbal, aXphaG9vckBtYXRoLnFhdS5lZHUucGs=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.