
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater., 21 September 2022
Sec. Metamaterials
Volume 9 - 2022 | https://doi.org/10.3389/fmats.2022.1015839
This article is part of the Research TopicAcoustic and Mechanical Metamaterials for Various Applications - Volume IIView all 8 articles
Low sound speed or low-density materials can be used as soft acoustic boundaries in water, potentially as low-frequency underwater sound insulation. This study uses a chiral structure to construct an acoustic metascreen with deep subwavelength thickness. The results show that the transmission coefficient of the metascreen decreases noticeably in the low-frequency range when adjusting the chiral structure. The displacement pattern and the effective acoustic impedance are used to investigate the sound insulation mechanism. Low sound speed and effective acoustic impedance are found in the anisotropic chiral structure, and an extensive range of quasi-longitudinal wave phase velocities from 116.70 m/s to 3935.48 m/s can be obtained by adjusting the structural parameters without changing the filling rate. Finally, the effect of the oblique incidence angle on the sound insulation of the metascreen is investigated.
The use of acoustic metascreens (Leroy et al., 2009; Leroy et al., 2015) has great significance in shielding unwanted noise radiation from underwater equipment to reduce the interference of underwater acoustic communication and prevent sonar detection (Hladky-Hennion and Decarpigny, 1991; Zhang et al., 2013; Lanoy et al., 2018; Chen Y. et al., 2020; Wu et al., 2020; Dong et al., 2021).
Conventionally, the design paradigm of the acoustic metascreen is using a soft material (e.g., silicon rubber) embedded periodically with cavities (Leroy et al., 2015). Calvo et al. (2015) designed a metascreen by embedding monolayer and multilayer arrays of disk-shaped cavities into rubber. Results showed that sound attenuation is evident near the monopole resonance frequency of the cavity, and disk-shaped cavities have more sound insulation advantages than near-spherical cavities. Yang et al. (2019) proposed a metascreen made of periodically perforated rubber layers with metal plates and revealed the sound insulation mechanism using the complex band mechanism. Cai et al. (2019) developed a general method to construct three-dimensional (3D)-soft metascreen using bubbles as local resonance units in a 3D-printed frame. The experimental results showed that the obstruction of underwater sound in a wide frequency range from 2 to 26 kHz was achieved. However, insulation for underwater sound at frequencies below 2 kHz has been less explored because of the high penetrability of long wavelengths.
Compared with the above metascreens based on local resonance or Bragg scattering, recent reports show that the metascreens based on a functional lattice can provide new design paradigms for low-frequency broadband waterborne sound insulation (Chen Z. et al., 2020; Wang et al., 2022; Zhao et al., 2022). It was found that bi-mode materials with optimal azimuth are favorable for achieving extremely low acoustic impedance, displaying efficient sound insulation in low-frequency domains. Strong anisotropy is required when bi-mode materials possess a positive Poisson’s ratio. By contrast, weak anisotropy benefits for low acoustic impedance when bi-mode materials have a negative Poisson’s ratio. However, whether materials without bi-mode characteristics can achieve low-acoustic impedances remains an open question.
Recently, chiral structures have attracted growing interest in designing mechanical and thermal metamaterials with intriguing phenomena like negative Poisson’s ratios (Lakes et al., 2015; Wu et al., 2019; Liu et al., 2021; Yin et al., 2021). Chiral structures have recently also been introduced to underwater sound absorption (An et al., 2021). However, to our knowledge, the characteristics of low acoustic impedance and low sound speed of chiral structure have not been investigated.
This study introduces an anisotropic chiral structure made of aluminum with high density and elastic modulus as underwater sound insulation. A lower sound speed effect, resulting in lower effective acoustic impedance, is found in this anisotropic chiral structure with a metal matrix. The sound insulation mechanism of the acoustic metascreen is revealed using effective parameters and displacement patterns. Finally, the effect of incidence angle on the sound insulation of the acoustic metascreen is discussed.
This work considers two-dimensional acoustic wave propagation between water and a metascreen in a Cartesian coordinate system. As illustrated in Figure 1A, a harmonic plane wave is incident on the metascreen along the x direction from the left semi-infinite water domain. The metascreen is comprises two cover plate panels embedded with periodically anisotropic chiral structures.
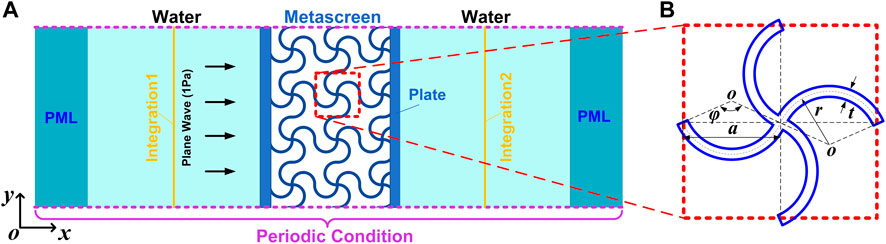
FIGURE 1. (A) Finite element model of sound transmission through a two-dimensional acoustic metascreen. (B) Schematic diagram of a unit cell from the metascreen.
The unit cell of the chiral structure is shown in Figure 1B. The unit cell consists of four identical arc beams connected at the head and distributed with rotational symmetry around the center junction. The chiral structure is characterized by four main parameters: the central angle
Full-wave simulations are performed using the Acoustic Solid interaction, Frequency Domain Interface of the COMSOL Multiphysics to evaluate the metascreens’ sound insulation capabilities. In the numerical model, the acoustic metascreen, which is infinite in the
Acoustic structural boundaries are applied to the two interfaces between the metascreen and water. Both horizontal purple dashed lines in Figure 1A represent periodic boundaries. A plane wave with 1 Pa amplitude is incident on the metascreen from the left side of the water domain. Both outer boundaries are set to perfectly matched layer (PML) conditions to simulate anechoic termination for the scattering wave. The transmission coefficient of sound energy is calculated using the ratio of the integral of the incident and transmitted sound fields at the solid yellow lines in Figure 1A.
Figure 2A compares the transmission coefficients of the metascreens embedded with different chiral structures. Here the metascreens are denoted as A0, A150, A190, and A230 for chiral structures with central angles of
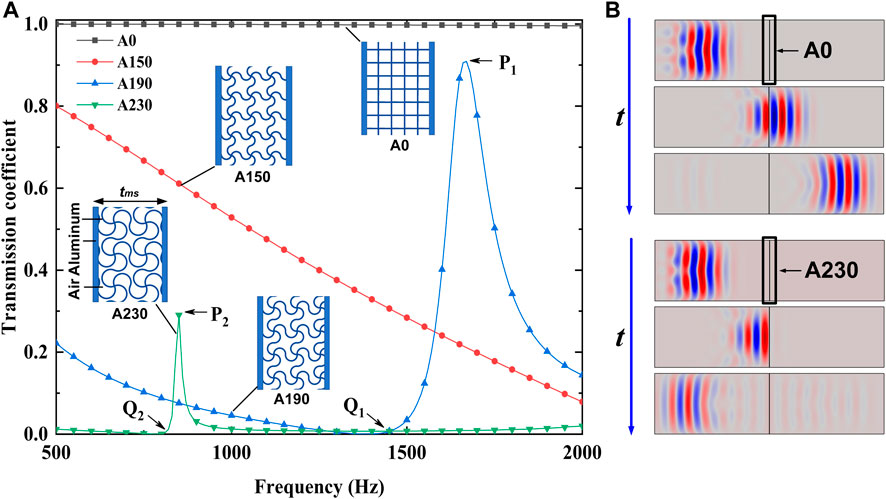
FIGURE 2. (A) The variation of the metascreen transmission coefficient frequency for different central angles φ. The inset diagrams show the A0, A150, A190, and A230 metascreens. (B) The time-domain sound transmission of A0 and A230 for an incident transient Gaussian pulse.
From Figure 2A, one can see that the metascreen transmission coefficient in the low-frequency band decreases noticeably with increasing central angle
Time-domain simulations are carried out to display the sound insulation performance of the acoustic metascreen more intuitively. The incidence of a Gaussian pulse with frequency around
The homogenization method (Bensoussan and Alain, 1978; Cheng et al., 2013) based on a unit cell is used to obtain the effective parameters of the chiral structures, which mainly determine the effective metascreen properties. According to the homogenization theory, the fourth effective elastic tensor of the chiral lattice material is
which can be calculated by
where
In addition, the displacement field
where
where
where
where
The effective parameters of the metascreens at low frequency can then be calculated as follows (Chen Y. et al., 2020; Wang et al., 2022):
where,
To intuitively observe the variation of the unit cell with the degree of chirality, Figure 3 shows the unit cells for increasing central angle
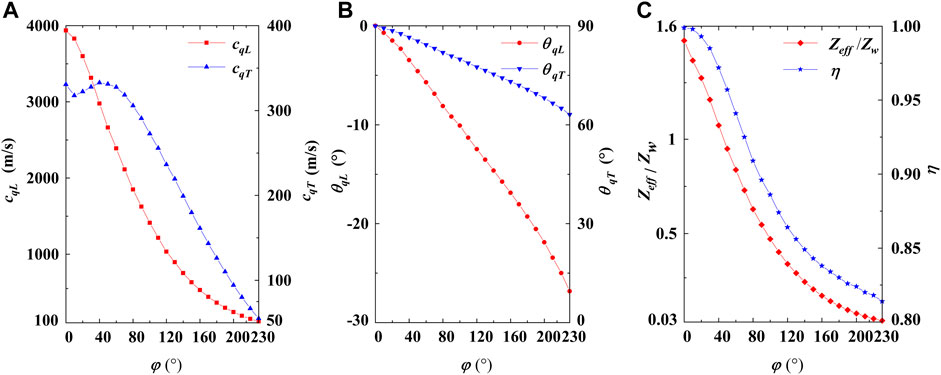
FIGURE 4. (A) The variation in phase velocities of the qL wave (cqL) and the qT wave (cqT) of the metascreens with central angle φ. (B) The variation in polarization angles θqL and θqT of the metascreens with central angle φ. (C) The variation in normalized impedance Zeff/Zw and polarization factor η of the metascreens with central angle φ.
As shown in Figure 4A, a significant decrease in the phase velocity of the qL wave
Figure 4C shows that, the effective acoustic impedance
To clearly show the effective parameters variations in Figure 4; Table 2 presents the effective parameters of the four metascreens embedded with chiral structures having central angles
The displacement deformation fields for A190 and A230 are investigated to explain the formation of their transmission coefficient peaks and valleys in Figure 2A. As shown in Figures 5A,B, at the transmission valley frequency, the displacement along the
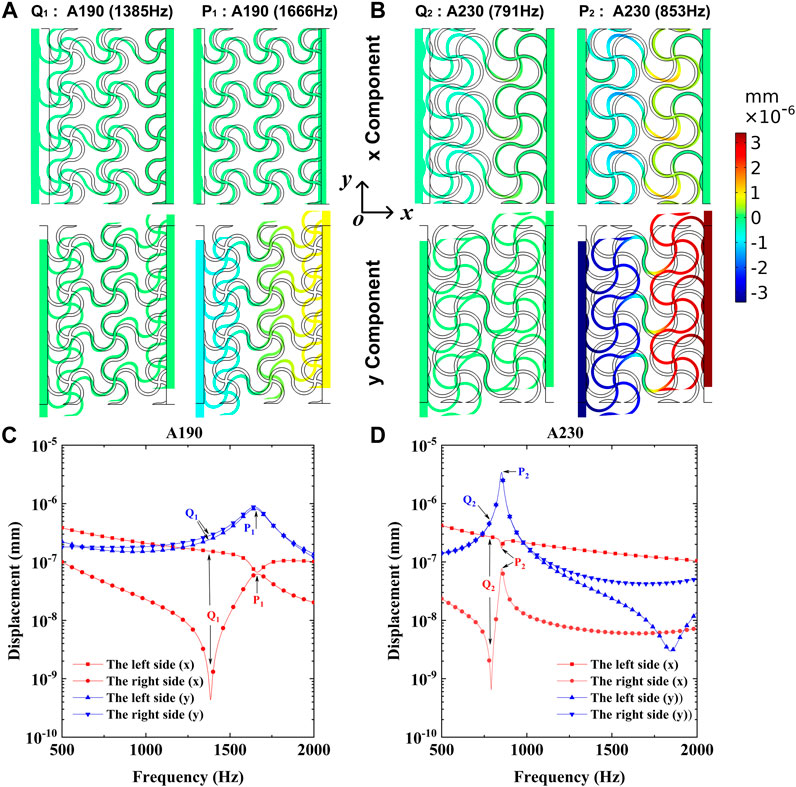
FIGURE 5. (A,B) are the displacement deformation fields at the transmission peak and valley frequencies, (C) and (D) are the average absolute displacements of the
One can also see from Figure 5 that the displacement along the
Finally, Figure 6 shows the effect of oblique incidence angle on the sound transmission coefficients for metascreens A0 and A230. One can see that A0 is almost transparent for waterborne sound at various oblique incidences (Figure 6A), although the transmission coefficient decreases to 0.8 at the 60° incidence angle. However, A230 maintains good underwater sound insulation performance at different oblique incidences (Figure 6B). Note that a new weak transmission peak appears when the incidence angle is above 28°. The displacement fields and the AAD can again interpret the underlying mechanisms of the A230 transmission peaks. Figures 6C–F show the displacement fields and the AAD for incidence angles of 15° and 45°. At the incidence angle of 15°, the displacement field and the AAD are similar to those at the normal incidence. The minimum displacement along the
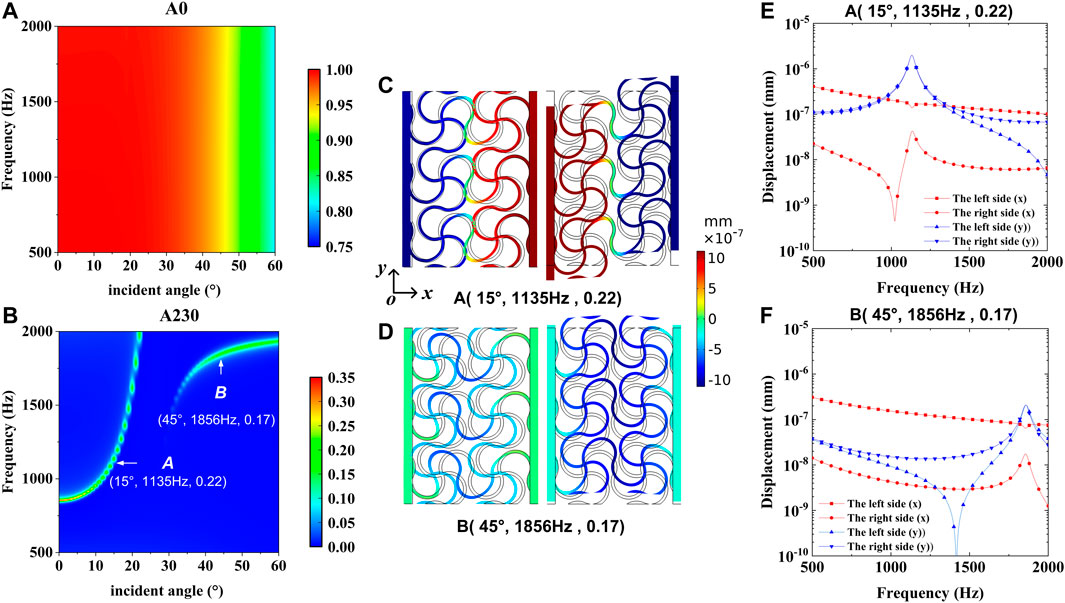
FIGURE 6. (A,B) are the acoustic transmission coefficients for metascreens A0 and A230, respectively, versus the incidence angle and frequency. (C,D) are the displacement fields at the transmission peak frequency points of A230 at 15° and 45° incidence angles, respectively. (E) and (F) show the average absolute displacement of A230 in the x and y components at 15° and 45° incidence angles, respectively.
The anisotropic chiral aluminum lattice is introduced to construct a metascreen for low-frequency underwater sound insulation. The results show that the metascreen transmission coefficient decreases noticeably in the low and broad frequency range with the degree of chirality for the same filling rate. The average transmission coefficient can be lowered to 0.0145 in the frequency range of 500–2000 Hz.
The effective acoustic properties of different metascreens are investigated using the homogenization method. It is found that an extensive quasi-longitudinal wave phase velocity range from 116.70 m/s to 3935.48 m/s can be obtained by adjusting the central angle without changing the filling rate. In addition, lower effective sound velocity and effective acoustic impedance of the metascreen can be achieved by increasing the degree of chirality, which contributes to low-frequency sound insulation.
The sound insulation mechanism is further investigated through the displacement pattern and effective acoustic impedance. The low phase velocity of the quasi-longitudinal wave and low polarization factor collectively lead to the low effective acoustic impedance of the metascreen. It is also shown that the shear resonance related to the extremely low phase velocity of the quasi-transverse wave results in the metascreen transmission peak.
The effect of oblique incidence angle on the metascreen’s sound insulation ability is also investigated, and the good sound insulation performance of the A230 metascreen is generally robust at different incidence angles. Overall, this study paves a promising avenue for anisotropic chiral structures with applications to underwater sound insulation.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
CW: Writing-original draft preparation, software, writing-review and editing. YW and HZ: Software, writing-review and editing. JZ, HY, DY, and JW: Writing-review and editing, supervision.
This work is supported by NSFC (Grant Nos. 52171327, 11991032, and 51805537).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
An, X., Lai, C., He, W., and Fan, H. (2021). Three-dimensional chiral meta-plate lattice structures for broad band vibration suppression and sound absorption. Compos. Part B Eng. 224, 109232. doi:10.1016/j.compositesb.2021.109232
Bensoussan, , and Alain, (1978). Asymptotic analysis for periodic structures/. North-Holland Pub. Co.
Cai, Z., Zhao, S., Huang, Z., Li, Z., Su, M., Zhang, Z., et al. (2019). Bubble architectures for locally resonant acoustic metamaterials. Adv. Funct. Mat. 29, 1906984. doi:10.1002/adfm.201906984
Calvo, D. C., Thangawng, A. L., Layman, J. C. N., Casalini, R., and Othman, S. F. (2015). Underwater sound transmission through arrays of disk cavities in a soft elastic medium. J. Acoust. Soc. Am. 138, 2537–2547. doi:10.1121/1.4931446
Chen, Y., Zhao, B., Liu, X., and Hu, G. (2020a). Highly anisotropic hexagonal lattice material for low frequency water sound insulation. Extreme Mech. Lett. 40, 100916. doi:10.1016/j.eml.2020.100916
Chen, Z., Yan, F., Negahban, M., and Li, Z. (2020b). Resonator-based reflective metasurface for low-frequency underwater acoustic waves. J. Appl. Phys. 128, 055305. doi:10.1063/5.0006523
Cheng, G., Cai, Y., and Xu, L. (2013). Novel implementation of homogenization method to predict effective properties of periodic materials. Acta Mech. Sin. 29, 550–556. doi:10.1007/s10409-013-0043-0
Dong, H. W., Zhao, S. D., Miao, X. B., Shen, C., Cheng, L., Zhao, Z., et al. (2021). Customized broadband pentamode metamaterials by topology optimization. J. Mech. Phys. Solids 152, 104407. doi:10.1016/j.jmps.2021.104407
Hladky-Hennion, A. C., and Decarpigny, J. N. (1991). Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: Application to Alberich anechoic coatings. J. Acoust. Soc. Am. 90, 3356–3367. doi:10.1121/1.401395
Lakes, R. S., Plesha, M, E., Li, J., and Chan, S. H. (2015). Controllable thermal expansion of large magnitude in chiral negative Poisson's ratio lattices. Phys. Status Solidi B 252, 1431–1434. doi:10.1002/pssb.201552158
Lanoy, M., Guillermic, R. M., Strybulevych, A., and Page, J. H. (2018). Broadband coherent perfect absorption of acoustic waves with bubble meta-screens. Appl. Phys. Lett. 113, 171907. doi:10.1063/1.5051341
Leroy, V., Strybulevych, A., Lanoy, M., Lemoult, F., Tourin, A., and Page, H. J. (2015). Super-absorption of acoustic waves with bubble meta-screens. Phys. Rev. B 91, 020301(R). doi:10.1103/PhysRevB.91.020301
Leroy, V., Strybulevych, A., Scanlon, M. G., and Page, J. H. (2009). Transmission of ultrasound through a single layer of bubbles. Eur. Phys. J. E 29, 123–130. doi:10.1140/epje/i2009-10457-y
Li, Y., Liang, B., Zou, X., and Cheng, J. (2013). Extraordinary acoustic transmission through ultrathin acoustic metamaterials by coiling up space. Appl. Phys. Lett. 103, 063509. doi:10.1063/1.4817925
Liu, J., Yan, D., Pang, W., and Zhang, Y. (2021). Design, fabrication and applications of soft network materials. Mat. TodayKidlingt. 49, 324–350. doi:10.1016/j.mattod.2021.05.007
Lu, M., Liu, X., Feng, L., Li, J., Huang, C., Chen, Y., et al. (2007). Extraordinary acoustic transmission through a 1D grating with very narrow apertures. Phys. Rev. Lett. 99, 174301. doi:10.1103/PhysRevLett.99.174301
Wang, Y., Zhao, H., Yang, H., Liu, J., Yu, D., and Wen, J. (2022). Topological design of lattice materials with application to underwater sound insulation. Mech. Syst. Signal Process. 171, 108911. doi:10.1016/j.ymssp.2022.108911
Wu, H., Hao, C., and Zhang, H. (2020). Underwater broadband sound insulation with chiral spiral structures. AIP Adv. 10, 125022. doi:10.1063/5.0025486
Wu, W., Hu, W., Qian, G., Liao, H., Xu, X., and Berto, F. (2019). Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mat. Des. 180, 107950. doi:10.1016/j.matdes.2019.107950
Yang, H., Xiao, Y., Zhao, H., Zhong, J., and Wen, J. (2019). On wave propagation and attenuation properties of underwater acoustic screens consisting of periodically perforated rubber layers with metal plates. J. Sound. Vib. 444, 21–34. doi:10.1016/j.jsv.2018.12.031
Yin, Y., Zhao, Z., and Li, Y. (2021). Theoretical and experimental research on anisotropic and nonlinear mechanics of periodic network materials. J. Mech. Phys. Solids 152, 104458. doi:10.1016/j.jmps.2021.104458
Zhang, Y., Wen, J., Zhao, H., Yu, D., Cai, L., and Wen, X. (2013). Sound insulation property of membrane-type acoustic metamaterials carrying different masses at adjacent cells. J. Appl. Phys. 114, 063515. doi:10.1063/1.4818435
Keywords: acoustic metascreen, chiral structure, underwater sound insulation, homogenization, effective parameter
Citation: Wang C, Zhao H, Wang Y, Zhong J, Yang H, Yu D and Wen J (2022) Low-frequency waterborne sound insulation by an acoustic metascreen with a metal chiral structure. Front. Mater. 9:1015839. doi: 10.3389/fmats.2022.1015839
Received: 10 August 2022; Accepted: 22 August 2022;
Published: 21 September 2022.
Edited by:
Fuyin Ma, Xi’an Jiaotong University, ChinaReviewed by:
Fengxian Xin, Xi’an Jiaotong University, ChinaCopyright © 2022 Wang, Zhao, Wang, Zhong, Yang, Yu and Wen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Honggang Zhao, emhoZzk2MDNAc2luYS5jb20=; Jihong Wen, d2Vuamlob25nQHZpcC5zaW5hLmNvbQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.