Tuning the ionic character of sodium dodecyl sulphate via counter-ion binding: An experimental and computational study

Solutions of surfactants exhibit remarkable features, such as a tunable amphiphilic character, which can further be varied for ionic surfactants through variations in their Coulombic interactions. These properties are very useful in many industrial applications such as in extraction, purification, and formulation processes, as detergents, wetting agents, or emulsifiers. Rather unexpectedly, the addition of tetrabutylammonium chloride ([N_4,4,4,4]Cl) to solutions of the ionic surfactant of sodium dodecyl sulphate (SDS) results in the appearance of a phase transition above the lower critical solution temperature (LCST), a property usually associated with non-ionic surfactants. The aim of this study is to provide a detailed nanoscopic scenario on the interaction between SDS micelles and [N_4,4,4,4]Cl moieties to better understand the nature of the LCST cloud point and how to confer it to a given ionic surfactant system. A coarse-grained molecular dynamics (CG-MD) computational framework, under the latest MARTINI 3.0 force field, was developed and validated using available literature data. The impact of [N_4,4,4,4]Cl concentration in the phase of SDS micellar aqueous solutions was then characterized and compared using experimental results. Specifically, dynamic light scattering (DLS) measurements and small-angle X-ray scattering (SAXS) profiles were obtained at different [N_4,4,4,4]⁺/[DS]^- molar ratios (from 0.0 to 1.0) and compared with the CG-MD results. A good agreement between computer simulations and experimental findings was obtained, reinforcing the suitability of GC-MD to simulate complex phase behaviors. When the [N_4,4,4,4]⁺/[DS]^- molar ratio is < 0.5, a weak impact of the cation in the micellar distribution was found whereas for ratios > 0.5, the system yielded clusters of enclosed small [DS]^- aggregates. Thus, the CG-MD simulations showed the formation of mixed [DS]^- and [N_4,4,4,4]⁺ aggregates with [N_4,4,4,4]⁺ cations acting as a bridge between small [DS]^- micelles. The CG-MD simulation framework developed in this work captured the role of [N_4,4,4,4]⁺ in the micellar phase transition whilst improving the results obtained with preceding computer models for which the limitations on capturing SDS and [N_4,4,4,4]Cl mixtures in aqueous solutions are also shown in detail.

1 Introduction

Stimuli-responsive systems can change their phase behavior after a temperature, magnetic field, light, or pH adjustment. Exploiting these properties allows for the design of novel and more efficient applications such as the purification of biomolecules, drug delivery nanocarriers, or the recovery of valuable compounds from wastewater (Ventura et al., 2017; Schaeffer et al., 2019a). Thermo-responsive systems can also be used for integrated reaction-separation processes (Ferreira et al., 2018; Morais et al., 2021). In this context, the reaction takes place under homogeneous conditions prior to the separation of products and catalysts/reactants into separate phases after the temperature change (Kohno et al., 2011; Ferreira et al., 2018). Thermo-responsive systems can exhibit an upper or lower critical solution temperature (UCST/LCST), depending on whether entropic (LCST) or enthalpic (UCST) terms dominate, led by solute-water interactions, mostly hydrogen bonding and strong polar interactions (Kohno and Ohno, 2012). Looking beyond the design of integrated reaction-separation systems, thermo-responsive systems were further demonstrated as draw solutions for forward osmosis desalination (Zhong et al., 2016) or heat storage media (Forero-Martinez et al., 2022).

Thermo-responsive systems presenting a LCST behavior are traditionally restricted to non-ionic polymeric and surfactant systems (Mukherjee et al., 2011) with few ionic systems exhibiting temperature dependent phase separation (Mukherjee et al., 2011; Naqvi and Kabir-ud-Din, 2018). However, aqueous solutions of bulky quaternary phosphonium or ammonium salts, often referred to as ionic liquids (ILs), were shown to phase separate upon heating with the cloud point dependent on the hydration properties of the anion (Gutowski et al., 2003; Martínez-Aragón et al., 2009; Freire et al., 2012; Schaeffer et al., 2018; Meyer et al., 2022). One example of such a system is the mixture of tetrabutylammonium halide ([N_4,4,4,4]X (X = Cl or Br) with the anionic surfactant sodium dodecyl sulphate (SDS) (Chauhan and Kaur, 2017). As an example, this aqueous [N_4,4,4,4]Cl/SDS mixture was applied towards the one-pot process for the solid–liquid extraction of violacein from Yarrowia lipolytica yeast biomass and its purification by estimating the LCST point using the cloud-point method to analyze the separation from contaminant proteins (Schaeffer et al., 2019b). Interestingly, the [N_4,4,4,4]X and SDS mixtures exhibit an anomalous temperature dependent behavior as a function of the [N_4,4,4,4]Cl concentration in SDS aqueous solutions (Mata et al., 2004; Schaeffer et al., 2019a). This system was experimentally characterized by cloud point measurements, dynamic light scattering (DLS), surface tension, (Bales and Zana, 2004; Mata et al., 2004), calorimetry (Mitra et al., 2007) or nuclear magnetic resonance (NMR) (Lin et al., 2013). Results indicate that the system properties result from extensive adsorption of the [N_4,4,4,4]⁺ cation of the [DS]^- micelles due to the low charge density, and therefore lower hydration, of the [DS]^- polar head, and large apolar volume of the symmetrical [N_4,4,4,4]⁺ ion. Nevertheless, these are all equilibrium-based measurements that only partially probe the dynamic nature of this system and the driving forces determining co-aggregation and phase separation. Considering the theoretical and practical relevance of conferring thermo-responsive behavior to ionic systems, a detailed understanding of the interactions and how these systematically vary with the molar ratio of [N_4,4,4,4]⁺ to [DS]^- is of interest.

The interactions at the nanoscale directing the self-assembly and aggregation in colloidal systems are rather complex and a difficult issue for experimentalists. Fortunately, molecular dynamics simulations provide the required level of detail to analyze the interactions between SDS and [N_4,4,4,4]Cl moieties and the complex cooperative self-assembly. For instance, E. Ritter et al. Berthod et al. (1991) carried out all-atom molecular dynamics (AA-MD) simulations with the COSMOmic (Klamt et al., 2008) package using preformed SDS micelles. In this work, a comprehensive analysis of micelle distributions for a wide number of surfactants (SDS, CTAB (cetyltrimethylammonium bromide), C₁₂E₁₀, Brij35, C₁₂E₂₃, Triton X-114 and Triton X-100 was developed, with good agreement to experiments, demonstrating that simulations can be a remarkable tool for predicting relevant properties of these micellar solutions. However, they were limited to study pre-assembled structures since AA-MD models cannot cope with the size/time scale to reproduce the self-assembly of relatively large structures. Manhub et al. Mahbub et al. (2019) studied the micellization of SDS and CTAB aqueous solutions and the impact of various salts at different temperatures using AA-MD simulations and the universal force field (UFF). They carried out experimental conductivity measurements to estimate the critical micelle concentrations, which was used as a reference for the MD simulations. MD results demonstrated that salts enhanced the interactions between the surfactants. The authors evaluated the formation of CTAB/SDS micelles and the complex interactions between both surfactants. The MD also demonstrated that the addition of salt enhanced the electrostatic interactions between SDS and CTAB moieties, in agreement with the experimental results. Tang et al. Tang et al. (2014) evaluated the effect of the diverse available force fields on the aggregation of SDS in water using AA-MD simulations. Using preformed structures, they found a low impact from the force field choice with small SDS aggregates, but vesicles rather than the expected rod-like structures were found when the SDS aggregate size was increased. Closer to the identified problematic, Liu et al. Liu et al. (2016a), Liu et al. (2016b) studied the influence of different tetraalkylammonium counterions (tetraalkylammonium [N_n,n,n,n]⁺, tetramethylammonium [N_1,1,1,1]⁺, tetraethylammonium [N_2,2,2,2]⁺, tetra propylammonium [N_3,3,3,3]⁺ and [N_4,4,4,4]⁺) on [DS]⁻ micelles using AA-MD simulations, focusing on the analysis of systems containing a single pre-formed micelle to investigate the various interaction patterns between the components.

However, time and size scale restrictions inherent in molecular dynamics atomistic models (AA-MD) limits their use to the initial stages of micelle formation, leaving out the relevant study of any inter micelle interactions and phase behaviour. (Illa-Tuset et al., 2018). The less detailed but more computationally efficient coarse-grained molecular dynamics (CG-MD) models can overcome such limitations, appearing as crucial tools to analyze the impact of [N_4,4,4,4]Cl on the phase behavior of SDS aqueous solutions. (Pérez-Sánchez et al., 2016; Chien et al., 2017; Illa-Tuset et al., 2018; Pérez-Sánchez et al., 2020). Progress towards this was made by Jalili et al. Jalili and Akhavan (2009) who used the MARTINI 2 CG-MD framework to model SDS aqueous solutions, with good agreement to previous AA-MD results (Gao et al., 2005; Sammalkorpi et al., 2007; Ritter et al., 2016) and to experimental micelle results. (Quina et al., 1995; Anachkov et al., 2012; Hammouda, 2013). LeBard et al. Lebard et al. (2012) performed CG-MD simulations to characterize the micellar distributions of three surfactants, including aqueous solutions of SDS. In that work, the authors conducted a comprehensive study regarding the impact of surfactant concentration on the aggregation number, noticing polydispersity of micelle sizes, and the impact that the type of hardware has on those values, with the CG-MD results compared with experimental literature data. The new method developed by the authors where CG-MD data is used as an input for the theoretical model, demonstrated that can predict critical micelle concentrations (CMC) in good agreement with literature data. However, LeBard et al. Lebard et al. (2012) used the HOOMD-Blue package for MD simulations and an ad hoc SDK force field for the SDS, with the consequence loss of transferability and generality offered by the MARTINI model and the GROMACS package. Ruiz-Morales et al. Ruiz-Morales and Romero-Martínez (2018) carried out CG-MD simulations with the MARTINI 2.2 model to evaluate the impact of the simulation box size on the critical micelle concentration and shear viscosity. They demonstrated the ability of MARTINI 2.2 for obtaining dynamic properties such as viscosity, finding a very good agreement with literature experimental data and improving upon the results of more detailed AA-MD models. Recently, Anogiannakis et al. Anogiannakis et al. (2020) used MARTINI 2.2 to perform CG-MD simulations of SDS and CTAB aqueous solutions. In that work they estimated the CMC, aggregation numbers and small angle neutron scattering (SANS) patterns at low concentrations, as well as the liquid crystal phase behavior. Specifically, the authors used the Dry MARTINI 2.2 forcefield where some adjustments were introduced in the non-bonded interactions to find a good agreement with literature data. However, the Dry MARTINI 2.2 model has some inherent limitations when compared with the explicit water MARTINI 2.2 version, since a new parameterization of all interactions must be carried out when new moieties are included in the system.

With the aim to find a general, transferable, and reliable computer model to tackle SDS and [N_4,4,4,4]Cl aqueous solutions, the MARTIN 2.2 model was initially selected. The regular and polarizable water models were benchmarked, exhibiting both advantages and disadvantages when reproducing experimental results of micelle distribution and the impact of [N_4,4,4,4]Cl on SDS aqueous solutions. Fortunately, with the advent of the recently released MARTINI 3.0 (42) and the validated SDS and [N_4,4,4,4]Cl CG-MD models, the advantages and disadvantages converged in the new MARTINI 3.0 as detailed below. Thus, the manuscript is organized as follows; the technical aspects of the CG-MD simulations and ad hoc experiments are described in the Methods section, as well as the topology and model benchmark. This is followed by the CG-MD results on the impact of [N_4,4,4,4]Cl in SDS aqueous solutions, which are presented for the selected model. Simulation snapshots are discussed regarding the characterization of the phase behavior, along with computed Small-angle X-ray scattering (SAXS) profiles that are compared with experimental results obtained for this study. Additionally, dynamic light scattering (DLS) and NMR experimental data were used to characterize the phase behavior.

2 Methodology

2.1 Simulation details

All simulations were performed with the 2019 GROMACS package (Lindahl et al., 2018), which integrates the equations of motion using the leapfrog algorithm (Hockney et al., 1974) with a 20 fs time step. The total potential energy entails bonded interactions for bond stretching and angle bending—bonds were compelled with the LINear Constraint Solver (LINCS) (Hess et al., 1997)—whereas non-bonded ones used the Lennard-Jones (LJ) potential and the regular Coulomb interaction function—long-range electrostatic interactions were assessed using the Particle-Mesh-Ewald (PME). (Darden et al., 1993). The non-bonded interactions were calculated with the Verlet cutoff scheme (potential-shift-Verlet modifier) and a cut-off of 1.2 nm. The temperature (298K and coupling time constant of 1.0 ps) and pressure (1 bar and isotropic coupling with a time constant of 24.0 ps) were set with the velocity-rescaling thermostat (Bussi et al., 2007) and Parrinello-Rahman barostat, (Parrinello and Rahman, 1981), respectively. The simulation boxes were created with Packmol, (Martínez et al., 2009), setting the molecules randomly, with periodic boundary conditions in all directions.

Prior to the NpT ensemble production runs, an energy minimization step was done using the steepest descent algorithm to avoid close contacts between molecules which could occur in the preparation of the initial simulation boxes. Afterwards, two equilibrium MD simulations were carried out on the NVT and NpT ensembles to establish the desired temperature and density, respectively. The total potential energy, pressure, temperature, and densities were monitored alongside the equilibrium steps and production runs to ensure the thermodynamic equilibrium. The Visual Molecular Dynamics (VMD) software package (Humphrey et al., 1996) was used to visualize the systems. The micellar distributions were analyzed using an in-house code (Jorge, 2008) based in the Hoshen–Kopelman cluster counting algorithm (Hoshen and Kopelman, 1976). Computed SAXS profiles in the MD simulations were obtained with the gmx saxs Gromacs tool which calculates the SAXS structure factors for given coarse-grained form factors based on Cromer’s method (Cromer and Mann, 1968).

2.2 Experimental methodology

Tetrabutylammonium chloride (97% purity) and sodium dodecyl sulfate (Pharmaceutical grade) were obtained from Sigma Aldrich (United States) and Panreac (Germany), respectively. A series of samples were prepared gravimetrically with varying proportions of SDS, [N_4,4,4,4]Cl and water molecules. The specific compositions are provided in Supplementary Table S1. Ultrapure, double distilled water, passed through a reverse osmosis system and further treated with a Milli-Q plus 185 water purification apparatus, (18.2 MΩ.cm at 25°C) was used for all experiments.

Small angle X-ray scattering (SAXS) measurements were made of each of these samples at the SAXS/WAXS beamline of the Australian Synchrotron. Samples were loaded into 1.5 mm quartz capillaries and sealed with epoxy. Scattering patterns were acquired at room temperature over 1 s, using an X-ray energy of 11.5 keV and a scattering vector range of 0.01–0.44 Å^-1. The 2D scattering profiles were converted to intensity vs. scattering vector, and the scattering contribution from an empty capillary subtracted, using the software Scatterbrain (http://archive.synchrotron.org.au/aussyncbeamlines/saxswaxs/software-saxswaxs).

¹H-NMR measurements were performed on a Bruker Avance 300 NMR spectrometer (Germany) operating at 300 MHz and 298 K. Samples were analyzed in a glass NMR tube with an added sealed capillary in a coaxial insert containing D₂O and trimethylsilyl propanoic acid as an internal reference, both purchased from SigmaAldrich (United States). The formation of aggregates was followed by dynamic light scattering (DLS) using a Zetasizer Nano-ZS photometer from Malvern Instruments (United Kingdom). Sample preparation for NMR and DLS were identical and contained a fixed SDS concentration of 2 wt%, with all samples prepared gravimetrically. Following the weighing of SDS, [N_4,4,4,4]Cl and H₂O, all samples were equilibrated for 24 h. Prior to the analyses, all samples were filtered through a nylon 0.45 μm syringe, sonicated in an ultrasonic bath for 5 min to promote particle dispersion and degassing and left to rest in a sealed quartz cuvette. DLS analyses were carried at 298 K, with an equilibration time of 120 s. Irradiation was performed at a wavelength of 565 nm by a helium-neon laser and scattered light was detected at a backscattering angle of 173°. The automatic mode was used for both measurements and data processing, the viscosity and refractive index of water was used. Analyses were performed in triplicate and extracted results are averages.

2.3 Molecular modelling and coarse-grained model validation

2.3.1 Validation of individual and mixed sodium dodecyl sulphate and [N_4,4,4,4]Cl aqueous solutions in MARTINI 2.2

The MARTINI 2.2 model (Marrink et al., 2007) CG model was chosen initially since it reproduces reasonably well the micelle distribution of SDS aqueous solutions. Thus, three apolar C₁ beads for the alkyl-chain tail and a charged Q_a (a meaning hydrogen bond acceptor) for the Sulphur head group were used (Jalili and Akhavan, 2009). The Q_d (d meaning hydrogen bond donor) was selected for the Na⁺ counterions whereas Q_a was chosen for Cl⁻. For [N_4,4,4,4]⁺, the ammonium center is represented with a Q₀ bead whilst the butyl groups are mapped with C₃ beads (Bastos et al., 2020). The P₄ and antifreeze BP₄ bead types, which implicitly include four water molecules, were selected to solvate the SDS system where 10% of BP₄ was included to avoid any unrealistic freezing of the regular MARTINI 2.2 water (Marrink et al., 2007). Supplementary Figure S1 illustrates the MARTINI 2.2 CG mapping for all molecules. Initially, a CG-MD simulation test was run for 3 μs with the aim to reproduce the micellar distribution of a 2 wt% of SDS concentration in aqueous solution. A spherical micellar solution was found with an averaged micelle aggregation number of N_agg = 60, in good agreement with experimental estimates N_agg ∼ 50–73 (Berthod et al., 1991; Itri and Amaral, 1991; Quina et al., 1995; Bales et al., 1998; Anachkov et al., 2012). Supplementary Figure S2A shows the final CG-MD simulation snapshot, and the micelle density profile was obtained with our cluster counting code displaying spherical micelles with an averaged diameter of Ø = 3.6 nm. Similarly, the [N_4,4,4,4]⁺ CG model was previously developed (Bastos et al., 2020) consisting of three apolar C₃ beads for the butyl groups and one Q₀ (0 meaning no hydrogen bond donor/acceptor capability) to map the nitrogen charged center. The Q_a was selected for the Cl⁻ counterions. To ensure that this system does not excessively aggregate in line with reported polarizable AA-MD results, (Dong et al., 2017), a simulation test of a 6 wt% of [N_4,4,4,4]Cl in aqueous solution was also run over 3 μs. As can be noticed in Supplementary Figure S2B, no evidence of aggregation was found where the simulation box density profile—obtained with the gmx density Gromacs tool—showed a homogeneous distribution of [N_4,4,4,4]Cl in the simulation box. The density of the simulation box was ρ = 0.93 g cm⁻³, in reasonable agreement with the experimental result of ρ = 1.018 g cm⁻³ (Jain et al., 2013).

Then, different concentrations of [N_4,4,4,4]Cl were included in a 2 wt% of SDS aqueous solution where the systems were arranged by randomly placing all molecules in the simulation box using the Packmol code (Martínez et al., 2009). In this manner, 0.1, 0.3, 0.5, 0.7, and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios were addressed to compare with DLS and NMR experiments carried out in this work. Therefore, the average hydrodynamic diameter (by volume) of aggregates in solution were obtained by DLS measurements and the results at different [N_4,4,4,4]⁺/[DS]^- ratios are shown in Supplementary Figure S3A. Furthermore, Supplementary Figure S3B shows the NMR shift of the mixture relative to that of the pure compounds in water, which was obtained to highlight the difference between SDS, [N_4,4,4,4]Cl aqueous solutions and their mixtures. Supplementary Figure S4 shows the simulation snapshots for 0.3, 0.5, and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios after 1.5 μs. Therefore, while the MARTINI 2.2 model reproduced SDS aqueous solutions very well in terms of the micellar distribution (Berthod et al., 1991; Itri and Amaral, 1991; Quina et al., 1995; Bales et al., 1998; Anachkov et al., 2012), whilst no clumped structures were seen in the 6 wt% [N_4,4,4,4]Cl aqueous solution simulation. (Dong et al., 2017). In addition, the 2 wt% of SDS aqueous solution exhibited spherical micelles with an averaged diameter ∅ ∼ 3.6 nm in reasonable agreement to what it was found in the DLS experiments at [N_4,4,4,4]⁺/[DS]^- = 0.0 (Supplementary Figure S3A). Unfortunately, the MARTINI 2.2 could not capture the micellar-to-clustered transition noticed in our experiments when [N_4,4,4,4]⁺/[DS]^- > 0.5 as shown in Supplementary Figure S3A. Conversely, prolate and rod like structures were obtained in our CG-MD simulations as shown in Supplementary Figure S4, mainly formed by small and joined [DS]^- aggregates, in contrast with the well-know SDS homogeneous micellar phase commonly found in the literature (Itri and Amaral, 1991; Bales et al., 1998). The solution with a ratio of 0.5 [N_4,4,4,4]⁺/[DS]^- shown in Supplementary Figure S4B exhibited a spherical aggregate formed by clumpled small [DS]^- aggregates with some interleaved [N_4,4,4,4]⁺ moieties in the center, acting as a bridge between them. Similarly, Supplementary Figure S4C displays a similar scenario for the solution with a ratio of [N_4,4,4,4]⁺/[DS]^- = 1.0 but the [N_4,4,4,4]⁺ moieties were homogeneously arranged in the spherical aggregate. Analogous scenarios were found for [N_4,4,4,4]⁺/[DS]^- ratios of 0.1 and 0.7 (not shown in Supplementary Figure S4) indicating that the MARTINI 2.2 framework cannot capture the micellar-to-clustered transition above the 0.5 ratio as displayed in the experiments (Supplementary Figure S3A). The simplicity of the regular MARTINI 2.2 water model, with a very limited energy landscape among other limitations (use of water antifreeze beads), could be the reason behind this issue.

2.3.2 Validation of individual and mixed sodium dodecyl sulphate and [N_4,4,4,4]Cl aqueous solutions with polarizable water in MARTINI 2.2

Since the polarizable water (PW) model available in MARTINI 2.2 offers a better perspective for the energy landscape, the PW model developed by Yesylevskyy et al. (2010) was used in the above systems. No clumping was found for the 6 wt% [N_4,4,4,4]Cl aqueous solution simulation test after 3 μs from, in agreement with literature (Dong et al., 2017). Then, the SDS 2 wt% aqueous solution was run to evaluate the impact of the polarizable water in the SDS micelle distribution. Unfortunately, small spherical micelles with an averaged aggregation number of N_agg = 20 were obtained after 1.5 μs, distant from the experimentally accepted values that are in the range of N_agg ∼ 50–73 (Berthod et al., 1991; Itri and Amaral, 1991; Quina et al., 1995; Bales et al., 1998; Anachkov et al., 2012). CG-MD simulations showed an averaged diameter of Ø ∼ 3.0 nm, exhibiting slightly smaller diameter when compared with the regular water model. Conversely, the polarizable water model offered a better perspective on tackling the impact of [N_4,4,4,4]Cl in the 2 wt% SDS aqueous solution as can be noticed in the experimental micelle size distribution when the for [N_4,4,4,4]Cl is increased as shown in Supplementary Figure S3A. Supplementary Figure S5 shows the CG-MD simulation snapshots for [N_4,4,4,4]⁺/[DS]^- ratios of 0.1, 0.3, 0.5, 0.7 and 1, after 1.5 μs. Consistent with experiments, Supplementary Figures 5A–C showed mono-phasic spherical [DS]^- micelle distributions surrounded by [N_4,4,4,4]⁺ moieties for [N_4,4,4,4]⁺/[DS]^- ratios of 0.1, 0.3, and 0.5. For ratios above 0.5, a clumpled and a biphasic system were formed for 0.7 and 1.0 ratios where a [N_4,4,4,4]⁺/[DS]^- and water rich phase were found, as illustrated in Supplementary Figures 5D–E. The 0.5 [N_4,4,4,4]⁺/[DS]^- ratio system seems the threshold for the micellar-to-clustered transition as observed in the experiments (Supplementary Figure S3A). Thus, the more realistic PW model was able to capture the impact of [N_4,4,4,4]Cl in SDS aqueous solution but this framework was limited by the poor SDS micelle size distribution obtained in the simulations.

2.3.3 Validation of individual and mixed sodium dodecyl sulphate and [N_4,4,4,4]Cl aqueous solutions in MARTINI 3.0

The recently released MARTINI 3.0 model developed by Souza et al. (2021) potentially overcomes most of the limitations of MARTINI 2.2. The new MARTINI 3 offers new interaction energies as well as an enhanced water model, including three scale options namely, W, SW, and TW with 4:1, 3:1, and 2:1 mapping, respectively. The SDS MARTINI 3 model developed by Vainikka et al. (2021), shown in Figure 1A, was selected to investigate the 2 wt% of SDS aqueous solution previously attempted. The water model used was the W with the 4:1 mapping with four water molecules per CG bead. Figure 1B displays the simulation snapshot after 3 μs, where spherical micelles were obtained with an averaged micelle aggregation number of N_agg = 35, slightly lower than literature results with an averaged diameter of Ø ∼ 3.3 nm (Supplementary Figure S6A), bigger than the DLS result as illustrated in Supplementary Figure S3A (Ø ∼ 2.0 nm at [N_4,4,4,4]⁺/[DS]^- = 0). However, it must be noted that this system displayed a polydisperse micelle size distribution with N_agg between 27 and 40, and Ø from 2.6 to 3.3 nm, close to the literature data and our DLS measurements (Itri and Amaral, 1991; Bales et al., 1998; Anachkov et al., 2012). The micelle size distribution was monitored during the simulation, reaching the plateau after 1 μs and continuing in equilibrium until the 3 μs of simulation time was reached. Nevertheless, this simulation was extended for an additional 3 μs with no trace of further micelle fusion processes, ensuring that micelle equilibrium was attained. Analogously, the new and more realistic [N_4,4,4,4]⁺ MARTINI 3 model (Souza et al., 2021) with four dummy beads (no mass and no Lennard-Jones interactions) with the aim to spread the charge around the ammonium center rather than a single point, was selected. The 6 wt% [N_4,4,4,4]Cl in aqueous solution simulation test was run for 3 μs from which no clumping was found, consistent with literature (Dong et al., 2017). Remarkably, the density of the simulation box was ρ = 1.02 g cm⁻³, in good agreement with the experimental density of ρ = 1.018 g cm⁻³ (Jain et al., 2013).

FIGURE 1

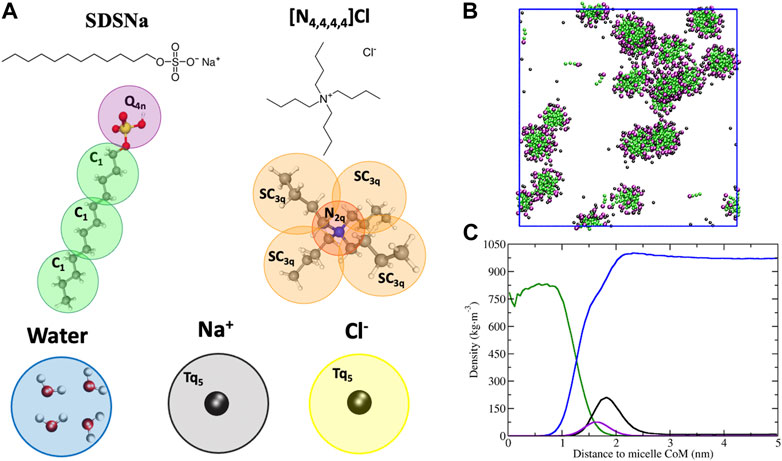
FIGURE 1. (A) CG mapping scheme for [DS]^-, [N_4,4,4,4]⁺, water, sodium and chloride counter ions in MARTINI 3. The [DS]^- consists of three C₁ beads for the alkyl tail (green) and a Q_4n bead type for the hydrophilic Sulphur head group (purple). (Vainikka et al., 2021). The [N_4,4,4,4]⁺ involves three SC_3q beads for the butyl groups (orange) and a N_2q bead type for the ammonium center (red) with a partial charge of 0.372, with four U dummy beads used to delocalize (partial charge 0.157 each) the head group charge in a more realistic way. (Souza et al., 2021). Cl⁻ and Na⁺ are represented by TQ₅ beads colored in yellow and grey, respectively, whereas the 4:1 mapping was selected for water. (B) Micellar solution obtained in the CG-MD simulation for 2 wt% SDS aqueous solution at 298K over 3 μs. (C) Averaged micelle density profile of the system shown in (B). The color code is as follows: [DS]^- alkyl tails in green, Sulphur head group in purple, sodium in black and water in blue. The water was removed in the simulation snapshot (B) for clarity.

Thus, the SDS and [N_4,4,4,4]Cl CG-MD MARTINI 3 models developed by Vainikka et al. (2021) and the W water model were selected to analyze the impact of [N_4,4,4,4]Cl in a 2 wt% SDS aqueous solution.

3 Results and discussion

Five [N_4,4,4,4]⁺/[DS]^- molar ratios, 0.0, 0.1, 0.3, 0.5, 0.7, and 1.0, were investigated in 2 wt% aqueous SDS solutions, with composition details provided in Supplementary Table S1, Figure 2 shows the CG-MD simulation snapshots after 2.5 μs of simulation time and Table 1 displays the N_agg and the averaged diameter, Ø, for the obtained aggregates. A homogeneous micellar solution was found in the SDS aqueous solution without [N_4,4,4,4]⁺ and 0.1 [N_4,4,4,4]⁺/[DS]^- ratios as illustrated in Figures 2A,B, exhibiting micelles with N_agg ∼ 35 whilst a Ø ∼ 3.3 nm was found in both systems (Table 1). The averaged micelle size obtained in the simulations were in good agreement with the DLS data displayed in Figure 3A where the solution without [N_4,4,4,4]Cl and for the [N_4,4,4,4]⁺/[DS]^- = 0.1 ratio exhibited similar micelle sizes Ø ∼ 2.0/3.0 nm.

FIGURE 2

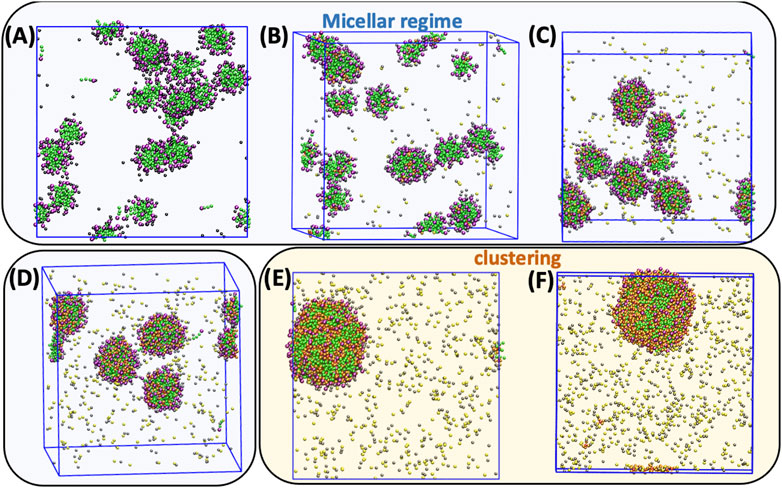
FIGURE 2. CG-MD simulation snapshots after for 2.5 μs for (A) 0.0, (B) 0.1 and (C) 0.3, (D) 0.5, (E) 0.7 and (F) 1.0 [N_4,4,4,4]⁺/[DS]^- molar ratios in a 2 wt% of SDS aqueous solution at 298 K. The color code is as follows: SDS alkyl tails and Sulphur charged headgroups are colored in green and purple, respectively. Chlorides are yellow, sodium grey, [N_4,4,4,4]⁺ butyl groups orange, and the ammonium centers are red whilst the dummy beads and water were not represented for clarity.

TABLE 1

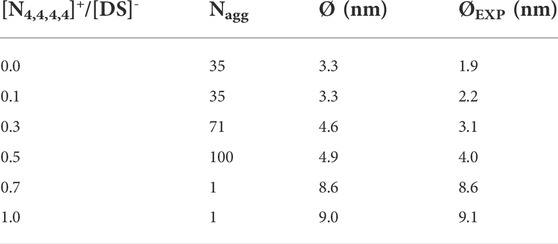
TABLE 1. Micelle size distribution obtained in the CG-MD simulations for 0.0, 0.1, 0.3 0.5, 0.7, and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios in the 2 wt% of SDS aqueous solution at 298 K. N_agg and Ø are the averaged aggregation number and diameter of the aggregates, respectively, obtained throughout the last 0.5 μs of simulation time.

FIGURE 3

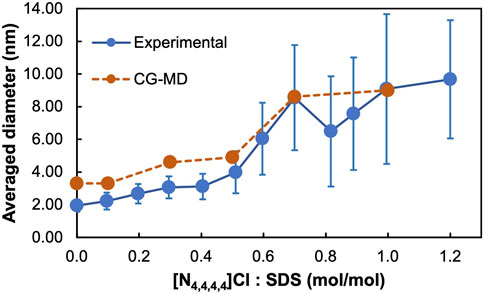
FIGURE 3. Experimental and CG-MD aggregate size distribution for the [N_4,4,4,4]⁺/[DS]^- molar ratios shown in Figure 2. DLS was used to obtain the experimental data where additional [N_4,4,4,4]⁺/[DS]^- molar ratios were measured. Bars in the experimental data correspond to half the base peak distribution and not the standard deviation.

The micelle density profile shown in Figure 4A is for the reference SDS aqueous solution (without [N_4,4,4,4]Cl) whilst Figure 4B shows how the [N_4,4,4,4]⁺ moieties (orange) and the Cl⁻ and Na⁺ counterions (yellow and grey colors, respectively) were mainly arranged over the micelle surface (denoted by maximum of the purple curve), and in the solution. A detailed perspective at the micelle surface for the above density profiles are provided in Supplementary Figures S6A–B. Similarly, the 0.3 ratio system yielded a homogeneous distribution of spherical micelles, as shown in Figure 2C, with N_agg ∼ 71 and Ø ∼ 4.6 nm (Table 1) but encompassing a slightly different micelle assembly. The DLS data pointed towards a similar micelle size with Ø ∼ 3.0/4.0 nm as shown in Figure 3A. The density profile shown in Figure 4C unveils the presence of SDS Sulphur headgroups (purple peaks) close to the aggregate center of mass (CoM) whereas the density of the [DS]^- alkyl tails (green) slightly decreased. This might indicate that [N_4,4,4,4]⁺ moieties were strongly absorbed and arranged in the micelle core. A detailed perspective can be seen in Supplementary Figure S6C showing that the [N_4,4,4,4]⁺ moieties and the Cl⁻ and Na⁺ counterions were arranged over the [DS]^- micelle surface as in the 0.1 ratio system.

FIGURE 4

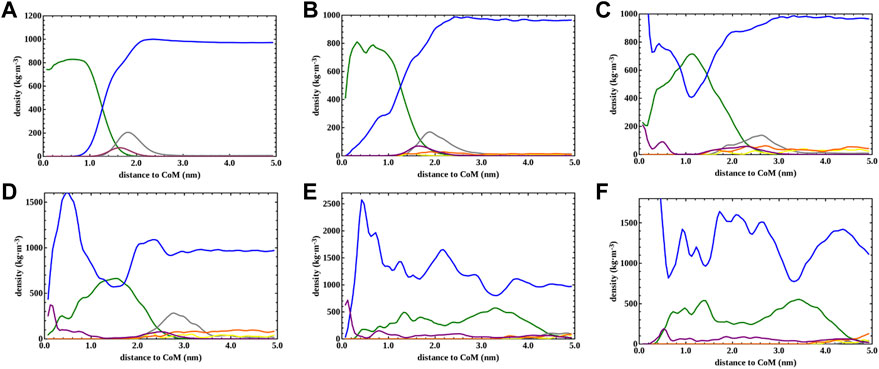
FIGURE 4. Averaged density profiles of the aggregates found in the CG-MD simulations for (A) 0.0, (B) 0.1, (C) 0.3, (D) 0.5, (E) 0.7 and (F) 1.0 [N_4,4,4,4]⁺/[DS]^- molar ratio systems shown in Figure 2. The last 0.5 μs of the simulation was taken to obtain the density profiles. The color code is as follows: [DS]^- alkyl tails and Sulphur charged headgroups are colored in green and purple, respectively. Sodium, chloride and water are in grey, yellow and blue, respectively, whereas [N_4,4,4,4]⁺ was in orange.

This arrangement was more noticeable in the system with a ratio of 0.5, which also exhibited a homogeneous distribution of swelled micelles, as can be seen in Figure 2D, with N_agg ∼ 100 and Ø ∼ 4.9 nm (Table 1) in good agreement with DLS data (Figure 3A) Ø ∼ 4.0 nm. However, the density profile presented in Figure 4D points towards those micelles being an amalgam of small [DS]^- aggregates, somehow resembling the structure of a blackberry fruit. As a matter of fact, the increased [N_4,4,4,4]⁺ absorption promoted a [DS]^- micelle core breakdown, resembling the above mentioned blackberry like structure, also giving access to some water molecules arrange inside the core structure (denoted by the blue maximum close to the CoM shown in Figure 4). The arrangement of some [N_4,4,4,4]⁺ moieties (orange) in between the [DS]^- connected aggregates can be seen in Figure 2D besides a noticeable increase of the aggregate size, indicating that the increased number of available [N_4,4,4,4]⁺ moieties induced a micelle swell. A different scenario was observed in the 0.7 system displaying one cluster as shown in Figure 2E, with N_agg ∼ 500 and Ø ∼ 8.6 nm (Table 1) in very good agreement with DLS experiments Ø ∼ 8.6 nm (Figure 3A). The simulation snapshot highlights the singular blackberry like structure, with the [N_4,4,4,4]⁺ moieties connecting small [DS]^- aggregates. The density profile shown in Figure 4E displays a homogeneous distribution of the [DS]^- headgroups (purple) alongside the aggregate as well as the [N_4,4,4,4]⁺ moieties (orange) and the counterions (grey and yellow) as shown in detail in Supplementary Figure S6E. When the number of [N_4,4,4,4]⁺ matched the [DS]^- moieties (ratio 1.0) the system also yielded a cluster with a Ø ∼ 8.7 nm in line with DLS estimate (Ø ∼ 9.1 nm) shown in Figure 3A, displaying the same structure and size as in the 0.7 ratio system. The aggregate structure obtained in the CG-MD simulation is shown in Figure 2F with its density profile is displayed in Figure 4F. In fact, the density profile resembles the one found in the 0.7 system. Supplementary Figure S6F highlights the similar [N_4,4,4,4]⁺ and counterion arrangement at the cluster surface.

The solvent accessible surface area (SASA) was obtained for [N_4,4,4,4]⁺ and SDS moieties for all 0.1, 0.3 0.5, 0.7, and 1.0 [N_4,4,4,4]⁺/[DS]^- solutions throughout the SASA calculation. SASA provides an estimation of the level of hydration/dehydration and these profiles are shown in Figure 5. Figure 5A illustrates how [N_4,4,4,4]⁺ moieties dehydrate in the SDS solutions when the concentration is increased. Thus, the difference of SASA between the 0.1 and 1.0 solutions was 1.5 nm², highlighting the fact that at low [N_4,4,4,4]⁺ concentrations, the [N_4,4,4,4]⁺ were mostly arranged at the SDS micelle surface as shown in the density profiles (Figures 4B,C). However, at 0.5 [N_4,4,4,4]⁺/[DS]^- ratio, the [N_4,4,4,4]⁺ were not only arranged at the SDS micelle surface but also inside, losing access to water as shown in Figure 5A (purple). This dehydration was more dramatic at 0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios, which can be seen by the shift between these and the regularly spaced SASA profiles observed in 0.1, 0.3, and 0.5 solutions. Thus, the noticeable change to lower SASA detected from 0.5 to 0.7 and 1.0 ratios (shift between purple and the orange and red color profiles) highlights the micellar-to-cluster phase transition also observed in the simulation snapshots of Figures 2E,F. Figure 5B displays the SASA for SDS moieties from higher-to-low SASA, the SDS at 0.0, 0.1, 0.3 and 0.5 [N_4,4,4,4]⁺/[DS]^- ratios exhibited a slightly higher access to water when compared with the 0.7 and 1.0 ratios as expected for micellar structures. In the first 250 ns of simulation, the 0.5 solution had a similar SASA profile to those of the 0.1 and 0.3 solutions. Then the SASA of the 0.5 solution rapidly dropped above 160 ns (see detail in the red circle in Figure 5B), displaying the same SASA seen for the 0.7 and 1.0 ratios, whereas the 0.1 and 0.3 profiles remained constant until 2,500 ns. Thus, an initial clustering process, promoted perhaps by a structural alteration of micelles promoted by the absorbed [N_4,4,4,4]⁺, could be the reason behind this behavior since the 0.5 [N_4,4,4,4]⁺/[DS]^- ratio seems to be the threshold [N_4,4,4,4]⁺ concentration above which a micellar-to-cluster transition occurred. In fact, the micelles observed in the simulation snapshots and density profiles in the 0.5 solution shown in Figure 2D and Figure 4D, respectively, resembled the blackberry fruit like structure denoted in the clusters for 0.7 and 1.0 ratios.

FIGURE 5

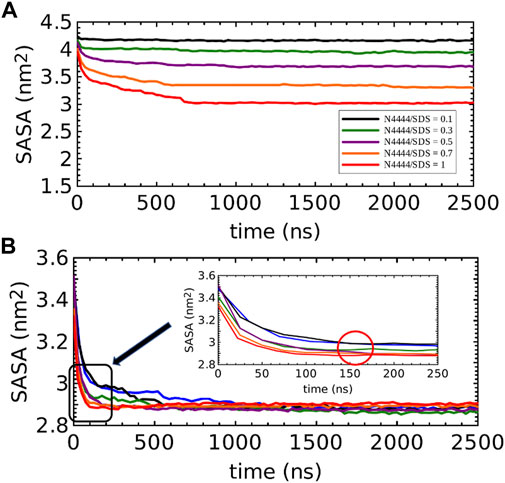
FIGURE 5. SASA profiles for the (A) [N_4,4,4,4]⁺ and (B) [DS]^- moieties, both for all 0.0, 0.1, 0.3, 0.5, 0.7, and 1.0 [N_4,4,4,4]⁺/[DS]^- molar ratio systems shown in Figure 2. The inset in Figure 5B zooms in the SASA profiles in the first 250 ns of simulation whilst the red circle guide the eye to emphasize the shift experienced for the 0.5 [N_4,4,4,4]⁺/[DS]^- ratio solution towards the SASA values of the clusters observed in the 0.7 and 1.0 solutions at 160 ns. SASA profile in (B) for the SDS solution without [N_4,4,4,4]⁺ is shown in blue color.

Overall, SASA results are in good agreement with our DLS and NMR experiments, revealing the micelle-to-clustering transition for [N_4,4,4,4]⁺/[DS]^- ratios > 0.5, being a threshold from an ionic system to a pseudo-nonionic one, assuming [N_4,4,4,4]⁺ cations between [DS]^- head groups. This transition could be due to depletion of H-bonds of water molecules around the butyl chains of [N_4,4,4,4]⁺ besides the [DS]^- at the micelle surface. This is associated with the entropy gain which is the major thermodynamic factor related to micellar aggregation and LCST transition.

With the aim to provide a clearer picture of the phases found in the CG-MD simulations, the computed SAXS profiles for the 0.0, 0.1, 0.3, 0.5, 0.7, and 1.0 [N_4,4,4,4]⁺/[DS]^- ratio systems were obtained using the last 0.5 μs of simulation time. In addition, experimental SAXS patterns were acquired of samples with these compositions. Figure 6 compares the computed SAXS profiles with their experimental counterparts. It must be pointed out that only a qualitative comparison between the computed and experimental SAXS profiles can be done due to the inherent size limitations of the simulation boxes. In fact, the simulation box sizes are ∼ 24 nm whereas the experimental samples are significantly larger. Additionally, the lack of atomistic details inherent in coarse-grained models make SAXS comparison with experiments even more difficult as also mentioned below. Furthermore, the experimental SAXS profiles were obtained using a 1 wt% SDS concentration, whilst 2 wt% was used in the CG-MD simulations due to the high computational cost of simulating diluted solutions. It must be noticed that the intensity of each computed SAXS profile was properly scaled with the aim to compare with the experimental ones. SAXS profiles can provide useful information of the phase behavior. In fact, in the pure SDS solution, the flat intensity profile at low q values indicates predominantly spherical or spheroidal micelles with repulsive interactions being the second the contribution of hydrophobic side chain distances. At higher [N_4,4,4,4]⁺/[DS]^- ratios, the intensity at low q increases drastically indicating aggregation and phase transition where the lack of the first peak exhibits a transition from repulsive to attractive inter micellar interactions (Kabir-ud-Din et al., 2006; Schäfer et al., 2020). Figures 6A–D show a similar pattern between computed and experimental SAXS profiles for 0.0, 0.1, 0.3, and 0.5 ratios, which are in qualitative good agreement with a homogeneous micelle distribution as can be seen in Figures 2A–D exhibiting both profiles a down trend of the intensity when low q values are approached. For 0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios, the computed and experimental SAXS profiles shown in Figures 6E,F displayed a similar pattern, both with an exponential increase of the intensity at low q, pointing towards a clustering process. This is in agreement with the [N_4,4,4,4]⁺/[DS]^- clusters observed in the CG-MD simulations (cf. Figures 2E,F) with the above-mentioned blackberry like structure. In this manner, the CG-MD simulations disclosed the impact of [N_4,4,4,4]Cl in the phase behavior of the SDS micelles where the [N_4,4,4,4]⁺ provided a positive charge character inside the SDS hydrophobic core. Thereby, in a 2 wt% SDS aqueous solution, at low [N_4,4,4,4]Cl concentrations ([N_4,4,4,4]⁺/[DS]^- ratios < 0.5) an homogeneous solution of [DS]^- micelles were in equilibrium and the inter micelle interactions were not affected by the absorbed [N_4,4,4,4]⁺ moieties. However, when the [N_4,4,4,4]Cl concentration is raised above the [N_4,4,4,4]⁺/[DS]^- ratio > 0.5, the inner positive and outer negative charge balance of the SDS micelles promoted the formation of [N_4,4,4,4]⁺/[DS]^- clusters as illustrated in Figures 2E,F. Thus, the electrostatic balance between the [DS]^- and [N_4,4,4,4]⁺ moieties seems to play the main role in the phase behavior as denoted in the evolution of the density profiles shown in Figure 4 and Supplementary Figure S6. In fact, if one focus in the second peaks of the experimental SAXS profiles as a function of the molar ratio displayed in Supplementary Figure S7, the trend could suggest a slight change in [DS]^- tail-tail distances. This might point towards that no micelle fusion but rather micelle clumping could be found resembling the above-mentioned blackberry structure.

FIGURE 6

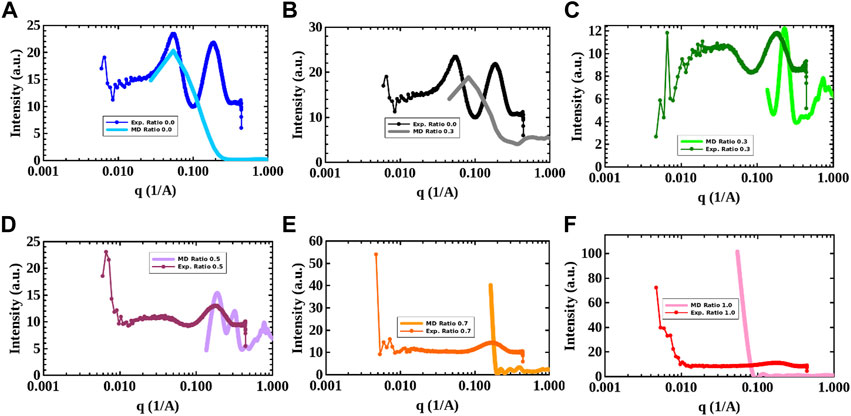
FIGURE 6. Computed and experimental SAXS profiles for the (A) 0.0, (B) 0.1, (C) 0.3, (D) 0.5, (E) 0.7, and (F) 1.0 [N_4,4,4,4]⁺/[DS]^- molar ratio systems shown in Figure 2. The SDS concentration in the experimental samples was 1wt% and the temperature was 298 K. Profiles colored in shadow are computed SAXS taken from the CG-MD simulations.

The primary aim of this comparative study was to computationally capture the experimental change in the SAXS profiles, with a focus on the low q values. When the [N_4,4,4,4]⁺/[DS]^- ratio is ≤ 0.5, the computed SAXS profiles tended towards lower intensities at low q values whilst > 0.5 the intensity increased at low q values. Thus, this variation in the experimental SAXS trend at low q values below and above the 0.5 ratio corresponds to, and supports, the micellar-to-clustering phase transition observed in the CG-MD simulation snapshots.

It must be pointed out that a direct correspondence of experimental and computed profiles is problematic due to the difference in molecular volumes when converting an atomistic description to a CG-bead one. Nevertheless, despite the expected discrepancies when comparing experimental and computed SAXS profiles, both clearly highlight a micellar-to-cluster phase transition when the [N_4,4,4,4]⁺/[DS]^- ratio is above 0.5.

4 Conclusion

A new CG-MD approach based on the recently released MARTIN 3.0 model was developed to model SDS aqueous solutions, and evaluate the impact of [N_4,4,4,4]Cl on the phase behavior. Literature computational and experimental data were used in the validation procedure. The experimental aggregation number of SDS micelles in aqueous solution was taken as a reference to evaluate different CG beads available in MARTINI 3.0. The non-bonded interaction energies of a previous SDS model based in MARTINI 2.2 were taken as reference to find their counterparts in MARTINI 3.0. Afterwards, a SDS aqueous solution at a concentration in the micellar regime was simulated and the aggregation number was in good agreement with literature data. The [N_4,4,4,4]⁺ MARTINI 3.0 model was already available in the literature, nevertheless, a strength test was carried out simulating a diluted [N_4,4,4,4]Cl aqueous solution to ensure that no excessive aggregation is observed. Then, five SDS aqueous solutions at different [N_4,4,4,4]Cl concentrations (0.1–1.0 [N_4,4,4,4]⁺/[DS]^- molar ratios) were simulated and the results were compared with SAXS experiments. The simulations showed how a regular SDS micellar solution (0.1 and 0.3 [N_4,4,4,4]⁺/[DS]^- ratios) yielded [DS]^-/[N_4,4,4,4]⁺ aggregates at higher [N_4,4,4,4]Cl concentrations (0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- ratios). The [N_4,4,4,4]⁺/[DS]^- solution at 0.5 M ratio separates the above mentioned phase behavior regimes, in good agreement with experiments. Accessible solvent surface areas (SASA) were obtained for the [N_4,4,4,4]⁺ and SDS in all [N_4,4,4,4]⁺/[DS]^- ratio solutions. The SASA profiles showed the dehydration of [N_4,4,4,4]⁺ moieties when their concentration is increased in the SDS solution, displaying the lowest values in 0.7 and 1.0 solutions when the system yielded clusters. In addition, experimental and computed SAXS profiles were obtained for the above [N_4,4,4,4]⁺/[DS]^- aqueous solutions. Computed SAXS profiles for 0.1 and 0.3 [N_4,4,4,4]⁺/[DS]^- ratios displayed a profile of characteristic spherical aggregates, in agreement with their experimental counterparts. For the 0.5 [N_4,4,4,4]⁺/[DS]^- molar ratio, the computed SAXS profile pointed out a micellar solution (as illustrated in the simulation snapshot) whereas the experimental counterpart indicated the presence of a cluster as also revealed in the 0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- solutions. The computed SAXS profile for 0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- solutions exhibited the presence of clusters in conjunction with micelles, also noticed in the simulation snapshots and in agreement with the experimental ones. Analyzing the simulation snapshots for these systems, the cluster were assembled through small SDS aggregates linked by the absorbed [N_4,4,4,4]⁺ moieties somehow resembling a blackberry fruit. Thus, in a SDS micellar aqueous solution, as soon as the [N_4,4,4,4]⁺ concentration is increased, the SDS micelles are gaining [N_4,4,4,4]⁺ moieties, resulting in swelling of the micelles. However, above a certain [N_4,4,4,4]⁺ concentration threshold, the absorbed [N_4,4,4,4]⁺ split the SDS micelle core, as can be seen in the simulation snapshots, providing a positive charge inside the micelle core. As a matter of fact, when the positive load is at least half of the negative charge of the SDS micelle surface, this impacts the inter micelle interactions, promoting a micelle fusion process to form a clustered structure as observed in the 0.7 and 1.0 [N_4,4,4,4]⁺/[DS]^- solutions.

This work demonstrates that the CG-MD MARTINI 3.0 model is a powerful tool to analyze processes at the nanoscale the self-assembly of SDS and [N_4,4,4,4]Cl aqueous solutions, and provide useful to complement the information obtained from experimental approaches.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

GP—conceptualization, data curation, investigation, molecular simulations, validation, writing original draft, review, and editing. NS—data curation, experimental DLS and NNMR measurements, review, and editing. TG—data curation, experimental SAXS measurements, review, and editing. JP—conceptualization, supervision, writing, review, and editing. JC—funding acquisition, conceptualization, supervision, writing, review, and editing.

Acknowledgments

This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 and LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC). CIEPQPF is supported by the Fundação para a Ciência e Tecnologia (FCT) through the projects UIDB/EQU/00102/2020 and UIDP/EQU/00102/2020. GáPé-Sá and NS acknowledge the national funds (OE), through FCT—Fundação para a Ciência e a Tecnologia, I.P., in the scope of the framework contract foreseen in the numbers 4, 5 and 6 of the article 23, of the Decree-Law 57/2016, of August 29^th, changed by Law 57/2017, of July 19^th. Part of this research was undertaken on the SAXS beamline at the Australian Synchrotron, part of ANSTO.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2022.1011164/full#supplementary-material

References

Anachkov, S. E., Danov, K. D., Basheva, E. S., Kralchevsky, P. A., and Ananthapadmanabhan, K. P. (2012). Determination of the aggregation number and charge of ionic surfactant micelles from the stepwise thinning of foam films. Adv. Colloid Interface Sci. 183-184, 55–67. doi:10.1016/j.cis.2012.08.003, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0001868612001285.

PubMed Abstract | CrossRef Full Text | Google Scholar

Anogiannakis, S. D., Petris, P. C., and Theodorou, D. N. (2020). Promising Route for the Development of a computational framework for self-assembly and phase behavior prediction of ionic surfactants using MARTINI. J. Phys. Chem. B 124 (3), 556–567. doi:10.1021/acs.jpcb.9b09915, Available from: https://pubs.acs.org/doi/10.1021/acs.jpcb.9b09915.

PubMed Abstract | CrossRef Full Text | Google Scholar

Bales, B. L., Messina, L., Vidal, A., Peric, M., and Nascimento, O. R. (1998). Precision relative aggregation number Determinations of SDS micelles using a Spin probe. A model of micelle surface hydration. J. Phys. Chem. B 102 (50), 10347–10358. doi:10.1021/jp983364a, Available from: https://pubs.acs.org/doi/10.1021/jp983364a.

CrossRef Full Text | Google Scholar

Bales, B. L., and Zana, R. (2004). Cloud point of aqueous solutions of tetrabutylammonium dodecyl sulfate is a function of the concentration of counterions in the aqueous phase. Langmuir 20 (5), 1579–1581. doi:10.1021/la0353935, Available from: https://pubs.acs.org/doi/10.1021/la0353935.

PubMed Abstract | CrossRef Full Text | Google Scholar

Bastos, H., Bento, R., Schaeffer, N., Coutinho, J. A. P., and Pérez-Sánchez, G. (2020). Using coarse-grained molecular dynamics to rationalize biomolecule solubilization mechanisms in ionic liquid-based colloidal systems. Phys. Chem. Chem. Phys. 22 (42), 24771–24783. doi:10.1039/D0CP04942E, Available from: http://xlink.rsc.org/?DOI=D0CP04942E.

PubMed Abstract | CrossRef Full Text | Google Scholar

Berthod, A., Borgerding, M. F., and Hinze, W. L. (1991). Investigation of the causes of reduced efficiency in micellar liquid chromatography. J. Chromatogr. A 556 (1–2), 263–275. doi:10.1016/s0021-9673(01)96226-0, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0021967301962260.

CrossRef Full Text | Google Scholar

Bussi, G., Donadio, D., and Parrinello, M. (2007). Canonical sampling through velocity rescaling. J. Chem. Phys. 126 (1), 014101. doi:10.1063/1.2408420, Available from: http://aip.scitation.org/doi/10.1063/1.2408420.

PubMed Abstract | CrossRef Full Text | Google Scholar

Chauhan, S., and Kaur, M. (2017). Modulation of aggregation behaviour of anionic surfactant in the presence of aqueous quaternary ammonium salts. J. Surfactants Deterg. 20 (3), 599–607. doi:10.1007/s11743-017-1949-5, Available from: http://doi.wiley.com/10.1007/s11743-017-1949-5.

CrossRef Full Text | Google Scholar

Chien, S-C., Pérez-Sánchez, G., Gomes, J. R. B., Cordeiro, M. N. D. S., Jorge, M., Auerbach, S. M., et al. (2017). Molecular simulations of the Synthesis of periodic Mesoporous Silica phases at high surfactant concentrations. J. Phys. Chem. C 121 (8), 4564–4575. doi:10.1021/acs.jpcc.6b09429, Available from: https://pubs.acs.org/doi/10.1021/acs.jpcc.6b09429.

CrossRef Full Text | Google Scholar

Cromer, D. T., and Mann, J. B. (1968). X-ray scattering factors computed from numerical Hartree–Fock wave functions. Acta Cryst. Sect. A 24 (2), 321–324. doi:10.1107/S0567739468000550,

CrossRef Full Text | Google Scholar

Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98 (12), 10089–10092. doi:10.1063/1.464397, Available from: http://aip.scitation.org/doi/10.1063/1.464397.

CrossRef Full Text | Google Scholar

Dong, D., Hooper, J. B., and Bedrov, D. (2017). Structural and dynamical properties of tetraalkylammonium bromide aqueous solutions: A molecular dynamics simulation study using a polarizable force field. J. Phys. Chem. B 121 (18), 4853–4863. doi:10.1021/acs.jpcb.7b01032, Available from: https://pubs.acs.org/doi/10.1021/acs.jpcb.7b01032.

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferreira, A. M., Passos, H., Okafuji, A., Tavares, A. P. M., Ohno, H., Freire, M. G., et al. (2018). An integrated process for enzymatic catalysis allowing product recovery and enzyme reuse by applying thermoreversible aqueous biphasic systems. Green Chem. 20 (6), 1218–1223. doi:10.1039/C7GC03880A, Available from: http://xlink.rsc.org/?DOI=C7GC03880A.

PubMed Abstract | CrossRef Full Text | Google Scholar

Forero-Martinez, N. C., Cortes-Huerto, R., Benedetto, A., and Ballone, P. (2022). Thermoresponsive ionic liquid/water mixtures: From Nanostructuring to phase separation. Molecules 27 (5), 1647. doi:10.3390/molecules27051647, Available from: https://www.mdpi.com/1420-3049/27/5/1647.

PubMed Abstract | CrossRef Full Text | Google Scholar

Freire, M. G., Cláudio, A. F. M., Araújo, J. M. M., Coutinho, J. A. P., Marrucho, I. M., Lopes, J. N. C., et al. (2012). Aqueous biphasic systems: A boost brought about by using ionic liquids. Chem. Soc. Rev. 41 (14), 4966. doi:10.1039/C2CS35151J, Available from: http://xlink.rsc.org/?DOI=c2cs35151j.

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, J., Ge, W., Hu, G., and Li, J. (2005). From homogeneous dispersion to MicellesA molecular dynamics simulation on the Compromise of the hydrophilic and hydrophobic effects of sodium dodecyl sulfate in aqueous solution. Langmuir 21 (11), 5223–5229. doi:10.1021/la047121n, Available from: https://pubs.acs.org/doi/10.1021/la047121n.

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutowski, K. E., Broker, G. A., Willauer, H. D., Huddleston, J. G., Swatloski, R. P., Holbrey, J. D., et al. (2003). Controlling the aqueous Miscibility of ionic liquids: Aqueous biphasic systems of water-Miscible ionic liquids and water-Structuring salts for recycle, Metathesis, and separations. J. Am. Chem. Soc. 125 (22), 6632–6633. doi:10.1021/ja0351802, Available from: https://pubs.acs.org/doi/10.1021/ja0351802.

PubMed Abstract | CrossRef Full Text | Google Scholar

Hammouda, B. (2013). Temperature effect on the Nanostructureof SDS micelles in water. J. Res. Natl. Inst. Stand. Technol. 118, 151. doi:10.6028/jres.118.008, Available from: https://nvlpubs.nist.gov/nistpubs/jres/118/jres.118.008.pdf.

PubMed Abstract | CrossRef Full Text | Google Scholar

Hess, B., Bekker, H., Berendsen, H. J. C., and Fraaije, J. G. E. M. (1997). Lincs: A linear constraint solver for molecular simulations. J. Comput. Chem. 18 (12), 1463–1472. Available from: http://doi.wiley.com/10.1002/%28SICI%291096-987X%28199709%2918%3A12%3C1463%3A%3AAID-JCC4%3E3.0.CO%3B2-H.

CrossRef Full Text | Google Scholar

Hockney, R., Goel, S., and Eastwood, J. (1974). Quiet high-resolution computer models of a plasma. J. Comput. Phys. 14 (2), 148–158. doi:10.1016/0021-9991(74)90010-2, Available from: http://linkinghub.elsevier.com/retrieve/pii/0021999174900102.

CrossRef Full Text | Google Scholar

Hoshen, J., and Kopelman, R. (1976). Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm. Phys. Rev. B 14 (8), 3438–3445. Available from: https://link.aps.org/doi/10.1103/PhysRevB.14.3438.

CrossRef Full Text | Google Scholar

Humphrey, W., Dalke, A., and Schulten, K. (1996). Vmd: Visual molecular dynamics. J. Mol. Graph. 14 (1), 33–38. doi:10.1016/0263-7855(96)00018-5, Available from: http://linkinghub.elsevier.com/retrieve/pii/0263785596000185.

PubMed Abstract | CrossRef Full Text | Google Scholar

Illa-Tuset, S., Malaspina, D. C., and Faraudo, J. (2018). Coarse-grained molecular dynamics simulation of the interface behaviour and self-assembly of CTAB cationic surfactants. Phys. Chem. Chem. Phys. 20 (41), 26422–26430. doi:10.1039/C8CP04505D Available from: http://xlink.rsc.org/?DOI=C8CP04505D.

PubMed Abstract | CrossRef Full Text | Google Scholar

Itri, R., and Amaral, L. Q. (1991). Distance distribution function of sodium dodecyl sulfate micelles by x-ray scattering. J. Phys. Chem. 95 (1), 423–427. doi:10.1021/j100154a074, Available from: https://pubs.acs.org/doi/10.1021/j100154a074.

CrossRef Full Text | Google Scholar

Jain, P., Sharma, S., and Shukla, R. K. (2013). Density and viscosity of tetrabutyl ammonium hydrogen sulphate and tetrabutyl ammonium chloride salts in aqueous and methanolic solution at 303 K. Phys. Chem. Liq. 51 (5), 547–566. doi:10.1080/00319104.2012.760084, Available from: https://www.tandfonline.com/doi/full/10.1080/00319104.2012.760084.

CrossRef Full Text | Google Scholar

Jalili, S., and Akhavan, M. (2009). A coarse-grained molecular dynamics simulation of a sodium dodecyl sulfate micelle in aqueous solution. Colloids Surfaces A Physicochem. Eng. Aspects 352 (1–3), 99–102. doi:10.1016/j.colsurfa.2009.10.007, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0927775709006104.

CrossRef Full Text | Google Scholar

Jorge, M. (2008). Molecular dynamics simulation of self-assembly of n -Decyltrimethylammonium bromide micelles. Langmuir 24 (11), 5714–5725. doi:10.1021/la800291p, Available from: http://pubs.acs.org/doi/abs/10.1021/la800291p.

PubMed Abstract | CrossRef Full Text | Google Scholar

Kabir-ud-Din, D. S., Sharma, D., Khan, Z. A., Aswal, V. K., and Kumar, S. (2006). Clouding phenomenon and SANS studies on tetra-n-butylammonium dodecylsulfate micellar solutions in the absence and presence of salts. J. Colloid Interface Sci. 302 (1), 315–321. doi:10.1016/j.jcis.2006.06.021, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0021979706005169.

PubMed Abstract | CrossRef Full Text | Google Scholar

Klamt, A., Huniar, U., Spycher, S., and Keldenich, J. (2008). COSMOmic: A Mechanistic approach to the calculation of Membrane−Water partition Coefficients and internal distributions within Membranes and micelles. J. Phys. Chem. B 112 (38), 12148–12157. doi:10.1021/jp801736k, Available from: https://pubs.acs.org/doi/10.1021/jp801736k.

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohno, Y., and Ohno, H. (2012). Ionic liquid/water mixtures: From hostility to conciliation. Chem. Commun. 48 (57), 7119. doi:10.1039/C2CC31638B, Available from: http://xlink.rsc.org/?DOI=c2cc31638b.

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohno, Y., Saita, S., Murata, K., Nakamura, N., and Ohno, H. (2011). Extraction of proteins with temperature sensitive and reversible phase change of ionic liquid/water mixture. Polym. Chem. 2 (4), 862. doi:10.1039/C0PY00364F, Available from: http://xlink.rsc.org/?DOI=c0py00364f.

CrossRef Full Text | Google Scholar

Lebard, D. N., Levine, B. G., Mertmann, P., Barr, S. A., Jusufi, A., Sanders, S., et al. (2012). Self-assembly of coarse-grained ionic surfactants accelerated by graphics processing units. Soft Matter 8 (8), 2385–2397. doi:10.1039/c1sm06787g,

CrossRef Full Text | Google Scholar

Lin, J-H., Chen, W-S., and Hou, S-S. (2013). NMR studies on effects of tetraalkylammonium bromides on micellization of sodium dodecylsulfate. J. Phys. Chem. B 117 (40), 12076–12085. doi:10.1021/jp403616p, Available from: https://pubs.acs.org/doi/10.1021/jp403616p.

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindahl, E., Abraham, M. J., Hess, B., and van der Spoel, D. (2018). GROMACS 2019 Source code. doi:10.5281/zenodo.2564764, Available at: https://doi.org/10.5281/zenodo.2424363.

CrossRef Full Text | Google Scholar

Liu, G., Li, R., Wei, Y., Gao, F., Wang, H., Yuan, S., et al. (2016). Molecular dynamics simulations on tetraalkylammonium interactions with dodecyl sulfate micelles at the air/water interface. J. Mol. Liq. 222, 1085–1090. doi:10.1016/j.molliq.2016.08.009, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0167732216307140.

CrossRef Full Text | Google Scholar

Liu, G., Zhang, H., Liu, G., Yuan, S., and Liu, C. (2016). Tetraalkylammonium interactions with dodecyl sulfate micelles: A molecular dynamics study. Phys. Chem. Chem. Phys. 18 (2), 878–885. doi:10.1039/C5CP05639J Available from: http://xlink.rsc.org/?DOI=C5CP05639J.

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahbub, S., Molla, M. R., Saha, M., Shahriar, I., Hoque, M. A., Halim, M. A., et al. (2019). Conductometric and molecular dynamics studies of the aggregation behavior of sodium dodecyl sulfate (SDS) and cetyltrimethylammonium bromide (CTAB) in aqueous and electrolytes solution. J. Mol. Liq. 283, 263–275. doi:10.1016/j.molliq.2019.03.045, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0167732219300200.

CrossRef Full Text | Google Scholar

Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., and de Vries, A. H. (2007). The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 111 (27), 7812–7824. doi:10.1021/jp071097f, Available from: http://pubs.acs.org/doi/abs/10.1021/jp071097f.

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez, L., Andrade, R., Birgin, E. G., and Martínez, J. M. (2009). Packmol: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 30 (13), 2157–2164. doi:10.1002/jcc.21224,

PubMed Abstract | CrossRef Full Text | Google Scholar

Martínez-Aragón, M., Burghoff, S., Goetheer, E. L. V., and de Haan, A. B. (2009). Guidelines for solvent selection for carrier mediated extraction of proteins. Sep. Purif. Technol. 65 (1), 65–72. doi:10.1016/j.seppur.2008.01.028, Available from: https://linkinghub.elsevier.com/retrieve/pii/S1383586608000543.

CrossRef Full Text | Google Scholar

Mata, J., Varade, D., Ghosh, G., and Bahadur, P. (2004). Effect of tetrabutylammonium bromide on the micelles of sodium dodecyl sulfate. Colloids Surfaces A Physicochem. Eng. Aspects 245 (1–3), 69–73. doi:10.1016/j.colsurfa.2004.07.009, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0927775704004194.

CrossRef Full Text | Google Scholar

Meyer, G., Schweins, R., Youngs, T., Dufrêche, J-F., Billard, I., and Plazanet, M. (2022). How temperature Rise can Induce phase separation in aqueous biphasic solutions. J. Phys. Chem. Lett. 13 (12), 2731–2736. doi:10.1021/acs.jpclett.2c00146, Available from: https://pubs.acs.org/doi/10.1021/acs.jpclett.2c00146.

PubMed Abstract | CrossRef Full Text | Google Scholar

Mitra, D., Chakraborty, I., Bhattacharya, S. C., and Moulik, S. P. (2007). Interfacial and solution properties of tetraalkylammonium bromides and their sodium dodecyl sulfate interacted products: A detailed Physicochemical study. Langmuir 23 (6), 3049–3061. doi:10.1021/la062830h, Available from: https://pubs.acs.org/doi/10.1021/la062830h.

PubMed Abstract | CrossRef Full Text | Google Scholar

Morais, E. S., Schaeffer, N., Freire, M. G., Freire, C. S. R., Coutinho, J. A. P., and Silvestre, A. J. D. (2021). Integrated production and separation of Furfural using an acidic-based aqueous biphasic system. ACS Sustain. Chem. Eng. 9 (36), 12205–12212. doi:10.1021/acssuschemeng.1c03733, Available from: https://pubs.acs.org/doi/10.1021/acssuschemeng.1c03733.

CrossRef Full Text | Google Scholar

Mukherjee, P., Padhan, S. K., Dash, S., Patel, S., and Mishra, B. K. (2011). Clouding behaviour in surfactant systems. Adv. Colloid Interface Sci. 162 (1), 59–79. doi:10.1016/j.cis.2010.12.005,

PubMed Abstract | CrossRef Full Text | Google Scholar

Naqvi, A. Z., and Kabir-ud-Din, D. S. (2018). Clouding phenomenon in amphiphilic systems: A review of five decades. Colloids Surfaces B Biointerfaces 165, 325–344. doi:10.1016/j.colsurfb.2018.01.060, Available from: https://linkinghub.elsevier.com/retrieve/pii/S0927776518300687.

PubMed Abstract | CrossRef Full Text | Google Scholar

Parrinello, M., and Rahman, A. (1981). Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 52 (12), 7182–7190. doi:10.1063/1.328693, Available from: http://aip.scitation.org/doi/10.1063/1.328693.

CrossRef Full Text | Google Scholar

Pérez-Sánchez, G., Chien, S-C., Gomes, J. R. B., Cordeiro Mn, D. S., Auerbach, S. M., Monson, P. A., et al. (2016). Multiscale model for the Templated Synthesis of Mesoporous Silica: The Essential role of Silica Oligomers. Chem. Mat. 28 (8), 2715–2727. doi:10.1021/acs.chemmater.6b00348, Available from: https://pubs.acs.org/doi/10.1021/acs.chemmater.6b00348.

CrossRef Full Text | Google Scholar

Pérez-Sánchez, G., Vicente, F. A., Schaeffer, N., Cardoso, I. S., Ventura, S. P. M., Jorge, M., et al. (2020). Unravelling the interactions between surface-Active ionic liquids and Triblock Copolymers for the design of thermal responsive systems. J. Phys. Chem. B 124 (32), 7046–7058. doi:10.1021/acs.jpcb.0c02992, Available from: https://pubs.acs.org/doi/10.1021/acs.jpcb.0c02992.

PubMed Abstract | CrossRef Full Text | Google Scholar

Quina, F. H., Nassar, P. M., Bonilha, J. B. S., and Bales, B. L. (1995). Growth of sodium dodecyl sulfate micelles with detergent concentration. J. Phys. Chem. 99 (46), 17028–17031. doi:10.1021/j100046a031, Available from: https://pubs.acs.org/doi/10.1021/j100046a031.

CrossRef Full Text | Google Scholar

Ritter, E., Yordanova, D., Gerlach, T., Smirnova, I., and Jakobtorweihen, S. (2016). Molecular dynamics simulations of various micelles to predict micelle water partition equilibria with COSMOmic: Influence of micelle size and structure. Fluid Phase Equilib. 422, 43–55. doi:10.1016/j.fluid.2016.03.006,

CrossRef Full Text | Google Scholar

Ruiz-Morales, Y., and Romero-Martínez, A. (2018). Coarse-grain molecular dynamics simulations to investigate the Bulk viscosity and critical micelle concentration of the ionic surfactant sodium dodecyl sulfate (SDS) in aqueous solution. J. Phys. Chem. B 122 (14), 3931–3943. doi:10.1021/acs.jpcb.7b10770, Available from: https://pubs.acs.org/doi/10.1021/acs.jpcb.7b10770.

PubMed Abstract | CrossRef Full Text | Google Scholar

Sammalkorpi, M., Karttunen, M., and Haataja, M. (2007). Structural properties of ionic detergent aggregates: A large-scale molecular dynamics study of sodium dodecyl sulfate. J. Phys. Chem. B 111 (40), 11722–11733. doi:10.1021/jp072587a, Available from: https://pubs.acs.org/doi/10.1021/jp072587a.

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaeffer, N., Kholany, M., Veloso, T. L. M., Pereira, J. L., Ventura, S. P. M., Nicaud, J-M., et al. (2019). Temperature-responsive extraction of violacein using a tuneable anionic surfactant-based system. Chem. Commun. 55 (59), 8643–8646. doi:10.1039/C9CC03831K Available from: http://xlink.rsc.org/?DOI=C9CC03831K.

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaeffer, N., Passos, H., Gras, M., Mogilireddy, V., Leal, J. P., Pérez-Sánchez, G., et al. (2018). Mechanism of ionic-liquid-based acidic aqueous biphasic system formation. Phys. Chem. Chem. Phys. 20 (15), 9838–9846. doi:10.1039/C8CP00937F Available from: http://xlink.rsc.org/?DOI=C8CP00937F.

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaeffer, N., Pérez-Sánchez, G., Passos, H., Gomes, J. R. B., Papaiconomou, N., and Coutinho, J. A. P. (2019). Mechanisms of phase separation in temperature-responsive acidic aqueous biphasic systems. Phys. Chem. Chem. Phys. 21 (14), 7462–7473. doi:10.1039/C8CP07750A Available from: http://xlink.rsc.org/?DOI=C8CP07750A.

PubMed Abstract | CrossRef Full Text | Google Scholar

Schäfer, K., Kolli, H. B., Killingmoe Christensen, M., Bore, S. L., Diezemann, G., Gauss, J., et al. (2020). Supramolecular packing Drives Morphological transitions of charged surfactant micelles. Angew. Chem. Int. Ed. Engl. 132 (42), 18750–18757. doi:10.1002/ange.202004522, Available from: https://onlinelibrary.wiley.com/doi/10.1002/ange.202004522.

CrossRef Full Text | Google Scholar

Souza, P. C. T., Alessandri, R., Barnoud, J., Thallmair, S., Faustino, I., Grünewald, F., et al. (2021). Martini 3: A general purpose force field for coarse-grained molecular dynamics. Nat. Methods 18 (4), 382–388. doi:10.1038/s41592-021-01098-3, Available from: http://www.nature.com/articles/s41592-021-01098-3.

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, X., Koenig, P. H., and Larson, R. G. (2014). Molecular dynamics simulations of sodium dodecyl sulfate micelles in water—the effect of the force field. J. Phys. Chem. B 118 (14), 3864–3880. doi:10.1021/jp410689m, Available from: https://pubs.acs.org/doi/10.1021/jp410689m.

PubMed Abstract | CrossRef Full Text | Google Scholar

Vainikka, P., Thallmair, S., Souza, P. C. T., and Marrink, S. J. (2021). Martini 3 coarse-grained model for type III Deep Eutectic solvents: Thermodynamic, structural, and extraction properties. ACS Sustain. Chem. Eng. 9 (51), 17338–17350. doi:10.1021/acssuschemeng.1c06521, Available from: https://pubs.acs.org/doi/10.1021/acssuschemeng.1c06521.

CrossRef Full Text | Google Scholar

Ventura, S. P. M., e Silva, F. A., Quental, M. V., Mondal, D., Freire, M. G., and Coutinho, J. A. P. (2017). Ionic-liquid-Mediated extraction and separation processes for Bioactive compounds: Past, present, and Future trends. Chem. Rev. 117 (10), 6984–7052. doi:10.1021/acs.chemrev.6b00550, Available from: https://pubs.acs.org/doi/10.1021/acs.chemrev.6b00550.

PubMed Abstract | CrossRef Full Text | Google Scholar

Yesylevskyy, S. O., Schäfer, L. V., Sengupta, D., and Marrink, S. J. (2010). Polarizable water model for the coarse-grained MARTINI force field. PLoS Comput. Biol. 6 (6), e1000810.

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhong, Y., Feng, X., Chen, W., Wang, X., Huang, K-W., Gnanou, Y., et al. (2016). Using UCST ionic liquid as a draw solute in forward osmosis to Treat high-Salinity water. Environ. Sci. Technol. 50 (2), 1039–1045. doi:10.1021/acs.est.5b03747, Available from: https://pubs.acs.org/doi/10.1021/acs.est.5b03747.

PubMed Abstract | CrossRef Full Text | Google Scholar