Explainable Artificial Intelligence for Mechanics: Physics-Explaining Neural Networks for Constitutive Models

(Artificial) neural networks have become increasingly popular in mechanics and materials sciences to accelerate computations with model order reduction techniques and as universal models for a wide variety of materials. However, the major disadvantage of neural networks remains: their numerous parameters are challenging to interpret and explain. Thus, neural networks are often labeled as black boxes, and their results often elude human interpretation. The new and active field of physics-informed neural networks attempts to mitigate this disadvantage by designing deep neural networks on the basis of mechanical knowledge. By using this a priori knowledge, deeper and more complex neural networks became feasible, since the mechanical assumptions can be explained. However, the internal reasoning and explanation of neural network parameters remain mysterious. Complementary to the physics-informed approach, we propose a first step towards a physics-explaining approach, which interprets neural networks trained on mechanical data a posteriori. This proof-of-concept explainable artificial intelligence approach aims at elucidating the black box of neural networks and their high-dimensional representations. Therein, the principal component analysis decorrelates the distributed representations in cell states of RNNs and allows the comparison to known and fundamental functions. The novel approach is supported by a systematic hyperparameter search strategy that identifies the best neural network architectures and training parameters. The findings of three case studies on fundamental constitutive models (hyperelasticity, elastoplasticity, and viscoelasticity) imply that the proposed strategy can help identify numerical and analytical closed-form solutions to characterize new materials.

1 Introduction

Data-driven models trained with deep learning algorithms have achieved tremendous successes in many research fields (LeCun et al., 2015). As the archetypical deep learning model, (artificial) neural networks and their variants are powerful predictors exceptionally well-suited for spatio-temporal data, such as mechanical tensor fields (Koeppe et al., 2020a). Each successive layer of a deep neural network learns to extract higher-level representations of the input and creates a data-driven model by supervised learning. Due to the large variety of layers and cells, neural networks are highly modular and successful for many applications (LeCun et al., 2015).

In mechanics and materials sciences, machine learning algorithms accelerate the development of new materials (Bock et al., 2019), provide model order reduction techniques and enable data-driven constitutive models. Likewise, machine and deep learning algorithms have become an active field of research in the related domain of tribology Argatov (2019); Argatov and Chai (2021). As one of the first works in mechanics, Ghaboussi et al. (1991) proposed a unified constitutive model with shallow neural networks that learn from experimental data. Further extensions reduced the required number of experimental samples (Ghaboussi et al., 1998), adjusted the hidden layer dimensionality during training (Ghaboussi and Sidarta, 1998), and approximated the stiffness matrix (Hashash et al., 2004). Theocaris and Panagiotopoulos (1995) used dense neural networks to model kinematic hardening (Theocaris and Panagiotopoulos, 1995) and identify parameters for the failure mode of anisotropic materials (Theocaris et al., 1997). Shin and Pande (2000) and Javadi et al. (2003, 2009); Javadi and Rezania (2009) proposed “intelligent finite elements”, neural network constitutive models that were applied to soils under cyclic loading and tunneling processes. Using context neurons in Recurrent Neural Networks (RNNs), Oeser and Freitag (2009), Graf et al. (2012), and Freitag et al. (2013) modeled elastoplastic and viscoelastic materials with fuzzy parameters. Bessa et al. (2017) proposed a data-driven analysis framework for materials with uncertain material parameters. For cantilever beams, Sadeghi and Lotfan (2017) used neural networks for nonlinear system identification and parameter estimation, while Koeppe et al. (2016) used dense neural networks to predict the displacement response. Extensions to continuum models resulted in linear “intelligent meta element” models of a cantilever beam (Koeppe et al., 2018a). To bridge the gap between atomistic and continuum mechanics, Teichert et al. (2019) trained integrable deep neural networks on atomistic scale models and successively approximated free energy functions. Stoffel et al. (2018) used dense neural networks to fit material data from high-velocity shock-wave tube experiments. Heider et al. (2020) investigated the frame invariance for graph-based neural networks predicting anisotropic elastoplastic material behavior. Huang et al. (2020) combined the proper orthogonal decomposition, manual history variables, and dense neural networks for hyperelasticity and plasticity. For materials applications, various data science methods have been successfully applied to simulation data and synthesized microstructures to analyze, characterize, and quantifify (e.g., Zhao et al. (2020); Altschuh et al. (2017)).

Despite the efforts to combine artificial intelligence and mechanics, the main disadvantage of neural networks remains: the learned parameters in black-box neural networks are challenging to interpret and explain (Breiman, 2001). Their high-level representations in deeper layers often elude human interpretation: what the neural network understood and how the individual parameter values can be explained remains incomprehensible. Coupled with insufficient data and limited computation capacities for past efforts, engineers and scientists mistrusted neural networks in favor of simpler models, whose fewer parameters could be easily interpreted and explained. Occam’s razor, the well-known problem-solving principle by William of Ockham (ca. 1,287–1,347), became an almost dogmatic imperative: the simpler model with fewer parameters must be chosen if two models are equally accurate. However, with the advent of deep learning, the concept of simple models has become ambiguous. The shared representations common in dense neural networks require potentially infinite numbers of parameters to model arbitrary functions (Hornik et al., 1989). To handle the large dimensionality of mechanical spatio-temporal data, extensive parameter sharing, utilized by recursions (Freitag et al., 2013; Freitag et al., 2017; Koeppe et al., 2017; Koeppe et al., 2018b; Koeppe et al., 2019) and convolutions (Koeppe et al., 2020a; Koeppe et al., 2020b; Wu P. et al., 2020), introduces assumptions based on prior knowledge and user-defined parameters, i.e., hyperparameters, to reduce the number of trainable parameters.

By deriving the prior assumptions on the deep learning algorithm from mechanical knowledge, the recent trend in computational mechanics, enhanced by neural networks, aims towards physics-informed neural networks. Lagaris et al. (1998) and Aarts and van der Veer (2001) imposed boundary and initial conditions on dense neural networks, which were trained to solve unconstrained partial differential equations by differentiating the neural network graphs. In Ramuhalli et al. (2005), the authors designed their neural network by embedding a finite element model, which used the neural network’s hidden layer to predict stiffness components and the output layer to predict the external force. Baymani et al. (2010) split the Stokes problem into three Poisson problems, approximated by three neural networks with superimposed boundary condition terms. In Rudd et al. (2014), a constrained backpropagation approach ensures that the boundary conditions are satisfied at each training step. The physics-informed neural network approach, as proposed by Raissi et al. (2019), employed two neural networks that contributed to the objective function. One physics-informed neural network mimicked the balance equation, while the second neural network approximated the potential function and pressure field. Yang and Perdikaris (2019) employed adversarial training to improve the performance of physics-informed neural networks. In Kissas et al. (2020), physics-informed neural networks model arterial blood pressure with magnetic resonance imaging data. Using the FEM to inspire a novel neural network architecture, Koeppe et al. (2020a) developed a deep convolutional recurrent neural network architecture that maps Dirichlet boundary constraints to force response and discretized field quantities in intelligent meta elements. Yao et al. (2020) used physics-informed deep convolutional neural networks to predict mechanical responses. Thus, using physics-informed approaches, neural networks with more parameters became feasible, whose architecture could be designed and explained using prior mechanical knowledge. However, the internal reasonings of the neural networks remained challenging to understand.

Complementary to the physics-informed approach, this work constitutes a new proof-of-concept approach towards a search approach radically different from the aforementioned design approach. Inspired by the explainable Artificial Intelligence (AI) research field (Bach et al., 2015; Arras et al., 2017; Alber et al., 2018; Montavon et al., 2018; Montavon et al., 2019; Samek et al., 2019), this novel approach elucidates the black box of neural networks to provide physics-explaining neural networks that complement the existing physics-informed neural networks. As a result, more powerful neural networks may be employed with confidence, since both the architectural design and the learned parameters can be explained.

This work has the objective to efficiently and systematically search neural network architectures for fundamental one-dimensional constitutive models and explain the trained neural networks. For this explanation, we propose a novel explainable AI method that uses the principal component analysis to interpret the cell states in RNNs. For the search, we define a wide hyperparameter search domain, implement an efficient search algorithm, and apply it to hyperelastic, viscoelastic, and elastoplastic constitutive models. After the search, the best neural network architectures are trained until they achieve low errors, and their generalization capabilities are tested. Finally, the developed explainable AI approach compares the temporal behavior of RNN cell states to known solutions to the fundamental physical problem, thereby demonstrating that neural networks without prior physical assumptions have the potential to inform mechanical research.

To the best of the authors’ knowledge, this work constitutes a first proof-of-concept study proposing a dedicated explainable AI strategy for neural networks in mechanics, as well as a novel approach within the general field of explainable AI. Unique to RNNs, which are popular in mechanics (Graf et al., 2010; Freitag et al., 2011, Freitag et al., 2017; Cao et al., 2016; Koeppe et al., 2018b, 2019; Wu L. et al., 2020), this work complements popular strategies for classification problems that investigate kernels in convolutional neural networks or investigate the data flow through neural networks, such as layer-wise relevance propagation (Bach et al., 2015; Montavon et al., 2019; Samek et al., 2019). Moreover, our new approach complements unsupervised approaches to find parsimonious and interpretable models for hyperelastic material behavior (Flaschel et al., 2021), which are one of the most recent representatives of the principle of simplicity. Finally, the systematic hyperparameter search strategy offers an alternative strategy to self-designing neural networks, which have successfully modeled anisotropic and elastoplastic constitutive behavior (Fuchs et al., 2021; Heider et al., 2021).

In Section 2.1, we briefly review the necessary preliminaries for RNN training as the foundation for the following sections. Section 2.2 details the systematic hyperparameter search strategy and explainable AI approach for data-driven constitutive models. For fundamental constitutive models, Section 3 demonstrates the developed approaches in three case studies. Finally, Section 4 discusses the approach and compares the results to related publications.

2 Materials and Methods

2.1 Preliminaries

2.1.1 Training Artificial Neural Networks

Dense feedforward neural networks are the fundamental building block of neural networks. They represent nonlinear parametric mappings NN from inputs x to predictions $\widehat{\mathit{y}}$ with L consecutive layers and trainable parameters θ:

$\mathrm{N}\mathrm{N}:\mathit{x};\mathit{\theta }\mathcal{\mapsto }\widehat{\mathit{y}}\text{with}\mathit{\theta }=\left\{({\mathit{W}}^{\left(1\right)},{\mathit{b}}^{\left(1\right)})\dots ({\mathit{W}}^{\left(L\right)},{\mathit{b}}^{\left(L\right)})\right\},(1)$

For dense feedforward neural networks, the parameters θ include the layer weights W^(l) and biases b^(l). Each layer l applies a linear transformation to the layer inputs x^(l), before a nonlinear activation function f^(l) returns the layer activations a^(l)

${\mathit{a}}^{\left(l\right)}={\mathrm{f}}^{\left(l\right)}\left({\mathit{z}}^{\left(l\right)}\right)\text{with}{\mathit{z}}^{\left(l\right)}={\mathit{W}}^{\left(l\right)}{\mathit{x}}^{\left(l\right)}+{\mathit{b}}^{\left(l\right)}\forall l=1\dots L.(2)$

Assembling and vectorizing these consecutive layers from x ≡a⁽⁰⁾ to $\widehat{\mathit{y}}\equiv {\mathit{a}}^{(L)}$ enables fast computations on Graphics Processing Units (GPUs) and Tensor Processing Units (TPUs).

Using supervised learning, neural network training identifies optimal parameters θ^opt, which minimize the difference between desired outputs and neural network predictions. From a wide variety of input-target samples $\left(\mathit{x},\mathit{y}\right)$, the task of predicting physical responses $\widehat{\mathit{y}}\approx \mathit{y}$ can be reformulated as a machine learning problem, where the prediction represents the expectation of the data probability distribution p^data (y∣x):

$\widehat{\mathit{y}}\left(\mathit{x}\right)\approx \mathbb{E}\left[{\mathrm{p}}^{\text{data}}\left(\mathit{y}\mid \mathit{x}\right)\right].(3)$

Assuming a single-peak distribution, e.g., a normal distribution ${\mathrm{p}}^{\text{data}}(\mathit{y}\mid \mathit{x})\approx \mathcal{N}(\mathit{y}\mid \mathit{x})$, the maximum likelihood estimation principle (cf. Goodfellow et al. (2016)) yields a compatible loss function $\mathcal{L}(\mathit{y},\widehat{\mathit{y}})$ for the prediction of physical values, such as the Mean Squared Error (MSE) averaged for batch size M and number of features F, i.e., $\mathcal{L}(\mathit{y},\widehat{\mathit{y}}):={(MF)}^{-1}\mathit{y}\cdot \widehat{\mathit{y}}$. Using this loss function to compute scalar errors ϵ, the contributions of each parameter to the error can be backpropagated to compute gradients and train the neural network with gradient descent. To ensure generalization to unknown samples, the datasets used are split (usually randomly) into training, validation, and test sets. Gradient descent with backpropagation is only performed on the training set, while the validation set safeguards against overfitting of the parameters θ. The test set safeguards against overfitting of the chosen hyperparameter values γ, which include, e.g., the dimensionalities of each layer dim (a^(l)) and the number of layers L.

Recurrent neural networks (Rumelhart et al., 1986) introduce time-delayed recursions to feedforward neural networks (Goodfellow et al., 2016). Thus, RNNs use parameter sharing to reuse parameters efficiently for sequential data-driven problems. Such sequential data x_t may be sorted according to the rate-dependent real time or a pseudo time. One straightforward implementation of an RNN cell introduces a single tensor-valued recursion as given by

${\bar{\mathit{x}}}_{t+1}={\left[\begin{array}{cc}\hfill {\mathit{x}}_{t+1}\hfill & \hfill {\mathit{a}}_t\hfill \end{array}\right]}^{\mathsf{T}},(4)$

${\mathit{c}}_{t+1}=\mathrm{f}\left(\mathit{W}{\bar{\mathit{x}}}_{t+1}+\mathit{b}\right),(5)$

${\mathit{a}}_{t+1}={\mathit{W}}^{\text{o}}{\mathit{c}}_{t+1}+{\mathit{b}}^{\text{o}}.(6)$

In Figure 1, the recurrent cell is depicted as a graph of two conventional dense layers and a time-delayed recursion of previous activation a_t. Subsequently embedded into a larger sequence tensor $\mathit{X}=\left[{\mathit{x}}_1\dots {\mathit{x}}_T\right]$, RNNs can be trained with backpropagation through time (Rumelhart et al., 1986).

FIGURE 1

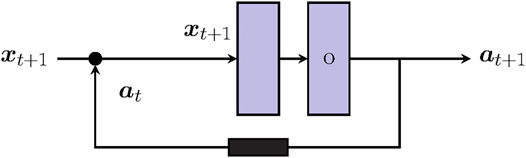
FIGURE 1. Visualization of a recurrent cell. The recurrent cell consists of two feedforward layers (light violet squares). A time-delayed recursion (black square) loops the activation of the first or last layer back as additional input to the cell.

However, simple RNNs (Eq. 4 to Eq. 6) suffer from unstable gradients and fading memory (Hochreiter and Schmidhuber, 1997; Greff et al., 2015), which motivated the development of RNNs with gates. These gating layers control the data flow, thereby stabilizing the gradients and mitigating the fading memory. The Long Short-Term Memory (LSTM) cell (Figure 2) (Hochreiter and Schmidhuber, 1997; Gers et al., 2000) and the Gated Recurrent Unit (GRU) (Cho et al., 2014) are the most common gated RNNs and demonstrated comparable performances (Chung et al., 2014). As in Eq. 4, the previous activation a_t is concatenated with the input x_t+1:

${\bar{\mathit{x}}}_{t+1}={\left[\begin{array}{cc}\hfill {\mathit{x}}_{t+1}\hfill & \hfill {\mathit{a}}_t\hfill \end{array}\right]}^{\mathsf{T}},(7)$

${\tilde{\mathit{x}}}_{t+1}={\bar{\mathit{x}}}_{t+1}\text{or}{\tilde{\mathit{x}}}_{t+1}={\left[\begin{array}{cc}\hfill {\bar{\mathit{x}}}_{t+1}\hfill & \hfill {\mathit{c}}_t\hfill \end{array}\right]}^{\mathsf{T}}.(8)$

FIGURE 2

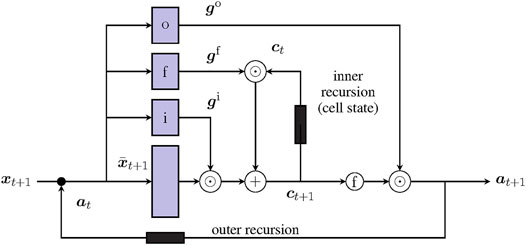
FIGURE 2. Visualization of an LSTM cell, which consists of multiple feedforward layers (light violet). Three gates, gⁱ, g^f, and g^o, control the data flow into the cell, within the cell, and out of the cell. Two recursions (black rectangles) ensure stable gradients across many time steps.

The gates process the adjusted input ${\tilde{\mathit{x}}}_{t+1}$ using dense layers, $\left({\mathit{W}}^{\text{i}},{\mathit{b}}^{\text{i}}\right)$, $\left({\mathit{W}}^{\text{f}},{\mathit{b}}^{\text{f}}\right)$, and $\left({\mathit{W}}^{\text{o}},{\mathit{b}}^{\text{o}}\right)$, and apply a sigmoid activation, which yields

${\mathit{g}}^{\text{i}}=\mathrm{s}\mathrm{i}\mathrm{g}({\mathit{W}}^{\text{i}}{\tilde{\mathit{x}}}_{t+1}+{\mathit{b}}^{\text{i}}),(9)$

${\mathit{g}}^{\text{f}}=\mathrm{s}\mathrm{i}\mathrm{g}({\mathit{W}}^{\text{f}}{\tilde{\mathit{x}}}_{t+1}+{\mathit{b}}^{\text{f}}),(10)$

${\mathit{g}}^{\text{o}}=\mathrm{s}\mathrm{i}\mathrm{g}\left({\mathit{W}}^{\text{o}}{\tilde{\mathit{x}}}_{t+1}+{\mathit{b}}^{\text{o}}\right).(11)$

Therein, gⁱ is the input gate activation, g^f the forget gate activation, and g^o the output gate activation, whose coefficient values are bounded between zero and one. Similar to Boolean masks, these gates control the data flow in the LSTM cell by

${\mathit{i}}_{t+1}={\mathit{g}}^{\text{i}}\odot \mathrm{f}\left(\mathit{W}{\bar{\mathit{x}}}_{t+1}+\mathit{b}\right),(12)$

${\mathit{c}}_{t+1}={\mathit{g}}^{\text{f}}\odot {\mathit{c}}_t+{\mathit{i}}_{t+1},(13)$

${\mathit{a}}_{t+1}={\mathit{g}}^{\text{o}}\odot \mathrm{f}\left({\mathit{c}}_{t+1}\right),(14)$

where the element-wise product ⊙ allows the gate tensors gⁱ, g^f, and g^o to control the incoming data flow into the cell c_t+1, to forget information from selected entries, and to output selected information as a_t+1. Despite being the foundation for the RNN reasoning and long-term memory, the cell states are often regarded as black boxes.

2.1.2 A Selection of Fundamental Constitutive Models

The systematic hyperparameter search and explainable AI approach will be demonstrated on three representative constitutive models, briefly reviewed in the following. These well-known models describe material effects, such as finite, lasting, and rate-dependent deformations. Since the ground truths for these one-dimensional models are known, the resulting neural network architectures from the hyperparameter search can be evaluated. Furthermore, for history-dependent material behaviors, the explainable AI approach can investigate the RNNs that best describe the constitutive models.

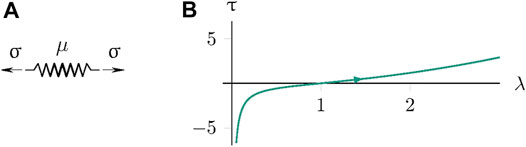
First, a hyperelastic constitutive model challenges neural networks to model finite strains and deal with the singular behavior of stretches that approach zero. The one-dimensional Neo-Hooke model (cf. Holzapfel (2000)) is regarded as one of the most straightforward nonlinear elastic material models. Therein, a single parameter μ describes the Cauchy stress τ as a function of the stretch λ:

$\mathrm{\tau }=\mu \left({\mathrm{\lambda }}^2-\frac{1}{\mathrm{\lambda }}\right).(15)$

Thus, the Neo-Hooke model offers the highest possible contrast to distributed neural network representations. In Figure 3, the corresponding rheological model (Figure 3A) and a loading and unloading cycle (Figure 3B) are depicted. The neural network approximation is challenged by stretch values near the origin, where the stress response exhibits singular behavior.

FIGURE 3

FIGURE 3. One-dimensional hyperelastic rheological model (A) and example load cycle (B).

Second, viscoelasticity represents the archetype of fading-memory material behavior (Truesdell and Noll, 2004), which poses a short-term temporal regression problem to the neural networks. Figure 4A introduces the Poynting-Thomson or standard linear viscoelastic solid model as an example for rate-dependent inelastic material behavior. As the elementary example for generalized Maxwell models, which use multiple parallel Maxwell branches to cover more decades in the frequency range, it exhibits the same principal relaxation and creep behavior (Markert, 2005), as depicted in Figure 4B–D.

FIGURE 4

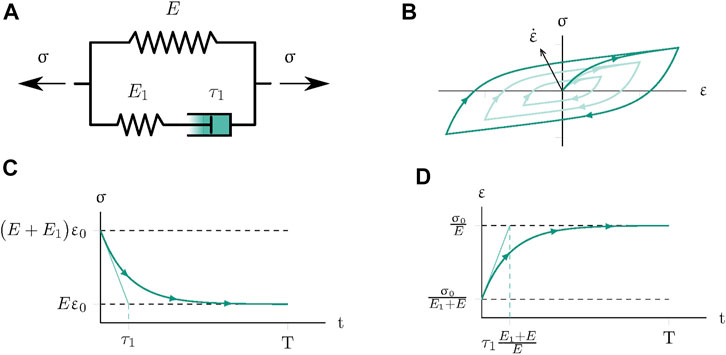
FIGURE 4. One-dimensional viscoelastic material behavior. (A) Poynting-Thomson rheological model. (B) Cyclic loading hysteresis for constant strain rates $\dot{\mathrm{\epsilon }}$. (C) Stress relaxation response to a unit-sized step ɛ(t) = ɛ₀ H(t). (D) Creep retardation response to a unit-sized step σ(t) = σ₀ H(t).

The additive decomposition of the stress σ and the evolution equations for each Maxwell branch i, as reviewed, e.g., in the textbook of Holzapfel (2000), yield

$3{\dot{\mathrm{\sigma }}}_i+\frac{{\mathrm{\sigma }}_i}{{\tau }_i}=E_i\dot{\mathrm{\epsilon }}\forall i=1\dots I,\text{and}(16)$

$\mathrm{\sigma }=E\mathrm{\epsilon }+\sum _i{\mathrm{\sigma }}_i.(17)$

For each branch i, σ_i represents the stress, τ_i the relaxation time, and E_i the modulus. The strain ɛ is shared by all Maxwell branches and the elastic spring with modulus E. For I = 1, Eqs 16, 17 yield

$\mathrm{\sigma }+{\tau }_1\dot{\mathrm{\sigma }}=E\mathrm{\epsilon }+{\tau }_1(E+E_1)\dot{\mathrm{\epsilon }}.(18)$

Many known excitations, e.g., unit steps σ(t) = σ₀ H(t) or ɛ(t) = ɛ₀ H(t) yield closed-form solutions described by the relaxation function R(t) and creep function C(t) (Simo and Hughes, 1998):

$\mathrm{\sigma }\left(\mathrm{t}\right)=\underset{-\infty }{\overset{\text{t}}{\int }}R\left(\mathrm{t}-\tilde{t}\right)\dot{\mathrm{\epsilon }}\left(\tilde{t}\right)d\tilde{t}\text{with}(19)$

$R\left(\mathrm{t}\right)=E+E_1\exp \left(-\frac{\mathrm{t}}{{\tau }_1}\right),(20)$

$\mathrm{\epsilon }\left(\mathrm{t}\right)=\underset{-\infty }{\overset{\text{t}}{\int }}C\left(\mathrm{t}-\tilde{t}\right)\dot{\mathrm{\sigma }}\left(\tilde{t}\right)d\tilde{t}\text{with}(21)$

$C\left(\mathrm{t}\right)=\left[\frac{1}{E+E_1}+\frac{E_1}{E\left(E+E_1\right)}\left(1-\exp \left(-\frac{\mathrm{t}E}{{\tau }_1\left(E+SEi\right)}\right)\right)\right].(22)$

For the general case of incremental excitations, numerical integration Eq. 16 with an implicit backward Euler scheme yields

$\begin{array}{cc}\hfill {\mathrm{\sigma }}_{\text{t}+\mathrm{\Delta }\mathrm{t}}=\frac{1}{c_{\mathrm{\sigma }1}}& \left[c_{e1}{\mathrm{\epsilon }}_{\text{t}+\mathrm{\Delta }\mathrm{t}}-c_{e0}{\mathrm{\epsilon }}_{\text{t}}+c_{\mathrm{\sigma }0}{\mathrm{\sigma }}_{\text{t}}\right]\hfill \\ \hfill \text{with}{c}_{\mathrm{\sigma }0}& =\frac{{\tau }_1}{\mathrm{\Delta }\mathrm{t}},c_{\mathrm{\sigma }1}=1+\frac{{\tau }_1}{\mathrm{\Delta }\mathrm{t}},\hfill \\ \hfill c_{\mathrm{ϵ}0}& =\frac{{\tau }_1}{\mathrm{\Delta }\mathrm{t}}(E+E_1),c_{\mathrm{ϵ}1}=E+\frac{{\tau }_1}{\mathrm{\Delta }\mathrm{t}}(E+E_1).\hfill \end{array}(23)$

Therein, σ_t and σ_t+Δt represent the stresses while ɛ_t and ɛ_t+Δt respectively represent the strains, respectively at the current and next increment. As a dissipative model, the dissipated energy can be described by the area surrounded by the hystereses, which depend on the strain rates (Figure 4B).

Finally, elastoplastic models exhibit path-dependent behavior with lasting deformations, i.e., long-term dependency behavior, and include potential discontinuities in the stress response, which need to be learned by the neural network. Numerical implementations of one-dimensional Prandtl-Reuss plasticity (Figure 5A) can be found, e.g., in Simo and Hughes (1998) or de Borst et al. (2012):

$\mathrm{\sigma }=E(\mathrm{\epsilon }-{\mathrm{\epsilon }}^{\text{P}}),(24)$

${\dot{\mathrm{\epsilon }}}^{\text{P}}=\gamma \mathrm{sign}\left(\mathrm{\sigma }-q_{\mathrm{\sigma }}\right)\text{and}{\dot{q}}_{\mathrm{\epsilon }}=\gamma \text{and}{\dot{q}}_{\mathrm{\sigma }}=\gamma H\mathrm{sign}\left(\mathrm{\sigma }-q_{\mathrm{\sigma }}\right),(25)$

$f_y(\mathrm{\sigma },q_{\mathrm{\epsilon }},q_{\mathrm{\sigma }})=|\mathrm{\sigma }-q_{\mathrm{\sigma }}|-({\mathrm{\sigma }}_Y+K{q}_{\mathrm{\epsilon }}).(26)$

FIGURE 5

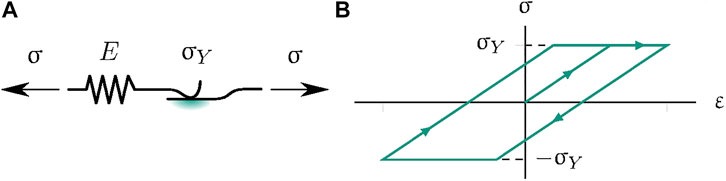
FIGURE 5. One-dimensional Prandtl-Reuss elastoplastic rheological model (A) with perfect plastic material behavior (B).

In Eqs 24 to 26, the main history variable is the plastic strain ɛ^P, whose evolution follows the yield step γ if a yield criterion f_y = 1 is met. In Figure 5B, the characteristic stress-strain curve of one-dimensional Prandtl-Reuss plasticity is shown.

2.2 Explainable Artificial Intelligence for Mechanics

2.2.1 Data-Driven Constitutive Models for Fundamental Material Behavior

Data-driven constitutive models and intelligent finite elements were one of the first applications of neural networks within the FEM (Ghaboussi et al., 1991; Ghaboussi et al., 1998; Ghaboussi and Sidarta, 1998; Javadi et al., 2009), since they leverage the flexibility of the FEM to the fullest. For a strain-driven problem, data-driven constitutive models can be defined by

$\mathrm{I}\mathrm{C}:\mathbf{\epsilon }{\mapsto }^{\mathit{Q}}\mathbf{\sigma },(27)$

where ɛ represents the strain and σ represents the stress. The history variables are gathered in Q, which may include both algorithmic history variables, such as the plastic strain ɛ^P, and recurrent neural network cell states C. As in the conventional FEM, the unified interface of inputs, outputs, and history variables enables a straightforward substitution of different data-driven constitutive models. For example, data-driven constitutive models, e.g., trained on experimental data (Stoffel et al., 2018), can substitute analytically derived constitutive models with trivial implementation effort. However, this flexibility massively increases the choice of conceivable neural network architectures and their defining hyperparameter configurations of data-driven constitutive models. Often, these hyperparameter configurations are chosen by the user or tuned using brute-force search algorithms.

2.2.2 Systematic Hyperparameter Search

Systematic hyperparameter search strategies constitute elegant and efficient solutions to finding optimal architectures and hyperparameter configurations. Hyperparameter search algorithms automatize the task of identifying advantageous neural network architectures and tuning hyperparameters γ to achieve good performance. Since neural networks are nonlinear function approximators with numerous parameters, the error surface is generally non-convex, high dimensional, potentially non-smooth, and noisy (Li et al., 2017). Furthermore, hyperparameters are interdependent, and the effects on the model remain unclear and problem-specific (Li et al., 2017), which often popularized brute force search algorithms, such as grid search (Bergstra and Bengio, 2012).

Grid search is the most fundamental search algorithm that seeks to cover the entire hyperparameter search domain. All possible combinations of user-defined hyperparameter values are tested one by one, with a fixed step size. The number and intervals of tested hyperparameter configurations Γ are set arbitrarily by the user, making the approach wasteful, inefficient, and infeasible for large numbers of hyperparameters.

Random search algorithms (Bergstra and Bengio, 2012) yield probabilistic approaches for larger numbers of hyperparameters. With enough trials, random search statistically explores the entire search space by testing a random selection of all possible combinations with varying step sizes. Thus, high-dimensional search spaces are explored faster, which makes random search a widely used search algorithm for hyperparameter-intensive neural networks (Bergstra and Bengio, 2012). Unfortunately, the computational effort of random search remains significant.

Therefore, this work follows approaches that increase the efficiency of the random search algorithm, leveraging the observation that the final performances of neural networks can be approximately assessed after a few epochs n, i.e., iterations that include the entire training dataset. The Successive Halving algorithm (Jamieson and Talwalkar, 2016), for example, trains randomly chosen hyperparameter configurations Γ = {γ⁽¹⁾…γ^(C)} for n epochs. After that, the lowest-performing configurations are discarded, while the best-performing configurations are trained further. Thus, the approach focuses the computational resources on promising hyperparameter configurations.

Unfortunately, the number of epochs to train before deciding on discarding low-performing configurations constitutes another hyperparameter, which depends on the mechanical problem. Either Successive Halving can explore more configurations C for fewer epochs n or investigate fewer configurations C for more epochs n per decision. Li et al. (2017) solved this exploration issue with the Hyperband search algorithm (Algorithm 1). By gathering groups of configurations in h brackets, Successive Halving can be applied for different numbers of epochs n_h per group. The first bracket s = h maximizes exploration to test many configurations C with Successive Halving, identifying promising positions even for vast search domains and non-convex or non-smooth loss functions. In the last bracket s = 0, fewer configurations are tested for the full number of epochs, similar to a conventional random search. This is advantageous if the search domain is narrow and the objective functions are convex and smooth. Thus, Hyperband combines efficient exploration and investigation of promising architectures and does not introduce additional hyperparameters to be tuned.

In this work, we combine Hyperband with aggressive early stopping, which discards solutions that are unlikely to improve further by monitoring moving averages of the validation errors. Independent of Hyperband, this additional logic further increases the efficiency of the search strategy for data-driven constitutive models. Thus, this fully automatized strategy identifies optimal neural network architectures for the given training and validation data without user interaction. The resulting hyperparameter configurations represent a ‘natural’ choice for the given problem, which merits further investigations into why this specific neural network was chosen.

ALGORITHM 1

ALGORITHM 1. Hyperband search (Li et al., 2017).

2.2.3 The Novel Explainable Artificial Intelligence Approach

If the problem allows, it is generally possible to identify and train an efficient neural network to achieve accurate results and generalize to unknown data with the systematic approach outlined above. However, in the past, the proven approximation capabilities of neural networks (Hornik et al., 1989) were often shunned because the magical black-box-generated results could not be explained. Given only finite dataset sizes, any machine learning algorithm may learn spurious or accidental correlations. Since neural networks naturally develop distributed high-dimensional representations in deep layers, the ‘reasoning’ of neural networks is notoriously difficult to verify. Thus, a trained neural network may generalize to validation and test datasets but found it’s decision-making on unphysical observations and biases in the dataset. The motivation of explainable AI is to unmask such ‘Clever Hans’ predictors¹ (Lapuschkin et al., 2019).

Many explainable neural network approaches, such as Layer-wise Relevance Propagation (LRP) (Bach et al., 2015; Arras et al., 2017; Montavon et al., 2018, Montavon et al., 2019), use the neural network graph to trace the activation back to its origin. In particular, such approaches are attractive for classification, because they can explain individual class labels, i.e., from single binary values to multiple inputs. For positive binary values, the activations can be traced back straightforwardly, explaining why the neural network chose the class associated with the binary value. However, multivariate regression problems are faced with a different problem: since the outputs are continuous, the neural network ‘reasoning’ must be interpretable over the full output ranges, including the origin. In particular, in balance equations, zero-valued residuals are at least as important as non-zero residuals and follow the same physical governing equations. Thus, for mechanical regression tasks, different explainable AI methods are necessary, which focus on the evolution of the high-dimensional representations.

As a new explainable AI approach using mechanical domain knowledge, our proposed approach focuses on the temporal evolution of mechanical quantities. Since time-variant problems in mechanics are often modeled by training RNNs on time-variant and path-dependent mechanical data (Freitag et al., 2011; Cao et al., 2016; Koeppe et al., 2019; Wu L. et al., 2020), we propose to use the Principal Component Analysis (PCA) to investigate recurrent cell states, e.g., in LSTM and GRU cells. Therefore, we interpret the time-variant cell states as statistical variables and use the PCA to identify the major variance directions in the distributed representations. With the original evolution equations and history variables known, major principal components can be compared with the known temporal evolution. If the cell states resemble the mechanical evolution equations of the algorithmic history variables, the neural network correctly understood the fundamental mechanical problem. For future materials, neural networks can thus be trained on new material test data, and the material can be possibly characterized by comparing the cell state principal components to known fundamental evolution equations.

The PCA (Pearson, 1901) constitutes an unsupervised learning algorithm that decorrelated data (Figure 6) (Goodfellow et al., 2016). As a linear transformation, the PCA identifies an orthonormal basis by maximizing the variance in the directions of the principal components. In the field of model order reduction and data analysis, the PCA is often used to compute proper orthogonal decompositions, which eliminate undesirable frequencies from mechanical problems and reduce the model dimensionality to achieve computational speed-up (cf. Freitag et al. (2017); Cao et al. (2016); Bamer et al. (2017); Huber (2021); Altschuh et al. (2017)). Used in this explainable AI approach, the PCA is not used to accelerate computations, but to analyze and explain neural network behavior.

FIGURE 6

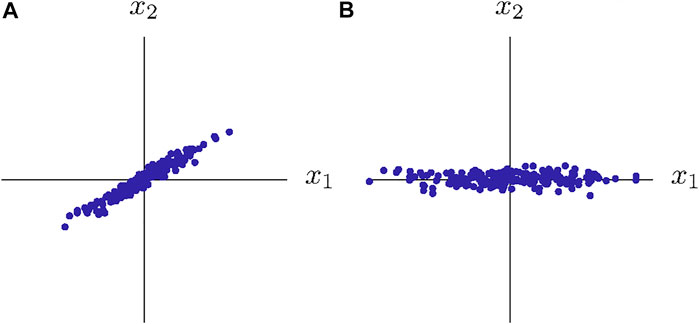
FIGURE 6. Feature decoupling using the PCA. The PCA identifies the directions with the highest variance in the original data (A) and enables the extraction of linearly independent features (B).

To compute the PCA on a dataset with correlated features (Figure 6A), the dataset of M samples x_m is collected in a dataset tensor X and centered feature-wise to $\bar{\mathit{X}}$:

$\mathit{X}={[{\mathit{x}}_1\dots {\mathit{x}}_M]}^{\mathsf{T}},(28)$

$\bar{\mathit{X}}=\mathit{X}-\mathbb{E}[\mathit{X}](29)$

Applied to the centered dataset tensor $\bar{\mathit{X}}$, the Singular Value Decomposition (SVD),

$\mathrm{SVD}:\bar{\mathit{X}}\mapsto \mathit{U},\mathbf{\Sigma },{\mathit{W}}^{\mathsf{T}},(30)$

decomposes $\bar{\mathit{X}}$ into the left-singular vectors U, the singular-value diagonal matrix Σ, and the right-singular vectors W. Conventionally, most SVD algorithms sort the singular vectors and singular values on the basis of the magnitude of the latter, where the highest singular value in Σ corresponds to the highest variance (i.e., frequency) in the dataset. Feature-wise contraction of the centered dataset $\bar{\mathit{X}}$ with W yields the decoupled data tensor $\bar{\mathit{x}}$:

$\bar{\mathit{x}}=\bar{\mathit{X}}\mathit{W}.(31)$

The reciprocal square root of the singular values $\sqrt{{\mathbf{\Sigma }}^{-1}}$ scales the decoupled dataset $\bar{\mathit{x}}$ down to unit variance.

To use the PCA on LSTM cell states c_t from Eq. 13, the data tensor C of sequence length T is assembled:

$\mathit{C}\equiv [{\mathit{c}}_1\dots {\mathit{c}}_T].(32)$

Equations 29 to 32 yield

$\bar{\mathit{C}}=\bar{\mathit{C}}\mathit{W}\text{with}\bar{\mathit{C}}=\mathit{C}-\mathbb{E}[\mathit{C}].(33)$

The columns ${\bar{\mathit{C}}}_t$ (t = 1 … T) of the decoupled state tensor $\bar{\mathit{C}}$ describe the temporal behavior of the cell in the principal axes. The associated singular value Σ_f divided by the sum of all singular values quantifies the relative importance of the corresponding principal components, i.e., how much each principal component explains the cell state variance. Often, most of the variance can be explained using the first three principal components, ${\bar{\mathit{c}}}^{\text{I}}$, ${\bar{\mathit{c}}}^{\text{II}}$, and ${\bar{\mathit{c}}}^{\text{III}}$, which describe the memory response of the majority of the cell units. To investigate the ability to explain the mechanical problem, the neural network’s major memory cell responses, ${\bar{\mathit{c}}}^{\text{I}}$, ${\bar{\mathit{c}}}^{\text{II}}$, and ${\bar{\mathit{c}}}^{\text{III}}$, are compared to the algorithmic history variables q.

This comparison demonstrates that the neural network understood temporal mechanical problems in line with the physically observed evolution laws.

Note that the ability to generalize, i.e., to achieve a reproducible and equally accurate result on unknown data, as outlined in Section 2.2.2, remains independent of the ability to model the result on correct physical assumptions, as described in this subsection. To achieve generalizable results, systematic hyperparameter tuning thus is the necessary prerequisite for the explainable AI approaches.

3 Results

The following three case studies demonstrate the systematic hyperparameter search strategy and the new explainable AI approach. First, the proposed systematic hyperparameter search strategy will be demonstrated in the scope of a case study for an intelligent nonlinear elastic constitutive model. Thereafter, the latter two case studies combine the systematic hyperparameter search strategy with explainable AI, in order to interpret inelastic time-variant constitutive behavior.

For all data-driven constitutive models, the same data-generation strategy provides training, validation, and test data. For a sequence length of T = 10000 and Ω = 5 phases of loading and unloading, we sample control values from a random normal distribution $\mathcal{N}(\mu =0,\sigma =1)$. Between those control values, a variety of ramping functions, e.g., linear, quadratic, or sinusoidal, interpolate the intermediate values to assemble stress- or strain-controlled loading sequences. The ramping functions are selected to cover a variety of constitutive responses based on the investigated constitutive models. Thereafter, the numerical implementation of each reference constitutive model generates M^total = 10000 samples, which are split randomly 70 %-15 %–15% into training, validation, and test set.

Three constitutive models are selected to demonstrate fundamental mechanical material behavior, including finite deformations, long-term temporal behavior, and rate dependency. To enhance interpretability, each one-dimensional constitutive model uses dimensionless and purely academic parameter values. Using preprocessing strategies, such as normalization and augmenting the input with explicit model parameters, models with arbitrary material parameter values can be created (Koeppe et al., 2018b; 2020a). First, an incompressible Neo-Hooke constitutive model ($\mu =\frac{1}{3}$) computes the nonlinear stress response to stretch-controlled loading. Due to the hyperelastic problem, all loading and unloading phases ω = 1…Ω use linear ramps. The investigated time-distributed dense neural network architectures receive the stretch λ as input and learn to predict the Cauchy stress σ. Second, a perfect Prandtl-Reuss elastoplasticity model (E = 1, σ_Y = 0.6) is subjected to strain-controlled loading. The phase interpolation functions are sampled randomly from linear, quadratic, square-root, exponential, sine, and half-sine ramping functions. The investigated RNN architectures use the strain ɛ to return the stress σ and plastic strain ɛ^P. Finally, a Poynting-Thomson constitutive model, defined by E = 1.0, E₁ = 0.5, and τ₁ = 0.1667 is integrated in time (T = 1) with an implicit backward Euler-scheme. The stress-controlled phases ω = 1…Ω include linear ramps and constant phases to investigate creeping behavior. The RNN architectures process the stress σ and return the strain ɛ and the viscous branch stress σ₁. For all neural networks, a final time-distributed dense layer of output size applies a linear transformation to cover the entire range of real values.

For the neural network architecture and the hyperparameters, the Hyperband algorithm (Li et al., 2017) systematically explores and investigates the high-dimensional search domain. During the training of each configuration, the Adam algorithm (Kingma and Ba, 2014) minimizes the MSE on the training set (N = 51 epochs) and reports the validation loss to evaluate the configuration in the scope of Hyperband. To avoid artificially penalizing specific weight values, neither L¹ nor L² regularization is used, optimizing the unconstrained MSE. In the Hyperband brackets, each step performed by the Successive Halving algorithm eliminates the worst configurations from all configurations by a factor of η = 3.7. In Table 1, the search domains for the recurrent and dense neural network architectures are described. The design variables, i.e., the layer width d^(l), the neural network depth L, the base learning rate α and the batch size M vary during all search trials. Moreover, for dense neural networks (hyperelastic material behavior), multiple activation functions are investigated by the algorithm, whereas for recurrent neural networks (viscoelastic and elastoplastic material behavior), the cell type of the reccurent cells become additional design variables. To limit the potentially infinite search space, the layer widths are selected to be identifcal for all layers and the design variables are varied in heurisically defined steps and ranges. After the search, we train the best configuration, as evaluated by the lowest MSE on the validation set, for the full duration of N = 301 epochs. The resulting parameter values θ^opt are used to evaluate the test set to compute the test errors.

TABLE 1

TABLE 1. Hyperband search domain for constitutive models.

For the last two case studies, the novel explainable neural network approach (Section 2.2.3), employing the PCA on the cell states, analyzes the best RNN architectures to explain the intelligent inelastic constitutive models.

The Kadi4Mat (Brandt et al., 2021) data management infrastructure stores, links, and describes the data generated in this publication. Published via the direct integration of Zenodo (Koeppe et al., 2021), the dataset includes the generated reference constitutive model dataset, the associated metadata of the constitutive and neural network models, and the serialized trained neural networks for different hyperparameter configurations at different epochs during training. The data storage with the associated metadata and connections enhances the systematic hyperparameter search strategy with the option for long-term data sustainability, e.g., by reusing previous search results and hyperparameter configurations for future models. Furthermore, the links between the dataset and the serialized neural network models provide a starting point for a bottom-up data ontology for machine learning in mechanics and material sciences. Subsequently formalized, the data ontology will provide semantic rules that describe the relations and workflows inherent to the research data, which will enable additional analysis and explainable AI approaches.

3.1 Systematic Investigation of Data-Driven Hyperelastic Constitutive Models

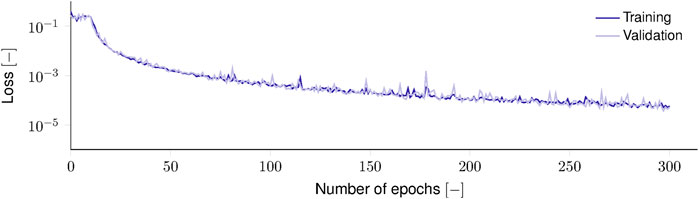
For the hyperelastic problem, the best-performing hyperparameters were a batch size of M = 64 and a base learning rate of α = 3 ⋅ 10^–3. A deep feedforward neural network with 5 hidden layers of width 112 and rectifier activation achieved the best performance. After training (Figure 7) for 301 epochs, the neural network achieves an MSE ϵ^MSE of 1.28 ⋅ 10^–5 on the training, 1.01 ⋅ 10^–5 on the validation, and 1.01 ⋅ 10^–5 on the test set. The same order of error magnitude on all three datasets indicates that the neural network achieved generalization. Figure 8 visualizes three randomly selected test samples. For the one-dimensional hyperelastic case, the data-driven constitutive model is in perfect agreement with the reference model.

FIGURE 7

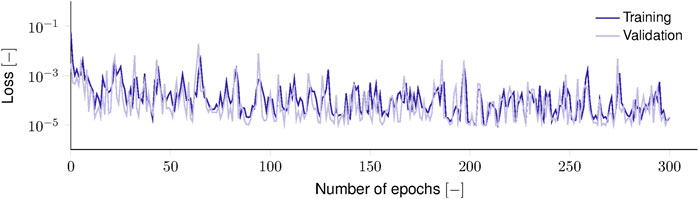
FIGURE 7. Training and validation loss during hyperelastic constitutive model training. Both losses rapidly reduce within the first 20 epochs before oscillating due to variance shift combined with the singular behavior of the stretch near the origin.

FIGURE 8

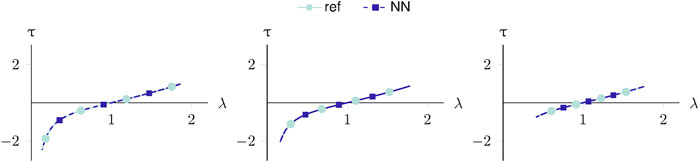
FIGURE 8. Three randomly selected stress-stretch curves for hyperelastic constitutive behavior. The data-driven constitutive model exactly matches the reference solution.

3.2 Explaining Data-Driven Elastoplastic Constitutive Models

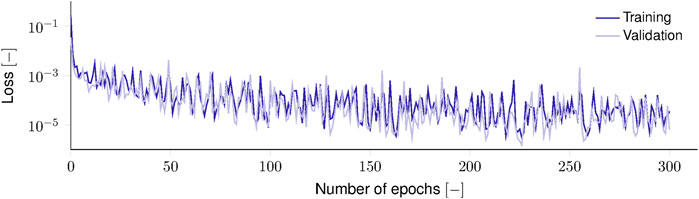
For the elastoplastic problem, the systematic search strategy identified a best-performing architecture, characterized by four LSTM cells, with a width of 52 units followed by a linear time-distributed dense layer with 2 units. For the training (Figure 9), a batch size of M = 32 and a base learning rate of α = 1 ⋅ 10^–3 resulted in the best result without overfitting, i.e., an MSE ϵ^MSE of 5.72 ⋅ 10^–5 on the training, 5.11 ⋅ 10^–5 on the validation, and 4.38 ⋅ 10^–5 on the test set.

FIGURE 9

FIGURE 9. Training and validation loss during elastoplastic constitutive model training.

To interpret and explain the RNN behavior, a random sample is extracted from the test set and evaluated using the data-driven constitutive model. The explainable AI approach uses the PCA on the concatenated cell states of all recurrent cells and yields the three principal components with the highest singular values. Expressed in the three major principal components and divided by their singular values, the cell states I, II, and III represent the joint response of the LSTM cell states. Figure 10 visualizes and compares the evolution of the stresses, strains, and history variables over the entire loading sequence.

FIGURE 10

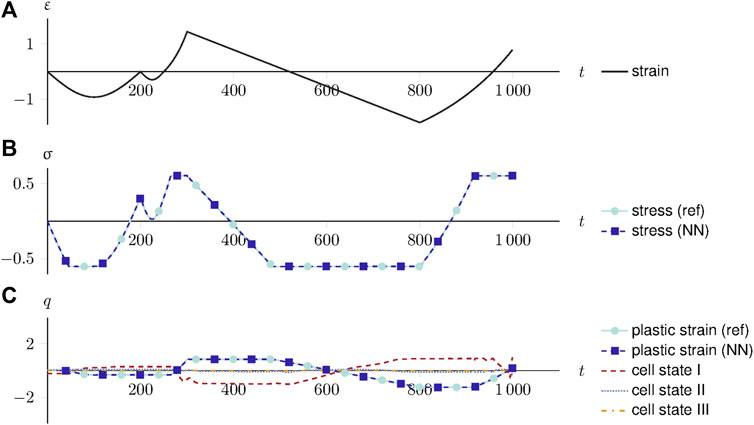
FIGURE 10. An explainable elastoplastic constitutive model. (A) The strain-driven loading over the time increments. (B) The stress response of the reference and data-driven constitutive model. (C) The plastic strain, compared to the three major principal components of the cell state. The cell states approximate the plastic strain (with a negative sign remedied by the output layer).

The neural network’s output predictions and the reference constitutive model match exactly, i.e., the stresses and plastic strain predictions are accurate. By comparing the plastic strain with the internal cell states, the learned function of the LSTM cells becomes apparent, which governs the neural network’s decision-making behavior. Without being trained directly, the cell states’ principal components learn to approximate the plastic strain evolution (with a negative sign). Since the PCA chooses the principal directions based on the variance, and the output layer can apply arbitrary weighting, the negative sign of the cell state does not affect the result. The second and third principal components do not contribute to the joint cell state response.

3.3 Explaining Data-Driven Viscoelastic Constitutive Models

For the viscoelastic problem, the Hyperband search found the best-performing architecture to be three GRU cells with 120 units, followed by a time-distributed dense layer (2 units and linear activation). For training convergence, a batch size of M = 32 and a base learning rate of α = 1 ⋅ 10^–3 achieved the best results. After training for the full 301 epochs (Figure 11), the neural network achieved a best MSE ϵ^MSE of 2.05 ⋅ 10^–7 on the training, 7.36 ⋅ 10^–7 on the validation, and 1.15 ⋅ 10^–6 on the test set, indicating generalization. Furthermore, since all samples are generated with unit variance and unit stiffness, the model approximates almost at the machine precision of the element-wise definition of the MSE performance metric ($\sim \mathcal{O}\left(10^7\right)$ for single-precision floating-point arithmetic).

FIGURE 11

FIGURE 11. Training and validation loss during viscoelastic constitutive model training.

Figure 12 exemplifies the explainable AI strategy on one randomly generated sample that was not used for training or validation. In the top row, the stress is plotted over the increments, which constitutes the input to the reference constitutive and neural network models. The second row compares the strain response of the reference and neural network models. The final row depicts the history variables q. The branch stress σ₁ is computed by both the reference and data-driven constitutive models. Both strain and branch stress match accurately, as indicated by the low test loss. Finally, the PCA on the GRU cell state over time yields the data-driven constitutive history variables, i.e., the three principal components with the highest singular values, which govern the major evolution of the data-driven constitutive model.

FIGURE 12

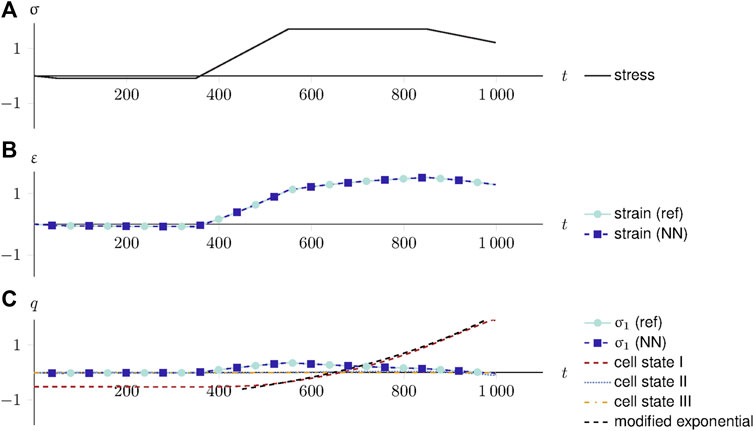
FIGURE 12. An explainable viscoelastic constitutive model. (A) The stress-driven loading over time. (B) The strain response of the reference and data-driven constitutive model. (C) The branch history stress compared to the three major principal components of the cell state. Instead of mimicking the history variables used to generate training data, the cell states learned a generic solution for viscoelasticity: a modified exponential function that can be shifted and scaled at will by the output layer.

Instead of approximating the history variables σ₁, used to generate the training data with backward Euler time integration, the first principal component of the cell states approximates a modified exponential function, correctly identifying the exponential behavior of viscoelasticity. Shifting, scaling, and changing the sign of a function represent trivial operations for previous and subsequent neural network layers. Thus, the weights of the RNN and the last dense layer can modify the cell output at will to assemble a solution, such as Eq. 21. The second and third principal components do not contribute to the joint cell state response.

4 Discussion

4.1 Results and Approach

The objectives of this publication were to systematically and automatically identify and train neural networks for data-driven constitutive models of fundamental material behavior and to explain the resulting recurrent neural networks’ behavior.

The test errors (2.45 ⋅ 10^–6 to 4.38 ⋅ 10^–5) approach machine precision for the single-precision floating-point arithmetic used to compute them. The neural network performance surpasses the elastoplastic constitutive model for uniaxial tension and compression in the recent works of Huang et al. (2020) (3.93 ⋅ 10^–2) and Alwattar and Mian (2019) (∼ 1 ⋅ 10^–5, as reported on the training set). For each of the case studies, the results were in the same order of magnitude for all datasets, regardless of whether they were shown to the neural networks during training (training dataset) or unknown to the neural network (validation and test dataset). The oscillations in the loss curves for the viscoelastic and hyperelastic cases can be attributed to the shift in randomly selected samples for each batch averaged over each epoch in combination with the stronger continuous nonlinearities of the problems. This suggests, that no overfitting occured and generalization to unknown data was achieved, despite the considerable number of trained parameters in some of the models identified by the search algorithm.

When using manual hyperparameter tuning, mechanical and physical 1257 knowledge, and machine learning expertise, considerably smaller neural networks with fewer parameters with fewer layers and units per layer are conceivable that could have been trained to achieve similar results. Limiting the capacity of machine learning models is one of the first and most important steps in achieving robust performance and generalization to unknown data. This limit is governed by the amount and variance of the data, which is considerably harder to generate in abundance for experimental data (cf. Argatov and Chai (2019)). Here, many best-practice applications and textbooks suggest choosing a neural network capacity slightly larger than strictly necessary and utilizing additional regularization schemes for optimal generalization performance (Goodfellow et al., 2016; Argatov and Chai, 2019). However, the objectives of this study were to demonstrate an automated and inductive strategy that requires minimal prior knowledge to automatically identify and train models and to help understand the resulting models, regardless of how many parameters were used. Therefore, the less-than-minimalistic models identified by the hyperparameter search algorithm posed a more difficult challenge for the novel explainable AI approach.

The results were achieved inductively, with minimal user input, through the application of a Hyperband-inspired systematic search strategy on mechanical data. To further improve the results of the neural networks, several approaches are conceivable, most of which are deductively derived from deep learning and mechanical domain knowledge. Ensemble learning and related regularizers, such as dropout (Srivastava et al., 2014), for example, are known to improve the quality of the results further (Srivastava et al., 2014; Goodfellow et al., 2016). Similarly, physics-informed and physics-guided approaches, as proposed by Raissi et al. (2019), Yang and Perdikaris (2019), or Kissas et al. (2020), use mechanical domain knowledge to improve neural network models of physical systems. In contrast, the data-driven constitutive models trained in this work represent an inductive, fundamental, and accurate approach that offers intuition for possible neural network architectures and hyperparameter configurations for higher-dimensional mechanical problems. In combination with the explainable AI approach, the data-driven constitutive models represent the first step towards physics-explaining neural networks.

Even beyond mechanics and materials sciences, applying the PCA to explain neural network cell states constitutes a novel and promising explainable AI method. The PCA investigation proposed in this work can explain the recurrent cell state behavior, despite the considerable size of the investigated architecture, compared to the one-dimensional fundamental problems. Due to the quality of the results and the explainability of the neural network, “Clever-Hans” predictors (Lapuschkin et al., 2019) can be ruled out. For material behavior where multiple physical effects affect the same observed features (e.g., viscoplasticity or ductile fracture), the global PCA used in this proof-of-concept study could be upgraded to provide local decompositions in combination with clustering algorithms.

As an explainable neural network approach in mechanics, the case studies demonstrate how neural networks can help to explain material behavior. For the elastoplastic problem, the recurrent cell state identified the same history variables used in computing the ground truth. For the viscoelastic problem, the data generation used numerical time-integration, but the neural network found a solution similar to the exponential closed-form solution. Therefore, if the ground truth is not known, e.g., when learning from raw experimental data, explainable neural network approaches can possibly identify underlying closed-form solutions. By characterizing new materials or material behavior, e.g., at extreme loading conditions, explainable AI can help guide researchers in mechanics and materials sciences towards new analytic closed-form solutions that elegantly model the materials in the desired ranges.

4.2 Concluding Remarks and Outlook

We proposed a step towards physics-explaining neural networks, which inductively complement existing deductive approaches for physics-informed and physics-guided neural networks. To that end, a systematic hyperparameter search strategy was implemented to identify the best neural network architectures and training parameters efficiently. For the analysis of the best neural networks, we proposed a novel explainable AI approach, which uses the PCA to explain the distributed representations in the cell states of RNNs.

The search strategy and explainable AI approach were demonstrated on data-driven constitutive models that learned fundamental material behavior, i.e., one-dimensional hyperelasticity, elastoplasticity, and viscoelasticity. For all case studies, the best neural network architectures achieved test errors in the order of 1 ⋅ 10^-5 to 1 ⋅ 10^-6. In particular, for hyperelasticity, the test error approached machine precision, despite the singular behavior for stretches approaching zero. For elastoplasticity, the novel explainable AI approach identified that the recurrent cell states learned history variables equivalent to the plastic strain, i.e., the history variables used to generate the original data. Remarkably, for viscoelasticity, the explainable AI approach found that the best performing neural network architecture used an exponential function as the basis for its decisions instead of the algorithmic history variables used to generate the training data.

These findings imply that systematic hyperparameter search, coupled with explainable AI, can help identify and characterize numerical and analytical closed-form solutions for constitutive models independent of the data origin. Thus, new materials can potentially be characterized with data originating from experiments, using the approach proposed in this work.

Future studies will apply and extend the proposed strategies to more complex material models. Of particular interest are viscoelastic materials subjected to strain rates that cover multiple decades, where conventional numerical models require numerous algorithmic history variables. Eventually, new materials, where the analytic closed-form solutions are as-of-yet unknown and numerical solutions are challenging to implement, can be characterized with developments based on the present work. Finally, applications beyond constitutive models are conceivable. For spatio-temporal problems, e.g., as given in Koeppe et al. (2020a), the explainable AI approach outlined in this work needs to be extended to leverage the spatial structure.

In forthcoming work, it is intended to extend the developed artificial intelligence approach within the Kadi4Mat (Brandt et al., 2021) framework to higher dimensional data containing 2D and 3D spatial plus temporal information to predict microstructure-mechanics correlations. The database used to train the neural network algorithms relies on digital twin data from synchronously conducted experiments and simulations of mechanically loaded polycrystalline and multiphase materials. Based on the training, the AI approach is applied to large-scale micromechanics-microstructure simulations so as to provide new insights, e.g., into mechanically induced nucleation events of new phases and grain variants or into microcrack probabilities. The combination of new AI concepts and advanced high-performance materials simulations shall establish an integral component of the research data infrastructure to enable computational methods for an accelerated design of new materials.

Data Availability Statement

The datasets generated and analyzed for this study can be found in the Zenodo repository https://zenodo.org/record/4699219.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors gratefully acknowledge financial support by the Federal Ministry of Education and Research (BMBF) and the Ministry of Science, Research and Art Baden-Württemberg as part of the Excellence Strategy of the German Federal and State Governments, through the projects FestBatt (project number 03XP0174E) and MoMaF - Science Data Center, and the state digitization strategy digital@bw (project number 57). The authors thank Leon Geisen for his editorial support.

Footnotes

¹Apparently, the horse ‘Clever Hans’ (1895–1916) could count and calculate, but, in fact, interpreted the expressions and gestures of the audience to find the correct answers.

References

Aarts, L. P., and van der Veer, P. (2001). Neural Network Method for Solving Partial Differential Equations. Neural Process. Lett. 14, 261–271. doi:10.1023/A:1012784129883

CrossRef Full Text | Google Scholar

Alber, M., Lapuschkin, S., Seegerer, P., Hägele, M., Schütt, K. T., Montavon, G., et al. (2018). iNNvestigate Neural Networks! ArXiv180804260 Cs Stat.

Google Scholar

Altschuh, P., Yabansu, Y. C., Hötzer, J., Selzer, M., Nestler, B., and Kalidindi, S. R. (2017). Data Science Approaches for Microstructure Quantification and Feature Identification in Porous Membranes. J. Membr. Sci. 540, 88–97. doi:10.1016/j.memsci.2017.06.020

CrossRef Full Text | Google Scholar

Alwattar, T., and Mian, A. (2019). Development of an Elastic Material Model for BCC Lattice Cell Structures Using Finite Element Analysis and Neural Networks Approaches. J. Compos. Sci. 3, 33. doi:10.3390/jcs3020033

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2019). An Artificial Neural Network Supported Regression Model for Wear Rate. Tribology Int. 138, 211–214. doi:10.1016/j.triboint.2019.05.040

CrossRef Full Text | Google Scholar

Argatov, I. I., and Chai, Y. S. (2021). Fretting Wear with Variable Coefficient of Friction in Gross Sliding Conditions. Tribology Int. 153, 106555. doi:10.1016/j.triboint.2020.106555

CrossRef Full Text | Google Scholar

Argatov, I. (2019). Artificial Neural Networks (ANNs) as a Novel Modeling Technique in Tribology. Front. Mech. Eng. 5, 30. doi:10.3389/fmech.2019.00030

CrossRef Full Text | Google Scholar

Arras, L., Montavon, G., Müller, K.-R., and Samek, W. (2017). “Explaining Recurrent Neural Network Predictions in Sentiment Analysis,” in Proceedings of the 8th Workshop on Computational Approaches to Subjectivity, Sentiment and Social Media Analysis, Copenhagen, Denmark (Association for Computational Linguistics), 159–168. doi:10.18653/v1/W17-5221

CrossRef Full Text | Google Scholar

Bach, S., Binder, A., Montavon, G., Klauschen, F., Müller, K.-R., and Samek, W. (2015). On Pixel-Wise Explanations for Non-Linear Classifier Decisions by Layer-Wise Relevance Propagation. PLoS One 10, e0130140. doi:10.1371/journal.pone.0130140

PubMed Abstract | CrossRef Full Text | Google Scholar

Bamer, F., Koeppe, A., and Markert, B. (2017). An Efficient Monte Carlo Simulation Strategy Based on Model Order Reduction and Artificial Neural Networks. Proc. Appl. Math. Mech. 17, 287–288. doi:10.1002/pamm.201710113

CrossRef Full Text | Google Scholar

Baymani, M., Kerayechian, A., and Effati, S. (2010). Artificial Neural Networks Approach for Solving Stokes Problem. Am 01, 288–292. doi:10.4236/am.2010.14037

CrossRef Full Text | Google Scholar

Bergstra, J., and Bengio, Y. (2012). Random Search for Hyper-Parameter Optimization. J. Mach. Learn. Res. 13, 281–305. doi:10.5555/2188385.2188395

CrossRef Full Text | Google Scholar

Bessa, M. A., Bostanabad, R., Liu, Z., Hu, A., Apley, D. W., Brinson, C., et al. (2017). A Framework for Data-Driven Analysis of Materials under Uncertainty: Countering the Curse of Dimensionality. Comput. Methods Appl. Mech. Eng. 320, 633–667. doi:10.1016/j.cma.2017.03.037

CrossRef Full Text | Google Scholar

Bock, F. E., Aydin, R. C., Cyron, C. J., Huber, N., Kalidindi, S. R., and Klusemann, B. (2019). A Review of the Application of Machine Learning and Data Mining Approaches in Continuum Materials Mechanics. Front. Mater. 6, 110. doi:10.3389/fmats.2019.00110

CrossRef Full Text | Google Scholar

Brandt, N., Griem, L., Herrmann, C., Schoof, E., Tosato, G., Zhao, Y., et al. (2021). Kadi4Mat: A Research Data Infrastructure for Materials Science. Data Sci. J. 20, 8. doi:10.5334/dsj-2021-008

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Statistical Modeling: The Two Cultures (With Comments and a Rejoinder by the Author). Statist. Sci. 16, 199–231. doi:10.1214/ss/1009213726

CrossRef Full Text | Google Scholar

Cao, B.-T., Freitag, S., and Meschke, G. (2016). A Hybrid RNN-GPOD Surrogate Model for Real-Time Settlement Predictions in Mechanised Tunnelling. Adv. Model. Simulation Eng. Sci. 3, 5. doi:10.1186/s40323-016-0057-9

CrossRef Full Text | Google Scholar

Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. ArXiv Prepr. ArXiv14061078. doi:10.3115/v1/d14-1179

CrossRef Full Text | Google Scholar

Chung, J., Gulcehre, C., Cho, K., and Bengio, Y. (2014). Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. ArXiv14123555 Cs.

Google Scholar

de Borst, R., Crisfield, M. A., Remmers, J. J. C., and Verhoosel, C. V. (2012). Nonlinear Finite Element Analysis of Solids and Structures. West Sussex, United Kingdom: Wiley.

Google Scholar

Flaschel, M., Kumar, S., and De Lorenzis, L. (2021). Unsupervised Discovery of Interpretable Hyperelastic Constitutive Laws. ArXiv201013496 Cs.

Google Scholar

Freitag, S., Graf, W., Kaliske, M., and Sickert, J. U. (2011). Prediction of Time-dependent Structural Behaviour with Recurrent Neural Networks for Fuzzy Data. Comput. Struct. 89, 1971–1981. doi:10.1016/j.compstruc.2011.05.013

CrossRef Full Text | Google Scholar

Freitag, S., Graf, W., and Kaliske, M. (2013). A Material Description Based on Recurrent Neural Networks for Fuzzy Data and its Application within the Finite Element Method. Comput. Struct. 124, 29–37. doi:10.1016/j.compstruc.2012.11.011

CrossRef Full Text | Google Scholar

Freitag, S., Cao, B. T., Ninić, J., and Meschke, G. (2017). Recurrent Neural Networks and Proper or Thogonal Decomposition With Interval Data for Real-Time Predictions of Mechanised Tunnelling Processes. Comput. Struct. 207, 258–273. doi:10.1016/j.compstruc.2017.03.020

CrossRef Full Text | Google Scholar

Fuchs, A., Heider, Y., Wang, K., Sun, W., and Kaliske, M. (2021). DNN2: A Hyper-Parameter Reinforcement Learning Game for Self-Design of Neural Network Based Elasto-Plastic Constitutive Descriptions. Comput. Struct. 249, 106505. doi:10.1016/j.compstruc.2021.106505

CrossRef Full Text | Google Scholar

Gers, F. A., Schmidhuber, J., and Cummins, F. (2000). Learning to Forget: Continual Prediction with LSTM. Neural Comput. 12, 2451–2471. doi:10.1162/089976600300015015

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghaboussi, J., and Sidarta, D. E. (1998). New Nested Adaptive Neural Networks (NANN) for Constitutive Modeling. Comput. Geotech. 22, 29–52. doi:10.1016/S0266-352X(97)00034-7

CrossRef Full Text | Google Scholar

Ghaboussi, J., Garrett, J., and Wu, X. (1991). Knowledge-Based Modeling of Material Behavior with Neural Networks. J. Eng. Mech. 117, 132–153. doi:10.1061/(asce)0733-9399(1991)117:1(132)

CrossRef Full Text | Google Scholar

Ghaboussi, J., Pecknold, D. A., Zhang, M., and Haj-Ali, R. M. (1998). Autoprogressive Training of Neural Network Constitutive Models. Int. J. Numer. Meth. Engng. 42, 105–126. doi:10.1002/(sici)1097-0207(19980515)42:1<105:aid-nme356>3.0.co;2-v

CrossRef Full Text | Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning. MIT Press.

Google Scholar

Graf, W., Freitag, S., Kaliske, M., and Sickert, J.-U. (2010). Recurrent Neural Networks for Uncertain Time-Dependent Structural Behavior. Comput.-Aided Civ. Infrastruct. Eng. 25, 322–323. doi:10.1111/j.1467-8667.2009.00645.x

CrossRef Full Text | Google Scholar

Graf, W., Freitag, S., Sickert, J.-U., and Kaliske, M. (2012). Structural Analysis with Fuzzy Data and Neural Network Based Material Description. Comput.-Aided Civ. Infrastruct. Eng. 27, 640–654. doi:10.1111/j.1467-8667.2012.00779.x

CrossRef Full Text | Google Scholar

Greff, K., Srivastava, R. K., Koutník, J., Steunebrink, B. R., and Schmidhuber, J. (2015). LSTM: A Search Space Odyssey. ArXiv150304069 Cs.

Google Scholar

Hashash, Y. M. A., Jung, S., and Ghaboussi, J. (2004). Numerical Implementation of a Neural Network Based Material Model in Finite Element Analysis. Int. J. Numer. Methods Eng. 59, 989–1005. doi:10.1002/nme.905

CrossRef Full Text | Google Scholar

Heider, Y., Wang, K., and Sun, W. (2020). SO(3)-invariance of Informed-Graph-Based Deep Neural Network for Anisotropic Elastoplastic Materials. Comput. Methods Appl. Mech. Eng. 363, 112875. doi:10.1016/j.cma.2020.112875

CrossRef Full Text | Google Scholar

Heider, Y., Suh, H. S., and Sun, W. (2021). An Offline Multi-Scale Unsaturated Poromechanics Model Enabled by Self-Designed/self-Improved Neural Networks. Int. J. Numer. Anal. Methods Geomech 45, 1212–1237. doi:10.1002/nag.3196

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzapfel, G. A. (2000). Nonlinear Solid Mechanics: A Continuum Approach for Engineering. Chichester ; New York: Wiley.

Google Scholar

Hornik, K., Stinchcombe, M., and White, H. (1989). Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 2, 359–366. doi:10.1016/0893-6080(89)90020-8

CrossRef Full Text | Google Scholar

Huang, D., Fuhg, J. N., Weißenfels, C., and Wriggers, P. (2020). A Machine Learning Based Plasticity Model Using Proper Orthogonal Decomposition. Comput. Methods Appl. Mech. Eng. 365, 113008. doi:10.1016/j.cma.2020.113008

CrossRef Full Text | Google Scholar

Huber, N. (2021). A Strategy for Dimensionality Reduction and Data Analysis Applied to Microstructure–Property Relationships of Nanoporous Metals. Materials 14, 1822. doi:10.3390/ma14081822

PubMed Abstract | CrossRef Full Text | Google Scholar

Jamieson, K., and Talwalkar, A. (2016). “Non-stochastic Best Arm Identification and Hyperparameter Optimization,” in Artificial Intelligence and Statistics, 240–248.

Google Scholar

Javadi, A., and Rezania, M. (2009). Intelligent Finite Element Method: An Evolutionary Approach to Constitutive Modeling. Adv. Eng. Inform. 23, 442–451. doi:10.1016/j.aei.2009.06.008

CrossRef Full Text | Google Scholar

Javadi, A. A., Tan, T. P., and Zhang, M. (2003). Neural Network for Constitutive Modelling in Finite Element Analysis. Comput. Assist. Mech. Eng. Sci. 10, 523–530. doi:10.1016/B978-008044046-0.50086-5

CrossRef Full Text | Google Scholar

Javadi, A., Tan, T., and Elkassas, A. (2009). “Intelligent Finite Element Method and Application to Simulation of Behavior of Soils under Cyclic Loading,” in Foundations of Computational Intelligence Volume 5. Studies in Computational Intelligence. Editors A. Abraham, A.-E. Hassanien, and V. Snášel (Springer Berlin Heidelberg). 317–338. doi:10.1007/978-3-642-01536-6_12

CrossRef Full Text | Google Scholar

Kingma, D., and Ba, J. (2014). Adam: A Method for Stochastic Optimization. ArXiv14126980 Cs.

Google Scholar

Kissas, G., Yang, Y., Hwuang, E., Witschey, W. R., Detre, J. A., and Perdikaris, P. (2020). Machine Learning in Cardiovascular Flows Modeling: Predicting Arterial Blood Pressure from Non-invasive 4D Flow MRI Data Using Physics-Informed Neural Networks. Comput. Methods Appl. Mech. Eng. 358, 112623. doi:10.1016/j.cma.2019.112623

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., and Markert, B. (2016). Model Reduction and Submodelling Using Neural Networks. PAMM 16, 537–538. doi:10.1002/pamm.201610257

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., Hernandez Padilla, C. A., and Markert, B. (2017). Neural Network Representation of a Phase-Field Model for Brittle Fracture. PAMM 17, 253–254. doi:10.1002/pamm.201710096

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., and Markert, B. (2018a). An Intelligent Meta-Element for Linear Elastic Continua. PAMM 18, e201800283. doi:10.1002/pamm.201800283

CrossRef Full Text | Google Scholar

Koeppe, A., Hernandez Padilla, C. A., Voshage, M., Schleifenbaum, J. H., and Markert, B. (2018b). Efficient Numerical Modeling of 3D-Printed Lattice-Cell Structures Using Neural Networks. Manuf. Lett. 15, 147–150. doi:10.1016/j.mfglet.2018.01.002

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., and Markert, B. (2019). An Efficient Monte Carlo Strategy for Elasto-Plastic Structures Based on Recurrent Neural Networks. Acta Mech. 230, 3279–3293. doi:10.1007/s00707-019-02436-5

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., and Markert, B. (2020a). An Intelligent Nonlinear Meta Element for Elastoplastic Continua: Deep Learning Using a New Time-Distributed Residual U-Net Architecture. Comput. Methods Appl. Mech. Eng. 366, 113088. doi:10.1016/j.cma.2020.113088

CrossRef Full Text | Google Scholar

Koeppe, A., Hesser, D. F., Mundt, M., Bamer, F., and Markert, B. (2020b). “Mechanik 4.0. Künstliche Intelligenz zur Analyse mechanischer Systeme,” in Handbuch Industrie 4.0: Recht, Technik, Gesellschaft. Editor W. Frenz (Berlin, Heidelberg: Springer), 553–567. doi:10.1007/978-3-662-58474-3_28

CrossRef Full Text | Google Scholar

Koeppe, A., Bamer, F., Selzer, M., Nestler, B., and Markert, B. (2021). Dataset: Explainable Artificial Intelligence for Mechanics: Physics-Informing Neural Networks for Constitutive Models. [Dataset]. doi:10.5281/zenodo.4699219

CrossRef Full Text | Google Scholar

Lagaris, I., Likas, A., and Fotiadis, D. (1998). Artificial Neural Networks for Solving Ordinary and Partial Differential Equations. IEEE Trans. Neural Netw. 9, 987–1000. doi:10.1109/72.712178

PubMed Abstract | CrossRef Full Text | Google Scholar

Lapuschkin, S., Wäldchen, S., Binder, A., Montavon, G., Samek, W., and Müller, K.-R. (2019). Unmasking Clever Hans Predictors and Assessing what Machines Really Learn. Nat. Commun. 10, 1096. doi:10.1038/s41467-019-08987-4

PubMed Abstract | CrossRef Full Text | Google Scholar

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep Learning. Nature 521, 436–444. doi:10.1038/nature14539

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A., and Talwalkar, A. (2017). Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 18, 6765–6816.

Google Scholar

Markert, B. (2005). Porous Media Viscoelasticity With Application To Polymeric Foams. No. II-12 in Report/Universität Stuttgart, Institut Für Mechanik (Bauwesen), Lehrstuhl II (Essen: Verl. Glückauf)

Google Scholar

Montavon, G., Samek, W., and Müller, K.-R. (2018). Methods for Interpreting and Understanding Deep Neural Networks. Digital Signal. Process. 73, 1–15. doi:10.1016/j.dsp.2017.10.011

CrossRef Full Text | Google Scholar

Montavon, G., Binder, A., Lapuschkin, S., Samek, W., and Müller, K.-R. (2019). “Layer-Wise Relevance Propagation: An Overview,” in Explainable AI: Interpreting, Explaining and Visualizing Deep Learning. Lecture Notes in Computer Science. Editors W. Samek, G. Montavon, A. Vedaldi, L. K. Hansen, and K.-R. Müller (Cham: Springer International Publishing), 193–209. doi:10.1007/978-3-030-28954-6_10

CrossRef Full Text | Google Scholar

Oeser, M., and Freitag, S. (2009). Modeling of Materials with Fading Memory Using Neural Networks. Int. J. Numer. Meth. Engng. 78, 843–862. doi:10.1002/nme.2518

CrossRef Full Text | Google Scholar

Pearson, K. (1901). LIII. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 2, 559–572. doi:10.1080/14786440109462720

CrossRef Full Text | Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

Ramuhalli, P., Udpa, L., and Udpa, S. (2005). Finite-element Neural Networks for Solving Differential Equations. IEEE Trans. Neural Netw. 16, 1381–1392. doi:10.1109/TNN.2005.857945

PubMed Abstract | CrossRef Full Text | Google Scholar

Rudd, K., Di Muro, G., and Ferrari, S. (2014). A Constrained Backpropagation Approach for the Adaptive Solution of Partial Differential Equations. IEEE Trans. Neural Netw. Learn. Syst. 25, 571–584. doi:10.1109/TNNLS.2013.2277601

PubMed Abstract | CrossRef Full Text | Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. Nature 323, 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Sadeghi, M. H., and Lotfan, S. (2017). Identification of Non-linear Parameter of a Cantilever Beam Model with Boundary Condition Non-linearity in the Presence of Noise: An NSI- and ANN-Based Approach. Acta Mech. 228, 4451–4469. doi:10.1007/s00707-017-1947-8

CrossRef Full Text | Google Scholar

W. Samek, G. Montavon, A. Vedaldi, L. K. Hansen, and K.-R. Müller (Editors) (2019). “Explainable AI: Interpreting, Explaining and Visualizing Deep Learning,” in Lecture Notes in Computer Science (Cham: Springer International Publishing). doi:10.1007/978-3-030-28954-6

CrossRef Full Text | Google Scholar

Shin, H. S., and Pande, G. N. (2000). On Self-Learning Finite Element Codes Based on Monitored Response of Structures. Comput. Geotech. 27, 161–178. doi:10.1016/S0266-352X(00)00016-1

CrossRef Full Text | Google Scholar

Simo, J. C., and Hughes, T. J. R. (1998). Computational Inelasticity. in Interdisciplinary Applied Mathematics. New York: Springer-Verlag. doi:10.1007/b98904

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G. E., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 15, 1929–1958. doi:10.5555/2627435.2670313

CrossRef Full Text | Google Scholar

Stoffel, M., Bamer, F., and Markert, B. (2018). Artificial Neural Networks and Intelligent Finite Elements in Non-linear Structural Mechanics. Thin-Walled Struct. 131, 102–106. doi:10.1016/j.tws.2018.06.035

CrossRef Full Text | Google Scholar

Teichert, G. H., Natarajan, A. R., Van der Ven, A., and Garikipati, K. (2019). Machine Learning Materials Physics: Integrable Deep Neural Networks Enable Scale Bridging by Learning Free Energy Functions. Comput. Methods Appl. Mech. Eng. 353, 201–216. doi:10.1016/j.cma.2019.05.019

CrossRef Full Text | Google Scholar

Theocaris, P. S., and Panagiotopoulos, P. D. (1995). Plasticity Including the Bauschinger Effect, Studied by a Neural Network Approach. Acta Mech. 113, 63–75. doi:10.1007/BF01212634

CrossRef Full Text | Google Scholar

Theocaris, P. S., Bisbos, C., and Panagiotopoulos, P. D. (1997). On the Parameter Identification Problem for Failure Criteria in Anisotropic Bodies. Acta Mech 123, 37–56. doi:10.1007/BF01178399

CrossRef Full Text | Google Scholar

Truesdell, C., and Noll, W. (2004). “The Non-Linear Field Theories of Mechanics,” in The Non-Linear Field Theories of Mechanics. Editors C. Truesdell, W. Noll, and S. S. Antman (Berlin, Heidelberg: Springer), 1–579. doi:10.1007/978-3-662-10388-3_1

CrossRef Full Text | Google Scholar

Wu, L., Nguyen, V. D., Kilingar, N. G., and Noels, L. (2020a). A Recurrent Neural Network-Accelerated Multi-Scale Model for Elasto-Plastic Heterogeneous Materials Subjected to Random Cyclic and Non-Proportional Loading Paths. Comput. Methods Appl. Mech. Eng. 369, 113234. doi:10.1016/j.cma.2020.113234

CrossRef Full Text | Google Scholar

Wu, P., Sun, J., Chang, X., Zhang, W., Arcucci, R., Guo, Y., et al. (2020b). Data-Driven Reduced Order Model with Temporal Convolutional Neural Network. Comput. Methods Appl. Mech. Eng. 360, 112766. doi:10.1016/j.cma.2019.112766

CrossRef Full Text | Google Scholar

Yang, Y., and Perdikaris, P. (2019). Adversarial Uncertainty Quantification in Physics-Informed Neural Networks. J. Comput. Phys. 394, 136–152. doi:10.1016/j.jcp.2019.05.027

CrossRef Full Text | Google Scholar

Yao, H., Gao, Y., and Liu, Y. (2020). FEA-Net: A Physics-Guided Data-Driven Model for Efficient Mechanical Response Prediction. Comput. Methods Appl. Mech. Eng. 363, 112892. doi:10.1016/j.cma.2020.112892

CrossRef Full Text | Google Scholar

Zhao, Y., Otto, S.-K., Brandt, N., Selzer, M., and Nestler, B. (2020). Application of Random Forests in ToF-SIMS Data. Proced. Comput. Sci. 176, 410–419. doi:10.1016/j.procs.2020.08.042

CrossRef Full Text | Google Scholar