Theoretical and Experimental Investigation on Dynamic Response of Asphalt Pavement Under Vibration Compaction

This study aims to investigate the dynamic response regulation by combining the theoretical analysis and field test under the vibration rolling condition. Based on the viscoelastic theory of a multilayer system, the dynamic stiffness method (DSM) incorporating multidimensional Fourier transform is proposed to solve the 3-dimensional (3D) dynamic response of pavement under vibration compaction. The stiffness matrix of each pavement layer and the global stiffness matrix of the whole pavement structure are obtained. By combining vibration load with boundary conditions, the 3D exact solution is obtained and validated by the finite element method. In addition, the field test is also conducted using a series of sensors and equipment (e.g., SmartRock sensor, acceleration sensor, temperature sensors, and non-nuclear density meter) to calibrate the theoretical model to determine the wave number and dynamic modulus during the vibration rolling process. Then, considering the factors during compaction, the rules of displacement variation and pavement acceleration are investigated in terms of modulus, thickness, and density. The results show that the 3D displacement and acceleration components both vibrate with high frequencies during compaction, and peak acceleration in the vertical direction prevails. For the vertical displacement, its distribution beneath the drum of the roller is almost even except that it drops to zero abruptly around the drum edge. The relationship between thickness and acceleration follows a linear function, and the acceleration on the pavement surface rises when the thickness increases. Although the density and modulus increase with rolling times, the effect of modulus on acceleration is more obvious and prominent than that of density. In summary, the DSM presented in this article provides a robust method to calculate the dynamic response of pavement under vibratory compaction and to back-calculate the modulus of compacted pavement layers. Moreover, the regulation also sheds insight on the understanding of vibration compaction mechanism that there is a potentially strong correlation between compaction state, modulus, and vibration acceleration.

1 Introduction

It is widely known that compaction is a key procedure in the construction process of asphalt pavement. Generally speaking, insufficient strength and poor durability are important reasons for asphalt pavement distresses, such as rutting, cracking, and water damage (Wang et al., 2009; Dan et al., 2022; Dan et al., 2020a; Hosseini et al., 2020). To a large extent, these distresses have been closely correlated with pavement compaction quality (Coleri et al., 2012; Xu and Chang, 2016; Jia et al., 2019; Wu et al., 2019; Jing et al., 2020). Although the importance of compaction is widely acknowledged nowadays, study on the compaction mechanism is still troubled with simplification and one-sidedness. In the field, the pavement construction process is affected by many complicating factors, such as exciting force, compaction work, amplitude, vibration frequency, and rolling speed (Coleri et al., 2012; Fares et al., 2014; Xu and Chang, 2016; Jia et al., 2019; Liu et al., 2019; Jing et al., 2020; Paulmichl et al., 2020; Liu et al., 2022). Specifically, there is little quantitative study as to how these factors affect the compaction and to what degree the effects are significant. It is, therefore, challenging to accurately reveal the compaction mechanism due to so many complex influencing factors. Additionally, it is difficult to detect the feedback information of pavement structure and analyze the physical and mechanical processes contained in the feedback information. In summary, there is a big gap between theory and practice for improving the compaction technology of asphalt pavement (Dan et al., 2020b).

Asphalt mixture is a type of pavement material with rheological properties and, thus, is generally compacted using the vibratory roller in engineering. In the compaction process, the vibratory roller not only runs on the pavement surface at a certain speed but also vibrates up and down at a certain frequency. Therefore, compared with traffic loading, the dynamic response of asphalt pavement in the process of vibration rolling is definitely different and requires special treatment. Many researchers carried out investigations on the dynamic response of asphalt pavement under various types of loading, and those methods can be roughly categorized into analytical approach and numerical simulation (Grundmann et al., 1999; Lu and Jeng, 2007; Lefeuvemesgouez and Mesgouez, 2008; Xu et al., 2008; Souza and Castro, 2012; Beskou et al., 2016; Dong and Ma, 2018; Roozbahany and Partl, 2019; Lv et al., 2020; Qian et al., 2020), with very limited experimental studies in the literature (Dong et al., 2012; Chen X et al., 2015; Shan et al., 2019; Li et al., 2020). In the analytical approach, the differential governing equation was usually established, and the analytical/semi-analytical solutions of pavement dynamic response were obtained by means of integral transformation (Bierer and Bode, 2007; Zhenning et al., 2016; Zhan et al., 2018; Liu et al., 2021a; Liu et al., 2021b). Most solutions treated the traffic loading as a moving concentrated, constant load or a moving load that changed harmonically with time. The studies on vibration of pavement mainly considered pavement roughness (Li et al., 2012; Lv et al., 2020), but few investigated the characteristics of dynamic response in the process of vibration compaction of pavement because the use of the analytical method is strongly affected by the complexity of the model itself (Lv et al., 2020; Zhao and Wang, 2020). In order to consider more complex situations, many researchers applied the finite element method to simulate the response of pavement under various dynamic loading. In addition, the discrete element method (DEM) is increasingly applied to quantify the internal stresses of aggregates during compaction from a microscopic perspective (Chen J et al., 2015; Liu et al., 2019; Si et al., 2019; Qian et al., 2020). Despite the general applicability of the finite and discrete element methods, the numerical simulation of dynamic pavement responses is usually time-consuming and inefficient (Wang et al., 2021). At present, the literature on the dynamic response of asphalt pavement structure under the combined action of moving and vibratory loading is relatively scarce, especially the theoretical aspects of vibration compaction.

Hence, taking into account the moving and vibratory characteristics of compaction loading, this work aims to study the three-dimensional (3D) dynamic response regulation in the compaction process and the influencing factors. A 3D model is to be established based on viscoelasticity theory for the pavement multilayer system, and the dynamic stiffness method will be used to derive the analytical solution for the purpose of a fast and efficient calculation. Furthermore, the dynamic response of asphalt pavement under the action of the vibratory roller is investigated in terms of displacement, acceleration, temperature, modulus, and compaction degree of the asphalt pavement.

2 Methodology

2.1 Assumptions

Although asphalt mixture is a complex three-phase material, the pavement is generally regarded as a multilayer elastic structure with infinite length in theoretical considerations (Bierer and Bode, 2007; Liu et al., 2021b). Previous research has pointed out that plastic deformation within the finite acting time of the vibratory roller is negligibly small, and the dynamic response process is, thus, regarded as a viscoelastic vibration (Wang et al., 2021). In addition, before the establishment of the model, the following assumptions need to be introduced:

(1) The roller–pavement vibration system is linear.

(2) The structure layers underneath the surface course are homogenous and isotropically elastic.

(3) The constitutive relationships of the structural layers satisfy Hook’s law.

(4) The displacement at a certain depth in the pavement is zero.

(5) The load vibrates freely on the road surface with a sinusoidal waveform, and the loading point is kept fixed. The pavement response with time can be illustrated according to different positions, which is expressed by x = vt (v is the moving speed of the road roller, t is the sampling time, and x is the distance to the observation point) (Dan et al., 2015; Wang et al., 2021).

2.2 Governing Equations

The 3D pavement with the Cartesian coordinate can be defined as follows. The origin is located at the pavement surface, and the z-, y- and x-axes are along the pavement depth direction, transverse direction, and longitudinal direction (driving of the vibratory roller), respectively.

Considering an asphalt pavement under vibration loading, the force equilibrium equation can be written as

$\{\begin{array}{c}\frac{\partial {\sigma }_x}{\partial x}+\frac{\partial {\tau }_{xy}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}=\rho \frac{{\partial }^2{u}_x}{\partial t^2}\\ \frac{\partial {\sigma }_y}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+\frac{\partial {\tau }_{yx}}{\partial x}=\rho \frac{{\partial }^2{u}_y}{\partial t^2}\\ \frac{\partial {\sigma }_z}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}=\rho \frac{{\partial }^2{u}_z}{\partial t^2}\end{array},(1)$

where u_z, u_y, and u_x are the displacement components in the z-, y-, and x- direction, respectively; σ_z, σ_y, and σ_x are the normal stress components accordingly; ρ is the density of the pavement material, and τ represents the shear stresses.

The strain–displacement and constitutive relationships are

$\{\begin{array}{c}{\epsilon }_x=\frac{\partial u_x}{\partial x},{\gamma }_{xy}=\frac{\partial u_x}{\partial y}+\frac{\partial u_y}{\partial x}\\ {\epsilon }_y=\frac{\partial u_y}{\partial y},{\gamma }_{yz}=\frac{\partial u_y}{\partial z}+\frac{\partial u_z}{\partial y}\\ {\epsilon }_z=\frac{\partial u_z}{\partial z},{\gamma }_{xz}=\frac{\partial u_x}{\partial z}+\frac{\partial u_z}{\partial x}\end{array},(2)$

$\{\begin{array}{l}{\epsilon }_x=\frac{1}{E}\left[{\sigma }_x-\mu \left({\sigma }_y+{\sigma }_z\right)\right]\\ {\epsilon }_y=\frac{1}{E}\left[{\sigma }_y-\mu \left({\sigma }_x+{\sigma }_z\right)\right]\\ {\epsilon }_z=\frac{1}{E}\left[{\sigma }_z-\mu \left({\sigma }_y+{\sigma }_x\right)\right]\\ {\gamma }_{xy}=\frac{1}{G}{\tau }_{xy},{\gamma }_{xz}=\frac{1}{G}{\tau }_{xz},{\gamma }_{zy}=\frac{1}{G}{\tau }_{zy}\end{array},(3)$

where ν, E, and G are Poisson’s ratio, Young’s elastic modulus, and shear modulus of the material.

Subsequently, Eqs 1–3 in the time domain are transformed into the frequency domain according to the Fourier transform method, as shown in Eqs 4–6,

$\{\begin{array}{c}\frac{\partial {\tilde{\sigma }}_x}{\partial x}+\frac{\partial {\tilde{\tau }}_{xy}}{\partial y}+\frac{\partial {\tilde{\tau }}_{zx}}{\partial z}+\rho {\xi }^2{\tilde{u}}_x=0\\ \frac{\partial {\tilde{\sigma }}_y}{\partial y}+\frac{\partial {\tilde{\tau }}_{zy}}{\partial z}+\frac{\partial {\tilde{\tau }}_{yx}}{\partial x}+\rho {\xi }^2{\tilde{u}}_y=0\\ \frac{\partial {\tilde{\sigma }}_z}{\partial z}+\frac{\partial {\tilde{\tau }}_{xz}}{\partial x}+\frac{\partial {\tilde{\tau }}_{yx}}{\partial y}+\rho {\xi }^2{\tilde{u}}_z=0\end{array},(4)$

$\{\begin{array}{c}{\tilde{\epsilon }}_x=\frac{\partial {\tilde{u}}_x}{\partial x},{\tilde{\gamma }}_{xy}=\frac{\partial {\tilde{u}}_x}{\partial y}+\frac{\partial {\tilde{u}}_y}{\partial x}\\ {\tilde{\epsilon }}_y=\frac{\partial {\tilde{u}}_y}{\partial y},{\tilde{\gamma }}_{yz}=\frac{\partial {\tilde{u}}_y}{\partial z}+\frac{\partial {\tilde{u}}_z}{\partial y}\\ {\tilde{\epsilon }}_z=\frac{\partial {\tilde{u}}_z}{\partial z},{\tilde{\gamma }}_{xz}=\frac{\partial {\tilde{u}}_x}{\partial z}+\frac{\partial {\tilde{u}}_z}{\partial x}\end{array},(5)$

$\{\begin{array}{l}{\tilde{\epsilon }}_x=\frac{1}{E}\left[{\tilde{\sigma }}_x-\mu \left({\tilde{\sigma }}_y+{\tilde{\sigma }}_z\right)\right]\\ {\tilde{\epsilon }}_y=\frac{1}{E}\left[{\tilde{\sigma }}_y-\mu \left({\tilde{\sigma }}_x+{\tilde{\sigma }}_z\right)\right]\\ {\tilde{\epsilon }}_z=\frac{1}{E}\left[{\tilde{\sigma }}_z-\mu \left({\tilde{\sigma }}_y+{\tilde{\sigma }}_x\right)\right]\\ {\tilde{\gamma }}_{xy}=\frac{1}{G}{\tilde{\tau }}_{xy},{\tilde{\gamma }}_{xz}=\frac{1}{G}{\tilde{\tau }}_{xz},{\tilde{\gamma }}_{zy}=\frac{1}{G}{\tilde{\tau }}_{zy}\end{array},(6)$

with

$\{\begin{array}{l}\lambda =\frac{\mu E}{\left(1+\mu \right)\left(1-2\mu \right)}\\ G=\frac{E}{2\left(1+\mu \right)}\end{array}.(7)$

Combining Eqs 5–7, the following equations can be obtained:

${\tilde{\sigma }}_x=\left(\lambda +2G\right)\frac{\partial {\tilde{u}}_x}{\partial x}+\lambda \left(\frac{\partial {\tilde{u}}_y}{\partial y}+\frac{\partial {\tilde{u}}_z}{\partial z}\right).(8)$

${\tilde{\sigma }}_y=\left(\lambda +2G\right)\frac{\partial {\tilde{u}}_y}{\partial y}+\lambda \left(\frac{\partial {\tilde{u}}_x}{\partial x}+\frac{\partial {\tilde{u}}_z}{\partial z}\right).(9)$

${\tilde{\sigma }}_z=\left(\lambda +2G\right)\frac{\partial {\tilde{u}}_z}{\partial z}+\lambda \left(\frac{\partial {\tilde{u}}_y}{\partial y}+\frac{\partial {\tilde{u}}_x}{\partial x}\right).(10)$

${\tilde{\tau }}_{xy}=G\left(\frac{\partial {\tilde{u}}_x}{\partial y}+\frac{\partial {\tilde{u}}_y}{\partial x}\right),{\tilde{\tau }}_{xz}=G\left(\frac{\partial {\tilde{u}}_x}{\partial z}+\frac{\partial {\tilde{u}}_z}{\partial x}\right),{\tilde{\tau }}_{zy}=G\left(\frac{\partial {\tilde{u}}_z}{\partial y}+\frac{\partial {\tilde{u}}_y}{\partial z}\right).(11)$

Taking the derivative of Eq. 10 with respect to x, we have

$\frac{{\partial }^2{\tilde{u}}_z}{\partial x\partial z}=\frac{1}{\left(\lambda +2G\right)}\frac{\partial {\tilde{\sigma }}_z}{\partial x}-\frac{\lambda }{\left(\lambda +2G\right)}\left(\frac{{\partial }^2{\tilde{u}}_y}{\partial x\partial y}+\frac{{\partial }^2{\tilde{u}}_x}{\partial x^2}\right).(12)$

Likewise, taking derivative of Eq. 8 with respect to x and then combining with Eq. 12, we obtain

$\frac{\partial {\tilde{\tau }}_{xz}}{\partial z}=-\frac{4G\left(\lambda +G\right)}{\lambda +2G}\frac{{\partial }^2{\tilde{u}}_x}{\partial x^2}-\frac{3\lambda G+2G^2}{\lambda +2G}\frac{{\partial }^2{\tilde{u}}_y}{\partial x\partial y}-G\frac{{\partial }^2{\tilde{u}}_x}{\partial y^2}-\frac{\lambda }{\lambda +2G}\frac{\partial {\tilde{\sigma }}_z}{\partial x}-\rho {\xi }^2{\tilde{u}}_x.(13)$

Similarly, taking derivative of Eqs 9, 10 with respect to y, we have

$\frac{\partial {\tilde{\tau }}_{yz}}{\partial z}=-\frac{4G\left(\lambda +G\right)}{\lambda +2G}\frac{{\partial }^2{\tilde{u}}_y}{\partial y^2}-\frac{3\lambda G+2G^2}{\lambda +2G}\frac{{\partial }^2{\tilde{u}}_x}{\partial x\partial y}-G\frac{{\partial }^2{\tilde{u}}_y}{\partial x^2}-\frac{\lambda }{\lambda +2G}\frac{\partial {\tilde{\sigma }}_z}{\partial y}-\rho {\xi }^2{\tilde{u}}_y.(14)$

In addition, the following equations can be obtained as well:

$\frac{\partial {\tilde{u}}_z}{\partial z}=\frac{1}{\lambda +2G}{\tilde{\sigma }}_z-\frac{\lambda }{\lambda +2G}\frac{\partial {\tilde{u}}_x}{\partial x}-\frac{\lambda }{\lambda +2G}\frac{\partial {\tilde{u}}_y}{\partial y}.(15)$

$\frac{\partial {\tilde{\sigma }}_z}{\partial z}=-\frac{\partial {\tilde{\tau }}_{zx}}{\partial x}-\frac{\partial {\tilde{\tau }}_{zy}}{\partial y}-\rho {\xi }^2{\tilde{u}}_z.(16)$

$\frac{\partial {\tilde{u}}_x}{\partial z}=\frac{1}{G}{\tilde{\tau }}_{xz}-\frac{\partial {\tilde{u}}_z}{\partial x}.(17)$

$\frac{\partial {\tilde{u}}_y}{\partial z}=\frac{1}{G}{\tilde{\tau }}_{zy}-\frac{\partial {\tilde{u}}_z}{\partial y}.(18)$

For Eqs 13–18 in the space domain, transforming into the frequency domain by performing the Fourier transform and then the governing equation can be given as follows

$\{\begin{array}{l}\frac{\partial {\tilde{\sigma }}_z}{\partial z}=-k\cdot j{\tilde{\tau }}_{zx}-s\cdot j{\tilde{\tau }}_{zy}-\rho {\xi }^2\cdot {\tilde{u}}_z\\ \frac{\partial j{\tilde{\tau }}_{xz}}{\partial z}=\left[\frac{4G\left(\lambda +G\right)}{\lambda +2G}{k}^2+G{s}^2-\rho {\xi }^2\right]\cdot j{\tilde{u}}_x+\frac{3\lambda G+2G^2}{\lambda +2G}ks\cdot j{\tilde{u}}_y+\frac{\lambda }{\lambda +2G}k\cdot {\tilde{\sigma }}_z\\ \frac{\partial j{\tilde{\tau }}_{yz}}{\partial z}=\left[\frac{4G\left(\lambda +G\right)}{\lambda +2G}{s}^2+G{k}^2-\rho {\xi }^2\right]\cdot j{\tilde{u}}_y+\frac{3\lambda G+2G^2}{\lambda +2G}ks\cdot j{\tilde{u}}_x+\frac{\lambda }{\lambda +2G}s\cdot {\tilde{\sigma }}_z\\ \frac{\partial {\tilde{u}}_z}{\partial z}=\frac{1}{\lambda +2G}{\tilde{\sigma }}_z-\frac{\lambda }{\lambda +2G}k\cdot j{\tilde{u}}_x-\frac{\lambda }{\lambda +2G}s\cdot j{\tilde{u}}_y\\ \frac{\partial j{\tilde{u}}_x}{\partial z}=\frac{1}{G}j{\tilde{\tau }}_{xz}+k\cdot {\tilde{u}}_z\\ \frac{\partial j{\tilde{u}}_y}{\partial z}=\frac{1}{G}j{\tilde{\tau }}_{zy}+s\cdot {\tilde{u}}_z\end{array}.(19)$

The abovementioned can be rearranged into a matrix form:

$\frac{\partial }{\partial z}\left[\begin{array}{l}{\tilde{\sigma }}_z\\ j{\tilde{\tau }}_{xz}\\ j{\tilde{\tau }}_{yz}\\ {\tilde{u}}_z\\ j{\tilde{u}}_x\\ j{\tilde{u}}_y\end{array}\right]=\left[\begin{array}{cccccc}0& -k& -s& -\rho {\xi }^2& 0& 0\\ \frac{\lambda k}{\lambda +2G}& 0& 0& 0& \frac{4G\left(\lambda +G\right)k^2}{\lambda +2G}+G{s}^2-\rho {\xi }^2& \frac{\left(3\lambda G+2G^2\right)ks}{\lambda +2G}\\ \frac{\lambda s}{\lambda +2G}& 0& 0& 0& \frac{\left(3\lambda G+2G^2\right)ks}{\lambda +2G}& \frac{4G\left(\lambda +G\right)s^2}{\lambda +2G}+G{k}^2-\rho {\xi }^2\\ \frac{1}{\lambda +2G}& 0& 0& 0& -\frac{\lambda k}{\lambda +2G}& -\frac{\lambda s}{\lambda +2G}\\ 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$G$}\right.& 0& k& 0& 0\\ 0& 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$G$}\right.& s& 0& 0\end{array}\right]\left[\begin{array}{l}{\tilde{\sigma }}_z\\ j{\tilde{\tau }}_{xz}\\ j{\tilde{\tau }}_{yz}\\ {\tilde{u}}_z\\ j{\tilde{u}}_x\\ j{\tilde{u}}_y\end{array}\right].(20)$

2.3 Stiffness Matrix for Multilayer Pavement System

On the basis of the established governing Eq. 20, it is necessary to simplify the governing equation to derivate the solution. First, we define

$B=\left[\begin{array}{cccccc}0& -k& -s& -\rho {\xi }^2& 0& 0\\ \frac{\lambda k}{\lambda +2G}& 0& 0& 0& \frac{4G\left(\lambda +G\right)k^2}{\lambda +2G}+G{s}^2-\rho {\xi }^2& \frac{\left(3\lambda G+2G^2\right)ks}{\lambda +2G}\\ \frac{\lambda s}{\lambda +2G}& 0& 0& 0& \frac{\left(3\lambda G+2G^2\right)ks}{\lambda +2G}& \frac{4G\left(\lambda +G\right)s^2}{\lambda +2G}+G{k}^2-\rho {\xi }^2\\ \frac{1}{\lambda +2G}& 0& 0& 0& -\frac{\lambda k}{\lambda +2G}& -\frac{\lambda s}{\lambda +2G}\\ 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$G$}\right.& 0& k& 0& 0\\ 0& 0& \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$G$}\right.& s& 0& 0\end{array}\right],(21)$

and Eq. 20 can be rewritten as

$\frac{\partial }{\partial z}{\left[\begin{array}{cccccc}{\tilde{\sigma }}_z& j{\tilde{\tau }}_{xz}& j{\tilde{\tau }}_{yz}& {\tilde{u}}_z& j{\tilde{u}}_x& j{\tilde{u}}_y\end{array}\right]}^T=B\cdot {\left[\begin{array}{cccccc}{\tilde{\sigma }}_z& j{\tilde{\tau }}_{xz}& j{\tilde{\tau }}_{yz}& {\tilde{u}}_z& j{\tilde{u}}_x& j{\tilde{u}}_y\end{array}\right]}^T.(22)$

According to the boundary condition shown in Figure 1, Eq. 22 can be solved readily.

${\left[\begin{array}{cccccc}{\tilde{\sigma }}_z^1& j{\tilde{\tau }}_{xz}^1& j{\tilde{\tau }}_{yz}^1& {\tilde{u}}_z^1& j{\tilde{u}}_x^1& j{\tilde{u}}_y^1\end{array}\right]}^T=e^{B{h}_1}{\left[\begin{array}{cccccc}{\tilde{\sigma }}_z^0& j{\tilde{\tau }}_{xz}^0& j{\tilde{\tau }}_{yz}^0& {\tilde{u}}_z^0& j{\tilde{u}}_x^0& j{\tilde{u}}_y^0\end{array}\right]}^T,(23)$

where ${\left[\begin{array}{cccccc}{\tilde{\sigma }}_z^1& j{\tilde{\tau }}_{xz}^1& j{\tilde{\tau }}_{yz}^1& {\tilde{u}}_z^1& j{\tilde{u}}_x^1& j{\tilde{u}}_y^1\end{array}\right]}^T$ and ${\left[\begin{array}{cccccc}{\tilde{\sigma }}_z^0& j{\tilde{\tau }}_{xz}^0& j{\tilde{\tau }}_{yz}^0& {\tilde{u}}_z^0& j{\tilde{u}}_x^0& j{\tilde{u}}_y^0\end{array}\right]}^T$ represent the boundary condition at h = h₁ and surface, respectively, and h₁ is the layer thickness.

FIGURE 1

FIGURE 1. Simplified model of vibration load.

Defining $T=e^{B{h}_1}$ and combining with the block matrix algorithm, Eq. 24 is obtained directly as follows:

$\left[\begin{array}{l}{\tilde{\sigma }}_z^0\\ j{\tilde{\tau }}_{xz}^0\\ j{\tilde{\tau }}_{yz}^0\\ {\tilde{\sigma }}_z^1\\ j{\tilde{\tau }}_{xz}^1\\ j{\tilde{\tau }}_{yz}^1\end{array}\right]=\left[\begin{array}{cc}-T_{21}^{-1}{T}_{22}& T_{21}^{-1}\\ T_{12}-T_{11}{T}_{21}^{-1}{T}_{22}& T_{11}{T}_{21}^{-1}\end{array}\right]\times \left[\begin{array}{l}{\tilde{u}}_z^0\\ j{\tilde{u}}_x^0\\ j{\tilde{u}}_y^0\\ {\tilde{u}}_z^1\\ j{\tilde{u}}_x^1\\ j{\tilde{u}}_y^1\end{array}\right].(24)$

Based on the relationship between the stress and displacement in the coordinate system, the following equations hold true:

$\left[\begin{array}{l}-{\tilde{\sigma }}_z^0\\ -j{\tilde{\tau }}_{xz}^0\\ -j{\tilde{\tau }}_{yz}^0\\ {\tilde{\sigma }}_z^1\\ j{\tilde{\tau }}_{xz}^1\\ j{\tilde{\tau }}_{yz}^1\end{array}\right]=\left[\begin{array}{cc}-T_{21}^{-1}{T}_{22}& T_{21}^{-1}\\ T_{12}-T_{11}{T}_{21}^{-1}{T}_{22}& T_{11}{T}_{21}^{-1}\end{array}\right]\times \left[\begin{array}{l}{\tilde{u}}_z^0\\ j{\tilde{u}}_x^0\\ j{\tilde{u}}_y^0\\ {\tilde{u}}_z^1\\ j{\tilde{u}}_x^1\\ j{\tilde{u}}_y^1\end{array}\right].(25)$

Here, the stiffness matrix can be defined as follows:

$\left[S\right]=\left[\begin{array}{cc}-T_{21}^{-1}{T}_{22}& T_{21}^{-1}\\ T_{12}-T_{11}{T}_{21}^{-1}{T}_{22}& T_{11}{T}_{21}^{-1}\end{array}\right]=\left[\begin{array}{cc}\left[S_{11}\right]& \left[S_{12}\right]\\ \left[S_{21}\right]& \left[S_{22}\right]\end{array}\right].(26)$

Any two layers of structure, layer i and layer i+1, are selected to obtain the global stiffness matrix of the multilayer pavement structure.

For layer i,

$\left[\begin{array}{l}-{\tilde{\sigma }}_z^{i-1}\\ -j{\tilde{\tau }}_{xz}^{i-1}\\ -j{\tilde{\tau }}_{yz}^{i-1}\\ {\tilde{\sigma }}_z^i\\ j{\tilde{\tau }}_{xz}^i\\ j{\tilde{\tau }}_{yz}^i\end{array}\right]=\left[\begin{array}{cc}\left[S_{11}^i\right]& \left[S_{12}^i\right]\\ \left[S_{21}^i\right]& \left[S_{22}^i\right]\end{array}\right]\times \left[\begin{array}{l}{\tilde{u}}_z^{i-1}\\ j{\tilde{u}}_x^{i-1}\\ j{\tilde{u}}_y^{i-1}\\ {\tilde{u}}_z^i\\ j{\tilde{u}}_x^i\\ j{\tilde{u}}_y^i\end{array}\right].(27)$

For layer i+1,

$\left[\begin{array}{l}-{\tilde{\sigma }}_z^i\\ -j{\tilde{\tau }}_{xz}^i\\ -j{\tilde{\tau }}_{yz}^i\\ {\tilde{\sigma }}_z^{i+1}\\ j{\tilde{\tau }}_{xz}^{i+1}\\ j{\tilde{\tau }}_{yz}^{i+1}\end{array}\right]=\left[\begin{array}{cc}\left[S_{11}^{i+1}\right]& \left[S_{12}^{i+1}\right]\\ \left[S_{21}^{i+1}\right]& \left[S_{22}^{i+1}\right]\end{array}\right]\times \left[\begin{array}{l}{\tilde{u}}_z^i\\ j{\tilde{u}}_x^i\\ j{\tilde{u}}_y^i\\ {\tilde{u}}_z^{i+1}\\ j{\tilde{u}}_x^{i+1}\\ j{\tilde{u}}_y^{i+1}\end{array}\right].(28)$

On the basis of the assumption that the layers are in complete contact with each other, combining Eqs 27, 28, we have

$\left[\begin{array}{c}-{\tilde{\sigma }}_z^{i-1}\\ -j{\tilde{\tau }}_{xz}^{i-1}\\ -j{\tilde{\tau }}_{yz}^{i-1}\\ 0\\ 0\\ 0\\ {\tilde{\sigma }}_z^{i+1}\\ j{\tilde{\tau }}_{xz}^{i+1}\\ j{\tilde{\tau }}_{yz}^{i+1}\end{array}\right]=\left[\begin{array}{ccc}\left[S_{11}^i\right]& \left[S_{12}^i\right]& 0\\ \left[S_{21}^i\right]& \left[S_{22}^i\right]+\left[S_{11}^{i+1}\right]& \left[S_{12}^{i+1}\right]\\ 0& \left[S_{21}^{i+1}\right]& \left[S_{22}^{i+1}\right]\end{array}\right]\times \left[\begin{array}{c}{\tilde{u}}_z^{i-1}\\ j{\tilde{u}}_x^{i-1}\\ j{\tilde{u}}_y^{i-1}\\ {\tilde{u}}_z^i\\ j{\tilde{u}}_x^i\\ j{\tilde{u}}_y^i\\ {\tilde{u}}_z^{i+1}\\ j{\tilde{u}}_x^{i+1}\\ j{\tilde{u}}_y^{i+1}\end{array}\right].(29)$

For the multilayer pavement system, the bottom layer is in complete contact with the rigid foundation bed. It thus can be regarded that the boundary condition at the bottom is zero for both stress and displacement. Therefore, the global stiffness matrix of the multilayer pavement system is given as follows:

$\left[\begin{array}{c}{f}_1\\ 0\\ 0\\ ⋮\\ 0\\ f_{n+1}\end{array}\right]=\left[\begin{array}{cccccc}\left[S_{11}^1\right]& \left[S_{12}^1\right]& 0& \cdots & 0& 0\\ \left[S_{21}^1\right]& \left[S_{22}^1+S_{11}^2\right]& \left[S_{12}^2\right]& \cdots & 0& 0\\ 0& \left[S_{21}^2\right]& \left[S_{22}^2+S_{11}^3\right]& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & \left[S_{22}^{n-1}+S_{11}^n\right]& \left[S_{12}^n\right]\\ 0& 0& 0& \cdots & \left[S_{21}^n\right]& \left[S_{22}^n\right]\end{array}\right]\left[\begin{array}{c}{d}_1\\ d_2\\ d_3\\ ⋮\\ d_n\\ d_{n+1}\end{array}\right],(30)$

where $f_1={\left[\begin{array}{ccc}-{\tilde{\sigma }}_z^0& -i{\tilde{\tau }}_{xz}^0& -i{\tilde{\tau }}_{yz}^0\end{array}\right]}^T$ and $d_i={\left[\begin{array}{ccc}{\tilde{u}}_z^{i-1}& i{\tilde{u}}_x^{i-1}& i{\tilde{u}}_y^{i-1}\end{array}\right]}^T$.

2.4 Vibration Load

Generally speaking, load distribution at the bottom of the vibratory roller drum is not uniform. For the sake of simulating the response of asphalt pavement as realistic as possible, the contact force between the pavement and drum is simplified as a semi-ellipse model in this study (Herrera et al., 2018). In addition, it is assumed that the eccentric block in the roller drum rotates around the rotating shaft at a certain angular speed ω₀, as shown in Figure 1.

Accordingly, description of the vibratory roller load can be simplified as follows:

$P=G_r+p=G_r+\frac{2b}{L}\sqrt{\frac{L^2}{4}-{\left(x-v_{0}t\right)}^2}\sin \left({\omega }_{0}t\right),(31)$

in which, $-\frac{L}{2}\mathrm{<}x\mathrm{<}\frac{L}{2};-\frac{W}{2}\mathrm{<}y\mathrm{<}\frac{W}{2}$, G_r is the roller gravity; L and W are widths along the x- and y-axes, respectively; b is load amplitude; v₀ is the speed of the vibratory roller, and ω₀ is the angular frequency.

In the practice of vibratory compaction, the moving speed of the roller is about 4.5 km/h, which can be neglected in the calculation and as such the exciting force is represented by (Bratu and Dobrescu, 2019)

$p_c=\frac{2b}{L}\sqrt{\frac{L^2}{4}-x^2}\sin \left({\omega }_{0}t\right).(32)$

Thus, the vibratory roller load is further simplified as follows:

$P_c=G_r+p_c=G+\frac{2b}{L}\sqrt{\frac{L^2}{4}-x^2}\sin \left({\omega }_{0}t\right).(33)$

3 Model validation and calibration

3.1 Numerical Comparison

For validating the analytical solution, the finite element method (FEM) is used to calculate the response of the pavement under the same conditions. For a balance between computational cost and accuracy, a 3D pavement model with 1310576 nodes is established, and the DLOAD subroutine is applied to simulate the vibration load. The mesh and model geometrics are illustrated in Figure 2, and the structural parameters are listed in Table 1.

FIGURE 2

FIGURE 2. FEM model: (A) meshing and (B) geometric and boundary conditions.

TABLE 1

TABLE 1. Structure and material information for the FEM model.

Comparison of solutions by the FEM and analytical method is presented in Figure 3. It can be seen that the displacement profiles in the z- and x-directions, as well as the peaks at the pavement midline obtained by the two methods, are consistent with each other. Furthermore, the spatial range of response to the vibration load is the same, between 15 m and 25 m. These agreements demonstrate the reliability and accuracy of the analytical method proposed in this article. Moreover, it should be pointed out that the FEM approach is highly time-consuming, which took over 2 hours in calculation in the present case. On the contrary, the developed analytical method only needed 143 s to obtain the solution in the frequency domain, and the inverse Fourier transform took another 5 s. Use of the analytical method enjoys a great advantage in computational efficiency while maintaining an equivalent accuracy.

FIGURE 3

FIGURE 3. Comparison between the FEM and analytical method.

3.2 Field Test and Calibration

In order to use the analytical method to analyze the dynamic response of asphalt mixture, the model parameters need to be calibrated by field test results because the modulus of loose asphalt mixture cannot be obtained during the rolling process. The pavement vibration rolling field test is performed on an asphalt bottom layer with a thickness of 8 cm in the Zheng–Xi Expressway in Guizhou Province, China. The asphalt mixture is a conventional AC-25 material. Table 2 shows the structural and material parameters for the test pavement. The vibratory roller is Dynapac CC624HF with double drums of which the operating weight is 13,600 kg, and the static weight at the front drum is 6,000 kg, with the drum dimension 1,300 mm (diameter) × 2,130 mm (width). The loading frequency of the drum is 51 Hz and excited force is about 166 kN. In the compaction process, the driving speed of the vibratory roller is 4.5 km/h.

TABLE 2

TABLE 2. Structural and material information for the test pavement.

During the vibration rolling process, SmartRock is placed in the mixture, and the field test data are collected via Bluetooth into a computer (Dan et al., 2020c). In the rolling direction, the data record area is selected approximately 25 m before and after the measuring point. After each rolling, a non-nuclear density meter is used to detect the compactness of the compacted mixture near the measuring point. In addition, to ensure the accuracy of the test, the roller moved at a constant speed when passing the observation point to mitigate the fluctuation of the signal. Figure 4 outlines the field test setup, sensor installation, and rolling process.

FIGURE 4

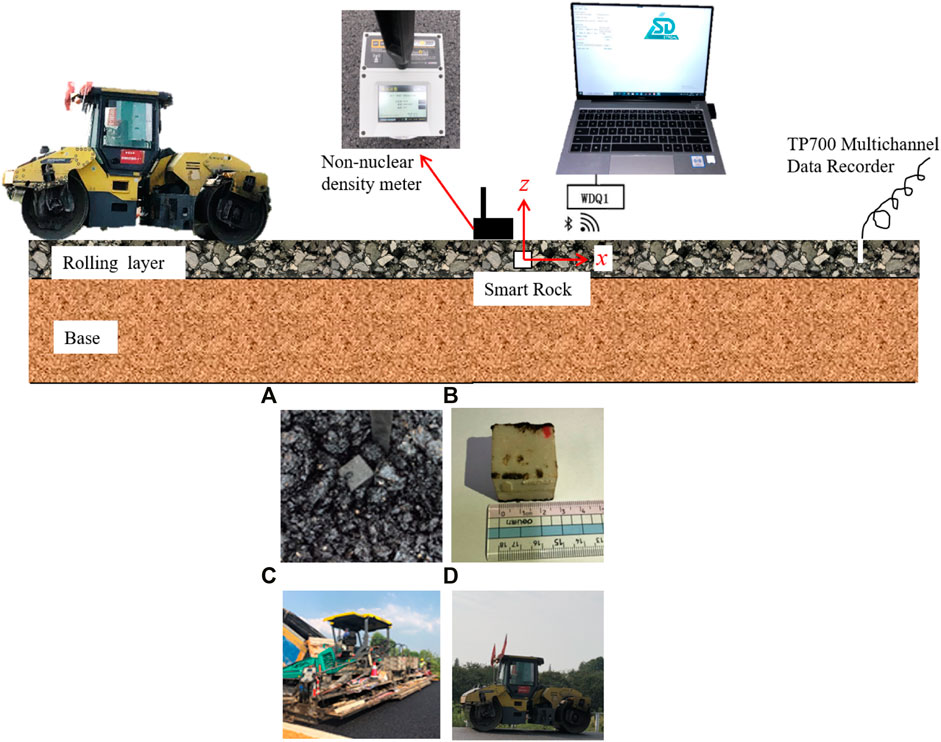
FIGURE 4. Schematic diagram of the field test arrangement and setting up the SmartRock: (A) embedment in mixture, (B) scale of the sensor, (C) field paving, and (D) rolling.

However, there are many types of equipment (paver, vibration roller, rubber-tired roller, etc.) in the field, which leads to interfering signals collected by SmartRock in the field test data. Hence, the band-pass filtering program is utilized to handle this issue. The acceleration curve of asphalt mixture after filtering is shown in Figure 5. Based on the pavement parameters substituted into the analytical model, the relationship between the peak acceleration and modulus is shown in Figure 6. In addition, using the field data, the dynamic modulus of asphalt mixture is back-calculated as 99 and 2057 MPa for the first and last rolling, respectively.

FIGURE 5

FIGURE 5. Time histories of acceleration in the field test.

FIGURE 6

FIGURE 6. Fitting curve of the relationship between peak acceleration and modulus.

The first rolling data of the field test are used to calibrate the model parameters in this study, and the calibrated acceleration is shown in Figure 7. The statistics criteria used in calibration are that the variance of acceleration in the z-direction reaches the minimum, and meanwhile, the root mean square error is minimized in all three directions between the calculated and measured accelerations. The comparison shows that the analytical solution agrees quite well with the field test data. The analytical solution captures the vibrations in acceleration over time. Also, the errors in fitting the peak values of all directions are minor, which are 9.5 × 10⁻³ g, 2.26 × 10⁻² g, and 9 × 10⁻⁴ g in the z-, y-, and x-directions, respectively.

FIGURE 7

FIGURE 7. Acceleration–time curve by calculation and test.

4 Analysis and Discussion

4.1 Vibration Displacement

It is well known that displacement is one of the noticeable dynamic responses of a pavement during the rolling process. Thus, a model is established to obtain the analytical solution of displacement for the structural and material parameters as shown earlier in Table 2.

Figure 8A presents the vertical displacement profiles of the pavement surface along the rolling and transverse directions. It can be seen in Figure 8A that the displacement is pronounced within the response range, and the displacement achieves the peak value at the loading point. The displacement beyond the load range vanishes rapidly.

FIGURE 8

FIGURE 8. Displacement profile in three directions, (A) vertical; (B) y-axis; and (C) x-axis.

Figure 8B shows y-axis displacement of the pavement surface, which is apparently different from vertical displacement. The displacement is zero at the load center and peaks immediately on the two sides with different signs, which agrees with the fact that asphalt mixture tends to move toward both sides of the contacting strip under rolling in the field. Figure 8C provides x-axis displacement of the pavement surface, which is generally similar with that in the y-direction.

During the rolling process, the dynamic response of the origin O changes with the moving roller. Based on the global stiffness matrix method, the displacement–time curves are obtained and shown in Figure 9.

FIGURE 9

FIGURE 9. The time histories of the displacement response at the origin.

Under the moving vibration load along the x-direction, the displacement of the observation point is shown in Figures 9B–D for the z-, y-, and x-directions. First, it can be found that the displacement of each direction vibrates along with the vibrating load. Then, in Figure 9B, it can be seen that u_z increases slowly with the approaching load and achieves peak value when the load moves toward the center. Moreover, in Figures 9C,D, it can be observed that the response regulation of displacement in the x- and y-directions is different from vertical displacement. Both u_y and u_x increase initially and decrease to zero at the center, and the displacement is opposite when the load moves away.

Apparently, the vertical displacement u_z is the largest and u_y is the smallest. It shows that the internal response is concentrated on the z-direction mostly during the rolling process. At the same time, the force is the smallest in the y-direction, which leads to the smallest displacement.

4.2 Vibration Acceleration

In the field test, it is impossible to detect the real-time displacement in the rolling process, but the acceleration can be monitored by the sensor. Thus, the acceleration of the observation point is calculated by the model, which is shown in Figure 10.

FIGURE 10

FIGURE 10. Acceleration of point O in the rolling process.

Figure 10 shows the acceleration curves of observation point O in z-, y-, and x-directions. It can be seen from the figure that there are many similarities in the acceleration of the three directions. The accelerations vibrate with the high frequency of the vibration load, and they all show a trend of increasing gradually when the load approaches and gradually decrease when the load moves away from the observation point. In addition, by comparing the peak values of accelerations in three directions, it is found that the peak value of z-direction acceleration is the largest (about 0.6362 g), and that of the y-direction is the smallest (about 0.08243 g), about 13% of the peak value of z-direction.

Essentially, acceleration may be affected by many factors, including the thickness of the compacted materials. For example, the thickness of the asphalt pavement is commonly between 4 and 8 cm, Figure 11 shows the relationship between thickness and acceleration, following a linear function, and the acceleration on the pavement surface rises when the thickness increases. It can be found that the acceleration in the z-direction increases from 0.1645 to 0.1797 g when the pavement thickness changes from 4 to 8 cm, respectively, and the increase percentage is about 9.2%.

FIGURE 11

FIGURE 11. Relationship between acceleration and thickness of compacted materials.

4.3 Modulus of the Pavement

During the rolling process of asphalt mixture, the modulus of pavement varies dramatically with the increase of rolling times, and the internal response of SmartRock embedded in asphalt mixture in the field experiment also changes dramatically. For further exploring the relationship between the internal response of asphalt mixture and the increase of compaction times, the peak values of acceleration in three directions during each rolling in the field test results (Figure 6) are plotted as scatter plots, as shown in Figure 12.

FIGURE 12

FIGURE 12. (A) Peak value of acceleration; (B) relation curve between modulus and acceleration.

It can be seen from Figure 12A that the peak acceleration decreases with the number of compaction times in general. The variation regulation of peak acceleration in the z- and x-directions is strongly correlated with the number of compaction times, and yet the peak acceleration in the y-direction is not. Generally, when the rolling times increase, the compactness of the mixture and, thus, its modulus gradually increase. Therefore, in order to analyze the influence of modulus on acceleration, the acceleration peak values in z- and y-directions are obtained by changing the material modulus parameters in the theoretical model, and the curve fitting is shown in Figure 12B. It can be understood from the figure that the peak accelerations in the z- and x-directions decrease sharply in the early stage with modulus. The reduction becomes gradual, and the accelerations tend to be stable with further modulus increase.

4.4 Pavement Compaction Degree

In general, during the rolling process, the density/compactness of the asphalt mixture also changes dramatically with the increase of compaction times. In the field test, the test points are marked after embedding SmartRock so that the non-nuclear densitometer is used to measure the density/compactness of the mixture in each pass.

Figure 13A demonstrates that the compactness of asphalt mixture gradually increases from 89.77% to 96.99%, with the increase of compaction times. After the asphalt mixture paved by the paver, the degree of compaction is 89.77%, when the asphalt mixture is in a relatively loose state. In early rolling, the degrees of compaction are 92.66% and 95.16% after the first and second rolling and the growth ratios are 3.2% and 2.7%, respectively. On the other hand, after the sixth and seventh rolling, the degrees of compaction are 97.19% and 96.99% and the increase percentages are 0.6% and −0.2%, respectively. Thus, the compaction degree increases rapidly initially and tends to be gentle subsequently, and the peak acceleration has the same variation regulation. Consequently, for further analyzing the influence of compactness on acceleration, the accelerations are calculated under different densities.

FIGURE 13

FIGURE 13. (A) Compactness during the rolling process; (B) influence of density on acceleration.

It can be seen from Figure 13B that the accelerations in all directions are almost identical under different densities, which is inconsistent with the field test (Figure 13A) in which acceleration decreases with increase in density. Based on the governing equation, it can be revealed that there are only three polynomials containing density ρ in the matrix B, that is, ρξ², $\frac{4G\left(\lambda +G\right)k^2}{\lambda +2G}+G{s}^2-\rho {\xi }^2$ and $\frac{4G\left(\lambda +G\right)s^2}{\lambda +2G}+G{k}^2-\rho {\xi }^2$, where G is the shear modulus. Obviously, when only the density ρ varies, Δρ is minor relative to the shear modulus G, and then Δρ is also very small for the matrix B, which leads to the calculated acceleration showing little variation. Hence, in the engineering practice, it can be concluded that although the density (degree of compaction) and modulus increase with the rolling times, the effect of modulus on acceleration is more obvious and prominent than that of density.

5 Summary and Conclusion

(1) In this study, investigations have been carried out to study the three-dimensional dynamic response of pavement under vibrating load. Based on the viscoelastic theory of the layered system and Fourier transform method, a set of differential governing equations of dynamic response is established under the vibration rolling load, which is simplified into a matrix form.

(2) Furthermore, the stiffness matrices of the multilayer system of asphalt pavement are derived, and the dynamic stiffness method is applied to solve the governing equation of the pavement structure under vibrating load. The proposed solution is validated by the FEM simulation and proven to be more efficient. Furthermore, the theoretical model is calibrated by the field test to determine the wave number and dynamic modulus during the vibration rolling process.

(3) The displacement always fluctuates under vibration loading with high frequency. The variation characteristics is that the displacement in z-direction increases sharply to a peak and then decreases sharply to zero, whereas the displacements in x- and y-directions rise to a peak value and then decrease to zero and subsequently increase reversely to a negative peak and then decrease to zero.

(4) For the vertical displacement, its distribution beneath the drum of the roller is almost even, except around the location of the drum edge, at which the displacement drops to zero sharply. For the displacements in the x- and y- directions, they reach the maximum not when the roller reaches the observation point but at a certain distance from it. Overall, vertical displacement dominates the deformation under vibration loading.

(5) The acceleration of the observation point has noticeable vibration state as the displacement, and the accelerations in the three directions gradually increase when the load approaches and gradually decrease when the load moves away. In addition, it can be found that the responses of peak acceleration in z- and x- directions are obviously dominant compared to those in the y- direction.

(6) Combined with the field test and the calculation results of the theoretical model in this study, it is found that the peak accelerations in z- and x-directions decrease and are correlated well with the modulus, while the peak acceleration in y-direction does not show a clear trend. In addition, although the density (degree of compaction) and modulus increase with the rolling times, the effect of modulus on acceleration is more obvious and prominent than that of density.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

H-YS: conceptualization, methodology, investigation, and writing—original draft preparation; H-CD: conceptualization, methodology, investigation, writing—review and editing, and funding acquisition; S-PW: methodology and writing—original draft preparation; XL: methodology, investigation, and writing—review and editing; HW: writing—review and editing, supervision, and resources.

Funding

This work was partially funded by the Natural Science Foundation of Hunan Province (CN) (Grant No. 2020JJ4702), the Jiangxi Transportation Science and Technology Foundation (CN) (Grant No. 2020H0028), and the Guizhou Transportation Science and Technology Foundation (CN) (Grant No. 2019-122-006).

Conflict of Interest

Author H-YS was employed by Power China Guiyang Engineering Corporation Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors especially appreciate Zhonghai Construction Co., Ltd. for assistance in the field test.

References

Beskou, N. D., Hatzigeorgiou, G. D., and Theodorakopoulos, D. D. (2016). Dynamic Inelastic Analysis of 3-D Flexible Pavements under Moving Vehicles: A Unified FEM Treatment. Soil Dyn. Earthquake Eng. 90, 420–431. doi:10.1016/j.soildyn.2016.09.018

CrossRef Full Text | Google Scholar

Bierer, T., and Bode, C. (2007). A Semi-analytical Model in Time Domain for Moving Loads. Soil Dyn. Earthquake Eng. 27 (12), 1073–1081. doi:10.1016/j.soildyn.2007.03.008

CrossRef Full Text | Google Scholar

Bratu, P., and Dobrescu, C. (2019). Dynamic Response of Zener-Modelled Linearly Viscoelastic Systems under Harmonic Excitation. Symmetry 11 (8), 1050. doi:10.3390/sym11081050

CrossRef Full Text | Google Scholar

Chen, J., Huang, B., Shu, X., and Hu, C. (2015). DEM Simulation of Laboratory Compaction of Asphalt Mixtures Using an Open Source Code. J. Mater. Civ. Eng. 27 (3), 04014130. doi:10.1061/(asce)mt.1943-5533.0001069

CrossRef Full Text | Google Scholar

Chen, X., Zhang, J., and Wang, X. (2015). Full-scale Field Testing on a Highway Composite Pavement Dynamic Responses. Transportation Geotechnics 4, 13–27. doi:10.1016/j.trgeo.2015.05.002

CrossRef Full Text | Google Scholar

Coleri, E., Harvey, J. T., Yang, K., and Boone, J. M. (2012). A Micromechanical Approach to Investigate Asphalt concrete Rutting Mechanisms. Construction Building Mater. 30, 36–49. doi:10.1016/j.conbuildmat.2011.11.041

CrossRef Full Text | Google Scholar

Dan, H.-C., He, L.-H., Zhao, L.-H., and Chen, J.-Q. (2015). Coupled Hydro-Mechanical Response of Saturated Asphalt Pavement under Moving Traffic Load. Int. J. Pavement Eng. 16 (2), 125–143. doi:10.1080/10298436.2014.937712

CrossRef Full Text | Google Scholar

Dan, H.-C., Zeng, H.-F., Zhu, Z.-H., Bai, G.-W., and Cao, W. (2022). Methodology for Interactive Labeling of Patched Asphalt Pavement Images Based on U-Net Convolutional Neural Network. Sustainability 14, 861. doi:10.3390/su14020861

CrossRef Full Text | Google Scholar

Dan, H.-C., Yang, D., Liu, X., Peng, A.-P., and Zhang, Z. (2020). Experimental Investigation on Dynamic Response of Asphalt Pavement Using SmartRock Sensor under Vibrating Compaction Loading. Construction Building Mater. 247, 118592. doi:10.1016/j.conbuildmat.2020.118592

CrossRef Full Text | Google Scholar

Dan, H.-C., Yang, D., Zhao, L.-H., Wang, S.-P., and Zhang, Z. (2020). Meso-scale Study on Compaction Characteristics of Asphalt Mixtures in Superpave Gyratory Compaction Using SmartRock Sensors. Construction Building Mater. 262, 120874. doi:10.1016/j.conbuildmat.2020.120874

CrossRef Full Text | Google Scholar

Dan, H. C., He, L. H., and Zhao, L. H. (2020). Experimental Investigation on the Resilient Response of Unbound Graded Aggregate Materials by Using Large-Scale Dynamic Triaxial Tests. Road Mater. Pavement Des. 21 (2), 434–451. doi:10.1080/14680629.2018.1500300

CrossRef Full Text | Google Scholar

Dong, Z., and Ma, X. (2018). Analytical Solutions of Asphalt Pavement Responses under Moving Loads with Arbitrary Non-uniform Tire Contact Pressure and Irregular Tire Imprint. Road Mater. Pavement Des. 19 (8), 1887–1903. doi:10.1080/14680629.2017.1354776

CrossRef Full Text | Google Scholar

Dong, Z., Tan, Y., Cao, L., and Li, S. (2012). Rutting Mechanism Analysis of Heavy-Duty Asphalt Pavement Based on Pavement Survey, Finite Element Simulation, and Instrumentation. J. Test. Eval. 40 (7), 1228–1237. doi:10.1520/jte20120162

CrossRef Full Text | Google Scholar

Fares, B., Sesh, C., and Musharraf, Z. (2014). Dynamical Response of Vibratory Rollers during the Compaction of Asphalt Pavements. J. Eng. Mech. 140 (7), 04014039. doi:10.1061/(asce)em.1943-7889.0000730

CrossRef Full Text | Google Scholar

Grundmann, H., Lieb, M., and Trommer, E. (1999). The Response of a Layered Half-Space to Traffic Loads Moving along its Surface. Archive Appl. Mech. (Ingenieur Archiv) 69 (1), 55–67. doi:10.1007/s004190050204

CrossRef Full Text | Google Scholar

Herrera, C., Alves Costa, P., and Caicedo, B. (2018). Numerical Modelling and Inverse Analysis of Continuous Compaction Control. Transportation Geotechnics 17, 165–177. doi:10.1016/j.trgeo.2018.09.012

CrossRef Full Text | Google Scholar

Hosseini, A., Faheem, A., Titi, H., and Schwandt, S. (2020). Evaluation of the Long-Term Performance of Flexible Pavements with Respect to Production and Construction Quality Control Indicators. Construction Building Mater. 230, 116998. doi:10.1016/j.conbuildmat.2019.116998

CrossRef Full Text | Google Scholar

Jia, T., He, T., Qian, Z., Lv, J., and Cao, K. (2019). An Improved Low-Cost Continuous Compaction Detection Method for the Construction of Asphalt Pavement. Adv. Civil Eng. 2019, 1–11. doi:10.1155/2019/4528230

CrossRef Full Text | Google Scholar

Jing, C., Zhang, J., and Song, B. (2020). An Innovative Evaluation Method for Performance of In-Service Asphalt Pavement with Semi-rigid Base. Construction Building Mater. 235, 117376. doi:10.1016/j.conbuildmat.2019.117376

CrossRef Full Text | Google Scholar

Lefeuvemesgouez, G., and Mesgouez, A. (2008). Ground Vibration Due to a High-Speed Moving Harmonic Rectangular Load on a Poroviscoelastic Half-Space. Int. J. Sol. Struct. 45 (11), 3353–3374. doi:10.1016/j.ijsolstr.2008.01.026

CrossRef Full Text | Google Scholar

Li, H., Wang, G., Qin, L., Wang, Q., and Wang, X. (2020). A Spectral Analysis of the Dynamic Frequency Characteristics of Asphalt Pavement under Live Vehicle Loading. Road Mater. Pavement Des. 21 (2), 486–499. doi:10.1080/14680629.2018.1506815

CrossRef Full Text | Google Scholar

Li, S., Yang, S., Chen, L., and Lu, Y. (2012). Effects of Parameters on Dynamic Responses for a Heavy Vehicle-Pavement-Foundation Coupled System. Ijhvs 19 (2), 207–224. doi:10.1504/ijhvs.2012.046835

CrossRef Full Text | Google Scholar

Liu, K., Xu, P., Wang, F., You, L., Zhang, X., and Fu, C. (2022). Assessment of Automatic Induction Self-Healing Treatment Applied to Steel Deck Asphalt Pavement. Automation in Construction 133, 104011. doi:10.1016/j.autcon.2021.104011 Accepted in 10 October 2021

CrossRef Full Text | Google Scholar

Liu, W., Gong, X., Gao, Y., and Li, L. (2019). Microscopic Characteristics of Field Compaction of Asphalt Mixture Using Discrete Element Method. J. Test. Eval. 47 (6), 4579–4594. doi:10.1520/jte20180633

CrossRef Full Text | Google Scholar

Liu, X., Li, Y., Lin, Y., and Banerjee, J. R. (2021). Spectral Dynamic Stiffness Theory for Free Vibration Analysis of Plate Structures Stiffened by Beams with Arbitrary Cross-Sections. Thin-Walled Structures 160, 107391. doi:10.1016/j.tws.2020.107391

CrossRef Full Text | Google Scholar

Liu, X., Zhao, X., Adhikari, S., and Liu, X. (2021). Stochastic Dynamic Stiffness for Damped Taut Membranes. Comput. Structures 248, 106483. doi:10.1016/j.compstruc.2021.106483

CrossRef Full Text | Google Scholar

Lu, J.-F., and Jeng, D.-S. (2007). A Half-Space Saturated Poro-Elastic Medium Subjected to a Moving point Load. Int. J. Sol. Structures 44 (2), 573–586. doi:10.1016/j.ijsolstr.2006.05.020

CrossRef Full Text | Google Scholar

Lv, Z., Qian, J. G., Shi, Z. H., and Gao, Q. (2020). Dynamic Responses of Layered Poroelastic Ground under Moving Traffic Loads Considering Effects of Pavement Roughness. Soil Dyn. Earthq. Eng. 130, 105996. doi:10.1016/j.soildyn.2019.105996

CrossRef Full Text | Google Scholar

Paulmichl, I., Adam, C., and Adam, D. (2020). Parametric Study of the Compaction Effect and the Response of an Oscillation Roller. Proc. Inst. Civil Eng. - Geotechnical Eng. 173 (4), 285–301. doi:10.1680/jgeen.19.00209

CrossRef Full Text | Google Scholar

Qian, G., Hu, K., Li, J., Bai, X., and Li, N. (2020). Compaction Process Tracking for Asphalt Mixture Using Discrete Element Method. Construction Building Mater. 235, 117478. doi:10.1016/j.conbuildmat.2019.117478

CrossRef Full Text | Google Scholar

Roozbahany, E. G., and Partl, M. N. (2019). Investigation of Asphalt Joint Compaction Using Discrete Element Simulation. Road Mater. Pavement Des. 20 (7), 1722–1734. doi:10.1080/14680629.2019.1594055

CrossRef Full Text | Google Scholar

Shan, J., Shao, H., Li, Q., and Sun, P. (2019). Comparison of Real Response and Theoretical Modeling of Pavement with Thick Asphalt Layers under Heavy Traffic Load. Adv. Civil Eng. 2019 (2), 1–11. doi:10.1155/2019/8097890

CrossRef Full Text | Google Scholar

Si, C., Zhou, X., You, Z., He, Y., Chen, E., and Zhang, R. (2019). Micro-mechanical Analysis of High Modulus Asphalt concrete Pavement. Construction Building Mater. 220, 128–141. doi:10.1016/j.conbuildmat.2019.06.019

CrossRef Full Text | Google Scholar

Souza, F. V., and Castro, L. S. (2012). Effect of Temperature on the Mechanical Response of Thermo-Viscoelastic Asphalt Pavements. Construction Building Mater. 30, 574–582. doi:10.1016/j.conbuildmat.2011.11.048

CrossRef Full Text | Google Scholar

Wang, H., Zhang, Q., and Tan, J. (2009). Investigation of Layer Contributions to Asphalt Pavement Rutting. J. Mater. Civ. Eng. 21 (4), 181–185. doi:10.1061/(asce)0899-1561(2009)21:4(181)

CrossRef Full Text | Google Scholar

Wang, S.-P., Dan, H.-C., Li, L., Liu, X., and Zhang, Z. (2021). Dynamic Response of Asphalt Pavement under Vibration Rolling Load: Theory and Calibration. Soil Dyn. Earthquake Eng. 143, 106633. doi:10.1016/j.soildyn.2021.106633

CrossRef Full Text | Google Scholar

Wu, H., Li, P., Nian, T., Zhang, G., He, T., and Wei, X. (2019). Evaluation of Asphalt and Asphalt Mixtures' Water Stability Method under Multiple Freeze-Thaw Cycles. Construction Building Mater. 228, 117089. doi:10.1016/j.conbuildmat.2019.117089

CrossRef Full Text | Google Scholar

Xu, B., Lu, J.-F., and Wang, J.-H. (2008). Dynamic Response of a Layered Water-Saturated Half Space to a Moving Load. Comput. Geotechnics 35 (1), 1–10. doi:10.1016/j.compgeo.2007.03.005

CrossRef Full Text | Google Scholar

Xu, Q., and Chang, G. K. (2016). Adaptive Quality Control and Acceptance of Pavement Material Density for Intelligent Road Construction. Automation in Construction 62, 78–88. doi:10.1016/j.autcon.2015.11.004

CrossRef Full Text | Google Scholar

Zhan, Y., Yao, H., and Lu, Z. (2018). Dynamic Response of the 3D Pavement-Transversely Isotropic Poroelastic Ground System to a Rectangular Moving Load. Soil Dyn. Earthquake Eng. 115, 394–401. doi:10.1016/j.soildyn.2018.06.037

CrossRef Full Text | Google Scholar

Zhao, J., and Wang, H. (2020). Dynamic Pavement Response Analysis under Moving Truck Loads with Random Amplitudes. J. Transp. Eng. Part. B: Pavements 146 (2), 04020020. doi:10.1061/jpeodx.0000173

CrossRef Full Text | Google Scholar

Zhenning, B. A., Liang, J., Lee, V. W., and Ji, H. (2016). 3D Dynamic Response of a Multi-Layered Transversely Isotropic Half-Space Subjected to a Moving point Load along a Horizontal Straight Line with Constant Speed. Int. J. Sol. Struct. 100, 427–445. doi:10.1016/j.ijsolstr.2016.09.016

CrossRef Full Text | Google Scholar