Effect of High Strain Rates on Adiabatic Shear Bands Evolution and Mechanical Performance of Dual-Phase Ti Alloy

In the present work, the adiabatic shear characteristics of our recently designed α + β dual-phase Ti alloy at different strain rates have been investigated by hat shaped specimen. The deformation process is divided into three stages: work hardening stage, steady stage, and unstable thermal softening stage. Along or near the shear deformation paths, the microvoids and the cracks can be captured at the strain rate of 1.8 × 10⁴ s⁻¹, 2.0 × 10⁴ s⁻¹, and 2.3 × 10⁴ s⁻¹, both of which contribute to the stable and unstable softening. It is found that dynamic stored energy of cold work will be significantly improved by the enhanced high strain rate. In the view of coupling analysis of inverse pole figure and grain boundary map, it seems that low angle grain boundaries present a good resistance to the formation of cracks and thermal softening. On the contrary, high angles grain boundaries are typically located in ASBs and their affecting regions, which is in line with the reported results. While the geometrical necessary dislocation (GND) density of adiabatic shear band (ASB) and its surroundings increased significantly, the width of the ASB becomes wider as the strain rate increases, which is consistent with the theory of sub-grain rotation dynamic recrystallization model. The formation of multiple ASBs in the corner position is schematically illustrated and the average elastic modulus and hardness of the ASB region are lower than the α and β phases, combined with the GND analysis, which proves that the ASB is a thermal softening zone in this experiment.

Introduction

Ti alloys are considered as ideal structural materials in aerospace and aircraft application, because of the characteristics of low density, high specific strength at both ambient and elevated temperatures, and excellent corrosion resistance (Lütjering and Williams, 2007). In the development of damage-tolerance Ti alloys, a great number of theoretical and experimental research efforts have focused on the formation and evolution of shear bands (Zener and Hollomon, 1944; Anand and Spitzig, 1980; Kuriyama and Meyers, 1986; Marchand and Duffy, 1988; Needleman, 1989; Grady, 1992; Xue et al., 2005; Bronkhorst et al., 2006), criterion for the formation (Nguyen, 1997), microstructure, and phase transition in the shear bands formed under extreme conditions. In particular, under the high strain rate, the narrow-sheared regions generally undergo the severe plastic deformation with intense enhanced temperature in a short time, which will result in the microstructure evolution in local region to form the so-called adiabatic shear band (ASB). In general, ASBs are considered as threshold of mutation damage of metals under dynamic load (Meyers et al., 2001; Walley, 2007). Moreover, ASB will be yielded at the high strain rate attributing to the competition between thermal softening and strain/stress-rate hardening within the local regions (El-Azab, 2008; Rittel et al., 2008; Guo et al., 2019; Hao et al., 2021). Therefore, it is essential to investigate the strain-rate-dependent mechanical properties and structural evolutions of advanced metal materials (Rittel et al., 2008; Guo et al., 2019; Reddy et al., 2020), thus, to reveal the foundations of corresponding plastic deformation behaviours (Hao et al., 2021).

In order to develop the advanced Ti alloys integrated the damage tolerance and high strength properties, a great amount of efforts have been completed investigating the high-strain rate shear behaviours of α Ti (Shahan and Taheri, 1993; Meyers et al., 1994; Chichili et al., 1998; Yang and Wang, 2006; Wang et al., 2007; Yang et al., 2010; Jiang et al., 2015; Kuang et al., 2017), Ti-6Al-4V alloy (Me-Bar and Shechtman, 1983; Grebe et al., 1985; Da Silva and Ramesh, 1997; Lee and Lin, 1998; Timothy and Hutchings, 2013; Sun et al., 2014a; b; Mendoza et al., 2015; Zhou et al., 2017), TC16 (Wang, 2008), near-β Ti5551 (Ran and Chen, 2018) and Ti5553 (Yan and Jin, 2020), β ones (Zhan et al., 2016), α + β dual-phase ones (Yang et al., 2011b; Mantri et al., 2018; Ben Boubaker et al., 2019; Danard et al., 2019; Kloenne et al., 2020; Lee et al., 2020), and so on. It is worth mentioning that the dual-phase materials (Wu et al., 2017; Hao et al., 2021; Zou et al., 2021) always present ultra-strong and ductile behaviors combining the solid solution strengthening, grain refinement effect, and precipitation hardening, which could excellently deal with the planar-defects-dominated plastic deformation behaviors (Hao et al., 2021). In particular, the α + β dule-phase Ti alloys, such as Ti-15Mo-3Nb-2.7Al-0.2Si (wt%) (Mantri et al., 2018), Ti-3Mo-3Cr-2Fe-2Al (Lee et al., 2020), Ti-10V-2Fe-3Al (Danard et al., 2019), Ti-0.85Al-4V-0.25Fe-0.25Si-0.15O (Kloenne et al., 2020), Ti-5Al-4Cr-4Mo-2Sn-2Zr (Ben Boubaker et al., 2019), Ti-6Al-2Cr-2Mo-2Nb-2Sn-2Zr (Hao et al., 2021), etc., display an excellent combination of ultimate tensile strength and ductility through optimizing the complex of deformation mechanisms (Hao et al., 2021). At various strain rates or high strain rate, multiple deformation mechanisms including twinning and dislocation can be captured (Hao et al., 2021). It is believed that the adiabatic shear zone is the source of crack initiation and propagation (Wang et al., 2007). The latest experimental work has reported that the ASB forms several microseconds after stress collapse and temperature rise reaches its maximum about 30 us after ASB formation (Guo et al., 2019). The traditional well-accepted thermal-softening mechanism of ASB should be double checked, calling for more research efforts to reveal the microstructure evolutions resulting in the local softening (Guo et al., 2019). Therefore, it is necessary to reveal their corresponding softening mechanisms, including the dynamic recrystallization, dynamic transformation, adiabatic heating, and morphologies texture evolution (Yang and Wang, 2006; Rittel et al., 2008; Osovski et al., 2012; Li et al., 2017; Lieou and Bronkhorst, 2018; Ben Boubaker et al., 2019; Hao et al., 2021).

In the present work, effects of high strain rates on ASB evolution and mechanical performance of α + β dual-phase alloy (Lee and Lin, 1998) are investigated. The hat-shaped specimens are utilized to study the formation mechanisms of ASB under dynamic load by the separated Hopkison pressure bar (SHPB) technology, thus, to reveal the corresponding deformation and softening behaviors. The microstructure evolutions are characterized in terms of optical microscope (OM), scanning electron microscope (SEM), electron backscattered diffraction (EBSD), and transmission electron microscope (TEM). The investigations of the formation process of ASB can further reveal the dynamic damage process of materials and provide important references for preventing material failure and fracture during high-speed deformation and extending the service life of materials.

Materials and Methods

In the present work, the hat-shaped specimens of the annealed forging α + β dual-phase Ti alloy was deformed at ambient temperature by means of separated Hopkinson pressure bar (SHPB), which conventionally captured the well-controlled and designed localized shear in the study of large strain and high strain rate deformation. The geometry of hat-shaped specimen together with their sections of investigated ones are presented in Figure 1. In order to avoid premature fracture failure of the sample and show more early behaviors of shear localization, the configuration of Hat with an outer diameter larger than inner diameter of Brim ring is selected. The dynamic compression test was carried out on a Φ14.7 mm diameter separated Hopkinson compression rod in the Dynamic Mechanics Laboratory of Beijing Institute of Technology, and the stress-strain curve under the condition of high strain rate was obtained. The detailed information about the system of experimental device including impact, bar incident bar, and transmitted bar can be found in our previous reports (Du et al., 2021). Through adjusting the air pressure of the incident bar to 0.60 atm, 0.80 atm, and 0.90 atm separately, the different strain rates and their stress-strain curves were obtained at the strain rate of 1.8 × 10⁴ s⁻¹, 2.0 × 10⁴ s⁻¹, and 2.3 × 10⁴ s⁻¹, respectively. Afterwards, the hat-shaped specimens were cut along the axis to trace the shear paths and the deformed microstructures.

FIGURE 1

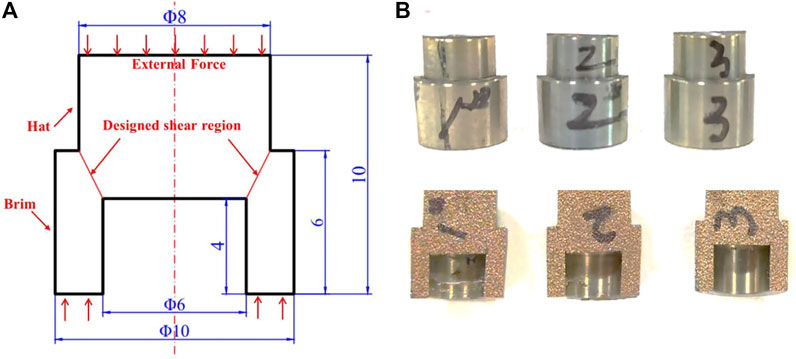
FIGURE 1. The diagrams of hat-shaped specimen, (A) the geometry of hat-shaped specimen; (B) the sections of investigated specimens.

The microstructure evolutions are characterized in terms of OM, SEM, EBSD, and TEM. Optical microstructure is observed by Nikon Eclipse LV150N optical microscope. The EBSD analysis is executed on field emission SEM of JEOL 7800F with the acceleration voltage at 20 kV, the probe current of 14 nA, and the scanning speed of 815 Hz (Du et al., 2021). It is worth mentioning that the size of scanning step is 0.15 m for the area of 0.16 mm², which is 1 m for the area of 2.88 mm².

Based on the model of the hat-shaped specimen proposed by Andrade et al., the shear parameters including shear stress ${\tau }_s$, shear strain ${\gamma }_s$ and shear strain rate $\dot{{\gamma }_s}$ can be calculated by the following equations (Andrade et al., 1994).

${\tau }_s\left(t\right)=\frac{E_0{A}_b}{A_s}{\epsilon }_t(1)$

${\gamma }_s=-\frac{C_0}{d_1-d_0}\underset{0}{\overset{t}{{\displaystyle \int }}}\left({\epsilon }_i-{\epsilon }_t\right)dt(2)$

$\dot{{\gamma }_s}=\frac{C_0}{d_1-d_0}\left({\epsilon }_i-{\epsilon }_t\right)(3)$

Here, the outside diameter of hat and inner diameter of brim are expressed as d₀ and d₁, respectively. C₀ is the elastic wave speed and E₀ is Young’s modulus of the Hopkinson bars. A_s and A_b represent the areas of the shear section and the cross section of transmitted bar. Correspondingly, the elastic strains of incident and transmitted bars are ε_i and ε_t, separately. It can be found that the severe shear strain can be obtained in the designed shear region, which is convent to capture the local shear deformation process and microstructure evolution (Du et al., 2021).

In order to calculate the width of ASB, the model reported by Grady and Kipp (Kipp and Grady, 1985; Grady, 1992; Landau et al., 2016) is utilized, which takes into account the energy dissipation in the process of ASB and can be expressed as:

$a_0={\left(\frac{9{\rho }^3{C}^2{\chi }^3}{{\tau }_b^3{\left(\frac{\partial \tau }{\partial \theta }\right)}^2\dot{\gamma }}\right)}^{1/4}(4)$

where ρ is the density, C the heat capacity, χ the thermal diffusivity, τ_b the flow stress, and $\dot{\gamma }$ the shear strain rate. The $(\partial \tau /\partial \theta )$ is the thermal softening coefficient, which is obtained from the work of Shahan and Taheri (1993). The material parameters were from the database of the Metflow software (Mitchell, 2007).

Results and Discussion

Figure 2 presents the typical microstructures of the as-received dual-phase Ti alloy (Lee and Lin, 1998) fabricated by Western Superconducting Material Technology Co., Ltd., which was forged at 920°C and annealed at T_β of 960°C afterward. The classical microstructures consisted of equiaxed α_p with average size of about 10 μm and coalesced secondary alpha phases (α_s) with thickness of about 0.9 μm. The phase fractions of α_p phases is about 46.2%.

FIGURE 2

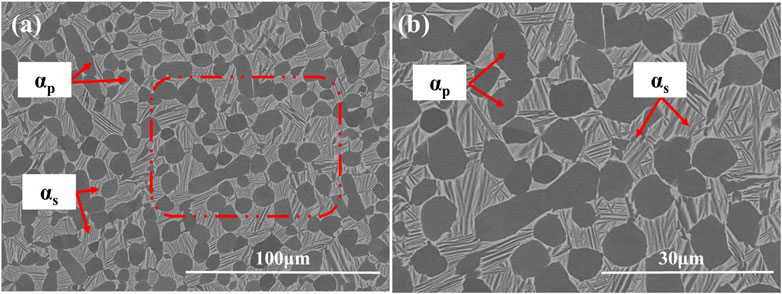
FIGURE 2. Microstructure characterizations of the as-received dual-phase Ti alloy, (A) the classical microstructures characterized by scanning electron microscope; (B) the enlarge zone of (A) highlighted by red rectangle.

Figure 3 shows the shear stress-shear strain response of hat-shaped specimens utilized in SHPB test at high strain rates of 1.8 × 10⁴ s⁻¹, 2.0 × 10⁴ s⁻¹, and 2.3 × 10⁴ s⁻¹. Referring to the static compression test, the stress-strain curve at high strain rate consisted of four stages, including the elastic deformation region, the strain hardening, the stbale softening, and the unstable softening. In particular, at the strain rate of 1.8 × 10⁴ s⁻¹, this alloy presents a maximum shear stress as high as 2016 MPa at the plastic deformation stage, indicating an excellent damage tolerance capability, as shown in Figure 3A. The shear stress increases with the improved shear strain and reaches a maximum as high as 2230 MPa with the shear strain of 0.123. In the range of shear strain from 0.123 to 0.165, the shear stress slowly decreased from the peak by 118 MPa attributing to the thermal softening during the adiabatic shear. It is worth mentioning that the dynamic stored deformation energy till to the work hardening stage can be characterized as the integration of the stress-strain curve.

FIGURE 3

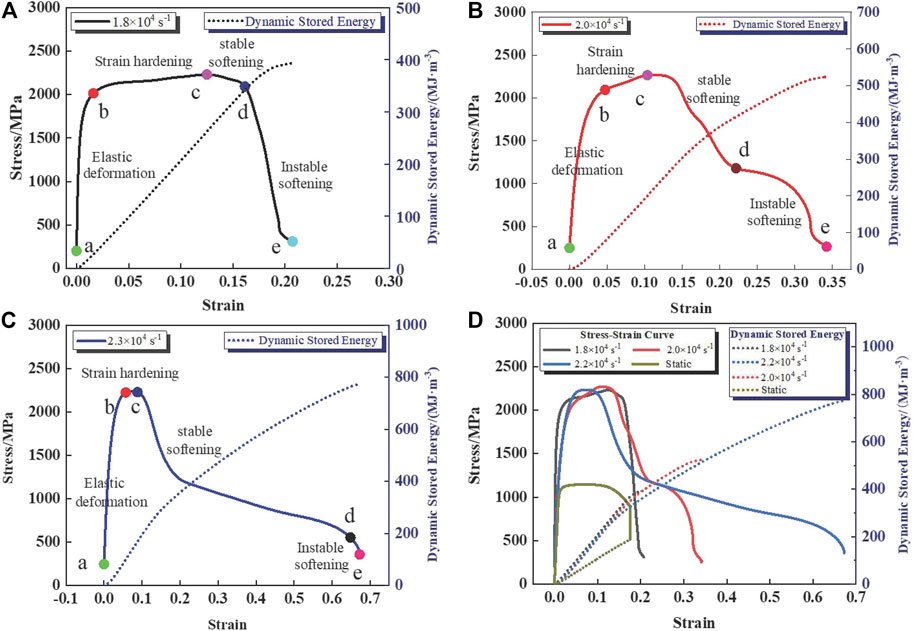
FIGURE 3. The stress-strain and the dynamic stored energy of dual-phase Ti alloy at various high strain rates, (A) 1.8 × 10⁴ s⁻¹; (B) 2.0 × 10⁴ s⁻¹; (C) 2.3 × 10⁴ s⁻¹; (D) the comparations of these three tests.

While Figures 3B,C show the stress-strain curve obtained at the higher strain rates of 2.0 × 10⁴ s⁻¹ and 2.3 × 10⁴ s⁻¹, their systematic comparations referring to the static ones are presented in Figure 3D. At the strain rate of 2.0 × 10⁴ s⁻¹, the shear stress increases with the improved shear strain and reaches a maximum as high as 2267 MPa with the shear strain of 0.111. In the range of shear strain from 0.111 to 0.143, the shear stress slowly decreased by 102 MPa from the peak attributing to the thermal softening during the adiabatic shear. When the strain reaches 0.217, the curve shows a plateau. On the contrary, the stress rapidly reaches the maximum under the strain rate of 2.3 × 10⁴ s⁻¹, and the strain strengthening and thermal softening effects in the plastic strain stage balance each other, as shown in Figure 3C. The stress reaches a peak of 2235 MPa at the strain of 0.099. The curve shows a plateau at the strain of 0.202, highlighting the thermal softening behaviors. It can be seen that the higher strain rate will result in the smaller plastic strain and strain to reach the peak stress, as displayed in Figure 3D. Moreover, it is found that dynamic stored energy of cold work (Rittel et al., 2008; Landau et al., 2016; Baik et al., 2021) will be significantly improved by the enhanced high strain rate, which are 393 MJ m⁻³, 524 MJ m⁻³, and 775 MJ m⁻³ for the strain rate of 1.8 × 10⁴ s⁻¹, 2.0 × 10⁴ s⁻¹, and 2.3 × 104 s⁻¹, respectively. Therefore, the dynamic recrystallization and ASB-mediated dominated softening mechanisms should be discussed.

In order to reveal aforementioned stable and unstable softening mechanisms, the multi-scales SEM characterizations of ASBs in the hat-shaped specimen at these three strain rates are shown in Figures 4–6, respectively. The additional numbers identify the typical features of selected regions. Under the shock loading conditions, the primary α phase on both sides of ASB is elongated and deformed along the shear direction, locating at transition area near the centre of the shear band and the matrix, as shown in Figures 4–6. Generally, the ASBs of the hat-shaped sample will start from the upper corner or the lower corner, which are mainly located at the α/β dual-phase colony structures. Along or near the shear deformation paths, the microvoids and the cracks can be captured at various strain rates, both of which contribute to the stable and unstable softening, as shown in Figures 4B–4, Figures 5A–5, B–4, and Figures 6B–5. It is understood that those microvoids are the preferred sites for nucleation and growth of cracks. When increasing the strain rate from 1.8 × 10⁴ s⁻¹ to 2.3 × 10⁴ s⁻¹, the width and length of microcracks are improved dramatically. Moreover, the width of ASB locating the main shearing/cracking path is dramatically enhanced by the increased strain rate, which is attributed to the higher dynamic stored energy of cold work than those at lower strain rate. Comparing to the width of ASB at 1.8 × 10⁴ s⁻¹, they are estimated to be 5–10 μm at 2.0 × 10⁴ s⁻¹ and larger than 10 μm at 2.3 × 10⁴ s⁻¹ based on the Grady-Kipp model expressed as Eq. 4. Furthermore, with the improved strain rate, the anomaly microstructural evolutions in the ASBs can be captured, which can be changed from the linear ASBs to the bowing vortex structures caused by the rotations of sub-grains and grains, as presented in Figures 6B–4, B–5.

FIGURE 4

FIGURE 4. The multi-scales SEM characterizations of adiabatic shear bands in the hat-shaped specimen at strain rate of 1.8 × 10⁴ s⁻¹ (Hao et al., 2021), (A) the left part; (B) the right part. The additional numbers identify the typical features of selected regions.

FIGURE 5

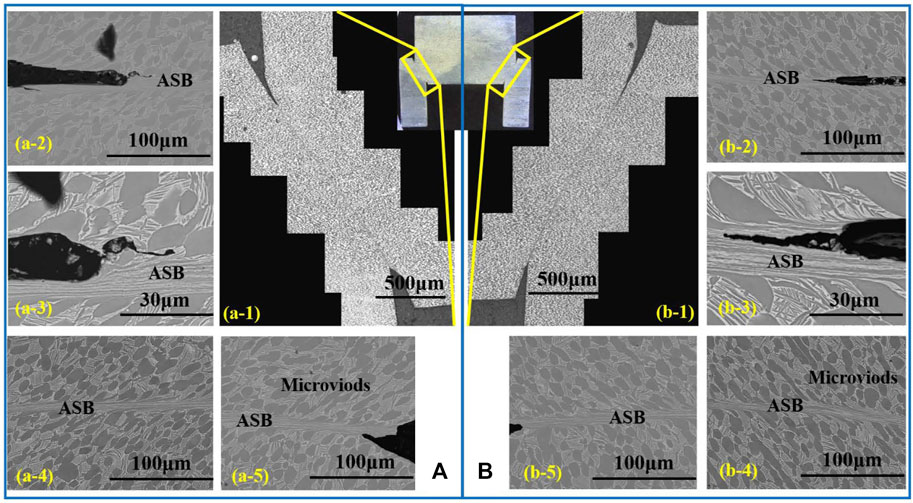
FIGURE 5. The multi-scales SEM characterizations of adiabatic shear bands in the hat-shaped specimen at strain rate of 2.0 × 10⁴ s⁻¹ s⁻¹, (A) the left part; (B) the right part. The additional numbers identify the typical features of selected regions.

FIGURE 6

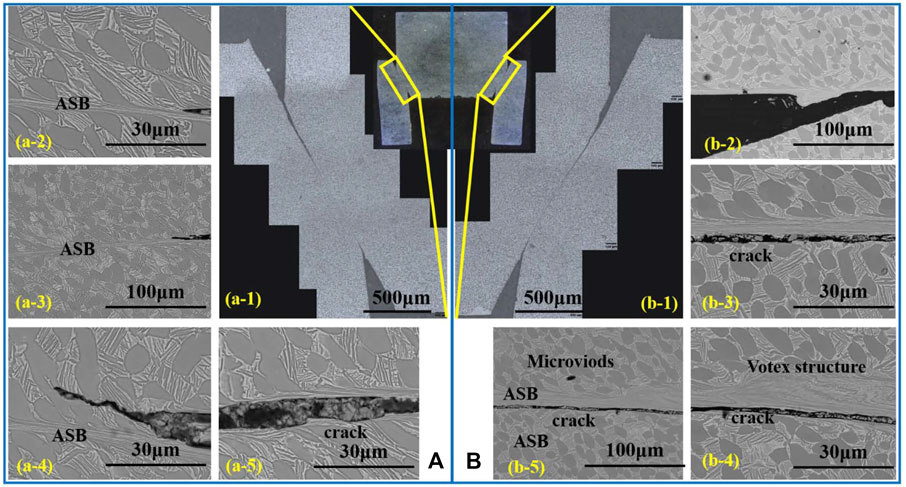
FIGURE 6. The multi-scales SEM characterizations of adiabatic shear bands in the hat-shaped specimen at strain rate of 2.3 × 10⁴ s⁻¹, (A) the left part; (B) the right part. The additional numbers identify the typical features of selected regions.

Taking the advantages of EBSD characterizations, the full scans of ASBs and the corresponding affecting zones in terms of the BC map, the geometrically necessary dislocation (GND) map, and the coupling analysis of IPF + GB at these three different strain rates are presented in Figures 7–9, respectively. The thickness of ASB affected zone resulting in the collaborating plastic deformation can be clearly captured by GND mapping. It can be seen that the GND density of ASB and its surroundings increased significantly when improving the strain rate, which also highlight the effect zone of ASBs. As dislocation density increases, dislocation entanglement forms a dislocation network, which is often considered a sign of work hardening. In fact, ASB eventually evolves into a softened area, during which thermoplastic instability occurs. When the material is under dynamic load, the heat generated by deformation cannot be transferred out in time to form a local “adiabatic temperature rise,” and the temperature rise causes the material to soften. When the softening effect is greater than the work hardening effect, a softened area will appear as the final observed adiabatic shear zone. Moreover, in the view of coupling analysis of inverse pole figure and grain boundary map (IPF + GB), it seems that low angle grain boundaries present a good resistance to the formation of cracks and the thermal softening. On the contrary, high angles grain boundaries are typically located in ASBs and their affecting regions, which is in line with our previous works (Hao et al., 2021) and the reported one in Ti (Timothy and Hutchings, 2013). With the guidance of grain boundary complexions (Grebe et al., 1985; Da Silva and Ramesh, 1997; Sun et al., 2014a), it is understood that the free volumes exist at the boundaries, constructing the weak bonded regions and contributing to the initiation of ASB.

FIGURE 7

FIGURE 7. The features of the hat-shaped sample in terms of back scattering (BC), geometrically necessary dislocation (GND) map, and the coupling analysis of inverse pole figure and grain boundary map (IPF + GB) at strain rate of 1.8 × 10⁴ s⁻¹.

FIGURE 8

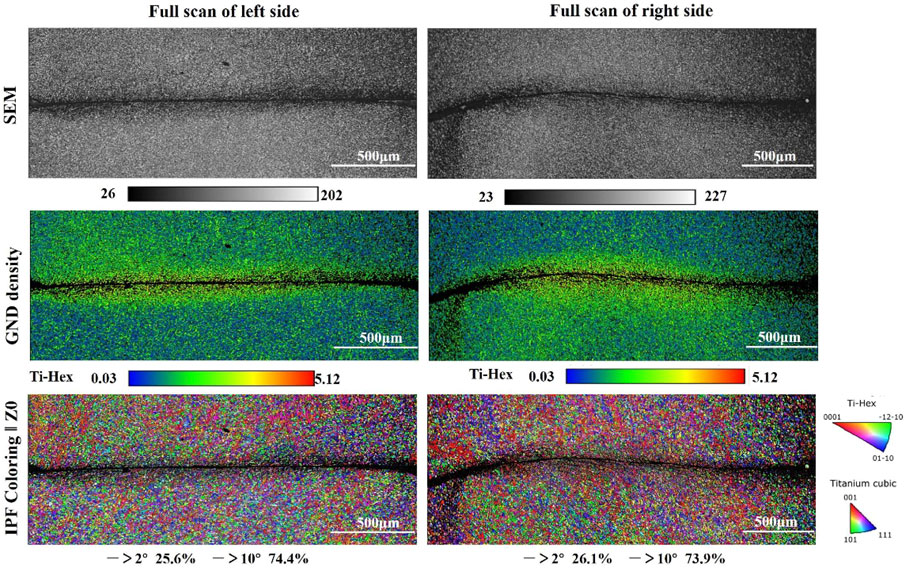
FIGURE 8. The features of the hat-shaped sample in terms of back scattering (BC), geometrically necessary dislocation (GND) map, and the coupling analysis of inverse pole figure and grain boundary map (IPF + GB) at strain rate of 2.0 × 10⁴ s⁻¹.

FIGURE 9

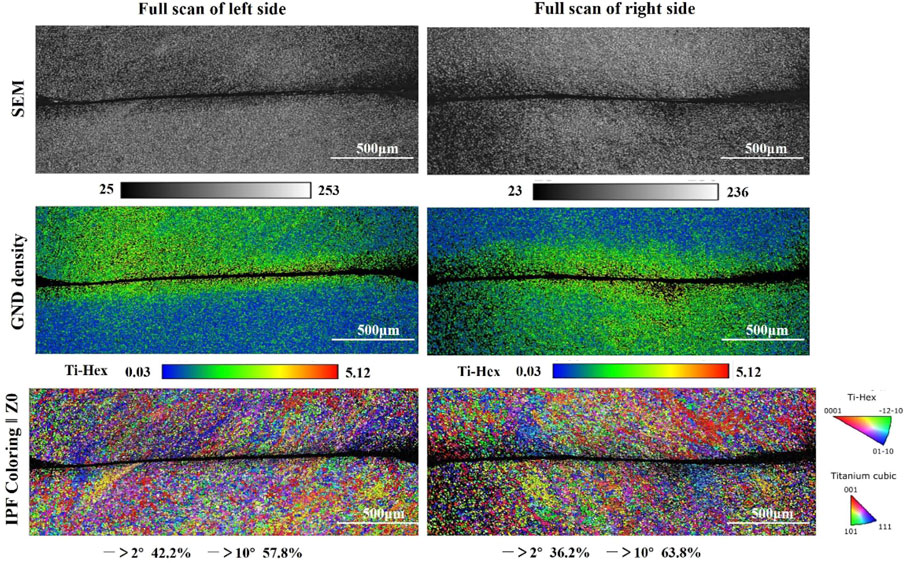
FIGURE 9. The features of the hat-shaped sample in terms of back scattering (BC), geometrically necessary dislocation (GND) map, and the coupling analysis of inverse pole figure and grain boundary map (IPF + GB) at strain rate of 2.3 × 10⁴ s⁻¹.

It is believed that dynamic recrystallization can be almost universally observed in the microstructure of ASBs (Rittel et al., 2008). The fine equiaxed sub-grains in the ASB are formed by dynamic recovery and continuous dynamic recrystallization (Yang et al., 2011a). As shown in Figure 10, the microstructures of the bottom corner position of shear region in left side of specimen are presented in terms of BC mapping and IPF mapping. Multiple very narrow ASBs can be observed in the BC map, as highlighted by those dash lines in Figure 10. It is worth mentioning that the multiple adiabatic shear bands in hat-shaped specimens during SHPB test are rarely reported, which can be captured in metallic materials during other dynamic impact tests, such as explosive collapse of a thick-walled cylinder (TWC) (Chichili et al., 1998; El-Azab, 2008) and ballistic impact test (Shahan and Taheri, 1993; Yang and Wang, 2006). Meanwhile, the un-indexable regions show more clearly the positions of multiple very narrow ASBs, where there are a great amount ultra-fine equiaxed sub-grains. Since one of them is found at the original bottom corner position of the sample before the plastic deformation, it is indicated that the formation of multiple ASBs is caused by the dramatic change of stress concentration in the bottom corner of the specimen. Therefore, multiple ASBs tend to be near parallel distributed along the shear direction, attributing to the concentrated plastic deformation in relatively narrow banded region near the bottom corner of the hat-shaped specimen during dynamic impact. Those regions between the adjacent very narrow ASBs presents stronger shear deformation microstructural characteristics than other regions. Moreover, according to the subgrain rotation dynamic recrystallization model (Meyers et al.), ASBs generate in metallic materials through four steps: (1) dislocations proliferate and distribute randomly during the initial stage of deformation; (2) dislocations rearrange to form elongated dislocation cells, known as the dynamic recovery; (3) elongated sub-grains generate from the dislocation cells as the deformation continues; (4) elongated sub-grains dissolve and rotate into equiaxed recrystallized micrograins.

FIGURE 10

FIGURE 10. The microstructure of the bottom corner position of shear region in left side of specimen obtained at the strain rate of 1.8 × 10⁴ s⁻¹, (A) BC map; (B) IPF coloring.

Conclusion

In summary, the adiabatic shear localization behavior of hat-shaped sample of α + β dual-phase Ti-6Al-2Cr-2Mo-2Nb-2Sn-2Zr alloy is investigated by SHPB test. Under the shock loading conditions, the primary α phase on both sides of ASB is elongated and deformed along the shear direction, locating at transition area near the centre of the shear band and the matrix. Generally, the ASBs of the hat-shaped sample will start from the upper corner or the lower corner, which are mainly located at the α/β dual-phase colony structures. Along or near the shear deformation paths, the microvoids and the cracks can be captured at various strain rates, both of which contribute to the stable and unstable softening. It is found that dynamic stored energy of cold work will be significantly improved by the enhanced high strain rate, which are 393 MJ m⁻³, 524 MJ m⁻³, and 775 MJ m⁻³ at the strain rate of 1.8 × 10⁴ s⁻¹, 2.0 × 10⁴ s⁻¹, and 2.3 × 10⁴ s⁻¹, respectively. In the view of coupling analysis of inverse pole figure and grain boundary map, it seems like that low angle grain boundaries present a good resistance to the formation of cracks and the thermal softening. On the contrary, high angles grain boundaries are typically located in ASBs and their affecting regions, which is in line with the reported results. The GND density of ASB and its surroundings increased significantly when improving the strain rate, which also highlight the effect zone of ASBs.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

Conceptualization, FH, KW, XL, HC, YF, and JL; methodology, FH, YM, CZ, HC, and WW; validation, YD, YM, CZ, HC, and WW; formal analysis, FH, JY, YM, CZ, YD, and WW; investigation, FH, JY, YM, CZ, YD, and WW; data curation, FH, YD, YM, and WW; writing—original draft preparation, FH, JY, YM, CZ, YD, and WW; writing—review and editing, KW, XL, HC, YF, and JL; visualization, FH, JY, YM, YD, and WW; supervision, KW, XL, HC, YF, and JL; project administration, WW and FH; funding acquisition, WW and FH. All authors have read and agreed to the published version of the manuscript.

Funding

This study received funding from the Science Challenge Project, grant number TZ2018002, and the Western Superconducting Technologies Co., Ltd., EPRCTC project 41422010505. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Conflict of Interest

Authors FH, YD, YM, HC, KW, YF, and XL were employed by Western Superconducting Technologies Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Anand, L., and Spitzig, W. A. (1980). Initiation of Localized Shear Bands in Plane Strain. J. Mech. Phys. Sol. 28, 113–128. doi:10.1016/0022-5096(80)90017-4

CrossRef Full Text | Google Scholar

Andrade, U., Meyers, M. A., Vecchio, K. S., and Chokshi, A. H. (1994). Dynamic Recrystallization in High-Strain, High-Strain-Rate Plastic Deformation of Copper. Acta Metallurgica et Materialia 42, 3183–3195. doi:10.1016/0956-7151(94)90417-0

CrossRef Full Text | Google Scholar

Baik, S.-I., Gupta, R. K., Kumar, K. S., and Seidman, D. N. (2021). Temperature Increases and Thermoplastic Microstructural Evolution in Adiabatic Shear Bands in a High-Strength and High-Toughness 10 wt.% Ni Steel. Acta Materialia 205, 116568. doi:10.1016/j.actamat.2020.116568

CrossRef Full Text | Google Scholar

Ben Boubaker, H., Mareau, C., Ayed, Y., Germain, G., and Tidu, A. (2019). Impact of the Initial Microstructure and the Loading Conditions on the Deformation Behavior of the Ti17 Titanium alloy. J. Mater. Sci. 55, 1765–1778. doi:10.1007/s10853-019-04014-5

CrossRef Full Text | Google Scholar

Bronkhorst, C. A., Cerreta, E. K., Xue, Q., Maudlin, P. J., Mason, T. A., and Gray, G. T. (2006). An Experimental and Numerical Study of the Localization Behavior of Tantalum and Stainless Steel. Int. J. Plasticity. 22, 1304–1335. doi:10.1016/j.ijplas.2005.10.002

CrossRef Full Text | Google Scholar

Chichili, D. R., Ramesh, K. T., and Hemker, K. J. (1998). The High-Strain-Rate Response of Alpha-Titanium: Experiments, Deformation Mechanisms and Modeling. Acta Materialia 46, 1025–1043. doi:10.1016/s1359-6454(97)00287-5

CrossRef Full Text | Google Scholar

Da Silva, M. G., and Ramesh, K. T. (1997). The Rate-Dependent Deformation and Localization of Fully Dense and Porous Ti-6Al-4V. Mater. Sci. Eng. A. 232, 11–22. doi:10.1016/s0921-5093(97)00076-2

CrossRef Full Text | Google Scholar

Danard, Y., Poulain, R., Garcia, M., Guillou, R., Thiaudière, D., Mantri, S., et al. (2019). Microstructure Design and In-Situ Investigation of TRIP/TWIP Effects in a Forged Dual-Phase Ti-10V-2Fe-3Al alloy. Materialia 8, 100507. doi:10.1016/j.mtla.2019.100507

CrossRef Full Text | Google Scholar

Du, Y.-X., Yang, X.-L., Li, Z.-S., Hao, F., Mao, Y.-C., Li, S.-Q., et al. (2021). Shear Localization Behavior in Hat-Shaped Specimen of Near-α Ti−6Al−2Zr−1Mo−1V Titanium alloy Loaded at High Strain Rate. Trans. Nonferrous Met. Soc. China 31, 1641–1655. doi:10.1016/s1003-6326(21)65604-2

CrossRef Full Text | Google Scholar

El-Azab, A. (2008). The Statistical Mechanics of Strain-Hardened Metals. Science 320, 1729–1730. doi:10.1126/science.1160003

PubMed Abstract | CrossRef Full Text | Google Scholar

Grady, D. E. (1992). Properties of an Adiabatic Shear-Band Process Zone. J. Mech. Phys. Sol. 40, 1197–1215. doi:10.1016/0022-5096(92)90012-q

CrossRef Full Text | Google Scholar

Grebe, H. A., Pak, H.-R., and Meyers, M. A. (1985). Adiabatic Shear Localization in Titanium and Ti-6 Pct Al-4 Pct V alloy. Metallurgical Trans. A. 16, 761–775. doi:10.1007/bf02814827

CrossRef Full Text | Google Scholar

Guo, Y., Ruan, Q., Zhu, S., Wei, Q., Chen, H., Lu, J., et al. (2019). Temperature Rise Associated with Adiabatic Shear Band: Causality Clarified. Phys. Rev. Lett. 122, 015503. doi:10.1103/PhysRevLett.122.015503

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, F., Du, Y., Li, P., Mao, Y., Lin, D., Wang, J., et al. (2021). Effect of High Strain Rate on Adiabatic Shearing of α+β Dual-Phase Ti Alloy. Materials 14, 2044. doi:10.3390/ma14082044

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., Chen, Z., Zhan, C., Chen, T., Wang, R., and Liu, C. (2015). Adiabatic Shear Localization in Pure Titanium Deformed by Dynamic Loading: Microstructure and Microtexture Characteristic. Mater. Sci. Eng. A. 640, 436–442. doi:10.1016/j.msea.2015.06.028

CrossRef Full Text | Google Scholar

Kipp, M. E., and Grady, D. E. (1985). Dynamic Fracture Growth and Interaction in One Dimension†. J. Mech. Phys. Sol. 33, 399–415. doi:10.1016/0022-5096(85)90036-5

CrossRef Full Text | Google Scholar

Kloenne, Z., Viswanathan, G., Fox, S., Loretto, M., and Fraser, H. L. (2020). Interface and colony Boundary Sliding as a Deformation Mechanism in a Novel Titanium alloy. Scripta Materialia 178, 418–421. doi:10.1016/j.scriptamat.2019.11.063

CrossRef Full Text | Google Scholar

Kuang, L., Chen, Z., Jiang, Y., Wang, Z., Wang, R., and Liu, C. (2017). Adiabatic Shear Behaviors in Rolled and Annealed Pure Titanium Subjected to Dynamic Impact Loading. Mater. Sci. Eng. A. 685, 95–106. doi:10.1016/j.msea.2017.01.011

CrossRef Full Text | Google Scholar

Kuriyama, S., and Meyers, M. A. (1986). Numerical Modeling of the Propagation of an Adiabatic Shear Band. Metallurgical Trans. A. 17, 443–450. doi:10.1007/bf02643951

CrossRef Full Text | Google Scholar

Landau, P., Osovski, S., Venkert, A., Gärtnerová, V., and Rittel, D. (2016). The Genesis of Adiabatic Shear Bands. Sci. Rep. 6, 37226. doi:10.1038/srep37226

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, S. W., Park, C. H., Hong, J.-K., and Yeom, J.-T. (2020). Development of Sub-Grained α+β Ti alloy with High Yield Strength Showing Twinning- and Transformation-Induced Plasticity. J. Alloys Comp. 813, 152102. doi:10.1016/j.jallcom.2019.152102

CrossRef Full Text | Google Scholar

Lee, W.-S., and Lin, C.-F. (1998). Plastic Deformation and Fracture Behaviour of Ti-6Al-4V alloy Loaded with High Strain Rate under Various Temperatures. Mater. Sci. Eng. A. 241, 48–59. doi:10.1016/s0921-5093(97)00471-1

CrossRef Full Text | Google Scholar

Li, J., Li, Y., Huang, C., Suo, T., and Wei, Q. (2017). On Adiabatic Shear Localization in Nanostructured Face-Centered Cubic Alloys with Different Stacking Fault Energies. Acta Materialia 141, 163–182. doi:10.1016/j.actamat.2017.09.022

CrossRef Full Text | Google Scholar

Lieou, C. K. C., and Bronkhorst, C. A. (2018). Dynamic Recrystallization in Adiabatic Shear Banding: Effective-Temperature Model and Comparison to Experiments in Ultrafine-Grained Titanium. Int. J. Plasticity. 111, 107–121. doi:10.1016/j.ijplas.2018.07.011

CrossRef Full Text | Google Scholar

Lütjering, G., and Williams, J. C. (2007). Titanium. Berlin: Springer-Verlag Berlin Heidelberg.

Google Scholar

Mantri, S. A., Choudhuri, D., Alam, T., Viswanathan, G. B., Sosa, J. M., Fraser, H. L., et al. (2018). Tuning the Scale of α Precipitates in β-Titanium Alloys for Achieving High Strength. Scripta Materialia 154, 139–144. doi:10.1016/j.scriptamat.2018.05.040

CrossRef Full Text | Google Scholar

Marchand, A., and Duffy, J. (1988). An Experimental Study of the Formation Process of Adiabatic Shear Bands in a Structural Steel. J. Mech. Phys. Sol. 36, 251–283. doi:10.1016/0022-5096(88)90012-9

CrossRef Full Text | Google Scholar

Me-Bar, Y., and Shechtman, D. (1983). On the Adiabatic Shear of Ti-6Al-4V Ballistic Targets. Mater. Sci. Eng. 58, 181–188. doi:10.1016/0025-5416(83)90044-7

CrossRef Full Text | Google Scholar

Mendoza, I., Villalobos, D., and Alexandrov, B. T. (2015). Crack Propagation of Ti alloy via Adiabatic Shear Bands. Mater. Sci. Eng. A. 645, 306–310. doi:10.1016/j.msea.2015.08.035

CrossRef Full Text | Google Scholar

Meyers, M. A., Nesterenko, V. F., Lasalvia, J. C., and Xue, Q. (2001). Shear Localization in Dynamic Deformation of Materials: Microstructural Evolution and Self-Organization. Mater. Sci. Eng. A. 317, 204–225. doi:10.1016/s0921-5093(01)01160-1

CrossRef Full Text | Google Scholar

Meyers, M. A., Subhash, G., Kad, B. K., and Prasad, L. (1994). Evolution of Microstructure and Shear-Band Formation in α-hcp Titanium. Mech. Mater. 17, 175–193. doi:10.1016/0167-6636(94)90058-2

CrossRef Full Text | Google Scholar

Mitchell, A. (2007). MeltFlow-VAR. 4.3 ed. Plymouth, US: Innovative Research, LLC.

Google Scholar

Needleman, A. (1989). Dynamic Shear Band Development in Plane Strain. J. Appl. Mech. 56, 1–9. doi:10.1115/1.3176046

CrossRef Full Text | Google Scholar

Nguyen, C. H. (1997). Analysis of Some Thermal Instability Criteria in the Adiabatic Shear Banding Process. J. Phys. IV France 07, C3-849–C3-854. doi:10.1051/jp4:19973143

CrossRef Full Text | Google Scholar

Osovski, S., Rittel, D., Landau, P., and Venkert, A. (2012). Microstructural Effects on Adiabatic Shear Band Formation. Scripta Materialia 66, 9–12. doi:10.1016/j.scriptamat.2011.09.014

CrossRef Full Text | Google Scholar

Ran, C., and Chen, P. (2018). Shear Localization and Recrystallization in High Strain Rate Deformation in Ti-5Al-5Mo-5V-1Cr-1Fe alloy. Mater. Lett. 232, 142–145. doi:10.1016/j.matlet.2018.08.095

CrossRef Full Text | Google Scholar

Reddy, V. S., Nath, P., Horbach, J., Sollich, P., and Sengupta, S. (2020). Nucleation Theory for Yielding of Nearly Defect-Free Crystals: Understanding Rate Dependent Yield Points. Phys. Rev. Lett. 124, 025503. doi:10.1103/PhysRevLett.124.025503

PubMed Abstract | CrossRef Full Text | Google Scholar

Rittel, D., Landau, P., and Venkert, A. (2008). Dynamic Recrystallization as a Potential Cause for Adiabatic Shear Failure. Phys. Rev. Lett. 101, 165501. doi:10.1103/physrevlett.101.165501

PubMed Abstract | CrossRef Full Text | Google Scholar

Shahan, A. R., and Taheri, A. K. (1993). Adiabatic Shear Bands in Titanium and Titanium Alloys: a Critical Review. Mater. Des. 14, 243–250. doi:10.1016/0261-3069(93)90078-a

CrossRef Full Text | Google Scholar

Sun, K., Yu, X., Tan, C., Ma, H., Wang, F., and Cai, H. (2014a). Effect of Microstructure on Adiabatic Shear Band Bifurcation in Ti-6Al-4V Alloys under Ballistic Impact. Mater. Sci. Eng. A. 595, 247–256. doi:10.1016/j.msea.2013.12.007

CrossRef Full Text | Google Scholar

Sun, K., Yu, X., Tan, C., Ma, H., Wang, F., and Cai, H. (2014b). Influence of Adiabatic Shear Bands Intersection on the Ballistic Impact of Ti-6Al-4V Alloys with Three Microstructures. Mater. Sci. Eng. A. 606, 257–267. doi:10.1016/j.msea.2014.03.091

CrossRef Full Text | Google Scholar

Timothy, S. P., and Hutchings, I. M. (2013). Initiation and Growth of Microfractures along Adiabatic Shear Bands in Ti-6AI-4V. Mater. Sci. Tech. 1, 526–530. doi:10.1179/mst.1985.1.7.526

CrossRef Full Text | Google Scholar

Walley, S. M. (2007). Shear Localization: A Historical Overview. Metall. Mat Trans. A. 38, 2629–2654. doi:10.1007/s11661-007-9271-x

CrossRef Full Text | Google Scholar

Wang, B. F. (2008). Adiabatic Shear Band in a Ti-3Al-5Mo-4.5V Titanium alloy. J. Mater. Sci. 43, 1576–1582. doi:10.1007/s10853-007-2330-2

CrossRef Full Text | Google Scholar

Wang, B. F., Yang, Y., Chen, Z. P., and Zeng, Y. (2007). Adiabatic Shear Bands in α-Titanium Tube under External Explosive Loading. J. Mater. Sci. 42, 8101–8105. doi:10.1007/s10853-007-1725-4

CrossRef Full Text | Google Scholar

Wu, G., Chan, K.-C., Zhu, L., Sun, L., and Lu, J. (2017). Dual-phase Nanostructuring as a Route to High-Strength Magnesium Alloys. Nature 545, 80–83. doi:10.1038/nature21691

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, Q., Gray, G. T., Henrie, B. L., Maloy, S. A., and Chen, S. R. (2005). Influence of Shock Prestraining on the Formation of Shear Localization in 304 Stainless Steel. Metall. Mat Trans. A. 36, 1471–1486. doi:10.1007/s11661-005-0239-4

CrossRef Full Text | Google Scholar

Yan, D. P., and Jin, X. (2020). Characterization of Shear Band Formation and Microstructure Evolution during Orthogonal Cutting of Ti-5553: Part I-Shear Angle, Strain and Strain Rate. J. Materi Eng. Perform. 29, 4063–4074. doi:10.1007/s11665-020-04880-0

CrossRef Full Text | Google Scholar

Yang, D. K., Cizek, P., Hodgson, P. D., and Wen, C. E. (2010). Microstructure Evolution and Nanograin Formation during Shear Localization in Cold-Rolled Titanium. Acta Materialia 58, 4536–4548. doi:10.1016/j.actamat.2010.05.007

CrossRef Full Text | Google Scholar

Yang, Y., Jiang, F., Zhou, B. M., Li, X. M., Zheng, H. G., and Zhang, Q. M. (2011a). Microstructural Characterization and Evolution Mechanism of Adiabatic Shear Band in a Near Beta-Ti alloy. Mater. Sci. Eng. A. 528, 2787–2794. doi:10.1016/j.msea.2010.12.053

CrossRef Full Text | Google Scholar

Yang, Y., Li, X. M., Tong, X. L., Zhang, Q. M., and Xu, C. Y. (2011b). Effects of Microstructure on the Adiabatic Shearing Behaviors of Titanium alloy. Mater. Sci. Eng. A. 528, 3130–3133. doi:10.1016/j.msea.2010.12.068

CrossRef Full Text | Google Scholar

Yang, Y., and Wang, B. F. (2006). Microstructure Evolution in Adiabatic Shear Band in α-Titanium. J. Mater. Sci. 41, 7387–7392. doi:10.1007/s10853-006-0811-3

CrossRef Full Text | Google Scholar

Zener, C., and Hollomon, J. H. (1944). Effect of Strain Rate upon Plastic Flow of Steel. J. Appl. Phys. 15, 22–32. doi:10.1063/1.1707363

CrossRef Full Text | Google Scholar

Zhan, H., Wang, G., Kent, D., and Dargusch, M. (2016). The Dynamic Response of a Metastable β Ti-Nb alloy to High Strain Rates at Room and Elevated Temperatures. Acta Materialia 105, 104–113. doi:10.1016/j.actamat.2015.11.056

CrossRef Full Text | Google Scholar

Zhou, T., Wu, J., Che, J., Wang, Y., and Wang, X. (2017). Dynamic Shear Characteristics of Titanium alloy Ti-6Al-4V at Large Strain Rates by the Split Hopkinson Pressure Bar Test. Int. J. Impact Eng. 109, 167–177. doi:10.1016/j.ijimpeng.2017.06.007

CrossRef Full Text | Google Scholar

Zou, C., Li, J., Wang, W. Y., Zhang, Y., Lin, D., Yuan, R., et al. (2021). Integrating Data Mining and Machine Learning to Discover High-Strength Ductile Titanium Alloys. Acta Materialia 202, 211–221. doi:10.1016/j.actamat.2020.10.056

CrossRef Full Text | Google Scholar