- 1School of Physical Science and Technology, Northwestern Polytechnical University, Xi’an, China
- 2The National Research Institute of Radio Spectrum Management, Xi’an, China
Topological material has been widely studied in recent years because of excellent physical properties. In this paper, a Weyl topological material composed of the double left-handed helixes is presented. It is demonstrated that the proposed structure possesses a two-dimensional complete topological nontrivial bandgap for a fixed kz in the microwave frequency, and the robust surface states are observed. This unique function provides a promising platform for the development of photonics and electromagnetics.
Introduction
Topological materials are an unusual material state, and the most interesting feature is that they can be distinguished strictly from all other materials using a mathematical concept called ‘topology’. This mathematical property enables topological materials to transmit electrical signals without dissipation. Topological materials can be realized firstly by electrons. It has become a significant research frontier due to the unique property of topological phase transition. Topological material has been investigated in the fields of optics and acoustics. (Klitzing et al., 1980; Bernevig et al., 2006; Konig et al., 2007; Hsieh et al., 2008; Xia et al., 2009; Zhang et al., 2009; Liu et al., 2018). The most attractive property of the topological materials is topologically protected edge states (two-dimensional systems)/surface states (three-dimensional systems). Electromagnetic wave can propagate in one-way without scattering in these edge/surface states (Yang et al., 2017; Yves ey al., 2017; Chaunsali et al., 2018; Wu et al., 2018). It is demonstrated that topological photonics can achieve many interesting phenomena, such as quantum Hall effect (Raghu and Haldane, 2008; Wang et al., 2008; Wang et al., 2009; Ye et al., 2019), quantum anomalous Hall effect (Fang and Wang, 2019; Mittal et al., 2019), quantum spin Hall effect (Christiansen et al., 2019; Slobozhanyuk et al., 2019; Sun et al., 2019; Zhirihin et al., 2019), and quantum valley Hall effect (Han et al., 2021; Jo et al., 2021).
Recently, Weyl degenerate state has been applied in the field of topological materials (Asadchy et al., 2021; Gao et al., 2016; Chen et al., 2016; Cheng et al., 2016; Yang et al., 2018; Kim et al., 2019a; Kim et al., 2019b; Wang et al., 2019; Ma et al., 2021; Lu et al., 2015; Yang et al., 2019; Yang et al., 2020). In the three-dimensional momentum space, Weyl point is a nodal point formed by the intersection of two linear nondegenerate dispersive bands. The additional mass term cannot be introduced in Weyl topological materials, and the band gap cannot be opened through perturbation. Therefore, Weyl topological materials have a very stable topological structure as compared with Dirac topological materials. With the development of topology, photonic Weyl topological materials have been studied as an emerging material with great potential. For instance, Gao et al. reported a novel type of plasmonic Weyl points in a naturally existing medium (Gao et al., 2016). Chen et al. proposed a topological photonic crystal that exhibits single, double and triple Weyl points (Chen et al., 2016). Yang et al. realized an idea Weyl point and helicoid surface states by using the three-dimensional photonic crystal composed of metallic inclusions (Yang et al., 2018). Wang et al. proposed a magnetized semiconductor and observed the photonic Weyl point and Fermi-arc surface states in the terahertz frequency by breaking the time reversal symmetry (Wang et al., 2019).
In this paper, we propose a Weyl topological material composed of double left-handed helixes. We demonstrate the existences of Weyl points and robust surface states in the present material. The Weyl topological material has a topological nontrivial bandgap in the bandwidth from 15.55 to 16.45 GHz, where the topologically protected surface state is observed.
Topological Material Design and Band Structure
Figure 1A shows a unit cell of the Weyl topological material composed of double left-handed metallic helixes with rotated by π each other. Figure 1B shows the proposed topological materials formed by the periodic arrangement of the unit cells in the xy plane, and stacking identical layers along the z direction. The helical structure has C2 symmetry, and the topological non-trivial phase is caused by the hyperbolic and chirality of the structure (Kim et al., 2019a). The proposed topological material is designed by using the High Frequency Structure Simulator (HFSS).
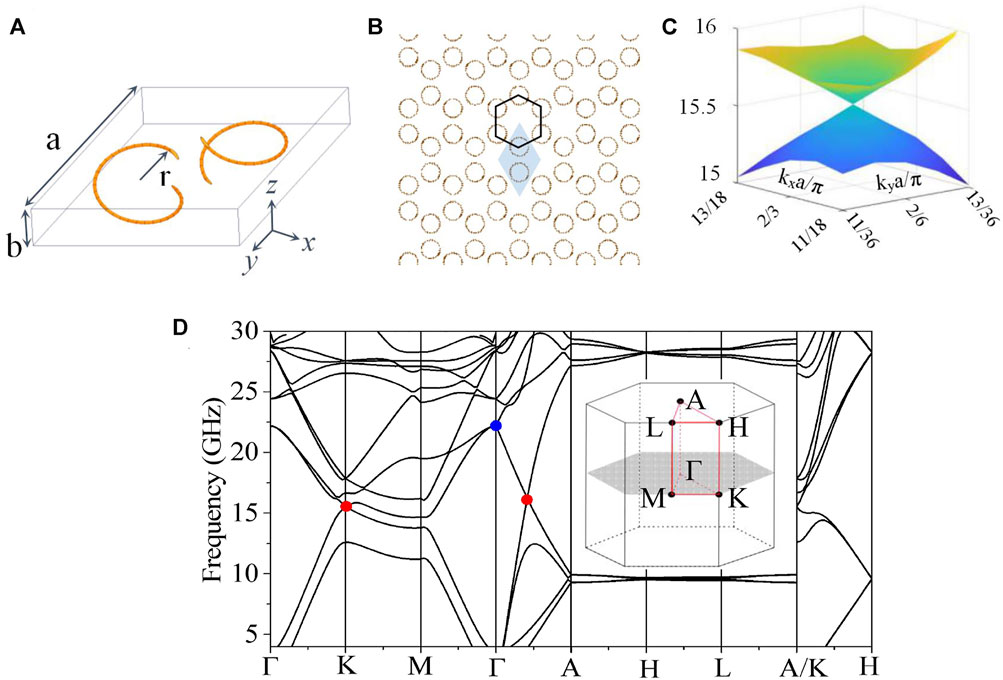
FIGURE 1. (A) Schematic diagram of the proposed unit cell of the topological material. The geometric parameters are shown as: lattice constant a = 12 mm, helix radius r = 2.5 mm, wire diameter w = 0.2 mm, lattice constant along the z axis h = 3 mm. The center distance between the two helixes b = 6tan(π/6). (B) Top view of a topological material arranged in a hexagonal lattice, and a blue shadow represents a unit cell. (C) Three-dimensional band structure in kzh = 0 plane for K point. (D) Band structure of the present topological material in the first Brillouin zone (inset). The red points represent Weyl points with the charge of +1, and the blue point represents Weyl point with the charge of −2.
It is well known that the dispersion of highly symmetric points in a honeycomb lattice can be represented by effective Hamiltonians. Combined Figures 1C,D, it can be seen that there is a Weyl point with frequency of 15.5 GHz at K point, the topological charge of Weyl point is +1. In addition, a Weyl point with topological charge +1 appears on the Γ-A line and a double Weyl point with topological charge -2 appears at the Brillouin zone center Γ. The double Weyl point in the Brillouin zone center Γ forms two Weyl point pairs with the other two Weyl points. The topological charge of a Weyl point can be calculated either by integrating Berry curvature on a closed surface enclosing the Weyl point (María Blanco de Paz et al., 2020). Weyl points can only move but never disappear under the perturbation of translational symmetry.
By selecting the reasonable value of kz, a topological nontrivial bandgap can be observed. Figures 2A–I show the band structure of the topological material in the planes of kzh = π/9, π/6, π/4, π/3, 7π/18, π/2, 2π/3, 5π/6, and 35π/36, respectively. Another band structure can also be achieved by converting kzh to -kzh (not shown in Figure 2). It is demonstrated that a topological nontrivial bandgap occurs as |kzh| > π/9. With the increasing of |kzh| from π/9 to π/4, the bandwidth of the gap increases. A widest bandgap from 15.55 to 16.45 GHz can be observed as |kzh| = π/4. However, as |kzh| > π/4, the bandwidth gradually decreases until it disappears.
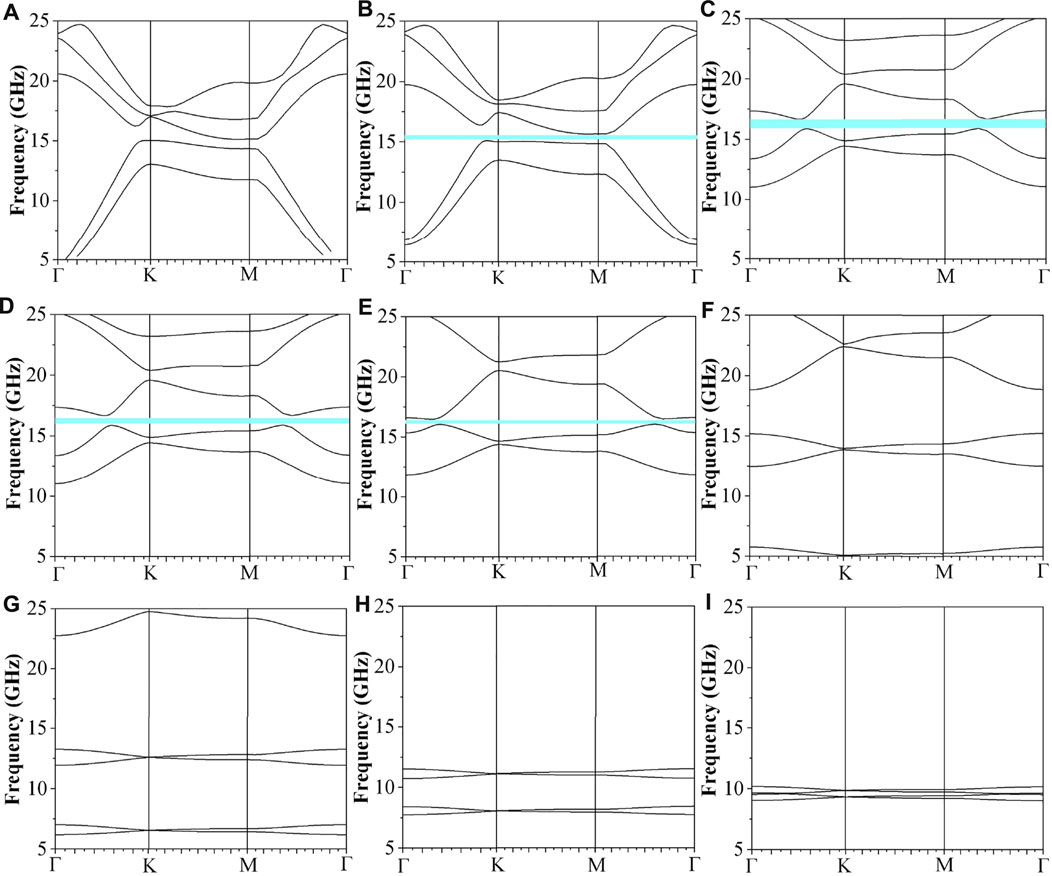
FIGURE 2. Band structures of the proposed topological material for various kzh. (A) kzh = π/9, (B) kzh = π/6, (C) kzh = π/4, (D) kzh = π/3, (E) kzh = 7π/18, (F) kzh = π/2, (G) kzh = 2π/3, (H) kzh = 5π/6, and (I) kzh = 35π/36. The cyan shaded area represents the nontrivial bandgap.
The Chern number of the band gap is equal to the sum of the Chern number of all the bands. For isolated bands, the Chern number is given by
Where
Robust Surface State of the Topological Material
In order to demonstrate topologically protected surface state in the proposed topological material, we arrange 16 unit cells along y-direction, as shown in Figure 3A. In the simulation, the y direction is set as the perfect electric conductor (PEC), and the other directions are set as periodic boundary conditions. Figure 3B shows the surface state dispersion of the topological material in the planes of kzh = π/4 and kzh = -π/4, of which red and blue line represent the surface states, and the black point represents bulk mode. It can be seen that the topological nontrivial bandgap appears around 16 GHz.
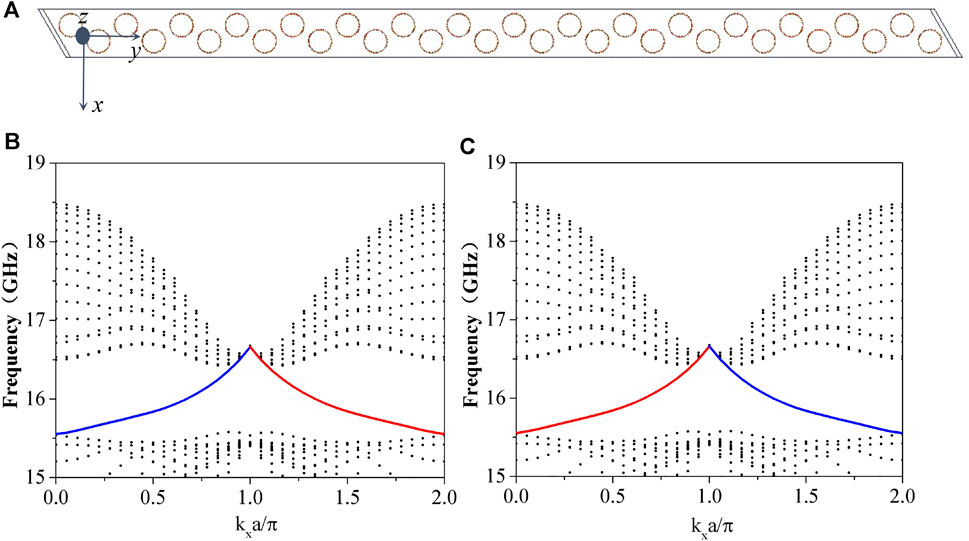
FIGURE 3. (A) Schematic diagram of the proposed topological material containing 16 unit cells. Surface state dispersion of the topological material in the planes of (B) kzh = π/4 and (C) kzh = −π/4, respectively. The black points represent bulk mode and the red (blue) solid line represent the surface states.
We further investigate the electric field distributions of the present topological material to demonstrate the surface state. Figures 4A,C are the electric field distributions of the surface state in the kzh = π/4 plane corresponding to the blue line mode and red line mode presented in Figure 3B, respectively. It can be seen that the electromagnetic waves are confined at the left edge and the right edge for the blue line mode and red line mode, respectively. Moreover, the electric field distributions show that energy flux direction of the surface state in the kzh = π/4 plane is counterclockwise. Figures 4B,D are the electric field distributions of the surface state in the kzh = −π/4 plane corresponding to the blue line and red line pattern presented in Figure 3C, respectively. Compared with the surface state in the kzh = π/4 plane, that energy flux direction of the surface state in the kzh = −π/4 plane is clockwise. In theory, the topologically protected surface state transmission is robust and without backscattering. To demonstrate this, we arrange the present topological materials in a stepped shape, as shown in Figure 4E. The step width, height, and length are 36 mm,
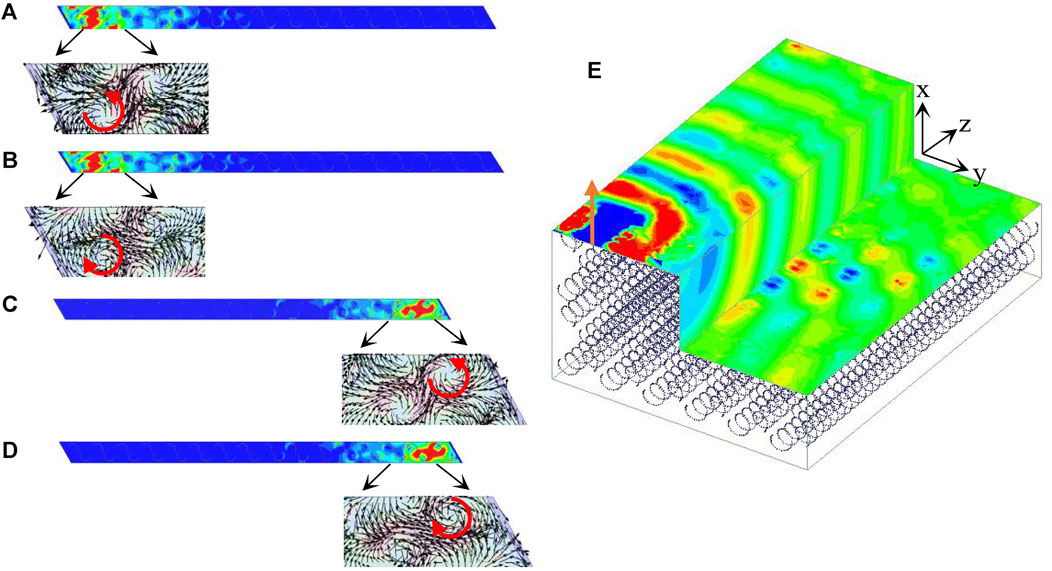
FIGURE 4. Simulated electric field distributions (Ez) in the planes of (A, C) kzh = π/4 corresponding to the blue line mode and red line mode presented in Figure 3B, respectively. Simulated electric field distributions (Ez) in the planes of (B, D) kzh = −π/4 corresponding to the blue line and red line pattern presented in Figure 3C, respectively. The arrows indicate the direction of the time-averaged energy flux. (E) x-component of electric field of surface waves at 15.85 GHz. The orange arrow represents the dipole source.
Conclusion
In conclusion, a Weyl topological material composed of the double left-handed helix is designed. We demonstrate the existences of Weyl points and robust surface states in the present material. It is shown that the double left-handed helix structure has a topological nontrivial bandgap at the frequency of 15.55–16.45 GHz, where the topologically protected surface state is observed. It can be expected that this surface state of backscattering suppression has potential applications in one-way waveguide and photonic integrated circuits.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.
Author Contributions
YL conceived the idea and supervised the project. LD, ML, and XZ performed the numerical simulations. KS, RJ, and XZ did the theoretical analysis. All authors contributed to the discussion. ML and YL co-wrote the article.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 11874301, 61805204, and 61601375), and the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No. 2020JM-094).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Asadchy, V. S., Guo, C., Zhao, B., and Fan, S. (2020). Sub‐Wavelength Passive Optical Isolators Using Photonic Structures Based on Weyl Semimetals. Adv. Opt. Mater. 8, 2000100. doi:10.1002/adom.202000100
Bernevig, B. A., Hughes, T. L., and Zhang, S.-C. (2006). Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 314, 1757–1761. doi:10.1126/science.1133734
Blanco de Paz, M., Devescovi, C., Giedke, G., Saenz, J. J., Vergniory, M. G., Bradlyn, B., et al. (2020). Tutorial: Computing Topological Invariants in 2D Photonic Crystals. Adv. Quan. Tech. 3, 1900117. doi:10.1002/qute.201900117
Chaunsali, R., Chen, C.-W., and Yang, J. (2018). Subwavelength and Directional Control of Flexural Waves in Zone-Folding Induced Topological Plates. Phys. Rev. B 97, 054307. doi:10.1103/PhysRevB.97.054307
Chen, W.-J., Xiao, M., and Chan, C. T. (2016). Photonic Crystals Possessing Multiple Weyl Points and the Experimental Observation of Robust Surface States. Nat. Commun. 7, 13038. doi:10.1038/ncomms13038
Cheng, X., Jouvaud, C., Ni, X., Mousavi, S. H., Genack, A. Z., and Khanikaev, A. B. (2016). Robust Reconfigurable Electromagnetic Pathways within a Photonic Topological Insulator. Nat. Mater 15, 542–548. doi:10.1038/nmat4573
Christiansen, R. E., Wang, F., Sigmund, O., and Stobbe, S. (2019). Designing Photonic Topological Insulators with Quantum-Spin-Hall Edge States Using Topology Optimization. Nanophotonics 8, 1363–1369. doi:10.1515/nanoph-2019-0057
Fang, K., and Wang, Y. (2019). Anomalous Quantum Hall Effect of Light in Bloch-Wave Modulated Photonic Crystals. Phys. Rev. Lett. 122, 233904. doi:10.1103/PhysRevLett.122.233904
Gao, W., Yang, B., Lawrence, M., Fang, F., Béri, B., and Zhang, S. (2016). Photonic Weyl Degeneracies in Magnetized Plasma. Nat. Commun. 7, 12435. doi:10.1038/ncomms12435
Han, Y., Fei, H., Lin, H., Zhang, Y., Zhang, M., and Yang, Y. (2021). Design of Broadband All-Dielectric Valley Photonic Crystals at Telecommunication Wavelength. Opt. Commun. 488, 126847. doi:10.1016/j.optcom.2021.126847
Hsieh, D., Qian, D., Wray, L., Xia, Y., Hor, Y. S., Cava, R. J., et al. (2008). A Topological Dirac Insulator in a Quantum Spin Hall Phase. Nature 452, 970–974. doi:10.1038/nature06843
Jo, M., Brasseur, P., Assouline, A., Fleury, G., Sim, H.-S., Watanabe, K., et al. (2021). Quantum Hall Valley Splitters and a Tunable Mach-Zehnder Interferometer in Graphene. Phys. Rev. Lett. 126, 146803. doi:10.1103/PhysRevLett.126.146803
Kim, M., Gao, W., Lee, D., Ha, T., Kim, T. T., Zhang, S., et al. (2019a). Extremely Broadband Topological Surface States in a Photonic Topological Metamaterial. Adv. Opt. Mater. 7, 1900900. doi:10.1002/adom.201900900
Kim, M., Lee, D., Lee, D., and Rho, J. (2019b). Topologically Nontrivial Photonic Nodal Surface in a Photonic Metamaterial. Phys. Rev. B 99, 235423. doi:10.1103/PhysRevB.99.235423
Klitzing, K. V., Dorda, G., and Pepper, M. (1980). New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 45, 494–497. doi:10.1103/physrevlett.45.494
König, M., Wiedmann, S., Brüne, C., Roth, A., Buhmann, H., Molenkamp, L. W., et al. (2007). Quantum Spin Hall Insulator State in HgTe Quantum Wells. Science 318, 766–770. doi:10.1126/science.1148047
Liu, Y., Guo, Q., Liu, H., Liu, C., Song, K., Yang, B., et al. (2018). Circular-Polarization-Selective Transmission Induced by Spin-Orbit Coupling in a Helical Tape Waveguide. Phys. Rev. Appl. 9, 054033. doi:10.1103/PhysRevApplied.9.054033
Lu, L., Wang, Z., Ye, D., Ran, L., Fu, L., Joannopoulos, J. D., et al. (2015). Experimental Observation of Weyl Points. Science 349, 622–624. doi:10.1126/science.aaa9273
Ma, S., Bi, Y., Guo, Q., Yang, B., You, O., Feng, J., et al. (2021). Linked Weyl Surfaces and Weyl Arcs in Photonic Metamaterials. Science 373, 572–576. doi:10.1126/science.abi7803
Mittal, S., Orre, V. V., Leykam, D., Chong, Y. D., and Hafezi, M. (2019). Photonic Anomalous Quantum Hall Effect. Phys. Rev. Lett. 123, 043201. doi:10.1103/PhysRevLett.123.043201
Raghu, S., and Haldane, F. D. M. (2008). Analogs of Quantum-Hall-Effect Edge States in Photonic Crystals. Phys. Rev. A. 78, 033834. doi:10.1103/PhysRevA.78.033834
Slobozhanyuk, A., Shchelokova, A. V., Ni, X., Hossein Mousavi, S., Smirnova, D. A., Belov, P. A., et al. (2019). Near-field Imaging of Spin-Locked Edge States in All-Dielectric Topological Metasurfaces. Appl. Phys. Lett. 114, 031103. doi:10.1063/1.5055601
Sun, X.-C., He, C., Liu, X.-P., Zou, Y., Lu, M.-H., Hu, X., et al. (2019). Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal. Crystals 9, 137. doi:10.3390/cryst9030137
Wang, D., Yang, B., Gao, W., Jia, H., Yang, Q., Chen, X., et al. (2019). Photonic Weyl Points Due to Broken Time-Reversal Symmetry in Magnetized Semiconductor. Nat. Phys. 15, 1150–1155. doi:10.1038/s41567-019-0612-7
Wang, Z., Chong, Y. D., Joannopoulos, J. D., and Soljačić, M. (2008). Reflection-Free One-Way Edge Modes in a Gyromagnetic Photonic Crystal. Phys. Rev. Lett. 100 (1), 013905. doi:10.1103/PhysRevLett.100.013905
Wang, Z., Chong, Y., Joannopoulos, J. D., and Soljačić, M. (2009). Observation of Unidirectional Backscattering-Immune Topological Electromagnetic States. Nature 461, 772–775. doi:10.1038/nature08293
Wu, Y., Chaunsali, R., Yasuda, H., Yu, K., and Yang, J. (2018). Dial-in Topological Metamaterials Based on Bistable Stewart Platform. Sci. Rep. 8, 112. doi:10.1038/s41598-017-18410-x
Xia, Y., Qian, D., Hsieh, D., Wray, L., Pal, A., Lin, H., et al. (2009). Observation of a Large-gap Topological-Insulator Class with a Single Dirac Cone on the Surface. Nat. Phys 5, 398–402. doi:10.1038/nphys1274
Yang, B., Guo, Q., Tremain, B., Barr, L. E., Gao, W., Liu, H., et al. (2017). Direct Observation of Topological Surface-State Arcs in Photonic Metamaterials. Nat. Commun. 8, 97. doi:10.1038/s41467-017-00134-1
Yang, B., Guo, Q., Tremain, B., Liu, R., Barr, L. E., Yan, Q., et al. (2018). Ideal Weyl Points and Helicoid Surface States in Artificial Photonic Crystal Structures. Science 359, 1013–1016. doi:10.1126/science.aaq1221
Yang, Y., Gao, Z., Feng, X., Huang, Y.-X., Zhou, P., Yang, S. A., et al. (2020). Ideal Unconventional Weyl Point in a Chiral Photonic Metamaterial. Phys. Rev. Lett. 125, 143001. doi:10.1103/PhysRevLett.125.143001
Yang, Y., Xia, J.-p., Sun, H.-x., Ge, Y., Jia, D., Yuan, S.-q., et al. (2019). Observation of a Topological Nodal Surface and its Surface-State Arcs in an Artificial Acoustic Crystal. Nat. Commun. 10, 5185. doi:10.1038/s41467-019-13258-3
Ye, W., Liu, Y., Liu, J., Horsley, S. A. R., Wen, S., and Zhang, S. (2019). Photonic Hall Effect and Helical Zitterbewegung in a Synthetic Weyl System. Light Sci. Appl. 8 (1), 49. doi:10.1038/s41377-019-0160-z
Yves, S., Fleury, R., Berthelot, T., Fink, M., Lemoult, F., and Lerosey, G. (2017). Crystalline Metamaterials for Topological Properties at Subwavelength Scales. Nat. Commun. 8, 16023. doi:10.1038/ncomms16023
Zhang, H., Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z., and Zhang, S.-C. (2009). Topological Insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a Single Dirac Cone on the Surface. Nat. Phys 5, 438–442. doi:10.1038/nphys1270
Keywords: topological material, Weyl point, surface state, band structure, nontrivial
Citation: Li M, Liu Y, Du L, Zhou X, Song K, Ji R and Zhao X (2022) Weyl Point and Nontrivial Surface States in a Helical Topological Material. Front. Mater. 8:805862. doi: 10.3389/fmats.2021.805862
Received: 31 October 2021; Accepted: 13 December 2021;
Published: 06 January 2022.
Edited by:
Yu Luo, Nanyang Technological University, SingaporeCopyright © 2022 Li, Liu, Du, Zhou, Song, Ji and Zhao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yahong Liu, eWhsaXVAbndwdS5lZHUuY24=; Xin Zhou, enhicmVlemVAMTYzLmNvbQ==
 Meize Li1
Meize Li1 Yahong Liu
Yahong Liu Kun Song
Kun Song