
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 24 December 2021
Sec. Metamaterials
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.802268
This article is part of the Research Topic Electromagnetic Metamaterials and Metasurfaces View all 7 articles
Inspired by the concept of miniaturized and integrated systems, an ultrathin and multifunctional metasurface device is highly desirable in microwave fields. It is an inherent characteristic that the two spin phase states of electromagnetic waves imparted by the geometric phase are always conjugate symmetric, i.e., the geometric phase produces anti-symmetrical phase responses between dual-orthogonal circular polarization states. So it is extremely crucial to break the conjugate constraints and realize the completely independent control of electromagnetic waves with dual-orthogonal circular polarization. Based on this perspective, ultrathin and bifunctional meta-devices operating in reflection mode are proposed to independently manipulate the left-handed and right-handed circularly polarized waves, which are constructed by anisotropic meta-atoms with synthetical geometric and propagation phases. It is worth noting that the component elements only need a single-layer structure with the thickness of 0.07λ0. Several design samples are presented to achieve functionalities of beam focusing, vortex wave generation, and beam deflection, respectively. Experiments are performed and show good consistence with the simulation results, successfully verifying the performance of the designed metasurfaces. The research results in this paper pave the way to design low-profile and bifunctional devices with independent controls of circularly polarized waves, which is expected to expand the working capacity of metasurfaces to realize complex electromagnetic wave manipulation with a new degree of freedom.
Metasurfaces, as a two-dimensional quasi-planar structure of metamaterials, have attracted extensive attention of researchers due to their novel electromagnetic (EM) response properties that are far superior to natural materials (Yu et al., 2011; Chen et al., 2016; Cui et al., 2017; Zhang et al., 2017; Chen et al., 2019; Sun et al., 2019). The existence of metasurfaces provides a new and unprecedented style to freely and flexibly manipulate the amplitude, phase, and polarization of EM waves (Hao et al., 2007; Liu et al., 2014; Lei and Yang, 2017; Li et al., 2018). In recent years, they have become an important application prospect in many fields, such as microwave (Wang et al., 2019; Mao et al., 2020; Xu et al., 2020), terahertz (Yu and Li, 2016; Qi et al., 2020; Liu et al., 2021) and optoelectronic (Kildishev et al., 2013; Chorsi and Gedney, 2016; Fan et al., 2017; Han et al., 2020) devices, and stealth (Zhong et al., 2017; Joy et al., 2021) and antenna (Pan et al., 2016; Moreno et al., 2018) technology. Specifically, various metasurfaces have been proposed to implement fantastic phenomena and applications in microwave regions, including anomalous reflection/refraction (Xu et al., 2016; Bao et al., 2019), beam focusing (Zhang et al., 2019; Yuan et al., 2020a), hologram imaging (Xie et al., 2019), vortex beams (Yang et al., 2019; Chen et al., 2021), and polarization conversion and absorbing devices (Xu et al., 2018b; Wang et al., 2020).
Generally speaking, a metasurface consists of numerous well-designed meta-atoms by regularly arranging an array. For a reflective metasurface, the meta-atoms mainly contain three parts, metallic resonator, dielectric spacer, and metal ground plate, and the working performance of the metasurface primarily depends on the structure of the metallic resonator. Once the meta-atom with producing predesigned functionality and EM phenomenon is customized, there are two generic manners to adjust its phase responses under different incident waves, that is, propagation phase and geometric phase (Mueller et al., 2017). The propagation phase can be regulated by changing the dimensions of the element and is usually used to achieve different functionalities under two orthogonal linearly polarized wave incidences (Yu and Li, 2016; Cai et al., 2017; Mueller et al., 2017). Moreover, the propagation phase is insensitive to orthogonal circularly polarized (CP) incident waves, due to that two orthogonal CP waves can be separately decomposed into the superposition of two orthogonal linearly polarized waves with equal magnitude but a + π/2 or − π/2 phase difference, and thus the propagation phase generates duplicate amplitude and phase responses for left-handed circularly polarized (LHCP) and right-handed circularly polarized (RHCP) incident waves (Ding et al., 2019; Yuan et al., 2020a; Zhang et al., 2021). The latter geometric phase, also referred to as Pancharatnam–Berry (PB) phase, is excited by rotating meta-atoms that make up the metasurface array and can produce the phase shift of twice the rotated angle under a CP incident wave (Bouchard et al., 2014; Xu et al., 2017; Yang et al., 2019; Chen et al., 2021; Gou et al., 2021). The geometric metasurface operating in a reflection manner can generate a desired functionality for output waves with opposite helicity to the incident waves. Therefore, the PB phase shows anti-symmetrical phase responses with equal values and opposite signs under the LHCP and RHCP waves illuminating the metasurface, which is the conjugate symmetry property of the PB phase theory and limits the manipulation for two orthogonal CP incident waves. In order to break the constraint of the geometric phase, the propagation phase is introduced to decouple the conjugate responses under orthogonal CP wave illumination (Mueller et al., 2017; Ding et al., 2019; Yin et al., 2019; Zhang et al., 2019; Yuan et al., 2020a; Yuan et al., 2020b; He et al., 2021; Wang et al., 2021).
To date, some element structures have been proposed and applied to form the metasurface arrays with the phase profiles combining propagation and geometric phases, to implement the completely independent control of two orthogonal CP waves in microwave, terahertz, and optical regions (Devlin et al., 2017; Xu et al., 2018a; Yin et al., 2019; Guo et al., 2020; Wang et al., 2021; Zheng et al., 2021). In the microwave field, the independent wavefront controls under CP waves illumination were demonstrated by utilizing the dual-layered anisotropic meta-atoms with low linearly polarized cross talk and imposing both the geometric and propagation phases of metasurfaces (Xu et al., 2018a; Ding et al., 2019). Additionally, a multilayer element structure with various geometric degrees of freedom was designed to realize simultaneous and independent phase modulation of both orthogonal CP-transmitted waves with a specific CP wave illumination (Zhang et al., 2019; Yuan et al., 2020a; Yuan et al., 2020b). Nevertheless, the multilayer structures may ensure the efficiency of the metasurface and the required helicity-decoupled phase but at the same increase the profile thickness and manufacturing complexity. Guo et al. theoretically and experimentally illustrated a broadband single-layered spin-decoupled metasurface based on quasi-I-shaped meta-atom and applied it to a dual-CP reflector antenna (Guo et al., 2020). Moreover, single-layer reflective metasurfaces composed of anisotropic meta-atoms with a thickness of 3 mm were proposed and performed functions including polarization beam splitting and orbital angular momentum (OAM) multiplexing at 5.8 GHz (He et al., 2021). Therefore, with the rapid development of modern miniaturized and integrated systems, it is of great importance to explore ultrathin and multifunctional devices that are programmed by introducing polarization-decoupled phases and could independently control orthogonal CP waves.
In this paper, single-layer ultrathin reflective metasurfaces are proposed to demonstrate multiple functionalities via the polarization-decoupled phase for dual orthogonal CP incident waves. They consist of anisotropic meta-atoms, which can realize well the independent control of orthogonal linearly polarized EM waves by using the propagation phase. The reflection matrix of a metasurface under the illumination of orthogonal CP waves is analyzed, and then the polarization-decoupling phase can be obtained by adjusting the geometric dimensions and rotating meta-atoms at specific angles, imposing the propagation phase and geometric phase simultaneously. On the basis of this concept, the designed metasurfaces can impose distinct phase profiles and respond differently to dual orthogonal CP waves, implementing independent manipulation for incident EM waves with left circular polarization (LCP) and right circular polarization (RCP) states. For proof of concept, we design three kinds of bifunctional metasurfaces operating in a reflection manner for three representative applications in the microwave domain. To be more specific, one of them achieves beam focusing with distinct focal lengths under the illumination of two orthogonal CP waves. Another one acts as an OAM multiplexor, which generates vortex waves with different topological charges when LHCP and RHCP waves separately illuminate the metasurface. Moreover, the third one is a beam deflector that can deflect two orthogonal CP incident waves by different reflection angles according to the generalized Snell’s reflection laws. The verification experiments are performed, and the results coincide well with the simulated ones.
The EM waves with orthogonal circular polarization states can be represented as the superposition of EM waves with two orthogonal linear polarization bases and expressed as follows:
where “ + ” and “ − ” represent a pair of orthogonal circular polarization states, namely, LCP and RCP waves in this paper, and the subscripts “x” and “y” are the coordinate components at the Cartesian coordinate system. When the EM waves are incident on the designed meta-atom structure, the reflected output wave polarization states are complex conjugates with respect to each input polarization state {|λ+⟩, |λ−⟩}; mathematically,
The above two expressions can be deduced and recast to obtain the Jones matrix, as follows:
Further, for two orthogonal CP incident waves, the Jones matrix of the element at coordinate (x, y) can be obtained by substituting Eq. 1; Eq. 2; Eq. 3:
In particular, the Jones matrix is unitary and symmetric, so it can be recast as its canonical form:
Then, the unknown quantities in Eq. 5 can be obtained through simple mathematical derivation with combining Eq. 4, as follows (Mueller et al., 2017; Xu et al., 2018a; Yuan et al., 2020b):
where the Jones matrix is framed based on the linear polarization coordinate base, and A is a diagonal matrix, whose elements are the eigenvalues of J, and Q is an orthogonal matrix, whose columns are the eigenvectors of J. The eigenvalues in matrix A impose the phase shifts φx and φy along the x- and y-polarized directions, while the eigenvectors impose the angular orientation θ of the meta-atoms relative to the reference coordinate system. Specially, the phase shifts φx and φy can be introduced using the propagation phase and attained by varying the dimensions of the anisotropic element along the x- and y-directions, and the angular orientation θ can be introduced using the geometric phase and attained by rotating the meta-atom in an anticlockwise direction. The above derived result can be understood as an integration of the propagation phase and geometric phase in a single meta-atom.
In general, on the basis of Eq. 6 and assigned spatial phase distributions ϕ+(x, y) and ϕ−(x, y) for the specific functionalities under LHCP and RHCP incident waves, the φx, φy, and θ of a meta-atom located at a concrete coordinate (x, y) can be calculated. Then, the metasurface array can be established using the eligible meta-atoms and applied to implement the independent manipulation for dual orthogonal CP incident waves.
Based on the above theoretical analysis, the anisotropic meta-atom plays an important role in designing the desired metasurfaces. Herein, an anisotropic element operating at 14 GHz is utilized, which consists of a top cross-shaped resonator, an intermediate dielectric substrate, and a bottom metal ground plate, as shown in Figure 1A. The middle spacer selects F4B as the dielectric material with a relative permittivity of 2.65 and a loss tangent of 0.001. The thickness of the F4B substrate is 1.5 mm, which is equivalent to 0.07λ0 (λ0 is the free space working wavelength at 14 GHz), and the thickness of the metal layers is 0.018 mm. The symmetric structure of the cross-shaped resonator imparts the anisotropic resonances along x- and y-directions for the meta-atom, guaranteeing the cross-coupling response between x- and y-polarized EM waves can be effectively eliminated. Therefore, the element has a specialty that its propagation phase under the illumination of orthogonal linearly polarized EM waves can be independently manipulated by varying its physical dimensions. As is shown in Figures 1B,D, the relationships of reflection phase and amplitude over frequency under the illumination of x-polarized EM waves are drawn for the unit cells applied in this work, from which we can obtain that the nearly linear reflection phase gradient within 360° and reflection amplitude higher than 0.98 are realized at 14 GHz. Moreover, the reflection phase differences (△φ = |φxx − φyy|) between two EM waves with orthogonal linear polarization states at 14 GHz are exhibited in Figure 1C for all unit cells, which are approximately equal to 180°. This approximate constant ensures that the reflection coefficients under the incidence of x- and y-polarized waves satisfy the relation of rxx = − ryy. Then, the desired bifunctional metasurfaces can be designed by employing the nine proposed representative unit cells with the combination of propagation and geometric phases. The desired phase profiles for bifunctional metasurfaces under incidences of two orthogonal CP waves and their layouts are displayed in Figure 2, where the two columns on the left separately depict the phase profiles under incidences of waves with LCP and RCP states, and the one column on the right draws the layouts of the three bifunctional metasurfaces for separately realizing the functions of 1) beam focusing, 2) vortex beam generation, and 3) beam deflection. It should be particularly noted that the designed metasurfaces are one single layer and the thickness is only 0.07λ0, which has an obvious advantage in realizing ultrathin design, compared with the other metasurfaces of the published literatures (Xu et al., 2018a; Meng et al., 2018; Ding et al., 2019; Guo et al., 2020; Zhang et al., 2021). Furthermore, a comparison between the proposed meta-atom and other reported reflection unit cells for realizing dual-polarization control in the microwave region is made and presented in Table 1.
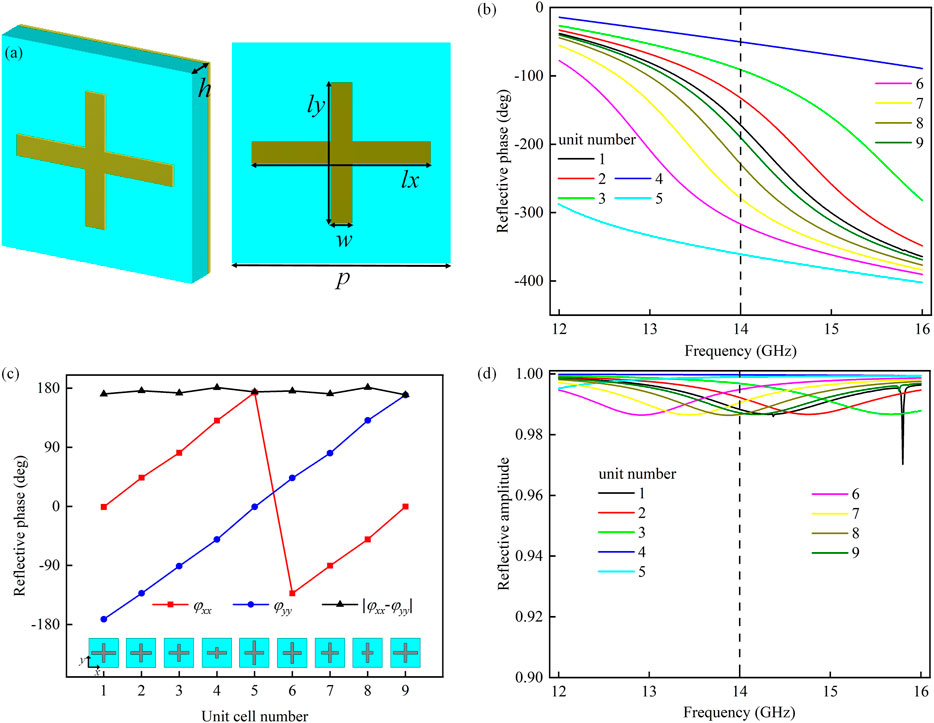
FIGURE 1. (A) Schematic of the proposed unit cell. The period p of the element is 10 mm, the thickness h of the dielectric substrate is 1.5 mm, the width w of the rectangular patch is 1 mm, and its lengths along the x and y directions are lx and ly, respectively. For the unit cells used in this work, their reflection phase and amplitude versus frequency under the illumination of x-polarized EM waves are plotted in (B,D). The extract reflection phases under the incidence of x- and y-polarized EM waves at 14 GHz are plotted in (C), where the black curve displays the phase difference between the two orthogonal linear polarized waves △φ = |φxx − φyy|.
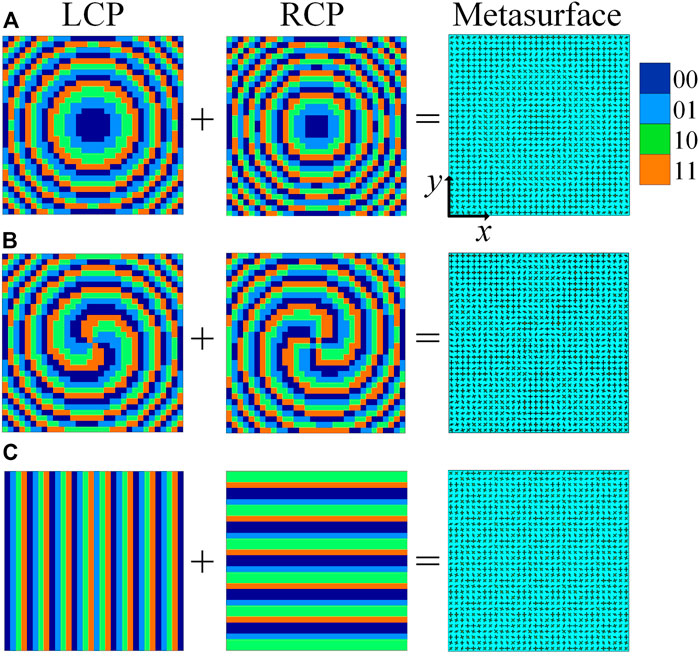
FIGURE 2. The desired phase profiles under incidences of two orthogonal CP waves in two columns on the left, and layouts of the designed metasurfaces in one column on the right, for (A) beam focusing, (B) vortex beam generation, and (C) beam deflection, where the phase is discretized into four levels, that is, 0°, 90°, 180°, and 270°.
In order to realize dual functionalities of generating focal beams with different focal lengths using a single metasurface, the spatial phase profiles can be obtained as follows:
where λ0 is the operating wavelength in free space at 14 GHz, fi (i = 1, 2) is the desired focal length, and (x, y) are the position coordinates for each meta-atom. In this work, a beam focusing reflective metasurface with different focal lengths under orthogonal CP waves incidence is proposed, which can efficiently focus the reflected wave with a focal length of f1 = 160 mm under LHCP wave incidence and with a focal length of f2 = 100 mm under RHCP wave incidence. According to Eqs 7a,b, different spatial phase profiles for orthogonal circular polarization can be calculated as shown in Figure 2A, in which the calculated continuous phase distributions are discretized into four levels without impairing the working efficiency of the metasurface, in order to simplify the design of the metasurface. Then, the specific phase shifts δx and δy along the x and y directions and angular orientation θ at each point for each element can be derived by substituting Eqs 7a,b with different fi into Eqs 6a,b,c. Furthermore, the metasurface operating at 14 GHz can be constructed using the nine representative elements, and it consists of 32 × 32 anisotropic subwavelength meta-atoms, occupying a total size of 320 mm × 320 mm. The focusing behavior of the metasurface can separately be characterized under LHCP and RHCP wave illumination through the commercial software CST Microwave Studio 2020, as depicted in Figure 3. The simulated normalized intensity distributions at the xoz planes under LHCP and RHCP wave incidence are presented in Figures 3A,C, respectively. It can be obviously seen that the focal spots separately locate at z = 160 mm and z = 100 mm for incident waves with LCP and RCP states. To further characterize the focusing performance, Figures 3B,D separately show the simulated and measured transverse normalized intensity distributions of the focal spots in the xoy planes at z = 160 mm under the LHCP wave incidence and z = 100 mm under the RHCP wave incidence, where the insets demonstrate the simulated and measured normalized focus intensity distributions in the corresponding xoy planes. By comparing the cross section and transverse normalized intensity profiles of the focus spots, the intensity distributions of simulation and measurement are observed to be in good agreement with each other. The full width at half maxima (FWHMs) of normalized intensity profiles of the focal spots are about 0.84λ0 under the LHCP incident wave and about 0.75λ0 under the RHCP incident wave from both simulation and measurement, indicating that a high-quality focus spot can indeed be produced. Here, the beam focusing metasurface is fabricated, and the near-field mapping measurement is performed in the microwave anechoic chamber (the detailed measurement process is illustrated in Experimental Section). As expected, the measured intensity distributions for reflected waves at the focal planes separately achieve a good focus under dual orthogonal CP incident waves, verifying the reliability of the designed metasurface.
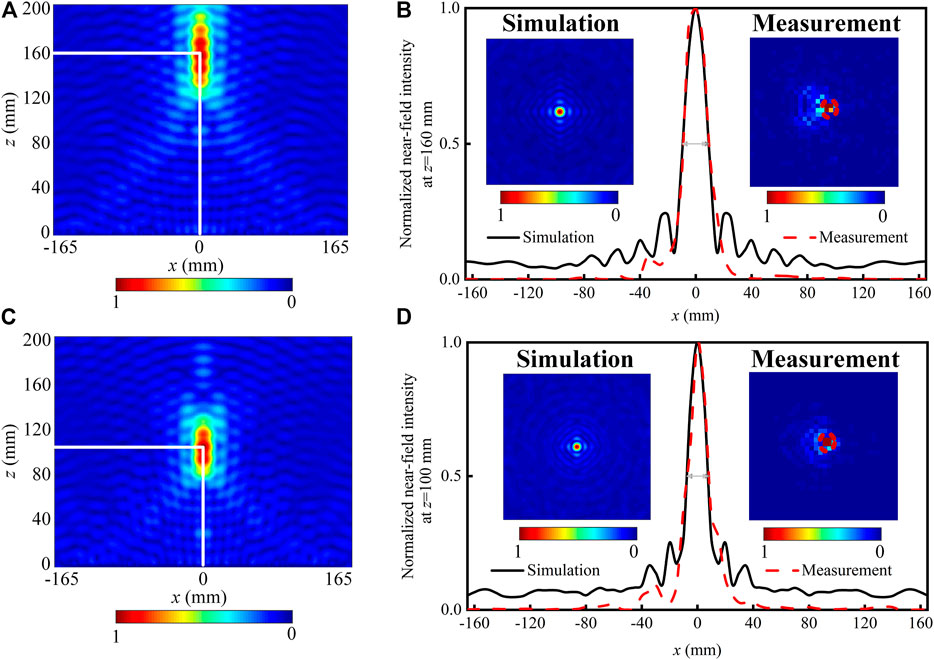
FIGURE 3. The numerically simulated normalized intensity distributions for beam focusing metasurface with dual focal lengths in xoz planes under (A) LHCP and (C) RHCP incident waves at 14 GHz, respectively. Simulated and measured transverse normalized intensity distributions of the focal spots in the xoy planes at (B) z = 160 mm under the LHCP wave incidence and (D) z = 100 mm under the RHCP wave incidence, and the insets show the simulated and measured normalized focus intensity distributions in the corresponding xoy planes.
In another aspect, an OAM-multiplexed metasurface for generating converged vortex waves with dual modes is designed. Two independent OAM modes can be generated and switched by reversing the helicity of the incident CP waves, i.e., a metasurface producing converged vortex beams with OAM modes of l1 = − 2 under the LHCP wave incidence and l2 = 3 under the RHCP wave incidence is constructed. The theoretical phase compensations of each element under the illumination of two orthogonal CP waves should satisfy the following equations:
where the focal length f1 is set to 160 mm. The calculated phase profiles under LCP and RCP incident waves and the metasurface layout are shown in Figure 2B, where the four phase states still are available and the continuous phase profiles are discretized into 2-bit levels. Then, by calculating the rotation angles and phase delays for orthogonal linear polarization states, the metasurface with dual OAM mode functionality can be constructed. With the LHCP wave illuminating the metasurface, the left-handed component of the reflected wave electric field is obtained at the sampling plane distanced 160 mm from the metasurface, as shown in Figures 4A,B. As expected, a donut-like intensity distribution and a helical phase pattern corresponding to the theoretical phase change of l1*2π and with the phase singularity at the center are observed. Likewise, similar results are obtained under the RHCP wave incidence, where the right-handed component of the reflected wave electric field exhibits the characteristic of a vortex wave with the OAM mode of l2 = 3, as depicted in Figures 4D,E. Herein, Fourier transform analysis of the sampling electric field is introduced to decompose the individual modes and quantify the purity of the OAM modes generated by the metasurface (Yang et al., 2019; Chen et al., 2021). Moreover, the OAM modes l from −5 to 5 are considered to calculate the energy weight (EW) under different modes. The corresponding mode spectra are drawn in Figures 4C,F, from which we can get the conclusion that the OAM mode of −2 with a ratio of 0.74 is mainly produced under the incident wave with the LCP state, and the OAM mode of 3 with a percentage of 0.71 is mainly produced under the incident wave with the RCP state, and other modes account for less than 0.05 and can be negligible because of the 2-bit discrete phase levels in the metasurface design process. The Fourier analysis results further certify the rationality of the design method.
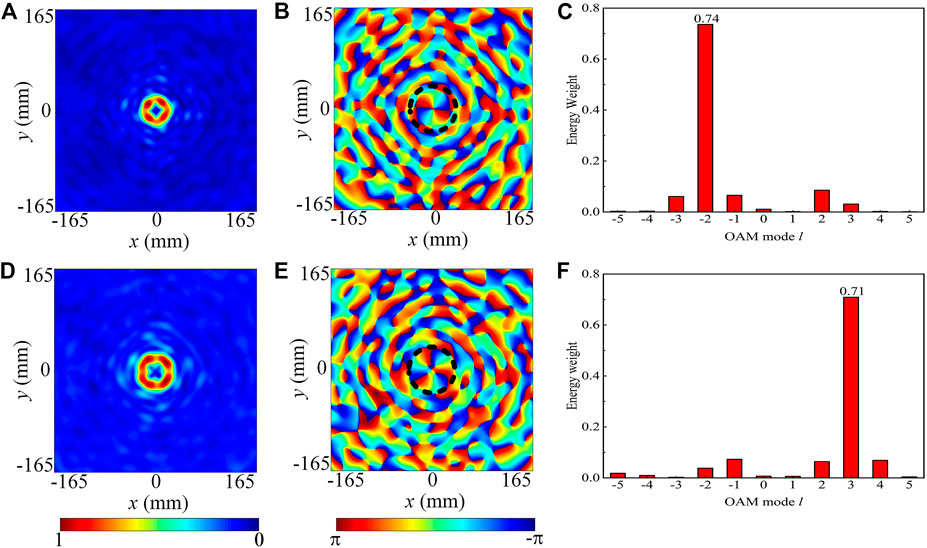
FIGURE 4. The numerically simulated results for the converging OAM-multiplexed metasurface at 14 GHz. The simulated normalized intensity and phase distributions in the xoy plane at z = 160 mm in (A,B) under LHCP wave incidence and in (D,E) under RHCP wave incidence, respectively. (C,F) depict the corresponding mode spectral analysis with the OAM modes of −2 under LHCP incident wave and 3 under RHCP incident wave, respectively.
For a better demonstration, the experimental measurements for the OAM multiplexed metasurface are performed, as shown in Figure 5 (as detailed in Experimental Section). The measured near-field intensity and phase results under LHCP and RHCP incident waves are separately shown in Figures 5A,B,D,E. In Figures 5A,B, a near-field intensity distribution with a nearly donut-shaped hollow profile and the spiral phase distribution clearly display the beams carrying OAM with the mode of −2 under the LHCP wave incidence. Similarly, the results depicted in Figures 5D,E indicate the generation of the converged vortex wave with the OAM mode of 3 under the RHCP wave illuminating the metasurface. Moreover, the measured 2D far-field scattering patterns at 14 GHz are separately displayed in Figures 5C,F for LHCP and RHCP incident waves with red dotted lines, and the corresponding simulated results are drawn with blue solid lines for comparison. It can be seen that the measurement results coincide well with the simulation results, and a clear drop occurs at the angle of 0° in keeping with the property of vortex beams. In Figure 5F, the simulated and measured results under RHCP wave incidence have a slight deviation at the peaks, which is attributed to two aspects: 1) inevitable fabrication errors and 2) an unavoidable slight offset between the aperture center of the transmitting antenna and the center of the metasurface, which leads to the slight difference between measured results and simulated results mainly caused by the slight off-axis deviation of the incident field and the quasi-planar wavefronts from the feeding horn antenna across the metasurface, compared to normally incident ideal-planar wavefronts considered in simulations. The simulated and measured results verify the effectiveness of generating dual-mode vortex waves by utilizing the proposed ultrathin reflective metasurface.
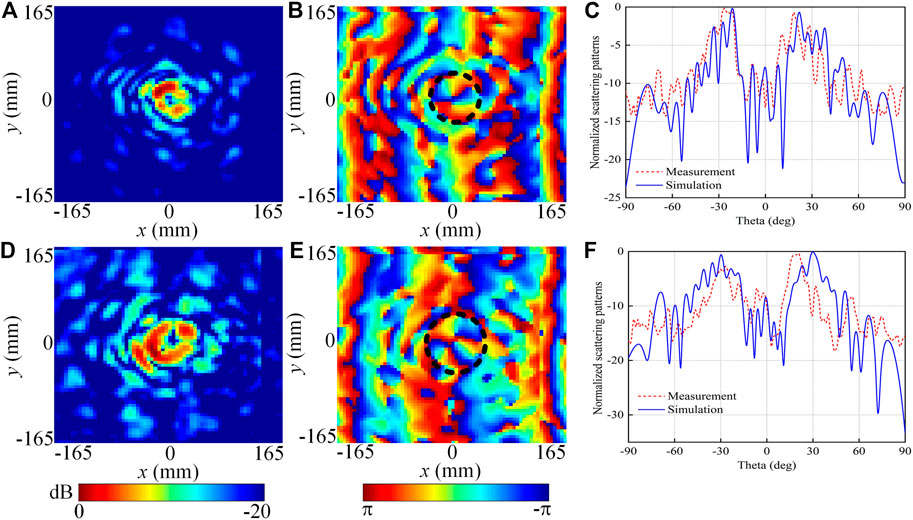
FIGURE 5. The experimentally measured results for the converging OAM-multiplexed metasurface at 14 GHz. The measured near-field distributions in the xoy plane at z = 160 mm in (A,B) under LHCP wave incidence and in (D,E) under RHCP wave incidence, respectively. (C,F) separately depict the comparisons of measured (dotted line) and simulated (solid line) far-field scattering patterns of the metasurface under LHCP wave incidence and under RHCP wave incidence.
Finally, the anomalous reflection behaviors of the designed metasurface between distinct functionalities depending on the polarization state of the incident wave are characterized and demonstrated based on this design scheme. The spatial phase profiles can be obtained by the following formula:
where α = 32.4° is the preset reflection angle along x direction and β = − 20.9° is the predesigned deflection angle along the y direction. We calculate the distinct spatial phase profiles for orthogonal circular polarization states, as depicted in Figure 2C. Then, the metasurface can be constructed with the identical method as described above. The full wave simulations are conducted to verify the performances of the designed metasurface. The simulated near-field results are shown in Figures 6D,E, in which it can be clearly observed that the simulated wavefront deflection angles of the reflected waves are in excellent agreement with the predesigned target deflection angles, for incident waves of the LCP and RCP states with a deflection angle of 32.4° along the x direction and a deflection angle of −20.9° along the y direction. Then, the 3D normalized far-field scattering patterns of the metasurface under dual orthogonal CP incident waves are drafted in a Cartesian coordinate system to more clearly demonstrate the functions of the metasurface, as depicted in Figure 6A. As shown, the reflected wave is deflected by −20.9° in the xoz plane when the plane wave in the RCP state is incident normally, and the reflected wave has a deviation angle of 32.4° in the yoz plane under the illumination of incident wave with the LCP state. In order to experimentally validate the performance of the designed metasurface, it has been fabricated and measured in the microwave anechoic chamber (refer to Experimental Section for details). The 2D-normalized scattering patterns of the simulated (blue solid line) and measured (red dotted line) ones in the yoz and xoz planes are shown in Figures 6B,C, respectively, corresponding to the results under the illumination of LHCP and RHCP incident waves. Except for the energy of main beams for measurements lower than the simulated ones, the deflection angles of the main beam of the reflected waves measured experimentally are exactly consistent with the expected, which may be due to the low power of the transmitting antenna used in the measurement. Therefore, the conclusion can be obtained that the measured results are in good match with the simulated ones, proving the feasibility and effectiveness of the designed method and metasurface.
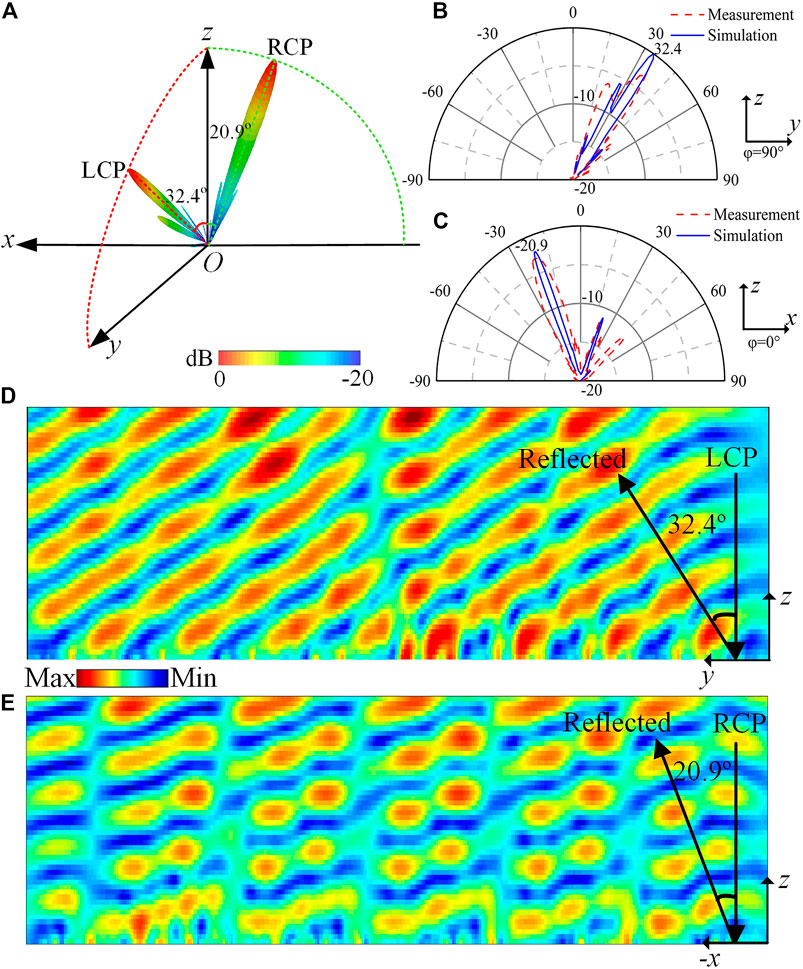
FIGURE 6. The schematic diagram of simulated 3D-normalized scattering patterns of the metasurface under dual orthogonal CP incident waves in (A). The corresponding simulated and measured 2D-normalized scattering patterns on the yoz plane under LHCP incident wave in (B) and xoz plane under RHCP incident wave in (C), respectively. The reflected electric field intensity distributions at 14 GHz on the yoz (along the x direction) and xoz (along the y direction) planes under the LHCP incident wave in (D) and RHCP incident wave in (E) shining the phase gradient metasurface, respectively.
The photographs of the three fabricated metasurface samples and the experimental environments are shown in Figure 7. The prototypes of the metasurfaces are fabricated using the printed circuit board (PCB) technique, as shown in Figure 7A, where the insets show zoomed parts for a clear illustration. Moreover, metasurface1 is applied to realize the function of beam focusing with different focal lengths under dual orthogonal CP incident waves; metasurface2 can separately generate converged vortex waves with the OAM modes of −2 and 3 under the waves with LCP and RCP states illuminating, while metasurface3 reflects the two normal incident plane waves with orthogonal CP states to two directions with different deflected angles. The near-field planar scanning system is exhibited in Figure 7B, which is mainly composed of a fixed platform, feeding antenna, position-controllable field probe, and vector network analyzer (VNA). During the measurement, the metasurface prototypes are illuminated with a dual CP horn antenna placed about 1.5 m away from the samples to ensure the incident wave to be a quasi-plane wave as used in simulations. The rectangular waveguide testing probe moves along the x and y directions to measure the intensity and phase wavefront distributions of the reflected wave. Moreover, the scanning planar area of 340 mm × 340 mm is perpendicular to the radiation beams. The near-field distributions of the beam focusing metasurface and the OAM multiplexed metasurface are performed by using the testing method. It should be noted that the distance between probe and metasurface should be adjusted to the focal lengths in the near-field experiments. The far-field measurement environment is presented in Figure 7C, where the samples and a dual CP horn antenna are placed on a board 1.5 m away from each other, and the board is fixed on a rotary stage and can freely rotate 360° in the horizontal plane. Here, the antenna is connected to a VNA and acts as a feeding antenna, whereas another CP horn antenna is placed far away from the rotating platform as a receiver to record far-field scattering patterns. The 2D-normalized far-field scattering patterns of the OAM-multiplexed metasurface and the beam deflection metasurface are performed at the measurement system.

FIGURE 7. Metasurface prototypes and the experimental setups.(A) Photographs of the fabricated samples. Illustration of the experimental setups for (B) near-field and (C) far-field measurements in the microwave anechoic chamber.
In conclusion, the theoretical method of the combining geometric phase and propagation phase has been utilized to design ultrathin spin-decoupled meta-devices. A single layer and ultrathin meta-atom operating at 14 GHz are proposed based on a cross-shaped resonator. Guided by the theoretical method, three distinct ultrathin bifunctional metasurfaces have been designed, simulated, and measured, which separately realize the functions of focusing with distinct focal lengths, vortex beams generation with different OAM modes, and beam deflection with different deflection angles and deflection directions, as the dual orthogonal CP waves illuminate the metasurfaces. Moreover, the simulated results have been validated by the microwave experiments, and good agreements are achieved between simulated and measured results, verifying the effectiveness of the theoretical method and the performance of the metasurfaces. The research results in this paper provide a new idea to design low-profile and multifunctional meta-devices and may be expected to significantly improve the capacity of the metasurface in future.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
WC and ZM proposed the idea. WC performed the metasurface design, numerical simulations, experiments, and manuscript writing. BQ and JZ participated in the data post-process. BQ, JZ, TN, and ZM analyzed the results and corrected the manuscript. All authors have read and agreed to the published version of the manuscript.
This work was supported in part by the National Key R&D Program of China (Grant No. 2019YFA0405403), in part by the National Natural Science Foundation of China (Grant No. 61631007) and in part by the Natural Science Foundation of Gansu Province (Grant No. 20JR10RA604).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Thanks are given to Dr. Yue Gou and Dr. Qian Ma from the State Key Laboratory of Millimeter Waves, School of Information Science and Engineering, Southeast University, for their sincere help during the experimental measurement.
Balthasar Mueller, J. P., Rubin, N. A., Devlin, R. C., Groever, B., and Capasso, F. (2017). Metasurface Polarization Optics: Independent Phase Control of Arbitrary Orthogonal States of Polarization. Phys. Rev. Lett. 118, 113901. doi:10.1103/PhysRevLett.118.113901
Bao, L., Wu, R. Y., Fu, X., Ma, Q., Bai, G. D., Mu, J., et al. (2019). Multi-beam Forming and Controls by Metasurface with Phase and Amplitude Modulations. IEEE Trans. Antennas Propagat. 67, 6680–6685. doi:10.1109/TAP.2019.2925289
Bouchard, F., De Leon, I., Schulz, S. A., Upham, J., Karimi, E., and Boyd, R. W. (2014). Optical Spin-To-Orbital Angular Momentum Conversion in Ultra-thin Metasurfaces with Arbitrary Topological Charges. Appl. Phys. Lett. 105, 101905. doi:10.1063/1.4895620
Cai, T., Tang, S., Wang, G., Xu, H., Sun, S., He, Q., et al. (2017). High-performance Bifunctional Metasurfaces in Transmission and Reflection Geometries. Adv. Opt. Mater. 5, 1600506. doi:10.1002/adom.201600506
Chen, H.-T., Taylor, A. J., and Yu, N. (2016). A Review of Metasurfaces: Physics and Applications. Rep. Prog. Phys. 79, 076401. doi:10.1088/0034-4885/79/7/076401
Chen, T., Tang, W., Mu, J., and Cui, T. J. (2019). Microwave Metamaterials. Annalen der Physik 531, 1800445. doi:10.1002/andp.201800445
Chen, W., Gou, Y., Ma, H., Niu, T., and Mei, Z. (2021). High-performance and Ultra-broadband Vortex Beam Generation Using a Pancharatnam-Berry Metasurface with an H-Shaped Resonator. J. Phys. D: Appl. Phys. 54, 255101. doi:10.1088/1361-6463/abedfa
Chorsi, H. T., and Gedney, S. D. (2017). Tunable Plasmonic Optoelectronic Devices Based on Graphene Metasurfaces. IEEE Photon. Technol. Lett. 29, 228–230. doi:10.1109/LPT.2016.2636813
Cui, T. J., Liu, S., and Zhang, L. (2017). Information Metamaterials and Metasurfaces. J. Mater. Chem. C 5, 3644–3668. doi:10.1039/C7TC00548B
Devlin, R. C., Ambrosio, A., Rubin, N. A., Mueller, J. P. B., and Capasso, F. (2017). Arbitrary Spin-To-Orbital Angular Momentum Conversion of Light. Science 358, 896–901. doi:10.1126/science.aao5392
Ding, G., Chen, K., Luo, X., Zhao, J., Jiang, T., and Feng, Y. (2019). Dual-helicity Decoupled Coding Metasurface for Independent Spin-To-Orbital Angular Momentum Conversion. Phys. Rev. Appl. 11, 044043. doi:10.1103/PhysRevApplied.11.044043
Fan, Q., Wang, D., Huo, P., Zhang, Z., Liang, Y., and Xu, T. (2017). Autofocusing Airy Beams Generated by All-Dielectric Metasurface for Visible Light. Opt. Express 25, 9285–9294. doi:10.1364/OE.25.009285
Gou, Y., Ma, H. F., Wu, L. W., Wang, Z. X., Xu, P., and Cui, T. J. (2021). Broadband Spin-Selective Wavefront Manipulations Based on Pancharatnam-berry Coding Metasurfaces. ACS Omega 6, 30019–30026. doi:10.1021/acsomega.1c04733
Guo, W.-L., Wang, G.-M., Ji, W.-Y., Zheng, Y.-L., Chen, K., and Feng, Y. (2020). Broadband Spin-Decoupled Metasurface for Dual-Circularly Polarized Reflector Antenna Design. IEEE Trans. Antennas Propagat. 68, 3534–3543. doi:10.1109/TAP.2020.2963945
Han, J., Intaravanne, Y., Ma, A., Wang, R., Li, S., Li, Z., et al. (2020). Optical Metasurfaces for Generation and Superposition of Optical Ring Vortex Beams. Laser Photon. Rev. 14, 2000146. doi:10.1002/lpor.202000146
Hao, J., Yuan, Y., Ran, L., Jiang, T., Kong, J. A., Chan, C. T., et al. (2007). Manipulating Electromagnetic Wave Polarizations by Anisotropic Metamaterials. Phys. Rev. Lett. 99, 063908. doi:10.1103/PhysRevLett.99.063908
He, X., Deng, L., Yang, Y., and Feng, B. (2021). Multifunctional Ultrathin Reflective Metasurface via Polarization-Decoupled Phase for Arbitrary Circularly or Elliptically Polarized Waves. Opt. Express 29, 12736–12749. doi:10.1364/OE.422664
Joy, V., Dileep, A., Abhilash, P. V., Nair, R. U., and Singh, H. (2021). Metasurfaces for Stealth Applications: A Comprehensive Review. J. Elec Materi 50, 3129–3148. doi:10.1007/s11664-021-08927-3
Kildishev, A. V., Boltasseva, A., and Shalaev, V. M. (2013). Planar Photonics with Metasurfaces. Science 339, 1232009. doi:10.1126/science.1232009
Lei, Z., and Yang, T. (2017). Converting State of Polarization with a Miniaturized Metasurface Device. IEEE Photon. Technol. Lett. 29, 615–618. doi:10.1109/LPT.2017.2675453
Li, H.-P., Wang, G.-M., Cai, T., Liang, J.-G., and Gao, X.-J. (2018). Phase- and Amplitude-Control Metasurfaces for Antenna Main-Lobe and Sidelobe Manipulations. IEEE Trans. Antennas Propagat. 66, 5121–5129. doi:10.1109/TAP.2018.2858181
Liu, L., Zhang, X., Kenney, M., Su, X., Xu, N., Ouyang, C., et al. (2014). Broadband Metasurfaces with Simultaneous Control of Phase and Amplitude. Adv. Mater. 26, 5031–5036. doi:10.1002/adma.201401484
Liu, W., Yang, Q., Xu, Q., Jiang, X., Wu, T., Wang, K., et al. (2021). Multifunctional All‐Dielectric Metasurfaces for Terahertz Multiplexing. Adv. Opt. Mater. 9, 2100506. doi:10.1002/adom.202100506
Mao, R., Wang, G., Cai, T., Liu, K., Wang, D., and Wu, B. (2020). Ultra-thin and High-Efficiency Full-Space Pancharatnam-berry Metasurface. Opt. Express 28, 31216–31225. doi:10.1364/OE.405086
Meng, X., Wu, J., Wu, Z., Qu, T., and Yang, L. (2018). Dual-polarized Reflectarray for Generating Dual Beams with Two Different Orbital Angular Momentum Modes Based on Independent Feeds in C- and X-Bands. Opt. Express 26, 23185–23195. doi:10.1364/OE.26.023185
Moreno, G., Yakovlev, A. B., Bernety, H. M., Werner, D. H., Xin, H., Monti, A., et al. (2018). Wideband Elliptical Metasurface Cloaks in Printed Antenna Technology. IEEE Trans. Antennas Propagat. 66, 3512–3525. doi:10.1109/TAP.2018.2829809
Pan, Y. M., Hu, P. F., Zhang, X. Y., and Zheng, S. Y. (2016). A Low-Profile High-Gain and Wideband Filtering Antenna with Metasurface. IEEE Trans. Antennas Propagat. 64, 2010–2016. doi:10.1109/TAP.2016.2535498
Qi, Y., Zhang, B., Liu, C., and Deng, X. (2020). Ultra-broadband Polarization Conversion Meta-Surface and its Application in Polarization Converter and Rcs Reduction. Ieee Access 8, 116675–116684. doi:10.1109/ACCESS.2020.3004127
Sun, S., He, Q., Hao, J., Xiao, S., and Zhou, L. (2019). Electromagnetic Metasurfaces: Physics and Applications. Adv. Opt. Photon. 11, 380–479. doi:10.1364/AOP.11.000380
Wang, H., Li, Y., Han, Y., Fan, Y., Sui, S., Chen, H., et al. (2019). Vortex Beam Generated by Circular-Polarized Metasurface Reflector Antenna. J. Phys. D: Appl. Phys. 52, 255306. doi:10.1088/1361-6463/ab1742
Wang, J., Yang, R., Ma, R., Tian, J., and Zhang, W. (2020). Reconfigurable Multifunctional Metasurface for Broadband Polarization Conversion and Perfect Absorption. IEEE Access 8, 105815–105823. doi:10.1109/ACCESS.2020.3000042
Wang, Z. X., Wu, J. W., Wu, L. W., Gou, Y., Ma, H. F., Cheng, Q., et al. (2021). High Efficiency Polarization‐Encoded Holograms with Ultrathin Bilayer Spin‐Decoupled Information Metasurfaces. Adv. Opt. Mater. 9, 2001609. doi:10.1002/adom.202001609
Xie, R., Zhai, G., Wang, X., Zhang, D., Si, L., Zhang, H., et al. (2019). High‐Efficiency Ultrathin Dual‐Wavelength Pancharatnam-Berry Metasurfaces with Complete Independent Phase Control. Adv. Opt. Mater. 7, 1900594. doi:10.1002/adom.201900594
Xu, H.-X., Han, L., Li, Y., Sun, Y., Zhao, J., Zhang, S., et al. (2018a). Completely Spin-Decoupled Dual-phase Hybrid Metasurfaces for Arbitrary Wavefront Control. Acs Photon. 6, 211–220. doi:10.1021/acsphotonics.8b01439
Xu, H.-X., Liu, H., Ling, X., Sun, Y., and Yuan, F. (2017). Broadband Vortex Beam Generation Using Multimode Pancharatnam-Berry Metasurface. IEEE Trans. Antennas Propagat. 65, 7378–7382. doi:10.1109/TAP.2017.2761548
Xu, H.-X., Wang, G.-M., Cai, T., Xiao, J., and Zhuang, Y.-Q. (2016). Tunable Pancharatnam-Berry Metasurface for Dynamical and High-Efficiency Anomalous Reflection. Opt. Express 24, 27836–27848. doi:10.1364/OE.24.027836
Xu, H. X., Hu, G., Jiang, M., Tang, S., Wang, Y., Wang, C., et al. (2020). Wavevector and Frequency Multiplexing Performed by a Spin‐Decoupled Multichannel Metasurface. Adv. Mater. Technol. 5, 1900710. doi:10.1002/admt.201900710
Xu, J., Li, R., Qin, J., Wang, S., and Han, T. (2018b). Ultra-broadband Wide-Angle Linear Polarization Converter Based on H-Shaped Metasurface. Opt. Express 26, 20913–20919. doi:10.1364/OE.26.020913
Yang, L.-J., Sun, S., and Sha, W. E. I. (2020). Ultrawideband Reflection-type Metasurface for Generating Integer and Fractional Orbital Angular Momentum. IEEE Trans. Antennas Propagat. 68, 2166–2175. doi:10.1109/TAP.2019.2948711
Yin, L.-Z., Huang, T.-J., Han, F.-Y., Liu, J.-Y., Wang, D., and Liu, P.-K. (2019). High-efficiency Terahertz Spin-Decoupled Meta-Coupler for Spoof Surface Plasmon Excitation and Beam Steering. Opt. Express 27, 18928–18939. doi:10.1364/OE.27.018928
Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J.-P., Capasso, F., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. science 334, 333–337. doi:10.1126/science.1210713
Yu, S., and Li, L. (2016). Generating Orbital Angular Momentum Beam Using Reflectarray in Thz Band. Proceedings of the IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO) (IEEE). July 2016. Beijing, China, 1–2. doi:10.1109/nemo.2016.7561634
Yuan, Y., Chen, S., Ratni, B., Wu, Q., Ding, X., Burokur, S. N., et al. (2020a). Bi-functional Meta-Device with Full Energy Utilization in Co- and Cross-Polarization fields. Appl. Phys. Lett. 117, 171602. doi:10.1063/5.0022989
Yuan, Y., Sun, S., Chen, Y., Zhang, K., Ding, X., Ratni, B., et al. (2020b). A Fully Phase‐Modulated Metasurface as an Energy‐Controllable Circular Polarization Router. Adv. Sci. 7, 2001437. doi:10.1002/advs.202001437
Zhang, L., Shuo, L., and Tie-jun, C. (2017). Theory and Application of Coding Metamaterials. 中国光学 10, 1–12. doi:10.3788/CO.20171001.000110.3788/co.20171001.0001b
Zhang, K., Yuan, Y., Ding, X., Ratni, B., Burokur, S. N., and Wu, Q. (2019). High-efficiency Metalenses with Switchable Functionalities in Microwave Region. ACS Appl. Mater. Inter. 11, 28423–28430. doi:10.1021/acsami.9b07102
Zhang, L., Guo, J., and Ding, T. (2021). Ultrathin Dual-Mode Vortex Beam Generator Based on Anisotropic Coding Metasurface. Sci. Rep. 11, 1–8. doi:10.1038/s41598-021-85374-4
Zheng, C., Li, J., Wang, G., Li, J., Wang, S., Li, M., et al. (2021). All-dielectric Chiral Coding Metasurface Based on Spin-Decoupling in Terahertz Band. Nanophotonics 10, 1347–1355. doi:10.1515/nanoph-2020-0622
Keywords: ultrathin, bi-functional, metasurface, spin-decoupling, beam focusing, vortex wave, beam deflection
Citation: Chen W, Qi B, Zhang J, Niu T and Mei Z (2021) Ultrathin Spin-Decoupled Meta-Devices for Independent Control of Electromagnetic Waves With Dual-Orthogonal Circular Polarization. Front. Mater. 8:802268. doi: 10.3389/fmats.2021.802268
Received: 26 October 2021; Accepted: 19 November 2021;
Published: 24 December 2021.
Edited by:
Wei-Xiang Jiang, Southeast University, ChinaReviewed by:
Jinhui Shi, Harbin Engineering University, ChinaCopyright © 2021 Chen, Qi, Zhang, Niu and Mei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhonglei Mei, bWVpemxAbHp1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.