Bond–Slip Law Between Steel Bar and Different Cement-Based Materials Considering Anchorage Position Function

The bond performance between steel bar and cement-based materials was the prerequisite for the two materials to work together, and previous studies showed that the bond behavior of the steel bars and cement-based materials will vary with the kinds of cement-based materials. For this reason, this paper adopted 12 direct pullout test specimens including three types of concrete and two types of steel bars. The strain of the steel bar at six measuring points was measured with a strain gauge. Based on the measured strain and free end slip of the steel bars, the distribution of steel stress, bond stress, and relative slip and the bond slip relation along the anchorage length were obtained and analyzed for different concrete and different steel bars. Based on these test results of steel strain and relative slip at six measuring points, the anchorage position function could be established in consideration of anchorage position, which was conducive to the establishment of an accurate bond–slip relationship. In addition, the anchorage length of the steel bar in Engineered Cementitious Composites (ECC) calculated from the equilibrium equation of critical limit state is only half of the anchorage length calculated in the current Code for Design of Concrete Structures (GB 50010-2010) in China. It is suggested to establish the critical anchorage length formula suitable for ECC in future studies.

Introduction

Cement-based materials are widely used in civil buildings, bridges, tunnels, and other fields because of its advantages of convenient supply of raw material, low cost, good durability, and so on (Fu et al., 2021; Lei et al., 2021; Lam et al., 2021; Wang et al., 2020; Wang et al., 2021a; Wang et al., 2021b; Zhang et al., 2021). As one of the advanced cement-based materials, Engineered Cementitious Composites (ECC) has received more and more attention from both engineers and researchers because of its superior strain-hardening behavior, crack control capability, and ductile property (Cai et al., 2021; Hu et al., 2019; Xiong et al., 2021a; Xiong et al., 2021b; Yu et al., 2021; Yu et al., 2017; Zhou et al., 2019). Experimental studies have confirmed that the ultimate tensile strain of ECC could exceed 3%, which is about 100–300 times as large as that of ordinary concrete and 5-10 times as large as that of steel bar (Li et al., 2002; Xu and Wang 2008). The bond performance between steel reinforcement and cement-based materials was the prerequisite for the two materials to work together and played an important role in ensuring reliable force transfer from the steel reinforcement to surrounding cement-based materials. Effective bonding between the steel bar and the cement-based material is essential for the two materials to work stably and cooperatively. Poor bonding performance will weaken the load-bearing capacity of the component, which will lead to structural failure.

Over the past years, many scholars have carried out some investigations on the bond performance of steel bars in ECC. Wang et al. (2015) carried out pullout tests to evaluate the influences of the properties of matrix materials on the bond behaviors between BFRP bars and cementitious materials and found that the bond strength of the ECC specimen was higher than that of the cement mortar specimen under the same cover thickness and embedment length. Lee et al. (2016) found that the bond strength between steel reinforcement and ECC could be significantly higher than that between steel reinforcement and normal concrete. Deng et al. (2018) carried out direct pullout tests of the steel bar in ECC by changing the bar diameter, bar shape, cover thickness, fiber volume content, and ECC strength and found that the ultimate bond strength of ECC and steel bars is better than the extreme bond strength of ordinary concrete and steel bars. Deng et al. (2018) also built the position function and proposed an accurate bond–slip relationship according to the distribution of bond stress along the anchorage length. Cai et al. (2020) investigated the bond–slip performance of steel reinforcement embedded in ECC as well as concrete and found that the bond strength between steel reinforcement and ECC was higher than that between steel reinforcement and concrete due to the superior tensile ductility of ECC. Xiao et al. (2021) carried out an direct pullout experiment to explore the influence of rebar diameter and type, cover layer thickness, embedment length, and fiber volume content on the bond behavior of the rebar embedded in ECC and found that as the embedment length increased, the bond stress distribution in the bonded section became increasingly nonuniform. Huang et al. (2020) examined the variation in bond stress along the anchorage length of glass fiber reinforced polymer (GFRP) bar tendons via strain gauges attached to the GFRP bars and established a more accurate bond stress and slip constitutive model of the GFRP bars and concrete. Hossain et al. (2020) performed pullout tests on specimens with different parameters such as bar type, bar diameter, embedded length, and concrete types to study the bond strength between GFRP bars and ECC and found that the bond strengths of GFRP bars embedded in the ECC were larger than that embedded in the normal concrete. As the foundation of finite element analysis and engineering design of reinforced concrete, the bond–slip relationship between steel bar and concrete will directly affect the reliability of analysis results. Krstulovic-opara et al. (1994) found that the bond performance was significantly affected by the tensile strength and strain capacity of the matrix. Therefore, compared with traditional cement-based materials such as concrete and fiber-reinforced concrete, the bond performance of steel bar in ECC may be quite different.

In the past few years, many studies have been conducted on the bond performance of deformed steel bars in concrete under service periods. According to the test results, various bond strength models and bond stress–slip constitutive models have been proposed assuming that the bonding stress is uniformly distributed over the embedded length, and the average bond stress is equal to the applied load divided by the contact area between the steel bar and the surrounding concrete (Zhao and Jin 2002). However, in practical engineering, the distribution of bond stress is different along the anchorage length. Therefore, it is necessary to take this difference into account to establish a more accurate bond–slip relationship. Previous studies have shown that the tensile strength and strain capacity of the matrix had a major impact on the bonding performance (Krstulovic-Opara et al., 1994; Choi et al., 2017). Therefore, the bond behavior of the steel bars in ECC may be different from the bond behavior of the steel bars in traditional brittle materials (such as concrete and fiber-reinforced concrete). For this reason, this paper adopted twelve direct pullout test specimens including three types of concrete and two types of steel bars. The strain of the steel bar at six measuring points was measured with strain gauges. Bonding stress could be calculated by these strains of the steel bar. Based on these test results of steel strain and relative slip at six measuring points, an accurate bond–slip relationship could be established in consideration of anchorage position.

Experimental Program

Materials

Engineered cementitious composites (ECC), normal strength concrete (NSC), and steel fiber-reinforced concrete (SFRC) were constituted with the mixture formulations provided in Table 1. The ECC and SFRC both contained Ordinary Portland cement (P.O 42.5R), Class Ⅰ high-calcium fly ash, silica sand, superplasticizer, and water. The difference between the ECC and SFRC is that polyvinyl alcohol (PVA) fiber is used in ECC, while steel fiber concrete contains steel fiber. The characteristics of PVA fiber and steel fiber used in this study are listed in Table 2. The NSC contained Ordinary Portland cement (P.O. 42.5R), river sand, gravel, water, and superplasticizer. The 28-day average compressive strengths of ECC, NSC, and SFRC are 48, 50, and 75 MPa, respectively.

TABLE 1

TABLE 1. Mix proportion used for the three types of concrete (by weight).

TABLE 2

TABLE 2. Characteristics of PVA fiber and steel fiber.

A common horizontal concrete mixer with a volume of 30 l was used to mix the components and prepare cement-based material samples, as shown in Figure 1. The dispersion of PVA fibers in the ECC is a key factor in achieving ideal mechanical properties. In this paper, the clusters of PVA fibers purchased from the market were placed in a plastic mold with a diameter of 150 mm and a height of 300 mm, and then the plastic mold was turned upside down on a smooth wooden board. Then, a demolding gun connected to the demolding air pump was inserted into the small hole at the bottom of the plastic mold, which can make PVA fibers evenly dispersed under the action of the airflow, as shown in Figure 2. The steel fibers were also evenly added into the SFRC mixture during the mixing process in order to avoid the congestion of the steel fibers. In order to test the tensile properties of ECC material, fresh ECC mixtures were poured into standard-size dog bone specimens, as shown in Figure 3A. The results of the tensile performance test showed that the ultimate tensile strain of ECC used in this paper exceeds 3% and met the requirements of ECC, as shown in Figure 3B. The design value of the tensile strength $f_{ty}$ of the ECC concrete was 4.58 MPa, and the testing and calculation procedures can be found in the literature (Xiao et al., 2021).

FIGURE 1

FIGURE 1. Production process of ECC specimens: (A) ECC material that has been stirred and (B) specimen casting.

FIGURE 2

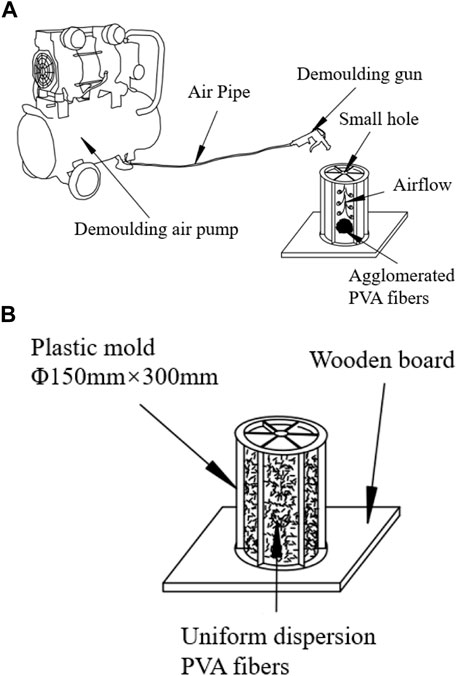
FIGURE 2. The uniform dispersion PVA fiber by a demolding air pump: (A) before PVA fiber dispersion and (B) after PVA fiber dispersion.

FIGURE 3

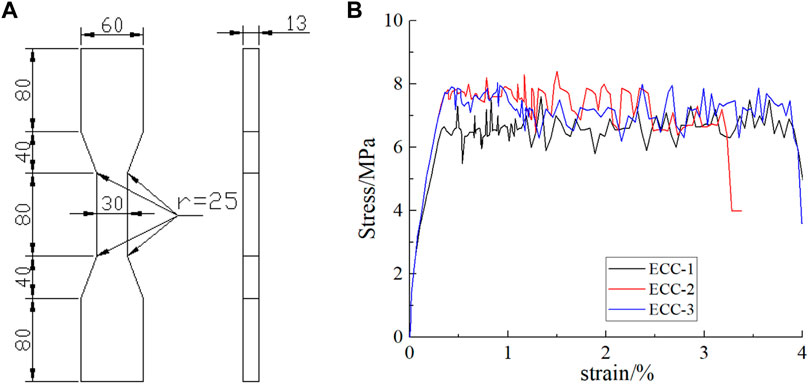
FIGURE 3. Design and tensile property of the adapted ECC in the experiment: (A) dimension of dog-bone specimen (Unit mm) and (B) tensile stress–strain curves of ECC.

Specimen Design

The pullout test is one of the most widely used test methods on investigating the bond performance between steel bar and cement-based materials due to the convenience of specimen manufacturing, the simple operation of test apparatus, and the easy analysis of the test results. In this paper, the pullout test was employed to study the bond performance between steel bar and cement-based materials. Direct pullout test specimen is to embed a steel bar horizontally into the concrete cube along its central axis. In order to ensure that the thickness of the protective layer is sufficient to make the failure mode of the specimen result in pullout failure, the side length of the concrete cube was designed to be 160 mm. A PVC pipe with a length of 60 mm was placed in the nonbonded region in the concrete cube, and the PVC pipe was filled with polyurethane foam to avoid concrete flowing into it during casting. The steel bar extends 50 mm from the free end and 360 mm from the loading end, and the length of the bond region was 100 mm, as shown in Figure 4. The experiment was divided into four groups, each of which consisted of three identical test specimens. The type of concrete used in the first three groups was different, and the type of steel bar used in the last group was different. Within the 100-mm anchorage length of each specimen, six strain gauges were pasted at equal intervals, each about 20 mm apart, as shown in Figure 4. The symbol E-C16 represents that the concrete of the specimen was ECC and the steel bar was ribbed steel bar with a diameter of 16 mm. The symbol E-C16R denoted that the concrete of the specimen was ECC and the steel bar was a plain round bar with a diameter of 16 mm. The symbol P-C16 meant that the concrete of the specimen was normal concrete and the steel bar was ribbed steel bar with a diameter of 16 mm. The symbol SF-C16 indicated that the concrete of the specimen was SFRC and the steel bar was ribbed steel bar with a diameter of 16 mm. The yield strength of the ribbed steel bar was 415.06 MPa and the yield strength of the plain round bar was 252.99 MPa and the testing data can be found in the literature (Xiao et al., 2021).

FIGURE 4

FIGURE 4. Details of test specimen (Unit: mm).

Experiment setup

The pullout test was carried out on the experimental machine shown in Figure 5. The concrete specimens with the embedded steel bar were placed in a self-made steel frame, which consisted of two 25-mm-thick square steel plates. The two square steel plates were connected to each other by four 20-mm-diameter steel rods located at the corners. The distance between the two steel plates was set to 50 cm to ensure there was sufficient space for the installation of linear variable differential transformers (LVDTs). There was a 30-mm-diameter hole in the center of the steel frame bottom plate to allow the steel bar to pass through. A universal testing machine with a maximum tensile force of 1,000 kN was adopted to apply the pullout load. The pullout load was applied at a rate of 0.5 mm/min in displacement loading mode until failure. Assuming that the bond stress is uniformly distributed along the longitudinal direction, the formula below can be used to calculate the average bond strength between steel bar and concrete:

$\tau =\frac{\mathrm{P}}{\mathrm{\pi }\mathrm{d}{\mathrm{l}}_{\mathrm{a}}}(1)$

where P denotes the pullout force, d represents the diameter of the steel bar, and $l_a$ means the length of the bond region. As shown in Figure 5, the BC segment was the bond region of the steel bar. The MM section was the upper surface of the concrete cubes close to the free end. The NN section was the lower surface of the concrete cubes close to the loading end. Two LVDTs were symmetrically mounted on the MM section to test the average displacement of the MM section $S_M$. An LVDT was placed at the free end of the steel bar (section AA) to test its displacement $S_A$. The TDS-530 data acquisition system was employed to obtain the test data. The net slip of the free end of the steel bar could be expressed as follows:

${\mathrm{S}}_{\mathrm{F}}=\frac{{\mathrm{S}}_{\mathrm{A}}-{\mathrm{S}}_{\mathrm{M}}}{2}(2)$

Since the BF segment was long and near the loading end, the loading force was large, and the deformation generated could not be ignored. Therefore, the deformation of the BF segment should be taken into consideration when calculating the net slip of the loading end. The deformation of the steel bar in segmented BF could be expressed as

$\mathrm{\Delta }{\mathrm{S}}_{\mathrm{B}\mathrm{F}}=\frac{\mathrm{P}}{{\mathrm{E}}_{\mathrm{S}}{\mathrm{A}}_{\mathrm{S}}}{\mathrm{L}}_{\mathrm{B}\mathrm{F}}(3)$

where ${\mathrm{E}}_{\mathrm{S}}$ denotes the elastic modulus of the steel bar, ${\mathrm{A}}_{\mathrm{S}}$ represents the cross-sectional area of the rebar, ${\mathrm{L}}_{\mathrm{B}\mathrm{F}}$ denotes the initial length of the steel bar in segment BF, and P refers to the pullout load. If ${\mathrm{S}}_{\mathrm{Z}}$ represented the displacement of the loading end of the universal testing machine, the net slip of the steel bar at the loading end can be expressed as follows:

$S_L=S_Z-\Delta S_{BF}(4)$

Therefore, the average relative slip of the steel bar and the matrix along the anchorage section could be expressed as follows:

$S=\frac{S_F+S_L}{2}(5)$

FIGURE 5

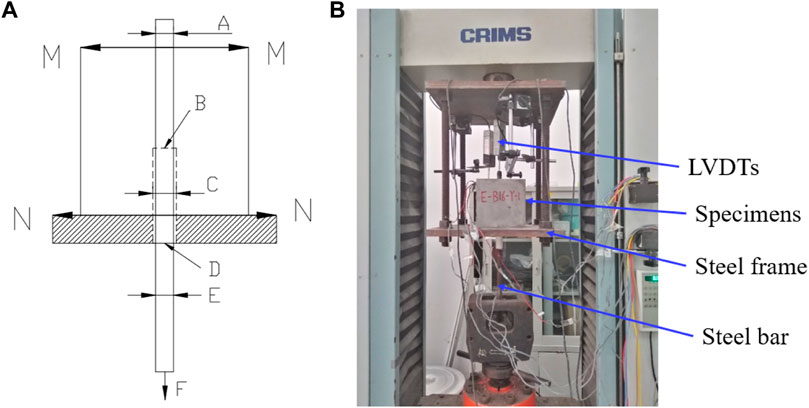
FIGURE 5. Schematic diagram of loading apparatus and measurement position: (A) diagrammatic view and (B) photograph.

Experimental Results and Discussion

Bond Stress-Slip Curves

The relationship of bond stress and slip was one of the most important experimental results for studying the bond performance between steel bars and concrete. The stress–slip relationships of the pullout tests of the four groups of the specimens in this paper are shown in Figure 6. For ordinary concrete P-C16, when the slip increased to about 1.5 mm, the tensile force slowly approached the ultimate load, and when the bond stress reached the maximum value, the concrete split due to the hoop tensile force exceeded the tensile strength of the concrete. The width of the cracks formed was relatively large in the form of brittle failure. For the SFRC SF-C16, the failure mode of SF-C16 was different from the failure mode of P-C16. Although there was a large crack the same as P-C16, the concrete of SF-C16 specimen did not split with brittle sound, forming a shear failure mode. In addition, the phenomenon of some steel fibers sinking was observed during casting of the concrete specimens, so the bond strength was lower than the results of other scholars, and the slip was lower than that of P-C16, which may be that the fiber sinking reduced the bond performance of steel bar and SFRC. Compared with P-C16 and SF-C16, the crack forms of specimen E-C16 were different. Although the failure mode was also shear failure, the surface of ECC specimen would find fine and intensive cracks that were hard to be observed by the naked eyes. The cracks were radially distributed from the center to the edge, and the number of the cracks on the surface of E-C16 was much more than that on the surface of P-C16 and SF-C16. This is attributed to that ECC had excellent crack control capability and ductile property. However, the shear strength of the pullout test ECC specimen E-C16R with a plain round bar was relatively small. At the initial stage, the shear stress of E-C16R was mainly supported by the chemical adhesion. Once the slip reached a certain value, the bond stress would decrease, and the slip would increase. The steel bar would be pulled out from the ECC, and it was difficult to find cracks on the surface of the specimen E-C16R, indicating that the bond performance was poor.

FIGURE 6

FIGURE 6. Bond–slip curve: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

The Distribution of Steel Stress Along the Anchorage Length

Since the strains of the steel bar under different loading levels could be measured by the strain gauges attached to the steel bar, the stress distribution of the steel bar along the anchorage length could be calculated, as shown in Figure7. The steel tension gradients of E-C16 and SF-C16 were the same, and their steel tension force started from 6 to 30 kN. The steel tension gradients of P-C16 were twice those of E-C16 and SF-C16 and the steel tension force of P-C16 started from 12 to 60 kN. As the bond strength of the specimen E-C16R was small, the tensile force of the steel bar was small as well and the steel tension force of E-C16R started from 1.5 to 3.5 kN. It is shown in Figure 7 that the stress distribution curves of the steel bars along the anchorage length were similar in the four types of specimens. The stresses of the steel bars were relatively gentle at the loading end and free end, but relatively steep in the middle. As the load increased, the stress of the steel bar at the loading end increased, but the free end did not change much. The comparison between the specimen E-C16 and SF-C16 showed that the gradient of the steel bar stress variation of E-C16 was smaller than that of SF-C16. This meant that the steel bar stress of E-C16 was relatively stable with the variation of the anchoring position. The stresses of the steel bars of E-C16 at the free end were obviously larger than those of SF-C16 with the increase in the reinforcement pulling force. This showed that the PVA fibers played a good bridge effect on the concrete matrix. When the tension force of the steel bar was the same, the stress of the steel bar in P-C16 at each anchorage position was larger than that in E-C16 and SF-C16. The stress gradient of the steel bar in P-C16 was relatively obvious, which indicated that the bond strength of P-C16 was relatively high. With the increase in the tension force of the steel bar, the stress of the steel bar in E-C16R showed a great change at the loading end, while the stress of the steel bar at the distance of 60 mm from the loading end decreases almost to zero. Such an obvious change indicated that the anchorage performance of E-C16R was significantly lower than that of the ribbed steel bar.

FIGURE 7

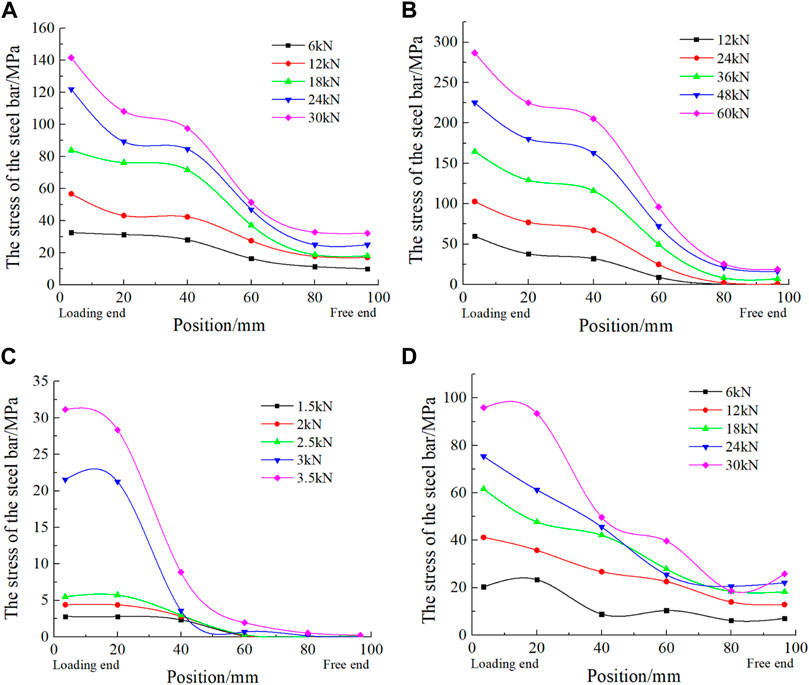
FIGURE 7. Distribution rule of the stress of the steel bar along the anchorage length: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

The Distribution of Bond Stress Along the Anchorage Length

In this paper, the strain gauge pasted on the surface of the steel bar was used to measure the strain of the steel bar at six measurement points along the bond region. Then the bond stress at each measurement point instead of the average stress of each interval was directly calculated according to the calculation method adopted in reference Xu and Wang (2008). Assuming that the strain of the steel bar was smoothly distributed in the bond region, and the bond region was divided into five sections by the measurement points, and the length of each section was h, the following formulas can then be obtained:

$\epsilon \left(x_i+h\right)=\epsilon \left(x_i\right)+h{\epsilon }^{\prime }\left(x_i\right)+\frac{h^2}{2!}{\epsilon }^{″}\left(x_i\right)+\frac{h^3}{3!}{\epsilon }^{″\prime }\left(x_i\right)+o\left(h^4\right)(6)$

$\epsilon \left(x_i-h\right)=\epsilon \left(x_i\right)-h{\epsilon }^{\prime }\left(x_i\right)+\frac{h^2}{2!}{\epsilon }^{″}\left(x_i\right)-\frac{h^3}{3!}{\epsilon }^{″\prime }\left(x_i\right)+o\left(h^4\right)(7)$

Eq. 7 is subtracted from Eq. 6:

${\epsilon }^{\prime }\left(x_i\right)=\frac{\epsilon \left(x_i+h\right)-\epsilon \left(x_i-h\right)}{2h}-\frac{h^2}{6}{\epsilon }^{″\prime }\left(x_i\right)+o\left(h^3\right)(8)$

Add Eqs 6, 7 to obtain:

${\epsilon }^{″}\left(x_i\right)=\frac{\epsilon \left(x_i+h\right)+\epsilon \left(x_i-h\right)}{h^2}+o\left(h^2\right)(9)$

Take the derivative of Eq. 9 and substitute it into the right-hand side of Eq. 8:

${\epsilon }^{\prime }\left(x_i\right)=\frac{\epsilon \left(x_i+h\right)-\epsilon \left(x_i-h\right)}{2h}-\frac{1}{6}\left({\epsilon }_{i+1}^{\prime }+{\epsilon }_{i-1}^{\prime }-2{\epsilon }_i^{\prime }\right)+o\left(h^3\right)(10)$

Ignore the error term and arrange $\delta {\epsilon }_i={\epsilon }_{i+1}-{\epsilon }_{i-1}$ to obtain the following formula:

${\epsilon }_{i-1}^{\text{'}}+4{\epsilon }_i^{\text{'}}+{\epsilon }_{i+1}^{\text{'}}=\frac{3}{h}\left({\epsilon }_{i+1}-{\epsilon }_{i-1}\right)=\frac{3}{h}\delta {\epsilon }_i(11)$

The following formula can be obtained from the microsegment equilibrium of the steel bar, as shown in Figure 8:

${\epsilon }_i^{\text{'}}={\tau }_i\frac{\pi d}{E_s{A}_s}=\frac{4{\tau }_i}{E_{s}d}(12)$

Substitute Eq. 12 into Eq. 11 to obtain the following formula:

${\tau }_{i-1}+4{\tau }_i+{\tau }_{i+1}=\frac{3E_{s}d}{4h}\delta {\epsilon }_i(13)$

Considering that its boundary conditions were ${\tau }_0={\tau }_n=0$, the bond stress could be obtained through the following equations:

$\left[\begin{array}{ccccccc}4& 1& & & & & \\ & 1& 4& 1& & & \\ & & & \mathrm{...}& \mathrm{...}& & \\ & & & & 1& 4& 1\\ & & & & & 1& 4\end{array}\right]\left\{\begin{array}{c}{\tau }_1\\ {\tau }_2\\ {\tau }_3\\ \mathrm{...}\\ {\tau }_i\\ \mathrm{...}\\ {\tau }_{n-2}\\ {\tau }_{n-1}\end{array}\right\}=\frac{3E_{s}d}{4h}\left\{\begin{array}{c}\delta {\epsilon }_1\\ \delta {\epsilon }_2\\ \delta {\epsilon }_3\\ \mathrm{...}\\ \delta {\epsilon }_i\\ \mathrm{...}\\ \delta {\epsilon }_{n-2}\\ \delta {\epsilon }_{n-1}\end{array}\right\}(14)$

where $E_s$ represents the elasticity modulus of steel bar, d denotes the diameter of steel, and ${\tau }_i$ and ${\epsilon }_i$ denote the bond stress and steel strain, respectively, at pint i. Equation 14 was a three-diagonal array equation that can be solved by the chase method. No matter how the measurement points of steel bar were arranged within the bond region, the equations could always form a strictly diagonally dominant matrix. Therefore, the numerical solution to the equations always existed and the bond stress of each strain measurement point can be calculated by software for calculation.

FIGURE 8

FIGURE 8. The microsegment equilibrium of steel bar.

Through Eq. 14, the bond stress under different uniaxial tensile loads was calculated. If these bond stresses were added up along the anchorage length, the bond stress multiplied by the circumference of the steel bar should be equal to the load applied to the steel bar at the loading end. If there was any difference between the two forces, the negative of the difference value should be adjusted according to the principle of equal distribution. Then, a smooth curve was used to express the general trend of the variations of the bond stress along the anchorage length, so that the area under the curve of bond stress distribution multiplied by the circumference of the steel bar was equal to the load applied to the steel bar at the loading end, and the curve of the distribution of bond stress along the anchorage length was obtained, as shown in Figure 9. The distance from the free end was defined as the X-coordinate, and the calculated stress in each strain recording point was defined as the Y-coordinate.

FIGURE 9

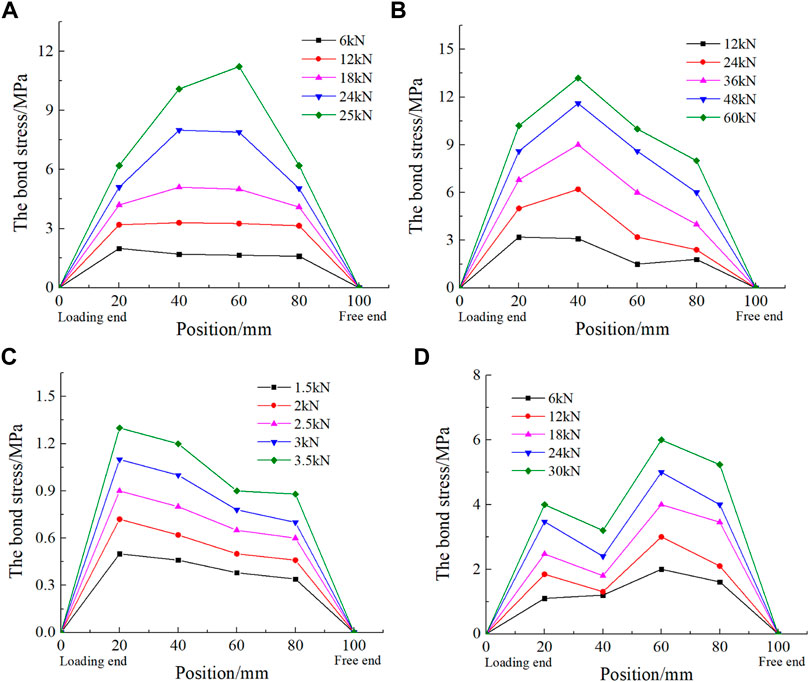
FIGURE 9. The relationship between bond stress and anchorage position: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

As is shown in Figure 9, no matter what kind of specimens, the distribution of bond stress along the anchorage length had a similar trend. That is, at each tensile load level, the stress along the anchorage length increased from the free end to the loading end. There were also some differences in the distribution of bond stress along the anchorage length for different specimens. For specimen E-C16, with the increase of the load applied to the steel bar at the loading end, the position of the maximum bond stress gradually approached the free end, and the stress in the middle of the anchorage position gradually became plump, indicating that the PVA fiber played a good bridging role. For specimen P-C16, at the initial stage of loading, the position of the maximum bond stress was close to the loaded end, but with the increase in the load applied to the steel bar at the loaded end, the stress at 60 mm away from the loaded end became plump and bore most of the tension force, gradually becoming the maximum bond stress. For specimen SF-C16, with the increase in tension force, the bond stress peak values of the specimen appeared at 20 and 60 mm away from the loading end. The peak points of the bond stress moved right with the increase in the tensile force. It was speculated that the good connection of steel fiber left and right hooks made the concrete work well together. For specimen E-C16R, the peak points of the bond stress mainly appeared at 40 mm away from the loading end, and the peak value of its bond stress at each tensile load level was far less than that of the specimen with the ribbed steel bar.

The Distribution of Relative Slip Along the Anchorage Length

From the measured slip of the loading end and the free end, the slip between steel bar and cement-based material at any position in the anchorage length could be calculated. It meant that this slip could be determined by the displacement difference between reinforcing bar and cement-based material at each point. In the test, the strain of the steel bar ${\epsilon }_{si}$ at each measuring point had been obtained by the method of the internal strain gauge, so the elongation of the steel bar micro-segment was $\Delta l_{si}={\epsilon }_{si}\Delta l$ ($\Delta l$ was the spacing between strain gauges 20 mm). The average stress ${\sigma }_{ci}$ and strain ${\epsilon }_{ci}$ of cement-based material around the steel bar can be calculated by the balance of micro-segments. Therefore, the micro-segment deformation of cement-based material was $\Delta l_{ci}={\epsilon }_{ci}\Delta l$. However, the stress distribution of cement-based materials in the cross section was not uniform. The stress at the steel bar interface was large, and the stress away from the steel bar interface was small. Meanwhile, the change in stress along the cross section varied related to the anchorage position. This change in trend was very obvious when near the loading end, but this changing trend was gentle when near the free end. Therefore, the inhomogeneous deformation coefficient ${\gamma }_c$ (the ratio of the interface strain to the average strain of the section) was introduced to consider this effect.

After obtaining the deformation of each microsegment and the deformation of the cement-based materials, the nonuniform deformation coefficient ${\gamma }_c$ can be calculated according to the relative slip of the loading end $s_l$ and the relative slip of the free end $s_f$.

$s_l=s_f+{\displaystyle \sum _{i=1}^n\left(\Delta l_{si}+{\gamma }_c\Delta l_{ci}\right)}(15)$

The relative slip $s_x$ between the steel bar and cement-based materials at x mm away from the free end could be expressed by Eq. 16:

$s_x=s_f+{\displaystyle \sum _{i=1}^m\left(\Delta l_{si}+{\gamma }_c\Delta l_{ci}\right)},m=\frac{x}{h}(16)$

where x is the distance away from the free end and h is the length of the bond region. According to the above method, the relative slip of the steel bar and cement-based materials at each point within the anchorage length could be calculated under any load, as shown in Figure 10.

FIGURE 10

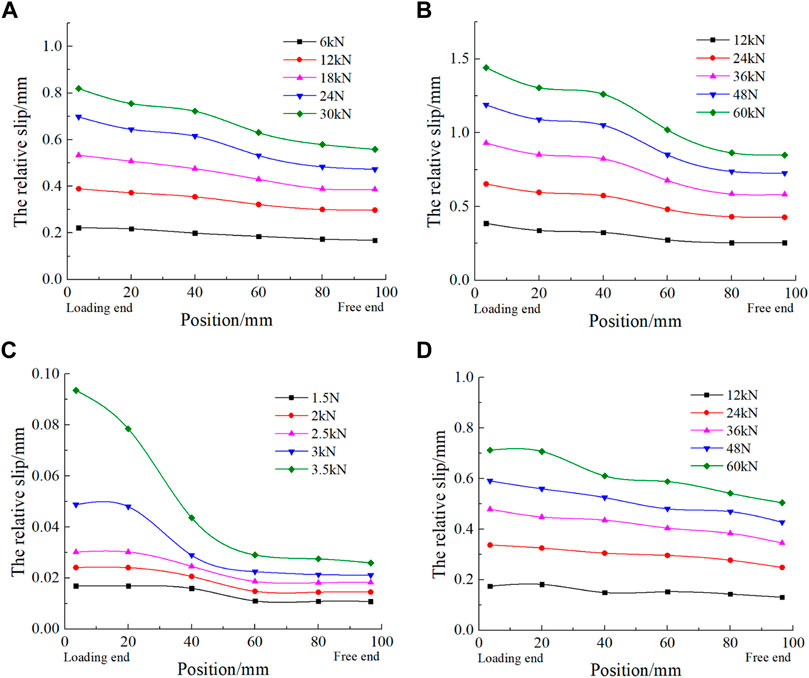
FIGURE 10. Relationship between slip and position: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

According to the result as shown in Figure 10, in the case of 12 and 24 kN, the relative slip fitting of the SFRC SF-C16 was very smooth, indicating that the adhesion force of the free end of the steel bar was lost at the early stage of the experiment and the shear lag effect was not obvious. However, for normal concrete specimens P-C16, the slip at the loading end was larger than that at the free end, and the shear lag effect occurred. For the E-C16 member with high toughness, the concrete integrity became better due to the connection between aggregates through PVA fiber with good hydrophilicity. The difference between the relative slip of the loading end and the relative slip of the free end was not particularly obvious, which indicated that ECC had good toughness and high ductility. Compared with specimen E-C16, it was obvious that the bond performance of E-C16R was very poor. Although the difference between the relative slip of the loading end and the relative slip of the free end was also not particularly obvious in the early stage, at the moment of the failure, the difference between the relative slip of the loading end and the relative slip of the free end became larger and the shear lag effect occurred.

The Variation of the Bond Slip Relation Along the Anchorage Length

Since the bond stress between steel bar and cement-based materials along the anchorage length would vary with the position, it was impossible to measure every strain of the steel bar along the anchorage length. In this paper, the bond–slip relationship was studied according to the anchorage points glued with strain gauges. Assuming that there was a bond–slip relationship at each measuring point, each specimen had a bond–slip relationship at the anchorage positions of 20, 40, 60, and 80 mm. According to the bond stress and its corresponding slip at each point along the anchorage length of the steel bar under all levels of load mentioned above, the bond–slip expressions at different positions could be fitted. After several trial calculations, it was found that the bond–slip relation at different anchorage points could be fitted by a cubic polynomial as follows:

$\tau =a+bs+c{s}^2+d{s}^3(17)$

where $\tau$ is the bond stress and its unit was MPa, and s is the bond–slip and its unit was mm. a, b, c, and d are the fitting parameters. The fitting result for the bond–slip relation of specimens E-C16, P-C16, E-C16R, and SF-C16 at the anchorage positions of 20, 40, 60, and 80 mm are listed in Tables 3–6, respectively. It can be seen from the data in these four tables that the cubic polynomial could fit the experimental data well. All the correlation coefficients were above 0.9, and all the variances were very small.

TABLE 3

TABLE 3. The fitting result for the bond-slip relation of specimens E-C16.

TABLE 4

TABLE 4. The fitting result for the bond–slip relation of specimens P-C16.

TABLE 5

TABLE 5. The fitting result for the bond–slip relation of specimens E-C16R.

TABLE 6

TABLE 6. The fitting result for the bond–slip relation of specimens SF-C16.

Figure 11 shows the bond slip curves of each specimen at different positions along the anchorage length in the loading process. It can be seen from the figure that the bond stress was not uniformly distributed at different anchorage points, but varied, obeying the cubic polynomial. Therefore, it was necessary to use the bonding test to establish the bond slip constitutive relation considering the influence of anchorage position.

FIGURE 11

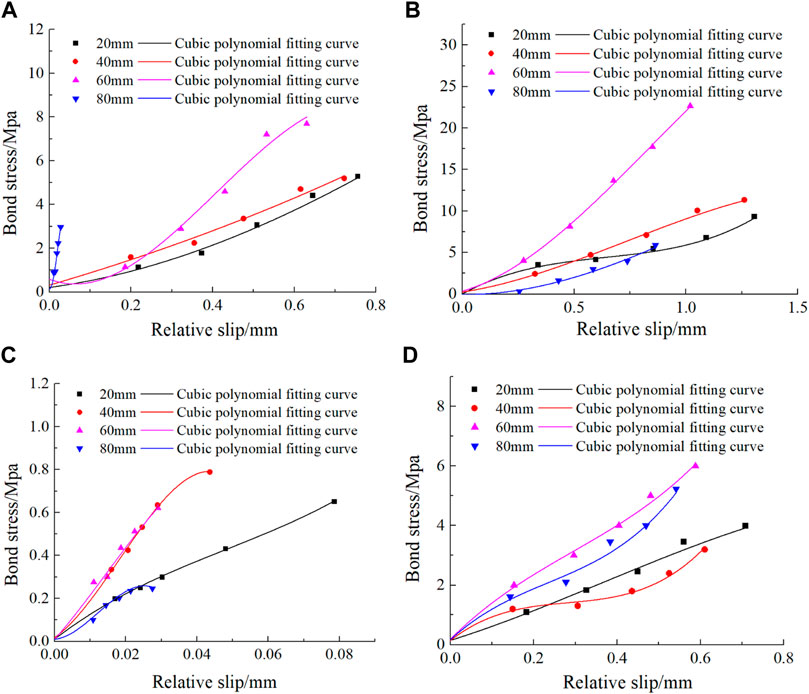
FIGURE 11. The relationship between bond stress and relative slip at different anchorage positions: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

Anchorage Position Function

The anchorage position function was a relative function that described the relative magnitude of the bond stiffness at different positions. Generally, the following methods were used to obtain the following: according to the abovementioned, the curve of the variation law of steel stress along the anchorage length was obtained firstly, and then the distribution of bond stress along the anchorage length was obtained by the stress of the steel bar. Next, the curve of the variation law of the relative slip along the anchorage length was drawn, and finally the distribution curve of bond stress $\tau$ at different anchorage positions under all slips was obtained. On the basis of these curves, the abscine value was divided by the anchorage length L, and the ordinate value was divided by its average bond stress, which was transformed into a normalized curve, and then the anchorage position function $\psi \left(x\right)$ was obtained by statistical regression. On the basis of Figure 12, the test data was simplified by a standardized method. The bond stress of each specimen at different anchorage positions was fitted; the fitting data results are listed in Tables 7, 8, where a, b, c, d, e, and f are the fitting coefficients and R² and S are the correlation coefficients and variance, respectively. According to correlation coefficient R², the fitting effect of the four polynomials was good for the three kinds of specimens E-C16R, E-C16, and P-C16, and their fitting correlation coefficient R2 was above 0.85, but the fitting effect of the four polynomials was poor for specimens SF-C16. Therefore, this paper adopted the fifth-degree polynomial to fit the test results of SF-C16 with the variance of 0.

FIGURE 12

FIGURE 12. Position function: (A) E-C16, (B) P-C16, (C) E-C16R, and (D) SF-C16.

TABLE 7

TABLE 7. The fitting results of specimens E-C16R, E-C16, and P-C16 at different anchorage positions.

TABLE 8

TABLE 8. The fitting results of specimens SF-C16 at different anchorage positions.

According to Tables 7, 8; Figure 12 above, the anchorage position functions of four different kinds of specimens could be obtained. The anchorage position function of the specimens E-C16 is as follows:

${\psi }_{\mathrm{E}}\left(\mathrm{x}\right)=0.016+4.52\left(\frac{\mathrm{x}}{\mathrm{L}}\right)-1.893{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^2-7.143{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^3+4.483{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^4(18)$

The anchorage position function of the specimens P-C16 is as follows:

${\psi }_{\mathrm{P}}\left(\mathrm{x}\right)=0.043-0.687\left(\frac{\mathrm{x}}{\mathrm{L}}\right)+21.33{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^2-45.06{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^3+22.96{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^4(19)$

The anchorage position function of the specimens E-C16R is as follows:

${\psi }_{\mathrm{E}\mathrm{R}}\left(\mathrm{x}\right)=-0.003+3.997\left(\frac{\mathrm{x}}{\mathrm{L}}\right)+0.373{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^2-12.472{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^3+8.108{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^4(20)$

The anchorage position function of the specimens SF-C16 is as follows:

${\psi }_{\mathrm{S}\mathrm{F}}\left(\mathrm{x}\right)=17.64\left(\frac{\mathrm{x}}{\mathrm{L}}\right)-119.27{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^2+312.51{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^3-338.13{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^4+127.26{\left(\frac{\mathrm{x}}{\mathrm{L}}\right)}^5(21)$

Since the number of test specimens was limited, the anchorage position function of the steel bars and cement-based materials discussed herein was mainly for comparison, and by comparison, the expression function varied with the change of cement-based materials. The bond–slip relation obtained by the pullout test could not reflect the influence of bond position, but in fact, the bond–slip constitutive relation varied with anchorage position. In order to describe this variation, an anchorage position function could be determined on the basis of the basic bond–slip relationship that was already known, and the bond–slip constitutive relation along anchorage length was expressed by multiplying the basic bond–slip relationship with the anchorage position function. The basic bond–slip relation adopted the average bond–slip constitutive relation $\tau =\phi \left(\mathrm{s}\right)$, then the bond–slip constitutive relation between steel bar and cement-based materials could be accurately described as:

$\tau \left(\mathrm{s},\mathrm{x}\right)=\phi \left(\mathrm{s}\right)\cdot \psi \left(\mathrm{x}\right)(22)$

where $\tau \left(\mathrm{s},\mathrm{x}\right)$ denotes the bond constitutive relation that varied with anchorage position. $\phi \left(\mathrm{s}\right)$ represents the average bond–slip relationship measured through the pullout test. $\psi \left(\mathrm{x}\right)$ is the anchorage position function, which could be taken according to Eqs 18–21.

Anchorage Length of the Steel Bar in ECC

There are two kinds of failure modes for the steel bar embedded in ECC under the tension force F: one is failure due to the steel bar being pulled apart; the other is failure due to the interface between the steel bar and ECC being sheared off. For the determined steel bar and ECC, the yield stress of the steel bar is a determined value, while the anchorage force applied by the ECC on the steel bar increases with the increase of the anchoring length La. When the anchorage length increases to a certain value, the anchorage force can be equal to the yield force of the steel bar, which means the anchorage failure occurs simultaneously with the yield of the steel bar. This particular anchorage length is called the “critical anchorage length.” The state in which the anchorage force is equal to the yield force of the steel bar is called “anchorage limit state.” It can be seen that the critical anchorage length is actually the minimum anchorage length that the steel bar cannot be pulled out in ECC when the tension force F reaches the yield force of the steel bar. The anchorage limit state is the state that the yield stress of the steel bar and the ultimate bond stress between the steel bar and ECC reach at the same time. Assume that under the critical limit state, the critical anchorage length of the steel bar in ECC is ${\mathrm{l}}_{\mathrm{c}\mathrm{r}}$. The tensile force of the steel bar is F and the yield strength of the steel bar is ${\mathrm{f}}_{\mathrm{y}}$. The diameter of the steel bar is d, and the bond stress of the interface between the steel bar and ECC is ${\mathrm{\tau }}_{\mathrm{u}}$, then the anchorage force applied by ECC on the steel bar can be calculated as follows:

$\mathrm{F}=\mathrm{\pi }\mathrm{d}{\mathrm{l}}_{\mathrm{c}\mathrm{r}}{\mathrm{\tau }}_{\mathrm{u}}(23)$

The relation between the force F applied on the steel bar and the yield strength of the steel bar ${\mathrm{f}}_{\mathrm{y}}$ can be calculated as follows:

$\mathrm{F}=\frac{\pi {\mathrm{d}}^2}{4}{\mathrm{f}}_{\mathrm{y}}(24)$

The calculation formula of critical anchorage length ${\mathrm{l}}_{\mathrm{c}\mathrm{r}}$ can be obtained from the equality of the above two expressions:

${\mathrm{l}}_{\mathrm{c}\mathrm{r}}=\frac{{\mathrm{f}}_{\mathrm{y}}\mathrm{d}}{4{\tau }_{\mathrm{u}}}(25)$

In this paper, the diameter of the ribbed steel bar is 16 mm, the yield strength of the ribbed steel bar is 400 MPa, and the design value of ECC’s tensile strength is 4.58 MPa. By substituting these values into Eq. 25, the critical anchorage length of the ribbed steel bar in ECC can be calculated to be 97 mm (${\mathrm{l}}_{\mathrm{a}}$ ≈6 days).

However, in the current Code for Design of Concrete Structures (GB 50010-2010) in China, when making full use of the tensile strength of the steel bar, the anchorage length of tensile steel bar should be calculated as follows:

${\mathrm{l}}_{\mathrm{a}}=\alpha \frac{{\mathrm{f}}_{\mathrm{y}}}{{\mathrm{f}}_{\mathrm{t}}}\mathrm{d}(26)$

where $\mathrm{\alpha }$ is called the shape coefficient of the steel bar, ${\mathrm{f}}_{\mathrm{t}}$ is called the design value of the tensile strength of the concrete, and ${\mathrm{f}}_{\mathrm{y}}$ is called the design value of the tensile strength of the steel bar. In this paper, the shape coefficient of the ribbed steel bar $\mathrm{\alpha }$ is 1.4, the design value of the tensile strength of the ECC ${\mathrm{f}}_{\mathrm{t}}$ is 4.58 MPa, and the design value of the tensile strength of the steel bar ${\mathrm{f}}_{\mathrm{y}}$ is 400 MPa. In this paper, the critical anchorage length of the ribbed steel bar with a diameter of 16 mm in ECC can be calculated to be 195.68 mm (${\mathrm{l}}_{\mathrm{a}}$ = 12.23 days) by substituting each of the above values into Eq. 26. It could be seen that it was safe and conservative to use Eq. 26 to calculate the anchorage length of the steel bar in ECC. Through the pullout test, we also found that when the anchorage length reached 100 mm, some of the steel bars reached the yield point. Therefore, in order to facilitate engineering application, it is suggested to establish the critical anchorage length formula suitable for ECC in future studies.

Conclusion

In this paper, experimental results for the influence of concrete type and steel bar type on the bond performance between steel bar and cement-based materials through the pullout test were presented and discussed. From this investigation, the following conclusions can be drawn:

1) Compared with failure modes of the pull-out specimens containing normal concrete (P-C16) and SFRC (SF-C16), it was found that fine and intensive cracks that were hard to be observed by naked eyes appeared on the surface of the pullout specimens containing ECC (E-C16). These cracks of E-C16 were radially distributed from the center to the edge, and the number of the cracks on the surface was much more than that on the other two specimens. This showed that ECC had excellent crack control capability and ductile property.

2) The strain of the steel bar at six measuring points was measured with strain gauge. Based on the measured strain and free end slip of the steel bars, the distribution of steel stress, bond stress, and relative slip and the bond slip relation along the anchorage length were obtained and analyzed for different concrete and different steel bars. Anchorage position function was established in consideration of anchorage position, which was conducive to the establishment of an accurate bond–slip relationship.

3) It was safe and conservative to use the calculation formula of critical anchorage length in the current Code for Design of Concrete Structures (GB 50010-2010) in China to calculate the critical anchorage length of the steel bar in ECC. It is suggested to establish the critical anchorage length formula suitable for ECC in future studies.

Author’s Note

Yuexiu Transport Infrastructure Co., Ltd. is mainly engaged in the investment, construction and operation management of toll highways, bridges and ports in Guangdong province and other high-growth provinces of China. In order to extend the service life of the bridge deck and substructure and to reduce material consumption over the life of the bridge and highway, all the authors participated the project on engineered cementitious composite materials and expect to particularly replace the traditional concrete expansion joints.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author Contributions

JX, XL, and HJ conceived and designed the study. MY, LL, FM, and DD performed the experiments. JX, MY, and ZH wrote the paper. JX, XL, and HJ reviewed and edited the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The research presented was funded by the National Natural Science Foundation of China (51778150) and the National Natural Science Foundation of China (51808133), Natural Science Foundation of Guangdong Province in China (2016A030313699), and Guangzhou Municipal Science and Technology Project China (201804010422).

Conflict of Interest

XL and MY were employed by the company Yuexiu Transport Infrastructure Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the National Natural Science Foundation of China for funding this project. The laboratory of school of civil and transportation engineering at Guangdong University of Technology is also gratefully acknowledged for providing all the resources required for this work.

References

Cai, J., Pan, J., Tan, J., and Li, X. (2020). Bond Behaviours of Deformed Steel Rebars in Engineered Cementitious Composites (ECC) and concrete. Construction Building Mater. 252, 119082. doi:10.1016/j.conbuildmat.2020.119082

CrossRef Full Text | Google Scholar

Cai, Z., Liu, F., Yu, J., Yu, K., and Tian, L. (2021). Development of Ultra-high Ductility Engineered Cementitious Composites as a Novel and Resilient Fireproof Coating. Construction Building Mater. 288, 123090. doi:10.1016/j.conbuildmat.2021.123090

CrossRef Full Text | Google Scholar

Choi, W.-C., Jang, S.-J., and Yun, H.-D. (2017). Bond and Cracking Behavior of Lap-Spliced Reinforcing Bars Embedded in Hybrid Fiber Reinforced Strain-Hardening Cementitious Composite (SHCC). Composites B: Eng. 108, 35–44. doi:10.1016/j.compositesb.2016.09.086

CrossRef Full Text | Google Scholar

Deng, M., Pan, J., and Sun, H. (2018). Bond Behavior of Steel Bar Embedded in Engineered Cementitious Composites under Pullout Load. Construction Building Mater. 168, 705–714. doi:10.1016/j.conbuildmat.2018.02.165

CrossRef Full Text | Google Scholar

Fu, C., Fang, D., Ye, H., Huang, L., and Wang, J. (2021). Bond Degradation of Non-uniformly Corroded Steel Rebars in concrete. Eng. Structures 226, 111392. doi:10.1016/j.engstruct.2020.111392

CrossRef Full Text | Google Scholar

Hossain, K. M. A., Alam, S., Anwar, M. S., and Julkarnine, K. M. Y. (2020). Bond Strength of Fibre-Reinforced Polymer Bars in Engineered Cementitious Composites. Proc. Inst. Civil Eng. - Construction Mater. 173 (1), 1–13. doi:10.1680/jcoma.17.00020

CrossRef Full Text | Google Scholar

Hu, B., Zhou, Y., Xing, F., Sui, L., and Luo, M. (2019). Experimental and Theoretical Investigation on the Hybrid CFRP-ECC Flexural Strengthening of RC Beams with Corroded Longitudinal Reinforcement. Eng. Structures 200, 109717. doi:10.1016/j.engstruct.2019.109717

CrossRef Full Text | Google Scholar

Huang, H., Yuan, Y., Zhang, W., Hao, R., and Zeng, J. (2020). Bond Properties between GFRP Bars and Hybrid Fiber-Reinforced concrete Containing Three Types of Artificial Fibers. Construction Building Mater. 250, 118857. doi:10.1016/j.conbuildmat.2020.118857

CrossRef Full Text | Google Scholar

Krstulovic-Opara, N., Watson, K. A., and Lafave, J. M. (1994). Effect of Increased Tensile Strength and Toughness on Reinforcing-Bar Bond Behavior. Cement and Concrete Composites 16 (2), 129–141. doi:10.1016/0958-9465(94)90007-8

CrossRef Full Text | Google Scholar

Lam, L., Huang, L., Xie, J.-H., and Chen, J.-F. (2021). Compressive Behavior of Ultra-high Performance concrete Confined with FRP. Compos. Structures 274, 114321. doi:10.1016/j.compstruct.2021.114321

CrossRef Full Text | Google Scholar

Lee, S. W., Kang, S.-B., Tan, K. H., and Yang, E.-H. (2016). Experimental and Analytical Investigation on Bond-Slip Behaviour of Deformed Bars Embedded in Engineered Cementitious Composites. Construction Building Mater. 127, 494–503. doi:10.1016/j.conbuildmat.2016.10.036

CrossRef Full Text | Google Scholar

Lei, W., Zeng, X., Yang, H., and Lv, X. (2021). Investigation and Application of Fractal Theory in Cement-Based Materials: A Review. Fractal Fractional 5 (4), 247. doi:10.3390/fractalfract5040247

CrossRef Full Text | Google Scholar

Li, V. C., Wu, C., Wang, S. X., Ogawa, A., and Saito, T. (2002). Interface Tailoring for Strain-Hardening Polyvinyl Alcohol Engineered Cementitious Composite (PVA-ECC). ACI Mater. J. 99 (5), 463–472. doi:10.1016/S0042-207X(02)00187-2

CrossRef Full Text | Google Scholar

Wang, H., Sun, X., Peng, G., Luo, Y., and Ying, Q. (2015). Experimental Study on Bond Behaviour between BFRP Bar and Engineered Cementitious Composite. Construction Building Mater. 95, 448–456. doi:10.1016/j.conbuildmat.2015.07.135

CrossRef Full Text | Google Scholar

Wang, L., Guo, F., Lin, Y., Yang, H., and Tang, S. W. (2020). Comparison between the Effects of Phosphorous Slag and Fly Ash on the C-S-H Structure, Long-Term Hydration Heat and Volume Deformation of Cement-Based Materials. Construction Building Mater. 250, 118807. doi:10.1016/j.conbuildmat.2020.118807

CrossRef Full Text | Google Scholar

Wang, L., Jin, M., Zhou, S., Tang, S., and Lu, X. (2021a). Investigation of Microstructure of C-S-H and Micro-mechanics of Cement Pastes under NH4NO3 Dissolution by 29Si MAS NMR and Microhardness. Measurement 185, 110019. doi:10.1016/j.measurement.2021.110019

CrossRef Full Text | Google Scholar

Wang, L., Li, G., Li, X., Guo, F., and Tang, S. (2021b). Influence of Reactivity and Dosage of MgO Expansive Agent on Shrinkage and Crack Resistance of Face Slab concrete. Cement and Concrete Composites 125, 104333. doi:10.1016/j.cemconcomp.2021.104333

CrossRef Full Text | Google Scholar

Xiao, J., Long, X., Ye, M., Jiang, H., Liu, L., and Zhai, K. (2021). Experimental Study of Bond Behavior between Rebar and PVA-Engineered Cementitious Composite (ECC) Using Pull-Out Tests. Front. Mater. 8, 15. doi:10.3389/fmats.2021.633404

CrossRef Full Text | Google Scholar

Xiong, Y., Xu, G., Wu, D., Fang, S., and Tang, Y. (2021a). Investigation of Using the Ceramic Polishing brick Powder in Engineered Cementitious Composites. J. Building Eng. 43, 102489. doi:10.1016/j.jobe.2021.102489

CrossRef Full Text | Google Scholar

Xiong, Y., Yang, Y., Fang, S., Wu, D., and Tang, Y. (2021b). Experimental Research on Compressive and Shrinkage Properties of ECC Containing Ceramic Wastes under Different Curing Conditions. Front. Mater. 8, 1. doi:10.3389/fmats.2021.727273

CrossRef Full Text | Google Scholar

Xu, S., and Wang, H. (2008). Experimental Study on Bond-Slip between Ultra High Toughness Cementitious Composites and Steel Bar. Eng. Mech. 25 (11), 53–061. doi:10.1016/S1872-5791(08)60058-5

CrossRef Full Text | Google Scholar

Yu, K., McGee, W., Ng, T. Y., Zhu, H., and Li, V. C. (2021). 3D-printable Engineered Cementitious Composites (3DP-ECC): Fresh and Hardened Properties. Cement Concrete Res. 143, 106388. doi:10.1016/j.cemconres.2021.106388

CrossRef Full Text | Google Scholar

Yu, K. Q., Wang, Y. C., Yu, J. T., and Xu, S. L. (2017). A Strain-Hardening Cementitious Composites with the Tensile Capacity up to 8. Construction Building Mater. 137, 410–419. doi:10.1016/j.conbuildmat.2017.01.060

CrossRef Full Text | Google Scholar

Zhang, J., Huang, J., Fu, C., Huang, L., and Ye, H. (2021). Characterization of Steel Reinforcement Corrosion in concrete Using 3D Laser Scanning Techniques. Construction Building Mater. 270, 121402. doi:10.1016/j.conbuildmat.2020.121402

CrossRef Full Text | Google Scholar

Zhao, Y., and Jin, W. (2002). Test Study on Bond Stress-Slip Relationship of concrete and Steel Bar. J. Building Structures 23 (1), 32–37. doi:10.1007/BF02960786

CrossRef Full Text | Google Scholar

Zhou, Y., Fu, H., Li, P., Zhao, D., Sui, L., and Li, L. (2019). Bond Behavior between Steel Bar and Engineered Cementitious Composite (ECC) Considering Lateral FRP Confinement: Test and Modeling. Compos. Structures 226, 111206. doi:10.1016/j.compstruct.2019.111206

CrossRef Full Text | Google Scholar