Coiling-Up Space Metasurface for High-Efficient and Wide-angle Acoustic Wavefront Steering

The recent advent of acoustic metasurface displays tremendous potential with their unique and flexible capabilities of wavefront manipulations. In this paper, we propose an acoustic metagrating made of binary coiling-up space structures to coherently control the acoustic wavefront steering. The acoustic wave steering is based on the in-plane coherent modulation of waves in different diffraction channels. The acoustic metagrating structure with a subwavelength thickness is realized with 3D printed two coiling-up space metaunits. By adjusting structural parameters of the metaunits, the −1st-order diffraction mode can be retained, and the rest of the diffraction orders are eliminated as much as possible through destructive interference, forming a high-efficiency anomalous reflection in the scattering field. The anomalous reflection performance of the designed metagrating is achieved over a wide range of incident angles with high efficiency.

Introduction

The recently appeared acoustic metasurfaces, as the two-dimensional (2D) version of metamaterials with subwavelength thicknesses, have shown outstanding capabilities in manipulating acoustic waves compared to natural materials (Li et al., 2013; Zhao et al., 2013; Ma et al., 2014; Xie et al., 2014; Xie et al., 2017; Assouar et al., 2018; Zhu et al., 2018; Chen et al., 2019; Long et al., 2020; Zhang et al., 2020). Metasurfaces originally have been introduced and progressed for manipulating electromagnetic waves (Yu et al., 2011; Yang et al., 2019; Guan et al., 2020a; Ding et al., 2020; Yuan et al., 2020; Fan et al., 2021) and then are expanded to steer the acoustic waves given that both of the them obey the generalized Snell’s law. Basically, the uniqueness of metasurfaces rested with their ability of easily adjusting the phase and/or amplitude so as to fully control the wave fields. At present, acoustic metasurfaces with various profiles have been proposed for different functions and applications, including (but not limited to) Helmholtz-resonator-like (Li et al., 2015; Wang et al., 2016; Zhang et al., 2021), membrane-type (Ma et al., 2014; Tang et al., 2019; Liu et al., 2020), and coiling-up space (Xie et al., 2014; Liang and Li, 2012; N. Almeida et al., 2021). By properly designing the inner structures of metasurfaces, a great deal of fascinating features has been realized, such as anomalous reflection and refraction (Liu et al., 2017; Li et al., 2018; Liu and Jiang, 2018; Qian et al., 2019; Su and Liu, 2020), asymmetric propagation (Shen et al., 2016; Li et al., 2017; Song et al., 2019), orbital angular momentum (Shi et al., 2019; Gao et al., 2021; Hou et al., 2021), near-perfect absorption (Zhu et al., 2019; Kumar and Lee, 2020; Donda et al., 2021; Liu et al., 2021a), beam focusing (Ma et al., 2018; Liu et al., 2021b; Xie and Hou, 2021), self-bending beams (Li and Assouar, 2015), acoustic cloaking (Jin et al., 2019; Li et al., 2019; Zhao et al., 2019; Fan et al., 2020; Zhou et al., 2021), and convolution operation and addition operation (Cao et al., 2021).

Most of the demonstrated metasurfaces for anomalous reflection based on generalized Snell’s law requires the arrangement of multi-metaunits with gradient indexes to provide additional phases of the scattered waves. Furthermore, the phase-gradient metasurface shows poor power efficiency due to mismatched wave impedances, because it cannot direct all incident energy to the required direction and eliminate the undesired scattered waves (Mohammadi Estakhri and Alù, 2016; Díaz-Rubio and Tretyakov, 2017). In addition, complex structural metaunits lead to unavoidable viscosity loss and non-negligible coupling effect between adjacent metaunits, and both of them will influence the efficiency of wavefront manipulation (Tang et al., 2021). Therefore, tremendous research studies have been devoted to achieving high-efficiency anomalous reflection. Retroreflector is a device that can reflect electromagnetic waves or acoustic waves back to the incident direction. Shen et al. proposed an acoustic retroreflector on the basis of conventional gradient-index metasurfaces without parasitic diffraction (Shen et al., 2018). Díaz-Rubio et al. presented a new synthesis method that introduces nonlocal response or local and nonsymmetric response into reflection and refraction, respectively. This method overcomes the radical limitations of traditional designs, permits complete control of the acoustic energy flow, and achieves perfect anomalous reflection and refraction (Díaz-Rubio and Tretyakov, 2017). Fu et al. investigated theoretically and experimentally phase gradient metagratings (PGMs), which can completely reverse the anomalous transmission and reflection through higher-order diffraction by changing the integer parity of the PGM design (Fu et al., 2019a). Li et al. induced self-induced surface waves into acoustic metasurfaces to meet the local power conservation requirements and cultivated an approach to design bianisotropic metasurfaces for arbitrary beam splitting and anomalous reflection with theoretically power efficiency of 100% (Li et al., 2020). However, these studies are proposed with complex theories and designed by metaunits with full phase range that make the designs difficulty to realize. Therefore, a new metasurface, i.e., metagrating, has been proposed to steer the acoustic wavefront with simpler methodology (Fu et al., 2019b; Fu et al., 2020a; Fu et al., 2020b). Guan et al. utilized metagrating to achieve helicity-switching and helicity-preserving performances in electromagnetic field (Guan et al., 2020b). Fu et al. reported a simple metagrating to achieve multifunctional reflection in acoustic field, which provides an alternative way for the manipulation of acoustic waves with high efficiency (Xie et al., 2017). However, this study is not yet verified in experiments.

In this paper, we propose an acoustic metagrating on the basis of the in-plane coherent modulation of acoustic waves in different diffraction channels, which does not need to be based on the generalized Snell’s law. The metagrating is made of binary coiling-up space metaunits to coherently control the wavefront steering. In our study, two 3D printed metaunits whose reflected waves satisfy the coherent condition are periodically arranged to form a metagrating that can realize high-efficiency anomalous reflection of acoustic waves. The validity of the wavefront manipulation method is proved in simulations and experiments. At last, the wide-angle characteristic of the designed metagrating is demonstrated in a range of 40° with high efficiency.

Materials and Methods

Because the propagation of acoustic waves follows the Huygens-Fresnel principle, the effect of acoustic diffraction can be easily understood. As shown in Figure 1A, the acoustic waves with an incident angle $\alpha$ incident on the surface of a grating. The grating constant is d. When the incident wavelength ${\lambda }_0$ is sufficiently short compared to the grating constant d, one or more diffraction modes could be motivated with a non-specular diffraction angle. Therefore, we can adjust d to remain one of the reflection diffraction modes and eliminated as much as possible by destructive interference, so as to realize anomalous reflection. This structure with optional diffraction modes is called metagrating, which combines the diffraction ability of the acoustic grating with the phase control capacity of the metasurface. The concept of metagrating renders a valid platform to realize the control of the acoustic wavefront. When a single-frequency acoustic wave travels in the same medium, the length difference of different transmission paths will cause phase difference between them. According to the two reflection paths in Figure 1A, the path difference can be calculated by the geometric analysis. When the value is an integer of the wavelength, constructive interference occurs, that is, it satisfies

$K{\lambda }_0=d\left(\sin {\beta }_K-\sin \alpha \right)(1)$

where K = 0, ±1, ±2, …, λ₀ is the wavelength, and ${\beta }_K$ is the reflected angle of diffraction order K. When the grating constant d satisfies Eq. 1, diffractions of different orders will occur in the acoustic field due to constructive interference. When K is 0, it is the normal specular reflection of 0th order. Metagrating is an artifical structure designed by the grating theory, which is made of metaunits instead of the traditional materials with different indexes. To obtain anomalous reflection based on acoustic metagrating, it is necessary to use two artificial metaunits in one grating period to eliminate the extra diffraction orders by means of destructive interference. Here, the −1st anomalous reflection is desired in our study. To make sure of the reflected acoustic waves without 2nd-order or higher-order diffraction components, the grating constant d and incident angle $\alpha$should satisfy

$2{\lambda }_0>d\left(1+\left|\sin \alpha \right|\right)(2)$

FIGURE 1

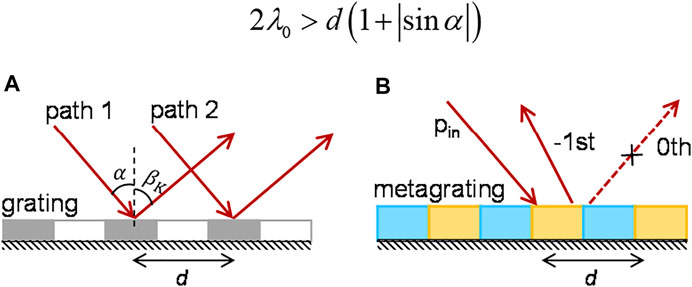
FIGURE 1. (A) The geometric paths of two parallel acoustic beams. (B) The schematic of a binary metagrating for coherent modulation of acoustic waves.

In this work, we hope to obtain the anomalous reflection with a −1st-order diffraction, so the designed metagrating should eliminate the 0th order and +1st-order diffraction. When $\alpha \ne {90}^o$, the essential condition for grating without +1st-order diffraction given by

${\lambda }_0>d\left(1-\left|\sin \alpha \right|\right)(3)$

Therefore, the anomalous reflection can be achieved by eliminating the 0th-order diffraction, as shown in Figure 1B. In this case, only two metaunits with phase difference of $\pi$ for constructive interference are needed in a grating period. As a result, the 0th-order reflection is eliminated, and only the −1st-order diffraction is remained.

The designed metagrating includes two coiling-up space metaunits, as shown in Figure 2A. Each metaunit is designed with width of m = 5 cm, height of p = 6 cm, and wall thickness of w = 4 mm. By adjusting the length of the branches in the metaunits, the propagation path of acoustic waves will be changed and the reflected phase will be modulated accordingly. The length of branches of unit A is l₁ = 3.18 cm, and parametric sweep of the length of branches in unit B is performed so that the reflected phase difference of the two metaunits is $\pi$ to eliminate the 0th-order acoustic wave as much as possible. In this case, the acoustic grating constant is d = 10 cm. When the wavelength${\lambda }_0$is slightly larger than the acoustic grating constant, with any incident angle $\alpha$, both (2) and (3) are all satisfied, which means that the acoustic waves are coherently controlled in different diffraction channels and higher-order diffraction modes are eliminated in the acoustic fields.

FIGURE 2

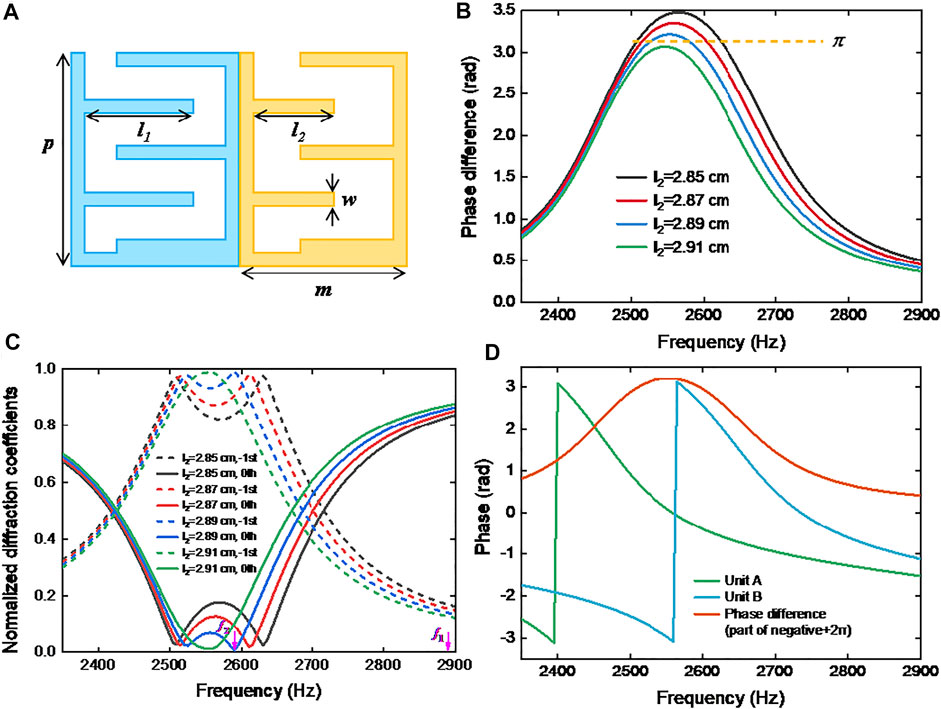
FIGURE 2. (A) The inner structures of the binary coiling-up space metaunits. (B) The reflection phase difference between unit A and unit B varying with l₂. (C) The normalized coefficients of each diffraction order in the reflection fields with difference l₂, where the dotted lines represent the −1st orders and the solid lines represents the 0th orders. (D) Phase curves (green and blue) and phase difference curves (orange) of unit A and unit B when the selected optimal structure l₂ = 2.89 cm.

The COMSOL Multiphysics software is used to perform the numerical of the distribution of the acoustic fields. The speed of acoustic waves and mass density of air are c₀ = 343 m/s and ρ₀ = 1.21 kg/m³, respectively, the incident angle $\alpha$is 45°, and the amplitude of the incident plane wave is 1 Pa. According to the diffraction equation, the −1st diffraction angle is ${\gamma }_1=\arcsin \left(\sin \alpha -\lambda /d\right)$. The phase difference between unit A and unit B is shown in Figure 2B; when l₂ = 2.85, 2.87, and 2.89 cm, there are two frequency points where the phase difference is $\pi$, and at l₂ = 2.91 cm, one frequency point of the phase difference is close to $\pi$. These frequencies are generally around 2,500–2,600 Hz. Figure 2C shows the normalized diffraction coefficients of diffraction modes. It can be seen that, for different values of l₂ of unit B, the normalized diffraction coefficients of the 0th-order and −1st-order diffractions of the unit B are different. For l₂ = 2.85, 2.87, and 2.89 cm, the 0th-order diffraction curve has two minimum frequency points, and the distance between the two minimum points gradually decreases with the increase of l₂. At the same time, there is a maximum frequency point between the two minimum values, and the normalized diffraction coefficients of 0th order at this point gradually decreases with the increase of l₂. When l₂ increases to 2.91 cm, there is only one minimum frequency point for 0th-order diffraction. It is in good agreement with the phase difference curves of the two metaunits in Figure 2B, that is, the closer the phase difference is to$\pi$, the smaller proportion of 0th order in the reflected fields. It also proves that the 0th-order diffraction in the reflected fields shows destructive interference due to the phase adjustment of the two metaunits. Meanwhile, this study also provides a strong proof of the validity of diffraction-based acoustic metagrating in wavefront control.

According to the discussions above, the 0th diffraction angle is 45° because of specular reflection and the −1st diffraction angle is ${\gamma }_1=\arcsin \left(\sin \alpha -\lambda /d\right)$according to the diffraction equation. Therefore, the normalized diffraction coefficients can be obtained by the normalization of integrals of far-field acoustic intensity around the diffraction angles. Under the consideration of the high efficiency of −1st-order diffraction, we choose l₂ = 2.89 cm and the workting frequency is f₂ = 2,590 Hz where the theoretical diffraction coefficient of anomalous reflection is 0.97. As shown in Figure 2D, the green and the blue curves represent the reflection phase of unit A and unit B, respectively, and the orange curve is the phase difference curve of the two. It is obvious that the phase difference curves of the two metaunits are much smoother than respective reflection phase curves, and anomalous reflection can also be achieved in a certain frequency bandwidth, although the theoretical efficiency is less than 100%.

Figure 3 shows the acoustic pressure distributions of incident waves and reflected waves at f₁ = 2,890 Hz and f₂ = 2,590 Hz. After comparison, it can be clearly seen that, when the incident angle is 45°, the 0th-order diffraction plays a dominant role at f₁, and the propagation of acoustic waves is specular reflection with a reflection angle ${\beta }_1$ of 45°. At f₂, the reflected acoustic waves are also plane waves, but the propagation direction is negative, coexisting with the incident acoustic wave on the same side of the interface normal. According to the acoustic pressure fields, the diffraction angle can be estimated to be about −38°, which is consistent with the diffraction angle calculated by the diffraction equation.

FIGURE 3

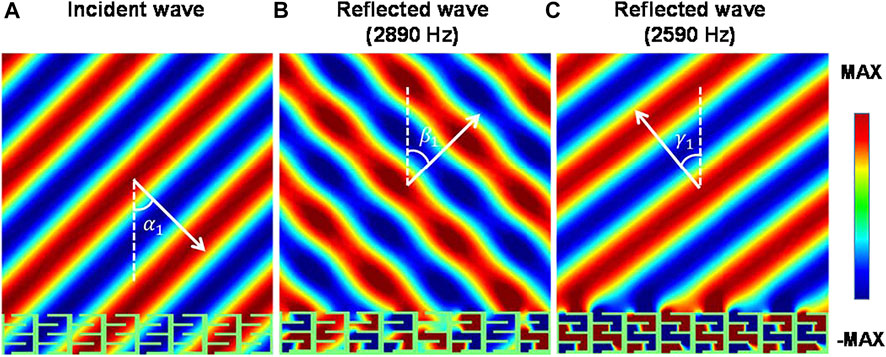
FIGURE 3. (A) Incident acoustic fields with plane wave. (B) Reflected pressure fields at non-working frequency f₁ = 2,890 Hz. (C) Reflected pressure fields at working frequency f₂ = 2,590 Hz.

Results

In simulation, the designed binary metagrating is used to achieve high-efficiency anomalous reflections. To further verify the wavefront manipulation capability of the designed metagrating, we prepare the model using 3D printing technology, and the printing material is polylactic acid. A scanning stage is used to perform the measurement, as shown in Figure 4A. A 2D waveguide is made of two paralleled plexiglass plates (1.2 × 2.2 m²), and absorbing sponges are installed around the waveguide closely to minimize the echo and environmental noise. To form a plane wave in the waveguide, a sine signal is generated by a computer and transmitted to an amplifier by a digital collector that converts the digital signal into an acoustic signal. A loudspeaker array is arranged on the top of the waveguide that is motivated by the amplifier. The acoustic pressure in the waveguide is measured by two microphones, one for detection and one for reference. Then, the acoustic signal is achieved and transmitted back to the computer by the collector through different channels.

FIGURE 4

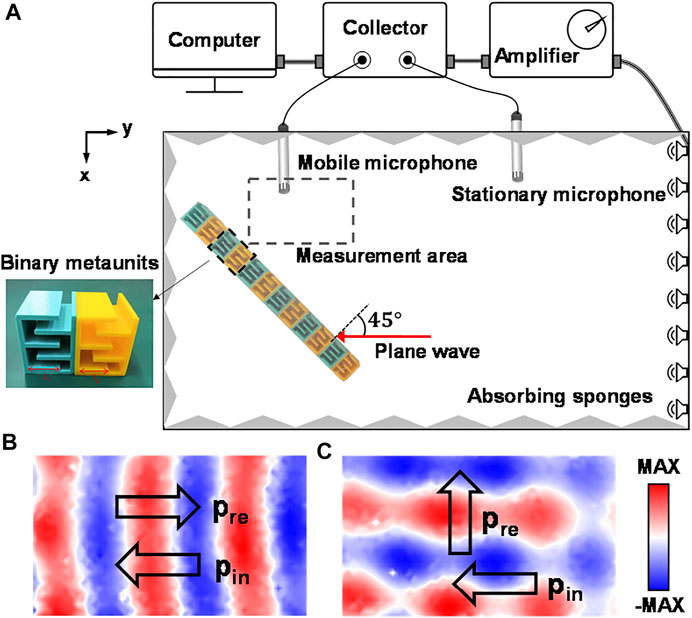
FIGURE 4. (A) Schematic diagram of experimental waveguide system. The dashed line box in the figure represents the measurement area where a single microphone is used to scan and measure acoustic pressure. The insert is the picture of the coiling-up space metaunits. (B) Total pressure fields after the plane acoustic wave passing through the sample. (C) Total pressure fields of plane acoustic wave passing through hard plane boundary.

When the incident angle $\alpha$ is 45°, the 3D printed metaunits are arranged periodically in the waveguide periodically. Because of the platform design, the loudspeaker array can only propagate acoustic waves along the long axis of the waveguide. We place the sample at an angle of 45°, which is equivalent to an incident angle of 45°. Microphone is used to scan the acoustic pressure value at multiple points and obtain the fields distribution in the area of the blue dashed line box. For comparison, we measured the total pressure fields after the plane acoustic waves incident into the metagrating and hard boundary plane, respectively. It is clear that there is a great difference between the two. When the reflective interface is hard boundary plane, the reflection angle is the same as the incident angle at 45°, and the incident waves and reflected waves interfere to form a standing wave field, as shown in Figure 4C. Figure 4B shows the total pressure fields when the reflective interface is a designed model. The pressure field is almost a plane wave along the horizontal direction, which is formed by the interference of the −1st-order diffraction and the incident acoustic waves.

As illustrated in all these simulations and experiments, the metagrating made of coiling-up space metaunits can modulate the reflection behavior of the objects effectively. It indicates that the metagrating provide a feasible means to realize wavefront control. The most outstanding feature of the metagrating is that each grating period contains only two metaunits for coherent modulation of waves, and it simplifies the process of realizing anomalous reflection greatly. Compared with acoustic metasurface with reflected phases from 0 to 2$\pi$ based on generalized Snell’s law, metagrating with only two reflected phases of 0 and $\pi$ is easier to obtain in experiment.

Discussion

Because metagrating is proposed on the basis of the coherent modulation of waves, the anomalous reflection performances of the designed metagrating with different incident angles are also studied in simulations. According to the diffraction equation of metagrating, the incident angle range for metagrating with −1st-order diffraction and without 1st-order diffraction is $\text{α}>18.6°$ when the working frequency is 2,590 Hz and the grating constant is 10 cm. The normalized −1st-order diffraction coefficients of the metgrating with varying incident angles are shown in Figure 5A. Over the range from $23°$ to $61°$, the normalized diffraction coefficients are larger than 0.85, where the phase difference between the binary metaunits approaches to $\text{π}$. It means that high-efficiency anomalous reflection is achieved over a wide range of incident angle of $38°$. The simulation results satisfy the predicted range of incident angles for the occurrence of −1st-order diffraction. However, under the incident angles that approach to $45°$, the efficiency of anomalous reflection do not reach the desired value of 1 because of partial destructive interference of the 0th diffractions of the binary metaunits.

FIGURE 5

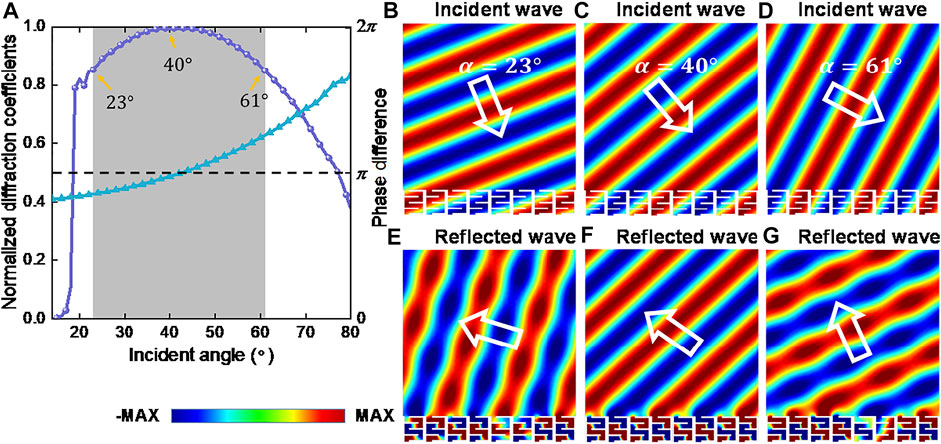
FIGURE 5. (A) Normalized −1st-order diffraction coefficients and phase difference between the binary metaunits at 2,590 Hz under different incident angles. The gray area represents the region of the value larger than 0.85. (B–D) Incident acoustic fields under incident angles of $23°$, $40°$, and $61°$. (E–G) Reflected acoustic fields under incident angles of $23°$, $40°$, and $61°$.

Here, we demonstrate the anomalous reflection performance under incident angles of $23°$, $40°$ and $61°$, where the normalized −1st-order diffraction coefficients are 0.85, 0.99, and 0.85, respectively. The incident acoustic fields are shown in Figures 5B–D, and the corresponding reflected acoustic fields are shown in Figures 5E–G. It can be seen that obvious anomalous reflections are acquired under the three incident angles. Therefore, the wide-angle performance of the designing metagrating is verified in simulations with high efficiency.

Conclusion

In summary, we proposed a kind reflective acoustic metasurface on the basis of the coherent control of acoustic wave for wide-angle acoustic wavefront control. By coherently modulating the reflected waves in different diffraction channels, the high-efficiency anomalous reflection is obtain over a wide range of incident angles with high efficiency. The major idea is to utilize the binary coiling-up space metaunits for the in-plane destructive interference of extra diffraction orders in an acoustic grating period and only remain one needed diffraction order. The feasibility has been verified both in simulations and experiments. Compared with the previous wavefront control method based on the generalized Snell’s law, the mechanism of coherent modulation of waves needs lower requirements on the number and phase control capability of metaunits and is valid in wide range of incident angles. This control method renders a feasible way for future research on the interaction between acoustic artificial microstructures and acoustic waves. In addition, to extend this method to a wideband, tunable acoustic metagrating is considered for the control of acoustic wavefront.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

YF and FZ conceived the idea and guided the research. FY and SC designed the metasurface. SC, FY, and KS prepared the samples, characterized the samples, and prepared the draft. All authors discussed the results and commented on the paper.

Funding

The authors would like to acknowledge financial support from National Natural Science Foundation of China (NSFC) (grants nos. 61771402, 12074314, and 11674266); NPU AoXiang New Star program; Science, Technology and Innovation Commission of Shenzhen Municipality (JCYJ20170817162221169); Shaanxi Province Postdoctoral Science Foundation (no. 2018BSHEDZZ64); and Natural Science Basic Research Plan in Shaanxi Province of China (nos. 2018JM6024 and 2020JM-145).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Assouar, B., Liang, B., Wu, Y., Li, Y., Cheng, J.-C., and Jing, Y. (2018). Acoustic Metasurfaces. Nat. Rev. Mater. 3, 460–472. doi:10.1038/s41578-018-0061-4

CrossRef Full Text | Google Scholar

Cao, W. K., Zhang, C., Wu, L. T., Guo, K. Q., Ke, J. C., Cui, T. J., et al. (2021). Tunable Acoustic Metasurface for Three-Dimensional Wave Manipulations. Phys. Rev. Appl. 15, 024026. doi:10.1103/PhysRevApplied.15.024026

CrossRef Full Text | Google Scholar

Chen, S., Fan, Y., Yang, F., Jin, Y., Fu, Q., Zheng, J., et al. (2019). Engineering Coiling‐Up Space Metasurfaces for Broadband Low‐Frequency Acoustic Absorption. Phys. Status Solidi RRL 13, 1900426. doi:10.1002/pssr.201900426

CrossRef Full Text | Google Scholar

Díaz-Rubio, A., and Tretyakov, S. A. (2017). Acoustic Metasurfaces for Scattering-free Anomalous Reflection and Refraction. Phys. Rev. B 96, 125409. doi:10.1103/PhysRevB.96.125409

CrossRef Full Text | Google Scholar

Ding, X., Wang, Z., Hu, G., Liu, J., Zhang, K., Li, H., et al. (2020). Metasurface Holographic Image Projection Based on Mathematical Properties of Fourier Transform. PhotoniX 1, 16. doi:10.1186/s43074-020-00016-8

CrossRef Full Text | Google Scholar

Donda, K., Zhu, Y., Merkel, A., Fan, S.-W., Cao, L., Wan, S., et al. (2021). Ultrathin Acoustic Absorbing Metasurface Based on Deep Learning Approach. Smart Mater. Struct. 30, 085003. doi:10.1088/1361-665X/ac0675

CrossRef Full Text | Google Scholar

Fan, S.-W., Zhao, S.-D., Cao, L., Zhu, Y., Chen, A.-L., Wang, Y.-F., et al. (2020). Reconfigurable Curved Metasurface for Acoustic Cloaking and Illusion. Phys. Rev. B 101, 024104. doi:10.1103/PhysRevB.101.024104

CrossRef Full Text | Google Scholar

Fan, Y., He, X., Zhang, F., Cai, W., Li, C., Fu, Q., et al. (2021). Fano-resonant Hybrid Metamaterial for Enhanced Nonlinear Tunability and Hysteresis Behavior. Research 2021, 1–9. doi:10.34133/2021/9754083

CrossRef Full Text | Google Scholar

Fu, Y.-Y., Tao, J.-Q., Song, A.-L., Liu, Y.-W., and Xu, Y.-D. (2020). Controllably Asymmetric Beam Splitting via gap-induced Diffraction Channel Transition in Dual-Layer Binary Metagratings. Front. Phys. 15, 52502. doi:10.1007/s11467-020-0968-2

CrossRef Full Text | Google Scholar

Fu, Y., Cao, Y., and Xu, Y. (2019). Multifunctional Reflection in Acoustic Metagratings with Simplified Design. Appl. Phys. Lett. 114, 053502. doi:10.1063/1.5083081

CrossRef Full Text | Google Scholar

Fu, Y., Shen, C., Cao, Y., Gao, L., Chen, H., Chan, C. T., et al. (2019). Reversal of Transmission and Reflection Based on Acoustic Metagratings with Integer Parity Design. Nat. Commun. 10, 2326. doi:10.1038/s41467-019-10377-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Fu, Y., Shen, C., Zhu, X., Li, J., Liu, Y., Cummer, S. A., et al. (2020). Sound Vortex Diffraction via Topological Charge in Phase Gradient Metagratings. Sci. Adv. 6, eaba9876. doi:10.1126/sciadv.aba9876

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, S., Li, Y., Ma, C., Cheng, Y., and Liu, X. (2021). Emitting Long-Distance Spiral Airborne Sound Using Low-Profile Planar Acoustic Antenna. Nat. Commun. 12, 2006. doi:10.1038/s41467-021-22325-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Guan, C., Li, H., Ding, X., Wang, Z., Zhang, K., Jin, M., et al. (2020). Dual-polarized Dual-Channel Helicity-Switching or Helicity-Preserving Retroreflectors Utilizing 1-bit Coding Metasurfaces. ACS Appl. Electron. Mater. 2, 3380–3389. doi:10.1021/acsaelm.0c00650

CrossRef Full Text | Google Scholar

Guan, C., Liu, J., Ding, X., Wang, Z., Zhang, K., Li, H., et al. (2020). Dual-polarized Multiplexed Meta-Holograms Utilizing Coding Metasurface. Nanophotonics 9, 3605–3613. doi:10.1515/nanoph-2020-0237

CrossRef Full Text | Google Scholar

Hou, Z., Ding, H., Wang, N., Fang, X., and Li, Y. (2021). Acoustic Vortices via Nonlocal Metagratings. Phys. Rev. Appl. 16, 014002. doi:10.1103/PhysRevApplied.16.014002

CrossRef Full Text | Google Scholar

Jin, Y., Fang, X., Li, Y., and Torrent, D. (2019). Engineered Diffraction Gratings for Acoustic Cloaking. Phys. Rev. Appl. 11, 011004. doi:10.1103/PhysRevApplied.11.011004

CrossRef Full Text | Google Scholar

Kumar, S., and Lee, H. P. (2020). Labyrinthine Acoustic Metastructures Enabling Broadband Sound Absorption and Ventilation. Appl. Phys. Lett. 116, 134103. doi:10.1063/5.0004520

CrossRef Full Text | Google Scholar

Li, H.-x., Rosendo-López, M., Zhu, Y.-f., Fan, X.-d., Torrent, D., Liang, B., et al. (2019). Ultrathin Acoustic Parity-Time Symmetric Metasurface Cloak. Research 2019, 1–7. doi:10.34133/2019/8345683

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Shen, C., Díaz-Rubio, A., Tretyakov, S. A., and Cummer, S. A. (2018). Systematic Design and Experimental Demonstration of Bianisotropic Metasurfaces for Scattering-free Manipulation of Acoustic Wavefronts. Nat. Commun. 9, 1342. doi:10.1038/s41467-018-03778-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Song, A., and Cummer, S. A. (2020). Bianisotropic Acoustic Metasurface for Surface-Wave-Enhanced Wavefront Transformation. Phys. Rev. Appl. 14, 044012. doi:10.1103/PhysRevApplied.14.044012

CrossRef Full Text | Google Scholar

Li, Y., and Assouar, M. B. (2015). Three-dimensional Collimated Self-Accelerating Beam through Acoustic Metascreen. Sci. Rep. 5, 17612. doi:10.1038/srep17612

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Jiang, X., Liang, B., Cheng, J.-c., and Zhang, L. (2015). Metascreen-based Acoustic Passive Phased Array. Phys. Rev. Appl. 4, 024003. doi:10.1103/PhysRevApplied.4.024003

CrossRef Full Text | Google Scholar

Li, Y., Liang, B., Gu, Z.-m., Zou, X.-y., and Cheng, J.-c. (2013). Reflected Wavefront Manipulation Based on Ultrathin Planar Acoustic Metasurfaces. Sci. Rep. 3, 2546. doi:10.1038/srep02546

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Shen, C., Xie, Y., Li, J., Wang, W., Cummer, S. A., et al. (2017). Tunable Asymmetric Transmission via Lossy Acoustic Metasurfaces. Phys. Rev. Lett. 119, 035501. doi:10.1103/PhysRevLett.119.035501

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., and Li, J. (2012). Extreme Acoustic Metamaterial by Coiling up Space. Phys. Rev. Lett. 108, 114301. doi:10.1103/PhysRevLett.108.114301

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, B., and Jiang, Y. (2018). Metasurface-based Angle-Selective Multichannel Acoustic Refractor. Appl. Phys. Express 11, 057301. doi:10.7567/apex.11.057301

CrossRef Full Text | Google Scholar

Liu, B., Ren, B., Zhao, J., Xu, X., Feng, Y., Zhao, W., et al. (2017). Experimental Realization of All-Angle Negative Refraction in Acoustic Gradient Metasurface. Appl. Phys. Lett. 111, 221602. doi:10.1063/1.5004005

CrossRef Full Text | Google Scholar

Liu, H., Wu, J. H., and Ma, F. (2021a). Dynamic Tunable Acoustic Metasurface with Continuously Perfect Sound Absorption. J. Phys. D: Appl. Phys. 54, 365105. doi:10.1088/1361-6463/ac0ab9

CrossRef Full Text | Google Scholar

Liu, J.-j., Liang, B., and Cheng, J.-c. (2021b). Focusing a Two-Dimensional Acoustic Vortex beyond Diffraction Limit on an Ultrathin Structured Surface. Phys. Rev. Appl. 15, 014015. doi:10.1103/PhysRevApplied.15.014015

CrossRef Full Text | Google Scholar

Liu, P., Chen, X., Xu, W., and Pei, Y. (2020). Magnetically Controlled Multifunctional Membrane Acoustic Metasurface. J. Appl. Phys. 127, 185104. doi:10.1063/1.5145289

CrossRef Full Text | Google Scholar

Long, Y., Zhang, D., Yang, C., Ge, J., Chen, H., and Ren, J. (2020). Realization of Acoustic Spin Transport in Metasurface Waveguides. Nat. Commun. 11, 4716. doi:10.1038/s41467-020-18599-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, G., Fan, X., Ma, F., de Rosny, J., Sheng, P., and Fink, M. (2018). Towards Anti-causal Green's Function for Three-Dimensional Sub-diffraction Focusing. Nat. Phys. 14, 608–612. doi:10.1038/s41567-018-0082-3

CrossRef Full Text | Google Scholar

Ma, G., Yang, M., Xiao, S., Yang, Z., and Sheng, P. (2014). Acoustic Metasurface with Hybrid Resonances. Nat. Mater 13, 873–878. doi:10.1038/nmat3994

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohammadi Estakhri, N., and Alù, A. (2016). Wave-front Transformation with Gradient Metasurfaces. Phys. Rev. X 6, 041008. doi:10.1103/PhysRevX.6.041008

CrossRef Full Text | Google Scholar

N. Almeida, G. d., Vergara, E. F., Barbosa, L. R., Lenzi, A., and Birch, R. S. (2021). Sound Absorption Metasurface with Symmetrical Coiled Spaces and Micro Slit of Variable Depth. Appl. Acoust. 183, 108312. doi:10.1016/j.apacoust.2021.108312

CrossRef Full Text | Google Scholar

Qian, J., Wang, Y., Yuan, S.-q., Sun, H.-x., and Liu, X.-j. (2019). Reflected Acoustic Wavefront Manipulation by an Ultrathin Metasurface Based on Three-Dimensional Generalized Snell's Law. Appl. Phys. Express 12, 094001. doi:10.7567/1882-0786/ab3492

CrossRef Full Text | Google Scholar

Shen, C., Díaz-Rubio, A., Li, J., and Cummer, S. A. (2018). A Surface Impedance-Based Three-Channel Acoustic Metasurface Retroreflector. Appl. Phys. Lett. 112, 183503. doi:10.1063/1.5025481

CrossRef Full Text | Google Scholar

Shen, C., Xie, Y., Li, J., Cummer, S. A., and Jing, Y. (2016). Asymmetric Acoustic Transmission through Near-Zero-index and Gradient-index Metasurfaces. Appl. Phys. Lett. 108, 223502. doi:10.1063/1.4953264

CrossRef Full Text | Google Scholar

Shi, C., Zhao, R., Long, Y., Yang, S., Wang, Y., Chen, H., et al. (2019). Observation of Acoustic Spin. Natl. Sci. Rev. 6, 707–712. doi:10.1093/nsr/nwz059

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, X., Chen, T., and Zhu, J. (2019). Frequency-selective Asymmetric Transmission via the Lossy Acoustic Metasurface. Appl. Phys. Express 12, 094006. doi:10.7567/1882-0786/ab3ab7

CrossRef Full Text | Google Scholar

Su, G., and Liu, Y. (2020). Amplitude-modulated Binary Acoustic Metasurface for Perfect Anomalous Refraction. Appl. Phys. Lett. 117, 221901. doi:10.1063/5.0032509

CrossRef Full Text | Google Scholar

Tang, S., Ren, B., Feng, Y., Song, J., and Jiang, Y. (2021). The Generation of Acoustic Airy Beam with Selective Band Based on Binary Metasurfaces: Customized on Demand. Appl. Phys. Lett. 119, 071907. doi:10.1063/5.0060032

CrossRef Full Text | Google Scholar

Tang, Y.-F., Liang, B., Yang, J., Yang, J., and Cheng, J.-c. (2019). Voltage-controlled Membrane-type Active Acoustic Metasurfaces with Ultrathin Thickness. Appl. Phys. Express 12, 064501. doi:10.7567/1882-0786/ab1277

CrossRef Full Text | Google Scholar

Wang, X.-P., Wan, L.-L., Chen, T.-N., Song, A.-L., and Du, X.-W. (2016). Broadband Reflected Wavefronts Manipulation Using Structured Phase Gradient Metasurfaces. AIP Adv. 6, 065320. doi:10.1063/1.4954750

CrossRef Full Text | Google Scholar

Xie, B., Tang, K., Cheng, H., Liu, Z., Chen, S., and Tian, J. (2017). Coding Acoustic Metasurfaces. Adv. Mater. 29, 1603507. doi:10.1002/adma.201603507

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, H., and Hou, Z. (2021). Nonlocal Metasurface for Acoustic Focusing. Phys. Rev. Appl. 15, 034054. doi:10.1103/PhysRevApplied.15.034054

CrossRef Full Text | Google Scholar

Xie, Y., Wang, W., Chen, H., Konneker, A., Popa, B.-I., and Cummer, S. A. (2014). Wavefront Modulation and Subwavelength Diffractive Acoustics with an Acoustic Metasurface. Nat. Commun. 5, 5553. doi:10.1038/ncomms6553

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, F., Fan, Y., Yang, R., Xu, J., Fu, Q., Zhang, F., et al. (2019). Controllable Coherent Perfect Absorber Made of Liquid Metal-Based Metasurface. Opt. Express 27, 25974–25982. doi:10.1364/oe.27.025974

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, N., Genevet, P., Kats, M. A., Aieta, F., Tetienne, J.-P., Capasso, F., et al. (2011). Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 334, 333–337. doi:10.1126/science.1210713

PubMed Abstract | CrossRef Full Text | Google Scholar

Yuan, Y., Zhang, K., Ratni, B., Song, Q., Ding, X., Wu, Q., et al. (2020). Independent Phase Modulation for Quadruplex Polarization Channels Enabled by Chirality-Assisted Geometric-phase Metasurfaces. Nat. Commun. 11, 4186. doi:10.1038/s41467-020-17773-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Cao, W. K., Wu, L. T., Ke, J. C., Jing, Y., Cui, T. J., et al. (2021). A Reconfigurable Active Acoustic Metalens. Appl. Phys. Lett. 118, 133502. doi:10.1063/5.0045024

CrossRef Full Text | Google Scholar

Zhang, Y., Cheng, H., Tian, J., and Chen, S. (2020). Frequency-Selected Bifunctional Coding Acoustic Metasurfaces. Phys. Rev. Appl. 14, 064057. doi:10.1103/PhysRevApplied.14.064057

CrossRef Full Text | Google Scholar

Zhao, J., Li, B., Chen, Z. N., and Qiu, C.-W. (2013). Redirection of Sound Waves Using Acoustic Metasurface. Appl. Phys. Lett. 103, 151604. doi:10.1063/1.4824758

CrossRef Full Text | Google Scholar

Zhao, W., Chu, H., Tao, Z., and Hang, Z. H. (2019). Acoustic Transmissive Cloaking Using Zero-index Materials and Metasurfaces. Appl. Phys. Express 12, 054004. doi:10.7567/1882-0786/ab14ad

CrossRef Full Text | Google Scholar

Zhou, H.-T., Fu, W.-X., Wang, Y.-F., Wang, Y.-S., Laude, V., and Zhang, C. (2021). Ultra-broadband Passive Acoustic Metasurface for Wide-Angle Carpet Cloaking. Mater. Des. 199, 109414. doi:10.1016/j.matdes.2020.109414

CrossRef Full Text | Google Scholar

Zhu, Y., Donda, K., Fan, S., Cao, L., and Assouar, B. (2019). Broadband Ultra-thin Acoustic Metasurface Absorber with Coiled Structure. Appl. Phys. Express 12, 114002. doi:10.7567/1882-0786/ab494a

CrossRef Full Text | Google Scholar

Zhu, Y., Hu, J., Fan, X., Yang, J., Liang, B., Zhu, X., et al. (2018). Fine Manipulation of Sound via Lossy Metamaterials with Independent and Arbitrary Reflection Amplitude and Phase. Nat. Commun. 9, 1632. doi:10.1038/s41467-018-04103-0

PubMed Abstract | CrossRef Full Text | Google Scholar