
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Mater. , 16 December 2021
Sec. Mechanics of Materials
Volume 8 - 2021 | https://doi.org/10.3389/fmats.2021.769879
This article is part of the Research Topic Recent Advances in Low-Positive, Zero, and Negative Thermal Expansion Materials: Fundamentals and Applications View all 5 articles
Negative thermal expansion (NTE) materials and structures exhibit the anomalous property of shrinking rather than expanding when heated. This work examines the potential of multi-material planar re-entrant and non-re-entrant honeycombs to exhibit anomalous thermal expansion properties. Expressions for the coefficient of thermal expansion as a function of the geometric parameters and intrinsic thermal expansion properties were derived for any in-plane direction. It was shown that re-entrant honeycombs, a metamaterial which is well known for its auxetic characteristics, can be made to exhibit NTE in specific directions when constructed from conventional positive thermal expansion (PTE) materials, provided that the slanting ligaments expand more than the vertical ligaments when heated and that the geometry is amenable. Conversely, it was shown that the construction of such honeycombs from NTE components will not necessarily result in a system which exhibits NTE in all directions. Furthermore, conditions which result in honeycombs demonstrating zero thermal expansion (ZTE) coefficients in specific directions were also explored.
One of the “anomalous phenomena” which has been given considerable attention in the past decades is that of “negative thermal expansion” (NTE), i.e., shrinkage, rather than expansion, of a sample when this is subjected to an increase in temperature (Takenaka, 2018; Chen et al., 2015; Evans et al., 1997). Over the years, several “nanoscale” NTE materials have been studied, which include polymers and other carbon-based compounds (Baughman and Turi, 1973; Baughman, 1973; Baughman and Galvão, 1993; Yoon et al., 2011; Fortes et al., 2011), zeolites and other oxides (Giddy et al., 1993; Swainson and Dove, 1995; Mary et al., 1996; Pryde et al., 1996; Evans et al., 1998; Couves et al., 1999; Marinkovic et al., 2005; Marinkovic et al., 2008; Tallentire et al., 2013) and metal organic frameworks (Henke et al., 2013; Coudert, 2015; Evans et al., 2017). Common mechanisms operating at the nanoscale include ones which manifest a “rotating squares” profile in one of their planes where NTE is manifested due to increased vibrational motion leading to closure of the motif with an increase in temperature (the Rigid Unit Mode, RUM, approach) (Pryde et al., 1997; Bieniok and Hammonds, 1998; Heine et al., 1999; Dove et al., 2000; Tao and Sleight, 2003; Dove, 2019) and the “wine-rack” mechanism where NTE results from a scissors-like deformation (Goodwin et al., 2008). A common characteristic of most of these studied systems is that the driving force leading to NTE is amplified vibrations of nanoscale “rigid units” with an increase in temperature which, due to geometry and restrictions imposed by the manner how these “rigid units” are connected, result in a net shrinkage in one (i.e., linear NTE) or more crystallographic directions.
The potential uses of NTE materials are numerous but in certain applications (e.g., construction and civil engineering applications) the quantities of material required are such that the cost of manufacture would be the decisive factor which determines whether or not NTE materials could be used. In that respect, in parallel to this “nano-level” work on NTE, there has also been a number of attempts to design systems where the thermal shrinkage effect (or no shrinkage at all, i.e., zero thermal expansion coefficient, ZTE) can be achieved at the macroscale, potentially at a lower cost (Lakes, 1996a; Lakes, 1996b; Sigmund and Torquato, 1997; Vandeperre and Clegg, 2003; Grima et al., 2007; Lakes, 2007; Miller et al., 2008; Grima et al., 2009; Grima et al., 2010a; Berger et al., 2011; Palumbo et al., 2011; Lehman and Lakes, 2012; Lehman and Lakes, 2013a; Lehman and Lakes, 2013b; Ellul and Grima, 2013; Gdoutos et al., 2013; Lehman and Lakes, 2014; Ha et al., 2016; Wang et al., 2016; Wei et al., 2016; Boatti et al., 2017; Ha et al., 2017; Cabras et al., 2019; Luo et al., 2019; Ni et al., 2019; Wu et al., 2019; Cauchi et al., 2020; Lim, 2020; Guo et al., 2021; Héripré et al., 2021). Such work typically involves the use of materials, usually conventional ones, which expand differently when heated. With careful design, this mismatch in thermal expansion can be used to achieve shrinkage in one or more directions (i.e., a net macroscale “apparent” or “effective” NTE). Examples of “macroscale NTE/ZTE” include the work based on the triangular elongation mechanism (Vandeperre and Clegg, 2003; Grima et al., 2007; Miller et al., 2008; Berger et al., 2011; Palumbo et al., 2011; Gdoutos et al., 2013; Wang et al., 2016; Wei et al., 2016; Cabras et al., 2019; Lim, 2020; Héripré et al., 2021) where the base of a triangular unit expands more than its side when heated, with the result that the triangle shortens; and systems incorporating bi-material strips which bend when heated (Lakes, 1996b; Lakes, 2007; Lehman and Lakes, 2012; Lehman and Lakes, 2013a; Ha et al., 2017; Ni et al., 2019; Wu et al., 2019; Cauchi et al., 2020; Lim, 2020) Apart from the fundamental work aimed at discovering new NTE materials and/or understand better how they work, a number of practical applications which stand to benefit from NTE materials have also been identified, particularly in the manufacture of materials and composites which demonstrate low or near-zero thermal expansion properties. (Romao et al., 2015)
The inspiration for present work, which also aims to focus on macroscale construction of NTE systems, comes primarily from the abundance of work available on hexagonal honeycombs which exhibit anomalous Poisson’s ratio properties, including, but not limited to, auxetic (Evans et al., 1991) (i.e., negative Poisson’s ratio) honeycombs. Research in the field of auxetic honeycombs (Abd El-Sayed et al., 1979; Almgren, 1985; Grima et al., 2010b; Gatt et al., 2015; Ashby and Michael, 1999; Gibson et al., 1982; Masters and Evans, 1996; Grima-Cornish et al., 2017; Evans et al., 1995; Pozniak et al., 2013; Lira et al., 2009; Huang et al., 2016) has shown that three types of topologically equivalent structures, their representative units shown in Figure 1, behave very differently when uniaxially stretched or compressed, which behaviour is dependent on the geometry and the manner how the honeycomb deforms when subjected to stress. More specifically, if the honeycombs deform exclusively through changes in the angles between the ligaments (idealised hinging model), when stretched in the Ox1 direction, the classical beehive-like hexagonal honeycombs shown in Figure 1B would get thinner (positive Poisson’s ratio), while the re-entrant ones shown in Figure 1A would get wider (negative Poisson’s ratio, auxetic) whilst the hybrid ones in Figure 1C would get neither thinner nor fatter (zero Poisson’s ratios) (Grima et al., 2010b; Attard and Grima, 2011; Grima and Attard, 2011). As discussed extensively elsewhere (Evans et al., 1995; Masters and Evans, 1996), similar properties are exhibited if the systems deform through flexure of the slanting ligaments. On the other hand, very different behaviour is observed if deformation is exclusively via changes in the length of the ligaments with the angles between them remaining constant (idealised stretching model). In such case, the standard hexagonal honeycomb exhibits auxeticity whist the re-entrant honeycomb exhibits standard positive Poisson’s ratio properties.
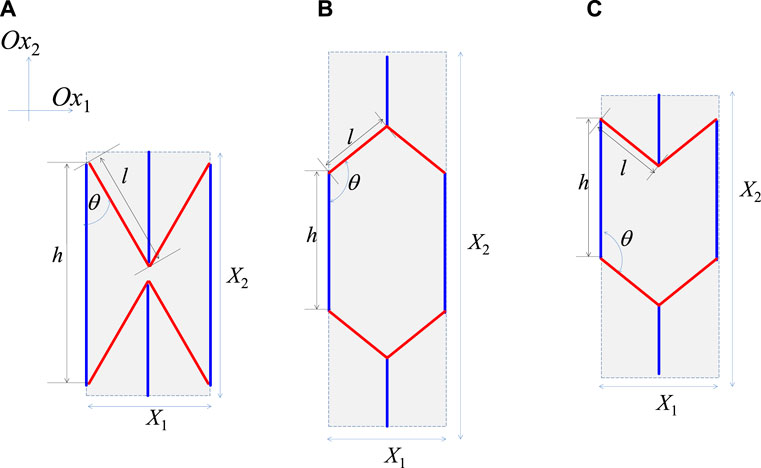
FIGURE 1. The three types of hexagonal honeycombs normally studied for their Poisson’s ratio properties: (A) The re-entrant honeycomb, well known for its negative Poisson’s ratio properties when it deforms through flexure or hinging; (B) the standard non-re-entrant honeycomb well known for its positive Poisson’s ratio properties when it deforms through flexure or hinging; and (C) the hybrid honeycomb better known for its zero Poisson’s ratio properties. In this work, which focuses on thermal expansion properties, the slanting ligaments (shown in red) are made of a different material from the vertical ligaments (shown in blue) with the slanting ligaments having thermal expansion αl and the vertical ligaments having thermal expansion αh.
Despite the extensive studies on these hexagonal honeycombs, including work on similar but more complex ones which may exhibit NTE (Lim, 2005; Ng et al., 2017; Zheng et al., 2018; Luo et al., 2019), the potential of the simplest of these systems, that is the standard re-entrant, non-re-entrant (convex) honeycomb, and the hybrid honeycombs have not yet been systematically explored. This work attempts to address this lacuna by attempting to assess the potential of such honeycombs (or rather a variation of them built from vertical and slanting ligaments having different thermal properties and which are welded together at the joints) to exhibit NTE, and, more generally, a pre-determined (controlled) thermal expansion coefficient (positive or negative).
A simple “proof of concept” of the potential of the re-entrant systems to exhibit anomalous properties is shown in Figure 2 and explained below, which together illustrate and explain how thermal shrinkage, or other anomalous thermal expansion properties, can occur. Illustrated in Figure 2A is the original re-entrant system at the reference temperature To with dimensions and geometric parameters h = 6, l = 2, and θ = 30°. The unit cell dimensions X1 and X2, defined as shown in Figure 1, are respectively given by:
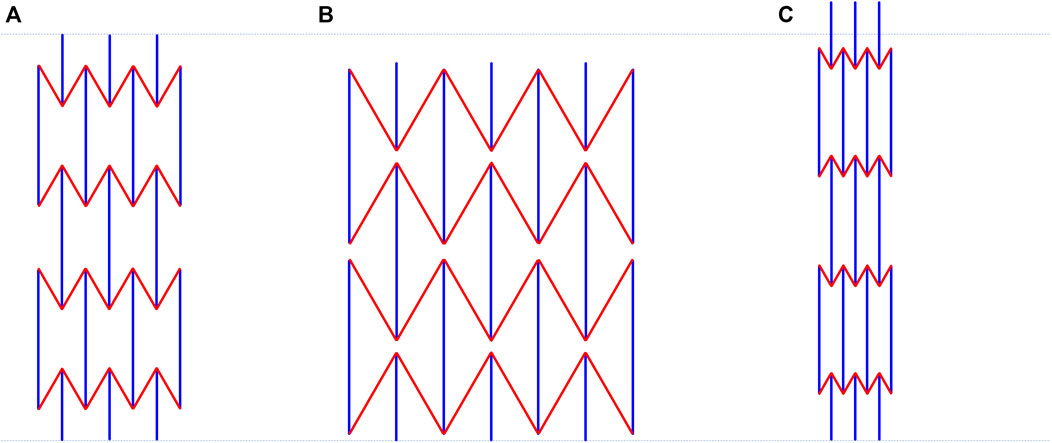
FIGURE 2. The effect of heat on re-entrant honeycombs with the slanting ligaments (shown in red) made from a different material to the vertical ligaments (shown in blue): (A) shows the geometry of the system at a temperature To whilst (B) and (C) show the geometry of the system at a higher temperature T = To + ΔT > To. In the case of (B), the ligaments have positive thermal expansion properties, with the slanting ligaments extending more than the vertical ones, whilst in (C) the ligaments have negative thermal expansion properties, with the slanting ligaments shrinking more than the vertical ones. The actual measurements and expansion properties are listed in Table 1.
If the honeycomb is built in a way that the slanting ligaments expand much more than the vertical ligaments when heated, with the angles between the ligaments remaining constant, then as clearly illustrated in Figure 2B, which shows a system at an elevated temperature T = To + ΔT where h = 7.5 (25% increase from 6), l = 4 (100% increase from 2) and θ remains at 30°, the system shrinks in the vertical Ox2 direction from X2 = 8.54 to X2 = 8.07 (5.44% shrinkage) but exhibits conventional thermal expansion in the horizontal Ox1 direction (see Table 1 for measurements). This confirms that, through their design, the re-entrant honeycombs have the capability to exhibit linear negative thermal expansion when constructed out of conventional positive thermal expansion (PTE) materials. Equally interesting is the effect shown in Figure 2C, which illustrates the effect of heat on a system constructed from NTE materials. In this specific case, the slanting ligaments shrink more than the vertical ligaments when heated, with the slanting ligaments shrinking from l = 2 to l = 1 (50% shrinkage) whilst the vertical ligaments only shrink from h = 6 to h = 5.5 (8.3% shrinkage). As illustrated in Figure 2C, despite the fact that every ligament in the system is shrinking, the system is manifesting a conventional positive thermal expansion in its vertical Ox2 direction of a rather substantial nature, thus proving (proof by contradiction) that intrinsic negative thermal expansion does not guarantee an overall macroscopic negative thermal expansion in all directions. For completeness’ sake, also reported in Table 1 are the properties of the analogous honeycombs having the standard convex non-re-entrant geometry (Figure 3i) and the hybrid semi-re-entrant geometry (Figure 3ii). Note that for the classical non-re-entrant honeycomb, the representative unit cell lengths of the systems are given by Eqs 1, 2 above. For the hybrid honeycomb, whilst the horizontal representative dimension X1 is still given by Eq. 1, the vertical representative dimension X2 is independent of l or the angles between the ligaments and is given by:
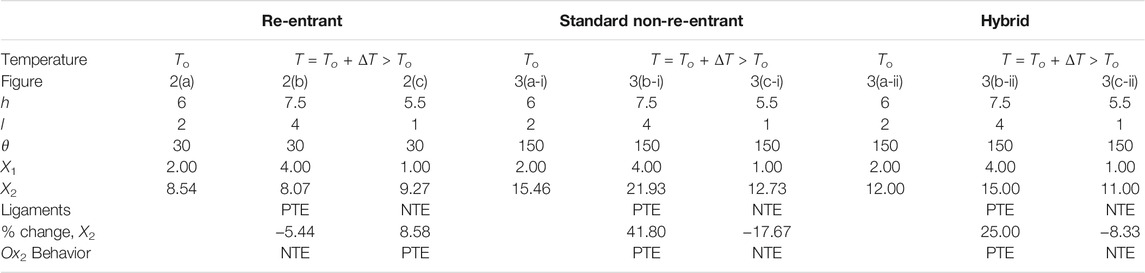
TABLE 1. The measurements and thermal expansion properties (in arbitrary units) related to the re-entrant, non-re-entrant and hybrid honeycombs shown in Figures 2–4 respectively.
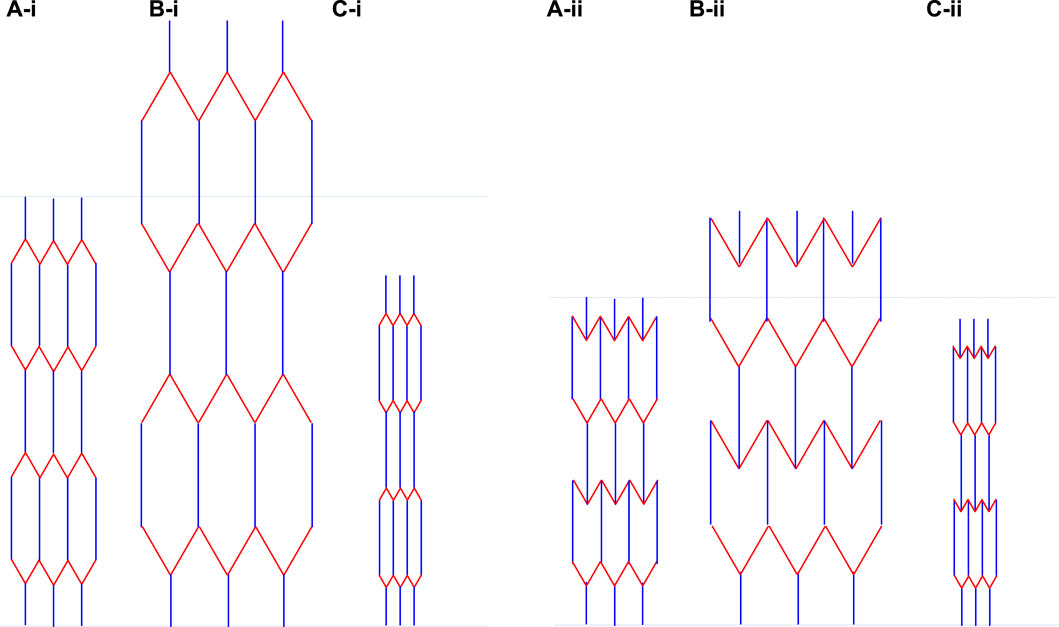
FIGURE 3. The effect of heat on the non-re-entrant honeycombs where (i) shows the standard convex honeycomb and (ii) shows the hybrid honeycombs. In both sets of honeycombs the slanting ligaments are made from a different material than the vertical ligaments (different ligaments shown by different colors). (A) shows the geometry of the systems at a temperature To whilst (B) and (C) show the geometry of the systems at a higher temperature T = To + ΔT > To. In the case of (B), the ligaments have positive thermal expansion properties, with the slanting ligaments extending more than the vertical ones, whilst in (C) the ligaments have negative thermal expansion properties, with the slanting ligaments shrinking more than the vertical ones. The actual measurements and expansion properties are listed in Table 1.
Note that as clearly illustrated in these figures and tables, in the case of the classical non-re-entrant and hybrid honeycombs, no anomalous thermal expansion characteristics are found when these systems are made from PTE ligaments.
Although the proof of principle presented above confirms the ability of the re-entrant structure made from two different materials to exhibit anomalous thermal expansion characteristics (including NTE), it cannot provide an adequate model that can be used to predict the extent of thermal expansion, positive or negative, that the system can experience when it is made from specific materials with predetermined thermal expansion properties and specific geometric features. As discussed elsewhere (Grima-Cornish et al., 2021), analytical modelling lends itself extremely well for such studies and provides a succinct manner of describing the properties of systems when subjected to a stimulus. Although a generalised analytical model can be derived which predicts the properties of the re-entrant, classical non-re-entrant, and hybrid honeycombs through the use of a single slightly more generalised version of the unit cells (e.g., one which describes the geometry in terms of two angles), for the sake of simplicity the model of the hybrid systems are derived separately.
As in any work involving analytical modelling, the validity or otherwise of any derived expressions depends primarily on the assumptions made and their applicability. In this case, the following assumptions will be made:
1) The honeycombs are constructed in a manner that a change in temperature will result exclusively in a change in length of the ligaments. In particular, it shall be assumed that the ligaments do not bend and the angles between them do not change.
2) The systems are made from ligaments of thermally responsive materials having dimensions which can be assumed to change linearly with a change in temperature within the temperature region of interest.
3) The honeycombs remain planar when heated and do not warp. When measuring the thermal expansion properties, the honeycombs are not being subjected to any additional mechanical load or stimulus (e.g., uniaxial stretching, shearing, etc.) apart from a change in temperature.
4) The systems must be physically realisable, i.e., X1, X2 > 0 and no part of the system should overlap with another. In practice this means that if the ligaments are all in the same plane, re-entrant systems must have:
It shall also be assumed that at a reference temperature To the vertical ligaments have length h and a linear thermal expansion coefficient of αh whilst the slanting ligaments have length l and a thermal expansion coefficient of αh, where the thermal expansion coefficients are defined by:
Thus, for all honeycombs studied (re-entrant, standard non-re-entrant and hybrid honeycombs), the change in X1 in the horizontal Ox1 direction as the temperature changes by an infinitesimally small amount dT is given by:
whilst for the re-entrant and standard non-re-entrant honeycombs, the corresponding change in X2 in the vertical Ox2 direction as the temperature changes by dT is given by:
and in the case of the hybrid honeycomb, the change in X2 is given by:
These changes in dimensions may be expressed as strains or as linear thermal expansion coefficients as follows:
1) In the Ox1 direction, for all three conformations:
2) In the Ox2 direction, for the re-entrant and standard non-re-entrant honeycombs:
and for the hybrid honeycombs:
Furthermore, since the systems as built, due to symmetry considerations, do not shear when heated, the strain tensor for the re-entrant and standard non-re-entrant honeycombs may expressed as:
which, through standard axis transformation techniques (Nye, 1957), may be transformed to give the strains at off-axis angles and hence the linear thermal expansion coefficients at any direction at an angle
Note that this expression, apart from predicting the thermal expansion coefficient in any direction, also suggests that maximum/minimum thermal expansion, including maximum NTE when present, occur at
Plots of the thermal expansion coefficient in the Ox2 direction for various re-entrant and non-re-entrant systems, plotted only for physically realisable systems where the slanting ligaments do not overlap, are shown in Figures 4, 5 for various combinations of (αl, αh) at different h/l ratios.
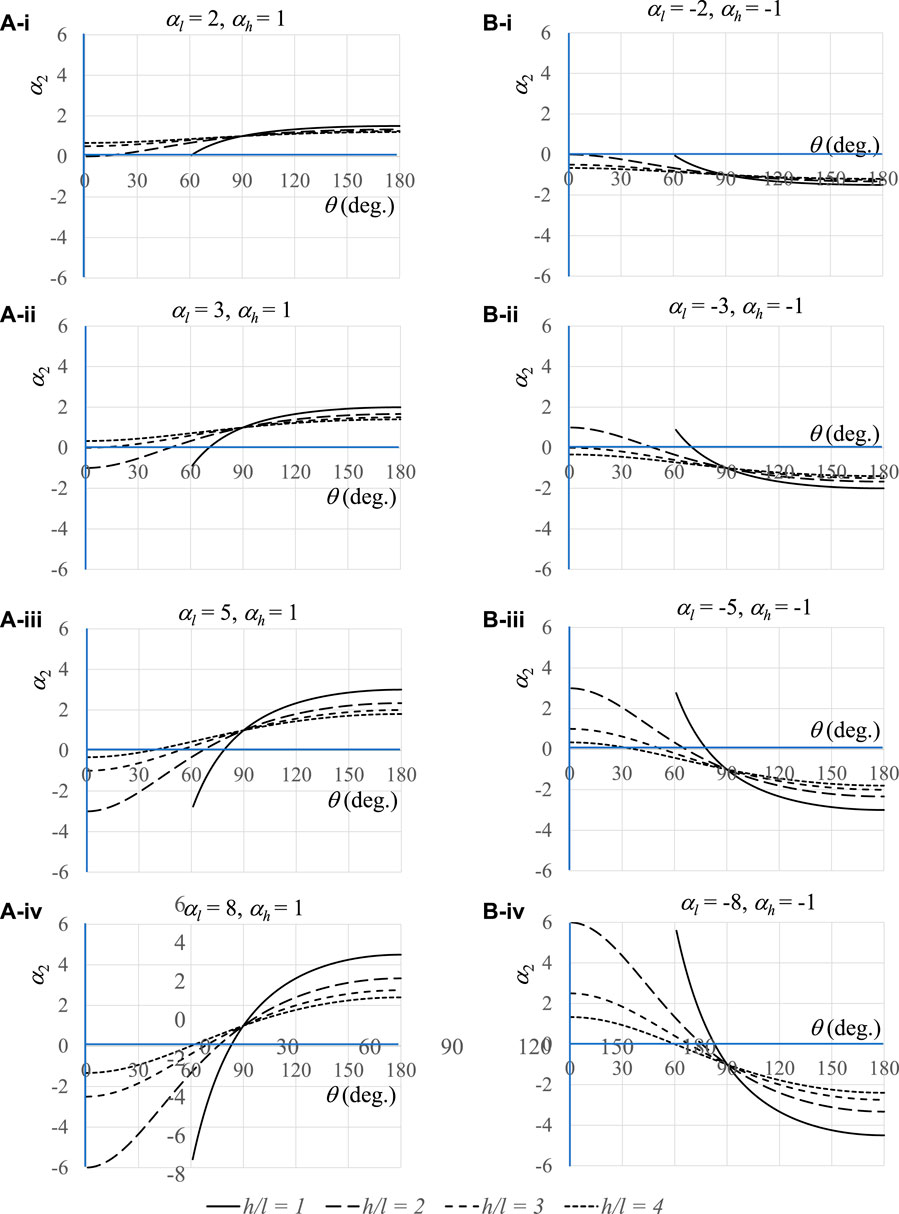
FIGURE 4. Plots of the coefficient of thermal expansion α2 in the Ox2 direction for various combinations of h/l and (αl, αh). Note that 0° < θ < 90°correspond to re-entrant honeycombs whilst 90° < θ < 180°correspond to the standard non-re-entrant honeycombs. The coefficients of thermal expansion are in arbitrary units and in (A) αl, αh > 0, and in (B) αl, αh < 0.
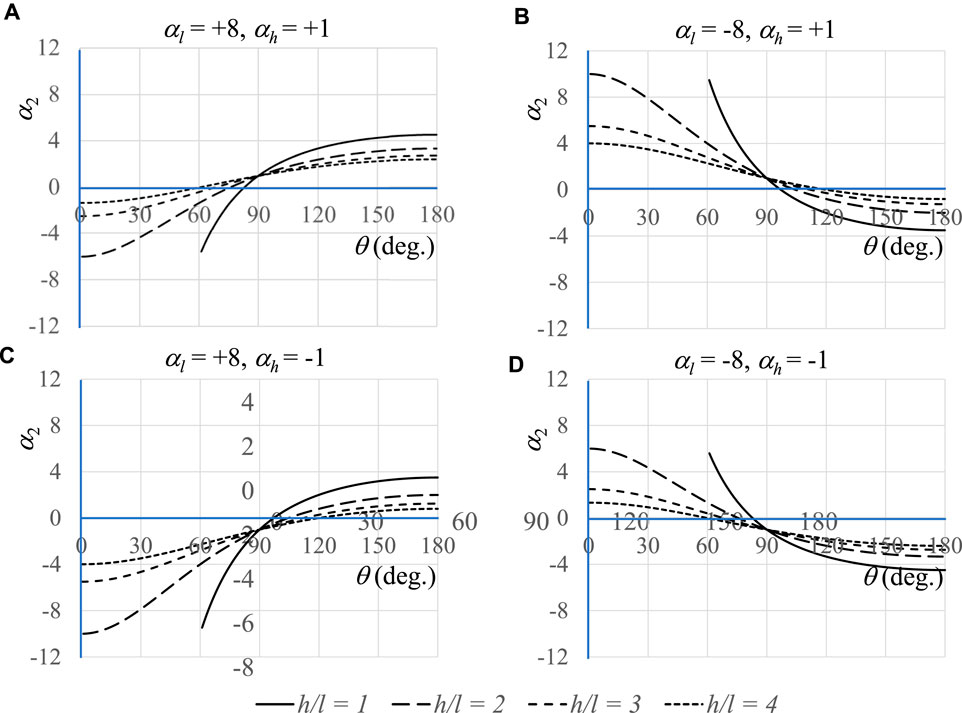
FIGURE 5. Plots of the coefficient of thermal expansion αl in the Ox2 direction for various combinations of h/l and the four combinations arising from αl = ±8, αh = ±1 where in (A) both ligaments have positive CTEs, (B) the slanting and vertical ligaments are made from NTE and PTE materials respectively, (C) the slanting and vertical ligaments are made from PTE and NTE materials respectively and (D) both ligaments have negative CTEs. Note that 0° < θ < 90° correspond to re-entrant honeycombs whilst 90° < θ < 180° correspond to the standard non-re-entrant honeycombs. The coefficients of thermal expansion are in arbitrary units. These plots suggest that for re-entrant configurations, maximum NTE is obtained if αl is positive and αh is negative. Conversely, for re-entrant configurations, maximum PTE is obtained if αl is negative and αh is positive.
The plots in Figures 4, 5 confirm that:
1) NTE can indeed be manifested from re-entrant systems made from ligaments exhibiting conventional thermal expansion properties, provided certain conditions are met, as discussed below.
2) For re-entrant honeycombs, intrinsic NTE properties of the ligaments do not guarantee an overall negative thermal expansion of the macrostructure since excessive shrinkage of the slanting ligaments when heating could lead to annihilation of the NTE effects and produce conventional macroscopic positive thermal expansion properties.
Note that similar plots can also be plotted for the thermal expansion coefficient in the Ox1 direction, but in this case, α1 would be independent of θ and equal to αl. Similar independence of θ is manifested by the thermal expansion coefficient in the Ox2 direction of the hybrid honeycombs but in this case, α2 would be equal to αh.
A better insight into the geometric and material property requirements to make the re-entrant honeycomb behave anomalously may be obtained by identifying the condition that results in a change in the sign of α2. From Eq. 12, this occurs when the numerator of the equation is equal to zero (the denominator is always positive), i.e.,:
meaning that:
Focusing first on achieving NTE from systems having positive αh and αl, when the condition in Eq. 18 is taken concurrently with the requirements that for physically realisable systems, as noted in Eq. 4, it is required that
which means that unless the CTE of the slanting ligaments is more than double that of the vertical ligaments, NTE cannot be achieved. This geometric constraint, also necessitates that
which in practice means the minimum value of
Moreover, once it is ascertained that
Eq. 23 rules out NTE from non-re-entrant systems for positive αh and αl since for such systems,
These conditions suggest that the maximum value of
Thus, in practice, to maximise the range of values of
Focusing now on the magnitude of NTE, it is evident from Eq. 12 that maximum NTE will be obtained if the magnitude of
An analysis of the behaviour of the systems when αl and αh are both negative suggests that the same arguments made above when αl and αh were both positive, are merely reversed. This may be easily appreciated through the plots in Figure 4B, which are a mirror image of the plots in Figure 4A, as well as through the equations above. As a corollary of this, the same conditions which resulted in NTE in the Ox2 directions when αl and αh were both positive, would now result in PTE in the Ox2 direction when αl and αh are both negative. Whilst this may be of less practical importance, it is a direct proof of the importance of design since the use of NTE materials will not guarantee that the final product would exhibit NTE. In fact, in this particular case of the re-entrant honeycomb, as shown in Figure 5, it would have been more beneficial to enhance NTE if αl was positive and αh was negative (and conversely, to enhance PTE if αl was negative and αh was positive). Note also that with such combinations of αl and αh, the re-entrant geometry is capable of manifesting magnified thermal expansion characteristics in the Ox2 direction.
At this point it is important to recognize that not all practical applications require maximisation of NTE, and in some cases it is more useful to be able to control the value of the thermal expansion coefficient and have it tailored to specific values, particularly a value of zero (zero thermal expansion, ZTE). ZTE in the Ox2 direction is obviously always obtained at the transition between NTE and PTE, or vice-versa, and the conditions which results in ZTE may be obtained from solving the equation α2 = 0, which in practice means solving Eq. 18. Thus, for systems with a given value of αh, αl, h and l, the value of θ which results in ZTE is given by:
This is only possible if
Although the discussion has focused on the thermal expansion properties in the Ox2 direction, the systems are generally anisotropic and the thermal expansion coefficient is dependent on the direction of measurement. Whilst this is clearly indicated by the fact that the thermal expansion properties in the Ox1 direction is always equal to the αl, it would still be useful to remember that the thermal expansion coefficient when measured off-axis will be different from when measured on-axis, with the sign and magnitude of this coefficient being dependent on h, l, θ, αh, αl, and ζ, the off-axis angle. To highlight the anisotropy, a selection of off-axis plots, where the thermal expansion coefficient is plotted as a polar plot against ζ, the direction of measurement, are shown in Figure 6. These plots were obtained for the specific systems when h = 2, l = 1, θ = 10°, αh = ±1, αl = ±8 and confirm that for the system where αh and αl are positive (i.e., αh = +1, αl = +8), maximum NTE is exhibited on-axis in the Ox2 direction. Furthermore, it should be noted that not all systems will exhibit NTE behaviour in certain directions and PTE behavior in others since this behaviour requires that α1 and α2 have different signs. In such cases, the change of sign (corresponding to an off-axis ZTE) would occur at off-axis angles ζo, obtained by setting Eq. 16 equal to zero and solving it to obtain:
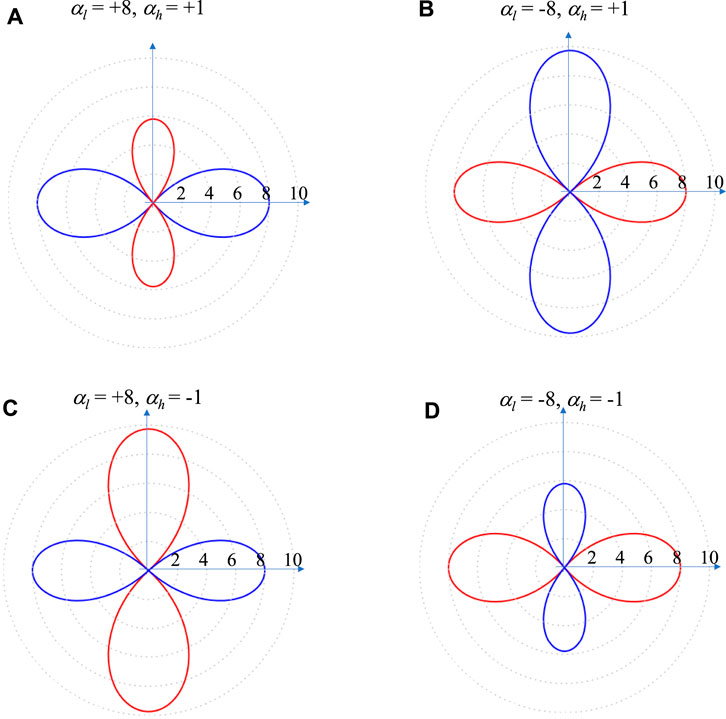
FIGURE 6. Plots of
Note that this expression is only solvable when α1 and α2 have different signs, which in turn requires that the difference in the thermal expansion coefficients of the constituent materials must be sufficiently large and the geometry must be amenable.
Another characteristic that should be highlighted is that in the plots shown in Figures 4, 5, whenever systems with θ angles close to 0° are realizable, the thermal expansion coefficient α2 was practically independent of the angle θ for small angles of θ. This is due to the fact that for small values of θ, the cosine of the angle is very close to +1 [for example, cos(10°) = 0.985 ≈ 1]. Thus, for small angles θ, the expression for α2 in Eq. 12 may be simplified to:
an expression which is simpler to understand and gives more leeway to manufacturers. Note that in such case of θ ≈ 0, the condition for near zero thermal expansion coefficients (ZTE) becomes:
which can be easily visualised since the expansion in h is cancelled by the expansion in l whilst for NTE we would require:
Note that for such systems to be physically realizable without risk of internal contact when the systems deform, h must generally be larger than twice l with an applicable safety margin.
Having considered the main characteristics associated with this model, it is important to highlight some of its strengths and limitations. The main limitation is that the work is entirely based on mathematical modelling and may be considered as highly idealistic in nature. For example, the analysis was performed using hypothetical materials rather than ones which are known to exist. This approach is justified by the fact that in this way, the model preserves its mathematical elegance which would otherwise be partially lost if actual non-integer values are used as parameters. Nevertheless, the ratios of thermal expansions required, i.e., at least double, are not unrealisable using real materials. Another limitation is that this study did not consider the design of the joint between the slanting and vertical ligaments. Ideally this joint should be such that it does not permit a change of angle and at the same time be small enough so as not to reduce the effective length of the ligaments. In practice, if the ligaments are of appropriate length and thickness, it is envisaged that these requirements could be met to a first approximation, simply by bolting or welding together the ligaments meeting at the joint. Nevertheless, it would be ideal if additional studies are carried out on this aspect. Here it should be mentioned that the lack of triangulation associated with some other similar macromodels offers the advantage that simple welding together of the ligaments at the joints may be sufficient to hold the structure together and the angles between the ligaments do not need to change (in fact, ideally they should not change).
A simple verification of the above considerations, including the possibility of obtaining NTE from re-entrant honeycombs made from conventional materials can be obtained from the results of the numerical simulations performed using the finite element analysis (FEA) software ANSYS on the representative unit of the honeycomb prototype shown in Figure 7A. This honeycomb is made of two different materials where the slanting ligaments have properties which are similar to that of zinc (linear thermal expansion coefficient of 30.2 × 10−6 K−1, Young’s modulus 108 GPa, Poisson’s ratio 0.25) whilst the material used for the vertical ligaments has properties which are similar to that of a steel alloy (linear thermal expansion coefficient of 9.9 × 10−6 K−1, Young’s modulus 215 GPa, Poisson’s ratio 0.28). Note also that the ligaments in these systems have a finite thickness t0 where in the limit where t0 tends to zero, the system would assume the idealized shape modelled analytically. For these specific simulations, l0 and h0 were set to 6 and 12 cm respectively, t0 was set as 3 mm whilst the angle θ was set at 30°. Simulations were performed using the 2D 8-node planar element, PLANE223, which allows for displacement along x and y directions caused by thermal loading. The procedure for meshing was as discussed in Cauchi et al. (2020), and to emulate a periodic system, the left-most nodes were constrained to have a zero displacement in the horizontal Ox1-direction, the bottom-most nodes were constrained to have a zero displacement in the vertical Ox2-direction, the right-most nodes were coupled in the Ox1-direction whilst the top-most nodes were coupled in the Ox2-direction. Thermal loads equivalent to a temperature change of +50 K were applied on each node to study temperature effects. As shown in Figure 7B, which shows the superimposed images of the deformed and undeformed systems (with a ×100 magnification of the displacements), the system behaves, to a first approximation, as predicted, i.e., shrinking in the vertical direction with a coefficient of thermal expansion α2 of −5.2 × 10−6 K−1 (analytical model predicts −5.6 × 10−6 K−1) and expanding in the horizontal direction with a coefficient of thermal expansion α1 of 29.5 × 10−6 K−1 (analytical model predicts −30.2 × 10−6 K−1).
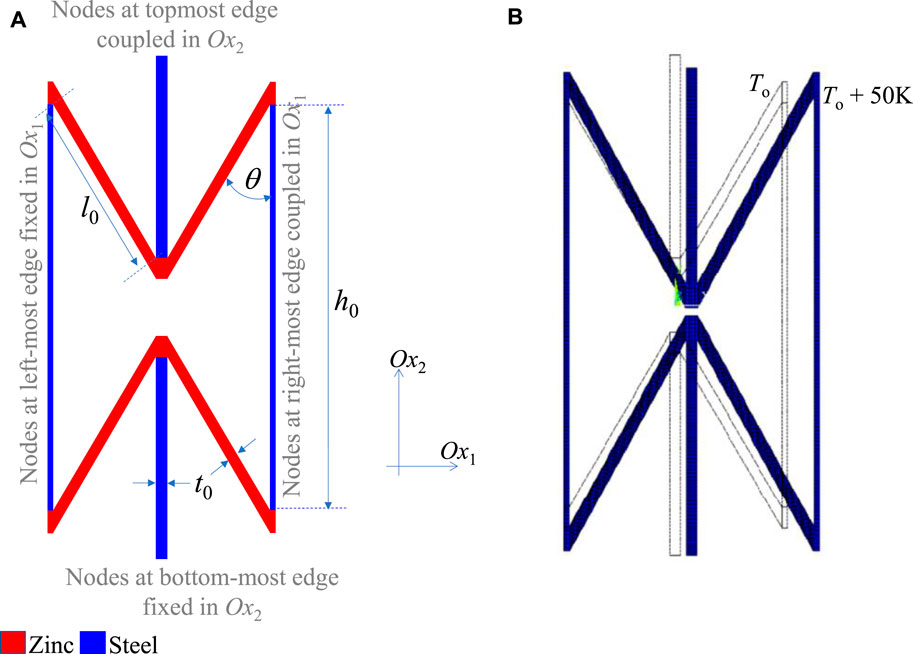
FIGURE 7. (A) The system modelled using FEA, which is made from slanting ligaments having zinc-like properties welded to vertical ligaments having steel like properties, and (B) images showing the heated and unheated system, at temperatures To + 50 K and To respectively, where the displacements are scaled up by a factor of x100 to aid visualisation. Note that the system shrinks in the vertical direction upon heating. Also note that the geometric parameters l0, h0, t0 and θ are set to 6 cm, 12 cm, 3 mm and 30° respectively, where, to satisfy the boundary conditions applied, the thickness of the full vertical ligaments are set at t0/2 to make a full thickness t0 when tessellated.
Nevertheless, probably the most important strength of these systems is that for this mechanism to operate, the geometry of the honeycombs remains that which is typically studied for generating auxeticity through flexure. Even more importantly, it is the slanting ligaments which need to have high thermal expansion coefficients, i.e., same ligaments which typically flex when a re-entrant honeycomb is stretched or compressed on-axis to generate negative Poisson’s ratio. Given that high coefficients of thermal expansions are typically manifested by softer materials, it may thus be hypothesized that the bi-material re-entrant honeycombs which would be designed to exhibit NTE are more than likely expected to be also auxetic, thus enhancing their multifunctionality. Such a hypothesis should ideally be tested, either through experimental work, or additional simulations using a more realistic finite-elements approach to definitely confirm that the well-known auxetic re-entrant honeycomb can been made even more versatile by exhibiting NTE or ZTE properties.
Finally, an important strength of this model is its versatility and ability to result in a very wide range of thermal expansion properties, which could be positive, negative or zero. Macrosystems such as this one which can exhibit tailor-made, possibly negative, thermal expansion properties that may be constructed from conventional materials offer the advantage that they can be mass-produced for use in applications requiring massive quantities, such as in civil and structural engineering and construction applications where issues associated with thermal mismatch are too well known. We envisage that the availability of expressions which can predict the thermal expansion properties as a function of geometry and the intrinsic properties of the constituent materials, when taken in conjunction with similar expressions presented elsewhere to predict the Poisson’s ratio of such honeycombs (Gibson et al., 1982; Masters and Evans, 1996; Attard and Grima, 2011) provide a most useful predictive tool to facilitate the design and manufacture of honeycombs with tailor-made thermal expansion and Poisson’s ratio properties for specific practical applications.
This work has examined the potential of multi-material planar re-entrant and non-re-entrant honeycombs to exhibit anomalous thermal expansion properties. An analytical model which can predict the coefficient of thermal expansion as a function of the geometric parameters and intrinsic thermal expansion properties was derived and analysed. Through this predictive model, it was shown that re-entrant honeycombs made from conventional positive thermal expansion materials can be re-designed to exhibit negative thermal expansion in specific directions, with maximum NTE being manifested in the direction of the vertical ligaments. It was shown that for such NTE to be manifested, the slanting ligaments must expand more than the vertical ligaments when heated and certain geometric requirements are met. In addition, it was postulated that the manner of construction is not likely to affect the Poisson’s ratio properties of such honeycombs with the result that these honeycombs can exhibit concurrent NTE and auxeticity (negative Poisson’s ratio).
It was also formally proved that 1) non-re-entrant honeycombs made from conventional PTE materials cannot exhibit NTE in any direction through this mechanism; 2) the use of NTE materials for the construction of re-entrant honeycombs does not guarantee that such honeycombs exhibit NTE in all directions, and 3) it is possible to construct honeycombs demonstrating zero thermal expansion (ZTE) coefficients in specific directions.
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
JG-C conceived this work, performed the proof of principle calculations and contributed extensively to the final article. JG derived the mathematical model. DA performed the FEA simulations. JG, DA, and KE supervised the work. All authors were involved in the discussion.
The authors gratefully acknowledge the support of the project A-ROW, grant No. R&I-2017-033-T, financed by the Malta Council for Science and Technology through FUSION: The R&I Technology Development Programme 2018.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abd El-Sayed, F. K., Jones, R., and Burgess, I. W. (1979). A Theoretical Approach to the Deformation of Honeycomb Based Composite Materials. Composites 10, 209–214. doi:10.1016/0010-4361(79)90021-1
Almgren, R. F. (1985). An Isotropic Three-Dimensional Structure with Poisson's Ratio =−1. J. Elast. 15, 427.
Ashby, L. J., and Michael, F. (1999). Gibson, Cellular Solids: Structure and Properties. Cambridge: Cambridge University Press.
Attard, D., and Grima, J. N. (2011). Modelling of Hexagonal Honeycombs Exhibiting Zero Poisson's Ratio. Phys. Stat. Sol. B. 248, 52–59. doi:10.1002/pssb.201083980
Baughman, R. H., and Galvão, D. S. (1993). Crystalline Networks with Unusual Predicted Mechanical and thermal Properties. Nature 365, 735–737. doi:10.1038/365735a0
Baughman, R. H. (1973). Negative thermal Expansion in Crystalline Linear Polymers. J. Chem. Phys. 58, 2976. doi:10.1063/1.1679607
Baughman, R. H., and Turi, E. A. (1973). Negative thermal Expansion of a Polydiacetylene Single crystal. J. Polym. Sci. A-2 Polym. Phys. 11, 2453–2466. doi:10.1002/pol.1973.180111213
Berger, J., Mercer, C., McMeeking, R. M., and Evans, A. G. (2011). The Design of Bonded Bimaterial Lattices that Combine Low Thermal Expansion with High Stiffness. J. Am. Ceram. Soc. 94, s42–s54. doi:10.1111/j.1551-2916.2011.04503.x
Bieniok, A., and Hammonds, K. D. (1998). Rigid Unit Modes and the Phase Transition and Structural Distortions of Zeolite Rho. Microporous Mesoporous Mater. 25, 193–200. doi:10.1016/s1387-1811(98)00207-8
Boatti, E., Vasios, N., and Bertoldi, K. (2017). Metamaterials: Origami Metamaterials for Tunable Thermal Expansion (Adv. Mater. 26/2017). Adv. Mater. 29, 1. doi:10.1002/adma.201770184
Cabras, L., Brun, M., and Misseroni, D. (2019). Micro-structured Medium with Large Isotropic Negative thermal Expansion. Proc. R. Soc. A. 475, 20190468. doi:10.1098/rspa.2019.0468
Cauchi, R., Attard, D., Grima-Cornish, J. N., and Grima, J. N. (2020). On the Design of Multimaterial Honeycombs and Structures with T‐Shaped Joints Having Tunable Thermal and Compressibility Properties. Phys. Status Solidi B. 257, 1900633. doi:10.1002/pssb.201900633
Chen, J., Hu, L., Deng, J., and Xing, X. (2015). Negative thermal Expansion in Functional Materials: Controllable thermal Expansion by Chemical Modifications. Chem. Soc. Rev. 44, 3522–3567. doi:10.1039/c4cs00461b
Coudert, F.-X. (2015). Responsive Metal-Organic Frameworks and Framework Materials: Under Pressure, Taking the Heat, in the Spotlight, with Friends. Chem. Mater. 27, 1905–1916. doi:10.1021/acs.chemmater.5b00046
Couves, J. W., Jones, R. H., Parker, S. C., Tschaufeser, P., and Catlow, C. R. A. (1999). Experimental Verification of a Predicted Negative thermal Expansivity of Crystalline Zeolites. J. Phys. Condens. Matter. 5, L329–L332. doi:10.1088/0953-8984/5/27/001
Dove, M. T. (2019). Flexibility of Network Materials and the Rigid Unit Mode Model: a Personal Perspective. Phil. Trans. R. Soc. A. 377, 20180222. doi:10.1098/rsta.2018.0222
Dove, M. T., Trachenko, K. O., Tucker, M. G., and Keen, D. A. (2000). Rigid Unit Modes in Framework Structures: Theory, Experiment and Applications. Rev. Mineralogy Geochem. 39, 1–33. doi:10.2138/rmg.2000.39.01
Ellul, B., and Grima, J. N. (2013). Modeling of thermal Expansion Coefficients of Composites with Disc Shaped Inclusions and Related Systems. Phys. Status Solidi B. 250, 2057–2061. doi:10.1002/pssb.201384227
Evans, J. D., Dürholt, J. P., Kaskel, S., and Schmid, R. (2017). Assessing Negative thermal Expansion in Mesoporous Metal–Organic Frameworks by Molecular Simulation J. Mater. Chem. A. 7, 24019. doi:10.1039/C9TA06644F
Evans, J. S. O., Mary, T. a., and Sleight, A. W. (1998). Negative Thermal Expansion in Sc2(WO4)3. J. Solid State. Chem. 137, 148–160. doi:10.1006/jssc.1998.7744
Evans, J. S. O., Mary, T. A., and Sleight, A. W. (1997). Negative thermal Expansion Materials. Physica B: Condensed Matter 241-243, 311–316. doi:10.1016/s0921-4526(97)00571-1
Evans, K. E., Alderson, A., and Christian, F. R. (1995). Auxetic Two-Dimensional Polymer Networks. An Example of Tailoring Geometry for Specific Mechanical Properties. Faraday Trans. 91, 2671. doi:10.1039/ft9959102671
Evans, K. E., Nkansah, M. A., Hutchinson, I. J., and Rogers, S. C. (1991). Molecular Network Design. Nature 353, 124. doi:10.1038/353124a0
Fortes, A. D., Suard, E., and Knight, K. S. (2011). Negative Linear Compressibility and Massive Anisotropic Thermal Expansion in Methanol Monohydrate. Science 331, 742–746. doi:10.1126/science.1198640
Gatt, R., Mizzi, L., Azzopardi, K. M., and Grima, J. N. (2015). A Force-Field Based Analysis of the Deformation Mechanism in α-cristobalite. Phys. Status Solidi B. 252, 1479–1485. doi:10.1002/pssb.201552133
Gdoutos, E., Shapiro, A. A., and Daraio, C. (2013). Thin and Thermally Stable Periodic Metastructures. Exp. Mech. 53, 1735–1742. doi:10.1007/s11340-013-9748-z
Gibson, L. J., Ashby, M. F., Schajer, G. S., and Robertson, C. I. (1982). The Mechanics of Two-Dimensional Cellular Materials. Proc. R. Soc. A. Math. Phys. Eng. Sci. 382, 25. doi:10.1098/rspa.1982.0087
Giddy, A. P., Dove, M. T., Pawley, G. S., and Heine, V. (1993). The Determination of Rigid-Unit Modes as Potential Soft Modes for Displacive Phase Transitions in Framework crystal Structures. Acta Cryst. Sect A. 49, 697–703. doi:10.1107/s0108767393002545
Goodwin, A. L., Keen, D. A., and Tucker, M. G. (2008). Large Negative Linear Compressibility of Ag3[Co(CN)6]. Proc. Natl. Acad. Sci. 105, 18708–18713. doi:10.1073/pnas.0804789105
Grima, J. N., and Attard, D. (2011). Molecular Networks with a Near Zero Poisson's Ratio. Phys. Stat. Sol. B. 248, 111–116. doi:10.1002/pssb.201083979
Grima, J. N., Farrugia, P. S., Gatt, R., and Zammit, V. (2007). A System with Adjustable Positive or Negative thermal Expansion. Proc. R. Soc. A. 463, 1585–1596. doi:10.1098/rspa.2007.1841
Grima, J. N., Gatt, R., and Ellul, B. (2009). A finite element analysis on the potential for negative thermal expansion and negative compressibility of triangular building blocks. Kuei Suan Jen Hsueh Pao/J. Chin. Ceram. Soc. 37, 743–748.
Grima, J. N., Oliveri, L., Attard, D., Ellul, B., Gatt, R., Cicala, G., et al. (2010). Hexagonal Honeycombs with Zero Poisson's Ratios and Enhanced Stiffness. Adv. Eng. Mater. 12, 855–862. doi:10.1002/adem.201000140
Grima, J. N., Oliveri, L., Ellul, B., Gatt, R., Attard, D., Cicala, G., et al. (2010). Adjustable and Negative thermal Expansion from Multilayered Systems. Phys. Stat. Sol. RRL 4, 133–135. doi:10.1002/pssr.201004076
Grima-Cornish, J. N., Grima, J. N., and Attard, D. (2021). Mathematical Modeling of Auxetic Systems: Bridging the gap between Analytical Models and Observation. Int. J. Mech. Mater. Eng. 16, 16. doi:10.1186/s40712-020-00125-z
Grima-Cornish, J. N., Grima, J. N., and Evans, K. E. (2017). On the Structural and Mechanical Properties of Poly(Phenylacetylene) Truss-like Hexagonal Hierarchical Nanonetworks. Phys. Status Solidi B. 254, 1700190. doi:10.1002/pssb.201700190
Guo, X., Ni, X., Li, J., Zhang, H., Zhang, F., Yu, H., et al. (2021). 2D Metamaterials: Designing Mechanical Metamaterials with Kirigami‐Inspired, Hierarchical Constructions for Giant Positive and Negative Thermal Expansion (Adv. Mater. 3/2021). Mater. 33, 217001. doi:10.1002/adma.202170016
Ha, C. S., Plesha, M. E., and Lakes, R. S. (2016). Chiral Three-Dimensional Lattices with Tunable Poisson's Ratio. Smart Mater. Struct. 25, 054005. doi:10.1088/0964-1726/25/5/054005
Ha, C. S., Plesha, M. E., and Lakes, R. S. (2017). Simulations of Thermoelastic Triangular Cell Lattices with Bonded Joints by Finite Element Analysis. Extreme Mech. Lett. 12, 101–107. doi:10.1016/j.eml.2016.10.013
Heine, V., Welche, P. R. L., and Dove, M. T. (1999). Geometrical Origin and Theory of Negative Thermal Expansion in Framework Structures. J. Am. Ceram. Soc. 82, 1793–1802. doi:10.1111/j.1151-2916.1999.tb02001.x
Henke, S., Schneemann, A., and Fischer, R. A. (2013). Massive Anisotropic Thermal Expansion and Thermo-Responsive Breathing in Metal-Organic Frameworks Modulated by Linker Functionalization. Adv. Funct. Mater. 23, 5990–5996. doi:10.1002/adfm.201301256
Héripré, E., Mehrez, M., and Constantinescu, A. (2021). FIB Manufactured Microstructures with Low Coefficients of thermal Expansion. Mech. Res. Commun. 114, 103667. doi:10.1016/j.mechrescom.2021.103667
Huang, J., Gong, X., Zhang, Q., Scarpa, F., Liu, Y., and Leng, J. (2016). In-plane Mechanics of a Novel Zero Poisson's Ratio Honeycomb Core. Composites B: Eng. 89, 67–76. doi:10.1016/j.compositesb.2015.11.032
Lakes, R. (1996). Dense Solid Microstructures with Unbounded Thermal Expansion. J. Mech. Behav. Mater. 7, 85.
Lakes, R. (1996). Cellular Solid Structures with Unbounded thermal Expansion. J. Mater. Sci. Lett. 15, 475–477. doi:10.1007/bf00275406
Lakes, R. (2007). Cellular Solids with Tunable Positive or Negative thermal Expansion of Unbounded Magnitude. Appl. Phys. Lett. 90, 221905. doi:10.1063/1.2743951
Lehman, J., and Lakes, R. S. (2014). Stiff, strong, Zero thermal Expansion Lattices via Material Hierarchy. Compos. Structures 107, 654–663. doi:10.1016/j.compstruct.2013.08.028
Lehman, J., and Lakes, R. (2012). Stiff Lattices with Zero thermal Expansion. J. Intell. Mater. Syst. Structures 23, 1263–1268. doi:10.1177/1045389x12445647
Lehman, J., and Lakes, R. (2013). Stiff Lattices with Zero thermal Expansion and Enhanced Stiffness via Rib Cross Section Optimization. Int. J. Mech. Mater. Des. 9, 213–225. doi:10.1007/s10999-012-9210-x
Lehman, J., and Lakes, R. (2013). Stiff, strong Zero thermal Expansion Lattices via the Poisson Effect. J. Mater. Res. 28, 2499–2508. doi:10.1557/jmr.2013.154
Lim, T.-C. (2005). Anisotropic and Negative thermal Expansion Behavior in a Cellular Microstructure. J. Mater. Sci. 40, 3275–3277. doi:10.1007/s10853-005-2700-6
Lira, C., Innocenti, P., and Scarpa, F. (2009). Transverse Elastic Shear of Auxetic Multi Re-entrant Honeycombs. Compos. Structures 90, 314–322. doi:10.1016/j.compstruct.2009.03.009
Luo, W., Xue, S., Zhang, M., Zhao, C., and Li, G. (2019). Bi-Material Negative Thermal Expansion Inverted Trapezoid Lattice Based on A Composite Rod. Materials 12, 3379. doi:10.3390/ma12203379
Marinkovic, B. A., Jardim, P. M., De Avillez, R. R., and Rizzo, F. (2005). Negative thermal Expansion in Y2Mo3O12. Solid State. Sci. 7, 1377–1383. doi:10.1016/j.solidstatesciences.2005.08.012
Marinkovic, B. A., Jardim, P. M., Rizzo, F., Saavedra, A., Lau, L. Y., and Suard, E. (2008). Complex thermal Expansion Properties of Al-Containing HZSM-5 Zeolite: A X-ray Diffraction, Neutron Diffraction and Thermogravimetry Study. Microporous Mesoporous Mater. 111, 110–116. doi:10.1016/j.micromeso.2007.07.015
Mary, T. A., Evans, J. S. O., Vogt, T., and Sleight, A. W. (1996). Negative Thermal Expansion from 0.3 to 1050 Kelvin in ZrW 2 O 8. Science 272, 90–92. doi:10.1126/science.272.5258.90
Masters, I. G., and Evans, K. E. (1996). Models for the Elastic Deformation of Honeycombs. Compos. Structures 35, 403–422. doi:10.1016/s0263-8223(96)00054-2
Miller, W., Mackenzie, D. S., Smith, C. W., and Evans, K. E. (2008). A Generalised Scale-independent Mechanism for Tailoring of thermal Expansivity: Positive and Negative. Mech. Mater. 40, 351–361. doi:10.1016/j.mechmat.2007.09.004
Ng, C. K., Saxena, K. K., Das, R., and Saavedra Flores, E. I. (2017). On the Anisotropic and Negative thermal Expansion from Dual-Material Re-entrant-type Cellular Metamaterials. J. Mater. Sci. 52, 899–912. doi:10.1007/s10853-016-0385-7
Ni, X., Guo, X., Li, J., Huang, Y., Zhang, Y., and Rogers, J. A. (2019). 2D Mechanical Metamaterials with Widely Tunable Unusual Modes of Thermal Expansion. Adv. Mater. 31, 1905405. doi:10.1002/adma.201905405
Nye, J. F. (1957). Physical Properties of Crystals : Their Representations by Tensors and Matrices. New York: Oxford University Press.
Palumbo, N. M. A., Smith, C. W., Miller, W., and Evans, K. E. (2011). Near-zero thermal Expansivity 2-D Lattice Structures: Performance in Terms of Mass and Mechanical Properties. Acta Materialia 59, 2392–2403. doi:10.1016/j.actamat.2010.12.037
Pozniak, A. A., Smardzewski, J., and Wojciechowski, K. W. (2013). Computer Simulations of Auxetic Foams in Two Dimensions. Smart Mater. Struct. 22, 084009. doi:10.1088/0964-1726/22/8/084009
Pryde, A. K. A., Hammonds, K. D., Dove, M. T., Heine, V., Gale, J. D., and Warren, M. C. (1996). Origin of the Negative thermal Expansion in and. J. Phys. Condens. Matter 8, 10973–10982. doi:10.1088/0953-8984/8/50/023
Pryde, A. K. A., Hammonds, K. D., Dove, M. T., Heine, V., Gale, J. D., and Warren, M. C. (1997). Rigid Unit Modes and the Negative thermal Expansion in ZrW2O8. Phase Transitions 61, 141–153. doi:10.1080/01411599708223734
Romao, C. P., Marinkovic, B. A., Werner-Zwanziger, U., and White, M. A. (2015). Thermal Expansion Reduction in Alumina-Toughened Zirconia by Incorporation of Zirconium Tungstate and Aluminum Tungstate. J. Am. Ceram. Soc. 98, 2858–2865. doi:10.1111/jace.13675
Sigmund, O., and Torquato, S. (1997). Design of Materials with Extreme thermal Expansion Using a Three-phase Topology Optimization Method. J. Mech. Phys. Sol. 45, 1037–1067. doi:10.1016/s0022-5096(96)00114-7
Swainson, I. P., and Dove, M. T. (1995). On the thermal Expansion of ?-cristobalite. Phys. Chem. Miner. 22, 61. doi:10.1007/bf00202681
Takenaka, K. (2018). Progress of Research in Negative Thermal Expansion Materials: Paradigm Shift in the Control of Thermal Expansion. Front. Chem. 6, 267. doi:10.3389/fchem.2018.00267
Tallentire, S. E., Child, F., Fall, I., Vella-Zarb, L., Evans, I. R., Tucker, M. G., et al. (2013). Systematic and Controllable Negative, Zero, and Positive Thermal Expansion in Cubic Zr1-xSnxMo2O8. J. Am. Chem. Soc. 135, 12849–12856. doi:10.1021/ja4060564
Tao, J. Z., and Sleight, A. W. (2003). The Role of Rigid Unit Modes in Negative thermal Expansion. J. Solid State. Chem. 173, 442–448. doi:10.1016/s0022-4596(03)00140-3
Vandeperre, L. J., and Clegg, W. J. (2003). Tailoring Strains Through Microstructural Design. Mater. Res. Soc. Symp. - Proc. 785, 389. doi:10.1557/proc-785-d11.4
Wang, Q., Jackson, J. A., Ge, Q., Hopkins, J. B., Spadaccini, C. M., and Fang, N. X. (2016). Lightweight Mechanical Metamaterials with Tunable Negative Thermal Expansion. Phys. Rev. Lett. 117, 1. doi:10.1103/physrevlett.117.175901
Wei, K., Chen, H., Pei, Y., and Fang, D. (2016). Planar Lattices with Tailorable Coefficient of thermal Expansion and High Stiffness Based on Dual-Material triangle Unit. J. Mech. Phys. Sol. 86, 173–191. doi:10.1016/j.jmps.2015.10.004
Wu, S.-C., Fecher, G. H., Shahab Naghavi, S., and Felser, C. (2019). Elastic Properties and Stability of Heusler Compounds: Cubic Co2YZ Compounds with L21 Structure. J. Appl. Phys. 125, 082523. doi:10.1063/1.5054398
Yoon, D., Son, Y.-W., and Cheong, H. (2011). Negative Thermal Expansion Coefficient of Graphene Measured by Raman Spectroscopy. Nano Lett. 11, 3227–3231. doi:10.1021/nl201488g
Keywords: negative thermal expansion, auxetic (negative Poisson ratio), honeycomb, re-entrant, metamaterials, architected materials
Citation: Grima-Cornish JN, Attard D, Evans KE and Grima JN (2021) Auxetic-Inspired Honeycomb Macrostructures With Anomalous Tailormade Thermal Expansion Properties Including “Negative” Heat-Shrinking Characteristics. Front. Mater. 8:769879. doi: 10.3389/fmats.2021.769879
Received: 02 September 2021; Accepted: 05 November 2021;
Published: 16 December 2021.
Edited by:
Bojan A. Marinkovic, Pontifical Catholic University of Rio de Janeiro, BrazilReviewed by:
Fabrizio Scarpa, University of Bristol, United KingdomCopyright © 2021 Grima-Cornish, Attard, Evans and Grima. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Joseph N. Grima, am9zZXBoLmdyaW1hQHVtLmVkdS5tdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.