Coupled Strengthening Effects by Lattice Distortion, Local Chemical Ordering, and Nanoprecipitates in Medium-Entropy Alloys

Extraordinary mechanical properties can be achieved in high-entropy alloys (HEAs) or medium-entropy alloys (MEAs) with nanoprecipitates. In the present study, the extra coupled strengthening effects by lattice distortion, local chemical ordering, and nanoprecipitates in the HEAs and MEAs with nanoprecipitates have been systematically investigated by large-scale molecular dynamics simulations. The moving of the dislocation can be slowed down, and the dislocation line shows a wavy configuration due to lattice distortion and local chemical ordering, resulting in strengthening. The degree of the wavy configuration increases and the sliding velocity of the dislocation decreases with increasing degrees of local chemical ordering. It is clearly indicated that the dislocation moves via nanoscale segment detrapping mechanism due to the effects of lattice distortion and local chemical ordering, resulting in roughened dislocation pathways for strengthening. The activated nanoscale segments are observed to be easier to detrap from the regions with stronger Co-Cr local chemical ordering and then propagate into the regions without such chemical ordering. These moving characteristics of the dislocation can delay the unpinning process from nanoprecipitates; thus, extra coupled strengthening effect has been revealed in the HEAs and MEAs with nanoprecipitates compared to pure Orowan’s strengthening.

Introduction

High-entropy alloys (HEAs) (Yeh et al., 2004; Cantor et al., 2004; Gludovatz et al., 2014; Schuh et al., 2015; George et al., 2020; LaRosa et al., 2019; Li et al., 2016; Lei et al., 2018; Jo et al., 2017; George et al., 2019; Shi et al., 2019) and/or medium-entropy alloys (MEAs) (Gludovatz et al., 2016; Miao et al., 2017; Yang M. et al., 2018a; Ma et al., 2018; Yang M. et al., 2019a; Wu et al., 2020; Sohn et al., 2019; Slone et al., 2019; Ding et al., 2018) are solid solution alloys consisting of three or more elements generally with equal atomic fraction. These HEAs and MEAs are generally single-phase materials and have high yield and ultimate strengths (Yeh et al., 2004; Cantor et al., 2004; Gludovatz et al., 2014; Schuh et al., 2015; George et al., 2020; LaRosa et al., 2019; Gludovatz et al., 2016; Miao et al., 2017; Yang T. et al., 2018b; Ma et al., 2018; Yang T. et al., 2019b; Wu et al., 2020; Sohn et al., 2019). Moreover, recently fabricated fcc HEAs and MEAs, such as FeCrMnCoNi HEA (Yeh et al., 2004; Cantor et al., 2004; Gludovatz et al., 2014; Schuh et al., 2015) and CoCrNi MEA (Gludovatz et al., 2016; Miao et al., 2017; Yang M. et al., 2018a; Ma et al., 2018; Yang M. et al., 2019a; Wu et al., 2020), can have high tensile ductility and exceptional fracture toughness and can have even better tensile and fracture properties at cryogenic temperature than at room temperature due to a transition of the dominant deformation mechanism from dislocation slip to deformation twinning (Gludovatz et al., 2014; Gludovatz et al., 2016).

Second-phase intermetallic compounds (IMCs) can generally enhance the yield strength of alloys, while the ductility in such alloys is diminished due to the localized strain concentration and the triggered microcracks around the brittle atomically ordered structures of IMCs (Gutierrez-Urrutia and Raabe, 2013; Kim et al., 2015). Coherent nanoprecipitates have been proven to be an effective strategy to achieve excellent synergy of strength and ductility in alloys (Jiang et al., 2017; Peng et al., 2020), and such microstructure design has been successfully applied in HEAs and MEAs recently to evade the strength–ductility dilemma (Yang T. et al., 2018b; Liang et al., 2018; Yang T. et al., 2019b; Ma et al., 2019; Tong et al., 2019; Du et al., 2020). For example, 3 at% Al and 3 at% Ti were added to a CoCrNi-based MEA to form fully coherent L12 precipitates, resulting in a yield strength of ∼2.0 GPa and a uniform elongation of ∼13% (Du et al., 2020). These coherent nanoprecipitates can minimize the elastic misfit strain of interfaces and relieve the stress/strain concentration during deformation and, at the same time, can provide Orowan-like hardening to enhance ductility in HEAs and MEAs.

The observed excellent mechanical properties in HEAs and MEAs can partly be attributed to the solid solution strengthening. Solid solution strengthening traditionally stems from the interaction of lattice dislocations with solutes (Varvenne et al., 2017; Labusch et al., 1972). The dislocation/solute interaction energy is typically high due to the distorted lattice by atomic size misfit and the more specific chemical core contributions (Varvenne et al., 2017; Labusch et al., 1972). The former factor can result in the interaction of the elastic stress field of dislocations with the strain field around the solute, while the latter factor can result in the different bonding environments within the stacking fault (SF) regions and the dislocation cores. Thus, the gliding of dislocations can be hindered by such interactions, requiring higher resolved shear stress for further plastic deformation. The traditional solid solution strengthening models (Varvenne et al., 2017; Labusch et al., 1972) were developed with an assumption of dilute alloys, while this assumption is clearly not valid any more in the case of HEAs and MEAs, where the definitions of solute and solvent break down (Okamoto et al., 2016; Varvenne et al., 2016a; Coury et al., 2019; Zhao and Nieh, 2017). Moreover, the models for solid solution strengthening were generally based on an assumption of a random distribution of atoms in the alloy, while more recently, chemical short-range order (CSRO) (Zhang et al., 2017; Li et al., 2019; Zhang et al., 2018; Zhang et al., 2020; Fantin et al., 2020; Varvenne et al., 2016b; Sadigh et al., 2012; Kostiuchenko et al., 2020) and local composition fluctuation (Jian et al., 2020) have also been found to play important roles in the mechanical behaviors of HEAs and MEAs. The local chemical structure/ordering and the local composition fluctuation can be experimentally characterized by extended X-ray absorption fine structure (EXAFS) techniques (Varvenne et al., 2016a; Zhang et al., 2017) and atomic resolution energy-dispersive X-ray spectroscopy (EDS) mapping using aberration-corrected TEM (Kostiuchenko et al., 2020; Zhang et al., 2020). The effects of local chemical ordering and local composition fluctuation on the solid solution strengthening have also be examined by molecular dynamics (MD) simulations in a few recent studies (Sadigh et al., 2012; Rao et al., 2017a; Ding et al., 2019; Li et al., 2019; Jian et al., 2020; Chen et al., 2021).

In the conventional alloy with nanoprecipitates, the elevated strengthening/hardening can be obtained by pinning dislocations at nanoparticles, the so-called Orowan’s strengthening/hardening. In the HEAs and MEAs without nanoprecipitates, the elevated strengthening/hardening can also be achieved by local chemical ordering. In HEAs and MEAs with nanoprecipitates, nanoprecipitates and local chemical ordering should both contribute to the strengthening/hardening. Moreover, these two strengthening effects might be coupled, and extra strengthening/hardening could be obtained due to this coupled effect, while the deformation mechanisms for this possible coupled effect are still unclear. In this regard, large-scale MD simulations have been conducted in the present study to investigate the a/2 < 110> edge dislocation sliding behaviors in a CoCrNi MEA with a wide variety of local chemical ordering and with/without nanoprecipitates. For the samples with nanoprecipitates, the coupled strengthening/hardening effects by nanoprecipitates and local chemical ordering can be considered.

Simulation Techniques

Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS, Plimpton, 1995) code has been utilized to perform the MD simulations and uncover the atomistic deformation mechanisms for the coupled strengthening/hardening in the CoCrNi MEA with a wide variety of local chemical ordering and with nanoprecipitates. The force reactions between atoms for the CoCrNi MEA were calculated by a regular EAM potential developed by Li et al. (Li et al., 2019) and an A-atom potential developed by Sadigh et al. (Sadigh et al., 2012). The A-atom potential—a hypothetical interatomic potential in pure metals—provides a mean-field representation of the three elements and ignores the effects of lattice distortion and local chemical ordering. For the samples without nanoprecipitates, the A-atom potential (Sadigh et al., 2012) was used to differentiate and identify the effects of lattice distortion and local chemical ordering on the strengthening/hardening, besides the regular EAM potential. The A-atom (average-atom) potential provides a mean-field representation of HEAs and MEAs, by approximating the interaction between any two constituent elements as a weighted average; thus, the lattice distortion effect can be eliminated by using the A-atom potential. Thus, for a sample with random distributions of elements, the simulations with the A-atom potential and the regular potential can identify the effect of lattice distortion on the strengthening/hardening. The effect of local chemical ordering on the strengthening/hardening can be simulated by using the regular potential and various samples with different degrees of local chemical ordering.

The equilibrium configurations with various degrees of local chemical ordering annealed at different temperatures (Ta, 450, 950, 1600 K) were obtained using the hybrid MD and Monte Carlo (MC) simulations under the variance-constrained semi-grand-canonical ensemble, and the other details about the hybrid MD and MC simulations can be referred to the previous research (Li et al., 2019).

In order to investigate the strengthening mechanisms, an a/2 < 110> edge dislocation, with line direction parallel to Z direction, was created using the continuum displacement field (Rao et al., 2017b) in the center of the simulation cells with the single crystal (bounded by $\left[\overline{1}10\right]$, $\left[111\right]$, and $\left[11\overline{2}\right]$ faces in the X, Y, and Z directions, respectively, Figure 1A) and with various degrees of local chemical ordering created by the aforementioned hybrid MD and MC simulations. The cell sizes were 110.96 × 12.40 × 41.72 nm³ (approximately 5.06 million atoms) for the CoCrNi MEA samples. The size of the cells in the X direction is selected to be large enough, giving enough time for dislocation movement without interacting with boundaries. The size of the cells in the Z direction (along the dislocation line) is also selected to be large enough to capture the characteristic length of roughed dislocation line and also to be large enough as compared to the characteristic length of local chemical ordering. The samples with nanoprecipitates were created by setting two spherical regions at specific positions as the rigid body, as shown in Figure 1B. The size of nanoprecipitates is 6 nm, and the interspacing of nanoprecipitates is 41.72 nm due to the periodic boundary condition along the Z direction. The projected distance along the X direction from the center of the nanoprecipitates to the center of the cells is 5 nm. The free boundary condition was imposed in the X direction, while the Z direction was set to be periodic. The position of the nanoprecipitate (the projected distance to the center of cells along the X direction), the size, and interspacing of nanoprecipitates definitely have strong influences on the strengthening effects. While the current research focuses on the coupled strengthening effects of lattice distortion, local chemical ordering, and nanoprecipitates, these effects of distance, size, and interspacing on the strengthening are excluded by keeping the same distance, size, and interspacing for various cells. Moreover, the nanoprecipitate is placed near the central position in order to make sure that the dislocation can bow out the nanoprecipitate completely before the leading parts of the dislocation touch the right boundary. Two thin rigid blocks with thickness of about 1 nm in the Y direction (upper and downer) were used as boundary planes for applying shear displacement, while the rest atoms were set to be mobile. The as-created samples were first fully relaxed under both the pressure 0 bar (along the Z direction) and the desired temperature (77 K) using the NPT ensemble prior to shear loading.

FIGURE 1

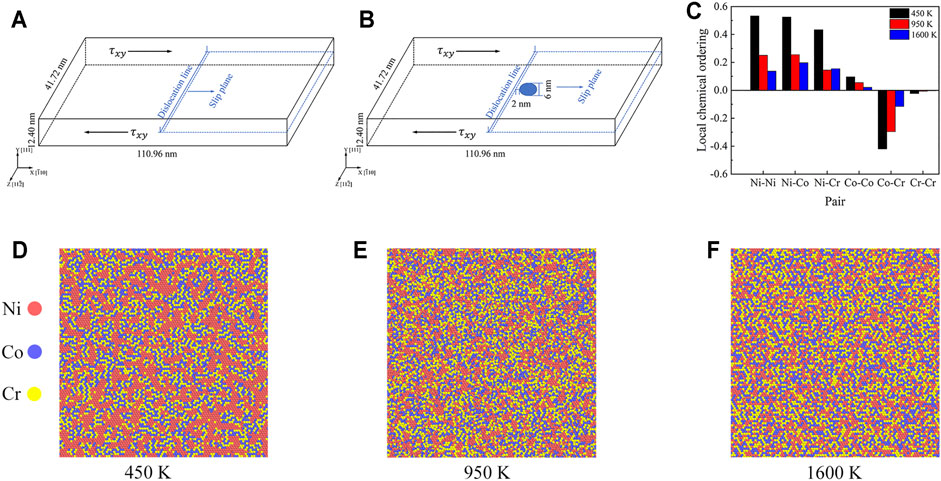
FIGURE 1. (A) Configuration for shear deformation on simulation cell with a straight a/2 < 110> edge dislocation and without nanoprecipitates. (B) Configuration for shear deformation on simulation cell with a straight a/2 < 110> edge dislocation and with nanoprecipitates. (C) The parameters of local chemical ordering for various pairs for the samples annealed at three different temperatures. (D) (E) (F) The typical atomic configurations with the detailed element distributions for the samples annealed at three different temperatures (Ta, 450, 950, 1600 K), in which the Ni atoms are colored in red, the Co atoms are colored in blue, and the Cr atoms are colored in yellow.

The shear strain was applied by subjecting the atoms in the upper and lower rigid blocks to a constant velocity (5.54 × 10^–2 m/s) in the X direction, giving a shearing strain rate of $1\times {10}^7/s$ and driving the dislocation for gliding toward the right side. In order to visualize the movement of the edge dislocation, the atoms were colored based on common neighbor analysis (CNA), in which gray color is for fcc atoms, red color is for hcp atoms (SF), and green color is for dislocation cores and free boundary atoms.

Results and Discussions

Figure 1C shows the local chemical ordering for samples annealed at three different temperatures (Ta, 450, 950, 1600 K), with local chemical ordering characterized by the pairwise multicomponent short-range order parameter (Antillon et al., 2019; de Fontaine, 1971). Here, only the first nearest-neighbor shell of the central atom is considered, since these parameters should play the most important role in the dislocation movement. As indicated in Figure 1C, the absolute values of ${\alpha }_{\text{Ni}-\text{Ni}}^1$, ${\alpha }_{\text{Ni}-\text{Co}}^1$, ${\alpha }_{\text{Ni}-\text{Cr}}^1$, ${\alpha }_{\text{Co}-\text{Co}}^1$, ${\alpha }_{\text{Co}-\text{Cr}}^1$, and ${\alpha }_{\text{Cr}-\text{Cr}}^1$ for various pairs increase with decreasing annealing temperatures. These parameters represent the pairwise multicomponent short-range order parameter: ${\alpha }_{\text{ij}}^1=\left(p_{ij}^1-C_j\right)/\left({\delta }_{ij}-C_j\right)$, where $p_{\text{ij}}^1$ is the average probability for finding a j-type atom around i-type atom in the first shell, $C_j$ is the average concentration of j-type atom in the system, and ${\delta }_{\text{ij}}$ is the Kronecker delta function. Moreover, ${\alpha }_{\text{Co}-\text{Cr}}^1$ and ${\alpha }_{\text{Cr}-\text{Cr}}^1$ are negative values. Figures 1D–F display the typical atomic configurations with the detailed element distributions for the samples annealed at three different temperatures (Ta, 450, 950, 1600 K). It is shown that the sample annealed at 1600 K shows a relatively random distribution of three elements, although a very weak trend for Ni clusters and interconnected Co-Cr clusters is observed. This means that only a very weak degree of local chemical ordering exists in the sample annealed at 1600 K. While with decreasing annealing temperature, dramatic local chemical ordering creates distinguishable nanoscale Ni domains and Co-Cr domains. Previous reports by EXAFS (Zhang et al., 2017) and MD simulations (Li et al., 2019) have also indicated that nanoscale Ni clusters could be formed, and the Cr atoms have a tendency to bond with Ni and Co atoms, instead of forming clusters by themselves. These observations suggest that the model CoCrNi system develops local Ni segregation and Co-Cr ordering, and the degree of local chemical ordering increases with decreasing annealing temperatures. It should be noted that the so-called local chemical ordering by these Ni clusters and Co-Cr clusters in the present study is very different from the CSRO for the VCoNi MEA in our recent study (Kostiuchenko et al., 2020), in which a repeating CSRO pattern across several neighboring atomic layers along the $\left[\overline{3}11\right]$ direction is observed: Co(Ni)-enriched/V-enriched/Co(Ni)-enriched/V-enriched.

For the samples without nanoprecipitates, the simulated shear stressstrain curves for the samples with various degrees of local chemical ordering and for the sample simulated by the A-atom potential are displayed in Figure 2A, in which the points for the edge dislocation moving with a displacement of 2 nm are marked by circles. For a carefully designed model with one edge dislocation in single crystal (in our case), the initial dislocation density is low, and no GBs are presented; thus, the shear stress should be only related to three parts: the first one is “intrinsic” lattice friction stress $\left({\tau }_{\text{FR}}\right)$, the second one is the strengthening due to the lattice distortion $\left({\tau }_{\text{LD}}\right)$, and the last one is the strengthening due to the local chemical ordering $\left({\tau }_{\text{LCO}}\right)$. Here, ${\tau }_{\text{FR}}$ is generally with a small magnitude and can be ignored for MEAs with severe lattice distortion and local chemical ordering. Thus, the reference shear stress for the edge dislocation moving with a displacement of 2 nm (when the leading partial dislocation touches the nanoprecipitate, this reference shear stress will be compared with the unpinning stress for the samples with nanoprecipitates) is plotted as a function of the degree of local chemical ordering in Figure 2B, in which the degree of local chemical ordering is represented by the values of ${\alpha }_{\text{Ni}-\text{Ni}}^1$. A small degree of local chemical ordering should exist even the samples are created by random functions; thus, the samples with zero degree of local chemical ordering are hardly obtained. Thus, a linear fitting is applied to the three data points for the samples annealed at three different temperatures (Ta, 450, 950, 1600 K) in Figure 2B, and this linear fitting line is extended to intercept with the ordinate. The intercepting point can be considered to be the strengthening by lattice distortion only (zero degree of local chemical ordering). The magnitude of lattice distortion can be quantified by the full width at half maximum (FWHM) for the radial distribution functions. The lattice distortion would contribute to the expansion of the FWHM, and larger lattice distortion leads to broader FWHW (Jian et al., 2020). As discussed earlier, both the local chemical ordering and the lattice distortion are not existing in the sample simulated by the A-atom potential. Thus, the difference of the reference shear stresses in Figure 2B for the intercepting point and for the sample simulated by the A-atom potential can approximately be considered as the strengthening effect of the lattice distortion. Moreover, the difference in the measured shear stresses among the samples annealed at different temperatures (Ta, 450, 950, 1600 K) can be considered as the strengthening effect of the local chemical ordering. It is indicated that both the lattice distortion and the local chemical ordering have influences on the strengthening, while the lattice distortion has a stronger impact on strengthening than local chemical ordering. Of course, the parameter of lattice distortion is dependent on the degree of local chemical ordering, and completely distinguishing the contributions from these two factors is a difficult task. Moreover, the reference shear stress increases with an increasing degree of the local chemical ordering.

FIGURE 2

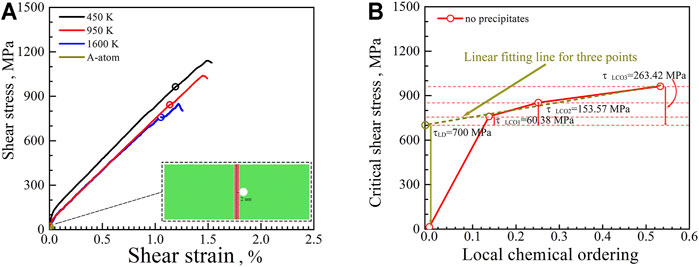
FIGURE 2. (A) Simulated shear stressstrain curves for the samples with various degrees of local chemical ordering and for the sample simulated by the A-atom potential (without nanoprecipitates). (B) The reference shear stress for the edge dislocation moving with a displacement of 2 nm as a function of the degree of local chemical ordering.

For the samples without nanoprecipitates, Figures 3A–C show the configurations and the movements of the edge dislocation at various applied shear strains for the sample simulated by the A-atom potential and for the samples annealed at 1,600 and 450 K, respectively. After relaxation, the as-created full edge dislocation displays a classical Shockley partial splitting along the dislocation core, that is, two partial dislocations separated by an SF. The average dissociation widths after relaxation for the samples annealed at 450 and 1600 K are observed to be smaller than those for the sample simulated by the A-atom potential. This observation indicates that the local chemical ordering can tune the local SF energy (SFE) for CoCrNi MEA, which is consistent with the previously reported results (Ding et al., 2018). As shown, the leading and trailing partials keep almost straight in the sample simulated by the A-atom potential after relaxation and during the movement of the dislocation, although the average dissociation width of SF changes under the shear stress during the movement. However, there are obvious fluctuations in the Shockley partial splitting widths along the dislocation line in the samples annealed at 450 and 1600 K after relaxation and during the movement of the dislocation, that is, the SF width varies along the dislocation line.

FIGURE 3

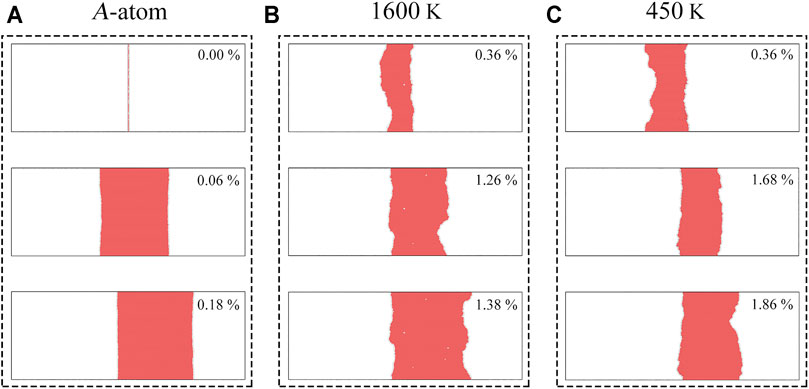
FIGURE 3. Snapshots at various applied shear strains for the configuration and the movement of the edge dislocation in (A) the sample without nanoprecipitates simulated by the A-atom potential; (B) the sample without nanoprecipitates annealed at 1600 K; (C) the sample without nanoprecipitates annealed at 450 K.

Moreover, the leading and trailing partial dislocation lines show the wavy configurations for the samples annealed at 450 and 1600 K. The fluctuations in SF width and the wavy configurations along the dislocation lines for the samples annealed at 450 and 1600 K can be attributed to the local chemical ordering, which results in roughened dislocation pathways for extra strengthening (Li et al., 2019). It is also observed that the shape of the wavy configuration for the dislocation line changes during the shear loading and during the movement of the edge dislocation for the samples annealed at 450 and 1600 K, which means that the sliding velocity is not uniform along the dislocation line during the shear loading and the gliding velocities for each segment on the dislocation line change significantly with time. It is interesting to note that some portion of the dislocation line moves faster than the other parts of the dislocation line under the applied shear strains, resulting in a roughened dislocation pathway in the samples annealed at 450 and 1600 K. The leading and trailing partial dislocations exhibit nanoscale curvatures along the dislocation line, leading to wavy dislocation lines and rugged SF ribbons.

In order to illustrate the degree of the wavy configurations, the normalized standard deviation of the local displacement in the leading partial dislocation as a function of the applied shear strain is plotted in Figure 4A for the sample simulated by the A-atom potential and for the samples annealed at 450 and 1600 K. In sharp contrast to the straight dislocation line (almost zero normalized standard deviation) for the sample simulated by the A-atom potential, it is clearly indicated that the degree of the wavy configurations is much larger for the sample simulated by the regular potential and increases with increasing degrees of local chemical ordering. At each time, the displacement is averaged along the dislocation line, and the averaged displacements for the leading partial dislocation are plotted as a function of shear strain for all samples in Figure 4B. It is observed that the slopes of these curves become larger and larger with increasing shear strain/time, which means that the gliding velocities become faster and faster with increasing applied shear strain. Previous research (Yuan and Wu, 2015; Peng et al., 2019) has also indicated that the dislocation gliding speed shows a strain/stress dependence for the same material, and the dislocation moves faster at higher strain/stress and can even move supersonically (i.e., at or over the speed of shear wave velocity) at ultrahigh applied strain/stress. It is indicated that the lattice distortion and the local chemical ordering have a significant impact on the moving velocity of the edge dislocation. The average moving velocity of the edge dislocation from the center to the right side of the simulated cell is estimated to be about 166.67 m/s for the sample simulated by the A-atom potential and be about 32.05 m/s, 26.04 m/s, and 23.81 m/s for the samples annealed at 1,600, 950, 450 K, respectively. The moving of the dislocations can be slowed down by the lattice distortion and the local chemical ordering, resulting in strengthening. Moreover, the average sliding velocity of the samples decreases with increasing degrees of local chemical ordering.

FIGURE 4

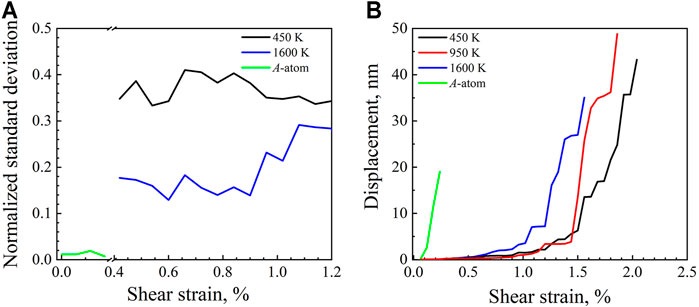
FIGURE 4. (A) Normalized standard deviation of the local displacement as a function of the shear strain for various samples without nanoprecipitates; (B) average displacements for the leading partial dislocation as a function of the shear strain for various samples without nanoprecipitates.

The motion characteristics of carrying plastic flow for the dislocation in the sample annealed at 450 K (without nanoprecipitates) are shown in Figure 5A. The long segment of the leading partial dislocation is considered, and a series of snapshots of the evolving dislocation line for gliding in the lattice are displayed in Figure 5A, in which the swept areas between two neighboring snapshots are highlighted in blue color. It is clearly indicated that the dislocation moves via nanoscale segment detrapping mechanism. Due to the varying moving velocity in different portions along the dislocation line, the dislocation line tends to bow out in soft regions and get trapped at hard regions acting as obstacle segments. Thus, the dislocation in the samples with local chemical ordering moves via a series of forward gliding of local nanoscale segments, and these segments move one at a time in an intermittent manner (i.e., one after another locally on the dislocation line), which is in sharp contrast with the sample simulated by the A-atom potential where the dislocation line moves smoothly by simultaneously propagating a long straight dislocation line. The correlation between nanoscale segment detrapping events and spatial deviations from local chemical ordering is displayed in Figure 5B. In Figure 5B, the swept areas of the activated nanoscale segments are marked by green lines, and the atoms are colored according to the ${\alpha }_{\text{Co}-\text{Cr}}^1$, and darker color means stronger Co-Cr local ordering (more negative ${\alpha }_{\text{Co}-\text{Cr}}^1$). It is interesting to note that the activated nanoscale segments seen in Figure 5A are observed to likely detrap from some of the local hard regions having stronger Co-Cr local chemical ordering and then propagate to the regions without such local chemical ordering. These moving characteristics for the samples with local chemical ordering and lattice distortion can result in the extra strengthening, which is very similar to the pinning strengthening by weak nanoparticles.

FIGURE 5

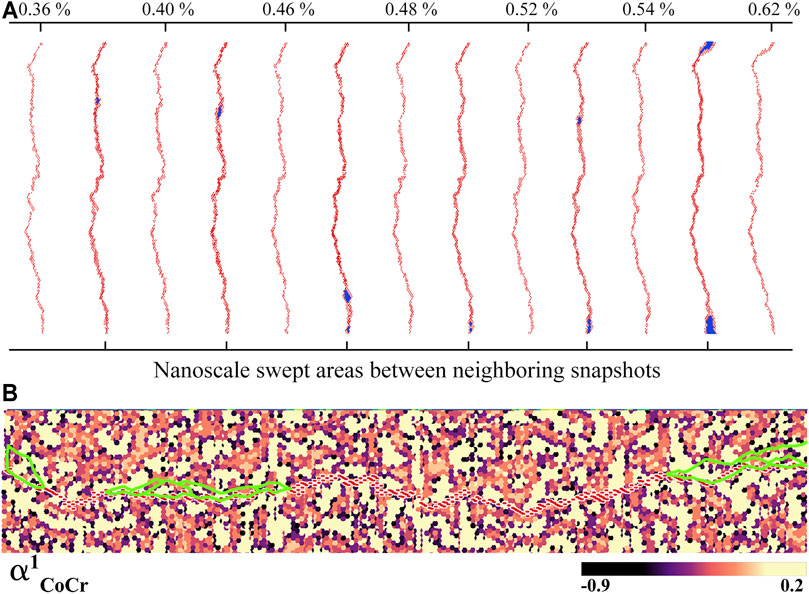
FIGURE 5. Dislocation motion via nanoscale segment detrapping mechanism for the sample annealed at 450 K (without nanoprecipitates). (A) Snapshots at varying shear strains showing nanoscale segment detrapping process, in which the swept areas between two neighboring snapshots are highlighted in blue color. (B) Correlation between nanoscale segment detrapping events and spatial deviations from local chemical ordering. (Atoms are colored according to the value of ${\alpha }_{\text{Co}-\text{Cr}}^1$.)

The simulated shear stress–strain curves for various samples with and without nanoprecipitates are shown in Figure 6A. In these curves, the points when the moving leading partial dislocation for the samples without nanoprecipitates reaches a displacement of 2 nm are marked by circles. It is interesting to note that the shear stressstrain curves for the samples without nanoprecipitates coincide very well with the corresponding samples with nanoprecipitates before the moving leading partial dislocation encounters the nanoprecipitate (at a displacement of 2 nm). However, the samples with nanoprecipitates display extra strengthening after the touching points, compared to the corresponding samples without nanoprecipitates. Moreover, the shear stress for the samples with nanoprecipitates reaches a maximum value and drops afterward due to the unpinning of the moving leading partial dislocation from the nanoprecipitate. These unpinning points are marked by squares in Figure 6A. Thus, the shear stress of the samples without nanoprecipitates for the toughing points and the shear stress of the samples with nanoprecipitates for the unpinning points are plotted as a function of the degree of local chemical ordering in Figure 6B, and the difference for these two critical shear stress can be considered for the extra strengthening by nanoprecipitates for various samples.

FIGURE 6

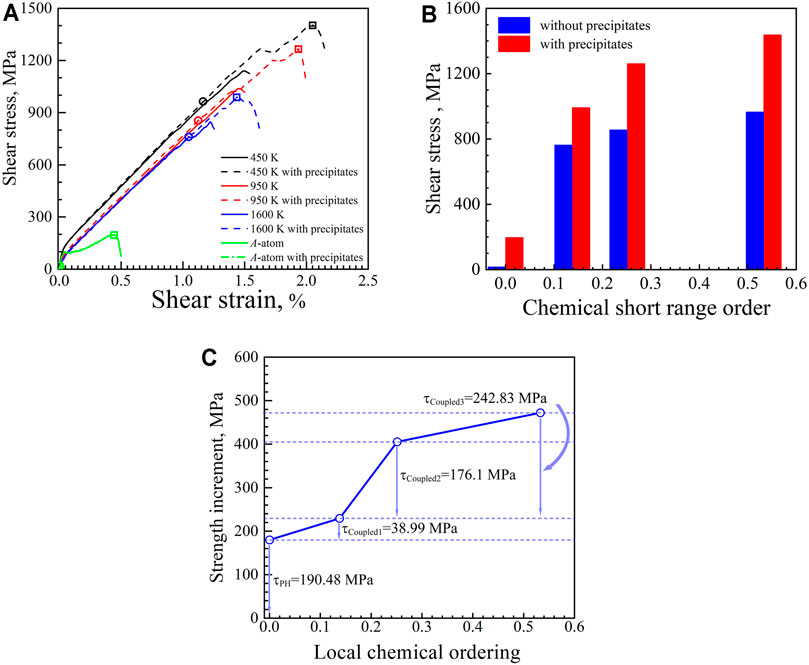
FIGURE 6. Coupling strengthening by lattice distortion, local chemical ordering, and nanoprecipitates. (A) Simulated shear stressstrain curves for various samples. (B) The critical shear stress ass a function of the degree of local chemical ordering. (C) The coupling strengthening effects as a function of the degree of local chemical ordering.

Then, the strength difference between the samples with nanoprecipitates and the corresponding samples without nanoprecipitates in Figure 6B is plotted as a function of the degree of local chemical ordering in Figure 6C. For the sample simulated by the A-atom potential, lattice distortion and local chemical ordering are not considered; thus, the strength difference (190.48 MPa) can be considered as the pure strengthening effect from the nanoprecipitates (pure Orowan’s strengthening). While the strength difference (229.47 MPa) for the sample annealed at 1600 K should be considered as the coupled strengthening effect from both the nanoprecipitates, the lattice distortion and the small degree of local chemical ordering, this coupled effect has an extra strengthening of 38.99 MPa besides pure Orowan’s strengthening of 190.48 MPa. The strength difference for the samples annealed at 950 and 450 K is 405.57 and 472.3 MPa, respectively. This indicates an extra coupled strengthening effect from both the nanoprecipitates and the local chemical ordering, and this extra coupled strengthening effect is 176.1, 242.83 MPa for the samples annealed at 950 and 450 K, respectively. It can be concluded that this extra coupled strengthening effect increases with an increasing degree of the local chemical ordering.

For the samples with nanoprecipitates, Figures 7A–C show the configurations and the movements of the edge dislocation at various applied shear strains for the sample simulated by the A-atom potential and for the samples annealed at 1,600 and 450 K, respectively. The snapshots at the unpinning points are also indicated in Figure 7. It is observed that the curvature of the leading partial dislocation at the unpinning points is very similar for all three samples. While the leading partial dislocation line is smooth for the sample simulated by the A-atom potential, the leading partial dislocation line shows ragged features for the two samples simulated by the regular potential. These ragged features are due to the nanoscale segment detrapping mechanism, which can slow down the dislocation sliding for strengthening. It is also interesting to note that both the lattice distortion and the local chemical ordering have a significant influence on the critical shear strain for the unpinning.

FIGURE 7

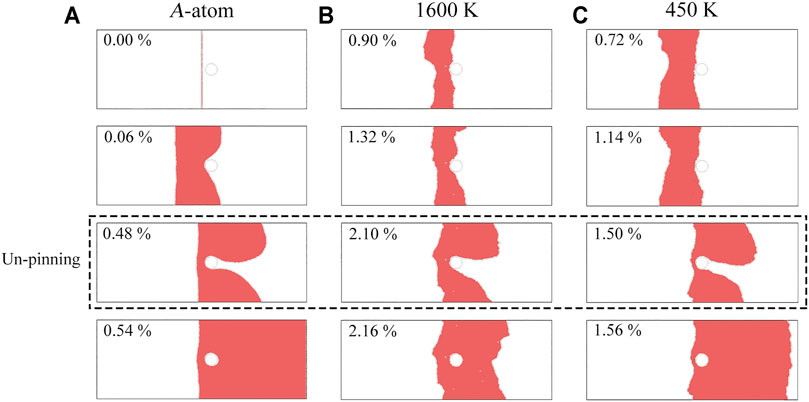
FIGURE 7. Snapshots at various applied shear strains for the configuration and the movement of the edge dislocation in (A) the sample with nanoprecipitates simulated by the A-atom potential; (B) the sample with nanoprecipitates annealed at 1600 K; (C) the sample with nanoprecipitates annealed at 450 K.

At each time, the displacement is averaged along the dislocation line, and the averaged displacements for the leading partial dislocation are plotted as a function of shear strain for all samples with nanoprecipitates in Figure 8A. The comparisons of the average displacements for the leading partial dislocation as a function of the shear strain for the samples with or without nanoprecipitates are displayed in Figures 8C–F. It is shown that the nanoprecipitates can significantly slow down the sliding of the edge dislocation, resulting in strengthening. Moreover, the normalized velocity decrement between the samples without nanoprecipitates until reaching a displacement of 2 nm and the samples with nanoprecipitates until unpinning from nanoprecipitates is plotted as a function of the degree of local chemical ordering in Figure 8B. As indicated, the normalized velocity decrement is smallest for the sample simulated by the A-atom potential and increases with an increasing degree of local chemical ordering. These observations indicate that the lattice distortion and the nanoprecipitates have a coupled effect on slowing down the sliding of the edge dislocation. The local chemical ordering and the nanoprecipitates also have coupled effects on slowing down the sliding of the edge dislocation, and this coupled effect increases with an increasing degree of local chemical ordering. Thus, these coupled effects on slowing down the sliding of the edge dislocation should be one of the origins for the coupled strengthening.

FIGURE 8

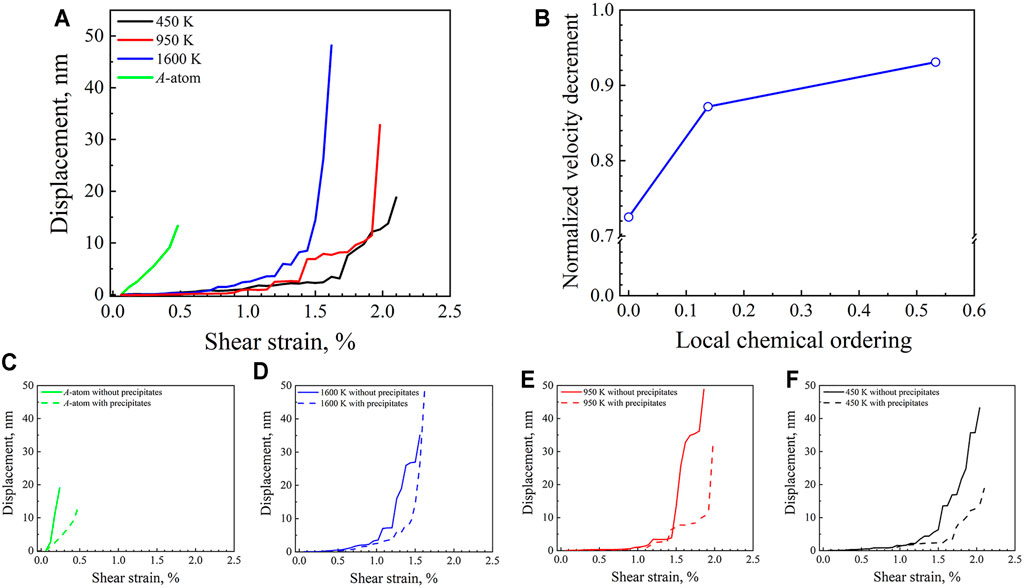
FIGURE 8. (A) Average displacements for the leading partial dislocation as a function of the shear strain for various samples with nanoprecipitates. (B) The normalized velocity decrement between the samples without nanoprecipitates until reaching a displacement of 2 nm and the samples with nanoprecipitates until unpinning from nanoprecipitates as a function of the degree of local chemical ordering. (C) (D) (E) (F) The comparisons of the average displacements for the leading partial dislocation as a function of the shear strain for the samples with or without nanoprecipitates.

In order to illustrate the possible atomistic mechanisms for the coupled effects on slowing down the sliding of the edge dislocation, snapshots at varying shear strains showing both processes of nanoscale segment detrapping and unpinning from the nanoprecipitate for the sample annealed at 450 K are shown in Figure 9A. In Figure 9A, the swept areas between two neighboring snapshots are highlighted in blue color. During the unpinning process from the nanoprecipitate, the leading partial dislocation is also observed to propagate via a series of forward gliding of local segments with nanoscale, and these segments are also found to move one at a time in an intermittent manner. Thus, the unpinning process from the nanoprecipitate is significantly delayed by these moving characteristics of nanoscale segment detrapping mechanism, resulting in coupled extra strengthening. For the unpinning process from the nanoprecipitate for the sample annealed at 450 K (with nanoprecipitates), the correlation between nanoscale segment detrapping events and spatial deviations from local chemical ordering is shown in Figure 9B. In Figure 9B, the swept areas of the activated nanoscale segments are also marked by green lines, and the atoms are also colored according to the value of ${\alpha }_{\text{Co}-\text{Cr}}^1$. Similar to the correlation for the corresponding sample without nanoprecipitates, the activated nanoscale segments seen in Figure 9B are also observed to likely detrap from some of the local hard regions having stronger Co-Cr local chemical ordering and then propagate to the regions without such local chemical ordering. Thus, the unpinning process from the nanoprecipitate is observed to be significantly delayed by these moving characteristics, resulting in extra coupled strengthening.

FIGURE 9

FIGURE 9. Dislocation motion via nanoscale segment detrapping mechanism for the sample annealed at 450 K (with nanoprecipitates). (A) Snapshots at varying shear strains showing nanoscale segment detrapping process, in which the swept areas between two neighboring snapshots are highlighted in blue color. (B) Correlation between nanoscale segment detrapping events and spatial deviations from local chemical ordering for the sample annealed at 450 K (with nanoprecipitates).

Summary and Concluding Remarks

High strength and strong strain hardening can be achieved in HEAs or MEAs with nanoprecipitates due to the effects of lattice distortion, local chemical ordering, and precipitation hardening. In the present study, large-scale molecular dynamics simulations have been utilized to investigate and reveal the extra coupled strengthening effects and the corresponding atomistic deformation mechanisms by lattice distortion, local chemical ordering, and nanoprecipitates. The main findings can be summarized as follows:

Both the lattice distortion and the local chemical ordering have impacts on the strengthening, while the lattice distortion has a stronger influence on the strengthening than the local chemical ordering. Moreover, a higher degree of the local chemical ordering results in higher strengthening. The moving of the dislocation can be slowed down, and the dislocation lines show the wavy configuration due to the lattice distortion and the local chemical ordering, resulting in strengthening. Moreover, the average sliding velocity of the dislocation is found to decrease, and the degree of the wavy configuration is observed to increase with an increasing degree of local chemical ordering.

The dislocation in the samples with local chemical ordering and lattice distortion moves via a series of forward gliding of local nanoscale segments, and these segments move one at a time in an intermittent manner, which is in sharp contrast with the sample simulated by the A-atom potential where the dislocation line moves smoothly by simultaneously propagating a long straight dislocation line. The activated nanoscale segments are observed to be easier to detrap from the regions with stronger Co-Cr local chemical ordering and then propagate into the regions without such chemical order. These moving characteristics via the nanoscale segment detrapping mechanism for the samples with local chemical ordering and lattice distortion can result in roughened dislocation pathways for strengthening.

Compared to pure Orowan’s strengthening, the extra coupled strengthening effect can be induced by lattice distortion, local chemical ordering, and nanoprecipitates, and this extra coupled strengthening effect increases with an increasing degree of the local chemical ordering. The lattice distortion, the local chemical ordering, and the nanoprecipitates are found to have a coupled effect on slowing down the sliding of the edge dislocation, and this coupled effect increases with an increasing degree of local chemical ordering, resulting in the coupled strengthening.

During the unpinning process from the nanoprecipitate, the dislocation is found to propagate via a series of forward gliding of local nano-segments (one at a time in an intermittent manner). Thus, the unpinning process from the nanoprecipitate is observed to be significantly delayed by these moving characteristics of nano-segment detrapping mechanism, resulting in coupled extra strengthening. The current results are found on the interactions between the a/2 < 110> edge dislocation, local chemical ordering, and nanoprecipitate. The present findings should be valid for other type of dislocations, while these investigations would be conducted in the future work due to the limitation of the paper length. The present findings should provide insights into understanding the strengthening and the strain hardening mechanisms in HEAs or MEAs with nanoprecipitates.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

FY and XW contributed to the conception and design of the study. WC performed the simulations and the analysis. FY wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This research was supported by the National Key R and D Program of China (Grant number 2017YFA0204402), the NSFC Basic Science Center Program for “Multiscale Problems in Nonlinear Mechanics” (Grant number 11988102), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant number XDB22040503), and the Development Project of China Railway (Grant number N2020J028).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Antillon, E., Woodward, C., Rao, S. I., Akdim, B., and Parthasarathy, T. A. (2019). A Molecular Dynamics Technique for Determining Energy Landscapes as a Dislocation Percolates through a Field of Solutes. Acta Materialia 166, 658–676. doi:10.1016/j.actamat.2018.12.037

CrossRef Full Text | Google Scholar

Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural Development in Equiatomic Multicomponent Alloys. Mater. Sci. Eng. A 375-377, 213–218. doi:10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Chen, X., Wang, Q., Cheng, Z., Zhu, M., Zhou, H., Jiang, P., et al. (2021). Direct Observation of Chemical Short-Range Order in a Medium-Entropy alloy. Nature 592, 712–716. doi:10.1038/s41586-021-03428-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Coury, F. G., Kaufman, M., and Clarke, A. J. (2019). Solid-solution Strengthening in Refractory High Entropy Alloys. Acta Materialia 175, 66–81. doi:10.1016/j.actamat.2019.06.006

CrossRef Full Text | Google Scholar

de Fontaine, D. (1971). The Number of Independent Pair-Correlation Functions in Multicomponent Systems. J. Appl. Cryst. 4, 15–19. doi:10.1107/s0021889871006174

CrossRef Full Text | Google Scholar

Ding, J., Yu, Q., Asta, M., and Ritchie, R. O. (2018). Tunable Stacking Fault Energies by Tailoring Local Chemical Order in CrCoNi Medium-Entropy Alloys. Proc. Natl. Acad. Sci. USA 115, 8919–8924. doi:10.1073/pnas.1808660115

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Q., Zhang, Y., Chen, X., Fu, X., Chen, D., Chen, S., et al. (2019). Tuning Element Distribution, Structure and Properties by Composition in High-Entropy Alloys. Nature 574, 223–227. doi:10.1038/s41586-019-1617-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Du, X. H., Li, W. P., Chang, H. T., Yang, T., Duan, G. S., Wu, B. L., et al. (2020). Dual Heterogeneous Structures lead to Ultrahigh Strength and Uniform Ductility in a Co-cr-ni Medium-Entropy alloy. Nat. Commun. 11, 2390. doi:10.1038/s41467-020-16085-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Fantin, A., Lepore, G. O., Manzoni, A. M., Kasatikov, S., Scherb, T., Huthwelker, T., et al. (2020). Short-range Chemical Order and Local Lattice Distortion in a Compositionally Complex alloy. Acta Materialia 193, 329–337. doi:10.1016/j.actamat.2020.04.034

CrossRef Full Text | Google Scholar

George, E. P., Curtin, W. A., and Tasan, C. C. (2020). High Entropy Alloys: A Focused Review of Mechanical Properties and Deformation Mechanisms. Acta Materialia 188, 435–474. doi:10.1016/j.actamat.2019.12.015

CrossRef Full Text | Google Scholar

George, E. P., Raabe, D., and Ritchie, R. O. (2019). High-entropy Alloys. Nat. Rev. Mater. 4, 515–534. doi:10.1038/s41578-019-0121-4

CrossRef Full Text | Google Scholar

Gludovatz, B., Hohenwarter, A., Catoor, D., Chang, E. H., George, E. P., and Ritchie, R. O. (2014). A Fracture-Resistant High-Entropy alloy for Cryogenic Applications. Science 345, 1153–1158. doi:10.1126/science.1254581

PubMed Abstract | CrossRef Full Text | Google Scholar

Gludovatz, B., Hohenwarter, A., Thurston, K. V. S., Bei, H., Wu, Z., George, E. P., et al. (2016). Exceptional Damage-Tolerance of a Medium-Entropy alloy CrCoNi at Cryogenic Temperatures. Nat. Commun. 7, 10602. doi:10.1038/ncomms10602

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutierrez-Urrutia, I., and Raabe, D. (2013). Influence of Al Content and Precipitation State on the Mechanical Behavior of Austenitic High-Mn Low-Density Steels. Scripta Materialia 68, 343–347. doi:10.1016/j.scriptamat.2012.08.038

CrossRef Full Text | Google Scholar

Jian, W.-R., Xie, Z., Xu, S., Su, Y., Yao, X., and Beyerlein, I. J. (2020). Effects of Lattice Distortion and Chemical Short-Range Order on the Mechanisms of Deformation in Medium Entropy alloy CoCrNi. Acta Materialia 199, 352–369. doi:10.1016/j.actamat.2020.08.044

CrossRef Full Text | Google Scholar

Jiang, S., Wang, H., Wu, Y., Liu, X., Chen, H., Yao, M., et al. (2017). Ultrastrong Steel via Minimal Lattice Misfit and High-Density Nanoprecipitation. Nature 544, 460–464. doi:10.1038/nature22032

PubMed Abstract | CrossRef Full Text | Google Scholar

Jo, Y. H., Jung, S., Choi, W. M., Sohn, S. S., Kim, H. S., Lee, B. J., et al. (2017). Cryogenic Strength Improvement by Utilizing Room-Temperature Deformation Twinning in a Partially Recrystallized VCrMnFeCoNi High-Entropy alloy. Nat. Commun. 8, 15719. doi:10.1038/ncomms15719

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, S.-H., Kim, H., and Kim, N. J. (2015). Brittle Intermetallic Compound Makes Ultrastrong Low-Density Steel with Large Ductility. Nature 518, 77–79. doi:10.1038/nature14144

PubMed Abstract | CrossRef Full Text | Google Scholar

Kostiuchenko, T., Ruban, A. V., Neugebauer, J., Shapeev, A., and Körmann, F. (2020). Short-range Order in Face-Centered Cubic VCoNi Alloys. Phys. Rev. Mater. 4, 113802. doi:10.1103/physrevmaterials.4.113802

CrossRef Full Text | Google Scholar

Labusch, R. (1972). Statistische theorien der mischkristallhärtung. Acta Metallurgica 20, 917–927. doi:10.1016/0001-6160(72)90085-5

CrossRef Full Text | Google Scholar

LaRosa, C. R., Shih, M., Varvenne, C., and Ghazisaeidi, M. (2019). Solid Solution Strengthening Theories of High-Entropy Alloys. Mater. Characterization 151, 310–317. doi:10.1016/j.matchar.2019.02.034

CrossRef Full Text | Google Scholar

Lei, Z., Liu, X., Wu, Y., Wang, H., Jiang, S., Wang, S., et al. (2018). Enhanced Strength and Ductility in a High-Entropy alloy via Ordered Oxygen Complexes. Nature 563, 546–550. doi:10.1038/s41586-018-0685-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Q.-J., Sheng, H., and Ma, E. (2019). Strengthening in Multi-Principal Element Alloys with Local-Chemical-Order Roughened Dislocation Pathways. Nat. Commun. 10, 3563. doi:10.1038/s41467-019-11464-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Pradeep, K. G., Deng, Y., Raabe, D., and Tasan, C. C. (2016). Metastable High-Entropy Dual-phase Alloys Overcome the Strength-Ductility Trade-Off. Nature 534, 227–230. doi:10.1038/nature17981

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Y.-J., Wang, L., Wen, Y., Cheng, B., Wu, Q., Cao, T., et al. (2018). High-content Ductile Coherent Nanoprecipitates Achieve Ultrastrong High-Entropy Alloys. Nat. Commun. 9, 4063. doi:10.1038/s41467-018-06600-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Y., Hao, J., Jie, J., Wang, Q., and Dong, C. (2019). Coherent Precipitation and Strengthening in a Dual-Phase AlNi2Co2Fe1.5Cr1.5 High-Entropy Alloy. Mater. Sci. Eng. A 764, 138241. doi:10.1016/j.msea.2019.138241

CrossRef Full Text | Google Scholar

Ma, Y., Yuan, F., Yang, M., Jiang, P., Ma, E., and Wu, X. (2018). Dynamic Shear Deformation of a CrCoNi Medium-Entropy Alloy with Heterogeneous Grain Structures. Acta Materialia 148, 407–418. doi:10.1016/j.actamat.2018.02.016

CrossRef Full Text | Google Scholar

Miao, J., Slone, C. E., Smith, T. M., Niu, C., Bei, H., Ghazisaeidi, M., et al. (2017). The Evolution of the Deformation Substructure in a Ni-Co-Cr Equiatomic Solid Solution Alloy. Acta Materialia 132, 35–48. doi:10.1016/j.actamat.2017.04.033

CrossRef Full Text | Google Scholar

Okamoto, N. L., Yuge, K., Tanaka, K., Inui, H., and George, E. P. (2016). Atomic Displacement in the CrMnFeCoNi High-Entropy Alloy - A Scaling Factor to Predict Solid Solution Strengthening. AIP Adv. 6, 125008. doi:10.1063/1.4971371

CrossRef Full Text | Google Scholar

Peng, S., Wei, Y., Jin, Z., and Yang, W. (2019). Supersonic Screw Dislocations Gliding at the Shear Wave Speed. Phys. Rev. Lett. 122, 045501. doi:10.1103/PhysRevLett.122.045501

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, S., Wei, Y., and Gao, H. (2020). Nanoscale Precipitates as Sustainable Dislocation Sources for Enhanced Ductility and High Strength. Proc. Natl. Acad. Sci. USA 117, 5204–5209. doi:10.1073/pnas.1914615117

PubMed Abstract | CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Rao, S. I., Varvenne, C., Woodward, C., Parthasarathy, T. A., Miracle, D., Senkov, O. N., et al. (2017a). Atomistic Simulations of Dislocations in a Model BCC Multicomponent Concentrated Solid Solution alloy. Acta Materialia 125, 311–320. doi:10.1016/j.actamat.2016.12.011

CrossRef Full Text | Google Scholar

Rao, S. I., Woodward, C., Parthasarathy, T. A., and Senkov, O. (2017b). Atomistic Simulations of Dislocation Behavior in a Model FCC Multicomponent Concentrated Solid Solution alloy. Acta Materialia 134, 188–194. doi:10.1016/j.actamat.2017.05.071

CrossRef Full Text | Google Scholar

Sadigh, B., Erhart, P., Stukowski, A., Caro, A., Martinez, E., and Zepeda-Ruiz, L. (2012). Scalable Parallel Monte Carlo Algorithm for Atomistic Simulations of Precipitation in Alloys. Phys. Rev. B 85, 184203. doi:10.1103/physrevb.85.184203

CrossRef Full Text | Google Scholar

Schuh, B., Mendez-Martin, F., Völker, B., George, E. P., Clemens, H., Pippan, R., et al. (2015). Mechanical Properties, Microstructure and thermal Stability of a Nanocrystalline CoCrFeMnNi High-Entropy alloy after Severe Plastic Deformation. Acta Materialia 96, 258–268. doi:10.1016/j.actamat.2015.06.025

CrossRef Full Text | Google Scholar

Shi, P., Ren, W., Zheng, T., Ren, Z., Hou, X., Peng, J., et al. (2019). Enhanced Strength-Ductility Synergy in Ultrafine-Grained Eutectic High-Entropy Alloys by Inheriting Microstructural Lamellae. Nat. Commun. 10, 489. doi:10.1038/s41467-019-08460-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Slone, C. E., Miao, J., George, E. P., and Mills, M. J. (2019). Achieving Ultra-high Strength and Ductility in Equiatomic CrCoNi with Partially Recrystallized Microstructures. Acta Materialia 165, 496–507. doi:10.1016/j.actamat.2018.12.015

CrossRef Full Text | Google Scholar

Sohn, S. S., Kwiatkowski da Silva, A., Ikeda, Y., Körmann, F., Lu, W., Choi, W. S., et al. (2019). Ultrastrong Medium-Entropy Single-phase Alloys Designed via Severe Lattice Distortion. Adv. Mater. 31, 1807142. doi:10.1002/adma.201807142

PubMed Abstract | CrossRef Full Text | Google Scholar

Tong, Y., Chen, D., Han, B., Wang, J., Feng, R., Yang, T., et al. (2019). Outstanding Tensile Properties of a Precipitation-Strengthened FeCoNiCrTi0.2 High-Entropy Alloy at Room and Cryogenic Temperatures. Acta Materialia 165, 228–240. doi:10.1016/j.actamat.2018.11.049

CrossRef Full Text | Google Scholar

Varvenne, C., Leyson, G. P. M., Ghazisaeidi, M., and Curtin, W. A. (2017). Solute Strengthening in Random Alloys. Acta Materialia 124, 660–683. doi:10.1016/j.actamat.2016.09.046

CrossRef Full Text | Google Scholar

Varvenne, C., Luque, A., and Curtin, W. A. (2016b). Theory of Strengthening in Fcc High Entropy Alloys. Acta Materialia 118, 164–176. doi:10.1016/j.actamat.2016.07.040

CrossRef Full Text | Google Scholar

Varvenne, C., Luque, A., Nöhring, W. G., and Curtin, W. A. (2016a). Average-atom Interatomic Potential for Random Alloys. Phys. Rev. B 93, 104201. doi:10.1103/physrevb.93.104201

CrossRef Full Text | Google Scholar

Wu, X., Yang, M., Jiang, P., Wang, C., Zhou, L., Yuan, F., et al. (2020). Deformation Nanotwins Suppress Shear Banding during Impact Test of CrCoNi Medium-Entropy alloy. Scripta Materialia 178, 452–456. doi:10.1016/j.scriptamat.2019.12.017

CrossRef Full Text | Google Scholar

Yang, M., Yan, D., Yuan, F., Jiang, P., Ma, E., and Wu, X. (2018a). Dynamically Reinforced Heterogeneous Grain Structure Prolongs Ductility in a Medium-Entropy alloy with Gigapascal Yield Strength. Proc. Natl. Acad. Sci. USA 115, 7224–7229. doi:10.1073/pnas.1807817115

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, M., Zhou, L., Wang, C., Jiang, P., Yuan, F., Ma, E., et al. (2019a). High Impact Toughness of CrCoNi Medium-Entropy alloy at Liquid-Helium Temperature. Scripta Materialia 172, 66–71. doi:10.1016/j.scriptamat.2019.07.010

CrossRef Full Text | Google Scholar

Yang, T., Zhao, Y. L., Luan, J. H., Han, B., Wei, J., Kai, J. J., et al. (2019b). Nanoparticles-strengthened High-Entropy Alloys for Cryogenic Applications Showing an Exceptional Strength-Ductility Synergy. Scripta Materialia 164, 30–35. doi:10.1016/j.scriptamat.2019.01.034

CrossRef Full Text | Google Scholar

Yang, T., Zhao, Y. L., Tong, Y., Jiao, Z. B., Wei, J., Cai, J. X., et al. (2018b). Multicomponent Intermetallic Nanoparticles and Superb Mechanical Behaviors of Complex Alloys. Science 362, 933–937. doi:10.1126/science.aas8815

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeh, J.-W., Chen, S.-K., Lin, S.-J., Gan, J.-Y., Chin, T.-S., Shun, T.-T., et al. (2004). Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 6, 299–303. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Yuan, F., and Wu, X. (2015). Size Effect and Boundary Type on the Strengthening of Nanoscale Domains in Pure Nickel. Mater. Sci. Eng. A 648, 243–251. doi:10.1016/j.msea.2015.09.071

CrossRef Full Text | Google Scholar

Zhang, F., Tong, Y., Jin, K., Bei, H., Weber, W. J., Huq, A., et al. (2018). Chemical Complexity Induced Local Structural Distortion in NiCoFeMnCr High-Entropy alloy. Mater. Res. Lett. 6, 450–455. doi:10.1080/21663831.2018.1478332

CrossRef Full Text | Google Scholar

Zhang, F. X., Zhao, S., Jin, K., Xue, H., Velisa, G., Bei, H., et al. (2017). Local Structure and Short-Range Order in a NiCoCr Solid Solution alloy. Phys. Rev. Lett. 118, 205501. doi:10.1103/physrevlett.118.205501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, R., Zhao, S., Ding, J., Chong, Y., Jia, T., Ophus, C., et al. (2020). Short-range Order and its Impact on the CrCoNi Medium-Entropy alloy. Nature 581, 283–287. doi:10.1038/s41586-020-2275-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, Y. Y., and Nieh, T. G. (2017). Correlation between Lattice Distortion and Friction Stress in Ni-Based Equiatomic Alloys. Intermetallics 86, 45–50. doi:10.1016/j.intermet.2017.03.011

CrossRef Full Text | Google Scholar