Numerical Investigation of Discrepancies Between Two-Dimensional and Three-Dimensional Acoustic Metamaterials

In order to get insight information of the band structure of acoustic metamaterials (AMMs) in condensed matter, periodic lattice structures are analyzed using Bloch’s theorem. Typical approaches of the band structure computation methods, topology optimization, and tunable abilities cannot overcome the gap between the two-dimensional (2D) AMMs theoretical and three-dimensional (3D) specimens’ experimental data yet. In this work, the variation in the results of the band structure obtained from the 2D mathematical model computed with respect to the 3D experimental models, and related cause of the variation is explored. The band structures and mode shapes of the 2D AMMs, quasi-2D models, and 3D specimen models are followed to reveal the boundary conditions and source for the observed differences in band structures. The cause for the discrepancies is verified by using the finite element method (FEM) with corresponding boundary conditions. It is found that outcomes from computational data of the 2D AMMs model are diverted significantly by means of bandgap, band structure, and stress distribution in counterparts of the 3D specimen model. This approach can provide assistance for computing the band structure of 2D AMMs for practical applications.

Introduction

Acoustic metamaterials (AMMs) are basically composite materials with a periodic structure composed of two or more elastic media (Kushwaha et al., 1993). Lately, AMMs have been attracted attention due to the distinctive characteristic of acoustic or elastic waves not being propagated at the specific frequency. Different from single-negative AMMs are mainly used for vibration isolation (An et al., 2020; Chen et al., 2021; Huang et al., 2021), AMMs with double-negative characteristics can be used in unique device designing such as acoustic cloaking (Chen and Chan, 2007; Munteanu and Chiroiu, 2011; Zheng et al., 2014), acoustic imaging (Deng et al., 2009; Molerón and Daraio, 2015; Laureti et al., 2016), waveguiding (Casadei et al., 2012; Cao et al., 2018; Ghasemi Baboly et al., 2018; Cao et al., 2019; Sirota et al., 2021), and acoustic focusing (Li et al., 2012; Al Jahdali and Wu, 2016; Chen et al., 2018). The tunable AMMs also be proposed to provide multiple functions, such as active acoustic metalens (Zhang et al., 2021) and tunable acoustic metasurface (Cao et al., 2021). and Exhibiting exclusive phenomena and feasibility to compute at ease in the counterpart of one- and three-dimensional (1D and 3D) AMMs, the two-dimensional (2D) AMMs have been studied at theoretical and experimental levels (Ding et al., 2010; Dorodnitsyn and Van Damme, 2016; Yu et al., 2017; An et al., 2018; Sang and Sandgren, 2018; Guo et al., 2019; Cheng et al., 2020; Sun et al., 2020; Wang et al., 2020). The general research is carried out the two steps, namely calculation of the band structures of 2D AMMs and experiment with the transmittance of corresponding specimens. The band structure can be obtained by theoretical or numerical methods under the applied 2D boundary conditions (Sigalas and Soukoulis, 1995; Axmann and Kuchment, 1999; Kafesaki and Economou, 1999; Cao et al., 2004a; b; Rabczuk et al., 2004; Ning et al., 2020; Wang et al., 2021). However, the used specimens during the experiments are actually 3D structures, which creates differences with respect to the 2D AMMs model for computing (Bertoldi et al., 2008; Mohammadi et al., 2008; Lv et al., 2013; Shan et al., 2014; Wang et al., 2014; Billon et al., 2019; Gao et al., 2019; Li et al., 2019; Faiz et al., 2020; Muhammad et al., 2020; Huo et al., 2021). The specimens for the experiments are arrayed in 2D periodically, while their physical structure scale is measured in 3D. Notably, the 2D AMMs model is a simplified ideal model, though the comparison of band structure computed by a model with experimental results can be devoid of some practical vibration modes, which may cause inconsistent results. The wave dispersion of the 2D AMMs model and its 3D specimens are analyzed, and significant differences are found in previous research (Krushynska et al., 2017). However, the height range of 3D cases in this research is limited to 0.1–0.5a, and the large height specimen is not considered. Typically, epoxy is used as a matrix material in AMMs, and such a relatively hard material can reduce the influence of the variation in height.

In this work, the computing models for 2D AMMs are defined to compute band structure and transmittance. The results are compared with the corresponding outcomes obtained by different 3D specimen models. In experiments, the specimen of 2D AMMs are actually 3D and 2D is its periodicity. In this case, there will be some difference between the 2D numerical computation results and 2D AMMs specimen experiments results. In this paper, we use the numerical computation results of 3D specimen models to investigate the discrepancies between its results and the 2D numerical computation results. The observed differences between them show the limitation of using computation results of 2D AMMs model to compare with experimental results. The two factors are analyzed to verify the variation i.e., the mode shape displacement distribution of each section along the $z$-axis and the mode shape stress distribution of each section along the $z$-axis. These analyses can be applied in the research on 2D periodic structures in solid-state physics, especially those with experiments.

Initially, the basic calculation based on the theories of 2D AMMs and corresponding specimens are briefly introduced. Thereafter, the difference in the calculated results are presented, and related reasons is verified. The final concluding remarks is given for detailed analyses.

Mathematical Model of Acoustic Metamaterials

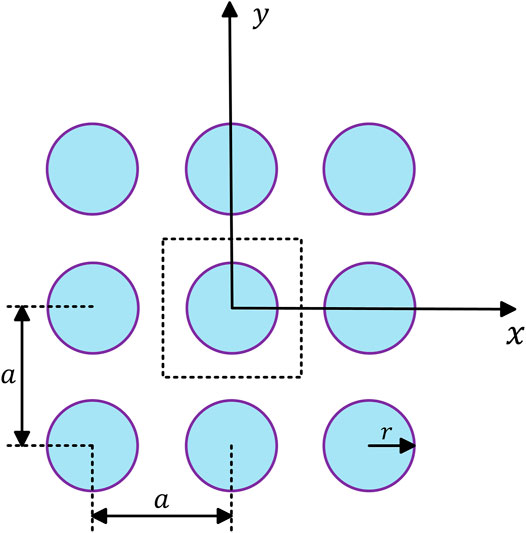
Here, a 2D AMMs consists of an array of straight and infinite cylinders arranged in a square matrix is considered. This kind of structure is widely used since the AMMs were studied(Mead, 1996; Krushynska et al., 2017; Mazzotti et al., 2019). Figure 1 illustrates the lattice structure, where $a$ denotes the lattice constant, and $r$ denotes the radius of the cylinder. The dash line area represents a unit cell. The cylinders are set parallel to the $z$-axis. By considering 2D AMMs, it is assumed that the elastic waves are propagated in the transverse plane i.e., perpendicular to the axis of the cylinder. The wave propagation mode in the $x \mathrm{-}y$ plane and the related Eigen-modes are called as $xy$ model.

FIGURE 1

FIGURE 1. The lattice structure of the 2D AMMs.

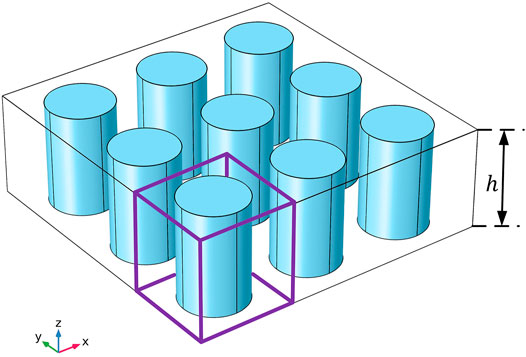
Based on the considered structure of the 2D AMMs, the corresponding specimen model is shown in Figure 2. It is worth noting that the unit cell of the specimen is 2D periodic array, while its physical structure model is appeared to be in 3D. The distribution of medium in the $x \mathrm{-}y$ plane is the same as the 2D model. By expending 2D AMMs model in the $z$-direction, the specimen model with a thickness of $h$ is determined, as can be seen in Figure 2.

FIGURE 2

FIGURE 2. The specimen model of the corresponding 2D AMMs.

The equation of motion of an elastic wave propagates in an isotropic medium, can be expressed as

$\begin{array}{c}\rho \frac{{\partial }^2{u}_i}{\partial t^2}=\frac{\partial {\sigma }_{ix}}{\partial x}+\frac{\partial {\sigma }_{iy}}{\partial y}+\frac{\partial {\sigma }_{iz}}{\partial z} \end{array}(1)$

where, $\rho$ is the density, $u$ is the displacement, and $\sigma$ is the stress. The higher-order terms with respect to small displacements are neglected in calculation.

In the case of 2D in-plane mode ($xy$ mode) and 3D specimen model, the stress $\mathit{\sigma }$ can be expanded in terms of sub-coordinates, respectively, as follows:

$\begin{array}{c}{\mathit{\sigma }}^{2D}={\left({\sigma }_x,{\sigma }_y,{\tau }_{xy}\right)}^T\end{array}(2)$

$\begin{array}{c}{\mathit{\sigma }}^{3D}={\left({\sigma }_x, {\sigma }_y, {\sigma }_z, {\tau }_{xy}, {\tau }_{yz}, {\tau }_{zx}\right)}^T\end{array}(3)$

The stress $\mathit{\sigma }$ can be expressed in terms of strain and elastic modulus by following relationships:

$\begin{array}{c}{\mathit{\sigma }}^{2D}={\mathbf{D}}^{2D}{\mathbf{\epsilon }}^{2D}\end{array}(4)$

$\begin{array}{c}{\mathit{\sigma }}^{3D}={\mathbf{D}}^{3D}{\mathbf{\epsilon }}^{3D}\end{array}(5)$

where, $\mathbf{D}$ is the elastic modulus, and $\epsilon$ is the strain. By substituting these equations into Eq. 1 yields

$\begin{array}{c}\rho {\omega }^2\mathit{u}+\left(\lambda +\mu \right)\nabla \left(\nabla \cdot \mathit{u}\right)+\mu {\nabla }^2\mathit{u}=0\end{array}(6)$

where, $\omega$ is the angular frequency, and $\mathit{u}$ is the displacement.

In 2D periodic array, the structure dimension is expended up to infinity in the $x$- and $y$-direction. Due to the periodicity of AMMs, Bloch’s theory can be applied to the mentioned relationships between the displacements $\mathit{u}$ as (Mead, 1996)

$\begin{array}{l}{\mathit{u}}_{A2}=e^{i{k}_{x}a}{\mathit{u}}_{A1},{\mathit{u}}_{A3}=e^{i{k}_{y}a}{\mathit{u}}_{A1}, {\mathit{u}}_{A4}=e^{i(k_x+k_y)a}{\mathit{u}}_{A1}\\ \begin{array}{c}{\mathit{u}}_{B2}=e^{i{k}_{y}a}{\mathit{u}}_{B1}, {\mathit{u}}_{B4}=e^{i{k}_{x}a}{\mathit{u}}_{B3}\end{array}\end{array}(7)$

where $A1$, $A2$, $A3,$ and $A4$ denote the four corners of a unit cell, and $B1$, $B2$, $B3$, and $B4$ denote the four connecting lines in a unit cell, as shown in Figure 3.

FIGURE 3

FIGURE 3. The schematic diagram of 2D unit cell and boundary conditions.

However, in the 3D specimen model, the unit cell has periodicity and finiteness in $x \mathrm{-}y$ plane and $z$-axis direction, respectively. By applying Bloch’s theory, the relationship of displacement $\mathit{u}$ can be described as

$\begin{array}{l}{\mathit{u}}_{A4}=e^{i{k}_{x}a}{\mathit{u}}_{A1},{\mathit{u}}_{A2}=e^{i{k}_{y}a}{\mathit{u}}_{A1},{\mathit{u}}_{A3}=e^{i(k_x+k_y)a}{\mathit{u}}_{A1}\\ {\mathit{u}}_{B4}=e^{i{k}_{x}a}{\mathit{u}}_{B2},{\mathit{u}}_{B12}=e^{i{k}_{x}a}{\mathit{u}}_{B10}\\ \begin{array}{c}{\mathit{u}}_{B3}=e^{i{k}_{y}a}{\mathit{u}}_{B1},{\mathit{u}}_{B11}=e^{i{k}_{y}a}{\mathit{u}}_{B9}\end{array}\\ {\mathit{u}}_{B8}=e^{i{k}_{x}a}{\mathit{u}}_{B5},{\mathit{u}}_{B6}=e^{i{k}_{y}a}{\mathit{u}}_{B5},{\mathit{u}}_{B7}=e^{i(k_x+k_y)a}{\mathit{u}}_{B5}\\ {\mathit{u}}_{C4}=e^{i{k}_{x}a}{\mathit{u}}_{C2},{\mathit{u}}_{C3}=e^{i{k}_{y}a}{\mathit{u}}_{C5}\end{array}(8)$

where, $A1-A8$ denote the eight corners of a unit cell, $B1 \mathrm{-}B12$ denote the twelve lines of a unit cell, and $C1 \mathrm{-}C6$ denote the six surfaces of a unit cell, as shown in Figure 4.

FIGURE 4

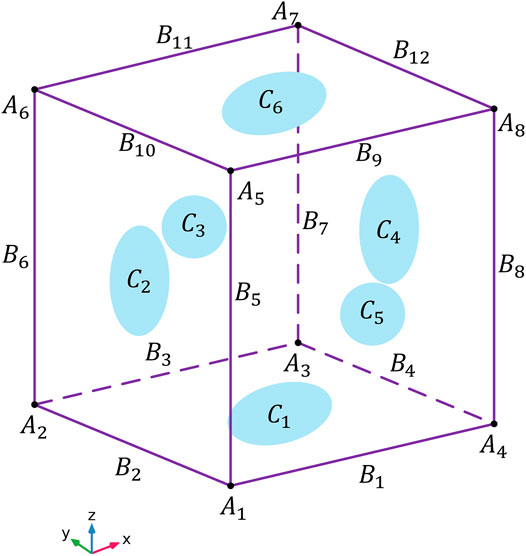
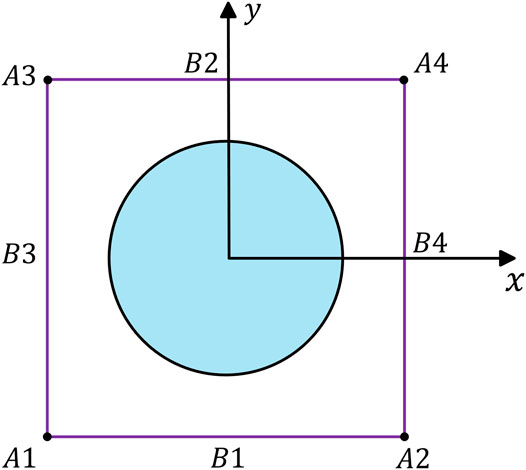
FIGURE 4. The schematic diagram of a unit cell in the 3D specimen model and its boundary conditions. The A, B, and C denote the points, lines, and surfaces nodes of the unit cell.

In order to apply the finite element method (FEM), the continuous systems need to be segmented into discrete one. The Eq. 6 can be expressed as the following equation

$\begin{array}{c}\left(\mathit{K}-{\omega }^2\mathit{M}\right)u=0\end{array}(9)$

Here, $\mathit{K}$ and $\mathit{M}$ are the structure stiffness and global mass matrices, respectively.

For a given value of the wave vector $\mathit{k}=(k_x,k_y)$, the eigenvalues of the Eq. 9 can give the resolution of the Eigen frequencies in terms of $\omega$. Since the 2D AMMs’ Bravais lattice is a square lattice, the first Brillouin zone has a shape of square. By taking the different wave vectors along the contours of irreducible Brillouin zone ($M-\text{Γ}-X-M$) as the Bloch wave vectors (Maurin et al., 2018), as shown in Figure 5A, the relationship between Eigen frequencies and Bloch wave vectors can be obtained, and the band structure of the 2D AMMs is determined. For the 3D specimen model, the physical structure scale is 3D, though the periodicity of the unit cell is considered in 2D. Therefore, the first Brillouin zone of the specimen model can be obtained. The first Brillouin zone and the contours of an irreducible Brillouin zone of the specimen model are similar to 2D AMMs’, as shown in Figure 5B.

FIGURE 5

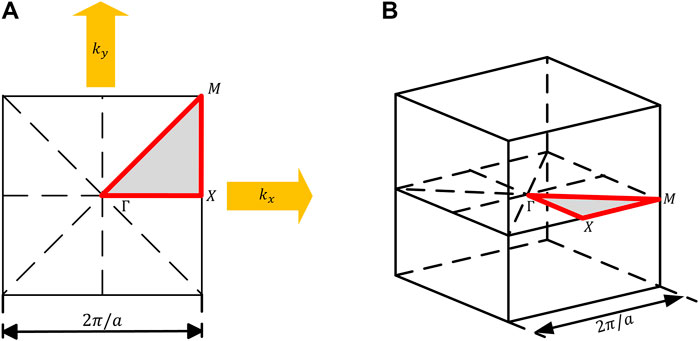
FIGURE 5. The Brillouin zone of (A) 2D AMMs and (B) 3D specimen model. The grey areas indicate the irreducible Brillouin zone and the red lines indicate their contours. $k_x$ and $k_y$ indicate the wave vectors in x- and y-direction, respectively.

Numerical Analyses

The band structure of the 2D AMMs model and corresponding 3D specimen model with different heights are computed to prove that there are the reasonable differences between them. The clear logic behind the differences is confirmed by computing the band structure of 2D AMMs’ specimens model i.e., 3D specimen model with modified physical conditions. The transmittance is also calculated to verify the accuracy of the band structure.

Differences Between the 2D Acoustic Metamaterials and 3D Specimens Model

In this example, a 2D AMMs, which consisted of straight and infinite cylinders arranged in the square matrix, as shown in Figure 1, with the lattice constant $a=15.5 \text{mm}$ and radius $r=5 \text{mm}$, is computed for its band structure. The materials of the cylinders and square matrix are lead and silicone rubber, respectively. The silicone rubber is a kind of viscoelastic material, and its viscous/damping effect is usually considered(Guo et al., 2019; Li et al., 2019). However, the effect of viscous/damping is neglected during the displacement tendency of the modes’ shape. The physical parameters of the lead and silicone rubber are listed in Table 1. The corresponding 3D specimen models with different heights$\left(h\right)$ are computed for their band structure. These specimen models can be considered as extending forms of the 2D AMM model in $z$-axis, as shown in Figure 2. The height parameter $h$ is set as $a\times {10}^{-1}$, $a\times {10}^{-0.5}$, $a\times {10}^0$, $a\times {10}^{0.5}$, and $a\times {10}^1$, respectively. The boundary conditions are set as described in the aforementioned mathematical models of AMMs.

TABLE 1

TABLE 1. Physical parameters of lead and silicone rubber (Kittel et al., 1996).

In addition to the band structure, the transmittance along the $\text{Γ} \mathrm{-}X$ direction is calculated by FEM to verify the accuracy of results of band structure. Mathematically, transmittance can be defined by

$\begin{array}{c}TL=10 {\log }_{10}\frac{W_{out}}{W_{in}}\end{array}(10)$

Here, $W_{in}$ and $W_{out}$ are the power of the incident wave and transmitted wave though the structure, respectively, and can be obtained by

$\begin{array}{c}{W}_{in}={\displaystyle \underset{{\text{Ω}}_{\text{in}}}{\iiint }\frac{1}{2}{\rho }_{in}{v}_{in}^{2}dV}\end{array}(11)$

$\begin{array}{c}{W}_{out}={\displaystyle \underset{{\text{Ω}}_{\text{out}}}{\iiint }\frac{1}{2}{\rho }_{out}{v}_{out}^{2}dV}\end{array}(12)$

where, ${\text{Ω}}_{\text{in}}$ and ${\text{Ω}}_{\text{out}}$ are the integration domains of the incident wave and transmitted wave, ${\rho }_{in}$ and ${\rho }_{out}$ are the density of these two domains, $v_{in}$ and $v_{out}$ are wave velocity of these two domains, respectively. The finite structure with 5 unit cells of 2D AMMs is constructed for the transmittance computation in $\text{Γ }\mathrm{-}X$ direction, as shown in Figure 6. The incident wave is a plane wave propagating in the $x$-direction (from left to right in Figure 6). In order to avoid the effect of wave reflection interference, the periodic boundary condition and the perfect matched layers are set in the 2D AMMs finite structure. The right domain is set to calculate the power of transmitted waves passing through 5 unit cells. For the 3D specimen model, the exactitude of their band structures is also substantiated by calculating the transmittance from the similar finite structure of 5 unit cells.

FIGURE 6

FIGURE 6. The finite structure for transmittance computation.

Based on the aforementioned structure, the band structure and the transmittance are computed. The dynamic responses of the system are investigated via FEM using the commercial software COMSOL Multiphysics. For wave propagation problems, using 12 degrees of freedom can generally obtain a solution with an error rate of less than 1%. With the quadratic elements used in FEM models, 6 second-order elements are sufficient for each wave period. Therefore, in order to determine the mesh size, the wavelength can be obtained by

$\begin{array}{c}{\lambda }_l=\frac{C_l}{f}\end{array}(13)$

$\begin{array}{c}{\lambda }_t=\frac{C_t}{f}\end{array}(14)$

where, ${\lambda }_l$ and ${\lambda }_t$ are wavelength of longitudinal waves and transverse waves, respectively, and $f$ is wave frequency. To ensure the accuracy of the results in the entire frequency range, $f$ should choose the maximum frequency 1200 Hz. The $C_l$ and $C_t$ are longitudinal speed of elastic wave and transverse speed of elastic wave, respectively, and can be expressed as

$\begin{array}{c}{C}_l=\sqrt{\frac{\lambda +2\mu }{\rho }}\end{array}(15)$

$\begin{array}{c}{C}_t=\sqrt{\frac{\mu }{\rho }}\end{array}(16)$

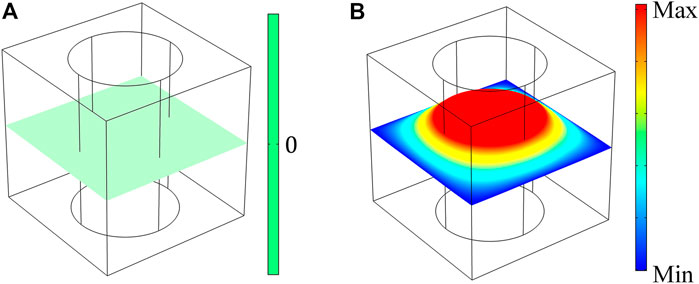
In order to get clarification for the difference in values, the quasi-2D AMMs model is considered. The ideal 2D AMMs models have no displacement along the z-axis direction. For specimen models, they are completely free and can have displacement in any direction. In order to make the connection between the two cases more clearly, a quasi-2D AMMs model as a midpoint is created. The quasi-2D AMMs model is based on the 3D specimen model and is restricted in the displacement along the z-axis direction. Thus, the additional boundary condition is

$\begin{array}{c}{u}_z=0\end{array}(17)$

where, $u_z$ is the medium displacement along the $z$-axis direction.

By sweeping the Bloch wave vector along the contour of an irreducible Brillouin zone (Figure 5), the corresponding band structure is obtained. By using different frequencies of the incident wave in the finite structure, the transmittance can be obtained. Figure 7 shows the band structure of the 2D AMMs model, quasi-2D model, and 3D specimen models with the given height of $a\times {10}^{-1}$, $a\times {10}^{-0.5}$, $a\times {10}^0$, $a\times {10}^{0.5}$, and $a\times {10}^1$, respectively. The band structure of the quasi-2D model and specimen model are shown on the left and right sides of each subfigure, respectively. The orange bars are used to show clearly the bandgap, as shown in Figure 7.

FIGURE 7

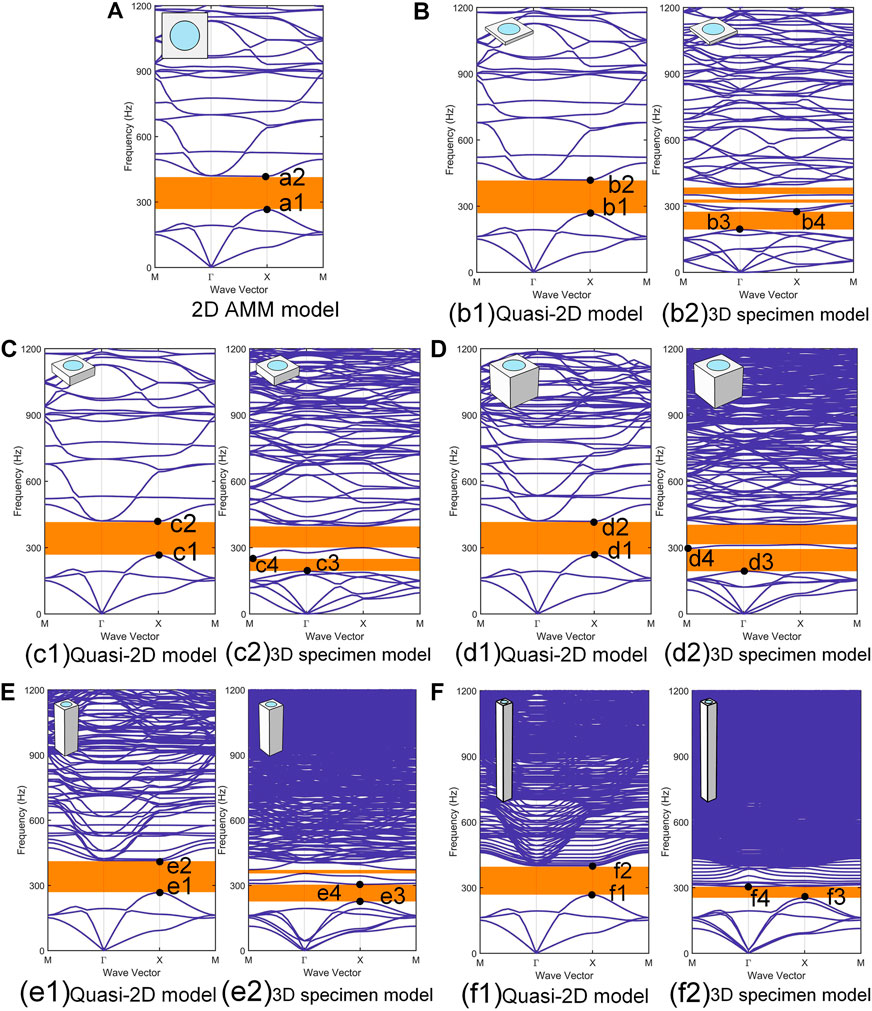
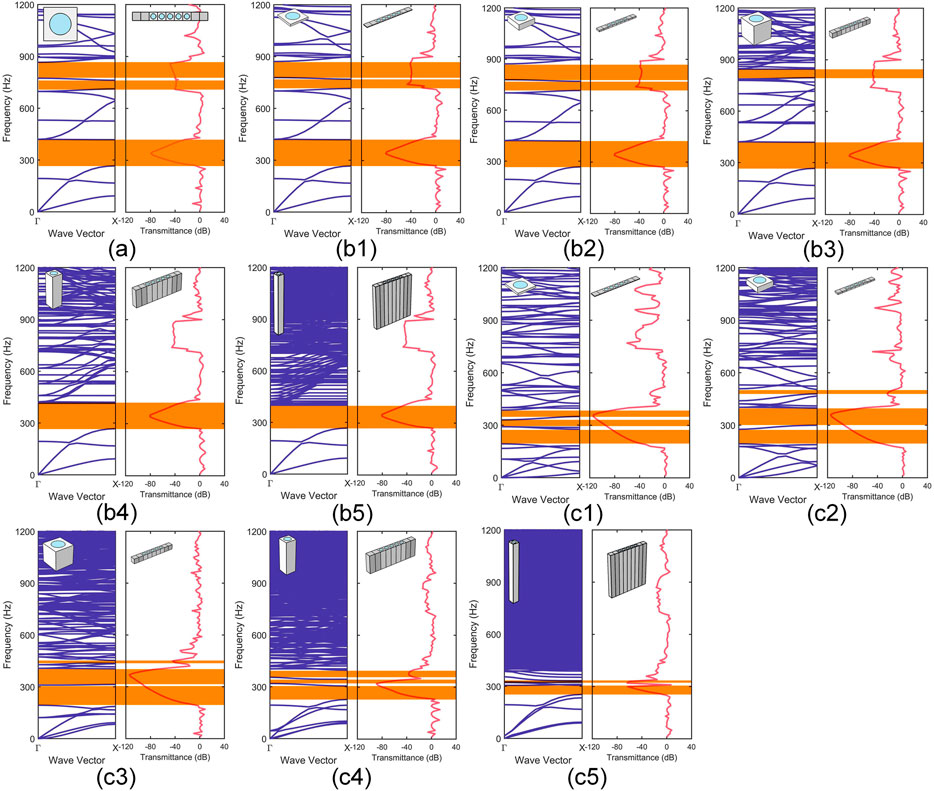
FIGURE 7. The band structure and corresponding transmittance of (A) 2D AMMs model and (b1, c1, d1, e1, f1) the quasi-2D models and (b2, c2, d2, e2, f2) specimen models with the height set as $a\times {10}^{-1}$, $a\times {10}^{-0.5}$, $a\times {10}^0$, $a\times {10}^{0.5}$, and $a\times {10}^1$ respectively.

The band structure of the 2D AMMs (Figure 7A) and quasi-2D model with smaller heights [Figure 7 (b1, c1, d1, e1, f1)] are similar. To evaluate band structure difference between 2D AMMs model and quasi-2D model quantitatively, the error rate of the energy band can be obtained by

$\begin{array}{c}{\mathit{ϵ}}_i=\frac{\left|f_{\text{quasi}-2\text{D}}-f_{2\text{D}}\right|}{f_{\text{quasi}-2\text{D}}}\end{array}(18)$

where, $\mathit{ϵ}$ is the error rates, the subscript $i$ represents $i$^th energy band, and $f$ represents the Eigen frequency. The Eigen frequency of the 2D AMMs and quasi-2D model are denoted by subscript 2D and quasi-2D, respectively. When the height of quasi-2D model is $a\times {10}^{-1}$, the average error rate of the first 20 band structure is ${\mathit{ϵ}}_{ave}={\displaystyle \sum }_{i=1}^{20}{\mathit{ϵ}}_i/20=0.0062$. According to the average error rate, there is nearly no difference between the 2D AMMs model and quasi-2D model with smaller heights. Figure 7 shows that with the height increases, band structure have greater differences. At the higher frequency, the variation in height is more sensitive. Though the change in band structure is significantly large, but the bandgap showed almost no change.

The band structure of the quasi-2D model [Figure 7 (b1, c1, d1, e1, f1)] and 3D specimen model [Figure 7 (b2, c2, d2, e2, f2)] with different heights showed a significant difference. Even at smaller heights [Figure 7 (b1, b2)], the band structure is significantly different. At a height of $a\times {10}^{-1}$, the quasi-2D model has one bandgap while the specimen model has three bandgaps under 1200 Hz. The band structure of the specimen model is more complicated. With increasing height, the quasi-2D model exhibited only one bandgap, however, the bandgap of the 3D specimen model is reduced from three to one. For the 3D specimen model, the high frequency of the band structure is more sensitive to create a variation in the height. This is similar to the quasi-2D model. In the frequency range below $300 \text{Hz}$, the band structures are indeed different, however, subtle variation is observed. In the frequency range from $300 \text{Hz}$ to $1200 \text{Hz}$, all the 3D specimen models with different heights showed more energy bands as compared to the 2D AMMs model. In this frequency range, the higher height of the 3D specimen model resulted in a large number of energy bands. With increasing height in the 3D specimen model, the range of the complete bandgap becomes smaller. The overall bandgap edge frequency of the 3D specimen model is lower than the 2D AMMs’.

In order to understand the physical mechanism due to the variation in the band structure, the mode shapes at the edges of the first bandgap are presented in Figure 8. By comparing the 2D AMMs and quasi-2D models, the obtained mode shape at the edges of the first bandgap are similar [Figure 8 (a1–f1), (a2–f2)]. The mode shapes of both upper edges and lower edges are observed as the translational motion mode. The movement of scatterer is dominant at the lower edges. At the upper edges, the movement of the matrix becomes dominant. This is a typical local resonance phenomenon. Further, by comparing the quasi-2D model and 3D specimen model, the observed mode shapes of both upper and lower edges showed a significant variation. The displacement fields of the quasi-2D model at the high-symmetry point $X$ are a translational motion mode [Figure 8 (b1–f1), (b2–f2)]. However, the corresponding bandgap at the lower edge mode shape is a torsional mode, as can be seen in [Figure 8 (b3, c3, d3)]. At the large height, the corresponding mode shape even becomes out-of-plane mode, as shown in [Figure 8 (e3, f3)]. These different mode shapes are caused by different heights of the 3D specimen model with respect to the different Eigen frequencies. The similarity between the quasi-2D model and 2D AMMs model creates an almost unchanged bandgap. Specifically, a noticeable large change in mode shapes of specimen models leads significant difference in the bandgap.

FIGURE 8

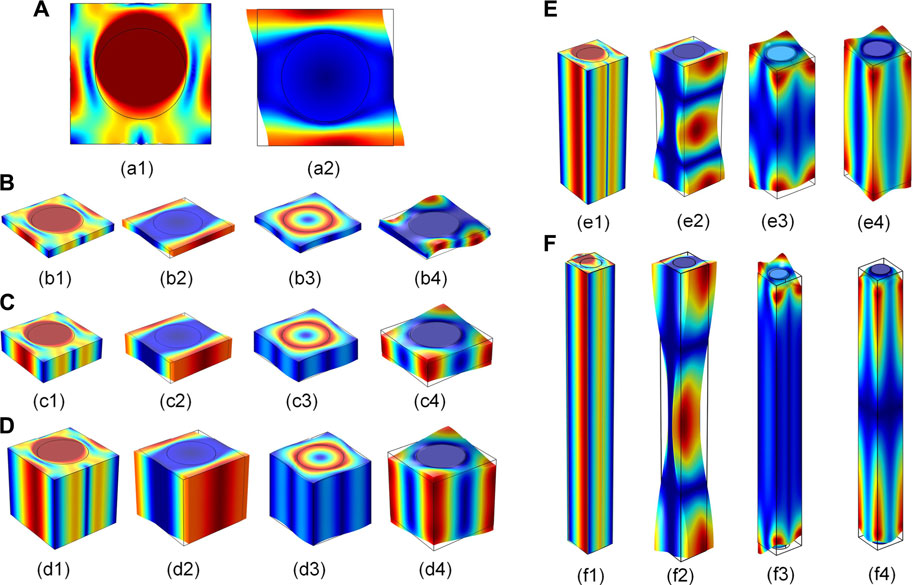
FIGURE 8. Mode shapes of the first bandgap edges in Figure 7.

According to the band structure and mode shapes of the different models above, a method to reduce the discrepancies between 2D AMMs and corresponding 3D specimen model is proposed. It is clear that at the lower height ($a\times {10}^{-1}$ and $a\times {10}^{-0.5}$), the band structure of quasi-2D model [Figure 7 (b1, c1)] and 2D AMMs model (Figure 7A) are almost the same. Compared with the 3D specimen model, the quasi-2D model displacement along z-axis is constrained. Thus, it is possible to use a lower height specimen and add roller constraint at upper and lower surfaces, which is perpendicular to the z-axis, to reduce the discrepancies. Even in a higher height, although the band structure of quasi-2D model [Figure 7(d1, e1, f1)] are different from 2D AMMs’, their bandgaps are almost the same. In the experiments, the transmittance usually be measured to verify the bandgaps. In this way, the experiments result from quasi-2D model will match the 2D AMMs’ well. Therefore, with the roller constraint at upper and lower surfaces, even at a higher height the discrepancies between 2D AMMs and 3D specimen model can be reduced.

The transmittance along $\text{Γ}-X$ direction is compared to the band structure in Figure 9. For 2D AMMs model (Figure 9A), quasi-2D model at lower height [Figure 9 (b1, b2)] and 3D specimen model [Figure 9 (c1–c5)], it is seen that two different kinds of results match well. This outcome makes two computation results mutually verify their correctness. While for quasi-2D model with higher height [Figure 9 (b3–b5)], the transmittance cannot match the $\text{Γ}-X$ bandgap. However, the transmittance of quasi-2D model consistent with the 2D AMMs’ at any height. This is reasonable because the mode shapes of 2D AMMs and quasi-2D model are similar. So their characteristics should be consistent. This phenomenon further validates feasibility of the method mentioned proposed above to reduce the discrepancies between 2D AMMs and 3D specimen model. This can also be verified from the analysis of the cause of the difference below.

FIGURE 9

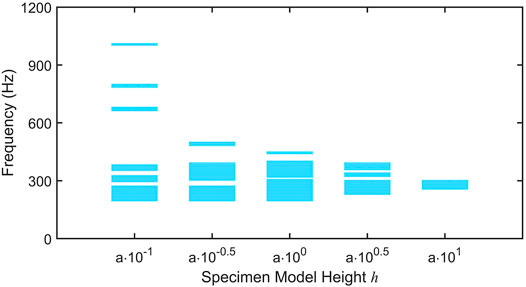
FIGURE 9. The Γ ̵X band structure and corresponding transmittance of (A) 2D AMMs model, (b1–b5) the quasi-2D model and (c1–c5) the specimen models with the height set as $a\times {10}^{-1}$, $a\times {10}^{-0.5}$, $a\times {10}^0$, $a\times {10}^{0.5}$, and $a\times {10}^1$ respectively.

The $\text{Γ} \mathrm{-}X$ bandgap frequency range of the 3D specimen models with respect to the different heights is illustrated in Figure 10. It is clearly seen that with variable height, the bandgap of the specimen models demonstrated an obvious different frequency range. It confirms a significant divergence in physical properties by means of the 3D specimen models with different heights.

FIGURE 10

FIGURE 10. The Γ ̵X bandgap frequency range of specimen models with the different heights.

The Bandgaps of Four-point Star and Cross Ligament Acoustic Metamaterials

In order to verify the prevalence of differences in the 3D specimen models with different heights, the investigations by considering two AMMs’ specimen models are carried out. Figure 11 shows the structures of two AMMs. The physical parameters of the matrix and scatterer are the same as the previous model i.e., silicone rubber and the lead, respectively, as listed in Table 1. The $\text{Γ} \mathrm{-}X$ bandgap frequency range of these two specimen models with different heights is illustrated in Figure 12. It is similar to the previously mentioned results (Figure 10) that the bandgap frequency range is notably disparate with different heights.

FIGURE 11

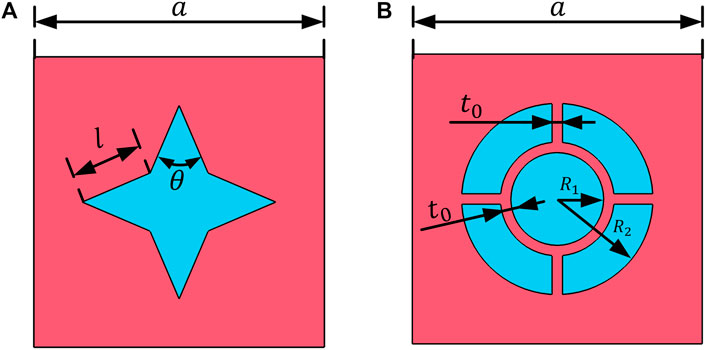
FIGURE 11. The structure of two AMMs. Red and blue represent the matrix and scatterer, respectively. (A) The four-point star AMMs with lattice constant $a=1.55 \text{cm}$, side length $l=0.35a$, and vertex $\theta =0.186 \text{rad}$. (B) The cross ligament AMMs with radius $R_1=0.16a$, radius $R_2=0.33a$, and ligament thickness $t_0=0.036a.$

FIGURE 12

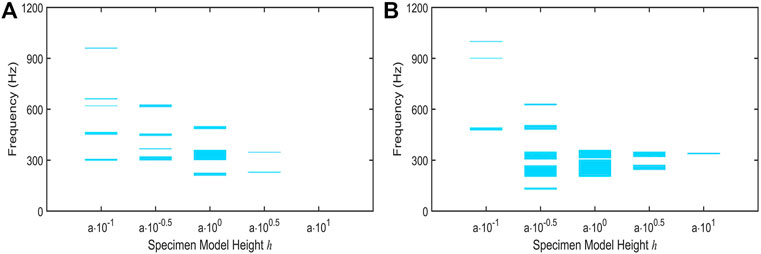
FIGURE 12. The $\text{Γ} \mathrm{-}X$ bandgap frequency range of (A) the four-point star and (B) the cross ligament specimen models with different heights.

Verification of the Existed Causes of Difference

To investigate the exact cause for the difference, the displacement along the $z$-axis of the 2D AMMs model and 3D specimen model are shown in Figure 13, and the stress distribution of the different sections along $z$-direction is illustrated in Figure 14. Firstly, as per the 2D AMMs model, it can be assumed as infinite in the $z$-axis direction. Therefore, there will be no displacement along the $z$-axis direction, as shown in Figure 13A. However, as per the 3D specimen model, the elastic waves not only propagate in the $x \mathrm{-}y$ plane but also in z-direction. The propagation of elastic waves caused medium displacement in the different sections along the $z$-axis. The variation in medium caused different motion modes that yield displacement along the $z$-axis direction, as shown in Figure 13B.

FIGURE 13

FIGURE 13. The displacement along the $z$-direction via(A) 2D AMMs model and (B) 3D specimen model.

FIGURE 14

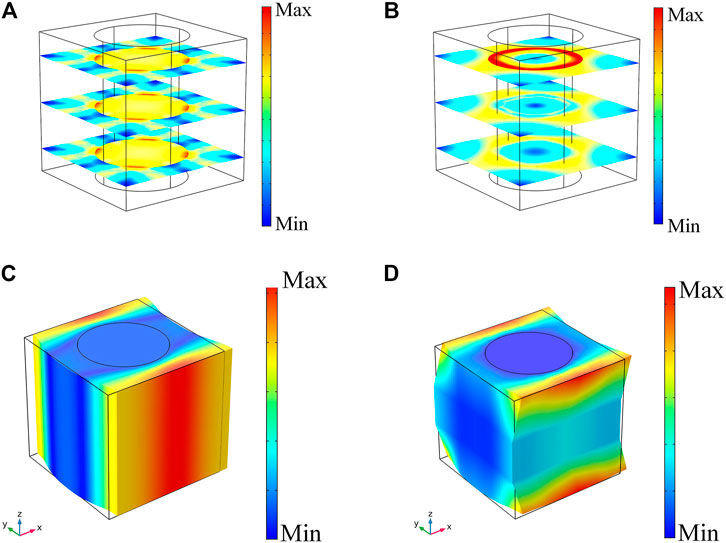
FIGURE 14. The stress distribution of different sections along $z$-direction. (A) 2D AMMs model and (B) 3D specimen model. The mode shapes of (C) ideal 2D AMMs model and (D) the 3D specimen model.

On the other hand, in the 2D AMMs model, stress distribution of each section along the $z$-axis is uniform due to the expended z-direction to the infinity, as shown in Figure 14A. However, in the 3D specimen model case, when the elastic waves propagate through the 3D specimen, which has finite height along $z$-direction, the stress distribution of the different sections along the $z$-axis is observed with variations, as shown in Figure 14B. This phenomenon can be verified by the model shapes of the mentioned two different cases. For an ideal 2D AMMs model, the model shape is devoid of bending along the $z$-direction owing to an infinite direction (Figure 14C). However, in counterparts of the case of 3D specimen models, the bending along z-direction exists in the model shape (Figure 14D). These different shapes cause the varied stress distribution and eventually resulted in the divergence in band structures.

As revealed above, the 2D AMMs and quasi-2D models showed quite similarities in results up to a certain extent. While the 2D AMMs and corresponding 3D specimen models showed a significant difference in the physical properties, and 3D specimen models with different heights have significant divergence in physical properties of materials. Therefore, the computation results of the 2D AMMs can be useful to get insight information from experimental results, meanwhile, data computed with 3D specimen models with different heights can provide reliability in terms of theoretical and experiments study. After noticeable differences between the 2D and 3D cases, 3D specimen models are indispensable especially for the larger heights and softer materials.

Conclusion

In this study, the difference in band structures between 2D AMMs and 3D specimen models are demonstrated and analyzed. The mathematical models of 2D AMMs and specimen models are reviewed to identify computation conditions in the band structure. The band structures are obtained by FEM and verified by transmittance behavior. The difference between the structure of the energy bands can prove that there are dissimilarities in the physical characteristics of 2D AMMs and 3D specimen models. It is noteworthy that variation in the height of unit cell can cause significant variation in band structures. The quasi-2D models’ band structures are also computed to investigate the true reason for variation in band structure. The changes of the mode shapes cause the variation, and these are revealed below. The mode shapes at the edges of the first bandgap are investigated. The other two 2D AMMs’ specimen models, namely four-point star and cross ligament AMMs with different heights are computed to verify divergent physical properties. The difference in the displacement along $z$-direction between 2D AMMs model and specimen model by means of the difference in the band structure is further verified by another crucial reason of the dissimilarity in stress distribution of different sections along the $z$-direction. These two reasons are clarified by modifying the boundary conditions to get the band structures of the specimen model. This can be a notification that to be cautious when using the computation results of 2D AMMs such as band structure to compare with the experimental results, which are represented by the specimen model in this paper. Consequently, for more accurate and rigorous results, especially which can be compared with experiments, the specimen model can provide better results with larger height and softer materials.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

WJ, HG, and PS conceived and designed the manuscript. YW and TY revised it. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the Project of National Natural Science Foundation of China (No. 52172371), and partly supported by the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, Program of Shanghai Academic/Technology Research Leader (No. 21XD1401100), and Technical Service Platform for Vibration and Noise Testing and Control of New Energy Vehicles (No. 18DZ2295900).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al Jahdali, R., and Wu, Y. (2016). High Transmission Acoustic Focusing by Impedance-Matched Acoustic Meta-Surfaces. Appl. Phys. Lett. 108 (3), 031902. doi:10.1063/1.4939932

CrossRef Full Text | Google Scholar

An, X., Fan, H., and Zhang, C. (2018). Elastic Wave and Vibration Bandgaps in Two-Dimensional Acoustic Metamaterials with Resonators and Disorders. Wave Motion 80, 69–81. doi:10.1016/j.wavemoti.2018.04.002

CrossRef Full Text | Google Scholar

An, X., Lai, C., Fan, H., and Zhang, C. (2020). 3D Acoustic Metamaterial-Based Mechanical Metalattice Structures for Low-Frequency and Broadband Vibration Attenuation. Int. J. Sol. Struct. 191-192, 293–306. doi:10.1016/j.ijsolstr.2020.01.020

CrossRef Full Text | Google Scholar

Axmann, W., and Kuchment, P. (1999). An Efficient Finite Element Method for Computing Spectra of Photonic and Acoustic Band-Gap Materials. J. Comput. Phys. 150 (2), 468–481. doi:10.1006/jcph.1999.6188

CrossRef Full Text | Google Scholar

Bertoldi, K., Boyce, M. C., Deschanel, S., Prange, S. M., and Mullin, T. (2008). Mechanics of Deformation-Triggered Pattern Transformations and Superelastic Behavior in Periodic Elastomeric Structures. J. Mech. Phys. Sol. 56 (8), 2642–2668. doi:10.1016/j.jmps.2008.03.006

CrossRef Full Text | Google Scholar

Billon, K., Ouisse, M., Sadoulet-Reboul, E., Collet, M., Butaud, P., Chevallier, G., et al. (2019). Design and Experimental Validation of a Temperature-Driven Adaptive Phononic crystal Slab. Smart Mater. Struct. 28 (3), 035007. doi:10.1088/1361-665x/aaf670

CrossRef Full Text | Google Scholar

Cao, W.-K., Wu, L.-T., Zhang, C., Ke, J.-C., Cheng, Q., Cui, T.-J., et al. (2019). Asymmetric Transmission of Acoustic Waves in a Waveguide via Gradient index Metamaterials. Sci. Bull. 64 (12), 808–813. doi:10.1016/j.scib.2019.01.002

CrossRef Full Text | Google Scholar

Cao, W. K., Wu, L. T., Zhang, C., Song, G. Y., Ke, J. C., Cheng, Q., et al. (2018). Acoustic Surface Waves on Three-Dimensional Groove Gratings with Sub-wavelength Thickness. Appl. Phys. Express 11 (8), 087301. doi:10.7567/apex.11.087301

CrossRef Full Text | Google Scholar

Cao, W. K., Zhang, C., Wu, L. T., Guo, K. Q., Ke, J. C., Cui, T. J., et al. (2021). Tunable Acoustic Metasurface for Three-Dimensional Wave Manipulations. Phys. Rev. Appl. 15 (2), 024026. doi:10.1103/PhysRevApplied.15.024026

CrossRef Full Text | Google Scholar

Cao, Y., Hou, Z., and Liu, Y. (2004a). Convergence Problem of Plane-Wave Expansion Method for Phononic Crystals. Phys. Lett. A 327 (2-3), 247–253. doi:10.1016/j.physleta.2004.05.030

CrossRef Full Text | Google Scholar

Cao, Y., Hou, Z., and Liu, Y. (2004b). Finite Difference Time Domain Method for Band-Structure Calculations of Two-Dimensional Phononic Crystals. Solid State Commun. 132 (8), 539–543. doi:10.1016/j.ssc.2004.09.003

CrossRef Full Text | Google Scholar

Casadei, F., Delpero, T., Bergamini, A., Ermanni, P., and Ruzzene, M. (2012). Piezoelectric Resonator Arrays for Tunable Acoustic Waveguides and Metamaterials. J. Appl. Phys. 112 (6), 064902. doi:10.1063/1.4752468

CrossRef Full Text | Google Scholar

Chen, C., Guo, Z., Liu, S., Feng, H., and Qiao, C. (2021). Hybrid Acousto-Elastic Metamaterials for Simultaneous Control of Low-Frequency Sound and Vibration. J. Appl. Phys. 129 (5), 054902. doi:10.1063/5.0028332

CrossRef Full Text | Google Scholar

Chen, D.-C., Zhu, X.-F., Wei, Q., Wu, D.-J., and Liu, X.-J. (2018). Broadband Acoustic Focusing by Airy-like Beams Based on Acoustic Metasurfaces. J. Appl. Phys. 123 (4), 044503. doi:10.1063/1.5010705

CrossRef Full Text | Google Scholar

Chen, H., and Chan, C. T. (2007). Acoustic Cloaking in Three Dimensions Using Acoustic Metamaterials. Appl. Phys. Lett. 91 (18), 183518. doi:10.1063/1.2803315

CrossRef Full Text | Google Scholar

Cheng, Q., Guo, H., Yuan, T., Sun, P., Guo, F., and Wang, Y. (2020). Topological Design of Square Lattice Structure for Broad and Multiple Band Gaps in Low-Frequency Range. Extreme Mech. Lett. 35, 100632. doi:10.1016/j.eml.2020.100632

CrossRef Full Text | Google Scholar

Deng, K., Ding, Y., He, Z., Zhao, H., Shi, J., and Liu, Z. (2009). Theoretical Study of Subwavelength Imaging by Acoustic Metamaterial Slabs. J. Appl. Phys. 105 (12), 124909. doi:10.1063/1.3153976

CrossRef Full Text | Google Scholar

Ding, C., Hao, L., and Zhao, X. (2010). Two-dimensional Acoustic Metamaterial with Negative Modulus. J. Appl. Phys. 108 (7), 074911. doi:10.1063/1.3493155

CrossRef Full Text | Google Scholar

Dorodnitsyn, V., and Van Damme, B. (2016). Two-dimensional Fluid-Filled Closed-Cell Cellular Solid as an Acoustic Metamaterial with Negative index. Phys. Rev. B 93 (13), 134302. doi:10.1103/PhysRevB.93.134302

CrossRef Full Text | Google Scholar

Faiz, M. S., Addouche, M., Zain, A. R. M., Siow, K. S., Chaalane, A., and Khelif, A. (2020). Experimental Demonstration of a Multichannel Elastic Wave Filter in a Phononic crystal Slab. Appl. Sci. 10 (13), 4594. doi:10.3390/app10134594

CrossRef Full Text | Google Scholar

Gao, N., Li, J., Bao, R.-h., and Chen, W.-q. (2019). Harnessing Uniaxial Tension to Tune Poisson's Ratio and Wave Propagation in Soft Porous Phononic Crystals: an Experimental Study. Soft Matter 15 (14), 2921–2927. doi:10.1039/C8SM02468E

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghasemi Baboly, M., Reinke, C. M., Griffin, B. A., El-Kady, I., and Leseman, Z. C. (2018). Acoustic Waveguiding in a Silicon Carbide Phononic Crystals at Microwave Frequencies. Appl. Phys. Lett. 112 (10), 103504. doi:10.1063/1.5016380

CrossRef Full Text | Google Scholar

Guo, F., Guo, H., Sun, P., Yuan, T., and Wang, Y. (2019). Study on Band gap Properties of Two-Dimensional Phononic Crystals Based on Generalized Viscoelastic Modeling. Mod. Phys. Lett. B 33 (32), 1950403. doi:10.1142/s0217984919504037

CrossRef Full Text | Google Scholar

Huang, H., Cao, E., Zhao, M., Alamri, S., and Li, B. (2021). Spider Web-Inspired Lightweight Membrane-type Acoustic Metamaterials for Broadband Low-Frequency Sound Isolation. Polymers 13 (7), 1146. doi:10.3390/polym13071146

PubMed Abstract | CrossRef Full Text | Google Scholar

Huo, S.-y., Chen, J.-j., Huang, H.-b., Wei, Y.-j., Tan, Z.-h., Feng, L.-y., et al. (2021). Experimental Demonstration of valley-protected Backscattering Suppression and Interlayer Topological Transport for Elastic Wave in Three-Dimensional Phononic Crystals. Mech. Syst. Signal Process. 154, 107543. doi:10.1016/j.ymssp.2020.107543

CrossRef Full Text | Google Scholar

Kafesaki, M., and Economou, E. N. (1999). Multiple-scattering Theory for Three-Dimensional Periodic Acoustic Composites. Phys. Rev. B 60 (17), 11993–12001. doi:10.1103/PhysRevB.60.11993

CrossRef Full Text | Google Scholar

Kittel, C., McEuen, P., and McEuen, P. (1996). Introduction to Solid State Physics. New York: Wiley.

Krushynska, A. O., Miniaci, M., Kouznetsova, V. G., and Geers, M. G. D. (2017). Multilayered Inclusions in Locally Resonant Metamaterials: Two-Dimensional versus Three-Dimensional Modeling. J. Vib. Acoust. 139 (2), 024501–024504. doi:10.1115/1.4035307

CrossRef Full Text | Google Scholar

Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71 (13), 2022–2025. doi:10.1103/PhysRevLett.71.2022

PubMed Abstract | CrossRef Full Text | Google Scholar

Laureti, S., Hutchins, D. A., Davis, L. A. J., Leigh, S. J., and Ricci, M. (2016). High-resolution Acoustic Imaging at Low Frequencies Using 3D-Printed Metamaterials. AIP Adv. 6 (12), 121701. doi:10.1063/1.4968606

CrossRef Full Text | Google Scholar

Li, D., Zigoneanu, L., Popa, B.-I., and Cummer, S. A. (2012). Design of an Acoustic Metamaterial Lens Using Genetic Algorithms. J. Acoust. Soc. Am. 132 (4), 2823–2833. doi:10.1121/1.4744942

CrossRef Full Text | Google Scholar

Li, J., Wang, Y., Chen, W., Wang, Y.-S., and Bao, R. (2019). Harnessing Inclusions to Tune post-buckling Deformation and Bandgaps of Soft Porous Periodic Structures. J. Sound Vib. 459, 114848. doi:10.1016/j.jsv.2019.114848

CrossRef Full Text | Google Scholar

Lv, H., Tian, X., Wang, M. Y., and Li, D. (2013). Vibration Energy Harvesting Using a Phononic crystal with point Defect States. Appl. Phys. Lett. 102 (3), 034103. doi:10.1063/1.4788810

CrossRef Full Text | Google Scholar

Maurin, F., Claeys, C., Deckers, E., and Desmet, W. (2018). Probability that a Band-gap Extremum Is Located on the Irreducible Brillouin-Zone Contour for the 17 Different Plane Crystallographic Lattices. Int. J. Sol. Struct. 135, 26–36. doi:10.1016/j.ijsolstr.2017.11.006

CrossRef Full Text | Google Scholar

Mazzotti, M., Bartoli, I., and Miniaci, M. (2019). Modeling Bloch Waves in Prestressed Phononic Crystal Plates. Front. Mater. 6, 74. doi:10.3389/fmats.2019.00074

CrossRef Full Text | Google Scholar

Mead, D. M. (1996). Wave Propagation in Continuous Periodic Structures: Research Contributions from Southampton, 1964-1995. J. Sound Vib. 190 (3), 495–524. doi:10.1006/jsvi.1996.0076

CrossRef Full Text | Google Scholar

Mohammadi, S., Eftekhar, A. A., Khelif, A., Hunt, W. D., and Adibi, A. (2008). Evidence of Large High Frequency Complete Phononic Band Gaps in Silicon Phononic crystal Plates. Appl. Phys. Lett. 92 (22), 221905. doi:10.1063/1.2939097

CrossRef Full Text | Google Scholar

Molerón, M., and Daraio, C. (2015). Acoustic Metamaterial for Subwavelength Edge Detection. Nat. Commun. 6 (1), 1–6. doi:10.1038/ncomms9037

CrossRef Full Text | Google Scholar

Muhammad, C. W., Lim, J. T. H., and Zhao, Z. (2020). Lightweight Architected Lattice Phononic Crystals with Broadband and Multiband Vibration Mitigation Characteristics. Extreme Mech. Lett. 41, 100994. doi:10.1016/j.eml.2020.100994

CrossRef Full Text | Google Scholar

Munteanu, L., and Chiroiu, V. (2011). On Three-Dimensional Spherical Acoustic Cloaking. New J. Phys. 13 (8), 083031. doi:10.1088/1367-2630/13/8/083031

CrossRef Full Text | Google Scholar

Ning, S., Yang, F., Luo, C., Liu, Z., and Zhuang, Z. (2020). Low-frequency Tunable Locally Resonant Band Gaps in Acoustic Metamaterials through Large Deformation. Extreme Mech. Lett. 35, 100623. doi:10.1016/j.eml.2019.100623

CrossRef Full Text | Google Scholar

Rabczuk, T., Belytschko, T., and Xiao, S. P. (2004). Stable Particle Methods Based on Lagrangian Kernels. Comput. Methods Appl. Mech. Eng. 193 (12-14), 1035–1063. doi:10.1016/j.cma.2003.12.005

CrossRef Full Text | Google Scholar

Sang, S., and Sandgren, E. (2018). Study of Two-Dimensional Acoustic Metamaterial Based on Lattice System. J. Vib. Eng. Technol. 6 (6), 513–521. doi:10.1007/s42417-018-0068-6

CrossRef Full Text | Google Scholar

Shan, S., Kang, S. H., Wang, P., Qu, C., Shian, S., Chen, E. R., et al. (2014). Harnessing Multiple Folding Mechanisms in Soft Periodic Structures for Tunable Control of Elastic Waves. Adv. Funct. Mater. 24 (31), 4935–4942. doi:10.1002/adfm.201400665

CrossRef Full Text | Google Scholar

Sigalas, M. M., and Soukoulis, C. M. (1995). Elastic-wave Propagation through Disordered And/or Absorptive Layered Systems. Phys. Rev. B 51 (5), 2780–2789. doi:10.1103/PhysRevB.51.2780

PubMed Abstract | CrossRef Full Text | Google Scholar

Sirota, L., Sabsovich, D., Lahini, Y., Ilan, R., and Shokef, Y. (2021). Real-time Steering of Curved Sound Beams in a Feedback-Based Topological Acoustic Metamaterial. Mech. Syst. Signal Process. 153, 107479. doi:10.1016/j.ymssp.2020.107479

CrossRef Full Text | Google Scholar

Sun, P., Zhang, Z., Guo, H., Liu, N., and Wang, Y. (2020). Hierarchical Square Honeycomb Metamaterials with Low-Frequency Broad Bandgaps and Flat Energy Bands Characteristics. J. Appl. Phys. 128 (23), 235102. doi:10.1063/5.0014846

CrossRef Full Text | Google Scholar

Wang, H., Zhang, Y., Lin, W., and Qin, Q.-H. (2020). A Novel Two-Dimensional Mechanical Metamaterial with Negative Poisson's Ratio. Comput. Mater. Sci. 171, 109232. doi:10.1016/j.commatsci.2019.109232

CrossRef Full Text | Google Scholar

Wang, L., Zheng, H., Zhao, M., Shi, L., and Hou, S. (2021). Petrov-Galerkin Method for the Band Structure Computation of Anisotropic and Piezoelectric Phononic Crystals. Appl. Math. Model. 89, 1090–1105. doi:10.1016/j.apm.2020.08.026

CrossRef Full Text | Google Scholar

Wang, P., Casadei, F., Shan, S., Weaver, J. C., and Bertoldi, K. (2014). Harnessing Buckling to Design Tunable Locally Resonant Acoustic Metamaterials. Phys. Rev. Lett. 113 (1), 014301. doi:10.1103/PhysRevLett.113.014301

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, X., Lu, Z., Cui, F., Cheng, L., and Cui, Y. (2017). Tunable Acoustic Metamaterial with an Array of Resonators Actuated by Dielectric Elastomer. Extreme Mech. Lett. 12, 37–40. doi:10.1016/j.eml.2016.07.003

CrossRef Full Text | Google Scholar

Zhang, C., Cao, W. K., Wu, L. T., Ke, J. C., Jing, Y., Cui, T. J., et al. (2021). A Reconfigurable Active Acoustic Metalens. Appl. Phys. Lett. 118 (13), 133502. doi:10.1063/5.0045024

CrossRef Full Text | Google Scholar

Zheng, L.-Y., Wu, Y., Ni, X., Chen, Z.-G., Lu, M.-H., and Chen, Y.-F. (2014). Acoustic Cloaking by a Near-Zero-index Phononic crystal. Appl. Phys. Lett. 104 (16), 161904. doi:10.1063/1.4873354

CrossRef Full Text | Google Scholar