- 1Department of Civil and Environmental Engineering, Politecnico di Milano, Milano, Italy
- 2Department of Mechanical Engineering, Politecnico di Milano, Milano, Italy
We show efficient elastic energy transfer and wave confinement through a graded array of resonators attached to an elastic beam. Experiments demonstrate that flexural resonators of increasing lengths allow to reduce wave scattering and to achieve the rainbow effect with local wavefield amplifications. We show that the definition of a monotonically decreasing distribution of the natural frequencies of the resonators along the wave propagation direction, is the preferable choice to increase the energy efficiency of the system. The proposed configuration is suitable for micro-fabrication, envisaging practical applications for micro-scale vibration energy harvesting.
1 Introduction
The study of novel metamaterial devices has attracted growing interest within the research community working in several fields of physics, such as electromagnetism (Pendry et al., 1999; Pendry, 2000) acoustics (Liu et al., 2000; Craster and Guenneau, 2013) and elasticity (Craster and Guenneau, 2017), amongst others. In the context of elastic waves, early designs based on Bragg scattering behavior due to material contrast were used to create bandgaps (Kushwaha et al., 1993; Vasseur et al., 2001; Khelif et al., 2003; Pennec et al., 2011; Laude, 2015) and to tailor specific wave behaviors often drawing ideas from the photonic crystal community. To push the operational regime of such systems toward lower frequencies, the exploitation of local resonance has received considerable attention (Liu et al., 2000; Miroshnichenko et al., 2010; Lemoult et al., 2011; Williams et al., 2015), especially for applications in geophysics, mechanical and civil engineering (Colombi et al., 2016a; Miniaci et al., 2016; Achaoui et al., 2017) involving common ambient spectra. While the concept was initially employed for vibration isolation purposes, it was later linked to a variety of phenomena including lensing (Colombi, 2016; Chaplain and Craster, 2019; Fuentes-Domínguez et al., 2021), localisation (Lott et al., 2020) or topological edge states (Pal and Ruzzene, 2017; Xia et al., 2020).
To capitalize on these recent metamaterial designs, energy harvesting is an attractive application: vibration-based energy harvesting has received considerable attention over the last 2 decades, aiming at powering devices using vibrational energy. A practical example consists in the opportunity to harvest energy from the environment to potentially remove the cost associated with battery replacement and avoid the waste of conventional batteries (Erturk and Elvin, 2013). Among the various possible energy harvesting methods, the ones based on piezoelectric materials are widely used due to their large power densities and ease of application (Anton and Sodano, 2007; Erturk and Inman, 2011). A recent line of work in this context exploits methods to locally concentrate the vibrational energy in the attempt to enhance the efficiency of piezoelectric devices. For instance, this can be achieved by focusing or localising acoustic/elastic wave energy in correspondence of the harvester using elastic mirrors, funnels (Carrara et al., 2013) defect modes (Qi et al., 2016), lenses (Tol et al., 2017; Allam et al., 2021), or black holes (Zhao et al., 2014). Another approach to amplify the wavefield relies on the rainbow effect, that effectively slows down waves and spatially separates frequency components. These systems are based on gradually varying periodic arrays of resonators to take advantage of local band-gaps to control wave propagation. The underlying physics, capable of inducing spatial segregation of frequency components, relies on the ability to locally decrease the propagation speed along the array. A similar wave speed reduction can be achieved through black-hole configurations that, however, rely on thickness modulations which reflect on a local stiffness decrease of the host medium, often undesired from the engineering perspective.
A graded array is instead formed by smoothly varying a particular parameter in space through a specific design of consecutive unit cells. Originally discovered in electromagnetism using axially non-uniform, linearly tapered, planar waveguides with cores of negative index material (Tsakmakidis et al., 2007), there has been a flurry of intensive research translating the rainbow effect into all flavors of classical wave propagation fields including acoustics (Romero-García et al., 2013; Zhu et al., 2013; Cebrecos et al., 2014; Chen et al., 2014), water waves (Bennetts et al., 2018) and fluid loaded elastic plates (Skelton et al., 2018), amongst others. Particular advances have been recently reported in elastic devices made of arrays of resonant rods for deep elastic substrates (Colombi et al., 2016b; Colombi et al., 2017; Colquitt et al., 2017; Chaplain et al., 2020a) to mode convert Rayleigh (R) into Shear (S) or Pressure (P) waves. Such graded line arrays of resonators have been theorised, designed and manufactured also for energy harvesting applications (Chaplain et al., 2020b; De Ponti et al., 2020; Alshaqaq and Erturk, 2021; De Ponti, 2021). In this context, rainbow reflection and trapping mechanisms are employed to enhance the interaction time between waves and the harvesting system, reporting higher power output as compared to ungraded designs. A straightforward implementation consists into a set of rod resonators of increasing height, which effectively couple with the motion of the A0 mode, with particularly strong interaction at the longitudinal resonance frequency of the rods (De Ponti et al., 2020). Even if the efficiency of the proposed designs has been verified numerically and experimentally, the use of axial resonators could be a problem for both fabrication and proper connection of the piezoelectric patches. Here, in contrast, we develop a more compact configuration based on a planar geometry with cantilever resonators. This system is also suitable for a piezoelectric deposition processes on the entire structure, yielding an overall smaller device with broadband features. In order to quantify the potential advantages of such rainbow device, we compare its performance to the case of a single resonating element and to an array with the same length and random grading law. We show that a monotonically decreasing distribution of the natural frequencies of the resonators yields stronger wavefield amplifications, which reflect on enhanced energy harvesting performance.
2 Rainbow Reflection Mechanics
We consider the system depicted in Figure 1A made of an elastic beam with attached an array of cantilevers of linearly increasing lengths. Due to the cross section symmetry, we focus the analysis on the wave propagation of the A0 flexural mode. It is worth to mention that a symmetry-broken cross-section or a non-null coupling between consecutive resonators may trigger different phenomena involving the excitation of waves with different polarization (De Ponti et al., 2021). Herein, we limit the analysis to the A0 mode and we consider all other supported modes as orthogonal to the excitation mechanism. The beam and the resonators are made of aluminium with Young modulus Ea = 70 GPa, Poisson ratio νa = 0.33 and density ρa = 2710 kg/m3. The beam is 500 mm long, 7 mm wide and 2 mm thick. The array is made of 9 unit cells of size a = 15 mm, with a linear grading law for the lengths of the resonators, from 16.75 to 27.75 mm, resulting in a grading angle of approximately 5.2°. By spatially varying the resonance frequency of the resonators attached to the beam (De Ponti et al., 2020; De Ponti, 2021) waves slow down with a reduction of both amplitude and wavelength (Figure 1B). Differently with respect to the acoustic wave compression (Chen et al., 2014), the array of resonators progressively absorbs energy from the beam, allowing for a wave amplitude reduction in the beam inside the array (De Ponti, 2021). We remark that there is a difference between rainbow reflection (hereafter implemented) and rainbow trapping, as delineated in Chaplain et al. (2020b). Rainbow reflection occurs when zero group velocity modes are met at band edge, while rainbow trapping when zero group velocity modes arises within the first Brillouin Zone due to the coupling between crossing modes. In both cases, the concurrent amplitude and wavelength reduction is a hallmark of energy transfer between the main structure and the resonators, and is used here for energy harvesting purposes. That is, our implementation in Figure 1C shows the arrangement of a set of piezoelectric patches and the electric circuit employed to transduce electric energy due to resonator motion in a tailored position along the beam. In here, we exploit the 31-mode of the piezoelectric patches connected to a resistive load to effectively harvest the elastic energy stored inside the target resonators.
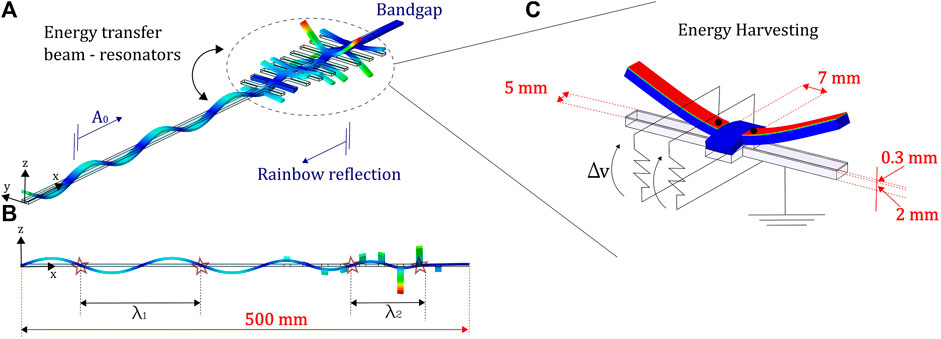
FIGURE 1. Schematic of the graded linear array of flexural resonators for energy harvesting. (A) By exciting the elastic beam with an A0 flexural wave, energy is efficiently transferred to the array of resonators. Such interaction reduces both the amplitude and the wavelength of the waves in the beam inside the array (B). Leveraging on this energy transfer mechanism, the elastic energy in the resonators can be used for piezoelectric energy harvesting (C).
The wave propagation properties of the system can be rigorously inferred by looking at the dispersion curves of a given cell inside the array. Provided the grading is gentle enough and provided the number of unit cells is sufficient, the global behaviour of the whole array can be deduced from the local dispersion curves of the constituent elements (Colombi et al., 2016b); in this way, the desired spatial selection by frequency properties, i.e. the rainbow behaviour of the system, is determined from the locally periodic structure at a given position. Figure 2A shows the numerical dispersion curves for the cell number 7 (where the cell numbering in the array goes from 1 for the shortest resonators to 9 for the longest). These dispersion curves are computed along the 1D irreducible Brillouin Zone using the finite elements software Abaqus (Smith, 2009), that incorporates the Bloch phase shift via Bloch-Floquet periodic boundary conditions in the attempt to study the unit cell containing two resonators. The resonators, later used for energy harvesting purposes, are 5 mm wide and 25 mm long. These values and the geometry of the attachments are chosen to ease the manufacturing of the specimen, but we remark that dynamically equivalent configurations can be achieved matching the desired natural frequency and the participating mass (Sugino et al., 2016). By inspecting the dispersion curves related to the bending of the resonators, we identify an in-phase and an out-of-phase mode, as shown in the inset in Figure 2A. This behaviour, which comes from having two resonators per cell, does not affect the response of the array since the antisymmetric mode cannot be excited with the symmetric A0 input. The spatial properties of the wavefield can be deduced from the local dispersion curves at a given frequency, as shown in Figure 2B. By increasing the length of the resonators along the spatial dimension, i.e. moving from (Pendry, 2000) to (Pennec et al., 2011), the dispersion curves shift towards lower frequencies. As a result, by fixing the frequency, the group velocity, vg = ∂ω/∂κ, smoothly reduces until zero. Such effect allows to slow down elastic waves inside the array and to confine waves in different positions depending on frequency. In addition, since the zero group velocity mode occurs at the band edge, it can couple with a backward propagating mode, which is typical of rainbow reflection (Chaplain et al., 2020b).
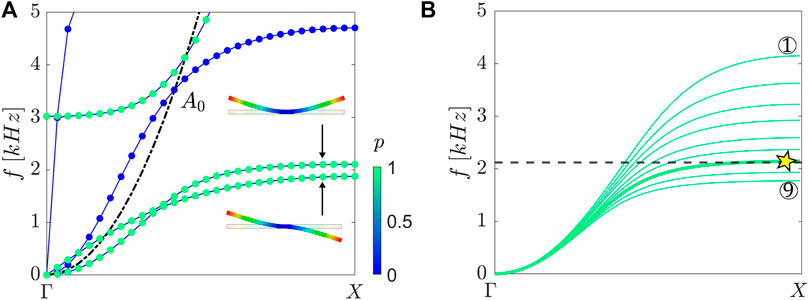
FIGURE 2. (A) Numerical dispersion curves for a periodic array of identical resonators of fixed length (here we take the resonator having length 25 mm that is then endowed with piezoelectric patches in the graded wedge); scatter points colours represent the wave polarization (green corresponding to the vertical motion, i.e. bending of the resonator). (B) In-phase bending mode for different resonators inside the array. Moving from short (Pendry, 2000) to long (Pennec et al., 2011) resonators at a given frequency the group velocity and the wavelength decrease, until the bandgap opening (here denoted with a yellow star in the position of the resonator number (Vasseur et al., 2001)).
To provide further insights on the energy transfer mechanism related to rainbow reflection, we compare the linear graded array to the case of a single cell, and to an array with a random grading law. The cells involved in the random configuration are the same adopted for the linear array but with a different arrangement of attachments, except for the target one. Figure 3 shows the three configurations, in which the target resonator, i.e. the one with the first flexural mode corresponding to the input frequency, is marked with a yellow star. We quantify the efficiency of each configuration by looking at the total energy density distributions along time, as shown in Figure 3. Such energy, denoted with Σ, can be decomposed in the contribution of the beam, Σbeam, and the resonators Σresonators. Each configuration is excited using a narrowband source at central frequency of 2 kHz, width Δf = 0.14 kHz, and time duration T = 15 ms. The numerical model employed is based on a finite element discretization of the system through Abaqus (Smith, 2009), using full 3D stress quadratic elements (C3D20). The analysis is performed opting for an implicit analysis based on the Hilber-Hughes-Taylor operator, with a constant time increment dt = 0.01 ms. The energy density for the beam and the resonators is obtained summing the strain and kinetic energy densities of the corresponding individual finite elements (FE) for each time instant. We notice that when a single cell is introduced on the elastic beam, low energy transfer is achieved (Figure 3A with a mean local energy density percentage in the resonators of about 12%. The linear array shows (Figure 3B) the strongest energy transfer, with a mean local energy density percentage in the resonators of about 76%. Finally, the random array shows a mean local energy density percentage in the resonators of about 68%.
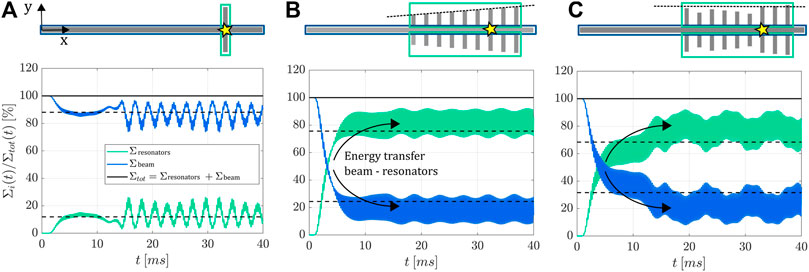
FIGURE 3. Total energy density distributions in time for the single cell (A), linear (B) and random array (C). Each system is forced using a tone burst of 15 ms at 2 kHz, able to excite the flexural resonace of the resonators in the cell marked with a yellow star. For the lone cell (A), weak energy transfer between the beam and the resonators is achieved. Adding a linear array of resonators (B) allows to increase the efficiency of energy transfer, providing strong energy confinement inside the resonators. A similar behaviour, but less efficient, is shown for the random array (C). To outline the differences in term of performance, the mean energy density along time is also reported with dashed black lines.
3 Experiments on Slow Waves for Energy Harvesting
A peculiar property of the rainbow reflection device is the capability to slow down array guided waves as they transverse the array. Such phenomenon allows for a longer interaction between the wave and the resonators, locally increasing the amplitude of the wavefield inside the resonators (De Ponti et al., 2020; De Ponti, 2021). To validate this effect, and the implications in terms of energy harvesting, we perform experimental tests in narrow and broad-band frequency regime. Figure 4 shows the experimental setup used for testing.

FIGURE 4. Experimental setup. The wavefield is measured using a 3D laser vibrometer (I). The beam is forced using an electrodynamic shaker (II), while the opposite side is suspended through elastic cables (III). A zoomed-in view of the lone cell (IV), linear array (V) and random array (VI) is reported in the right insets.
At the right boundary, a LDS v406 electrodynamic shaker is rigidly connected to the beam through a thick aluminium plate with high strength adhesive, to provide excitation. At the opposite boundary, the structure is suspended through elastic cables that do not affect the dynamics of the system. The wavefield on the elastic beam is measured through a Polytec 3D Scanner Laser Doppler Vibrometer (SLDV), which is able to separate the out-of-plane velocity field in both space and time. The same narrow-band excitation input used in the numerical model is synchronously started with the acquisition which, in turn, is averaged in time to decrease the noise. Figure 5 shows the experimental Fast Fourier Transform (FFT) of the wavefield for the single cell (Figure 5A), the linear (Figure 5B) and random array (Figure 5C) at different time instants. The corresponding input (blue arrow) and reflected waves (green arrow) measured for different time instants along the plain beam before the resonators are reported for the different configurations. It can be noticed that a stronger slowing effect is achieved for the linear array, since the wave reflection is not visible before the array at 5 ms. After a certain amount of time, such effect vanishes and the three configurations are similar in terms of wave reflection.
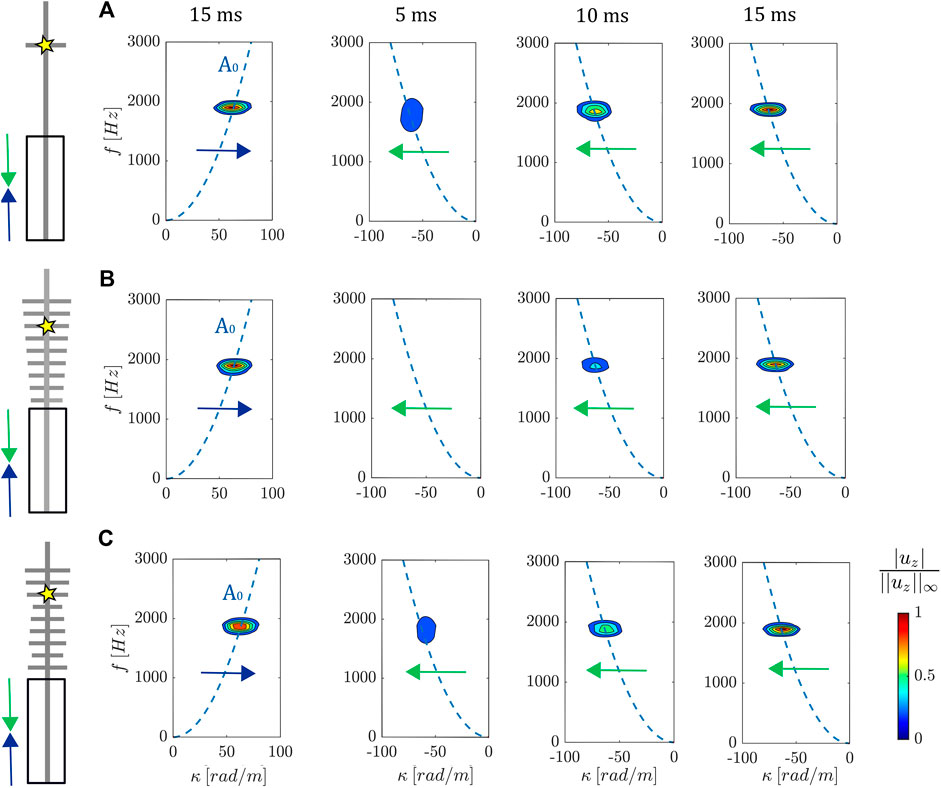
FIGURE 5. Experimental Fast Fourier Transform (FFT) of the wavefield measured on the plain beam for the lone cell (A), linear (B) and random array (C). Waves are backscattered when the input A0 wave reaches the target cell marked with the yellow star. Since the linear graded array (B) provides a smooth reduction of the wave group velocity, it shows lower reflections with respect to the other two cases (A, C). While this effect is notably marked at small time increments (e.g. 5 and 10 ms), it slowly vanishes in time (e.g. 15 ms), confirming the inherently reflective properties of the system.
We experimentally show the rainbow effect in the linear array by applying a broadband frequency sweep in the range 1.6–4.2 kHz. Figure 6A shows a space-frequency analysis of the experimental data. Depending on the frequency, waves stop at different spatial positions, corresponding to the bandgap opening. Moreover, we notice that the amplitude and the wavelength of the mode shapes decrease inside the array, until the amplitude vanishes in correspondence of the position of the resonating element, which is well predicted by numerical results (dashed white line). We then quantify the advantages of such mechanism for energy harvesting by placing piezoelectic PZT-5H patches (Ep = 61 GPa, νp = 0.31, ρp = 7800 kg/m3, dielectric constant
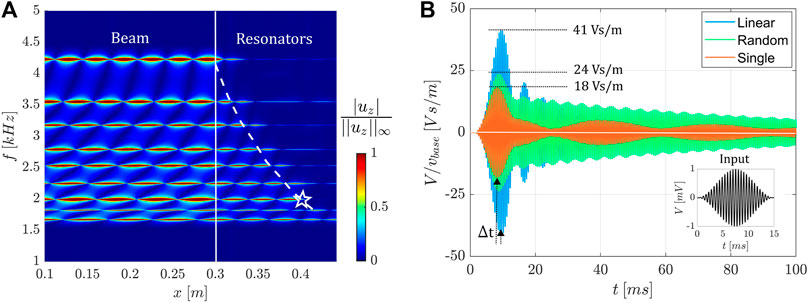
FIGURE 6. (A) Space-frequency analysis of the experimental data superimposed to numerical predictions (dashed white line) from dispersion curves. (B) Open circuit output voltage for the linear, random and single cell configuration, corresponding to the input excitation frequency marked with the white star in (A). The linear grading provides the maximum output voltage and time delay.
4 Conclusion
In conclusion, we have demonstrated potential advantages in using graded arrays of flexural resonators for efficient elastic energy confinement. The array capability of slowing down waves enables a strong energy transfer to the resonators, which then reflects in enhanced energy harvesting performances. This effect is stronger for a monotonically decreasing distribution of the natural frequencies of the resonators, due to the longest interaction time between the wave and the array. We remark that the system can be frequency-tuned simply by adding masses at the tip of the cantilever resonators: this design can be employed to match applications and scenarios characterized low frequency ambient spectra. Also, we remark that the present configuration can be suitably employed for energy harvesting applications and can be scaled at the micro-scale for the implementation of next generation vibration energy harvesting devices.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
JMDP, AC, and RA initiated the project. JMDP and LI carried out the numerical studies and created the figures. ER and FB helped with the laboratory experiment. JMDP wrote the article. All the authors contributed to the editing of the article.
Funding
The support of the H2020 FET-proactive project MetaVEH under grant agreement No. 952039.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We also gratefully acknowledge the Italian Ministry of Education, University and Research for the support provided through the Project “Department of Excellence LIS4.0—Lightweight and Smart Structures for Industry 4.0.”
References
Achaoui, Y., Antonakakis, T., Brûlé, S., Craster, R. V., Enoch, S., and Guenneau, S. (2017). Clamped Seismic Metamaterials: Ultra-low Frequency Stop Bands. New J. Phys. 19, 063022. doi:10.1088/1367-2630/aa6e21
Allam, A., Sabra, K., and Erturk, A. (2021). Sound Energy Harvesting by Leveraging a 3D-Printed Phononic crystal Lens. Appl. Phys. Lett. 118, 103504. doi:10.1063/5.0030698
Alshaqaq, M., and Erturk, A. (2021). Graded Multifunctional Piezoelectric Metastructures for Wideband Vibration Attenuation and Energy Harvesting. Smart Mater. Struct. 30, 015029. doi:10.1088/1361-665x/abc7fa
Anton, S. R., and Sodano, H. A. (2007). A Review of Power Harvesting Using Piezoelectric Materials (2003-2006). Smart Mater. Struct. 16, R1–R21. doi:10.1088/0964-1726/16/3/r01
Bennetts, L. G., Peter, M. A., and Craster, R. V. (2018). Graded Resonator Arrays for Spatial Frequency Separation and Amplification of Water Waves. J. Fluid Mech. 854, R4. doi:10.1017/jfm.2018.648
Carrara, M., Cacan, M. R., Toussaint, J., Leamy, M. J., Ruzzene, M., and Erturk, A. (2013). Metamaterial-inspired Structures and Concepts for Elastoacoustic Wave Energy Harvesting. Smart Mater. Struct. 22, 065004. doi:10.1088/0964-1726/22/6/065004
Cebrecos, A., Picó, R., Sánchez-Morcillo, V. J., Staliunas, K., Romero-García, V., and Garcia-Raffi, L. M. (2014). Enhancement of Sound by Soft Reflections in Exponentially Chirped Crystals. AIP Adv. 4, 124402. doi:10.1063/1.4902508
Chaplain, G. J., De Ponti, J. M., Colombi, A., Fuentes-Dominguez, R., Dryburg, P., Pieris, D., et al. (2020). Tailored Elastic Surface to Body Wave Umklapp Conversion. Nat. Commun. 11, 3267, 1–8. doi:10.1038/s41467-020-17021-x
Chaplain, G. J., and Craster, R. V. (2019). Flat Lensing by Graded Line Meta-Arrays. Phys. Rev. B 99 (R), 220102. doi:10.1103/physrevb.99.220102
Chaplain, G. J., Pajer, D., De Ponti, J. M., and Craster, R. V. (2020). Delineating Rainbow Reflection and Trapping with Applications for Energy Harvesting. New J. Phys. 22, 063024. doi:10.1088/1367-2630/ab8cae
Chen, Y., Liu, H., Reilly, M., Bae, H., and Yu, M. (2014). Enhanced Acoustic Sensing through Wave Compression and Pressure Amplification in Anisotropic Metamaterials. Nat. Commun. 5, 5247. doi:10.1038/ncomms6247
Colombi, A., Colquitt, D., Roux, P., Guenneau, S., and Craster, R. V. (2016). A Seismic Metamaterial: The Resonant Metawedge. Sci. Rep. 6 (1), 27717, 1–6. doi:10.1038/srep27717
Colombi, A., Ageeva, V., Smith, R. J., Clare, A., Patel, R., Clark, M., et al. (2017). Enhanced Sensing and Conversion of Ultrasonic Rayleigh Waves by Elastic Metasurfaces. Sci. Rep. 7 (1), 6750. doi:10.1038/s41598-017-07151-6
Colombi, A. (2016). Resonant Metalenses for Flexural Waves in Plates. The J. Acoust. Soc. America 140, EL423–EL428. doi:10.1121/1.4967179
Colombi, A., Roux, P., Guenneau, S., Gueguen, P., and Craster, R. V. (2016). Forests as a Natural Seismic Metamaterial: Rayleigh Wave Bandgaps Induced by Local Resonances. Sci. Rep. 6, 19238. doi:10.1038/srep19238
Colquitt, D. J., Colombi, A., Craster, R. V., Roux, P., and Guenneau, S. R. L. (2017). Seismic Metasurfaces: Sub-wavelength Resonators and Rayleigh Wave Interaction. J. Mech. Phys. Sol. 99, 379–393. doi:10.1016/j.jmps.2016.12.004
Craster, R. V., and Guenneau, S. (2013). Acoustic Metamaterials, Negative Refraction, Imaging, Lensing and Cloaking. Springer Series in Materials Science, 1–324.
Craster, R. V., and Guenneau, S. (2017). World Scientific Handbook of Metamaterials and Plasmonics: Volume 2: Elastic, Acoustic and Seismic Metamaterials. Singapore: World Scientific.
De Ponti, J. M., Colombi, A., Riva, E., Ardito, R., Braghin, F., Corigliano, A., et al. (2020). Experimental Investigation of Amplification, via a Mechanical Delay-Line, in a Rainbow-Based Metamaterial for Energy Harvesting. Appl. Phys. Lett. 117, 143902. doi:10.1063/5.0023544
De Ponti, J. M., Iorio, L., Riva, E., Ardito, R., Braghin, F., and Corigliano, A. (2021). Selective Mode Conversion and Rainbow Trapping via Graded Elastic Waveguides. Phys. Rev. Appl. 16, 034028. doi:10.1103/physrevapplied.16.034028
Fuentes-Domínguez, R., Yao, M., Colombi, A., Dryburgh, P., Pieris, D., Jackson-Crisp, A., et al. (2021). Design of a Resonant Luneburg Lens for Surface Acoustic Waves. Ultrasonics 111, 106306. doi:10.1016/j.ultras.2020.106306
Khelif, A., Djafari-Rouhani, B., Vasseur, J. O., and Deymier, P. A. (2003). Transmission and Dispersion Relations of Perfect and Defect-Containing Waveguide Structures in Phononic Band gap Materials. Phys. Rev. B 68, 024302. doi:10.1103/physrevb.68.024302
Kushwaha, M. S., Halevi, P., Dobrzynski, L., and Djafari-Rouhani, B. (1993). Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 71, 2022–2025. doi:10.1103/physrevlett.71.2022
Laude, V. (2015). Phononic Crystals Artificial Crystals for Sonic, Acoustic, and Elastic Waves. Berlin: De Gruyter.
Lemoult, F., Fink, M., and Lerosey, G. (2011). Acoustic Resonators for Far-Field Control of Sound on a Subwavelength Scale. Phys. Rev. Lett. 107, 064301. doi:10.1103/PhysRevLett.107.064301
Liu, Z., Zhang, X., Mao, Y., Zhu, Y. Y., Yang, Z., Chan, C. T., et al. (2000). Locally Resonant Sonic Materials. Science 289, 1734–1736. doi:10.1126/science.289.5485.1734
Lott, M., Roux, P., Seydoux, L., Tallon, B., Pelat, A., Skipetrov, S., et al. (2020). Localized Modes on a Metasurface through Multiwave Interactions. Phys. Rev. Mater. 4, 065203. doi:10.1103/physrevmaterials.4.065203
Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016). Large Scale Mechanical Metamaterials as Seismic Shields. New J. Phys. 18, 083041. doi:10.1088/1367-2630/18/8/083041
Miroshnichenko, A. E., Flach, S., and Kivshar, Y. S. (2010). Fano Resonances in Nanoscale Structures. Rev. Mod. Phys. 82, 2257–2298. doi:10.1103/revmodphys.82.2257
Pal, R. K., and Ruzzene, M. (2017). Edge Waves in Plates with Resonators: an Elastic Analogue of the Quantum valley Hall Effect. New J. Phys. 19, 025001. doi:10.1088/1367-2630/aa56a2
Pendry, J. B., Holden, A. J., Robbins, D. J., and Stewart, W. J. (1999). Magnetism from Conductors and Enhanced Nonlinear Phenomena. IEEE Trans. Microwave Theor. Techn. 47, 2075–2084. doi:10.1109/22.798002
Pendry, J. B. (2000). Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969. doi:10.1103/physrevlett.85.3966
Pennec, Y., Rouhani, B. D., Li, C., Escalante, J. M., Martinez, A., Benchabane, S., et al. (2011). Band Gaps and Cavity Modes in Dual Phononic and Photonic Strip Waveguides. AIP Adv. 1, 041901. doi:10.1063/1.3675799
Qi, S., Oudich, M., Li, Y., and Assouar, B. (2016). Acoustic Energy Harvesting Based on a Planar Acoustic Metamaterial. Appl. Phys. Lett. 108, 263501. doi:10.1063/1.4954987
Romero-García, V., Picó, R., Cebrecos, A., Sánchez-Morcillo, V. J., and Staliunas, K. (2013). Enhancement of Sound in Chirped Sonic Crystals. Appl. Phys. Lett. 102, 091906. doi:10.1063/1.4793575
Skelton, E. A., Craster, R. V., Colombi, A., and Colquitt, D. J. (2018). The Multi-Physics Metawedge: Graded Arrays on Fluid-Loaded Elastic Plates and the Mechanical Analogues of Rainbow Trapping and Mode Conversion. New J. Phys. 20, 053017. doi:10.1088/1367-2630/aabecf
Smith, M. (2009). ABAQUS/Standard User’s Manual, Version 6.9. Providence, RI: Dassault Systèmes Simulia Corp.
Sugino, C., Leadenham, S., Ruzzene, M., and Erturk, A. (2016). On the Mechanism of Bandgap Formation in Locally Resonant Finite Elastic Metamaterials. J. Appl. Phys. 120, 134501. doi:10.1063/1.4963648
Tol, S., Degertekin, F. L., and Erturk, A. (2017). Phononic crystal Luneburg Lens for Omnidirectional Elastic Wave Focusing and Energy Harvesting. Appl. Phys. Lett. 111, 013503. doi:10.1063/1.4991684
Tsakmakidis, K. L., Boardman, A. D., and Hess, O. (2007). 'Trapped Rainbow' Storage of Light in Metamaterials. Nature 450, 397–401. doi:10.1038/nature06285
Vasseur, J. O., Deymier, P. A., Chenni, B., Djafari-Rouhani, B., Dobrzynski, L., and Prevost, D. (2001). Experimental and Theoretical Evidence for the Existence of Absolute Acoustic Band Gaps in Two-Dimensional Solid Phononic Crystals. Phys. Rev. Lett. 86, 3012–3015. doi:10.1103/physrevlett.86.3012
Williams, E. G., Roux, P., Rupin, M., and Kuperman, W. A. (2015). Theory of Multiresonant Metamaterials forA0Lamb Waves. Phys. Rev. B 91, 104307. doi:10.1103/physrevb.91.104307
Xia, Y., Erturk, A., and Ruzzene, M. (2020). Topological Edge States in Quasiperiodic Locally Resonant Metastructures. Phys. Rev. Appl. 13, 014023. doi:10.1103/physrevapplied.13.014023
Zhao, L., Conlon, S. C., and Semperlotti, F. (2014). Broadband Energy Harvesting Using Acoustic Black Hole Structural Tailoring. Smart Mater. Struct. 23, 065021. doi:10.1088/0964-1726/23/6/065021
Keywords: metamaterials, piezoelectricity, energy harvesting, resonators, rainbow effect
Citation: De Ponti JM, Iorio L, Riva E, Braghin F, Corigliano A and Ardito R (2021) Enhanced Energy Harvesting of Flexural Waves in Elastic Beams by Bending Mode of Graded Resonators. Front. Mater. 8:745141. doi: 10.3389/fmats.2021.745141
Received: 21 July 2021; Accepted: 04 October 2021;
Published: 05 November 2021.
Edited by:
Fuyin Ma, Xi’an Jiaotong University, ChinaReviewed by:
Ming Yuan, Nanjing University of Posts and Telecommunications, ChinaXiao-shuang Li, Hebei University, China
Copyright © 2021 De Ponti, Iorio, Riva, Braghin, Corigliano and Ardito. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jacopo Maria De Ponti, amFjb3BvbWFyaWEuZGVwb250aUBwb2xpbWkuaXQ=
†ORCID ID: Jacopo Maria De Ponti, orcid.org/0000-0002-6155-2031; Luca Iorio, orcid.org/0000-0002-9515-9334; Emanuele Riva, orcid.org/0000-0001-6773-9000; Francesco Braghin, orcid.org/0000-0002-0476-4118; Alberto Corigliano, orcid.org/0000-0002-1285-2724; Raffaele Ardito, orcid.org/0000-0002-4271-9190
 Jacopo Maria De Ponti
Jacopo Maria De Ponti Luca Iorio1†
Luca Iorio1† Emanuele Riva
Emanuele Riva Francesco Braghin
Francesco Braghin Alberto Corigliano
Alberto Corigliano Raffaele Ardito
Raffaele Ardito