Nonlinear Buckling of Fixed Functionally Graded Material Arches Under a Locally Uniformly Distributed Radial Load

Functionally graded material (FGM) arches may be subjected to a locally radial load and have different material distributions leading to different nonlinear in-plane buckling behavior. Little studies is presented about effects of the type of material distributions on the nonlinear in-plane buckling of FGM arches under a locally radial load in the literature insofar. This paper focuses on investigating the nonlinear in-plane buckling behavior of fixed FGM arches under a locally uniformly distributed radial load and incorporating effects of the type of material distributions. New theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches under a locally uniformly distributed radial load that are subjected to three different types of material distributions are derived. The comparisons between theoretical and ANSYS results indicate that the theoretical solutions are accurate. In addition, the critical modified geometric slendernesses of FGM arches related to the switches of buckling modes are also derived. It is found that the type of material distributions of the fixed FGM arches affects the limit point buckling loads and bifurcation buckling loads as well as the nonlinear equilibrium path significantly. It is also found that the limit point buckling load and bifurcation buckling load increase with an increase of the modified geometric slenderness, the localized parameter and the proportional coefficient of homogeneous ceramic layer as well as a decrease of the power-law index p of material distributions of the FGM arches.

Introduction

Arch structure has been widely used in the practice, because of the unique characteristics about aesthetics and safety. Arch structure is often subjected to different forms of load and different boundary constraints in practical engineering, which may lead to structural damage of arches. (Timoshenko et al., 1962), (Schreyer, 1972) and (Plaut and Raymond, 1990) started the research of arches early. Then, (Bradford et al., 2002) researched the in-plane buckling behavior of symmetrical cross-section arches under a central point load. (Pi et al., 2002) used an energy method to build the nonlinear equilibrium equation and the buckling equilibrium equation of arches, and the analytical result of nonlinear buckling was obtained. (Pi et al., 2008) also presented a theoretical research on the nonlinear in-plane buckling of pin-ended circular arches subjected to a central point load with rotational restraints elastic end. (Pi and Bradford, 2009) developed the virtual work approach was used to establish post-buckling equilibrium differential equation and the nonlinear buckling, and the exact solution of the nonlinear bifurcations. (Cai and Feng, 2010) carried out the in-plane buckling of parabolic arches whose rotational stiffness of supports increases according to loaded. (Cai et al., 2012) carried out the buckling equations and nonlinear equilibrium by virtual work principal method. (Cai et al., 2013) also analyzed the buckling equilibrium path according to the bistable strut by using fixed arches subjected to a central point load. According to the principle of virtual work, (Han et al., 2016) studied the in-plane nonlinear buckling behavior of circular arches with elastic horizontal supports under a uniform radial load. (Yan et al., 2017) made an analytical study about the non-uniform shallow arch subjected to a central point load. (Pi et al., 2017) revealed in-plane buckling of fixed shallow circular arches with the arbitrary radial point load. (Lu et al., 2018) explored the nonlinear in-plane buckling and post-buckling behavior of the fixed arches subjected to a localized uniform radial load. (Lu et al., 2020) also explored effects of movement and rotation of supports on nonlinear instability of fixed shallow arches under a localized uniform radial load. (Hu et al., 2021) presented an analytical investigates for nonlinear buckling of pin-ended arch-beam structures. In addition to the optimization of the cross section can make the stability of the structure better (Chen and Young, 2021; Chen et al., 2021), the improvement of material engineering technology also can make the stability of the structure better.

Most of the arches studied in the above literatures are homogeneous solid materials, however, functionally graded material (FGM) has been widely used because their mechanical properties are better than those of homogeneous materials in recent years. FGM arches are usually composed of two or more materials, which can contribute to the superior performance of each material, but the stress and buckling of FGM arches become complicated. (Bateni and Eslami, 2015) conducted nonlinear buckling behavior of FG circular arches under the uniformly radial load using an analytical method. (Simsek, 2016) assumed the material properties of the beam vary as the power-law form in both axial and thickness directions. (Al-shujairi and Mollamahmutoğlu, 2018) concerned with the sandwich FG micro-beams is made of the ceramic-metal FG skin and homogenous ceramic core, based on the classical rule and the Mori-Tanaka homogenization scheme of composite material properties of the part of the FG sandwich size according to beam changes continuously by the thickness of the beam. For different boundary condition analysis, (Bateni and Eslami, 2014) explored the nonlinear in-plane buckling behavior of FGMs arches. Simply supported–simply supported and clamped–clamped boundary conditions are considered as two types of well-known symmetric boundary conditions for this analysis. (Simsek, 2016) investigated first two-dimensional FGM to research the buckling of beams with different boundary conditions, using adding auxiliary functions the boundary conditions are met. For different load form analysis, (Rastgo et al., 2005) explored the spatial buckling of pinned FGM arches being subjected to a thermal loading for using the Galerkin method. (Song and Li, 2008) using Kirchhoff” s assumption conducted nonlinear governing equations of FG arches under thermal and mechanical loads. (Asgari et al., 2014) focused the nonlinear thermo-elastic behavior of pin-ended FGM arches. The stability equation of the nonlinear primary equilibrium path was developed using adjacent equilibrium criterion. (Moita et al., 2018) studied the discrete model of the structural by the theory of high order shear deformation, and the finite element formulation is carried out to meet general FGM plate-shell type structures. (Yang et al., 2020a; Yang et al., 2020b; Yang et al., 2020c; Yang et al., 2021a; Yang et al., 2021b) have published a series of papers on in-plane buckling and free vibrations of functionally graded composite arches with graphene reinforcements. However, FGM arches may be subjected to a locally radial load and have different material distributions leading to different nonlinear in-plane buckling behavior. Little studies is presented about effects of the type of material distributions on the nonlinear in-plane buckling of FGM arches under a locally radial load in the literature.

This paper, therefore, aims at studying the in-plane buckling of a fixed functionally graded material arch under a locally uniformly distributed radial load incorporating effects of the type of material distributions. To illustrate the nonlinear in-plane buckling behavior of FGM arches, three types of material distributions containing functionally graded material layer and homogeneous material layer are considered. Theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches under a locally uniformly distributed radial load that are subjected to three different types of material distributions are derived. Comparisons with the ANSYS results present the theoretical solutions are enough accurate. The critical modified geometric slendernesses of FGM arches that are switches of buckling modes are also derived. In addition, the effects of the proportional coefficient of homogeneous ceramic layer, the type and power-law index p of material distributions on the buckling load and critical modified geometric slendernesses are discussed and examined.

Material Distribution of Functionally Graded material Arches

The FGM shallow arches under a locally uniformly distributed radial load q with a central angle $2\Theta$, and radius R and length S are made from ceramic Al₂O₃ and metal Al, as shown in Figure 1. In addition, 2c represents the subtended angle of the arch segment where the locally uniformly distributed radial load acts, also as shown in Figure 1. The total cross-sectional thickness and width are h and b, respectively.

FIGURE 1

FIGURE 1. FGM arch under a locally uniformly distributed radial load.

In this research, the metal-ceramic material Al-Al₂O₃ is adopted. According to power-law function, the FGM arch through the thickness are graded continuously as

$\Xi ={\Xi }_m{V}_m+{\Xi }_c{V}_c,(1)$

where ${\Xi }_c$ and ${\Xi }_m$ are the properties of ceramic and metal, respectively. $V_c$ and $V_m$ is the volume fraction of ceramic and metal, and they meet the following conditions as

$V_m+V_c=1.(2)$

In order to illustrate the nonlinear in-plane buckling behavior of FGM arches, three types of material distributions containing functionally graded material layer and homogeneous material layer are considered, including Type A, Type B, and Type C as shown in Figure 2. The cross-section of Type A represents that the top layer is the metal layer with the thickness $\alpha h$ and the material distributions of bottom layer is that the weight fraction of metal increase from the top surface to the bottom and the weight fraction of ceramic decrease from the top surface to the bottom surface. The cross-section of Type B have three layers, the middle layer of Type B is the metal layer with the thickness $\alpha h$, the top and bottom layers of Type B is symmetric about the midline of the cross-section, and the material distributions of bottom layer of Type B is same to the bottom layer of Type A. The cross-section of Type C have four layers, the top and the bottom layers of Type C is the metal layer with the thickness $\alpha h\text{/}2$, the second and third layers of Type B is symmetric about the midline of the cross-section, and the material distributions of the second layer of Type C is same to the bottom layer of Type A.

FIGURE 2

FIGURE 2. Type A, Type B and Type C of material distributions of FGM arch.

The volume fractions $V_c$ for three distribution modes that are shown in Figure 2 are expressed as

$\text{Type}\mathbf{ }\text{A: }{V}_c=\{\begin{array}{cc}{\left[\frac{z+0.5h}{\left(1-\alpha \right)h}\right]}^p& -0.5h\le z\le \left(0.5-\alpha \right)h,\\ 1& \left(0.5-\alpha \right)h\le z\le 0.5h\end{array}(3)$

$\text{Type}\mathbf{ }\text{B: }{V}_c=\{\begin{array}{cc}{\left[\frac{z+0.5h}{0.5\left(1-\alpha \right)h}\right]}^p& -0.5h\le z\le -0.5\alpha h,\\ 1& -0.5\alpha h\le z\le 0.5\alpha h\\ {\left[\frac{-z+0.5h}{0.5\left(1-\alpha \right)h}\right]}^p& 0.5\alpha h\le z\le 0.5h\end{array}(4)$

and

$\text{Type}\mathbf{ }\text{C: }{V}_c=\{\begin{array}{cc}1& -0.5h\le z\le -0.5\left(1-\alpha \right)h\\ {\left[-\frac{z}{0.5\left(1-\alpha \right)h}\right]}^p& -0.5\left(1-\alpha \right)h\le z\le 0,\\ {\left[\frac{z}{0.5\left(1-\alpha \right)h}\right]}^p& 0\le z\le 0.5\left(1-\alpha \right)h\\ 1& 0.5\left(1-\alpha \right)h\le z\le 0.5h\end{array}(5)$

where p is the power-law index of material distributions and $\alpha$ is the proportional coefficient of homogeneous ceramic layer. According to Eq. 1, the elastic modulus of FGM arch can be expressed as (Bateni and Eslami, 2015).

$E\left(z\right)=E_m\left(1-V_c\right)+E_c{V}_c(6)$

where $E_c$ and $E_m$ are the elastic modulus of ceramic and metal, respectively.

Nonlinear Equilibrium

The nonlinear in-plane buckling behavior of a fixed FGM arch subjected to a locally uniformly distributed radial load is investigated, which is shown in Figure 1. The potential energy Π of the FGM arch can then be given by

$\Pi =\frac{1}{2}{\displaystyle {\int }_{-\Phi }^{\Phi }Rb}{\displaystyle {\int }_{-h/2}^{h/2}E\left(z\right){\epsilon }^{2}dzd\varphi }-R^2{\displaystyle {\int }_{-\Phi }^{\Phi }q\tilde{v}{H}_1\left(\varphi ,c\right)}d\varphi (7)$

with the function $H_1\left(\varphi ,c\right)$ being given by

$H_1\left(\varphi ,c\right)=\text{Heaviside}\left(\varphi +c\right)-\text{Heaviside}\left(\varphi -c\right),(8)$

where $\text{Heaviside}\left(\right)$ represents Heaviside function. The longitudinal strain of an arbitrary point at the cross-section can be expressed as

$\epsilon ={\epsilon }_m+{\epsilon }_b(9)$

where ${\epsilon }_m$ and ${\epsilon }_b$ are the membrane and bending strains of the FGM arch, respectively, which are given by

${\epsilon }_m=-\tilde{v}+\frac{1}{2}{{\tilde{v}}^{\prime }}^2+{\tilde{w}}^{\prime },(10)$

${\epsilon }_b=-\frac{z{\tilde{v}}^{″}}{R}(11)$

with $\tilde{w}=w/R$ and $\tilde{v}=v/R$, where $({)}^{\prime }\equiv d()/d\varphi$, z is the coordinate of the point P₀ at the cross-sectional axis oz, w and v are the axial and radial displacements respectively.

For nonlinear equilibrium of FGM arch using the principle of minimum total potential energy, the variation of the total potential energy obtained from Eq. 7 should vanish as

$\delta \Pi ={\displaystyle {\int }_{-\Theta }^{\Theta }Rb}{\displaystyle {\int }_{-h/2}^{h/2}E\left(z\right)\epsilon \delta \epsilon dzd\varphi }-R^2{\displaystyle {\int }_{-\Theta }^{\Theta }q\delta \tilde{v}{H}_1\left(\varphi ,c\right)}d\varphi =\text{0}(12)$

By substituting Eqs 10, 11 into Eq. 12, the Eq. 12 can then be rewritten as

$\delta \Pi ={\displaystyle {\int }_{-\Theta }^{\Theta }\left[-NR\left(\delta {\tilde{w}}^{\prime }-\delta \tilde{v}+{\tilde{v}}^{\prime }\delta {\tilde{v}}^{\prime }\right)-M\delta {\tilde{v}}^{″}\right]}d\varphi -R^2{\displaystyle {\int }_{-\Theta }^{\Theta }q\delta \tilde{v}{H}_1\left(\varphi ,c\right)}d\varphi =\text{0}(13)$

where N and M are the axial and bending actions of the FGM arch, respectively, which can be given by

$N=-A_k\left({\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)+\frac{B_k}{R}{\tilde{v}}^{″}(14)$

$M=B_k\left({\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)-\frac{D_k}{R}{\tilde{v}}^{″}(15)$

with $A_k$, $B_k$, and $D_k$ being the stiffness components of the FGM arch, respectively, which are defined as

$\left\{A_k{B}_k{D}_k\right\}=b{\displaystyle \underset{-\text{0}\text{.}5h}{\overset{0.5h}{\int }}E\left(z\right)\left\{1z{z}^2\right\}\text{dz}}.(16)$

When material distributions of the FGM arch is subjected to Type A, the stiffness components of the FGM arch $A_k$, $B_k$, and $D_k$ can be given by

$A_k=\frac{bh\left\{\left[\left(E_c-E_m\right)\alpha +E_m\right]p+E_c\right\}}{p+1}(17)$

$B_k=\frac{b{h}^{2}p\left(1-\alpha \right)\left(E_c-E_m\right)\left(\alpha p+\alpha +1\right)}{2p^2+6p+4}(18)$

$\begin{array}{c}{D}_k=\frac{b{h}^3{p}^2\left\{\left(E_c-E_m\right)\left[\left(4{\alpha }^3-6{\alpha }^2+3\alpha -1\right)p+12{\alpha }^3-12{\alpha }^2+3\alpha -3\right]+E_c\left(6+p\right)\right\}}{12\left(p^3+6p^2+11p+6\right)}\\ +\frac{b{h}^3\left\{\left[\left(8{\alpha }^3-6{\alpha }^2+6\alpha -8\right)\left(E_c-E_m\right)+11E_c\right]p+6E_c\right\}}{12\left(p^3+6p^2+11p+6\right)}\end{array}(19)$

When material distributions of the FGM arch is subjected to Type B, the stiffness components of the FGM arch $A_k$, $B_k$, and $D_k$ can be given by

$A_k=\frac{bh\left\{\left[\left(E_c-E_m\right)\alpha +E_m\right]p+E_c\right\}}{p+1}(20)$

$B_k=0(21)$

$\begin{array}{c}{D}_k=\frac{b{h}^3{p}^2\left\{\left(E_c-E_m\right)\left[p\left({\alpha }^3-1\right)+3{\alpha }^3+3{\alpha }^2-6\right]+E_c\left(6+p\right)\right\}}{12\left(p^3+6p^2+11p+6\right)}\\ +\frac{b{h}^3\left[\left(2{\alpha }^3+3{\alpha }^2+6\alpha -11\right)\left(E_c-E_m\right)p+E_c\left(11p+6\right)\right]}{12\left(p^3+6p^2+11p+6\right)}\end{array}(22)$

When material distributions of the FGM arch is subjected to Type C, the stiffness components of the FGM arch $A_k$, $B_k$, and $D_k$ can be given by

$A_k=\frac{bh\left\{\left[\left(E_c-E_m\right)\alpha +E_m\right]p+E_c\right\}}{p+1}(23)$

$B_k=0(24)$

$D_k=\frac{b{h}^3\left[\left(E_c-E_m\right)\left({\alpha }^3-3{\alpha }^2+3\alpha \right)p+E_{m}p+3E_c\right]}{12p+36}(25)$

Integrating Eq. 13 by parts, the differential equilibrium equations of a FGM arch under a locally uniformly distributed radial load can be derived as

${\left(NR\right)}^{\prime }=\text{0}(26)$

$NR+{\left(NR{\tilde{v}}^{\prime }\right)}^{\prime }-M^{″}-q{R}^2{{\rm H}}_1\left(\varphi ,c\right)=0(27)$

By Substituting Eq. 14 into Eq. 15, the bending action of the FGM arch can be given by

$M=-\left(D_{\text{k}}-\frac{B_k^2}{A_k}\right)\frac{{\tilde{v}}^{″}}{R}-\frac{B_k}{A_k}N(28)$

By Substituting Eqs. 26, 28 into Eq. 27, Eq. 27 can then be rewritten as

$\frac{{\tilde{v}}^{iv}}{{\varpi }^2}+{\tilde{v}}^{″}=\frac{qR{{\rm H}}_1\left(\varphi ,c\right)}{N}-1(29)$

where $\varpi$ is non-dimensional axial force parameter, which is given by

${\varpi }^2=\frac{N{R}^2}{\kappa }(30)$

with $\kappa$ being the equivalent stiffness of the FGM arch, which is defined as

$\kappa =D_{\text{k}}-\frac{B_k^2}{A_k}(31)$

Meanwhile, the essential boundary conditions at the both ends of FGM arch

$\tilde{v}=0,\tilde{w}=0,\mathrm{and}{\tilde{v}}^{\prime }=0\mathrm{at}\varphi =\pm \Theta (32)$

also need to be satisfied. The non-dimensional radial displacement $\tilde{v}$ of a FGM arch can be determined by solving Eq. 29 under the boundary conditions obtained from Eq. 32.

$\begin{array}{c}\tilde{v}=\frac{P\left[\cos \left(\varpi \varphi \right)\left({\beta }_2-\cos {\beta }_1\sin {\beta }_2\right)-{\beta }_2\left({\beta }_1\sin {\beta }_1+\cos {\beta }_1\right)+\sin {\beta }_2\right]}{{\varpi }^2\sin {\beta }_1}+\frac{{\beta }_1^2-{\mu }^2{\varphi }^2}{2{\varpi }^2}\\ +\frac{{\beta }_1\left[\cos {\beta }_1-\cos \left(\varpi \varphi \right)\right]}{{\varpi }^2\sin {\beta }_1}+\frac{P{{\rm H}}_1\left(\varphi ,c\right)\left[2\cos {\beta }_2\cos \left(\varpi \varphi \right)+{\beta }_2^2+{\left(\varpi \varphi \right)}^2-2\right]}{2{\varpi }^2}\\ -\frac{P{{\rm H}}_2\left(\varphi ,c\right)\left[\sin \left(\varpi \varphi \right)\sin {\beta }_2-\varpi \varphi {\beta }_2\right]}{{\varpi }^2}\end{array}(33)$

where ${\beta }_1=\mu \Theta$ and ${\beta }_2=\mu c=\eta {\beta }_1$ with $\eta =c/\Theta$, the non-dimensional locally uniformly distributed radial load P is expressed as

$P=\frac{Q}{2cN}\mathrm{with}Q=2cqR,(34)$

and the ${\text{H}}_2\left(\varphi ,c\right)$ is expressed as

${\text{H}}_2\left(\varphi ,c\right)=-1+Heaviside\left(-c+\varphi \right)+Heaviside\left(-c+\varphi \right).(35)$

Equation 33 indicates that the non-dimensional radial displacement $\tilde{v}$ is dependent on P and $\varpi$, and so it is necessary to calculate the relationship of the axial force with the locally uniformly distributed radial load.

Therefore, substituting Eq. 33 into Eq. 14, and integrating it along the arch length results in

$\begin{array}{c}2\Phi N={\displaystyle {\int }_{-\Theta }^{\Theta }\left[-A_k\left({\tilde{w}}^{\prime }-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)+\frac{B_k}{R}{\tilde{v}}^{″}\right]}d\varphi \\ ={\displaystyle {\int }_{-\Theta }^{\Theta }-A_k\left(-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)d\varphi -{\displaystyle {\int }_{-\Theta }^{\Theta }{A}_k\left({\tilde{w}}^{\prime }\right)d\varphi }+{\displaystyle {\int }_{-\Theta }^{\Theta }\frac{B_k}{R}{\tilde{v}}^{″}d\varphi },}\\ ={\displaystyle {\int }_{-\Theta }^{\Theta }-A_k\left(-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)d\varphi -{\tilde{w}|}_{-\Theta }^{\Theta }+{\left(\frac{B_k}{R}{\tilde{v}}^{\prime }\right)|}_{-\Theta }^{\Theta }}\end{array}(36)$

Considering the essential boundary conditions obtained from Eq. 32, the Eq. 36 can be rewritten as

$2\Phi N={\displaystyle {\int }_{-\Theta }^{\Theta }-A_k\left(-\tilde{v}+\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)}d\varphi \Rightarrow {\displaystyle {\int }_{-\Theta }^{\Theta }\left(\tilde{v}-\frac{{{\tilde{v}}^{\prime }}^2}{2}\right)}d\varphi +\frac{2\Phi N}{A_k}=0,(37)$

Subsequently, Calculating Eq. 37 leads to a quadratic equilibrium equation, as

$A_1{P}^2+B_{1}P+C_1=0,(38)$

where the coefficients $A_1$, $B_1$ and $C_1$ are expressed as

$\begin{array}{c}{A}_1=\frac{\left[3{\beta }_2^2+5{\sin }^2{\beta }_2-{\beta }_2\sin \left(2{\beta }_2\right)\right]\cos {\beta }_1+2{\beta }_2\left({\beta }_2\cos {\beta }_2-4\sin {\beta }_2\right)}{4{\beta }_1^3\sin {\beta }_1}-\frac{5\sin \left(2{\beta }_2\right)}{8{\beta }_1^3}\\ +\frac{{\beta }_2^2\left(2{\sin }^2{\beta }_1+1\right)+{\sin }^2{\beta }_2-2{\beta }_2\sin {\beta }_2\cos {\beta }_1}{4{\beta }_1^2{\sin }^2{\beta }_1}+\frac{6{\cos }^2{\beta }_2+9-4{\beta }_1^2}{12{\beta }_1^3}\end{array}(39)$

$B_1=\frac{2\sin {\beta }_2-{\beta }_2\left(\cos {\beta }_1+\cos {\beta }_2\right)}{2{\beta }_1^2\sin {\beta }_1}+\frac{\sin {\beta }_2\cos {\beta }_1-{\beta }_2}{2{\beta }_1{\sin }^2{\beta }_1},(40)$

$C_1=\frac{2{\cos }^2{\beta }_1+1}{12{\sin }^2{\beta }_1}-\frac{\cos {\beta }_1}{4{\beta }_1\sin {\beta }_1}+\frac{\kappa {\beta }_1^2}{A_k{\left({\lambda }_{s}h\right)}^2}(41)$

with λ_s being the modified geometric slenderness of the FGM arch, respectively, which can be express as

${\lambda }_s=\frac{S\Theta }{2h}(42)$

By solving Eq. 38, the relationship of the axial force with the locally uniformly distributed radial load can be obtained. Then, by substituting those relationship into Eq. 33, the non-dimensional radial displacement $\tilde{v}$ can be obtained. Finally, the relationship of the locally uniformly distributed radial load with the non-dimensional radial displacement can be established, and the nonlinear instability behavior of FGM arches can be analyzed.

Buckling Analysis

Limit Point Buckling and Bifurcation Buckling

The FGM arches under the locally uniformly distributed radial load may buckle in a limit point mode. According to the theory of (Lu et al., 2018) for an arches under the locally uniformly distributed radial load, the upper and lower limit point buckling loads can be derived using routine calculus, and the equation of equilibrium between ${\beta }_1$ and P at the upper and lower limit points can be expressed as

$A_2{P}^2+B_{2}P+B_2=0(43)$

where

$A_2=\frac{{\beta }_1\partial A_1}{\partial {\beta }_1}-4A_1,B_2=\frac{{\beta }_1\partial B_1}{\partial {\beta }_1}-2B_1,C_2=\frac{{\beta }_1\partial C_1}{\partial {\beta }_1}(44)$

Therefore, the upper and lower limit point buckling loads can be obtained by solving Eqs 38, 43 simultaneously.

It can be found that the Eq. 43 for equilibrium of limit point buckling mode of the FGM arches are the same as those for the homogeneous arches (Lu et al., 2018). Similarly, refer to limit point buckling theory of the homogeneous arches under the locally uniformly distributed radial load, the axial force parameter ${\beta }_{b1}$ and the axial force N in the FGM arch during lowest possible limit point buckling are respectively given by

${\beta }_{b1}=\pi \text{ and }N=\frac{{\pi }^2\kappa }{{\left(S/2\right)}^2}=N_{E1}(45)$

In addition, also refer to the above theory of homogeneous arch, the central displacement ${\tilde{v}}_{sc}$ corresponding to the lowest buckling load of the FGM arch as

$\begin{array}{c}{\tilde{v}}_{sc}=\frac{{\Theta }^2}{2}-\frac{2{\Theta }^2}{2{\pi }^2\left({\beta }_2+\sin {\beta }_2\right)}\left[{\beta }_2\left({\pi }^2-2\right)+\pi \left(1-\cos {\beta }_2\right)-2\sin {\beta }_2-\frac{{\beta }_2^2\pi }{2}\right]\\ \pm 2{\Theta }^2\sqrt{\frac{1}{{\pi }^2}\left(\frac{B}{{\pi }^2}+\frac{5}{3}\right)-\frac{4\kappa }{A_k{\left({\lambda }_{s}h\right)}^2}}\end{array}(46)$

with

$\begin{array}{c}B=\frac{\left(5\pi -6{\beta }_2\right)\cos {\beta }_2-6{\beta }_2}{{\beta }_2+\sin {\beta }_2}+{\beta }_2^2+9+2{\left(\pi -{\beta }_2\right)}^2\left(\frac{1}{{\beta }_2+\sin {\beta }_2}-1\right)\\ +\frac{{\beta }_2\left(\cos {\beta }_2+1\right)\left(2{\beta }_2-5\pi \right)-{\beta }_2^2\left(9{\pi }^2-10\pi {\beta }_2+3{\beta }_2^2\right)}{{\left({\beta }_2+\sin {\beta }_2\right)}^2}\end{array}(47)$

The Eq. 46 has a real solution only when

$\frac{1}{{\pi }^2}\left(\frac{B}{{\pi }^2}+\frac{5}{3}\right)-\frac{4\kappa }{A_k{\left({\lambda }_{s}h\right)}^2}\ge 0(48)$

from which the modified geometric slenderness ${\lambda }_s$ of the lowest buckling load of the FGM arch can be obtained once the type of the cross section and the locally uniformly distributed radial load are given.

The FGM arches under the locally uniformly distributed radial load may buckle in a bifurcation mode. The equation of equilibrium of the FGM arch in the primary equilibrium path is obtained from Eq. 29. Similarly, the differential equation of equilibrium of the FGM arch in the case of infinitely close to the bifurcation equilibrium path can be given by

$\frac{{\tilde{v}}^{iv}+{\tilde{v}}_b^{iv}}{{\varpi }^2}+{\tilde{v}}^{″}+{{\tilde{v}}^{″}}_b=P{\text{H}}_1\left(\varphi ,c\right)-1(49)$

Therefore, the equation for equilibrium of bifurcation mode of the FGM arches can be built by substituting Eq. 29 into Eq. 49 as

$\frac{{\tilde{v}}_b^{iv}}{{\varpi }^2}+{{\tilde{v}}^{″}}_b=0(50)$

It’s can be found that the equation for equilibrium of bifurcation mode of the FGM arches are the same as those for the homogeneous arches (Lu et al., 2018). Similarly, refer to bifurcation buckling theory of the homogeneous arches, the axial force parameter ${\beta }_{b1}$ and the axial force N in the arch during bifurcation are respectively given by

${\beta }_{b1}=1.4303\pi \text{ and }N=\frac{{\left(1.4303\pi \right)}^2\kappa }{{\left(S/2\right)}^2}=N_{E2}(51)$

In addition, the parameter ${\beta }_{b2}$ for bifurcation mode can then be expressed as

${\beta }_{b2}=1.4303\pi \frac{c}{\Theta }(52)$

By substituting Eqs 51, 52 into Eq. 39, the equation of equilibrium between ${\beta }_{b1}$ and P at the upper and lower bifurcation points can be expressed as

$A_3{P}^2+B_{3}P+C_3=0(53)$

where

$\begin{array}{l}{A}_3=\frac{5{\sin }^2{\beta }_{b2}-{\beta }_{b2}\sin \left(2{\beta }_{b2}\right)}{4{\beta }_{b1}^4}+\frac{4{\beta }_{b2}{\cos }^2{\beta }_{b2}-5\sin \left(2{\beta }_{b2}\right)}{8{\beta }_{b1}^3}+\frac{3\eta \left(\eta +1\right)}{4{\beta }_{b1}^2}+\frac{{\eta }^2\left(3-2\eta \right)}{6}\\ +\frac{\eta \left({\beta }_{b2}\cos {\beta }_{b2}-5\sin {\beta }_{b2}\right)}{2{\beta }_{b1}^2\sin {\beta }_{b1}}+\frac{{\beta }_{b2}^2+{\sin }^2{\beta }_{b2}}{4{\beta }_{b1}^2{\sin }^2{\beta }_{b1}}\end{array}(54)$

$B_3=\frac{3\sin {\beta }_{b2}-{\beta }_{b2}\cos {\beta }_{b2}}{2{\beta }_{b1}^2\sin {\beta }_{b1}}-\frac{\eta }{{\beta }_{b1}}\left(\frac{1}{2}-\frac{1}{{\beta }_{b1}}\right)(55)$

$C_3=\frac{1}{12{\sin }^2{\beta }_1}-\frac{1}{12{\beta }_1^2}+\frac{\kappa {\beta }_{b1}^2}{A_k{\left({\lambda }_{s}h\right)}^2}(56)$

with

$\eta =\frac{c}{\Theta }(57)$

The bifurcation buckling load of a FGM arch under a locally uniformly distributed radial load can be obtained once the localized parameter η is given.

Comparisons of Theoretical Solutions with ANSYS Results

According to Donnell’s shallow shell theory, in the ANSYS models of FGM arch, the geometry of the rectangular section was, the width b = 0.14 m, the total thickness h = 0.07 m, the power-law index p = 1 and the proportional coefficient of homogeneous ceramic layer $\alpha$= 0.2. In addition, the geometric slenderness of the FGM arch S/h = 100. The Young’s modulus of the metal-ceramic material Al-Al₂O₃ are 70GPa and 380GPa, respectively.

When a multilayer for metal-ceramic material Al-Al₂O₃ is used to simulate a continuous gradient properties, the accuracy of the FGM arch model increases with an increase of the number of layers of metal-ceramic material Al-Al₂O₃. As demonstrated in Figure 3, when material distributions of the FGM arch is subjected to Type A (Figure 3A), the cross-section of the FGM arch have 101 layers, the first layer is a homogeneous ceramic layer, and the second to the 101st layers are gradient layers from ceramic to metal. When material distributions of the FGM arch is subjected to Type B (Figure 3B), the cross-section of the FGM arch have 201 layers, the first to the 100st layers are gradient layers from metal to ceramic, the 101st is a homogeneous ceramic layer, and the 102st to the 201st layers are gradient layers from ceramic to metal. When material distributions of the FGM arch is subjected to Type C (Figure 3C), the cross-section of the FGM arch have 202 layers, the first layer is a homogeneous ceramic layer, the second to the 101st layers are gradient layers from ceramic to metal, the 102st to the 201st layers are gradient layers from metal to ceramic, the 101st is a homogeneous ceramic layer, and the last layer is a homogeneous ceramic layer.

FIGURE 3

FIGURE 3. ANSYS model of material distributions of FGM arch (A) Type A (B) Type B (C) Type C (D) ANSYS model with boundary conditions.

In addition, the proposed theoretical solution of the buckling equilibrium path, the limit point and bifurcation buckling load for the FGM arches under the locally uniformly distributed radial load are validated by ANSYS finite element results. Convergence researches for using the shell element shell181 of ANSYS show that 80 elements can produce convergent results. Therefore, 80 shell181 elements are chosen to simulate the FGM arches (Figure 3D).

Comparisons of the theoretical solutions of Eqs. 33, 38 for the limit point buckling equilibrium path and the limit point buckling load of the FGM arches with the corresponding ANSYS results are plotted in Figure 4. The variation curves of the dimensionless locally uniformly distributed radial load Q/(2N_Ec2Θ) with the dimensionless central displacement v_c/f are plotted in Figure 4A for material distributions of the FGM arch being subjected to Type A, in Figure 4B for material distributions of the FGM arch being subjected to Type B, and in Figure 4C for material distributions of the FGM arch being subjected to Type C, where the locally uniformly distributed radial load with $\eta =0.5$, the modified geometric slenderness ${\lambda }_s=4$ and $N_{Ec2}={\left(1.4303\pi \right)}^2{E}_{c}b{h}^3/\left[12{\left(S/2\right)}^2\right]$. It can be seen from Figures 4A–C that the theoretical solutions for the limit point buckling equilibrium path and the limit point buckling load of the FGM arches are highly consistent with the corresponding ANSYS results.

FIGURE 4

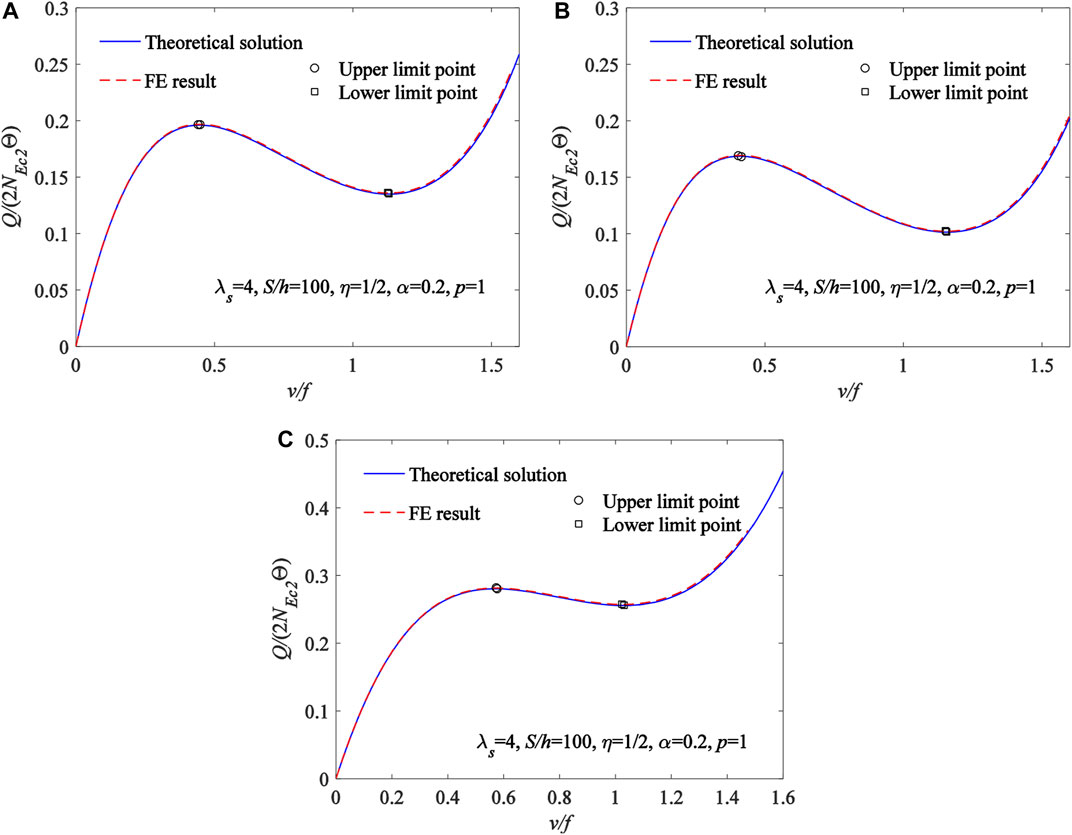
FIGURE 4. Comparisons of the theoretical solutions for the limit point buckling with the corresponding ANSYS results (A) Type A (B) Type B (C) Type C.

Comparisons of the theoretical solutions of Eqs 33, 53 for bifurcation buckling equilibrium path and the bifurcation buckling load of the FGM arches with the corresponding ANSYS results are plotted in Figure 5. The variation curves of the dimensionless locally uniformly distributed radial load Q/(2N_Ec2Θ) with the dimensionless central displacement v_c/f are plotted in Figure 5A for material distributions of the FGM arch being subjected to Type A, in Figure 5B for material distributions of the FGM arch being subjected to Type B, and in Figure 5C for material distributions of the FGM arch being subjected to Type C, where the locally uniformly distributed radial load with $\eta =0.75$, the modified geometric slenderness ${\lambda }_s=8$. It can be seen from Figures 5A–C that the theoretical solutions for bifurcation buckling equilibrium path and the bifurcation buckling load of the FGM arches are highly consistent with the corresponding ANSYS results.

FIGURE 5

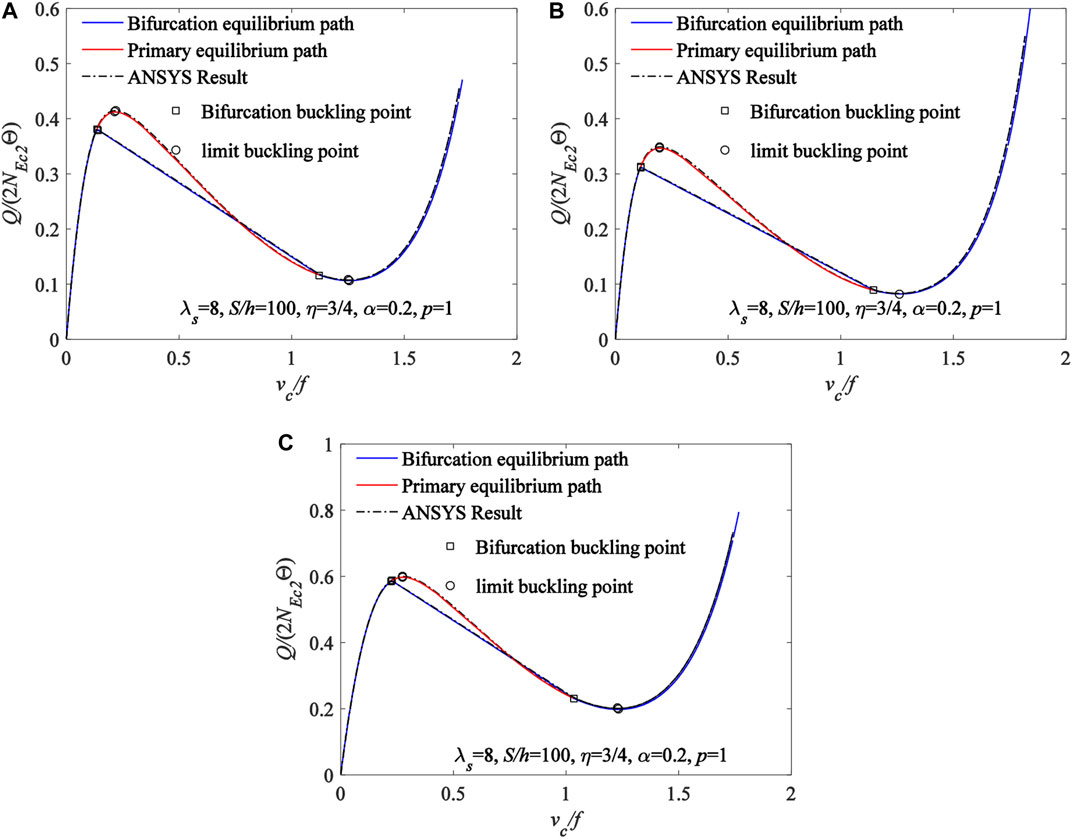
FIGURE 5. Comparisons of the theoretical solutions for the bifurcation buckling with the corresponding ANSYS results (A) Type A (B) Type B (C) Type C.

Hence, the theoretical solutions of Eqs 33, 38, 53 can be used to predict the buckling equilibrium path, the limit point and bifurcation buckling load for the FGM arches under the locally uniformly distributed radial load.

Limit Point Buckling Analysis

This section investigates the effects of the localized parameter η of locally uniformly distributed radial load, the type and the power-law index p of material distributions of the FGM arch on the limit point buckling equilibrium path and the limit point buckling load for FGM arches under a locally uniformly distributed radial load.

Under the locally uniformly distributed radial load, the limit point buckling equilibrium path obtained from Eqs 33, 38 for FGM arches having different localized parameter η are plotted in Figure 6A with the variation curves of v_c/f vs Q/(2N_Ec2Θ), and in Figure 6B with the variation curves of N/N_Ec2vs Q/(2N_Ec2Θ), where the modified geometric slenderness ${\lambda }_s=4$, the power-law index p = 1, the proportional coefficient of homogeneous ceramic layer $\alpha$= 0.2, the geometric slenderness S/h = 100 and the material distributions of FGM arches are subjected to Type A. Also plotted in Figure 6 are the limit points given by Eqs 38, 43. In Figure 6, when the upper limit point is reached, the load system and limit point buckling equilibrium path of FGM arches snaps through to the remote equilibrium branch, and the displacement become very large. Therefore, the upper limit point is the limit point buckling load. It can also be seen from Figure 6 that the localized parameter η has a significant effect on the limit point buckling equilibrium path and the limit point buckling load, the limit point buckling load increases with an increase of localized parameter η, which indicates that FGM arches having a larger length of the locally uniformly distributed radial loading segment are more prone to limit point buckling.

FIGURE 6

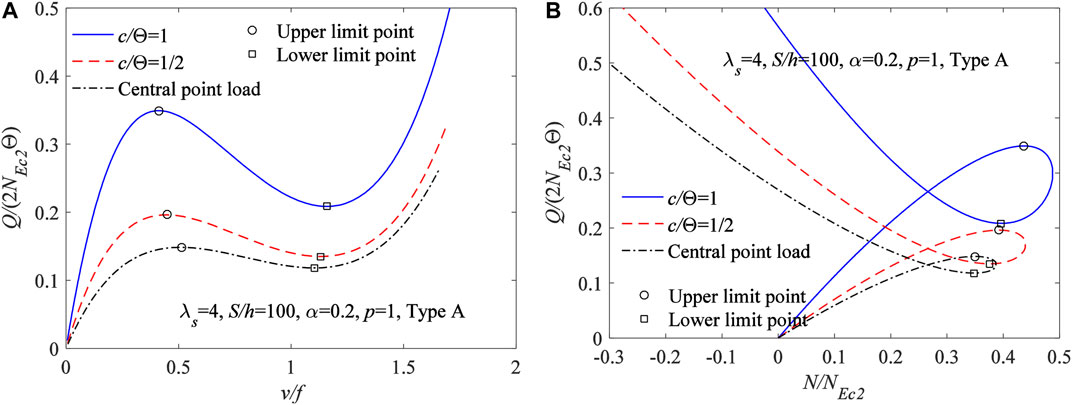
FIGURE 6. Limit point buckling equilibrium path for FGM arches having different localized parameter (A)v_c/f vs Q/(2N_Ec2Θ) (B)N/N_Ec2vs Q/(2N_Ec2Θ).

In addition, the limit point buckling equilibrium path obtained from Eqs 33, 38 for FGM arches having different type of material distributions are plotted in Figure 7A with the variation curves of v_c/f vs Q/(2N_Ec2Θ), and in Figure 7B with the variation curves of N/N_Ec2vs Q/(2N_Ec2Θ), where ${\lambda }_s=4$, η = 0.5, $\alpha$= 0.2, S/h = 100, p = 1. It can be seen from Figure 7 that the type of material distributions has a significant effect on the limit point buckling equilibrium path and the limit point buckling load, Type C has a largest limit point buckling load among Type A, Type B and Type C, which indicates that under the same proportion of metal and ceramic materials, the distribution of ceramics on the upper and lower surfaces of the cross-section can greatly improve the stability of the FGM arch.

FIGURE 7

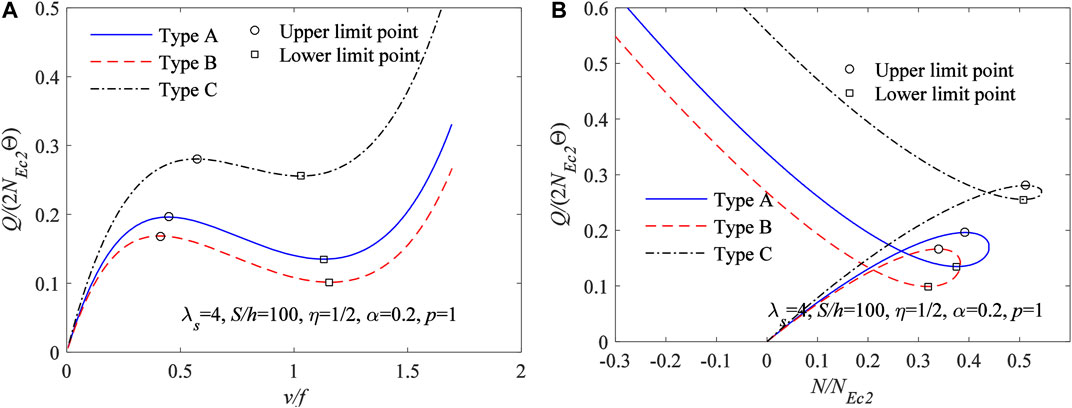
FIGURE 7. Limit point buckling equilibrium path for FGM arches having different type of material distributions (A)v_c/f vs Q/(2N_Ec2Θ) (B)N/N_Ec2vs Q/(2N_Ec2Θ).

Similarly, Figure 8A plots the variation curves of v_c/f vs Q/(2N_Ec2Θ) and Figure 8B plots the variation curves of N/N_Ec2vs Q/(2N_Ec2Θ) for FGM arches having different power-law index p, where ${\lambda }_s=4$, η = 0.5, $\alpha$= 0.2, S/h = 100 and the material distributions of FGM arches are subjected to Type A. It can also be seen from Figure 8 that the power-law index p has a significant effect on the limit point buckling equilibrium path and the limit point buckling load, the limit point buckling load increases with a decrease of the power-law index p, which indicates that FGM arches having a smaller power-law index p of material distributions are more prone to limit point buckling.

FIGURE 8

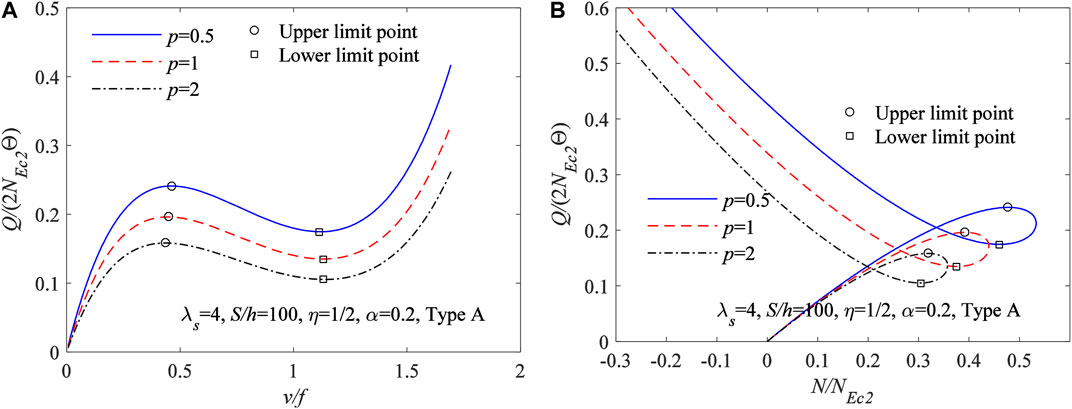
FIGURE 8. Limit point buckling equilibrium path for FGM arches having different power-law index of material distributions (A)v_c/f vs Q/(2N_Ec2Θ) (B)N/N_Ec2vs Q/(2N_Ec2Θ).

Furthermore, the influences of the modified geometric slenderness ${\lambda }_s$, the type and the power-law index p of material distributions of the FGM arch, the proportional coefficient of homogeneous ceramic layer $\alpha$ and the localized parameter η of the locally uniformly distributed radial load on the limit point buckling load of the FGM arch are studied in detail as well. The variation curves of η vs Q/(2N_Ec2Θ) are plotted in Figure 9A for a FGM arch having different modified geometric slenderness ${\lambda }_s$, in Figure 9B for a FGM arch having different type of material distributions, in Figure 9C for a FGM arch having different power-law index p of material distributions and in Figure 9D for a FGM arch having different proportional coefficient of homogeneous ceramic layer $\alpha$. It can be seen again from Figure 9 that the limit point buckling load increases with an increase of localized parameter η. It can be seen from Figure 9A that the limit point buckling load increases with an increase of modified geometric slenderness ${\lambda }_s$. It can be seen again from Figure 9B that Type C has a largest limit point buckling load among Type A, Type B and Type C. In addition, because the composition proportion of ceramics increases with an increase of the proportional coefficient of homogeneous ceramic layer $\alpha$ and a decrease of the power-law index p of material distributions of the FGM arch. Therefore, Figures 9C,D show the limit point buckling load increases with an increase of the proportional coefficient of homogeneous ceramic layer $\alpha$ and a decrease of the power-law index p of material distributions of the FGM arch, and the power-law index p has a more obvious effect on the limit point buckling load.

FIGURE 9

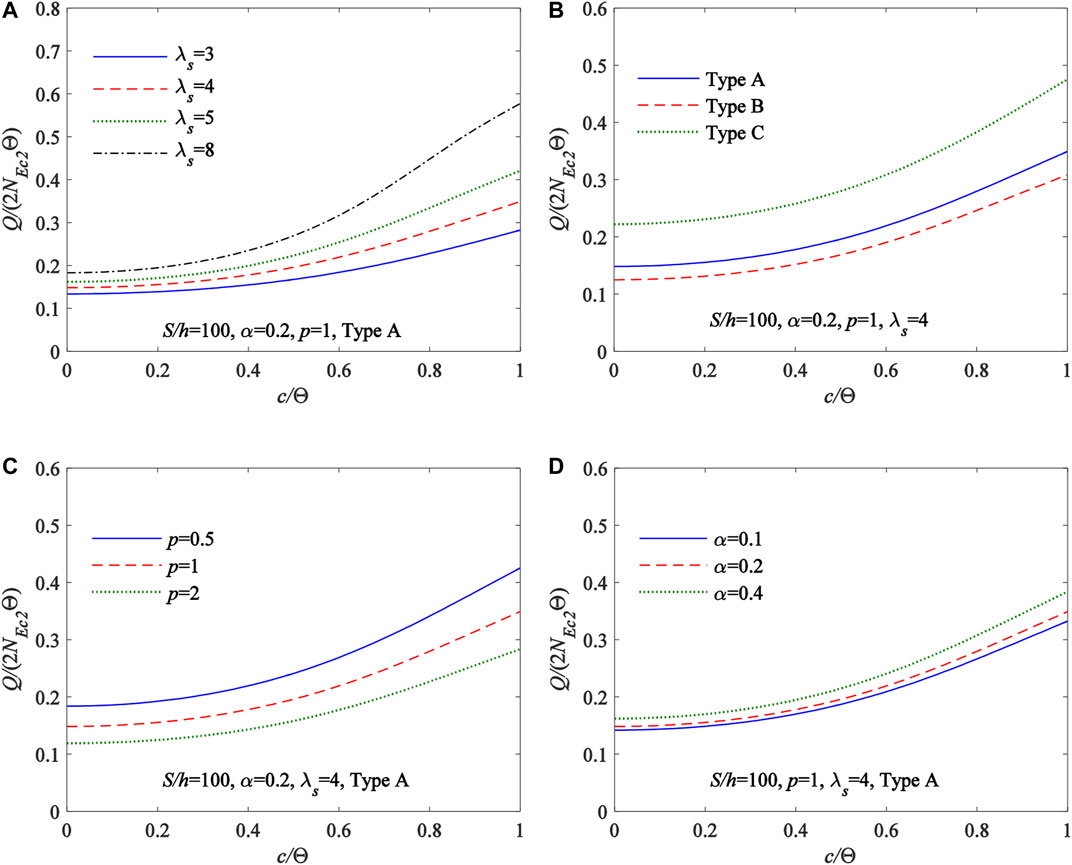
FIGURE 9. η vs Q/(2N_Ec2Θ) (A) different modified geometric slenderness (B) different type of material distributions (C) different power-law index p of material distributions (D) different proportional coefficient of homogeneous ceramic layer.

Bifurcation Buckling Analysis

This section investigates the effects of the localized parameter η of locally uniformly distributed radial load, the type of material distributions of the FGM arch on the bifurcation buckling equilibrium path and the bifurcation buckling load for FGM arches under a locally uniformly distributed radial load.

Under the locally uniformly distributed radial load, the bifurcation buckling equilibrium path obtained from Eqs 33, 53 for FGM arches having different localized parameter η are plotted in Figure 10A with the variation curves of v_c/f vs Q/(2N_Ec2Θ), and in Figure 6B with the variation curves of N/N_Ec2vs Q/(2N_Ec2Θ), where the modified geometric slenderness ${\lambda }_s=8$, the power-law index p = 1, the proportional coefficient of homogeneous ceramic layer $\alpha$= 0.2, the geometric slenderness S/h = 100 and the material distributions of FGM arches are subjected to Type A. Also plotted in Figure 10 are the bifurcation buckling points given by Eq. 53. In Figure 10, the upper bifurcation buckling point is on the primary equilibrium path and bifurcation buckling equilibrium path, when this point is reached, the load decreases with an increase of the central displacement, and the dimensionless axial force parameter axial force N/N_Ec2 still unchanged during this moment. When lower bifurcation buckling point is reached, the equilibrium path of the FGM arch returns from the bifurcation buckling equilibrium path back to the primary equilibrium path.

FIGURE 10

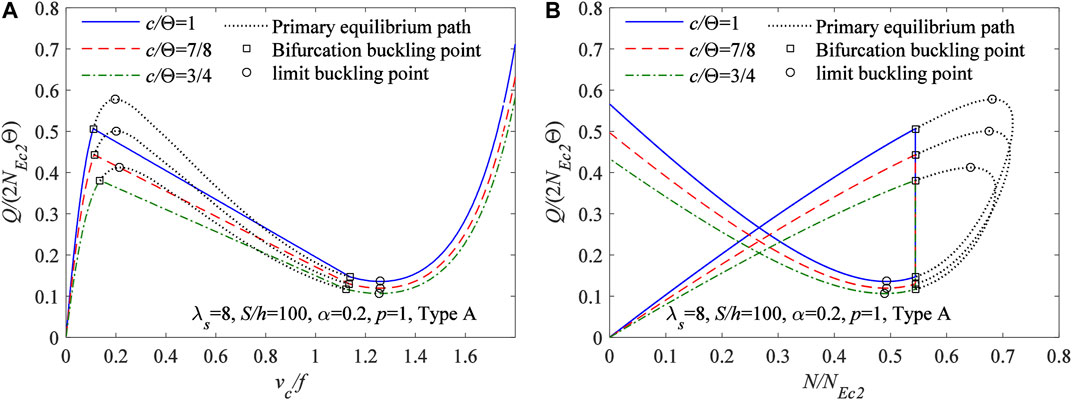
FIGURE 10. Bifurcation equilibrium path for FGM arches having different localized parameter (A)v_c/f vs Q/(2N_Ec2Θ) (B)N/N_Ec2vs Q/(2N_Ec2Θ).

It can also be seen from Figure 10 that the localized parameter η has a significant effect on the bifurcation buckling equilibrium path and the bifurcation buckling load, the bifurcation buckling load increases with an increase of localized parameter η, which indicates that FGM arches having a larger length of the locally uniformly distributed radial loading segment are more prone to bifurcation buckling.

In addition, the bifurcation buckling equilibrium path obtained from Eqs 33, 53 for FGM arches having different type of material distributions are plotted in Figure 11A with the variation curves of v_c/f vs Q/(2N_Ec2Θ), and in Figure 11B with the variation curves of N/N_Ec2vs Q/(2N_Ec2Θ), where ${\lambda }_s=8$, η = 0.5, $\alpha$= 0.2, S/h = 100, p = 1. It can be seen from Figure 11 that the type of material distributions has a significant effect on the bifurcation buckling equilibrium path and the limit point buckling load, Type C has a largest bifurcation buckling load among Type A, Type B and Type C, which indicates again that under the same proportion of metal and ceramic materials, the distribution of ceramics on the upper and lower surfaces of the cross-section can greatly improve the stability of the FGM arch.

FIGURE 11

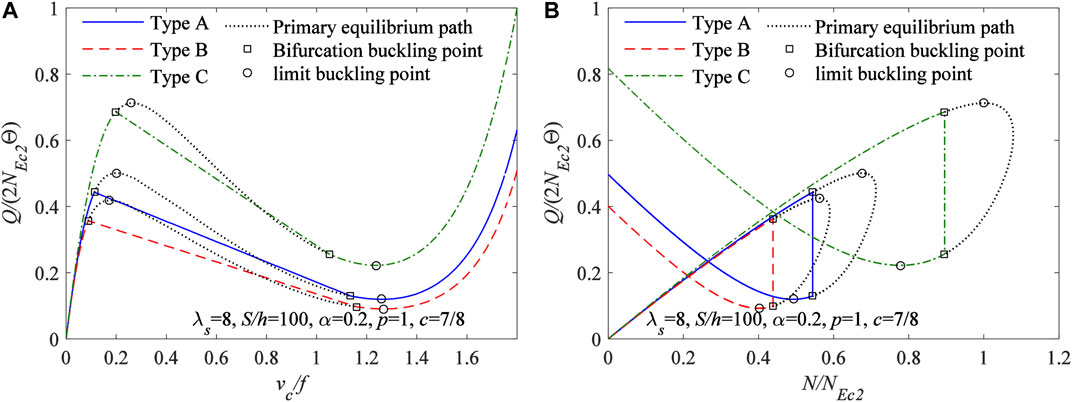
FIGURE 11. Bifurcation equilibrium path for FGM arches having different type of material distributions (A)v_c/f vs Q/(2N_Ec2Θ) (B)N/N_Ec2vs Q/(2N_Ec2Θ).

Furthermore, the influences of the localized parameter η of locally uniformly distributed radial load, the type of material distributions and the modified geometric slenderness ${\lambda }_s$ of the FGM arch on the limit point buckling load and bifurcation buckling load of the FGM arch are studied in detail as well. The variation curves of ${\lambda }_s$vs Q/(2N_Ec2Φ) are plotted in Figure 12A for a Type A FGM arch having different localized parameter η, in Figure 12B for a Type B FGM arch having different localized parameter η and in Figure 12C for a Type C FGM arch having different localized parameter η. It can be seen from Figure 12 that the limit point buckling load and bifurcation buckling load increase with an increase of the modified geometric slenderness ${\lambda }_s$ and the localized parameter η. It can also be seen from Figure 12 that Type C has a largest limit point buckling load and bifurcation buckling load among Type A, Type B and Type C. In addition, Figure 12 shows that the limit point buckling loads are initially larger than the bifurcation buckling loads, and then smaller than the bifurcation buckling loads while the modified geometric slenderness ${\lambda }_s$ reaches a certain value. However, when η = 0.25, the limit point buckling loads are larger than the bifurcation buckling loads with any modified geometric slenderness ${\lambda }_s$. Therefore, the modified geometric slenderness ${\lambda }_s$ that is a switches of bifurcation buckling domination and limit point buckling domination may not exist within a certain range of the localized parameter η.

FIGURE 12

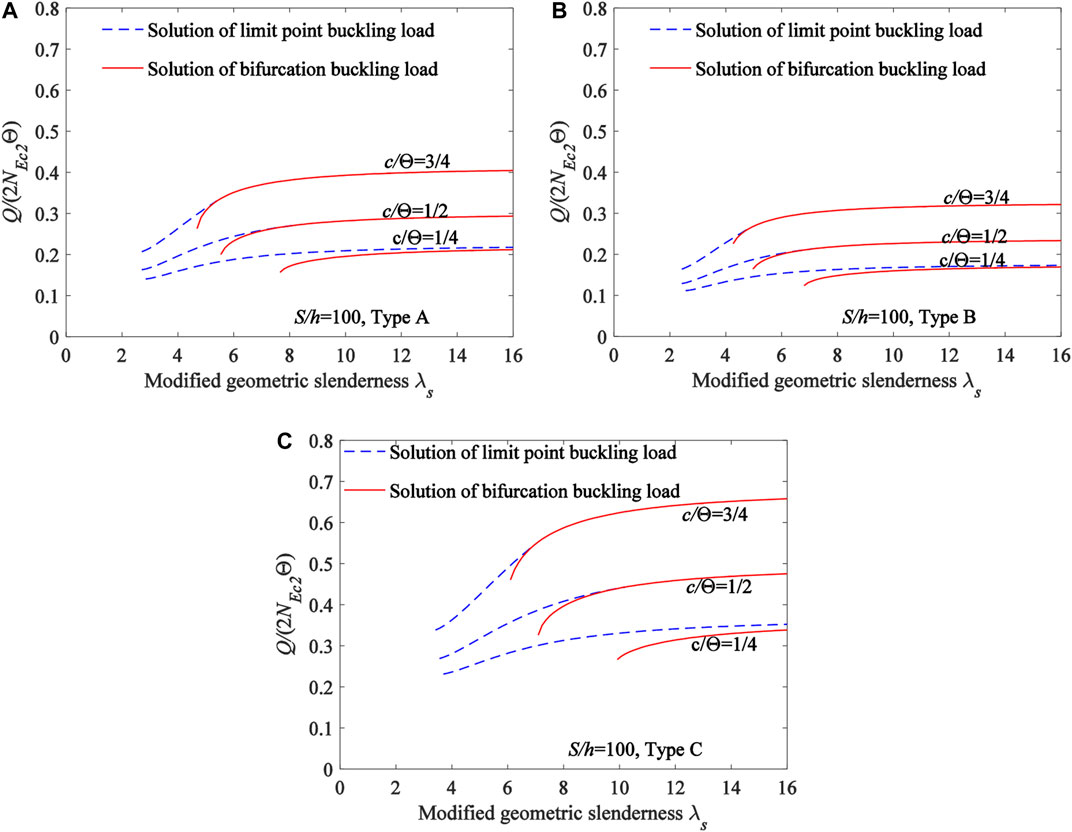
FIGURE 12. Limit point buckling load and bifurcation buckling load of the FGM arch (A) Type A (B) Type B (C) Type C.

Criteria for Switches of Buckling Mode of Functionally Graded Material Arch

It can be seen from the above research that fixed FGM arches under a locally uniformly distributed radial load may buckle in a limit point buckling mode or in a bifurcation buckling mode. The buckling equilibrium path for FGM arches having different modified geometric slenderness are plotted in Figure 13 with the variation curves of v_c/f vs Q/(2N_Ec2Θ), where η = 0.75, $\alpha$= 0.2, S/h = 100, p = 1 and the material distributions of FGM arches are subjected to Type A. Figure 13A shows that when ${\lambda }_s=2.586$, the buckling equilibrium path is in the lowest limit point buckling mode, which only has a inflection point, this mode is a switches of limit point buckling and no limit point buckling. Figure 13B shows when ${\lambda }_s=4$, the buckling equilibrium path is in the limit point buckling mode, which has two limit point. Figure 13C shows when ${\lambda }_s=4.67$, the buckling equilibrium path is in the lowest bifurcation buckling mode, which only has a bifurcation buckling point, this mode is a switches of bifurcation buckling and limit point buckling. Figure 13D shows when ${\lambda }_s=5$, the buckling equilibrium path is in the bifurcation buckling mode, which has two bifurcation buckling point. Figure 13E shows when ${\lambda }_s=5.45$, the buckling equilibrium path is in the lowest bifurcation buckling dominant mode, which has the same upper limit point and upper bifurcation buckling point, this mode is a switches of bifurcation buckling domination and limit point buckling domination. Figure 13F shows when ${\lambda }_s=8$, the buckling equilibrium path is in the bifurcation buckling dominant mode. Therefore, the modified geometric slenderness ${\lambda }_s$ of a fixed FGM arch play an important role in determining its buckling mode.

FIGURE 13

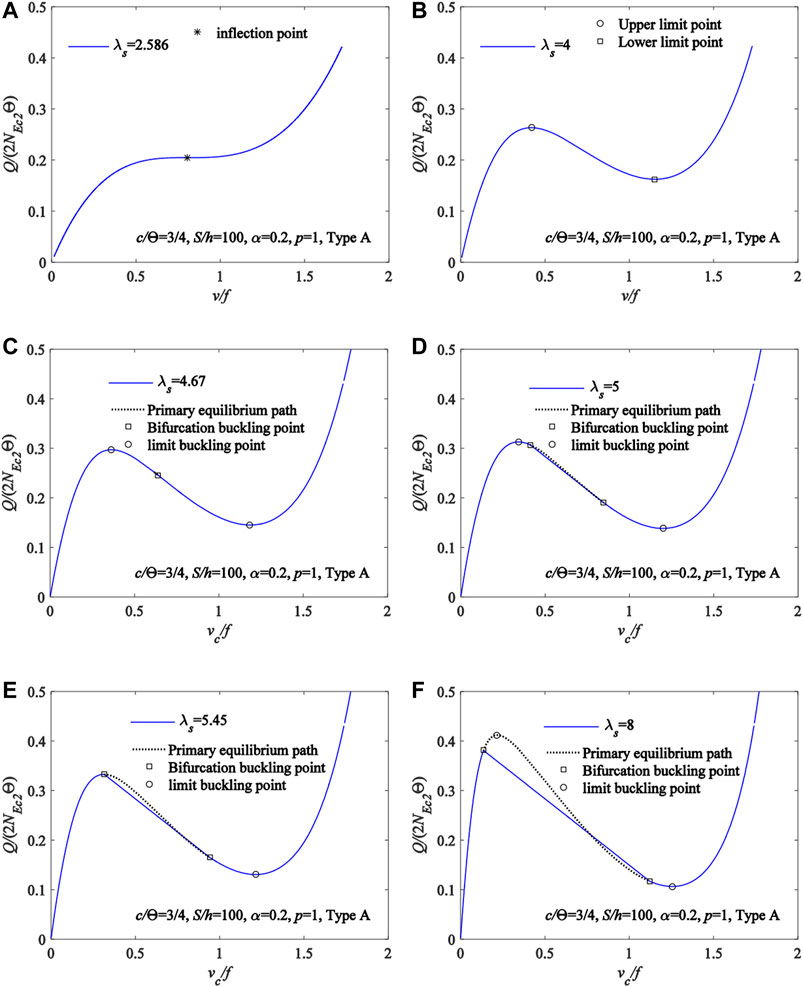
FIGURE 13. Buckling equilibrium path for FGM arches having different modified geometric slenderness (A)${\lambda }_s=2.586$(B)${\lambda }_s=4$(C)${\lambda }_s=4.67$(D)${\lambda }_s=5$(E)${\lambda }_s=5.45$(F)${\lambda }_s=8$.

The modified geometric slenderness λ_s obtained from Eq. 48 can make fixed FGM arches lose its stability in the lowest limit buckling mode. This modified geometric slenderness λ_sl can be expressed as

${\lambda }_s\ge {\lambda }_{sl}=\frac{2\pi }{h}\sqrt{\frac{\kappa \pi }{A_k\left(\frac{B}{{\pi }^2}+\frac{5}{3}\right)}}(58)$

The modified geometric slenderness λ_s obtained from Eq. 53 can make fixed FGM arches lose its stability in the lowest bifurcation buckling mode. This modified geometric slenderness λ_sb1 can be expressed as

${\lambda }_s\ge {\lambda }_{sb1}=\frac{1}{h}\sqrt{\frac{\kappa {\beta }_{b1}^2}{A_k\left(\frac{B_3^2}{4A_3}-\frac{1}{12{\sin }^2{\beta }_{b1}}+\frac{1}{12{\beta }_{b1}^2}\right)}},(59)$

When the fixed FGM arches lose its stability in the lowest bifurcation buckling dominant mode, the modified geometric slenderness λ_sb2 corresponding to this mode can be obtained by equaling the upper bifurcation instability load to the upper limit point buckling load.

Typical variation curves of the localized parameter η vs the modified geometric slenderness λ_s are shown in Figure 14A for FGM arches having different type of material distributions, in Figure 14B for FGM arches having different power-law index p of material distributions and in Figure 14C for FGM arches having different proportional coefficient of homogeneous ceramic layer $\alpha$, where S/h = 100. It can be seen from Figure 14 that the localized parameter η has a significant effect on the modified geometric slenderness λ_sb1, λ_sb2, and a slightly effect on the modified geometric slenderness λ_sl, the modified geometric slenderness λ_sl, λ_sb1, and λ_sb2 increase with a decrease of the localized parameter η of the locally uniformly distributed radial load. Figure 14 defines four regions, region I corresponding to FGM arches with λ_s < λ_sl is subjected to the no buckling mode, region II corresponding to FGM arches with λ_sl < λ_s < λ_sb1 is subjected to the limit point buckling mode, region III corresponding to FGM arches with λ_sb1 < λ_s < λ_sb2 is subjected to the bifurcation buckling mode, region IV corresponding to FGM arches with λ_s > λ_sb2 is subjected to the bifurcation buckling dominant mode. In addition, it can be seen from Figure 14A that the type of material distributions has a significant effect on the modified geometric slenderness λ_sl, λ_sb1 and λ_sb2, Type C has largest modified geometric slenderness λ_sl, λ_sb1 and λ_sb2 among Type A, Type B and Type C, Figures 14B,C shows the modified geometric slenderness λ_sl, λ_sb1 and λ_sb2 increase with an decrease of the power-law index p of material distributions and the proportional coefficient of homogeneous ceramic layer $\alpha$.

FIGURE 14

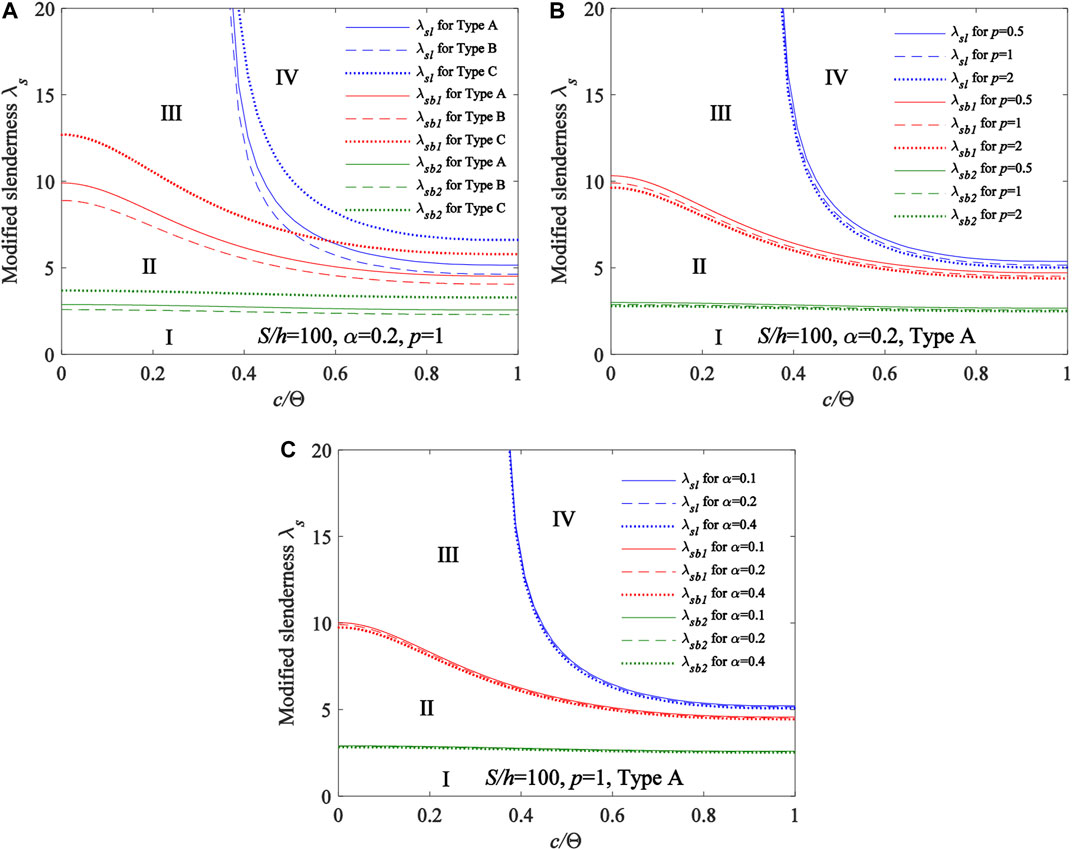
FIGURE 14. Localized parameter η vs Modified geometric slenderness λ_sl, λ_sb1, and λ_sb2(A) different type of material distributions (B) different power-law index p of material distributions (C) different proportional coefficient of homogeneous ceramic layer.

Conclusion

Theoretical studies of the nonlinear in-plane buckling of a fixed circular functionally graded material (FGM) arches under a locally uniformly distributed radial load have been explored in this paper. It was found that fixed FGM arches under a locally uniformly distributed radial load may buckle in a limit point buckling mode or in a bifurcation buckling mode. Theoretical solutions for the limit point buckling load and bifurcation buckling loads and nonlinear equilibrium path of the fixed FGM arches that are subjected to three different types of material distributions were obtained. It was found that the type of material distributions of the fixed FGM arches slight the limit point buckling loads and bifurcation buckling loads as well as the nonlinear equilibrium path significantly. Type C had a largest limit point buckling load and a largest bifurcation buckling load among Type A, Type B and Type C, it indicated that under the same proportion of metal and ceramic materials, the distribution of ceramics on the upper and lower surfaces of the cross-section can greatly improve the stability of the FGM arch. In addition, the limit point buckling load and bifurcation buckling load also increase with an increase of the modified geometric slenderness ${\lambda }_s$ and the localized parameter η and the proportional coefficient of homogeneous ceramic layer $\alpha$ as well as a decrease of the power-law index p of material distributions of the FGM arch.

The critical modified geometric slendernesses λ_sl, λ_sb1, and λ_sb2 that are switches of buckling modes were also derived. The localized parameter η has a significant effect on the modified geometric slenderness λ_sb1, λ_sb2, and limited effect on the modified geometric slenderness λ_sl, the modified geometric slenderness λ_sl, λ_sb1, and λ_sb2 increase with a decrease of the localized parameter η of the locally uniformly distributed radial load. It was found that Region I corresponding to FGM arches with λ_s < λ_sl is subjected to the no buckling mode, region II corresponding to FGM arches with λ_sl < λ_s < λ_sb1 is subjected to the limit point buckling mode, region III corresponding to FGM arches with λ_sb1 < λ_s < λ_sb2 is subjected to the bifurcation buckling mode, region IV corresponding to FGM arches with λ_s > λ_sb2 is subjected to the bifurcation buckling dominant mode. In addition, it was also found that the type of material distributions has a significant effect on the modified geometric slenderness λ_sl, λ_sb1 and λ_sb2, Type C has the largest modified geometric slenderness λ_sl, λ_sb1 and λ_sb2 among Type A, Type B and Type C, and the modified geometric slenderness λ_sl, λ_sb1 and λ_sb2 increase with an decrease of the power-law index p of material distributions and the proportional coefficient of homogeneous ceramic layer $\alpha$. Theoretical solutions for FGM arches under a locally uniformly distributed radial load derived in this paper would be useful as a reference for the design of buckling of the FGM arches in the future.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

HL: Data curation, Formal analysis, Investigation, Methodology, Software, Visualization, Writing-review and editing. JZ: Formal analysis, Validation, Writing-review and editing. ZY: Formal analysis, Investigation, Methodology, Writing-original draft. AL: Data curation, funding acquisition. JZ: Project administration.

Funding

This work was funded by (Characteristic innovation projects of colleges and universities in Guangdong Province) with grant number (2019KTSCX190) and (National Natural Science Foundation of China) with grant number (51908146).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-shujairi, M., and Mollamahmutoğlu, C. (2018). Buckling and Free Vibration Analysis of Functionally Graded sandwich Microbeams Resting on Elastic Foundation by Using Non Local Strain Gradient Theory in Conjunction with Higher Order Shear Theories under thermal Effect. Compos. Part. B 154, 292–312. doi:10.1016/j.compositesb.2018.08.103

CrossRef Full Text | Google Scholar

Asgari, H., Bateni, M., Kiani, Y., and Eslami, M. R. (2014). Non-linear Thermo-Elastic and Buckling Analysis of FGM Shallow Arches. Compos. Struct. 109, 75–85. doi:10.1016/j.compstruct.2013.10.045

CrossRef Full Text | Google Scholar

Bateni, M., and Eslami, M. R. (2015). Non-linear In-Plane Stability Analysis of FG Circular Shallow Arches under Uniform Radial Pressure. Thin-Walled Structures 94, 302–313. doi:10.1016/j.tws.2015.04.019

CrossRef Full Text | Google Scholar

Bateni, M., and Eslami, M. R. (2014). Non-linear In-Plane Stability Analysis of FGM Circular Shallow Arches under central Concentrated Force. Int. J. Non-Linear Mech. 60, 58–69. doi:10.1016/j.ijnonlinmec.2014.01.001

CrossRef Full Text | Google Scholar

Bradford, M. A., Uy, B., and Pi, Y.-L. (2002). In-plane Elastic Stability of Arches under a central Concentrated Load. J. Eng. Mech. 128, 710–719. doi:10.1061/(asce)0733-9399(2002)128:7(710)

CrossRef Full Text | Google Scholar

Cai, J., and Feng, J. (2010). Buckling of Parabolic Shallow Arches when Support Stiffens under Compression. Mech. Res. Commun. 37, 467–471. doi:10.1016/j.mechrescom.2010.05.004

CrossRef Full Text | Google Scholar

Cai, J., Xu, Y., Feng, J., and Zhang, J. (2012). In-plane Elastic Buckling of Shallow Parabolic Arches under an External Load and Temperature Changes. J. Struct. Eng. 138, 1300–1309. doi:10.1061/(asce)st.1943-541x.0000570

CrossRef Full Text | Google Scholar

Cai, J., Zhou, Y., and Feng, J. (2013). Post-buckling Behavior of a Fixed Arch for Variable Geometry Structures. Mech. Res. Commun. 52, 74–80. doi:10.1016/j.mechrescom.2013.07.002

CrossRef Full Text | Google Scholar

Chen, M.-T., and Young, B. (2021). Beam-column Design of Cold-Formed Steel Semi-oval Hollow Non-slender Sections. Thin-walled Structures 162, 107376. doi:10.1016/j.tws.2020.107376

CrossRef Full Text | Google Scholar

Chen, M.-T., Young, B., Martins, A. D., Camotim, D., and Dinis, P. B. (2021). Experimental Investigation on Cold-Formed Steel Lipped Channel Beams Affected by Local-Distortional Interaction under Non-uniform Bending. Thin-walled Structures 161, 107494. doi:10.1016/j.tws.2021.107494

CrossRef Full Text | Google Scholar

Han, Q., Cheng, Y., Lu, Y., Li, T., and Lu, P. (2016). Nonlinear Buckling Analysis of Shallow Arches with Elastic Horizontal Supports. Thin-Walled Structures 109, 88–102. doi:10.1016/j.tws.2016.09.016

CrossRef Full Text | Google Scholar

Hu, C.-F., Li, Z., and Hu, Q.-S. (2021). On Non-linear Behavior and Buckling of Arch-Beam Structures. Eng. Structures 239 (2), 112214. doi:10.1016/j.engstruct.2021.112214

CrossRef Full Text | Google Scholar

Lu, H., Liu, A., Pi, Y.-L., Bradford, M. A., Fu, J., and Huang, Y. (2018). Localized Loading and Nonlinear Instability and post-instability of Fixed Arches. Thin-Walled Structures 131, 165–178. doi:10.1016/j.tws.2018.06.019

CrossRef Full Text | Google Scholar

Lu, H. W., Liu, L. L., Liu, A. R., Pi, Y.-L., Bradford, M. A., and Huang, Y. H. (2020). Effects of Movement and Rotation of Supports on Nonlinear Instability of Fixed Shallow Arches. Thin-Walled Structures 122, 2020. doi:10.1016/j.tws.2020.106909

CrossRef Full Text | Google Scholar

Moita, J. S., Araújo, A. L., Correia, V. F., Mota Soares, C. M., and Herskovits, J. (2018). Material Distribution and Sizing Optimization of Functionally Graded Plate-Shell Structures. Composites B: Eng. 142, 263–272. doi:10.1016/j.compositesb.2018.01.023

CrossRef Full Text | Google Scholar

Pi, Y.-L., Bradford, M. A., and Liu, A. (2017). Nonlinear Equilibrium and Buckling of Fixed Shallow Arches Subjected to an Arbitrary Radial Concentrated Load. Int. J. Str. Stab. Dyn. 17 (8), 1750082. doi:10.1142/s0219455417500821

CrossRef Full Text | Google Scholar

Pi, Y.-L., and Bradford, M. A. (2009). Non-linear In-Plane Postbuckling of Arches with Rotational End Restraints under Uniform Radial Loading. Int. J. Non-Linear Mech. 44 (9), 975–989. doi:10.1016/j.ijnonlinmec.2009.07.003

CrossRef Full Text | Google Scholar

Pi, Y.-L., Bradford, M. A., and Tin-Loi, F. (2008). Non-linear In-Plane Buckling of Rotationally Restrained Shallow Arches under a central Concentrated Load. Int. J. Non-Linear Mech. 43 (1), 1–17. doi:10.1016/j.ijnonlinmec.2007.03.013

CrossRef Full Text | Google Scholar

Pi, Y.-L., Bradford, M. A., and Uy, B. (2002). In-plane Stability of Arches. Int. J. Sol. Structures 39 (1), 105–125. doi:10.1016/s0020-7683(01)00209-8

CrossRef Full Text | Google Scholar

Plaut, R. H., and Raymond, H. (1990). Buckling of Shallow Arches with Supports that Stiffen when Compressed. J. Eng. Mech. 116 (4), 973–976. doi:10.1061/(asce)0733-9399(1990)116:4(973)

CrossRef Full Text | Google Scholar

Rastgo, A., Shafie, H., and Allahverdizadeh, A. (2005). Instability of Curved Beams Made of Functionally Graded Material under Thermal Loading. Int. J. Mech. Mater. Des. 2, 117–128. doi:10.1007/s10999-005-4446-3

CrossRef Full Text | Google Scholar

Schreyer, H. L. (1972). The Effect of Initial Imperfections on the Buckling Load of Shallow Circular Arches. J. Appl. Mech. 39 (2), 445–450. doi:10.1115/1.3422698

CrossRef Full Text | Google Scholar

Simsek, M. (2016). Buckling of Timoshenko Beams Composed of Two-Dimensional Functionally Graded Material (2D-FGM) Having Different Boundary Conditions. Compos. Struct. 49, 304–314. doi:10.1016/j.compstruct.2016.04.034

Google Scholar

Song, X., and Li, S. R. (2008). Nonlinear Stability of Fixed-Fixed Fgm Arches Subjected to Mechanical and thermal Loads. Amr 33-37, 699–706. doi:10.4028/www.scientific.net/amr.33-37.699

CrossRef Full Text | Google Scholar

Timoshenko, S. P., Gere, J. M., Prager, W., Gere, J. M., and Prager, W. (1962). Theory of Elastic Stability, Second Edition. J. Appl. Mech. 29 (1), 220–221. doi:10.1115/1.3636481

CrossRef Full Text | Google Scholar

Yan, S.-t., Shen, X., Chen, Z., and Jin, Z. (2017). On Buckling of Non-uniform Shallow Arch under a central Concentrated Load. Int. J. Mech. Sci. 133, 330–343. doi:10.1016/j.ijmecsci.2017.08.046

CrossRef Full Text | Google Scholar

Yang, Z., Feng, C., Yang, J., Wang, Y., Lv, J., Liu, A., et al. (2020a). Geometrically Nonlinear Buckling of Graphene Platelets Reinforced Dielectric Composite (GPLRDC) Arches with Rotational End Restraints. Aerospace Sci. Tech. 107, 106326. doi:10.1016/j.ast.2020.106326

CrossRef Full Text | Google Scholar

Yang, Z., Zhao, S., Yang, J., Lv, J., Liu, A., and Fu, J. (2020b). In-plane and Out-Of-Plane Free Vibrations of Functionally Graded Composite Arches with Graphene Reinforcements. Mech. Adv. Mater. Structures, 1–11. doi:10.1080/15376494.2020.1716420

CrossRef Full Text | Google Scholar

Yang, Z., Tam, M., Zhang, Y., Kitipornchai, S., Lv, J., and Yang, J. (2020c). Nonlinear Dynamic Response of FG Graphene Platelets Reinforced Composite Beam with Edge Cracks in thermal Environment. Int. J. Str. Stab. Dyn. 20, 2043005. doi:10.1142/s0219455420430051

CrossRef Full Text | Google Scholar

Yang, Z., Liu, A., Yang, J., Lai, S.-K., Lv, J., and Fu, J. (2021a). Analytical Prediction for Nonlinear Buckling of Elastically Supported FG-GPLRC Arches under a central point Load. Materials 14 (8), 2026. doi:10.3390/ma14082026

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Z., Wu, D., Yang, J., Lai, S.-K., Lv, J., Liu, A., et al. (2021b). Dynamic Buckling of Rotationally Restrained FG Porous Arches Reinforced with Graphene Nanoplatelets under a Uniform Step Load. Thin-Walled Structures 166, 108103. doi:10.1016/j.tws.2021.108103

CrossRef Full Text | Google Scholar