- 1School of Mechanical Engineering, Chengdu University, Chengdu, China
- 2Institute of Materials Science, Technical University of Darmstadt, Darmstadt, Germany
- 3School of Energy and Power Engineering, Dalian University of Technology, Dalian, China
Electronic fitness function (EFF, achieved by the electrical transport properties) as a new quantity to estimate thermoelectric (TE) performance of semiconductor crystals is usually used for screening novel TE materials. In recent years, because of the high EFF values, an increasing number of two-dimensional materials have been predicted to have the potential for TE applications via high-throughput calculations. Among them, the GeS2 monolayer has many interesting physical properties and is being used for industrial applications. Hence, in this work, we systematically investigated the TE performance, including both electronic and thermal transport properties, of the GeS2 monolayer with first-principles calculations. The results show that the structure of the GeS2 monolayer at 700 K is thermally unstable, so we study its TE performance only at 300 and 500 K. As compared with other typical TE monolayers, the GeS2 monolayer exhibits excellent electronic transport properties but a relatively high lattice thermal conductivity of 5.71 W m−1 K−1 at 500 K, and thus an unsatisfactory ZT value of 0.23. Such a low ZT value indicates that it is necessary to consider not only the electron transport properties but also the thermal transport properties to screen the thermoelectric materials with excellent performance through high-throughput calculations.
Introduction
In the past decades, the development of environment-friendly renewable energy has been the main task since it has alleviated the current global energy crisis and the greenhouse effect to some extent (Biswas et al., 2012; Wang and Wu, 2012; Tan et al., 2016). Thermoelectric (TE) materials, which are capable of converting waste heat into electricity directly and reversibly without air pollution, have attracted intense attention (Bell 2008; Wang et al., 2016; Wang et al., 2017). The conversion efficiency is characterized by a dimensionless figure of merit,
High-throughput computations are usually used to screen high-performance functional materials according to their EFF (electronic fitness function) values, which is a new quantity to estimate TE performance of materials, such as SnSe2 (Jia et al., 2020) and SnO (Miller et al., 2017). As a chalcogenide material, GeS2 has interesting physical properties and is being used for industrial applications, such as photodetection (Yang et al., 2019), photoresistor, or antireflection coating (Málek and Shánělová, 1999). Especially, glassy germanium disulfide has been heavily studied for many years (Lucovsky et al., 1974; Tichý et al., 1982; Weinstein et al., 1982) and was still the subject of recent experimental investigations (Petri and Salmon, 2001). Besides, the 1T-CdI2–type GeS2 monolayer was recently reported to have potential as a promising TE material due to its highest peak EFF value (0.3 × 10−19 W5/3 ms−1/3 K−2) for p-type carriers (Sarikurt et al., 2020). However, the high EFF value only reflects its strong electron transport performance, but the thermal transport property of the GeS2 monolayer is not yet clear. Most importantly, there has not been a focus on the TE performance of GeS2 monolayers that integrate electrical transport and thermal transport. Consequently, the further exploration of the electronic and thermal transport properties of the GeS2 monolayer is quite reasonable and desirable.
In this work, the TE properties of two-dimensional (2D) isotropic GeS2 are comprehensively studied based on first-principles calculations combined with the Boltzmann transport theory. The results show that this monolayer exhibits great electronic properties, for example, high PF value (3.4 mW m−1 K−2) at 300 K, which is consistent with the high EFF values obtained with high-throughput computations. However, due to the unsatisfactory thermal transport properties, the ZT value of 2D GeS2 can only reach 0.23 at 500 K. This study suggests that the GeS2 monolayer has poor TE performance, thus proving that the method of predicting high-efficiency TE materials according to the EFF values obtained via high-throughput computations may be incomplete.
Computational Details
In this study, our first-principles calculations are performed by using density functional theory (DFT), as implemented in the Vienna Ab initio Simulation Package (VASP) (Kresse and Hafner, 1993; Kresse and Furthmüller, 1996a; Kresse and Furthmüller, 1996b). The generalized gradient approximation (GGA) (Perdew et al., 1996; Zhang et al., 2018) with Perdew–Burke–Ernzerhof (PBE) parametrization (Qiao et al., 2018) is applied as the exchange–correlation potential. For obtaining the accurate electronic structure, the Heyd–Scuseria–Ernzerhof hybrid functional (HSE06) (Heyd et al., 2003) is adopted to describe the exchange–correlation energy. The cutoff energy of 550 eV is set for the plane-wave basis, and the Brillouin zones are sampled with 15 × 15 × 1 Monkhorst–Pack special k-point meshes for 2D GeS2. The convergence criteria for energy and force are 1 × 10−5 eV and 1 × 10−4 eV/Å, respectively, which is accurate enough and used in many studies (Sun et al., 2003). To avoid the effect of layer–layer interactions, a sufficiently large vacuum layer of 20 Å is constructed perpendicular to the layer plane in all the calculated structures.
In order to obtain
where
The electronic transport properties are obtained by employing the Boltzmann transport equation combined with the relaxation time approximation (RTA) via the BoltzTraP2 code with a denser 31 × 31 × 1 k-point sampling (Madsen et al., 2018). Although RTA tends to overestimate power factors, because of computational convenience, we still adopt this approximation. It was also used in a study on the electronic transport properties of two-dimensional triphosphides (InP3, GaP3, SbP3, and SnP3) (Sun et al., 2020). The relaxation time τ is calculated using deformation potential (DP) theory combined with the effective mass approximation (Bardeen and Shockley, 1950) as shown below:
where ħ,
Results and Discussion
Geometrical Characteristics and Electronic Structures
The optimized structure of 2D GeS2 possesses a trigonal structure, with the P
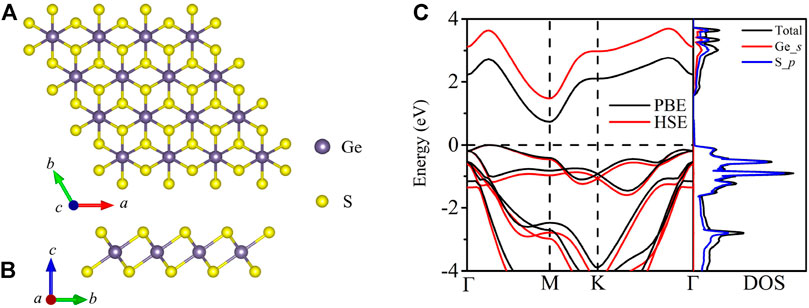
FIGURE 1. Crystal structure of top views (A) and side view (B) for monolayer GeS2. Electronic band structure and DOS (states/eV/u.c.) (C) for monolayer GeS2.
Stability and Phonon Dispersion
To confirm the thermal stability of monolayer GeS2, ab initio molecular dynamics (AIMD) simulations are performed between 300 and 700 K with a time period up to 4 ps. The results as given in Figure 2 show that the average values of the total energy remain nearly constant after 1 ps at 300 and 500 K. However, the curve at 700 K still declines after 1 ps. Besides, the structures are well maintained and all the atoms in monolayer GeS2 are vibrating around their equilibrium positions at 300 and 500 K, but the atom distribution is disordered at 700 K, which suggests that the structure is unstable at 700 K. Consequently, we choose 300 and 500 K as the typical temperatures to study the TE properties of the GeS2 monolayer.
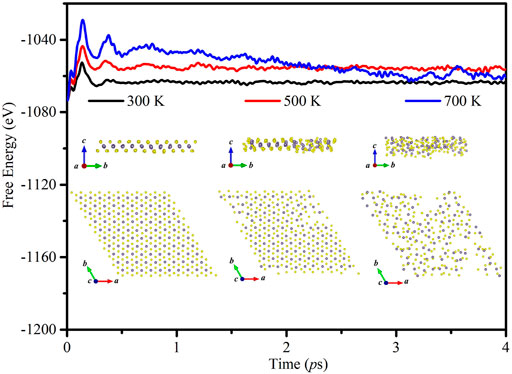
FIGURE 2. Free energy fluctuations with respect to time in AIMD simulations and equilibrium structures for the GeS2 monolayer obtained via AIMD simulations at 300, 500, and 700 K.
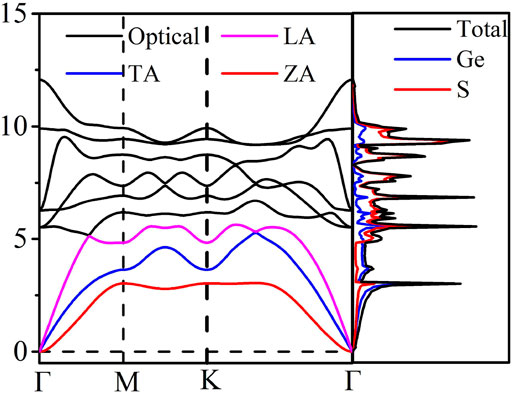
Next, we focus on the thermal properties of the GeS2 monolayer and figure out the phonon spectrum and phonon DOS as given in Figure 3 to confirm its dynamic stability. There are nine phonon branches found in the phonon dispersion since there are three atoms in the unit cell. Among them, the three lowest vibration frequency branches are the out-of-plane flexural acoustic branch (ZA), the in-plane linear transverse acoustic branch (TA), and the longitudinal acoustic branch (LA), respectively. From Figure 3, one can see that no imaginary phonon branches are observed in the phonon dispersion, suggesting that the GeS2 monolayer is dynamically stable. It is noted that there is no overlapped part among acoustic and optical branches, which suggests that the coupling effect of acoustic–acoustic modes and acoustic–optical modes is extremely weak. This phenomenon may lead to high lattice thermal conductivity. Also, the phonon DOS distribution shows that the acoustic branches are dominated by the heaviest Ge atoms, and the relatively light S atoms mostly contribute to the optical branches.
Thermal Transport Properties
Next, the thermal transport properties of the GeS2 monolayer are obtained based on the second- and third-order IFCs. The lattice thermal conductivities in the temperature range of 200–700 K are shown in Figure 4A. It shows that the calculated intrinsic
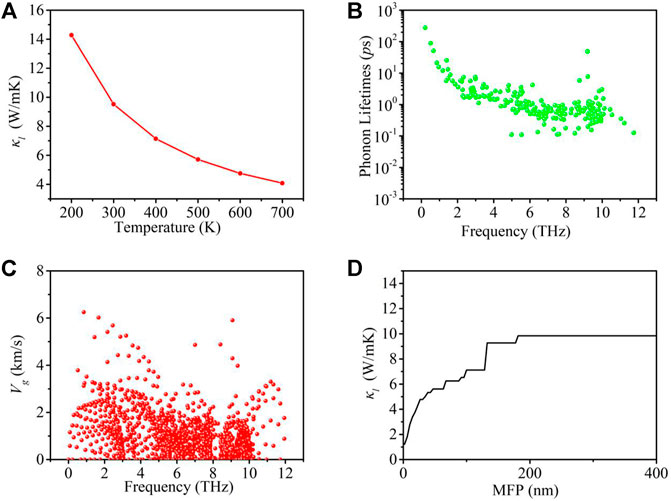
FIGURE 4. (A)
To further understand the thermal transport behavior of the GeS2 monolayer,
where CV,
Electronic Transport Properties
The Seebeck coefficient of the GeS2 monolayer is given in Figure 5A. It is noted that with the carrier concentration increasing from 1011 to 1014 cm−2, the absolute value of the Seebeck coefficient |S| of n- and p-type GeS2 decreases at the temperatures of 300 and 500 K, which can be explained by the following equation (Guo, Hu et al., 2013):
where kB, e, h, m*, and n are the Boltzmann constant, electron charge, Planck constant, effective mass, and carrier concentration, respectively. In addition, it can be seen that the absolute value of the Seebeck coefficient |S| of n- and p-type GeS2 increases as the temperature increases from 300 to 500 K with the carrier concentration at the range of 1011–1014 cm−2. Besides, the |S| for p-type GeS2 is larger than that for n-type GeS2 at a given carrier concentration under 300 and 500 K due to the larger effective mass. For example, the Seebeck coefficient of 696 μV K−1 for the p-type system is larger than that of 620 μV K−1 for the n-type system along the x-axis at 500 K with a carrier concentration of 1 × 1011 cm−2. The |S| is comparable with that of another FeOCl-type monolayer, Al2I2Se2, which was reported as a promising TE material (Qi et al., 2021). In addition, the comparison of calculated thermoelectric parameters at 300 K between GeS2 and Al2I2Se2 monolayers has been made in Table 1.
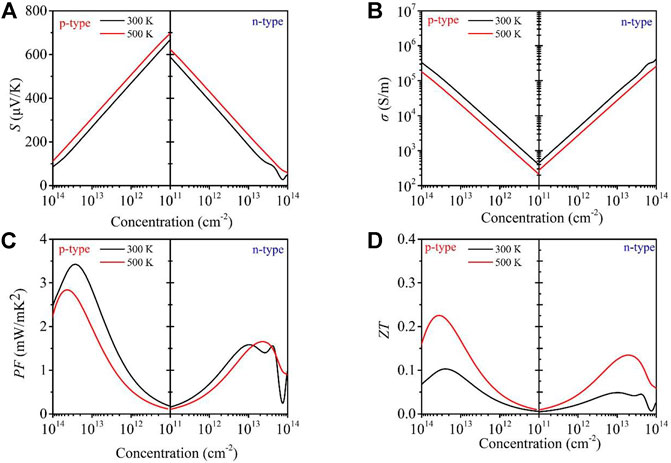
FIGURE 5. Calculated Seebeck coefficient S (A), electrical conductivity σ (B), power factor PF(C), and (D)ZT values as a function of carrier concentration at different temperatures (300 and 500 K, respectively) for monolayer GeS2.

TABLE 1. Comparison of calculated thermoelectric parameters (
The relaxation time, mobility, and effective mass are shown in Table 2. Based on the calculated relaxation time, the σ as σ/τ within the constant RTA is obtained, as shown in Figure 5B. It can be seen that the σ of both n- and p-type systems increases with the increase in carrier concentration at a given temperature, which can be explained with the following formula (Snyder et al., 2020):
where n is the carrier concentration and μ is the mobility of the charge carrier. In addition, σ decreases with the increasing temperature because of more frequent scattering of electrons and lower relaxation time at a higher temperature. As can be clearly noticed, the σ of the n-type system is larger than that of the p-type system due to the larger effective mass for n-type GeS2 at a given temperature and carrier concentration. For example, the value of σ for n-type GeS2 is 287 S/m, which is larger than that for p-type GeS2 (210 S/m) at 500 K with a carrier concentration of 1 × 1011 cm−2.
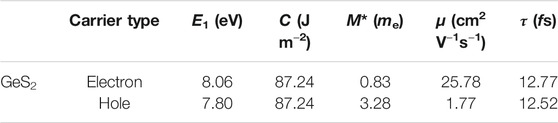
TABLE 2. DP constant E1, elastic constant C, effective mass m*, carrier mobility μ, and relaxation time τ of the GeS2 monolayer at room temperature. me represents the rest mass of the electron.
The power factor PF = (S2σ) of the GeS2 monolayer is calculated combined with the Seebeck coefficient and electrical conductivity, as shown in Figure 5C. Due to the opposite changes of
Dimensionless Figure of Merit (ZT)
Combining the thermoelectric transport parameters obtained above, the ZT values of n- and p-type GeS2 monolayers are estimated, as plotted in Figure 5D. It can be found that the maximum ZT values for the p-type system are larger than those for the n-type system at 300 and 500 K due to the higher PF values of p-type GeS2. At the temperature of 500 K, an optimal ZT value of 0.23 for the p-type system can be reached, which is almost twice the value of 0.13 for the n-type system. The maximum ZT value is smaller than those of most TE materials, like SnSe (2.6 at 923 K) (Zhao et al., 2014) and GeAs2 (2.78 at 800 K) (Wang et al., 2017), suggesting that the TE performance of the GeS2 monolayer is not as good as the prediction with high-throughput computations indicated, which is attributed to its high lattice thermal conductivity. Therefore, only considering the EFF values without thermal transport properties for predicting the TE performance of materials is incomplete.
Conclusion
Motivated by the prediction with high-throughput computations, we systematically study the TE performance of the GeS2 monolayer via first-principles calculations combined with Boltzmann transport theory. Our results show that the electronic transport properties exhibit great performance, consistent with the prediction of high EFF. Specifically, the largest PF value of the GeS2 monolayer reaches 3.4 mW m−1 K−2 at 300 K because of its high electrical conductivity. However, we also find that its lattice thermal conductivity is as high as 9.52 Wm−1 K−1 at 300 K, resulting in an unsatisfactory ZT value (0.1) for the p-type system. Additionally, the highest ZT value is only 0.23 at 500 K. This work suggests that the GeS2 monolayer is not suitable for TE applications; thus, the prediction of EFF values by high-throughput computations is incomplete.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
XW conceived the idea. XW conducted the simulation and analysis. All authors participated in the writing and correction of the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful for the financial support provided by the Education Department of Sichuan Province, China (18ZB0133), the Applied Basic Research Programs of Sichuan Province, China (2018JY0062), and the Research Project of Chengdu University, China (2018XZB17).
References
Bardeen, J., and Shockley, W. (1950). Deformation Potentials and Mobilities in Non-polar Crystals. Phys. Rev. 80, 72–80. doi:10.1103/physrev.80.72
Bell, L. E. (2008). Cooling, Heating, Generating Power, and Recovering Waste Heat with Thermoelectric Systems. Science 321, 1457–1461. doi:10.1126/science.1158899
Biswas, K., He, J., Blum, I. D., Wu, C.-I., Hogan, T. P., Seidman, D. N. D., et al. (2012). High-performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature 489, 414–418. doi:10.1038/nature11439
Carrete, J., Mingo, N., and Curtarolo, S. (2014). Low thermal Conductivity and Triaxial Phononic Anisotropy of SnSe. Appl. Phys. Lett. 105, 101907. doi:10.1063/1.4895770
Chen, W., Pöhls, J.-H., Hautier, G., Broberg, D., Bajaj, S., Aydemir, U., et al. (2016). Understanding Thermoelectric Properties from High-Throughput Calculations: Trends, Insights, and Comparisons with experiment. J. Mater. Chem. C 4, 4414–4426. doi:10.1039/c5tc04339e
Guo, D., Hu, C., Xi, Y., and Zhang, K. (2013). Strain Effects to Optimize Thermoelectric Properties of Doped Bi2O2Se via Tran-Blaha Modified Becke-Johnson Density Functional Theory. J. Phys. Chem. C 117, 21597–21602. doi:10.1021/jp4080465
Guo, R., Wang, X., Kuang, Y., and Huang, B. (2015). First-principles Study of Anisotropic Thermoelectric Transport Properties of IV-VI Semiconductor Compounds SnSe and SnS. Phys. Rev. B 92, 115202. doi:10.1103/physrevb.92.115202
Heremans, J. P., Jovovic, V., Toberer, E. S., Saramat, A., Kurosaki, K., Charoenphakdee, A., et al. (2008). Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States. Science 321, 554–557. doi:10.1126/science.1159725
Heyd, J., Scuseria, G. E., and Ernzerhof, M. (2003). Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 118, 8207–8215. doi:10.1063/1.1564060
Hicks, L. D., and Dresselhaus, M. S. (1993). Effect of Quantum-Well Structures on the Thermoelectric Figure of merit. Phys. Rev. B 47, 12727–12731. doi:10.1103/physrevb.47.12727
Jia, T., Feng, Z., Guo, S., Zhang, X., and Zhang, Y. (2020). Screening Promising Thermoelectric Materials in Binary Chalcogenides through High-Throughput Computations. ACS Appl. Mater. Inter. 12, 11852–11864. doi:10.1021/acsami.9b23297
Jonson, M., and Mahan, G. D. (1980). Mott's Formula for the Thermopower and the Wiedemann-Franz Law. Phys. Rev. B 21, 4223–4229. doi:10.1103/physrevb.21.4223
Kresse, G., and Furthmüller, J. (1996a). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 6, 15–50. doi:10.1016/0927-0256(96)00008-0
Kresse, G., and Furthmüller, J. (1996b). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54, 11169–11186. doi:10.1103/physrevb.54.11169
Kresse, G., and Hafner, J. (1993). Ab Initiomolecular Dynamics for Liquid Metals. Phys. Rev. B 47, 558–561. doi:10.1103/PhysRevB.47.558
Li, W., Carrete, J., A. Katcho, N., and Mingo, N. (2014). ShengBTE: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Li, B., Wang, H., Kawakita, Y., Zhang, Q., Feygenson, M., Yu, H. L., et al. (2018). Liquid-like thermal Conduction in Intercalated Layered Crystalline Solids. Nat. Mater 17, 226–230. doi:10.1038/s41563-017-0004-2
Li, M., Wang, N., Jiang, M., Xiao, H., Zhang, H., Liu, Z., et al. (2019). Improved Thermoelectric Performance of Bilayer Bi2O2Se by the Band Convergence Approach. J. Mater. Chem. C 7, 11029–11039. doi:10.1039/c9tc02188d
Li, R., Li, X., Xi, L., Yang, J., Singh, D. J., and Zhang, W. (2019). High-Throughput Screening for Advanced Thermoelectric Materials: Diamond-Like ABX2 Compounds. ACS Appl. Mater. Inter. 11, 24859–24866. doi:10.1021/acsami.9b01196
Liu, W.-S., Zhao, L.-D., Zhang, B.-P., Zhang, H.-L., and Li, J.-F. (2008). Enhanced Thermoelectric Property Originating from Additional Carrier Pocket in Skutterudite Compounds. Appl. Phys. Lett. 93, 042109. doi:10.1063/1.2965123
Lucovsky, G., Galeener, F. L., Keezer, R. C., Geils, R. H., and Six, H. A. (1974). Structural Interpretation of the Infrared and Raman Spectra of Glasses in the alloy systemGe1−xSx. Phys. Rev. B 10, 5134–5146. doi:10.1103/physrevb.10.5134
Málek, J., and Shánělová, J. (1999). Viscosity of Germanium Sulfide Melts. J. Non-Crystalline Sol. 243, 116–122. doi:10.1016/s0022-3093(98)00823-0
Madsen, G. K. H., Carrete, J., and Verstraete, M. J. (2018). BoltzTraP2, a Program for Interpolating Band Structures and Calculating Semi-classical Transport Coefficients. Comput. Phys. Commun. 231, 140–145. doi:10.1016/j.cpc.2018.05.010
Miller, S. A., Gorai, P., Aydemir, U., Mason, T. O., Stevanović, V., Toberer, E. S., et al. (2017). SnO as a Potential Oxide Thermoelectric Candidate. J. Mater. Chem. C 5, 8854–8861. doi:10.1039/c7tc01623a
Nielsen, M. D., Ozolins, V., and Heremans, J. P. (2013). Lone Pair Electrons Minimize Lattice thermal Conductivity. Energy Environ. Sci. 6, 570–578. doi:10.1039/c2ee23391f
Ortiz, B. R., Adamczyk, J. M., Gordiz, K., Braden, T., and Toberer, E. S. (2019). Towards the High-Throughput Synthesis of Bulk Materials: Thermoelectric PbTe-PbSe-SnTe-SnSe Alloys. Mol. Syst. Des. Eng. 4, 407–420. doi:10.1039/c8me00073e
Ouyang, T., Jiang, E., Tang, C., Li, J., He, C., and Zhong, J. (2018). Thermal and Thermoelectric Properties of Monolayer Indium Triphosphide (InP3): a First-Principles Study. J. Mater. Chem. A. 6, 21532–21541. doi:10.1039/c8ta07012a
Pei, Y., LaLonde, A., Iwanaga, S., and Snyder, G. J. (2011). High Thermoelectric Figure of merit in Heavy Hole Dominated PbTe. Energ. Environ. Sci. 4, 2085. doi:10.1039/c0ee00456a
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/physrevlett.77.3865
Petri, I., and Salmon, P. S. (2001). A Neutron Diffraction Study of Glassy GeS2. J. Non-Crystalline Sol. 293-295, 169–174. doi:10.1016/s0022-3093(01)00667-6
Qi, H., Sun, Z., Wang, N., Qin, G., Zhang, H., and Shen, C. (2021). Two-dimensional Al2I2Se2: A Promising Anisotropic Thermoelectric Material. J. Alloys Compd. 876, 160191. doi:10.1016/j.jallcom.2021.160191
Qiao, L., Zhang, S., Xiao, H. Y., Singh, D. J., Zhang, K. H. L., Liu, Z. J., et al. (2018). Orbital Controlled Band gap Engineering of Tetragonal BiFeO3 for Optoelectronic Applications. J. Mater. Chem. C 6, 1239–1247. doi:10.1039/c7tc04160h
Row, D. M., Shukla, V. S., and Savvideset, N. (1981). Phonon Scattering at Grain Boundaries in Heavily Doped fine-grained Silicon-Germanium Alloys. Nature 290, 765–766. doi:10.1038/290765a0
Sarikurt, S., Kocabaş, T., and Sevik, C. (2020). High-throughput Computational Screening of 2D Materials for Thermoelectrics. J. Mater. Chem. A. 8, 19674–19683. doi:10.1039/d0ta04945j
Shi, H. L., Parker, D., Du, M. H., and Singhet, D. J. (2015). Connecting Thermoelectric Performance and Topological-Insulator Behavior: Bi2Te3 and Bi2Te2Se from First Principles. Phys. Rev. Appl. 3, 014004. doi:10.1103/physrevapplied.3.014004
Snyder, G. J., and Toberer, E. S. (2008). Complex Thermoelectric Materials. Nat. Mater 7, 105–114. doi:10.1038/nmat2090
Snyder, G. J., Snyder, A. H., Wood, M., Gurunathan, R., Snyder, B. H., and Niu, C. (2020). Weighted Mobility. Adv. Mater. 32, 2001537. doi:10.1002/adma.202001537
Sun, G., Kürti, J., Rajczy, P., Kertesz, M., Hafner, J., and Kresse, G. (2003). Performance of the Vienna Ab Initio Simulation Package (VASP) in Chemical Applications. J. Mol. Struct. Theochem 624, 37–45. doi:10.1016/s0166-1280(02)00733-9
Sun, Z., Yuan, K., Chang, Z., Bi, S., Zhang, X., and Tang, D. (2020). Ultra-low thermal Conductivity and High Thermoelectric Performance of Two-Dimensional Triphosphides (InP3, GaP3, SbP3 and SnP3): a Comprehensive First-Principles Study. Nanoscale 12, 3330–3342. doi:10.1039/c9nr08679j
Tan, G., Zhao, L.-D., and Kanatzidis, M. G. (2016). Rationally Designing High-Performance Bulk Thermoelectric Materials. Chem. Rev. 116, 12123–12149. doi:10.1021/acs.chemrev.6b00255
Tang, Y., Gibbs, Z. M., Agapito, L. A., Li, G., Kim, H.-S., Nardelli, M. B., et al. (2015). Convergence of Multi-valley Bands as the Electronic Origin of High Thermoelectric Performance in CoSb3 Skutterudites. Nat. Mater 14, 1223–1228. doi:10.1038/nmat4430
Tian, Z., Garg, J., Esfarjani, K., Shiga, T., Shiomi, J., and Chen, G. (2012). Phonon Conduction in PbSe, PbTe, and PbTe1−xSexfrom First-Principles Calculations. Phys. Rev. B 85, 184303. doi:10.1103/physrevb.85.184303
Tichý, L., Tříska, A., Barta, Č., Tichá, H., and Frumar, M. (1982). Optical Gaps from 'mean' Bond Energy in Ge1−x S X and Ge K Sb M S N Non-crystalline Solids. Philosophical Mag. B 46, 365–376. doi:10.1080/13642818208246447
Togo, A., Oba, F., and Tanaka, I. (2008). First-principles Calculations of the Ferroelastic Transition between Rutile-type andCaCl2-typeSiO2at High Pressures. Phys. Rev. B 78, 134106. doi:10.1103/physrevb.78.134106
Wang, Z. L., and Wu, W. (2012). Nanotechnology-Enabled Energy Harvesting for Self-Powered Micro-/Nanosystems. Angew. Chem. Int. Ed. 51, 11700–11721. doi:10.1002/anie.201201656
Wang, F. Q., Zhang, S., Yu, J., and Wang, Q. (2015). Thermoelectric Properties of Single-Layered SnSe Sheet. Nanoscale 7, 15962–15970. doi:10.1039/c5nr03813h
Wang, X., Wang, Z. L., and Yang, Y. (2016). Hybridized Nanogenerator for Simultaneously Scavenging Mechanical and thermal Energies by Electromagnetic-Triboelectric-Thermoelectric Effects. Nano Energy 26, 164–171. doi:10.1016/j.nanoen.2016.05.032
Wang, F. Q., Guo, Y., Wang, Q., Kawazoe, Y., and Jena, P. (2017). Exceptional Thermoelectric Properties of Layered GeAs2. Chem. Mater. 29, 9300–9307. doi:10.1021/acs.chemmater.7b03279
Wang, N., Li, M., Xiao, H., Zu, X., and Qiao, L. (2020). Layered LaCuOSe: a Promising Anisotropic Thermoelectric Material. Phys. Rev. Appl. 13, 024038. doi:10.1103/physrevapplied.13.024038
Weinstein, B. A., Zallen, R., Slade, M. L., and Mikkelsen, J. C. (1982). Pressure-optical Studies of GeS2glasses and Crystals: Implications for Network Topology. Phys. Rev. B 25, 781–792. doi:10.1103/physrevb.25.781
Yang, J., Xi, L., Qiu, W., Wu, L., Shi, X., Chen, L., et al. (2016). On the Tuning of Electrical and thermal Transport in Thermoelectrics: an Integrated Theory-experiment Perspective. NPJ Comput. Mater. 2, 15015. doi:10.1038/npjcompumats.2015.15
Yang, Y., Liu, S. C., Wang, X., Li, Z., Zhang, Y., Zhang, G., et al. (2019). Polarization‐Sensitive Ultraviolet Photodetection of Anisotropic 2D GeS 2. Adv. Funct. Mater. 29, 1900411. doi:10.1002/adfm.201900411
Yuan, J., Cai, Y., Shen, L., Xiao, Y., Ren, J.-C., Wang, A., et al. (2018). One-dimensional Thermoelectrics Induced by Rashba Spin-Orbit Coupling in Two-Dimensional BiSb Monolayer. Nano Energy 52, 163–170. doi:10.1016/j.nanoen.2018.07.041
Yuan, K., Sun, Z., Zhang, X., Gong, X., and Tang, D. (2020). A First-Principles Study of the Thermoelectric Properties of Rhombohedral GeSe. Phys. Chem. Chem. Phys. 22, 1911–1922. doi:10.1039/c9cp05153h
Zhang, Y., Ke, X. Z., ChenYang, C. F. J., and Kent, P. R. C. (2009). Thermodynamic Properties of PbTe, PbSe, and PbS: First-Principles Study. Phys. Rev. B. 80, 024304. doi:10.1103/physrevb.80.024304
Zhang, S., Xiao, H. Y., Peng, S. M., Yang, G. X., Liu, Z. J., Zu, X. T., et al. (2018). Band-Gap Reduction in (BiCrO3)(m)/(BiFeO3)(n) Superlattices: Designing Low-Band-Gap Ferroelectrics. Phys. Rev. Appl. 10, 044004. doi:10.1103/physrevapplied.10.044004
Keywords: GeS2 monolayer, thermoelectric, transport property, high-throughput calculations, first-principles calculations
Citation: Wang X, Feng W, Shen C, Sun Z, Qi H, Yang M, Liu Y, Wu Y and Wu X (2021) The Verification of Thermoelectric Performance Obtained by High-Throughput Calculations: The Case of GeS2 Monolayer From First-Principles Calculations. Front. Mater. 8:709757. doi: 10.3389/fmats.2021.709757
Received: 14 May 2021; Accepted: 01 June 2021;
Published: 05 July 2021.
Edited by:
Guangzhao Qin, Hunan University, ChinaReviewed by:
Ning Wang, University of Electronic Science and Technology of China, ChinaLei Wang, University of Science and Technology of China, China
Bingke Li, Nanyang Institute of Technology, China
Copyright © 2021 Wang, Feng, Shen, Sun, Qi, Yang, Liu, Wu and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaoqiang Wu, d3V4aWFvcWlhbmdAY2R1LmVkdS5jbg==
 Xiaolian Wang1
Xiaolian Wang1 Xiaoqiang Wu
Xiaoqiang Wu