Computational Geometry-Based 3D Yarn Path Modeling of Wound SiCf/SiC-Cladding Tubes and Its Application to Meso-Scale Finite Element Model

The filament winding process is a competitive performing technology for nuclear fuel cladding tubes due to its high automation. The study of the yarn path on the mandrel surface is vital to design and produce the cladding tube with the desired mechanical properties, reducing manufacturing time and costs. The geodesic and semi-geodesic trajectories are used to create a 3D yarn path in this paper. A 3D yarn path optimization method based on the principle of minimum potential energy is proposed to simulate the overlap effect in accord with the real winding process. The finite element (FE) mesh based on the 3D yarn path has been used for the mechanical analysis of the cladding tube. The embedded region constraint is applied to define the interaction between the matrix mesh and the yarn mesh to model the meso-structure of the cladding tube. Based on the meso-scale FE model, the mechanical behavior of the wound SiC_f/SiC nuclear fuel cladding tube is studied in detail. The results show that due to the neglect of the overlap effect, the conventional laminate model overestimates the cladding tube strength. The proposed meso-scale FE model can accurately predict the failure of the cladding tube. The results also confirm that the creation of a 3D yarn path and the derived meso-scale FE model, representing an accurate wound structure, are of importance to the prediction of the performance of the cladding tube.

Introduction

Continuous SiC fiber-reinforced SiC matrix (SiC_f/SiC) composites have been used in high temperature applications, such as nuclear fuel cladding tubes and aerospace propulsion systems (Naslain, 2004). Similar to other fiber-reinforced composites, the properties of SiC_f/SiC composites mainly depend on the parameters of the fiber reinforcement, including fiber volume fraction, fiber orientation, and fiber architecture. In most cases, relatively high fiber volume fractions can be achieved by optimizing the performing process. As a result, the design of the fiber architecture and fiber orientation is essential to improve the comprehensive mechanical properties of the tubular cladding (Katoh et al., 2014). Three suitable performing processes are generally adopted for cladding tubes, including filament winding, 2D braiding, and 3D braiding (Sauder, 2014). The highest fiber volume fraction and strength are obtained by the filament winding (Figure 1) (Kim et al., 2015a). Moreover, the winding process can offer better yarn placement accuracy, and the fiber breakage will be minimized by eliminating yarn-to-yarn friction compared with braiding. Consequently, the winding process is a competitive processing technology for the cladding tube performing.

FIGURE 1

FIGURE 1. The filament winding technique for nuclear fuel cladding tube. (A) Filament winding process on a 4-axis filament winding machine. (B) SiC fiber wound preform (Kim et al., 2015a); (C) SiC_f/SiC nuclear fuel cladding tube.

Due to the high degree of automation, the winding process is an economical and rapid performing technology for the cladding tube. Nonetheless, it lacks an efficient design process that takes specific processing parameters into account. The processing parameters of the winding process determine the properties of the wound tube, such as the coverage rate, winding angle, areal weight, and so on. Since the cost of SiC_f/SiC composite forming is high, the trial-and-error method is more unaffordable compared with resin-based composites. Therefore, the gap between the properties and processing parameters has to be bridged using a numerical processing model in which the fiber architecture can be precisely captured. Then, the mechanical properties of the cladding tubes can be optimized and precisely predicted by meso-scale FE model.

In order to predict the fiber architecture in a wound structure, it is crucial to study the winding trajectory during the winding process. Simões et al. (1993) visualized the winding trajectory (geodesic and non-geodesic) as a polyline and simplified the mandrel shape as a wireframe model. However, only a single winding trajectory was simulated, rather than a path showing the width of the yarn. Several works of the literature (Hongya et al., 2007; Xianfeng et al., 2010; Zu et al., 2012) used a similar approach to simulate the winding process for other mandrel shapes, such as toroidal tanks, S-elbows, aircraft inlets, and vanes. Nonetheless, they were not real filament winding simulations because no consideration was given to the cross-section shape of yarn in the model. The paths of yarns on the elbow were generated by Li et al. (2005), while all the yarns appeared on the same layer, ignoring overlap effect. During the winding process, the former winding yarns are always covered by the latter ones. Fu et al. (2016) developed an algorithm to visualize the winding process of axisymmetric vessels in real-time, facilitating the engineers to check whether the distribution of yarns is reasonable and whether there is any collision during the winding process. The visualization simulation of the latter yarns covering the former yarns was achieved by OpenGL graphics display technology. The thickness of the yarns was also not taken into consideration in the simulation, in which the paths were always on the original mandrel surface. In fact, the yarns stack up on the mandrel surface as the winding process proceeds, leading to a renewal of the mandrel surface. These simulations fail to model the phenomenon of yarns accumulation on the mandrel surface, leading to the fact that real yarn architecture in the wound parts cannot be obtained from the simulation results. In other words, it is just a pseudo-3D filament winding simulation. For the accurate prediction of the cladding tube mechanical properties, real yarn architecture is necessary for meso-scale FE model. Several works of the literature focus on the effect of winding angle on the wound tube mechanical properties with conventional laminate model while ignoring the effect of the real yarn architecture (Gunasegaran et al., 2013; Sulaiman et al., 2013).

This work develops an efficient virtual tool based on computational geometry for the design of the SiC_f/SiC-cladding tubes, whose reinforcements are performed using the filament winding technique. The real yarn architecture modeling includes the generation of 3D yarn paths and overlap between yarns. The geodesic and semi-geodesic trajectories are developed to generate the 3D yarn paths totally covering the mandrel. Then, the L-BFGS algorithm is applied to path optimization, which can obtain the real 3D yarns architecture with an overlap effect. With real yarns architecture, the embedded region constraint is used in the meso-scale FE modeling. The meso-scale FE model can avoid the weakness of the laminate model, which ignores the overlap effect.

Physically Realistic 3D Paths Generation for Yarns

Yarn Centerline Creation

To simplify the process of modeling the 3D path of a wound yarn, a reasonable procedure is to first calculate the trajectory of the yarn centerline and then assign a yarn width and thickness to the centerline. The process of calculating the yarn centerline involves calculating the geodesic and semi-geodesic on the mandrel surface, as well as the winding pattern generation. As shown in Figure 2A, the yarn centerline consists of three kinds of trajectories, which are circular arc, helix, and semi-geodesic. When the cylindrical surface is expanded into a rectangle (Figure 2B), both the arcs and the helixes are shown as straight lines, for they are both geodesics (the geodesic is a straight line after the developable surface is spread). In contrast, the semi-geodesics are shown as curves, which means that its winding angle, i.e., the angle from the meridional direction to the yarn direction (Koussios, 2004), varies according to the z-coordinate.

FIGURE 2

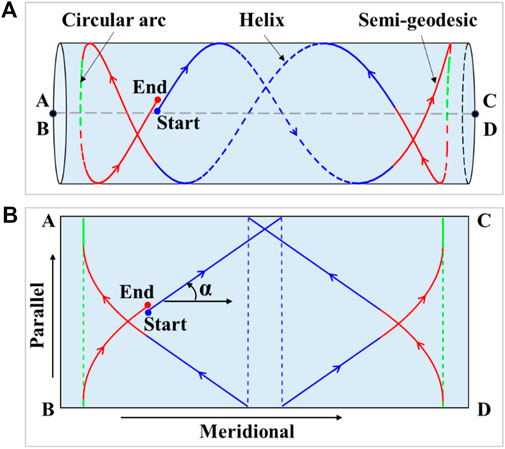
FIGURE 2. (A) Yarn centerline along one cycle on the cylindrical surface; (B) yarn centerline along one cycle after the cylindrical surface is spread.

A parametric representation of the helix and circle can be made by the following:

$\{\begin{array}{c}x=Rcos\left(\varphi \right),y=Rsin\left(\varphi \right),z=C\varphi helix\\ x=Rcos\left(\varphi \right),y=Rsin\left(\varphi \right),z=C circle\end{array}(1)$

where R is the cylinder radius, $\phi$ is the rotation angle from the x-axis, and C is a constant. The winding angle, α, can be given by the following:

$\{\begin{array}{c}\alpha =arctan\left(R/C\right) helix\\ \alpha =\pi /2 circle\end{array}(2)$

The semi-geodesic has a variable winding angle and is used to reverse yarn motion direction at both ends of the mandrel. However, compared with the geodesic, the semi-geodesic trajectory can lead to yarn slippage on the mandrel. In order to maintain the mechanical stability of the yarn, it is essential to ensure that the ratio of the frictional force and the normal pressure acting on the yarn is less than the friction coefficient μ between the yarn and the mandrel. This equilibrium condition could be expressed by differential geometric quantities, geodesic curvature, and the normal curvature, which can be written as follows (De Carvalho et al., 1995; Koussios, 2004; Koussios et al., 2004; Kim et al., 2005; Vargas Rojas et al., 2014):

$\frac{\text{d}\alpha }{\text{d}z}=\frac{\eta {\text{sin}}^2\alpha }{R\text{cos}\alpha }(3)$

where $\eta$ is slip coefficient, it must satisfy $0\mathrm{⩽}\eta \mathrm{⩽}\mu$.

Through integral $\underset{z_0}{\overset{z}{{\displaystyle \int }}}\text{d}t=\underset{{\alpha }_0}{\overset{\alpha }{{\displaystyle \int }}}\frac{R\text{cos}\alpha \text{d}\alpha }{\eta {\text{sin}}^2\alpha }$, the analytical solution of Eq. 3 can be written as follows:

$z-z_0=\frac{R}{\eta }\left(\frac{1}{\text{sin}{\alpha }_0}-\frac{1}{\text{sin}\alpha }\right)(4)$

where ${\alpha }_0$ and $z_0$ are the winding angle and axial position of the start point, respectively.

In order to maintain a constant length increment ds along the semi-geodesic, the step size of z is calculated in the following way:

$\Delta z=z_{i+1}-z_i=ds\cdot cos\left(\alpha \right)(5)$

The relationship between rotation angle ${\varphi }_{i+1}$ and ${\varphi }_i$ can be expressed as follows:

${\varphi }_{i+1}={\varphi }_i+{\displaystyle \underset{z_i}{\overset{z_{i+1}}{\int }}\frac{\text{tan}\left[\alpha \left(z\right)\right]}{R}}dz(6)$

To have the yarn cover the mandrel uniformly, the total rotation angle experienced during a cycle must be designed according to the particular winding pattern. The winding pattern is formed by the yarn going back and forth along the mandrel and crossing and overlapping itself at certain points. Once the helix and semi-geodesic trajectories are determined, the yarn usually dwells in both ends of the mandrel when α = π/2 for a certain angle of $\Delta {\varphi }_{dwell}$, forming a circular arc. $\Delta {\varphi }_{dwell}$ can be expressed as follows:

$\{\begin{array}{c}\Delta {\varphi }_{dwell}=\pi -\frac{1}{2}mod\left(\Delta {\varphi }_n-\frac{2\pi d}{N}, 2\pi \right)\\ N=ceil\left(\frac{2\pi R}{b}\text{cos}\left(\alpha \right)\right)\end{array}(7)$

where $\Delta {\varphi }_n$ is the rotation angle experienced by helixes and semi-geodesics in a cycle; N is the number of cycles required to completely cover the mandrel; b is yarn width; d governs the pattern formed during the winding (Johansen et al., 1998), it must satisfy $1\mathrm{⩽}d<N$ , and the ratio $d/N$ is non-reducible. After N cycles, the yarn will eventually cover the mandrel (Figure 3).

FIGURE 3

FIGURE 3. Yarn centerline along all cycles in one layer.

Yarn Width and Thickness Modeling

Many different yarn cross-sections have been presented over the years to indicate the actual condition of the yarn before and after tension is applied. These studies have mainly been carried out for representative volume elements (RVE) or advanced fiber placement (AFP) techniques (Potluri and Manan, 2007; Ansar et al., 2011; Kim et al., 2015b; Vernet and Trochu, 2016). Commonly used yarn cross-section shapes include rectangular, ellipsoidal, lenticular, and so on. However, in the filament winding process, the yarn is expanded into a flat shape with a rectangular cross-section. Hence, our work considers the yarn cross-section as a rectangular cross-section, and the shape remains consistent throughout the winding process.

As shown in Figure 4A, based on the centerline of the yarn path $T_{\left(0\right)}$, multiple parallel trajectories are obtained by geodesic offsets on the mandrel surface to describe the yarn width (Fu et al., 2016). The multiple parallel trajectories are represented by a set of $B=\left\{T_{\left(i\right)}\mathrm{\mid }i=\mathrm{0,1},\mathrm{...},2m\right\}$, where m is the number of equal parts of the half yarn width. Each trajectory $T_{\left(i\right)}=\left\{P_{\left(i,j\right)}\mathrm{\mid }j=\mathrm{0,1},\mathrm{...},n\right\}$ is composed of a sequence of discrete points of $P_{\left(i,j\right)}$, where n is the number of all discrete points along the centerline $T_{\left(0\right)}$. All parallel trajectories are then raised by one yarn thickness along the outer normal of the mandrel surface to describe the yarn thickness (Figure 4B), so the number of trajectories in set B is doubled to 4m + 2.

FIGURE 4

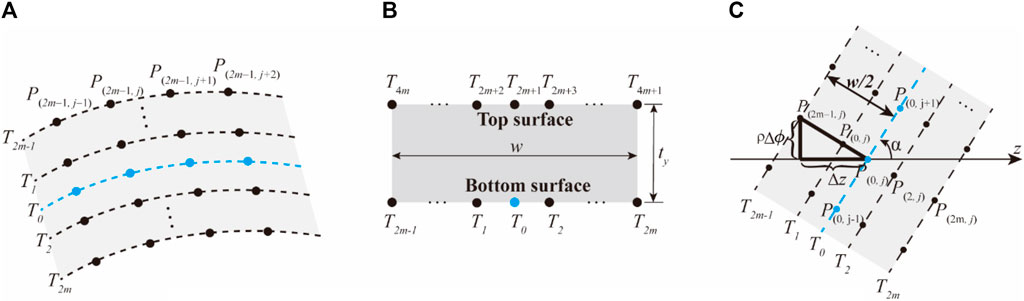
FIGURE 4. Representation of the width and thickness of a yarn. (A) Representation of the width of yarn; (B) yarn cross-section expressed as a rectangle; (C) position of multiple parallel trajectories of a yarn path in relation to the centerline.

On the cylindrical surface, the geodesic offsets are easy to calculate. $T_{\left(i\right)}=\left\{i=1,\mathrm{...},4m+1\right\}$ can be obtained from $T_{\left(0\right)}$ according to the winding angle, the distance from the mandrel axis, the width, and thickness of the yarn. As shown in Figure 4C, assuming the cylindrical coordinate of a point $P_{\left(0,j\right)}$ on $T_{\left(0\right)}$ is $\left({\rho }_{\left(0,j\right)}, {\phi }_{\left(0,j\right)}, z_{\left(0,j\right)}\right)$, the variation of the rotation angle $\phi$ and the axial coordinate $z$ corresponding to the half yarn width can be written as $\Delta \phi =\frac{w\cdot \text{cos}\alpha }{2\rho }$ and $\Delta z=\frac{w\cdot \text{sin}\alpha }{2}$, respectively, where w is the yarn width. The points $P_{\left(2i-1,j\right)}\left(i=1,\mathrm{...},m-1\right)$ are uniformly distributed over the width between $P_{\left(2m-1,j\right)}$ and $P_{\left(0,j\right)}$, its cylindrical coordinates can be expressed as follows:

$P_{\left(2i-1,j\right)}=\left({\rho }_{\left(\mathrm{2i-1},j\right)}, {\phi }_{\left(0,j\right)}-\Delta \varphi \frac{i}{m}, z_{\left(0,j\right)}-\Delta z\frac{i}{m}\right)(8)$

Points $P_{\left(2i+2m,j\right)}\left(i=1,\mathrm{...},m\right)$ have the same $\varphi$ and $z$ with $P_{\left(2i-1,j\right)}\left(i=1,\mathrm{...},m\right)$. Compared with point $P_{\left(2i-1,j\right)}$, point $P_{\left(2i+2m,j\right)}$ is $t$ further from the mandrel surface, where $t$ is the yarn thickness. The cylindrical coordinates of $P_{\left(2i+2m,j\right)}$ can be expressed as follows:

$P_{\left(2i+2m,j\right)}=\left({\rho }_{\left(0,j\right)}+t, {\phi }_{\left(0,j\right)}-\Delta \varphi \frac{i}{m}, z_{\left(0,j\right)}-\Delta z\frac{i}{m}\right)(9)$

Similarly, for points $P_{\left(2i,j\right)}$ and $P_{\left(2i+2m+1,j\right)}$, we can get the following:

$\{\begin{array}{c}{P}_{\left(2i,j\right)}=\left({\rho }_{\left(0,j\right)}, {\phi }_{\left(0,j\right)}+\Delta \varphi \frac{i}{m}, z_{\left(0,j\right)}+\Delta z\frac{i}{m}\right)\\ P_{\left(2i+2m+1,j\right)}=\left({\rho }_{\left(0,j\right)}+t, {\phi }_{\left(0,j\right)}+\Delta \varphi \frac{i}{m}, z_{\left(0,j\right)}+\Delta z\frac{i}{m}\right)\end{array}(10)$

Overlap Processing

As soon as the yarn crosses another part of itself in the winding process, overlap will occur. Assuming that the yarn is always in contact with the mandrel surface or a previous part of itself, a point on the current yarn path obtains a new radial distance ${\rho }_{new}=\rho +t$ in the cylindrical coordinate whenever the current part of the yarn encounters a previous part of itself. Then, if the current part of the yarn crosses with a new part of the yarn later, the radial distance in cylindrical coordinate continues to increase, i.e., ${\rho }_{new}=\rho +2t$.

Figure 5 shows a schematic representation of the overlap processing of two yarns (yarn A and yarn B). Yarn A can be regarded as the part of the yarn wound first and yarn B as the part of the yarn wound later. If there is no overlap processing, yarn B interferes with yarn A at the intersection (Figure 5A), the paths of yarn A and B are on the original mandrel surface. It fails to represent the yarn accumulation on the mandrel surface. After eliminating interference, the 3D path of yarn B is shown in Figure 5B. Intuitively, it is clear that the behavior of yarn B does not conform to physical reality; its distance from the mandrel surface changes abruptly before and after crossing yarn A and therefore, its path appears discontinuous. The underlying reason for the discontinuity is that the radial distance of points on yarn B in the cylindrical coordinate is updated by integer multiples of the yarn thickness during the overlap process.

FIGURE 5

FIGURE 5. Generation of physically realistic 3D paths for yarns. (A) Before interference processing; (B) the discontinuous 3D paths of yarns after interference processing; (C) continuous 3D paths of yarns after optimization.

During the winding process, the yarn is subjected to winding tension. As a result, the tensioned yarn B temporarily leaves the mandrel surface before and after crossing the underlying yarn A. In a stable winding process, the mechanical behavior of the yarn should conform to the principle of minimum potential energy. It is important to note that the yarn sliding in the tangential direction receives a tension constraint and can be considered as having no tendency to slip (the friction force in this direction is zero), so the tension of the yarn can be considered as equal everywhere. Then the elongation of the yarn, $\epsilon$, can be defined as follows:

$\epsilon =\frac{F}{EA}(11)$

where F, E, and A denote the tension, the modulus in the length direction of the yarn, and the cross-section area of the yarn, respectively.

Ignoring first the cross-section of the yarn and denoting $P_{\left(i,j\right)}\left(i=\mathrm{0,1},\mathrm{...},n\right)$ by $P_j$, the deformation energy, $U$, of yarn B, can be expressed as follows:

$U=\frac{1}{2}EA\epsilon {\displaystyle \sum }_{j=0}^{n-1}\left|P_j{P}_{j+1}\right|(12)$

For the displacement constraint of $P_j\left(j=1,\mathrm{...},n-1\right)$, its coordinates φ and z are obtained based on the previous calculation of the centerline trajectory and cannot be changed. Otherwise, it deviates from the intended winding path. And the coordinate ρ is obtained based on a simplified overlap processing. In fact, the current value of ρ is the minimum value that guarantees the yarn B will not interfere geometrically with the mandrel and yarn A. It does not ensure that the 3D yarn path is physically real, and the actual ρ can be larger than that value. In a word, yarn B acts as a discrete connected system, $P_j$ can only move to the outer normal direction of the mandrel, and its final radial coordinate ${\tilde{\rho }}_j$ must satisfy ${\tilde{\rho }}_j\mathrm{⩾}{\rho }_j$. In the above displacement adjustment process, the support reaction force does not do any work. Hence, the total potential energy of the whole system is equal to the total elastic energy and it can be given as follows:

$\Pi =\frac{1}{2}EA\epsilon {\displaystyle \sum }_{j=0}^{n-1}\left|P_j{P}_{j+1}\right|(13)$

where $\Pi$ denotes the total potential energy of yarn B.

According to the principle of minimum potential energy (Chandrupatla et al., 2002), under the displacement constraint, the potential energy can be used as the objective function, and the discrete connected system of yarn B will remain in mechanical equilibrium only when the potential energy of the whole system is minimized. Considering that the coefficient, E, A and $\epsilon$ are constants, so the objective function can be simplified as follows:

$Q\left({\tilde{\rho }}_j\right)={\displaystyle \sum }_{j=0}^{n-1}\left|P_j{P}_{j+1}\right|(14)$

The physical meaning of Eq. 14 is that the equilibrium state of the yarn B, determined according to the principle of minimum potential energy, is in fact, also intuitively the shape of the shortest path of the yarn B.

It can be proven that the shortest total path is equivalent to the smallest sum of squared path lengths under the current constraint (the proof process is omitted here). Therefore, the objective function can be transformed into the following:

$\tilde{Q}\left({\tilde{\rho }}_j\right)={\displaystyle \sum }_{j=0}^{n-1}{\left|P_j{P}_{j+1}\right|}^2(15)$

The new objective function, $\tilde{Q}$, can be understood as the sum of the elastic energy of a zero-length spring with a stiffness of 2 between $P_j$ and $P_{j+1}$. It is more suitable for optimal solving than Q because the expression does not contain a root sign, which is beneficial to improve the computational efficiency.

Yarn B has a rectangular cross-section in practical optimization, and its 3D path consists of many trajectories $T_{\left(i\right)}=\left\{i=0,\mathrm{...},4m+1\right\}$. Take, for example, one of these trajectories, $T_{\left(i\right)}\left(0\mathrm{⩽}i\mathrm{⩽}2m\right)$, which is on the lower surface of yarn B and composed of ordered points $P_{\left(i,j\right)}\left(i=\mathrm{0,1},\mathrm{...},n\right)$ with cylindrical coordinates of $\left({\rho }_{\left(i,j\right)}, {\phi }_{\left(i,j\right)}, z_{\left(i,j\right)}\right)$. It is assumed that the points $P_{\left(i,j\right)}$$\left(j=\mathrm{1,2},\dots ,2m-1\right)$ will be raised to position ${\tilde{P}}_{\left(i,j\right)}$, and the cylindrical coordinates of ${\tilde{P}}_{\left(i,j\right)}$ can be written as $\left({\rho }_{(i,j+1)}+{\delta }_{\left(i,j+1\right)}^2, {\phi }_{(i,j+1)}, z_{(i,j+1)}\right)$, which naturally satisfy the displacement constraint.

The square of the length of the line segment ${\tilde{P}}_{\left(i,j\right)}{\tilde{P}}_{\left(i,j+1\right)}$ can be written as follows:

$\begin{array}{l}{\left|{\tilde{P}}_{\left(i,j\right)}{\tilde{P}}_{\left(i,j+1\right)}\right|}^2={\left(\left({\rho }_{\left(i,j\right)}+{\delta }_{(i,j)}^2\right)\cdot \text{cos}\left({\phi }_{\left(i,j\right)}\right)-\left({\rho }_{(i,j+1)}+{\delta }_{(i,j+1)}^2\right)\cdot \text{cos}\left({\phi }_{(i,j+1)}\right)\right)}^2\\ +{\left(\left({\rho }_{\left(i,j\right)}+{\delta }_{(i,j)}^2\right)\cdot \text{sin}\left({\phi }_{\left(i,j\right)}\right)-\left({\rho }_{(i,j+1)}+{\delta }_{(i,j+1)}^2\right)\cdot \text{sin}\left({\phi }_{(i,j+1)}\right)\right)}^2+{\left(z_{\left(i,j\right)}-z_{(i,j+1)}\right)}^2\end{array}(16)$

The objective function $\tilde{Q}\left({\tilde{\rho }}_j\right)$, which becomes a quadratic polynomial in the variable ${\delta }_{(i,j)}$$\left(j=\mathrm{1,2},\dots ,2m-1\right)$, which can be written as follows:

$\tilde{Q}\left({\delta }_{(i,j)}\right)={\displaystyle \sum }_{j=0}^{n-1}{\left|{\tilde{P}}_{\left(i,j\right)}{\tilde{P}}_{\left(i,j+1\right)}\right|}^2(17)$

The value of ${\delta }_{(i,j)}$ corresponding to the minimum value of this objective function is the solution to this optimization problem. We use the L-BFGS (Nocedal, 1980) method to solve this optimization problem, which is the most common method for solving unconstrained nonlinear programming problems and has the advantages of fast convergence and low memory overhead often found in various machine learning algorithms. In order to apply the L-BGFS algorithm, the gradient function of the objective function $\tilde{Q}\left({\delta }_{(i,j)}\right)$ with respect to the variable ${\delta }_{(i,j)}$ must be provided.

$\frac{\partial \tilde{Q}}{\partial {\delta }_{(i,j)}}=4\left[2\left({\rho }_{\left(i,j\right)}+{\delta }_{(i,j)}^2\right)-\left({\rho }_{\left(i,j-1\right)}+{\delta }_{(i,j-1)}^2\right)\text{cos}\left({\phi }_{\left(i,j-1\right)}-{\phi }_{\left(i,j\right)}\right)-\left({\rho }_{\left(i,j+1\right)}+{\delta }_{\left(i,j+1\right)}^2\right)\text{cos}\left({\phi }_{\left(i,j+1\right)}-{\phi }_{\left(i,j\right)}\right)\right]{\delta }_{\left(i,j\right)}(18)$

The optimized 3D path of the yarn is shown in Figure 5C. It can be seen that the shape of the yarn B becomes smooth and leaves the surface of the mandrel before and after crossing yarn A, conforming to physical reality.

As shown in Figure 6, the 3D path modeling strategy for wound yarn was applied to the fuel cladding tube. The main geometrical and processing parameters are listed below:

• The width and thickness of the SiC_f yarn are 1.1 and 0.1 mm, respectively;

• The diameter of the mandrel is 20 mm the effective winding length is 100 mm;

• The winding angle is 45°and the winding pattern is 41/1.

FIGURE 6

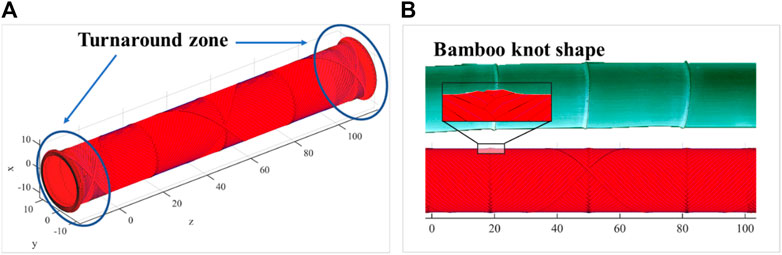
FIGURE 6. (A) Simulated 3D path of yarn in wound preform; (B) the winding pattern has a “bamboo knot” shape.

The simulated 3D path of yarn shows the “bamboo knot” structure of the wound part (Figure 6B). The winding path in the turnaround zone is semi-geodesic and the winding angle changes from the 45°to 90°, where yarn enrichment occurs and the thickness is, therefore, thicker than that in the other areas, which is also consistent with reality.

Meso-Scale Finite Element Modeling and Analysis

The 3D winding path already provides a geometric model of the yarn, which can be meshed to generate the meso-scale FE model. Based on the meso-scale FE model, the structural analysis can be performed. The numerical results of the wound tube model will be compared with the laminated tube model that is often used as a simplification. The discrepancies between these two models will be investigated in detail.

Nuclear Fuel Cladding Tube Modeling

As seen in Figure 7A, the tube has a length of 100 mm, an inner diameter of 20 mm, and a wall thickness of 0.5 mm. The wound yarns have 153,504 C3D8R elements, and the matrix has 77,952 elements (Figure 7B), while the laminated tube has 103,936 elements (Figure 7C). The global fiber volume fraction is 28% for both wound and laminated tubes. The input material properties are listed in Table 1, calculated from the micro-UD model (Feng et al., 2020). The SiC matrix has Young’s modulus of 300 GPa and a Poisson ratio of 0.14.

FIGURE 7

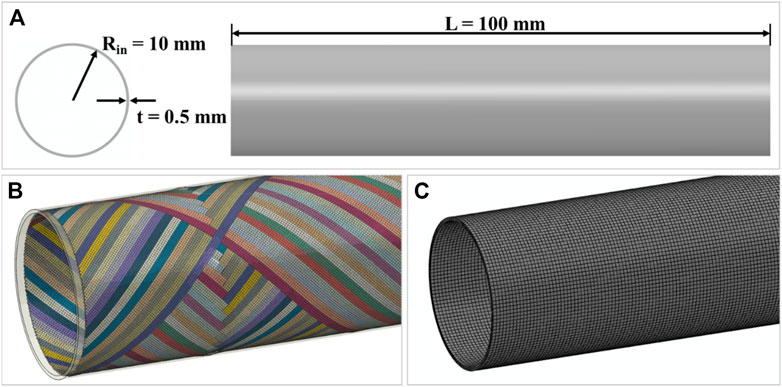
FIGURE 7. The FE model of the nuclear cladding tube: (A) the dimension of the tube with a length of 100 mm and a thickness of 0.5 mm; (B) the wound mesh integrated with the matrix using embedded constraint; (C) the laminated tube. The global fiber volume fractions are identical at 28%.

TABLE 1

TABLE 1. Input mechanical properties for yarn and laminate, calculated from micro-UD model (Feng et al., 2020).

The embedded element technique is used to specify that an element or group of elements is embedded in “host” elements. As shown in Figure 8A, the matrix mesh is the host mesh, and the yarn mesh is the embedded mesh. Abaqus searches for the geometric relationships between nodes of the embedded elements and the host elements. If a node of an embedded element lies within a host element, the translational degrees of freedom at the node are eliminated and the node becomes an “embedded node.” The translational degrees of freedom of the embedded node are constrained to the interpolated values of the corresponding degrees of freedom of the host element (Tabatabaei et al., 2014). Figure 8B shows the displacement boundary conditions at both ends of the tube. The load is applied directly to the master node at the end of the tube. Then the master node transfers the load to the slave nodes at both ends of the tube through continuum distributing constraints by weight. Take the axial tension condition as an example, the three translational degrees of freedom of the left master node are set to zero, and the tension load is applied through the axial displacement of the right master node.

FIGURE 8

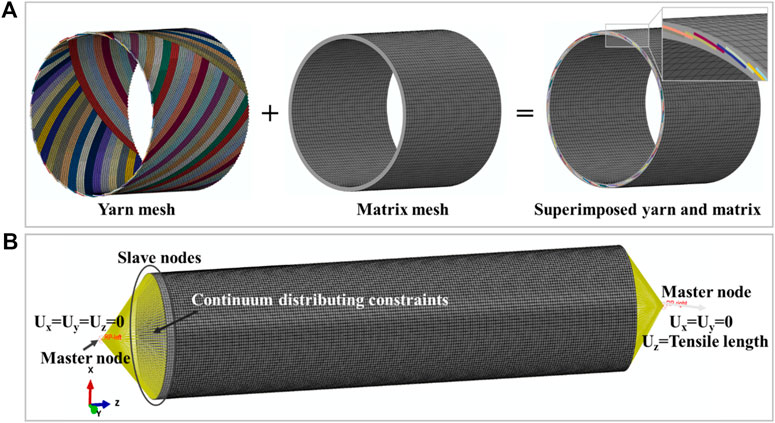
FIGURE 8. (A) Define the constraints between the yarn and the matrix by domain superposition technique; (B) displacement constraints at both ends of the tube.

Numerical Results

With the obtained mesh (Figure 7B) and material properties (Table 1), the meso-scale FE model of the cladding tube can be applied to structural optimization. Generally, the model of the laminated tube with identical fiber orientations are often used to predict the major mechanical properties, e.g., apparent modulus and strength, as a simplified substitute. However, the weakening effect of the yarn waviness and interlocks caused by the overlap effect has not yet been specifically investigated in the previous work of cladding tube design. The mechanical stresses on the cladding tubes are small, and the main risk is the mechanical failure during a sudden axial movement (Sauder, 2014), which will result in axial tensile or compressive stresses. In addition, the weakness of the SiC_f/SiC composite is the low shear strength, which is reflected in the axial tensile condition where the fiber direction is exactly the maximum shear stress. Therefore, in the following discussion, an equivalent tensile loading will be applied to the tube; the apparent moduli of the wound tube and laminated tube will be calculated and compared.

Figure 9A shows that the global axial tensile moduli of the wound and laminated tubes are quasi equivalent. The global tensile modulus of the laminated tube is 322.0 GPa, and the global tensile modulus of the wound tube is 322.2 GPa. The deviation is negligible. In such a circumstance, the meso-scale FE model can be used to predict the apparent moduli of the cladding tube, especially under complex service loadings.

FIGURE 9

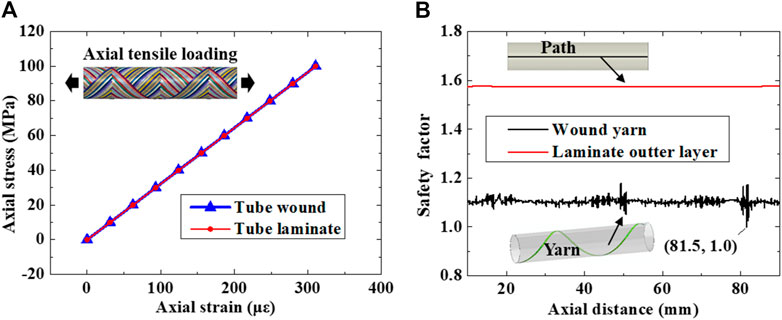
FIGURE 9. The mechanical response of wound and laminated tubes under global axial tensile loading. (A) the global tension moduli; (B) the safety factor of shear stress.

Although the calculated moduli of the wound tube and the laminated tube present good agreement, the local stress states are totally different since the waviness and interlock of the yarn cause stress concentration, which will introduce an earlier damage initiation and final failure of the cladding tube. Shear stress is the typical stress state of the tube under axial tension and the shear stress safety factor is demonstrated in Figure 9B. The safety factor is defined as the ratio of the shear stress and shear strength (the shear strengths of SiC_f/SiC are 60.1 and 78.8 MPa when the fiber volume fraction is 70 and 28% (Feng et al., 2020)). For the wound tube, the shear stress is extracted from the nodes along the yarn on which the maximum stress is located, and for the laminated tube, the shear stress is extracted from the nodes along the axial direction. According to our assumption, the safety factors in the wound yarns are almost 36.7% lower than that of the laminated tube. The lowest safety factor occurs at the “bamboo knot” in the yarn, which means that the damage initiation will occur here due to stress concentration caused by the overlap effect, which cannot be reflected in the laminated tube model. Figure 10A shows the global shear stress just before the damage of the yarn, and it can be seen that the maximum shear stress in the wound tube yarn is 20% greater than the stress in the laminated tube. At the same time, a higher fiber volume fraction will lead to a reduction in shear strength, so the difference in safety factor between the two models is greater than the difference in shear stress. In such a context, with the same fiber volume fraction, the wound tube and the laminated one have similar values of moduli but quite different apparent strengths. The stress concentration and higher local fiber volume fraction result in a lower strength for wound tubes. This result confirms that a precise wound structure on meso-scale is indispensable for the property prediction of the cladding tube.

FIGURE 10

FIGURE 10. The shear stresses of tubes. (A) wound tube; (B) laminated tube.

Summary and Conclusion

In this paper, an efficient filament winding virtual tool considering the overlap effect of the yarn for SiC_f/SiC nuclear fuel cladding tube is developed, which not only stimulates the 3D yarn laying path on the mandrel surface but also generates a meso-scale FE model of the cladding tube. The centerline (geodesic and semi-geodesic) of the 3D yarn path is calculated based on the analytical method and then the path is obtained by offsetting the centerline in the width and thickness directions of the yarn increasing efficiency in trajectory calculation. An innovative overlap processing algorithm based on the principle of minimum potential energy is proposed to obtain a continuous 3D path, which reflects the real yarns architecture. The comparisons of the apparent mechanical properties between the proposed meso-scale FE model and the conventional laminated model prove that the laminated tube model overestimates the structural strength, which results from the laminated model ignoring the yarn overlap effect. Non-uniformity of fiber volume fraction can also lead to earlier damage. In conclusion, the stress concentration caused by the overlap effect must be considered and optimized in the design. In the future, the proposed filament winding virtual tool will be applied to study the mechanical properties of nuclear fuel cladding tubes under complex loading cases.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding authors.

Author Contributions

JT carried out the investigation, methodology, data curation, software, writing-original draft preparation, visualization, and formal analysis. GZ performed data curation, software, methodology, writing-reviewing, and editing. JW, YD, YF, YC, and CZ contributed to software and validation. SX did the implementation of the computer code and supporting algorithms and testing of existing code components. QH and JX carried out project administration, supervision, and funding acquisition. JX contributed to writing-reviewing and editing, project administration, supervision, and funding acquisition.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52075526) and the Dalian University of Technology 2019 Discipline Platform Fund (No. 1000-82212201). The authors also gratefully acknowledge the National Key Research and Development Program (No.2018YFB1107500), the “Ningbo 3315 Plan Innovation Team” (No. 2017A-28-C), the “Transformational Technologies for Clean Energy and Demonstration,” and the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA21010205).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ansar, M., Xinwei, W., and Chouwei, Z. (2011). Modeling Strategies of 3D Woven Composites: A Review. Compos. Structures 93 (8), 1947–1963. doi:10.1016/j.compstruct.2011.03.010

CrossRef Full Text | Google Scholar

Chandrupatla, T. R., Belegundu, A. D., Ramesh, T., and Ray, C. (2002). Introduction to Finite Elements in Engineering. Upper Saddle River, NJ: Prentice-Hall.

De Carvalho, J., Lossie, M., Vandepitte, D., and Van Brussel, H. (1995). Optimization of Filament-Wound Parts Based on Non-geodesic Winding. Composites manufacturing 6 (2), 79–84. doi:10.1016/0956-7143(95)99647-b

CrossRef Full Text | Google Scholar

Feng, Y., Wang, J., Shang, N., Zhao, G., Zhang, C., Tang, J., et al. (2020). Multiscale Modelling of SiCf/SiC Nuclear Fuel Cladding Based on FE-Simulation of Braiding Process. Front. Mater. 7, 473.

Google Scholar

Fu, J., Yun, J., Kim, J.-S., and Jung, Y. (2016). Real-time Graphic Visualization of Filament Band Winding for Fiber-Reinforced Cylindrical Vessels. J. Compos. Mater. 50 (16), 2165–2175. doi:10.1177/0021998315602325

CrossRef Full Text | Google Scholar

Gunasegaran, V., Prashanth, R., and Narayanan, M. (2013). Experimental Investigation and Finite Element Analysis of Filament Wound GRP Pipes for Underground Applications. Proced. Eng. 64, 1293–1301. doi:10.1016/j.proeng.2013.09.210

CrossRef Full Text | Google Scholar

Hongya, F., Xianfeng, W., Zhenyu, H., and Yunzhong, F. (2007). Abnormal Shape Mould Winding. Chin. J. Aeronautics 20 (6), 552–558. doi:10.1016/s1000-9361(07)60081-8

CrossRef Full Text | Google Scholar

Johansen, B. S., Lystrup, A., and Jensen, M. T. (1998). CADPATH: a Complete Program for the CAD-, CAE- and CAM-Winding of Advanced Fibre Composites. J. Mater. Process. Tech. 77 (1-3), 194–200. doi:10.1016/s0924-0136(97)00417-2

CrossRef Full Text | Google Scholar

Katoh, Y., Ozawa, K., Shih, C., Nozawa, T., Shinavski, R. J., Hasegawa, A., et al. (2014). Continuous SiC Fiber, CVI SiC Matrix Composites for Nuclear Applications: Properties and Irradiation Effects. J. Nucl. Mater. 448 (1-3), 448–476. doi:10.1016/j.jnucmat.2013.06.040

CrossRef Full Text | Google Scholar

Kim, B. C., Weaver, P. M., and Potter, K. (2015). Computer Aided Modelling of Variable Angle Tow Composites Manufactured by Continuous Tow Shearing. Compos. Structures 129, 256–267. doi:10.1016/j.compstruct.2015.04.012

CrossRef Full Text | Google Scholar

Kim, C.-U., Kang, J.-H., Hong, C.-S., and Kim, C.-G. (2005). Optimal Design of Filament Wound Structures under Internal Pressure Based on the Semi-geodesic Path Algorithm. Compos. Structures 67 (4), 443–452. doi:10.1016/j.compstruct.2004.02.003

CrossRef Full Text | Google Scholar

Kim, D., Lee, H.-G., Park, J. Y., and Kim, W.-J. (2015). Fabrication and Measurement of Hoop Strength of SiC Triplex Tube for Nuclear Fuel Cladding Applications. J. Nucl. Mater. 458, 29–36. doi:10.1016/j.jnucmat.2014.11.117

CrossRef Full Text | Google Scholar

Koussios, S., Bergsma, O. K., and Beukers, A. (2004). Filament Winding. Part 1: Determination of the Wound Body Related Parameters. Composites A: Appl. Sci. Manufacturing 35 (2), 181–195. doi:10.1016/j.compositesa.2003.10.003

CrossRef Full Text | Google Scholar

Koussios, S. (2004). Filament Winding: A Unified Approach. Delft University of Technology.

Li, H., Liang, Y., and Bao, H. (2005). CAM System for Filament Winding on Elbows. J. Mater. Process. Technol. 161 (3), 491–496. doi:10.1016/j.jmatprotec.2004.07.093

CrossRef Full Text | Google Scholar

Naslain, R. (2004). Design, Preparation and Properties of Non-oxide CMCs for Application in Engines and Nuclear Reactors: an Overview. Composites Sci. Tech. 64 (2), 155–170. doi:10.1016/s0266-3538(03)00230-6

CrossRef Full Text | Google Scholar

Nocedal, J. (1980). Updating Quasi-Newton Matrices with Limited Storage. Math. Comp. 35 (151), 773. doi:10.1090/s0025-5718-1980-0572855-7

CrossRef Full Text | Google Scholar

Potluri, P., and Manan, A. (2007). Mechanics of Non-orthogonally Interlaced Textile Composites. Composites Part A: Appl. Sci. Manufacturing 38 (4), 1216–1226. doi:10.1016/j.compositesa.2006.04.008

CrossRef Full Text | Google Scholar

Sauder, C. (2014). Ceramic Matrix Composites: Nuclear Applications, Ceramic Matrix Composites: Materials, Modeling and Technology, 609–646. doi:10.1002/9781118832998.ch22

CrossRef Full Text

Simões, J. A. O., Wu, S.-T., and Loseries, F. (1993). Visual Simulation of the Geodesic and Non-geodesic Trajectories of the Filament Winding, Graphics Modeling and Visualization in Science and Technology. Springer, 199–215. doi:10.1007/978-3-642-77811-7_16

CrossRef Full Text

Sulaiman, S., Borazjani, S., and Tang, S. H. (2013). “Finite Element Analysis of Filament-Wound Composite Pressure Vessel under Internal Pressure,” in IOP Conference Series: Materials Science and Engineering (IOP Publishing), 012061. doi:10.1088/1757-899x/50/1/012061

CrossRef Full Text | Google Scholar

Tabatabaei, S. A., Lomov, S. V., and Verpoest, I. (2014). Assessment of Embedded Element Technique in Meso-FE Modelling of Fibre Reinforced Composites. Compos. Structures 107, 436–446. doi:10.1016/j.compstruct.2013.08.020

CrossRef Full Text | Google Scholar

Vargas Rojas, E., Chapelle, D., Perreux, D., Delobelle, B., and Thiebaud, F. (2014). Unified Approach of Filament Winding Applied to Complex Shape Mandrels. Compos. Structures 116, 805–813. doi:10.1016/j.compstruct.2014.06.009

CrossRef Full Text | Google Scholar

Vernet, N., and Trochu, F. (2016). Analysis and Modeling of 3D Interlock Fabric Compaction Behavior. Composites Part A: Appl. Sci. Manufacturing 80, 182–193. doi:10.1016/j.compositesa.2015.10.024

CrossRef Full Text | Google Scholar

Xianfeng, W., Jun, X., and Liwei, W. (2010). Winding Pattern Design and Simulation of S-Elbow. Chin. J. Aeronautics 23 (5), 573–577. doi:10.1016/s1000-9361(09)60256-9

CrossRef Full Text | Google Scholar

Zu, L., Zhang, D., Xu, Y., and Xiao, D. (2012). Integral Design and Simulation of Composite Toroidal Hydrogen Storage Tanks. Int. J. Hydrogen Energ. 37 (1), 1027–1036. doi:10.1016/j.ijhydene.2011.03.026

CrossRef Full Text | Google Scholar