An Advanced Finite Element Modeling for the Failure of Notched Ceramic Matrix Composite With TFP Patch Reinforcement

An advanced modeling strategy for notched ceramic matrix composite coupons with patch reinforcement was proposed to investigate the failure mechanisms. This model considered the tailored fiber–placed (TFP) yarn details obtained from the design phase and the embedded element concept which was used to successfully overcome the meshing difficulties. Inter-ply “glue” layers were simulated using the surface-based contact cohesive element method, so the delamination due to interfacial material discontinuity and damage can be well reproduced and analyzed. For composite ply, the energy-based composite progressive damage model that is independent of the mesh size was applied. Virtual test campaign was performed with a variety of geometrical and material parameters, and the damage and failure mechanisms based on the stress analysis can be revealed to support the design optimization of patch reinforcement.

Introduction

Continuous silicon carbide fiber–reinforced silicon carbide ceramic matrix (SiC_f/SiC) composites are considered to be candidate accident-tolerant fuel (ATF) cladding materials due to their excellent ablation resistance, corrosion resistance, and radiation tolerance (Snead et al., 2007). However, despite the substantial achievements, there are still some key problems that need to be solved to satisfy the requirement of engineering application. For example, it is often inevitable to manufacture open holes or notches in the engineering composite components. In the assembling process of SiC_f/SiC composite flame holders (Berdoyes et al., 2005), some hole flanges are needed for joining (Figure 1A). In the roller kiln or tunnel kiln system, there are also some holes in the silicon carbide ceramic beam and rod for assembly (Figures 1B,C). Nevertheless, the SiC_f/SiC composites have the properties of high hardness and brittleness, and the stress concentration caused by notches, holes, or attachment points is a threat to structural safety and reliability.

FIGURE 1

FIGURE 1. SiC ceramic matrix open-hole composite components: (A) flame holders; (B) beam; (C) rod.

The presence of a hole or notch in a composite laminate is associated with stress concentration and out-of-plane stresses and will produce a change in the failure mechanisms and a failure strength reduction of the laminate compared to a laminate without a notch. In the breakage of an open hole or notch laminate subjected to engineering loads, several failure mechanisms can be observed including matrix cracking, fiber breakage, and delamination. Consequently, local reinforcement around an open hole or notch is often required in the composite structure design. Although the mechanical joining technique with bolted reinforcement widely used in the traditional engineering materials such as steel, aluminum, or plastic provides an easy engineering solution, the drilled holes required for the bolted joints in the composite laminate will further remarkably reduce the strength of the structure by additional fiber breakage and delamination. The detailed damage introduced by the drilling process can be found in the works of Hocheng and Tsao (2006), Tsao and Hocheng (2004), and Srinivasa Rao et al. (2008). Consequently, innovative reinforcement methods for the composite laminate with an open hole or notch are required in engineering structure design.

The tailored fiber placement (TFP) technology that is based on embroidery machines was developed by the Institute of Polymer Research Dresden (Crothers et al.; Gliesche and Feltin; Rothe and Feltin, 1994). According to the designed reinforcement paths, the machine will stitch a yarn onto a base material in almost any desired orientation. Other than isotropic materials whose stress concentration can be only reduced by geometrical optimization, the anisotropic materials, such as FRPs, can be optimized based on the tailored fiber orientations that locally follow the principal stresses. Therefore, the maximum properties can be achieved along the fiber direction. Meanwhile, the stress concentration introduced by notches can be efficiently reduced to the largest extent. Gliesche et al. (2003) applied the TFP technique to a notched textile composite specimen. It was reported that the damage of the reinforced sample started outside of the reinforced area. The strength of the sample was 94% that of the un-notched specimen and 33% higher than that of the one without reinforcement.

The notched sample has been numerically studied since the 1970s. Earlier researchers employed the finite element (FE) method (Hillerborg et al., 1976; Kwon and Berner, 1995; Kwon and Craugh, 2001), in which the damage modes were considered and micromechanical constitutive law was applied. Thereafter, continuum damage modeling (CDM) (Chang and Chang, 1987; Davila et al., 2005; Forghani et al., 2013) and discrete modeling, e.g., cohesive element method (Turon et al., 2010), were developed to study the damage caused by stress concentration.

In contrast to the sample with an open hole or with traditional reinforcements, however, the notched sample reinforced by the TFP patch has rarely been studied. Koricho et al. (2015) investigated the TFP-made specimen in comparison with drilled composite samples, both experimentally and numerically. The FE model of Koricho was based on the 2D Hashin failure criterion. Temmen et al. developed a tool chain to optimize the TFP process. The Puck failure criterion was adopted in order to distinguish the fiber rupture from the inter-fiber fracture of the stitched yarn. Gliesche et al. (2003) carried out research on the reinforcement of the TFP patch on the unidirectional laminate. However, the work of Koricho, Temmen, and Gliesche did not explicitly reproduce the single yarn embedded in the patch that exhibited high inhomogeneity. Meanwhile, the ply–ply and patch–sample interfacial properties, which affect the damage initiation location and propagation, were not accounted for.

Furthermore, the studies on mechanical properties of the reinforced sample with an open hole or notch are mainly focused on polymer matrix composites rather than ceramic matrix composites. This is partly due to the fact that ceramic matrix composite technology is still being developed and the ceramic matrix composite experiments are time-, money-, and energy-consuming. However, the stress concentrations caused by a hole or notch are inevitable with the gradual application of ceramic matrix composite materials. As a result, it is vital to investigate the strength of open-hole ceramic matrix composites and the related reinforcement methods.

In this paper, an advanced three-dimensional modeling strategy for the TFP patch–reinforced ceramic matrix composite sample with an open hole is presented. It possesses the following features:

1) The placed yarn that is consolidated in the patch is fully simulated as a piece-wise orthotropic material using solid elements. It is nested in the matrix mesh using the “embedded element technique.”

2) To predict the material damage of the yarn and the sample with an open hole that is strengthened by woven fabrics, an energy-based damage evolution mode proposed by Maimí et al. (2007) is applied. The damage in a ply is triggered by the maximum stress failure criterion.

3) The interface between the TFP patch and the composite sample, as well as those between plies in the composite sample, is simulated using the surface-based cohesive behavioral properties, which can well represent a quasi-zero-thickness cohesive layer.

A Python script is written to automatically generate the FE model according to user definitions, e.g., coupon size, hole diameter, size of the reinforcement, number of plies, fiber orientations, and material properties. With this FE model, the progressive damage of the TFP yarn, woven composite plies, and interfacial delamination can be analyzed. The model is applied to investigate the damage mechanism of the patch-reinforced sample with a variety of geometrical and material parameters. The results provide a promising opportunity for quick design and optimization.

Model Construction

TFP Yarn Mesh

Following the designed pattern in CAD software (Figures 2A, C), the yarn is placed and stitched onto the base material to produce the reinforcement (Figures 2B, D). With the chemical vapor infiltration (CVI) technique, the TFP reinforcement could be consolidated within the SiC matrix to produce the composite reinforcement patches. Thereafter, the patch and the sample could be joined with the Ti₃SiC₂ tapes and the in situ reaction TiC gradient layer via FAST (Zhou et al., 2018), while the open holes of the patch and base sample are aligned together to form the TFP patch reinforcement.

FIGURE 2

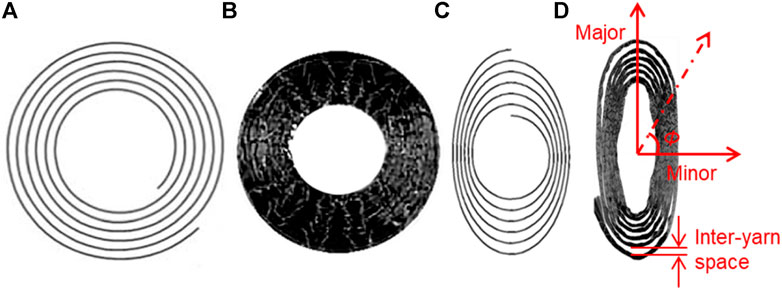
FIGURE 2. TFP patches: (A,C) TFP patterns designed in CAD software; (B,D) stitched yarns (Gliesche et al., 2003).

The TFP pattern is defined in CAD software in the format of “STandard for the Exchange of Product model data” (STP), from which the points’ coordinates can be extracted. Based on these point coordinates, the yarn’s 3D mesh is generated (Figure 3A). Each element is defined with a local coordinate that follows the local fiber orientation (Figure 3B). A typical feature is demonstrated in Figure 2D that the stitched yarn has a transitional cross-sectional area and inter-yarn space. The yarn width and space gradually reduce to the minimum, respectively, when the angle $\varphi$ decreases from 90° to 0°. This feature can be well reproduced in the given mesh (Figures 3A,C). During the change of the width, the cross-sectional area of the yarn is maintained constantly. Thus, the yarn thickness of the mesh varies inversely proportional to the yarn width.

FIGURE 3

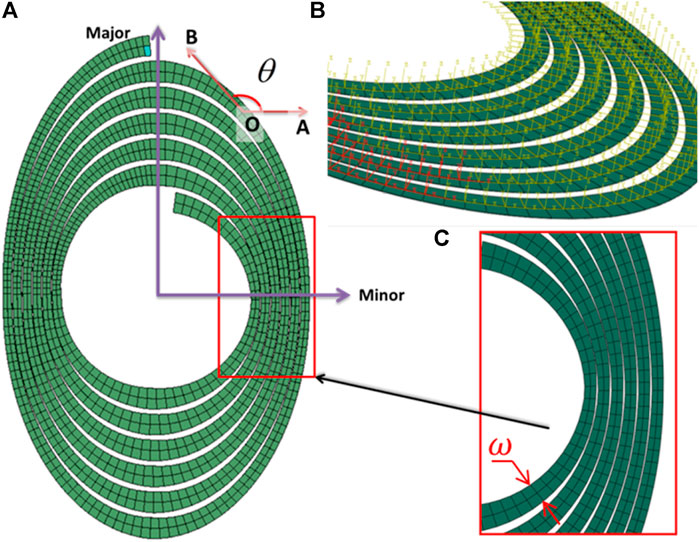
FIGURE 3. Mesh of the TFP yarn: (A) 3D solid mesh generated following the pattern in Figure 2C, (B) orthotropic material with local fiber orientation definition, and (C) transitional yarn width and inter-yarn space.

The instant width of the TFP yarn can be calculated as

$\omega =\{\begin{array}{l}{\omega }_0\left[\frac{2\left(1-\eta \right)}{\pi }\left(\theta -0.5\pi \right)+\eta \right],\theta \in \left[0,\pi \right]\hfill \\ {\omega }_0\left[\frac{2\left(1-\eta \right)}{\pi }\left(\theta -0.5\pi \right)+\eta \right],\theta \in (-\pi ,0],\hfill \end{array}(1)$

where the angle $\theta \in \left(-\pi ,\pi \right]$ is the angle between the horizontal axis OA and the tangent line OB (Figure 3A). O is an arbitrary point on the TFP path. $\eta$is the width reduction factor from measurement. ${\omega }_{\text{0}}$ is the maximum width of the yarn on the major axis, while $\eta ·{\omega }_{\text{0}}$ is the minimum width on the minor axis. Apparently, $\omega$ reaches ${\omega }_{\text{0}}$ when $\theta$ equals zero or $\pi$ and has the minimum when $\theta$ is $\pm \text{0}\text{.}5\pi$. To keep the cross-sectional area constant, the instant thickness at point O is

$T=\frac{{\omega }_0·T_0}{\omega }.(2)$

where $T_0$ is the yarn thickness on the major axis.

TFP Patch Reinforcement

The geometric outer contour of the TFP patch reinforcement is a standard circle or a standard ellipse with a hole. In the traditional continuous model, the matrix mesh is obtained by Boolean subtraction of the TFP patch and the yarn mesh. However, the extremely tiny inter-yarn space between yarns makes the matrix mesh too small, which leads to poor mesh quality and high computational cost.

An alternative is the “mesh superposition technique” (McGlockton et al., 2003; Yang and Cox, 2010), with which the yarn mesh is embedded into the mesh of the matrix material (Figure 4). Actually, the “mesh superposition technique” is a method of multi-point constraints in Abaqus. Geometrically, the matrix mesh includes the yarn mesh. The matrix mesh is the host mesh, which is considered an independent model from the point of view of translational degrees of freedom (DOFs). The kinematic constraints are created between the nodes of the embedded and the host elements. The translational degrees of freedom of the embedded node are interpolated as the values of the DOFs of the surrounding host nodes.

FIGURE 4

FIGURE 4. “Mesh superposition technique” applied to the TFP patch: (A) circular patch and (B) elliptical patch. The yarn mesh is embedded into the matrix mesh to avoid the meshing difficulties at the places where the inter-yarn space is extremely tiny.

The mesh superposition technique is an effective solution to the problem of composite meshing, as the volume mesh of the separate parts is much simpler and more efficient than that in a full model.

Sample With Open Hole

As shown in Figure 5A, the coupon is partitioned into specific sections (1) and (2), to apply the local refined structural mesh. The locally well-structured mesh serves the purpose of dealing with high stress concentration near the hole.

FIGURE 5

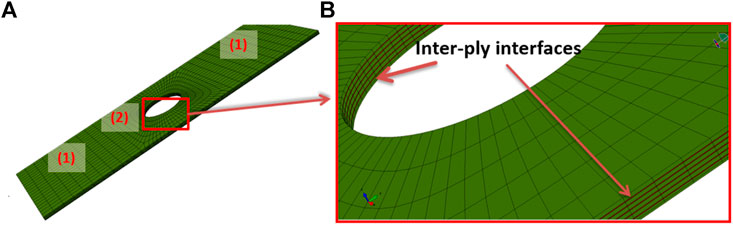
FIGURE 5. Sample with an open hole: (A) a locally refined mesh is used to deal with stress concentration; (B) inter-ply interfaces are modeled using the “surface-based cohesive behavior model.”

In Figure 5B, each ply of the composite is modeled. There are two ways to create the interface between neighboring plies or between the TFP patch and the base laminate sample: “cohesive element,” and “surface-based cohesive behavior model” (SBCBM). Compared to the cohesive element, the SBCBM, which correlates the inter-ply traction and separation between plies, is physically realistic and numerically efficient. Usually, the inter-ply interface is so thin that the thickness, which is normally needed by cohesive elements, is negligibly small and hard to obtain. Moreover, the SBCBM does not require the contacting surface pair possessing a coincident mesh by sharing common nodes. Bonded by the SBCBM, an FE model of the single-side TFP-patched composite laminate sample is assembled together and demonstrated in Figure 6. This model contains 28,376 elements, which are linear solid elements C3D8 containing eight integration points, and 40,876 nodes in total. The model will be solved using the Abaqus explicit solver.

FIGURE 6

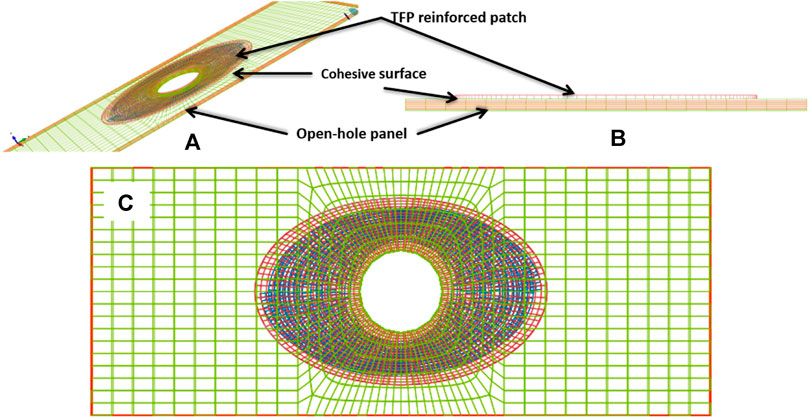
FIGURE 6. The whole set of TFP-reinforced coupons where the TFP patch and plies are assembled together using the SBCBM: (A) ISO view of the model, (B) side view of the model, and (C) top view.

Material Models

Interfacial Models

Traction–Separation Failure Model

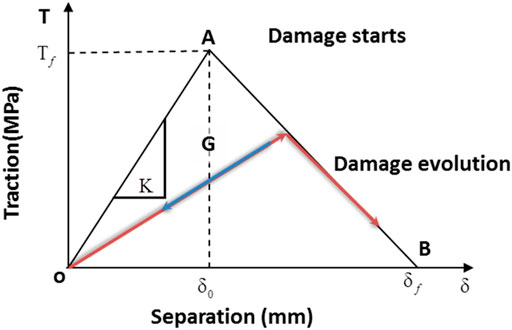
As aforementioned, the ply interfaces are modeled using the SBCBM. The corresponding linear damage evolution is demonstrated in Figure 7. Instead of using strain and stress, this damage evolution model is a correlation between the traction force and the separation displacement. In the elastic zone ($\delta <{\delta }_0$), no material damage occurs. Once the traction reaches $T_f$ (A in Figure 7), the interfacial material starts to degrade by irreversibly losing its properties (A to B). After B, the interface loses all the properties and delamination takes place. The corresponding separation displacements to points A and B are ${\delta }_{\text{0}}$ and ${\delta }_f$, respectively. Under a three-dimensional stress state, the separation $\delta$ stands for ${\delta }_n$,${\delta }_s$, and ${\delta }_t$, while the traction $T$represents $t_n$, $t_s$, and $t_t$. The subscripts n, s, and t mean the normal direction, first shear direction, and second shear direction, respectively. The critical fracture energy $G$ ($G_I$, $G_{II}$, and $G_{III}$ for Mode I, II, and III fracture energies, respectively) and cohesive strength ($t_n^0$, $t_s^0$, and $t_t^0$) should be provided as inputs. The initial stiffness $K$ is automatically selected by the system as contact penalty.

FIGURE 7

FIGURE 7. Linear damage evolution of the traction–separation model.

When the damage evolution is assumed to be linear as shown in Figure 7, the fracture energy $G$ is represented as

$G=\frac{1}{2}{T}_f{\delta }_f.(3)$

The fracture energies, $G_I$, $G_{II}$, and$G_{III}$ can be obtained through the double cantilever bending (DCB) test, end notched flexure (ENF) test, and edge crack torsion (ECT) test, respectively. In contrast, the cohesive strength $T_f$ is difficult to retain directly. They can be, nevertheless, reversely calculated by fitting the simulation results to the experimental data (Diehl, 2008).

Damage Model

The damage initiation is triggered by the quadratic nominal stress criterion, as shown in the following equation:

${\left(\frac{\langle t_n\rangle }{t_n^0}\right)}^2+{\left(\frac{t_s}{t_s^0}\right)}^2+{\left(\frac{t_t}{t_t^0}\right)}^2=1.(4)$

The Macaulay brackets $\langle \cdot \rangle$ imply that compressive stress will not cause delamination. The mixed mode damage is governed by Benzeggagh–Kenane mixed mode behavior (Benzeggagh and Kenane, 1996):

$G_I+\left(G_{II}-G_I\right){\left\{\frac{G_{II}+G_{III}}{G_I+G_{II}+G_{III}}\right\}}^{\xi }=G.(5)$

where $\xi$ is the material constant determined by experiments. $G$ is the crucial fracture energy obtained from the experiment, too. It is very convenient when the fracture energy along the first and second shear directions is the same ($G_s=G_t$). Then, Eq. 5 is rewritten as

$G_n+\left(G_s-G_n\right){\left\{\frac{2G_s}{G_n+2G_s}\right\}}^{\xi }=G.(6)$

Considering the interfacial properties for epoxy matrix composites and SiC matrix composites are different, the different input data are listed in Table 1.

TABLE 1

TABLE 1. Interfacial properties for SiC matrix composites (Choi and Kowalik, 2008; Liu et al., 2016).

Composite Ply Model

Continuum Damage Model

Muñoz et al. (2015) proposed a continuum damage model to describe the progressive damage of the composite ply. Five damage functions that represent fiber loading directions are defined in Table 2.

TABLE 2

TABLE 2. Damage activation functions for a composite ply (Muñoz et al., 2015).

In Table 2, the symbols $\phi$, $E$, $S$, $\epsilon$, and $\tau$ stand for the damage activation function, Young’s modulus, the strength, the strain, and the shear stress, respectively. The superscripts t and c mean tension and compression, respectively. In the post-damage phase, the compliance matrix was defined as follows (Maimí et al., 2007):

$\mathit{C}=\left[\begin{array}{ccc}\frac{1}{\left(1-d_1\right)E_{11}}& -\frac{{\mu }_{12}}{E_1}& \text{0}\\ & \frac{1}{\left(1-d_2\right)E_{22}}& \text{0}\\ sym& & \frac{1}{\left(1-d_6\right)G_{12}}\end{array}\right],(7)$

where $\mathit{C}$ is the compliance matrix; $d_N$ (N = 1, 2, 6) are the damage variables; and $\mathit{\mu }$ is Poisson’s ratio.

After the onset of damage, the damage propagation is controlled by damage activation functions $F_N$ (N = 1+, 1−, 2+, 2−, 6), corresponding to loadings applied to the material in the local frame. N = 1+, 1− represents tensile failure and compressive failure in direction 1. N = 2+, 2− represents tensile failure and compressive failure in direction 2. N = 6 represents in-plane shear failure. The damage activation functions have the following expression:

$F_N={\phi }_N-r_N\le 0,(8)$

where $r_N$ (N = 1+, 1−, 2+, 2−, 6) define the elastic boundary in the post-damage phase, before further damage takes place. Maimí et al. (2007) related $r_N$ to the damage variables $d_N$ (N=1+, 1−, 2+, 2−, 6) by exponential law:

$d_N=1-\frac{1}{r_N}\exp \left({\text{A}}_{\text{N}}\left(1-{\text{r}}_{\text{N}}\right)\right),(9)$

where $A_N$ (N = 1+, 1−, 2+, 2−, 6) are material-dependent coefficients, defined as

$A_N=\frac{2l^{\ast }{X}_N^2}{2E_N{G}_N-l^{\ast }{X}_N^2},(10)$

where $E_N$, $X_N$, and $G_N$ (N = 1+, 1−, 2+, 2−, 6) are the elastic moduli, strengths, and fracture energies. $l^{\ast }$stands for the characteristic length of a finite element. The parameter $A_N$, according to Bazant’s model (Bažant and Oh, 1983), guarantees that the damage propagation and energy release are independent of the mesh size (Maimí et al., 2007). The fracture energies G_N control element deletion.

Input of Consolidated TFP Yarn and Woven Laminates

The consolidated TFP yarn can be treated as a homogeneous and transverse isotropic material. The strength components, stiffness components, and Poisson’s ratios of the impregnated yarns are calculated (Table 3) using Chamis’s equations (Chamis et al., 2013) based on the properties of constituents provided by Presby et al. (2019) (Table 4).

TABLE 3

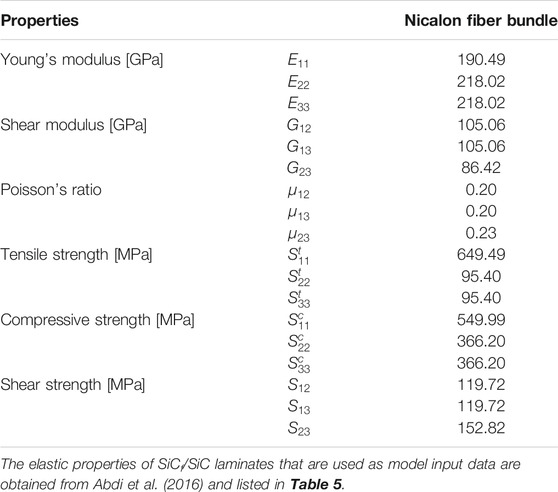
TABLE 3. Mechanical properties of the fiber bundle consolidated with the SiC matrix, calculated using Chamis’s equations (fiber volume fraction $V_f$ = 26.42%).

TABLE 4

TABLE 4. Typical mechanical properties of the fiber and matrix (Presby et al., 2019).

Numerical Tests

Numerical Tests on Notched Sample

Strength Prediction

A comprehensive study on strength and fracture criteria in fabric composite samples with a circular hole was carried out by virtual test. The detailed elastic properties of the woven SiC_f/SiC composite samples that contain [0, 45, −45, 0] plies are listed in Table 5.

TABLE 5

TABLE 5. Elastic properties of SiC_f/SiC woven composites (Abdi et al., 2016).

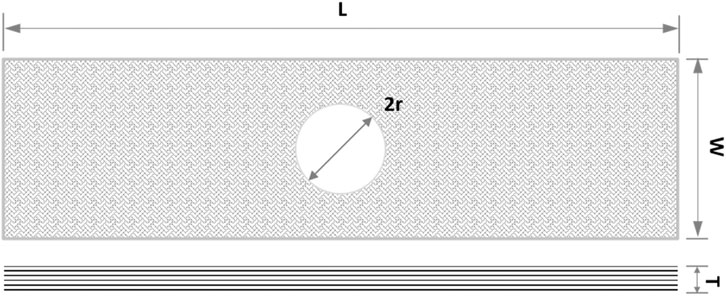
To run a calculation, the necessary material properties as input for the model are already provided in Material Models. The dimensions of the notched sample are described in Figure 8. The radius of the hole varies from 2 to 10 mm, in order to investigate the dependence of failure on hole size.

FIGURE 8

FIGURE 8. Dimensions of the sample: L = 150 mm, W = 40 mm, T = 1 mm, and r = 2–10 mm.

The calculated strengths of the drilled sample with different hole radii (2–10 mm) are listed in Table 6. The residual strength of the laminate with an open-hole radius of 10 mm is only 36.32% of the strength of the un-notched laminate. In this case, it is necessary to adopt reinforcement methods for the composite laminate with an open hole or notch.

TABLE 6

TABLE 6. Predicted results of the notched woven SiC_f/SiC composite sample: the sample’s width is 40 mm.

Stress Analysis

In Figure 9, the tension and shear contours immediately before the damage onset for a [0, 45, −45, 0] laminate, which has a hole radius of R = 10 mm, are demonstrated. The stress concentration factor, which is defined as the ratio of the maximum tensile stress value on the edge of the hole (Figures 9A–D) to the value of external tensile stress (90 MPa), is 4.4 and 2.2 for 0^o and 45^o plies, respectively. The external tensile stress means loading force divided by the material cross-section without the hole. The stress concentration factor indicates that the fiber rupture will take place firstly in 0^o plies and then extend to ±45^o plies (Figure 10). Under the on-axis loading, the ±45^o plies (Figures 9F, G) bear the shear loadings effectively, three times those of 0^o plies (legends in Figures 9E, H).

FIGURE 9

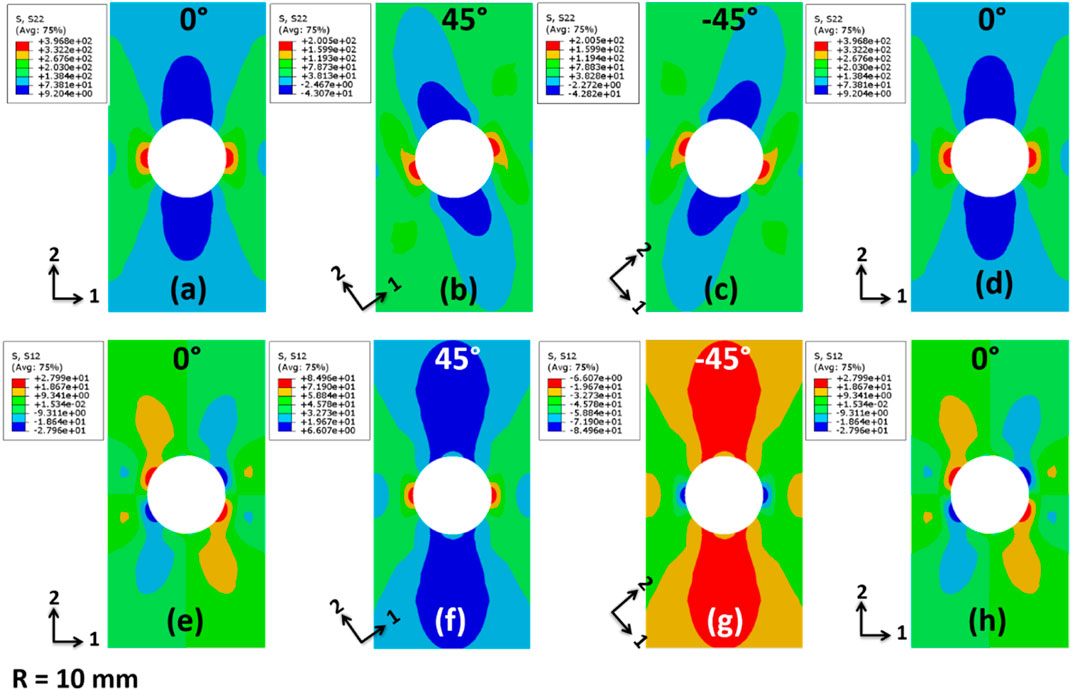
FIGURE 9. Stress contours of [0, 45, –45, 0] laminates immediately before damage onset (tensile stress $\sigma =96$ MPa): (A–D) plot of tensile stresses along the fiber direction; (E–H) in-plane shear stress.

FIGURE 10

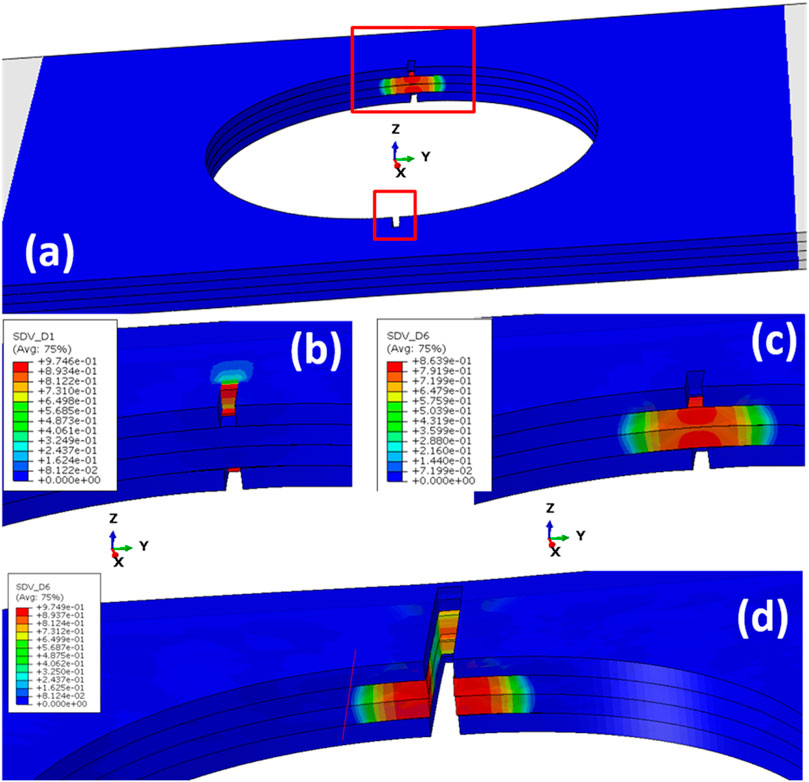
FIGURE 10. Damage development: (A) damage onset; (B) cracks propagate in 0^o plies (external tensile stress $\sigma =122$ MPa), (C) shear damage already accumulated in ±45^o plies (external tensile stress $\sigma =122$ MPa); (D) cracks propagate to ±45^o plies while the external tensile stress snaps back to 118 MPa. SDV_D1 and SDV_D6 stand for damage variables $d_N$, where N equals ±1 and 6, respectively.

When element deletion is activated, the aforementioned damage initiation and propagation can be clearly demonstrated, as shown in Figure 10. The cracks (due to fiber rupture, damage variable $d_1=\text{ 0}\text{.}99$) start in 0^o plies when the sample is applied with external stress that equals 122 MPa (Figures 10A, B). At this moment, except the shear damage (Figure 10C), there is no fiber rupture occurring in ±45^o plies (Figure 10B). The cracks propagate in 0^o plies till the applied stress reaches 146 MPa, and suddenly, the ±45^o plies are torn while applied stress snaps back to 118 MPa (Figure 10D).

Delamination

It is obvious that stress concentration “amplifies” the loading at the hole circumference. Furthermore, due to high material discontinuity at the interfaces between the 0^o ply and the 45^o ply, the in-plane shear stress (Figure 11A) and out-of-plane shear stress (Figures 11B, C) help to form the mild interfacial damage (Figure 11D) in an early stage when the external stress is only 45 MPa. Remarkable delamination presents when the 0^o laminate starts to degrade (Figure 11E), when the external load reaches 90 MPa. The delamination grows fast till the final failure (Figure 11F). The delamination between ±45^o plies, where the in-plane shear and out-of-plane shear are neglectable, is milder than that between the 0^o ply and the 45^o ply (Figures 11D, E).

FIGURE 11

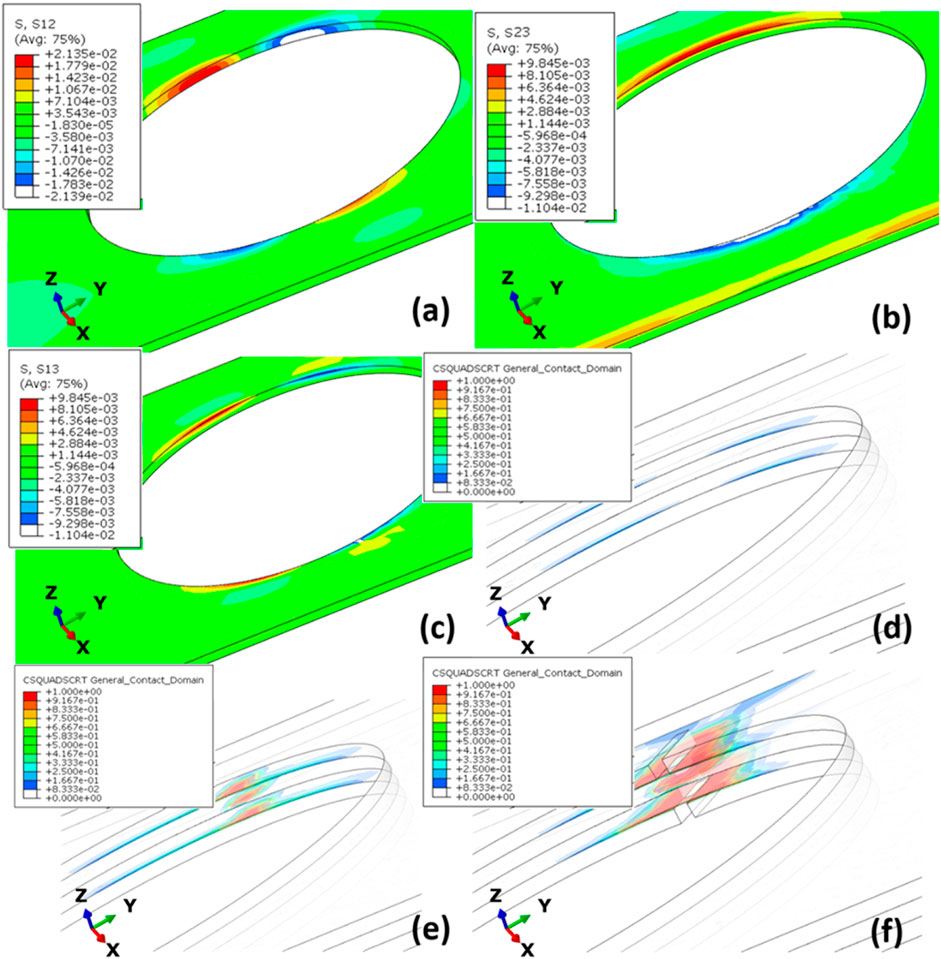
FIGURE 11. Delamination evolution: (A) in-plane shear stress at the interfaces between the 0^o ply and the 45^o ply, (B, C) out-of-plane shear stress between the 0^o ply and the 45^o ply, (D) interface damage starts when the external tensile stress is 45 MPa, (E) delamination starts when 0^o plies start to damage (tensile stress $\sigma =90$ MPa), and (F) crack grows accompanied with massive delamination.

Numerical Tests on Notched Sample With Patch Reinforcement

With the help of the FE model, virtual test campaign is carried out for notched samples reinforced by circular annular (CA) and elliptical annular (EA) patches, based on the patching parameters listed in Table 7.

TABLE 7

TABLE 7. Patching parameters to be studied in virtual test campaign.

The dimensions of the virtual test samples are delineated in Figure 12A, where the patch matrix material is set to invisible. The geometrical parameters of the samples are as follows: L = 150 mm, W = 60 mm, T = 2 mm, r = 10 mm, D = 47 mm, a = 41 mm, and b = 80 mm, where D, a, and b are the outer diameter of the CA patch and outer major axis and minor axis of the EA patch, respectively. The single-side reinforced (SSR) and double-side reinforced (DSR) samples are sketched in Figure 12B.

FIGURE 12

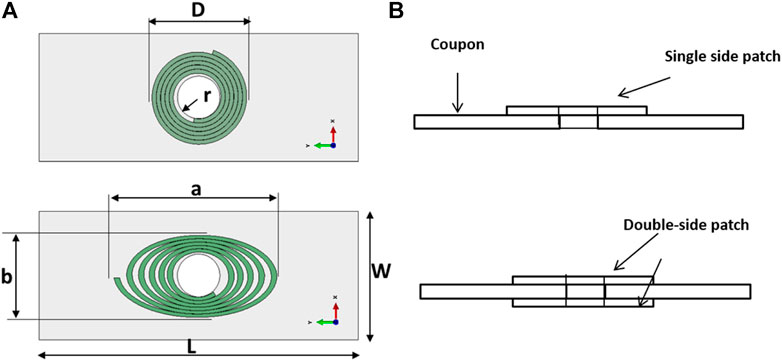
FIGURE 12. Sketches of the virtual test samples: (A) sketches of the CA- and EA-reinforced samples; (B) sketches of SSR and DSR samples. The dimensions of the sample are L = 150 mm, W = 60 mm, T = 2 mm, r = 10 mm, D = 47 mm, a = 41 mm, and b = 80 mm.

Study on Patching Parameters

In Figures 13A, B, the ultimate applied stress and apparent moduli of the CA patch–reinforced sample, as well as those of the undrilled sample and drilled sample, are delineated. The abbreviations OP, NP, WS, WD, YS, and YD represent the original sample without hole, sample with a hole, and drilled sample with woven SSR, with woven DSR, with TFP SSR, and with TFP DSR, respectively. From Figures 13A, B, two conclusions can be drawn: 1) The TFP patch exhibits overwhelming advantages in terms of enhancing the strength. In contrast to the woven fabric, the TFP yarn seems to be more efficient in resisting the maximum principal stress. 2) DSR samples show higher strengths and moduli than SSR samples. SSR (Figure 13C) cannot omit the stress concentration on the un-patched side (Figure 13E), where the damage and crack occur earlier. In contrast, the DSR samples (Figure 13D), where the same total amount of reinforcement (evenly separated on double sides) as in SSR is used, can ideally balance the load, eliminate the stress concentration, and delay the damage onset (Figure 13F).

FIGURE 13

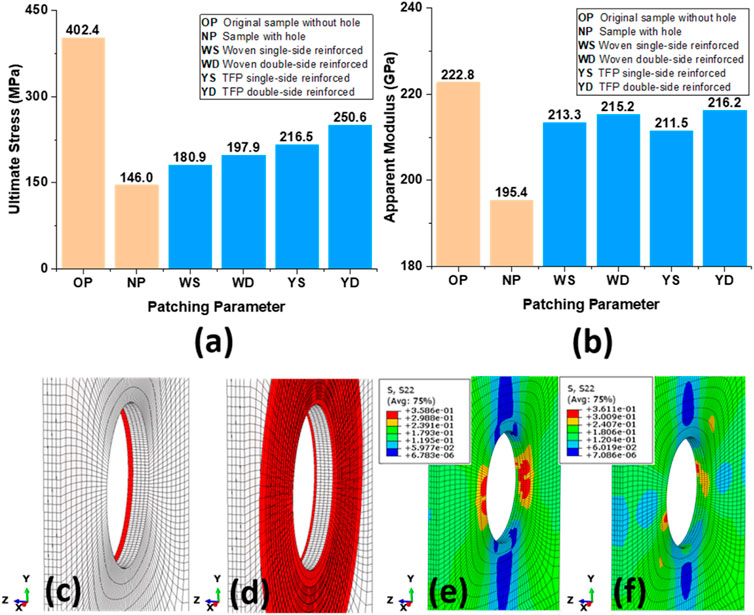
FIGURE 13. Study on patching parameters: (A) comparison of ultimate stress, (B) comparison of apparent moduli, (C) SSR sample, (D) DSR sample, (E) S22 contour for the SSR sample, and (F) S22 contour for the DSR sample.

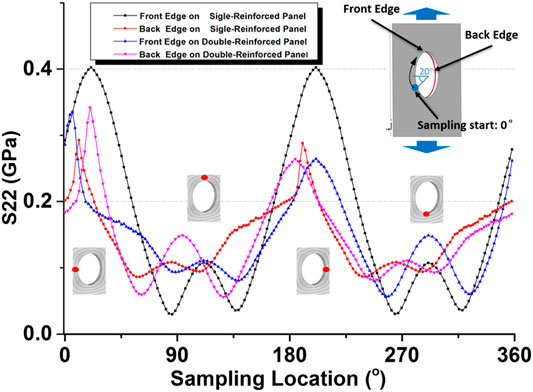
In order to analyze the stress distribution around the hole, S22 contours are sampled clockwise from the front and back sides of the sample along the hole edges (Figure 14). For the SSR sample, the back edge has patch reinforcement, while the front has not (Figures 13C, E). It is worth noting that the stress (solid-square–symboled curve in Figure 14) obtained from the front edge in Figures 13C, E shows larger oscillation and higher peak values of 400 MPa, while the edge with patch reinforcements reads a value of about 350 MPa. This higher local stress leads to earlier damage onset and well explains the aforementioned conclusion ii).

FIGURE 14

FIGURE 14. S22 distribution on the edges of the hole of the SSR sample and DSR sample.

Study on Patch Shape

In Figures 15A, B, the ultimate applied stress and apparent moduli for CA and EA patch–reinforced samples, as well as those of the undrilled and drilled samples, are delineated. Obviously shown in Figures 15A, B, the EA patches exert more effectiveness in enhancing the apparent properties of the drilled samples. The TFP DSR can increase the strength from 146 MPa up to 319 MPa, 79% of the strength (402 MPa) of the undrilled sample (Figure 15A). The apparent modulus increases from 195.4 GPa up to 235.1 GPa, higher than that of the undrilled one (222.8 GPa) (Figure 15B).

FIGURE 15

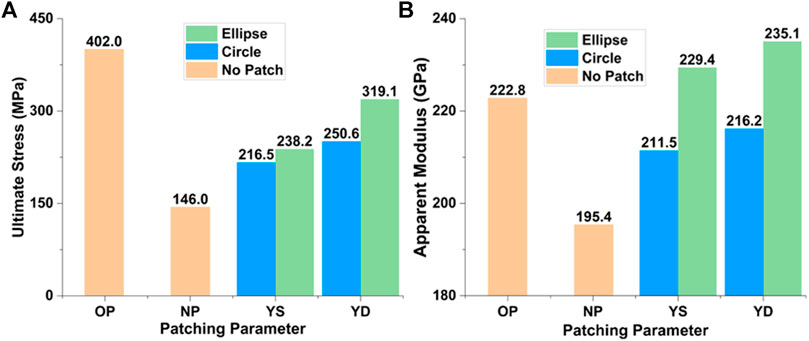
FIGURE 15. Study on patch shape: (A) comparison of ultimate tensile stress; (B) comparison of apparent moduli. The abbreviations YS and YD represent the drilled sample with TFP SSR and TFP DSR, respectively.

The S22 distributions on the edges of the hole for circular annular (CA) and elliptical annular (EA) TFP patch–reinforced samples are extracted and compared in Figure 16. Stress curves are extracted from both sides of the SSR sample. The stress curves on the unpatched side show higher oscillations. The peak values of the CA-patched sample reach 415 MPa, 15 MPa higher than that of the EA-patched sample. This indicates that the former has an earlier damage initiation and thus lower strength (Figure 15A). Comparing the stress curves from the patched side, the curve (solid triangles) of the EA-patched sample is much flatter than the CA counterpart (solid circles), which suggests the EA patch has more efficiency in reducing the local stress concentration.

FIGURE 16

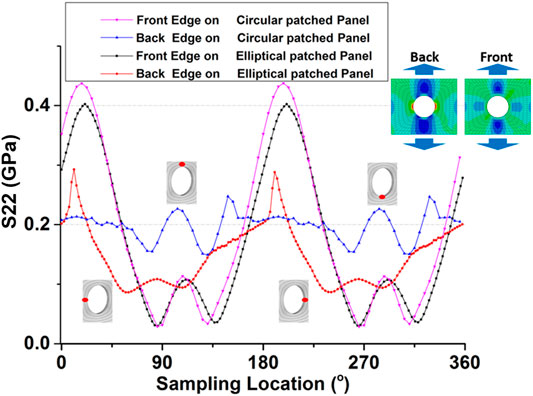
FIGURE 16. S22 distribution on the edges of the hole of CA- and EA-TFP single-side reinforced (SSR) samples.

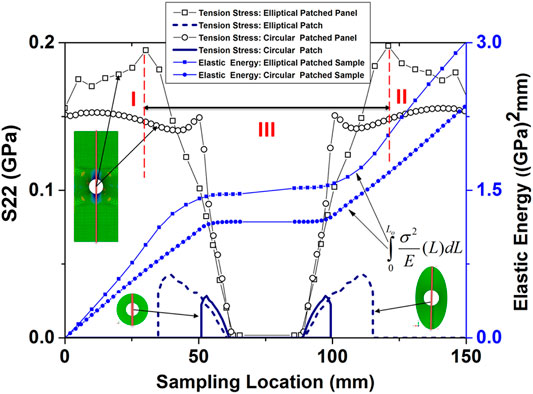
The tensile stress along the longitudinal axis of the notched coupons and patches (vertical red lines sketched on the sample and patches) on the contacted surfaces of the EA and CA patch–reinforced samples is extracted along with and without the nominal elastic energy along the axes (Figure 17). Stress curves are extracted from the patch side of the SSR sample. When applied with the same external strain, the former stress curve shows higher values in zones I and II (outside of the patching area). The local stress reaches the maximum of 200 MPa on the boundary between zones I and III, as well as that between zones II and III. This implies that the damage will take place on the drilled sample next to the edge of the patch when the patch is strong enough and perfectly bonded.

FIGURE 17

FIGURE 17. Tensile stress (S22) along the longitudinal axes of the patched samples and patches.

The total elastic energy stored in the sample can be represented as

$G_e={\displaystyle {\int }_V\frac{{\sigma }^2}{E}}dv=\overline{E}·{\overline{\epsilon }}^2·V,(11)$

where $G_e$ is the total elastic energy and $\sigma$, $\overline{\epsilon }$, $V$, $E$, and $\overline{E}$ are the local stress, the external strain, the total volume of the sample, Young’s modulus, and the apparent Young’s modulus, respectively. Using the above equation, the apparent tensile modulus can be evaluated. To explain the reason why the elliptical TFP single-side reinforced sample possesses a higher apparent modulus than the circular TFP single-side reinforced sample (229.4 vs. 211.5 GPa) (Figure 15B), a concept of nominal elastic energy can be introduced as

${}_{ne}G=w·{\displaystyle {\int }_0^L\frac{{\sigma }^2\left(l\right)}{E}dl={}_{ne}\overline{E}·{\overline{\epsilon }}^2·w·L},(12)$

where L and w are the length of the sample and the width of the elements lying on the loading sampling path. ${}_{ne}G$ and ${}_{ne}\overline{E}$ are the nominal elastic energy stored in the elements along the sampling path shown in Figure 17 and the nominal elastic modulus, respectively. The tensile stress $\sigma$ is the function of the nodal coordinate on the loading path, as demonstrated in Figure 17. Hence, the ratio of the nominal moduli, $R_n$, for elliptical and circular TFP single-side reinforced samples reads

$R_n=\frac{{\overline{E}}_{Ellip}}{{\overline{E}}_{Circ}}=\frac{ne{G}_{Ellip}^s+ne{G}_{Ellip}^P}{ne{G}_{Circ}^s+ne{G}_{Circ}^P}=\frac{{\displaystyle {\int }_0^L\frac{Ellip{\sigma }_S^2\left(l\right)}{E_S}}dl+{\displaystyle {\int }_0^L\frac{Ellip{\sigma }_P^2\left(l\right)}{E_P}}dl}{{\displaystyle {\int }_0^L\frac{circ{\sigma }_S^2\left(l\right)}{E_S}}dl+{\displaystyle {\int }_0^L\frac{circ{\sigma }_P^2\left(l\right)}{E_P}}dl},(13)$

where subscripts and superscripts “Ellip,” “Circ,” “S,” and “P” stand for elliptical and circular patches and the drilled sample and patch, respectively. The integrals in the above equation are calculated and presented in Figure 17, too. It is apparent that $R_n$ is larger than 1.0. The factor $R_n$ reveals the reason why the apparent modulus of the elliptical TFP single-side reinforced sample (229.4 GPa) is larger than that of the circular one (211.5 GPa) (Figure 15B). By applying the same deformation, more elastic energy is stored in the elliptical patch and zones I and II of the drilled coupon for the elliptical TFP single-side reinforced sample than for the counterpart.

Conclusion

In this work, an advanced progressive damage FE model for the notched ceramic matrix composite laminate reinforced by the special TFP composite patch has been established. An energy-based composite progressive damage model that is independent of the mesh size is applied. This model also accounts for the TFP yarn details that are inherited from TFP path design. The embedded element concept is used to successfully avoid the meshing difficulties. The inter-ply “glue” layer is simulated using the surface-based contact method, and the delamination due to interfacial material discontinuity and damage can be well reproduced and analyzed. A virtual test campaign was carried out based on a variety of geometrical and material parameters. Based on the stress analysis, the related damage mechanism was revealed. From the FE analysis, the following conclusions can be drawn:

1) The optimized TFP patch is more efficient in minimizing the stress concentration around the hole edges than the woven fabric.

2) The double-side reinforcement, compared to the single-side counterpart, reduces the stress concentration introduced by the geometrical asymmetry on the unpatched side and thus highly increases the modulus and strength.

3) The elliptical patch has shown better mechanical performance. The apparent strength reaches 79% of the un-notched sample, while the modulus exceeds that of the original sample.

In summary, the proposed FE model well simulated the damage behavior of the patch-reinforced ceramic matrix composite sample. Through the FE analysis, the double-side elliptical sample reinforced by the TFP yarn is highly recommended. In the future work, nevertheless, to correctly predict the orientation of crack propagation, especially that in 45^o plies, the enhanced FE method or the orientated mesh should be utilized.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding authors.

Author Contributions

GZ carried out investigation, ran the software, contributed to testing code components, and wrote the first draft of the manuscript. JT performed the methodology. GZ, JT, JW, YC, and YF curated the data. JW, YC, and YF were responsible for modeling and simulation. YC, SX, XJ, SZ, and JX contributed to supervision and funding acquisition. SL revised the first draft of the manuscript. SZ and JX contributed to project administration. GZ and JX contributed to supporting algorithms and reviewed and edited the paper.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52075526) and the Dalian University of Technology 2019 Discipline Platform Fund (No. 1000-82212201). The authors also gratefully acknowledge the National Key Research and Development Program (No. 2018YFB1107500), the “Ningbo 3315 Plan Innovation Team” (No. 2017A-28-C), the “Transformational Technologies for Clean Energy and Demonstration,” the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDA21010205), and the financial support from the National Young Talents Program of China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdi, F., Godines, C., Morscher, G. N., Choi, S., Villa Montero, M., Han, Z., et al. (2016). Foreign Object Damage and Fatigue after Impact Simulations on Flat and Curved Hi Nicalon and Hi Nicalon Type S (Mi Sic) Specimens at Room and 1200 C Using Building Block Approach in Turbo Expo: Power for Land, Sea, and Air. V006T002A007: American Society of Mechanical Engineers. doi:10.1115/gt2016-58086

CrossRef Full Text | Google Scholar

Bažant, Z. P., and Oh, B. H. (1983). Crack Band Theory for Fracture of concrete. Matériaux et Construction 16, 155–177. doi:10.1007/BF02486267

CrossRef Full Text | Google Scholar

Benzeggagh, M. L., and Kenane, M. (1996). Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/epoxy Composites with Mixed-Mode Bending Apparatus. Composites Sci. Tech. 56, 439–449. doi:10.1016/0266-3538(96)00005-X

CrossRef Full Text | Google Scholar

Berdoyes, I., Thebault, J., Bouillon, E., and Solide, S. P. (2005). Improved SiC/SiC and C/C Materials Applications Parts. Eur. Congr. Adv. Mater. Process., 1–7.

Google Scholar

Chamis, C. C., Abdi, F., Garg, M., Minnetyan, L., Baid, H., Huang, D., et al. (2013). Micromechanics-based Prqogressive Failure Analysis Prediction for WWFE-III Composite Coupon Test Cases. J. Compos. Mater. 47, 2695–2712. doi:10.1177/0021998313499478

CrossRef Full Text | Google Scholar

Chang, F.-K., and Chang, K.-Y. (1987). A Progressive Damage Model for Laminated Composites Containing Stress Concentrations. J. Compos. Mater. 21, 834–855. doi:10.1177/002199838702100904

CrossRef Full Text | Google Scholar

Choi, S. R., and Kowalik, R. W. (2008). Interlaminar Crack Growth Resistances of Various Ceramic Matrix Composites in Mode I and Mode II Loading. J. Eng. Gas Turbines Power 130. doi:10.1115/1.2800349

CrossRef Full Text | Google Scholar

Crothers, P. J., Drechsler, K., Feltin, D., Herszberg, I., and Bannister, M.. The Design and Application of Tailored Fibre placementFailure Criteria for FRP Laminates. 11. International Conference On Composite Materials, 39, 323–345. doi:10.1177/0021998305046452

CrossRef Full Text | Google Scholar

Davila, C.G., Camanho, P. P., and Rose, C.A. (2005). Failure Criteria for FRP Laminates. J. Compos. Mater. 39, 323-345. doi:10.1177/0021998305046452

CrossRef Full Text | Google Scholar

Diehl, T. (2008). On Using a Penalty-Based Cohesive-Zone Finite Element Approach, Part II: Inelastic Peeling of an Epoxy-Bonded Aluminum Strip. Int. J. Adhes. Adhesives 28, 256–265. doi:10.1016/j.ijadhadh.2007.06.004

CrossRef Full Text | Google Scholar

Forghani, A., Zobeiry, N., Vaziri, R., Poursartip, A., and Ellyin, F. (2013). A Non-local Approach to Simulation of Damage in Laminated Composites. Lancaster, PA: DEStech Publications, Inc.

Gliesche, K., and Feltin, D. Automated Manufacture of Textile Reinforcements by Tailored Fiber Placement. International Symposium on Composites Manufacturing for Aircraft Structures, 30–31.

Google Scholar

Gliesche, K., Hübner, T., and Orawetz, H. (2003). Application of the Tailored Fibre Placement (TFP) Process for a Local Reinforcement on an "Open-Hole" Tension Plate from Carbon/epoxy Laminates. Composites Sci. Tech. 63, 81–88. doi:10.1016/S0266-3538(02)00178-1

CrossRef Full Text | Google Scholar

Hillerborg, A., Modéer, M., and Petersson, P.-E. (1976). Analysis of Crack Formation and Crack Growth in concrete by Means of Fracture Mechanics and Finite Elements. Cement Concrete Res. 6, 773–781. doi:10.1016/0008-8846(76)90007-7

CrossRef Full Text | Google Scholar

Hocheng, H., and Tsao, C. C. (2006). Effects of Special Drill Bits on Drilling-Induced Delamination of Composite Materials. Int. J. Machine Tools Manufacture 46, 1403–1416. doi:10.1016/j.ijmachtools.2005.10.004

CrossRef Full Text | Google Scholar

Koricho, E. G., Khomenko, A., Fristedt, T., and Haq, M. (2015). Innovative Tailored Fiber Placement Technique for Enhanced Damage Resistance in Notched Composite Laminate. Compos. Structures 120, 378–385. doi:10.1016/j.compstruct.2014.10.016

CrossRef Full Text | Google Scholar

Kwon, Y. W., and Berner, J. M. (1995). Micromechanics Model for Damage and Failure Analyses of Laminated Fibrous Composites. Eng. Fracture Mech. 52, 231–242. doi:10.1016/0013-7944(95)00017-P

CrossRef Full Text | Google Scholar

Kwon, Y. W., and Craugh, L. E. (2001). Progressive Failure Modeling in Notched Cross-Ply Fibrous Composites. Appl. Compos. Mater. 8, 63–74. doi:10.1023/A:1008909000755

CrossRef Full Text | Google Scholar

Liu, H. T., Yang, L. W., Sun, X., Cheng, H. F., Wang, C. Y., Mao, W. G., et al. (2016). Enhancing the Fracture Resistance of Carbon Fiber Reinforced SiC Matrix Composites by Interface Modification through a Simple Fiber Heat-Treatment Process. Carbon 109, 435–443. doi:10.1016/j.carbon.2016.08.047

CrossRef Full Text | Google Scholar

Maimí, P., Camanho, P. P., Mayugo, J. A., and Dávila, C. G. (2007). A Continuum Damage Model for Composite Laminates: Part II - Computational Implementation and Validation. Mech. Mater. 39, 909–919. doi:10.1016/j.mechmat.2007.03.006

CrossRef Full Text | Google Scholar

Mcglockton, M. A., Cox, B. N., and Mcmeeking, R. M. (2003). A Binary Model of Textile Composites: III High Failure Strain and Work of Fracture in 3D Weaves. J. Mech. Phys. Sol. 51, 1573–1600. doi:10.1016/S0022-5096(03)00038-3

CrossRef Full Text | Google Scholar

Muñoz, R., Martínez-Hergueta, F., Gálvez, F., González, C., and Llorca, J. (2015). Ballistic Performance of Hybrid 3D Woven Composites: Experiments and Simulations. Compos. Structures 127, 141–151. doi:10.1016/j.compstruct.2015.03.021

CrossRef Full Text | Google Scholar

Presby, M. J., Mansour, R., Manigandan, K., Morscher, G. N., Abdi, F., Godines, C., et al. (2019). Characterization and Simulation of Foreign Object Damage in Curved and Flat SiC/SiC Ceramic Matrix Composites. Ceramics Int. 45, 2635–2643. doi:10.1016/j.ceramint.2018.10.207

CrossRef Full Text | Google Scholar

Rothe, H., and Feltin, D. (1994). Textile Constructions that Conform to Power Flux-Novel Reinforcement Structures for Composite. Proc. TECTEXTIL Frankfurt.

CrossRef Full Text | Google Scholar

Snead, L. L., Nozawa, T., Katoh, Y., Byun, T.-S., Kondo, S., and Petti, D. A. (2007). Handbook of SiC Properties for Fuel Performance Modeling. J. Nucl. Mater. 371, 329–377. doi:10.1016/j.jnucmat.2007.05.016

CrossRef Full Text | Google Scholar

Srinivasa Rao, B., Rudramoorthy, R., Srinivas, S., and Nageswara Rao, B. (2008). Effect of Drilling Induced Damage on Notched Tensile and Pin Bearing Strengths of Woven GFR-Epoxy Composites. Mater. Sci. Eng. A 472, 347–352. doi:10.1016/j.msea.2007.03.023

CrossRef Full Text | Google Scholar

Temmen, H., Degenhardt, R., and Raible, T.. Tailored fibre placement optimization tool. 25th International Congress of Aeronautical Sciences, 44, 1085–1090. doi:10.1016/j.ijmachtools.2004.02.019

CrossRef Full Text | Google Scholar

Tsao, C. C., and Hocheng, H. (2004). Taguchi Analysis of Delamination Associated with Various Drill Bits in Drilling of Composite Material. Int. J. Mach. Tools Manuf. 44 (10), 1085-1090. doi:10.1016/j.ijmachtools.2004.02.019

CrossRef Full Text | Google Scholar

Turon, A., Camanho, P. P., Costa, J., and Renart, J. (2010). Accurate Simulation of Delamination Growth under Mixed-Mode Loading Using Cohesive Elements: Definition of Interlaminar Strengths and Elastic Stiffness. Compos. Structures 92, 1857–1864. doi:10.1016/j.compstruct.2010.01.012

CrossRef Full Text | Google Scholar

Yang, Q. D., and Cox, B. (2010). Predicting Failure in Textile Composites Using the Binary Model with Gauge-Averaging. Eng. Fracture Mech. 77, 3174–3189. doi:10.1016/j.engfracmech.2010.08.004

CrossRef Full Text | Google Scholar

Zhou, X., Liu, Z., Li, Y., Li, Y., Li, P., Huang, F., et al. (2018). SiC Ceramics Joined with an In-Situ Reaction Gradient Layer of TiC/Ti3SiC2 and Interface Stress Distribution Simulations. Ceramics Int. 44, 15785–15794. doi:10.1016/j.ceramint.2018.05.255

CrossRef Full Text | Google Scholar