Application of 3D Balanced Growth Theory to the Formation of Bulk Amorphous Alloys

Since the emergence of amorphous alloys as a new class of materials, efficiency improvements have been made in optimizing the fabrication process, the mechanization of alloy formation, and the size of the alloys themselves. Amorphous alloys have been used in precision instruments as they possess excellent magnetic properties, corrosion resistance, wear resistance, high strength, hardness, toughness, high electrical resistivity, and electromechanical coupling properties. Because their hysteresis losses are lower than those of traditional transformer cores, the conversion efficiency of equipment has been significantly improved, thereby saving energy and protecting the environment. Hence, amorphous iron cores have replaced traditional materials. Amorphous alloys also show excellent performance as anti-corrosion and wear-resistant coatings. The process of preparing amorphous alloys starts with an amorphous alloy film obtained by evaporation deposition and then proceeds to the use of a high cooling rate ribbon spinning method to finally obtain a thin strip of an amorphous alloy. A widely used method of copper mold suction casting is then used to prepare the bulk amorphous alloy. The sizes of amorphous alloys have been continually increasing, which has resulted in increasingly serious challenges, such as cooling rate and thermal stability limitations. In addition, crystals can form at low cooling rates. The latent heat of crystallization is released when crystals are formed, which causes damage to the amorphous area so that the size of amorphous alloys is reduced. Because of these difficulties, new processes that eliminate the cooling rate gradient, such as 3D additive manufacturing, ultrasonic production, and mold design, combined with the concept of “entropy control” component design and the economic theory of “balanced development,” lead to a three-dimensional bulk amorphous alloy being proposed. The theory of balanced growth provides a new concept for the development and application of bulk amorphous alloys. This review offers a retrospective view of recent studies of amorphous alloys and provides a description of the formation of amorphous alloys and amorphous phases and the criteria required to predict the successful formation of amorphous alloys. Then, we address the problem of size limitation confronting current production methods. The three-dimensional balanced growth theory of bulk amorphous alloys was formulated from a flexible adaptation of the balanced growth theory of economics. We have confidence that the production and development of bulk amorphous alloys have a bright future.

Introduction

Amorphous and crystalline substances are both ubiquitous forms of matter found in nature. The discovery of amorphous alloys represents a great step forward in the progress of science, which opens up many different fields for applications involving these materials. The study of bulk amorphous alloys, in particular, has become the research frontier in the field of amorphous alloys generally. Since their discovery in the 1960s, these alloys, also known as metallic glasses, have been widely used in high-precision and civil fields because of their unique properties. For example, their high specific strength, excellent corrosion resistance, soft magnetic properties, and unique net forming ability have aroused the interest of researchers in several scientific and engineering disciplines. However, the size of amorphous alloys is one of the important factors limiting their application, which has therefore become a hot research topic. From the perspective of the development of amorphous alloys, from the initial increase in cooling rate to the synthesis of amorphous alloys by adding precious metals and other elements, and finally to the theory of entropy regulation used in their design to increase their size, it has been found that the main factors affecting their formation are their amorphous forming ability and the external cooling rate (Takeuchi and Inoue, 2001). Based on this research, exploring new theoretical methods and improving the development of the preparation technology are the key approaches to overcoming the size limitations of bulk amorphous alloys.

Amorphous metals were first discovered in 1938. At that time, many people thought that metals could not be solidified into an amorphous form, but the German physicist Kramer (1934) has prepared Sn amorphous films using numerous evaporation–deposition experiments. This method has been verified and improved on by subsequent researchers and has been developed to prepare amorphous thin films by electrodeposition, which became the earliest form of amorphous coating technology. Through a mercury undercooling experiment in 1950, Turnbull (1952) has proposed that increasing the cooling rate can force the metal to melt far away from its equilibrium state and reach the deep undercooling zone to form an amorphous state; the faster the cooling rate, the more obvious is this phenomenon. The theory can then be extended to any metal melt. If the cooling rate is fast enough, the melt solidifies to form a glass without diffusion. Thus, Turnbull’s theory has laid a theoretical foundation for the development of amorphous alloys. The deep eutectic point and the reduced glass temperature (T_rg), which is related to the melting point (Cohen and Turnbull, 1958, Cohen and Turnbull, 1959), have been proposed, and the kinetic theory of amorphous formation was perfected with Uhlmann (1977). Combined with classical nucleation theory and phase transformation theory, the basic factors affecting the amorphous formation, such as cooling rate and undercooling, were put forward. In 1960, in order to prove these theoretical conjectures, Klement et al. (1960) have used a cooling rate as high as 105–10⁶ K/s to prepare amorphous alloy samples with a thickness of only 20 μm. This was the first time in the history of amorphous alloy development that a true example of an amorphous alloy had been prepared by an artificial method. However, due to the limitations of this technology, it is difficult to attain the high cooling rates required for their preparation, which hinders the further development of amorphous alloys.

With more intensive research, in the late 1960s, Chen (1974) has studied the glass-forming ability of a palladium-based alloy system at Bell Labs in the United States and prepared a Pd-Cu-Si metal glass rod with millimeter diameter. By this time, a breakthrough in the size of amorphous alloys had been achieved, from initial thin films to millimeter-sized rods, by adding various precious metals. In order to avoid the limitations of these metals, Inoue et al. (1989) have prepared millimeter-sized amorphous alloys of Mg-Cu-Si and La-Al-Ni by adding non-precious metals. From this, amorphous alloys of Zr, Zn, Cu, Sr, Ti, and other systems with excellent properties were prepared by metal mold casting. The critical size achieved by Inoue et al. (1990), Jiao et al. (2010), and Li et al. (2012) was greater than 1 mm, and the preparation conditions were no longer as harsh as before. Following these breakthroughs, the size of bulk metallic glasses and bulk amorphous alloys was on the order of millimeters. Inoue has obtained multicomponent bulk metallic glasses not only by improving the preparation technology but also by improving the composition of the alloy system and reducing the cooling rate, thereby obtaining amorphous alloy samples with a critical size of centimeters. Metal mold casting technology has also laid the foundations for modern copper mold suction casting technology. At the same time, Greer (1993) has put forward the “confusion principle” (Li and Zhang, 2017). Inspired by these continuous improvements, Inoue summarized the law of formation of bulk amorphous alloys, known as “Inoue’s three principles,” as follows: 1) the alloy system consists of at least three elements; 2) the three main constituent elements must have a sufficiently large difference in their atomic sizes; 3) high heats of mixing released should exist between the components. The theory has guided the formation and development of amorphous alloys ever since.

In the history of the development of amorphous alloys, the breakthroughs in their sizes have gone from thin films to millimeter rods, to amorphous films, to bulk amorphous alloys, and from rapid cooling technology to copper mold casting, then to improvements in composition. The purpose of increasing the cooling rate and improving alloy composition is to improve their amorphous forming ability, which is a crucial factor in the formation of amorphous alloys.

Formation Ability of Amorphous Alloys

Development of Formation Ability

The formation of amorphous alloys is a complex process and is an intuitive manifestation of the comprehensive effect of dynamics, thermodynamics, structure, and other factors in the process of solidification transformation, which can characterize the difficulties experienced in the transition from the liquid to the glassy state in alloy systems. In decades of research, the ability to form amorphous alloys has been constantly discussed, and new insights have supplemented scientists’ knowledge and understanding of this process.

Amorphous alloys can be prepared by improving the cooling rate. It is generally believed that the stronger the metal’s ability to form an amorphous alloy, the larger the size of the amorphous sample that forms under the same cooling conditions. Based on this, Lin and Johnson (1995) have proposed the critical cooling rate (R_c) to characterize the forming ability of an amorphous alloy, as given by Eq. (1)

$R_{\text{c}}=\mathbf{d}T/\mathbf{d}t=10/D^2,(1)$

where T is temperature, t is time, and D is critical size. Johnson et al. (2011) have explained that nucleation is controlled by different mechanisms in the shallow supercooled liquid region from the melting temperature (T_m) to the “nose tip” temperature and in the deep supercooled liquid region from the “nose tip” temperature to the glass transition temperature (T_g). Figure 1 shows that, in the shallow supercooled liquid region, crystallization is controlled by nucleation. In this temperature range, the growth rate of the crystal nucleus is very large and, as long as the crystal nucleus appears, it is easier to form crystals. However, it is relatively easy to nucleate in the deep supercooled liquid region, but the growth of the crystal nucleus is more difficult, which is achieved by the long-range diffusion of atoms. Crystallization is inhibited by controlling the diffusion process of atoms to form the amorphous alloy.

FIGURE 1

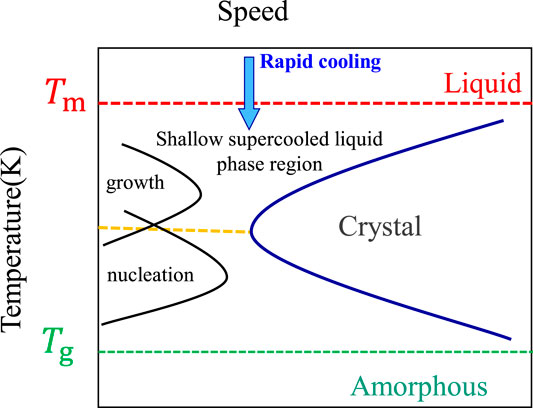
FIGURE 1. Time–temperature transition (3T) from alloy melt to amorphous alloy (Wang, 2013).

Turnbull (1969) has put forward the famous criterion of amorphous forming ability according to classical nucleation theory; that is, the reduced temperature T_r is used to measure the amorphous forming ability of a liquid, as given by Eq. (2):

$T_{\text{rg}}=T_{\text{g}}/T_{\text{m}}.(2)$

As shown in Figure 2, when $T_{\text{rg}}>2/3$, there is no heterogeneous nucleation during solidification, the viscosity of the liquid metal is very high, and the rate of homogeneous nucleation is very low so that it is easier to form an amorphous state. When $T_{\text{rg}}=1/2$, the amorphous alloy must be obtained at a higher cooling rate.

FIGURE 2

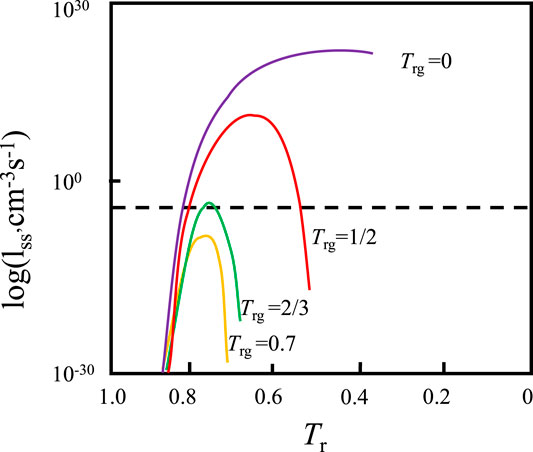
FIGURE 2. Relationship between reduction temperature and the logarithm of the nucleation rate in Turnbull’s amorphous formation theory (Wang, 2013).

In addition to using the reduced glass temperature T_rg to characterize the interval between the melting temperature and the glass transition temperature, some researchers have also used the supercooled liquid region ΔT_x ($\text{Δ}{T}_x=T_x-T_{\text{g}}$, where T_x is the initial crystallization temperature) to indirectly reflect the glass-forming ability (Inoue et al., 1990). Generally speaking, the larger the width of ΔT_x in the supercooled liquid region, the higher the thermal stability and the stronger the crystallization resistance.

Based on the above research and the “confusion principle” put forward by Greer, the conclusion is that the more the alloy components, the more difficult the long-range diffusion of atoms and the higher the probability of random close packing (Greer, 1993).

The development and progress of science is a dialectical process. In 2004, Cantor et al. (2004) and others developed more than 20 kinds of alloy systems based on the principle of chaos. Amorphous alloys could not be obtained in any other way, which were called multicomponent alloys at the time. Yeh et al. (2004) have later put forward the concept of high-entropy alloys; then, in 2008, Zhang et al. (2008) have summarized the law of phase formation of multicomponent alloy systems. Thus, although the classical amorphous formation criterion has been a very important guiding factor, it also has some limitations. However, with the continuous development of the criterion of amorphous forming ability, from Greer’s “confusion principle” to “Inoue’s three principles,” the thermodynamic parameter of entropy plays an important role in amorphous alloy formation.

There has been a considerable amount of discussion about the role of entropy in amorphous alloy formation. Classical nucleation theory and crystal growth theory both emphasize the effect of the liquid–solid Gibbs free energy difference ΔG_l–s and the thermodynamic interfacial energy. The kinetic melt viscosity η (or the relaxation time τ and the diffusion coefficient) is an important parameter for determining the formation of amorphous alloys. In classical nucleation theory, when the temperature is lower than the melting point T_m, the melt enters a supercooled state, and the critical radius R_c at which stable nuclei can form in the supercooled liquid is given by thefollowing Eq. (3):

$R_{\text{c}}=\frac{2\sigma }{\text{Δ}{G}_{\text{l}-\text{s}}}.(3)$

The critical nuclear energy E_c needed to form this crystal nucleus is given by Eq. (4):

$E_{\text{c}}=\frac{16\text{π}{\sigma }^2}{3\text{Δ}{G}_{\text{l}-\text{s}}^2}.(4)$

The free energy difference ΔG_l–s between the solid and liquid phases is the driving force for crystal formation. Thus, to obtain an amorphous alloy, it is necessary to reduce the free energy difference between the solid and liquid phases so that the shape of nuclear energy increases, which means that it is not easy to form crystals, which tend to form amorphously. The equation for the simplified free energy difference was given by Johnson (1986), as Eq. (5):

$\text{Δ}{G}_{\text{l}-\text{s}}=\text{Δ}{S}_{\text{f}}\text{Δ}T\frac{2T}{T_{\text{m}} + T},(5)$

where ΔS_f represents the melting entropy, that is, the entropy difference between the solid and liquid phases near the melting point. It can be seen from Eq. 5 that when ΔS_f decreases, ΔG_l–s also decreases, which is beneficial to the formation of amorphous alloys. When the number of components in the alloy system increases, compared with a traditional alloy, ΔS_f near the melting point of the solid–liquid phase also decreases. Therefore, from the point of view of thermodynamics, the increase in entropy is beneficial to the formation of amorphous alloys.

As solidification is the process of atom nucleation and growth through long-range diffusion, the formation of amorphous crystals is also affected by kinetic factors. For a multicomponent alloy system, when R > R_c, the melt enters a supercooled state. As the temperature decreases, the viscosity of the melt becomes ever larger, causing the diffusion of atoms to be hindered, deviating from the equilibrium state of the system, and forming an amorphous state. Accordingly, the relationship between liquid configuration entropy and viscosity coefficient, established by Adam and Gibbs (1965), is given by Eq. (6):

$\eta ={\eta }_0\mathbf{e}\mathbf{x}\mathbf{p}\left(\frac{A}{T{S}_{\text{con}}}\right),(6)$

where A is a constant and η0 is the reference dynamic viscosity coefficient under one atmosphere. It can be seen that with an increase in the number of components, the configuration entropy will increase, and the decrease in the viscosity coefficient η means that the fluidity of the melt increases, which is conducive to the long-range diffusion of atoms and is unfavorable for the formation of amorphous alloys. Therefore, from a dynamic point of view, the increase in entropy is not conducive to the formation of amorphous alloys.

In terms of structure, one of the “Inoue three principles” states that there must be a sufficiently large atomic size difference σ between the atoms of the constituent elements. An atomic size difference of greater than 12% is the most conducive. The compact and random stacking structure can improve the amorphous forming ability effectively (Egami and Waseda, 1984). The free volume model is used to analyze the influence of atomic size differences. In this model, the viscosity coefficient η is expressed as follows (Spaepen, 1977):

$1/\eta =A\mathbf{e}\mathbf{x}\mathbf{p}(-K/V_{\text{f}}),(7)$

where A and K are constants and V_f is the free volume. The relationship between the free volume and the self-diffusion coefficient of the liquid can be approximately expressed by the Stokes–Einstein equation, as given by Eq. (8):

$D=(k_{\text{B}}T/6\pi r_0)/\eta ,(8)$

where k_B is the Boltzmann constant and r₀ is the molecular diameter. When the atomic size is uneven, a closely stacked structure will be formed, the free volume will decrease, the solid–liquid interface of the alloy can be increased, the viscosity of the melt will increase, and the long-range diffusion of atoms will be hindered. Unlike a crystal, the short-range local atomic arrangement of an amorphous alloy is composed mainly of icosahedral clusters, such as in the La-Al-TM (TM = transition metal) alloy, which has been shown by high-resolution transmission electron microscopy (XRD) and neutron scattering (Chen and Ma, 2011).

In contrast, the mismatch entropy S_σ (one component of the configuration entropy) is used to discuss the effect of S_σ on the formation of amorphous alloys. The standardized mismatch entropy $S_{\sigma }/k_{\text{B}}$ is usually used to describe the degree of mismatch between atoms in the system and to reflect the elastic properties of the system. Previous calculations by Takeuchi et al. (2013) have shown that the standardized mismatch entropy $S_{\sigma }/k_{\text{B}}$ is related to the atomic size difference, as given by the following Eq. (9)

$S_{\sigma }/k_{\text{B}}\sim {(\delta /22)}^2.(9)$

When the atomic size difference is large, the interaction between atoms is strong, and it is not easy to form a stable structure. In addition, when nonmetallic elements such as Si are added to the alloy system, the bonding mode of the latter becomes more complex, and the metals with a strong ability to form amorphous alloys with Si or Sn can do so more easily. Therefore, the mismatch entropy is related to the atomic size difference δ. The larger the atomic size difference, the greater the mismatch entropy. From the structural conditions of amorphous formation, the increase in the misalignment entropy helps increase the amorphous formation capacity. However, it is worth noting that the influence of structure is also different in different alloy systems. Generally speaking, an increase in entropy is beneficial to the formation of amorphous alloys at the structural level. It can be seen from Figure 3 that the formation region of the amorphous phase is for δ > 9, −49 ≤ ΔHmix ≤ −5.5 kJ/mol, 7 ≤ ΔSmix ≤ 16 J/(K·mol) (Guo et al., 2013); that is to say, when the alloy composition parameters involved fall within this range, the multicomponent alloy formed will be amorphous, for which Li et al. (2017) and others have confirmed the accuracy of their predictions.

FIGURE 3

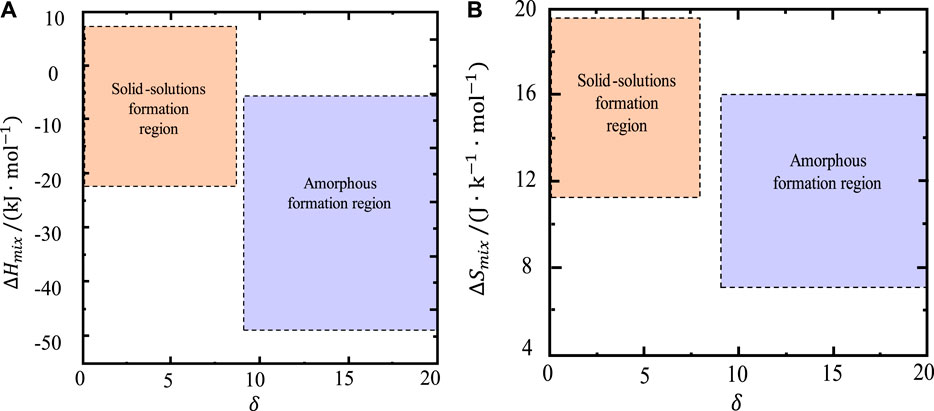
FIGURE 3. (A) ΔHmix—δ and (B) ΔSmix—δ plots showing the phase selection in high-entropy bulk metallic glass (HE-BMG) alloys (Li et al., 2017).

In researching and discussing amorphous formation ability, the effects of the various factors involved are found to be very complex. In terms of the effects of the above thermodynamic and kinetic parameters on amorphous alloy formation, there is no unified parameter for measuring, estimating, and predicting amorphous alloy formation, where the inclusion of too many parameters leads to confusion and a lack of understanding.

Recently, Wang et al. (2020) have discussed the synergistic and competitive relationship between enthalpy and entropy in the process of amorphous alloy formation. They have found a certain relationship between the melting entropy and melting point T_m, the critical cooling rate R_c, the classical amorphous formation parameter $T_{\text{g}}/T_{\text{m}}$, and the kinetic melt viscosity. Entropy is considered to be more suitable as a thermodynamic representative parameter of the amorphous formation energy. Unlike the relationship between the entropy of melting and its parameters in kinetics, the enthalpy or entropy caused by different structures in thermodynamics has different numerical values. Therefore, these thermodynamic parameters of different materials and different systems need a structural parameter to normalize the entropy of melting, aiding discussion of the differences. The structural parameter is the Beads number (Tu et al., 2016), reflecting the degree of freedom of molecular rotation or orientation and can be used as a normalized parameter to avoid this problem. The feasibility of using this parameter has been confirmed from studies of drug molecules and intermetallic compounds, but whether it is the most crucial parameter remains to be seen. Thus far, the above discussion has been about the parameters of amorphous forming ability, but its effectiveness and widespread use need to be proved for a greater number of different alloy systems.

The Effect of Rare Earth Elements on the Glass-Formation Ability of Amorphous Alloys

The electronic shells structure of rare earth elements can usually be represented by 4f ⁿ5d¹6s², and n is from 0 to 14. With the increase of atomic number, the 4f electron shell is gradually filled, and the neighboring rare earth elements only differ by one electron in the 4f atomic orbital. Therefore, the physical and chemical properties of the elements are similar. From the perspective of the electronic shells structure of rare earth elements, they have a high electronic valence, large atomic radius, strong polarization, and therefore strong chemical activity, which can form oxides, sulfides, chlorides, fluorides, hydroxides, and carbonates and many other compounds. Compared with ordinary metals and alloys, it has some unique effects, among which adding a proper amount of rare earth elements into the amorphous alloy can effectively improve the glass-formation ability. As early as 1989, Ning Yuantao et al. systematically studied the influence of La, Ce, Pr, and other eight rare earth elements on the thermal stability of PdSi_16.5 amorphous alloy (Ning Yuantao et al., 1989). The results showed that rare earth elements, especially heavy rare earth elements, could significantly improve the thermodynamic parameters of the amorphous alloy, including characteristic transition temperature T_θ [T_g (glass transition temperature), T_x (initial crystallization temperature), T_p (peak crystallization temperature), and T_rg (reduced glass temperature)]. As mentioned above, T_g (glass transition temperature), T_x (initial crystallization temperature), and T_rg (reduced glass temperature) are classical parameters to describe the formation ability of amorphous alloys, and the improvement of these parameters contributes to the glass-formation ability (GFA). The crystallization activation energy is the increase in the critical nucleation energy of crystallization, as described in Eq. 4, which is conducive to the formation of amorphous alloys.

Adding rare earth elements to amorphous alloys is an effective method to increase the size of amorphous alloys and improve the GFA. Yong et al. (2000) investigated the changes of adding different contents of rare earth metal yttrium in Zr₅₅Al₁₅Ni₁₀Cu₂₀ alloys. The results were observed by XRD, DSC, and DTA measurements. The effect of yttrium addition on the alloy phase change was observed. As shown in Figure 4, with the addition of 1–4% yttrium, the crystalline peak diffraction becomes gradually lesser and weaker. When the amount of yttrium reaches 4%, almost no crystalline diffraction peaks were observed. However, when the yttrium content continued to increase to 6%, part of the crystal phase was precipitated. Therefore, the proper addition of yttrium could inhibit the formation of the crystal phase and improve the GFA. At the same time, the same trend was also confirmed by DTA and DSC measurements; that is, the appropriate addition of yttrium could reduce the melting temperature T_m of the alloy. As shown in Figure 5 and Figure 6, with the heating rate of 0.67 K/s, the DTA test results showed an obvious glass transformation process when the amount of yttrium was 2 and 4%, and the subcooled liquid region ($\Delta T=T_x-T_g$) was widened. In order to explore the influence of rare earth element yttrium on the thermodynamic parameters, the samples were prepared under the conditions of raw material purity and low vacuum. With the heating rate of 0.33 K/s, DSC test results showed that the supercooled liquid phase ΔT reaches the maximum value when the addition amount reaches 2% and the glass transition temperature T_rg is reduced to the maximum value when the addition amount is 4%. The larger ΔT and Trg are, the easier it is to form an amorphous state and the lower the critical cooling rate will be. The results of the thermodynamic analysis also prove that the appropriate addition of yttrium can improve the GFA under low raw material purity and low vacuum conditions. In 2006, similar results were obtained by adding yttrium to Cu-Zr-Al amorphous alloy, as shown in Figure 7, as the yttrium content increases from 0.5 to 2.5 at.%, XRD patterns of the resultant alloys generally show a diffusive amorphous hump with only a few small crystallization peaks, and especially, there are no obvious crystallization peaks observed for the sample with 2% yttrium (Zhang et al. 2006). Moreover, the fusion entropy was calculated after adding yttrium as the added yttrium in the Cu-Zr-Al alloy system is larger than 2 at.%, ΔSf decreases. As a result, the total free energy barrier will decrease, thus facilitating the formation of the crystalline phases of Cu₁₀Zr₇ and CuZr.

FIGURE 4

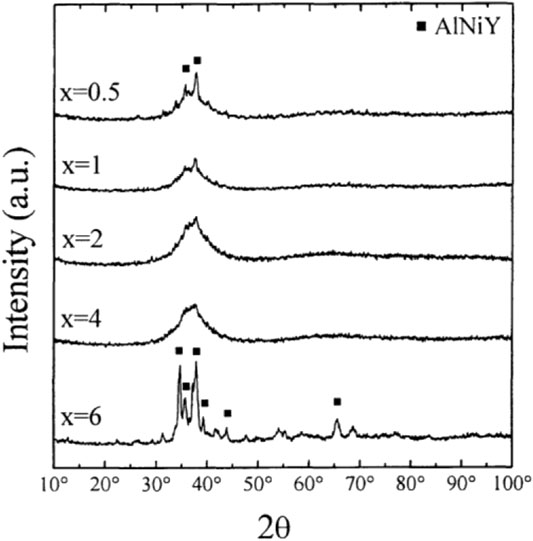
FIGURE 4. XRD patterns of the (Zr₆₅Al₈₅Ni₁₀Cu₂₀)_100-xY_x. © 2000 The Japan Institute of Metals (Yong et al., 2000).

FIGURE 5

FIGURE 5. DTA curves of (Zr₆₅Al₈₅Ni₁₀Cu₂₀)_100-xY_x, alloy with a heating rate of 0.33K/s: (A) DSC curves of (Zr₆₅Al₈₅Ni₁₀Cu₂₀)₉₈Y₂, alloy with a heating rate of 0.67K/s; (B) © 2000 The Japan Institute of Metals (Yong et al., 2000).

FIGURE 6

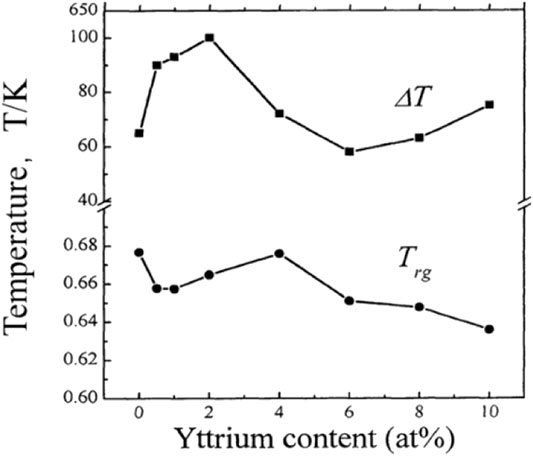
FIGURE 6. ΔT and Trg changes with x of (Zr₆₅Al₈₅Ni₁₀Cu₂₀)_100-xY_x alloys. © 2000 The Japan Institute of Metals (Yong et al., 2000).

FIGURE 7

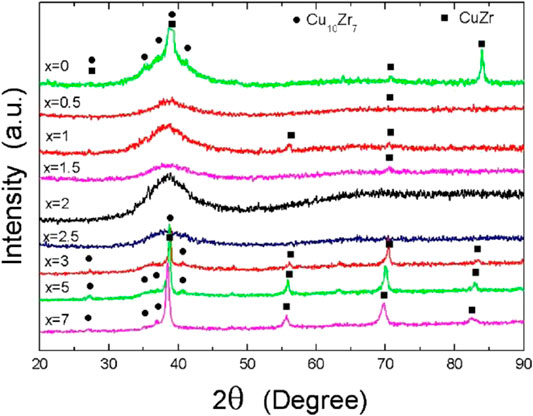
FIGURE 7. Color online XRD patterns of (Cu_0.48Zr_0.48Al_0.04)_100-xY_x, x = 0–7 at.% alloys with a diameter of 3 mm. The crystalline phases are identified to be CuZr and Cu₁₀Zr₇ phases. © 2006 American Institute of Physics (Zhang et al., 2006).

The influence of adding a proper amount of rare earth elements to the amorphous alloy on the amorphous formation ability can be summarized as follows:

1) The atomic radius of rare earth elements is larger than that of ordinary metal elements, and the atomic size difference δ is larger after adding rare earth elements, making the entropy ΔS larger.

2) The addition of rare earth elements can effectively improve the stability of characteristic transition temperature Tθ to external temperature variation.

3) The addition of rare earth elements makes the liquidus decrease; thus, the eutectic temperature decreases and the crystal structure is not easy to form.

4) Rare earth elements are more likely to combine with impurity elements when forming compounds such as oxides and carbides. It can scavenge the impurities via the formation of innocuous oxides and carbides and reduce the heterogeneous nucleation.

Prediction of Amorphous Phase Formation

In the previous discussion, the forming ability of amorphous alloys was analyzed from the point of view of thermodynamics and kinetics. Entropy and enthalpy alone cannot control the formation of the amorphous phase. In the Gibbs thermodynamic equation, the formation of amorphous alloys is only expressed as the interaction of entropy and enthalpy. However, in order to describe which parameter of entropy and enthalpy contributes more to the formation of amorphous alloy, it is necessary to express the proportional relationship between entropy and enthalpy. Taking into account the factors of entropy of mixing, enthalpy of mixing, and melting temperature, Ω parameter is proposed, as expressed by the following Equ. (9)

$\Omega =\frac{T_{\text{m}}\text{Δ}{S}_{\text{mix}}}{\text{Δ}{H}_{\text{mix}}},(10)$

where ΔS_mix is the entropy of mixing, ΔH_mix is the enthalpy of mixing, and T_m is the melting point of the mixture. When Ω > 1, the effect of TΔS_mix is larger than that of ΔH_mix, which becomes the dominant factor. According to Eq. 4, the free energy difference between the solid and liquid phases decreases and the alternative nuclear energy of the crystal nucleus increases so that it is more favorable to the formation of an amorphous phase. In contrast, if Ω < 1, ΔH_mix is the main factor, the difference in free energy between the solid and liquid phases is larger, and the driving force for the formation of the crystal phase is greater, which is not conducive to the formation of an amorphous phase. Synthesizing the role of the atomic size difference δ in the formation of the amorphous phase and drawing a two-dimensional diagram of Ω–δ, as shown in Figure 8, the amorphous phase falls in the range of parameter values Ω < 1, δ ≥ 5%. The Ω parameter can predict whether the amorphous phase can be formed before the formation of the alloy in order to adjust the composition and improve the accuracy and efficiency of the process.

FIGURE 8

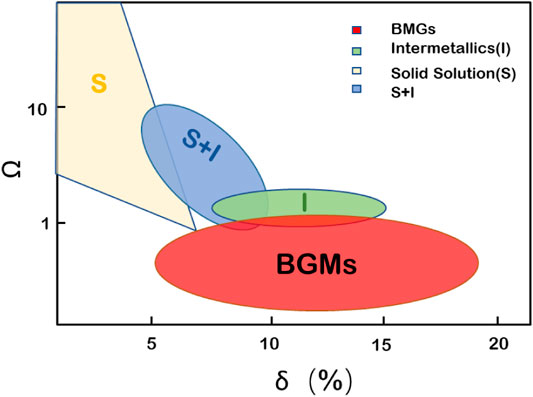
FIGURE 8. Relationship between the parameters Ω and δ of multicomponent alloys and the amorphous phase region (Yang and Zhang, 2012).

Theory of Three-Dimensional Balanced Growth

The capacity for amorphous alloy formation belongs to the internal factors of the process, just as the cooling rate is the external factor affecting amorphous formation. Currently, of the more mature technologies available for the preparation of amorphous alloys, arc melting–copper mold suction casting is the most commonly used method. As shown in Figure 9, the main problem with this technique is that during the suction casting of the copper mold, the upper and lower temperature gradients are different, resulting in different cooling rates. Crystallization occurs when the melt close to the upper suction gate is cooled, resulting in the amorphous alloy sample not being a completely amorphous structure, and the size and quality of the amorphous sample are therefore limited. Based on this research, how to eliminate the cooling rate gradient has become the key to solving this problem; hence, the method of three-dimensional balanced growth is proposed. The core of this method is the balanced growth of amorphous alloys. The term “balanced growth” comes from the classical economic theory of balanced growth (Nath and Zong, 1963; Xia and Wang, 2005). This is designed to achieve mutual coordination and common growth of various industries and departments through large-scale investment in various sectors of the national economy at the same time. As representatives of the theory of balanced growth, Rosenstein-Rodin and Knox have believed that to promote the balanced development of the national economy, the government must invest economic and policy support according to the needs of the development of various regions, industries, and fields to ensure the development of backward areas, industries, and fields. Taking an opposing view of balanced growth, the economist Herman put forward the counterbalancing theory of “unbalanced growth” and thought that government support would lead to inertia in economic development and hence put forward the concept of an economic “development pole.” Some of the areas with rapid economic development promote the economic development of more backward areas. The policy of regional economic development implemented in China draws lessons from this theory. The current regional economic development, urban agglomeration, and the two Silk Road development belts promote the economic development of the eastern and western regions and the coastal inland areas to achieve the development of the point belt and the line to finally realize the highest ideal of common prosperity. Considering this economic theory, there are similarities and differences to be observed between the amorphous process of copper mold suction casting and the development of the economy. During suction casting, part of the melt’s temperature that first enters the mold is quite different from that of the mold, which can be cooled rapidly in a short time, and the cooling rate is greater than the critical cooling rate. The amorphous state is formed and, with a gradual increase in the melt, the temperature in the mold and the inner environment of the mold increases, which affects the cooling rate of the melt. (From the axial point of view, the size of the amorphous formation is uneven; from the radial point of view, at present, because the diameter of the existing bulk amorphous alloy is small, there is little difference in the cooling rate between the core and the surface.) Such a state of unbalanced growth is similar to the “development pole” of economic theory, with rapid development in some regions and a more prominent economic level. In the regions with slow development, the economy lags. Economic development and the growth of amorphous alloys both hope to finally achieve the goal of balanced growth. This concept is applied to solve the phenomenon of nonequilibrium growth in the preparation of amorphous alloys. As with the investment in primitive and regional fields in economics, there is a cooling rate gradient in the process of suction casting of amorphous alloys, and their formation in different parts of the process is different. By reforming the original copper mold, the part with a slow cooling rate can increase it and realize balanced growth of the amorphous alloy.

FIGURE 9

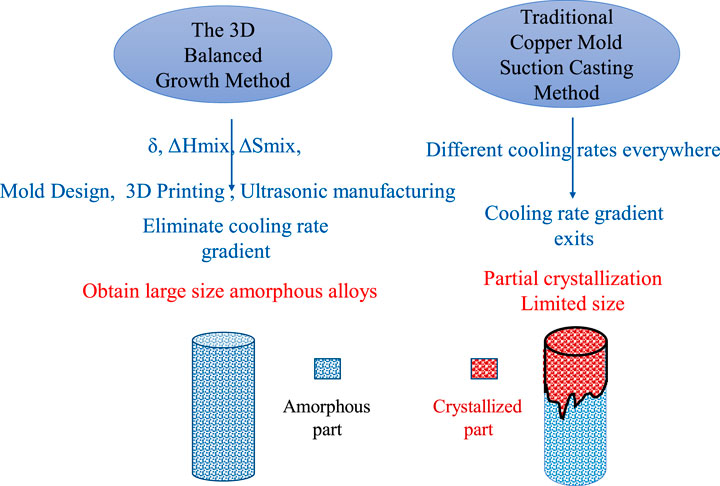
FIGURE 9. Comparison between the three-dimensional balanced growth method and traditional copper mold suction casting.

A schematic diagram of the copper mold is shown in Figure 10. On the basis of the original copper mold, the cylindrical copper mold has a uniform series of holes punched in the side, and the thermocouple is connected symmetrically on both sides. The thermocouple is a common device for measuring and controlling the temperature. The temperature signal can be converted into a voltage and the apparatus does not need an external power supply. Having high sensitivity, it is often used to measure the temperature of gases or liquids in the furnace and the pipe and the surface temperature of the solid. Using a thermocouple, the temperature changes during the suction casting of the copper mold can be monitored in real time, thus reflecting the rate of cooling. The position of the slower cooling rate is judged according to the signal transmitted by the thermocouple, and then the input cooling medium or phase change materials, such as gallium-indium alloy, absorb heat during phase transformation and achieve a cooling effect on the melt in the mold, which increases the cooling rate. The cooling rate gradient is approximately zero (there are cooling rate gradients in both axial and radial directions, as well as the axial cooling rate gradient, shown in Figure11), thus eliminating the cooling rate gradient to achieve the effect of balanced growth.

FIGURE 10

FIGURE 10. Schematic diagram of the mold design.

FIGURE 11

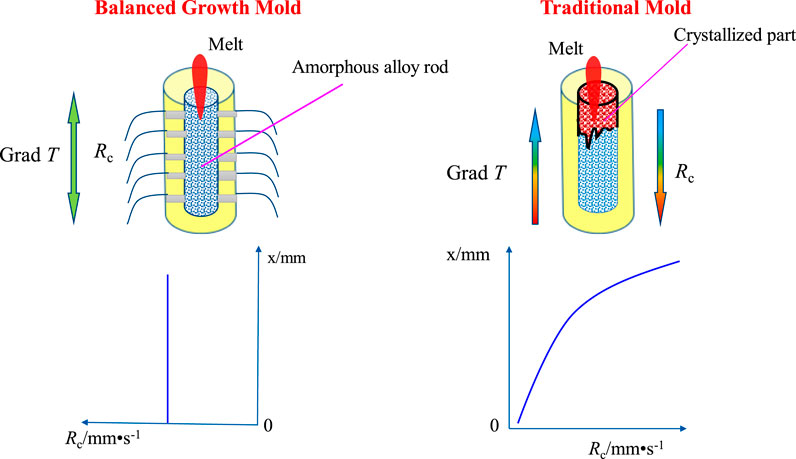
FIGURE 11. Comparison of the cooling rate gradients of an amorphous alloy growing in a balanced mold and a traditional mold.

The core aim of the three-dimensional balanced growth theory is to eliminate the cooling rate gradient, but it is not limited to this objective. First, the design of alloy composition is based on the design concept of “entropy regulation:” 1) δ > 12%; 2) the enthalpy of mixing ΔH_mix should be sufficiently negative; 3) the entropy of mixing ΔS_mix should be within a certain range. Theoretically, the three different parameters described above take different values when measured from three different angles. Second, the cooling rate of each point reaches relative equilibrium and increases in the three spatial dimensions. Finally, the amorphous alloy is obtained by 3D printing, ultrasonic manufacturing, thermoplastic processing, and other preparation techniques, which is also balance in three-dimensional space. In general, there are three dimensions in terms of composition design, elimination of cooling rate gradient, and preparation technology.

In the latest research on the size of bulk amorphous alloys, the size of La amorphous alloy was 100 mm (Li et al., 2021); that is, multilayer components have succeeded in being stacked by thermoplastic processing. In this process, a cooling system was added to the thermoplastic equipment, the temperature was added to the supercooled liquid region, and pressure was formed when the alloy melt became viscous. The function of the cooling system is to quickly cool the viscous melt thus formed below the glass transition temperature in order to form an amorphous alloy. Because the size of the component is very small, when the sample is cooled in the cooling system, the cooling rate gradient can be ignored, which can ensure the integrity of the amorphous state of the alloy. An increase in the three-dimensional size of the amorphous alloy can be obtained by this new process.

Conclusion and Prospects

The development of amorphous alloys has gone through three stages, as shown in Figure 12. From 1947 to 1990, amorphous alloys were obtained mainly by rapid cooling technology, and the cooling rate could reach 10⁶ K/s (Klement et al., 1960). The amorphous alloy samples prepared were mainly thin films and ribbons with a thickness of less than 1 mm. The invention of rod-like amorphous alloys was further developed when Chen and others have added precious metals, with a diameter of 1 mm and components of 2 mm, which are called low-entropy traditional metal glasses. This was the first stage in the development of amorphous alloys. Inoue et al. (1990) proposed the law of amorphous formation. By increasing the range of components and improving the composition of the amorphous alloy system, millimeter metallic glass was first prepared, which broke through the long-standing amorphous size limit. Entropy, a thermodynamic parameter, has become an important parameter for the regulation of amorphous systems. During this period, Cantor et al. (2004) have discovered multicomponent alloys, and Yeh et al. (2004) put forward the concept of high-entropy alloys. A high-entropy system can form not only amorphous but also ordered solid solutions, and high-entropy amorphous alloys can be obtained by controlling the proportions of components in the threshold range. The increase in the range of added components promotes the formation of an amorphous state and reduces the cooling rate of amorphous alloys, which in turn promotes the progress of amorphous industrial production, which is the second stage in the development of amorphous alloys. The three-part balanced growth theory described in this article, which regulates the composition of the alloy with the best formation ability from the point of view of entropy and achieves balanced growth by eliminating the cooling rate gradient, is expected to break through the bottleneck that hampers the development of bulk amorphous alloy size and open a new stage in amorphous alloy research.

FIGURE 12

FIGURE 12. Development stages in amorphous alloy research.

As an important type of new materials, amorphous alloys have been a subject worthy of in-depth study since their discovery. Although landmark progress has been achieved in the field of amorphous alloy research, many problems remain to be solved. For example, what is the physical nature of amorphous alloys, from what perspective can amorphous alloys be analyzed in order to better understand their properties, and what parameters can be used to evaluate and predict the formation of amorphous alloys more intuitively, uniformly, and objectively? There are still many challenges worth exploring in this field, and future studies should take into account the theory of three-dimensional balanced growth proposed in this review to help widen this horizon.

Author Contributions

YZ contributed to the conception of the study and to theoretical guidance; YW designed the mold and wrote the manuscript; TZ helped to carry out the analysis of the results and contributed to the study with constructive discussions.

Funding

The authors would like to thank: (1) The Guangdong Basic and Applied Basic Research Foundation (Grant No. 2019B1515120020), (2) The State Key Laboratory for Advanced Metals and Materials (2020-Z08) in the University of Science and Technology Beijing 2020Z-08 for their financial assistance for this project. This work is also supported by the Funds for Creative Research Groups of China (No. 51921001).

Conflict of Interest

TZ was employed by Dongguan Eontec Advanced Materials Research Institute Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our gratitude to all those who helped us during the writing of this thesis. We would like to thank YaSong Li, who helped us to understand the structure of the preparation equipment and made the design plan of the mold. We would also like to thank XueHui Yan, who has offered us valuable suggestions in my academic studies, and has provided us with inspiring advice. Without their patient help, insightful criticism, and expert discussion, this thesis could not have been completed.

References

Adam, G., and Gibbs, J. H. (1965). On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids. J. Chem. Phys. 43, 139–146. doi:10.1063/1.1696442

CrossRef Full Text | Google Scholar

Cantor, B., Chang, I. T. H., Knight, P., and Vincent, A. J. B. (2004). Microstructural Development in Equiatomic Multicomponent Alloys. Mater. Sci. Eng. A 375-377, 213–218. doi:10.1016/j.msea.2003.10.257

CrossRef Full Text | Google Scholar

Chen, H. S. (1974). Thermodynamic Considerations on the Formation and Stability of Metallic Glasses. Scripta Metall. 22, 505. doi:10.1016/0001-6160(74)90112-6

CrossRef Full Text | Google Scholar

Cheng, Y. Q., and Ma, E. (2011). Atomic-level Structure and Structure-Property Relationship in Metallic Glasses. Prog. Mater. Sci. 56, 379–473. doi:10.1016/j.pmatsci.2010.12.002

CrossRef Full Text | Google Scholar

Cohen, M. H., and Turnbull, D. (1958). Concerning Reconstructive Transformation and Formation of Glass. J. Chem. Phys. 29, 1049.

CrossRef Full Text | Google Scholar

Cohen, M. H., and Turnbull, D. (1959). Molecular Transport in Liquids and Glasses. J. Chem. Phys. 31, 1164–1169. doi:10.1063/1.1730566

CrossRef Full Text | Google Scholar

Egami, T., and Waseda, Y. (1984). Atomic Size Effect on the Formability of Metallic Glasses. J. Non-Crystalline Sol. 64, 113–134. doi:10.1016/0022-3093(84)90210-2

CrossRef Full Text | Google Scholar

Greer, A. L. (1993). Confusion by Design. Nature 366, 303–304. doi:10.1038/366303a0

CrossRef Full Text | Google Scholar

Guo, S., Hu, Q., Ng, C., and Liu, C. T. (2013). More Than Entropy in High-Entropy Alloys: Forming Solid Solutions or Amorphous Phase. Intermetallics 41, 96–103. doi:10.1016/j.intermet.2013.05.002

CrossRef Full Text | Google Scholar

Inoue, A., Kita, K., Zhang, T., and Masumoto, T. (1989). An Amorphous La₅₅Al₂₅Ni₂₀ Alloy Prepared by Water Quenching. Mater. Trans. JIM 30, 722–725. doi:10.2320/matertrans1989.30.722

CrossRef Full Text | Google Scholar

Inoue, A., Zhang, T., Masumoto, T., Jiao, W., Zhao, K., Xi, X. K., et al. (1990). Zr–Al–Ni Amorphous Alloys with High Glass Transition Temperature and Significant Supercooled Liquid Region Zinc-Based Bulk Metallic Glasses. Mater. Trans. Jimnon-cryst. Sol. 31, 177–183. doi:10.2320/matertrans1989.31.17720103561867

CrossRef Full Text | Google Scholar

Jiao, W., Zhao, K., Xi, X. K., Zhao, D. Q., Pan, M. X., and Wang, W. H. (2010). Zinc-Based Bulk Metallic Glasses. Non-Cryst. Solids 356, 1867.

Johnson, W. L., Kaltenboeck, G., Demetriou, M. D., Schramm, J. P., Liu, X., Samwer, K., et al. (2011). Beating Crystallization in Glass-Forming Metals by Millisecond Heating and Processing. Science 332, 828–833. doi:10.1126/science.1201362

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, W. (1986). Thermodynamic and Kinetic Aspects of the crystal to Glass Transformation in Metallic Materials. Prog. Mater. Sci. 30, 81–134. doi:10.1016/0079-6425(86)90005-8

CrossRef Full Text | Google Scholar

Klement, W., Willens, R. H., and Duwez, P. (1960). Non-crystalline Structure in Solidified Gold-Silicon Alloys. Nature 187, 869–870. doi:10.1038/187869b0

CrossRef Full Text | Google Scholar

Kramer, J. (1934). Über Nichtleitende Metallmodifikationen. Ann. Phys. 411, 37–64. doi:10.1002/andp.19344110104

CrossRef Full Text | Google Scholar

Li, H. F., Zhao, K., Wang, Y. B., Zheng, Y. F., and Wang, W. H. (2012). Study on Bio-Corrosion and Cytotoxicity of a Sr-Based Bulk Metallic Glass as Potential Biodegradable Metal. J. Biomed. Mater. Res. 100b, 368–377. doi:10.1002/jbm.b.31958

CrossRef Full Text | Google Scholar

Li, H., Li, Z., Yang, J., Ke, H. B., Sun, B., Yuan, C. C., et al. (2021). Interface Design Enabled Manufacture of Giant Metallic Glasses. Sci. China Mater. 64, 964–972. doi:10.1007/s40843-020-1561-x

CrossRef Full Text | Google Scholar

Li, R. X., and Zhang, Y. (2017). Entropy and Glass Formation. J. Acta Physica Sinica -Chinese Edition 66, 17.

Google Scholar

Li, Y., Zhang, W., and Qi, T. (2017). New Soft Magnetic Fe25Co25Ni25(P, C, B)25 High Entropy Bulk Metallic Glasses with Large Supercooled Liquid Region. J. Alloys Compounds 693, 25–31. doi:10.1016/j.jallcom.2016.09.144

CrossRef Full Text | Google Scholar

Lin, X. H., and Johnson, W. L. (1995). Formation of Ti-Zr-Cu-Ni Bulk Metallic Glasses. J. Appl. Phys. 78, 6514–6519. doi:10.1063/1.360537

CrossRef Full Text | Google Scholar

Nath, S. K., and Zong, S. (1963). The Theory of Balanced Growth. Dig. Foreign Soc. Sci. 10, 24.

Google Scholar

Ning, Y. T., and Li, Y. N. (1989). Effect of Rare Earth Elements on thermal Stability of Amorphous PdSi_16.5 alloy. Acta Metallurgica Sinica (04), j126–131.

Google Scholar

Spaepen, F. (1977). A Microscopic Mechanism for Steady State Inhomogeneous Flow in Metallic Glasses. Acta Metallurgica 25, 407–415. doi:10.1016/0001-6160(77)90232-2

CrossRef Full Text | Google Scholar

Takeuchi, A., Amiya, K., Wada, T., Yubuta, K., Zhang, W., and Makino, A. (2013). Entropies in alloy Design for High-Entropy and Bulk Glassy Alloys. Entropy 15, 3810–3821. doi:10.3390/e15093810

CrossRef Full Text | Google Scholar

Takeuchi, A., and Inoue, A. (2001). Quantitative Evaluation of Critical Cooling Rate for Metallic Glasses. Mater. Sci. Eng. A 304-306, 446–451. doi:10.1016/s0921-5093(00)01446-5

CrossRef Full Text | Google Scholar

Tu, W., Li, X., Chen, Z., Liu, Y. D., Labardi, M., Capaccioli, S., et al. (2016). Glass Formability in Medium-Sized Molecular Systems/pharmaceuticals. I. Thermodynamics vs. Kinetics. J. Chem. Phys. 144, 174502. doi:10.1063/1.4947476

PubMed Abstract | CrossRef Full Text | Google Scholar

Turnbull, D. (1952). Kinetics of Solidification of Supercooled Liquid Mercury Droplets. J. Chem. Phys. 20, 411–424. doi:10.1063/1.1700435

CrossRef Full Text | Google Scholar

Turnbull, D. (1969). Under what Conditions Can a Glass Be Formed? Contemp. Phys. 10, 473–488. doi:10.1080/00107516908204405

CrossRef Full Text | Google Scholar

Uhlmann, D. R. (1977). Glass Formation. J. Non-Crystalline Sol. 25, 42–85. doi:10.1016/0022-3093(77)90090-4

CrossRef Full Text | Google Scholar

Wang, L. M., Liu, R. P., and Tian, Y. J. (2020). Enthalpy and Entropy in the Formation of Amorphous Materials: Competition or Synergy. Acta Phys. Sin. 69, 19. doi:10.7498/aps.69.20200707

CrossRef Full Text | Google Scholar

Wang, W. H. (2013). Essence and Characteristics of Amorphous Matter. Pro. Phys. 33, 177.

Google Scholar

Xia, J. W., and Wang, B. (2005). A Summary of the Theories of Balanced and Unbalanced Industrial Growth Abro. Econ. Rev. J. 9, 76.

Google Scholar

Yang, X., and Zhang, Y. (2012). Prediction of High-Entropy Stabilized Solid-Solution in Multi-Component Alloys. Mater. Chem. Phys. 132, 233–238. doi:10.1016/j.matchemphys.2011.11.021

CrossRef Full Text | Google Scholar

Yeh, J.-W., Chen, S.-K., Lin, S.-J., Gan, J.-Y., Chin, T.-S., Shun, T.-T., et al. (2004). Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel alloy Design Concepts and Outcomes. Adv. Eng. Mater. 6, 299–303. doi:10.1002/adem.200300567

CrossRef Full Text | Google Scholar

Yong, Z., Pan, M. X., Zhao, D. Q., Wang, R. J., Wang, W. H., et al. (2000). Formation of Zr-Based Bulk Metallic Glasses from Low Purity of Materials by Yttrium Addition. Mate. Trans. JIM 41 (11), 1410–1414.

Google Scholar

Zhang, Y., Chen, J., Chen, G. L., and Liu, X. J. (2006). Glass Formation Mechanism of Minor Yttrium Addition in CuZrAl Alloys. Appl. Phys. Lett. 89, 131904. doi:10.1063/1.2357160

CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, Y. J., Lin, J. P., Chen, G. L., and Liaw, P. K. (2008). Solid-solution Phase Formation Rules for Multi-Component Alloys. Adv. Eng. Mater. 10, 534–538. doi:10.1002/adem.200700240

CrossRef Full Text | Google Scholar