Determination of Vacancy Formation Energies in Binary UZr Alloys Using Special Quasirandom Structure Methods

The use of predictive models to examine defect production and migration in metallic systems requires a thorough understanding of the energetics of defect formation and migration. In fully miscible alloys, atomistic properties will all have a range of values that are heavily dependent on local atomic configurations. In this work we have used the atomistic simulation tool Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) to investigate the impact of first nearest neighbor configuration on vacancy formation energies at 0 K in γ-U-Zr alloys of varying Zr concentrations. The properties of randomly generated alloy microstructures were also compared with those produced as special quasi-random structures (SQS) using the “mcsqs” code within the Alloy Theoretic Automated Toolkit. Results have confirmed that local configuration can have a significant impact on measured properties and must be considered when characterizing miscible alloy systems. Results also indicated that the generation method of the random structure (i.e., via random species assignment or a method of enforced randomness) does not result in a measurable difference in average vacancy formation energies in miscible U-Zr systems.

1 Introduction

The use of predictive models to examine defect production and migration in metallic systems requires a thorough understanding of the energetics of defect formation and migration. In fully miscible alloys, atomistic properties are heavily dependent on local atomic configurations, and can vary significantly across the volume of even a homogeneous alloy mixture. One such atomistic property is the vacancy formation energy ($E_v$), which is a very important material property that is frequently required for continuum and Monte Carlo simulations of materials (Soisson, 2006; Badillo et al., 2015; Piochaud et al., 2016). It plays a significant role in governing the diffusion and formation of point defects in materials, and must be parameterized accurately for the specific material system to allow for representative simulations. In alloy systems, such as the U-Zr alloy system examined in this work, the vacancy formation energy is a function of local atomic arrangement and must be tracked separately for the two species, since continuum methods such as phase field or Monte Carlo methods must track which species is removed to form the defect. The $E_v$ for elemental uranium has been explored extensively in both experiments and computational calculations, with a mono-vacancy formation energy of 1.20 ± 0.25 eV being reported by Matter et al. (1980). $E_v$ in Zr metal has not been studied as extensively, with different authors reporting values over a large range of energies (1.68 eV by Korzhavyi et al. (1999) and 2.1 eV by Le Bacq et al. (1999). Additional reported values for $E_v$ in elemental uranium and zirconium are provided in Tables 1,2 in section Results and Discussion.

TABLE 1

TABLE 1. Vacancy formation energies in bcc uranium.

TABLE 2

TABLE 2. Vacancy formation energies in bcc zirconium.

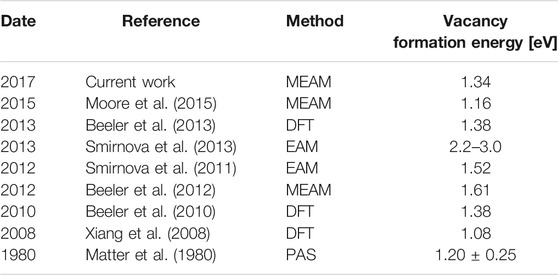
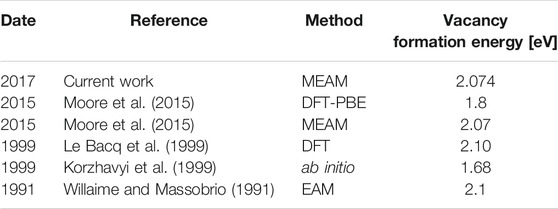
For this work, the Modified Embedded Atom Method (MEAM) based interatomic potential for U-Zr developed by Moore et al. (2015) was used. This potential was developed to simulate γ-U-Zr alloys at operational temperatures. The uranium portion of this potential was designed to recreate the properties of γ-phase uranium at high temperatures, but was also fit to the elastic properties and lattice constant of γ-phase uranium at 0 K. However, the γ-phase of pure uranium is unstable at 0 K, and must be stabilized through the application of an external pressure. Due to this mechanical instability, calculations of properties by other common simulation methods such as density functional theory (DFT) or ab initio calculations cannot be performed, due to their reliance on the presence of an equilibrium state at 0 K (Moore et al., 2015). However, through the use of a volume or pressure constraint in molecular dynamics simulations, simulations of pure γ-phase uranium can be performed. It is also important to note that the presence of a small atom percentage of an alloying element can stabilize the γ-phase of uranium, meaning that all of the studied U-Zr alloy compositions in this work were stable without requiring additional constraints.

It is common practice in molecular dynamics (MD) modeling of metallic alloys to populate the lattice structure via random atom placement. Bulk material properties of crystals generated in this way can closely mimic the properties of real crystals; however, due to the finite nature of any modeled supercell, the random population of lattice sites may deviate from “perfect” randomness on a local scale. To address this issue, Wei et al. (1990) proposed a method of generating “special quasirandom structures” (SQS) that would more closely mimic the configuration average of an infinite perfectly random ${\text{A}}_{1-x}$B_x alloy, and can be generated in sizes as small as $N=8$. SQS “supercells” can be generated, and then combined into a larger lattices if bulk properties needed to be tested. The process of generating SQS is provided in Wei et al. (1990), where multisite correlation functions are used to determine if a randomly generated microstructure mimics the ensemble averages that would be expected for an infinite random alloy. This is done to ensure that there are not regions within the randomly generated microstructure that statistically would be considered not random, thereby ensuring that properties determined using SQS are representative of a homogeneously mixed alloy. In their original work, Wei et al. (1990) found that a supercell size of $N=8$ was sufficient to mimic the first and second nearest neighbor correlation functions for a binary alloy, and $N=64$ was sufficient to mimic the correlation functions for the third nearest neighbors. For this work, SQS’s of 2000 atoms and 250 atoms were developed using the stochastic SQS generation system that was implemented in the “mcsqs” code by van de Walle et al. (2013). The 250 atom structures were then repeated to produce a single system containing 2,000 atoms.

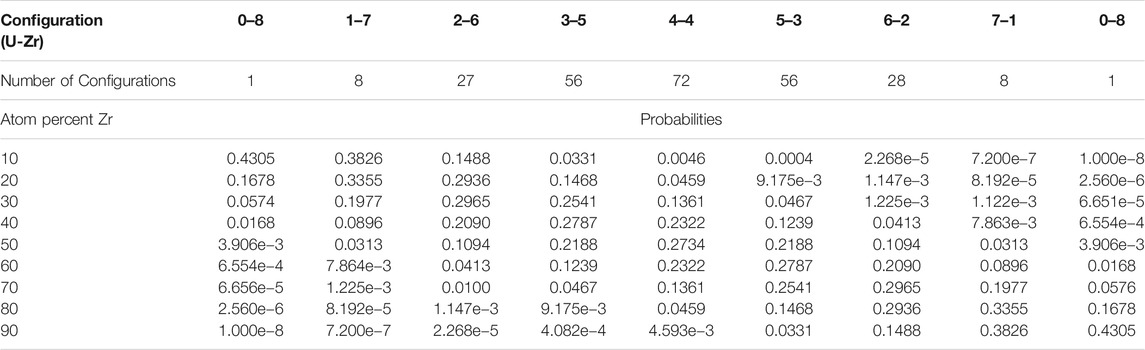
For any alloy, there exists a distribution of possible vacancy formation energies due to the species arrangement and thermal oscillations of the atoms in the neighboring sites (Zhao et al., 2016). For this work, to examine the impact of different configurations of nearest neighbor sites on vacancy formation energy, all 256 possible nearest neighbor configurations for a binary bcc alloy were examined for each atom percentage and vacancy type tested. However, not all configurations are equally likely to occur in all alloys with differing atom percentages (e.g., all eight nearest neighbor lattice positions of a vacancy in a U-10%Zr alloys being filled by Zr atoms, etc.)

In a perfectly random binary alloy, the probability of an atom of species A inhabiting any given lattice position can be defined by the concentration of that species in the bulk lattice, $C_A$, while the probability of species B inhabiting the same lattice position can be defined as the concentration of species B in the lattice, $C_B$. For a number of lattice positions z, the probability that i lattice positions are inhabited by species A and $z-i$ lattice positions are inhabited by species B can be defined as

$C_A^i{C}_B^{z-i}(1)$

This probability refers to the probability of i species A atoms and $z-i$ species B atoms inhabiting specific lattice positions. For each species distribution in z lattice positions, with i atoms of species A and $z-i$ atoms of species B, the total number of configurations with that species distribution can be described by the following expression:

$\frac{z!}{i!\left(z-i\right)!}(2)$

Finally, the expression that defines the probability of having a specific species distribution in z lattice positions in a binary alloy can be expressed as the product of the probability of having the species distribution in a particular configuration and the total number of possible configurations for that species distribution, resulting in a binomial probability distribution (Kim, 1984),

$P=\frac{z!}{\left(z-i\right)!i!}{C}_A^i{C}_B^{z-i}for\left(0\le i\le z\right)(3)$

In a BCC structure, there are eight first nearest neighbor sites and 6 s nearest neighbor sites. For a binary BCC alloy, there then exist 256 unique first nearest neighbor configurations and 104 unique second nearest neighbor configurations, combining for a total of 26,624 unique local configurations around a single atomic position, which in a binary system can be one of two different species. To account for this the results of all possible configurations were compared with results for the configurations with atom percentages that were reasonable when compared to the atom percentage of the alloy as a whole.

All MD simulations were performed with a supercell consisting of 10 × 10 × 10 unit cells held in an NVE ensemble.

2 Methods

2.1 Interatomic Potential of Uranium-Zirconium

Molecular dynamics simulations model interactions between atoms via interatomic potential functions that are used to calculate the force on any atom in the system caused by the other N−1 atoms in the system. A primary advantage of interatomic potential functions over first principle calculations is that potentials can be used for the calculation of larger scale atomic properties at temperature, as well as the ability to perform calculations on systems with many atoms. This is particularly advantageous for materials such as γ-uranium, which is mechanically unstable at 0 K (Moore et al., 2015). For this work, a modified embedded atom method, or MEAM, potential was used. MEAM potentials are modified versions of embedded atom method potentials (EAM), which are semi-empirical potentials that express cohesive energy in terms of embedding energies, with the atoms in the system being embedded in an electron gas. The difference between MEAM and EAM potentials is that MEAM potentials account for angular forces, which are present in certain materials that form directional bonds (Beeler et al., 2012). Full descriptions and comparisons of EAM and MEAM potentials have been completed in other works (Beeler et al., 2012; Foiles and Baskes, 2012), and only a short description of the theory will be included here. A more complete description of MEAM potentials is also provided in the Supplementary Material, paraphrased from Beeler et al. (2012). The general equation for the interatomic potential for both EAM and MEAM is shown by Eq. 4.

$E={\displaystyle \sum _i\left[F_i\left(\overline{{\rho }_i}\right)+\frac{1}{2}{\displaystyle \sum }_{j\ne i}{\varphi }_{ij}\left(R_{ij}\right)\right]}(4)$

In this equation, E represents the energy of the atoms i, ${\varphi }_{ij}$ represents the pair potential between atoms i and j, $\overline{\rho }$ is the effective electron density, and $F_i$ is the embedding function, which introduces many-body effects. For EAM potentials, the background electron density is taken to be the linear superposition of the spherically averaged atomic electron densities (${\rho }^0$), whereas in MEAM, angular effects are considered (Beeler et al., 2012).

Vacancy formation energies can be calculated for a bulk lattice using the following equation,

$E_f=E_{\left(n-1\right)}-\frac{n-1}{n}{E}_{\left(n\right)}(5)$

where $E_{\left(n-1\right)}$ is the energy of the system with a single vacancy, $E_{\left(n\right)}$ is the energy of the perfect lattice, and n is the total number of atoms in the perfect lattice (Beeler et al., 2012). This equation was used due to the emphasis of this work on the impact of local atomic configuration and alloy composition on the value of the vacancy formation energy with respect to irradiation, rather than desiring a global minimum value for use in determining the concentration of thermal vacancies Zhang and Sluiter (2015), Ruban (2016).

2.2 Special Quasirandom Structures Generation Procedures

For the generation of SQS, three input files were used with the “mcsqs” code from the Alloy Theoretic Automated Toolkit (ATAT) (van de Walle and Asta, 2002; van de Walle et al., 2002; Hart and Forcade, 2008; van de Walle et al., 2013; Liu et al., 2017). The first input file (by default rndstr.in, but this can be changed with the −1 = filename option in the command line) defines the structure of the alloy and the ratio of the components. This input file must be made by the user. The second input file (by default clusters.out, but this can be changed with the −cf = filename option in the command line) tells the code what clusters must be considered while generating the SQS. This input file can be generated by code by using the command

$mcsqs-2=\dots -3=\dots$

where −2 and −3 define the ranges of pairs and triplets, while in the same directory as rndstr.in. For the purpose of this work, the range of pairs was set to 6 Angstroms, and the range of triplets was set to 8 Angstroms. The third input file used was sqscell. out, which defines the supercell that “mcsqs” will use while generating the SQS. This input file is required only if the user requires a supercell of a specific shape. For the purpose of this work, a cubic supercell was used, to allow for ease of comparison between the SQS structure and the cubic structures that LAMMPS generates. To generate the SQS, the command

$mcsqs-n=\dots -rc$

must be used, where −n defines the number of atoms that will be placed within the supercell, and −rc tells the code to use the supercell defined in sqscell.out. For the code to work, the value for −n must be an integer, and the number of atoms must match with the size of the supercell provided in sqscell.out.

To run multiple ATAT sequences in parallel, the command −ip = ... can be added to the previous command, with an integer following the equals sign. This integer will be appended to the names of the output files produced by the code. The produced SQS will be found in the output file bestsqs(i). out, which will have the dimensions of the unit cell and the supercell, and then the xyz location and type of each atom in the supercell in units of the specified lattice parameter. The file bestcorr.out tracks the correlations of the best SQS that has been found. For the purpose of this work, the code was stopped after the first SQS was generated.

2.3 Molecular Dynamics Procedures

2.3.1 Random Structures

All of the random structures used for this work were produced by Plimpton (1995) LAMMPS. To produce a random structure, the dimensions of the supercell must be given in terms of unit cells, and the lattice parameter of the unit cell must be provided. Also, the structure of the unit cell must be specified (bcc, fcc, etc…). LAMMPS will produce a homogeneous structure with the specified dimensions and structure. To create a random alloy, the set command is used, which allows the user to specify what percentage of atoms should be replaced by a specified atom type. Each alloy was minimized to energy (unitless) and force (eV/Angstrom) stopping tolerances of 1.0e−15. After running the initial minimization on the as-generated crystal, the atom at the center of the supercell was removed, and the alloy was again run for one time-step, then minimized to the same tolerance limits. For each random supercell generated by LAMMPS, the calculation of the vacancy formation energy was performed for both zirconium and uranium vacancies by setting the atom type of the atom that was to be removed to the desired element. To prevent the mechanical instability of pure uranium at 0 K from influencing the results of simulations performed with pure uranium, the energy minimization step was only performed on the first nearest neighbors and second nearest neighbors of the vacancy.

2.3.2 Special Quasirandom Structures

LAMMPS has the ability to import supercell structures through the use of the read_data command. After the supercell structure is read into the LAMMPS, the same process for the determination of the vacancy formation energy was used. For the 2,000 atom SQS structures, a MATLAB script was used that determined the atom type of the atom at the center of the supercell, and found the xyz coordinates of the closest atom to the center of the supercell that was of the other type. For the 250 SQS structures, the atom at the center of the supercell was removed, and random atoms within the structure were chosen until an atom of the different type was found. Then, two runs were performed for each SQS, one where the atom at the center of the supercell was removed, and then a run where the atom of the opposite type was removed. In this way, the structure of the SQS was preserved.

3 Results and Discussion

Using LAMMPS, vacancy formation energies were calculated for the random structures and the SQS by minimizing the energy of the lattice as it was produced, then removing an atom from the center of the structure, minimizing the energy, and then taking the difference between the energies before and after the removal of the atom, as described by Eq. 5 in the Section Methods. All of these simulations were performed at a temperature of 0 K.

Figures 1, 2 compare the vacancy formation energies for the removal of zirconium and uranium atoms, respectively, for structures that were generated using the SQS method and by random atom placement. SQS can not be generated for pure metals, so only a single LAMMPS simulation was performed to determine the $E_v$ of uranium and zirconium in pure uranium and zirconium metals. Tabulated results for the $E_v$ in the pure metals can be seen in Tables 1,2, compared with results from other works. The value of 1.34 eV obtained for the uranium $E_v$ in pure uranium at 0 K agrees well with the value of 1.38 eV produced by Beeler et al. using a MEAM potential for γ-uranium in LAMMPS (Beeler et al., 2013).

FIGURE 1

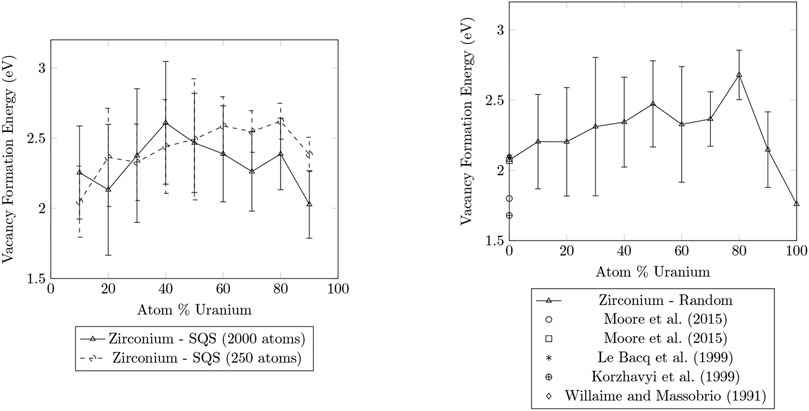
FIGURE 1. Plots of the vacancy formation energies for the removal of zirconium calculated for SQS and random structures of U-Zr alloy ranging from 0$\text{\%}$ to 100$\text{\%}$ U.

FIGURE 2

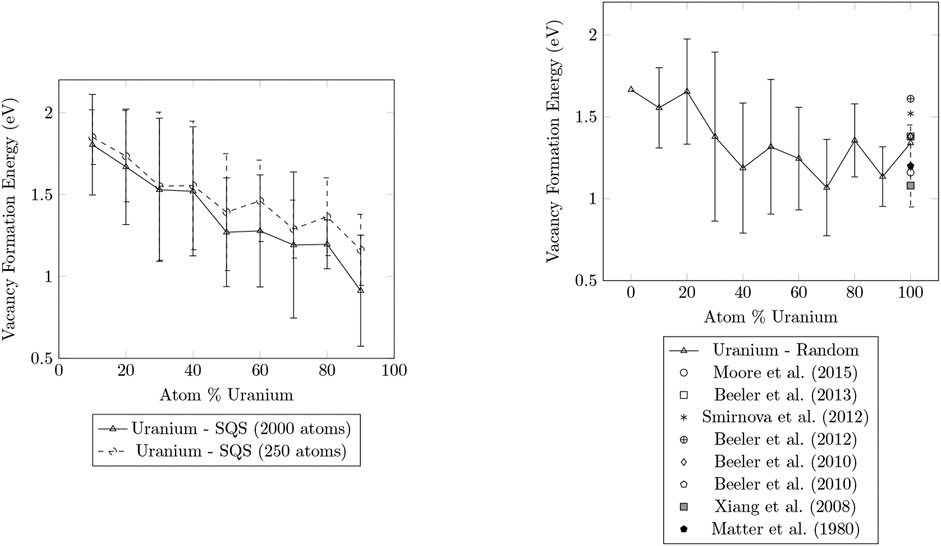
FIGURE 2. Plots of the vacancy formation energies for the removal of uranium calculated for SQS and random structures of U-Zr alloy ranging from 0$\text{\%}$ to 100$\text{\%}$ U.

For the $E_v$ of zirconium, the value seems to be fairly constant with changing atom percent of uranium, with any variation in the lines being within two standard deviations. The value of 2.074 eV obtained for the zirconium $E_v$ in pure zirconium matches very well with the results of 2.07 and 2.10 eV attained by Willaime and Massobrio (1991), Le Bacq et al. (1999), and Moore et al. (2015), respectively.

The results for the vacancy formation energies of the 2000 atom SQS structures and the random structures were in good agreement. The $E_v$ for the 250 atom SQS structures tended to be higher than those from the random and the 2,000 atom SQS structures at higher uranium percentages; however, this difference never exceeded more than one standard deviations, indicating that it was not a true difference in the properties between the structures. One important note is that random alloys produced by LAMMPS do not have exact atom percentages, with the atom percentages for each run being randomly distributed around the specified percent, with a maximum deviation of a few percentage points. Atom percentages for SQS structures are exact.

To examine the impact of local configuration on the vacancy formation energy, all possible nearest neighbor configurations were tested for the U-Zr alloy system for both uranium and zirconium vacancies. It has been shown in previous studies that the vacancy formation energy in binary alloys is highly dependent on the species distribution in both the first and second nearest neighbor sites (del Rio et al., 2011). For the simulations performed for this work only the first nearest neighbor configurations were varied, while keeping the second nearest neighbor configurations as they were generated. Therefore, the impact of second nearest neighbor configurations on the vacancy formation energy cannot be determined from the collected data.

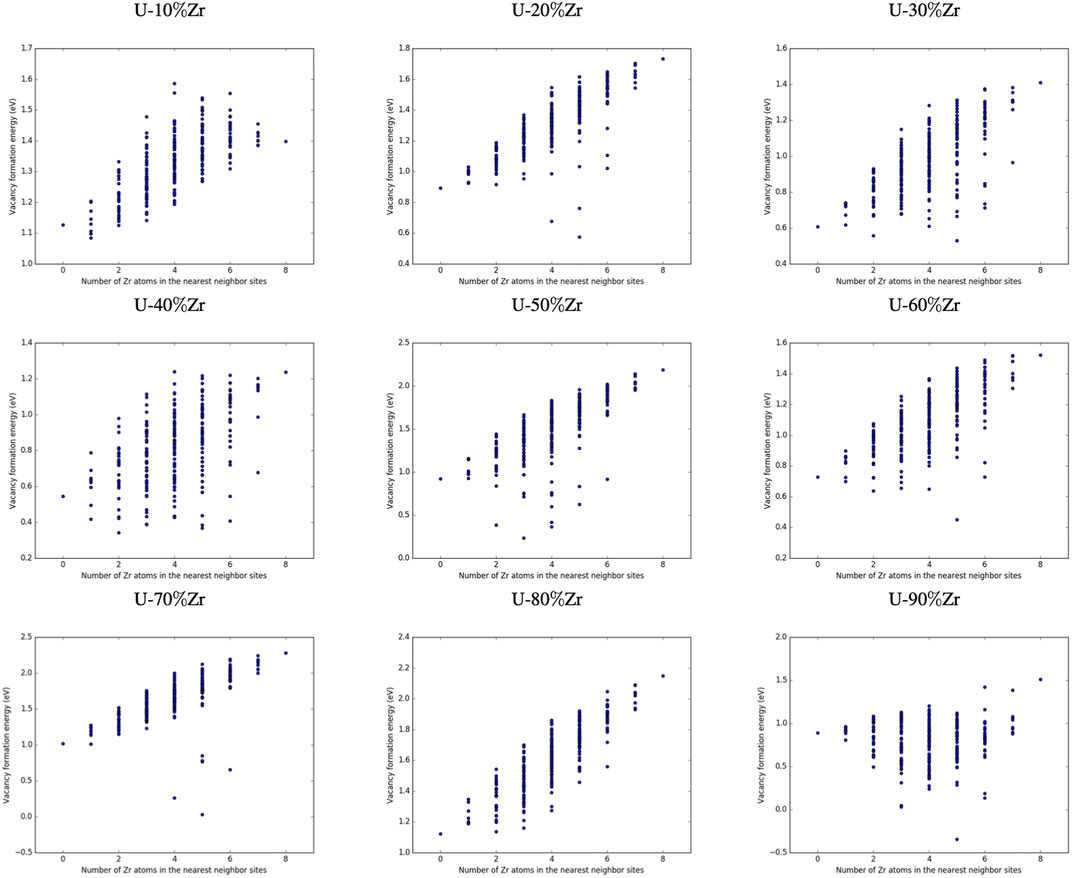
It is important to note that not all local atomic configurations are equally likely in an alloy with a set concentration. For example based on the probabilities provided in Table 3, a U-10%Zr alloy will have a 96.2% chance that there will be three or fewer zirconium atoms in nearest neighbor sites, and a 99.55% chance that there will be four or fewer zirconium atoms in nearest neighbor positions. Therefore, when considering the impact that different configurations have on the average vacancy formation energy for a given material composition, it is valid to sample configurations based on their probability of occuring.

TABLE 3

TABLE 3. Probability of zirconium inhabiting a number of nearest neighbor positions in U-Zr alloy.

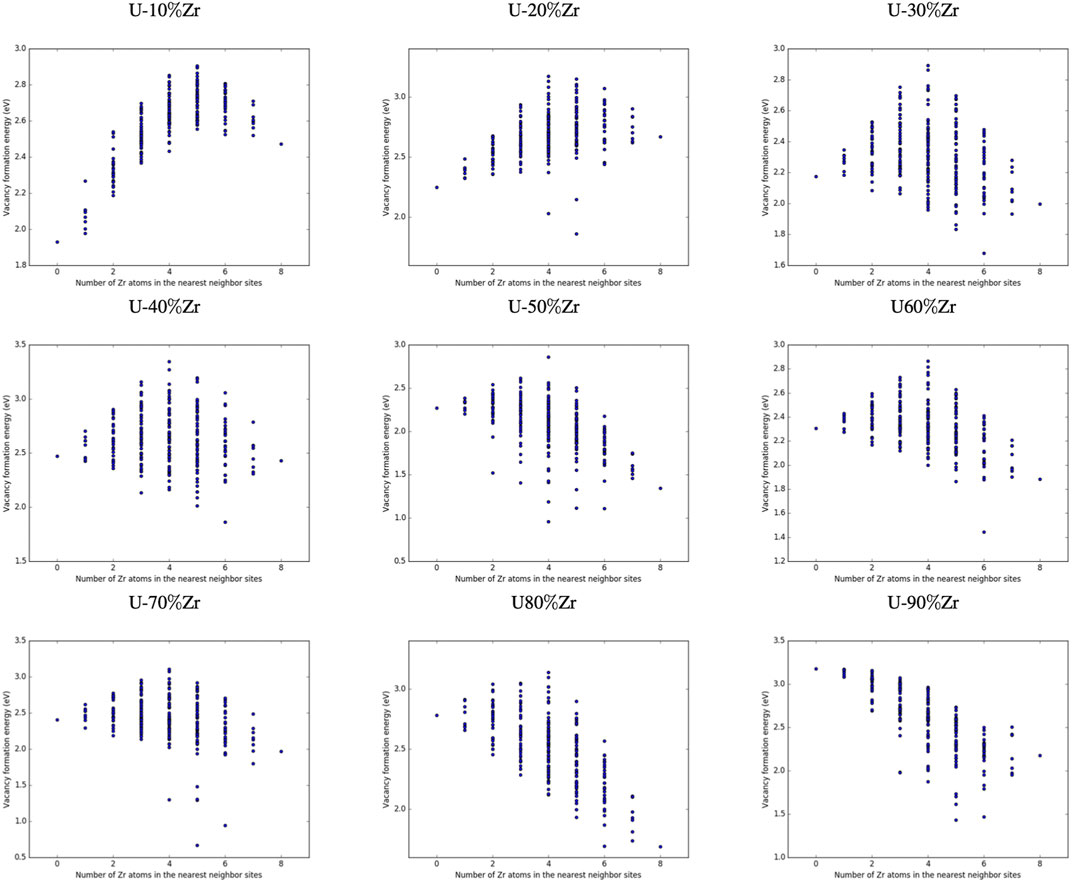
Figures 3, 4 show the vacancy formation energy as a function of local atomic composition and configuration calculated for a zirconium and uranium vacancy in U-10%Zr alloy, respectively. Each data point represents the $E_v$ for a particular nearest neighbor configuration with the number of Zr atoms specified along the x-axis. The plots of the $E_v$ results for the 256 configurations at different atom percentages can be seen in Figures 5, 6. All of the simulations for Figures 5, 6 were performed in randomly generated supercells with the nearest neighbors adjusted manually.

FIGURE 3

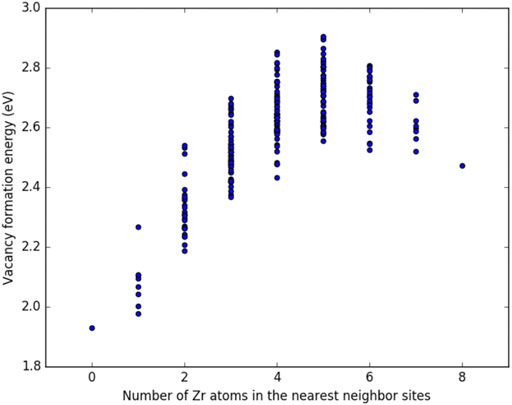
FIGURE 3. Plot of the vacancy formation energy for removing a zirconium atom from a U-10$\text{\%}$ Zr alloy. Each data point represents the vacancy formation energy for a particular configuration for the number of Zr atoms in the nearest neighbor sites as specified by the x-axis position.

FIGURE 4

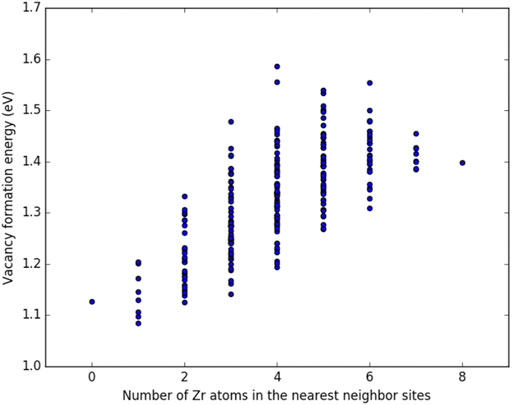
FIGURE 4. Plot of the vacancy formation energy for removing a uranium atom from a U-10$\text{\%}$ Zr alloy. Each data point represents the vacancy formation energy for a particular configuration for the number of Zr atoms in the nearest neighbor sites as specified by the x-axis position.

FIGURE 5

FIGURE 5. Configuration $E_v$ of zirconium vacancies for different atom percentages.

FIGURE 6

FIGURE 6. Configuration $E_v$ of uranium vacancies for different atom percentages.

By examining Figures 3, 4, it can be seen that the energy required to remove either a uranium or zirconium atom from a U-10%Zr alloy generally increases as the total number of Zr atoms in nearest neighbor positions increases. In the case of removal of Zr, there is a slight drop in $E_v$ as the number of zirconium atoms in nearest neighbor sites increases from five atoms to eight atoms, while the trend in the removal of uranium consistently increases with increasing zirconium atoms in nearest neighbor positions. This trend could be interpreted as an increase in the vacancy formation energy near positions where the local atomic concentrations deviate significantly from the composition of the alloy. This exact trend is observed in Figure 5, where the U-10%Zr, U-20%Zr, U-80%Zr, and U-90%Zr alloy compositions all show the trend of increasing $E_v$ as the local composition differs significantly from that of the alloy. For the middle concentrations (U-30%Zr to U-70%Zr), very similar trends are observed where there is a slight decreasing trend in $E_v$ with an increasing number of zirconium nearest neighbors. In the case of the dependence of $E_v$ on local atomic composition for the removal of uranium atoms, the same trend is observed for all alloy compositions, where the energy required to form a vacancy by removing a uranium atom always increases as the number of zirconium nearest neighbors increases.

Determining specific trends in how the local arrangement of the species (i.e., species clumped together or distributed evenly across the nearest neighbor sites) impacts the formation energy of vacancies is difficult, particularly since this will also depend on the composition and arrangement of the second nearest neighbor atoms, which were not manipulated in this study, as well as the alloy composition. Examination of specific configurations by hand was performed for a series of initial alloy compositions and configurations, and it was determined that $E_v$ is higher when the different species are grouped together into adjacent nearest neighbor sites, and that $E_v$ decreases as the species are spread out as much as possible.

4 Conclusions

The formation energies of uranium and zirconium vacancies in U-Zr binary bcc alloys were determined using MD simulations with a MEAM potential. Non-linear dependence on atom percent was observed for both uranium and zirconium vacancies. Good agreement was found for the $E_v$ of both pure uranium and pure zirconium with the works of Matter et al. (1980), Beeler et al. (2010), and Beeler et al. (2013) and for uranium and Willaime and Massobrio (1991), Le Bacq et al. (1999), and Moore et al. (2015) for zirconium.

The impact of crystal generation method on $E_v$ was examined by generating the alloys both as random alloys and as SQS. It was found that, for the supercell size used in our MD simulations, there is no statistically significant difference between the vacancy formation energies in the crystals generated by the two methods. This indicates that the supercell size used in our simulations was sufficiently large to mimic a truly random structure. Additional work could be performed to determine the supercell size where a random alloy ceases to perform similarly to SQS structures, which are intended to mimic perfectly random systems.

The effect of local atomic configuration on $E_v$ was examined by varying the configuration of atoms in the nearest neighbor sites around a vacancy in U-Zr alloys. It was observed that for both uranium and zirconium, the configuration of nearest neighbor atoms did have an impact on the $E_v$. The removal energy of uranium was found to increase with increasing Zr nearest neighbors up until an atom fraction of 90% Zr, where no strong dependence on nearest neighbor configuration was found. The removal energy of zirconium was found to increase with increasing Zr nearest neighbors in low atom percent Zr alloys, and decrease with increasing Zr nearest neighbors in alloys with Zr atom percentages higher than percent. It was observed that $E_v$ increased when the nearest neighbors were arranged in a manner that grouped atoms of the same species together, while $E_v$ was found to decrease as the species were evenly distributed across the nearest neighbor sites.

With a better understanding of the $E_v$ in γ-U-Zr alloys, additional work can be performed with the examination of defect diffusion via vacancies, as well as the formation of defects due to radiation damage events. This work could also support the development or improvement of conventional interatomic potentials for alloys, or as a possible data source for machine learning interatomic potentials or machine learnining-based simulation techniques. Further insight into the relationship between the $E_v$ and local atomic configuration could be explored through the use of DFT simulations.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

CD conceptualized and initiated the ideas in this work, DV performed calculations and made modifications to initial ideas based on results and consultation with CD. DV wrote the initial draft and CD edited and revised the paper draft.

Funding

CD would like to acknowledge funding from the G.W. Woodruff Fellowship. CD and DV acknowledge support from Department of Energy Nuclear Energy UNiveristy Progranms Office.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank the reviewers of this work for their help in improving the quality of this work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.692660/full#supplementary-material

References

Badillo, A., Bellon, P., and Averback, R. S. (2015). A Phase Field Model for Segregation and Precipitation Induced by Irradiation in Alloys. Model. Simul. Mater. Sci. Eng. 23, 035008. doi:10.1088/0965-0393/23/3/035008

CrossRef Full Text | Google Scholar

Beeler, B., Deo, C., Baskes, M., and Okuniewski, M. (2012). Atomistic Properties of γ Uranium. J. Phys. Condens. Matter 24, 075401. doi:10.1088/0953-8984/24/7/075401

PubMed Abstract | CrossRef Full Text | Google Scholar

Beeler, B., Deo, C., Baskes, M., and Okuniewski, M. (2013). First Principles Calculations of the Structure and Elastic Constants of α, β and γ Uranium. J. Nucl. Mater. 433, 143–151. doi:10.1016/j.jnucmat.2012.09.019

CrossRef Full Text | Google Scholar

Beeler, B., Good, B., Rashkeev, S., Deo, C., Baskes, M., and Okuniewski, M. (2010). First Principles Calculations for Defects in U. J. Phys. Condens. Matter 22, 505703. doi:10.1088/0953-8984/22/50/505703

PubMed Abstract | CrossRef Full Text | Google Scholar

del Rio, E., Sampedro, J. M., Caturla, M. J., Caro, M., et al. (2011). Formation Energy of Vacancies in FeCr Alloys: Dependence on Cr Concentration. J. Nucl. Mater. 408, 18–24. doi:10.1016/j.jnucmat.2010.10.021

CrossRef Full Text | Google Scholar

Foiles, S. M., and Baskes, M. I. (2012). Contributions of the Embedded-Atom Method to Materials Science and Engineering. MRS Bull. 37, 485–491. doi:10.1557/mrs.2012.93

CrossRef Full Text | Google Scholar

Hart, G. L. W., and Forcade, R. W. (2008). Algorithm for Generating Derivative Structures. Phys. Rev. B 77, 224115. doi:10.1103/PhysRevB.77.224115

CrossRef Full Text | Google Scholar

Kim, S. M. (1984). Vacancy Formation Energies in Disordered Alloys. Phys. Rev. B 30, 4829–4832. doi:10.1103/PhysRevB.30.4829

CrossRef Full Text | Google Scholar

Korzhavyi, P. A., Abrikosov, I. A., Johansson, B., Ruban, A. V., and Skriver, H. L. (1999). First-principles Calculations of the Vacancy Formation Energy in Transition and noble Metals. Phys. Rev. B 59, 11693–11703. doi:10.1103/PhysRevB.59.11693

CrossRef Full Text | Google Scholar

Le Bacq, O., Willaime, F., and Pasturel, A. (1999). Unrelaxed Vacancy Formation Energies in Group-IV Elements Calculated by the Full-Potential Linear Muffin-Tin Orbital Method: Invariance with crystal Structure. Phys. Rev. B 59, 8508–8515. doi:10.1103/PhysRevB.59.8508

CrossRef Full Text | Google Scholar

Liu, Z. T. Y., Burton, B. P., Khare, S. V., and Gall, D. (2017). First-principles Phase Diagram Calculations for the Rocksalt-Structure Quasibinary Systems TiN-ZrN, TiN-HfN and ZrN-HfN. J. Phys. Condens. Matter 29, 035401. doi:10.1088/0953-8984/29/3/035401

PubMed Abstract | CrossRef Full Text | Google Scholar

Matter, H., Winter, J., and Triftshäuser, W. (1980). Investigation of Vacancy Formation and Phase Transformations in Uranium by Positron Annihilation. J. Nucl. Mater. 88, 273–278. doi:10.1016/0022-3115(80)90283-4

CrossRef Full Text | Google Scholar

Moore, A. P., Beeler, B., Deo, C., Baskes, M. I., and Okuniewski, M. A. (2015). Atomistic Modeling of High Temperature Uranium-Zirconium alloy Structure and Thermodynamics. J. Nucl. Mater. 467, 802–819. doi:10.1016/j.jnucmat.2015.10.016

CrossRef Full Text | Google Scholar

Piochaud, J. B., Nastar, M., Soisson, F., Thuinet, L., and Legris, A. (2016). Atomic-based Phase-Field Method for the Modeling of Radiation Induced Segregation in Fe-Cr. Comput. Mater. Sci. 122, 249–262. doi:10.1016/j.comatsci.2016.05.02110.1016/j.commatsci.2016.05.021

CrossRef Full Text | Google Scholar

Plimpton, S. (1995). Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 117, 1–19. doi:10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

Ruban, A. V. (2016). Thermal Vacancies in Random Alloys in the Single-Site Mean-Field Approximation. Phys. Rev. B 93, 134115. doi:10.1103/PhysRevB.93.134115

CrossRef Full Text | Google Scholar

Smirnova, D. E., Starikov, S. V., and Stegailov, V. V. (2011). Interatomic Potential for Uranium in a Wide Range of Pressures and Temperatures. J. Phys. Condens. Matter 24, 015702. doi:10.1088/0953-8984/24/1/015702

PubMed Abstract | CrossRef Full Text | Google Scholar

Smirnova, D. E., Kuksin, Y. A., Starikov, S. V., Stegailov, V. V., Rest, J., Insepov, Z., et al. (2013). A Ternary EAM Interatomic Potential for U-Mo Alloys with Xenon. Model. Simul. Mater. Sci. Eng. 21, 035011. doi:10.1088/0965-0393/21/3/035011

CrossRef Full Text | Google Scholar

Soisson, F. (2006). Kinetic Monte Carlo Simulations of Radiation Induced Segregation and Precipitation. J. Nucl. Mater. 349, 235–250. doi:10.1016/j.jnucmat.2005.11.003

CrossRef Full Text | Google Scholar

van de Walle, A., Asta, M., and Ceder, G. (2002). The alloy Theoretic Automated Toolkit: A User Guide. Calphad 26, 539–553. doi:10.1016/S0364-5916(02)80006-2

CrossRef Full Text | Google Scholar

van de Walle, A., Tiwary, P., de Jong, M., Olmsted, D. L., Asta, M., Dick, A., et al. (2013). Efficient Stochastic Generation of Special Quasirandom Structures. Calphad 42, 13–18. doi:10.1016/j.calphad.2013.06.006

CrossRef Full Text | Google Scholar

Walle, A. v. d., and Asta, M. (2002). Self-driven Lattice-Model Monte Carlo Simulations of alloy Thermodynamic Properties and Phase Diagrams. Model. Simul. Mater. Sci. Eng. 10, 521–538. doi:10.1088/0965-0393/10/5/304

CrossRef Full Text | Google Scholar

Wei, S.-H., Ferreira, L. G., Bernard, J. E., and Zunger, A. (1990). Electronic Properties of Random Alloys: Special Quasirandom Structures. Phys. Rev. B 42, 9622–9649. doi:10.1103/PhysRevB.42.9622

CrossRef Full Text | Google Scholar

Willaime, F., and Massobrio, C. (1991). Development of anN-Body Interatomic Potential for Hcp and Bcc Zirconium. Phys. Rev. B 43, 11653–11665. doi:10.1103/PhysRevB.43.11653

CrossRef Full Text | Google Scholar

Xiang, S., Huang, H., and Hsiung, L. M. (2008). Quantum Mechanical Calculations of Uranium Phases and Niobium Defects in γ-uranium. J. Nucl. Mater. 375, 113–119. doi:10.1016/j.jnucmat.2007.11.003

CrossRef Full Text | Google Scholar

Zhang, X., and Sluiter, M. H. F. (2015). Ab Initioprediction of Vacancy Properties in Concentrated Alloys: The Case of Fcc Cu-Ni. Phys. Rev. B 91, 174107. doi:10.1103/PhysRevB.91.174107

CrossRef Full Text | Google Scholar

Zhao, S., Stocks, G. M., and Zhang, Y. (2016). Defect Energetics of Concentrated Solid-Solution Alloys from Ab Initio Calculations: Ni0.5Co0.5, Ni0.5Fe0.5, Ni0.8Fe0.2 and Ni0.8Cr0.2. Phys. Chem. Chem. Phys. 18, 24043–24056. doi:10.1039/C6CP05161H

PubMed Abstract | CrossRef Full Text | Google Scholar