- 1Xi’an Modern Chemistry Research Institute, Xi’an, China
- 2College of Mechanical and Vehicle Engineering, Hunan University, Changsha, China
Composed of metallic layers and composite plies, fiber metal laminates (FMLs) combine inherent advantages of metals and composites. The phenomenon of anomalous response behavior, in which the permanent deformation is in the opposite direction to the incoming pressure wave, has been discovered in dynamic responses of monolithic plate subjected to impulsive loading. In this study, dynamic responses of FML plates of various configurations are examined and compared against the responses of a monolithic plate using finite element analysis. It is found that under the load condition in which an anomalous dynamic behavior of an aluminum plate is observed, FMLs oscillate a few cycles before resting on permanent deformation, and the laminate thickness strongly affects the final deflection, which could be in the counter-intuitive direction or near the initial position of zero deflection depending on configuration and specification of FMLs. In addition, interaction of damage accumulation with deflection responses is investigated. The findings of this study can be useful for optimal design of FMLs intended for usage under extreme loadings.
Introduction
Composite materials are composed of two or more different substances, each with its own characteristics, combined to achieve superior properties than the constituent materials (Lapczyk and Hurtado, 2007; Guo et al., 2021). Having witnessed a rapidly development, composite materials are widely used in erospace, automotive, electrical, construction, and other fields (Ameri, Moradi and Talebitooti, 2020; Wanchoo et al., 2021). Active research on the dynamic behavior of composite materials includes rate dependence of mechanical properties (Wang et al., 2021), constitutive models (Zhan et al., 2021), damage evolution such as shear softening upon dynamic loading (Tang et al., 2017), and etc.
Fiber-metal laminates (FMLs) are made of thin metal layers alternating with composite layers having a unidirectional, cross-ply, or fabric structure (Vasiliev and Morozov, 2018). FMLs combine advantages of fiber-reinforced composite materials and metals, possessing high specific strength, fatigue resistance, and excellent impact resistance (Andrew et al., 2019; Nicolinco et al., 2021). A particular important application of FMLs is using them in conditions that involving severe and extreme loads to absorb energies (Sasso et al., 2019; Jia et al., 2021). The dynamic responses of FMLs under various loading conditions have drawn research interest. One category is the study of projectile impacts, including FMLs under low-speed and high-speed projectile impacts (Lee et al., 2018; Li et al., 2018; Sharma et al., 2021), multiple impacts with the same total energy (Yao et al., 2019), the influence of projectile deformability (Sangsefidi et al., 2021), and etc.
Impulsive loading is characterized by high intensity and short duration. While metal plates made of aluminum alloys or steel (Chen and Hao, 2014; Micallef et al., 2016; Cerik, 2017; Zhang et al., 2020), stiffened structures (Zhao et al., 2020; Fu et al., 2021; Kong et al., 2021), as well as other innovative forms of structures (Sun et al., 2019; Zhou and Jing, 2020; Jing et al., 2021) under impulsive loads have been intensively studied, FMLs subjected to intensive short duration loading, however, are far from being well understood. The involved complexities include the wide range of changes in strain rate under blast loading (Zhang et al., 2018; Xu et al., 2020), interaction of fragments with blast waves (Dhari, 2021), modeling of interfacial debonding between adjacent plies (Soutis et al., 2011), and sensitivity to the load characteristics (Karagiozova et al., 2010).
Anomalous dynamic responses, also knowns as counter-intuitive behaviors, have been found in ductile metal objects subjected to a pressure pulse. The final deflections are in the direction opposite to that of the pressure applied during the pulse. Since the discovery of this interesting dynamic behavior (Symonds and Yu, 1985), theoretical, experimental, and numerical studies have been conducted on the counter-intuitive behavior of beams and plates under impact and impulse loads. It has been realized that the counter-intuitive behavior is related with the elastic-plastic non-linearity and the compressive instability (Dong et al., 2011). Under impulsive loading conditions, the negative phase due to the momentum of air that generates an overexpansion has been found to have significant influence on the occurrence of counter-intuitive behaviors (Aune et al., 2016). Attention to counter-intuitive behavior is deserved because it is an unstable configuration that a small loading less than the failure level might leads to catastrophic results (Ma et al., 2015). However, the responses of FMLs are not clear in the dynamically anomalous regime that has been observed for monolithic metal plates. Hence, unexpected but potentially disastrous consequences of counter-intuitive behavior can be a critical factor restricting extensive usage of FMLs.
In this study, dynamic responses of FML plates subjected to impulsive loads are investigated, with special focus to anomalous response behavior. First, dynamic responses of a monolithic metal plate are studied and validated. Then, same impulsive loading conditions are applied to FML plates of varying configurations. The differences between monolithic and FML plates are examined. Lastly, the damage induced during the dynamic responses is investigated, and implications on FML design and structural applications are discussed. Materials and Methods is devoted to description devotes to the materials and modeling considerations. In Results and Discussions, numerical results are discussed. Conclusions are summarized in Conclusion.
Materials and Methods
In this study, FMLs are composed of two thin aluminum layers bonded with fiber composite layers. A coding system denoted by
In the present study, three types of FML panels with varying layer thickness and fiber orientation are studied as shown in Figure 1. The thickness versus weight trade-off is always an important consider in FML applications. Thus, the total thickness is set to the same value for all FML panels; the performance of different FML configurations can then be evaluated.
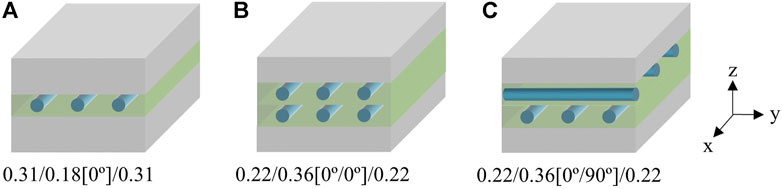
FIGURE 1. Schematics of FMLs with varying layer thickness and fiber orientation for (A) 0.31/0.18[0°]/0.31 (B) 0.22/0.36[0°/0°]/0.31 and (C) 0.22/0.36[0°/90°]/0.31.
Dynamic responses of FML plates subjected to impulsive loads are studied via numerical simulations. The plate dimensions are

TABLE 1. Material parameters of fiber-reinforced composites (Lapczyk and Hurtado, 2007).
Metal Constitutive Relation
In order to simulate large elastoplastic deformation of metal, the rate of deformation is decomposed into elastic and plastic parts as
where
where
where
where
where
where
Since materials undergo rapid plastic deformation subjected to impulsive loads, the adiabatic process is assumed. The rate of temperature rise is defined as
where

TABLE 2. Material parameters for the metal constitutive relation (Aune et al., 2017).
Modeling of Fiber Reinforced Polymer
Because of geometrical feature of the FML plates having a thickness significantly smaller than the other dimensions, the aluminum and composites layers are modeled using shell elements. Composite layups can be composed of plies made of different materials in different orientations. To simplify the model, the shell composite layup model in ABAQUS that discretizes only the reference surfaces for each ply is used, and thus fibers and matrix are not explicitly modeled.
The failure criteria of fiber-reinforced composite materials adopt the Hashin’s theory (Hashin and Rotem, 1973; Hashin, 1980) that has been implemented in the commercial finite element package ABAQUS. Four different modes of failure are considered including fiber rupture in tension, fiber buckling and kinking in compression, matrix cracking under transverse tension and shearing, and matrix crushing under transverse compression and shearing. The initiation criterion is expressed as
where
When damage begins to accumulate, each failure mode has its own damage evolution and a damage index in the range of 0–1 as the measure of damage. Using the energy-based linear damage evolution law, the fracture energies
Modeling Considerations for Adhesive Layers
The degradation of bonding adhesive layer between metal and composite layers in an FML significantly reduce the rigidity and eventually lead to interlaminar delamination. Thus, the adhesive behavior of bonded neighboring layers must be taken into consideration. In this study, the surface-based cohesive behavior model available in ABAQUS is used.
The linear elastic traction-separation behavior is assumed in the surface-based cohesive model. Material properties used to define the elastic behavior of adhesive are summarized in Table 3. The debonding process consists of three phases, i.e., damage initiation, damage evolution and complete failure. This study uses the quadratic separation criterion to characterize damage initiation represented as
where

TABLE 3. Material parameters for cohesive behavior (Lapczyk and Hurtado, 2007).
The law of damage evolution describes the degradation rate of stiffness once the initiation criterion is reached. The energy-based exponential damage evolution law is adopted, and the power law criterion is used to describe the interaction of mixed modes as (Camanho and Davila, 2002)
where
where
where
Modeling of Impulsive Loading
A primary goal of this study is to investigate the anomalous dynamic response that is highly sensitive to the applied loads, hence the load function is of critical importance. While many studies use simplified pulse shapes such as triangles or rectangles in their numerical simulations, an in-house code specifically developed for modeling the impulsive pressure is ported to commercial finite element software via user defined subroutines in the present study.
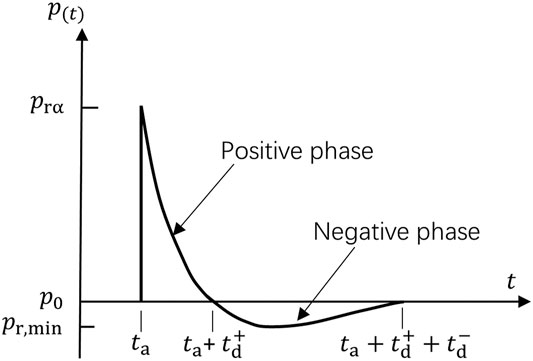
The pressure-time history is comprised of positive and negative phases as shown in Figure 2. The pressure profile is characterized by the ambient pressure
The required input parameters for the impulsive load function are the location of source and equivalent charge weight. The scaled distance using the Hopkinson-Cranz scaling law can be used to describe the intensity of shock loading as
where
The reflected pressure considering the angle of incidence
where
Since
Where
Results and Discussions
Dynamic Response of a Monolithic Metal Plate
In this subsection, the dynamic response of an aluminum plate under impulsive loading is studied and compared against experimental results available in literature. The dimensions of the plate are
The deflection at the plate center is shown in Figure 3, indicating radically different dynamic responses of the plate subjected to impulsive loads of varying intensity. The final deflection of the plate under the impulsive load of
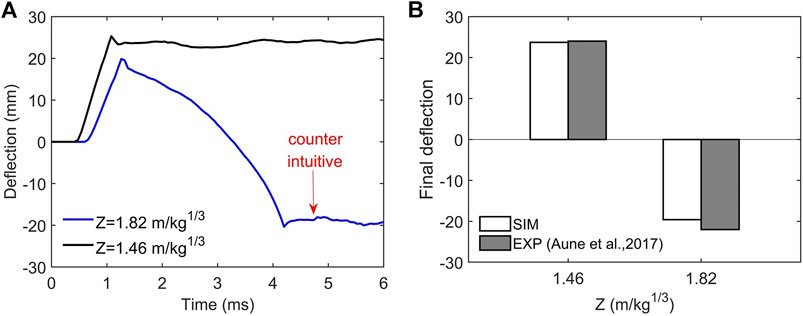
FIGURE 3. Dynamic responses of a monolithic metal plate. (A) The deflection time histories at the plate center. (B) The final deflections under two impulsive loads defined in terms of the scaled distance
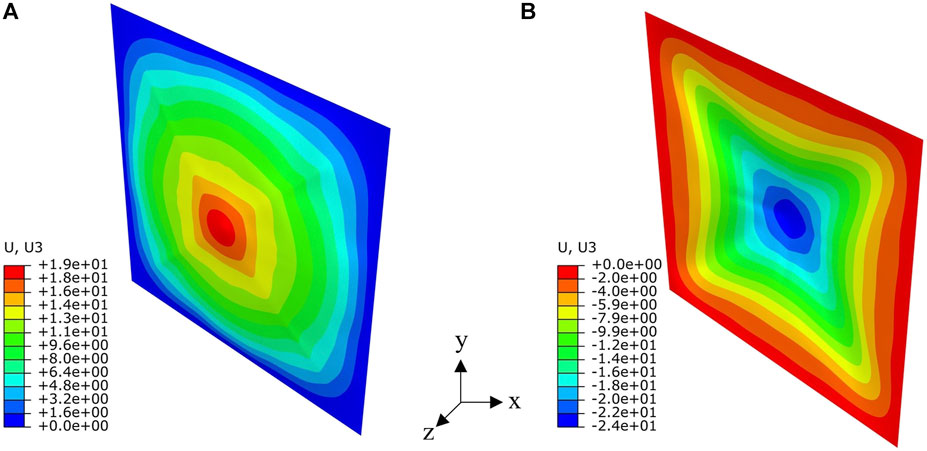
FIGURE 4. Final permantent deformation of metal plate subjected to impulsive loads of (A)
Dynamic Responses of Fiber-Metal Laminate Plates
We then study dynamic responses of FML plates and examine the difference in comparison to the responses of the monolithic metal plate. The geometries and material properties have been summarized in Materials and Methods. The thickness of the FML plates under consideration is identical to that of the aluminum plate studied in Dynamic Response of a Monolithic Metal Plate, so a quantitative comparison in dynamic responses can be made between monolithic and FML plates.
Figure 5A plots the deflection time histories at the plate center with the impulsive load of
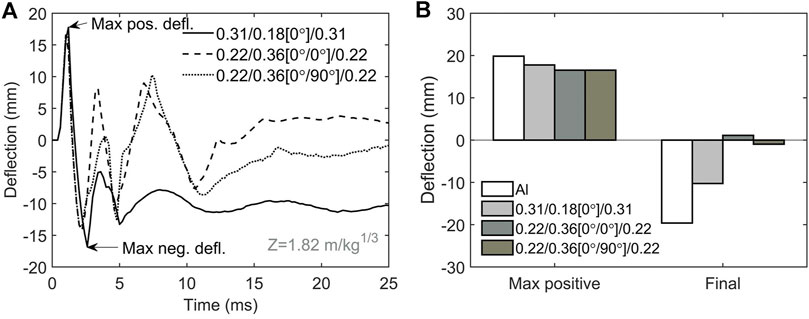
FIGURE 5. Dynamic responses of FML plates under the impulsive load of
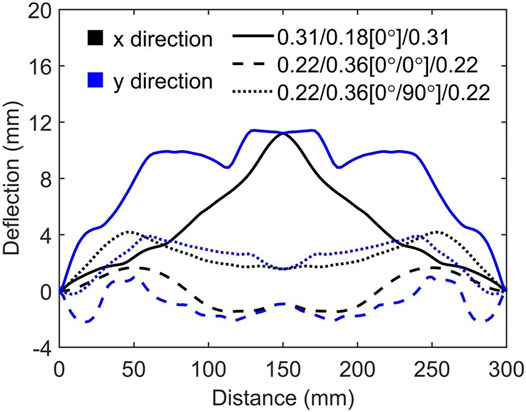
Figure 6 shows the final deformation profiles of FML plates. For the
Given the considerable difference in the slope of deflection near the plate edges, we further inspect the state of stress triaxiality defined as the ratio of the hydrostatic mean stress to the von Mizes equivalent stress, i.e.,
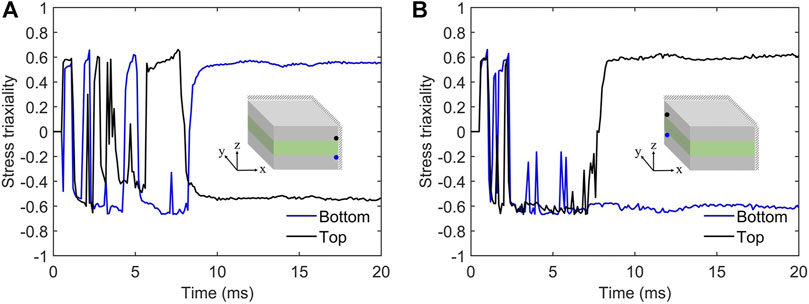
FIGURE 7. The evolution of stress triaxiality of the 0.22/0.36 [0°/0°]/0.22 plate under the impulsive load of
Next, we examine the dynamic responses of FML plates subjected to higher intensity of impulsive loading with the scaled distance
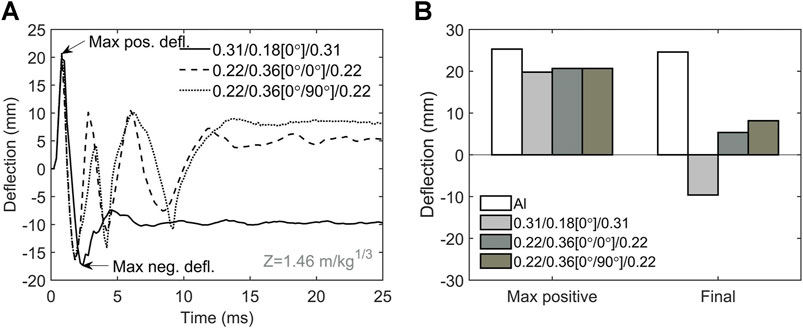
FIGURE 8. Dynamic responses of FML plates under the impulsive load of
Damage of Fiber-Metal Laminate Plates
For all three FML plates subjected to the scaled pulse
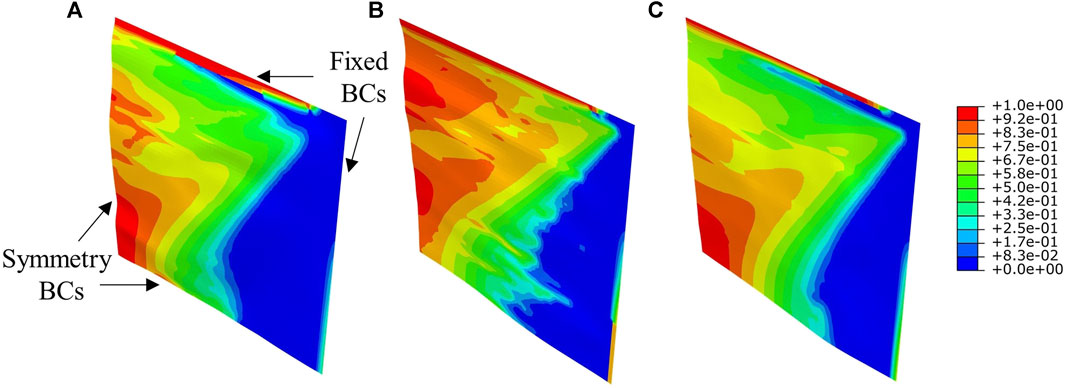
FIGURE 9. Matrix tension damage of the composite layer under the impulsive load of
The degradation and eventual failure of bonding between two cohesive surfaces are major concerns for applications using FMLs. Figure 10 shows the damage evolution at various locations of the 0.22/0.36 [0°/0°]/0.22 plate. Overall, the top cohesive interface, which is closer to the source of impulsive loading, suffers severer damage than the bottom cohesive interface; plate edges sustain more damage than the center, which is closer to the source though. Although damage is produced, no debonding takes place for both
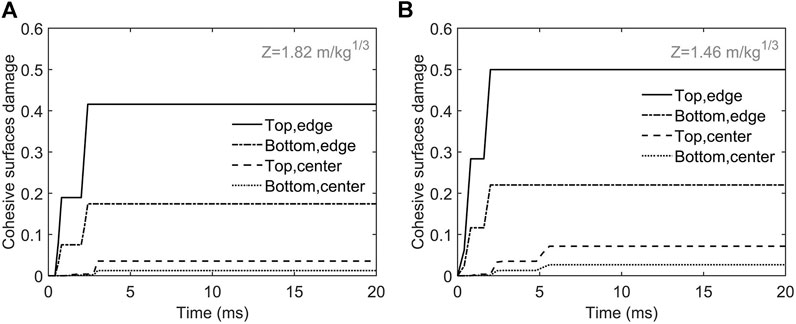
FIGURE 10. The damage evolution at various locations of the 0.22/0.36 [0°/0°]/0.22 plate. (A) With the impulsive load of
It is worth pointing out that although the impulsive loading is applied normal to the plate surface, localized sliding can occur between layers. To illustrate this phenomenon, the displacements along the
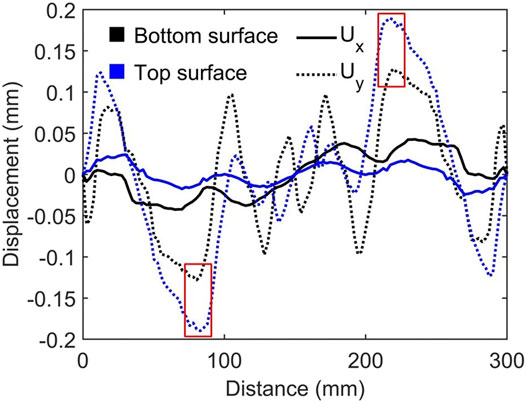
FIGURE 11. The displacements along the x- and y-centerlines of the 0.22/0.36 [0°/0°]/0.22 plate under the impulsive load of
Lastly, in order to clearly understand the damage of FML during the dynamic response, the energy dissipated by damage is plotted as shown in Figure 12. In the case of impulsive load
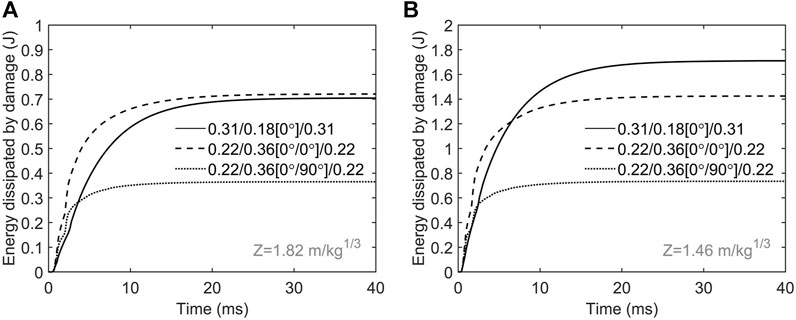
FIGURE 12. Energy dissipated by damage with (A) the impulsive load of
Conclusion
Dynamic responses of FML plates subjected to impulsive loads are investigated, with special focus to anomalous response behavior. Modeling considerations include high strain-rate ductile plasticity, failure criteria for fiber reinforced polymer, degradation of adhesive layers, and validated pressure pulses that strongly affect predictions of counter-intuitive behaviors under impulsive loadings. Different FML configurations under impulsive loadings are examined.
First, dynamic responses of a monolithic plate made of aluminum are examined. A counter-intuitive behavior with the final permanent deflection in the opposite direction to the incoming load is predicted numerically. This anomalous behavior vanishes as the loading intensity, which is characterized by the scaled distance, decreases by 20%. The numerical predictions are validated against experimental results available in literature.
Under the same loading conditions, dynamic responses of FML plates of different configurations are studied. Remarkably different responses are noticed. While the maximum positive deflections of FML plates are consistently reduced in all cases, the final permanent deformation shows a wide disparity among FML configurations and load intensities. Under the load condition in which an anomalous dynamic behavior of the aluminum plate is observed, FMLs oscillate before resting on permanent deformation, and the laminate configuration and specification strongly affect the final deflection, which might hold position in the counter-intuitive direction opposite to the incoming pulse or in the vicinity of the initial position with small permanent deflection. Interestingly, after decreasing the scaled distance such that the anomalous behavior vanishes for the aluminum plate, a counter-intuitive behavior still exists in the FML plate that has a thinner composite layer than the other FML plates.
On one hand, the anomalous behavior is related with the elastic-plastic non-linearity and the compressive instability; on the other, interaction with damage accumulation in plates made of FMLs deserves attention. It is found that in the studied loading cases, stress triaxialities in different layers as well as along different directions are noticed to be quite different, suggesting different state of deformation such as tension or shear. Lastly, although matrix damage due to tension is the main failure mechanism in the present study, localized sliding is noticed between layers.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
HZ, JZ, and WL conceived and designed the study. JZ, WL, and BM carried out the simulation work. HZ, JZ, and WL reviewed and edited the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work was financially supported by the Open Collaboration and Innovation Fund of Xi’an Modern Chemistry Research Institute.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ameri, B., Moradi, M., and Talebitooti, R. (2021). Effect of Honeycomb Core on Free Vibration Analysis of Fiber Metal Laminate (FML) Beams Compared to Conventional Composites. Compos. Structures 261 (May 2020), 113281. doi:10.1016/j.compstruct.2020.113281
Andrew, J. J., Srinivasan, S. M., Arockiarajan, A., and Dhakal, H. N. (2019). Parameters Influencing the Impact Response of Fiber-Reinforced Polymer Matrix Composite Materials: A Critical Review. Compos. Structures 224 (December), 111007. doi:10.1016/j.compstruct.2019.111007
Aune, V., Fagerholt, E., Hauge, K. O., Langseth, M., and Børvik, T. (2016). Experimental Study on the Response of Thin Aluminium and Steel Plates Subjected to Airblast Loading. Int. J. Impact Eng. 90, 106–121. doi:10.1016/j.ijimpeng.2015.11.017
Aune, V., Valsamos, G., Casadei, F., Larcher, M., Langseth, M., and Børvik, T. (2017). Numerical Study on the Structural Response of Blast-Loaded Thin Aluminium and Steel Plates. Int. J. Impact Eng. 99, 131–144. doi:10.1016/j.ijimpeng.2016.08.010
Bao, Y., and Wierzbicki, T. (2004). A Comparative Study on Various Ductile Crack Formation Criteria. J. Eng. Mater. Technol. Trans. ASME 126 (3), 314–324. doi:10.1115/1.1755244
Bassi, A., Genna, F., and Symonds, P. S. (2003). Anomalous Elastic-Plastic Responses to Short Pulse Loading of Circular Plates. Int. J. Impact Eng. 28 (1), 65–91. doi:10.1016/S0734-743X(02)00036-2
Camanho, P. P., and Davila, C. D. (2002). Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials. Washington, DC: National Aeronautics and Space Administration, Report No.: NASA/TM-2002-211737.
Cerik, B. C. (2017). Damage Assessment of Marine Grade Aluminium Alloy-Plated Structures Due to Air Blast and Explosive Loads. Thin-Walled Structures 110 (October), 123–132. doi:10.1016/j.tws.2016.10.021
Chen, W., and Hao, H. (2014). Experimental Investigations and Numerical Simulations of Multi-Arch Double-Layered Panels under Uniform Impulsive Loadings. Int. J. Impact Eng. 63, 140–157. doi:10.1016/j.ijimpeng.2013.08.012
Dhari, R. S. (2021). A Numerical Study on Cross Ply Laminates Subjected to Stray Fragments Impact Loading. Compos. Structures 261 (January), 113563. doi:10.1016/j.compstruct.2021.113563
Dong, Q., Li, Q. M., and Zheng, J. Y. (2011). Further Study on Counter-intuitive Response of Single-Degree-Of-Freedom Structures. Int. J. Impact Eng. 38 (5), 305–308. doi:10.1016/j.ijimpeng.2010.10.033
Fu, T., Zhang, M., Zheng, Q., Zhou, D., Sun, X., and Wang, X. (2021). Scaling the Response of Armor Steel Subjected to Blast Loading. Int. J. Impact Eng. 153, 103863. doi:10.1016/j.ijimpeng.2021.103863
Greenhalgh, E. (2009). Failure Analysis and Fractography of Polymer Composites. Chennai, TN: Elsevier. doi:10.1533/9781845696818
Guo, Q., Yao, W., Li, W., and Gupta, N. (2021). Constitutive Models for the Structural Analysis of Composite Materials for the Finite Element Analysis: A Review of Recent Practices. Compos. Structures 260 (August), 113267. doi:10.1016/j.compstruct.2020.113267
Hashin, Z., and Rotem, A. (1973). A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 7 (4), 448–464. doi:10.1177/002199837300700404
Hashin, Z. (1980). ‘Failure Criteria for Unidirectional Mr !’. J. Appl. Mech. 47 (June), 329–334. doi:10.1115/1.3153664
Jia, S., Wang, F., Zhou, J., Jiang, Z., and Xu, B. (2021). Study on the Mechanical Performances of Carbon Fiber/epoxy Composite Material Subjected to Dynamical Compression and High Temperature Loads. Compos. Structures 258 (December 2020), 113421. doi:10.1016/j.compstruct.2020.113421
Jing, L., Liu, K., Su, X., and Guo, X. (2021). Experimental and Numerical Study of Square Sandwich Panels with Layered-Gradient Foam Cores to Air-Blast Loading. Thin-Walled Structures 161 (January), 107445. doi:10.1016/j.tws.2021.107445
Karagiozova, D., Langdon, G. S., Nurick, G. N., and Chung Kim Yuen, S. (2010). Simulation of the Response of Fibre-Metal Laminates to Localised Blast Loading. Int. J. Impact Eng. 37 (6), 766–782. doi:10.1016/j.ijimpeng.2009.04.001
Kong, X., Zhou, H., Kuang, Z., Zheng, C., Li, X., Wu, W., et al. (2021). Corrected Method for Scaling the Dynamic Response of Stiffened Plate Subjected to Blast Load. Thin-Walled Structures 159, 107214. doi:10.1016/j.tws.2020.107214
Lapczyk, I., and Hurtado, J. A. (2007). Progressive Damage Modeling in Fiber-Reinforced Materials. Composites A: Appl. Sci. Manufacturing 38 (11), 2333–2341. doi:10.1016/j.compositesa.2007.01.017
Lee, D.-W., Park, B.-J., Park, S.-Y., Choi, C.-H., and Song, J.-I. (2018). Fabrication of High-Stiffness Fiber-Metal Laminates and Study of Their Behavior under Low-Velocity Impact Loadings. Compos. Structures 189 (November 2017), 61–69. doi:10.1016/j.compstruct.2018.01.044
Li, Q. M., Dong, Q., and Zheng, J. Y. (2008). Counter-intuitive Breathing Mode Response of an Elastic-Plastic Circular Ring Subjected to Axisymmetric Internal Pressure Pulse. Int. J. Impact Eng. 35 (8), 784–794. doi:10.1016/j.ijimpeng.2007.07.002
Li, X., Zhang, X., Guo, Y., Shim, V. P. W., Yang, J., and Chai, G. B. (2018). Influence of Fiber Type on the Impact Response of Titanium-Based Fiber-Metal Laminates. Int. J. Impact Eng. 114 (October 2017), 32–42. doi:10.1016/j.ijimpeng.2017.12.011
Ma, J., Fan, F., Wu, C., and Zhi, X. (2015). Counter-intuitive Collapse of Single-Layer Reticulated Domes Subject to Interior Blast Loading. Thin-Walled Structures 96, 130–138. doi:10.1016/j.tws.2015.08.001
Micallef, K., Fallah, A. S., Curtis, P. T., and Louca, L. A. (2016). On the Dynamic Plastic Response of Steel Membranes Subjected to Localised Blast Loading. Int. J. Impact Eng. 89, 25–37. doi:10.1016/j.ijimpeng.2015.11.002
Ng, T. Y., and Daolin, X. (2002). Multiple Stability and Unpredictable Outcomes in the Chaotic Vibrations of Euler Beams. J. Vibration Acoust. Trans. ASME 124 (1), 126–131. doi:10.1115/1.1426072
Nicolinco, C., Mahboob, Z., Chemisky, Y., Meraghni, F., Oguamanam, D., and Bougherara, H. (2021). Prediction of the Compressive Damage Response of Flax-Reinforced Laminates Using a Mesoscale Framework. Composites Part A: Appl. Sci. Manufacturing 140, 106153. doi:10.1016/j.compositesa.2020.106153
Sangsefidi, M., Sabouri, H., Mir, M., and Hasanpour, A. (2021). High-velocity Impact Response of Fiber Metal Laminates: Experimental Investigation of Projectile's Deformability. Thin-Walled Structures 159 (September), 107169. doi:10.1016/j.tws.2020.107169
Sasso, M., Mancini, E., Dhaliwal, G. S., Newaz, G. M., and Amodio, D. (2019). Investigation of the Mechanical Behavior of CARALL FML at High Strain Rate. Compos. Structures 222 (April), 110922. doi:10.1016/j.compstruct.2019.110922
Sharma, A. P., Velmurugan, R., Shankar, K., and Ha, S. (2021). High-velocity Impact Response of Titanium-Based Fiber Metal Laminates. Part I: Experimental Investigations. Int. J. Impact Eng. 152 (February), 103845. doi:10.1016/j.ijimpeng.2021.103845
Soutis, C., Mohamed, G., and Hodzic, A. (2011). Modelling the Structural Response of GLARE Panels to Blast Load. Compos. Structures 94 (1), 267–276. doi:10.1016/j.compstruct.2011.06.014
Sun, G., Zhang, J., Li, S., Fang, J., Wang, E., and Li, Q. (2019). Dynamic Response of Sandwich Panel with Hierarchical Honeycomb Cores Subject to Blast Loading. Thin-Walled Structures 142 (April), 499–515. doi:10.1016/j.tws.2019.04.029
Symonds, P. S., and Yu, T. X. (1985). Counterintuitive Behavior in a Problem of Elastic-Plastic Beam Dynamics. J. Appl. Mech. Trans. ASME 52 (3), 517–522. doi:10.1115/1.3169093
Tang, Y. L., Wu, R. F., Jiao, Z. M., Shi, X. H., Wang, Z. H., and Qiao, J. W. (2017). Shear Softening of Ta-Containing Metallic Glass Matrix Composites upon Dynamic Loading. Mater. Sci. Eng. A 704 (March), 322–328. doi:10.1016/j.msea.2017.08.046
Vasiliev, V. V., and Morozov, E. V. (2018). Advanced Mechanics of Composite Materials and Structures. Chennai, TN: Elsevier.
Wanchoo, P., Matos, H., Rousseau, C.-E., and Shukla, A. (2021). Investigations on Air and Underwater Blast Mitigation in Polymeric Composite Structures - A Review. Compos. Structures 263 (January), 113530. doi:10.1016/j.compstruct.2020.113530
Wang, M., Li, Y., Chen, B., Shi, D., Umeda, J., Kondoh, K., et al. (2021). The Rate-dependent Mechanical Behavior of CNT-Reinforced Aluminum Matrix Composites under Tensile Loading. Mater. Sci. Eng. A 808 (November 2020), 140893. doi:10.1016/j.msea.2021.140893
Xu, M., Yang, Y., Lei, H., Wang, P., Li, X., Zhang, Z., et al. (2020). Dynamic Response of Fiber Metal Laminates Subjected to Localized High Impulse Blast Loading. Compos. Structures 243 (December 2019), 112216. doi:10.1016/j.compstruct.2020.112216
Yao, L., Sun, G., He, W., Meng, X., and Xie, D. (2019). Investigation on Impact Behavior of FMLs under Multiple Impacts with the Same Total Energy: Experimental Characterization and Numerical Simulation. Compos. Structures 226 (June), 111218. doi:10.1016/j.compstruct.2019.111218
Zhan, J., Yao, X., Han, F., and Zhang, X. (2021). A Rate-dependent Peridynamic Model for Predicting the Dynamic Response of Particle Reinforced Metal Matrix Composites. Compos. Structures 263 (November 2020), 113673. doi:10.1016/j.compstruct.2021.113673
Zhang, K. F., Liang, M. Z., Li, X. Y., and Lu, F. Y. (2020). A Study on Fracture of Metal Plate under the Detonation Wave Interaction. Int. J. Impact Eng. 145 (July), 103665. doi:10.1016/j.ijimpeng.2020.103665
Zhang, S., Caprani, C. C., and Heidarpour, A. (2018). Strain Rate Studies of Pultruded Glass Fibre Reinforced Polymer Material Properties: A Literature Review. Construction Building Mater. 171, 984–1004. doi:10.1016/j.conbuildmat.2018.03.113
Zhao, N., Yao, S., Zhang, D., Lu, F., and Sun, C. (2020). Experimental and Numerical Studies on the Dynamic Response of Stiffened Plates under Confined Blast Loads. Thin-Walled Structures 154 (May), 106839. doi:10.1016/j.tws.2020.106839
Keywords: Composites, FML, dynamic responses, impulsive loads, damage evolution
Citation: Zhai H, Zhu J, Mao B and Liu W (2021) Analysis of Anomalous Dynamic Responses of Fiber Metal Laminates Under Pulse Loading. Front. Mater. 8:683851. doi: 10.3389/fmats.2021.683851
Received: 22 March 2021; Accepted: 21 April 2021;
Published: 07 May 2021.
Edited by:
Ping Xiang, Central South University, ChinaReviewed by:
Rulin Shen, Central South University, ChinaFei Han, Dalian University of Technology, China
Zhanqi Cheng, Zhengzhou University, China
Copyright © 2021 Zhai, Zhu, Mao and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenyang Liu, bGl1d2VueWFuZ0BobnUuZWR1LmNu
 Hongbo Zhai1
Hongbo Zhai1 Jianwei Zhu
Jianwei Zhu Wenyang Liu
Wenyang Liu