Uniform Strain-Dependent Thermal Conductivity of Pentagonal and Hexagonal Silicene

Two-dimensional (2D) pentagonal monolayer structures have shown promising characteristics and fascinating physical and chemical properties. The disparate strain-dependent thermal conductivity of two-dimensional penta-structures was reported, but the difference between the silicon-based pentagonal and hexagonal structures is barely researched. In this work, based on first-principles calculations, we studied the strain-modulated phonon transport behavior of two 2D pentagonal (penta-SiH and bilayer penta-Si) and one hexagonal silicene structures (H-silicene), of which the penta-SiH and H-silicene mean the structures are hydrogenated for the purpose of thermodynamical stability. We found that the silicon-based pentagonal structure also presented a different strain-dependent thermal conductivity from other pentagonal materials, such as penta-graphene, penta-SiC, or penta-SiN. Moreover, even with the similar strain-dependent thermal transport behavior in penta-SiH and bilayer penta-silicene, we find that the governing mechanism is still different. For both pentagonal silicene structures, the thermal conductivity presents a large improvement at first as the tensile strain increases from 0 to 10% and then stabilizes with a strain larger than 10%. A detailed analysis shows that the in-plane modes contributed the most part to the group velocity enhancement under strains in penta-SiH which is opposite from the bilayer penta-graphene, although the phonon group velocity and phonon lifetime of both structures increase with applied strain. On the other hand, a similarity was found in pentagonal silicene and hexagonal silicene despite the differences in geometry structures. Furthermore, based on the detailed analysis between the pentagonal (penta-SiH) and hexagonal silicene structures (H-silicene), the difference in out-of-plane phonon scattering cannot be ignored: different major scattering channels of the out-of-plane flexural modes result in different thermal conductivity sensitivity to strains, and the disparity in anharmonicity leads to different thermal conductivity under no strain.

1 Introduction

Graphene is a very promising two-dimensional (2D) material due to its fantastic mechanical, electronic, and transport properties (Zhang et al., 2005; Balandin et al., 2008; Lindsay et al., 2010; Balandin, 2011; Liu et al., 2014). The discovery of graphene has generated extensive studies of 2D nanostructures, which have become a hot field of nanoscale materials and nanotechnology (Novoselov et al., 2004; Geim, 2009; Novoselov et al., 2012; Ferrari, 2014). While most of the monolayer structures share a similar hexagonal lattice structure, like graphene and boron nitride (BN) (Hu et al., 2014), recently, a new 2D carbon allotrope which is entirely composed of carbon pentagons and resembles the Cairo pentagonal tiling called penta-graphene was proposed from the first-principles calculation and was confirmed to be thermodynamically and mechanically stable (Zhang et al., 2015). Since the prediction of penta-graphene, lots of research studies on its properties have been conducted (Chen et al., 2016; Liu et al., 2016). Meanwhile, researchers also devoted efforts in finding other pentagonal monolayer structures, such as penta-SiC and penta-BN (Li et al., 2015; Lopez-Bezanilla and Littlewood, 2015; Zhang et al., 2016). Recently, some results of pentagonal silicene were published, which indicate its thermodynamic unstability (Ding and Wang, 2015). However, the H-decorated penta-silicene (penta-SiH) showed a stable structure and a great promise for excellent mechanical and electronic properties. Furthermore, a particular type of bilayer penta-silicene (penta-Si) is found to have even lower energy than all of the known hexagonal silicene bilayers, and therefore forms the most stable bilayer silicon material predicted so far (Aierken et al., 2016). On the other hand, experimental evidence of the existence of the pentagonal silicon monolayer structure was also published recently (Cerda et al., 2016). Thus, the pentagonal silicene could be a very important semiconductor material in the future for the materials community.

Among all the concerned physical properties of nanomaterials, thermal conductivity is always a very important property that is involved in various applications. However, the thermal property of the pentagonal silicene structure has still not been reported as well as the difference in the thermal behavior between hexagonal and pentagonal silicene structures. Motivated by the current situation, a first-principles study to investigate the thermal properties of both the monolayer penta-SiH and bilayer penta-Si structure is reported in this article. Beyond that, different thermal conductivity response to the tensile strain between hexagonal and pentagonal silicene is also discussed. We find that for pentagonal silicene, thermal conductivity increases under tensile strains (both monolayer and bilayer); meanwhile, for the hexagonal structure, the H-decorated silicene (H-silicene) presents a similar response to strains with the original silicene. We find a unified strain tuned thermal conductivity but with a different mechanism in pentagonal and hexagonal silicene.

2 Methodology

By solving the phonon Boltzmann transport equation (BTE) with interatomic force constants evaluated from first-principles calculations, the intrinsic lattice thermal conductivity (κ) can be obtained. The lattice thermal conductivity is calculated from the solution of the BTE as below (Li et al., 2014):

${\kappa }_i^{\alpha \beta }=\frac{1}{k_B{T}^2\Omega N}{\displaystyle \sum _{\lambda }{f}_0\left(f_0+1\right){\left(\hslash {\omega }_{\lambda }\right)}^2{v}_{{\alpha }_i\lambda }{F}_{{\beta }_i\lambda },}(1)$

where α and β denote the three directions (x, y, or z); $k_B$ is the Boltzmann constant; T, $\Omega$, and N are the temperature, system volume, and the number of q points, respectively; λ is the phonon mode that consists of both wave vector q and phonon branch ν; $f_0$ refers to the equilibrium Bose–Einstein distribution function; $\hslash$ is the reduced Planck constant; ${\omega }_{\lambda }$ and $v_{\alpha ,\lambda }$ are the phonon frequency and phonon group velocity, respectively. The $F_{\beta ,\lambda }$ can be written as (Li et al., 2014)

$F_{\beta ,\lambda }={\tau }_{\lambda }\left(v_{\beta ,\lambda }+{\Delta }_{\lambda }\right),(2)$

where ${\tau }_{\lambda }$ is the phonon lifetime under the relaxation time approximation (RTA) and ${\Delta }_{\lambda }$ is a correction term to deal with the inaccuracy of the RTA value while solving BTE iteratively. The RTA result for thermal conductivity can be obtained when ${\Delta }_{\lambda }=0$. Furthermore, Eq. 1 can be rewritten in the form of volumetric phonon-specific heat $\left(C_{ph}\right)$ (Turney et al., 2009) as

${\kappa }_i^{\alpha \beta }=\frac{1}{N}{\displaystyle \sum }_{\lambda }{c}_{ph,\lambda }{v}_{\alpha ,\lambda }{v}_{\beta ,\lambda }{\tau }_{\lambda }.(3)$

There are three dominant phonon-scattering mechanisms considered in our calculations, which are the intrinsic phonon–phonon scattering, the isotopic disorder, and the phonon boundary scattering. The intrinsic scattering rate from the three-phonon scattering processes is calculated as (Li et al., 2014)

$\frac{1}{{\tau }_{\lambda }}=\frac{1}{N}\left({\displaystyle \sum }_{{\lambda }_2{\lambda }_3}{\Gamma }_{\lambda {\lambda }_2{\lambda }_3}^{+}+\frac{1}{2}{\displaystyle \sum }_{{\lambda }_2{\lambda }_3}{\Gamma }_{\lambda {\lambda }_2{\lambda }_3}^{-}\right),(4)$

where ${\lambda }_2$ and ${\lambda }_3$ denote the second and third phonon mode scattering with phonon mode λ, and ${\Gamma }_{\lambda {\lambda }_2{\lambda }_3}^{\pm }$ and ${\Gamma }_{\lambda {\lambda }_2{\lambda }_3}^{-}$ refer to the intrinsic three-phonon scattering rate for the absorption process $\left(\lambda +{\lambda }_2\to {\lambda }_3\right)$ and emission process $\left(\lambda \to {\lambda }_2+{\lambda }_3\right)$, respectively. The isotopic scattering is calculated by Tamura’s formula (Tamura, 1983):

$\frac{1}{{\tau }_{\lambda \lambda \text{'}}^{iso}}=\frac{\pi {\omega }^2}{2}{\displaystyle \sum _{i}g\left(i\right)|e_{\lambda }^{\ast }\left(i\right)\cdot e_{\lambda \text{'}}\left(i\right){|}^2\delta \left({\omega }_{\lambda }-{\omega }_{\lambda \text{'}}\right)},(5)$

where $g\left(i\right)={\displaystyle \sum f_s\left(i\right){\left[1-m_s\left(i\right)/m\left(i\right)\right]}^2}$ is the Pearson deviation coefficient of the masses $m_s\left(i\right)$ of isotopes s of atom i.

All the first-principles calculations are performed based on the density functional theory (DFT) using the Vienna ab initio simulation package (VASP) (Kresse, 1996) with the projector augmented wave pseudopotentials (PAW) (Kresse, 1999). The Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1996) of generalized gradient approximation (GGA) is chosen as the exchange correlation functional, and the plane waves with a kinetic energy cutoff of 500 eV are used to expand the valance electron wave functions. This potential is also chosen by other researchers in many of the previous DFT calculations and is proved to be correct and accurate (Zhang et al., 2015; Chen et al., 2016; Li et al., 2015; Zhang et al., 2016). The electronic step and ionic step stop criteria are ${10}^{-8}$ and ${10}^{-7}$ eV, respectively. The Monkhorst–Pack (Monkhorst and Pack, 1976) k-mesh with a grid density of 0.25 Å⁻¹ is used in the geometry relaxation and static calculations. All the structures are fully optimized until the maximum Hellmann–Feynman force is no larger than ${10}^{-8}$ eV/Å. A $4\times 4\times 1$ supercell is used to calculate the dynamical matrix and the anharmonic force constants. For the latter, up to the fifth nearest neighbors and $64\times 64\times 1$ ($64\times 64\times 1$ for the bilayer penta-Si) q-mesh samples of the first Brillouin zone are considered. Tensile strains are generated by stretching the optimized lattice constant of unstrained structure $a_0$ in both in-plane directions by the same certain percentage $\epsilon =\left(a-a_0\right)/a_0$, where a is the lattice constant of the strained structures.

3 Results and Discussion

3.1 Structures

Figure 1 illustrates the atomic structure of the H-decorated penta-silicene (penta-SiH) sheet (Figures 1A,B) and its phonon dispersion curve, as well as its phonon density of states (pDOS) (Figure 1C). The lattice constant is 5.31 Å, and the buckling height is 2.45 Å. Similar to penta-graphene, in original penta-silicene (no H-decorated), both $s{p}^2$ and $s{p}^3$ hybrid bonds exist between Si atoms with the length of 2.25 Å and 2.37 Å, respectively. However, because the $s{p}^2$ bonding between Si atoms will be dehybridized into $s{p}^3$ like, these Si atoms will have the tendency to distort the pentagonal structure and thus induce the instability of the structure (Cahangirov et al., 2009; Sahin et al., 2009; Ding and Wang, 2015) Thus, the H decoration is necessary to realize the stability of penta-silicene. The H atoms can be decorated on top of Si2 atoms, which still maintain the Si pentagon integrity as shown in Figure 1A. After decoration, the bond length between Si atoms is 2.37 Å, indicating the only existence of $s{p}^3$ hybrid bonds between Si atoms. Because of the significant mass difference between Si and H atoms, there are two gaps around 15 and 40 THz in the phonon dispersion curves. Comparing the phonon dispersion curve and the pDOS results between penta-SiH and bilayer penta-silicene (Figure 1F), we can find that the high frequency bands (<15 THz) are mostly contributed by H atoms. And due to these bandgaps, the phonon scattering channels are decreased.

FIGURE 1

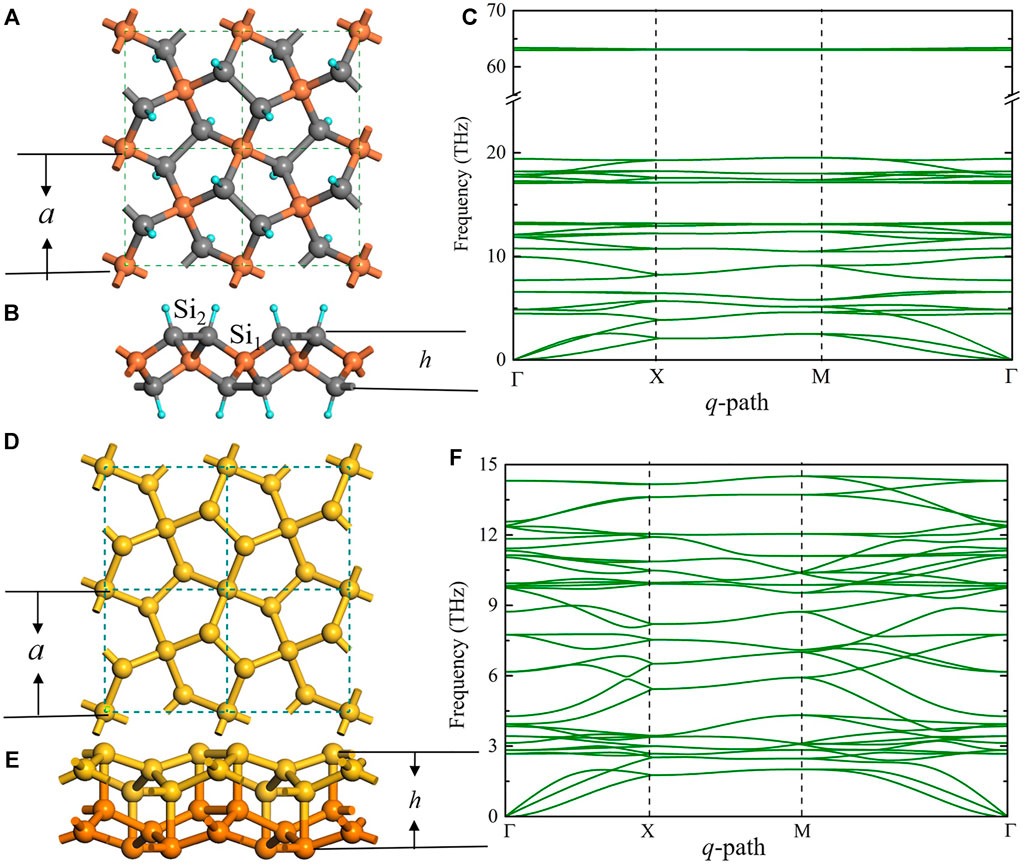
FIGURE 1. (A) Top view of the H-decorated silicene structure (penta-SiH). The smallest dashed square indicates the unit cell of the pentagonal structure. (B) The side view of the same structure, where a is the lattice constant and h is the buckling distance. Si1 (dark yellow) and Si2 (dark gray) represent the Si atom with and without H atom decoration, respectively. (C) Phonon dispersion curve and the phonon density of state (pDOS) of penta-SiH. (D) and (E) Top view and the side view of the bilayer penta-Si structure, respectively, where a is the lattice constant and h is the buckling distance. Yellow and orange atoms represent the different layers of the bilayer structure. (F) Phonon dispersion curve and the pDOS of the bilayer penta-Si structure.

As mentioned above, bilayer penta-Si is another stable pentagonal silicene structure. By directly stacking two monolayer pentagonal silicene together (AA-stacking), the Si2 atoms in each layer interact with each other and eliminate the unsaturated hanging bond, making the structure thermodynamically stable. Figures 1D,E show the crystal structure of the bilayer penta-Si, and the absence of imaginary frequency in the phonon dispersion as shown in Figure 1F illustrates the thermodynamical stability. For bilayer penta-Si, the lattice constant is 5.895 Å, and the buckling height is 3.43 Å. The bond length between all Si atoms is 2.46 Å (including the vertical bonds between two layers). From Figure 1C, we can see that all the phonon bands are below 15 THz, which yields the previous conclusion that in penta-SiH, the H atoms contribute to the high frequency bands (<15 THz), while Si atoms do the rest. In addition, phonon dispersion of bilayer penta-Si is very similar to that of penta-SiH for the low frequency part (15 THz), especially for acoustic phonon branches, implying the similarity in the thermal transport behavior, as we will see later.

3.2 Thermal Conductivity

In Figure 2, we demonstrate the strain-modulated lattice thermal conductivity of penta-SiH (Figure 2A) and bilayer penta-Si (Figure 2B), as well as the thermal conductivity under no strains with its phonon specific heat $\left(C_{ph}\right)$, group velocity $\left(v_g\right)$, and phonon lifetime (τ) replaced by their respective values of the strained structure. Unlike penta-graphene, the thermal conductivity of penta-SiH exhibits 90% improvement from 73.8 $W/mK$ to 138.3 $W/mK$ when the tensile strain increases from 0 to 10%. However, even at the highest value, the thermal conductivity of penta-SiH is still smaller than that of the unstrained penta-graphene (197 $W/mK$) (Liu et al., 2016). When the tensile strain is larger than 10%, the thermal conductivity reaches a converged value, showing little change with the strain increasing.

FIGURE 2

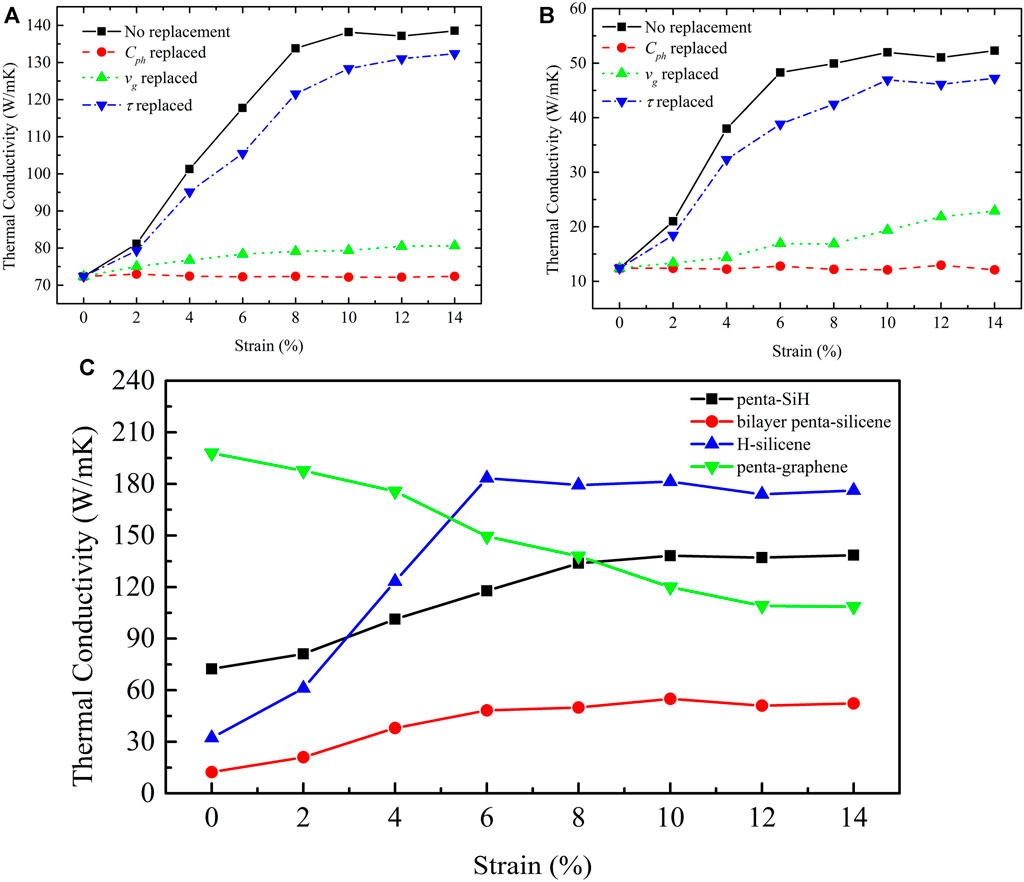
FIGURE 2. Intrinsic lattice thermal conductivity of penta-SiH (A) and bilayer penta-Si (B). “Replaced” means that the corresponding term was replaced by the value at certain strains and the other term stayed with non-strain values. (C) Comparison of the strain-dependent intrinsic lattice thermal conductivity among penta-SiH, bilayer penta-Si, H-silicene, and penta-graphene.

For bilayer penta-Si, the thermal conductivity presents a very similar trend as penta-SiH; that is, the thermal conductivity increases from 10 to 40 $W/mK$ with the strain increasing from 0 to 6%, and then does not have a noticeable change when the strain is increased further, despite the absolute value being lower by a factor of 3. The thermal conductivity tendency is consistent with our previous phonon dispersion results. It is also common that the thermal conductivity of the multilayer structure is much lower than that of the monolayer structure, such as the case of graphene and MoS₂ (Li et al., 2013; Cai et al., 2014; Wei et al., 2014). On the other hand, for both penta-SiH and bilayer penta-Si, from the cross-calculation results, we can see that the strain-dependent phonon lifetime perfectly reproduces the change trend of the thermal conductivity, while the phonon group velocity increases a little, and the specific heat barely changes. Thus, we can conclude that for penta-SiH and bilayer penta-Si, the major reason of the thermal conductivity change upon tension is the same and originates from the strain-modulated phonon lifetime.

3.3 Phonon Group Velocity and Phonon Lifetime

To further clarify how the strain tunes the thermal conductivity in penta-SiH and bilayer penta-Si, for both structures, we first compare the phonon dispersion curves under some typical strains, especially for the acoustic branches. Figure 3A shows the phonon dispersion of three acoustic phonon branches of penta-SiH, namely, the flexural acoustic (FA), longitudinal acoustic (LA), and transverse acoustic (TA) branches, along the q-path from $\Gamma$ to X at some typical strains. It is clearly seen that the dispersion of FA branches is stiffened with strain increasing, indicating the increase of the phonon group velocity of FA modes, which would finally result in the increasing of lattice thermal conductivity. For LA branches, the change is barely visible, and for TA branches, only the part of the phonon modes shows an increased frequency, indicating the small enhancement in phonon group velocity of TA modes. For bilayer penta-Si (Figure 4A), it is interesting to find that the acoustic phonon branches show a similar strain-dependent behavior as that of penta-SiH. That is to say, when the strain is increased, the phonon group velocity of both LA and TA also increases (phonon modes are stiffened), which is similar to penta-SiH. However, contradictory from penta-SiH, the FA branches of bilayer penta-Si are not stiffened under higher strains but tangle together, and thus show little changes. We believe the difference is induced by the inherent layered structure of the bilayer penta-Si. For both structures, the tensile strain reduces the structure buckling. For monolayer penta-SiH, this change leads to an obvious stiffen of FA modes, but for bilayer penta-Si due to the bilayer structure, the LA and TA modes are more sensitive to the strain than the FA modes.

FIGURE 3

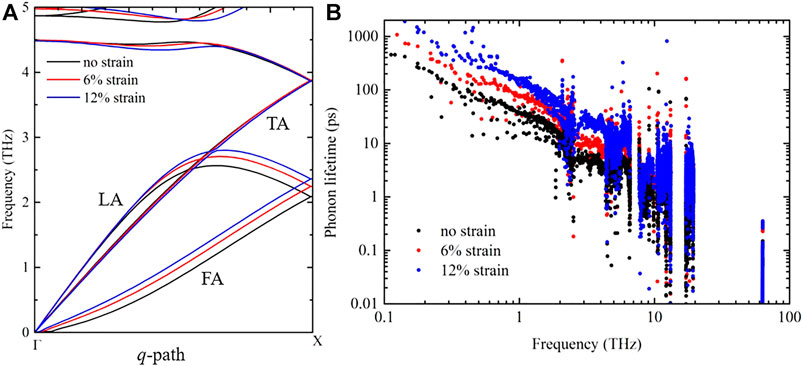
FIGURE 3. (A) Phonon dispersion curves of acoustic phonon branches of penta-SiH along the $\Gamma -X$ direction at typical tensile strains. For brevity, only the acoustic phonon branches are shown. The three acoustic phonon branches are labeled with FA (flexural acoustic), TA (transvers acoustic), and LA (longitudinal acoustic). (B) The corresponding frequency-dependent phonon lifetime of penta-SiH.

FIGURE 4

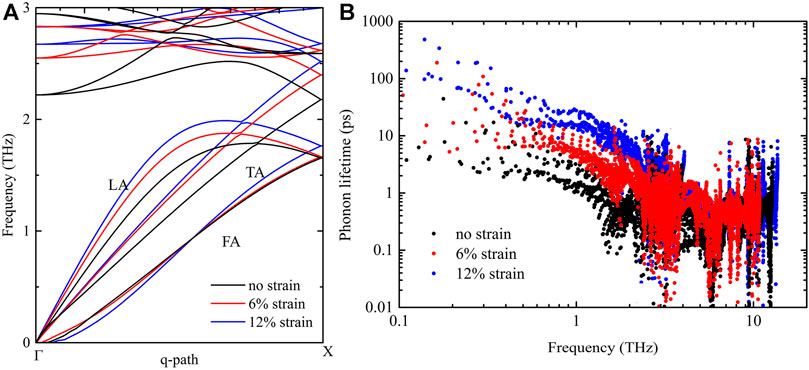
FIGURE 4. (A) Phonon dispersion curves of acoustic phonon branches of bilayer penta-Si along the $\Gamma -X$ direction at typical tensile strains. (B) Frequency-dependent phonon lifetime of bilayer penta-Si at typical tensile strains.

Although it is common that the thermal conductivity of the multilayer structure is much lower than that of the monolayer structure, we are still interested in digging out the fundamental reason. Figure 3B shows the phonon lifetime of penta-SiH under some typical strains, from which the phonon lifetime improvement under increased strains can be clearly observed. The lifetime of low-frequency phonons increases by about 10 times from 1 $ps$-100 $ps$ to 10 $ps$-1000 $ps$, when the strain is enhanced from 0 to 12%. These results are consistent with the previous cross-calculated results (Figure 2). For bilayer penta-Si, the results are shown in Figure 4B. Not surprisingly, the phonon lifetime shares a very similar tendency with penta-Si. However, the absolute value of the phonon lifetime is completely different. For example, when comparing unstrained cases, almost all the phonon lifetime of bilayer penta-Si is under 100 $ps$, while for penta-SiH, the phonons with a lifetime higher than 100 $ps$ are evident. The difference in the phonon lifetime explains the difference in the absolute value of thermal conductivity between the two structures (Figure 2).

In addition, our earlier results (Xie et al., 2016) show that the thermal conductivity of monolayer silicene can also be largely tuned by the tensile strains, which present a similar tendency with the current pentagonal silicene structure. To further explore the mechanism of strain-tuned thermal conductivity in pentagonal and hexagonal silicene, we also calculated the thermal conductivity of H-decorated silicene (H-silicene) under strains. In Figure 2C, we compare the strain-dependent thermal conductivity among H-silicene, penta-SiH, and bilayer penta-Si. The thermal conductivity of the unstrained H-silicene is found to be lower than that of penta-SiH but higher than that of bilayer penta-Si. With the strain increasing, thermal conductivity of H-silicene increases most rapidly and becomes higher than that of penta-SiH when the strain is larger than 4%. The thermal conductivity reaches the highest value at 6% strain and then decreases slightly when the strain continuously increases. This trend is similar with that of the bare silicene (Xie et al., 2016). Comparing the absolute value with bare silicene (Xie et al., 2016), it is also worth noting that at large strains (<6%), the H decoration has little effect on the thermal conductivity of silicene.

To further investigate the mechanism of thermal conductivity changes under strains, the phonon dispersion curve and lifetime of H-silicene are also calculated. Figure 5A shows the acoustic phonon branches of H-silicene under typical strains. It is very interesting to find that even with the fundamentally different geometry structure, the phonon branches of pentagonal and hexagonal silicene still respond similarly to the tensile strains. The FA branch is stiffened when the strain is increased, indicating the enhancement of phonon group velocity of FA modes. While for TA and LA branches, although the changes are more obvious than penta-SiH, these changes still cannot result in the considerably large changes of group velocity. On the other hand, from the strain-modulated phonon lifetime as shown in Figure 5B, we know that the phonon lifetime of H-silicene increases rapidly with the strains. The lifetime of acoustic phonons increases by more than 10 times when the strain is increased from 0 to 8%. We believe this is the main reason responsible for the rapid increase of thermal conductivity upon tension. To make a short conclusion, the pentagonal H decorated silicene (penta-SiH) and hexagonal H-silicene share a very similar thermal transport behavior under tensile strains despite their different geometry structures. The mechanism underlying the strain-tuned thermal conductivity is also similar; that is, both the phonon group velocity and phonon lifetime increase under strain, except that the phonon lifetime increases more rapidly and obviously in the hexagonal H-silicene structure.

FIGURE 5

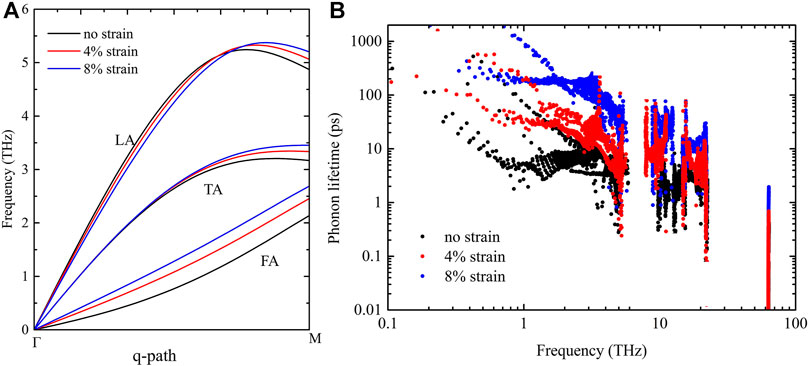
FIGURE 5. (A) Phonon dispersion curves of acoustic phonon branches of hexagonal H-silicene along the $\Gamma -M$ direction at typical tensile strains. The three acoustic phonon branches are labeled with FA (flexural acoustic), TA (transvers acoustic), and LA (longitudinal acoustic). (B) Frequency-dependent phonon lifetime of hexagonal H-silicene at typical tensile strains.

3.4 Thermal Contribution, Scattering Channel, and Anharmonicity

Despite the similar mechanism and phenomenon between penta-SiH and H-silicene, it is very interesting to find that the thermal conductivity of H-silicene is smaller than that of penta-SiH when no strain is applied, but became higher when the strain is larger than 4%. Based on the above analysis, it is concluded that the difference is due to the rapid increasing of the phonon relaxation time. Nevertheless, a further investigation of its physical picture is also necessary. First of all, the thermal conductivity contribution from acoustic phonon branches is calculated. Figure 6 gives the thermal conductivity contribution from the in-plane modes (TA and LA) and the out-plane modes (FA), both the absolute value [(a) for penta-SiH and (b) for H-silicene] and percentage value [(c) for penta-SiH and (d) for H-silicene]. It is unexpected to find that the contribution of acoustic modes showed a very different tendency under strains. For penta-SiH, the out-plane mode (FA) plays a major role (contribution $>$50%) with no strain applied. With the strain increasing, the contribution from in-plane modes (TA and LA) contributed the most part of thermal contribution ($>$50% when the strain $>$4 and $>$60% at the maximum strain). As for the absolute value, the contribution from in-plane modes increased rapidly under strains, while the out-plane contribution showed a rather slow increase. For H-silicene, the result is similar when we look at the absolute value; that is, the contribution from in-plane modes increased rapidly with strains, while the out-plane mode presented a slow increasing tendency under strains. Additionally, compared to penta-SiH, the absolute value of FA modes in H-silicene increased more rapidly under increasing strains, which led to the rapid increase of the total thermal conductivity (Figure 2C).

FIGURE 6

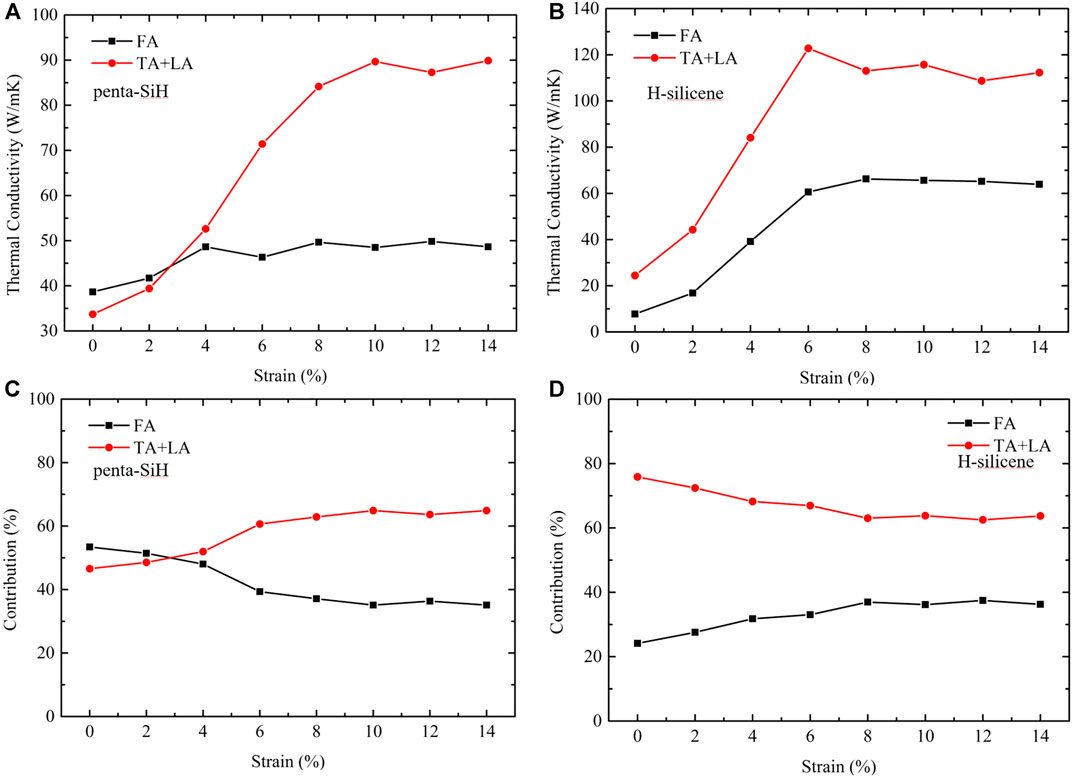
FIGURE 6. Thermal conductivity contribution from in-plane (TA and LA) and out-plane (FA) acoustic phonon modes of penta-SiH (a, c) and H-silicene (b, d). (A) and (B) The absolute value. (C) and (D) The percentage value.

However, the percentage results of H-silicene are very different from those of penta-SiH. Similar to the bare silicene, the in-plane modes contribute the most part of the thermal conductivity (nearly 80% under no strain). With the increasing strains, the contribution from the out-plane mode also increased (from 25 to 37%), but the out-plane modes always contribute the most part (more than 60%) of thermal conductivity. Considering our previous discussion about group velocity, the group velocity of FA modes showed a rather obvious increase under strains, which can be the reason of the contribution percentage change in H-silicene. However, the penta-SiH and H-silicene showed very similar group velocity changes under strains, but share very different contribution percentage changes from H-silicene.

Figure 7 gives the total phonon scattering rate of three acoustic phonon modes in penta-SiH (a) and H-silicene (b) under strains. For TA and LA modes, the scattering rate of both penta-SiH and H-silicene presented a significant drop under strains, but for FA modes, the difference cannot be ignored in the two materials. In penta-SiH, FA modes present a much more gentle decreasing tendency than TA and LA modes, while in H-silicene, the FA modes decreased as rapidly as the rest of the two phonon branches. This different scattering rate change tendency between FA modes and TA/LA modes in penta-SiH explains its contribution tendency in Figures 6A,C. On the other hand, due to the rapidly decreasing scattering rate of all three acoustic phonon modes, thermal conductivity of H-silicene increased more rapidly than that of penta-SiH under strains, which results in a higher value when the strain is larger than 4%. To further investigate the FA mode scattering differences between penta-SiH and H-silicene, we looked deeply into its scattering channels. Figures 7C,D display some typical scattering channel of FA modes in penta-SiH and H-silicene, respectively. From the results, it is obvious that the major scattering channel in the two structures is different. For penta-SiH, FA modes are more likely to scatter with the optical modes ($\mathrm{FA}\pm \mathrm{O}\to \mathrm{O}$ and $\mathrm{FA}\pm \mathrm{TA}/\mathrm{LA}\to \mathrm{O}$ dominate the highest scattering rate), while for H-silicene, the phonon scattering between acoustic phonons dominates the major part of the scattering channel ($\mathrm{FA}\to \mathrm{FA}\pm \mathrm{FA}$, $\mathrm{FA}\to \mathrm{TA}/\mathrm{LA}/\mathrm{FA}$ showed the highest scattering rate). When applying strains, for H-silicene, the structure became flatter, due to which the out-plane scattering between Si atoms was restricted, which leads to the significant decrease in the scattering rate of FA modes in H-silicene. However, for penta-SiH, the scattering with optical phonon (which was mostly donated by H atoms) dominated the most part of the FA mode scattering. Meanwhile, the situation between H atoms and Si atoms changed little under strains; thus, the scattering rate of FA modes presented a gentle decreasing under strains.

FIGURE 7

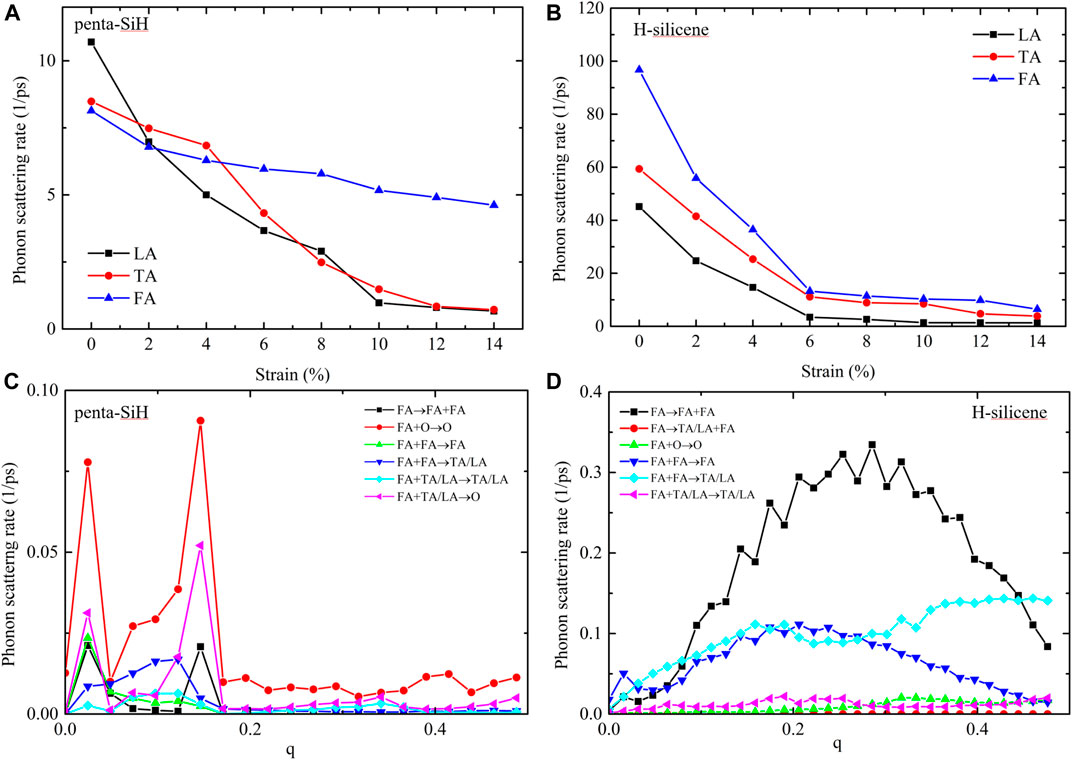
FIGURE 7. The total phonon scattering rates of FA, TA, and LA modes of penta-SiH (A) and H-silicene (B). (C) Some typical phonon scattering channels of FA modes in penta-SiH. (D) Some typical phonon scattering channels of FA modes in H-silicene.

On the other hand, we believe that the change of scattering channels is also connected with the system symmetry. Penta-SiH has the crystal symmetry of the space group$P{42}_{1}m$, which contains two screw axis in the $x-y$ plane ($2_1\left(x,\frac{1}{4},0\right)\left[\frac{1}{2},\mathrm{0,0}\right]$ and $2_1\left(\frac{1}{4},y,0\right)\left[0,\frac{1}{2},0\right]$). Thus, when applying strains, the symmetry operators of out-of-plane direction are affected by the decreased buckling height, which leads to the behavior of the FA scattering rate. On the contrary, for H-silicene, the space group is $P3m1$, which has no rotation axis in the $x-y$ plane. Therefore, even though the buckling height is also decreased under strains, the scattering rate of FA modes presents the same changes as the TA/LA modes do.

As we discussed above, different from the graphene/penta-graphene system, the similarity of thermal behavior between penta-SiH and H-silicene is obvious. To fundamentally understand this similarity from the atomic level, the orbital hybridization based on the projected electronic band structure and electron density of states (DOS) in the reciprocal space is shown in Figures 8A,B. In both H-silicene and penta-SiH, we only calculated the orbital hybridization of Si atoms. For H-silicene, as shown in Figure 8A, the $p_z$ orbital is distinctively hybridized with s/$p_x$/$p_y$, contributing to the $s{p}^3$ hybridization and leading to the buckled structure in H-silicene. This is similar with the silicene, where $p_z$ orbital shows a weaker hybridization with the other three orbitals, thus forming a weak π bond as well as the $s{p}^3$ bonding (Qin et al., 2017). In contrast, for penta-SiH, the $p_z$ orbital also hybridizes with the s/$p_x$/$p_y$ orbitals, except that the hybridization is more obvious and stronger, indicating a stronger $s{p}^3$ bonding between Si atoms. Thus, we believe that the similarity in thermal conductivity behavior between H-silicene and penta-SiH is due to the similar $s{p}^3$ bonding between Si atoms. However, although with the same Si $s{p}^3$ bonding, the bond may present different anharmonicity due to the different geometry structure. Anharmonicity is one of the key factors that affect the thermal conductivity. Anharmonicity describes the deviation of the energy profile from a harmonic profile. As an illustration, we displaced the center Si atom of the penta-SiH and H-silicene along the z direction around its equilibrium location to induce the bond changes and study the total energy change as a function of the displacement to characterize the structure anharmonicity. In Figures 8C,D, the harmonic (quadratic) fittings of the energy change profiles show that penta-SiH has a more harmonic structure than H-silicene, as indicated by the smaller deviation from the harmonic well. This difference in anharmonicity results in higher thermal conductivity for penta-SiH than H-silicene for the unstrained state.

FIGURE 8

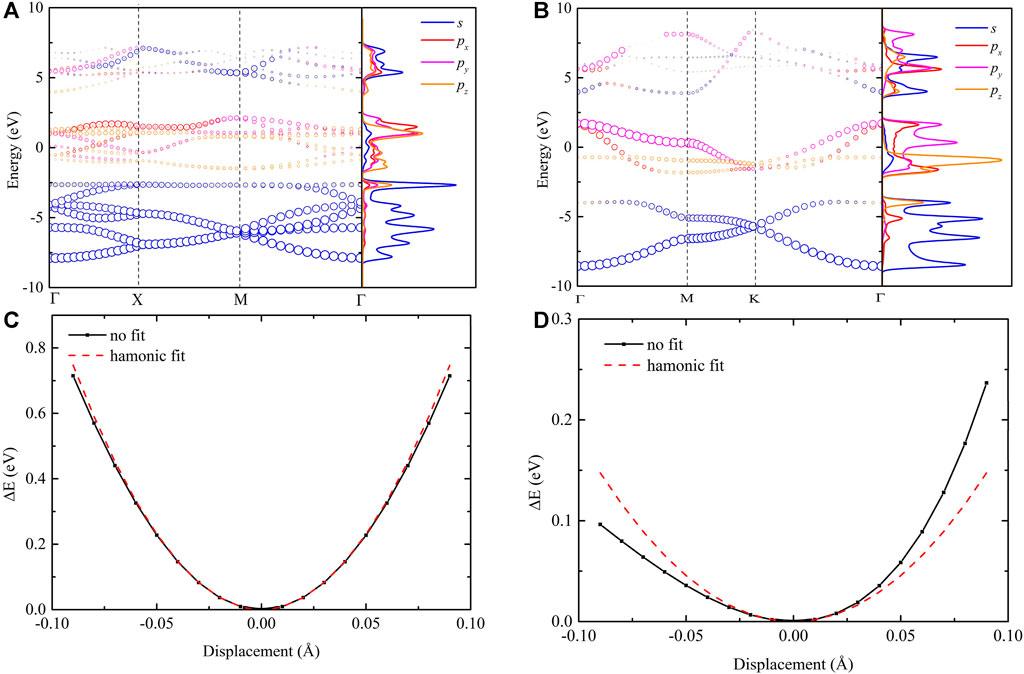
FIGURE 8. (Top) Orbital projected electronic structures projected on s, $p_x$, $p_y$ and $p_z$ orbitals of Si atom in penta-SiH (A) and H-silicene (B), respectively. (Bottom) The total energy change as a function of displacement of Si atoms in penta-SiH (C) and H-silicene (D) as well as harmonic fitting (red dashed line), respectively.

4 Conclusions

To summarize, with first-principles calculations, we find that the lattice thermal conductivity of two 2D pentagonal silicene structures (penta-SiH and bilayer penta-Si) possesses strain dependence different from penta-graphene. Although both pentagonal silicene structures share a very similar thermal transport behavior under tensile strains, the governing mechanism is quite different. For both pentagonal silicene structures, the thermal conductivity first shows a large improvement (90% for penta-SiH and 400% for bilayer penta-Si) as tensile strain increases from 0 to 10% and then stabilizes with a strain larger than 10%. A detailed analysis shows that the phonon group velocity and phonon lifetime of both structures increase with applied strain, and the phonon lifetime plays the major role in the improvement of thermal conductivity. On the other hand, based on the detailed analysis between the pentagonal silicene structure (penta-SiH) and the hexagonal silicene structure (H-silicene), we find that despite their similarity in the thermal behavior under strains, their difference in out-of-plane phonon scattering cannot be ignored. Different major scattering channels of the out-of-plane flexural modes result in different thermal conductivity sensitivity to strains, and the disparity in anharmonicity leads to the different thermal conductivity under no strains. Through our calculations and analysis, we conclude that the pentagonal silicene structure shares very similar properties with the hexagonal silicene structure, which suggests that the pentagonal silicene structures might also be very promising for future nanoelectronic applications.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

HL appreciates the financial support from the National Natural Science Foundation of China (No. 11904296), Fundamental Research Funds for the Central Universities (No. SWU119002), and the Natural Science Foundation of Chongqing (cstc2020jcyj-msxm0803).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.683503/full#supplementary-material

References

Aierken, Y., Leenaerts, O., and Peeters, F. M. (2016). A First-Principles Study of Stable Few-Layer Penta-Silicene. Phys. Chem. Chem. Phys. 18, 18486–18492. doi:10.1039/c6cp03200a

PubMed Abstract | CrossRef Full Text | Google Scholar

Balandin, A. A. (2011). Thermal Properties of Graphene and Nanostructured Carbon Materials. Nat. Mater. 10, 569–581. doi:10.1038/nmat3064

PubMed Abstract | CrossRef Full Text | Google Scholar

Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872

PubMed Abstract | CrossRef Full Text | Google Scholar

Cahangirov, S., Topsakal, M., Akturk, E., Sahin, H., and Ciraci, S. (2009). Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium. Phys. Rev. Lett. 102, 236804. doi:10.1103/PhysRevLett.102.236804

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, Y., Lan, J., Zhang, G., and Zhang, Y. W. (2014). Lattice Vibrational Modes and Phonon Thermal Conductivity of Monolayer Mos 2. Phys. Rev. B 89, 035438. doi:10.1103/physrevb.89.035438

CrossRef Full Text | Google Scholar

Cerda, J. I., Slawinska, J., Le Lay, G., Marele, A. C., Gomez-Rodriguez, J. M., and Davila, M. E. (2016). Unveiling the pentagonal nature of perfectly aligned single-and double-strand si nano-ribbons on ag (110). Nat. Commun. 7. doi:10.1038/ncomms13076

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Schusteritsch, G., Pickard, C. J., Salzmann, C. G., and Michaelides, A. (2016). Two Dimensional Ice from First Principles: Structures and Phase Transitions. Phys. Rev. Lett. 116, 025501. doi:10.1103/physrevlett.116.025501

PubMed Abstract | CrossRef Full Text | Google Scholar

Ding, Y., and Wang, Y. (2015). Hydrogen-induced Stabilization and Tunable Electronic Structures of Penta-Silicene: a Computational Study. J. Mater. Chem. C. 3, 11341–11348. doi:10.1039/C5TC02504D

CrossRef Full Text | Google Scholar

Ferrari, A. C. (2014). Science and Technology Roadmap for Graphene, Related Two-Dimensional Crystals, and Hybrid Systems. Nanoscale 7, 4598–4810. doi:10.1039/C4NR01600A

CrossRef Full Text | Google Scholar

Geim, A. K. (2009). Graphene: Status and Prospects. Science 324, 1530–1534. doi:10.1126/science.1158877

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, S., Lozada-Hidalgo, M., Wang, F. C., Mishchenko, A., Schedin, F., Nair, R. R., et al. (2014). Proton Transport through One-Atom-Thick Crystals. Nature 516, 227–230. doi:10.1038/nature14015

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G. (1996). Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B. 54, 11169–11186. doi:10.1103/PhysRevB.54.11169

CrossRef Full Text | Google Scholar

Kresse, G. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Li, F., Tu, K., Zhang, H., and Chen, Z. (2015). Flexible Structural and Electronic Properties of a Pentagonal B 2 C Monolayer via External Strain: A Computational Investigation. Phys. Chem. Chem. Phys. 17, 24151–24156. doi:10.1039/c5cp03885e

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W., Carrete, J., Katcho, A., and Mingo, N. (2014). Shengbte: A Solver of the Boltzmann Transport Equation for Phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015

CrossRef Full Text | Google Scholar

Li, W., Carrete, J., and Mingo, N. (2013). Thermal Conductivity and Phonon Linewidths of Monolayer Mos2 from First Principles. Appl. Phys. Lett. 103, 253103. doi:10.1063/1.4850995

CrossRef Full Text | Google Scholar

Lindsay, L., Broido, D., and Mingo, N. (2010). Flexural Phonons and Thermal Transport in Graphene. Phys. Rev. B. 82, 115427. doi:10.1103/physrevb.82.115427

CrossRef Full Text | Google Scholar

Liu, H., Qin, G., Lin, Y., and Hu, M. (2016). Disparate Strain Dependent Thermal Conductivity of Two-Dimensional Penta-Structures. Nano Lett. 16, 3831–3842. doi:10.1021/acs.nanolett.6b01311

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H. K., Lin, Y., and Luo, S. N. (2014). Grain Boundary Energy and Grain Size Dependences of Thermal Conductivity of Polycrystalline Graphene. J. Phys. Chem. C. 118, 24797–24802. doi:10.1021/jp508035b

CrossRef Full Text | Google Scholar

Lopez-Bezanilla, A., and Littlewood, P. B. (2015). σ–π-band Inversion in a Novel Two-Dimensional Material. J. Phys. Chem. C. 119, 19469–19474. doi:10.1021/acs.jpcc.5b04726

CrossRef Full Text | Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B. 13, 5188–5192. doi:10.1103/PhysRevB.13.5188

CrossRef Full Text | Google Scholar

Novoselov, K. S., Fal’ko, V. I., Colombo, L., Gellert, P. R., Schwab, M. G., and Kim, K. (2015). A Roadmap for Graphene. Nature 490, 192–200. doi:10.1038/nature11458

CrossRef Full Text | Google Scholar

Novoselov, K. S., Geim, A. K., Morozov, S. V., Jiang, D., Zhang, Y., Dubonos, S. V., et al. (2004). Electric Field Effect in Atomically Thin Carbon Films. Science 306, 666–669. doi:10.1126/science.1102896

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Qin, Z., Qin, G., Zuo, X., Xiong, Z., and Hu, M. (2017). Orbitally Driven Low Thermal Conductivity of Monolayer Gallium Nitride (gan) with Planar Honeycomb Structure: a Comparative Study. Nanoscale 9, 4295–4309. doi:10.1039/c7nr01271c

PubMed Abstract | CrossRef Full Text | Google Scholar

Sahin, H., Cahangirov, S., Topsakal, M., Bekaroglu, E., Akturk, E., Senger, R. T., et al. (2009). Monolayer Honeycomb Structures of Group-Iv Elements and Iii-V Binary Compounds: First-Principles Calculations. Phys. Rev. B. 80, 155453. doi:10.1103/PhysRevB.80.155453

CrossRef Full Text | Google Scholar

Tamura, S. (1983). Isotope Scattering of Dispersive Phonons in Ge. Phys. Rev. B. 27, 858. doi:10.1103/physrevb.27.858

CrossRef Full Text | Google Scholar

Turney, J., Landry, E., McGaughey, A., and Amon, C. (2009). Predicting Phonon Properties and Thermal Conductivity from Anharmonic Lattice Dynamics Calculations and Molecular Dynamics Simulations. Phys. Rev. B. 79, 064301. doi:10.1103/physrevb.79.064301

CrossRef Full Text | Google Scholar

Wei, X., Wang, Y., Shen, Y., Xie, G., Xiao, H., Zhong, J., et al. (2014). Phonon Thermal Conductivity of Monolayer Mos2: A Comparison with Single Layer Graphene. Appl. Phys. Lett. 105, 103902. doi:10.1063/1.4895344

CrossRef Full Text | Google Scholar

Xie, H., Ouyang, T., Germaneau, E., Qin, G., Hu, M., and Bao, H. (2016). Large Tunability of Lattice Thermal Conductivity of Monolayer Silicene via Mechanical Strain. Phys. Rev. B. 93, 075404. doi:10.1103/physrevb.93.075404

CrossRef Full Text | Google Scholar

Zhang, S., Zhou, J., Wang, Q., Chen, X., Kawazoe, Y., and Jena, P. (2015). Penta-graphene: A New Carbon Allotrope. Proc. Natl. Acad. Sci. 112, 2372–2377. doi:10.1073/pnas.1416591112

CrossRef Full Text | Google Scholar

Zhang, S., Zhou, J., Wang, Q., and Jena, P. (2016). Beyond Graphitic Carbon Nitride: Nitrogen-Rich Penta-Cn2 Sheet. J. Phys. Chem. C. 120, 3993–3998. doi:10.1021/acs.jpcc.5b12510

CrossRef Full Text | Google Scholar

Zhang, Y., Tan, Y. W., Stormer, H. L., and Kim, P. (2005). Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene. Nature 438, 201–204. doi:10.1038/nature04235

PubMed Abstract | CrossRef Full Text | Google Scholar