Gas Bubble Evolution in Polycrystalline UMo Fuels Under Elastic-Plastic Deformation: A Phase-Field Model With Crystal-Plasticity

In monolithic UMo fuels, the interaction between the Al cladding and large gas bubble volumetric swelling causes both elastic-plastic and creep deformation. In this work, a phase-field model of gas bubble evolution in polycrystalline UMo under elastic-plastic deformation was developed for studying the dynamic interaction between evolving gas bubble/voids and deformation. A crystal plasticity model, which assumes that the plastic strain rate is proportional to resolved shear stresses of dislocation slip systems on their slip planes, was used to describe plastic deformation in polycrystalline UMo. Xe diffusion and gas bubble evolution are driven by the minimization of chemical and deformation energies in the phase-field model, while evolving gas bubble structure was used to update the mechanical properties in the crystal plasticity model. With the developed model, we simulated the effect of gas bubble structures (different volume fractions and internal gas pressures) on stress-strain curves and the effect of local stresses on gas bubble evolution. The results show that 1) the effective Young’s modulus and yield stress decrease with the increase of gas bubble volume fraction; 2) the hardening coefficient increases with the increase of gas bubble volume fraction, especially for gas bubbles with higher internal pressure; and 3) the pressure dependence of Xe thermodynamic and kinetic properties in addition to the local stress state determine gas bubble growth or shrinkage. The simulated results can serve as a guide to improve material property models for macroscale fuel performance modeling.

Introduction

The measured thickness increase of a UMo fuel meat in monolithic UMo plate-type fuel as a function of the local fission density is shown in Figure 1. The profile of an irradiated UMo fuel plate and gas bubble structures at different fission densities are also shown in Figure 1. Irradiation results in a nonuniform thickness of the UMo fuel meart and large changes in the gas bubble structure with respect to fission density. The interaction between gas bubble volumetric swelling of the UMo fuel meat and the Al cladding in monolithic UMo fuels results in a non-uniform stress field in both the UMo fuel meat and Al cladding, which drives elastic-plastic and/or creep deformation, defect diffusion, and microstructure evolution (Kim et al., 2013; Meyer et al., 2014; Meyer et al., 2017; Ozaltun and Rabin, 2017; Medvedev et al., 2018). The fission product induced swelling generates high stresses within both the fuel and the cladding, leading to plasticity and creep. The interaction of gas bubble swelling with this induced mechanical deformation will subsequently affect the nature of gas bubble evolution, due to accommodation of stress. On the other hand, since the gas bubbles have different thermo-mechanical properties from UMo matrix, the evolution of gas bubbles impacts the thermo-mechanical properties of the entire fuel system. Therefore, to predict the fuel performance including mechanical integrity, geometric stability, and stable irradiation behavior, it is crucial to validate the correlation among deformation, gas bubble evolution, and material properties, and develop physics-based constitutive equations of swelling, elastic-plastic deformation, and creep.

FIGURE 1

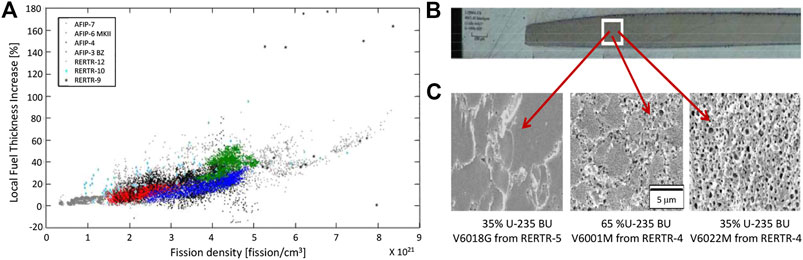
FIGURE 1. Experimental results reproduced from references (Kim et al., 2013; Meyer et al., 2017). (A) UMo fuel meat thickness change vs. fission density (Meyer et al., 2017), (B) profile of radiated UMo fuel meat, and (C) evolution of recrystallized grains and gas bubbles in UMo fuel meat (Kim et al., 2013).

The existing constitutive models for swelling, elastic-plastic deformation, and creep utilized in monolithic UMo fuel performance modeling (Miller et al., 2010; Ozaltun and Rabin, 2017; Medvedev et al., 2018; Yan et al., 2019) are empirical and developed primarily by fitting experimental data (Burkes et al., 2010; Burkes and Wachs, 2010; Kim et al., 2013) and secondarily to fit the results of finite element analyses. The mechanisms of deformations such as plastic and creep deformation and the coupling of gas bubble structure, stress, and property evolution are not sufficiently considered, which limits the predictive capability of the existing models.

In the absence of irradiation damage, a number of microstructure-dependent plastic and creep deformation models have been developed (Deutchman et al., 2012; Cottura et al., 2016; Wu and Sandfeld, 2017; Yang et al., 2018). A homogenized crystal plasticity FEM Model (Deutchman et al., 2012), which uses crystal plasticity parameters (such as activation energy, passing stress and activation volume) provided by a dislocation-density based crystal plasticity modeling, was developed to study the effect of various microstructures (precipitate shape and volume fraction, and channel width) on plastic deformation in Ni based superalloys. An empirical constitutive model-based phase-field model (Tsukada et al., 2011), which uses the von Mises yield criterion for plastic deformation and a simple creep evolution equation, was developed to study the evolution of microstructure and inelastic (plastic and creep) deformation during high temperature creep in nickel-based superalloys. Yang et al. (2018) developed a phase-field model combining a simple creep damage model (Vladimirov et al., 2009) and a dislocation dynamics model (Wu and Sandfeld, 2017) for studying the evolution of ${\gamma }^{\prime }/\gamma$ phases during creep in nickel-based single crystal superalloys. Phase-field models of diffusive transformations with dislocation density based plastic deformation (Cottura et al., 2016), grain boundary sliding with crystal plasticity deformation (Cheng et al., 2019), and continuum dislocation dynamic-based crystal plasticity (Koslowski et al., 2002; Koslowski and Ortiz, 2004; Zeng et al., 2016), in addition to continuum dislocation dynamics-based crystal plasticity (Hochrainer et al., 2014; Hochrainer et al., 2016), have also been developed to study dislocation structure evolution during deformation. These models strengthen the simulation capability in studying the interaction between phase separation, dislocation structure evolution, and plastic deformation. Previously, the authors have developed a number of microstructure evolution models in UMo fuels including gas bubble superlattice formation (Hu et al., 2016), radiation-induced recrystallization (Hu et al., 2017), and defect clustering with non-equilibrium gas bubble association growth (Hu et al., 2020). In this work, we leverage the existing computational capability of gas bubble evolution and crystal plasticity to develop a phase-field model of gas bubble evolution in polycrystalline UMo fuels under elastic-plastic deformation to study the effect of gas bubble structures, such as volume fraction and internal pressures, on mechanical properties as well as the effect of local stress on gas bubble evolution.

Phase-Field Model of Gas Bubble Evolution in Polycrystalline UMo Under Elastic-Plastic Deformation

We consider gas bubble evolution in a representative volume of polycrystalline UMo in monolithic UMo fuels as shown in Figure 2. The axes $xyz$ denote the global coordinate while $x_{\beta }{y}_{\beta }{z}_{\beta }$ is the local coordinate of grain $\beta$. The orientation of grain $\beta$ in the global coordinate is described by the Euler angle $\left({\varphi }_{\beta },{\theta }_{\beta },{\psi }_{\beta }\right)$. The volumetric swelling associated with fission gas bubbles in a UMo fuel meat is constrained by the Al cladding, which produce stresses, and both plastic and creep deformation. The interaction between gas bubble swelling and inelastic deformation affects gas bubble growth as well as stress and strain, and hence, fuel performance. To describe the gas bubble evolution in the polycrystalline UMo under irradiation and inelastic (plastic plus creep) deformation, two sets of field variables are used to describe the microstructure. One set is the order parameters ${\eta }_{\beta }\left(\mathit{r},t\right)$ and $\chi \left(\mathit{r},t\right)$. ${\eta }_{\beta }\left(\mathit{r},t\right)$ describes the grain orientations and $\chi \left(\mathit{r},t\right)$ describes the gas bubbles. ${\eta }_{\beta }\left(\mathit{r},t\right)$ is equal to 1 inside grain $\beta$, 0 outside the grain $\beta$, and varies from 0 to 1 across the grain boundaries. The order parameter $\chi \left(\mathit{r},t\right)$ is equal to 1 inside gas bubbles, 0 outside gas bubbles, and varies from 0 to 1 across the interface between gas bubble and matrix. The other set of field variables includes defect concentrations $c_{li }\left(n,\mathit{r},t\right)$ and $c_{\text{Xe}}\left(\mathit{r},t\right)$. $c_{li }\left(n,\mathit{r},t\right),$ describes the concentrations of vacancy and interstitial clusters; where $li$ denotes a cluster with defect $i$ which could be vacancy or interstitial, while $l$ means cluster or loop, and $n$ is the number of defect $i$ in the cluster $li$. $c_{\text{Xe}}\left(\mathit{r},t\right)$ describes the concentration of fission gas atoms, here treated as Xe, and $\mathit{r},t$ are global coordinate and time, respectively.

FIGURE 2

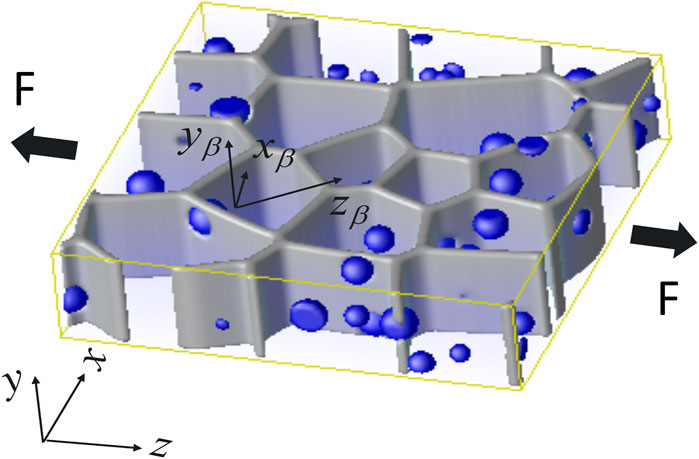
FIGURE 2. Illustration of polycrystalline UMo with distributed gas bubbles, where F is the applied force.

A phase-field model of grain growth (Chen, 2002) is used to generate polycrystalline structures. The grain boundaries are defined by a shape function $\eta \left(\mathit{r},t\right)=2{\displaystyle {\sum }_{\beta =1}^{{\beta }_0}{\left(1-{\eta }_{\beta }\right)}^2}$, which has the value of 0 inside the grains and continuously varies to 1 at the center of grain boundaries, and ${\beta }_0$ is the total number of grains in the simulation cell. Grain boundaries and gas bubbles are structural defects, which are sinks for vacancies and interstitials. The spatial distribution of sinks can be defined by $\theta \left(\mathit{r},t\right)=\eta \left(\mathit{r},t\right)+{\chi }^2\left(\mathit{r},t\right)$.

In UMo fuels, ²³⁵U fission generates high-energy neutrons and fission fragments that cause radiation damage. A cluster dynamics model (Mansur, 1994; Kohnert and Wirth, 2015; Brimbal et al., 2016; Kohnert et al., 2018) is used to describe the evolution of vacancies, interstitials, and their clusters in polycrystalline structures with distributed gas bubbles. The generation of gas atoms, vacancies, and interstitials are calculated with the fission product yields and the kinetic energy distribution of the fission products. Grain boundaries, gas bubbles, and dislocations are treated as sink and emission sites of defects. The description of the cluster dynamics model of defect evolution is given in (Hu et al., 2020). In this work, we focused on the static or dynamic interaction between elastic-plastic deformation and gas bubbles. For simplicity, we assumed that interstitial concentration is low and fission gas Xe atoms occupy the vacancy or vacancy cluster sites. For a given Xe concentration, the vacancy concentration affects thermodynamic and kinetic properties such as lattice mismatch and diffusivity. So only Xe concentration $c_{\text{Xe}}\left(\mathit{r},t\right)$ is taken into account in this work.

The KKS model (Kim et al., 1999) is used to describe the gas bubble evolution in polycrystalline UMo. The total free energy $G$ of the system is formulated as a functional of the order parameter field $\chi (\mathit{r},t)$ and concentration field $c_{\text{Xe}}\left(\mathit{r},t\right)$ as

$G={\displaystyle {\int }_V\left[\left\{1-h\left(\chi \right)\right\}{f}_m\left(c_m\right)+h\left(\chi \right)f_b\left(c_b\right)+wg\left(\chi \right)+\frac{\kappa }{2}{\left(\nabla \chi \right)}^2+f_{def}\right]}\text{d}v(1)$

where V is the material volume of the simulation cell, $c_m$ and $c_b$ are the Xe concentration in matrix and as bubble phases, respectively, $f_m\left(c_m\right)$ and $f_b\left(c_b\right)$ are the free energy density of matrix and gas bubble, respectively, $h\left(\chi \right)$ is a shape function having values between 0 and 1, $g\left(\chi \right)$ is the double-well potential, $w$ is the double-well potential height, $\kappa$ is the gradient energy coefficient, and $f_{def}$ is the deformation energy density. The shape function $h\left(\chi \right)$ and the double-well potential are selected as:

$h\left(\chi \right)={\chi }^3\left(10-15\chi +6{\chi }^2\right)(2)$

$g\left(\chi \right)={\chi }^2{\left(1-\chi \right)}^2(3)$

For simplicity, the free-energy densities are approximated as quadratic functions of concentrations:

$f_m\left(c_m\right)=f_0\left[A_{1m}+A_{2m}{c}_m+A_{3m}{c}_m^2\right](4)$

$f_b\left(c_b\right)=f_0\left[A_{1b}+A_{2b}{c}_b+A_{3b}{c}_b^2\right](5)$

where $A_{im}$ and $A_{ib},\left(i=\mathrm{1,2,3}\right)$ are free energy coefficients and $f_0$ is a parameter which scales the chemical driving force, which is related to the deformation energy driving force of Xe diffusion in the matrix.

The KKS model assumes that 1) at any material point the chemical potentials of the matrix and gas bubble phases are the same; and 2) Xe concentration is conserved. These two assumptions are described as:

${\frac{\partial f_m}{\partial c_m}|}_{c_m=c_m^{\ast }}={\frac{\partial f_b}{\partial c_b}|}_{c_b=c_b^{\ast }},(6)$

$c_{\text{Xe}}\left(\mathit{r},t\right)=c_m^{\ast }\left(\mathit{r},t\right) \left[1-h\left(\chi \right)\right]+c_b^{\ast }\left(\mathit{r},t\right)h\left(\chi \right),(7)$

From Eqs 6, 7, we obtain a single solution of $c_m^{\ast }\left(\mathit{r},t\right)$ and $c_b^{\ast }\left(\mathit{r},t\right)$.

The temporal evolution of the field variables are given by Allen-Cahn (Cahn and Allen, 1977) and Cahn-Hilliard (Cahn, 1961) equations:

$\frac{\partial c_{\text{Xe}}\left(\mathit{r},t\right)}{\partial t}=\nabla \frac{D\left(\chi ,{\eta }_{m }\right)}{f_{c_{\text{Xe}}{c}_{\text{Xe}}}}\cdot \nabla \left[\frac{\partial f\left(c_{\text{Xe}}\right)}{\partial c_{\text{Xe}}}+\frac{\partial f_{def}}{\partial c_{\text{Xe}}}\right],(8)$

$\frac{\partial \chi \left(\mathit{r},t\right)}{\partial t}=L\left\{\begin{array}{c}-\frac{\partial }{\partial \chi }\left(\frac{\kappa }{2}{\left|\nabla \chi \right|}^2\right)+h^{\prime }\left(\chi \right)\left[f_m\left(c_m^{\ast }\right)-f_b\left(c_b^{\ast }\right)-\left(c_m^{\ast }-c_b^{\ast }\right)\frac{\partial f_m\left(c_m^{\ast }\right)}{\partial c_m^{\ast }}\right]\\ -w{g}^{\prime }\left(\chi \right)-\frac{\partial f_{def}}{\partial \chi }\end{array}\right\},(9)$

where $D\left(\chi ,{\eta }_{m }\right)$ is the diffusion of Xe, the order parameters $\chi$ and ${\eta }_{m }$ are used to describe an inhomogeneous Xe diffusivity, $L$ is the interfacial mobility coefficient, and $f\left(c_{\text{Xe}}\right)=\left\{1-h\left(\chi \right)\right\}{f}_m\left(c_m\right)+h\left(\chi \right)f_b\left(c_b\right)$ is the total free energy density.

There are three unknown model parameters in the evolution Eqs 8, 9, i.e., $w$, $\kappa$, and $L$. These parameters can be determined by material properties including interface thickness $2\lambda$, interface energy $\gamma$, and interface mobility$\nu$. Analyzing the equilibrium properties of the kinetic Eqs 8, 9 via thin interface limit analysis (Kim et al., 1999; Hu et al., 2007), the relationships can be obtained:

$\gamma =\frac{\sqrt{\kappa w}}{3\sqrt{2}},(10)$

$2\lambda =\alpha \sqrt{\frac{2\kappa }{w},}(11)$

where $\alpha$ is a coefficient that depends on the definition of the interface and is set to $\alpha =2.2$, and the parameter $L$ can be obtained from thin interface analysis (Hu et al., 2020). But for a diffusion-controlled process like the gas bubble evolution in this work, $L$ can be chosen to be a large value to ensure a stable solution. The deformation energy density, $f_{def}$, in Eq. 2 depends on the local elastic-plastic energy. The calculation methods incorporating elastic-plastic energy will be described in Elastic-Plastic Deformation Under Crystal Plasticity Framework and Material Properties of UMo.

Elastic-Plastic Deformation Under Crystal Plasticity Framework

With the assumption of small deformation, the deformation energy density can be calculated by:

$f_{def}=\frac{1}{2}{C}_{ijkl}\left(\mathit{r}\right){\epsilon }_{ij}^e{\epsilon }_{kl}^e-{\sigma }_{ij}^{appl}{\overline{\epsilon }}_{ij},(12)$

where $C_{ijkl}\left(\mathit{r}\right)$ is the elastic constant tensor, ${\epsilon }_{ij}^e$ is the elastic strain, ${\sigma }_{ij}^{appl}$ is the applied stress tensor, and ${\overline{\epsilon }}_{kl}$ is the average strain tensor.

The elastic strain is expressed as

${\epsilon }_{ij}^e={\epsilon }_{ij}-{\epsilon }_{ij}^{\ast },(13)$

where ${\epsilon }_{ij}$ is the total strain and ${\epsilon }_{ij}^{\ast }$ is the total eigenstrain associated with lattice mismatch between the matrix and the pressured gas bubble and plastic deformation. The eigenstrain is defined as

${\epsilon }_{ij}^{\ast }\left(\mathit{r},t\right)={\epsilon }_0\left(c_{\text{Xe}}\right){\delta }_{ij}h\left(\chi \right)+{\epsilon }_{ij}^p\left(\mathit{r},t\right),(14)$

where ${\epsilon }_0\left(c_{\text{Xe}}\right)$ is the eigenstrain of gas bubbles which can be estimated by the equation of state of Xe gas phase inside the gas bubble, ${\delta }_{ij}$ is the Kronecker delta function, and ${\epsilon }_{ij}^p\left(\mathit{r},t\right)$ is the plastic strain which is calculated from crystal plasticity theory.

According to crystal plasticity theory, the plastic strain rate at the point $\mathit{r}$ inside grain $\beta$ can be generally calculated as (Ma and Roters, 2004; Ma et al., 2006):

${\dot{\mathit{\epsilon }}}^{\beta p}\left(\mathit{r}\right)={\displaystyle \sum _{s=1}^N{\mathit{m}}^s\left(\mathit{r}\right){\dot{\gamma }}^s\left(\mathit{r}\right)}={\dot{\gamma }}_0{\displaystyle \sum _{s=1}^N{\mathit{m}}^s\left(\mathit{r}\right){\left(\frac{\left|{\mathit{m}}^s\left(\mathit{r}\right):\mathit{\sigma }\left(\mathit{r}\right)\right|}{{\tau }_0^s\left(\mathit{r}\right)}\right)}^n\mathrm{sgn}\left({\mathit{m}}^s\left(\mathit{r}\right):{\mathit{\sigma }}^{\prime }\left(\mathit{r}\right)\right)},(15)$

where ${\dot{\gamma }}^s\left(\mathit{r}\right)$, ${\tau }_0^s\left(\mathit{r}\right)$, and ${\mathit{m}}^s\left(\mathit{r}\right)$, are the shear strain rate, the critical resolved shear stress, and the Schmid tensor, respectively. The superscript s denotes the slip system s at material point $\mathit{r}$, and N is the total number of the slip systems of the crystal at material point $\mathit{r}$. ${\dot{\gamma }}_0$ is a normalization factor and n is the stress exponent (inverse of the rate-sensitivity exponent). ${\mathit{\sigma }}^{\prime }\left(\mathit{r}\right)$ is the deviatoric stress tensor. The Schmid tensor is a dyadic tensor and is calculated using:

${\mathit{m}}^s=\frac{1}{2b}\left({\mathit{b}}^s\otimes {\mathit{n}}^s+{\mathit{n}}^s\otimes {\mathit{b}}^s\right),(16)$

where ${\mathit{b}}^s$ and ${\mathit{n}}^s$ are the Burger’s vector and the normal direction of slip system s at point $\mathit{r}$ inside grain $\beta$. Then, the total plastic strain rate is calculated as

${\dot{\mathit{\epsilon }}}^p\left(\mathit{r}\right)={\displaystyle {\sum }_{\beta =1,\dots ,{\beta }_0}{\dot{\mathit{\epsilon }}}^{\beta p}\left(\mathit{r}\right){\eta }_{\beta }\left(\mathit{r}\right)},(17)$

We use ${\mathit{A}}_{\beta }=\left(a_{ij}^{\beta }\right)$ denoting the rotation matrix of the local coordinate of grain $\beta$. The coordinate transfer of the second order tensor $\epsilon$, such as stress, strain and diffusivity tensors, from local coordinate to global can be written as

${\epsilon }_{\text{global}}={\mathit{A}}_{\beta }{\epsilon }_{\text{local}}{\mathit{A}}_{\beta }^T,(18)$

where ${\mathit{A}}_{\beta }^T$ is the transpose of ${\mathit{A}}_{\beta }$. With the Euler angles of grain $\beta$, the components of the rotation matrix are given as

$\begin{array}{l}{\mathit{A}}_{\beta }=\left[\begin{array}{ccc}{a}_{11}^{\beta }& a_{12}^{\beta }& a_{13}^{\beta }\\ a_{21}^{\beta }& a_{22}^{\beta }& a_{23}^{\beta }\\ a_{31}^{\beta }& a_{32}^{\beta }& a_{33}^{\beta }\end{array}\right]=\\ \left[\begin{array}{ccc}\cos {\psi }_{\beta }\cos {\phi }_{\beta }\cos {\theta }_{\beta }-\sin {\phi }_{\beta }\sin {\theta }_{\beta }& -\cos {\psi }_{\beta }\cos {\phi }_{\beta }\cos {\theta }_{\beta }-\sin {\phi }_{\beta }\cos {\theta }_{\beta }& \sin {\psi }_{\beta }\cos {\phi }_{\beta }\\ \cos {\psi }_{\beta }\cos {\phi }_{\beta }\cos {\theta }_{\beta }+\cos {\phi }_{\beta }\sin {\theta }_{\beta }& -\cos {\psi }_{\beta }\sin {\phi }_{\beta }\sin {\theta }_{\beta }+\cos {\phi }_{\beta }\cos {\theta }_{\beta }& \sin {\psi }_{\beta }\sin {\phi }_{\beta }\\ -\sin {\psi }_{\beta }\cos {\theta }_{\beta }& \sin {\psi }_{\beta }\sin {\theta }_{\beta }& \cos {\psi }_{\beta }\end{array}\right],\end{array}(19)$

Assuming that gas bubble phase has isotropic elastic constants $C_{ijkl}^b$ and the single crystal UMo has anisotropic elastic constant $C_{ijkl}^M$, the elastic constant tensor in the global coordinate, can be described as

$C_{ijkl}\left(\mathit{r}\right)= {\displaystyle \sum _{\beta =1,{\beta }_0}{C}_{pqst}^M{a}_{ip}^{\beta }{a}_{jq}^{\beta }{a}_{ks}^{\beta }{a}_{lt}^{\beta }{\eta }_{\beta }\left(\mathit{r},t\right)}+ C_{ijkl}^b\chi \left(\mathit{r},t\right),(20)$

To calculate deformation energy density in Eq. 12, we need to solve the shear strain rate ${\dot{\gamma }}^s\left(\mathit{r}\right)$ from Eq. 15. In this work, a formulation based on FFTs (Lebensohn et al., 2012) is employed to solve for the shear strain rate ${\dot{\gamma }}^s\left(\mathit{r}\right)$.

Here we summarize the method as follows. At time $t+\Delta t$, the total strain includes elastic strains and plastic strains at a material point r:

${\mathit{\epsilon }}^{t+\Delta t}\left(\mathit{r}\right)={\mathit{\epsilon }}^{e,t+\Delta t}\left(\mathit{r}\right)+{\mathit{\epsilon }}^{p,t}\left(\mathit{r}\right)+{\dot{\mathit{\epsilon }}}^{p,t+\Delta t}\left(\mathit{r}\right)\Delta t,(21)$

where $\mathit{\epsilon }\left(\mathit{r}\right)$ represents the total strain tensor, ${\mathit{\epsilon }}^e\left(\mathit{r}\right)$ is the elastic strain tensor, ${\mathit{\epsilon }}^p\left(\mathit{r}\right)$ is the viscoplastic strain tensor, and ${\dot{\mathit{\epsilon }}}^p\left(\mathit{r}\right)$ is the viscoplastic strain rate tensor. The viscoplastic strain rate ${\dot{\mathit{\epsilon }}}^p\left(\mathit{r}\right)$ is constitutively related to the local deviatoric stress, ${\mathit{\sigma }}^{\prime }\left(\mathit{r}\right)=\mathit{\sigma }\left(\mathit{r}\right)-p\left(\mathit{r}\right)\mathit{I}$, where $p\left(\mathit{r}\right)=\left(1/3\right)\left[{\sigma }_{11}\left(\mathit{r}\right)+{\sigma }_{22}\left(\mathit{r}\right)+{\sigma }_{33}\left(\mathit{r}\right)\right]$ and I being the hydrostatic stresses and a unit matrix, respectively, via a sum over the N active slip systems described by Eq. 15.

The Euler implicit time discretization scheme is used to solve the solution of Eq. 21. The expression, in small strains, of the stress tensor at material point r at $t+\Delta t$ is given by

${\mathit{\sigma }}^{t+\Delta t}\left(\mathit{r}\right)=\mathit{c}\left(\mathit{r}\right):{\mathit{\epsilon }}^{e,t+\Delta t}\left(\mathit{r}\right)=\mathit{c}\left(\mathit{r}\right):\left[{\mathit{\epsilon }}^{t+\Delta t}\left(\mathit{r}\right)-{\mathit{\epsilon }}^{p,t}\left(\mathit{r}\right)-{\dot{\mathit{\epsilon }}}^{p,t+\Delta t}\left(\mathit{r}\right)\Delta t\right],(22)$

where $\mathit{\sigma }\left(\mathit{r}\right)$ is the Cauchy stress tensor, and $\mathit{c}\left(\mathit{r}\right)=\left\{c_{ijkl}\left(\mathit{r}\right)\right\}$ is the elastic stiffness tensor. The stresses must satisfy the stress equilibrium equation

${\sigma }_{ij,j}^{t+\Delta t}\left(\mathit{r}\right)=0(23)$

and associated boundary conditions.

For known plastic deformation strain ${\mathit{\epsilon }}^{p,t}\left(\mathit{r}\right)$ at step t, the stress ${\mathit{\sigma }}^{t+\Delta t}\left(\mathit{r}\right)$, strain ${\mathit{\epsilon }}^{t+\Delta t}\left(\mathit{r}\right)$, and plastic strain rate ${\dot{\mathit{\epsilon }}}^{p,t+\Delta t}\left(\mathit{r}\right)$ at time step $t+\Delta t$ can be obtained by the following two steps:

Step 1. Seek solutions of ${\mathit{\tau }}^{t+\Delta t}\left(\mathit{r}\right)$ and ${\mathit{e}}^{t+\Delta t}\left(\mathit{r}\right)$ for the following equations

$\begin{array}{l}{\mathit{\tau }}^{t+\Delta t}\left(\mathit{r}\right)=\mathit{c}\left(\mathit{r}\right):\left[{\mathit{e}}^{t+\Delta t}\left(\mathit{r}\right)-{\mathit{\epsilon }}^{p,t}\left(\mathit{r}\right)\right],\\ \text{or}\\ \mathit{\tau }\left(\mathit{r}\right)=\mathit{c}\left(\mathit{r}\right):\left[\mathit{e}\left(\mathit{r}\right)-{\mathit{\epsilon }}^{p,t}\left(\mathit{r}\right)\right],\end{array}(24)$

by removing the superscript $t+\Delta t$, and keep the previous time step superscript t. The stress, $\mathit{\tau }\left(\mathit{r}\right)$, satisfies the equilibrium Eq. 23:

${\tau }_{ij,j}\left(\mathit{r}\right)=0(25)$

The strains, $\mathit{e}\left(\mathit{x}\right)$, are related to the displacements, $\mathit{u}\left(\mathit{r}\right)$, as follows:

$e_{ii}=u_{i,i},e_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right),i\ne j,(26)$

Combining Eqs 24, 25, we have

${\tau }_{ij}\left(\mathit{r}\right)=c_{ijkl}\left(\mathit{r}\right)\left(e_{kl}\left(\mathit{r}\right)-{\epsilon }_{kl}^{p,t}\left(\mathit{r}\right)\right)=c_{ijkl}\left(\mathit{r}\right)\left(u_{k,l}\left(\mathit{r}\right)-{\epsilon }_{kl}^{p,t}\left(\mathit{r}\right)\right),(27)$

We use iteration and FFT to solve Eqs 25, 27 and let the obtained stresses and displacements satisfy the given boundary condition. The boundary condition is satisfied in the concept of average values. For example,

(1) For a polycrystal under uniaxial tensile stress along the x₁-axis with a strain rate of ${\dot{\epsilon }}_{11}$, the boundary condition is given by ${\overline{e}}_{11}={\overline{\epsilon }}_{11}^t+{\dot{\epsilon }}_{11}\Delta t$ and ${\overline{\tau }}_{22}={\overline{\tau }}_{33}={\overline{\tau }}_{23}={\overline{\tau }}_{13}={\overline{\tau }}_{12}=0$ where ${\overline{\epsilon }}_{11}^t$ is the average value of ${\epsilon }_{11}^t$ from the previous step t and is known for the current step.

(2) For a polycrystal under a constant pressure stress ${\sigma }_0$ along the x₁-axis with a shear strain rate ${\dot{\epsilon }}_{12}$ and a fixed side-boundary condition to mimic billet material inside a die chamber, the boundary condition can be expressed as ${\overline{\tau }}_{11}={\sigma }_0$, ${\overline{e}}_{22}={\overline{e}}_{33}={\overline{e}}_{23}={\overline{e}}_{13}=0$ and ${\overline{e}}_{12}={\overline{\epsilon }}_{12}^t+{\dot{\epsilon }}_{12}\Delta t$, where ${\overline{\epsilon }}_{12}^t$ is known for the current step, similar to ${\overline{\epsilon }}_{11}^t$.

Stresses, ${\tau }_{ij}\left(\mathit{r}\right)$, and strains, $e_{ij}\left(\mathit{r}\right)$, can be obtained through an iteration procedure (Hu and Chen, 2001).

Step 2. To get the final solutions of ${\mathit{\sigma }}^{t+\Delta t}\left(\mathit{r}\right)$, ${\mathit{\epsilon }}^{t+\Delta t}\left(\mathit{r}\right)$, and ${\dot{\mathit{\epsilon }}}^{p,t+\Delta t}\left(\mathit{r}\right)$, or $\mathit{\sigma }\left(\mathit{r}\right)$, $\mathit{\epsilon }\left(\mathit{r}\right)$, and ${\dot{\mathit{\epsilon }}}^p\left(\mathit{r}\right)$ without the superscript t+Δt for Eqs 21, 22 under given boundary conditions, a residual function $R_{ij}\left(\mathit{r}\right)$ is introduced (Lebensohn et al., 2012):

$R_{ij}\left(\mathit{r}\right)={\sigma }_{ij}\left(\mathit{r}\right)-{\tau }_{ij}\left(\mathit{r}\right)+c_{ijkl}^0\left[{\epsilon }_{kl}\left(\mathit{r}\right)-e_{kl}\left(\mathit{r}\right)\right],(28)$

where ${\tau }_{ij}\left(\mathit{r}\right)$ and $e_{ij}\left(\mathit{r}\right)$, have been obtained from Step 1, and ${\sigma }_{ij}\left(\mathit{r}\right)$ and ${\epsilon }_{ij}\left(\mathit{r}\right)$ will be solved through nullification of $R_{ij}\left(\mathit{r}\right)$ coupled with Eqs. 15, 22. The nullification of Eq. 15 is solved using a Newton-Raphson (N-R) scheme, i.e.,

${\sigma }_{ij}^{\left(l+1\right)}\left(\mathit{r}\right)={\sigma }_{ij}^{\left(l\right)}\left(\mathit{r}\right)-{\left[{\left(\frac{\partial R_{ij}}{\partial {\sigma }_{ij}}\right)}^{-1}\right]}^{\left(l\right)}{R}_{ij}^{\left(l\right)}\left(\mathit{r}\right),(29)$

where the superscript l denotes the l-th iteration step. The iteration is stopped when $\left|R_{ij}\right|$ is less than a predetermined value. Through this step, we can finally get ${\sigma }_{ij}\left(\mathit{r}\right)$, ${\epsilon }_{ij}\left(\mathit{r}\right)$, and ${\dot{\epsilon }}_{ij}^p\left(\mathit{r}\right)$ for the given boundary condition and time step.

For materials with strength hardening, ${\tau }_0^s\left(\mathit{r}\right)$ varies with ${\dot{\gamma }}^s\left(\mathit{r}\right)$. For example, linear strength hardening can be expressed by $\Delta {\tau }_0^s=H{\displaystyle {\sum }_{s=1}^N{\dot{\gamma }}^s\left(\mathit{r}\right)\Delta t}$ with H being a constant. In such a case, ${\tau }_0^s\left(\mathit{r}\right)$ in Eq. 16 is replaced by

${\tau }_0^{s,t+\Delta t}\left(\mathit{r}\right)={\tau }_0^{s,t}\left(\mathit{r}\right)+\Delta {\tau }_0^s={\tau }_0^{s,t}\left(\mathit{r}\right)+H{\displaystyle \sum _{s=1}^N{\dot{\gamma }}^{s,t}\left(\mathit{r}\right)\Delta t},(30)$

Through Steps 1 and 2, ${\sigma }_{ij}\left(\mathit{r}\right)$, ${\epsilon }_{ij}\left(\mathit{r}\right)$, and, ${\dot{\epsilon }}_{ij}^p\left(\mathit{r}\right)$ are obtained. With a known strength hardening law such as Eq. 30, the shear strain rate ${\dot{\gamma }}^s\left(\mathit{r}\right)$ can be obtained from Eq. 15.

Material Properties of UMo

The thermal and mechanical properties of UMo that depend on temperature and neutron fluence (Medvedev et al., 2018) have been assessed by experiments (Farrell and King, 1979; Polkinghorne and Lacy, 1991; Kaufman, 1999; Farrell; Meyer et al., 2016). The temperature dependence of Young’s modulus $E$ (GPa) is expressed as (Beghi, 1968),

$E\left(T\right)=110.84-72.926\times {10}^{-3}T-1.8718\times {10}^{-5}{T}^2,294\le T\le 873\text{K}(31)$

where T is the temperature (K).

The Poisson’s ratio was adapted from (Burkes et al., 2010) and it is constant 0.324. The temperature dependence of yield strength ${\sigma }_y$ is expressed as (Klein),

${\sigma }_y=-1.2727\times {10}^{-6}{T}^3+2.430\times {10}^{-3}{T}^2-2.4285T+1478.6, 300\le \text{T}\le 866\text{K},(32)$

Since we do not have the yield stress of single crystal UMo, Eq. 32 is used to estimate the critical resolved stress in the crystal plasticity model. Formation energy and migration energy of Xe are calculated by atomistic simulations (Smirnova et al., 2012; Smirnova et al., 2013; Smirnova et al., 2015).

Both experiments and atomistic simulations show that gamma UMo has isotropic elastic properties. Thus, two of the three elastic moduli, i.e., Young’s modulus $E$, Shear modulus $G,$ and Poisson’s ratio $v$, can describe the elastic properties of UMo. In this work, the temperature is set to be 500 K, which is approximately the operation temperature of UMo fuels in high performance research reactors (Meyer et al., 2016). From Eqs 30, 32, $E$ is 70 GPa and the yield strength ${\sigma }_y$ is 0.718 GPa at T = 500 K. The constant H in Eq. 30 is set to be $5.0\times {10}^6\text{Pa}.$ γ−UMo has a body-centered cubic (bcc) structure, where 24 slip systems are often activated during deformation; $12\cdot \left\{110\right\}\overline{1}11$ and $12\cdot \left\{211\right\}\overline{1}11$ systems. The crystal plasticity model is general and can consider all the slip systems. For model validation, only $12\cdot \left\{110\right\}\overline{1}11$ slip systems are considered in the simulations. In addition, the evolution of radiation defects such as vacancies, interstitials, and their clusters are not considered in the current phase-field model, whereas only Xe diffusion and Xe gas bubble evolution are taken into account. Table 1 lists the model parameters in the simulations.

TABLE 1

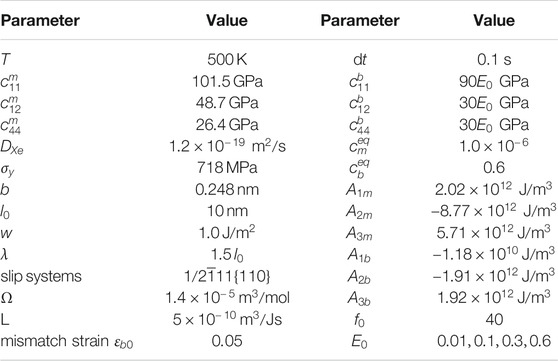
TABLE 1. Model parameters of crystal plasticity and phase-field model of gas bubble evolution for UMo crystals.

Results

Figure 2 illustrates the simulation cell with dimensions of $128l_0\times 32l_0\times 128l_0$, cylindrical grains along y-direction, and distributed gas bubbles. The average grain size in the xz plane is about 340 nm, which is on the order of the typical grain size observed in recrystallized grains in UMo fuels. Periodic boundaries conditions are applied in the x-, y-, and z- directions and a strain along the z-direction is applied to perform tensile or compressive deformation. In this work, the developed model was applied to: 1) study the effect of gas bubble structures on mechanical response; and 2) study the effect of stresses and stress-dependent thermodynamic and kinetic properties on gas bubble evolution.

Effect of Gas Bubble Structures on Mechanical Properties

Three gas bubble structures with gas bubble volume fractions $\left(V_f=3.5\%,6.7\%,\text{and}9.7\% \right)$ are generated with a phase-field model of gas bubble evolution in polycrystalline structures. Gas bubbles, which have an average gas bubble size of 100 nm in diameter are randomly distributed in the simulation cell. It is assumed that bubbles are pressurized and that the pressure is associated with the lattice mismatch between the gas phase and the matrix UMo phase. The lattice mismatch is described by an eigenstrain tensor ${\epsilon }_{ij}^{gb\ast }={\epsilon }_{b0}{\delta }_{ij}{c}_b^{\ast }\left(\mathit{r},t\right)h\left(\chi \right)$, where $c_b^{\ast }\left(\mathit{r},t\right)$ is the Xe concentration inside the gas bubble, $h\left(\chi \right)$ is the shape function defined by Eq. 3, ${\delta }_{ij}$ is the Kronecker-Delta function, and ${\epsilon }_{b0}$ is the mismatch strain. For the first order approximation, if the bulk modulus, pressure, and Xe equilibrium concentration inside the gas bubble are $B_{gb}$, $p_{gb}$ and $c_b^{eq}$, respectively, the mismatch strain can be estimated by ${\epsilon }_{b0}=\left(p_{gb}/B_{gb} c_b^{eq}\right)$. In principle, the equation of state (EOS) of Xe gas phase (Harrison, 1969; Hu et al., 2017; Beeler et al., 2020) can be used to estimate the bulk modulus $B_{gb}$ and the equilibrium Xe concentration for given a pressure, hence, the mismatch strain ${\epsilon }_0$. From the EOS (Beeler et al., 2020), when the internal pressure is about 2 GPa the bulk modulus is about 30 GPa. Here, we assigned the elastic constants of the gas phase to be $c_{11}^b=90E_{0 }\text{GPa}$, $c_{12}^b=30E_{0 }\text{GPa}$ and $c_{44}^b=30E_{0 }\text{GPa}$, the bulk modulus B_gb is $50E_{0}GPa$, and the Poisson’s ratio is $0.125$, where $E_{0 }$ is a parameter which depends on the pressure $p_{gb}$ and the concentration $c_b^{eq}$ inside the gas bubble. Pressure, equilibrium concentration, and lattice mismatch inside gas bubbles change with the local stresses and chemistry (local vacancy and Xe concentrations) in UMo fuels in service. For evolving gas bubbles, the molar volume is calculated by the Xe concentration inside the gas bubble. With the molar volume, the pressure and bulk modulus can be calculated with the EOS. To study the effect of steady state gas bubble structures on mechanical response, we can prescribe fixed values of $c_b^{eq}$ and ${\epsilon }_0$, which are listed in Table 1, and vary $E_{0 }$ to describe the pressure inside the gas bubbles.

Stress Field Around Pressured Gas Bubbles

In the elastic-plastic deformation model, the iteration approach (Hu and Chen, 2001) is used to solve the mechanical equilibrium equations and the stress field in an elastic inhomogeneous material with a distribution of stress-free strains as described in Eq. 15. The stress field around gas bubbles with average radius of 50 nm and different internal pressures ($\left(P_{gb}=0.07,0.60,1.2\text{and}2.1\text{GPa}\right)$) under elastic deformation is calculated. Stress fields on the middle plane around gas bubbles are presented in Figure 3. The light black lines denote the grain boundary while the white circles show the interfaces between gas bubble and matrix. It is found that the pressure $\left(P=-\left({\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}\right)/3\right)$ inside the gas bubbles is uniform which is in agreement with Eshelby’s solution (Eshelby, 1957), and the shear stress $\left({\sigma }_{13}\right)$ around the gas bubble is larger than the yield stress of UMo $\left(0.718\text{GPa}\right)$ when the internal pressure is larger than 1 GPa. The internal pressure inside nano-sized gas bubbles may reach a few GPa according to MD simulations (Xiao and Long, 2014; Hu et al., 2017; Beeler et al., 2020), but with the increase of gas bubble size, the pressure decreases. In addition, a stress field associated with the cladding constraint in UMo monolithic fuels might increase the stresses in the matrix. Therefore, the internal pressure and the cladding constraint may result in plastic deformation in UMo under service.

FIGURE 3

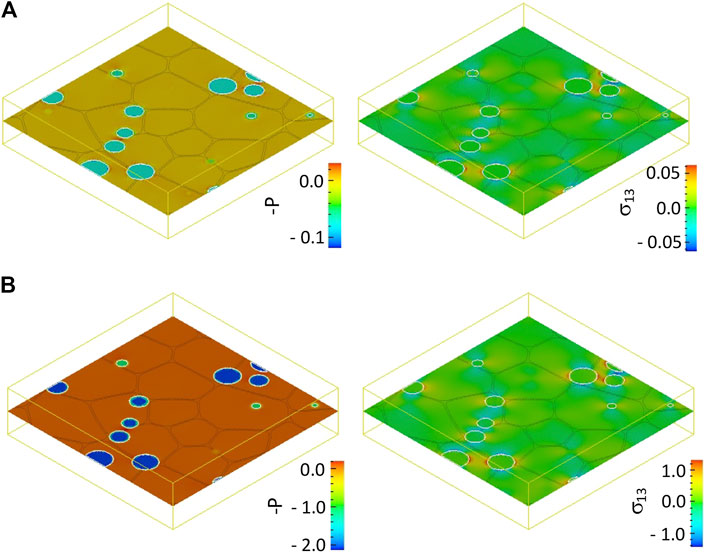
FIGURE 3. Pressure $\left(P\right)$ and shear stress $\left({\sigma }_{13}\right)$ distributions on the plane S for gas bubbles with internal pressures of (A) 0.07 GPa and (B) 2.1 GPa. The units of pressure and stress is GPa.

Effect of Gas Bubble Structures on Stress-Strain Curves

Gas bubble structures with different volume fractions $\left(V_f=3.5\%,6.7\%,\text{and}9.7\%\right)$ and different initial internal pressures $\left(P_{gb}=0.07,\text{and}1.2\text{GPa}\right)$ are used to study the effect of gas bubble structures on stress-strain curves under elastic-plastic deformation. In the simulations, a strain rate of $\text{d}{\overline{\epsilon }}_{33}/\text{d}t=3\times {10}^{-4}$ (1/s) (the other strain components are zero, ${\overline{\epsilon }}_{ij}=0$ ) is applied in z-direction for tensile deformation while $\text{d}{\overline{\epsilon }}_{33}/\text{d}t=-3\times {10}^{-4}$ (1/s) is applied for compressive deformation. Xe concentration in the matrix is set to be $5\times {10}^{-5}$ and the stress-free strain associated with Xe induced lattice change in the matrix is set to be 0.1. Figure 4A,B presents the effect of gas bubble structures on stress-strain curves under tensile and compress deformation. The black curves are the stress-strain curves in polycrystalline structures with Xe concentration of $5\times {10}^{-5}$, but without gas bubbles. The results in Figure 4A are stress strain curves for gas bubbles with a low initial internal pressure of $P_{gb}=0.07\text{GPa}$, while the results in Figure 4B are for gas bubbles with a higher initial internal pressure of $P_{gb}=1.2\text{GPa}$. Because of the lattice mismatch associated with distributed Xe in the matrix and the internal pressure inside gas bubbles, a residual stress field is present. The residual stress, which is a compressive stress field due to a positive stress-free strain, shifts the total stress at applied strain of zero to a negative value. The negative stress value is marked by the small circle in the stress-strain curves. It can be seen that the effect of gas bubble volume fraction on the stress shift at an applied strain of ${\overline{\epsilon }}_{33}=0$ is small, especially for the case of gas bubbles with a low internal pressure $P_{gb}=0.07\text{GPa}$. For gas bubbles with high pressure, the stress shift increases with the increase of gas bubble volume fraction which can be seen by zooming in on the stress-strain curves at ${\overline{\epsilon }}_{33}=0$ in Figure 4B. For the simulation conditions, the residual stress is mainly determined by the distributed Xe (its concentration and stress-free strain) in the matrix. If the matrix vacancy is rich, the distributed vacancies and Xe results in the reduction of UMo lattice constant, and the stress-free strain is negative. It is expected that the residual stress is a tensile stress field due to a negative stress-free strain, and the stress-strain curves shift to a positive value at ${\overline{\epsilon }}_{33}=0$.

FIGURE 4

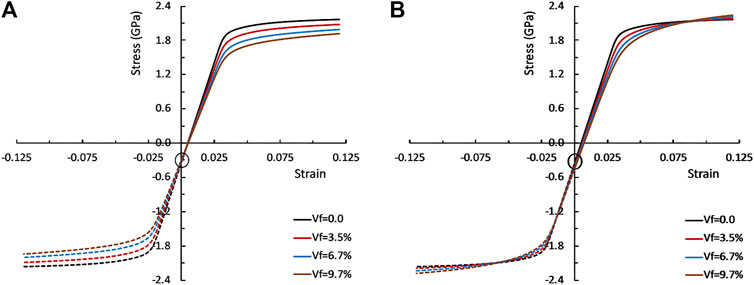
FIGURE 4. Effect of gas bubble volume fraction and internal pressure on stress strain curves. Results shown are for gas bubbles with a pressure of (A)$P_{gb}=0.07\text{GPa}$, (B)$P_{gb}=1.2\text{GPa}$. Both tensile and compressive stresses are applied.

Comparing the results in Figure 4, we can conclude that 1) for all the cases the effective Young’s modulus, which is the slope at the linear part of the stress-strain curves, decreases with the increase of gas bubble volume fraction. This is expected because the gas phase has a lower Young’s modulus than that of the matrix UMo phase. 2) The Young’s modulus depends on both gas bubble structure (gas bubble volume fraction and internal pressure) and applied stress (tensile or compress). 3) the yield stress decreases with the increase of gas bubble volume fraction. The yield stress has a similar dependence on gas bubble structure and applied stress as that of the Young’s modulus; and 4) the hardening coefficient increases with the increase of gas bubble volume fraction, especially for gas bubbles with higher internal pressures, which is indicated by the slop of stress-strain curves in the plastic deformation stage.

The strain hardening is determined by the plastic strain rate. The distributions of plastic strain ${\epsilon }_{13}^p$ on the center plane S in polycrystalline structures with gas bubble volume fraction 9.7% at different applied strain ${\overline{\epsilon }}_{33}$ are shown in Figure 5. The results in Figures 5A,B are for gas bubbles with pressure of $P_{gb}=0.07\text{GPa}$ and $P_{gb}=1.2\text{GPa}$ under tensile deformation, respectively. Before the applied strain reaches ${\overline{\epsilon }}_{33}=0.02$, the deformation is elastic and the plastic strain is zero as shown in Figure 5. It is observed that plastic deformation first takes place near the gas bubble interface, particularly at the interface region of two nearby gas bubbles as shown ${\overline{\epsilon }}_{33}=0.054$, where the stress concentration is higher than that at the interface of an isolate gas bubble, as shown in Figure 3A. With the increase of applied strain, plastic strain increases. The plastic strain in regions with yellow color has a positive sign while the plastic strain in regions with green color has a negative sign. The flaky pattern of plastic strain $\left({\epsilon }_{13}^p\right)$ distribution at ${\overline{\epsilon }}_{33}=0.1$ indicates the formation of shear bands where shear strain has a uniform and high value. Figure 6 plots the distributions of the shear stress component ${\sigma }_{13}$ on the center plane S at ${\overline{\epsilon }}_{33}=0.1$. The white lines show the <101> directions. From the results in Figure 6, we can see that 1) most bands of shear stress ${\sigma }_{13}$ align along the <101> directions while the effect of grain orientation on shear stress ${\sigma }_{13}$ is minor. The isotropic elastic properties of UMo, which has the Zener ratio $\left(2C_{44}/\left(C_{11}-C_{12}\right)\right)$ of 1, can explains the grain orientation independence of shear stresses, and 2) the alignment of gas bubbles along the <101> direction enhances the shear stress bands for both cases of gas bubbles (with low and high initial pressures). Compared with the shear stress, the bands of shear plastic strain $\left({\epsilon }_{13}^p\right)$ shown in Figure 5 does not well align along the <101> directions. This is because dislocation sliding depends not only on the resolved shear stress but also grain orientations. The red and blue of the color bar in Figures 5, 6 present the maximum and minimum values of shear strain (or stress) in the simulation cell during deformation for a given gas bubble structure with low (or high) pressure. Comparing the maximum values in the color bars in Figures 5, 6 we can see that both the maximum plastic strain and shear stress for gas bubbles with low pressure are larger but more localized near the gas bubbles than that for gas bubbles with high pressure. In other words, the shear stress and strain fields around gas bubbles with a low gas pressure is more inhomogeneous than those around gas bubbles with a high gas pressure. We also calculated the evolution of total shear plastic strain in the simulation cell during the deformation. The results show that the total plastic strain for a system with low pressure gas bubbles is higher than that for a system with high pressure gas bubbles. Therefore, we can conclude that the more inhomogeneous a stress field is, the less strain hardening is. And the gas bubble dependence of hardening behavior showed in Figure 4 is attributed to the inhomogeneous stress induced inhomogeneous plastic deformation.

FIGURE 5

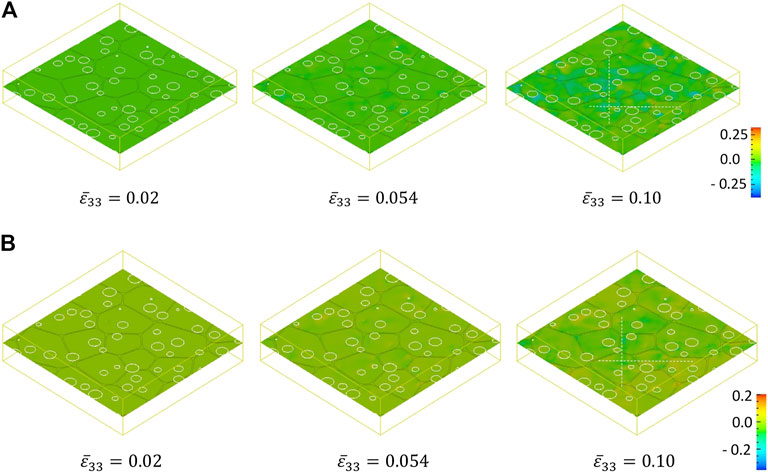
FIGURE 5. Distributions of plastic strain ${\epsilon }_{13}^p$ on the plane S in polycrystalline structures with gas bubble volume fraction 9.7% at different applied strains $\left({\overline{\epsilon }}_{33}=0.02,0.054,\text{and}0.10\right)$. (A) gas bubbles with initial pressure $P_{gb}=0.07\text{GPa}$ and (B) gas bubbles with initial pressure $P_{gb}=1.2\text{GPa}$.

FIGURE 6

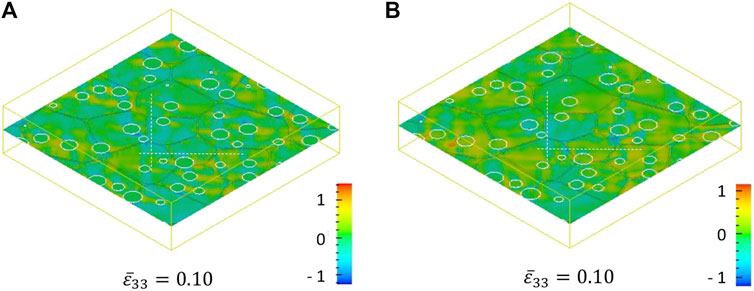
FIGURE 6. Distribution of shear stress ${\sigma }_{13}$ at ${\overline{\epsilon }}_{33}=0.1$. (A) gas bubble with initial internal pressure $P_{gb}=0.07\text{GPa}$, and (B) gas bubble with initial internal pressure $P_{gb}=1.2\text{GPa}$.

For a given gas bubble structure, the average pressures $\left(P=\left({\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}\right)/3\right)$ in the matrix and inside gas bubbles are calculated during deformation. Figure 7 shows the average pressure in terms of applied strain. The circle on the curves presents the pressure associated with the residual stress at applied strain ${\overline{\epsilon }}_{33}=0.0$. Under tensile deformation the pressure P in the matrix changes from negative to positive. This means that the average volume of atoms in matrix increases. As a result, the formation energies of defects with positive lattice misfit such as large solutes and self-interstitials should decrease, and their migration energy should decrease. In contrast, under compressive deformation, the pressure P in the matrix simply becomes more negative. This causes the formation energies and migration energy of defects with positive lattice misfit (such as Xe substitutionals or interstitials) to increase. The average pressure inside the gas bubbles also depends on the applied strain. Based on the equation of state of the gas phase, which describes the correlation between gas atom concentration and pressure, the gas concentration inside gas bubbles should decrease with a pressure decrease. Therefore, the average pressure changes in the matrix and inside the gas bubble affect the thermodynamic and kinetic properties of diffusive defects in the matrix and inside gas bubbles, as well as the gas bubble evolution.

FIGURE 7

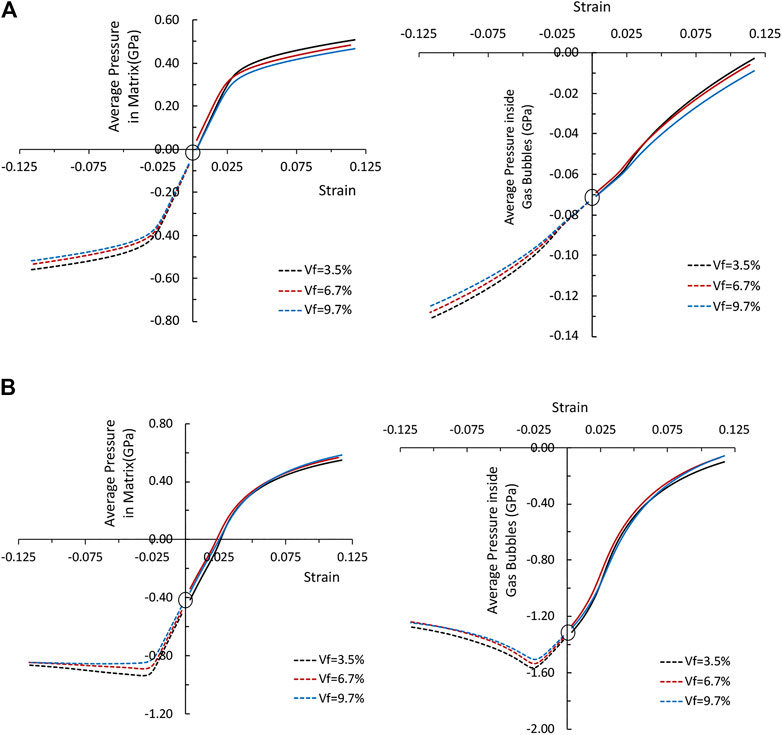
FIGURE 7. Average pressure vs applied strain in matrix and inside gas bubbles in UMo with gas bubbles, (A) for gas bubbles with initial internal pressure 0.07 GPa, and (B) for gas bubbles with initial internal pressure 1.2 GPa.

Effect of Elastic-Plastic Deformation on Gas Bubble Evolution

The gas bubble evolution model presented in Section Phase-Field Model of Gas Bubble Evolution in Polycrystalline UMo Under Elastic-Plastic Deformation requires thermodynamic and kinetic properties including diffusivities and the equilibrium concentration of Xe in the matrix and inside gas bubbles. We describe the diffusivity and equilibrium concentration as a function of average pressure in the matrix and inside gas bubbles. In principle, these thermodynamic and kinetic properties can be obtained from atomic simulations (Valikova and Nazarov, 2008; Sueoka et al., 2012). For instance, the equation of state of Xe gas phase can be used to determine the correlation between the equilibrium Xe concentration and pressure inside gas bubbles. The pressure dependent formation energy of Xe in the matrix can be used to develop the chemical free energy of Xe in the matrix phase, and the pressure dependent migration energy can be used to assess the correlation between Xe diffusivity and pressure. Since we don’t have the data for UMo, a linear correlation of the thermodynamic and kinetic properties in terms of pressure near the equilibrium state are used to validate the effect of elastic-plastic deformation on gas bubbles.

In the simulations, an initial Xe concentration of 0.005 and distributed gas bubbles with a volume fraction 3.5% and initial pressure 2.1 GPa are introduced into polycrystalline UMo. The stress-free strain, ${\epsilon }_0$, of Xe in the matrix is assumed to be 0.1 or −0.1. The positive ${\epsilon }_0$ describes a state which is Xe-rich in the matrix, causing a compressive lattice environment, while the negative ${\epsilon }_0$ describes a vacancy-rich state in the matrix, causing a tensile lattice environment. For a given initial structure, the pressure of the residual stress is chosen as the equilibrium state. The equilibrium Xe concentrations in the matrix and gas phase are calculated by $c_i^{eq}\left(P_i\right)=\left(c_i^{eq}\left(P_{i0}\right)+{\omega }_i\left(P_i-P_{i0}\right)c_i^{eq}\left(P_{i0}\right)\right)/\left(P_{i,\max }-P_{i0}\right)$. $P_{i0}$ is the pressure of the residual stress at the equilibrium state. $P_{i,\max }$ is the maximum pressure in different gas bubble structures for a give applied strain, $i=b\text{or}m$, which denote the gas bubble and the matrix, respectively. ${\omega }_i$ is a coefficient which is set to be 0.3, allowing a maximum 30% change of equilibrium concentration for the pressure changes. The pressure $P_{i,\max }$ is estimated from the data in Figure 7. For simplicity, the pressure dependence of Xe diffusivity assumes that the diffusivity of Xe in a vacancy-rich environment, i.e., ${\epsilon }_0=-0.1$, is one order magnitude larger than that in a Xe-rich environment, ${\epsilon }_0=0.1$. The rest of the model parameters of the phase-field model are listed in Table 1.

The simulations are carried out in three steps: 1) apply a strain rate, $\text{d}{\overline{\epsilon }}_{33}/\text{d}t=3\times {10}^{-4}\left(1/\text{s}\right)$ or $\text{d}{\overline{\epsilon }}_{33}/\text{d}t=-3\times {10}^{-4}\left(1/\text{s}\right)$, up to a total applied strain of ${\overline{\epsilon }}_{33}=0.05$ for a tensile stress state, or ${\overline{\epsilon }}_{33}=-0.05$ for a compressive stress state; 2) update the diffusivity and equilibrium concentrations in the matrix and inside gas bubbles based on the average pressures; 3) simulate the gas bubble evolution with the phase-field model, update gas bubble structures, elastic and plastic properties; update the elastic-plastic solution every 1,000 diffusion time steps, and return to step 2) to simulate the dynamic interaction between elastic deformation and gas bubble evolution. Figure 8 shows the final gas bubble structures at time $t=240\text{h}$ for four simulation cases, and Figure 9 plots the evolution of gas bubble volume fraction. The circle at $t=0$ shows the volume fraction of initial gas bubbles. The solid lines present the gas bubble evolution under tensile stress states while the dashed lines denote the cases under compressive stress states. The results demonstrate that 1) a tensile stress state leads to gas bubble growth, while a compressive stress states causes a slight shrink of gas bubbles; 2) a vacancy rich environment promotes gas bubble growth under a tensile stress state while it prevents gas bubble from shrinking under a compressive stress state.

FIGURE 8

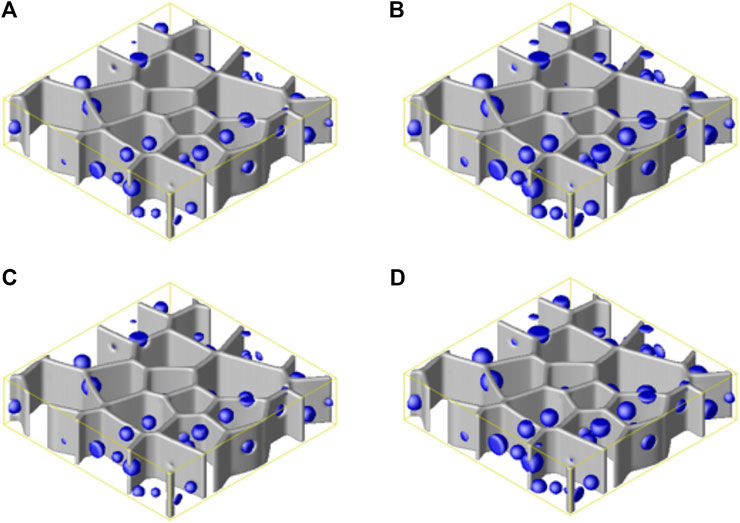
FIGURE 8. Gas bubble structures at time $t=240\text{h}$. (A) Xe rich ${\epsilon }_0=0.1$ under compressive stress state ${\overline{\epsilon }}_{33}=-0.05$, (B) Xe rich ${\epsilon }_0=0.1$ under tensile stress state ${\overline{\epsilon }}_{33}=0.05$, (C) vacancy rich ${\epsilon }_0=-0.1$ under compressive stress state ${\overline{\epsilon }}_{33}=-0.05$, (D) vacancy rich ${\epsilon }_0=-0.1$ under tensile stress state ${\overline{\epsilon }}_{33}=0.05$.

FIGURE 9

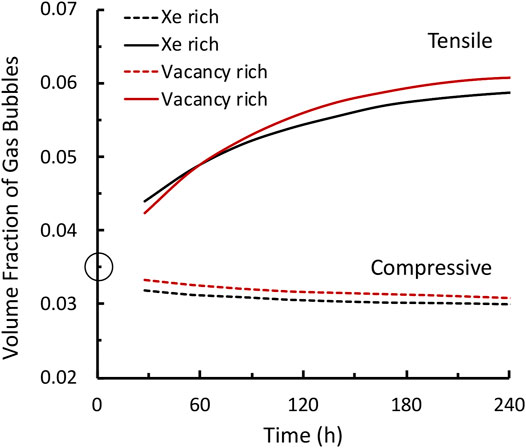
FIGURE 9. Effect of local stress state and thermodynamic and kinetic properties of defects on gas bubble evolution.

Figure 10 shows the Xe concentration distribution on the center plane S at time $t=240\text{h}$ for the four simulation cases. From the color bar it can be seen that under a compressive stress state the Xe concentration inside the gas bubble, which is shown in Figures 10A, C, is about 0.75, which is an increase from 0.6 at the initial state due to the increase of internal pressure. The Xe concentration inside the gas bubble under a tensile stress state, which is shown in Figures 10B, D, changes from 0.6 at the initial state to around 0.4 due to the reduction of internal pressure inside gas bubbles. The white lines show the contour of the order parameter, $\chi$, in the phase-field model which is equal to 0.5, representing the interface of gas bubbles and matrix. It is interesting to find that the gas bubbles no longer have a spherical shape. The gas bubble shape change can be explained by the fact that an inhomogeneous stress field around the gas bubble results in an inhomogeneous plastic deformation, pressure, and non-uniform equilibrium concentration, hence, different interface evolution kinetics. Experimental data also show the gas bubbles have an irregular shape (Miller et al., 2015; Gan et al., 2017). Beside the factor of elastic-plastic deformation, the solid fission phase precipitation on the interior of the gas bubble surface can also affects the gas bubble interface evolution kinetics, hence, the gas bubble shape.

FIGURE 10

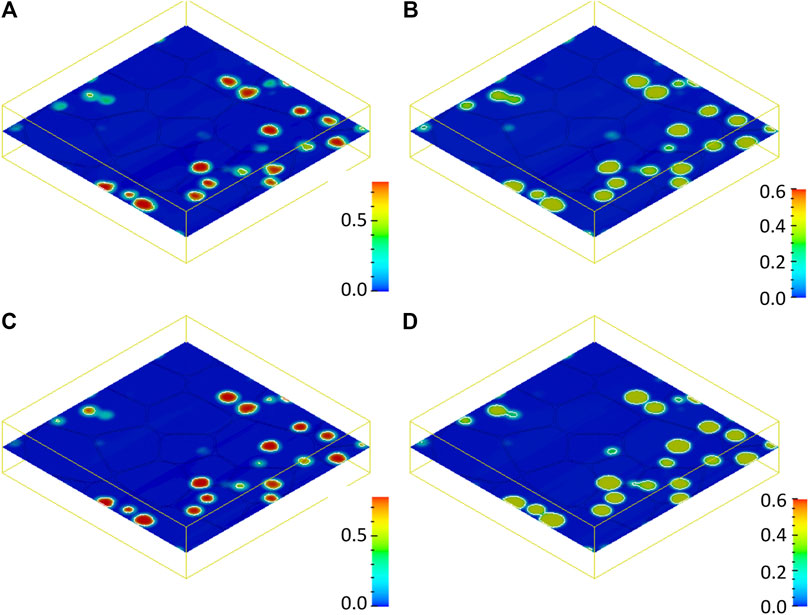
FIGURE 10. Xe concentration distribution on the center plane S at time $t=240\text{h}$. (A) Xe rich ${\epsilon }_0=0.1$ under compressive stress state ${\overline{\epsilon }}_{33}=-0.05$, (B) Xe rich ${\epsilon }_0=0.1$ under tensile stress state ${\overline{\epsilon }}_{33}=0.05$, (C) vacancy rich ${\epsilon }_0=-0.1$ under compressive stress state ${\overline{\epsilon }}_{33}=-0.05$, (D) vacancy rich ${\epsilon }_0=-0.1$ under tensile stress state ${\overline{\epsilon }}_{33}=0.05$.

Conclusion

In this work we developed a phase-field model of gas bubble evolution in polycrystalline UMo under elastic-plastic deformation. Plastic strain rate-based crystal plasticity is employed to describe the elastic-plastic deformation. The effect of local pressure on the thermodynamic and kinetic properties of Xe is taken into account. With the developed model, we simulated the effect of gas bubble structures (different volume fraction and internal pressure) on stress-strain curves and the effect of local stress fields on gas bubble evolution. The results show that 1) the effective Young’s modulus decreases with the increase of gas bubble volume fraction; 2) the yield stress decreases with the increase of gas bubble volume fraction; 3) the hardening coefficient increases with the increase of gas bubble volume fraction, especially for gas bubbles with higher internal pressure; 4) a tensile stress state leads to gas bubble growth while a compressive stress states causes a slight shrink of gas bubbles; 5) a vacancy rich environment promotes gas bubble growth under a tensile stress state while preventing gas bubble shrinkage under a compressive stress state; and 6) an inhomogeneous stress field around the gas bubble results in an inhomogeneous plastic deformation, pressure, and non-uniform equilibrium concentration, hence, an irregular gas bubble shape. The results demonstrate that the developed model is capable of studying the effect of gas bubble structures on mechanical properties and studying the dynamic interaction between elastic-plastic deformation and evolving gas bubbles. However, additional thermodynamic and kinetic properties, such as the effect of pressure on chemical free energy and mobility of Xe in matrix and gas phases, are required for more quantitative simulations. The model also needs to be extended to take radiation defect accumulation and potential creep deformation into account.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SH: model and code development, simulation, visualization, and writing-original draft and editing. BB: conceptualization, writing-review and editing.

Funding

This work was supported by the U.S. Department of Energy, National Nuclear Security Administration Office of Material Management and Minimization, under DE-AC07–05ID14517. Pacific Northwest National Laboratory is a multiprogram national laboratory operated by Battelle Memorial Institute for the U.S. Department of Energy under DE-AC05–76RL01830. Computations were performed on the Constance cluster at Pacific Northwest National Laboratory.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmats.2021.682667/full#supplementary-material.

References

Beeler, B., Hu, S., Zhang, Y., and Gao, Y. (2020). A Improved Equation of State for Xe Gas Bubbles in γU-Mo Fuels. J. Nucl. Mater. 530, 151961. doi:10.1016/j.jnucmat.2019.151961

CrossRef Full Text | Google Scholar

Beghi, G. (1968). Gamma Phase Uranium-Molybdenum Fuel Alloys. EURATOM Report No: EUR-4053e. Brussels, Europe: European Atomic Energy Community-EURATOM. Van Muysewinkel, Ispra - Italy.

Brimbal, D., Fournier, L., and Barbu, A. (2016). Cluster Dynamics Modeling of the Effect of High Dose Irradiation and Helium on the Microstructure of Austenitic Stainless Steels. J. Nucl. Mater. 468, 124–139. doi:10.1016/j.jnucmat.2015.11.007

CrossRef Full Text | Google Scholar

Burkes, D. E., G. S., K., and Wachs, D. M., Thermaphysical Properties of U-10Mo Alloy. INL/EXT-10-19373, (2010).

Google Scholar

Burkes, D. E., Papesch, C. A., Maddison, A. P., Hartmann, P. J., and Rice, F. J. (2010). Thermo-physical Properties of DU-10 wt.% Mo Alloys. J. Nucl. Mater. 403 (1-3), 160–166. doi:10.1016/j.jnucmat.2010.06.018

CrossRef Full Text | Google Scholar

Cahn, J. W., and Allen, S. M. (1977). A Microscopic Theory for Domain Wall Motion and its Experimental Verification IN Fe-Al Alloy Domain Growth Kinetics. J. Phys. Colloques. 38, C7–C51. doi:10.1051/jphyscol:1977709

CrossRef Full Text | Google Scholar

Cahn, J. W. (1961). On Spinodal Decomposition. Acta Metallurgica 9 (9), 795–801. doi:10.1016/0001-6160(61)90182-1

CrossRef Full Text | Google Scholar

Chen, L.-Q. (2002). Phase-field Models for Microstructure Evolution. Annu. Rev. Mater. Res. 32, 113–140. doi:10.1146/annurev.matsci.32.112001.132041

CrossRef Full Text | Google Scholar

Cheng, T.-L., Wen, Y.-H., and Hawk, J. A. (2019). Diffuse Interface Approach to Modeling crystal Plasticity with Accommodation of Grain Boundary Sliding. Int. J. Plasticity 114, 106–125. doi:10.1016/j.ijplas.2018.10.012

CrossRef Full Text | Google Scholar

Cottura, M., Appolaire, B., Finel, A., and Le Bouar, Y. (2016). Coupling the Phase Field Method for Diffusive Transformations with Dislocation Density-Based crystal Plasticity: Application to Ni-Based Superalloys. J. Mech. Phys. Sol. 94, 473–489. doi:10.1016/j.jmps.2016.05.016

CrossRef Full Text | Google Scholar

Deutchman, H. Z., Phillips, P. J., Zhou, N., Samal, M. K., Ghosh, S., Wang, Y., et al. (2012). “Deformation Mechanisms Coupled With Phase Field And Crystal Plasticity Modeling In A High Temperature Polycrystalline Ni-Based Superalloy,” in Superalloys 2012: 12th International Symposium on Syperalloys. TMS. doi:10.7449/2012/superalloys_2012_25_33

CrossRef Full Text | Google Scholar

Eshelby, J. D. (1957). The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proceeding R. Soc. A 241 (1226), 376–396.

Google Scholar

Farrell, K., and King, R. (1979). “Tensile Properties of Neutron- Irradiated 6061 Aluminum Alloy in Annealed and Precipitation-Hardened Conditions,” in Effects of Radiation on Structural Materials. Editor J. Sprague, and D. Kramer (West Conshohocken, PA: ASTM International), 440–449. doi:10.1520/STP38180S

Google Scholar

Farrell, K. Assessment Of Aluminum Structural Materials For Service Within The ANS Reflector Vessel in Report Number ORNL/TM-13049. 1995. Oak Ridge/TN: Oak Rige National Laboratory. doi:10.2172/201578

CrossRef Full Text

Gan, J., Miller, B. D., Keiser, D. D., Jue, J. F., Madden, J. W., Robinson, A. B., et al. (2017). Irradiated Microstructure of U-10Mo Monolithic Fuel Plate at Very High Fission Density. J. Nucl. Mater. 492, 195–203. doi:10.1016/j.jnucmat.2017.05.035

CrossRef Full Text | Google Scholar

Harrison, J. W. (1969). An Extrapolated Equation of State for Xenon for Use in Fuel Swelling Calculations. J. Nucl. Mater. 31 (1), 99–106. doi:10.1016/0022-3115(69)90047-6

CrossRef Full Text | Google Scholar

Hochrainer, T., Sandfeld, S., Zaiser, M., and Gumbsch, P. (2014). Continuum Dislocation Dynamics: Towards a Physical Theory of crystal Plasticity. J. Mech. Phys. Sol. 63, 167–178. doi:10.1016/j.jmps.2013.09.012

CrossRef Full Text | Google Scholar

Hochrainer, T. (2016). Thermodynamically Consistent Continuum Dislocation Dynamics. J. Mech. Phys. Sol. 88, 12–22. doi:10.1016/j.jmps.2015.12.015

CrossRef Full Text | Google Scholar

Hu, S. Y., and Chen, L. Q. (2001). A Phase-Field Model for Evolving Microstructures with strong Elastic Inhomogeneity. Acta Materialia 49 (11), 1879–1890. doi:10.1016/s1359-6454(01)00118-5

CrossRef Full Text | Google Scholar

Hu, S. Y., Murray, J., Weiland, H., Liu, Z. K., and Chen, L. Q. (2007). Thermodynamic Description and Growth Kinetics of Stoichiometric Precipitates in the Phase-Field Approach. Calphad 31 (2), 303–312. doi:10.1016/j.calphad.2006.08.005

CrossRef Full Text | Google Scholar

Hu, S., Burkes, D. E., Lavender, C. A., Senor, D. J., Setyawan, W., and Xu, Z. (2016). Formation Mechanism of Gas Bubble Superlattice in UMo Metal Fuels: Phase-Field Modeling Investigation. J. Nucl. Mater. 479, 202–215. doi:10.1016/j.jnucmat.2016.07.012

CrossRef Full Text | Google Scholar

Hu, S., Joshi, V., and Lavender, C. A. (2017). A Rate-Theory-Phase-Field Model of Irradiation-Induced Recrystallization in UMo Nuclear Fuels. JOM 69 (12), 2554–2562. doi:10.1007/s11837-017-2611-4

CrossRef Full Text | Google Scholar

Hu, S., Setyawan, W., Joshi, V. V., and Lavender, C. A. (2017). Atomistic Simulations of Thermodynamic Properties of Xe Gas Bubbles in U10Mo Fuels. J. Nucl. Mater. 490, 49–58. doi:10.1016/j.jnucmat.2017.04.016

CrossRef Full Text | Google Scholar

Hu, S. Y., Setyawan, W., Beeler, B. W., Gan, J., and Burkes, D. E. (2020). Defect Cluster and Nonequilibrium Gas Bubble Associated Growth in Irradiated UMo Fuels – a Cluster Dynamics and Phase Field Model. J. Nucl. Mater. 542, 152441. doi:10.1016/j.jnucmat.2020.152441

CrossRef Full Text | Google Scholar

Kaufman, J. G. (1999). Properties of aluminum alloys: tensile, creep and fatigue data at high and low temperatures. 3rd Edn. Novelty, OH: ASM International.

Kim, S. G., Kim, W. T., and Suzuki, T. (1999). Phase-field Model for Binary Alloys. Phys. Rev. E 60 (6), 7186–7197. doi:10.1103/physreve.60.7186

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, Y. S., Hofman, G. L., and Cheon, J. S. (2013). Recrystallization and Fission-Gas-Bubble Swelling of U-Mo Fuel. J. Nucl. Mater. 436 (1-3), 14–22. doi:10.1016/j.jnucmat.2013.01.291

CrossRef Full Text | Google Scholar

Klein, J. L. “Uranium and its Alloys,” in Nuclear Reactor Fuel Elements. Editor A. R. Kaufmann 1662 (New York, NY: Wiley), 31.

Google Scholar

Kohnert, A. A., and Wirth, B. D. (2015). Cluster Dynamics Models of Irradiation Damage Accumulation in Ferritic Iron. II. Effects of Reaction Dimensionality. J. Appl. Phys. 117 (15), 154306. doi:10.1063/1.4918316

CrossRef Full Text | Google Scholar

Kohnert, A. A., Wirth, B. D., and Capolungo, L. (2018). Modeling Microstructural Evolution in Irradiated Materials with Cluster Dynamics Methods: A Review. Comput. Mater. Sci. 149, 442–459. doi:10.1016/j.commatsci.2018.02.049

CrossRef Full Text | Google Scholar

Koslowski, M., and Ortiz, M. (2004). A Multi-phase Field Model of Planar Dislocation Networks. Model. Simul. Mater. Sci. Eng. 12 (6), 1087–1097. doi:10.1088/0965-0393/12/6/003

CrossRef Full Text | Google Scholar

Koslowski, M., Cuitiño, A. M., and Ortiz, M. (2002). A Phase-Field Theory of Dislocation Dynamics, Strain Hardening and Hysteresis in Ductile Single Crystals. J. Mech. Phys. Sol. 50 (12), 2597–2635. doi:10.1016/s0022-5096(02)00037-6

CrossRef Full Text | Google Scholar

Lebensohn, R. A., Kanjarla, A. K., and Eisenlohr, P. (2012). An Elasto-Viscoplastic Formulation Based on Fast Fourier Transforms for the Prediction of Micromechanical fields in Polycrystalline Materials. Int. J. Plasticity 32-33, 59–69. doi:10.1016/j.ijplas.2011.12.005

CrossRef Full Text | Google Scholar

Ma, A., and Roters, F. (2004). A Constitutive Model for Fcc Single Crystals Based on Dislocation Densities and its Application to Uniaxial Compression of Aluminium Single Crystals. Acta Materialia 52 (12), 3603–3612. doi:10.1016/j.actamat.2004.04.012

CrossRef Full Text | Google Scholar

Ma, A., Roters, F., and Raabe, D. (2006). A Dislocation Density Based Constitutive Model for crystal Plasticity FEM Including Geometrically Necessary Dislocations. Acta Materialia 54 (8), 2169–2179. doi:10.1016/j.actamat.2006.01.005

CrossRef Full Text | Google Scholar

Mansur, L. K. (1994). Theory and Experimental Background on Dimensional Changes in Irradiated Alloys. J. Nucl. Mater. 216, 97–123. doi:10.1016/0022-3115(94)90009-4

CrossRef Full Text | Google Scholar

Medvedev, P. G., Ozaltun, H., Robinson, A. B., and Rabin, B. H. (2018). Shutdown-induced Tensile Stress in Monolithic Miniplates as a Possible Cause of Plate Pillowing at Very High Burnup. Nucl. Eng. Des. 328, 161–165. doi:10.1016/j.nucengdes.2018.01.004

CrossRef Full Text | Google Scholar

Meyer, M. K., Gan, J., Jue, J. F., Keiser, D. D., Perez, E., Robinson, A., et al. (2014). Irradiation Performance of U-Mo Monolithic Fuel. Nucl. Eng. Technol. 46 (2), 169–182. doi:10.5516/net.07.2014.706

CrossRef Full Text | Google Scholar

Meyer, M., Rabin, B. H., Cole, J., Glagolenko, I., Jones, W., Jue, J. F., et al. (2016). Research and Development Report for U-Mo Monolithic Fuel. Technical Report, INL/EXT-17-40975. Idaho Falls: Idaho National Laboratory.

Meyer, M., Rabin, B. H., Cole, J., Glagolenko, I., Jones, W., Jue, J. F., et al. (2017). Preliminary Report on U-Mo Monolithic Fuel for Research Reactors. Technical Report, INL/EXT-17-40975. Idaho Falls: Idaho National Laboratory.

Miller, G. K., Burkes, D. E., and Wachs, D. M. (2010). Modeling thermal and Stress Behavior of the Fuel-Clad Interface in Monolithic Fuel Mini-Plates. Mater. Des. 31 (7), 3234–3243. doi:10.1016/j.matdes.2010.02.016

CrossRef Full Text | Google Scholar

Miller, B. D., Gan, J., Keiser, D. D., Robinson, A. B., Jue, J. F., Madden, J. W., et al. (2015). Transmission Electron Microscopy Characterization of the Fission Gas Bubble Superlattice in Irradiated U–7 wt%Mo Dispersion Fuels. J. Nucl. Mater. 458, 115–121. doi:10.1016/j.jnucmat.2014.12.012

CrossRef Full Text | Google Scholar

Ozaltun, H., and Rabin, B. H. (2017). Thermo-mechanical Performance Assessment of Selected Plates from MP-1 High Power Experiments, in Proceedings of the ASME 2017 Nuclear Forum collocated with the ASME 2017 Power Conference Joint With ICOPE-17, the ASME 2017 11th International Conference on Energy Sustainability, and the ASME 2017 15th International Conference on Fuel Cell Science, Engineering and Technology. ASME 2017 Nuclear Forum, Charlotte, NC, June 26–30, 2017. ASME. doi:10.1115/nuclrf2017-3271

CrossRef Full Text

Polkinghorne, S. T., and Lacy, J. M. (1991). Thermo-physical and Mechanical Properties of ATR Core Materials. EG&G Inc. Technical Report, PG-T-91-031. Idaho Falls: Idaho National Laboratory.

Smirnova, D. E., Starikov, S. V., and Stegailov, V. V. (2012). New Interatomic Potential for Computation of Mechanical and Thermodynamic Properties of Uranium in a Wide Range of Pressures and Temperatures. Phys. Met. Metallogr. 113 (2), 107–116. doi:10.1134/s0031918x12020147

CrossRef Full Text | Google Scholar

Smirnova, D. E., Kuksin, A. Y., Starikov, S. V., Stegailov, V. V., Insepov, Z., Rest, J., et al. (2013). A Ternary EAM Interatomic Potential for U-Mo Alloys with Xenon. Model. Simulation Mater. Sci. Eng. 21 (3), 1–24. doi:10.1088/0965-0393/21/3/035011

CrossRef Full Text | Google Scholar

Smirnova, D. E., Kuksin, A. Y., Starikov, S. V., and Stegailov, V. V. (2015). Atomistic Modeling of the Self-Diffusion in γ-U and γ-U-Mo. Phys. Met. Metallogr. 116 (5), 445–455. doi:10.1134/s0031918x1503014x

CrossRef Full Text | Google Scholar

Sueoka, K., Kamiyama, E., and Kariyazaki, H. (2012). A Study on Density Functional Theory of the Effect of Pressure on the Formation and Migration Enthalpies of Intrinsic point Defects in Growing Single crystal Si. J. Appl. Phys. 111 (9), 093529. doi:10.1063/1.4712632

CrossRef Full Text | Google Scholar

Tsukada, Y., Murata, Y., Koyama, T., Miura, N., and Kondo, Y. (2011). Creep Deformation and Rafting in Nickel-Based Superalloys Simulated by the Phase-Field Method Using Classical Flow and Creep Theories. Acta Materialia 59 (16), 6378–6386. doi:10.1016/j.actamat.2011.06.050

CrossRef Full Text | Google Scholar

Valikova, I. V., and Nazarov, A. V. (2008). Simulation of Characteristics Determining Pressure Effects on the Concentration and Diffusivity of Vacancies in BCC Metals: A New Approach. Phys. Met. Metallogr. 105 (6), 544–552. doi:10.1134/s0031918x08060033

CrossRef Full Text | Google Scholar

Vladimirov, I. N., Reese, S., and Eggeler, G. (2009). Constitutive Modelling of the Anisotropic Creep Behaviour of Nickel-Base Single crystal Superalloys. Int. J. Mech. Sci. 51 (4), 305–313. doi:10.1016/j.ijmecsci.2009.02.004

CrossRef Full Text | Google Scholar

Wu, R., and Sandfeld, S. (2017). A Dislocation Dynamics-Assisted Phase Field Model for Nickel-Based Superalloys: The Role of Initial Dislocation Density and External Stress during Creep. J. Alloys Compd. 703, 389–395. doi:10.1016/j.jallcom.2017.01.335

CrossRef Full Text | Google Scholar

Xiao, H. X., and Long, C. S. (2014). A Modified Equation of State for Xe at High Pressures by Molecular Dynamics Simulation. Chin. Phys. B 23 (2), 1–5. doi:10.1088/1674-1056/23/2/020502

CrossRef Full Text | Google Scholar

Yan, F., Jian, X., and Ding, S. (2019). Effects of UMo Irradiation Creep on the Thermo-Mechanical Behavior in Monolithic UMo/Al Fuel Plates. J. Nucl. Mater. 524, 209–217. doi:10.1016/j.jnucmat.2019.07.006

CrossRef Full Text | Google Scholar

Yang, M., Zhang, J., Wei, H., Gui, W., Su, H., Jin, T., et al. (2018). A Phase-Field Model for Creep Behavior in Nickel-Base Single-crystal Superalloy: Coupled with Creep Damage. Scripta Materialia 147, 16–20. doi:10.1016/j.scriptamat.2017.12.008

CrossRef Full Text | Google Scholar

Zeng, Y., Hunter, A., Beyerlein, I. J., and Koslowski, M. (2016). A Phase Field Dislocation Dynamics Model for a Bicrystal Interface System: An Investigation into Dislocation Slip Transmission across Cube-On-Cube Interfaces. Int. J. Plasticity 79, 293–313. doi:10.1016/j.ijplas.2015.09.001

CrossRef Full Text | Google Scholar