Deformation Texture Evolution in Flat Profile AlMgSi Extrusions: Experiments, FEM, and Crystal Plasticity Modeling

In the present work, the deformation textures during flat profile extrusion from round billets of an AA6063 and an AA6082 aluminium alloy have been numerically modeled by coupling FEM flow simulations and crystal plasticity simulations and compared to experimentally measured textures obtained by electron back-scatter diffraction (EBSD). The AA6063 alloy was extruded at a relatively low temperature (350°C), while the AA6082 alloy, containing dispersoids that prevent recrystallization, was extruded at a higher temperature (500°C). Both alloys were water quenched at the exit of the die, to maintain the deformation texture after extrusion. In the center of the profiles, both alloys exhibit a conventional $\beta$-fiber texture and the Cube component, which was significantly stronger at the highest extrusion temperature. The classical full-constraint (FC)-Taylor and the Alamel grain cluster model were employed for the texture predictions. Both models were implemented using the regularized single crystal yield surface. This approach enables activation of any number and type of slip systems, as well as accounting for strain rate sensitivity, which are important at 350°C and 500°C. The strength of the nonoctahedral slips and the strain-rate sensitivity were varied by a global optimization algorithm. At 350°C, a good fit could be obtained both with the FC Taylor and the Alamel model, although the Alamel model clearly performs the best. However, even with rate sensitivity and nonoctahedral slip systems invoked, none of the models are capable of predicting the strong Cube component observed experimentally at 500°C.

Introduction

Extrusion is an extensively used thermal–mechanical process to produce aluminium profiles for a range of applications. The properties of the profiles, for example, mechanical, fatigue, fracture, corrosion, as well as surface appearance, are strongly dependent on the underlying microstructure and texture, and the desired characteristics of these different properties may vary with applications (Ralston et al., 2010; Dumoulin et al., 2012; Donati et al., 2013). Moreover, in many cases, it is challenging to provide extruded profiles with a consistent and homogenous grain structure and texture both along the length and through the cross section of the profiles. It is, thus, of great importance to understand and be able to predict (model) how different microstructures and textures are generated and how they evolve during and after extrusion, as basis for controlling the final appearance and properties of extruded profiles (Ralston et al., 2010; Dumoulin et al., 2012; Donati et al., 2013).

The deformation texture after extrusion can be numerically predicted by coupling FEM flow simulations and crystal plasticity models. Aukrust et al. (1997) predicted the deformation texture for flat profile extrusions using the FC- and Relaxed-Constraints (RC)-Taylor model, while Perocheau and Driver (2000) made use of the RC-Taylor hypothesis and a viscoplastic constitutive law for their texture simulations. The deformation texture predictions and their through thickness variations were compared to corresponding experiments and showed reasonable qualitative agreement. At the same time, it was shown that the predictions were improved by considering the nonoctahedral slip systems for high-temperature deformations. More recently, the present authors have modeled the overall deformation texture for extruded round profiles, using the FC-Taylor model and Alamel-type models and deformation histories along different particle paths provided by FEM flow simulations, to predict the through thickness texture variations (Zhang et al., 2018b). Compared to experiments, the Alamel model gave the best predictions.

In the present work, the deformation texture evolutions of extruded flat profiles of AA6xxx aluminium alloys have been numerically investigated and discussed in view of corresponding extrusion experiments. The extrusion trials were carried out in a mini-press laboratory extrusion set-up with immediate water quenching of the profiles at the exit of the die, which made it possible to ‘freeze’ the deformation texture prior to possible spontaneous recrystallization of the profiles at the die exit. The experimentally textures were characterized by the electron back-scatter diffraction technique (EBSD) in scanning electron microscopy (SEM).

In order to model the deformation texture evolution during extrusion, FEM simulations are carried to provide the strain, strain rate, and temperature along the center particle path. The simulations serve as input to an appropriate deformation texture (crystal plasticity) model. Since this is hot deformation, a special focus is put on the effect of nonoctahedral slip and strain-rate sensitivity on the deformation texture evolution. A careful analysis of the deformation history obtained from the FEM simulations provides information on how the deformation conditions change during extrusion, from the container, through the die, and into the extruded profile, and serves as basis to interpret the as-extruded deformation textures. The novelty of the present work is partly related to the use of the Alamel grain cluster model, in addition to the FC-Taylor model, to model the deformation texture evolution during flat profile extrusion. Furthermore, the fact that both models were implemented using the regularized single crystal yield surface approach, enables any number and type of slip systems (i.e., including nonoctahedral slip), as well as accounting for strain rate sensitivity. These aspects strongly influence the predicted texture during hot deformation, like extrusion, and have in the present work been fitted to experiments with the implementation of an optimization procedure.

Materials and Methods

Experimental

The alloys considered in this work, were direct chill cast, then homogenized, extruded, and finally water quenched. An AA6063 alloy (chemical composition in wt% Si 0.4; Mg 0.5; Fe 0.096; Mn 0.017; Ti 0.01; Ga 0.012; Al remaining) and an AA6082 alloy (chemical composition in wt% Si 1.0; Mg 0.7; Fe 0.17; Mn 0.5; Zn 0.01; Al remaining) were investigated. The latter alloy contains dispersoids to suppress recrystallization.

For the AA6063 alloy, billets of 22 mm length and with a 20 mm diameter were machined from the homogenized material and then extruded into rectangular flat profiles of 1.3 mm thickness and 3 mm width in a laboratory scale direct extrusion set-up. This corresponds to an extrusion ratio of 80, which is within the typical extrusion ratio range in the extrusion industry. Prior to extrusion, the container, billet, die, and ram were heated together to the desired testing temperature, which for the results presented in this study were 350°C. The extrusions were performed at a ram speed of 4.5 mm/s and with a ram stroke of 9 mm. At the exit of the die, the extruded profiles were immediately pushed into cold water, which enabled the extruded material to be below 300°C within 2 s after the end of deformation. The low extrusion temperature of 350°C was chosen to prevent possible fast static recrystallization during quenching and thus to preserve the deformed microstructure and texture after extrusion. The ram speed was chosen to provide a profile exit speed comparable to industrial practice of similar alloys. The initial microstructure showed an equiaxed grain structure with an average grain size of diameter of 90 μm. While the material contained primary particles (constituents) with an average diameter of 1.4 μm and volume fraction of about 0.4%, this alloy did not contain second-phase particles (dispersoids) to suppress recrystallization.

For comparison with another alloy, which does not easily recrystallize after deformation, even at higher extrusion temperatures, experiments were also carried out with an AA6082 alloy. In this case, round billets of 100 mm in diameter were extruded into flat bars of 10 mm thickness and 78.5 mm in width, which corresponds to an extrusion ratio of 10. The as-cast textures of both alloys were random. AA6063 and AA6082 are chosen for the present study as they are commonly used extrusion alloys.

The textures of the as-extruded profiles were obtained by EBSD in a field emission scanning electron microscope (FESEM) equipped with the TSL orientation imaging microscopy (OIM) software points. Orientation distribution functions (ODF) were employed to illustrate the textures. The experimental deformation texture of the AA6063 alloy has been presented in an earlier work, and for further experimental details, it is referred to this work (Zhang et al., 2018a).

FEM Simulations

During extrusion, each material point in the billet will go through different and complicated deformation histories, in terms of strain rate, temperature, pressure, and strain, which will vary with time and position. In order to predict the extrusion microstructure and texture, an accurate description of the deformation history in terms of these quantities is thus required. The initial step of the modeling exercise is to perform flow simulations by FEM, to provide the deformation history along relevant particle paths as output for the subsequent modeling (Aukrust et al., 1997; Zhang et al., 2015).

In the present work, a commercial FEM code HyperXtrude, assuming steady-state flow, was employed to provide the deformation history along desired path lines. Due to the symmetry of the extrusion profile and the set-up, only a quarter of the geometry was simulated. Hexahedral brick elements were used with a very fine mesh resolution in the bearing channel region, to capture the variations in the deformation field in this region with adequate accuracy. Rigid boundaries were considered for the container and the die towards the aluminium. The temperature of 350°C was specified for the container and the die. A heat transfer coefficient of 10,000 W/(m²K) was used and full sticking assumed between the aluminium and the container and between the aluminium and the die surface. In the bearing channel, on the other hand, where the experimental set-up used parallel bearings, a full-slip condition was assumed in the simulations, since it can be expected that the bearings are relieved due to die deflection during extrusion.

The Sellars–Tegart constitutive equation was used to describe the hot deformation during the extrusion (Sellars and McG. Tegart, 1972), for which the steady state effective flow stress, $\overline{\sigma }$, is given as

$\overline{\sigma }=\frac{1}{\alpha }{\sinh }^{-1}{\left(\frac{Z}{A}\right)}^{\frac{1}{n}} (1)$

where Z = $\overline{\epsilon }\exp \frac{Q}{\mathrm{RT}}$ is the Zener–Hollomon parameter, $Q$ is the activation energy, $R$ is the universal gas constant, $T$ is the absolute temperature, and $\alpha , A, n$, and $Q$ are temperature independent material constants. The parameter values used for the AA6063 alloy in this work are obtained from the literature (Sheppard and Jackson, 1997) and is given in Table 1. These parameters are based on fitting of experimental compression and torsion data over a range of temperatures and strain rates relevant for the present work.

TABLE 1

TABLE 1. Material constants of the Sellars–Tegart constitutive equation for AA6063.

The deformation history for the center path (crossing of the horizontal and vertical symmetry planes), which ends at the exit of the 3 mm long bearing channel, was exported for further analysis and texture postsimulations.

Note that, FEM simulations were not carried out for the AA6082 alloy. The AA6082 has a different chemical composition; thus, the parameters of the constituent Eq. 1, including temperature, are different. The geometrical set-up is also different with a considerable smaller extrusion ratio. For the purpose of a qualitative comparison, the deformation path of the AA6063 was applied also for the texture simulations of the AA6082. This does not justify a quantitative comparison of simulated and measured textures. However, as it turns out, the extrusion texture contains a very strong Cube component that cannot be captured even qualitatively by the models. Note that an earlier reported texture of AA6082 (Ryen et al., 2004), measured after extrusion at a similar temperature, but with a higher extrusion ratio of about 50, showed a very similar, slightly sharper texture, with an even stronger Cube component.

The same modeling approach has recently been applied for the extrusion of round profiles of the same alloy (Zhang et al., 2018b). As compared to the previous work, only the center deformation path is considered for the subsequent texture simulations in the present work.

Crystal Plasticity Modeling

Two different crystal plasticity models, i.e., the FC-Taylor and the advanced Lamel model (Alamel) (Van Houtte et al., 2005) have been considered in this work.

The main assumption of the FC-Taylor model is that each single crystal experiences the same deformation as the polycrystalline aggregate (Van Houtte, 1988b), which implies that the FC-Taylor model ignore grain interactions. In Alamel-type models, on the other hand, local interactions across grain boundaries are considered by relaxing the constraints on the shear strain components, while constraints are imposed on the corresponding stress component. The Alamel model considers a cluster containing a common grain boundary and the two adjunct grains or regions. In the Alamel model, the grain boundary is represented by its normal vector and the shear components related with the normal of the common grain boundary can be relaxed.

Both the FC-Taylor and the Alamel model were implemented using the regularized single crystal yield surface (Holmedal, 2020). This approach enables activation of any number and type of slip systems in a very robust way. Moreover, the exponent $a$ of the single crystal yield function is directly associated to the strain rate sensitivity defined by the power law (Hutchinson, 1976),

${\tau }^s={\tau }_0\text{sgn}\left({\dot{\gamma }}^s\right){\left|\frac{{\dot{\gamma }}^s}{{\dot{\gamma }}_0}\right|}^m(2)$

As pointed out by Holmedal (2020),

$m=\frac{1}{a-1}(3)$

In the FC-Taylor model, elastic deformation is neglected, i.e., the velocity gradient $\mathbf{L}$ provided by FEM simulations, is assumed to be equal to the plastic velocity gradient, ${\mathbf{L}}^{\text{p}}$. After transformation into the crystal frame (quantities denoted by a hat) it reads ${\widehat{\mathbf{L}}}^{\text{p}}=\mathbf{Q}{\mathbf{L}}^{\text{p}}{\mathbf{Q}}^{\text{T}}$, where $\mathbf{Q}$ is a rotation matrix between the global (laboratory) and the local (crystal) frame. In the crystal frame, for each time increment, the deviatoric Cauchy stress $\widehat{\mathbf{\sigma }}$ is found by solving the system of six nonlinear equations

${\widehat{\mathbf{D}}}^{\text{p}}=\dot{\lambda }\frac{\partial f}{\partial \widehat{\mathbf{\sigma }}}\text{and}f\left(\widehat{\mathbf{\sigma }}\right)=0(4)$

by the Newton–Raphson method with line search (Scherzinger, 2017). ${\widehat{\mathbf{D}}}^{\text{p}}=\text{sym}\left({\widehat{\mathbf{L}}}^{\text{p}}\right)$ is the plastic strain rate, $f$ is the single crystal yield function, and $\dot{\lambda }$ is the plastic multiplier equal to the plastic work rate. The constitutive spin in the crystal frame, ${\widehat{\mathbf{W}}}^{\text{c}}$, is calculated as

${\widehat{\mathbf{W}}}^{\text{c}}={\widehat{\mathbf{W}}}^{\text{p}}-{\displaystyle \sum }_s{\widehat{\mathbf{\Omega }}}^s{\dot{\gamma }}^s(5)$

where ${\widehat{\mathbf{W}}}^{\text{p}}=\text{skew}\left({\widehat{\mathbf{L}}}^{\text{p}}\right)$ is the plastic spin, ${\dot{\gamma }}^s$ is the slip rate on the slip system $s$, ${\widehat{\mathbf{\Omega }}}^{\mathit{s}}$ is the skew-symmetric part of the Schmid matrix ${\mathbf{m}}^s={\mathbf{b}}^s\otimes {\mathbf{n}}^s$, with the slip direction, ${\mathbf{b}}^s$, and the slip plane normal, ${\mathbf{n}}^s$. The orientation matrix of the single crystal is updated according to

$\dot{\mathit{Q}}=\mathrm{-}{\widehat{\mathbf{W}}}^{\text{c}}\mathbf{Q}(6)$

In the Alamel model, in order to solve the plastic slip in the cluster, the nonlinear system given in Eq. 4 is solved simultaneously for both grains. In addition, these are coupled by two nonlinear equations reading

${\sigma }_{23}^{\text{B},\text{G}1}-{\sigma }_{23}^{\text{B},\text{G}2}=0,(\mathrm{7a})$

${\sigma }_{13}^{\text{B},\text{G}1}-{\sigma }_{13}^{\text{B},\text{G}2}=0.(\mathrm{7b})$

Here, ${\sigma }_{ij}^{\text{B},\text{G}x}$ represents the $ij$-th Cauchy stress component of the grain $x$ expressed in the boundary frame in a cluster. Solving Eqs. 7a results in two relaxation shears $r_{23}$ and $r_{13}$ so that

${\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B},\text{G}1}={\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B}}+\left(\begin{array}{ccc}0& 0& r_{13}\\ 0& 0& r_{23}\\ 0& 0& 0\end{array}\right)\text{and}{\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B},\text{G}2}={\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B}}-\left(\begin{array}{ccc}0& 0& r_{13}\\ 0& 0& r_{23}\\ 0& 0& 0\end{array}\right)(8)$

where ${\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B},\text{G}x}$ is the plastic velocity gradient of grain $x$ in the boundary frame, ${\left({\mathbf{L}}^{\text{p}}\right)}^{\text{B}}$ is the plastic velocity gradient prescribed by FEM and rotated into the boundary frame. After solving the relaxations and both grains, the update of respective orientation matrices is done in a similar fashion as Eqs. 5, 6.

Besides the octahedral slip systems $\left\{111\right\}\langle 1\overline{1}0\rangle$, also the three nonoctahedral slip system classes $\left\{110\right\}\langle 1\overline{1}0\rangle$, $\left\{001\right\}\langle 1\overline{1}0\rangle$, and $\left\{112\right\}\langle 1\overline{1}0\rangle$ are considered here (Maurice and Driver, 1997a; Maurice and Driver, 1997b). The initial texture of the billet material is assumed to be random and is represented by a set of 1,000 randomly distributed orientations (uniformly distributed in Euler space). As described above, the considered grain interactions in the Alamel-type models take place on the common grain boundary shared by two adjacent grains. A set of 500 randomly distributed normal vectors in the spatial space are taken to represent the initial orientations of the grain boundaries, and they will reorientate during the deformation.

The crystal plasticity models use the deformation history provided by the FEM continuum plasticity flow simulations, notably the velocity gradient tensor $\mathbf{L}$ and the time increment $\text{Δ}t$, to update the texture. The final deformation texture is exported to and analyzed using the MTEX toolbox in the Matlab software (Hielscher and Schaeben, 2008).

Results

Experimental Results

The microstructure of the AA6063 profile extruded at T = 350°C, has been presented in a previous work (Zhang et al., 2018a). The as-extruded material for this condition shows a fibrous structure, i.e., a nonrecrystallized deformation structure. The overall texture in the form the ODF, representative for the center region, is shown in Figure 1A. It is noted that the texture is quite strong, with the Cu-component 26 times random, S 30 times random, Brass 20 times random, while Cube is only 3.6 times random.

FIGURE 1

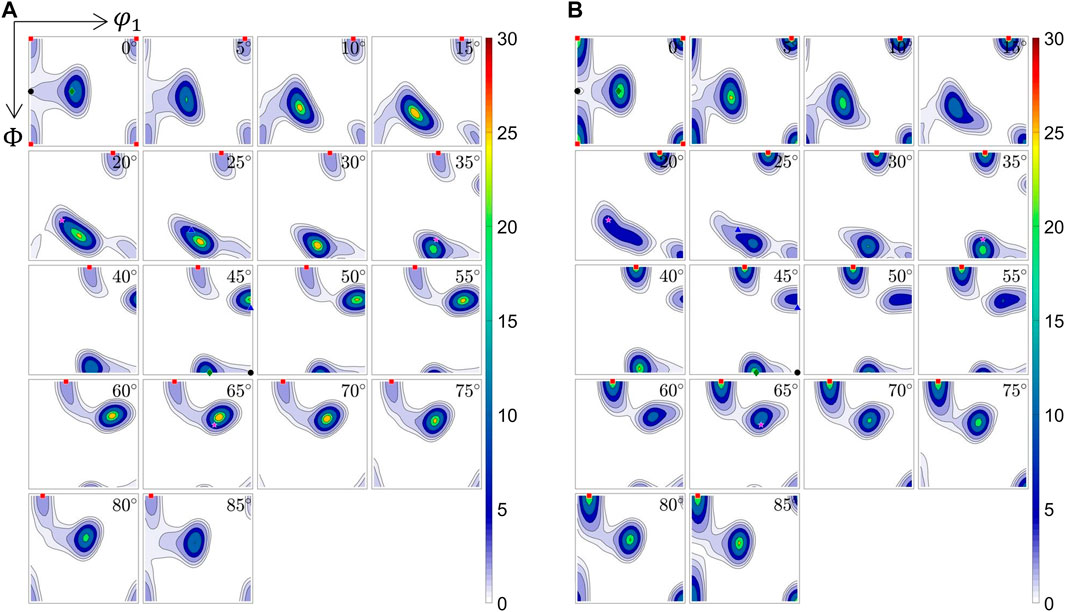
FIGURE 1. The experimental texture of the as-extruded profile in the form of ODF for the center region (A) AA6063 extruded at 350°C and (B) AA6082 extruded at 500°C.

For comparison, the deformation texture of the AA6082 alloy extruded at 500°C has also been recorded (Figure 1B). Also, this alloy, even at this high extrusion temperature, is in a fibrous, nonrecrystallized state after extrusion, and can as such be compared with the AA6063 alloy extruded at 350°C. Although different chemical compositions and extrusion ratios, the most important difference in this context is the extrusion temperature. The intensities of the main texture components are listed in Table 2. It is interesting to note that the texture is quite different, with the most notable difference the much stronger Cube (intensity 25). The relative intensities for the Copper, S, and Brass are also clearly different.

TABLE 2

TABLE 2. Intensity of the beta-fiber texture components and Cube texture in the AA6063 and AA6082 alloys extruded at different temperatures.

FEM Flow Simulations

The deformation microstructure is characterized by its deformation substructure and associated texture. As already mentioned, coupled FEM simulations and crystal plasticity (CP) modeling has recently successfully been performed to provide texture predictions comparable to the experiments (Zhang et al., 2015; Zhang et al., 2018b). In principle, any CP model can be used, nonetheless advanced CP models such as Alamel-type models have shown to perform better than the FC-Taylor model in predicting the deformation texture. The initial texture and the velocity gradient $\mathbf{L}$ along particle paths provided by the HyperXtrude FEM simulations are the main input to the CP models. The deformation texture simulations are realized by including just conventional octahedral slip as well as with also nonoctahedral slip systems included (Maurice and Driver, 1997a; Maurice and Driver, 1997b).

The deformation characteristics can be analyzed by means of the FEM flow simulations, using the same method developed by (Zhang et al., 2018b). Evolution of the strain rate along the center path is illustrated in Figure 2. It follows from Figure 2 that the accumulated strain increases slowly far from the die inlet. At $\text{Γ}=-10\text{mm}$, the strainrate increases rapidly, which corresponds to the flow into the extrusion gap.

FIGURE 2

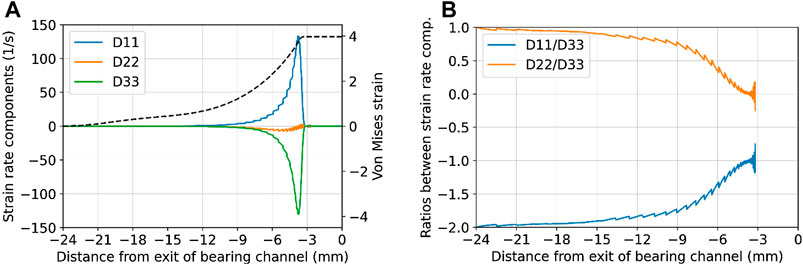
FIGURE 2. Deformation mode analysis for the center deformation path; (A) plot of components of the deformation rate tensor; (B) ratios between these components.

With the definitions 1 = ED (extrusion direction), 2 = TD (transverse direction), and 3 = ND (normal direction, we have for uniaxial tension/compression

$\frac{{\dot{\epsilon }}_{22}}{{\dot{\epsilon }}_{33}}=1\text{and}\frac{{\dot{\epsilon }}_{11}}{{\dot{\epsilon }}_{33}}=-2(9)$

while for plane strain compression,

$\frac{{\dot{\epsilon }}_{22}}{{\dot{\epsilon }}_{33}}=0\text{and}\frac{{\dot{\epsilon }}_{11}}{{\dot{\epsilon }}_{33}}=-1(10)$

From Figure 2, we clearly see that the flow changes from uniaxial tension in the container, to plane strain compression as one approach the bearings.

It is well known that during uniaxial tension of fcc alloys, a double $\langle 100\rangle /\langle 111\rangle$ fiber texture develops (Zhang et al., 2018b). Consistent with the deformation analysis above, this is also what is observed experimentally by analyzing the texture of the material in the container (of the AA6063 alloy extruded at 350°C) before it enters the die (not shown in this paper), with a double $\langle 111\rangle$ and $\langle 100\rangle$ fiber texture, where the $\langle 111\rangle$ component is considerably stronger than the $\langle 100\rangle$. This was also what was previously observed during round profile extrusion of the same alloy. It is then interesting to see how these two components individually further develop during plane strain compression, which is the dominant deformation mode the material experiences during the die. This is analyzed in the Discussion part.

FEM Extrusion Texture Predictions

Rate-Sensitive CP Models With Only the Octahedral Slip Systems

The deformation texture was predicted by coupled FEM and CP modeling. Two different CP rate-insensitive models have been considered in this work, i.e., the FC-Taylor and the Alamel model. A description of both these models can be found in Mánik and Holmedal (2013); Mánik and Holmedal (2014) and Zhang et al. (2015). The FC-Taylor model ignores any grain interactions, whereas the Alamel model assumes grain interaction locally at the grain boundary by allowing relaxations of the strain constraints. Both models were formulated and implemented based on the regularized single crystal yield surface (Holmedal, 2020). This approach allows to introduce rate-sensitive behavior as well as activation of arbitrary number and type of slip systems in a robust way. In the first set of trials, only conventional octahedral slips were considered, i.e., the twelve $\left\{111\right\}\langle 110\rangle$ slip systems.

The texture predictions were conducted for the center path. Applying the velocity gradient and the temperature as a function of time, as predicted by the FEM simulations for the center path of the AA6063 alloy, the texture after extrusion was predicted by the CP models for this given deformation history for both alloys, in lack of detailed FEM simulations for the AA6082, as discussed above. The predicted results were processed in the MTEX toolbox in the Matlab software. When generating the ODF, the same parameters were used as for processing the experimental EBSD data.

As far as it concerns the predicted textures for the rate-insensitive variants of both the FC-Taylor and the Alamel model with only the octahedral slip, it is referred to a previous work (Zhang et al., 2018a).

Figure 3 shows the effect of the strain-rate sensitivity on the intensity of texture components obtained by the FC-Taylor (a, c) and Alamel model (b, d) with octahedral slips only. For the case of T = 350°C (Figures 3A,B), for a realistic strain-rate sensitivity expected to be between 0.1–0.2, the model predicted well Cube and Cu component intensities, while S and Brass were underpredicted, and Goss was significantly overpredicted. The too weak Brass component prediction occurred at both temperatures and is expected from Taylor type models (Mánik and Holmedal, 2014; Van Houtte, 1988a). For the case of 500°C (Figures 3C,D), the Alamel model predicted a significantly too low Cube, while the ED-rotated Cube, i.e., the Goss component, was too strong. The correct prediction of the Cube is important, because it is commonly assumed that the strong Cube, often present after recrystallization of hot deformed Al-alloys, stems from Cube already present in the deformed conditions (Daaland and Nes, 1996; Vatne et al., 1996).

FIGURE 3

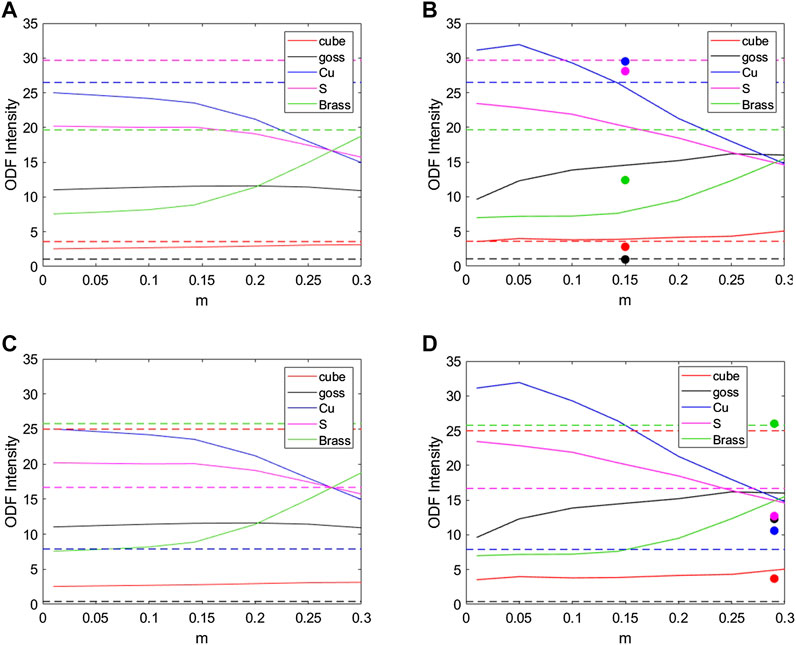
FIGURE 3. Intensities of texture components as functions of the strain-rate sensitivity. Predicted by the Alamel model by solid lines in (B) and (D), and computed by the FC-Taylor model by solid lines in (A) and (C) compared to measured values (dashed horizontal lines) for (A) and (B) T 350°C and (C) and (D) T 500°C. The filled circles in (B) and (D) indicate the results from the Alamel model with the optimal parameters including nonoctahedral slips (Table 3).

Rate-Sensitive Models With Both Octahedral and Nonoctahedral Slip Systems

Maurice and Driver (1997a), Maurice and Driver (1997b) have shown that nonoctahedral slip may play a role at higher deformations temperatures. The deformation texture calculations are therefore made, including possible additional nonoctahedral slip systems, i.e., $\left\{110\right\}\langle 1\overline{1}0\rangle$, $\left\{001\right\}\langle 1\overline{1}0\rangle$, and $\left\{112\right\}\langle 1\overline{1}0\rangle$.

Both the strain rate sensitivity and the critical stresses of the nonoctahedral slip systems depend on the temperature. Several values have been previously suggested in the literature (Falkinger et al., 2020). Typically, the relative strengths of the nonoctahedral slips with respect to the octahedral slips are within the range of 0.75–1.5, the strain-rate sensitivity varies from 0.1 to 0.3, see e.g., (Perocheau et al., 1998; Falkinger et al., 2020).

In order to test the ability of the CP models to predict the measured textures, quantitatively at 350°C and qualitatively at 500°C, the strength of the nonoctahedral slips as well as the strain-rate sensitivity were varied by a global optimization algorithm within the given range until the best fit between the predicted and the measured texture was found. Strain-rate sensitivity variations were in the range from 0.1 to 0.4, the critical stresses of the nonoctahedral slips between 0.5 and 2, where the factor 2 represents deactivation of the given slip. The strength of the octahedral slips was fixed to unity. The particle swarm optimization algorithm in Matlab software (Mezura-Montes and Coello, 2011) was used for optimization. A brief outline of the algorithm is as follows:

1. The particle swarm algorithm begins by creating the initial particles and assigning them initial velocities.

2. It evaluates the objective function at each particle location and determines the best (lowest) function value and the best location.

3. It chooses new velocities, based on the current velocity, the particles’ individual best locations, and the best locations of their neighbors and iteratively updates the particles locations.

For the case of T = 350°C, the residual $\mathrm{ℛ}$ to be minimized was defined in the least-square sense as

$\mathrm{ℛ}={\left(\frac{I_{\text{Cube}}^{\text{mod}}}{I_{\text{Cube}}^{\text{exp}}}-1\right)}^2+{\left(\frac{I_{\text{Goss}}^{\text{mod}}}{I_{\text{Goss}}^{\text{exp}}}-1\right)}^2+{\left(\frac{I_{\text{Cu}}^{\text{mod}}}{I_{\text{Cu}}^{\text{exp}}}-1\right)}^2+{\left(\frac{I_{\text{S}}^{\text{mod}}}{I_{\text{S}}^{\text{exp}}}-1\right)}^2+{\left(\frac{I_{\text{Brass}}^{\text{mod}}}{I_{\text{Brass}}^{\text{exp}}}-1\right)}^2(11)$

where $I_{\text{X}}^{\text{exp}}$ and $I_{\text{X}}^{\text{mod}}$ are intensities of the $X$ texture component, read from the experimentally measured and the predicted ODFs, respectively. A global minimum was found for both the FC Taylor and the Alamel model, the corresponding model parameters are listed in Table 3.

TABLE 3

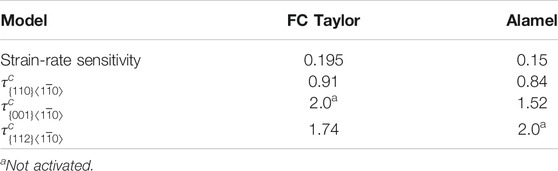
TABLE 3. Case of AA6063, T = 350°C. The best-fit relative critical resolved shear stress (CSSR) for the three nonoctahedral slip systems considered in the texture optimization for FC Taylor and Alamel, respectively.

In both models, ${\tau }_{\left\{111\right\}\langle 1\overline{1}0\rangle }^c=1$. The final residuals were 0.285 and 0.2 for the FC Taylor and the Alamel, respectively. The simulated ODFs having closest match with the experimentally measured texture for AA6063 T = 350°C are shown in Figure 4 and those for AA6082 T = 500 °C in Figure 5, and the intensities of the individual components are compared in Figure 6.

FIGURE 4

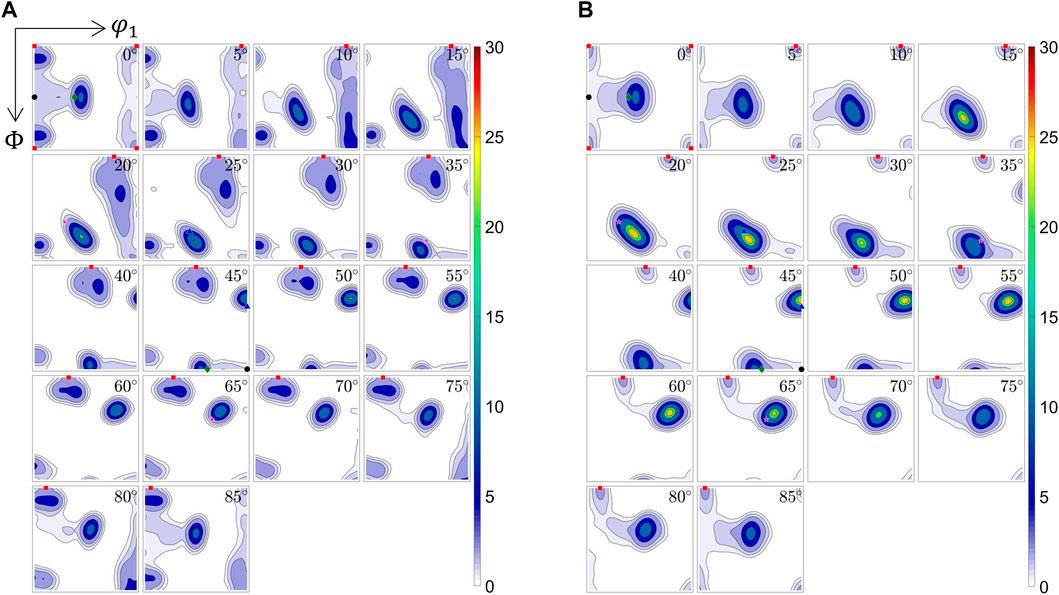
FIGURE 4. Texture predictions computed by (A) FC-Taylor and (B) Alamel models with parameters giving the best match with the experimentally measured texture for AA6063, T 350°C.

FIGURE 5

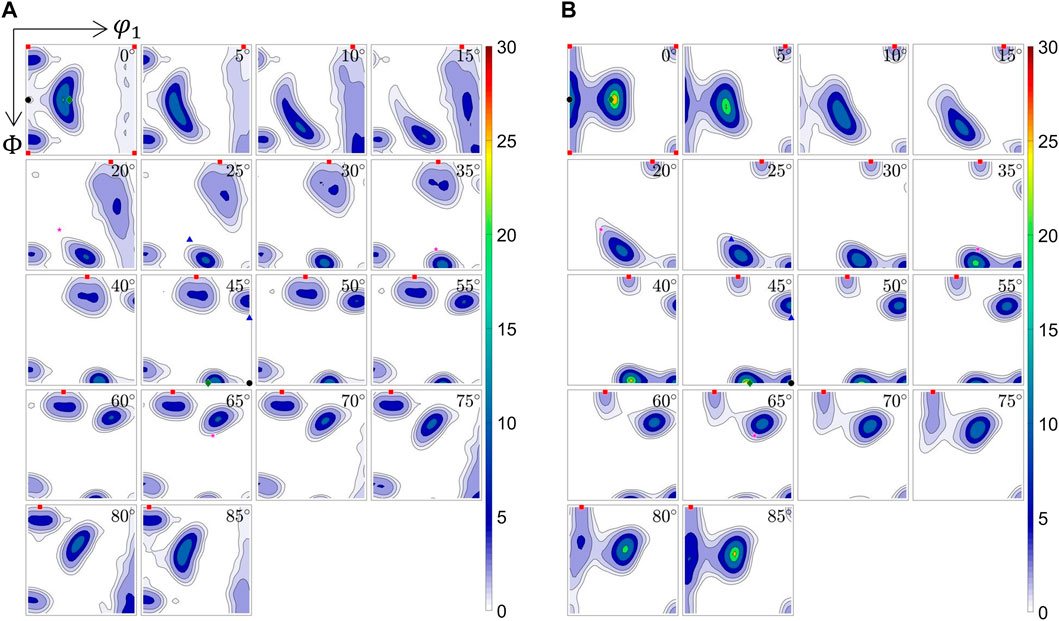
FIGURE 5. Texture predictions computed by (A) FC-Taylor and (B) Alamel models with parameters giving the best match with the experimentally measured texture for AA6082, T 500°C.

FIGURE 6

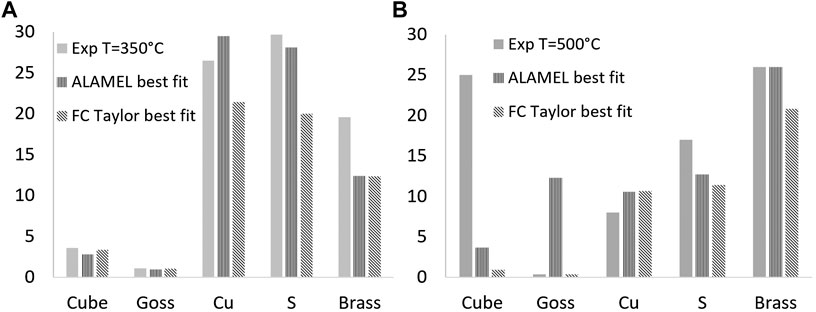
FIGURE 6. Predicted and measured texture component intensities for (A) AA6063 T 350°C, (B) AA6082 T 500°C.

Both the strain-rate sensitivity and the critical resolved shear stresses that give the best fit for both models are within physically reasonable limits. According to Table 3, slip on the $\left\{110\right\}$ planes has the lowest critical resolved shear stress, which means that this class of slip systems contributes more to the overall slip solution than slip on $\left\{001\right\}$ and $\left\{112\right\}$ planes, which have higher critical resolved shear stresses. The FC-Taylor model develops an extra undesired texture component, i.e., ∼10° ED rotated Cube, which is not present in the Alamel’s prediction. As this component is not stable for the plane-strain compression, it would continue to rotate if the deformation had continued.

For the case of AA6082, T = 500°C (Figure 5), neither of the texture models used can predict as high content of the Cube component as measured (intensity 25) (Figure 1B and Discussion chapter). Due to this, and because of the inaccuracy by applying the strain path from the AA6063 simulation also for the AA6082 texture simulation, the residual in the global optimization problem was instead chosen as $\mathrm{ℛ}=\underset{V}{{\displaystyle \int }}{\left(I^{\text{exp}}\mathrm{-}{I}^{\text{mod}}\right)}^2\text{d}V$, i.e., to minimize the texture index of the difference between experimental and modeled textures. A global minimum was found for both the FC Taylor and the Alamel model, the corresponding model parameters are listed in Table 4.

TABLE 4

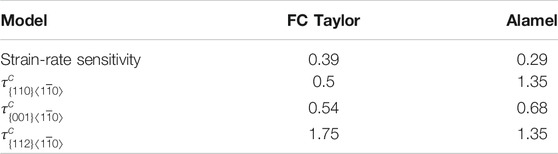
TABLE 4. Case of AA6082, T = 500°C. The best-fit relative critical resolved shear stress (CSSR) for the three nonoctahedral slip systems considered in the texture optimization for FC Taylor and Alamel, respectively.

In both models, ${\tau }_{\left\{111\right\}\langle 1\overline{1}0\rangle }^c=1$. The final residuals were 2.330 and 1.8 for the FC Taylor and the Alamel, respectively. The simulated ODFs with the optimal set of parameters with respect to the experimentally measured texture for AA6082 T = 500°C are shown in Figure 5, and the intensities of the individual components are compared in Figure 6B.

A reasonable fit for S, Brass, and Cu components was obtained by both models. However, none of the models was capable to predict the strong Cube component observed experimentally after extrusion at this temperature. For the Alamel model, the optimal solution for the overall ODF resulted in the strong overprediction of Goss component.

Discussion

Influence of the Nonoctahedral Slip Systems on Texture Prediction

The results presented in Figure 6 show that by allowing slip on both octahedral and nonoctahedral slip systems, both FC Taylor and Alamel models were capable to model all the main components of the experimental texture after extrusion at 350°C. However, the Alamel model distinguished itself when considering the overall texture comparison. The activation of the nonoctahedral slip systems has proven to be crucial for obtaining good texture predictions. Figures 3B,D compare the Alamel model predictions for 350°C and 500°C, respectively, without considering slip on the nonoctahedral planes to the optimal solution obtained by the global optimization. The sole activation of the octahedral slip leads to strong overprediction of Goss, regardless of the strain-rate sensitivity. The effect of the activation of $\left\{110\right\} \langle 1\overline{1}0\rangle$ and $\left\{112\right\} \langle 1\overline{1}0\rangle$ slip systems at two different strain-rate sensitivities, i.e., $m=0.1$ and 0.25, for the Alamel model (quite similar in the FC Taylor) is shown in Figure 7. Two main conclusions can be made:

1. Slip on the $\left\{110\right\}$ planes can supress evolution of Goss.

2. Slip on the $\left\{112\right\}$ planes can promote evolution of Goss and Cube.

FIGURE 7

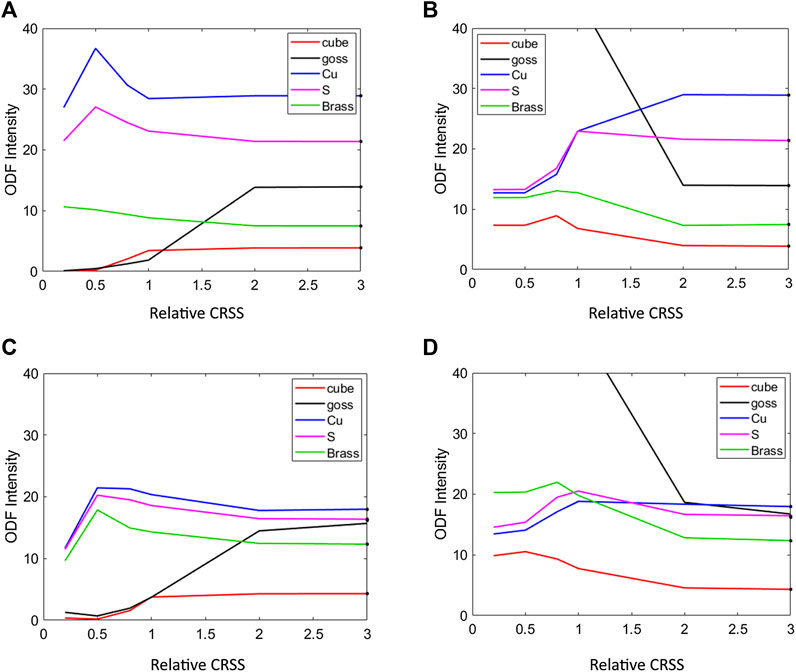
FIGURE 7. Effect of the strain rate sensitivity and the activation of the non-octahedral slip systems on the texture component intensity prediction in the Alamelmodel. (A) m = 0.1, octahedral slip + $\left\{110\right\}\langle 1\overline{1}0\rangle$(B) m = 0.1, octahedral slip + $\left\{112\right\}\langle 1\overline{1}0\rangle$(C) m = 0.25, octahedral slip + $\left\{110\right\}\langle 1\overline{1}0\rangle$(D) m = 0.25, octahedral slip +$\left\{112\right\}\langle 1\overline{1}0\rangle$.

Activation of the nonoctahedral slip systems affects the other texture components than Goss to somewhat less extent. Based on this observation, the reason for the very low Goss in the measured extrusion at 350°C is probably due to the activation of the $\left\{110\right\}$ slip planes.

The good overall texture fit provided by the Alamel model for 350°C was not achieved for the case of 500°C. The individual predictions for the Cu, S, and Brass components are reasonably good; however, poor predictions for Goss and Cube are obtained. At 500°C, the strain-rate sensitivity is expected to be moderately high, i.e., in the range of 0.2–0.3. Figure 7D shows that by including the $\left\{112\right\}\langle 1\overline{1}0\rangle$ the amount of Cube can be increased with a strain rate sensitivity in this range. However, this is accompanied by a large increase in the Goss component, which clearly contradicts the experiments, in which quite limited Goss is observed. In any case, none of the current models, irrespective of parameters, are capable of predicting an intensity of Cube as high as ∼25. For AA6082, one can argue that some error in the simulated texture should be expected, due to performing the simulation based on the strain path obtained from the AA6063 FEM simulation, which has an extrusion ratio of 80 as compared to 10 for the AA6082. With a higher extrusion ratio, a slightly sharper texture is expected, as well as some redistribution of the strength of the texture components. However, an even stronger Cube component was observed for extrusion of AA6082 at a similar temperature but with a higher, more comparable extrusion ratio (Ryen et al., 2004). Hence, the error introduced by using an unprecise strain path is small compared to the significant error not predicting the strong Cube component.

It is suspected that the large amount of Cube observed in AA6082 extruded at 500°C is not representative for the true deformation texture, but rather a result of fast recovery or early recrystallization of Cube at this high temperature.

Through Extrusion Texture Evolution Prediction

One of the main objectives behind the use of the texture model is to study and explain the origin of Cube texture component, as its presence in the deformation texture is believed to have important influence on the recrystallization of hot deformed Al-alloys (Daaland and Nes, 1996; Vatne et al., 1996). The clue to get any Cube at all is the deformation mode characteristics of the extrusion (Figure 2). The initial dominating deformation mode is uniaxial tension producing the $\langle 100\rangle$ and $\langle 111\rangle$ axisymmetric texture fibers. The Cube component is part of the $\langle 100\rangle$ fiber and remains present through further deformation close to and in the die, where the deformation mode is mainly plane strain compression. The good texture prediction at 350°C provided by the Alamel model legitimates to use this model for assessing the texture evolution through the whole extrusion process.

Figure 8 shows texture component developments through the extrusion process, predicted by the Alamel model with parameters that give the best fit of the measured texture at 350°C. During the uniaxial tensile deformation mode, the $\langle 111\rangle$ fiber, here represented by the $\left\{011\right\}\langle 1\overline{1}1\rangle$ and Cu components, develops stronger than the $\langle 100\rangle$ fiber, represented by Cube and Goss components. The texture approximately at the end of the uniaxial tensile mode, i.e., at strain of 1.5 is shown in Figure 9A. During the following deformation mode of plane strain compression, the $\langle 111\rangle$ fiber rotates into the $\beta$-fiber and forms the classical plane strain deformation texture (note interchanging of intensities between the $\left\{011\right\}\langle 1\overline{1}1\rangle$ tensile component and Brass both in Figures 8, 9). The Cube continues to develop further during the last part of the extrusion where a mixed deformation mode took place, probably at the expense of Goss. Finally, the plane strain compression causes the intensity of the Cube to fall to approximately half the intensity. It is interesting to note that no Cube comes from the $\langle 111\rangle$ fiber.

FIGURE 8

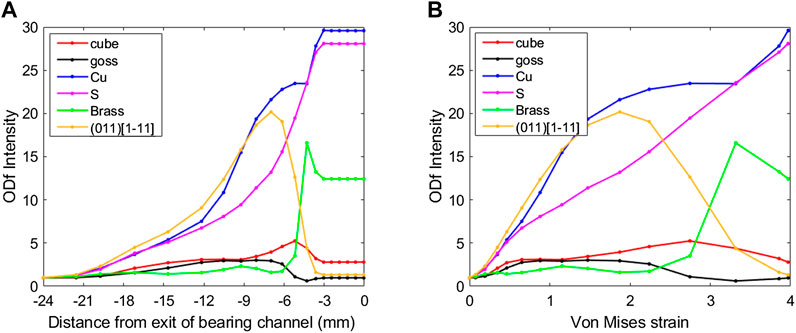
FIGURE 8. Through-extrusion texture components development prediction by the Alamel model with parameters giving the best fit to the measured texture at 350°C, plotted as a function of (A) the Von Mises strain, (B) distance from exit of bearing channel along the extrusion direction.

FIGURE 9

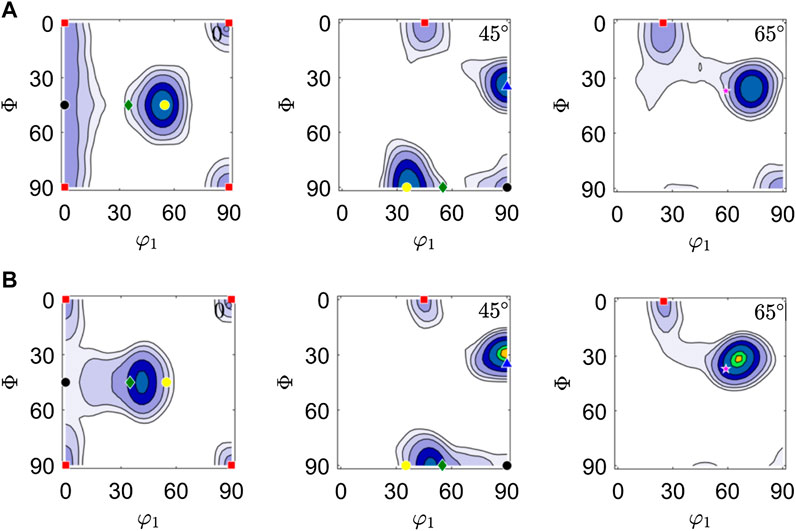
FIGURE 9. Texture predictions (A) after Von Mises strain of ∼1.5, which approximately corresponds to the transition from the uniaxial tensile mode to plane-strain compression mode; (B) at the end of the extrusion process.

Conclusions

In the present work, the evolution of deformation textures during flat profile extrusion of AA6xxx aluminium alloys have been investigated numerically, by coupling FEM flow simulations and crystal plasticity simulations and compared to experiments. The simulations are based on implementations of the FC-Taylor at the Alamel grain cluster model, which allow for variations in strain-rate sensitivity and the inclusion of any type and number of nonoctahedral slip systems. The numerical simulated textures are compared to the measured ones and discussed. To assess the quality of the texture predictions at 350°C and 500°C, the strength of the nonoctahedral slips as well as the strain-rate sensitivity were varied by a global optimization algorithm. At 350°C, fairly good fits were obtained both with the FC Taylor and the Alamel model, and the selected optimal parameters had reasonable values as compared to their expected physical interpretations. Nonetheless, the Alamel model provided a significantly better overall texture prediction, predicting all the major texture components with correct intensities. A reasonable, qualitative fit for S, Brass, and Cu components can also be obtained at 500°C by both models. However, none of the models are capable of predicting the strong Cube component observed experimentally after extrusion at this temperature. Both models, in particular the Alamel model, tend to predict a too strong Goss component at 500°C, while this component can be suppressed by the activation of $\left\{110\right\} \langle 1\overline{1}0\rangle$ slip systems at the lower strain rate sensitivity at 350°C. Owing to strain rate sensitivity and activation of nonoctahedral slip systems, high predictability was obtained for 350°C. However, for 500°C, the poor predictions are likely due to that dislocation slip is no longer the sole responsible mechanism.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

KZ was involved in experiments and initial texture simulations. TM was involved in texture simulations and texture optimization. AIA was involved in texture simulations. BH and KM was involved in supervision, interpretation, funding acquisition, and suggestions. KM, TM, KZ, and BH wrote the manuscript. All authors discussed the results and reviewed and edited the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research work has been supported by the IPN project COSMETEX (228918/O30) in Norway. The financial support by the Research Council of Norway and the industrial partner SAPA AS (Now Hydro Extruded Solutions) is gratefully acknowledged. We are grateful to Antonio Segatori, Hydro Extruded Solutions, Finspång, Sweden, for providing the extruded profiles for the texture analyses, and to Trond Aukrust, SINTEF Industry, Norway, for providing the FEM extrusion results, which are basis for the texture simulations.

References

Aukrust, T., Tjøtta, S., Vatne, H. E., and Van Houtte, P. (1997). Coupled FEM and texture modelling of plane strain extrusion of an aluminium alloy. Int. J. Plast. 13, 111–125. doi:10.1016/s0749-6419(97)00003-x

CrossRef Full Text | Google Scholar

Daaland, O., and Nes, E. (1996). Origin of cube texture during hot rolling of commercial Al-Mn-Mg alloys. Acta Mater. 44, 1389–1411. doi:10.1016/1359-6454(95)00290-1

CrossRef Full Text | Google Scholar

Donati, L., Segatori, A., El Mehtedi, M., and Tomesani, L. (2013). Grain evolution analysis and experimental validation in the extrusion of 6XXX alloys by use of a Lagrangian FE code. Int. J. Plast. 46, 70–81. doi:10.1016/j.ijplas.2012.11.008

CrossRef Full Text | Google Scholar

Dumoulin, S., Engler, O., Hopperstad, O. S., and Lademo, O. G. (2012). Description of plastic anisotropy in AA6063-T6 using the crystal plasticity finite element method. Model. Simulat. Mater. Sci. Eng. 20, 20. doi:10.1088/0965-0393/20/5/055008

CrossRef Full Text | Google Scholar

Falkinger, G., Simon, P., and Mitsche, S. (2020). Viscoplastic self-consistent modeling of the through-thickness texture of a hot-rolled Al-Mg-Si plate. Metall. Mater. Trans. 51, 3066–3075. doi:10.1007/s11661-020-05743-y

CrossRef Full Text | Google Scholar

Hielscher, R., and Schaeben, H. (2008). A novel pole figure inversion method: specification of theMTEXalgorithm. J. Appl. Crystallogr. 41, 1024–1037. doi:10.1107/s0021889808030112

CrossRef Full Text | Google Scholar

Holmedal, B. (2020). Regularized yield surfaces for crystal plasticity of metals. Crystals 10, 1076. doi:10.3390/cryst10121076

CrossRef Full Text | Google Scholar

Hutchinson, J. W. (1976). Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. Roy. Soc. Lond. Math. Phys. Sci. 348, 101–127.

Google Scholar

Mánik, T., and Holmedal, B. (2013). Additional relaxations in the Alamel texture model. Mater. Sci. Eng. 580, 349–354. doi:10.1016/j.msea.2013.05.071

CrossRef Full Text | Google Scholar

Mánik, T., and Holmedal, B. (2014). Review of the Taylor ambiguity and the relationship between rate-independent and rate-dependent full-constraints Taylor models. Int. J. Plast. 55, 152–181. doi:10.1016/j.ijplas.2013.10.002

CrossRef Full Text | Google Scholar

Maurice, C., and Driver, J. H. (1997a). Hot rolling textures of f.c.c. metals-Part I. Experimental results on Al single and polycrystals. Acta Mater. 45, 4627–4638. doi:10.1016/s1359-6454(97)00115-8

CrossRef Full Text | Google Scholar

Maurice, C., and Driver, J. H. (1997b). Hot rolling textures of f.c.c. metals-Part II. Numerical simulations. Acta Mater. 45, 4639–4649. doi:10.1016/s1359-6454(97)00117-1

CrossRef Full Text | Google Scholar

Mezura-Montes, E., and Coello Coello, C. A. (2011). Constraint-handling in nature-inspired numerical optimization: past, present and future. Swarm and Evolutionary Computation. 1, 173–194. doi:10.1016/j.swevo.2011.10.001

CrossRef Full Text | Google Scholar

Perocheau, F., Driver, J. H., and Aukrust, T. (1998). “A viscoplastic simulation of texture evolution during extrusion of an aluminium alloy,” in Texture and anisotropy of polycrystals. Editor R. A. Schwarzer (Aedermannsdor, Switzerland: Trans Tech Publications), 377–382.

CrossRef Full Text | Google Scholar

Perocheau, F., and Driver, J. H. (2000). Texture gradient simulations for extrusion and reversible rolling of FCC metals. Int. J. Plast. 16, 73–89. doi:10.1016/s0749-6419(99)00048-0

CrossRef Full Text | Google Scholar

Ralston, K. D., Birbilis, N., and Davies, C. H. J. (2010). Revealing the relationship between grain size and corrosion rate of metals. Scripta Mater. 63, 1201–1204. doi:10.1016/j.scriptamat.2010.08.035

CrossRef Full Text | Google Scholar

Ryen, Ø., Holmedal, B., Li, S., Houtte, P. v., Roven, H. J., and Nes, E. (2004). “Plastic anisotropy in recrystallized and unrecrystallized extruded aluminium profiles,” in 9th international conference on aluminium alloys, August, 2004. Editors J. F. Nie, A. J. Morton, and B. C. Muddle (Brisbane, Australia: © Institute of Materials Engineering Australasia Ltd), 1004–1009.

Google Scholar

Scherzinger, W. M. (2017). A return mapping algorithm for isotropic and anisotropic plasticity models using a line search method. Comput. Methods Appl. Mech. Eng. 317, 526–553. doi:10.1016/j.cma.2016.11.026

CrossRef Full Text | Google Scholar

Sellars, C. M., and Tegart, W. J. M. (1972). Hot workability. Int. Metall. Rev. 17, 1–24. doi:10.1179/imtlr.1972.17.1.1

CrossRef Full Text | Google Scholar

Sheppard, T., and Jackson, A. (1997). Constitutive equations for use in prediction of flow stress during extrusion of aluminium alloys. Mater. Sci. Technol. 13, 203–209. doi:10.1179/mst.1997.13.3.203

CrossRef Full Text | Google Scholar

Van Houtte, P. (1988a). A comprehensive mathematical formulation of an extended Taylor-Bishop-hill model featuring relaxed constraints, the Renouard-Wintenberger theory and a strain rate sensitivity model. Textures Microstruct. 8, 313–350. doi:10.1155/tsm.8-9.313

CrossRef Full Text | Google Scholar

Van Houtte, P. (1988b). A comprehensive mathematical formulation of an extended taylor-bishop-hill model featuring relaxed constraints, the renouard-wintenberger theory and a strain rate sensitivity model. Textures Microstruct. 8, 313–350. doi:10.1155/tsm.8-9.313

CrossRef Full Text | Google Scholar

Van Houtte, P., Li, S. Y., Seefeldt, M., and Delannay, L. (2005). Deformation texture prediction: from the Taylor model to the advanced Lamel model. Int. J. Plast. 21, 589–624. doi:10.1016/j.ijplas.2004.04.011

CrossRef Full Text | Google Scholar

Vatne, H. E., Furu, T., and Nes, E. (1996). Nucleation of recrystallised grains from cube bands in hot deformed commercial purity aluminium. Mater. Sci. Technol. 12, 201–210. doi:10.1179/mst.1996.12.3.201

CrossRef Full Text | Google Scholar

Zhang, K., Marthinsen, K., Holmedal, B., Aukrust, T., and Segatori, A. (2015). Coupled FEM and Alamel-type polycrystal plasticity modelling applied to extrusion of aluminium alloys. Aluminium Two Thousand World Congress and International Conference on Extrusion and Benchmark ICEB 2015, Florence, Italy, 12.-15 May, 2015. Editors L. Donati and L. Tomesani. Materials Today-Proceedings 2, 4898-4903.

CrossRef Full Text | Google Scholar

Zhang, K., Marthinsen, K., Holmedal, B., Aukrust, T., and Segatori, A. (2018a). “Evolution in texture and through thickness variations in Al-Mg-Si-extrusions: experiments and modelling,” in International conference on aluminium alloys (ICAA16). Montreal, Canada: Canadian Institute of Mining, Metallurgy & Petroleum, McGill University.

Google Scholar

Zhang, K., Marthinsen, K., Holmedal, B., Aukrust, T., and Segatori, A. (2018b). Through thickness variations of deformation texture in round profile extrusions of 6063-type aluminium alloy: experiments, FEM and crystal plasticity modelling. Mater. Sci. Eng. 722, 20–29. doi:10.1016/j.msea.2018.02.081

CrossRef Full Text | Google Scholar