Experimental Investigation on Failure Behaviors of G50 Ultra-High Strength Steel Targets Struck by Tungsten Alloy Spherical Fragments at High Velocity

An experimental investigation is presented into the failure behaviors of the G50 ultra-high strength steel targets struck by tungsten alloy spherical fragments at high velocity. The depth of penetration and the crater volume of G50 steel targets at velocities ranging from 923 to 1,807 m/s are obtained by ballistic gun experiments. A conic-like crater is observed in the G50 steel target after impact by a tungsten alloy spherical fragment, which is different from that in the experiments of low strength steel targets. It is believed that the eroding and fragmentation of the tungsten fragment during the penetration process give rise to this phenomenon. In addition, several tensile cracks are found both at the crater surface and the crater bottom, which are considered to be caused by tensile stress induced by the superposition of rarefaction waves at some local areas of the impacted interface. Numerical simulations of the penetration of tungsten alloy fragments into G50 steel targets are performed to predict failure features of the targets. It is shown that the numerical results are in good agreement with available experimental results.

Introduction

In modern warfare, the fragment anti-missile warhead is widely applied to intercept and destroy the incoming missile. The warhead is a key component of the missile to destroy the targets. Its capability against fragments penetration is an important prerequisite to ensure the completion of the given mission. Due to its low price and high strength, G50 (28CrMnSiNi4MoNb) ultra-high strength steel, a kind of low alloy steel without cobalt, has been widely used as material for penetrating warhead shell (Zhang et al., 2019). Tungsten alloy has become the main choice for the design of anti-missile warhead fragments with its good physical and mechanical capabilities of high density, small attenuation coefficient and strong ability of piercing armor. Therefore, it is of great significance to study the damage characteristics of G50 ultra-high strength steel under the impact of tungsten alloy fragments for designing the penetrating warhead shell.

The failure characteristics of tungsten alloy projectiles penetrating into steel targets have been studied over decades due to the continually military interest. Martineau et al. (2004) studied the penetration characteristics of the high-strength low-alloy (HSLA-100) steel impacted by 6.4 mm diameter tungsten carbide spheres at velocities ranging from 0.8 to 2.5 km/s experimentally. The results demonstrate that the diameter of the resulting crater increases linearly as a function of impact velocities. But the relationship between the depth of penetration and the impact velocity is non-linear. Schaer and Herrwerth (2001) proposed a theoretical model to predict the depth of penetration of tungsten projectiles with rotationally symmetric ellipsoid shape into semi-infinite targets at hypervelocity. The shape influences of projectiles on the depth of penetration were further discussed by additional numerical simulations. Hohler and Stilp (1977) conducted a series of tests to obtain the penetration characteristics of tungsten alloy rods into semi-infinite armored steel targets. The corresponding test data have become the standard reference data for theoretical analysis and numerical simulations. Anderson et al. (1995) and Anderson and Walker (1995) proposed an engineering model in accordance of the penetration mechanism and failure features of hypervelocity penetration of metallic targets impacted by cylindrical tungsten projectiles. Wu (1999) conducted an series of experiments to study the failure mechanism of 93 W alloy fragments of 2–4 g penetrating into armored steel targets at velocities ranging from 500 to 1,300 m/s. The fracture properties of 93 W alloy fragments were discussed intensively. Duan et al. (2003) conducted the experiments of two kinds of steel target plates (45# steel and 30CrMnMo) penetrated by sintered tungsten alloy projectiles. The microstructures of the targets showed that no adiabatic shear band was observed in the low strength 45# steel. While there were several kinds of adiabatic shear bands in the high strength 30CrMnMo steel under similar impact conditions which is also observed in perforation experiments of several kinds of steel targets (Atapek and Karagoz, 2010; Atapek, 2013). Rama Subba Reddy et al. (2019) conducted the ballistic tests of an amour steel against a scaled-down tungsten alloy projectile at velocities ranging from 900 to 1,400 m/s. Microstructural observations performed by SEM showed that the mushroom head of projectile is formed and cracks occurs originally at the both sides of the remnant and propagates to the head and the tungsten alloy projectile fails due to the adiabatic shear localization after deforming severely.

However as our knowledge G50 (28CrMnSiNi4MoNb) ultra-high strength steel penetrated by tungsten alloy fragments have not been investigated before. In this paper, an experimental investigation is reported into the failure characteristics of ultra-high strength steel targets subjected to impact by tungsten alloy fragments at velocity ranging from 923 to 1870 m/s which are still lacking. The expected results may provide a significantly experimental and theoretical basis for the design of the penetrating warhead shell.

Experiments

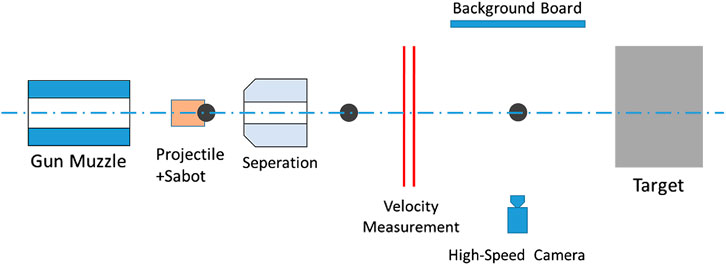
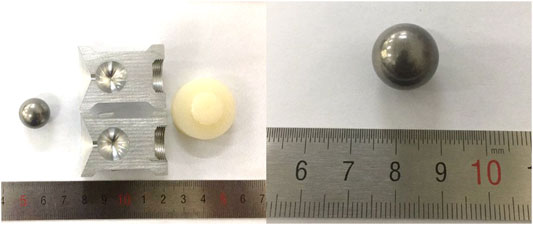
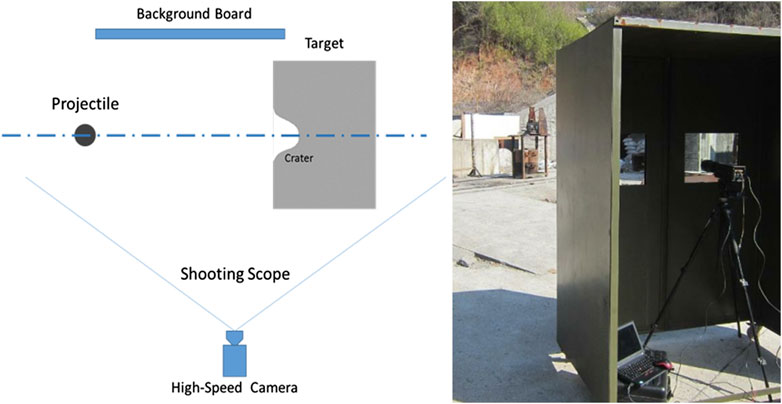
The plate material used in the experiments is a kind of low alloy steel without cobalt, ultra-high strength G50 steel which is supplied by ChangChen Special Steel Co. and the tungsten alloy is supplied by Xi'an Huashan Tungsten Products Co., Ltd. The chemical composition of G50 steel is given in Table 1. The experiment arrangement for the present tests is shown in Figure 1. The G50 ultra-high strength steel targets with the thickness of 100 mm was struck normally by the 15 mm diameter tungsten alloy spherical fragments with velocities ranging from 923 to 1870 m/s. The fragments were fired from a Φ30 mm ballistic gun after placed in a specifically designed sabot which is shown in Figure 2. The velocity measurement placed between the gun and target was used to measure the velocity of fragments. High-speed camera was further used to calibrate the impact velocity.

TABLE 1

TABLE 1. Chemical composition of G50 steel in wt%.

FIGURE 1

FIGURE 1. Sketch of the experiment setup.

FIGURE 2

FIGURE 2. Tungsten alloy fragment and specifically designed sabot.

The 15 mm diameter spherical fragments used in the experiment are made from W93 tungsten alloy, with density of 17.6 g/cm³ and total mass of 31 g. Assembled fragments with the sabot are shown in Figure 2. By adjusting the mass of the propellant, the velocity of fragments can be controlled in the range from 900 to 1,800 m/s. The G50 target was placed on a steel base as shown in Figure 3.

FIGURE 3

FIGURE 3. G50 steel target and velocity measurement.

The velocities of tungsten alloy fragments were measured by a pair of sensor aluminum foils which formed a part of electrical circuits and were connected to a multi-channel velocity measurement system. Then the time it takes the fragment to fly between two aluminum foils was recorded by the sensor. The velocity of fragments could be calculated from dividing the distance between two aluminum foils by the time interval. The high-speed camera system was used to record the flight attitude and penetration process of fragments as shown in Figure 4.

FIGURE 4

FIGURE 4. The layout of high-speed camera system.

Results and Discussions

Figure 5 shows the cut plane view of G50 steel targets. The experimental observations show that there are no obvious residual tungsten alloy fragments at the bottom of the crater, which suggests that the fragments are broken into pieces and ejected out of the crater during the penetration. It can be found from the G50 steel target after impact that a raised lip on the front surface combined with spall is produced by the tungsten alloy fragment and layered cracks occurs at the rough crater surface. The crater formed in the G50 steel target after impact by a tungsten alloy spherical fragment is conic-like, which is different from that in the low strength steel target tests.

FIGURE 5

FIGURE 5. Photographs of cross sections of G50 steel target after impact by a tungsten alloy spherical fragment. (A)v = 923 m/s (B)v = 1,158 m/s (C)v = 1,426 m/s (D)v = 1,600 m/s (E)v = 1,800 m/s, and (F)v = 1,870 m/s.

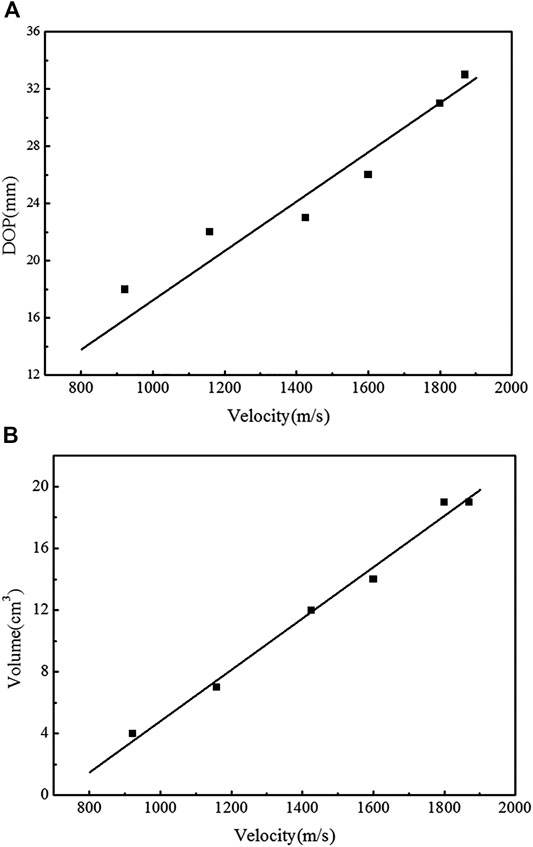
The depth of penetration and the crater volume of six shots are summarized in Table 2. Figure 6 shows the experimental data of the depth of penetration and the crater volume at different impact velocities, respectively. It is shown that both the depth of penetration and the crater volume increase nearly linearly with the increase of impact velocities.

TABLE 2

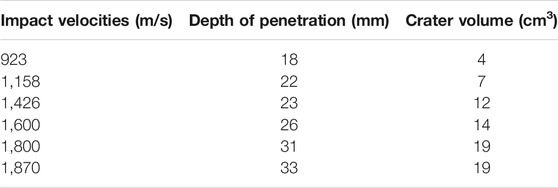
TABLE 2. Depth of penetration and crater volume of the G50 steel targets at different impact velocities.

FIGURE 6

FIGURE 6. (A) Depth of penetration, and (B) crater volumes.

Much effort Zhao et al. (2015) and Wang et al. (2013) has been dedicated toward the cratering features of tungsten alloy projectiles penetrating into ductile metallic targets with low yield strength (such as low carbon steel). The schematic diagrams of the penetration process are shown in Figure 7. When the projectile penetrates into the ductile metallic targets at high velocities, the stress at the projectile-target interface is much higher than the dynamic yield strength of projectile material. The projectile materials deformed and eroded at the projectile-target interface. The target material flows in a hydrodynamic manner in the depth and radial directions when intruded by a projectile. A raised lip on the front surface produced by the tungsten alloy fragment appears due to the effect of the rarefaction wave which is a typical phenomenon of the high velocity penetration when the impact pressure exceeds the strength of the target material. After the transient entrance phase, the projectile is continuously eroded, and intrudes the targets with the crater expanding and deepening to form a uniform cylindrical target crater under the effect of pressure and inertia.

FIGURE 7

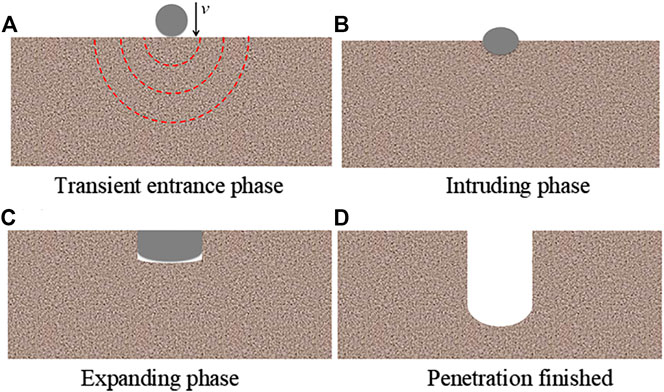
FIGURE 7. Schematical diagrams of penetration process of low carbon steel target impacted by a tungsten ball (Zhao et al., 2015). (A) Transient entrance phase, (B) intruding phase, (C) expanding phase, and (D) penetration finished.

However as to our knowledge, much fewer researches were found to investigate the failure features and penetration mechanism of G50 ultra-high strength steel targets impacted by tungsten alloy fragments. According to the failure features and penetration mechanism of the G50 steel target impacted by the tungsten alloy fragment, the pressure at the projectile-target interface is extremely high, and due to the strong rarefaction wave produced by boundary effect stretches target surface, a raise lip with spall are produced by rarefaction wave. With the increase of the impact velocity, the impact pressure and strength of the rarefaction wave increases, which makes the tensile spall area on the front surface of the target larger. It is also demonstrated that the failure mode of G50 steel develops from ductile fracture to semi-brittle fracture under high tensile strain rate. Obvious macro-cracks can be observed on the crater surface, which is slightly undulating in a wavy manner. At the surface of the crater, grain distortion flow is considered to be caused due to the adiabatic shear, and a severely deformed strip parallel distribution appears. At the same time, there are macro tensile cracks deepening into the targets, which suggests that local tensile failure occurs in the G50 target under the effect of the tungsten alloy fragment penetration.

During the penetration process, under the conditions of high temperature, high pressure and high strain rate, inhomogeneous stress distribution in the tungsten fragment occurs, and the fragment continuously erodes to “mushroom-like” head and the products of erosion are ejected out of the target. Local sudden unloading of craters, and the tensile stress are produced by the unloading wave interaction. Meanwhile, the adiabatic shear bands around the target crater greatly reduces the material strength in this area. Under the influence of shear stress, micro-cracks are nucleating, propagating and penetrating in the shear bands, and then macro-cracks are generated in the local unloading area.

With the penetration process going on, the random macro-cracks in the thickness direction occurs and the material departs from the target locally, which make the stress distribution concentrate, macro-cracks propagate and material locally fails in the tungsten alloy fragment. The front section of the fragment sharpens, which reduces the contact area between the fragment and the target, and thus the penetration resistance decreases. Figure 8 shows the schematic diagrams of failure features of tungsten alloy fragments penetrating into G50 steel target at high speed. It can be inferred that the failure mode of the target and the fragment is closely related.

FIGURE 8

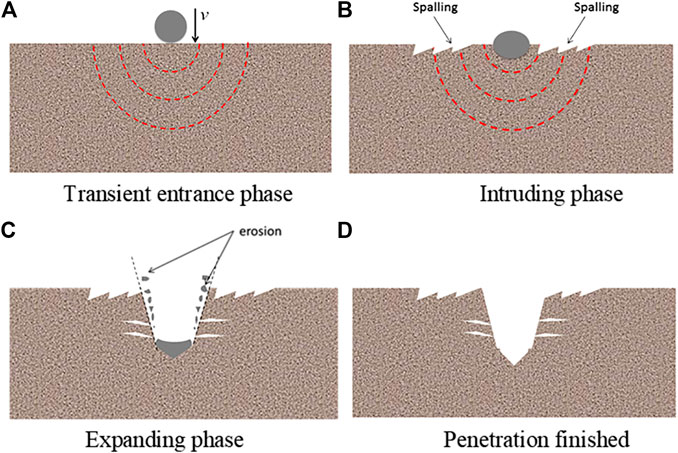
FIGURE 8. Schematical diagram of penetration process G50 steel target impacted by a tungsten ball (Zhao et al., 2015). (A) Transient entrance phase, (B) intruding phase, (C) expanding phase, and (D) penetration finished.

According to the dynamic cavity expansion theory, the radial stress on the cavity surface of the ideal elasto-plastic material is (Forrestal and Luk, 1988):

${\sigma }_r=\frac{2Y}{3}\left[\ln \left(\frac{2E}{3Y}\right)+1\right]+\frac{3}{2}\rho u^2(1)$

where Y is the yield strength, E is the elastic modulus, $\rho$ is the material density, and u is the cavity surface expansion velocity. According to Eq. (1), the radial stress on the cavity surface is closely correlated to the yield strength of the target plate. G50 steel has a ultra-high yield strength of 1,590 MPa (Wang et al., 2009), which makes a high radial stress. The higher radial stress acted on tungsten alloy fragments will cause greater stress concentration and inhomogeneous distribution of stress in the fragments. Greater concentration and inhomogeneous distribution of stress in the fragments will consequently lead the inhomogeneity and concentration of deformation, which finally lead the fragment break and fall into pieces.

In order to further investigate and verify the reason of conic-like crater forming, numerical simulations on the penetration of the tungsten alloy spherical fragment into the G50 steel target at velocities ranging from 923 to 1,870 m/s were carried out. Among them, Johnson-Cook constitutive relations and Gruneisen EOS are adopted for both the G50 steel target. The flow stress of Johnson-Cook model can be expressed in the following form:

$\sigma =\left(A+B{\overline{\epsilon }}^n\right)\left(1+C\ln {\dot{\epsilon }}^{\ast }\right)\left(1-T^{\ast m}\right)(2)$

where $\sigma$ is the flow stress, A, B, C, n, m are constant parameters, ${\dot{\epsilon }}^{\ast }=\dot{\epsilon }/{\dot{\epsilon }}_0$, ${\dot{\epsilon }}_0$ is the reference strain rate which is taken to be 10⁻⁵/s $T^{\ast }=\left(T-T_r\right)/\left(T_m-T_r\right)$, $T_r$ is the reference temperature, $T_m$ is the melt temperature, $\overline{\epsilon }$ is the equivalent plastic stain. The parameters of constitutive relation are shown in Table 3 (Wang et al., 2009). The equation of Gruneisen EOS can be expressed in the following form:

$P=\{\begin{array}{cc}\frac{{\rho }_0{C}^2\mu \left[1+\left(1-\frac{\gamma }{2}\right)\mu -\frac{a^2}{2}\mu \right]}{1-\left(S_1-1\right)\mu -S_2\frac{{\mu }^2}{\mu +1}-S_3\frac{{\mu }^3}{{\left(\mu +1\right)}^2}}& \mu \ge 0\\ {\rho }_0{C}^2\mu +\left(\gamma +a\mu \right)E& \mu <0\end{array}(3)$

where P is the pressure, E is the relative internal energy, ${\rho }_0$ is the initial density, C₀ is the intercept of the curve of v_s to v_p, S₁, S₂, S₃ are parameter of the curve of v_s to v_p, v_s and v_p are the velocities of shock wave and particles respectively. $\mu$ is the volume strain, $\gamma$ is the Gruneisen constant, a is the correction factor which is taken to be zero in this study. The parameters of EOS are listed in Table 4 (Li and Chen, 2001). Plastic kinematic model is used for tungsten alloy fragments and the parameters are listed in Table 5.

TABLE 3

TABLE 3. Constitutive properties for the G50 steel target and tungsten alloy spherical fragment.

TABLE 4

TABLE 4. Parameters of EOS for G50 steel target.

TABLE 5

TABLE 5. Material parameter for the tungsten alloy fragments.

The finite element model is shown in Figure 9A. According to the symmetry of the model, 1/2 3-D solid model was established. The mesh for the fragment consisted of 78,609 elements with an elements size of 0.25 mm. The diameter and thickness of G50 target plate are 80 and 40 mm. The mesh for the targets consisted of 1,389,216 hexahedral elements. The unit sized of 0.5 mm were used to mesh the model and the grids in the circular area with a radius of 40 mm near the impact point is locally encrypted with the unit sized of 0.25 mm. Symmetric constraints are applied on the plane of symmetry, and the boundary conditions are reinforced around the target plate.

FIGURE 9

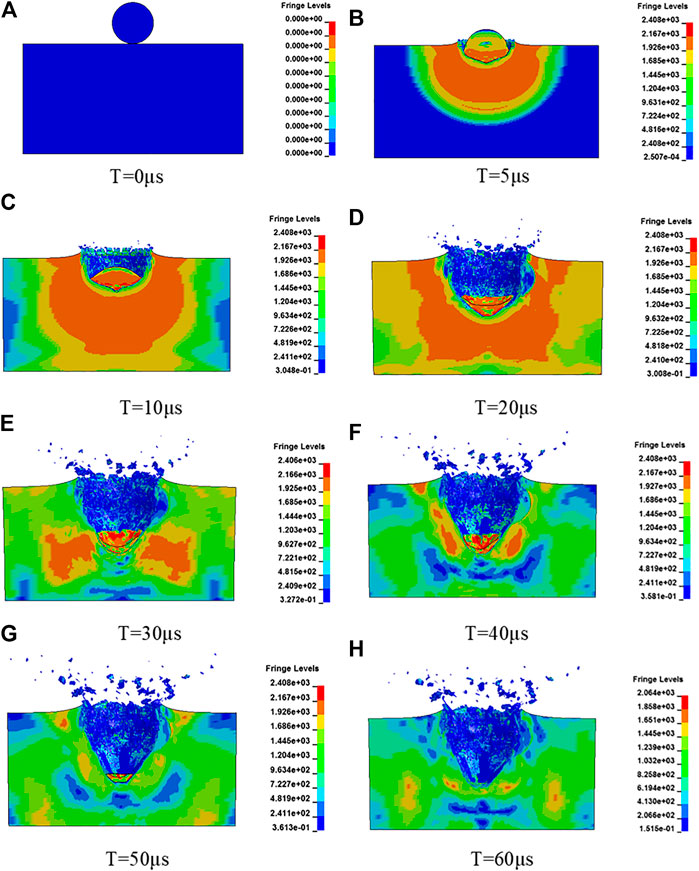
FIGURE 9. Schematic diagrams of penetration of tungsten sphere into G50 steel at the impact velocity of 1,800 m/s at different times. (A)T = 0 µs, (B)T = 5 µs, (C)T = 10 µs, (D)T = 20 µs, (E)T = 30 µs, (F)T = 40 µs, (G)T = 50 µs, and (H)T = 60 µs.

The depth of penetration predicted by present model is 27 mm which is in good agreement with experimental data. The crater volume predicted by numerical simulation is 14.5 cm³ approximately while the crater volume obtained by experiment is 19 cm³. It should be mentioned here that the crate volume obtained by experiments includes the volume in tensile spall area which is not included in numerical results. This may be the reason why the crater volume obtained by experiments is higher than that predicted by numerical simulations.

A sequence of six images at different time, illustrating the section view of the fragment penetrating into the G50 steel target at impact velocity of 1,800 m/s are shown in Figure 9. At the transient entrance phase, the fragment deforms and forms a conic-like head with hemi-spherical part behind. With the fragment being continuously eroded, the material of the hemi-spherical part of the fragment flows into the conic-like head and the erosion products of the fragment form debris which is ejected out of the crater until the hemi-spherical part is completed eroded. The conic-like craters formed due to the shape of the fragment’ head. It is noteworthy that the configuration of crater obtained by the numerical simulation is similar with the experimental observation, which verifies that the tungsten fragment falls into pieces during the penetration process.

Conclusion

G50 ultra-high strength steel, which has been widely used as warhead shell, is a low alloy steel without cobalt. The ballistic gun experiments of the G50 steel target struck normally by the tungsten alloy fragment at impact velocities ranging from 923 to 1,807 m/s has been conducted by using the commercially available software, LS-DYNA. The depth of penetration, crater volume and failure behaviors of G50 steel targets were obtained. The ballistic experimental results show that the crater is conic-like in the G50 steel target after struck by a tungsten alloy spherical fragment, which is different from that in the low strength steel target tests. It can be observed in the G50 steel target after impact that obvious layer cracks in the crimps of the crater surface and a raised lip on the front surface combined with spall produced by the tungsten alloy fragment. These phenomena mentioned above provide evidence that the tungsten fragment is eroded, sharpened and break into pieces during the penetration process. In addition, several tensile cracks are found in G50 steel targets, which are considered to be caused by tensile stress induced by the superposition of rarefaction at some local areas of the impacted interface.

Numerical simulations of the penetration of a tungsten alloy fragment into the G50 steel target were carried out to predict failure characteristics of the G50 target. It is noteworthy that the configuration of crater obtained by numerical simulations is similar with the experimental observations, which provide evidence that the tungsten fragment falls into pieces during the penetration process.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

HP and WS annotate and maintain research data for initial use. LuZ and LJ conduct investigation process and perform the experiments and data collection. FX is responsible for the research activity planning and execution. ZX performs the numerical simulations. LiZ and LuZ write the initial draft.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Nomenclature

Y yield strength
E elastic modulus
$\rho$ material density
u cavity surface expansion velocity
A, B, N parameters related to strain hardening relations in Johnson-Cook constitutive model
C parameter related to strain rate effect in Johnson-Cook constitutive model
M parameter related to temperature softening effect in Johnson-Cook constitutive model
T_melt melting temperature
P pressure
v_s velocities of shock wave
v_p velocities of particles
S₁, S₂, S₃ parameter of the curve of v_s to v_p
$\gamma$ Gruneisen constant
$\mu$ volume strain
${\sigma }_{\text{y}}$ _{yield stress}
E_t plastic modulus

References

Anderson, C. E., Hohler, R. V., and Walker, J. D. (1995). Time-resolved penetration of long rods into targets. Int. J. Impact Eng. 16 (1), 1–18. doi:10.1016/0734-743X(94)E0030-Y

CrossRef Full Text | Google Scholar

Anderson, C. E., and Walker, J. D. (1995). An analytic expression for P/L for WA long rods into armor steel. Shock Compress. Condens. Matter 14, 1135–1138. doi:10.1063/1.50782

CrossRef Full Text | Google Scholar

Atapek, S. (2013). Development of a new armor steel and its ballistic performance. Defence Sci. J. 63 (3), 271–277. doi:10.14429/dsj.63.1341

CrossRef Full Text | Google Scholar

Atapek, S., and Karagoz, S. (2010). Ballistic impact behaviour of a tempered bainitic steel against 7.62 mm armour piercing projectile. Defence Sci. J. 61 (1), 81–87. doi:10.14429/dsj.61.411

CrossRef Full Text | Google Scholar

Duan, Z. Q., Li, S. X., and Huang, D. W. (2003). Microstructures and adiabatic shear bands formed by ballistic impact in steels and tungsten alloy. Fatig. Fract. Eng. Mater. Struct. 26 (12), 1119–1126. doi:10.1046/j.1460-2695.2003.00705.x

CrossRef Full Text | Google Scholar

Forrestal, M. J., and Luk, V. K. (1988). Dynamic spherical cavity-expansion in a compressible elastic-plastic solid. J. Appl. Mech. 55, 275–279. doi:10.1115/1.3173672

CrossRef Full Text | Google Scholar

Hohler, V., and Stilp, A. J. (1977). “Penetration of steel and high density rods in semi-infinite targets,” in Proceedings of the 3rd International Symposium on ballistics. Karlsruhe, FRG, 23–25

Google Scholar

Li, K. H., and Chen, D. O. (2001). A constitutive model of materials under high temperature and pressure. Chin. J. High Press. Phys. 15 (1), 24–31. doi:10.1063/1.4850040

CrossRef Full Text | Google Scholar

Martineau, R. L., Prime, M. B., and Duffey, T. (2004). Penetration of HSLA-100 steel with tungsten carbide spheres at striking velocities between 0.8 and 2.5 km/s. Int. J. Impact Eng. 30 (5), 505–520. doi:10.1016/S0734-743X(03)00080-0

CrossRef Full Text | Google Scholar

Ponguru Senthil, P., Rama Subba Reddy, P., and Sreekantha Reddy, T. (2019). Scaled WHA long rod projectile impact against an armour steel. Human Fact. Mech. Eng. Def. Safe. 13, 33–39. doi:10.1007/s41314-019-0018-4

CrossRef Full Text | Google Scholar

Schaer, F. K., and Herrwerth, M. (2001). Shape effects in hypervelocity impact on semi-infinite metallic targets. Int. J. Impact Eng. 26, 699–711. doi:10.1016/s0734-743x(99)00141-4

CrossRef Full Text | Google Scholar

Wang, K. H., Zhang, Y., and Ming, L. (2009). Experimental research on the mechanical properties of G50 alloy steel. Acta Armamentarii 30 (S2), 247–250. doi:10.21236/ad0724289

CrossRef Full Text | Google Scholar

Wang, Q. T., Zhang, Q. M., Zhai, Z., and Liu, X. (2013). Character of carter for tungsten spheres with a high-velocity penetrating into a medium-thick steel plate. J. Vib. Shock 32 (23), 121–125. doi:10.1063/1.4914669

CrossRef Full Text | Google Scholar

Wu, X. (1999). Research on penetration theory and experiment of tungsten alloy spherical fragment against finite thickness target. PhD Thesis, Chinese. Beijing: Beijing institute of technology

Google Scholar

Zhang, Y., Li, J., Li, C., Kejian, L., Kessam, S., and Pengjun, C. (2019). Effect of heat treatment on mechanical properties of G50 ultra-high strength steel. Heat Treat. Metals. 1, 54–56. doi:10.5220/0007525300100014

CrossRef Full Text | Google Scholar

Zhao, X. X., Wang, S. S., and Xu, Y. X. (2015). Crater diameter calculation model of tungsten sphere impacting low carbon steel plate at high velocity. Trans. Beijing Inst. Technol. 35 (12), 1217–1221. doi:10.15918/j.tbit1001-0645.2015.12.002

CrossRef Full Text | Google Scholar