- 1College of Civil Engineering, Nanjing Forestry University, Nanjing, China
- 2School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu, China
To investigate the similarities and differences of mechanical behavior between the bamboo-concrete connections and the wood-concrete connections, thirty-six specimens were tested through push-out tests with the material type (bamboo or wood), concrete strength and dowel diameter as test parameters. In addition to the linear variable displacement transducer the digital image correlation was also used to obtain the slip distribution of the whole field of the specimens, which was conducive to the further detailed analysis of the slip distribution and a comprehensive understanding of the load-slip relationship. The results showed that the failure modes of the bamboo-concrete connections were similar to that of the wood-concrete connections, such as the concrete failure near the joint and the dowels bending in different degrees. The load-slip curves of the two kinds of connections were similar, which could be summarized as the elastic section, strengthening section and descending section. The shear stiffness and capacity of bamboo-concrete connections were higher than that of wood-concrete connections, and the shear capacity increased with the increase of dowel diameter and concrete strength. The slip distribution of the left and right sides of the specimen was basically identical. The load-transfer performance of the dowel was excellent. Finally, the prediction method of shear capacity and load-slip curve model of composite connections were proposed and verified to be effective.
Introduction
The bamboo/wood-concrete composite system usually consist of a bamboo/wood part in the tensile zone, a concrete layer in the compressive zone, and a connection between bamboo/wood and concrete. Thus, the mechanical properties of each material are used in efficient ways. Bamboo/wood-concrete composite system are used in bridges and buildings (Dias et al., 2016; Sebastian et al., 2016; Shan et al., 2017). Because of the low density and renewability of bamboo/wood, bamboo/wood-concrete composite system show several advantages over reinforced concrete structures, including better efficiency in terms of strength to self-weight ratio, and better seismic and environmental friendly performance (Shan et al., 2020).
At present, many countries are short of wood resources. The wood supply in many areas is insufficient, so it is necessary to find a renewable material with excellent mechanical properties to replace wood. It is feasible to develop engineered bamboo to realize more effective utilization of bamboo (Li et al., 2019), especially in the countries where bamboo resources are abundant (Tian et al., 2019). Among them, bamboo scrimber is the most widely used engineering bamboo at present. The material performance and preparation technology of bamboo scrimber had been investigated by many researchers. Yu et al. (2017) investigated the manufacturing process and basic properties of bamboo scrimber. Wei et al. (2016, 2018, 2020a, 2020c), Chen et al. (2020c) performed tests on the mechanical properties of bamboo scrimber, including axial tension, axial compression, eccentric compression and bending. Shangguan et al. (2015), Zhong et al. (2017) studied the compressive properties and bending properties of bamboo scrimber. Xu et al. (2017), Cui et al. (2018) tested the tensile properties at elevated temperatures and thermal performance of bamboo scrimber. It could be found from the current research results that the bamboo scrimber could meet the requirements of structural materials.
However, the serviceability limit of flexural members is determined by deformation rather than strength in most cases. The bamboo flexural members have the defects of insufficient bearing capacity, low section stiffness, and insufficient spanning capacity (Chen et al., 2020a; Chen et al., 2020b; Wei et al., 2020b), which is similar to the wood flexural members. To enhance the flexural performance, the wood-concrete composite structure was proposed. For this structure, the performance of shear connections plays an important role in the composite effect of composite structure. Auclair et al. (2016) found the ductility and the performance of the wood-concrete beams could be improved by changing the concrete shell diameter and steel core diameter of connectors. Martins et al. (2016) developed a wood-concrete composite component for the floor. Three connection systems were tested. In the push-out test, the connection with dowel connectors was the best. Sebastian et al. (2016) tested the wood–concrete composite beams with different screw thread connectors. The beams with fully threaded screw connectors presented an excellent ductility, and the beams with partially threaded screw connections exhibited a good bearing capacity. Jiang et al. (2017) studied the early behavior of shear connections with screw. The results showed that the strength and stiffness of screw connections increase rapidly in the first seven days. Khorsandnia et al. (2018) studied the numerical models for the analysis of the wood-concrete composite beams with panelised reinforced concrete slabs.
Based on the reference of wood-concrete composite structure, bamboo-concrete composite (BCC) structure was proposed. Due to the obvious differences between bamboo and wood in fiber structure, manufacturing technology and mechanical properties, etc., it was not appropriate to apply the research results of wood-concrete composite structure indiscriminately to bamboo-concrete composite structure. Wei et al. (2017b, 2017c), Wang et al. (2020) had carried out the four-point bending tests and push-out test on two types of BCC structures with different connections. The results indicated that two connections showed a remarkable bearing capacity and the ductility of the perforated plate shear connections was larger. Shan et al. (2017) conducted the push-out test on six types of connections for glubam-concrete composite beams, and four kinds of connectors suitable for BCC structure are recommended. Shan et al. (2020) carried out short-term bending tests on glued laminated bamboo and concrete composite beams. Four-point bending tests were conducted on nine full-scale BCC beams with four types of connectors. All BCC beams showed excellent behavior and the 200 mm long notch connection exhibited higher bearing capacity. With the development of various engineering materials (Ding et al., 2018; Zhang et al., 2018), fiber reinforced polymer had been widely used in the reinforcement of structural members (Wei et al., 2017a; Ding et al., 2019; Zhang et al., 2020). Wei et al. (2014) presented a new fiber reinforced polymer-bamboo-concrete composite structure. The bearing capacity and section rigidity were significantly improved. The mechanical properties of the novel composite beams were intermediate between the full-composite and non-composite.
However, the similarities and differences of mechanical properties of bamboo-concrete and wood-concrete shear connections are rarely studied. Therefore, a series of bamboo-concrete specimens and wood-concrete specimens were tested under static push-out loading in this paper. Except for the material (bamboo or wood), other parameter the two kinds of specimens were set in the same and symmetric way. The interface slip was measured by the digital image correlation (DIC) and the linear variable displacement transducer (LVDT). The failure modes, load-slip relationship, shear stiffness, shear capacity, and slip distribution were discussed.
Materials and Methods
Materials
Bamboo and Wood
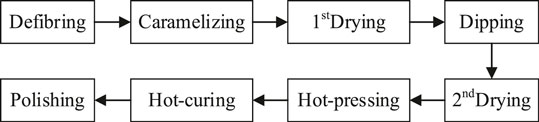
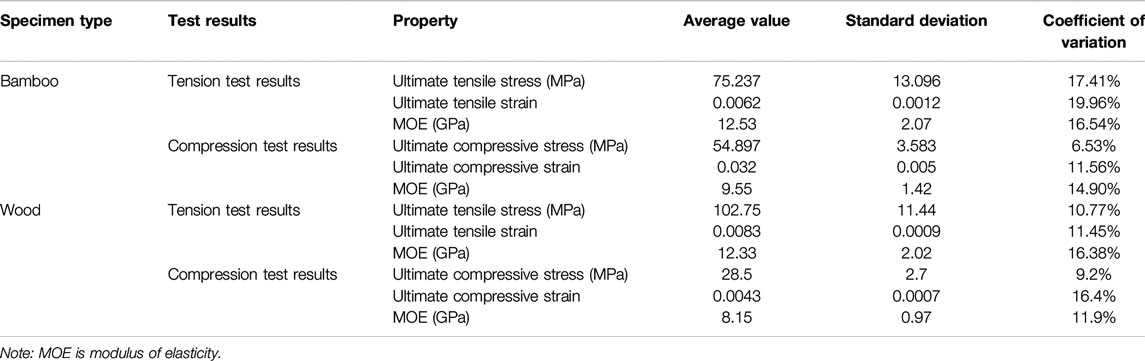
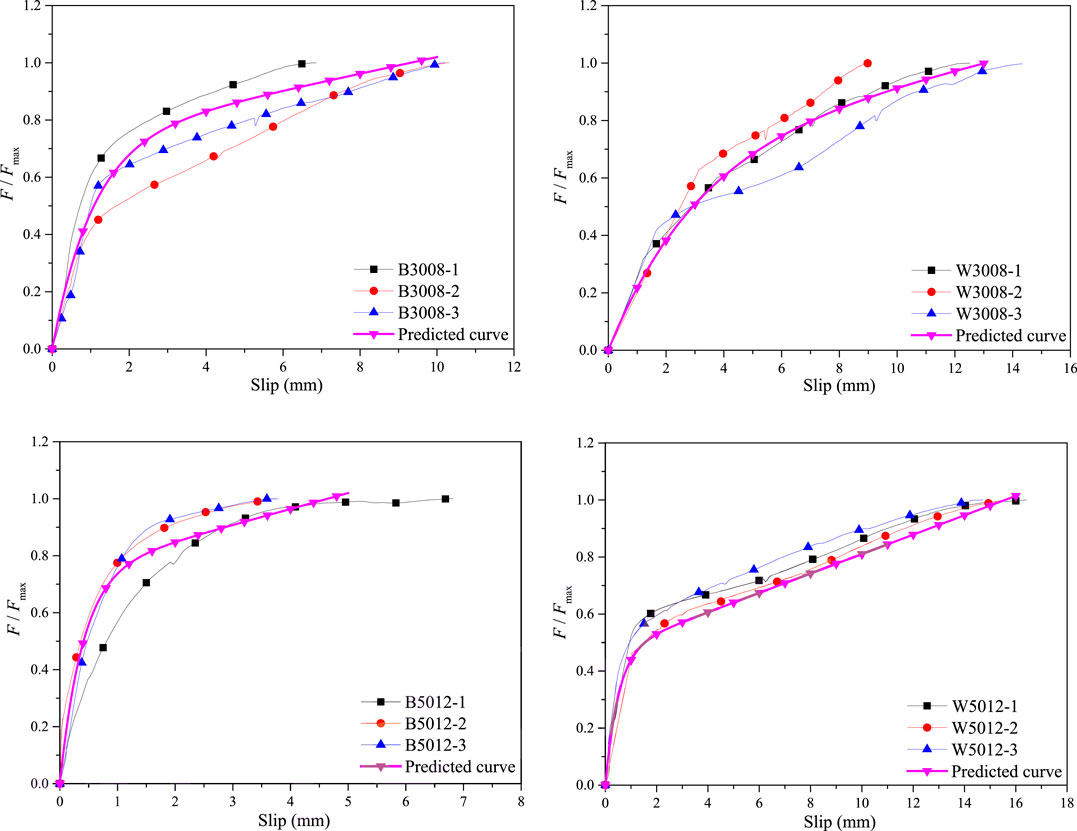
Bamboo scrimber used in this test is made up of bamboo fibers that had been dried, impregnated, and pressed under high pressure and high temperature conditions. The key manufacturing process is shown in Figure 1. In this test, the impregnation rate of adhesive is about 5% of the dry weight of bamboo fibers, the average density is 1,100 kg/m3, and the moisture content is between 6.0% and 8.0%. According to ASTM D143-09 (ASTM International, 2009), 10 tensile specimens (25 × 10 × 455 mm, TB-1 to TB-10) and 10 compressive specimens (50 × 50 × 150 mm, CB-1 to CB-10) were tested for the mechanical properties of bamboo scrimber. The test setup, stress-strain curves, and mechanical properties of the bamboo specimens are shown in Figures 2 and 3 and Table 1, respectively.

FIGURE 2. Specimens of bamboo scrimber and wood. (A) Tension specimen size (units: mm). (B) Tension specimen of bamboo scrimber. (C) Tensile specimens of wood. (D) Compression specimen of bamboo scrimber. (E) Compression specimens of wood.
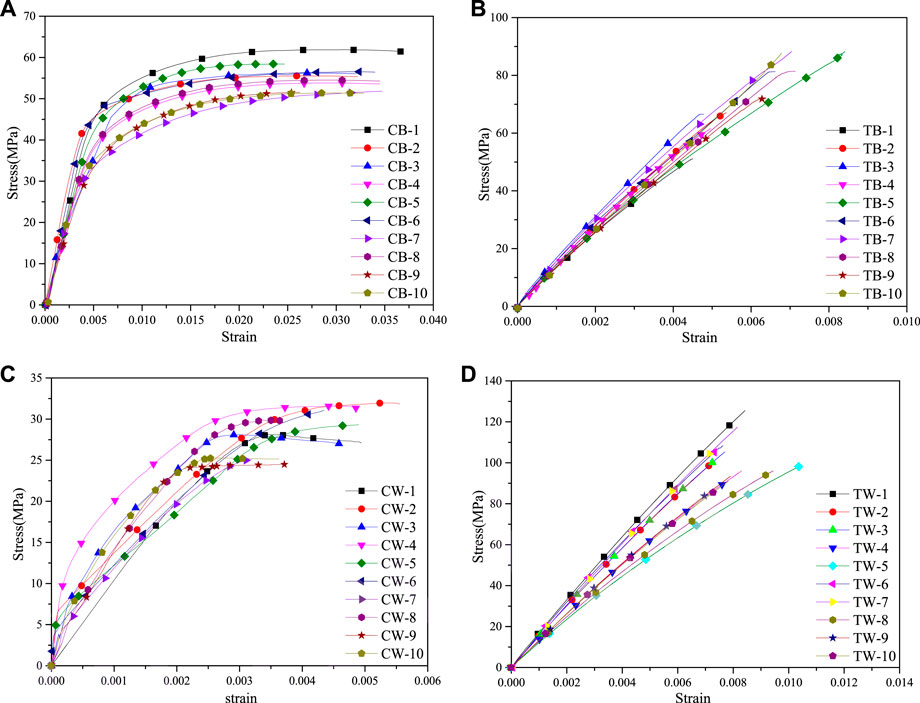
FIGURE 3. Stress-strain curves of specimens. (A) Bamboo scrimber compression specimens. (B) Bamboo scrimber tensile specimens. (C) Wood compression specimens. (D) Wood tensile specimens.
The wood used in this test was made of pinus sylvestris, which is a kind of popular timber. The number, size, and test method of wood tensile specimens (TW-1 to TW-10) and compressive specimens (CW-1 to CW-10) were the same as that of the bamboo scrimber specimens. The test setup, stress-strain relationship, and mechanical properties of the wood specimens are shown in Figures 2 and 3 and Table 1, respectively.
Concrete
Two kinds of concrete with different strength were used in this test. Three cylinders (φ150 × 300 mm) of C30 and C50 were tested. The average compressive strength and modulus of elasticity of C30 were 34.7 MPa and 33.3 GPa, respectively. The average compressive strength and modulus of elasticity of C50 were 58.0 MPa and 37.3 GPa, respectively.
Dowel
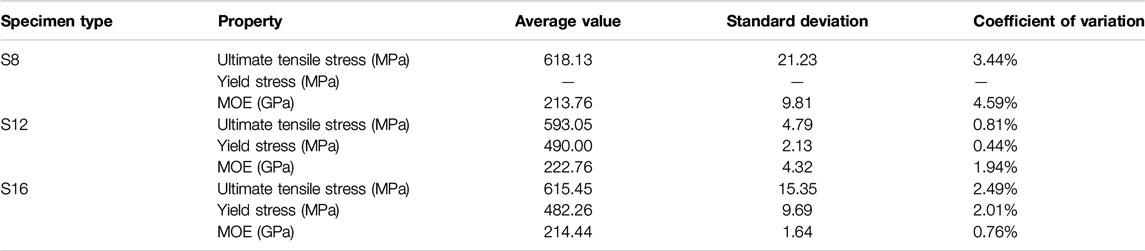
The dowels used in this experiment were ribbed steel bars with 8, 12, and 16 mm in diameter. Three bars of each diameter were selected for the tensile test. The average strength of dowel tensile specimens was shown in Table 2.
Adhesives
The adhesive used in this test was the epoxy resin adhesive, which was mainly used for the connection between dowel and bamboo (wood) hole. Its main function was to ensure the stress transfer and avoid sliding friction between them. According to the manufacturer’s statement, the average tension strength, modulus of elasticity, and ultimate tensile strain of the epoxy resin adhesives were 67.7 MPa, 2.9 GPa, and 0.029, respectively.
Specimen Preparation
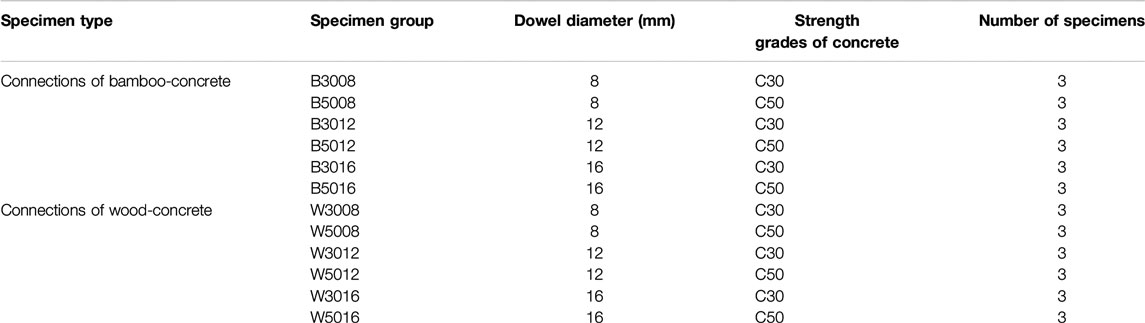
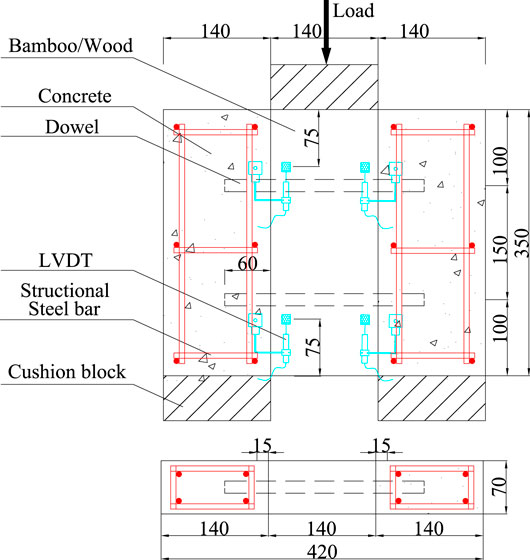
Eighteen bamboo-concrete connections and 18 wood-concrete connections were processed with the material type (bamboo or wood), concrete strength and dowel diameter as test parameters in this experiment. Table 3 listed the details of these specimens. The number of specimen is based on the principle of material + concrete strength + dowel diameter, B represents bamboo, W represents wood, for example, B3008 represents BCC structure, in which the concrete strength grade is C30 and dowel diameter is 8 mm. Additionally, the number “- 1/2/3” referred to the three specimens with the same sizes in each group. As shown in Figure 4, the specimens consists of two concrete blocks (140 × 350 × 70 mm) and one bamboo (wood) block (140 × 350 × 70 mm). The bamboo (wood) block was located in the middle of the specimen, the concrete blocks were arranged on both sides connected. The dowel passed through the reserved hole of the bamboo (wood) block, extending 60 mm into concrete blocks both sides, respectively. The concrete is strengthened by the 8 mm diameter constructional steel bars in the direction of length, width, and height.
Push-Out Test
A 3,000 kN hydraulic actuator was used in the push-out tests. After pre-loading (510 kN load) to eliminate the influence of specimen clearance, the test was started with the loading speed of 0.2 mm/min. When the specimen approached failure, the loading speed changed to 0.5 mm/min. The details of test setup were illustrated in Figure 4. The interface slip between the concrete block and the bamboo block was measured by two methods. The first method was the LVDT. Four displacement meters were fixed on the concrete blocks near the interface, and the measuring rods were fixed at the same level on the bamboo block near the interface (Figure 5). The second method was the DIC. After the surface of the specimen was polished and cleaned, uniformly distributed spots are set up for camera recognition. After equipment calibration, two image collectors were used to continuously collect the deformation images of the specimens during the entire test process (Figure 6). In the test, the acquisition frequency of LVDT was the same as that of DIC, and the data was collected once every 3 s. After the pre-loading was completed, LVDT and DIC started to collect at the same time.

FIGURE 6. Digital image correlation measurement. (A) Optical imaging system. (B) Calibration before collection of data.
Test Results and Discussion
Observations and Failure Modes
Figure 7 shows the failure modes of the wood-concrete composite connections. When the load approached 70–85% ultimate capacity, the diagonal crack occurred in the concrete block near the interface. When load increased up to the ultimate load, there were many cracks and even spalling of the concrete surface. Subsequently, the load dropped continuously and slowly until the end of the test. When the load value dropped to about 35% ultimate capacity, the concrete blocks on both sides were destroyed along the cracks.

FIGURE 7. Typical failure mode of wood-concrete connection. (A) Cracks on the concrete surface. (B) Concrete failure and dowel bending at joint. (C) Large area failure of concrete. (D) Wood holes deformation. (E) Bending mode.
Figure 8 shows the failure modes of the bamboo-concrete composite connections. The cracks began to appear on concrete block near the joint under 60–80% ultimate load, and the cracks expanded around as the load increases. When load reached up to the ultimate load, the concrete near the dowels were destroyed, which caused the load value to drop rapidly. When the load value dropped to about 30% ultimate load, the concrete blocks on both sides were failed.
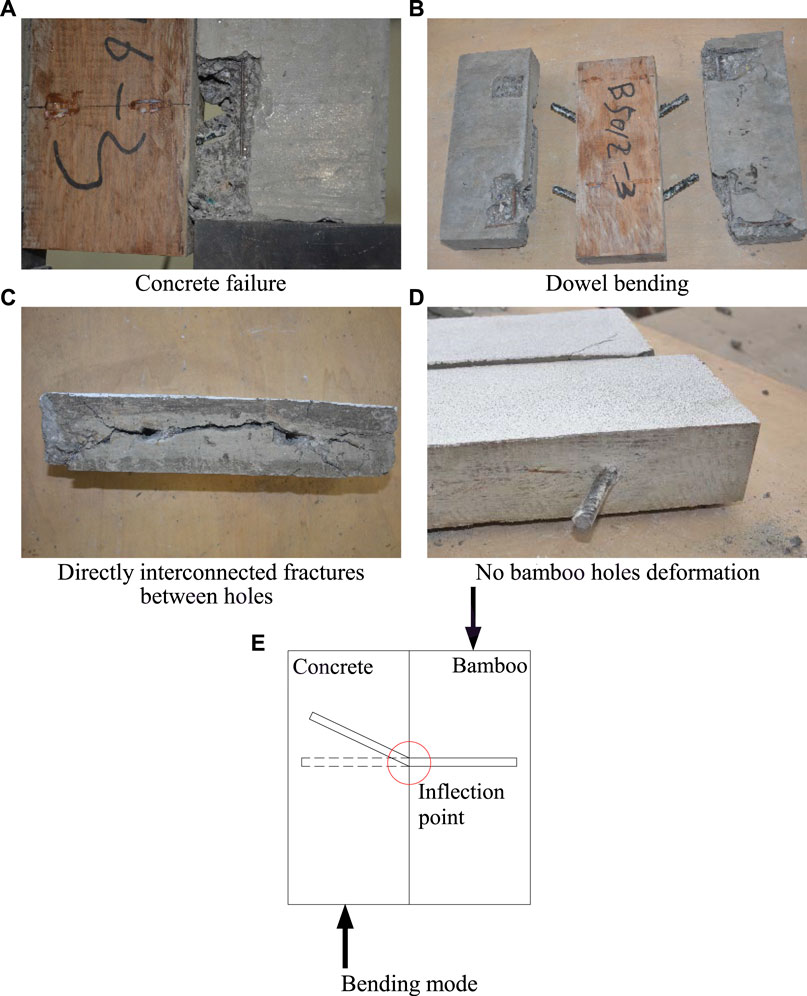
FIGURE 8. Typical failure mode of bamboo-concrete connection. (A) Concrete failure. (B) Dowel bending. (C) Directly interconnected fractures between holes. (D) No bamboo holes deformation. (E) Bending mode.
To sum up, the failure modes of the wood-concrete composite connections and bamboo-concrete composite connections were not significantly different, which could be defined as the moderate failure considering that the specimens had large plastic deformation after the ultimate load. After testing, the concrete slab was carefully removed, the directly interconnected fractures between the dowel holes and the dowels bending to different degrees could be found. The difference was that the wood holes were deformed while the bamboo holes were not, which could intuitively reflect the reason for the different shear stiffness and shear capacity of two kinds of specimens. Compared with wood, the higher strength of bamboo led to the different position of the inflection point of dowels.
Load-Slip Curves
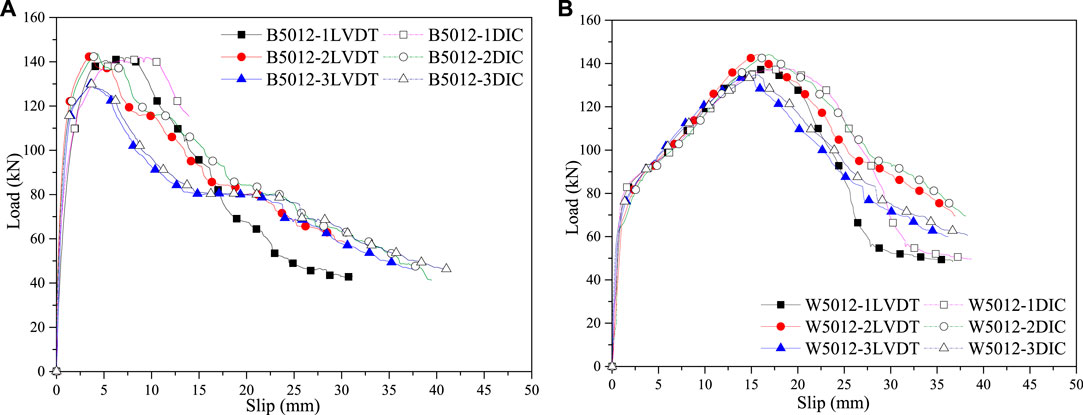
As showed in Figure 9, the load-slip curves of the two kinds of connections were similar, which could be summarized as the elastic section, strengthening section and descending section. The load-slip curves were basically linear at the first elastic section (0–60% ultimate load). The load-slip curves were nonlinear, and the increasing rates of the interface slip were obviously accelerated at the second strengthening section (60–100% ultimate load). At the third descending section, the load dropped and the slip increased continuously until the end of the test.
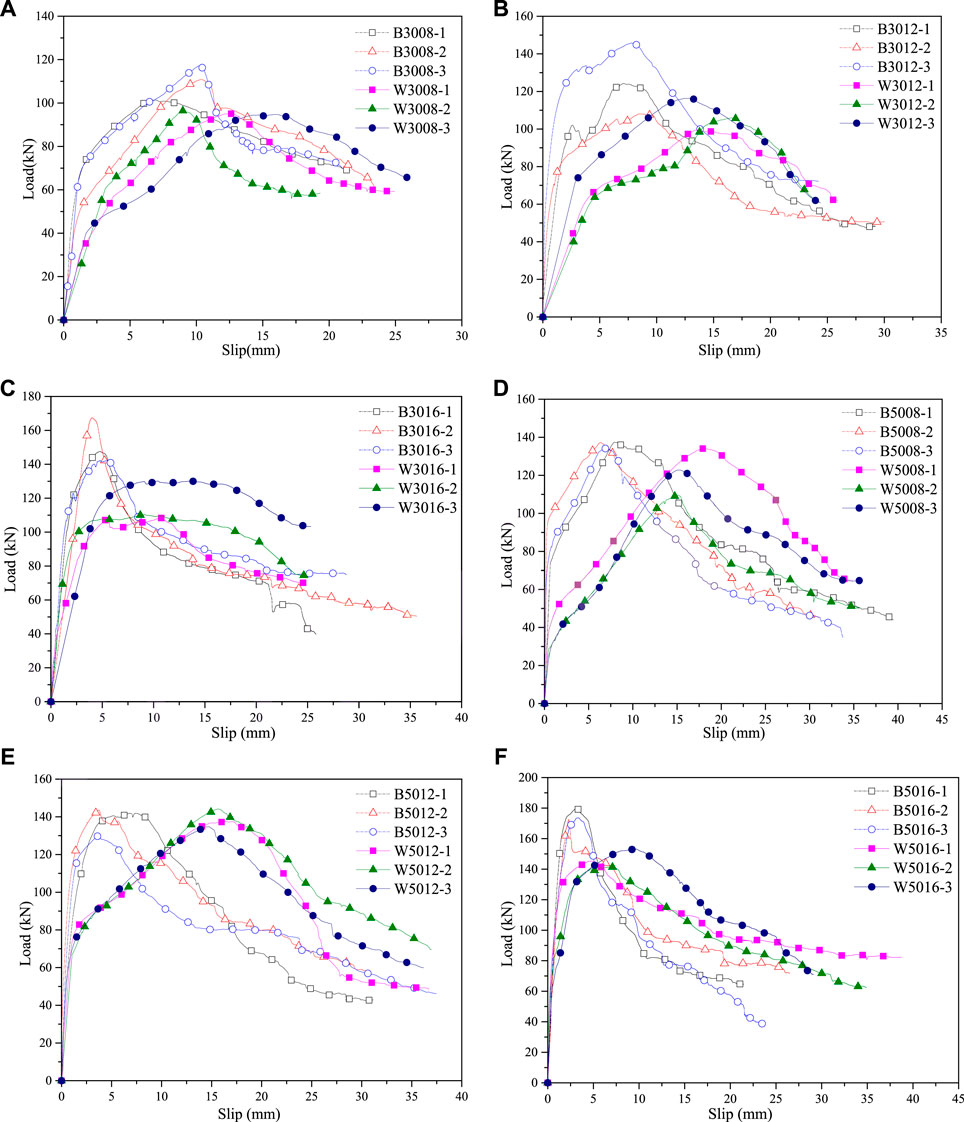
FIGURE 9. Comparison of load-slip curves of bamboo-concrete and wood-concrete connections. (A) 3008, (B) 3012, (C) 3016, (D) 5008, (E) 5012, and (F) 5016.
Besides, it could be found that the slip values corresponding to the ultimate load of wood-concrete specimens were larger than those of bamboo-concrete specimens. After passing the ultimate load point, the curves of bamboo-concrete specimens decreased rapidly, while the curves of wood-concrete specimens decreased slowly. The slip corresponding to the ultimate load decreased with the dowel diameter increase.
To verify the reliability of the measurement results based on DIC, B5012 group, and W5012 group were selected for comparison. The load-slip curves are shown in Figure 10. It could be seen that the LVDT results were basically the same as the DIC results.
Shear Stiffness
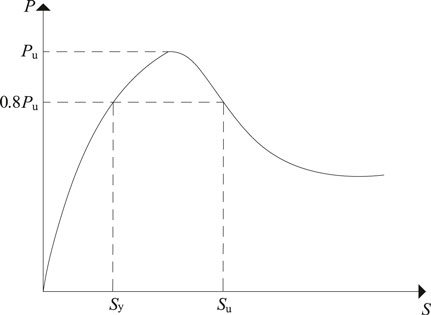
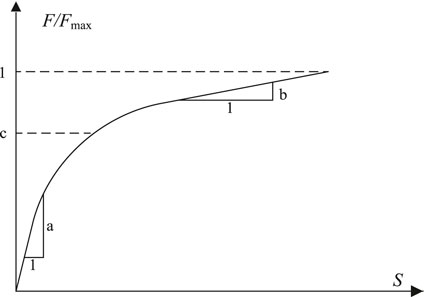
According to Eurocode 5 (European Union, 2006), the shear stiffness K (Eq. 1) and the ductility coefficient D (Eq. 2) were calculated, respectively. The Ductility coefficient model is shown in Figure 11.
where p is the load value, kN; Pu is the ultimate load, kN; S is the slip value, mm; Su and Sy are the slip value corresponding the different load as showed in Figure 11, mm.
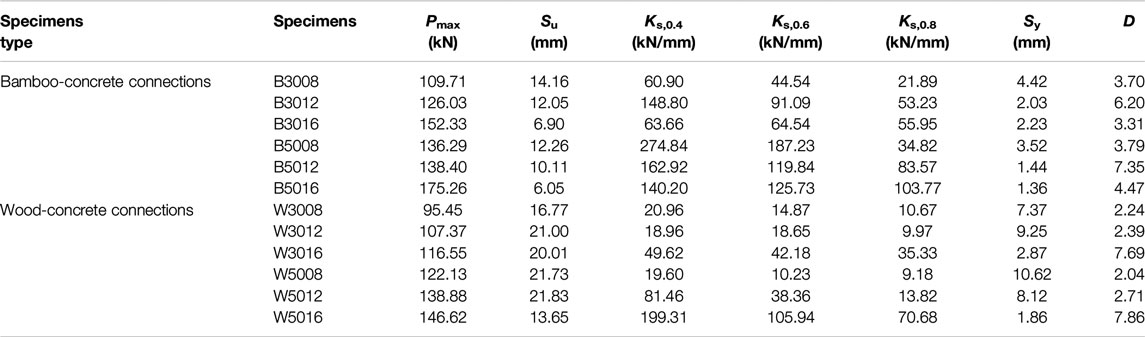
The results of the stiffness and ductility of all specimens are shown in Table 4, and the data are the average values of each group of specimens. The following findings could be obtained from the table. The values of Ks,0.4, Ks,0.6 and Ks,0.8 of all specimens showed a decreasing trend in general. The shear stiffness of bamboo-concrete connections were more than 19% higher than that of wood-concrete connections. According to the second section of this paper, the compressive strength and modulus of elasticity of bamboo are 1.93 and 1.17 times of that of wood. The different mechanical properties of two kinds of materials led to the difference of the stiffness and ductility of composite connections. The ductility of the bamboo-concrete specimens with 12 mm diameter dowels and the wood-concrete specimens with 16 mm diameter dowels was the best among all specimens. The increase of concrete strength could improve the stiffness of all specimens, but the change of concrete strength had little effect on the ductility of all specimens.
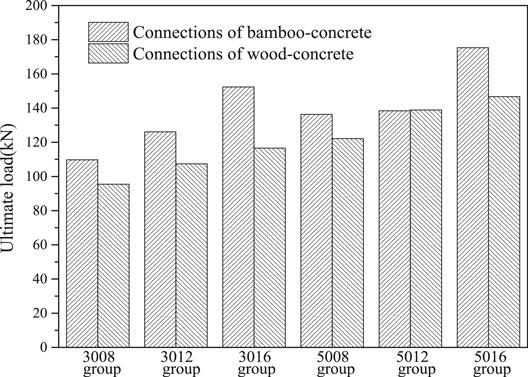
Shear Capacity
The average value of ultimate shear capacity of each group of specimens was showed in Figure 12. The ultimate capacity of bamboo-concrete specimens was up to 31% larger than that of wood-concrete specimens at most. The main reason could be considered that the higher strength of bamboo resulted in the higher shear capacity of bamboo-concrete connections. The ultimate shear capacity increased with the increase of dowel diameter and concrete strength.
Slip Distribution
The distribution of relative slip could not be obtained by LVDT, which could get only a limited number of relative slip values at the designated positions. The relative slip values between bamboo/wood and concrete at all positions of the specimen could be obtained by DIC. Base on DIC, the displacement of the whole field is shown in Figure 13A. Considering that the height of the specimen was 350 mm, as shown in Figure 13B, thirteen points (vertical spacing 25 mm) were selected along the height of the specimen on both sides of the interface. The difference value of displacement between two points in parallel position were calculated to represent the relative slip value.
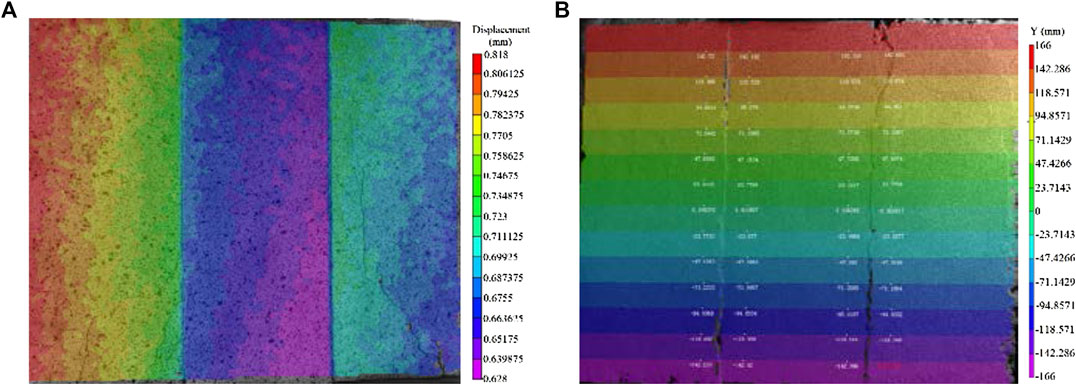
FIGURE 13. Test results and post-processing methods based on digital image correlation. (A) The cloud picture of slip. (B) Selection of analysis points near the interface.
The variation of slip along the specimens height on both sides of the interface was analyzed. The slip distributions of bamboo-concrete specimens under the test loads of 40, 60, 80, 100, 120, and 140 kN are shown in Figure 14. The slip distributions of wood-concrete specimens under the test loads of 40, 60, 80, 100, and 120 kN are shown in Figure 15.
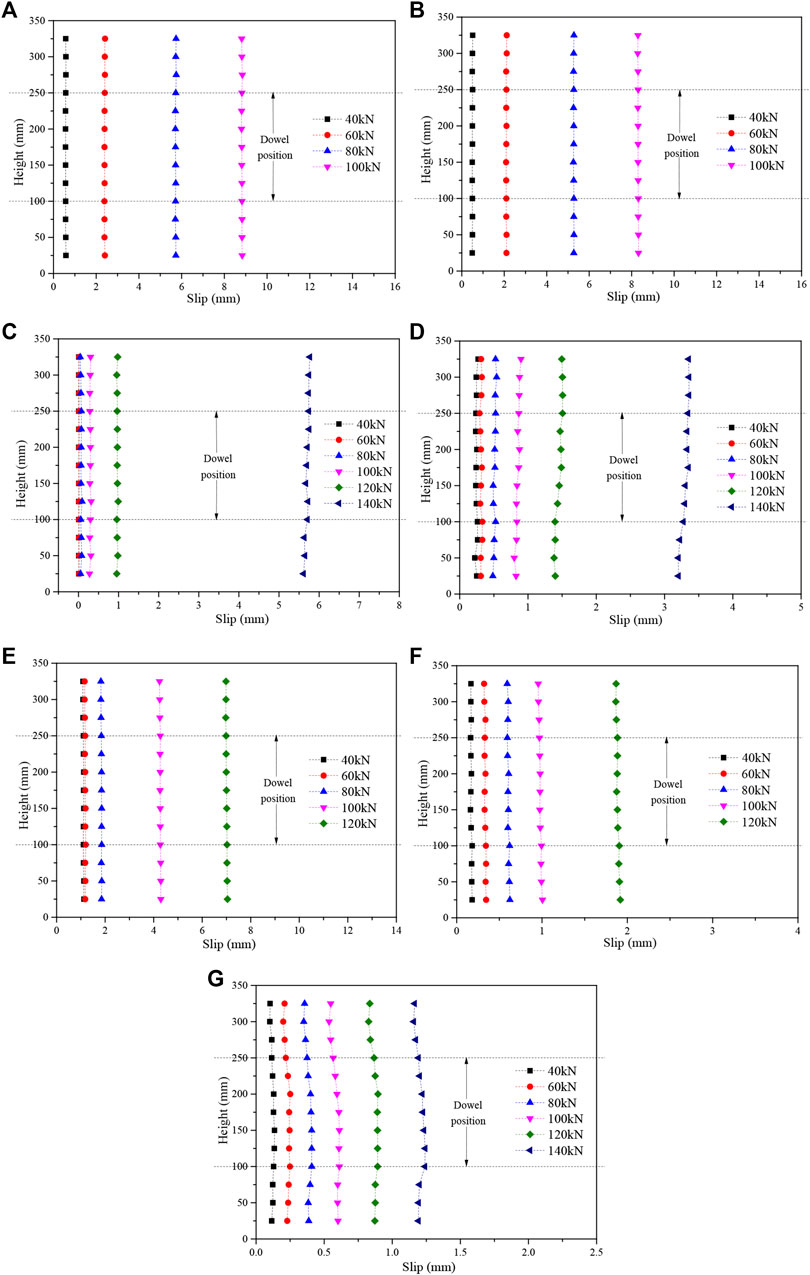
FIGURE 14. The curves of the slip of bamboo-concrete specimens along interface height. (A) B3008-2 left, (B) B3008-2 right, (C) B3012-3 right, (D) B3016-1 right, (E) B5008-1 right, (F) B5012-3 right, (G) B5016-2 right.
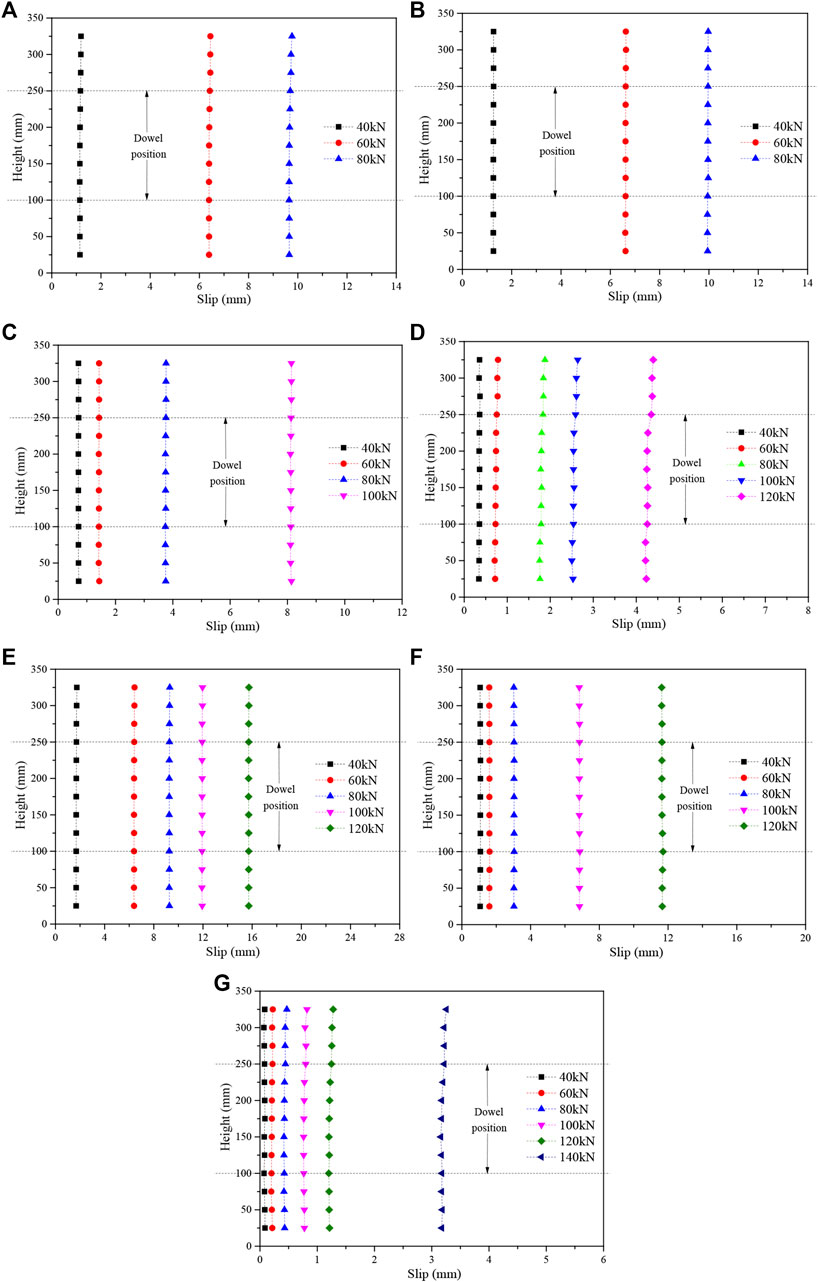
FIGURE 15. The curves of slip of wood-concrete specimens along interface height. (A) W3008-3 left, (B) W3008-3 right, (C) W3012-3 right, (D) W3016-2 right, (E) W5008-3 right, (F) W5012-2 right, (G) W5016-1 right.
Combined with Figures 14 and 15, the summary was as follows. The distribution of the slip of the wood-concrete specimens and the bamboo-concrete specimens was similar. The relative slip values of the left and right sides of the specimen were basically identical, indicating that there was no visible offset load in the testing process. The line connecting 13 points at different heights was basically a straight line, which means that the force transmission was stable without sudden change. At the later stage of the test, there was a higher increase amplitude of the slip with the same load increment, which indicated a decrease in shear stiffness of composite specimens. The slip decreased with the increase of the dowel diameter and the concrete strength grade.
Theoretical Analysis
Shear Capacity
In reference to the calculation equation of shear capacity of the steel-concrete composite structure and wood-concrete composite structure, this paper attempted to find a suitable analytical methodologies of shear capacity of the bamboo/wood-concrete composite connections.
Ceccotti Model
Ceccotti (2002) proposed that the shear strength of the wood-concrete system should be analyzed according to three modes: the failure of the timber side (Eq. 3), the failure of the dowel (Eq. 4), and the concrete side (Eq. 5), and the minimum of the three values should be taken as the shear capacity of the connection.
where, Q is the shear capacity of the single dowel, N; As is section area of the dowel, mm2; fu is the ultimate tensile strength of dowel, MPa; γv is the safety factor, generally γv = 1.25; d is the dowel diameter, mm; fh is compression strength of wood parallel to the grain, MPa; fck is the compressive strength of concrete cylinder, MPa; Ec is the elastic modulus of concrete, MPa; My is the moment value corresponding to the formation of plastic hinges of the dowel, It could be calculated according to Eq. 6.
Saulius Model
Saulius et al. (2007) proposed that there were three failure modes of the wood-concrete connection: hingeless yield mode (Eq. 7), single hinge yield mode (Eq. 8), and double hinge yield mode (Eq. 9), as shown in Figure 16.
1. Calculation equation of shear capacity of dowel in hingeless yield mode:
2. Calculation equation of shear capacity of dowel in single hinge yield mode:
3. Calculation equation of shear capacity of dowel in double hinge yield mode:
where, Q is the shear capacity of the single dowel, N; lE is the length of the dowel into the wood, mm; d is the dowel diameter, mm; fh is compression strength of wood parallel to the grain, MPa; My is the moment value corresponding to the dowel plastic hinge formation.
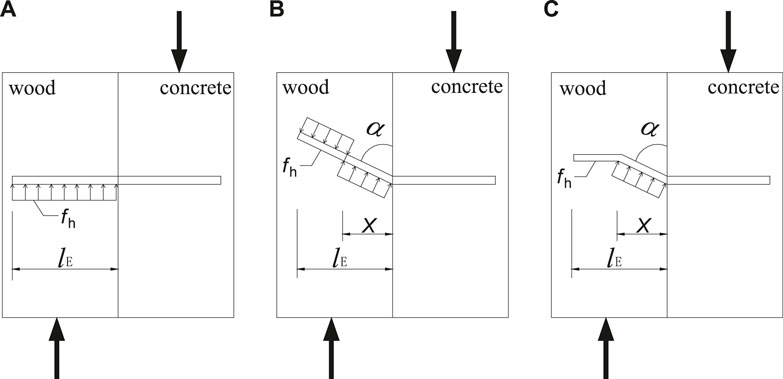
FIGURE 16. Stress analysis of three yield modes. (A) Hingless yield mode, (B) single hinge yield mode, and (C) double hinge yield mode.
The bending angle of the dowel was small in this test. So α was larger, which was greater than 80°, sinα was approximately 1. So the shear capacity under the three yield modes could be expressed as Eq. 10.
European Code
According to Eurocode 4 (European Union, 2006), the shear capacity of the steel-concrete composite system was the smaller of the two values calculated by Eqs. 11 and 12.
where, α is the influence coefficient of dowel length, when 3 ≤ h/d ≤ 4, a = 0.2 [(h/d + 1)] ≤ 1.0, when h/d ≥ 4, α = 1; As is section area of the dowel, mm2; fu is the ultimate tensile strength of dowel, MPa; γv is the partial safety factor, generally γv = 1.25; d is the dowel diameter, mm; fck is the standard compressive strength of concrete cylinder, MPa; Ec is the elastic modulus of concrete, MPa.
Chinese Code
The influence of the minimum tensile strength and yield value of the dowel is further considered in the Chinese Code GB50017-2013 (Chinese Committee for Standardization, 2013). The shear capacity could be calculated by Eq. 13.
where, As is section area of the dowel, mm2; fc is the standard compressive strength of concrete cube, MPa; Ec is the elastic modulus of concrete, MPa; γ is the ratio of the minimum tensile strength to the yield strength of the dowel; f is the design value of dowel tensile strength, MPa.
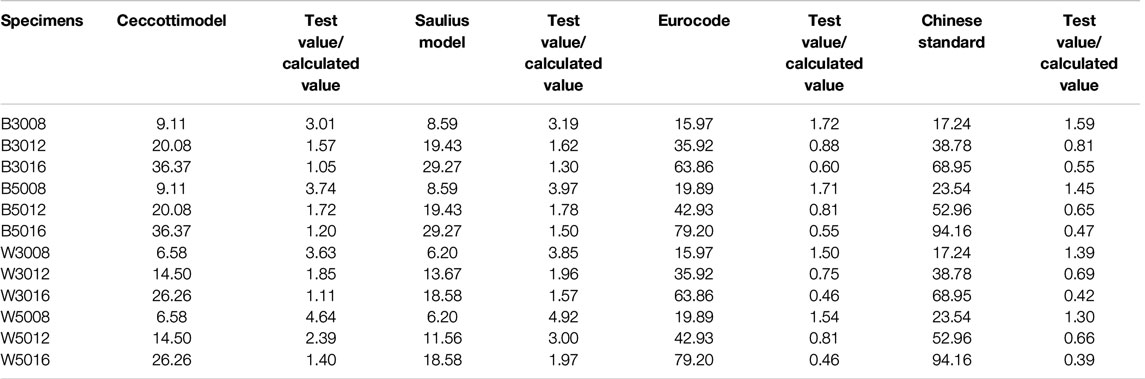
In this test, two dowels passed through the reserved hole of the bamboo/wood block and formed four shear connectors with the concrete blocks. To divide the test load by four to get the shear capacity of a single connector. The actual shear capacity and theoretical shear capacity of all specimens were showed in Table 5.
It could be found from the table that increasing the dowel diameter could improve the shear capacity of the specimens according to the theoretical calculation. In contrast, the shear capacity changed little with the dowel diameter according in the test. Through preliminary analysis, the reasons for the differences could be summarized as follows.
The influence of dowel bending in the wood was considered, but the influence of concrete strength was not considered in the theoretical equation of wood-concrete connection. The influence of concrete strength was considered, but steel strength was not considered in the theoretical equation of the steel-concrete connection. In general, Saulius model was more in line with the actual failure mode of this paper. In this paper, it was suggested that the ratio (fc/fh) of compressive strength of concrete to that of bamboo/wood should be added as a parameter, and it was suggested to add the revised parameters α, β to modify the Saulius model.
My could be calculated according to the Eq. 15.
By using mathematical statistics method to fit the results of each specimen, it could be concluded that α1 = 1.5, β1 = 0.5; α2 = 3, β2 = 0.4. The revised equation was as follows.
where, Q is the shear capacity of the single dowel, N; fu is the ultimate tensile strength of dowel, MPa; d is the dowel diameter, mm; lE is the dowel length into bamboo (wood), mm; fh is the compression strength of bamboo (wood) parallel to the grain, MPa; fc is the standard compressive strength of concrete cube, MPa.
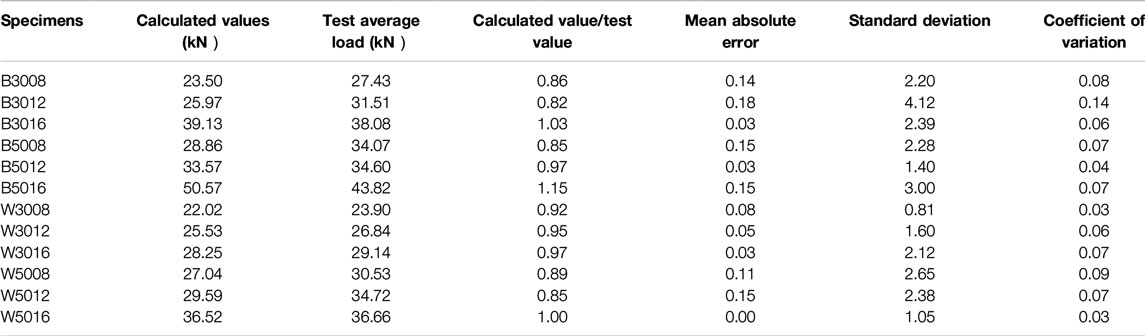
The shear capacity of the specimens was calculated by the above Eq. 16 and compared with the test value. As provided in Table 6, there was a good correlation between the test values and the values calculated by the revised equation. The result also proved the necessity of considering the influence of concrete compressive strength in the calculation of shear capacity.
Load-Slip Curves
Dias (2012) used a three-parameter model to describe the rising segment of the load-slip curves of wood-concrete connections, as shown in Figure 17 and Eq. 17. In this paper, the model was proposed to describe the upward section of the load-slip curve of the bamboo-concrete connections.
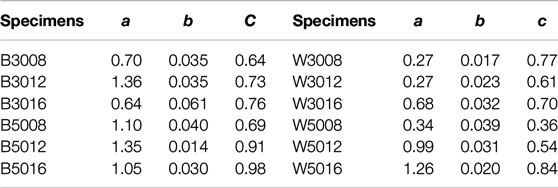
where, a, b, c are the parameters, s is the slip, F is the load, Fmax is the ultimate load. The values of a, b, and c of all specimens were fitted by mathematical software. The results were shown in Table 7.
After analyzing the results, it was suggested to take values of a, b, and c according to the following Eqs. 18–20.
where, Ks,0.4 and Ks,0.6 are the secant slip modulus at the 40% and 60% of the ultimate shear capacity, respectively. sest is the slip value corresponding to the ultimate load.
According to the above Eqs. 18–20 the values of a, b, and c of all specimens were calculated, then the results were brought into Eq. 17 for further calculation. It could be found that the prediction curve was more consistent with the actual test curve. Groups 3,008 and 5,012 were representatives, as shown in Figure 18. The predicted curves were consistent with the test curves. It was verified that this method could better express the load-slip relationship of this test. Therefore, the proposed model (Eq. 17) can better express the load-slip relationship of this type of bamboo/wood-concrete connection.
Conclusions
This paper reports an experimental research on the bamboo-concrete connections and the wood-concrete connections to study the similarities and differences of mechanical properties between them. The interface slip of the specimens was measured by the LVDT and the DIC. The failure mode, the load-slip relationship, the shear stiffness, the shear capacity and the slip distribution of the specimens were studied. The following conclusions could be drawn:
1. The failure modes of bamboo-concrete connections were similar to that of wood-concrete connections, which could be defined as the moderate failure considering that the specimens had large plastic deformation after the ultimate load. The concrete surface of the specimens was cracked seriously or even peeled off locally. The directly interconnected fractures between the dowel holes and the dowels bending to different degrees could be found. The difference was that the wood holes were deformed, while no bamboo holes deformation.
2. The load-slip curves of wood-concrete specimens and bamboo-concrete specimens were similar, which could be summarized as elastic section, strengthening section and descending section. The shear stiffness of bamboo-concrete connections were more than 19% higher than that of wood-concrete connections. With the increase of concrete strength, the shear stiffness of the specimen increased and the deflection of the specimen changed little. The ultimate capacity of bamboo-concrete specimens was up to 31% larger than that of wood-concrete specimens at most. The ultimate shear capacity increased with the increase of dowel diameter and concrete strength. The different strength and modulus of elasticity of two kinds of materials led to the difference of the mechanical properties of composite connections.
3. According to the data measured by DIC, it could be found that the slip distribution of the wood-concrete specimens and the bamboo-concrete specimens was similar. The relative slip values of the left and right sides of the specimen were basically identical, indicating that there was no visible offset load in the testing process. The line connecting points at different heights was basically a straight line, which means that the force transmission was stable without sudden change.
4. Revised parameters α, β and the ratio (fc/fh) were added to revise the Saulius model to predict the shear capacity for the bamboo (wood)-concrete connections, and the modified model could provide satisfactory calculating results. Based on Dias model, a new model was proposed to describe the rising segment of the load-slip curves of the bamboo (wood)-concrete connection, and the predicted curves were consistent with the test curves.
Data Availability Statement
All datasets generated for this study are included in the article/Supplementary Material.
Author Contributions
ZW contributed to the analysis of the data and discussion of the obtained results and was a major contributor in writing the manuscript. YW contributed to the design of this analysis study. JJ and KZha contributed to the examination of all of the tests. KZhe contributed to the verification of data. All authors contributed to the article and approved the submitted version.
Funding
The authors acknowledge the contribution of the Natural Science Foundation of China (51778300, 51208262); the Natural Science Foundation (BK20191390), Key Research and Development Project (BE2020703) and “Qinglan Project” of Jiangsu Province, China; the “Six talent peaks project” in Jiangsu Province (JZ-017), China; the Natural Science Foundation (ACKYC20046) of Anhui University of Finance and Economics, China.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest
Acknowledgments
The authors gratefully acknowledge Longlong Zhao, for their assistance in the experiments. The authors would further like to thank Jiawen Bai and Bo Yang.
References
ASTM International (2009). ASTM D143-09, standard test methods for small clear specimens of timber. West Conshohocken, PA: ASTM International.
Auclair, S. C., Sorelli, L., and Salenikovich, A. (2016). A new composite connector for timber-concrete composite structures. Constr. Build. Mater. 112, 84–92. doi:10.1016/j.conbuildmat.2016.02.025
Ceccotti, A. (2002). Composite concrete-timber structures. Prog. Struct. Eng. Mater. 4, 264–275. doi:10.1002/pse.126
Chen, G., Wu, J., Jiang, H., Zhou, T., Li, X., and Yu, Y. (2020a). Evaluation of OSB webbed laminated bamboo lumber box-shaped joists with a circular web hole. J. Build. Eng. 29, 101129. doi:10.1016/j.jobe.2019.101129
Chen, G., Yu, Y., Li, X., and He, B. (2020b). Mechanical behavior of laminated bamboo lumber for structural application: an experimental investigation. Eur. J. Wood Prod. 78, 53–63. doi:10.1007/s00107-019-01486-9
Chen, S., Wei, Y., Hu, Y., Zhai, Z., and Wang, L. (2020c). Behavior and strength of rectangular bamboo scrimber columns with shape and slenderness effects. Mater. Today. Commun. 25, 101392. doi:10.1016/j.mtcomm.2020.101392
Cui, Z., Xu, M., Chen, Z., and Xiang, J. (2018). Experimental study on thermal performance of bamboo scrimber at elevated temperatures. Constr. Build. Mater. 182, 178–187. doi:10.1016/j.conbuildmat.2018.06.124
Dias, A., Skinner, J., Crews, K., and Tannert, T. (2016). Timber-concrete-composites increasing the use of timber in construction. Eur. J. Wood Prod. 74, 443–451. doi:10.1007/s00107-015-0975-0
Dias, A. M. P. G. (2012). Analysis of the nonlinear behavior of timber-concrete connections. J. Struct. Eng. 138, 1128–1137. doi:10.1061/(asce)st.1943-541x.0000523
Ding, L., Liu, X., Wang, X., Huang, H., and Wu, Z. (2018). Mechanical properties of pultruded basalt fiber-reinforced polymer tube under axial tension and compression. Constr. Build. Mater. 176, 629–637. doi:10.1016/j.conbuildmat.2018.05.036
Ding, L., Shi, J., Wang, X., Liu, Y., Jin, Y., and Wu, Z. (2019). Bond behavior between basalt fiber-reinforced polymer rebars and coral-reef-sand concrete conditioned in saline solution. Struct. Concr. 21, 659–672. doi:10.1002/suco.201900106
European Union (2006). Eurocode 4, design of composite steel and concrete structures–part 1-1: general rules and rules for buildings. Brussels, Belgium: European Union.
European Union (2006). Eurocode 5, design of timber structures–part 1-1: general-common rules and rules for buildings. Brussels, Belgium: European Union. EN 1995-1-1.
Chinese Committee for Standardization (2013). G. B. 50017-2003, Code for design of steel structures, Beijing, China: China Construction Industry Press.
Jiang, Y., Hong, W., Hu, X., Crocetti, R., Wang, L., and Sun, W. (2017). Early-age performance of lag screw shear connections for glulam-lightweight concrete composite beams. Constr. Build. Mater. 151, 36–42. doi:10.1016/j.conbuildmat.2017.06.063
Khorsandnia, N., Valipour, H., and Bradford, M. (2018). Deconstructable timber-concrete composite beams with panelised slabs: finite element analysis. Constr. Build. Mater. 163, 798–811. doi:10.1016/j.conbuildmat.2017.12.169
Li, H., Zhang, H., Qiu, Z., Su, J., Wei, D., Lorenzo, R., et al. (2019). Mechanical properties and stress strain relationship models for bamboo scrimber. J. Renew. Mater. 8, 13–27. doi:10.32604/jrm.2020.09341
Martins, C., Dias, A. M. P. G., Costa, R., and Santos, P. (2016). Environmentally friendly high performance timber–concrete panel. Constr. Build. Mater. 102, 1060–1069. doi:10.1016/j.conbuildmat.2015.07.194
Saulius, K., Audronis, K., and Balys, V. (2007). Mechanical behaviour of timber-to-concrete connections with inclined screws. J. Civ. Eng. Manag. 13, 201–207. doi:10.3846/13923730.2007.9636437
Sebastian, W. M., Mudie, J., Cox, G., Piazza, M., Tomasi, R., and Giongo, I. (2016). Insight into mechanics of externally indeterminate hardwood-concrete composite beams. Constr. Build. Mater. 102, 1029–1048. doi:10.1016/j.conbuildmat.2015.10.015
Shan, B., Wang, Z. Y., Li, T. Y., and Xiao, Y. (2020). Experimental and analytical Investigations on short-term behavior of glubam-concrete composite beams. J. Struct. Eng. 146, 04019217. doi:10.1061/(ASCE)ST.1943-541X.0002517
Shan, B., Xiao, Y., Zhang, W. L., and Liu, B. (2017). Mechanical behavior of connections for glubam-concrete composite beams. Constr. Build. Mater. 143, 158–168. doi:10.1016/j.conbuildmat.2017.03.136
Shangguan, W., Zhong, Y., Xing, X., Zhao, R., and Ren, H. (2015). Strength models of bamboo scrimber for compressive properties. J. Wood Sci. 61, 120–128. doi:10.1007/s10086-014-1444-9
Tian, L.-m., Kou, Y.-f., and Hao, J.-p. (2019). Axial compressive behaviour of sprayed composite mortar–original bamboo composite columns. Constr. Build. Mater. 215, 726–736. doi:10.1016/j.conbuildmat.2019.04.234
Wang, Z., Wei, Y., Li, N., Zhao, K., and Ding, M. (2020). Flexural behavior of bamboo–concrete composite beams with perforated steel plate connections. J. Wood Sci. 66, 1–20. doi:10.1186/s10086-020-1854-9
Wei, Y., Ji, X., Duan, M., and Li, G. (2017a). Flexural performance of bamboo scrimber beams strengthened with fiber-reinforced polymer. Constr. Build. Mater. 142, 66–82. doi:10.1016/j.conbuildmat.2017.03.054
Wei, Y., Ji, X. W., Duan, M. J., Zhao, L. L., and Li, G. F. (2018). Model for axial stress-strain relationship of bamboo scrimber. Acta Mater. Compos. Sin. 35, 572–579 [in Chinese, with English summary]. doi:10.13801/j.cnki.fhclxb.20170608.002
Wei, Y., Ji, X. W., Zhou, M. Q., Zhao, L. L., and Duan, M. J. (2017b). Mechanical properties of bamboo-concrete composite structures with dowel-type connections. Trans. Chin. Soc. Agric. Eng. 33, 65–72 [in Chinese, with English summary]. doi:10.11975/j.issn.1002-6819.2017.03.009
Wei, Y., Li, N., Wu, G., Duan, M. J., and Li, G. F. (2017c). Load-slip behavior of perforated plate connections of bamboo-concrete. J. Southeast. Univ. 47, 1167–1173. doi:10.3969/j.issn.1001-0505.2017.06.014
Wei, Y., Tang, S., Ji, X., Zhao, K., and Li, G. (2020a). Stress-strain behavior and model of bamboo scrimber under cyclic axial compression. Eng. Struct. 209, 110279, [It is English paper]. doi:10.1016/j.engstruct.2020.110279
Wei, Y., Wu, G., Li, G. F., Zhang, Q. S., and Jiang, S. X. (2014). Mechanical behavior of novel FRP-bamboo-concrete composite beams. J. Central. South. Univ. 45, 4384–4392 [in Chinese, with English summary. Available at: JournalArticle/5b435954c095d716a4c75fab]
Wei, Y., Yan, S., Zhao, K., Dong, F., and Li, G. (2020b). Experimental and theoretical investigation of steel-reinforced bamboo scrimber beams. Eng. Struct. 223, 111179. doi:10.1016/j.engstruct.2020.111179
Wei, Y., Zhao, K., Hang, C., Chen, S., and Ding, M. (2020c). Experimental study on the creep behavior of recombinant bamboo. J. Renew. Mater. 8, 251–273. doi:10.32604/jrm.2020.08779
Wei, Y., Zhou, M. Q., and Yuan, L. D. (2016). Mechanical performance of glulam bamboo columns under eccentric loading. Acta Mater. Compos. Sin. 33, 379–385 [in Chinese]. doi:10.13801/j.cnki.fhclxb.20150703.002
Xu, M., Cui, Z., Chen, Z., and Xiang, J. (2017). Experimental study on compressive and tensile properties of a bamboo scrimber at elevated temperatures. Constr. Build. Mater. 151, 732–741. doi:10.1016/j.conbuildmat.2017.06.128
Yu, Y., Liu, R., Huang, Y., Meng, F., and Yu, W. (2017). Preparation, physical, mechanical, and interfacial morphological properties of engineered bamboo scrimber. Constr. Build. Mater. 157, 1032–1039. doi:10.1016/j.conbuildmat.2017.09.185
Zhang, Y., Peng, H., and Lv, W. (2018). Shear stress transfer model for evaluating the fracture behaviour of SHCCs for RC shear strengthening. Mag. Concr. Res. 70, 512–517. doi:10.1680/jmacr.17.00104
Zhang, Y., Wei, Y., Bai, J., Wu, G., and Dong, Z. (2020). A novel seawater and sea sand concrete filled FRP-carbon steel composite tube column: concept and behaviour. Compos. Struct. 246, 112421. doi:10.1016/j.compstruct.2020.112421
Keywords: bamboo-concrete shear connections, wood-concrete shear connections, dowel-type connector, mechanical behavior, comparative study
Citation: Wang Z, Wei Y, Jiang J, Zhao K and Zheng K (2020) Comparative Study on Mechanical Behavior of Bamboo-Concrete Connections and Wood-Concrete Connections. Front. Mater. 7:587580. doi: 10.3389/fmats.2020.587580
Received: 26 July 2020; Accepted: 31 August 2020;
Published: 28 September 2020.
Edited by:
Jun Wu, Huazhong University of Science and Technology, ChinaCopyright © 2020 Wang, Wei, Jiang, Zhao and Zheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yang Wei, d3k3OEBuamZ1LmVkdS5jbg==
 Zhiyuan Wang1,2
Zhiyuan Wang1,2 Yang Wei
Yang Wei Kaiqi Zheng
Kaiqi Zheng