
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Mater. , 07 December 2020
Sec. Energy Materials
Volume 7 - 2020 | https://doi.org/10.3389/fmats.2020.578791
Heterostructures based on two-dimensional (2D) materials have attracted intense attention in recent decades due to their unusual and tunable physics/chemical properties, which can be converted into promising engineering applications ranging from electronics, photonics, and phononics to energy recovery. A fundamental understanding of thermal transport in 2D heterostructures is crucial importance for developing micro-nano devices based on them. In this review, we summarized the recent advances of thermal transport in 2D heterostructures. Firstly, we introduced diverse theoretical approaches and experimental techniques for thermal transport in low-dimensional materials. Then we briefly reviewed the thermal properties of various 2D single-phase materials beyond graphene such as hexagonal boron nitride (h-BN), phosphorene, transition metal dichalcogenides (TMDs) and borophene, and emphatically discussed various influencing factors including structural defects, mechanical strain, and substrate interactions. Moreover, we highlighted thermal conduction control in tailored nanosystems—2D heterostructures and presented the associated underlying physical mechanisms, especially interface-modulated phonon dynamics. Finally, we outline their significant applications in advanced thermal management and thermoelectrics conversion, and discuss a number of open problems on thermal transport in 2D heterostructures.
The excellent physicochemical properties of graphene (superior thermal stability, high conductivity, favorable mechanical strength, broadband absorption) have inspired great interest not only in its fundamental and applied aspects, but also in exploring other two-dimensional (2D) materials. Subsequently, numerous post-graphene 2D materials ranging from hexagonal boron nitride (h-BN) (Jo et al., 2013), silicene (Vogt et al., 2012), transition-metal dichalcogenide (TMDC) like MoS2 (Smithe et al., 2018) and MoSe2 (Zhang et al., 2013), to phospherene (Chen et al., 2018c) and borophene (Ranjan et al., 2019) have been synthesized, and present diversified electronic, thermal and optical properties, which could be complementary to those of graphene. For example, compared to the zero band-gap of graphene, MoS2 exhibit direct band gap, making it an attractive material for nanoelectronic applications like field-effect transistors with a high on–off ratio and low power consumption (Chang et al., 2013). Another example, stanene, a single-layer buckled honeycomb structure of Tin atom, is demonstrated to be near-room-temperature quantum anomalous Hall effect (Wu et al., 2014) and ultra-low thermal conductivity (Cherukara et al., 2016), which is particularly suited for thermoelectric devices. Furthermore, 2D organic carbon nitride materials as graphene derivatives exhibited high photocatalytic activity owing to their interface interaction, and can be used as the next-generation highly effective photocatalyst (Zhao et al., 2018a; Zhao et al., 2021).
Recently, research on heterostructures composed of distinct 2D materials has captured much attention because their emergence could bring novel exciting physical properties beyond either of the individual component monolayer structures and provide additional degrees of freedom for device engineering. Normally, heterostructures are divided into two classes: in-plane heterostructures where two 2D materials are stitched seamlessly into a shared plane with an atomically sharp 1D interface; van der Waals (vdW) heterostructures where distinct 2D materials are stacked vertically with non-bonded vdW forces between adjacent layers. Benefited from the progresses in the microtechnology, high-quality graphene/h-BN in-plane heterostructures can be synthesized via chemical vapor deposition (CVD) method, and their compositional and structural diversities could translate into greater freedom for tuning the physical properties such as the presence of a metal-insulator transition (Ci et al., 2010; Liu et al., 2014d). Based on the same preparation method, the integration of MoS2, MoSe2 or WSe2 monolayers into a heterostructure has provided the possibility to produce strong localized photoluminescence and in-plane p-n junctions, showing perspectives in phototransistors and field-effect transistor (Huang et al., 2014; Li et al., 2015). The advantages of in-plane heterostructures mainly contain simpler band alignment, more distinct phase separation and strong interfacial action (Li et al., 2015). Compared to in-plane heterostructures which demands the matched lattice structures of constituent materials, vdW heterostructures intrinsically create an ultra-clean interface regardless of the typical interfacial lattice-matching constraints, which is crucial for tunneling devices that suffer from interfacial defects and dislocations. Additionally, vdW heterostructures offer new mechanisms for manipulating the properties of emergent device via the stacking sequence, the relative rotation between adjacent layers as well as interlayer spacing. A few pioneering works have reported prototypical field-effect-transistor with graphene-based (Bertolazzi et al., 2013; Georgiou et al., 2013) or phosphorus vdW heterostructures (Kang et al., 2016), photodiodes based on MoS2/WSe2 stacks (Roy et al., 2015), and high-efficiency photovoltaic cells based on graphene/WS2 vertical junctions (Iannaccone et al., 2018). On the other hand, the non-bonded vdW interactions of adjacent layers can preserve the electronic properties of each layer, and help resolve a critical challenge that the poor electronic quality of 2D layered materials deposited on SiO2 substrates (Yankowitz et al., 2019). For instance, the quality of graphene encapsulated in h-BN is dramatically improved, and possesses high mobility and ballistic transport over tens of micrometers, which approaches those of suspended graphene (Wang et al., 2013a). It is reported h-BN/phosphorus/h-BN sandwiched heterostructure exists high field-effect mobility and high on-off ratios at room temperature, and the embed phosphorus remains intact and preserves high quality (Chen et al., 2015b). In a word, the physicochemical properties of different heterostructures are closely linked to material composition and structural configuration, representing the significance of structure-property relations.
Thermal transport in 2D heterostructures is not only of a fundamental issue in physics but also crucial to engineering applications. On the one hand, heat dissipation arising from charge carrier scattering processes has to be considered in the development of such nanostructures for electronic and photoelectric devices because the generation of waste Joule heat often leads to the formation of high-temperature hot spots in devices (Wang et al., 2017d), which severely affect the stability and performance of devices. Hence, the choice of 2D building blocks with high thermal conductivity helps to alleviate Joule heat dissipation, and a deeper understanding of the underlying mechanisms for heat conduction across the heterogeneous interface would aid in the design of functional devices. On the other hand, low thermal conductivity materials are necessary for the application in thermoelectric devices converting waste heat into electrical energy. The introduction of 2D heterostructures probably causes increasing Seebeck coefficient and lowering thermal conductivity based on carrier-energy filtering or quantum confinement effects. Compared to dissipating heat and thermoelectric generator, the design of functional thermal devices such as rectifier, transistor, and logical gate to handle heat signals requires controllable thermal transport. In fact, the structural diversities combined with structural defect and external stress field can realize the rich diversity of thermal properties in 2D heterostructures, and enables them to be used in different thermal fields. From another perspective, the interfaces of heterostructures make the thermal transport mechanisms deviate from that in single 2D materials and conventional bulk materials, either through inducing a contact thermal resistance or new phonon modes. For example, it is reported that the thermal conductivity of graphene and graphene nanoribbons (GNRs) monotonously decreases with the tensile strain due to phonon softening (Wei et al., 2011; Shen et al., 2014; Guo et al., 2020), while the load of tensile strain of graphene/h-BN in-plane heterostructures significantly enhance the interfacial thermal conductance owing to improving the alignment of out-of-plane phonon modes near the interface (Ong et al., 2016). Further research demonstrates that the thermal conductivity of graphene/h-BN superlattices first increases and then decreases with increasing the tensile strain, which stems from the competition between in-plane phonons softening and flexural phonons stiffening (Zhu and Ertekin, 2015). Furthermore, some abnormal thermal phenomena such as thermal rectification (TR) (Yuan et al., 2015; Zhang et al., 2018), negative differential thermal resistance (NDTR) (Chen et al., 2017b), thermal bandgap (Zhu and Ertekin, 2014b) and thermophoresis (Mandelli et al., 2017) have been reported in 2D heterostructures, and sparked heated debate.
As we know, phonons are the main heat carriers in semiconductors like TMDCs and silicene, and insulators like h-BN. Specifically, the ultra-high thermal conductivity of graphene dominated by phonons has raised the exciting prospect for heat removal in electronic devices and peculiar phonon transport properties, as reviewed by (Nika and Balandin, 2012; Xu et al., 2014c; Al and Farías, 2016; Xu et al., 2016b; Nika and Balandin, 2017) which has also laid the solid basis for other emerging 2D materials. Phonon transport in novel 2D materials and their heterostuctures probably differs from that in graphene because of crystal structures and atom species, suggesting that the existing knowledge of graphene couldn’t be transplanted to them directly. Fortunately, sustaining advances of theory and experiment offers microscopic details from the atomistic level to the device scale. To date, the thermal properties of 2D materials beyond graphene have been discussed in many previous review articles. Regarding to the progress of theoretical approaches and experimental techniques in 2D materials, please refer to (Cahill et al., 2014; Wang et al., 2017d; Zeng et al., 2018b; Fu et al., 2019) For the phonon transport in phosphorene, borophenes, TMDs and other 2D materials, please refer to (Gu et al., 2018; Qin and Hu, 2018; Chen and Chen, 2020a; Li et al., 2020a; Zhao et al., 2020b) For a detailed survey of thermoelectricity applications of 2D materials, please refer to (Dollfus et al., 2015; Zhang and Zhang, 2017a; Li et al., 2020b). In this review, we not only summarizes the existing results of phonon transport in pristine 2D materials and their heterostuctures, but also gives a physical picture of various phonon scattering mechanisms induced by interior imperfections or external field, to pave the way for better thermal management in practical devices. In Theoretical Approaches and Experimental Measurements, we introduced diverse theoretical approaches and experimental techniques for investigating heat conduction in low-dimensional nanostructures. In Thermal Transport in Some Typical 2D Materials, we briefly reviewed the unique thermal properties of several typical 2D materials. In Thermal Transport in 2D Heterostructures, we highlighted the manipulation of heat conduction in tailored nanosystems—2D heterostructures and present the associated underlying transport mechanisms, especially interface-modulated phonon dynamics. Finally, we show the potential applicability of 2D heterostructures in advanced thermal and thermoelectrics devices, and give the conclusions and a brief outlook.
Currently, different theoretical method have been developed to study the thermal transport properties of 2D materials, principally including the Boltzmann transport equation (BTE), atomistic Green’s functions (AGF) and molecular dynamics (MD) simulations. Note that the latter two are especially suitable for describing phonon transmission/scattering across an interface in 2D heterostructures.
MD simulations with classical potentials are a powerful technique to handle many-body problems at the atomistic level. Here, all-order anharmonic effect is inherently contained in atomistic interactions, differing from that in BTE and AGF. At present, the MD method is widely adopted to study phonon transport problems such as structural effect and various influences like doping, defect, strain and substate. Note that the accuracy of classical MD calculations depends on the quality of the inter-atomic potentials. Recently, intensive efforts have been conducted to construct reliable potential function from the calculations of first principles (Rowe et al., 2018). In practice, equilibrium MD (EMD) and nonequilibrium MD (NEMD) simulations are adopted to extract the thermal properties of 2D materials. In EMD, the calculation of thermal conductivity is based on the Green–Kubo formula or Einstein Relation ration (Sellan et al., 2010; Sevik et al., 2011). For NEMD, both sides of sample are connected to a hot and cold reservoir, respectively. After sufficient run-time, the stationary-state heat flux and temperature are obtained to calculate thermal conductivity in terms of Fourier’s law of heat conduction,
Obviously, the obtained thermal conductivity using the two methods does not provide microscopic perspective into thermal conduction in crystals. For this, a spectral energy density (SED) technique on the base of harmonic lattice dynamics and EMD calculations has been developed to extract mode–resolved thermal conductivity (Thomas et al., 2010; Qiu and Ruan, 2012a). However, the contribution of some long wavelengths phonons can’t be contained in the simulation results because of size effect (Xie et al., 2016; Gu et al., 2018). As a result, the calculated thermal conductivity is sensitive to the size of simulation domain. Note that the NEMD method has also been applied to study interface-modulated phonon dynamics such as graphene/MoS2 (Liu et al., 2017a), graphene/phosphorene in-plane heterostructures (Liu et al., 2018a) and graphene/h-BN (Xu et al., 2014a) MoS2/WSe2 (Zhang et al., 2017b), phosphorene/graphene vdW heterostructures (Liang et al., 2018).
The presence of phonon-interface scattering will produce thermal resistance, also called as Kapitza thermal resistance. The phenomenon could be partly explained by the acoustic mismatch model (AMM) and the diffuse mismatch model (DMM), which is good for some simple material (Kakodkar and Feser, 2017). While for 2D heterostructrues, both kinds of theoretical models are likely to fail because of the dimensionality mismatch and limited thickness of actual system. In addition to this, the models couldn’t give a detailed picture for interfacial thermal transport as AGF calculation. For this, a spectral decomposition of interfacial thermal conductance method based on NEMD simulations is developed by (Sääskilahti et al., 2015) and extended by (Zhou and Hu, 2017c), offering a detailed description of inelastic effects. Under nonequilibrium steady state, the spectrally resolved heat flux between two atoms i and j is given by
where
where
where
Additionally, the phonon wave-packet (PWP) method based on wavelet transforms and MD simulation has also developed to calculate the phonon transmission coefficient. A detailed derivation process is referred to the articles by (Schelling and Phillpot, 2003). The advantage of the PWP method is that the phonon scattering process could be observed directly from the simulation, not just the transmission result as the AGF. The basic idea of PWP is to form a phonon wave packet so that it is localized in both real space and reciprocal space. To produce a wave packet at wave vector
where
As we know, phonons have wave nature. The AGF method can rigorously include wave effects on a discrete atomic lattice. Actually, this method was initially developed to handle quantum electron transport in nanostructures (Fan and Chen, 2010; Chen et al., 2018a; Deng et al., 2018; Zeng et al., 2018a; Chen et al., 2019a; Zhou et al., 2019; Fan et al., 2020). By making a few careful substitutions, the approach has been extended to study phonon transport in a wide variety of nanostructures (Xu et al., 2009; Peng and Chen, 2014; Zhou et al., 2017b; He et al., 2019) especially suitable for low-dimensional hetrostuctures such as Si/Ge (Tian et al., 2012b), graphene/h-BN (Peng et al., 2017), MoS2/metal (Yan et al., 2016b) interfaces and others (Ma et al., 2016). Here, we simply introduce this method from the numerical simulation point of view. The phonon Hamiltonian of entire system is consisting of three parts, namely Left (L), Center (C) and Right (R) regions, the matrix form can be written as
where
Where
The surface Green’s function usually solved recursively or using the decimation technique. According to Caroli formula, the phonon transmission coefficient as phonon frequency is represented as
where
Here
Diagonalizing
where
By summing over the subscript m and n, the total phonon transmission in Eq. 9 can be obtained. If there is significant nonlinear effect in the central scattering region, the third-order force constant can be consierded as a perturbation of harmonic system. The three-phonon scattering self-energy
where
From the particle-based picture perspective, phonon transport is governed by the BTE, where phonons obey the Bose-Einstein distribution function
where
where
where
here
The measurement of thermal conductivity or interfacial thermal conductance (ITC) in 2D nanostructures is helpful to grasp the law of phonon transport. At present, the optothermal Raman and microbridge techniques are the most common method for measuring the thermal properties of 2D materials. In addition the 3ω and time-domain thermoreflectance (TDTR) techniques have been adopted to obtain ITC. Because of space limitation, we briefly introduce some measurement results for 2D materials and discuss the measurement errors.
With the aid of optothermal Raman technique, the thermal conductivity measurement of single-layer graphene was reported by (Balandin et al., 2008), and the obtained value ranges from 2,000 to 5,000 Wm−1 K−1 at room temperature. Analogously, the thermal conductivity of bilayer graphene was also identified (Li et al., 2014a), coinciding with the theoretical predictions (Nika et al., 2014). Furthermore (Malekpour et al., 2016), reported that the room-temperature thermal conductivity of defective graphene reduces from 1800 to 400 Wm−1K−1 when the defect density induced by electron beam irradiation slightly increases from 0.0005 to 0.005%. (Chen et al., 2012) measured the thermal conductivity of graphene with different 13C isotope concentrations, and revealed that 50% concentration results in a 50% reduction in thermal conductivity. Except graphene, this technique has also applied to black phosphorous (Luo et al., 2015) MoS2 and MoSe2 (Zhang et al., 2015c), In a word, although the uncertainty of the optical absorption coefficient, weak temperature-dependence of Raman peak shift and uncertainty of contact thermal resistance will affect the measurement accuracy, the optothermal Raman measurement is still a simple and effective method to measure the thermal conductivity of 2D structures.
The microbridge technique was initially used to measure the thermal conductivity of 1D nanostructures (Li et al., 2003), and then was applied in 2D materials (Pettes et al., 2011). For example, (Xu et al., 2014b) experimentally found the logarithmic dependence of thermal conductivity on the sample length L (
The ITC measurement of in-plane heterostructures is quite challenging compared to that of vdW interfaces. There exist far fewer measurements on the ITC. Usually, the measured ITC of graphene/substrate interface is in the range from 20 to 100 MWm−2 K−1 at 300 K. Taking this value as reference, the measured ITC MoS2/substrate interface is considerably smaller. Using the TDTR-based approach, (Lee et al., 2015b) reported that the ITC of MoS2/metal thin-films interface is ∼26 MW m−2 K−1. Moreover, the optothermal Raman measurement indicated that the ITC of MoS2/SiO2 interface is about 1.94 MW m−2 K−1 (Taube et al., 2015). Analogously, (Behranginia et al., 2018) reported that the ITC between WSe2/SiO2 interface ranges from 10 to 32 MW m−2 K−1 via analyzing the temperature-dependence of the low-frequency shear mode. (Chen et al., 2014) measured the ITC of vertically stacked graphene/h-BN interface and found that the value reaches 7.4 MW/m2K at room temperature, which stems from the remaining organic residues at the interface.
It is well known that single-layer graphene possesses ultra-high room-temperature thermal conductivity. The results of thermal conductivity measurements for graphene have been discussed in Molecular Dynamics Simulations. Note that the measured values are closely related to experimental approaches, external condition (strain, substrate), sample size (length, layer-thickness) and quality (like point-defect, isotopic abundance, grain size). Hence, theoretical simulations could provide deeper insight into concerning the thermal property of graphene. Using the PBT method combined in conjunction with the force-constant model, (Lindsay et al., 2010) claimed that the flexural acoustic (ZA) phonons contribute 70–80% of heat conduction in graphene, which is ascribed to the existence of selection rules in phonon scattering processes. The phenomenon has also been confirmed by others research groups based on similar theoretical approach (Fugallo et al., 2014; Lindsay et al., 2014). Using the BTE method and Raman technique, (Seol et al., 2010) reported that the thermal transport contribution from ZA modes for graphene is as large as 77%, and this ratio is decreased by the substrate or organic residues (Pettes et al., 2011). Recently, using the iterative BTE method, (Lee et al., 2015a) found that there is an obvious hydrodynamic phonon transport in graphene over a wide temperature range due to the presence of strong N scattering processes. Subsequently, (Machida et al., 2020) experimentally showed an extremely high thermal conductivity in the very thin graphite samples (8.5-micrometer-thick) at higher temperature, which extends the hydrodynamic regime from cryogenic to room temperatures. That is, there are three phonon transport behaviors, namely ballistic, diffusive and hydrodynamic transport. Furthermore, (Al and Farías, 2016) outlined the phonon dynamics in supported graphene, and revealed the physical picture of phonon-substrate scattering. (Nika and Balandin, 2017) minutely discussed the mode-resolved thermal conductivity in graphene. In addition, our previous work highlighted the manipulation of thermal transport in graphene from the viewpoint of the wave/particle nature of phonons (Chen and Chen, 2020a). (Dollfus et al., 2015) summarized experimental and theoretical results about the thermoelectric properties of graphene and its derivatives, and described how the poor thermoelectric performance of graphene achieves high thermoelectric figures by tuning on a wide range both the thermal and electronic transport based on different strategies of nanostructuring and bandgap engineering. Those studies on thermal transport of graphene have stimulated great interest in exploring other emerging 2D materials, as shown in Figure 1.
Monolayer h-BN is also called “white graphene” because of their similar honeycomb structure. Unlike zero band-gap graphene, h-BN with 5.8 eV band-gap has been viewed as the top ranked candidate for the dielectric material in electronic devices or the new nonmetal catalyst in the field of photocatalysis (Zhao et al., 2019). It was reported that the electron mobility of graphene electronic devices supported on few-layer h-BN far outweighs that supported on silicon dioxide (SiO2) because of the atomically smooth surface of h-BN (Serrano et al., 2007). In addition, h-BN also holds high chemical stability, strong mechanical strength and good thermal property. The basal-plane thermal conductivity of high-quality bulk h-BN sample could reach up to 390 W m−1 K−1 at 300 K (Geick et al., 1966), which shows great potential in current-generation dielectric materials. For sing-layer h-BN, the BTE calculations indicated that the system’s thermal conductivity is about 600 Wm−1 K−1 (Lindsay and Broido, 2011), but the EMD results showed that the value is 400 Wm−1 K−1 (Sevik et al., 2011).
Experimentally, because the intensity of Raman peaks in h-BN is very weak, the optothermal Raman method may not be applicable for h-BN. (Zhou et al., 2014) found only 5% optical absorption for nine-layer h-BN in optothermal Raman measurment, and the obtained thermal conductivity was 227–280 m−1 K−1. Using the microbridge method, (Jo et al., 2013) reported that the thermal conductivity of an 11-layer sample reaches ∼360 W m−1 K−1 at 300 K, approaching the value of bulk h-BN (Lindsay and Broido, 2011). Actually, the accurate measurement of thermal properties of 2D heterostructures still has a long way to go.
Silicene possesses a buckled honeycomb atomic arrangement of Si atoms. There is a spin-orbit coupling of 1.55 meV owing to the breaking of mirror symmetry in this bucked structure. In addition, silicene can be easily integrated into electronic devices (Liu et al., 2013a). From the view of the heat dissipation of electronic devices, the influence of buckled structure on phonon transport is well worth exploring. Based on the BTE method, (Gu and Yang, 2015) demonstrated the thermal conductivity of silicene is only a fifth of that of bulk silicon (140 W m−1 K−1). Moreover, it was also found the contribution of ZA modes to the thermal conductivity of silicene is about 7.5%. Similarly, (Xie et al., 2014a) found the relaxation times of acoustic phonon modes with long-wavelength are now close to zero at
Based on different MD simulations, the calculated thermal conductivity for silicene ranged from 5 to 50 W m−1 K−1, which could be ascribed to the adopted empirical potentials including the Tersoff potential, embedded-atom method (MEAM) potential, optimized Stillinger-Weber potential (Zhang et al., 2014a; Liu et al., 2014b). Compared with planar 2D materials, the structure buckling has important effect on the phonon transport in silicene via providing additional scattering or breaking the symmetry selection rule. As a result, there is an unusual thermal response to the applied tensile strain in silicene: a small strain can enhance the thermal conductivity while further increase will cause the decrease of thermal conductivity. That is differentiated from the monotone decreasing with tensile strain for graphene (Hu et al., 2013). This can be explained as follows: for a small strain, the bucked configuration becomes flat because of bond rotation, rendering the enhancement of in-plane stiffness and facilitating phonon transport; under large strain, the Si-Si bonds are significantly elongated and the in-plane stiffness weakens, lowering the thermal conductivity. However, the experimental study of thermal transport in silicene hasn’t been reported by now.
Unlike graphene and h-BN with single atomic layer, a transition metal layer is sandwiched between two chalcogenide atomic layers for TMDs. In general, these TMDs possess a finite bandgap, and are suitable for many electronic and photonic applications (Zhao et al., 2020a). Owing to the difference of lattice structure between TMDs and graphene, TMDs demonstrates different thermal transport properties (Zhao et al., 2020b). Clearly, the strong covalent bonds between the carbon atoms result in a high thermal conductivity of graphene. By comparison, the transition metal-chalcogen bond is weak because of its special sandwich structure, raising the particularity of phonon properties. Besides the crystal structure, the atomic masses are another factor affecting the thermal conductivity of TMDs. A large mass difference between transition metal and chalcogen atoms often induces substantial phonon-gap (Jiang, 2014). For instance, the phonon gap in WS2 achieves 3.3 THz, and some three-phonon processes (like acoustic + acoustic
MoS2 and MoSe2 as the most typical TMDs have been experimentally fabricated (Keyshar et al., 2017), and their thermal transport properties have also been widely explored. (Wei et al., 2014) claimed that the thermal conductivity of MoS2 is about 26 Wm−1 K−1 at room temperature using BTE method under the RTA assumption. Analogously, (Gu and Yang, 2014) reported the thermal conductivity of MoSe2 is 54 Wm−1 K−1 under the iterative solution, which is over 20% than that under the RTA assumption. Furthermore, the relative contribution of different phonon polarization branches to thermal conductivity resembles the case in silicene rather than graphene because MoS2 is not an individual atomic plane. (Cai et al., 2014) predicted a room-temperature thermal conductivity of 23.2W Wm−1K−1 for MoS2 by solving the AGF. Based on NEMD simulations, (Hong et al., 2016b) showed that the thermal conductivities of MoS2 and MoSe2 are 110.43 and 43.88 Wm−1 K−1, respectively. Lately, 2D MXenes, namely hexagonal transition metal carbides/nitrides, are highly attractive because of their promising technological applications such as energy storage, thermoelectric conversion and flexible devices (Ma et al., 2014; Sarikurt et al., 2018). Clearly, the performance of aforementioned devices strongly depends on the thermal transport properties of constituent material. As we know, low thermal conductivity and excellent conductor are desired in thermoelectric devices, while micro-nano electronic devices require the material with high thermal conductivity. Some previous studies demonstrated that the heat dissipation is a major challenge for MXene-based devices owing to their large aspect ratios and heterogeneous structures. For example, (Hemmat et al., 2019) found the ITC of Ti3C2Tz/SiO2 interface is the range of 10–27 MW m−2 K−1 under different annealing temperatures, and a similar range of ITC was obtained in Ti3C2/SiO2 interface with or without AlOx encapsulation (Yasaei et al., 2018). On the other hand, the in-plane thermal conductivity of MXenes has also been studied. For instance, (Guo et al., 2018) demonstrated that the thermal transport performance in luorine-terminated Ti2CTz exceeds that in oxygen-terminated one, but is comparable to that of bare Ti2C using BTE method. Analogously, (Gholivand et al., 2019) reported that compared to oxygen-terminated Ti3C2Tz, the fluorine-terminated structure has remarkable advantage in heat dissipation. In another theoretical study, (Sarikurt et al., 2018) investigated the influences of transition metals and surface functionalization on the thermal conductivity of M2CO2, and the obtained results showed that their thermal conductivities range from 15-60 Wm−1 K−1.
Experimentally, the optothermal Raman method was used to measure the room-temperature thermal conductivities of 1-layer and 11-layer MoS2, and the obtained values were ∼34.5 Wm−1 K−1 (Liu et al., 2018a) and ∼52 Wm−1 K−1 (Sahoo et al., 2013), respectively, which exceeds the results calculated from the NEMD method (Wang et al., 2016). Meanwhile, the measured value for 4-layer MoS2 was in the range of 44∼50 Wm−1 K−1 by thermal bridge method (Jo et al., 2014). In addition, the temperature-dependent thermal conductivity of substrate-supported MoS2 was extracted from the optothermal Raman method, and the measured room-temperature thermal conductivity was 62.2 Wm−1 K−1, but reduced to 7.45 W Wm−1 K−1 at 450 K (Taube et al., 2015). Apart from MoS2, (Peimyoo et al., 2015) used the optothermal Raman method to determine the thermal conductivity of monolayer and bilayer CVD-grown WS2. The measured values are 32 and 53 Wm−1 K−1 for monolayer and bilayer WS2 at 300 K, respectively. Analogously, (Zhang et al., 2015c) reported that the room-temperature thermal conductivity of monolayer MoSe2 is 59 ± 18 Wm−1 K−1. The similar phonon and Raman scattering in different kinds of TMDs have been discussed earlier. It is believed that other than phonon frequency due to the different mass between Mo and W atom, the common features of 1 L, 2 L and bulk structures in both MoS2 and WS2 should be similar. (Yan et al., 2013) demonstrated a low thermal conductivity of 9 W m−1 K−1 for TaSe2 with a thickness of 45 nm. The experimental discrepancies were primarily due to the sample quality like surface disorders, and the measurement error. Most recently, (Liu and Li, 2018c) experimentally observed that the thermal conductivity of Ti3C2Tz to be 55.88 Wm−1 K−1, Note that neither explicit configuration nor surface termination atoms are clarified in this study.
Phosphorene as a 2D puckered honeycomb structure possesses high carrier mobility and large direct band-gap (∼1.5 eV) (Liu et al., 2014c), indicating abundant nanoelectronic applications. In addition, phosphorene has shown promising application in thermoelectrics devices (Fei et al., 2014). Actually, either electrical or thermoelectrical devices strong depend on the thermal transport properties of phosphorene. Hence, the investigation of the thermal conductivity of such 2D material is necessary.
Theoretically, the thermal conductivity of phosphorene has been explored using different methods including EMD (Xu et al., 2015), BTE under RAT (Zhu et al., 2014a) or iterative rule (Qin et al., 2016). For example, (Qin et al., 2016) showed that the simulated thermal conductivity along zigzag (ZZ) and armchair (AC) directions are respectively 15.33 Wm−1 K−1 and 4.59 Wm−1 K−1 using the iterative BTE method. The low thermal conductivity could be understood from the softening transverse optical (TO) phonons resulted from the long-ranged interaction in phosphorene structure. Combined the spectral energy density (SED) technique with EMD simulations, the ZZ and AC -direction thermal conductivity were predicted to be 152.7 and 33 Wm−1 K−1 in phosphorene, respectively (Xu et al., 2015). (Zhu et al., 2014a) used the RTA to predict the thermal conductivity of black phosphorene of 84 Wm−1 K−1 (24 Wm−1 K−1) in the ZZ (AC) direction (armchair) at 300 K. Although the results reported are discrepant from different research groups, the thermal transport anisotropy behaviors have been clearly demonstrated for all techniques. To understand the phenomenon, the thermal conductivity contribution from ZA modes has also been calculated, which corresponds to 16% (8%) for the case of the ZZ (AC) direction (Qin et al., 2016). That is analogous to silicene (7.5%) but different from graphene (75%), because the hinge-like structure of phosphorene broken the selection rule in three phonon processes. Recently, (Zhao et al., 2018b) thought that the large anisotropic thermal transport stems from phonon group velocity rather than relaxation time. To be specific, the speed of sound velocity
Considering the limitations of synthesis technique, only few experiments were performed to extract the thermal conductivity of different thicknesses phosphorene films. Based on the measurement of micro-Raman spectroscopy, (Luo et al., 2015) demonstrated that the thermal conductivity of a 15 nm thick sample is ∼40 Wm−1 K−1 (20 Wm−1 K−1) along AC (ZZ) direction and decreases with the decrease of film thick. That is, the thermal conductivity anisotropic level has negative relation with film thickness, as shown in Figure 1. Another example, (Jang et al., 2015) adopted the TDTR method to investigate the thermal transport properties of silicon-supported thin films, and claimed that the thermal conductivity anisotropic ratio is about 2.5. Using the thermal bridge method, (Lee et al., 2015b) showed that when the thickness of phosphorous flakes reduces from 300 to 50 nm, the ZZ (AC) direction thermal conductivity drops to 12 from 27 Wm−1 K−1 (5 from 15 Wm−1 K−1). The first-principle calculation revealed the anisotropic thermal transport stems from orientation-dependent phonon dispersion and phonon–phonon scattering based on first-principle calculation. By comparison, the out-of-plane thermal transport is independent of the thickness of phosphorene film. Interestingly, (Su and Zhang, 2015) performed the optothermal Raman method to evaluate the substrate effect on the thermal conductivity phosphorene film, and the measured results indicated that the introduction of SiO2/Si substrate can enhance the thermal conductivity by more than one fold. The novel phenomenon seems to contradict the generally held notion held notion that the substrates have negative effect on the thermal conductivity of 2D materials.
Borophene is quite unique because there are rich hexagonal holes distributions in the triangular lattice such as the structure of borophene is mixed by triangle lattice and hexagonal lattice. At present borophene sheets with different phases and borophene nanoribbons have been experimentally synthesized on various substrates using the molecular beam epitaxy (MBE) approaches. For example, (Mannix et al., 2015) fabricated borophene sheets on the Ag (111) surface and found the planar islands with single atoms thickness occur at substrate temperature 570 and 650 K. Combined with theoretical calculations, the two phases of borophene can be identified as
It is well known that light atomic mass and strong interatomic interaction are the crucial factors for the high thermal conductance of a nanostructure. Compared to carbon atom, the atomic mass of boron is light, and the Young’s module of borophene is close to that of graphene (Li et al., 2018a), indicating that borophene probably possesses superior thermal conductivity as high as that of graphene. Using AGF method, (Zhou et al., 2017a) found the phonon thermal conductance of
2D heterostructures provide possibilities for high-performance optoelectronic devices. Modern advanced fabrication techniques like molecular beam epitaxy and epitaxial growth techniques enable the in-plane heterostructures with atomically sharp interfaces (Liu et al., 2013b; Gao et al., 2013; Li et al., 2015). Nevertheless, because of lattice matching constraints, only certain combinations of materials can enable continued heteroepitaxial growth. On the other hand, the presence of interfaces in heterostructures also induces some novel properties that are distinct from the parent materials. In particular, the lattice mismatch-induced strain would change the force environment of atoms, which cause the deformation of 2D crystalline structures and the variation of phonon spectra. At present, the ITC measurement of in-plane heterostructures is quite challenging compared to that of vdW interfaces. Hence, theoretical simulations provide a convenient way to understand interfacial thermal transport of in-plane heterostructures.
Benefitting from the mall lattice mismatch between grpahene and h-BN, their in-plane heterostructures as a typical case have been successfully synthesized (Gao et al., 2013). The simulated results of EMD method showed that the thermal conductivity along the vertical-interface direction is limited by the less conductive component (h-BN) and is insensitive to the details of the interface (Song and Medhekar, 2013), while that along the parallel-interface direction stabilises a constant which approaches the average of the parent materials, and gradually declines with increasing BN composition. The vibrational eigen-mode analysis reveals that increasing the BN composition would cause intermediate-frequency phonons to be localised in graphene domain (Chen et al., 2016b). (Hong et al., 2016c) studied the effect of sample length and ambient temperature on the ITC in graphen/h-BN in-plane heterostructures via NEMD method, and showed that the ITC varies from 1.9 to 4.5 GW/m2K as the sample length in the range from 20∼100 nm and rising temperature could obviously enhance the ITC. Based on the same method and analogous models, (Liu et al., 2019a) found that increasing the number of atomic row can elevate (lower) the ITC in the zigzag (armchair) interface topography. To understand the mechanism of phonon transmission/scattering at interface, (Feng et al., 2017) calculated the temperatures of phonons under the framework of NEMD simulations. Taking graphene/h-BN planar interfaces as example, the temperature jump of the ZA mode is only 10∼20% of the overall temperature jump because there is considerable overlap between the acoustic branches of graphene and h-BN, while that of the ZO mode is as high as 220% of the overall one, stemming from the negligible coupling at the interface, as shown in Figure 2. Moreover, when interface mixing is introduced, the contribution ratio of ZA mode to the overall temperature jump increases from 19 to 41% and that of the in-plane modes decrease, indicating that a certain number of heat transfer channels shifts from the ZA mode to the TA/LA modes. Using AGF method, (Ong et al., 2016) demonstrated that alternating the bond orientation and type at the interface significantly affect the scattering and transmission of higher frequency modes. In the case of the zigzag-bond interface, the bonding type is able to dramatically alter the preferred orientation of the transverse optical (TO) phonons.
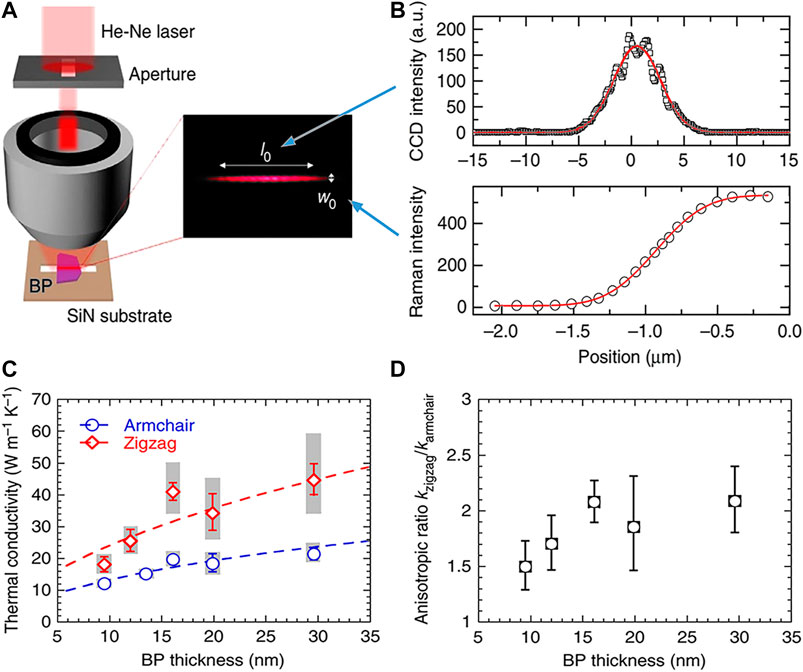
FIGURE 2. (A) The diagram of experimental procedures. (B) The lengthwise profile and the knife-edge-measured widthwise integrated profile of the laser focal line, corresponding to a Gaussian function. (C) The measured thermal conductivities of multiple BP films along AC and ZZ directions, respectively. Dashed lines denote the theoretical modeling results. (D) The anisotropic ratio of thermal conductivity for different phosphorus thickness. Reproduced from (Luo et al., 2015) with permission from Nature Publishing Group.
During the crystal preparation process, a series of defects like single-vacancy (SV), stone−wales (SW) ineluctably exist in heterostructures. (Sutter et al., 2011) experimentally prepared graphene/h-BN in-plane heterostructures via a sequential CVD growth method, and pointed out that the interface of prepared heterostrucutres will be intermixing when the growth temperature becomes high. Based on NEMD simulations, (Liu et al., 2016) showed that the topological defect near the graphene/h-BN interface could promote the interfacial thermal transport, which may be attributable to the localization of the stress fields. Analogously, (Li et al., 2018b) systematically studied the influences of SV and SW interfacial defects on the ITC in the in-plane heterostructures. The results indicated that the ITC quickly decreases with SV concentration but slowly with SW defects, and ultimately remain unchanged for large concentration. The phonon spectra and stress distribution analysis revealed that the regression of in-plane modes induced by SV defects results in the reduced thermal conductivity. Moreover, (Gao and Xu, 2017) reported that the existence of SW interfacial defects can realize the regulation of phonon transport direction, being equivalent to applying mechanical tensile strain. More recently, (Ni et al., 2019) reported the dependence of thermal conductivity on interface composition diffusion in graphene/h-BN in-plane heterostructures, and demonstrated that the system’s thermal conductivity is closely related to the interface composition diffusion length because of the Anderson localization of phonons. (Liang et al., 2020) found that the ITC decreases with the increase of layer number n and saturates at n = 3 in multilayer in-plane graphen/h-BN heterostructures. Even so, the asymptotic value still surpasses that in monolayer heterostructures.
Graphene/h-BN superlattices as special hetrostructures were forecasted to own numerous excellent properties like good thermoelectric performance (Yokomizo and Nakamura, 2013) and opto-electronics properties (Liu et al., 2013b). Using AGF method, (Jiang et al., 2011b) reported that there is a minimum in the period length
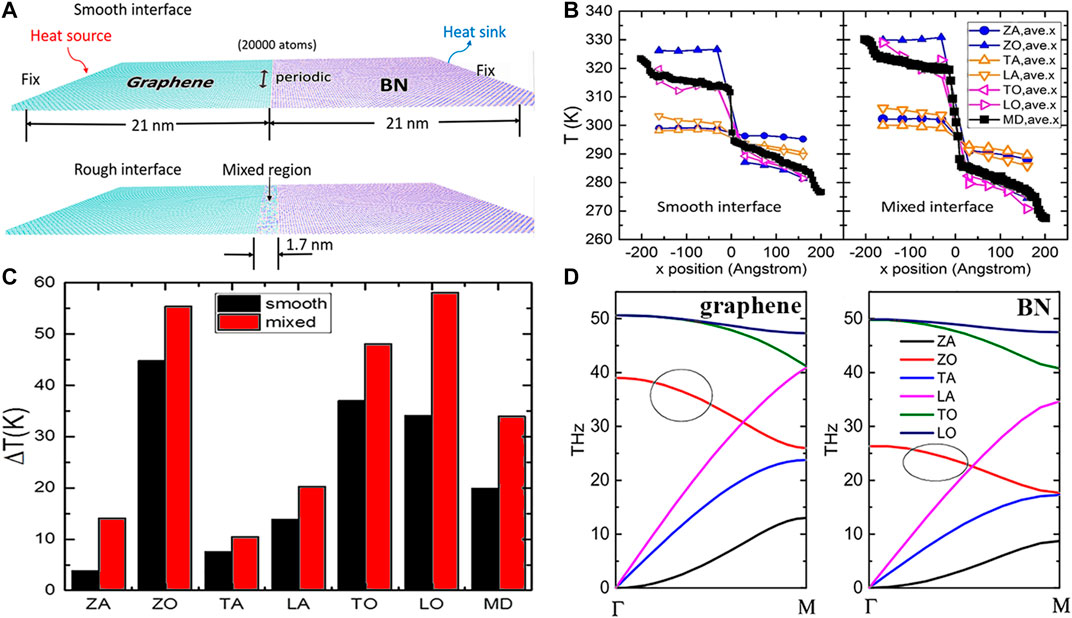
FIGURE 3. (A) NEMD simulation setups for graphene/h-BN with smooth/rough interfaces, (B) The overall temperature profile in NEMD and the spectral phonon temperatures for the six branches, (C) The phonon branch temperature jumps, (D) The phonon dispersion relations of graphene and h-BN. Note that the ZO branches have negligible frequency overlap. Reproduced from (Feng et al., 2017) with permission from American Chemical Society.
Except for graphene/h-BN in-plane heterostructures, some previous research also focused on the interfacial thermal transport across other 2D heterojunctions. Combined the first-principles with NEMD methods, (Liu et al., 2017a) indicated that the ITC of graphene/MoS2 in-plane heterostructure is higher than covalently bonded graphene/metal interfaces. Here, every Mo-C bond could act as a heat transfer channel. (Liu et al., 2014a) explored the dependence of ITC on temperature and strain in graphene/silicene in-plane heterostructure, and concluded that high temperature and small strain is beneficial to improve the ITC. In this work, it is worth noting that when the heat flux imposed into the system is lower than 42 GW m−2, the value ITC almost varies with increasing the heat flux, corresponding to the Fourier heat conduction; while it exceeds the critical value, a low-frequency kinetic wave is stimulated, constructing an extra channel for the non-Fourier heat transfer. (Qin et al., 2019) found that the ITC of MoS2/WSe2 in-plane heterostructure is about 10% of that of graphene/h-BN heterojunction because of strong phonon scatterings at the interface, which could be useful for thermoelectric applications. (Liu et al., 2018a) claimed that the ITC of phosphorene-based coplanar heterostructures doesn’t present obvious anisotropy as the thermal conductivity of phosphorene because the interfacial anharmonicity results in a “mixing” effect for phonon transport. Moreover, the dependence of ITC on strain is very sensitive to the interface morphology, which can be understood by the analysis of stress distribution and phonon spectra overlap.
Benefitting from the progress of ingenious experimental methods, the synthesis of vdW heterostructures via self-assembly technology has achieved an unprecedented degree of control and accuracy, and provides new insights to explore structure-function relationship (Frisenda et al., 2018) and to assemble complex devices (Abidi et al., 2018; Ding et al., 2018b) which are able to be tuned by stacking sequence, orientation, interlayer coupling, and external field. For example, graphene/hBN vdW heterostructures were prepared via an all-dry poly (methyl methacrylate) transfer process using polyvinylalcohol as the water-soluble sacrificial layer, which can avoid the polymer residual problem and prevent contamination from chemical solutions (Tien et al., 2016). Another example is that monolayer WS2 and MoS2 can be directly deposited on h-BN by CVD, which maintain their intrinsic bandgap of 2.01 and 1.85 eV (Fu et al., 2016), indicating a high quality of heterostructures with uniform distribution and a clean interface being developed. Thermal properties of vdW heterostructures is of great interest because it is highly relevant to the functionality, performance and reliability of such heterostructures-enabled devices.
For bilayer graphene/h-BN heterostructures, there are periodic moire patterns on graphene layer. Three typical stacking configurations including AA, AB, AB′ stacking have been verified in experimental results. Moreover, different moire patterns may also affect the phonon transport in such heterostructures. In terms of the analysis of phonon dispersion, (Jung et al., 2012) found that the AB stacking is superior to the AA stacking for graphene/h-BN vdW heterostructures. (Zhang et al., 2017c) carried out the NEMD simulations to calculate the thermal conductivity of h-BN-supported graphene, and demonstrated that the system’s thermal conductivity is reduced only 23% compared to the suspended case. That is because the force environment of graphene is barely affected by h-BN substrate. Additionally, they also discovered that the thermal transport properties strongly depend on the stacking ways of vdW heterostructures. Based on AGF method, (Yan et al., 2016a) showed that when the interlayer spacing between grapheme and h-BN layers is small, the perpendicular heat conduction is determined by in-plane acoustic modes. Another important finding in this work is that the ITC could be enhanced by more than 50% from C-N matched to C-B matched interface. Using the same method, (Wang et al., 2013b) found that the thermal conductance of graphene coupled with h-BN greatly reduces at low temperatures but can be still preserved as high as 96% that of graphene at room temperature. This could be explained by the fact that the h-BN coupling affects the out-of-plane vibrations, linearizing the flexural phonon modes and suppressing the transmittance. However, it has a minor effect on the in-plane vibrations, leaving the TA and LA phonons unchanged. Furthermore, the effect of different layers of h-BN (N) on the thermal conductance of graphene has also been studied, and the results showed that the presence of multi-layers h-BN (
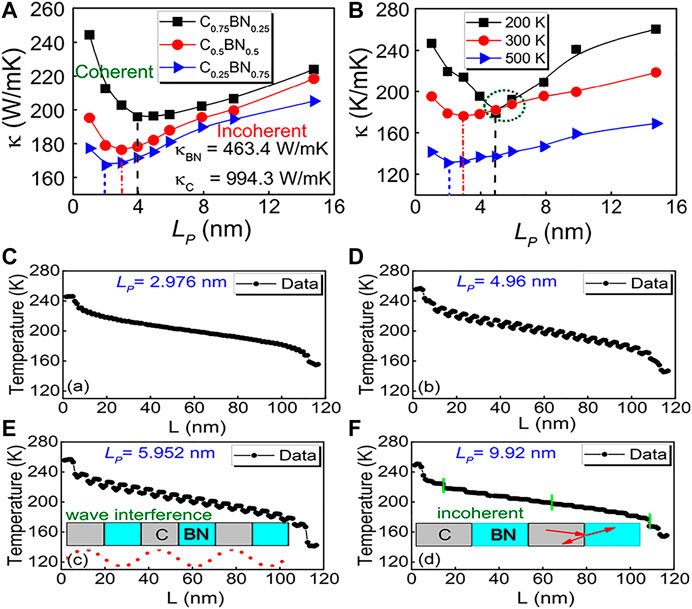
FIGURE 4. The thermal conductivity of graphene/h-BN superlattice as a function of
Apart from graphene/h-BN vdW heterostructure, the ITC of other vdW heterostructures have also been investigated. Based on MD simulations, (Pei et al., 2017) showed that constructing the graphene/phosphorene/graphene sandwiched structures can elevate the thermal stability and thermal conductivity of phosphorene. (Liang et al., 2018) found that the in-plane thermal transport in graphene/phosphorene vdW heterostructures exists obvious anisotropy and increasing the interlayer coupling could enhance the thermal conductivity of phosphorene layer because of phonons stiffening. With the aid of NEMD simulations, (Zhang et al., 2016) found defect, hydrogenation and compressive strain can increase the ITC of graphene/phosphorene/grapheme multilayer structures. By BTE method, the room-temperature thermal conductivity of MoS2/MoSe2 bilayer heterostructure was predicted to be 25.4 Wm−1 K−1 (Ma et al., 2019), which is intermediate between MoSe2 and MoS2. Moreover, it was also found that increasing temperature will decrease the in-plane thermal conductivity, but increase the ITC. (Gao et al., 2016) showed that the interlayer coupling can reduce the in-plane thermal conductivity of graphene layer in graphene/MoS2 bilayer heterostructure, but barely affects the thermal transport in MoS2 layer. Similar phenomenon has been reported in the h-BN/silicene bilayer heterostructure by (Cai, et al., 2016). More importantly, they also found that the electronic and phonon transport are dominated by the silicone and h-BN layers, repectively, which realizes the decupling of phonon and electron transport. (Hong et al., 2018) summarized systematically the ITC of different grapheme-based heterostructurs, and the obtained results range from 2.8 to 25 M WK−1 m−2 at temperature range from 100 to 700 K. In a word, the ITC can be modulated by temperature, contact pressure, hydrogenation and vacancy defects. Experimentally, the ITC measurement of vdW heterostructures has been reported in previous studies. Using the Raman optothermal technique, (Liu et al., 2017c) observed that the ITC of MoS2/h-BN vdW heterostructure (∼17 MW m−2 K−1) is a third of that of graphene/h-BN one (∼52 MW m−2 K−1). That is because the lighter mass of carbon atoms leads to larger frequency range that can be available for phonon transmission from the graphene to h-BN region. Another example, (Kim et al., 2018) used the space-resolved Raman spectroscopy technique to show that the doping level regulated by high electric field is beneficial to the spatial heat dissipation of graphene/h-BN devices, particularly close to the temperature of graphene breakdown.
The manipulation of thermal transport in 2D heterostructres is crucial for the design of micro-nano devices based on them. However, since thermal transport is carried by a large population of phonons spanning a frequency spectrum and existing diverse interactions, controlling phonon transport is actually a complex task. Basically, the phonon scattering processes could be enhanced by introducing structural defects like isotopes, vacancy or dislocation, substrates, chemisorption, and strain. Note that using the mentioned-above controlling method, only the phonons with short wavelengths gets scattered efficiently by above tuning methods, while some long-wavelength phonons are nearly not influenced. Recently, a new thinking for manipulating phonon transport on the base of the wave nature of phonons like interference or local resonance has drawn considerable attention. Besides, the pseudospins and topological effects of phonons as new quantum degrees of freedom might be utilized to manipulate phonons (Gao et al., 2018; Liu et al., 2019b; Xiong et al., 2018).
During the preparation of 2D materials, point-defect, isotopes and grain boundaries, inevitably resides in samples. The presence of imperfections normally introduces phonon scattering and thus causes decreasing thermal conductivity. The effect of randomly distributed isotopes was studied in h-BN via BTE calculations (Lindsay and Broido, 2011), demonstrating that the reduced thermal conductivity is the result of high-frequency phonon modes scattering induced by mass difference. Using AGF method, (Mingo et al., 2010) found that the presence of isotope clustering could strengthen the cross section scattering. Analogously, (Morooka et al., 2008) demonstrated two interesting phonon transport behavior in GNRs with SW-defects: the first is that there is edge heat flux and the second is the appearance of circulating heat flux near SW defect. Subsequently, (Jiang et al., 2011a) showed that the probability of phonon transmission across the Si-doped region in graphene is very low, causing a significant reduction of thermal conductivity. (Huang et al., 2013) reported the influence of extended line-defects on the thermal conductance of GNRs, and showed that the modulation of the relative orientation between line-defect and transport direction can substantially change the system’s thermal conductance. With aid of the NEMD simulations, (Ding et al., 2015) indicated the thermal conductivity of MoS2 is reduced by over 60% for a 0.5% mono-Mo vacancy concentration. The analysis of SDE revealed that the reduction of thermal conductivity in defective MoS2 is mainly determined by the phonon relaxation time. Analogously, (Zhou and Chen, 2015) found that the presence of nanoholes in graphyne nanoribbons will result in the intensive localization of phonons. In particular, a thought of “nanodomains in 2D alloy” has been proposed (Gu and Yang, 2016), because alloying can strongly scatter the high-frequency phonons, as shown in Figure 5. Moreover, (Ding et al., 2016) found that an unexpected enhancement of the ITC is observed when vacancy defects are introduced at the interface layers. The defect-induced enhancement in thermal transport is attributed to the increased friction and thus enhanced phonon coupling at the interfaces. Using the suspended thermal bridge method, (Aiyiti et al., 2018) experimentally verified that the introduction of defect is an effective approach to lower the thermal conductivity of few layer MoS2.
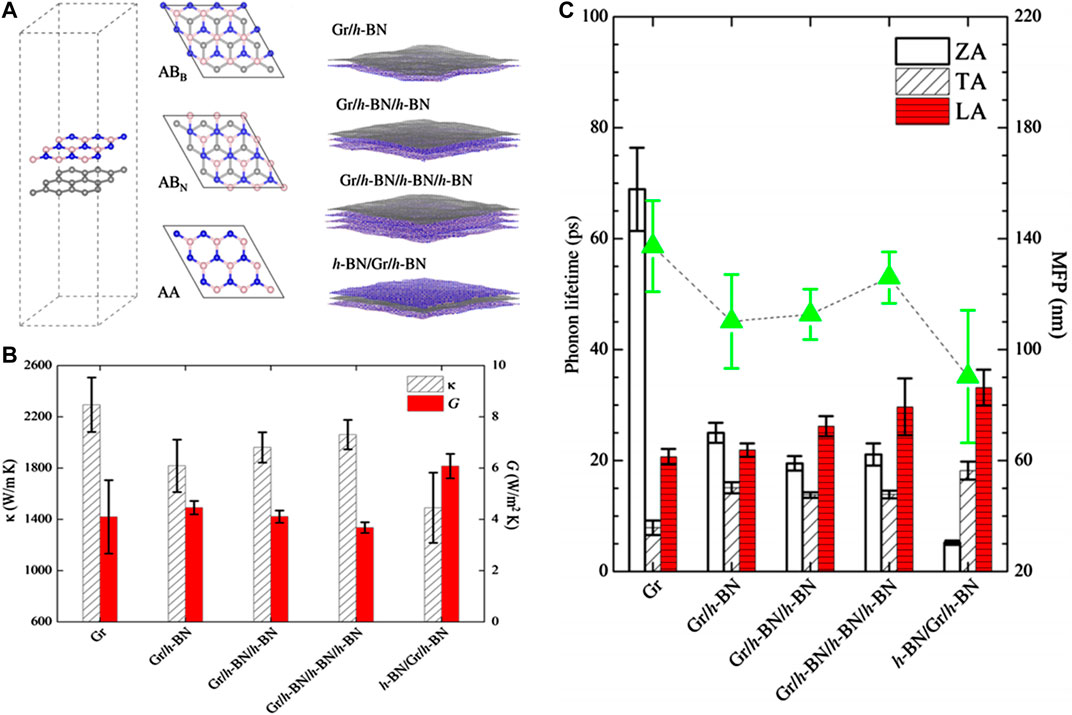
FIGURE 5. (A) Schematic of the graphene and h-BN heterostructures used in MD simulations, Gray, pink, and blue balls represent C, B, and N atoms, respectively. (B) Thermal conductivity (
Mechanical strain as a regular method has been widely applied to modulate the physical properties of 2D materials. In general, the thermal conductivities of 2D planar nanostructures like graphene or graphyne monotonically decrease with increasing the tensile strain because of phonon softening, which lowers the phonon group velocity (Wei et al., 2011). By contrast, in the buckled 2D materials like silicene or phosphorene, the dependence of thermal conductivity on the tensile strain shows a transition from the initial increase to subsequent reduction variation. For instance, based on MD simulations, (Fan et al., 2017) demonstrated that the loading of tensile strain can increase the relaxation times of ZA phonon modes in graphene. Using BTE method under RTA, (Kuang et al., 2016) reported that the applied tensile strain can either reduce or increase the thermal conductivity of graphene, which depends on the sample length. Apart from graphene, (Jiang et al., 2013) demonstrated that the thermal conductivity of MoS2 monotonically decreases with the increase of tensile strain. (Xie et al., 2016) performed the BTE simulations to study the controllable thermal conductivity in monolayer silicene by mechanical strain. Here, there was an up-and-down relation between the obtained thermal conductivity and the tensile strain, because a small tensile strain is able to partially recover the selection rule that only exists in 2D planar nanostructure. While the tensile strain becomes large, the appearance of phonon softening lowers the phonon group velocity. Moreover, using NEMD method, (Zhu and Ertekin, 2015) reported that the thermal conductivity of graphene/h-BN superlattice initially increases to a peak value, after which it then decreases with further strain. The non-monotonic curve was considered as a competition between in-plane softening and flexural stiffening of phonons. (Chen et al., 2017c) showed that as a compressive strain of 0.18 is applied in the graphene/black phosphorus vdW heterostructures, the ITC increase more than 15-fold compared to the strain-free value. The significant enhancement of ITC induced by compressive strain could be understood from the following two aspects. The first is that the applied normal pressure on the multilayer structures clearly strengths the interlayer coupling. The second is that the compressive strain also enhances the shear interaction between the interlayers and thus improves the thermal transport contribution from in-plane phonons. Experimentally, (Guo et al., 2020) reported the tensile strain dependence of the thermal conductivity of monolayer graphene using optothermal Raman method. The measured results demonstrated that under a 0.12% biaxial tensile strain, the system’s thermal conductivity drops approximately by 20% at 350 K, which verifies the previous theoretical literatures prediction (Varshney et al., 2018). Similar phenomenon has also been reported in polycrystalline multilayer graphene based on the microbridge measurement (Zeng et al., 2020c). Additionly, using TDTR method, (Meng et al., 2019) showed that a 9% cross-plane compressive strain can cause the 7-fold increase of the cross-plane thermal conductivity of multilayer MoS2, which is available for improving MoS2-based device performance and stability, as shown in Figure 6. The analysis of lattice dynamics and phonon spectroscopy revealed that the drastic increase of cross-plane thermal conductivity with pressure is mainly the result of strengthened interlayer forces and enhanced group velocity of longitudinal acoustic phonons, while the saturation of thermal conductivity above 15 GPa is associated with the combined effects from increasing group velocity and reduced phonon lifetimes. It is conceivable that the observed phenomena should occur in most vdW heterosturctues.
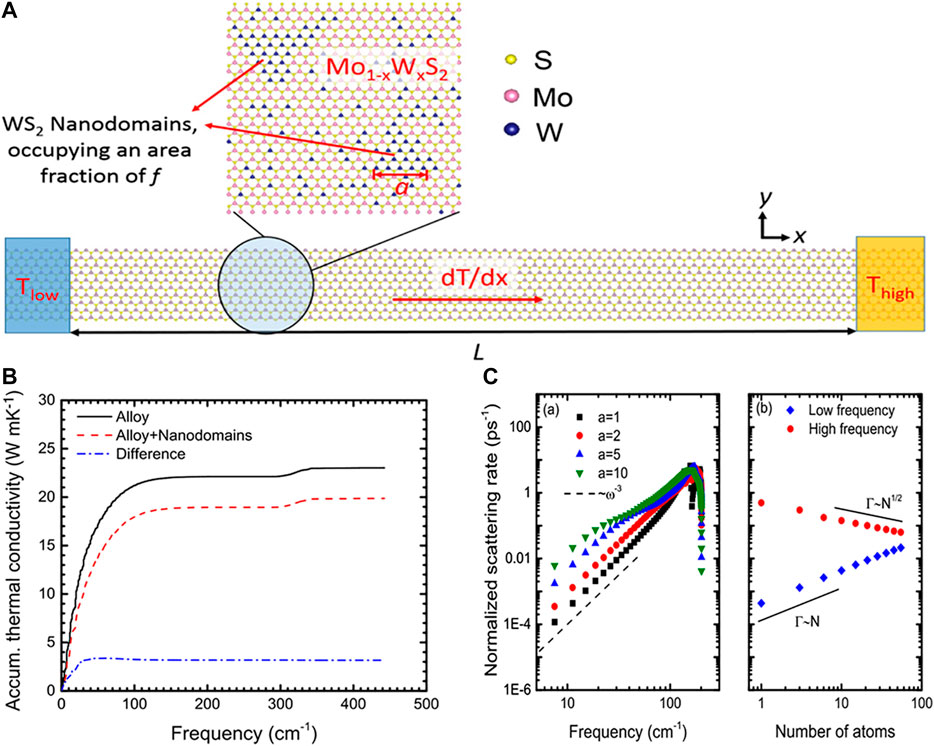
FIGURE 6. A typical atomic configuration for the Mo1−xWxS2 alloy embedded with triangular WS2 nanodomains (B) The accumulative thermal conductivity of Mo0.5W0.5S2 with and without nanodomains embedded as a function phonon frequency. (C) The phonon nanodomain scattering rates of LA phonons from the
The third common approach to modulate the thermal conductivity of 2D heterostructres is chemical functionalization. Using SED technology, (Pei et al., 2011; Kim et al., 2012) found that the hydrogenation coverage dependence of thermal conductivity in functionalized graphene shows a U-shaped variation, similar to the composition dependence of thermal conductivity in Si/Ge alloy (Xie et al., 2020). (Mu et al., 2014) reported that a 5% oxidation coverage leads to a 90% reduction of thermal conductivity in graphene samples. It can be explained from the following two aspects: one is that the existence of the oxygen atoms adds phonon-impurity scattering; the other is that the reflection symmetry of pristine graphene plane is destructed owing to oxygen coverage, which enhances the scattering of flexural modes. In some cases, hydrogenation is beneficial for the thermal transport in 2D materials. According to the BTE calculated results, (Wu et al., 2016) demonstrated that the hydrogenations can enhance the phonon transport in penta-graphene (up to 76% increase), which ascribes to the wakening anharmonicity of C-C bond. Using EMD method, (Yang et al., 2018) found that when the coverage of the adsorbed groups exceeds 0.1, the thermal conductivity of functioned h-BN remains constant (about 100 Wm−1 K−1), which are still sufficiently thermally conductive as fillers of composites. (Hong et al., 2016a) showed that the ITR of graphene/phosphorene bilayer heterostructure increases monotonically with the hydrogen coverage in graphene layer. The maximum addition of 84.5% is observed at 12% hydrogen coverage. The enhanced thermal transport can be understood that an extra H–P heat dissipation channel is created in addition to that between C–P atoms and the absorbed H atoms on graphene behave as scattering centers, thereby enhancing the graphene’s lateral to flexural direction phonon coupling which indirectly strengthens the thermal transmission from graphene to phosphorene. (Liang et al., 2018) found that the in-plane thermal conductivity of phosphorene layer in graphene/phosphorene vdW heterostrucutres is significantly improved by hydrogenating the graphene layer.
When 2D materials or related heterostructres are integrated for device applications, their thermal transport properties have been drastically altered on account of the phonon-substrate scattering. The heat generated in device geometry may flow in the sample, and is dissipated directly into the substrate through their interfaces. (Sadeghi et al., 2013) experimentally observed that when the number of layers in SiO2–supported few-layer graphene achieves 34, the system’s thermal conductivity almost equated with the natural graphite, because there are long-wavelength out-of-plane phonons and partially diffusive interface-phonon scattering in thick sample. In general, the substrate will cause the enhancement of optical phonon scattering in 2D materials (Berciaud et al., 2009). In terms of SED analysis, (Qiu et al., 2012b) argued that the substrate effect is responsible for the reduction of the phonon relaxation time of ZA modes. Interestingly, (Su and Zhang, 2015) experimentally demonstrated that the SiO2 substrate could double the thermal conductivity of phosphorene film, which differs from the case in SiO2-supported CNTs (Ong et al., 2011). Based on EMD simulations, (Chen et al., 2016a) revealed that the degree of thermal transport anisotropy can be significantly enhanced in supported phosphorene. That was because the substrate effect significantly suppresses the ZA modes that dominate the thermal transport along armchair direction. (Li et al., 2018c) found that the ITC of graphene/h-BN in-plane heterostructrue is enhanced as it couples with a SiO2 substrate, which ascribes to the increase of thermal transport channels. Similar simulated results have been reported in asymmetric graphene/h-BN in-plane heterosturctures (Sandonas et al., 2017).
Considering that phonons are waves of the atomic lattice, it is natural to think phonons interference, which could be used to regulate thermal transport (Chen et al., 2005; Xie et al., 2018a; Xie et al., 2018b; Zeng et al., 2020a). Actually, in periodic superlattice, phonons would be reflected by the periodic interfere as that the photons in photonic crystals. To produce the interference patterns, it should satisfy the following two conditions. First, the interface roughness is much less than the phonon wavelength, in which the phase of phonons could be preserved after undergoing interface scattering. However, the wavelengths of most phonons at room temperature are rather short in superlattice. Hence, atomically smooth interface are required for distinct phonon interference. Second, the spacing of two adjacent interfaces (namely period length) should also be relatively short so that propagating phonons will not be scattered before being reflected at the interfaces. For this, the coherent phonons consisting of the constructive interference of incident and reflected phonons could preserve their phases across multiple interfaces. That is, when the period length is sufficiently long, phonons are difficult to produce interference patterns, and so the phonon transport is diffusive and corresponding thermal conductivity monotonically increases with the number of scattering interfaces. From the kinetic theory perspective, the phonon interference might generate a phonon-gap, and decline the system’s thermal conductivity to some extent. More importantly, the interference could flatten the phonon dispersion in a large frequency range, which affects the group velocity, as discussed in In-Plane Heterostructures. Note that the strict condition of phonon interference actually limits the applications of one-dimensional superlattice.
Lately, a metamaterial constructed by arrays of pillars on the nanofilms/nanowires has attracted more and more attention. The presence of nanopillars causes the formation of various resonant modes in the whole frequency range. If the resonant modes have the same polarization and frequency with the propagating modes from the base material, both kinds of phonons will hybridize due to the band anticrossing effect, and the phonon group velocity is lowered. The advantage of this design is that the long-wavelength phonons can be effectively controlled. For instance, using BTE method, (Davis and Hussein, 2014) calculated the thermal conductivity of nanopillared silicon thin films, and found that the obtained value is less than half of that in pristine nanowires. This is attributed to the hybridizations taking place at both subwavelength and superwavelength frequencies. Moreover, based on the NEMD simulations, (Xiong et al., 2016) reported that introducing resonant structures to alloying structures could achieve ultra-low thermal conductivity (0.9 Wm−1 K−1). It can be understood that the local resonance effect impedes the transport of low-frequency phonons and alloying can effectively scatter high-frequency phonons. Subsequent studies also confirmed this conclusion (Liu et al., 2018b; Nomura et al., 2018). Apart from silicon-based nanostrucutres, (Ma et al., 2018) reported a reduction of half thermal conductivity in nanopillared GNRs compared to pristine nanoribbons. It was also found that isotopic doping in nanopillars is conducive to phonon transport, because doping could weaken the hybridization degree. By designing the pristine/branched GNR junctions, (Chen et al., 2018b) proposed a high-performance thermal rectifier where its TR ratio is as high as 400% under a small temperature bias. The underlying mechanism was found to be that when the longitudinal phonons exists obvious local resonance for the negative heat flux. Experimentally, (Anufriev et al., 2017) observed a reduced thermal conductivity in silicon films by attaching aluminum pillars. However, they argued that the reduction of thermal conductivity originates from interface roughness induced by the metal deposition rather than phonon local resonance. In other words, the validity of phonon local resonance lowering thermal conductivity is still not clear. Furthermore, the design 2D hole-based phononic crystal is another feasible method to manipulate phonon transport. (Feng and Ruan, 2016) claimed that the thermal conductivity of graphene phononic crystal (GPC) is three orders of magnitude lower than the pristine one and decreases exponentially with increasing porosity. The vibrational eigen-mode analysis revealed that the phonon localization and phonon back scattering around the nanopores are the major factor responsible for the ultra-low thermal conductivity of GPC. Similar results have also been reported in some other studies (Hu et al., 2019). Analogously, (Cui et al., 2018a) reported that the thermal conductivity of silicene phononic crystal is not sensitive to temperature but strongly depends on the porosity ratio, as that in 3D phononic crystal (Hopkins et al., 2011). There were three reasons for that, namely increasing phonon scatterings, inducing phonon localization and phonon coherent effects.
From the point of view of informatics, phonons as heat carriers can be also used for data storage and processing, namely called phononics. Various thermal devices (corresponding to the electronic counterparts) like rectifier, transistor, and logic gate have been conceptualized (Li et al., 2012; Jia et al., 2020), making the design of thermal logic circuits possible. Then, some of them are gradually realized via designing different sophisticated nanojunctions. To be specific, thermal rectifier as basic components that enables heat flow preferentially in one direction has been explored both theoretically and experimentally. For example, (Chang et al., 2006) experimentally observed the TR phenomenon in gradual mass-loading BN nanotubes opened the active regulation of heat flux in low-dimensional materials (Chang et al., 2006). After that, numerous architecture models like graded core-shell nanowires (Liu et al., 2014e), asymmetric nanobibbons (Zhang and Zhang, 2011; Sandonas et al., 2017; Li et al., 2018c) and phase change materials (Kang et al., 2018) have been proposed to use as nanoscale thermal rectifiers. For example, the TR ratio of the single-layer Y-shaped GNRs was predicted to be about 45% under a normalized temperature bias (
Apart from geometric asymmetry and mass asymmetry, the introduction of functionalized or defected engineering is also able to realize efficient TR effect. (Pal and Puri, 2014) proposed asymmetrically polymer-functionalized carbon nanotubes (CNTs) to obtain high TR ratio. When the applied temperature bias was 40 K, the TR ratio could be as high as 204% in this complex structure. From this work, it can be summarized that the structural asymmetry and the strong temperature dependence of vibration density of states are two necessary conductions to obtain high TR ratio. (Melis et al., 2015) reported that the TR ratio is about 54% in pristine/hydrogenated graphene heterojuction with triangular morphology. (Hu et al., 2017) proposed the thought of improving TR performance by tendering multi thermal rectifiers. (Nobakht et al., 2018) studied TR in defect-engineered graphene with asymmetric holing arrangements. It was found that the TR ratio increases as porosity increases, and can reach as high as 78% at room temperature with triangular hole arrangement with porosity of 75%, enabling effective and precise TR. Using microbridge method, (Wang et al., 2017a) experimentally demonstrated the measured TR ratio is about 26% in asymmetric defect graphene, which is ascribed to temperature and space dependence of thermal conductivity. It is worth pointing out that the aforementioned good TR effect commonly requires large temperature bias and delicate nanostructures namely complicated synthetic procedures, which limits the practical applications. Recently, phase change materials show promising potential in high-performance thermal rectifier. Utilizing the crystalline polymer nanofiber/cross-linked polymer nanofiber heterojunctions, (Zhang and Luo, 2015b) constructed a new thermal rectifier and its workflow was that the polymer nanofiber portion undergoes a phase transition and its thermal conductivity dramatically alters under temperature gradient. As a result, a 20 K temperature bias stimulated ∼100% TR ratio. Detailed spectral analysis revealed that the large TR ratio was ascribed to by the vibrational mismatch of sulfur and carbon atoms. (Kang et al., 2018) developed an analytical framework upon a material architecture for actualizing one type of nonlinear thermal transport, and applied the analytical framework to a junction comprising two phase-change materials (polyethylene and vanadium dioxide). The results showed that such heterojunction has a maximal theoretical rectification factor of approximately 140%. However, associated problems include slow phase change and narrow temperature range, thus hindering practical applications.
Actually, constructing nanojunctions is an effective method to implement efficient thermal rectifier. Base on NEMD simulations, (Yang et al., 2017) demonstrated that the TR ratio is as high as 1,200% in graphene/CNTs junction under 300 K temperature bias, approaching the actual application, which is considered as the formation of standing wave along negative heat flux direction. (Chen et al., 2019b) reported a high TR ratio of 334% in carbon/h-BN heteronanotubes can achieve 334%. Similar phenomenon has also been found in gaphene/h-BN in-plane heterostructures (Chen et al., 2016d). Note that a moderate C/BN ratio and parallel arrangement help improve the TR ratio in CBN hybrids (Chen et al., 2016b). (Dong et al., 2019) reported that the TR ratio in Au/CNTs heterojunctions decreases with the number of the molecular bridges but increases with the length of CNTs, reaching 375% under 60 K temperature bias. (Sandonas et al., 2017) indicated that the TR ratio in supported graphene/h-BN in-plane heterojunctions increases from 8.8 to 79% by lowering the substrate temperature. Recently, (Wei et al., 2019) proposed a new thermal rectifier base on multilayer graphene-based with interlayer gradient functionalization. The TR mechanism was that the vocational of each graphene layer exists obvious difference. (Chen et al., 2020b) reported a distinct TR effect in asymmetric graphene/h-BN vdW heterostructure. Moreover, the TR ratio increased rapidly with the interlayer coupling level, as shown in Figure 7A. Detailed spectral analyses revealed that for strong interlayer coupling, the low-frequency phonons presents the characteristic of localized modes along negative heat flux direction, while
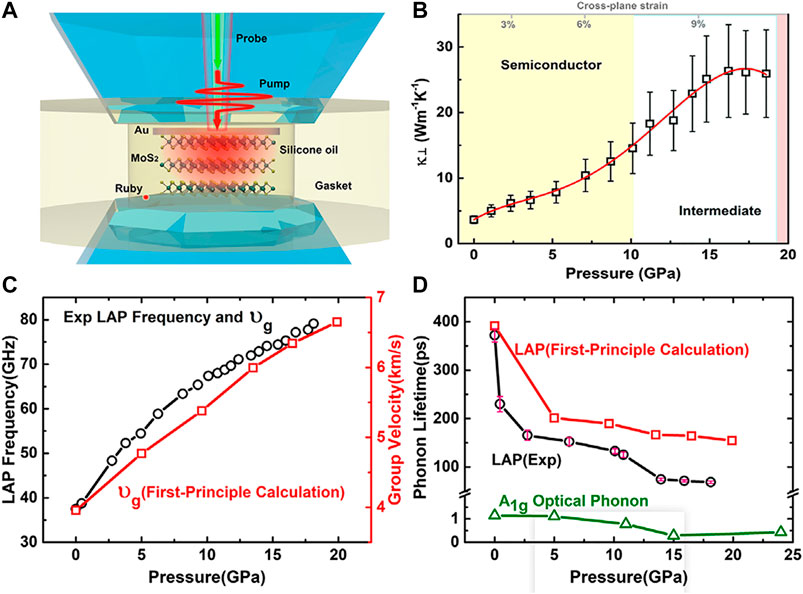
FIGURE 7. (A) Schematic of thermal conductivity measurement with a diamond anvil cell integrated with a picosecond TRTR, (B) Extracted cross-plane thermal conductivity (dominated by phonons) as a function of pressure. The red curve is included only as a guide to the eye, (C) Pressure-dependent coherent longitudinal acoustic phonons (LAP) frequencies extracted from coherent phonon spectroscopy (CPS) measurements (black circles) and LAP group velocities from first-principles calculations (red squares), (D) Pressure-dependent LAP lifetimes extracted from CPS measurements (black circles) and from first-principles calculations (red squares), as well as lifetimes of A1g optical phonons extracted from Raman measurements (green triangles). Reproduced from (Meng et al., 2019) with permission from American Physical Society.
Apart from TR effect, another crucial thermal transport phenomenon is negative differential thermal resistance (NDTR) in which heat flux is inversely correlated with thermal bias. Actually, NDTR is the foundation not only for thermal switching, but also for thermal memory. By now, the phenomenon has been widely investigated in non-linear lattice models (Chan et al., 2014). Some obtained results showed that the existence of interface effect is a requirement for generating NDTR. Subsequently, (Ai et al., 2012) found that the phenomenon of NDTR only exists in single-layer GNRs with appropriate width. For multi-layer GNRs, NDTR regime becomes gradually smaller and even disappears with increasing the number of layers. By designing sandwiched nanofluids, (Li et al., 2019) demonstrated that the heat flux is suppressed and even prohibited when temperature bias becomes sufficiently large, because nanofluids are adsorbed on the solid surface under negative temperature bias, and the free fluid molecules is decreased. Furthermore, (Chen et al., 2017b) studied the nonlinear thermal transport in graphene/h-BN in-plane heterostructure and showed that when
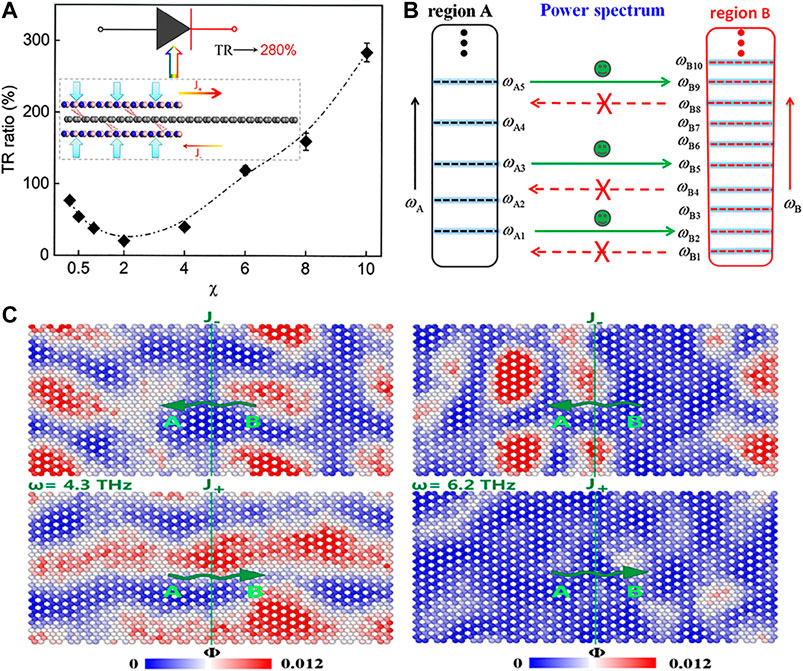
FIGURE 8. (A) The dependence of the TR ratio on the coupling strength
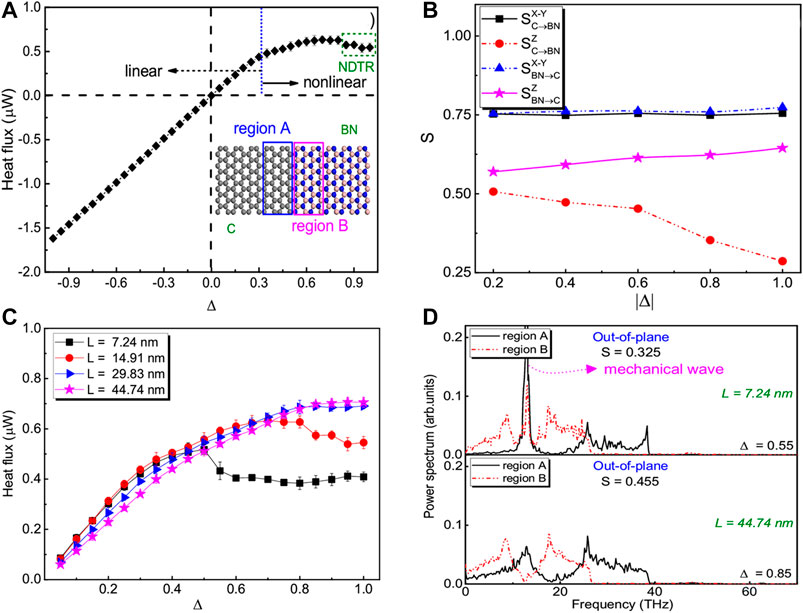
FIGURE 9. (A) Heat flux
Thermoelectric materials enable heat energy to directly convert into electric power. The efficiency of thermoelectric conversion is determined by a dimensionless parameter, namely figure-of-merit (
Reducing dimensionality as an important strategy for enhancing thermoelectric performance has been proposed by (Heremans et al., 2013), and its working mechanisms are as follows: 1) the size-quantization in low-dimensional nanostrucutres facilitates increasing the Seebeck coefficient; 2) the phonon-boundary scatterings can reduces the system’s thermal conductivity. In fact, it has reported that the electronic transmission exists obvious fluctuation within the first conductance band for asymmetric GNRs, and consequently the Seebeck coefficient is enhanced (Xie et al., 2012; Cao et al., 2019). (Yokomizo and Nakamura, 2013) demonstrated that the value of
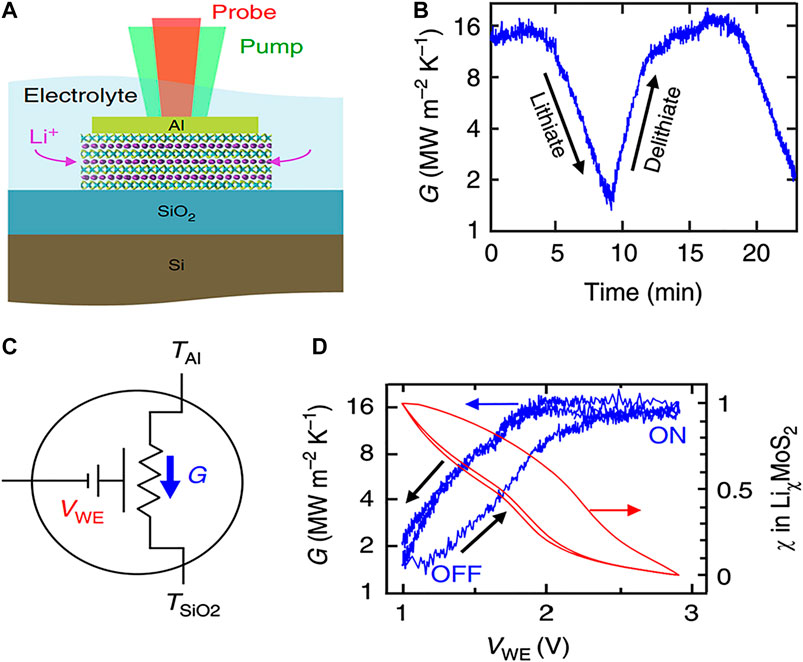
FIGURE 10. (A) The working principle of such device. (B) The measurement of cross-plane thermal conductance during the electrochemical cycle, (C) The gating voltage VWE that is applied between Li and Al/MoS2 electrodes changes the thermal conductance G. (D) Thermal conductance and average lithium composition χ plotted as a function of voltage, indicating significant hysteresis between charge and discharge curves. Reproduced from (Sood et al., 2018) with permission from Nature Publishing Group.
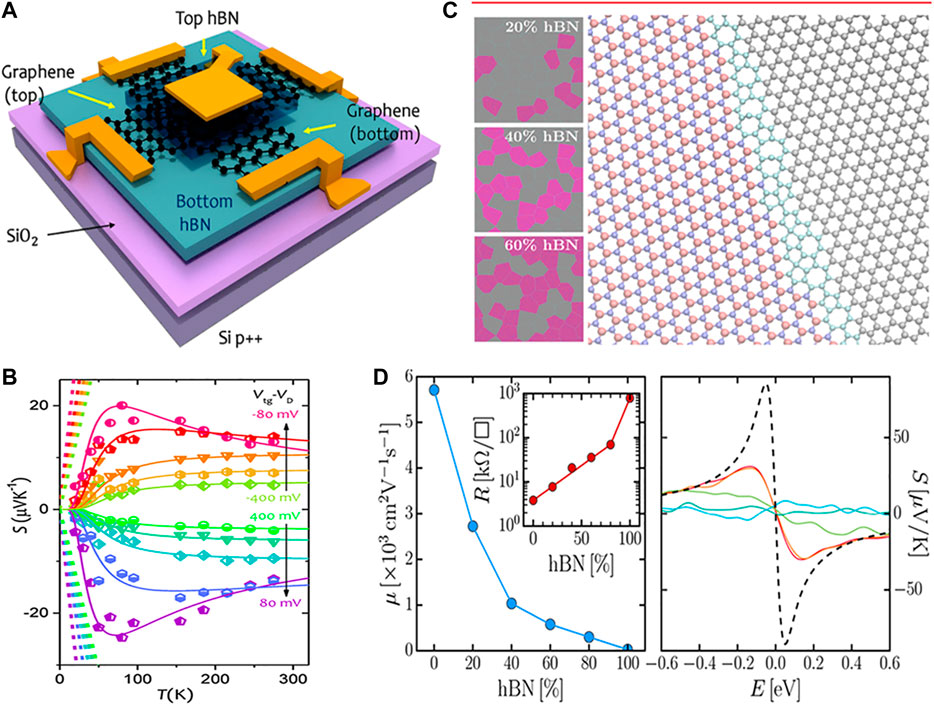
FIGURE 11. (A) Schematic of the h-BN-encapsulated twisted-bilayer graphene device geometry including the contact pads used for the cross-plane thermoelectricity measurement. (B) Temperature dependence of the Seebeck coefficient for different
To sum up, 2D heterostructures have great potential for the applications of thermoelectric conversion. However, theoretical calculations still have large limitations due to the limitation of computation cost and the handing question of van der Waals force in the DFT calculation. In particular, the electron–phonon coupling was not considered in the calculation process. In fact, some previous studies have indicated that the electron–phonon coupling can severely affect the electron transport properties such as spin filter and magnetoresistances (Liu et al., 2017b; Li and Chen, 2017). Again, (Zhu et al., 2019) found that the presence of bipolar effect in SnP3 could lower the system thermal conductivity and help enhance the ZT value (∼3.4). Hence, new theoretical method including multiparticle coupling is necessary to predict the thermoelectric performance of nanostructurs.
In this review, we have introduced various experimental and theoretical methods for the thermal transport in low-dimensional materials. Then, the thermal transport properties of 2D materials and their in-plane/vdW heterostructures were discussed. Furthermore, we have summarized different thoughts to manipulate thermal conductivity. In practical terms, the introduction of isotopes, dislocation, substrates, chemisorption, and strain can strength diffuse phonon scattering (particle-like), which is valid with a limited range of high-frequency phonons. Meanwhile, the wave nature of phonons like interference or local resonance can regulate low-frequency phonons. The diversity of thermal properties in 2D heterostructures indicates important potential applications in thermoelectric, thermal dissipation and thermal devices fields, which needs further investigations.
Advanced fabrication techniques have made multistage circuit integration of 2D heterostructures possible, and resolving the thermal dissipation across the interfaces also looms ahead when designing nanodevices. Considering that heat transfer in semiconductor device is carried by a large population of phonons spanning a frequency spectrum and existing diverse interactions, controlling phonon transport is actually a complex task in these nanostructures and some important questions are still not clear. First, the phonon transport in nanostructures under coupling multi-field effect like electron-phonon or magneton-phonon couplings is in the primary stage of development. Some already obtained results are based on either theoretical models or based on multiple hypotheses, and haven’t been verified by experiments. Second, because of the multi-scale character of phonon transport, the accurate control of phonon transport in specific frequency range remains surprisingly difficult. Moreover, the anomalous non-Fourier transport caused by the excitation of the kinetic wave needs further confirmation in experiment. Third, on the experiment side, the accurate measurement of thermal properties of 2D heterostructures still has a long way to go.
X-KC, Y-JZ and K-QC conceived the manuscript. All authors reviewed and discussed the manuscript.
This work was supported by the National Key Research and Development Program of China (No. 2017YFB0701602), by the National Natural Science Foundation of China (Nos. 11674092, 11904161), by Hunan Provincial Natural Science Foundation of China (No. 2018JJ3421), by the Scientific Research Fund of Hunan Provincial Education Department (No. 18C0454) and by the Open Fund of Hunan Provincial Key Laboratory of Advanced Materials for New Energy Storage and Conversion (No. 2018TP1037-202004).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abidi, I. H., Weng, L.-T., Wong, C. P. J., Tyagi, A., Gan, L., Ding, Y., et al. (2018). New approach to unveiling individual atomic layers of 2D materials and their heterostructures. Chem. Mater. 30, 1718–1728. doi:10.1021/acs.chemmater.7b05371
Ai, B. Q., Zhong, W. R., and Hu, B. (2012). Dimension dependence of negative differential thermal resistance in graphene nanoribbons. J. Phys. Chem. C 116, 13810–13815. doi:10.1021/jp303431k
Aiyiti, A., Hu, S., Wang, C., Xi, Q., Cheng, Z., Xia, M., et al. (2018). Thermal conductivity of suspended few-layer MoS2. Nanoscale 10, 2727–2734. doi:10.1039/c7nr07522g
Al Taleb, A., and Farías, D. (2016). Phonon dynamics of graphene on metals. J. Phys. Condens. Matter 28, 103005. doi:10.1088/0953-8984/28/10/103005
Anufriev, R., Yanagisawa, R., and Nomura, M. (2017). Aluminium nanopillars reduce thermal conductivity of silicon nanobeams. Nanoscale 9, 15083–15088. doi:10.1039/c7nr05114j
Balandin, A. A., Ghosh, S., Bao, W., Calizo, I., Teweldebrhan, D., Miao, F., et al. (2008). Superior thermal conductivity of single-layer graphene. Nano Lett. 8, 902–907. doi:10.1021/nl0731872
Barrios-Vargas, J. E., Mortazavi, B., Cummings, A. W., Martinez-Gordillo, R., Pruneda, M., Colombo, L., et al. (2017). Electrical and thermal transport in coplanar polycrystalline graphene–hBN heterostructures. Nano Lett. 17, 1660–1664. doi:10.1021/acs.nanolett.6b04936
Behranginia, A., Hemmat, Z., Majee, A. K., Foss, C. J., Yasaei, P., Aksamija, Z., et al. (2018). Power dissipation of WSe2 field-effect transistors probed by low-frequency Raman thermometry. ACS Appl. Mater. Interfaces 10, 24892–24898. doi:10.1021/acsami.8b04724
Berciaud, S., Ryu, S., Brus, L. E., and Heinz, T. F. (2009). Probing the intrinsic properties of exfoliated graphene: Raman spectroscopy of free-standing monolayers. Nano Lett. 9, 346–352. doi:10.1021/nl8031444
Bertolazzi, S., Krasnozhon, D., and Kis, A. (2013). Nonvolatile memory cells based on MoS2/graphene heterostructures. ACS Nano 7, 3246–3252. doi:10.1021/nn3059136
Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Fan, S., Goodson, K. E., et al. (2014). Nanoscale thermal transport. II. 2003–2012. App. Phys. Rev. 1, 011305 . doi:10.2172/1160069
Cai, Y., Lan, J., Zhang, G., and Zhang, Y. W. (2014). Lattice vibrational modes and phonon thermal conductivity of monolayer MoS2. Phy. Rev. B. 89 (3), 035438. doi:10.1103/physrevb.89.035438
Cai, Y., Pei, Q. X., Zhang, G., and Zhang, Y. W. (2016). Decoupled electron and phonon transports in hexagonal boron nitride-silicene bilayer heterostructure. J. Appl. Phys. 119 (6), 065102. doi:10.1063/1.4941534
Cao, X. H., Wu, D., Feng, Y.-X., Zhou, W.-X., Tang, L.-M., and Chen, K.-Q. (2019). Effect of electrophilic substitution and destructive quantum interference on the thermoelectric performance in molecular devices. J. Phys. Condens. Matter 31, 345303. doi:10.1088/1361-648x/ab2299
Chan, H. K., He, D., and Hu, B. (2014). Scaling analysis of negative differential thermal resistance. Phys. Rev. E 89 (5), 052126. doi:10.1103/physreve.89.052126
Chang, C. W., Okawa, D., Majumdar, A., and Zettl, A. (2006). Solid-state thermal rectifier. Science 314, 1121–1124. doi:10.1126/science.1132898
Chang, H. Y., Yang, S., Lee, J., Tao, L., Hwang, W.-S., Jena, D., et al. . (2013). High-performance, highly bendable MoS2 transistors with high-k dielectrics for flexible low-power systems. ACS Nano, 7, 5446–5452. doi:10.1021/nn401429w
Chen, X.-K., and Chen, K.-Q. (2020a). Thermal transport of carbon nanomaterials. J. Phys. Condens. Matter 32, 153002. doi:10.1088/1361-648x/ab5e57
Chen, K. Q., Li, W. X., Duan, W., Shuai, Z., and Gu, B. L. (2005). Effect of defects on the thermal conductivity in a nanowire. Phys. Rev. B 72 (4), 045422. doi:10.1103/physrevb.72.045422
Chen, S., Wu, Q., Mishra, C., Kang, J., Zhang, H., Cho, K., et al. (2012). Thermal conductivity of isotopically modified graphene. Nat. Mater.. 11, 203–207. doi:10.1038/nmat3207
Chen, C. C., Li, Z., Shi, L., and Cronin, S. B. (2014). Thermal interface conductance across a graphene/hexagonal boron nitride heterojunction. App. Phy. Lett. 104 (8), 081908. doi:10.1063/1.4866335
Chen, X., Wu, Y., Wu, Z., Han, Y., Xu, S., Wang, L., et al. (2015b). High-quality sandwiched black phosphorus heterostructure and its quantum oscillations. Nat. Commun.. 6, 7315. doi:10.1038/ncomms8315
Chen, J., Chen, S., and Gao, Y. (2016a). Anisotropy enhancement of thermal energy transport in supported black phosphorene. J. Phys. Chem. Lett. 7, 2518–2523. doi:10.1021/acs.jpclett.6b00858
Chen, X.-K., Xie, Z.-X., Zhou, W.-X., and Chen, K.-Q. (2016b). The thermal conductivity in hybridised graphene and boron nitride nanoribbons modulated with strain. J. Phys. D Appl. Phys. 49, 115301. doi:10.1088/0022-3727/49/11/115301
Chen, X. K., Xie, Z. X., Zhou, W. X., Tang, L. M., and Chen, K. Q.. (2016c). Phonon wave interference in graphene and boron nitride superlattice. Appl. Phys. Lett. 109 (2), 023101. doi:10.1063/1.4958688
Chen, X.-K., Xie, Z.-X., Zhou, W.-X., Tang, L.-M., and Chen, K.-Q. (2016d). Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction. Carbon 100, 492–500. doi:10.1016/j.carbon.2016.01.045
Chen, T., Li, H., Zhang, Y., Liu, D., Chao, Y., and Wang, L. (2017a). Parity effects induced by the resonant electronic states coupling in polyacetylene-based devices. J. Electron. Mater. 46, 5121–5126. doi:10.1007/s11664-017-5501-1
Chen, X. K., Liu, J., Peng, Z. H., Du, D., and Chen, K. Q. (2017b). A wave-dominated heat transport mechanism for negative differential thermal resistance in graphene/hexagonal boron nitride heterostructures. Appl. Phys. Lett. 110 (9), 091907. doi:10.1063/1.4977776
Chen, Y., Zhang, Y., Cai, K., Jiang, J., Zheng, J.-C., Zhao, J., et al. (2017c). Interfacial thermal conductance in graphene/black phosphorus heterogeneous structures. Carbon 117, 399–410. doi:10.1016/j.carbon.2017.03.011
Chen, T., Guo, C., Xu, L., Li, Q., Luo, K., Liu, D., et al. (2018a). Modulating the properties of multi-functional molecular devices consisting of zigzag gallium nitride nanoribbons by different magnetic orderings: a first-principles study. Phys. Chem. Chem. Phys. 20, 5726. doi:10.1039/c7cp07467k
Chen, X.-K., Liu, J., Xie, Z.-X., Zhang, Y., Deng, Y.-X., and Chen, K.-Q. (2018b). A local resonance mechanism for thermal rectification in pristine/branched graphene nanoribbon junctions. Appl. Phys. Lett. 113, 121906. doi:10.1063/1.5053233
Chen, X., Chen, C., Levi, A., Houben, L., Deng, B., Yuan, S., et al. (2018c). Large-velocity saturation in thin-film black phosphorus transistors. ACS Nano, 12, 5003–5010. doi:10.1021/acsnano.8b02295
Chen, T., Xu, L., Li, Q., Li, X., and Long, M. (2019a). Direction and strain controlled anisotropic transport behaviors of 2D GeSe-phosphorene vdW heterojunctions. Nanotechnology 30, 445703. doi:10.1088/1361-6528/ab375b
Chen, X.-K., Xie, Z.-X., Zhang, Y., Deng, Y.-X., Zou, T.-H., Liu, J., et al. (2019b). Highly efficient thermal rectification in carbon/boron nitride heteronanotubes. Carbon 148, 532–539. doi:10.1016/j.carbon.2019.03.073
Chen, X.-K., Pang, M., Chen, T., Du, D., and Chen, K.-Q. (2020b). Thermal rectification in asymmetric graphene/hexagonal boron nitride van der Waals heterostructures. ACS Appl. Mater. Interfaces 12, 15517–15526. doi:10.1021/acsami.9b22498
Cherukara, M. J., Narayanan, B., Kinaci, A., Sasikumar, K., Gray, S. K., Chan, M. K. Y., et al. (2016). Ab initio-based bond order potential to investigate low thermal conductivity of stanene nanostructures. J. Phys. Chem. Lett. 7, 3752–3759. doi:10.1021/acs.jpclett.6b01562
Ci, L., Song, L., Jin, C., Jariwala, D., Wu, D., Li, Y., et al. (2010). Atomic layers of hybridized boron nitride and graphene domains. Nat. Mater.. 9, 430–435. doi:10.1038/nmat2711
Cui, L., Shi, S., Li, Z., Wei, G., and Du, X. (2018a). Reduction of thermal conductivity in silicene nanomesh: insights from coherent and incoherent phonon transport. Phys. Chem. Chem. Phys. 20, 27169–27175. doi:10.1039/c8cp03993c
Cui, X., Ouyang, T., Li, J., He, C., Tang, C., and Zhong, J. (2018b). Enhancing the thermoelectric performance of gamma-graphyne nanoribbons by introducing edge disorder. Phys. Chem. Chem. Phys. 20, 7173–7179. doi:10.1039/c7cp08154e
da Silva, C., Saiz, F., Romero, D. A., and Amon, C. H. (2016). Coherent phonon transport in short-period two-dimensional superlattices of graphene and boron nitride. Phy. Rev. B 93, 125427. doi:10.1103/physrevb.93.125427
Davis, B. L., and Hussein, M. I. (2014). Thermal conductivity reduction by local resonance. Phys. Rev. Lett. 112 (5), 055505. doi:10.1103/physrevlett.112.055505
Deng, Y.-X., Chen, S.-Z., Zeng, Y., Zhou, W.-X., and Chen, K.-Q. (2017). Large spin rectifying and high-efficiency spin-filtering in superior molecular junction. Org. Electron. 50, 184–190. doi:10.1016/j.orgel.2017.07.046
Deng, Y.-X., Chen, S.-Z., Zeng, Y., Feng, Y., Zhou, W.-X., Tang, L.-M., et al. (2018). Spin gapless semiconductor and half-metal properties in magnetic penta-hexa-graphene nanotubes. Org. Electron. 63, 310–317. doi:10.1016/j.orgel.2018.09.046
Ding, Z., Pei, Q.-X., Jiang, J.-W., and Zhang, Y.-W. (2015). Manipulating the thermal conductivity of monolayer MoS2 via lattice defect and strain engineering. J. Phys. Chem. C 119, 16358–16365. doi:10.1021/acs.jpcc.5b03607
Ding, Z., Pei, Q.-X., Jiang, J.-W., Huang, W., and Zhang, Y.-W. (2016). Interfacial thermal conductance in graphene/MoS2 heterostructures. Carbon 96, 888–896. doi:10.1016/j.carbon.2015.10.046
Ding, G., He, J., Gao, G. Y., and Yao, K. (2018a). Two-dimensional MoS2-MoSe2 lateral superlattice with minimized lattice thermal conductivity. J. Appl. Phys. 124, 165101. doi:10.1063/1.5051067
Ding, Y., Zhou, N., Gan, L., Yan, X., Wu, R., Abidi, I. H., et al. (2018b). Stacking-mode confined growth of 2H-MoTe2/MoS2 bilayer heterostructures for UV-vis-IR photodetectors. Nanomater. Energy 49, 200–208. doi:10.1016/j.nanoen.2018.04.055
Dollfus, P., Nguyen, V. H., and Saint-Martin, J. (2015). Thermoelectric effects in graphene nanostructures. J. Phys. Condens. Matter 27, 133204. doi:10.1088/0953-8984/27/13/133204
Dong, Y., Diao, C., Song, Y., Chi, H., Singh, D. J., and Lin, J. (2019). Molecular bridge thermal diode enabled by vibrational mismatch. Phys. Rev. Appl. 11, 024043. doi:10.1115/mnhmt2019-3905
Fan, Z. Q., and Chen, K. Q. (2010). Negative differential resistance and rectifying behaviors in phenalenyl molecular device with different contact geometries. Appl. Phys. Lett. 96 (5), 053509. doi:10.1063/1.3309708
Fan, Z., Pereira, L. F. C., Hirvonen, P., Ervasti, M. M., Elder, K. R., Donadio, D., et al. (2017). Thermal conductivity decomposition in two-dimensional materials: application to graphene. Phys. Rev. B 95, 144309. doi:10.1103/physrevb.95.144309
Fan, Z.-Q., Zhang, Z.-H., and Yang, S.-Y. (2020). High-performance 5.1 nm in-plane Janus WSeTe Schottky barrier field effect transistors. Nanoscale 12, 21750. doi:10.1039/d0nr05269h
Fei, R., Faghaninia, A., Soklaski, R., Yan, J.-A., Lo, C., and Yang, L. (2014). Enhanced thermoelectric efficiency via orthogonal electrical and thermal conductances in phosphorene. Nano Lett. 14, 6393–6399. doi:10.1021/nl502865s
Feng, T., and Ruan, X. (2016). Ultra-low thermal conductivity in graphene nanomesh. Carbon 101, 107–113. doi:10.1016/j.carbon.2016.01.082
Feng, T., Yao, W., Wang, Z., Shi, J., Li, C., Cao, B., et al. (2017). Spectral analysis of nonequilibrium molecular dynamics: spectral phonon temperature and local nonequilibrium in thin films and across interfaces. Phys. Rev. B 95, 195202. doi:10.1103/physrevb.95.195202
Frisenda, R., Navarro-Moratalla, E., Gant, P., Pérez De Lara, D., Jarillo-Herrero, P., Gorbachev, R. V., et al. (2018). Recent progress in the assembly of nanodevices and van der Waals heterostructures by deterministic placement of 2D materials. Chem. Soc. Rev. 47, 53–68. doi:10.1039/c7cs00556c
Fu, L., Sun, Y., Wu, N., Mendes, R. G., Chen, L., Xu, Z., et al. (2016). Direct growth of MoS2/h-BN heterostructures via a sulfide-resistant alloy. ACS Nano 10, 2063–2070. doi:10.1021/acsnano.5b06254
Fu, Y., Hansson, J., Liu, Y., Chen, S., Zehri, A., Samani, M. K., et al. (2019). Graphene related materials for thermal management. 2D Mater. 7 (1), 012001. doi:10.1088/2053-1583/ab48d9
Fugallo, G., Cepellotti, A., Paulatto, L., Lazzeri, M., Marzari, N., and Mauri, F. (2014). Thermal conductivity of graphene and graphite: collective excitations and mean free paths. Nano Lett. 14, 6109–6114. doi:10.1021/nl502059f
Gao, Y., and Xu, B. (2017). Controllable interface junction, in-plane heterostructures capable of mechanically mediating on-demand asymmetry of thermal transports. ACS Appl. Mater. Interfaces 9, 34506–34517. doi:10.1021/acsami.7b11508
Gao, Y., Zhang, Y., Chen, P., Li, Y., Liu, M., Gao, T., et al. (2013). Toward single-layer uniform hexagonal boron nitride-graphene patchworks with zigzag linking edges. Nano Lett. 13, 3439–3443. doi:10.1021/nl4021123
Gao, Y., Liu, Q., and Xu, B. (2016). Lattice mismatch dominant yet mechanically tunable thermal conductivity in bilayer heterostructures. ACS Nano 10, 5431–5439. doi:10.1021/acsnano.6b01674
Gao, M., Zhang, W., and Zhang, L. (2018). Nondegenerate chiral phonons in graphene/hexagonal boron nitride heterostructure from first-principles calculations. Nano Lett. 18, 4424–4430. doi:10.1021/acs.nanolett.8b01487
Ma, R., Perry, C. H., and Rupprecht, G. (1966). Normal modes in hexagonal boron nitride. Phys. Rev. 146, 543. doi:10.1103/physrev.146.543
Georgiou, T., Jalil, R., Belle, B. D., Britnell, L., Gorbachev, R. V., Morozov, S. V., et al. (2013). Vertical field-effect transistor based on graphene–WS2 heterostructures for flexible and transparent electronics. Nat. Nanotechnol.. 8, 100–103. doi:10.1038/nnano.2012.224
Gholivand, H., Fuladi, S., Hemmat, Z., Salehi-Khojin, A., and Khalili-Araghi, F. (2019). Effect of surface termination on the lattice thermal conductivity of monolayer Ti3C2Tz MXenes. J. Appl. Phys. 126, 065101. doi:10.1063/1.5094294
Gu, X., and Yang, R. (2014). Phonon transport in single-layer transition metal dichalcogenides: a first-principles study. Appl. Phys. Lett. 105, 131903. doi:10.1063/1.4896685
Gu, X., and Yang, R. (2015). First-principles prediction of phononic thermal conductivity of silicene: a comparison with graphene. J. Appl. Phys. 117 (2), 025102. doi:10.1063/1.4905540
Gu, X., and Yang, R. (2016). Phonon transport in single-layer MO1−x Wx S2 alloy embedded with WS2 nanodomains. Phys. Rev. B 94, 075308. doi:10.1103/physrevb.94.075308
Gu, X., Wei, Y., Yin, X., Li, B., and Yang, R. (2018). Colloquium: phononic thermal properties of two-dimensional materials. Rev. Mod. Rhys 90, 041002. doi:10.1103/revmodphys.90.041002
Guo, Z., Miao, N., Zhou, J., Pan, Y., and Sun, Z. (2018). Coincident modulation of lattice and electron thermal transport performance in MXenes via surface functionalization. Phys. Chem. Chem. Phys. 20, 19689–19697. doi:10.1039/c8cp02564a
Guo, M., Qian, Y., Qi, H., Bi, K., and Chen, Y. (2020). Experimental measurements on the thermal conductivity of strained monolayer graphene. Carbon 157, 185–190. doi:10.1016/j.carbon.2019.10.027
He, J., Li, D., Ying, Y., Feng, C., He, J., Zhong, C., et al. (2019). Orbitally driven giant thermal conductance associated with abnormal strain dependence in hydrogenated graphene-like borophene. Npj Comput. Mater 5, 47. doi:10.1038/s41524-019-0183-2
Hemmat, Z., Yasaei, P., Schultz, J. F., Hong, L., Majidi, L., Behranginia, A., et al. (2019). Tuning thermal transport through atomically thin Ti3C2TzMXene by current annealing in vacuum. Adv. Funct. Mater. 29, 1805693. doi:10.1002/adfm.201805693
Heremans, J. P., Dresselhaus, M. S., Bell, L. E., and Morelli, D. T. (2013). When thermoelectrics reached the nanoscale. Nat. Nanotechnol. 8, 471. doi:10.1038/nnano.2013.129
Hong, Y., Zhang, J., and Zeng, X. C. (2016a). Interlayer thermal conductance within a phosphorene and graphene bilayer. Nanoscale 8, 19211–19218. doi:10.1039/c6nr07977f
Hong, Y., Zhang, J., and Zeng, X. C. (2016b). Thermal conductivity of monolayer MoSe2 and MoS2. J. Phys. Chem. C 120, 26067–26075. doi:10.1021/acs.jpcc.6b07262
Hong, Y., Zhang, J., and Zeng, X. C. (2016c). Thermal contact resistance across a linear heterojunction within a hybrid graphene/hexagonal boron nitride sheet. Phys. Chem. Chem. Phys. 18, 24164–24170. doi:10.1039/c6cp03933b
Hong, Y., Ju, M. G., Zhang, J., and Zeng, X. C. (2018). Phonon thermal transport in a graphene/MoSe2 van der Waals heterobilayer. Phys. Chem. Chem. Phys. 20, 2637–2645. doi:10.1039/c7cp06874c
Hopkins, P. E., Reinke, C. M., Su, M. F., Olsson, R. H., Shaner, E. A., Leseman, Z. C., et al. (2011). Reduction in the thermal conductivity of single crystalline silicon by phononic crystal patterning. Nano Lett. 11, 107–112. doi:10.1021/nl102918q
Hu, M., Zhang, X., and Poulikakos, D. (2013). Anomalous thermal response of silicene to uniaxial stretching. Phy. Rev. B 87, 195417. doi:10.1103/physrevb.87.195417
Hu, S., An, M., Yang, N., and Li, B. (2017). A series circuit of thermal rectifiers: an effective way to enhance rectification ratio. Small 13, 1602726. doi:10.1002/smll.201602726
Hu, S., Zhang, Z., Jiang, P., Ren, W., Yu, C., Shiomi, J., et al. (2019). Disorder limits the coherent phonon transport in two-dimensional phononic crystal structures. Nanoscale 11, 11839–11846. doi:10.1039/c9nr02548k
Huang, H., Xu, Y., Zou, X., Wu, J., and Duan, W. (2013). Tuning thermal conduction via extended defects in graphene. Phys. Rev. B 87, 205415. doi:10.1103/physrevb.87.205415
Huang, C., Wu, S., Sanchez, A. M., Peters, J. J. P., Beanland, R., Ross, J. S., et al. (2014). Lateral heterojunctions within monolayer MoSe2-WSe2 semiconductors. Nat. Mater.. 13, 1096–1101. doi:10.1038/nmat4064
Hung Nguyen, V., Nguyen, M. C., Nguyen, H.-V., Saint-Martin, J., and Dollfus, P. (2014). Enhanced thermoelectric figure of merit in vertical graphene junctions. Appl. Phys. Lett. 105, 133105. doi:10.1063/1.4896915
Iannaccone, G., Bonaccorso, F., Colombo, L., and Fiori, G. (2018). Quantum engineering of transistors based on 2D materials heterostructures. Nat. Nanotechnol. 13, 183–191. doi:10.1038/s41565-018-0082-6
Jang, W., Bao, W., Jing, L., Lau, C. N., and Dames, C. (2013). Thermal conductivity of suspended few-layer graphene by a modified T-bridge method. Appl. Phys. Lett. 103, 133102. doi:10.1063/1.4821941
Jang, H., Wood, J. D., Ryder, C. R., Hersam, M. C., and Cahill, D. G. (2015). Anisotropic thermal conductivity of exfoliated black phosphorus. Adv. Mater.. 27, 8017–8022. doi:10.1002/adma.201503466
Jia, P. Z., Zeng, Y. J., Wu, D., Pan, H., Cao, X. H., Zhou, W. X., et al. . (2019). Excellent thermoelectric performance induced by interface effect in MoS2/MoSe2 van der Waals heterostructure. J. Phys.: condens. Matter 32 (5), 055302. doi:10.1088/1361-648x/ab4cab
Jia, P.-Z., Wu, D., Zhang, Q.-Q., Zhou, W.-X., Fan, Z.-Q., Feng, Y.-X., et al. (2020). Design of thermal metamaterials with excellent thermal control functions by using functional nanoporous graphene. Phys. Status Solidi RRL 14, 2000333. doi:10.1002/pssr.202000333
Jiang, J.-W., Wang, B.-S., and Wang, J.-S. (2011a). First principle study of the thermal conductance in graphene nanoribbon with vacancy and substitutional silicon defects. Appl. Phys. Lett. 98, 113114. doi:10.1063/1.3567768
Jiang, J. W., Wang, J. S., and Wang, B. S. (2011b). Minimum thermal conductance in graphene and boron nitride superlattice. Appl. Phys. Lett. 99(4), 043109. doi:10.1063/1.3619832
Jiang, J.-W., Park, H. S., and Rabczuk, T. (2013). Molecular dynamics simulations of single-layer molybdenum disulphide (MoS2): Stillinger-Weber parametrization, mechanical properties, and thermal conductivity. J. Appl. Phys. 114, 064307. doi:10.1063/1.4818414
Jiang, J. W.. (2014). Phonon bandgap engineering of strained monolayer MoS2. Nanoscale 6, 8326–8333. doi:10.1039/c4nr00279b
Jo, I., Pettes, M. T., Kim, J., Watanabe, K., Taniguchi, T., Yao, Z., et al. (2013). Thermal conductivity and phonon transport in suspended few-layer hexagonal boron nitride. Nano Lett. 13, 550–554. doi:10.1021/nl304060g
Jo, I., Pettes, M. T., Ou, E., Wu, W., and Shi, L. (2014). Basal-plane thermal conductivity of few-layer molybdenum disulfide. Appl. Phys. Lett. 104, 201902. doi:10.1063/1.4876965
Jung, J., Qiao, Z., Niu, Q., and MacDonald, A. H. (2012). Transport properties of graphene nanoroads in boron nitride sheets. Nano Lett. 12, 2936–2940. doi:10.1021/nl300610w
Kakodkar, R. R., and Feser, J. P. (2017). Probing the validity of the diffuse mismatch model for phonons using atomistic simulations. Phys. Rev. B 95, 125434. doi:10.1103/physrevb.95.125434
Kang, J., Jariwala, D., Ryder, C. R., Wells, S. A., Choi, Y., Hwang, E., et al. (2016). Probing out-of-plane charge transport in black phosphorus with graphene-contacted vertical field-effect transistors. Nano Lett., 16, 2580–2585. doi:10.1021/acs.nanolett.6b00144
Kang, H., Yang, F., and Urban, J. J. (2018). Thermal rectification via heterojunctions of solid-state phase-change materials. Phys. Rev. Appl. 10 (2), 024034. doi:10.1103/physrevapplied.10.024034
Keyshar, K., Berg, M., Zhang, X., Vajtai, R., Gupta, G., Chan, C. K., et al. (2017). Experimental determination of the ionization energies of MoSe2, WS2, and MoS2 on SiO2 using photoemission electron microscopy. ACS Nano 11, 8223–8230. doi:10.1021/acsnano.7b03242
Kim, J. Y., Lee, J.-H., and Grossman, J. C. (2012). Thermal transport in functionalized graphene. ACS Nano 6, 9050–9057. doi:10.1021/nn3031595
Kim, D., Kim, H., Yun, W. S., Watanabe, K., Taniguchi, T., Rho, H., et al. (2018). Energy dissipation mechanism revealed by spatially resolved Raman thermometry of graphene/hexagonal boron nitride heterostructure devices. 2D Mater. 5 (2), 025009. doi:10.1088/2053-1583/aaab14
Kuang, Y., Lindsay, L., Shi, S., Wang, X., and Huang, B. (2016). Thermal conductivity of graphene mediated by strain and size. Heat Mass Tran. 101, 772–778. doi:10.1016/j.ijheatmasstransfer.2016.05.072
Lee, S., and Lindsay, L. (2017). Hydrodynamic phonon drift and second sound in a (20, 20) single-wall carbon nanotube. Phys. Rev. B 95, 184304. doi:10.1103/physrevb.95.184304
Lee, S., Broido, D., Esfarjani, K., and Chen, G. (2015a). Hydrodynamic phonon transport in suspended graphene. Nat. Commun.. 6, 6290. doi:10.1038/ncomms7290
Lee, S., Yang, F., Suh, J., Yang, S., Lee, Y., Li, G., et al. (2015b). Anisotropic in-plane thermal conductivity of black phosphorus nanoribbons at temperatures higher than 100 K. Nat. Commun. 6, 9573. doi:10.1038/ncomms9573
Li, B.-L., and Chen, K.-Q. (2017). Effects of electron-phonon interactions on the spin-dependent Seebeck effect in graphene nanoribbons. Carbon 119, 548–554. doi:10.1016/j.carbon.2017.04.069
Li, D., Wu, Y., Kim, P., Shi, L., Yang, P., and Majumdar, A. (2003). Thermal conductivity of individual silicon nanowires. Appl. Phys. Lett. 83, 2934–2936. doi:10.1063/1.1616981
Li, N., Ren, J., Wang, L., Zhang, G., Hänggi, P., and Li, B. (2012). Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045. doi:10.1103/revmodphys.84.1045
Li, H., Ying, H., Chen, X., Nika, D. L., Cocemasov, A. I., Cai, W., et al. (2014a). Thermal conductivity of twisted bilayer graphene. Nanoscale 6, 13402–13408. doi:10.1039/c4nr04455j
Li, W., Carrete, J., Katcho, N. A., and Mingo, N. (2014b). ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput. Phys. Commun. 185, 1747–1758. doi:10.1016/j.cpc.2014.02.015
Li, M.-Y., Shi, Y., Cheng, C.-C., Lu, L.-S., Lin, Y.-C., Tang, H.-L., et al. (2015). Epitaxial growth of a monolayer WSe2-MoS2 lateral p-n junction with an atomically sharp interface. Science 349, 524–528. doi:10.1126/science.aab4097
Li, D., He, J., Ding, G., Tang, Q., Ying, Y., He, J., et al. (2018a). Stretch-driven increase in ultrahigh thermal conductance of hydrogenated borophene and dimensionality crossover in phonon transmission. Adv. Funct. Mater. 28, 1801685. doi:10.1002/adfm.201801685
Li, M., Zheng, B., Duan, K., Zhang, Y., Huang, Z., and Zhou, H. (2018b). Effect of defects on the thermal transport across the graphene/hexagonal boron nitride interface. J. Phys. Chem. C 122, 14945–14953. doi:10.1021/acs.jpcc.8b02750
Li, T., Tang, Z., Huang, Z., and Yu, J. (2018c). Substrate effects on the thermal performance of in-plane graphene/hexagonal boron nitride heterostructures. Carbon 130, 396–400. doi:10.1016/j.carbon.2018.01.017
Li, W., Kong, L., Chen, C., Gou, J., Sheng, S., Zhang, W., et al. (2018d). Experimental realization of honeycomb borophene. Sci. Bull. 63, 282–286. doi:10.1016/j.scib.2018.02.006
Li, F., Wang, J., Xia, G., and Li, Z. (2019). Negative differential thermal resistance through nanoscale solid-fluid-solid sandwiched structures. Nanoscale 11, 13051–13057. doi:10.1039/c9nr01606f
Li, D., Gao, J., Cheng, P., He, J., Yin, Y., Hu, Y., et al. (2020a). 2D boron sheets: structure, growth, and electronic and thermal transport properties. Adv. Funct. Mater.. 30, 1904349. doi:10.1002/adfm.201904349
Li, D., Gong, Y., Chen, Y., Lin, J., Khan, Q., Zhang, Y., et al. (2020b). Recent progress of two-dimensional thermoelectric materials. Nano-Micro Lett. 12, 36. doi:10.1007/s40820-020-0374-x
Liang, T., Zhang, P., Yuan, P., and Zhai, S. (2018). In-plane thermal transport in black phosphorene/graphene layered heterostructures: a molecular dynamics study. Phys. Chem. Chem. Phys. 20, 21151–21162. doi:10.1039/c8cp02831a
Liang, T., Zhou, M., Zhang, P., Yuan, P., and Yang, D. (2020). Multilayer in-plane graphene/hexagonal boron nitride heterostructures: insights into the interfacial thermal transport properties. Int. J. Heat Mass Tran. 151, 119395. doi:10.1016/j.ijheatmasstransfer.2020.119395
Lindsay, L., and Broido, D. A. (2011). Enhanced thermal conductivity and isotope effect in single-layer hexagonal boron nitride. Phys. Rev. B 84, 155421. doi:10.1103/physrevb.84.155421
Lindsay, L., Broido, D. A., and Mingo, N. (2009). Lattice thermal conductivity of single-walled carbon nanotubes: beyond the relaxation time approximation and phonon-phonon scattering selection rules. Phys. Rev. B 80, 125407. doi:10.1103/physrevb.80.125407
Lindsay, L., Broido, D. A., and Mingo, N. (2010). Flexural phonons and thermal transport in graphene. Phys. Rev. B 82, 115427. doi:10.1103/physrevb.82.115427
Lindsay, L., Li, W., Carrete, J., Mingo, N., Broido, D. A., and Reinecke, T. L. (2014). Phonon thermal transport in strained and unstrained graphene from first principles. Phys. Rev. B 89, 155426. doi:10.1103/physrevb.89.155426
Liu, R., and Li, W. (2018c). High-thermal-stability and high-thermal-conductivity Ti3C2Tx MXene/poly (vinyl alcohol) (PVA) composites. ACS Omega 3, 2609–2617. doi:10.1021/acsomega.7b02001
Liu, H., Gao, J., and Zhao, J. (2013a). Silicene on substrates: a way to preserve or tune its electronic properties. J. Phys. Chem. C 117, 10353–10359. doi:10.1021/jp311836m
Liu, Z., Ma, L., Shi, G., Zhou, W., Gong, Y., Lei, S., et al. (2013b). In-plane heterostructures of graphene and hexagonal boron nitride with controlled domain sizes. Nat. Nanotechnol.. 8, 119. doi:10.1038/nnano.2012.256
Liu, B., Baimova, J. A., Reddy, C. D., Dmitriev, S. V., Law, W. K., Feng, X. Q., et al. (2014a). Interface thermal conductance and rectification in hybrid graphene/silicene monolayer. Carbon 79, 236–244. doi:10.1016/j.carbon.2014.07.064
Liu, B., Reddy, C. D., Jiang, J., Zhu, H., Baimova, J. A., and Dmitriev, S. V. (2014b). Thermal conductivity of silicene nanosheets and the effect of isotopic doping. J. Phys. D Appl. Phys. 47, 165301. doi:10.1088/0022-3727/47/16/165301
Liu, H., Neal, A. T., Zhu, Z., Luo, Z., Xu, X., Tománek, D., et al. . (2014c). Phosphorene: an unexplored 2D semiconductor with a high hole mobility. ACS Nano 8, 4033–4041. doi:10.1021/nn501226z
Liu, L., Park, J., Siegel, D. A., McCarty, K. F., Clark, K. W., Deng, W., et al. (2014d). Heteroepitaxial growth of two-dimensional hexagonal boron nitride templated by graphene edges. Science 343, 163–167. doi:10.1126/science.1246137
Liu, Y.-Y., Zhou, W.-X., Tang, L.-M., and Chen, K.-Q. (2014e). An important mechanism for thermal rectification in graded nanowires. Appl. Phys. Lett. 105, 203111. doi:10.1063/1.4902427
Liu, X., Zhang, G., and Zhang, Y.-W. (2015). Graphene-based thermal modulators. Nano Res. 8, 2755–2762. doi:10.1007/s12274-015-0782-2
Liu, X., Zhang, G., and Zhang, Y.-W.. (2016). Topological defects at the graphene/h-BN interface abnormally enhance its thermal conductance. Nano Lett. 16, 4954–4959. doi:10.1021/acs.nanolett.6b01565
Liu, X., Gao, J., Zhang, G., and Zhang, Y.-W. (2017a). MoS2-graphene in-plane contact for high interfacial thermal conduction. Nano Res. 10, 2944–2953. doi:10.1007/s12274-017-1504-8
Liu, Y.-Y., Li, B.-L., Chen, S.-Z., Jiang, X., and Chen, K.-Q. (2017b). Effect of room temperature lattice vibration on the electron transport in graphene nanoribbons. Appl. Phys. Lett. 111, 133107. doi:10.1063/1.4999127
Liu, Y., Ong, Z. Y., Wu, J., Zhao, Y., Watanabe, K., Taniguchi, T., et al. (2017c). Thermal conductance of the 2D MoS2/h-BN and graphene/h-BN interfaces. Sci. Rep. 7, 43886. doi:10.1038/srep43886
Liu, X., Gao, J., Zhang, G., and Zhang, Y.-W. (2018a). Design of phosphorene/graphene heterojunctions for high and tunable interfacial thermal conductance. Nanoscale, 10, 19854–19862. doi:10.1039/c8nr06110f
Liu, Y.-Y., Zeng, Y.-J., Jia, P.-Z., Cao, X.-H., Jiang, X., and Chen, K.-Q. (2018b). An efficient mechanism for enhancing the thermoelectricity of nanoribbons by blocking phonon transport in 2D materials. J. Phys. Condens. Matter 30, 275701. doi:10.1088/1361-648x/aac7f5
Liu, F., Zou, R., Hu, N., Ning, H., Yan, C., Liu, Y., et al. (2019a). Enhancement of thermal energy transport across the graphene/h-BN heterostructure interface. Nanoscale 11, 4067–4072. doi:10.1039/c8nr10468a
Liu, Y., Xu, Y., and Duan, W. (2019b). Three-dimensional topological states of phonons with tunable pseudospin physics. Research 2019, 5173580. doi:10.34133/2019/5173580
Luo, Z., Maassen, J., Deng, Y., Du, Y., Garrelts, R. P., Lundstrom, M. S., et al. (2015). Anisotropic in-plane thermal conductivity observed in few-layer black phosphorus. Nat. Commun.. 6, 8572. doi:10.1038/ncomms9572
Ma, Z., Hu, Z., Zhao, X., Tang, Q., Wu, D., Zhou, Z., et al. (2014). Tunable band structures of heterostructured bilayers with transition-metal dichalcogenide and MXene monolayer. J. Phys. Chem. C 118, 5593–5599. doi:10.1021/jp500861n
Ma, D., Ding, H., Meng, H., Feng, L., Wu, Y., Shiomi, J., et al. (2016). Nano-cross-junction effect on phonon transport in silicon nanowire cages. Phys. Rev. B 94, 165434. doi:10.1103/physrevb.94.165434
Ma, D., Wan, X., and Yang, N. (2018). Unexpected thermal conductivity enhancement in pillared graphene nanoribbon with isotopic resonance. Phys. Rev. B 98, 245420. doi:10.1103/physrevb.98.245420
Ma, J.-J., Zheng, J.-J., Zhu, X.-L., Liu, P.-F., Li, W.-D., and Wang, B.-T. (2019). First-principles calculations of thermal transport properties in MoS2/MoSe2 bilayer heterostructure. Phys. Chem. Chem. Phys. 21, 10442–10448. doi:10.1039/c9cp01702j
Machida, Y., Matsumoto, N., Isono, T., and Behnia, K. (2020). Phonon hydrodynamics and ultrahigh-room-temperature thermal conductivity in thin graphite. Science 367, 309–312. doi:10.1126/science.aaz8043
Mahapatra, P. S., Sarkar, K., Krishnamurthy, H. R., Mukerjee, S., and Ghosh, A. (2017). Seebeck coefficient of a single van der Waals junction in twisted bilayer graphene. Nano Lett. 17, 6822–6827. doi:10.1021/acs.nanolett.7b03097
Malekpour, H., Ramnani, P., Srinivasan, S., Balasubramanian, G., Nika, D. L., Mulchandani, A., et al. (2016). Thermal conductivity of graphene with defects induced by electron beam irradiation. Nanoscale 8, 14608–14616. doi:10.1039/c6nr03470e
Mandelli, D., Leven, I., Hod, O., and Urbakh, M. (2017). Sliding friction of graphene/hexagonal–boron nitride heterojunctions: a route to robust superlubricity. Sci. Rep. 7, 10851. doi:10.1038/s41598-017-10522-8
Mannix, A. J., Zhou, X.-F., Kiraly, B., Wood, J. D., Alducin, D., Myers, B. D., et al. (2015). Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs. Science 350, 1513–1516. doi:10.1126/science.aad1080
Mazzamuto, F., Nguyen, V. H., Apertet, Y., Caër, C., Chassat, C., Saint-Martin, J., et al. (2011). Enhanced thermoelectric properties in graphene nanoribbons by resonant tunneling of electrons. Phys. Rev. B 83, 235426. doi:10.1103/physrevb.83.235426
Melis, C., Barbarino, G., and Colombo, L. (2015). Exploiting hydrogenation for thermal rectification in graphene nanoribbons. Phys. Rev. B 92, 245408. doi:10.1103/physrevb.92.245408
Meng, X., Pandey, T., Jeong, J., Fu, S., Yang, J., Chen, K., et al. . (2019). Thermal conductivity enhancement in MoS2 under extreme strain. Phys. Rev. Lett. 122, 155901. doi:10.1103/physrevlett.122.155901
Mingo, N., Esfarjani, K., Broido, D. A., and Stewart, D. A. (2010). Cluster scattering effects on phonon conduction in graphene. Phys. Rev. B 81 (4), 045408. doi:10.1103/physrevb.81.045408
Morooka, M., Yamamoto, T., and Watanabe, K. (2008). Defect-induced circulating thermal current in graphene with nanosized width. Phys. Rev. B 77, 033412.
Mortazavi, B., Le, M.-Q., Rabczuk, T., and Pereira, L. F. C. (2017). Anomalous strain effect on the thermal conductivity of borophene: a reactive molecular dynamics study. Phys. E 93, 202–207. doi:10.1016/j.physe.2017.06.012
Mu, X., Wu, X., Zhang, T., Go, D. B., and Luo, T. (2014). Thermal transport in graphene oxide–from ballistic extreme to amorphous limit. Sci. Rep.. 4, 3909. doi:10.1038/srep03909
Mu, X., Zhang, T., Go, D. B., and Luo, T. (2015). Coherent and incoherent phonon thermal transport in isotopically modified graphene superlattices. Carbon 83, 208–216. doi:10.1016/j.carbon.2014.11.028
Narducci, D. (2011). Do we really need high thermoelectric figures of merit? A critical appraisal to the power conversion efficiency of thermoelectric materials. Appl. Phys. Lett. 99, 102104. doi:10.1063/1.3634018
Ni, Y., Zhang, H., Hu, S., Wang, H., Volz, S., and Xiong, S. (2019). Interface diffusion-induced phonon localization in two-dimensional lateral heterostructures. Int. J. Heat Mass Tran. 144, 118608. doi:10.1016/j.ijheatmasstransfer.2019.118608
Nika, D. L., and Balandin, A. A.. (2012). Two-dimensional phonon transport in graphene. J. Phys.: condens. Matter 24 (23) 233203. doi:10.1088/0953-8984/24/23/233203
Nika, D. L., and Balandin, A. A. (2017). Phonons and thermal transport in graphene and graphene-based materials. Rep.Prog. Phys. 80 (3), 036502. doi:10.1088/1361-6633/80/3/036502
Nika, D. L., Cocemasov, A. I., and Balandin, A. A.. (2014). Specific heat of twisted bilayer graphene: engineering phonons by atomic plane rotations. App. Phy. Lett. 105, 031904. doi:10.1063/1.4890622
Nobakht, A. Y., Gandomi, Y. A., Wang, J., Bowman, M. H., Marable, D. C., Garrison, B. E., et al. (2018). Thermal rectification via asymmetric structural defects in graphene. Carbon 132, 565–572. doi:10.1016/j.carbon.2018.02.087
Nomura, M., Shiomi, J., Shiga, T., and Anufriev, R. (2018). Thermal phonon engineering by tailored nanostructures. J. Appl. Phys. 57, 080101. doi:10.1364/opj.2018.31acj4
Ong, Z. Y., Pop, E., and Shiomi, J. (2011). Reduction of phonon lifetimes and thermal conductivity of a carbon nanotube on amorphous silica. Phys. Rev. B 84, 165418. doi:10.1103/physrevb.84.165418
Ong, Z. Y., Zhang, G., and Zhang, Y. W. (2016). Controlling the thermal conductance of graphene/h−BN lateral interface with strain and structure engineering. Phys. Rev. B 93 (7), 075406. doi:10.1103/physrevb.93.075406
Ouyang, T., Chen, Y., Xie, Y., Wei, X. L., Yang, K., Yang, P., et al. (2010). Ballistic thermal rectification in asymmetric three-terminal graphene nanojunctions. Phys. Rev. B 82, 245403. doi:10.1103/physrevb.82.245403
Pak, A. J., and Hwang, G. S.. (2016). Theoretical analysis of thermal transport in graphene supported on hexagonal boron nitride: the importance of strong adhesion due to π-bond polarization. Phys. Rev. Appl. 6 (3), 034015. doi:10.1103/physrevapplied.6.034015
Pal, S., and Puri, I. K.. (2014). Thermal rectification in a polymer-functionalized single-wall carbon nanotube. Nanotechnology 25, 345401. doi:10.1088/0957-4484/25/34/345401
Pal, S., and Puri, I. K.. (2015). Thermal and gate using a monolayer graphene nanoribbon. Small 11, 2910–2917. doi:10.1002/smll.201303888
Pei, Q.-X., Sha, Z.-D., and Zhang, Y.-W. (2011). A theoretical analysis of the thermal conductivity of hydrogenated graphene. Carbon 49, 4752–4759. doi:10.1016/j.carbon.2011.06.083
Pei, Q.-X., Zhang, X., Ding, Z., Zhang, Y.-Y., and Zhang, Y.-W. (2017). Thermal stability and thermal conductivity of phosphorene in phosphorene/graphene van der Waals heterostructures. Phys. Chem. Chem. Phys. 19, 17180–17186. doi:10.1039/c7cp02553j
Peimyoo, N., Shang, J., Yang, W., Wang, Y., Cong, C., and Yu, T. (2015). Thermal conductivity determination of suspended mono-and bilayer WS2 by Raman spectroscopy. Nano Res. 8, 1210–1221. doi:10.1007/s12274-014-0602-0
Peng, X.-F., and Chen, K.-Q. (2014). Thermal transport for flexural and in-plane phonons in graphene nanoribbons. Carbon 77, 360–365. doi:10.1016/j.carbon.2014.05.039
Peng, X. F., Chen, K. Q., Wan, Q., Zou, B. S., and Duan, W. (2010). Quantized thermal conductance at low temperatures in quantum wire with catenoidal contacts. Phys. Rev. B 81, 195317. doi:10.1103/physrevb.81.195317
Peng, X.-F., Zhou, X., Tan, S.-H., Wang, X.-J., Chen, L.-Q., and Chen, K.-Q. (2017). Thermal conductance in graphene nanoribbons modulated by defects and alternating boron-nitride structures. Carbon 113, 334–339. doi:10.1016/j.carbon.2016.11.066
Pettes, M. T., Jo, I., Yao, Z., and Shi, L.. (2011). Influence of polymeric residue on the thermal conductivity of suspended bilayer graphene. Nano Lett. 11, 1195–1200. doi:10.1021/nl104156y
Qin, G., and Hu, M. (2018). Thermal transport in phosphorene. Small 14, 1702465. doi:10.1002/smll.201702465
Qin, G., Zhang, X., Yue, S. Y., Qin, Z., Wang, H., Han, Y., et al. (2016). Resonant bonding driven giant phonon anharmonicity and low thermal conductivity of phosphorene. Phy. Rev. B 94, 165445. doi:10.1103/physrevb.94.165445
Qin, H., Pei, Q.-X., Liu, Y., and Zhang, Y.-W. (2019). The mechanical and thermal properties of MoS2-WSe2 lateral heterostructures. Phys. Chem. Chem. Phys. 21, 15845–15853. doi:10.1039/c9cp02499a
Qiu, B., and Ruan, X. (2012a). Reduction of spectral phonon relaxation times from suspended to supported graphene. Appl. Phys. Lett. 100, 193101. doi:10.1063/1.4712041
Qiu, B., Wang, Y., Zhao, Q., and Ruan, X. (2012b). The effects of diameter and chirality on the thermal transport in free-standing and supported carbon-nanotubes. Appl. Phys. Lett. 100, 233105. doi:10.1063/1.4725194
Ranjan, P., Sahu, T. K., Bhushan, R., Yamijala, S. S., Late, D. J., Kumar, P., et al. (2019). Freestanding borophene and its hybrids. Adv. Mater.. 31, 1900353. doi:10.1002/adma.201900353
Ravichandran, J., Yadav, A. K., Cheaito, R., Rossen, P. B., Soukiassian, A., et al. (2014). Crossover from incoherent to coherent phonon scattering in epitaxial oxide superlattices. Nat. Mater.. 13, 168–172. doi:10.1038/nmat3826
Rosul, M. G., Lee, D., Olson, D. H., Liu, N., Wang, X., Hopkins, P. E., et al. (2019). Thermionic transport across gold-graphene-WSe2 van der Waals heterostructures. Sci. Adv. 5, eaax7827. doi:10.1126/sciadv.aax7827
Rowe, P., Csányi, G., Alfè, D., and Michaelides, A.. (2018). Development of a machine learning potential for graphene. Phys. Rev. B 97 (5), 054303. doi:10.1103/PhysRevB.97.054303
Roy, T., Tosun, M., Cao, X., Fang, H., Lien, D.-H., Zhao, P., et al. (2015). Dual-gated MoS2/WSe2 van der Waals tunnel diodes and transistors. ACS Nano 9, 2071–2079. doi:10.1021/nn507278b
Sääskilahti, K., Oksanen, J., Volz, S., and Tulkki, J. (2015). Frequency-dependent phonon mean free path in carbon nanotubes from nonequilibrium molecular dynamics. Phys. Rev. B 91, 115426. doi:10.1103/physrevb.91.115426
Sadeghi, M. M., Jo, I., and Shi, L. (2013). Phonon-interface scattering in multilayer graphene on an amorphous support. Proc. Natl. Acad. Sci. U. S. A 110, 16321–16326. doi:10.1073/pnas.1306175110
Sadeghi, H., Sangtarash, S., and Lambert, C. J.. (2016). Cross-plane enhanced thermoelectricity and phonon suppression in graphene/MoS2 van der Waals heterostructures. 2D Mater. 4 (1), 015012. doi:10.1088/2053-1583/4/1/015012
Sahoo, S., Gaur, A. P. S., Ahmadi, M., Guinel, M. J.-F., and Katiyar, R. S. (2013). Temperature-dependent Raman studies and thermal conductivity of few-layer MoS2. J. Phys. Chem. C 117, 9042–9047. doi:10.1021/jp402509w
Sandonas, L. M., Cuba-Supanta, G., Gutierrez, R., Dianat, A., Landauro, C. V., and Cuniberti, G. (2017). Enhancement of thermal transport properties of asymmetric Graphene/h-BN nanoribbon heterojunctions by substrate engineering. Carbon 124, 642–650. doi:10.1016/j.carbon.2017.09.025
Sarikurt, S., Çakır, D., Keçeli, M., and Sevik, C. (2018). The influence of surface functionalization on thermal transport and thermoelectric properties of MXene monolayers. Nanoscale 10, 8859–8868. doi:10.1039/c7nr09144c
Schelling, P. K., and Phillpot, S. R. (2003). Multiscale simulation of phonon transport in superlattices. J. Appl. Phys. 93, 5377–5387. doi:10.1063/1.1561601
Sellan, D. P., Landry, E. S., Turney, J. E., McGaughey, A. J., and Amon, C. H. (2010). Size effects in molecular dynamics thermal conductivity predictions. Phys. Rev. B 81, 214305. doi:10.1103/physrevb.81.214305
Seol, J. H., Jo, I., Moore, A. L., Lindsay, L., Aitken, Z. H., Pettes, M. T., et al. (2010). Two-dimensional phonon transport in supported graphene. Science, 328, 213–216. doi:10.1126/science.1184014
Serrano, J., Bosak, A., Arenal, R., Krisch, M., Watanabe, K., Taniguchi, T., et al. (2007). Vibrational properties of hexagonal boron nitride: inelastic X-ray scattering and ab initio calculations. Phy. Rev. Lett. 98 (9), 095503. doi:10.1103/PHYSREVLETT.98.095503
Sevik, C., Kinaci, A., Haskins, J. B., and Çağın, T. (2011). Characterization of thermal transport in low-dimensional boron nitride nanostructures. Phys. Rev. B, 84 (8), 085409. doi:10.1103/physrevb.84.085409
Shen, X., Lin, X., Jia, J., Wang, Z., Li, Z., and Kim, J.-K. (2014). Tunable thermal conductivities of graphene oxide by functionalization and tensile loading. Carbon 80, 235–245. doi:10.1016/j.carbon.2014.08.062
Smithe, K. K. H., English, C. D., Suryavanshi, S. V., and Pop, E.. (2018). High-field transport and velocity saturation in synthetic monolayer MoS2. Nano Lett. 18, 4516–4522. doi:10.1021/acs.nanolett.8b01692
Song, J., and Medhekar, N. V. (2013). Thermal transport in lattice-constrained 2D hybrid graphene heterostructures. J. Phys. Condens. Matter 25, 445007. doi:10.1088/0953-8984/25/44/445007
Sood, A., Xiong, F., Chen, S., Wang, H., Selli, D., Zhang, J., et al. . (2018). An electrochemical thermal transistor. Nat. Commun.. 9, 4510. doi:10.1038/s41467-018-06760-7
Su, L., and Zhang, Y. (2015). Temperature coefficients of phonon frequencies and thermal conductivity in thin black phosphorus layers. App. Phys. Lett. 107 (7), 071905. doi:10.1063/1.4928931
Sun, H., Li, Q., and Wan, X. G. (2016). First-principles study of thermal properties of borophene. Phys. Chem. Chem. Phys. 18, 14927–14932. doi:10.1039/c6cp02029a
Sutter, P., Lahiri, J., Albrecht, P., and Sutter, E.. (2011). Chemical vapor deposition and etching of high-quality monolayer hexagonal boron nitride films. ACS Nano 5, 7303–7309. doi:10.1021/nn202141k
Taube, A., Judek, J., Łapińska, A., and Zdrojek, M.. (2015). Temperature-dependent thermal properties of supported MoS2 monolayers. ACS Appl. Mater. Interfaces 7, 5061–5065. doi:10.1021/acsami.5b00690
Thomas, J. A., Turney, J. E., Iutzi, R. M., Amon, C. H., and McGaughey, A. J. (2010). Predicting phonon dispersion relations and lifetimes from the spectral energy density. Phys. Rev. B 81, 081411. doi:10.1115/ihtc14-22262
Tian, H., Xie, D., Yang, Y., Ren, T. L., Zhang, G., Wang, Y. F., et al. (2012a). A novel solid-state thermal rectifier based on reduced graphene oxide. Sci. Rep.. 2, 523. doi:10.1038/srep00523
Tian, Z., Esfarjani, K., and Chen, G. (2012b). Enhancing phonon transmission across a Si/Ge interface by atomic roughness: first-principles study with the Green's function method. Phys. Rev. B 86, 235304. doi:10.1103/physrevb.86.235304
Tien, D. H., Park, J.-Y., Kim, K. B., Lee, N., Choi, T., Kim, P., et al. (2016). Study of graphene-based 2D-heterostructure device fabricated by all-dry transfer process. ACS Appl. Mater. Interfaces 8, 3072–3078. doi:10.1021/acsami.5b10370
Tran, V.-T., Saint-Martin, J., and Dollfus, P.. (2015). High thermoelectric performance in graphene nanoribbons by graphene/BN interface engineering. Nanotechnology 26 (49), 495202. doi:10.1088/0957-4484/26/49/495202
Varshney, V., Lee, J., Brown, J. S., Farmer, B. L., Voevodin, A. A., and Roy, A. K. (2018). Effect of length, Diameter, chirality, Deformation, and strain on contact Thermal conductance between single-Wall carbon nanotubes. Front. Mater 5, 17. doi:10.3389/fmats.2018.00017
Vogt, P., De Padova, P., Quaresima, C., Avila, J., Frantzeskakis, E., Asensio, M. C., et al. (2012). Silicene: compelling experimental evidence for graphenelike two-dimensional silicon. Phys. Rev. Lett. 108, 155501. doi:10.1103/physrevlett.108.155501
Wang, L., Meric, I., Huang, P. Y., Gao, Q., Gao, Y., Tran, H., et al. (2013a). One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617. doi:10.1126/science.1244358
Wang, X., Huang, T., and Lu, S. (2013b). High performance of the thermal transport in graphene supported on hexagonal boron nitride. Appl. Phys. Express 6 (7), 075202. doi:10.7567/apex.6.075202
Wang, Y., Vallabhaneni, A., Hu, J., Qiu, B., Chen, Y. P., and Ruan, X. (2014). Phonon lateral confinement enables thermal rectification in asymmetric single-material nanostructures. Nano Lett. 14, 592–596. doi:10.1021/nl403773f
Wang, Y., Zhang, K., and Xie, G. (2016). Remarkable suppression of thermal conductivity by point defects in MoS2 nanoribbons. Appl. Surf. Sci. 360, 107–112. doi:10.1016/j.apsusc.2015.10.235
Wang, H., Hu, S., Takahashi, K., Zhang, X., Takamatsu, H., and Chen, J. (2017a). Experimental study of thermal rectification in suspended monolayer graphene. Nat. Commun. 8, 15843. doi:10.1038/ncomms15843
Wang, X., Hong, Y., Chan, P. K. L., and Zhang, J. (2017b). Phonon thermal transport in silicene-germanene superlattice: a molecular dynamics study. Nanotechnology 28, 255403. doi:10.1088/1361-6528/aa71fa
Wang, X., Wang, M., Hong, Y., Wang, Z., and Zhang, J. (2017c). Coherent and incoherent phonon transport in a graphene and nitrogenated holey graphene superlattice. Phys. Chem. Chem. Phys. 19, 24240–24248. doi:10.1039/c7cp04219a
Wang, Y., Xu, N., Li, D., and Zhu, J. (2017d). Thermal properties of two dimensional layered materials. Adv. Funct. Mater. 27, 1604134. doi:10.1002/adfm.201604134
Ward, A., and Broido, D. A. (2010). Intrinsic phonon relaxation times from first-principles studies of the thermal conductivities of Si and Ge. Phys. Rev. B81 (8) 085205. doi:10.1103/physrevb.81.085205
Wei, N., Xu, L., Wang, H.-Q., and Zheng, J.-C.. (2011). Strain engineering of thermal conductivity in graphene sheets and nanoribbons: a demonstration of magic flexibility. Nanotechnology 22, 105705. doi:10.1088/0957-4484/22/10/105705
Wei, X., Wang, Y., Shen, Y., Xie, G., Xiao, H., Zhong, J., et al. (2014). Phonon thermal conductivity of monolayer MoS2: a comparison with single layer graphene. Appl. Phys. Lett. 105, 103902. doi:10.1063/1.4895344
Wei, A., Lahkar, S., Li, X., Li, S., and Ye, H.. (2019). Multilayer graphene-based thermal rectifier with interlayer gradient functionalization. ACS Appl. Mater. Interfaces 11, 45180–45188. doi:10.1021/acsami.9b11762
Wu, S. C., Shan, G., and Yan, B.. (2014). Prediction of near-room-temperature quantum anomalous Hall effect on honeycomb materials. Phys. Rev. Lett. 113, 256401. doi:10.1103/physrevlett.113.256401
Wu, X., Varshney, V., Lee, J., Zhang, T., Wohlwend, J. L., Roy, A. K., et al. (2016). Hydrogenation of penta-graphene leads to unexpected large improvement in thermal conductivity. Nano Lett. 16, 3925–3935. doi:10.1021/acs.nanolett.6b01536
Wu, D., Cao, X.-H., Chen, S.-Z., Tang, L.-M., Feng, Y.-X., Chen, K.-Q., et al. (2019). Pure spin current generated in thermally driven molecular magnetic junctions: a promising mechanism for thermoelectric conversion. J. Mater. Chem. A 7, 19037–19044. doi:10.1039/c9ta04642a
Wu, D., Cao, X. H., Jia, P. Z., Zeng, Y. J., Feng, Y. X., Tang, L. M., et al. (2020). Excellent thermoelectric performance in weak-coupling molecular junctions with electrode doping and electrochemical gating. Sci. China Phys. Mech 63, 276811. doi:10.1007/s11433-019-1528-y
Xie, Z. X., Tang, L. M., Pan, C. N., Li, K. M., Chen, K. Q., and Duan, W.. (2012). Enhancement of thermoelectric properties in graphene nanoribbons modulated with stub structures. Appl. Phys. Lett. 100, 073105. doi:10.1103/physrevb.93.075404
Xie, G., Guo, Y., Li, B., Yang, L., Zhang, K., Tang, M., et al. . (2013). Phonon surface scattering controlled length dependence of thermal conductivity of silicon nanowires. Phys. Chem. Chem. Phys. 15, 14647–14652. doi:10.1039/c3cp50969a
Xie, H., Hu, M., and Bao, H. (2014a). Thermal conductivity of silicene from first-principles. Appl. Phys. Lett. 104, 131906. doi:10.1063/1.4870586
Xie, Z.-X., Zhang, Y., Yu, X., Li, K.-M., and Chen, Q. (2014b). Ballistic thermal conductance by phonons through superlattice quantum-waveguides. J. Appl. Phys. 115, 104309. doi:10.1063/1.4868595
Xie, H., Ouyang, T., Germaneau, É., Qin, G., Hu, M., and Bao, H. (2016). Large tunability of lattice thermal conductivity of monolayer silicene via mechanical strain. Phys. Rev. B 93, 075404. doi:10.1103/physrevb.93.075404
Xie, F., Fan, Z.-Q., Chen, K.-Q., Zhang, X.-J., and Long, M.-Q. (2017). Influence of anchoring groups on single-molecular junction conductance: theoretical comparative study of thiol and amine. Org. Eelctron 50, 198–203. doi:10.1016/j.orgel.2017.07.052
Xie, G., Ding, D., and Zhang, G. (2018a). Phonon coherence and its effect on thermal conductivity of nanostructures. Adv. Phys. X 3, 1480417. doi:10.1080/23746149.2018.1480417
Xie, G., Ju, Z., Zhou, K., Wei, X., Guo, Z., Cai, Y., et al. (2018b). Ultra-low thermal conductivity of two-dimensional phononic crystals in the incoherent regime. Npj Comput. Mater 4, 21. doi:10.1038/s41524-018-0076-9
Xie, Z.-X., Yu, X., Chen, X.-K., Zhou, W.-X., Shi, Y.-M., and Zhang, L.-F. (2020). Modulation of thermal transport in AlxGa1−xAs alloy nanowires with varying compositions. Appl. Phys. Lett. 116 (14), 143102. doi:10.1063/5.0003961
Xiong, S., Sääskilahti, K., Kosevich, Y. A., Han, H., Donadio, D., and Volz, S.. (2016). Blocking phonon transport by structural resonances in alloy-based nanophononic metamaterials leads to ultralow thermal conductivity. Phys. Rev. Lett. 117 (2), 025503. doi:10.1103/physrevlett.117.025503
Xiong, G., Xing, Y., and Zhang, L. (2018). Interfacial thermal transport via one-dimensional atomic junction model. Front. Energy Res. 6, 6. doi:10.3389/fenrg.2018.00006
Xu, W., and Zhang, G. (2016a). Remarkable reduction of thermal conductivity in phosphorene phononic crystal. J. Phys. Condens. Matter 28, 175401. doi:10.1088/0953-8984/28/17/175401
Xu, Y., Chen, X., Gu, B.-L., and Duan, W. (2009). Intrinsic anisotropy of thermal conductance in graphene nanoribbons. Appl. Phys. Lett. 95, 233116. doi:10.1063/1.3272678
Xu, W., Zhang, G., and Li, B. (2014a). Interfacial thermal resistance and thermal rectification between suspended and encased single layer graphene. J. Appl. Phys. 116, 134303. doi:10.1063/1.4896733
Xu, X., Pereira, L. F., Wang, Y., Wu, J., Zhang, K., Zhao, X., et al. . (2014b). Length-dependent thermal conductivity in suspended single-layer graphene. Nat. Commun.. 5, 3689. doi:10.1038/ncomms4689
Xu, Y., Li, Z., and Duan, W. (2014c). Thermal and thermoelectric properties of graphene. Small 10, 2182–2199. doi:10.1002/smll.201303701
Xu, W., Zhu, L., Cai, Y., Zhang, G., and Li, B. (2015). Direction dependent thermal conductivity of monolayer phosphorene: parameterization of Stillinger-Weber potential and molecular dynamics study. J. Appl. Phys. 117, 214308. doi:10.1063/1.4922118
Xu, X., Chen, J., and Li, B. (2016b). Phonon thermal conduction in novel 2D materials. J. Phys. Condens. Matter 28, 483001. doi:10.1088/0953-8984/28/48/483001
Yan, Z., Jiang, C., Pope, T. R., Tsang, C. F., Stickney, J. L., Goli, P., et al. (2013). Phonon and thermal properties of exfoliated TaSe2 thin films. J. Appl. Phys. 114, 204301. doi:10.1063/1.4833250
Yan, Z., Chen, L., Yoon, M., and Kumar, S. (2016a). Phonon transport at the interfaces of vertically stacked graphene and hexagonal boron nitride heterostructures. Nanoscale 8, 4037–4046. doi:10.1039/c5nr06818e
Yan, Z., Chen, L., Yoon, M., and Kumar, S. (2016b). The role of interfacial electronic properties on phonon transport in two-dimensional MoS2 on metal substrates. ACS Appl. Mater. Interfaces 8, 33299–33306. doi:10.1021/acsami.6b10608
Yang, X., Yu, D., and Cao, B.. (2017). Giant thermal rectification from single-carbon nanotube-graphene junction. ACS Appl. Mater. Interfaces 9, 24078–24084. doi:10.1021/acsami.7b04464
Yang, N., Zeng, X., Lu, J., Sun, R., and Wong, C.-P. (2018). Effect of chemical functionalization on the thermal conductivity of 2D hexagonal boron nitride. Appl. Phys. Lett. 113, 171904. doi:10.1063/1.5050293
Yankowitz, M., Ma, Q., Jarillo-Herrero, P., and LeRoy, B. J. (2019). van der Waals heterostructures combining graphene and hexagonal boron nitride. Nat. Rev. Phys. 1, 112–125. doi:10.1038/s42254-018-0016-0
Yasaei, P., Hemmat, Z., Foss, C. J., Li, S. J., Hong, L., Behranginia, A., et al. (2018). Enhanced thermal boundary conductance in few-layer Ti3C2 MXene with encapsulation. Adv. Mater.. 30, 1801629. doi:10.1002/adma.201801629
Yokomizo, Y., and Nakamura, J. (2013). Giant Seebeck coefficient of the graphene/h-BN superlattices. Appl. Phys. Lett. 103, 113901. doi:10.1063/1.4820820
Yuan, K., Sun, M., Wang, Z., and Tang, D. (2015). Tunable thermal rectification in silicon-functionalized graphene nanoribbons by molecular dynamics simulation. Int. J. Therm. Sci. 98, 24–31. doi:10.1016/j.ijthermalsci.2015.07.004
Zeng, J., Chen, K.-Q., and Tong, Y.-X. (2018a). Covalent coupling of porphines to graphene edges: quantum transport properties and their applications in electronics. Carbon 127, 611–617. doi:10.1016/j.carbon.2017.11.047
Zeng, Y. J., Liu, Y. Y., Zhou, W. X., and Chen, K. Q.. (2018b). Nanoscale thermal transport: theoretical method and application. Chin. Phys. B 27 (3), 036304. doi:10.1088/1674-1056/27/3/036304
Zeng, Y.-J., Wu, D., Cao, X.-H., Feng, Y.-X., Tang, L.-M., and Chen, K.-Q. (2020a). Significantly enhanced thermoelectric performance of molecular junction by twist angle dependent phonon interference effect. J. Mater. Chem. A 8, 11884–11891. doi:10.1039/d0ta02423f
Zeng, Y. J., Wu, D., Cao, X. H., Zhou, W. X., Tang, L. M., and Chen, K. Q. (2020b). Nanoscale organic thermoelectric materials: measurement, theoretical models, and optimization strategies. Adv. Funct. Mater. 30, 1903873. doi:10.1002/adfm.201903873
Zeng, Y., Lo, C.-L., Zhang, S., Chen, Z., and Marconnet, A. (2020c). Dynamically tunable thermal transport in polycrystalline graphene by strain engineering. Carbon 158, 63–68. doi:10.1016/j.carbon.2019.11.060
Zhang, T., and Luo, T. (2015b). Thermal diodes: giant thermal rectification from polyethylene nanofiber thermal diodes. Small 11, 4656. doi:10.1002/smll.201570222
Zhang, G., and Zhang, H.. (2011). Thermal conduction and rectification in few-layer graphene Y Junctions. Nanoscale 3, 4604–4607. doi:10.1039/c1nr10945f
Zhang, G., and Zhang, Y.-W. (2017a). Thermoelectric properties of two-dimensional transition metal dichalcogenides. J. Mater. Chem. C 5, 7684–7698. doi:10.1039/c7tc01088e
Zhang, Y., Chang, T.-R., Zhou, B., Cui, Y.-T., Yan, H., Liu, Z., et al. (2013). Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol.. 9, 111–115. doi:10.1038/nnano.2013.277
Zhang, X., Xie, H., Hu, M., Bao, H., Yue, S., Qin, G., et al. (2014a). Thermal conductivity of silicene calculated using an optimized Stillinger-Weber potential. Phy. Rev. B 89, 054310. doi:10.1103/physrevb.89.054310
Zhang, Y., Xie, Z.-X., Yu, X., Wang, H.-B., and Li, K.-M. (2014b). Ballistic thermal transport in a cylindrical semiconductor nanowire modulated with bridge contacts. Journal of Applied Physics 116, 144304. doi:10.1063/1.4897548
Zhang, J., Hong, Y., and Yue, Y. (2015a). Thermal transport across graphene and single layer hexagonal boron nitride. J. Appl. Phys. 117, 134307. doi:10.1063/1.4916985
Zhang, X., Sun, D., Li, Y., Lee, G.-H., Cui, X., Chenet, D., et al. (2015c). Measurement of lateral and interfacial thermal conductivity of single-and bilayer MoS2 and MoSe2 using refined optothermal Raman technique. ACS Appl. Mater. Interfaces 7, 25923–25929. doi:10.1021/acsami.5b08580
Zhang, Y.-Y., Pei, Q.-X., Mai, Y.-W., and Lai, S.-K. (2016). Interfacial thermal conductance in multilayer graphene/phosphorene heterostructure. J. Phys. D Appl. Phys. 49, 465301. doi:10.1088/0022-3727/49/46/465301
Zhang, J., Hong, Y., Wang, X., Yue, Y., Xie, D., Jiang, J., et al. (2017b). Phonon thermal properties of transition-metal dichalcogenides MoS2 and MoSe2 heterostructure. J. Phys. Chem. C 121, 10336–10344. doi:10.1021/acs.jpcc.7b02547
Zhang, Z., Hu, S., Chen, J., and Li, B. (2017c). Hexagonal boron nitride: a promising substrate for graphene with high heat dissipation. Nanotechnology 28, 225704. doi:10.1088/1361-6528/aa6e49
Zhang, Y., Pei, Q.-X., Wang, C.-M., Yang, C., and Zhang, Y.-W. (2018). Interfacial thermal conductance and thermal rectification of hexagonal BCnN/graphene in-plane heterojunctions. J. Phys. Chem. C 122, 22783–22789. doi:10.1021/acs.jpcc.8b08015
Zhang, Y., Chen, S.-Z., Xie, Z.-X., Yu, X., Deng, Y.-X., Chen, X.-H., et al. (2019). Spin-resolved transport properties of DNA base multi-functional electronic devices. Phys. Lett. 383, 2069–2075. doi:10.1016/j.physleta.2019.03.034
Zhao, G., Cheng, Y., Wu, Y., Xu, X., and Hao, X. (2018a). New 2D carbon nitride organic materials synthesis with huge-application prospects in CN photocatalyst. Small 14, 1704138. doi:10.1002/smll.201704138
Zhao, Y., Zhang, G., Nai, M. H., Ding, G., Li, D., Liu, Y., et al. (2018b). Probing the physical origin of anisotropic thermal transport in black phosphorus nanoribbons. Adv. Mater. 30, 1804928. doi:10.1002/adma.201804928
Zhao, G., Wang, A., He, W., Xing, Y., and Xu, X. (2019). 2D new nonmetal photocatalyst of sulfur‐doped h‐BN nanosheeets with high photocatalytic activity. Adv. Mater. Interfaces 6, 1900062. doi:10.1002/admi.201900062
Zhao, G., Cheng, Y., Sun, P., Ma, W., Hao, S., Wang, X., et al. (2020a). Biocarbon based template synthesis of uniform lamellar MoS2 nanoflowers with excellent energy storage performance in lithium-ion battery and supercapacitors. Electrochim. Acta 331, 135262. doi:10.1016/j.electacta.2019.135262
Zhao, Y., Cai, Y., Zhang, L., Li, B., Zhang, G., and Thong, J. T. L. (2020b). Thermal transport in 2D semiconductors-considerations for device applications. Adv. Funct. Mater. 30, 1903929. doi:10.1002/adfm.201903929
Zhao, G., Hao, S., Guo, J., Xing, Y., Zhang, L., and Xu, X. (2021). Design of p-n homojunctions in metal-free carbon nitride photocatalyst for overall water splitting. Chin. J. Catal. 42, 501–509. doi:10.1016/s1872-2067(20)63670-1
Zhou, W.-X., and Chen, K.-Q. (2015). Enhancement of thermoelectric performance in β-graphyne nanoribbons by suppressing phononic thermal conductance. Carbon 85, 24–27. doi:10.1016/j.carbon.2014.12.059
Zhou, Y., and Hu, M. (2017c). Full quantification of frequency-dependent interfacial thermal conductance contributed by two- and three-phonon scattering processes from nonequilibrium molecular dynamics simulations. Phys. Rev. B 95, 115313. doi:10.1103/physrevb.95.115313
Zhou, H., Zhu, J., Liu, Z., Yan, Z., Fan, X., Lin, J., et al. (2014). High thermal conductivity of suspended few-layer hexagonal boron nitride sheets. Nano Res. 7, 1232–1240. doi:10.1007/s12274-014-0486-z
Zhou, H., Cai, Y., Zhang, G., and Zhang, Y. W. (2017a). Superior lattice thermal conductance of single-layer borophene. Npj 2D Mater. Appl. 1, 14. doi:10.1038/s41699-017-0018-2
Zhou, Y.-H., Zhang, X., Ji, C., Liu, Z.-M., and Chen, K.-Q. (2017b). The length and hydrogenation effects on electronic transport properties of carbon-based molecular wires. Org. Electron. 51, 332–340. doi:10.1016/j.orgel.2017.09.031
Zhou, Y., Zheng, X., Cheng, Z.-Q., and Chen, K.-Q. (2019). Current superposition law realized in molecular devices connected in parallel. J. Phys. Chem. C 123, 10462–10468. doi:10.1021/acs.jpcc.9b01812
Zhou, W. X., Cheng, Y., Chen, K. Q., Xie, G., Wang, T., and Zhang, G. (2020a). Thermal conductivity of amorphous materials. Adv. Funct. Mater. 30, 1903829. doi:10.1002/adfm.201903829
Zhou, W.-X., Wu, D., Xie, G., Chen, K.-Q., and Zhang, G. (2020b). α-Ag2S: a ductile thermoelectric material with high ZT. ACS Omega 5, 5796–5804. doi:10.1021/acsomega.9b03929
Zhu, T., and Ertekin, E. (2014b). Phonon transport on two-dimensional graphene/boron nitride superlattices. Phys. Rev. B 90, 195209. doi:10.1103/physrevb.90.195209
Zhu, T., and Ertekin, E. (2015). Resolving anomalous strain effects on two-dimensional phonon flows: the cases of graphene, boron nitride, and planar superlattices. Phys. Rev. B 91, 205429. doi:10.1103/physrevb.91.205429
Zhu, L., Zhang, G., and Li, B. (2014a). Coexistence of size-dependent and size-independent thermal conductivities in phosphorene. Phy. Rev. B 90, 214302. doi:10.1103/physrevb.90.214302
Zhu, W., Liang, L., Roberts, R. H., Lin, J.-F., and Akinwande, D.. (2018). Anisotropic electron–phonon interactions in angle-resolved Raman study of strained black phosphorus. ACS Nano 12, 12512–12522. doi:10.1021/acsnano.8b06940
Zhu, X.-L., Liu, P.-F., Zhang, J., Zhang, P., Zhou, W.-X., Xie, G., et al. (2019). Monolayer SnP3: an excellent p-type thermoelectric material. Nanoscale 11, 19923–19932. doi:10.1039/c9nr04726c
Keywords: two-dimensional materials, heterostructures, thermal conductivity, phonon property, thermoelectric
Citation: Chen X-K, Zeng Y-J and Chen K-Q (2020) Thermal Transport in Two-Dimensional Heterostructures. Front. Mater. 7:578791. doi: 10.3389/fmats.2020.578791
Received: 01 July 2020; Accepted: 09 November 2020;
Published: 07 December 2020.
Edited by:
Weifeng Li, Shandong University, ChinaCopyright © 2020 Chen, Chen and Zeng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ke-Qiu Chen, a2VxaXVjaGVuQGhudS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.