Numerical Simulation of Water Transport in Unsaturated Recycled Aggregate Concrete

The old mortar attached to recycled aggregate (RA) is the main reason for the difference in water movement between RA concrete (RAC) and natural aggregate concrete. In this study, considering the old and new interfacial transition zones, a five-phase composite model for describing the water transport and distribution in RAC is established at the mesoscale. The key parameters describing water unsaturated transport in two types of mortar, saturated hydraulic conductivity (K_s) and van Genuchten model parameters (α, n), are obtained through the constant-head permeability test and isothermal adsorption test. By using the finite element method, the numerical simulations of unsaturated moisture movement in the homogeneous mortar, natural aggregate concrete, and five-phase RAC are systematically carried out. The proposed water transport model in the matrix is validated by comparison with the available experimental findings from the literature. The results show that the model can well predict unsaturated water transport in cement-based materials, including RAC. A parameter sensitivity analysis is undertaken to ascertain the main influencing factors of water transport in RAC. It is concluded that the RA replacement rate (R_ra), the thickness of the old mortar (d_m), and the aggregate volume fraction (F_a) are the primary parameters affecting moisture movement in RAC.

Introduction

With the rapid progress of infrastructure construction, two contradictions have gradually emerged. One is the imbalance between excessive and unsustainable exploitation of natural resources and the ever-growing requirements of building materials. Another is that the increasing wastes from construction and demolition conflicts with inadequate waste disposal methods. This phenomenon poses a severe threat to the economic development and ecological equilibrium in many countries and regions all over the world (Oikonomou, 2005; Xiao et al., 2012; Fraj and Idir, 2017; Tam et al., 2018; Lam et al., 2019; Song et al., 2020). Thus, processing the construction waste into recycled aggregates (RAs) instead of the natural aggregates (NAs) is known as an effective way to resolve these two contradictions. However, compared with NA concrete (NAC), RA concrete (RAC) whose applications are limited to low-level civil construction works are rarely used in modern infrastructure construction due to the inferior performance of RA caused by its complicated composition.

As is known to all, there are at least two interface transition zones (ITZs) in RAC (Tam et al., 2005; Xiao et al., 2013): 1) the old ITZ between NA and its adhered old cement mortar, which already exist in RA; and 2) the new ITZ between the RA and new cement mortar. Compared to traditional concrete, this caused more defects in mechanical properties and more significant hidden dangers of durability problems (Bao et al., 2020a; Wang et al., 2020). Thus far, investigations mainly focused on the mechanical properties of RAC (Folino and Xargay, 2014; Kim and Yun, 2014; Velay-Lizancos et al., 2018; Wang and Xiao, 2018; Munir et al., 2020), yet still limited in durability problems.

Most of the durability degradation mechanisms of cement-based materials can almost be attributed to the distribution and migration of moisture which either causes physical damage to the concrete structure such as freeze-thaw cycles (Zhang et al., 2017b; Wang et al., 2019; Bao et al., 2020b) (Zhang et al., 2017b; Bao et al., 2020b) or carries deleterious agents, such as chloride and sulfate, into the interior of cement-based materials (Phillipson et al., 2007; Tian et al., 2020; Zhang et al., 2020). Thus far, there are few experimental methods to study water transport directly. Neutron radiography is an excellent non-destructive testing method (Zhang et al., 2017a). However, inhomogeneous moisture distribution in the thickness direction caused by the complex structure of RAs will result in the moisture distribution overlap during the imaging process and eventually lead to abnormal images. As for other advanced non-destructive testing techniques such as X-ray computed tomography and nuclear magnetic resonance, there are also certain limitations. X-ray computed tomography (Smyl et al., 2016; Xue et al., 2020) has higher resolution than neutron imaging and can realize spatial detection of structures relatively faster, yet limited by the distinction between matrix and moisture. Nuclear magnetic resonance (Rucker-Gramm and Beddoe, 2010; Wyrzykowski et al., 2017; McDonald et al., 2020) is sensitive to hydrogen nucleus, however, it is limited by its parameters setting (such as the determination of surface relaxation rate) and imaging resolution. Thus, numerical methods may be an effective method for moisture distribution research.

In recent years, some contributions have been made to improve the mass transfer theory of cement-based materials by using numerical simulation methods. For example, considering the coupling effect of moisture and heat, Burkan Isgor and Razaqpur (2004) developed a macroscopic spatial and temporal simulation of the carbonation front advancement in cracked concrete. Based on Voronoi tessellation, Wang et al. (2016) presented a 2D numerical lattice model of mass transport in concrete on the mesoscale level to study the migration of moisture and chloride ions in cracked concrete under the action of dry and wet cycles. According to the theory of computational mechanics, Caggiano et al. (2018) conducted mesoscopic numerical simulation research on water transport of concrete under capillary action by combining zero-thickness interface and pipe elements. On the basis of the unsaturated flow theory, Li et al. (2017, 2018) carried out a numerical simulation study on the moisture distribution characteristic of ITZ and the crack network. Zhao K. et al. (2020) carried out study on chloride transport in cement mortar during drying process which evaluates the influence of diffusion and convection on chloride transport by experiments and numerical simulation. Zhao H. et al. (2020) proposed a coupled hygro-thermo-chemical model, and accurately predicted the three stage of coupled humidity and temperature filed via numerical and experimental method. However, there are still few studies on numerical simulation of the mass transfer process in RAC, especially lacking the water unsaturated transport research.

For the purpose of revealing the water migration in a heterogeneous RAC of multiple phases, this work is aimed to find the water transport characteristic in RAC and calculate the distribution of water content at any elapsed time instead of developing a complicated model for water transport in real RAC. The model in this paper focused on the mesoscale, whereby RAC was idealized as a five-phase composite porous media made up of two kinds of ITZs, two types of mortars, and NCs. Nonlinear diffusion equations based on unsaturated flow theory, were used to describe the water movement, and solved by the finite element method (FEM). And the model parameters were determined by the experimental method in this paper.

Unsaturated Flow Theory

In principle, the moisture migration in cement-based materials is dominated by two mechanisms: permeability and absorption. If the cement-based materials are thoroughly saturated with water, Darcy’s law can be used to describe the process of moisture movement, i.e., permeability. Nevertheless, saturated flow is the exception, and most building constructions can not serve in a saturated state so that capillary absorption should be considered as the primary mechanism of water transport. According to the work of Swartzendruber (1969) in the field of soil, the extended Darcy’s law can be used as the governing equation for describing water unsaturated transport,

$\mathrm{u}=-K\left(\mathrm{\Theta }\right)\nabla \mathrm{\Psi } (1)$

where u is the flow velocity (LT⁻¹); K(Θ) is the unsaturated hydraulic conductivity which is also known as unsaturated permeability (LT⁻¹); $\mathrm{\Psi }$ is the capillary potential (L); $\mathrm{\nabla }$ is the Gradient tensor operator (L⁻¹). $\mathrm{\Theta }$ denotes the normalized water content (–), and it can be written as

$\mathrm{\Theta }=\frac{\theta -{\theta }_{\mathrm{r}}}{{\mathrm{\theta }}_{\mathrm{s}}-{\theta }_{\mathrm{r}}} 0\le \mathrm{\Theta }\le 1 (2)$

where $\theta$, denoted the ratio of water volume to sample bulk volume, is the volumetric water content (–); ${\theta }_{\mathrm{r}}$ is the residual water content (i.e., the water content at dry condition, generally 0) (–) (Lockington et al., 1999), and ${\theta }_{\text{s}}$ is the saturated water content (i.e., the water content in the saturated condition) (–).

In fluid mechanics, the law of conservation of mass is expressed as a Continuity Equation, which is as follows:

$\frac{\partial \theta }{\partial t}+\nabla u=0(3)$

Combining Eq. 1 with Eq. 3 leads to the fundamental equation of unsaturated flow, namely the Richards’ equation

$\frac{\partial \theta }{\partial t}=\nabla K\left(\mathrm{\Theta }\right)\nabla \mathrm{\Psi }(4)$

Usually, Richards’ equation can also be expressed in another two equivalent forms:

$\left(1\right)\text{\hspace{1em}Θ\hspace{0.5em}based\hspace{0.5em}form}:\frac{\partial \mathrm{\Theta }}{\partial t}-\nabla D\left(\mathrm{\Theta }\right)\nabla \mathrm{\Theta }=0$

$\left(2\right)\text{\hspace{1em}Ψ\hspace{0.5em}based\hspace{0.5em}form}:C\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}-\nabla \cdot K\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }=0$

where $C\left(\mathrm{\Psi }\right)=\frac{d\mathrm{\Theta }}{d\dot{\mathrm{\Psi }}}$

A serious limitation of the Θ-based Richards Equation is that the materials of interest must be homogeneous. However, RAC is a kind of multiple-phase composite material which can not be considered as a homogeneous material. In this way, across the interfaces between different phases, the distribution of water content becomes discontinuous. In other words, the Ψ-based form, which can balance the saturation and the capillary potential well, is more suitable for this study.

In Eq. 1, the unsaturated hydraulic conductivity K(Θ) can hardly be obtained experimentally for cementitious materials. According to soil mechanics theory, it can be well estimated by the most widely used model, Mualem equation (Mualem, 1976),

$K\left(\mathrm{\Theta }\right)=K_{\mathrm{s}}{\mathrm{\Theta }}^{\mathit{l}}{\left[1-{\left(1-{\mathrm{\Theta }}^{\frac{1}{m}}\right)}^m\right]}^2(5)$

where $m$ is the van Genuchten parameter (–), usually simplified to $m=1/\left(1-n\right);$l is a constant equal to −0.5 for cementitious materials (–); $K_{\mathrm{s}}$ is the saturated hydraulic conductivity, also known as permeability (LT⁻¹). The relationship between saturation Θ and capillary potential Ψ can be easily established by van Genuchten model (van Genuchten, 1980),

$\mathrm{\Theta }\left(\mathrm{\Psi }\right)=\{\begin{array}{ll}{\left[\frac{1}{1+{\left(\alpha \mathrm{\Psi }\right)}^n}\right]}^m\hfill & \mathrm{\Psi }<0\hfill \\ 1\hfill & \mathrm{\Psi }\ge 0\hfill \end{array}(6)$

with α (L⁻¹) and n as fitting constants and properties of the material. These parameters can adequately describe the water retention curve of cement-based materials, so as to express the unsaturated water transport characteristics of different phase under capillary suction.

Determination and Validation of Parameters

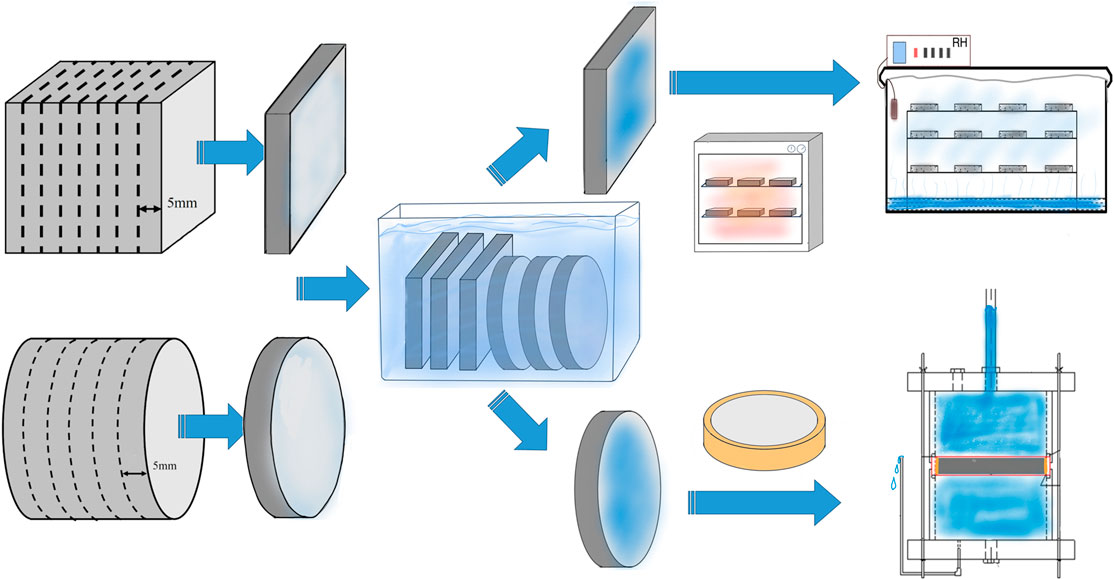
In order to solve the governing equation, the first issue is to determine the parameters (i.e., K_s, α, and n) of different phases. Since the data for cementitious materials are sparse, to ensure the accuracy and effectiveness of the simulation results, adsorption tests, and static pressure penetration tests were conducted in this work. The process is as shown in Figure 1.

FIGURE 1

FIGURE 1. Process of specimens’ preparation.

Materials and Specimen Preparation

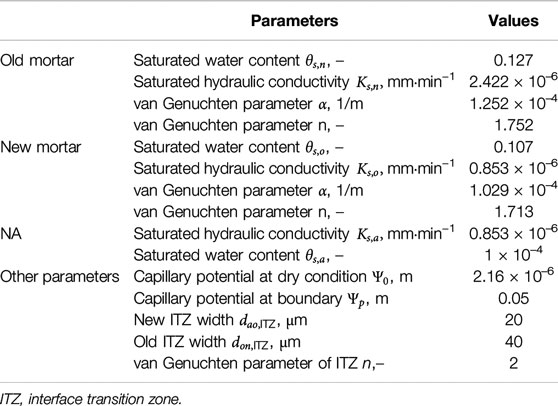
Ordinary Portland cement 52.5 type and river sand with a maximum grain size of 5 mm were used to prepare the mortar specimen. Cube specimens with the side length of 70.7 mm and cylinder specimens with the size of Φ100 mm × 50 mm were prepared separately. All these specimens were demolded after 24 h and then cured in water at an ambient temperature of 20 ± 2°C. After 7 days, specimens were cut into slices of 5 mm thin and then soaked in water for 90 days to minimize the negative impact of hydration on subsequent tests. The mix proportion was determined, according to the research of Zhang et al. (2017a), as shown in Table 1.

TABLE 1

TABLE 1. Mix proportion of cement mortar, kg/m³ (The permission has been obtained from the copyright holders).

Isothermal Adsorption Test

The adsorption isotherm is the basis for studying the properties related to water transport of materials. In order to obtain the van Genuchten parameters α and n, it is necessary to achieve the time-dependent adsorption curves. The following experiments were therefore carried out.

In the beginning, different humidity environments need to be established. Five inorganic salts were selected to prepare supersaturated salt solutions namely MgCl₂, NaBr, NaCl, KCl, and K₂SO₄, by whose theoretical humidity that they can regulate is 33, 58, 76, 86, and 98%, respectively. Correspondingly, five humidity chambers with different salt solutions were prepared in a constant temperature and humidity room [T = 20 ± 2°C and relative humidity (RH) = 50 ± 2%]. The RH (–) of each chamber was measured repeatedly by using humidity sensors until it reached a steady state (the fluctuation in 24 h did not exceed ±1.5%). The actual RH were shown in Table 2.

TABLE 2

TABLE 2. Relative humidity of supersaturated salt solution.

Secondly, the cured square sheet specimens of M1 and M2 were dried to a constant weight at 105 C (mass variation in 7 days is less than 0.01 g), and the dried mass was recorded as $m_{\mathrm{d}}$. Six pieces of M1 and M2 specimens had been placed and numbered in each humidity chambers, followed by a long-term test. After 3 months, the specimens were weighed every 7 days until the constant weight was reached. Each specimen’s mass $m$ at this time was the mass with the adsorption reached equilibrium. Then these specimens were soaked into the water again until saturated, and the water-saturated mass $m_{\mathrm{s}}$ was recorded. By transforming Eq. 2 as follows,

$\mathrm{\Theta }=\frac{\theta -{\theta }_{\mathrm{r}}}{{\theta }_{\mathrm{s}}-{\theta }_{\mathrm{r}}}=\frac{m-m_{\mathrm{d}}}{m_{\mathrm{s}}-m_{\mathrm{d}}} (7)$

the relationship between $\mathrm{\Theta }$ and RH can then be successfully established. According to this relationship, the isothermal adsorption curves were plotted, as shown in Figure 2A.

FIGURE 2

FIGURE 2. (A) Isothermal adsorption curves and (B) water retention curves of M1 and M2.

The relationship between hydrostatic pressure and RH can be described by the Kelvin-Laplace equation,

$P_{\mathrm{w}}=\frac{{\rho }_{\mathrm{w}}\mathrm{R}\mathrm{T}}{M_{\mathrm{w}}}\ln \left(\mathrm{R}\mathrm{H}\right) (8)$

where P_w denotes the hydrostatic pressure (L⁻¹ MT⁻²), $P_{\mathrm{w}}={\rho }_{\mathrm{w}}g\mathrm{\Psi }$; ${\rho }_{\mathrm{w}}$ is the water density, ${\rho }_{\mathrm{w}}=1g/\mathrm{c}{\mathrm{m}}_3$; R denotes the ideal gas constant, which is 8.3144 J/(mol K); T is the Kelvin temperature, which is 293.15 K in this paper; M_w denotes the relative molecular weight of water. Combining Eq. 6 with Eq. 8 leads to the following equation,

$\mathrm{\Theta }=[\begin{array}{ll}{\{\frac{1}{1+{[\alpha \frac{\mathrm{R}\mathrm{T}}{M_{\mathrm{w}}g}\mathrm{l}\mathrm{n}\left(\mathrm{R}\mathrm{H}\right)]}^n}\}}^{\frac{1}{1-n}}\hfill & \mathrm{\Psi }<0\hfill \\ 1\hfill & \mathrm{\Psi }\ge 0\hfill \end{array}(9)$

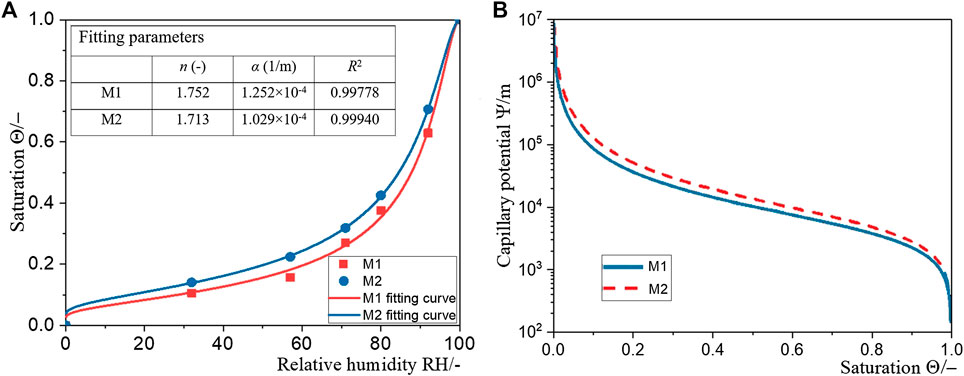
The value of α and n were obtained by fitting Eq. 9, as shown in Figure 2A.

The isotherm adsorption curves fitted in Figure 2A can be transformed into water retention curves in Figure 2B by Eq. 6. The saturation can be easily converted into capillary potential according to these curves, and the initial condition value and boundary condition value of the matrix can be determined quantitatively. It can be manifested from the profiles that when the capillary potential reaches Ψ = −2.16 × 10⁻⁶ mm, the saturation of M1 and M2 is almost equal to zero (that is, the dry state).

The Static Pressure Penetration Test

In Richards’ equation, the value of saturated hydraulic conductivity K_s is also an important parameter to define the properties of the matrix material, which can be obtained by the static pressure penetration test. The pressure penetration apparatus shown in Figure 3A is manufactured according to the research of Ludirdja and Young (1989).

FIGURE 3

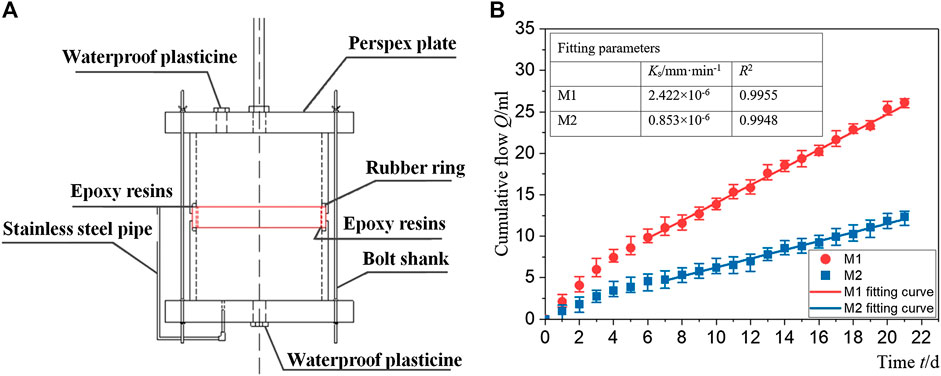
FIGURE 3. Static pressure test: (A) penetration apparatus, and (B) curves of cumulative volume of water permeated vs. time for M1 and M2.

Firstly, each mortar specimen was wrapped with the rubber ring and sealed at the junction by epoxy resin to prevent water leakage. And then, the upper chamber, the rubber ring, and the lower chamber were connected in sequence. The lower chamber was filled with water until the liquid level in the stainless-steel pipe reached the top. In the same way, the upper chamber and the pipette were filled with water carefully to 305 mm. The top of the stainless-steel pipe was kept horizontal with the upper surface of the specimen so that the water at the top will penetrate through the specimen into the lower chamber under the single action of water pressure and flow out from the stainless-steel pipe. The volume change of the water in the pipette was recorded every 24 h as q_i (L³), and then water was filled again to 305 mm height. Due to the little change of water level within 24 h, the specimens can be considered to be under the load of a constant head at all times. The above procedure was repeated until q_i reached a constant value. The relationship between $Q$ (that is, the accumulated amount of q_i) and observation time $t$ was plotted in Figure 3B. $K_{\mathrm{s}}$ can be obtained by fitting the following Eq. 10,

$K_{\mathrm{s}}=\frac{QL}{hAt}(10)$

where L denotes the thickness of the specimen (L); A denotes the permeability area (L²), which is the cut surface area of each specimen; h denotes the water head (L), which is the distance from the liquid surface at the top of the pipette to each specimen.

Validation of the Models

It is difficult to measure the distribution of moisture in non-transparent cement-based materials by experimental methods, and the process of non-destructive testing is also limited. Therefore, in order to verify the accuracy of the theoretical model and parameters, the results of the neutron radiography test carried out by Zhang et al. (2017a) were chosen to compare with the simulation results in this paper. The specimens used in the analysis are mortar specimens with a water-cement ratio of 0.6, whose mix proportion is the same as that of M1 in Table 1. The prepared mortar specimen was cut into thin slices of 100 mm × 100 mm × 25 mm and sealed with aluminum foil tape around to prevent moisture intrusion from other boundaries instead of the bottom surface (Figure 4A). The sealed specimen was placed in a flume for the capillary water absorption experiment, and the neutron radiography test was administered in the meantime.

FIGURE 4

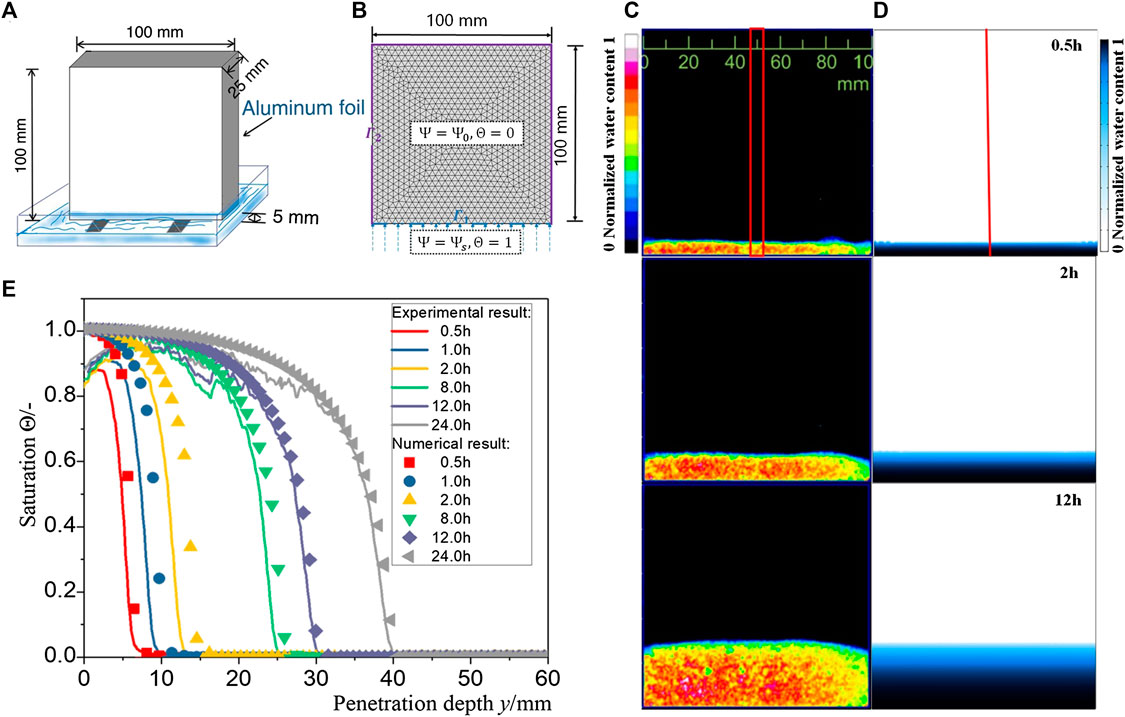
FIGURE 4. (A) Schematic and (B) model of water absorption test, and the comparison of experimental and numerical results: (C) the neutron images of water distribution by Zhang et al. (2017a) (The permission has been obtained from the copyright holders), (D) water distribution cloud maps by numerical simulation, and (E) one-dimensional water distribution profiles by Zhang et al. (2017a) (The permission has been obtained from the copyright holders).

According to the capillary absorption test, the cement mortar absorption model can be established, as shown in Figure 4B. The matrix is initially in a dry state and can only contact the water through the bottom boundary. The remaining boundaries do not exchange water with the outside environment. Therefore, the initial condition and boundary condition can be expressed by

$\{\begin{array}{l}{\mathrm{\Psi }|}_{t=0}={\mathrm{\Psi }}_{0,m}\hfill \\ {\mathrm{\Psi }}_{{\mathrm{\Gamma }}_{\mathrm{1}}}={\mathrm{\Psi }}_{p,m}\hfill \\ {\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_2}=f=0\hfill \end{array}\begin{array}{l}\mathrm{\Psi }\in \mathrm{\Omega }\hfill \\ \mathrm{\Psi }\in {\mathrm{\Gamma }}_1\hfill \\ \mathrm{\Psi }\in {\mathrm{\Gamma }}_2\hfill \end{array}(11)$

where $\mathrm{\Omega }$ is the mortar matrix; ${\mathrm{\Gamma }}_1$ and ${\mathrm{\Gamma }}_2$ are the water absorption boundaries of the mortar specimen and the remaining boundaries, respectively, Γ₁∪Γ₂ = Γ; $f$ denotes the flow velocity through boundary ${\mathrm{\Gamma }}_2$ (LT⁻¹); ${\mathrm{\Psi }}_{0,m}$ is the capillary potential at matrix saturation of 0 (L); ${\mathrm{\Psi }}_{p,m}$ is the capillary potential at matrix saturation of 1 (L). The parameters for numerical computation are listed in Table 3.

TABLE 3

TABLE 3. Summary of parameters for M1.

The cloud maps of water distribution at different times can be obtained by employing numerical simulation, and the results are compared with the experimental results of neutron imaging. By comparing Figures 4C,D, it can be observed intuitively that the moisture in the specimen is absorbed upward from the lower surface of the specimen under the action of the capillary adsorption force. Due to the inhomogeneity of the mortar composite, the water front is not completely parallel to the water absorption surface, and the water distribution at different coordinates is also slightly different. However, these differences did not substantially affect the results. The distribution of water front illustrates that the water transport is almost one-dimensional parallel to the bottom of the boundary, and the movement of the water front slows down gradually with time elapsing. The simulated position of the water front at different times shows good agreement with the experimental results.

The marked central area shown in Figures 4C,D is selected for quantitative analysis to obtain numerical and experimental water distribution shown in Figure 4E. It can be seen quantitatively that the water distribution along the y-axis in the simulation results is roughly the same as that in the test results. The difference between the simulation results and the test results mainly comes from the following points: a) The mortar model is simplified to a homogeneous model structure whereby water is uniformly distributed in the horizontal direction. However, in the capillary absorption test, due to various factors such as uneven distribution of sand particles and insufficient hydration, the results will inevitably be different from the idealized model’s. Sand and insufficient hydration will cause the lag of unsaturated water transport. b) In the capillary water absorption test, the sample needs to be dried by oven. High temperature will damage the material, enhance the connectivity of the pores, and accelerate the process of water transport in the matrix. c) The inhomogeneity of the mortar specimens causes the saturation water content at each position to be different, so it is inevitable to underestimate or overestimate the saturation of certain areas after normalization by the formula. However, the influence of these errors is very weak and within an acceptable range, thus overall results show well agreement. This agreement suggests that the numerical model and substitute parameters correctly describe the capillary absorption process in the cement mortar matrix, which provides a guarantee for the accuracy of subsequent studies on water unsaturated transport in RAC.

Transport Analysis for Recycled Aggregate Concrete

Mesoscale Recycled Aggregate Concrete Model

Considering that the polygonal aggregate has a huge amount of calculation for the simulation and the limited influence on water transport (Li et al., 2016; Liu et al., 2018), the round aggregates are used in our study to simplify the calculation. As mentioned before, the essential difference between RAC and NAC is the coarse aggregate. Compared to NA, RAC can not be considered as traditional aggregate-matrix two-phase material structure nor aggregate-ITZ-matrix three-phase material structure because of the old mortar attached to old NA. The old ITZ initially existed between the old aggregate and the old mortar, and new ITZ gradually forms between the old mortar and the new mortar after setting. As a consequence, in order to describe the migration of water in RAC more accurately, the five-phase RAC model consisting of old aggregate, old mortar paste, old ITZ, new mortar paste, and new ITZ were established by simplifying the actual RA into a concentric circle model (Figure 5A).

FIGURE 5

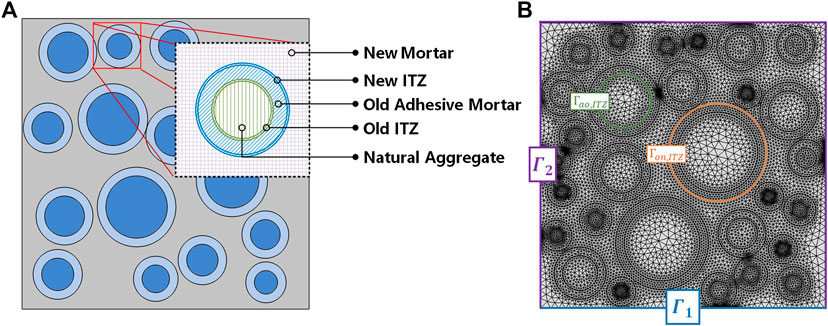
FIGURE 5. Mesoscale structure of recycled aggregate concrete: (A) schematic diagrams and (B) finite element meshes diagrams.

By means of the Monte Carlo method, in other words, cyclically putting concentric circles of different sizes into a square area until it reaches the expected area fraction (i.e., coarse aggregate volume fraction), the two-dimensional RAC random aggregate model can be established. This process was achieved by randomly generating NC aggregate center coordinates, radius, and adhesive mortar thickness and running a set of MATLAB codes. The meshed RAC model is shown in Figure 5B.

Definition of Interface Transition Zones Phase

According to the description of the smooth plate crack flow method (Chen et al., 2013; Li et al., 2017), a variant of extended Darcy’s law was adopted to describe the water flow in ITZ. In this way, ITZs in the model will have no geometric width, and water transport in it might be simplified to flow along interior boundaries between the two different phases. The governing equation of water transport in the crack is as follows,

$\{\begin{array}{l}{d}_{\mathrm{I}\mathrm{T}\mathrm{Z}}{C}_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}+{\nabla }_T\times \left[d_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(-K_{ \mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right){\nabla }_{\mathrm{T}}\mathrm{\Psi }\right)\right]=f_{\mathrm{a}}+f_{\mathrm{o}}\hfill \\ d_{\mathrm{I}\mathrm{T}\mathrm{Z}}{C}_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}+{\nabla }_T\times \left[d_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(-K_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right){\nabla }_{\mathrm{T}}\mathrm{\Psi }\right)\right]=f_{\mathrm{o}}+f_{\mathrm{n}}\hfill \end{array} (12)$

where $d_{\mathrm{I}\mathrm{T}\mathrm{Z}}$ is the ITZ width, and ${\nabla }_{\text{T}}$ denotes the tangential derivatives of ITZ. $f_i$ is the exchange item (i.e., the flow rate) between ITZ and matrix, the subscript i represents the three matrix NA(a), old adhesive mortar (o), and new mortar (n). Since the width of ITZ is far smaller than that of the matrix, the capillary potential at the two sides of it is identical to $\mathrm{\Psi }$. Therefore $f_i$ can be expressed as follows

$\{\begin{array}{l}{-K_n\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_{\mathrm{o}\mathrm{n},\mathrm{I}\mathrm{T}\mathrm{Z}}}=f_{\mathrm{n}} \mathrm{\Psi }\in {\mathrm{\Gamma }}_{\mathrm{o}\mathrm{n},\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \\ {-K_o\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_{\mathrm{o}\mathrm{n},\mathrm{I}\mathrm{T}\mathrm{Z}}}=f_{\mathrm{o}} \mathrm{\Psi }\in {\mathrm{\Gamma }}_{\mathrm{o}\mathrm{n},\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \\ {-K_a\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_{\mathrm{a}\mathrm{n},\mathrm{I}\mathrm{T}\mathrm{Z}}}=f_{\mathrm{a}} \mathrm{\Psi }\in {\mathrm{\Gamma }}_{\mathrm{a}\mathrm{o},\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \\ {-K_o\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_{\mathrm{a}\mathrm{o},\mathrm{I}\mathrm{T}\mathrm{Z}}}=f_{\mathrm{o}} \mathrm{\Psi }\in {\mathrm{\Gamma }}_{\mathrm{a}\mathrm{o},\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \end{array} (13)$

where ${\mathrm{\Gamma }}_{j,\mathrm{I}\mathrm{T}\mathrm{Z}}$ is different interfaces. $K_i$ is the hydraulic conductivity of different matrix.$K_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)$ in Eq. 12 denotes the unsaturated hydraulic conductivity of ITZ,

$K_{\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)=K_{\mathrm{s},\mathrm{I}\mathrm{T}\mathrm{Z}}{\mathrm{\Theta }}^{\mathit{l}}{\left[1-{\left(1-{\mathrm{\Theta }}^{\frac{1}{m}}\right)}^m\right]}^2 (14)$

where l is a constant equal to −0.5 for cementitious materials (–); $m$ is the van Genuchten parameter (–), $m=1-1/n$. It is reported that the value of n is generally between 1 and 2, fluctuating little in similar materials. In this work, n is assumed as 2 for ITZs. $K_{s,\text{ITZ}}\left(\mathrm{\Psi }\right)$ is the saturated hydraulic conductivity of ITZ. According to the cubic law (Witherspoon et al., 1980; Wang et al., 2016), the relationship between $K_{s,\mathrm{I}\mathrm{T}\mathrm{Z}}$ and width can be expressed as Eq. 15

$K_{\mathrm{s}, \mathrm{I}\mathrm{T}\mathrm{Z}}=\frac{d_{\mathrm{I}\mathrm{T}\mathrm{Z}}^3}{12l_{\mathrm{I}\mathrm{T}\mathrm{Z}}}\frac{\rho g}{\mu } (15)$

where μ is the viscous coefficient of water. With these formulations above, the ITZ domain can be idealized as a porous and zero-model-thickness interface with higher hydraulic conductivity in RAC.

Definition of Natural Aggregate and Mortar Phases

The pore structure determines the mass transfer performance of cementitious material. Since the pore structure of RC is different from NC, the water transfer law in RAC is naturally different from NAC. The migration velocity of water in the matrix can be regarded as a function of the characteristics of the RAC’s different phases. In other words, correctly distinguishing and defining the properties of each phase to represent its pore structure characteristic in numerical simulation is an essential factor in ascertaining the water distribution in RAC. In this model, both the cement mortar phase and the aggregate phase are considered as the porous material so that the water transport in them follows the Richards’ Equation (i.e., Eq. 3). Consequently, combining the previously mentioned theory of water transport in the matrix, the governing equation of water transport in recycled concrete can be obtained, which is expressed as follows,

$\{\begin{array}{l}{C}_n\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}-\nabla K_n\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }=0 \mathrm{\Psi }\in {\mathrm{\Omega }}_n\hfill \\ C_o\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}-\nabla K_o\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }=0 \mathrm{\Psi }\in {\mathrm{\Omega }}_o\hfill \\ C_a\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}-\nabla K_a\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }=0 \mathrm{\Psi }\in {\mathrm{\Omega }}_a\hfill \\ d_{ao,\mathrm{I}\mathrm{T}\mathrm{Z}}C\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}+\nabla \left(d_{ao,\mathrm{I}\mathrm{T}\mathrm{Z}}{K}_{ao,\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }\right)=0 \mathrm{\Psi }\in {\mathrm{\Gamma }}_{ao,\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \\ d_{on,\mathrm{I}\mathrm{T}\mathrm{Z}}C\left(\mathrm{\Psi }\right)\frac{\partial \mathrm{\Psi }}{\partial t}+\nabla \left(d_{on,\mathrm{I}\mathrm{T}\mathrm{Z}}{K}_{om,\mathrm{I}\mathrm{T}\mathrm{Z}}\left(\mathrm{\Psi }\right)\nabla \mathrm{\Psi }\right)=0 \mathrm{\Psi }\in {\mathrm{\Gamma }}_{on,\mathrm{I}\mathrm{T}\mathrm{Z}}\hfill \end{array} (16)$

And the initial and boundary condition can be expressed as

$\{\begin{array}{l}{\mathrm{\Psi }|}_{t=0}={\mathrm{\Psi }}_0\hfill \\ {\mathrm{\Psi }}_{{\mathrm{\Gamma }}_1}={\mathrm{\Psi }}_p\hfill \\ {\frac{\partial \mathrm{\Psi }}{\partial \left\{n\right\}}|}_{{\mathrm{\Gamma }}_2}=f=0\hfill \end{array}\begin{array}{l}\mathrm{\Psi }\in \mathrm{\Omega }\hfill \\ \mathrm{\Psi }\in {\mathrm{\Gamma }}_1\hfill \\ \mathrm{\Psi }\in {\mathrm{\Gamma }}_2\hfill \end{array}(17)$

In the Eq. 16, if the governing equation in domain ${\mathrm{\Omega }}_o$ is replaced with that in domain ${\mathrm{\Omega }}_n$, the unsaturated transport simulation of NAC can be implemented.

Compared with the new cement mortar matrix, due to various factors such as crushing and grinding, the micro-cracks of the old adhesive mortar and the old ITZ increase, and their saturated water content and permeability also increase accordingly. This means that the saturated water content ${\theta }_s$ and hydraulic conductivity $K_s$ of new mortar are higher than these of old adhesive mortar. For this purpose, the parameters of M1 and M2 are used to describe the old adhesive mortar and new mortar in the model, respectively. Considering the extremely low water absorption rate, NA can be regarded as an impermeable porous media. It is found through trial calculation that, when $K_s\left(\mathrm{N}\mathrm{A}\right)/K_s\left(\mathrm{m}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\right)\le 1\times {10}^{-6}$, ${\theta }_s\left(\mathrm{N}\mathrm{A}\right)/{\theta }_s\left(\mathrm{M}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\right)\le 1\times {10}^{-3}$, there is hardly water movement in NA. To simplify the calculation, the $K_s$ and ${\theta }_s$ are assumed as 1 × 10^–20 m/sec and 0.0001 in this work. The parameter settings of RAC are summarized in Table 4.

TABLE 4

TABLE 4. Summary of material parameters for recycled aggregate concrete.

Validation of the Recycled Aggregate Concrete Models

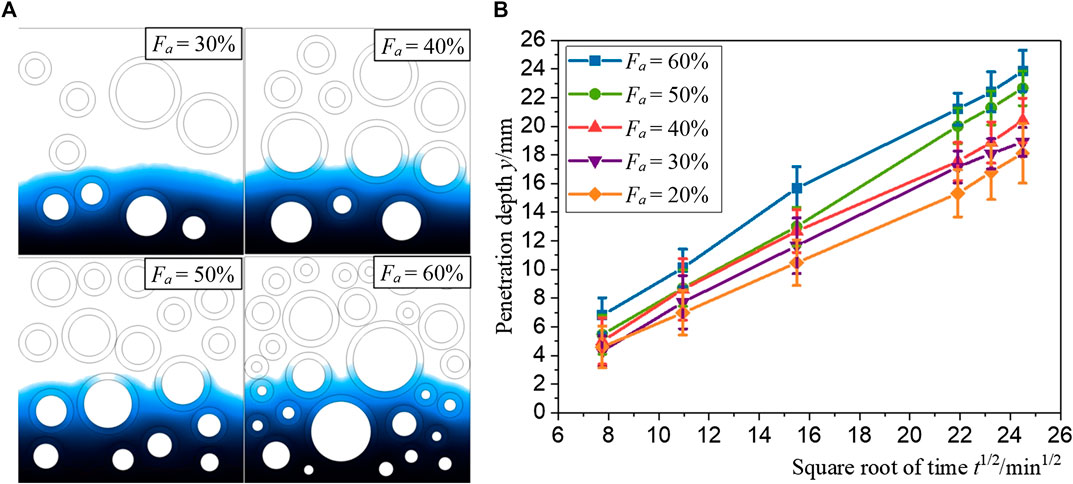
To verify the accuracy of the model, we compared the simulation results with the capillary water absorption test results of Bao et al. (2020a) which is shown in Figures 6A,B. It is illustrated that, both the macroscopic water absorption and the microscopic water penetration depth, the simulation results agree well with experimental results. The differences are mainly due to the following factors: a) There is a slight difference in water cement ratio between experiment (W/C = 0.39) and simulation (W/C = 0.40) which might cause differences in results; b) There are some uncertainties in practice, such as the insufficient hydration and the heterogeneity of mortar matrix, which is difficult to achieve by numerical model; c) Although a complex RA model has been established, it is still a simplified form of practical RA. These factors may cause small changes in the results but will not have a substantial impact on the conclusions. Hence one can conclude that the RAC model used in this study is accurate and reliable.

FIGURE 6

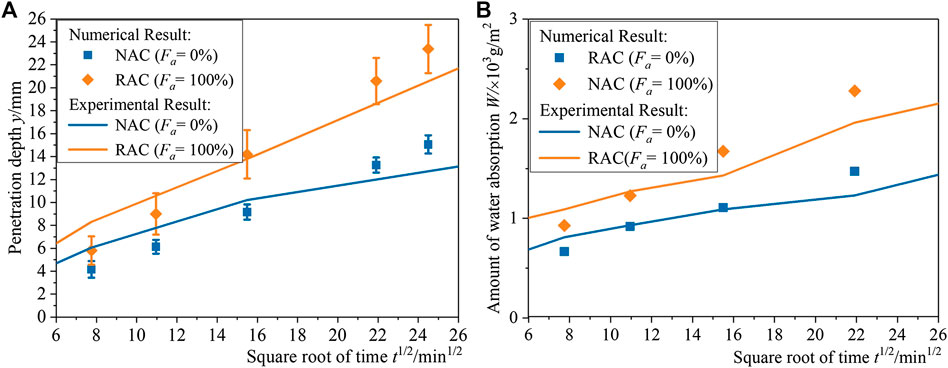
FIGURE 6. Comparison of numerical results and the experimental results of Bao et al. (2020a) on (A) water penetration depth and (B) amount of water absorption (The permission has been obtained from the copyright holders).

Modeling Results of Water Uptake in Recycled Aggregate Concrete and Natural Aggregate Concrete

Equation 16 was implemented in the commercial finite element software, COMSOL Multiphysics, the multi-field coupled FEM simulation program, and the cloud map of water distribution of NAC and RAC at different times were obtained to describe the 2D water distribution in RAC and NAC at different times (Figures 7A,B).

FIGURE 7

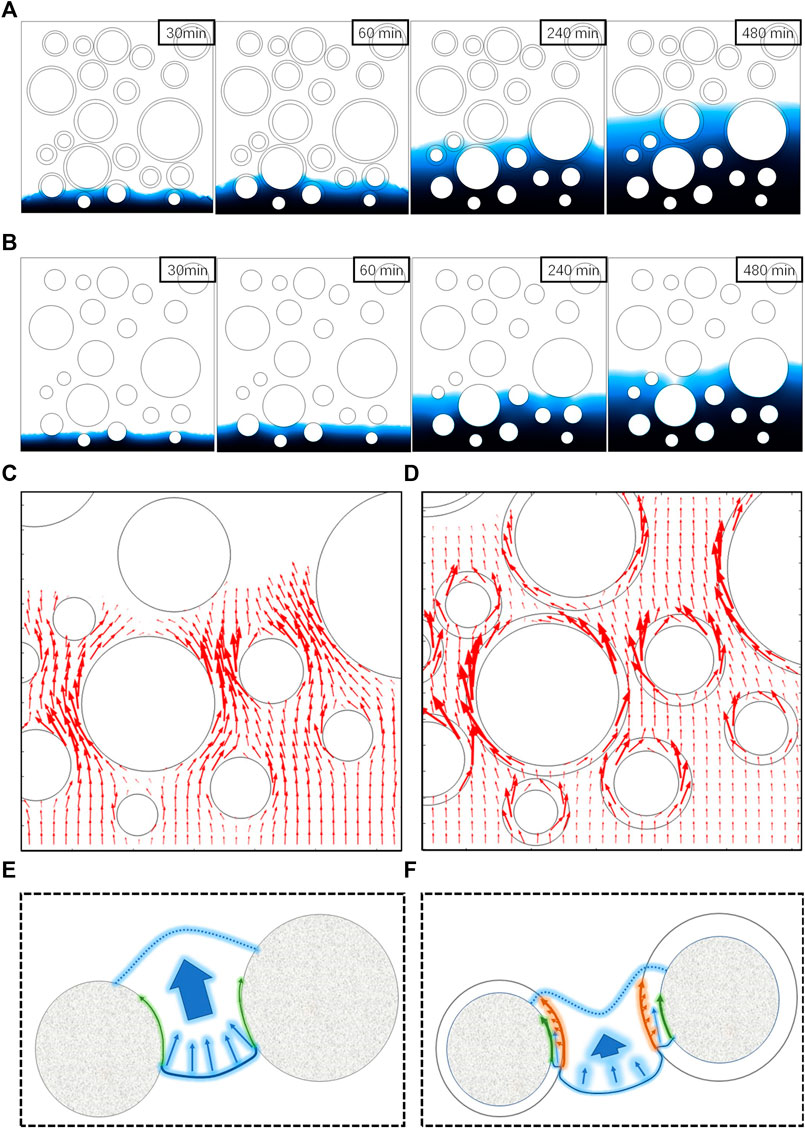
FIGURE 7. Comparison of numerical simulation results between recycled aggregate concrete (RAC) and natural aggregate concrete (NAC): cloud maps of water distribution in (A) RAC and (B) NAC, the arrow diagram of flow flux in (C) RAC and (D) NAC, and the schematic of water movement characteristic between aggregates in (E) RAC and (F) NAC.

It can be seen that, as t = 30 min, the water front in RAC has wholly surpassed the marked aggregate, and the water front behind the aggregate penetrates deeper than it in the mortar matrix. While the moisture penetrating speed in NAC slows down, and the water front in the mortar penetrates is deeper. When t = 60 min, the difference in the penetration depth is more prominent. The peak of the water front has reached a depth of about 13 mm in RAC, while barely about 7 mm in NAC.

Despite considering the influence of ITZ of NAC, the hindrance effect of NA on water transport is much higher than the promoting effect of ITZ. By comparing the flow flux arrow diagram shown in Figures 7C,D, one can see in NAC that although the flow velocity of ITZ is higher than that of the ordinary mortar matrix, it is still lower than the moisture transmission in the narrow and long domain between NAs. However, in RAC, the flow velocity between RAs is relatively low, and the main flow velocity is concentrated in the old adhesive mortar and ITZ area. This phenomenon can be explained that water only moves in the matrix and single ITZ on condition that NA is assumed as impermeable, whereby the real water transport area is equivalent to narrowing. Thus, due to the limitation of water transport capacity, the vast majority of water still crowds in the mortar matrix, so that the convex surface of the water front is formed between the aggregates (Figure 7E). However, the old mortar and the double ITZs are all weak areas for RAC. Both of the porosity and hydraulic conductivity are relatively large. On the one hand, similar to NAC, the water absorption of RAC is accelerated due to the existence of ITZ. On the other hand, as moving in ITZ, water also transfers rapidly into the old mortar whose capillary pressure is higher than that of the new mortar, which further accelerates the penetration of water. Because of the higher penetration velocity in RA, the convex surface of the moisture front is formed behind RA (Figure 7F).

The relationship between the water penetration depth and the square root of the time were plotted in Figure 8, which is approximated to a positive linear correlation. The slope of the curve corresponds to the velocity of water uptake, which indicated that the water absorption velocity in RAC is much larger than the other two materials. As t = 600 min, the penetration depth of water in RAC even reaches 1.6 times that in NAC. By comparing NAC and cement mortar, it can be illustrated that the penetration depth in RAC always slightly lags behind in cement mortar, which confirms that the hindrance effect of NA on moisture is stronger than the promoting effect of single ITZ as mentioned before. However, the error bars of moisture penetration in NAC shows lower variability, which indicates that NA and single ITZ have limited effects on water uptake. Instead, this situation is quite different in RAC. “Convenient access” of RA occupies a dominant position in water transport, which leads to the increased influence of matrix heterogeneity, and then causes larger variability of penetration depth showed in profile. This feature can also be found intuitively in the cloud map in Figures 7A,B, as t = 480 min.

FIGURE 8

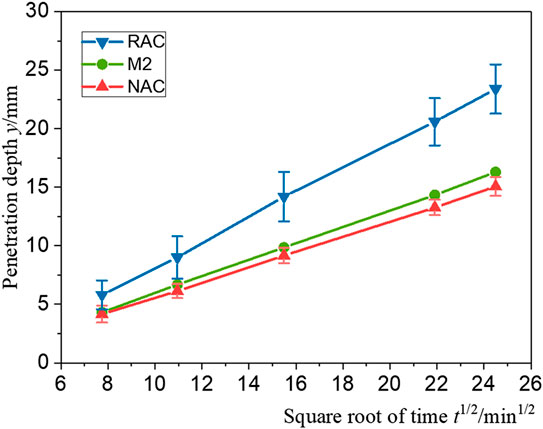
FIGURE 8. The profiles of water penetration depth in recycled aggregate concrete (RAC), natural aggregate concrete (NAC), and cement mortar at different time.

Parameter Sensitivity

The previous content illustrates the critical role RA plays in unsaturated absorption of RAC. Therefore, it is necessary to conduct a more detailed study on the impact of aggregate. For this purpose, parameter sensitivity analyses on RA replacement rate ($R_{ra}$), the thickness of old mortar (d_m) and the RA volume fraction ($F_a$) were implemented.

Effect of Recycled Aggregate Replacement Rate on Water Absorption

$R_{\mathrm{r}\mathrm{a}}$ refers to the volume ratio of RA to all aggregates, which is assumed to be the area ratio in 2D condition. To investigate its influence on the water absorption of RAC, five $R_{\mathrm{r}\mathrm{a}}$ of 0, 25, 50, 75, and 100% were used, and then a random aggregate model was generated.

As shown in Figure 9A, it can be learned that with the $R_{\mathrm{r}\mathrm{a}}$ increases, the penetration depth of the water front advances slightly. By observing the marked red area, the difference in water distribution can be distinguished. Figure 9B shows the water penetration depth against the different square root of t, with the given values of $R_{\mathrm{r}\mathrm{a}}$. One can see that with the increase of R, water uptake is gradually accelerated, and the depth of water penetration also obviously increases. The reason for this phenomenon is mainly that the appearance of old adhesion mortar and double ITZs increase the overall capillary potential macroscopically, thereby enhance the water absorption performance of concrete. It can be found that water penetration depth in concrete with $R_{\mathrm{r}\mathrm{a}}$ of 50% advances nearly 5 mm more than it with $R_{\mathrm{r}\mathrm{a}}$ of 0%, which is almost equivalent to 1.35 times depth of the latter. It can also be seen that the volatility of the water front gradually rises with the $R_{\mathrm{r}\mathrm{a}}$ becoming greater. It can be attributed that the increase of RA causes greater heterogeneity of concrete matrix by randomly increasing weak areas. This phenomenon evidences that it is necessary to reduce water absorption performance of RA if higher $R_{\mathrm{r}\mathrm{a}}$ are pursued.

FIGURE 9

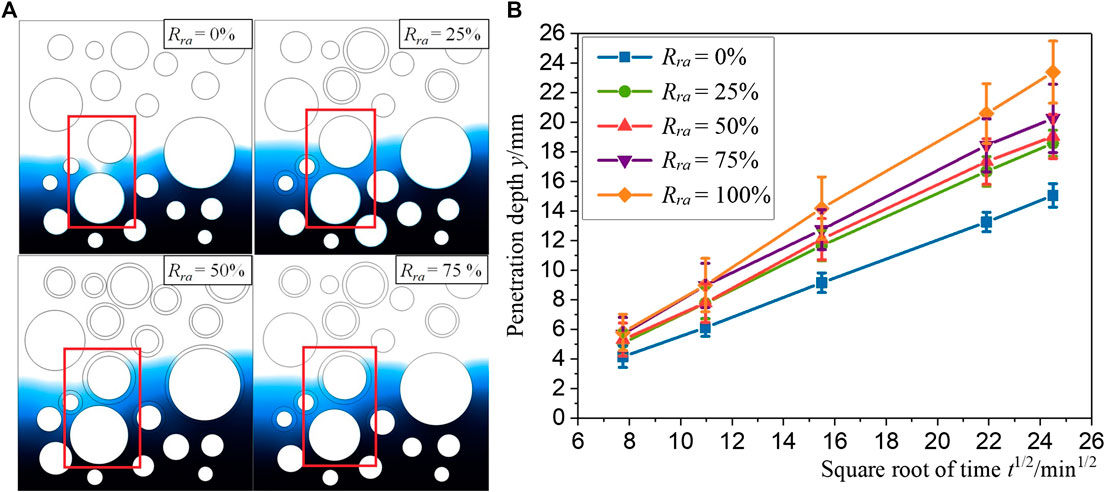
FIGURE 9. (A) 2D cloud diagram and (B) profiles of moisture distribution with different R_ra (F_a = 50%).

Effect of Thickness of Old Mortar on Water Absorption

To investigate the influence of old adhesive mortar on water movement in RAC, without changing the size of the NC, the RAC model is generated. Figure 10A indicates that with the increase of $d_m$, wet front reaches much deeper. The quantitative depth of water penetration over time can be learned in Figure 10B. In the beginning, it indicates no significant difference. However, the influence of $d_m$ becomes noticeable over time. The reason might be that the increase of $d_m$ directly leads to the increase of volumetric ratio of old mortar to NA, which increases the overall porosity of RA and accelerates water movement. It is worth to mention that radius of NA is reduced to keep $F_a$ unchanged. This means that when $d_m$ increases, it not only promotes moisture absorption, but also reduces the blocking effect of the aggregate on the moisture. Therefore, in order to improve the durability of RAC, it is necessary to minimize d_m as much as possible.

FIGURE 10

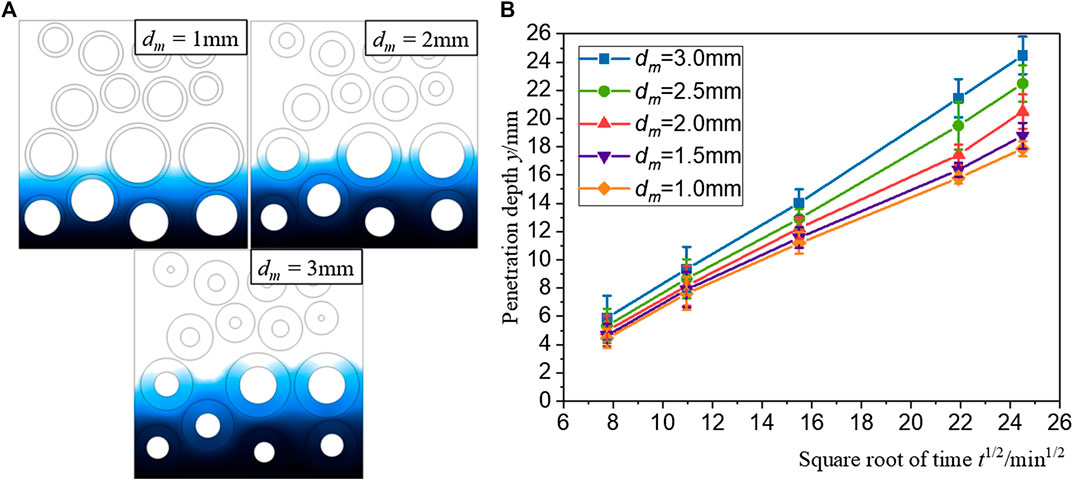
FIGURE 10. (A) 2D cloud diagram and (B) profiles of moisture distribution with different d_m (F_a = 50%).

Effect of Recycled Aggregate Volume Fraction on Water Absorption

$F_{\text{a}}$ refers to the volume ratio of RA to the concrete matrix, which is assumed to area ratio in the 2D model. The presence of adhesive mortar and ITZ plays a certain role in promoting water transport, and that of NA plays a certain role in inhibiting water transport. When the $F_{\text{a}}$ changes, the volume fraction of adhesive mortar and old aggregate has also changed accordingly. To investigate the influence of $F_{\text{a}}$, a RA model with $d_m$ of 1.5 mm and particle size of 5–20 mm is generated.

The cloud map in Figure 11A shows that the change in F_a causes the difference in moisture distribution. However, this change seems to be reflected only in the difference of water front tortuosity instead of the depth. The water penetration depth of different $F_{\text{a}}$ plotted against the square root of time is shown in Figure 11B The profiles show that the slope slightly increases with the growth of volume fraction, which signifies that the velocity of water absorption increases. In Validation of the RAC Models, it has been reported that the hindrance effect of NA in NAC is the reason for the lower water absorption velocity than in cement mortar. In this section, one can see when $F_{\text{a}}$ is relatively low, there is no RA in lower area of the concrete model, which makes the early moisture absorption only proceed in the mortar matrix and caused a lower velocity of moisture absorption during the first 60 min. This result indicates that the promoting effect of the old mortar exceeds the hindrance effect of NAs.

FIGURE 11

FIGURE 11. (A) 2D cloud diagram and (B) profiles of moisture distribution with different F_a.

Conclusions

In this paper, the influence of aggregates and ITZs on the water transport performance of concrete are studied by combining the FEM and unsaturated theory. The numerical simulation approach is reported to evaluate the unsaturated transport process in RAC. The following conclusion can be drawn:

• On the basis of the non-homogeneous characteristic of concrete, the five-phase RAC model consisting of old aggregate, old adhesive mortar, old ITZ, new mortar, and new ITZ is established on the mesoscopic level. The capillary absorption equation in unsaturated RAC is reasonably derived, and the model parameters required in the equation are determined by the experimental method. The accuracy of the model and parameters are validated by comparing experimental data.

• The double ITZs and old mortar in RAC provide a more convenient channel for moisture movement, which results in moisture preferentially transporting along the aggregate instead of the new mortar matrix and causing the forefront of the wet front always forming behind the RA. This transmission mode greatly accelerates the capillary absorption rate of water in the concrete, thereby seriously threatening the durability of this concrete.

• The parameter sensitivity analysis of recycled concrete is conducted. It is found that as the thickness of the old adhesive mortar and the replacement rate of RA increase, the water absorption velocity in RAC is significantly accelerated. The moisture uptake velocity increases with the growth of aggregate volume fraction, but the amplitude is relatively small, which shows that the hindrance effect of NA on moisture is offset by the promotion effect of adhesive mortar with dual ITZs.

Data Availability Statement

All datasets presented in this study are included in the article.

Author Contributions

The corresponding author is responsible for ensuring that the descriptions are accurate. ZL: writing original draft, implementation of the numerical simulation and data curation. PZ: Formulation of overarching research goals and aims. JB: development of methodology. YH: investigation, modifying and editing.

Funding

Financial support for on-going projects by the Natural Science Foundation of China (51922052, U1706222, 51778309), Natural Science Foundation of Shandong Province (ZR2018JL018, ZR2019PEE001) and Open Research Fund Program of State Key Laboratory of Hydroscience and Engineering (SKLHSE-2019-C-04) is gratefully acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Bao, J., Li, S., Zhang, P., Ding, X., Xue, S., Cui, Y., et al. (2020a). Influence of the incorporation of recycled coarse aggregate on water absorption and chloride penetration into concrete. Constr. Build. Mater. 239, 117845. doi:10.1016/j.conbuildmat.2019.117845

CrossRef Full Text | Google Scholar

Bao, J., Xue, S., Zhang, P., Dai, Z., and Cui, Y. (2020b). Coupled effects of sustained compressive loading and freeze‐thaw cycles on water penetration into concrete. Struct. Concr. 2020, 1–11. doi:10.1002/suco.201900200

CrossRef Full Text | Google Scholar

Burkan Isgor, O., and Razaqpur, A. G. (2004). Finite element modeling of coupled heat transfer, moisture transport and carbonation processes in concrete structures. Cem. Concr. Compos. 26 (1), 57–73. doi:10.1016/s0958-9465(02)00125-7

CrossRef Full Text | Google Scholar

Caggiano, A., Said Schicchi, D., Mankel, C., Ukrainczyk, N., and Koenders, E. A. B. (2018). A mesoscale approach for modeling capillary water absorption and transport phenomena in cementitious materials. Comput. Struct. 200, 1–10. doi:10.1016/j.compstruc.2018.01.013

CrossRef Full Text | Google Scholar

Chen, B., Song, E., and Cheng, X. (2013). “Plane-symmetrical simulation of flow and heat transport in fractured geological media: a discrete fracture model with comsol,” in Multiphysical testing of soils and shales (Berlin, Germany: Springer), 149–154.

Google Scholar

Folino, P., and Xargay, H. (2014). Recycled aggregate concrete – mechanical behavior under uniaxial and triaxial compression. Constr. Build. Mater. 56, 21–31. doi:10.1016/j.conbuildmat.2014.01.073

CrossRef Full Text | Google Scholar

Fraj, A. B., and Idir, R. (2017). Concrete based on recycled aggregates – recycling and environmental analysis: a case study of Paris’ region. Constr. Build. Mater. 157, 952–964. doi:10.1016/j.conbuildmat.2017.09.059

CrossRef Full Text | Google Scholar

Kim, S.-W., and Yun, H.-D. (2014). Evaluation of the bond behavior of steel reinforcing bars in recycled fine aggregate concrete. Cem. Concr. Compos. 46, 8–18. doi:10.1016/j.cemconcomp.2013.10.013

CrossRef Full Text | Google Scholar

Lam, P. T. I., Yu, A. T. W., Wu, Z., and Poon, C. S. (2019). Methodology for upstream estimation of construction waste for new building projects. J. Clean. Prod. 230, 1003–1012. doi:10.1016/j.jclepro.2019.04.183

CrossRef Full Text | Google Scholar

Li, X., Chen, S., Xu, Q., and Xu, Y. (2017). Modeling the three-dimensional unsaturated water transport in concrete at the mesoscale. Comput. Struct. 190, 61–74. doi:10.1016/j.compstruc.2017.05.005

CrossRef Full Text | Google Scholar

Li, X., Chen, S., Xu, Q., and Xu, Y. (2018). Modeling capillary water absorption in concrete with discrete crack network. J. Mater. Civ. Eng. 30 (1), 04017263. doi:10.1061/(asce)mt.1943-5533.0002122

CrossRef Full Text | Google Scholar

Li, X., Xu, Y., and Chen, S. (2016). Computational homogenization of effective permeability in three-phase mesoscale concrete. Constr. Build. Mater. 121, 100–111. doi:10.1016/j.conbuildmat.2016.05.141

CrossRef Full Text | Google Scholar

Liu, Q.-f., Feng, G.-l., Xia, J., Yang, J., and Li, L.-y. (2018). Ionic transport features in concrete composites containing various shaped aggregates: a numerical study. Compos. Struct. 183, 371–380. doi:10.1016/j.compstruct.2017.03.088

CrossRef Full Text | Google Scholar

Lockington, D., Parlange, J.-Y., and Dux, P. (1999). Sorptivity and the estimation of water penetration into unsaturated concrete. Mater. Struct. 32 (5), 342. doi:10.1007/BF02479625

CrossRef Full Text | Google Scholar

Ludirdja, D., Berger, R. L., and Young, J. F. (1989). Simple method for measuring water permeability of concrete. ACI Mater. J. 86 (5), 433–439. doi:10.14359/2000

CrossRef Full Text | Google Scholar

McDonald, P. J., Istok, O., Janota, M., Gajewicz-Jaromin, A. M., and Faux, D. A. (2020). Sorption, anomalous water transport and dynamic porosity in cement paste: a spatially localised 1H NMR relaxation study and a proposed mechanism. Cem. Concr. Res. 133, 106045. doi:10.1016/j.cemconres.2020.106045

CrossRef Full Text | Google Scholar

Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12 (3), 513–522. doi:10.1029/WR012i003p00513

CrossRef Full Text | Google Scholar

Munir, M. J., Kazmi, S. M. S., Wu, Y.-F., Patnaikuni, I., Zhou, Y., and Xing, F. (2020). Stress strain performance of steel spiral confined recycled aggregate concrete. Cem. Concr. Compos. 108, 103535. doi:10.1016/j.cemconcomp.2020.103535

CrossRef Full Text | Google Scholar

Oikonomou, N. D. (2005). Recycled concrete aggregates. Cem. Concr. Compos. 27 (2), 315–318. doi:10.1016/j.cemconcomp.2004.02.020

CrossRef Full Text | Google Scholar

Phillipson, M. C., Baker, P. H., Davies, M., Ye, Z., McNaughtan, A., Galbraith, G. H., et al. (2007). Moisture measurement in building materials: an overview of current methods and new approaches. Build. Serv. Eng. Res. Technol. 28 (4), 303–316. doi:10.1177/0143624407084184

CrossRef Full Text | Google Scholar

Rucker-Gramm, P., and Beddoe, R. E. (2010). Effect of moisture content of concrete on water uptake. Cem. Concr. Res. 40 (1), 102–108. doi:10.1016/j.cemconres.2009.09.001

CrossRef Full Text | Google Scholar

Smyl, D., Hallaji, M., Seppänen, A., and Pour-Ghaz, M. (2016). Quantitative electrical imaging of three-dimensional moisture flow in cement-based materials. Int. J. Heat Mass Tran. 103, 1348–1358. doi:10.1016/j.ijheatmasstransfer.2016.08.039

CrossRef Full Text | Google Scholar

Song, Q., Zhao, H., Jia, J., Yang, L., Lv, W., Bao, J., et al. (2020). Pyrolysis of municipal solid waste with iron-based additives: a study on the kinetic, product distribution and catalytic mechanisms. J. Clean. Prod. 258, 120682. doi:10.1016/j.jclepro.2020.120682

CrossRef Full Text | Google Scholar

Swartzendruber, D. (1969). “The flow of water in unsaturated soils,” in Flow through porous media. Editor R. J. M. De Weist (New York, NY: Academic Press), 215–292.

Google Scholar

Tam, V. W. Y., Gao, X. F., and Tam, C. M. (2005). Microstructural analysis of recycled aggregate concrete produced from two-stage mixing approach. Cem. Concr. Res. 35 (6), 1195–1203. doi:10.1016/j.cemconres.2004.10.025

CrossRef Full Text | Google Scholar

Tam, V. W. Y., Soomro, M., and Evangelista, A. C. J. (2018). A review of recycled aggregate in concrete applications (2000–2017). Constr. Build. Mater. 172, 272–292. doi:10.1016/j.conbuildmat.2018.03.240

CrossRef Full Text | Google Scholar

Tian, Y., Zhang, P., Zhao, K., Du, Z., and Zhao, T. (2020). Application of Ag/AgCl sensor for chloride monitoring of mortar under dry-wet cycles. Sensors 20 (5), 1394. doi:10.3390/s20051394

CrossRef Full Text | Google Scholar

van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Velay-Lizancos, M., Vazquez-Burgo, P., Restrepo, D., and Martinez-Lage, I. (2018). Effect of fine and coarse recycled concrete aggregate on the mechanical behavior of precast reinforced beams: comparison of FE simulations, theoretical, and experimental results on real scale beams. Constr. Build. Mater. 191, 1109–1119. doi:10.1016/j.conbuildmat.2018.10.075

CrossRef Full Text | Google Scholar

Wang, C., and Xiao, J. (2018). Evaluation of the stress-strain behavior of confined recycled aggregate concrete under monotonic dynamic loadings. Cem. Concr. Compos. 87, 149–163. doi:10.1016/j.cemconcomp.2017.12.012

CrossRef Full Text | Google Scholar

Wang, L., Bao, J., and Ueda, T. (2016). Prediction of mass transport in cracked-unsaturated concrete by mesoscale lattice model. Ocean Eng. 127, 144–157. doi:10.1016/j.oceaneng.2016.09.044

CrossRef Full Text | Google Scholar

Wang, R., Yu, N., and Li, Y. (2020). Methods for improving the microstructure of recycled concrete aggregate: a review. Constr. Build. Mater. 242, 118164. doi:10.1016/j.conbuildmat.2020.118164

CrossRef Full Text | Google Scholar

Wang, Y., Cao, Y., Zhang, P., Ma, Y., Zhao, T., Wang, H., et al. (2019). Water absorption and chloride diffusivity of concrete under the coupling effect of uniaxial compressive load and freeze-thaw cycles. Constr. Build. Mater. 209, 566–576. doi:10.1016/j.conbuildmat.2019.03.091

CrossRef Full Text | Google Scholar

Witherspoon, P. A., Wang, J. S. Y., Iwai, K., and Gale, J. E. (1980). Validity of Cubic Law for fluid flow in a deformable rock fracture. Water Resour. Res. 16 (6), 1016–1024. doi:10.1029/WR016i006p01016

CrossRef Full Text | Google Scholar

Wyrzykowski, M., McDonald, P. J., Scrivener, K. L., and Lura, P. (2017). Water redistribution within the microstructure of cementitious materials due to temperature changes studied with ¹H NMR. J. Phys. Chem. C 121 (50), 27950–27962. doi:10.1021/acs.jpcc.7b08141

CrossRef Full Text | Google Scholar

Xiao, J., Li, W., Corr, D. J., and Shah, S. P. (2013). Effects of interfacial transition zones on the stress–strain behavior of modeled recycled aggregate concrete. Cem. Concr. Res. 52, 82–99. doi:10.1016/j.cemconres.2013.05.004

CrossRef Full Text | Google Scholar

Xiao, J., Li, W., Fan, Y., and Huang, X. (2012). An overview of study on recycled aggregate concrete in China (1996–2011). Constr. Build. Mater. 31, 364–383. doi:10.1016/j.conbuildmat.2011.12.074

CrossRef Full Text | Google Scholar

Xue, S., Zhang, P., Bao, J., He, L., Hu, Y., and Yang, S. (2020). Comparison of Mercury Intrusion Porosimetry and multi-scale X-ray CT on characterizing the microstructure of heat-treated cement mortar. Mater. Charact. 160, 110085. doi:10.1016/j.matchar.2019.110085

CrossRef Full Text | Google Scholar

Zhang, P., Dai, Y., Wang, W., Yang, J., Mo, L., Guo, W., et al. (2020). Effects of magnesia expansive agents on the self-healing performance of microcracks in strain-hardening cement-based composites (SHCC). Mater. Today Commun. 25, 101421. doi:10.1016/j.mtcomm.2020.101421

CrossRef Full Text | Google Scholar

Zhang, P., Hou, D., Liu, Q., Liu, Z., and Yu, J. (2017a). Water and chloride ions migration in porous cementitious materials: an experimental and molecular dynamics investigation. Cem. Concr. Res. 102, 161–174. doi:10.1016/j.cemconres.2017.09.010

CrossRef Full Text | Google Scholar

Zhang, P., Wittmann, F. H., Vogel, M., Müller, H. S., and Zhao, T. (2017b). Influence of freeze-thaw cycles on capillary absorption and chloride penetration into concrete. Cem. Concr. Res. 100, 60–67. doi:10.1016/j.cemconres.2017.05.018

CrossRef Full Text | Google Scholar

Zhao, H., Jiang, K., Yang, R., Tang, Y., and Liu, J. (2020). Experimental and theoretical analysis on coupled effect of hydration, temperature and humidity in early-age cement-based materials. Int. J. Heat Mass Transf. 146, 118784. doi:10.1016/j.ijheatmasstransfer.2019.118784

CrossRef Full Text | Google Scholar

Zhao, K., Qiao, Y., Zhang, P., Bao, J., and Tian, Y. (2020). Experimental and numerical study on chloride transport in cement mortar during drying process. Constr. Build. Mater. 258, 119655. doi:10.1016/j.conbuildmat.2020.119655

CrossRef Full Text | Google Scholar