Coupled Transport of Sulfate and Chloride Ions With Adsorption Effect: A Numerical Analysis

In the marine environment, reinforced concrete will suffer from chloride ion erosion and sulfate ion erosion at the same time. However, most scholars only study the interaction mechanism between chloride ion and sulfate ion, and the consideration of physical adsorption and chemical combination caused by hydration products is not perfect. Based on the law of conservation of mass, this study integrates the relationship between porosity and hydration time, the weakening of chemical binding of sulfate ions to chloride ions into the mathematical model, establishes the coupling transport model of sulfate and chloride, and verifies the rationality of the model by comparing with the measured data. And then, the physical adsorption and chemical binding of chloride ions under the action of sulfate ions were quantitatively analyzed. It is found that chemical binding is dominant and sulfate ion will reduce the chemical binding effect of chloride ion. With the decrease of the initial water/cement ratio, the diffusion depth of free chloride ion will also decrease.

Introduction

The concrete structure is widely used admittedly in Ocean Engineering, for example, subsea tunnel engineering which tests the durability extremely. Concrete is buried under the seafloor for a long time to withstand the erosion of sea salt, which will not only cause damage to the concrete structure but also affect the normal service life of the building (Banthia et al., 2005; Choinska et al., 2007; Ghazy and Bassuoni, 2017; Montoya and Nagel, 2020; Wang et al., 2020a; Xu et al., 2020; Zhou et al., 2020). In the marine environment, the porous nature of concrete determines that it will inevitably be eroded by sea salt. This kind of erosion can be divided into two types, one is the diffusion of ions, the other is the combination of ions (Song et al., 2008; Medeiros et al., 2009). As we all know, there are many reasons for the damage of reinforced concrete structure, such as corrosion and expansion of reinforcement, resulting in concrete cracking and damage (Sofia and Alexandre, 2018; Wang et al., 2020b), loss of setting the strength of the concrete itself (Neville, 2004), mechanical wear of concrete structure surface (Fiorio, 2005), etc. In the marine environment, corrosion of reinforcement is mainly caused by the diffusion of chloride ions, while the loss of concrete strength is mainly caused by the chemical reaction of sulfate ions.

At present, many scholars have discussed the combination of chloride ions in concrete. Dhir et al. (1996) reported the results of the determination of the chloride binding capacity of Ground Granulated Blast-furnace Slag (GGBS) slurry. It was found that the higher the concentration of aluminate, the stronger the chloride binding capacity. Zhu et al. (2012) through exploring the influence of different types of chloride salts on the binding capacity of chloride ions in concrete, found that the binding capacity of chloride ions corresponding to calcium chloride is the strongest, while that of sodium chloride and potassium chloride is the weakest. Arya and Xu (1995) studied the influence of different types of cement on the chloride binding capacity. The chloride binding capacity was successively enhanced, and the order was GGBS, Pulverized Fuel Ash (PFA), and Ordinary Portland Cement (OPC). It is observed that although GGBS has the strongest chloride binding capacity, OPC concrete has the strongest corrosion resistance. Tang and Nilsson (1993) studied the sorption of chloride ions on OPC concrete under different water/cement ratio and aggregate content. The results showed that the sorption capacity of chlorine ion was closely related to the content of CSH gel, but had nothing to do with water/cement ratio and aggregate content. Geiker et al. (2007) studied the prediction and analysis of chloride binding capacity in OPC concrete by different salt types. The results showed that the ratio of chloride binding capacity to free chloride content in pore solution was the largest when AFm content was high. Jensen et al. (1999) tested the influence of different components of cement paste and mortar, as well as the different exposure conditions on the self-entry of chloride into the concrete. It was found that the combination of chloride ions changed the shape of the entrance profile of the model. Martin-Pérez et al. (2000) discussed the influence of three kinds of bind isothermal curves on the chloride ion permeability profile with a finite difference method and evaluated the service life of reinforced concrete in this way. Yoon et al. (2014) proposed the use of calcined layered double hydroxides to prevent chloride induction, which greatly improved the durability of reinforced concrete, not only adsorbed the memory effect in aqueous solution but also had a higher binding capacity than the original layered double hydroxides in cement-based materials. The effect of fly ash and slag on the binding capacity of chloride ion in the sulfate environment (Castellote et al., 1999; Xu et al., 2013; Geng et al., 2015). The results show that the addition of fly ash and slag increases the release of chloride ions.

Through the reading of the above literature, it is found that most of the researchers only study and discuss the diffusion law of combined chloride ion and free chloride ion under the action of a single factor. However, it is still shallow to discuss and study the combined chloride ion under the action of multi-factor and multi mechanism, which is divided into physically adsorbed chloride ion and chemically combined chloride ion. In this study, a multi-factor coupled chloride diffusion model is proposed. It will take into account the reduction of chloride binding to chloride ions, the adsorption, and chemical action of hydrated calcium silicate gel, and the quantitative analysis of free chlorine ions, physisorption chlorine ions, and chemically bound chloride ions through the PDE module of the finite element analysis software COMSOL. In this model, the diffusion coefficient of free chloride ion in a porous solution is established by considering the interaction between ions. Besides, it is assumed that there is no calcium corrosion under the coupling effect of sulfate and chloride, that is, the adsorbed free chloride ions do not have biological understanding adsorption. It is worth noting that even though the physically adsorbed chloride ions cannot be moved, they still carry electric charges.

Modeling

The time-depth relationship model of porous Fick law is adopted for chloride diffusion in concrete (Valdes-Parada et al., 2007):

$\begin{array}{ll}{\epsilon }_{tot}\frac{\partial C_{cl}}{\partial t}+div{J}_{cl}=0& (1)\end{array}$

where ε_tot is the total porosity of concrete (m³/m³); C_cl is the total chloride ion concentration (%); t is the erosion time (s); J_cl is the material flux of the corresponding component (m/s).

Hirao et al. (2005) have studied that the cement hydration products in concrete have the binding ability to chloride ions, which are mainly calcium silicate hydrate (CSH) and calcium monosulfate hydrate (AFm). Among them, CSH is mainly physical adsorption, while AFm is mainly chemical binding (Florea and Brouwers, 2012). In this model, Equation (2-a) transformation is still carried out according to the law of conservation of mass. The difference is that only the chemical binding term of chloride ions is modeled as a sink term. The reason is that as long as there is calcium aluminate, the chemisorption of chloride ions in the combination will react with it. In the final analysis, it is only related to the concentration of reactants. Therefore, when considering the chloride ion transport of chemisorption, we use the form of sink term to model separately, see Equation (2-b). Add the part of chloride ions physically adsorbed to the first item of Equation (1). Component C_cl is divided into two parts, one is free chloride ion concentration, the other is physical adsorption chloride ion concentration.

$\begin{array}{ll}{\epsilon }_{tot}\frac{\partial (C_{pa}+C_f)}{\partial t}+div{J}_{cl}+Q(C_{cb})=0& (\mathrm{2-a})\end{array}$

$\begin{array}{ll}Q(C_{cb})=\frac{\partial C_{cb}}{\partial t}& (\mathrm{2-b})\end{array}$

$\begin{array}{ll}{C}_{cb}=f(C_f)& (\mathrm{2-c})\end{array}$

$\begin{array}{ll}{C}_{cb}=\beta C_f^{\alpha }& (\mathrm{2-d})\end{array}$

$\begin{array}{ll}{C}_T=C_{pa}+C_{cb}+C_f& (\mathrm{2-e})\end{array}$

where C_cb is the concentration of chemically bound chloride ions (%); C_pa is the concentration of chloride ions adsorbed in the double layer region (Chatterji and Kawamura, 1992), that is, the concentration of physically adsorbed chloride ion (%); C_f is the concentration of free chloride ion in pore solution (%); Q(C_cb) is the sink term which is a function of chemically bound chloride ions (1/s); C_T is the concentration sum of free chloride ion, chemically bound chloride ion, and physically adsorbed chloride ion at the depth z from the erosion surface (%).

Hirao et al. (2005) through the study of the adsorption and combination of chloride ions by cement hydration products, found that ettringite, and calcium hydroxide does not have the ability of physical adsorption of chloride ions. However, through the comparison between the final model and the measured data, it is found that there may be a weak chemical combination. It can be seen from Carrara et al. (2016) that the concentration of chemically bound chloride ion is a function of the concentration of free chloride ion, using Carrara et al. (2016) research model (β = 0.4366, α = 0.58), see Equation (2-d). According to Ishida and Maekawa (1999), the total porosity of chloride in concrete is divided into two categories, one is gel porosity and the other is capillary porosity, see Equation (3-a). Considering that the porosity of concrete is related to the degree of hydration of cement, Masi et al. (1997) established a functional relationship between the degree of hydration α and the time of hydration t by studying the hydration process from calcium aluminate to the hydration product. See Equation (3-b) for the specific expression.

$\begin{array}{ll}{\epsilon }_{tot}={\epsilon }_{gl}+{\epsilon }_{cp}& (\mathrm{3-a})\end{array}$

$\begin{array}{ll}\alpha =1-0.5\left[{(1+1.67\tau )}^{-0.6}+{(1+0.29\tau )}^{-0.48}\right]& (\mathrm{3-b})\end{array}$

where ε_gl is the gel porosity (m³/m³); ε_cp is the capillary porosity (m³/m³); α is the degree of hydration of cementitious materials; τ is the time consumed in the hydration process(day).

Hansen (1986) has derived the formula for calculating the porosity and capillary porosity of the gel through the formula derived from the experimental data of (Powers and Brownyards, 1948).

$\begin{array}{ll}{\epsilon }_{gl}=\frac{(\frac{w_0}{c})-0.36\alpha }{(\frac{w_0}{c})+0.32}& (\mathrm{4-a})\end{array}$

$\begin{array}{ll}{\epsilon }_{cp}=\frac{0.19\alpha }{(\frac{w_0}{c})+0.32}& (\mathrm{4-b})\end{array}$

where $\frac{w_0}{c}$ is the initial water/cement ratio in the form of mass fraction (kg/kg).

The results show that the presence of Jin et al. (2019) sulfate ions will reduce the chemical binding capacity of chloride ions, and Equation (5-a) is used for calculation when the relationship between combined chloride and free chloride is non-linear. Because sulfate ion reacts mainly with calcium hydroxide and aluminate hydrate in concrete (Sun et al., 2013), it has little effect on the physical adsorption of chloride ion. In this study, the chemical binding weakening model of chloride ions under the influence of sulfate ions established by Jin et al. (2019) is used, see Equation (5-d). The specific derivation process is as follows.

$\begin{array}{ll}{R}_0=\frac{\partial C_b}{\partial C_f}& (\mathrm{5-a})\end{array}$

$\begin{array}{ll}{C}_b=C_{cb}+C_{pa}& (\mathrm{5-b})\end{array}$

$\begin{array}{ll}{C}_{pa}=\frac{\text{K}{C}_f}{1+\text{N}{C}_f}& (\mathrm{5-c})\end{array}$

$\begin{array}{ll}R=\frac{\partial C_b}{\partial C_f}(a+b{C}_{S{O}_4^{2-}}^c)& (\mathrm{5-d})\end{array}$

$\begin{array}{ll}{C}_{cb,S{O}_4^{2-}}=R{C}_f-C_{pa}& (\mathrm{5-e})\end{array}$

$\begin{array}{ll}Q(C_{cb,S{O}_4^{2-}})=\frac{\partial C_{cb,S{O}_4^{2-}}}{\partial t}& (\mathrm{5-f})\end{array}$

where R₀ is the ability of chloride binding without the influence of sulfate ion; C_b is the total bound chloride concentration at depth z (%); and are fitting parameters (Carrara et al., 2016) (K = 0.1228, N = 0.0747); R is the chloride binding capacity under the influence of sulfate ion; $C_{cb,S{O}_4^{2-}}$ is the chemical binding content of chloride ion under the action of sulfate ion; $Q\left(C_{cb,S{O}_4^{2-}}\right)$ is the sink term produced by the action of sulfate ion (1/s); a, b, and c are fitting parameters (Jin et al., 2019), respectively (a = 1, b = −0.011, c = 1.31); $C_{S{O}_4^{2-}}$ is the free sulfate ion concentration (%).

In saturated concrete, ions are mainly transmitted to the medium in the form of diffusion. However, not all ions are presented in dynamic form. Static ions can be divided into two categories: one is physically adsorbed ions, the other is chemically combined ions. As mentioned above, although the physically adsorbed ions in static ions still carry charges, they cannot move. As we all know, only the free ions can conduct electricity. In this model, Einstein's law is used to establish the diffusion coefficient of free chloride ion in pore solution, see Equation (6).

$\begin{array}{ll}{D}_f=R_{g}T\frac{{\Lambda }_{c{l}^{-}}}{z_{c{l}^{-}}^2{F}^2}& (6)\end{array}$

where D_f is the diffusion coefficient of chloride ion in the pore solution (m²/s); R_g is the universal gas constant (J/K·mol); T is the ambient temperature (K); ${\Lambda }_{c{l}^{-}}$ is the molar conductivity of free chloride ion in porous solution (Sm²/mol); $z_{c{l}^{-}}$ is the chloride ion valence (= −1); F is the Faraday constant (c/mol).

As we all know, the conductivity of mobile ion in solution is closely related to its concentration. In 1929 Onsager deduced the theoretical model of conductivity and concentration through the concept of the ion-atmosphere. However, this model is only applicable to dilute solution with ion concentration C ≤ 0.005 mol/l, not to the solution with higher concentration. Chandra and Bagchi (1989) modified the Onsager model and proposed an ion conductivity that can calculate the ion concentration up to 2,000 mmol/L, see Equation (7).

$\begin{array}{ll}{\Lambda }_{c{l}^{-}}={\Lambda }_{c{l}^{-}}^{\infty }-(G{z}_{c{l}^{-}}^2+H{z}_{c{l}^{-}}^3{w}_{c{l}^{-}}{\Lambda }_{c{l}^{-}}^{\infty })\sqrt{C_f}& (7)\end{array}$

where ${\Lambda }_{c{l}^{-}}^{\infty }$ is the limit molar conductivity of free chloride ion in infinite dilution solution when the ambient temperature is 25°C, the corresponding ${\Lambda }_{c{l}^{-}}^{\infty }$ is 7.635 × 10⁻³[Sm²/mol]; G and H are parameters related to temperature, ion type, and medium; $w_{c{l}^{-}}$ is the influence coefficient considering ion activity.

Here, G, H, and $w_{c{l}^{-}}$ are calculated by Equations (8-a) to (8-c), respectively.

$\begin{array}{ll}G=\frac{\sqrt{2\pi }e{F}^2}{3\pi \eta \sqrt{1000{\epsilon }_0{\epsilon }_{r}RT}}& (\mathrm{8-a})\end{array}$

$\begin{array}{ll}H=\frac{\sqrt{2\pi }e{F}^2}{3\sqrt{1000}{({\epsilon }_0{\epsilon }_{r}RT)}^{\frac{3}{2}}}& (\mathrm{8-b})\end{array}$

$\begin{array}{ll}{w}_{c{l}^{-}}=2\left[1-{\left(\frac{1}{2}{\displaystyle \sum _{i=1}^n}\frac{{\Lambda }_{c{l}^{-}}^{\infty }}{{\Lambda }_{c{l}^{-}}^{\infty }+{\Lambda }_i^{\infty }}\right)}^{\frac{1}{2}}\right]& (\mathrm{8-c})\end{array}$

where e is the elementary charge (c); ε₀ is the vacuum dielectric constant (c²/J·m); ε_r is the relative permittivity of water; ${\Lambda }_i^{\infty }$ is the limit molar conductivity of all ions in the pore solution (Sm²/mol); n is the total number of ions; η is the viscosity coefficient of medium water (see Table 1 for specific parameter values). The conductivity and ionic radius values are given in Table 2.

TABLE 1

Table 1. Parameter value in calculation formula of conductivity and free chloride ion diffusion coefficient.

TABLE 2

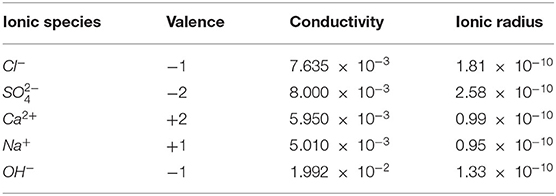
Table 2. Parameter value of ions in pore solution (Chatterji and Kawamura, 1992).

It is not only the interaction between ions but also the tortuosity of aggregate and pore structure that affects the diffusion of free chloride. Therefore, it is necessary to introduce tortuosity to correct the diffusion coefficient in the flux (see Equation 9).

$\begin{array}{ll}{J}_{cl}=-\frac{{({\epsilon }_{cp}+{\epsilon }_{gl})D}_f}{\Omega }\nabla C_f& (9)\end{array}$

where Ω is the tortuosity of ion transport in porous media (Ω = 192), the calculation of tortuosity is based on the method used by Ahmad et al. (2005). The tortuosity and porosity are both inherent properties of materials, but the former reflects the complexity of the transport path, which further affects the ion transport. Specifically, the larger the tortuosity is, the more difficult the transport is, and vice versa (see Figure 1).

FIGURE 1

Figure 1. Tortuosity of concrete solid phase.

By substituting Equations (2-a), (2-b), (3-a), and (9) into Equation (1), the following free chloride transport model can be obtained.

$\begin{array}{ll}\begin{array}{l}[\left({\epsilon }_{tot}-1\right)\frac{d{C}_{pa}}{d{C}_f}+{\epsilon }_{tot}\hfill \\ +\frac{\partial C_b}{\partial C_f}(a+b{C}_{S{O}_4^{2-}}^c)]\frac{\partial C_f}{\partial t}=\nabla \left({\epsilon }_{tot}\frac{D_f}{\Omega }\nabla C_f\right)\hfill \end{array}& (10)\end{array}$

Equation (10) with the help of the COMSOL finite element analysis software, a one-dimensional solution of the two-dimensional geometric model is carried out for the model. The specific operation details are as follows. First, two-dimensional graphics (such as squares) are created in the geometry module. Here, it is emphasized that the creation of two-dimensional/three-dimensional graphics is only for a better presentation of the solution results. From the perspective of diffusion, Equation (10) is essentially one-dimensional. In this paper, the interface of partial differential equation in the form of a coefficient is selected for the transient solution. See Figure 2, 578 domain elements, and 60 boundary elements, that is, the number of triangles or quadrilaterals in 2D geometry. Among them, boundary elements are the number of triangles included in the boundary. For the mathematical model with complex boundary conditions, it needs to be rezoning. In this model, the boundary conditions are set as fixed values, so no modification is needed. It is worth noting that the fitting parameters involved in this paper are all derived from the results of reference concrete (without any mineral admixture). If we want to simulate the concrete with mineral admixture, the retest is needed to determine the parameters.

FIGURE 2

Figure 2. Physical field control grid.

Numerical Verification

Based on the test data of Sandberg (1999) by Equation (10), the OPC concrete slab with a length of 100 cm, a width of 70 cm, and a thickness of 10 cm was immersed in seawater for 14 months in the literature. Here, the way of immersion is to use half of the immersion and half of the exposure in the thickness direction. Notice that this model only validates the submerged part of the test block. The specific mix proportion is 390 kg/m³ dry weight cement, 0.5 water/cement ratio, 0–8 mm grain size sand, its density is 853 kg/m³, 8–16 mm gravel aggregate, which is 787 kg/m³. Through the comparison between the model and the measured data and error analysis, it is found that the calculation results are in good agreement with the experimental data. In the model, the surface concentration of free chloride ion is 1.05%, and the initial concentration value is 0. Because the concentration of chloride ion in the marine environment is about 7 times the concentration of sulfate ion, and assuming that the surface ion content of concrete to meet this relationship, the surface concentration of sulfate ion is 0.15%. As shown in Figure 3, the curve of free chloride ion concentration in concrete pore solution with 14 months, $\frac{w}{c}=0.5$ in the immersion area with diffusion depth is depicted. Figure 4 shows the free chloride concentration (C_f) Test values, calculated values, and relative error values at different depths. Here, the relative error is expressed as a percentage. Through comparison, it is found that the maximum error is not more than 10%. It can be found from Figure 3 that the chloride concentration gradient decreases with the increase of depth.

FIGURE 3

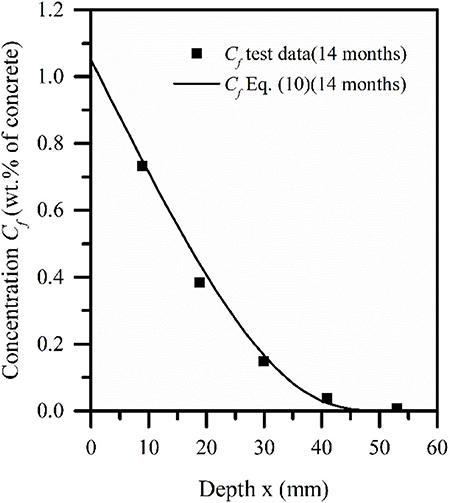
Figure 3. Simulation and test comparison of free chloride ion of concrete slab exposed to marine environment for 14 months.

FIGURE 4

Figure 4. Error analysis of calculation value and test value.

Based on Equations (10) and (2-e), the test data of Tumidajski et al. (1995) are verified. In the literature, 50 type cement is used for mix design, which is 370 kg/m³, 1, 107 kg/m³ coarse aggregate, 148 kg/m³ water, and 738 kg/m³ fine aggregate. The size of a concrete specimen is 75 mm × 75 mm × 300 mm, and it is cured in a 100% humidity environment for 28 days. In this model, the surface concentration of free chloride ion is 1.05%, the initial concentration value is 0, the surface concentration of sulfate ion is 0.05%, the initial concentration value is 0, and see Figure 6 for concentration distribution of free chloride ions under time and depth. Figure 5 depicts the concentration distribution curve of concrete beams corroded by chloride ion and sulfate ion in a multi-component solution for 3, 6, and 12 months in a saturated state. It can be seen from Figures 5, 6 that with the increase of time, the internal diffusion depth of concrete is also increasing and the increasing range is decreasing. Through the comparison between the numerical model Equation (2-e) and the measured data, it is found that the error value of the rest points decreases obviously with the increase of the diffusion depth, except for the points close to the erosion surface, which may be caused by the loss of ion concentration during the measurement. The reason why the point close to the erosion surface is more consistent with other points may be due to the measurement time, but on the whole, the calculated value of the model is in good agreement with the measured data. This model can well-reflect the trend of ion concentration.

FIGURE 5

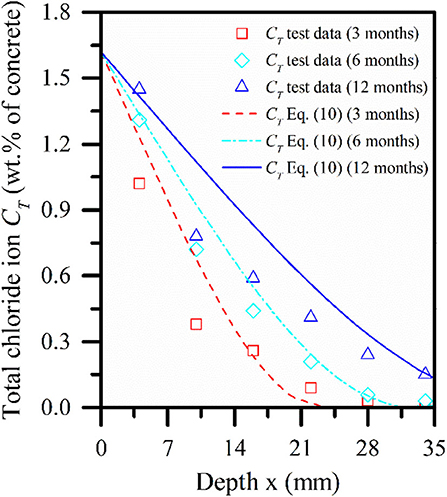
Figure 5. Simulation and test comparison of total chloride ions in concrete beams exposed for 3, 6, and 12 months.

FIGURE 6

Figure 6. Concentration distribution of free chloride ions under time and depth.

Results and Discussion

Effect of Physical Adsorption and Chemical Binding on Chloride Transport

This section discusses the analysis based on Sandberg's test data. Equations (2-d) and (5-c), respectively represent the chloride ion content of chemical binding and physical adsorption at different concentrations of free chloride ion. Figure 7 shows the change curve of free chloride ion content with depth in 14 months pore solution of the concrete slab in immersion area, the distribution curve of chloride ion concentration in pore solution considering adsorption effect, and the curve of total chloride ion in chemical combination.

FIGURE 7

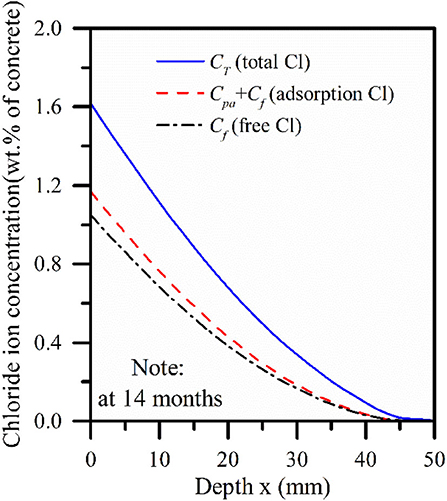
Figure 7. The free chloride ion calculated by the model includes the physical adsorption and the total chloride concentration curve.

It can be found from Figure 7 that the content of the chemical binding part is more than 5 times that of the physical adsorption part, and the effect is more obvious with the increase of diffusion depth. Therefore, it can be found that chemical binding plays a leading role while physical adsorption and chemical binding are simultaneously applied to the concrete interior. However, physical adsorption and chemical binding did not change the chloride concentration transport trend, and the three showed the same diffusion law. Figure 8 describes the curve of chloride concentration with time under the action of physical adsorption and chemical combination. It can be found in Figure 8 that compared with physical adsorption, chemical binding still dominates, and chemical binding takes place faster than physical adsorption.

FIGURE 8

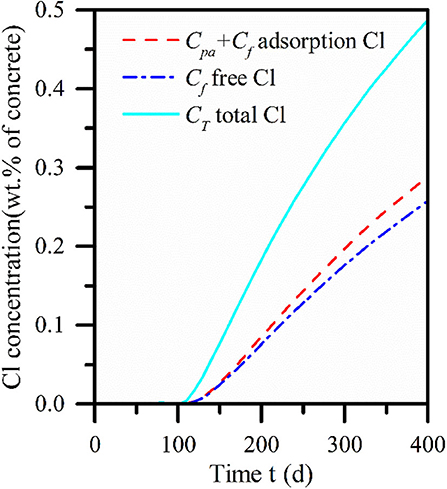
Figure 8. Three forms of concrete interior calculated by model: the free chloride, the chloride of including the physical adsorption and the total chloride.

The Effect of Sulfate Ion on the Concentration of Chemically Bound Chloride Ion

Dehwah et al. (2002) studied the effect of cement alkalinity on chloride corrosion in OPC concrete and Sulfate Resistant Portland Cement Concrete (SRPC). It was found that the binding capacity of chloride decreased with the increase of sulfate ion concentration in pore solution. Shaheen and Pradhan (2015), respectively studied the determination of free chloride ion content in the mixed solution with the same chloride ion concentration by 3, 6, and 12% sulfate ion. The results showed that the free chloride ion concentration decreased with the increase of sulfate ion concentration. In this study, the chemical binding model established by Hirao et al. (2005), see Equation (2-d) and based on Paul's experimental data for quantitative analysis.

Figure 9 depicts the change curve of the concentration of chemically bound chloride ions with depth under the action of chemical binding. It can be seen from Figure 9 that sulfate ions cause a decrease of chemically bound chloride ions, which verifies the correctness of the model. It can also be found that in the depth range of 0–45 mm, there is a linear relationship between the chemically bound chloride ions and the diffusion depth, which decreases with the increase of the erosion depth. Figure 10 depicts the relationship between the concentration of chemically bound chloride ions and the depth of diffusion under different concentrations of sulfate ions. It can be seen from Figure 10 that with the increase of sulfate ion concentration, the concentration of chemically bound chloride ion at the same depth decreases continuously, and the decreased amplitude increases with the increase of sulfate ion concentration at the same step length. When the concentration of sulfate ion reaches more than 1.7%, the curve is segmented, and the decrease of the content of chemically bound chloride ion in the range of 0–5 mm is much higher than that in the range of 5–50 mm. This is consistent with the conclusion of Dehwah et al. (2002).

FIGURE 9

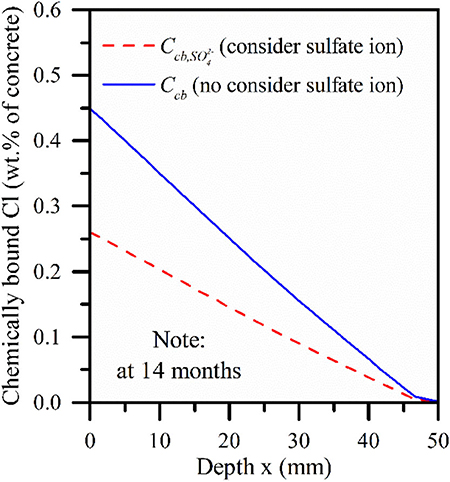
Figure 9. Chemical binding curve of chloride ion: red solid line (sulfate ion is considered), blue solid line (sulfate ion is not considered).

FIGURE 10

Figure 10. Concentration of chemically bound chloride ions at different sulfate ion concentrations.

Effect of Initial Water/Cement Ratio on Free Chloride Diffusion

Based on Equation (10), the law of chloride diffusion under different initial water/cement ratio was studied. As above, Paul test data is still used as a reference. Figure 11 depicts the diffusion curve of free chloride ion in concrete under different water/cement ratios, among which the blue solid line represents the diffusion curve of free chloride ion eroded for 6 months in Paul's literature. It can be seen from Figure 11 that the diffusion depth of free chloride ion decreases with the decrease of water/cement ratio, which is 31, 30, 27.5, and 23.3 mm in turn. It can be seen that the decreased amplitude has an increasing trend.

FIGURE 11

Figure 11. Free chloride concentration under different initial water-cement ratio.

Figure 11 shows that the decrease of the water/cement ratio does not change the diffusion rule of free chloride ion. It only reduces the penetration of free chloride ions.

Conclusions

Through the verification of the mathematical model, it is shown that the model can be used to predict the diffusion process of chloride ions into the concrete. After discussing the coupled transport model of sulfate and chloride, the following conclusions can be obtained:

• The diffusion of chloride in concrete can be reflected more truly by separately modeling of chloride binding and integrating the relationship between porosity and hydration time into the mathematical model.

• It is found that the chemical binding at different depths is more than 5 times the content of physical adsorption chloride ions. However, chemical binding and physical adsorption do not change the diffusion trend of chloride ions.

• The results show that sulfate ion can reduce the chemical binding capacity of chloride ion. With the increase of sulfate ion concentration, the trend is increasingly obvious. When the concentration of sulfate ion is more than 1.7%, the curve of the change of the chemical bound chloride ion with the depth is segmented.

• With the decrease of the initial water/cement ratio, the diffusion depth of free chloride ion decreased. When the initial water/cement ratio increases in the same step (H = 0.05), it can be found that the increasing speed of diffusion depth slows down.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

JX: conceptualization, methodology, and writing—review and editing. RM: data curation and writing—original draft. JZ and XD: data curation, visualization, and investigation. PW and WS: suggestions and supervision. All authors contributed to the article and approved the submitted version.

Funding

This project was supported by the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 19KJB560004), China Postdoctoral Science Foundation (No. 2019M661693), National Natural Science Foundation of China (Nos. 51578497, U1706222, 51608286, and 51708483), National Key R&D Program of China (No. 2017YFB0309904), Natural Science Foundation of Shandong province (No. 2019GSF110006), and the Source Innovation Program of Qingdao City (No. 17-1-1-13-jch).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmad, S., Azad, A. K., and Loughlin, K. F. (2005). “A study of permeability and tortuosity of concrete,” in Conference on Our World in Concrete and Structures, Vol. 45 (Singapore), 23–30.

Google Scholar

Arya, C., and Xu, Y. (1995). Effect of cement type on chloride binding and corrosion of steel in concrete. Cement Concrete Res. 25, 893–902. doi: 10.1016/0008-8846(95)00080-V

CrossRef Full Text | Google Scholar

Banthia, N., Biparva, A., and Mindess, S. (2005). Permeability of concrete under stress. Cement Concrete Res. 35, 1651–1655. doi: 10.1016/j.cemconres.2004.10.044

CrossRef Full Text | Google Scholar

Carrara, P., Lorenzis, L. D., and Bentz, D. P. (2016). Chloride diffusivity in hardened cement paste from microscale analyses and accounting for binding effects. Model. Simul. Mater. Sci. Eng. 24, 1–26. doi: 10.1088/0965-0393/24/6/065009

PubMed Abstract | CrossRef Full Text | Google Scholar

Castellote, M., Andrade, C., and Alonso, C. (1999). Chloride-binding isotherms in concrete submitted to non-steady-state migration experiments. Cement Concrete Res. 29, 1799–1806. doi: 10.1016/S0008-8846(99)00173-8

CrossRef Full Text | Google Scholar

Chandra, A., and Bagchi, B. (1989). Breakdown of onsager's conjecture on distance dependent polarization relaxation in solvation dynamics. J. Chem. Phys. 91, 2594–2598. doi: 10.1063/1.457020

CrossRef Full Text | Google Scholar

Chatterji, S., and Kawamura, M. (1992). Electrical double layer, ion transport and reactions in hardened cement paste. Cement Concrete Res. 22, 774–782. doi: 10.1016/0008-8846(92)90101-Z

CrossRef Full Text | Google Scholar

Choinska, M., Khelidj, A., Chatzigeorgiou, G., and Pijaudier-Cabot, G. (2007). Effects and interactions of temperature and stress-level related damage on permeability of concrete. Cement Concrete Res. 37, 79–88. doi: 10.1016/j.cemconres.2006.09.015

CrossRef Full Text | Google Scholar

Dehwah, H., Austin, S., and Maslehuddin, M. (2002). Effect of cement alkalinity on pore solution chemistry and chloride-induced reinforcement corrosion. ACI Mater. J. 99, 227–233. doi: 10.14359/11967

CrossRef Full Text | Google Scholar

Dhir, R. K., El-Mohr, M. A. K., and Dyer, T. D. (1996). Chloride binding in GGBS concrete. Cement Concrete Res. 26, 1767–1773. doi: 10.1016/S0008-8846(96)00180-9

CrossRef Full Text | Google Scholar

Fiorio, B. (2005). Wear characterisation and degradation mechanisms of a concrete surface under ice friction. Construct. Build. Mater. 19, 366–375. doi: 10.1016/j.conbuildmat.2004.07.020

CrossRef Full Text | Google Scholar

Florea, M., and Brouwers, H. (2012). Chloride binding related to hydration products part?: ordinary portland cement. Cement Concrete Res. 42, 282–290. doi: 10.1016/j.cemconres.2011.09.016

CrossRef Full Text | Google Scholar

Geiker, M., Nielsen, E. P., and Herfort, D. (2007). Prediction of chloride ingress and binding in cement paste. Mater. Struct. 40, 405–417. doi: 10.1617/s11527-006-9148-2

CrossRef Full Text | Google Scholar

Geng, J., Easterbrook, D., Li, L. Y., and Mo, L. (2015). The stability of bound chlorides in cement paste with sulfate attack. Cement Concrete Res. 68, 211–222. doi: 10.1016/j.cemconres.2014.11.010

CrossRef Full Text | Google Scholar

Ghazy, A., and Bassuoni, M. T. (2017). Resistance of concrete to different exposures with chloride-based salts. Cem. Concr. Res. 101, 144–158. doi: 10.1016/j.cemconres.2017.09.001

CrossRef Full Text | Google Scholar

Hansen, T. C. (1986). Physical structure of hardened cement paste: a classical approach. Mater. Struct. 19, 423–436. doi: 10.1007/BF02472146

CrossRef Full Text | Google Scholar

Hirao, H., Yamada, K., Takahashi, H., and Zibara, H. (2005). Chloride binding of cement estimated by binding isotherms of hydrates. J. Adv. Concrete Technol. 3, 77–84. doi: 10.3151/jact.3.77

CrossRef Full Text | Google Scholar

Ishida, T., and Maekawa, K. (1999). An integrated computational system for mass/energy generation, transport, and mechanics of materials and structures. Doboku Gakkai Ronbunshu. 627, 13–25. doi: 10.2208/jscej.1999.627_13

CrossRef Full Text | Google Scholar

Jensen, O. M., Hansen, P. F., Coats, A. M., and Glasser, F. P. (1999). Chloride ingress in cement paste and mortar. Cement Concrete Res. 29, 1497–1504. doi: 10.1016/S0008-8846(99)00131-3

CrossRef Full Text | Google Scholar

Jin, Z., Sun, W., Zhao, T., and Li, Q. (2019). Chloride binding in concrete exposed to corrosive solutions. J. Chin. Ceramic Soc. 37, 1068–1072. doi: 10.1109/CLEOE-EQEC.2009.5194697

CrossRef Full Text | Google Scholar

Martin-Pérez, B., Zibara, H., Hooton, R. D., and Thomas, M. D. A. (2000). A study of the effect of chloride binding on service life predictions. Cement Concrete Res. 30, 1215–1223. doi: 10.1016/S0008-8846(00)00339-2

CrossRef Full Text | Google Scholar

Masi, M., Colella, D., Radaelli, G., and Bertolini, L. (1997). Simulation of chloride penetration in cement-based materials. Cement Concrete Res. 27, 1591–1601. doi: 10.1016/S0008-8846(97)00200-7

CrossRef Full Text | Google Scholar

Medeiros, M. H. F., Filho, J. H., and Helene, P. (2009). Influence of the slice position on chloride migration tests for concrete in marine conditions. Mar. Struct. 22, 128–141. doi: 10.1016/j.marstruc.2008.09.003

CrossRef Full Text | Google Scholar

Montoya, R., and Nagel, V. (2020). Capillary water absorption and chloride transport into mortar samples: a finite element analysis. Front. Mater. 7:28. doi: 10.3389/fmats.2020.00028

CrossRef Full Text | Google Scholar

Neville, A. (2004). The confused world of sulfate attack on concrete. Cement Concrete Composit. 34, 1275–1296. doi: 10.1016/j.cemconres.2004.04.004

CrossRef Full Text | Google Scholar

Powers, T. C., and Brownyards, T. L. (1948). Studies of the physical properties of hardened cement paste. Portland Chem. Assoc. 22, 53–66.

Google Scholar

Sandberg, P. (1999). Studies of chloride binding in concrete exposed in a marine environment. Cement Concrete Res. 29, 473–477. doi: 10.1016/S0008-8846(98)00191-4

CrossRef Full Text | Google Scholar

Shaheen, F., and Pradhan, B. (2015). Effect of chloride and conjoint chloride–sulfate ions on corrosion of reinforcing steel in electrolytic concrete powder solution (ECPS). Construct. Build. Mater. 101, 99–112. doi: 10.1016/j.conbuildmat.2015.10.028

CrossRef Full Text | Google Scholar

Sofia, R., and Alexandre, B. J. (2018). Chloride ingress into structural lightweight aggregate concrete in real marine environment. Mar. Struct. 61, 170–187. doi: 10.1016/j.marstruc.2018.05.008

CrossRef Full Text | Google Scholar

Song, H. W., Lee, C. H., and Ann, K. Y. (2008). Factors influencing chloride transport in concrete structures exposed to marine environments. Cement Concrete Composit. 30, 113–121. doi: 10.1016/j.cemconcomp.2007.09.005

CrossRef Full Text | Google Scholar

Sun, C., Chen, J., Zhu, J., Zhang, M., and Ye, J. (2013). A new diffusion model of sulfate ions in concrete. Constr. Build. Mater. 39, 39–45. doi: 10.1016/j.conbuildmat.2012.05.022

CrossRef Full Text | Google Scholar

Tang, L., and Nilsson, L. O. (1993). Chloride binding capacity and binding isotherms of OPC pastes and mortars. Cement Concrete Res. 23, 247–253. doi: 10.1016/0008-8846(93)90089-R

CrossRef Full Text | Google Scholar

Tumidajski, P. J., Chan, G. W., Feldman, R. F., and Strathdee, G. (1995). A boltzmann-matano analysis of chloride diffusion. Cement Concrete Res. 25, 1556–1566. doi: 10.1016/0008-8846(95)00149-7

CrossRef Full Text | Google Scholar

Valdes-Parada, F. J., Ochoa-Tapia, J. A., and Alvarez-Ramirez, J. (2007). Effective medium equations for fractional Fick's law in porous media. Phys. Stat. Mech. Appl. 373, 339–353. doi: 10.1016/j.physa.2006.06.007

CrossRef Full Text | Google Scholar

Wang, P., Jiao, M., Hu, C., Tian, L., Zhao, T., Lei, D., et al. (2020b). Research on bonding and shrinkage properties of SHCC-repaired concrete beams. Materials 13, 1557–1574. doi: 10.3390/ma13071757

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Wang, Y., Zhao, T., Xiong, C., Xu, P., Zhou, J., et al. (2020a). Effectiveness protection performance of an internal blending organic corrosion inhibitor for carbon steel in chloride contaminated simulated concrete pore solution. J. Adv. Concrete Technol. 18, 116–128. doi: 10.3151/jact.18.116

CrossRef Full Text | Google Scholar

Xu, J., Peng, C., Wan, L., Wu, Q., and She, W. (2020). Effect of crack self-healing on concrete diffusivity: mesoscale dynamics simulation study. ASCE J. Mater. Civil Eng. 32:04020149. doi: 10.1061/(ASCE)MT.1943-5533.0003214

CrossRef Full Text | Google Scholar

Xu, J., Zhang, C., Jiang, L., Tang, L., Gao, G., and Xu, Y. (2013). Releases of bound chlorides from chloride-admixed plain and blended cement pastes subjected to sulfate attacks. Const. Build. Mater. 45, 53–59. doi: 10.1016/j.conbuildmat.2013.03.068

CrossRef Full Text | Google Scholar

Yoon, S., Moon, J., Bae, S., Duan, X., Giannelis, E., and Monteiro, P. (2014). Chloride adsorption by calcined layered double hydroxides in hardened Portland cement paste. Mater. Chem. Phys. 145, 376–386. doi: 10.1016/j.matchemphys.2014.02.026

CrossRef Full Text | Google Scholar

Zhou, Y., Cai, J., Chen, R. X., Hou, D., Xu, J., Lv, K., et al. (2020). The design and evaluation of a smart polymer-based fluids transport inhibitor. J. Clean. Prod. 257, 1–12. doi: 10.1016/j.jclepro.2020.120528

CrossRef Full Text | Google Scholar

Zhu, Q., Jiang, L., Chen, Y., Xu, J. X., and Mo, L. (2012). Effect of chloride salt type on chloride binding behavior of concrete. Construct. Build. Mater. 37, 512–517. doi: 10.1016/j.conbuildmat.2012.07.079

CrossRef Full Text | Google Scholar

GLOSSARY