On the Role of Hydrolyzable Metal Cations in the Adsorption of Anionic Surfactants on Negatively Charged Surfaces

The role of hydrolyzable metal ions in the adsorption of anionic surfactants on a negatively charge surface is studied by electrophoresis and phase transfer experiments. The notion that the presence of such hydrolyzable species (activators) can promote flotation is not new, but a detailed mechanistic explanation is lacking. We relate the role of activators to the phenomenon of overcharging, which has been studied rather extensively within colloid and interface science. The experiments conducted in this article show that overcharging is a necessary condition for the adsorption of an anionic surfactant on a negatively charged surface and that the hydrophobization of the studied particles is most effective when overcharging is most pronounced.

1. Introduction

In the flotation of mineral particles, one often relies on the adsorption of collectors for an effective hydrophobization of the target particles. If the ore to be floated has a very diverse mineralogical composition, there is quite a number of collectors that may selectively adsorb on the target particles. If, however, one is concerned with mineral assemblies that are majorly composed of oxides and silicates, the issue of finding a sufficiently selective collector becomes considerably more difficult. In principle one could try ionic surfactants and rely on electrostatics to achieve selectivity. For an anionic surfactant this would require that the valuable particles are positively charged and all other particles be negatively charged for the anionic surfactant to be electrostatically repelled. Here one relies on a sufficiently large difference between the points of zero charge of the minerals. However, as many oxides and silicates are negatively charged in practical pH ranges this is not a universal option for silicate-oxide systems. Similar reasoning applies to the selective separation of fine particles across liquid-liquid interfaces, a process the present authors are concerned with Machunsky et al. (2009), and Leistner et al. (2014, 2019).

An appealing alternative to the hydrophobization routes just described is the use of certain inorganic electrolytes to promote the adsorption of an ionic surfactant. Within the flotation literature these inorganic electrolytes are known as activators (Schubert, 1996; Furstenau and Pradip, 2005). Common to all activators is the fact that they show a more or less pronounced, pH-dependent speciation in aqueous solution. By speciation it is understood that hydrolyzed metal cations exist in certain pH ranges and these are precisely the pH ranges where best flotation results are obtained with negatively charged particles and anionic collectors (Fuerstenau et al., 1965). The mechanistic idea behind these activators is that they act as a linker between the anionic surfactant and the similarly charged surface. Schubert (1996) summarizes that the probable mechanism is the adsorption of the activator in the Stern layer and Furstenau and Pradip (2005) state that the hydrolyzed species show such a high surface activity that they adsorb on any sort of adsorbent and thus provide said link.

The behavior of such hydrolyzed metal electrolytes has attracted interest in colloid and interface science as well (for reviews see Lyklema, 2006, 2013), where it was noticed that the colloid stability is affected quite drastically by such electrolytes. Furthermore, the phenomenon of overcharging—a more or less sudden sign reversal of the ζ-potential as a function of electrolyte concentration—was studied quite intensively.

In this article we will bring the information collected on the overcharging phenomenon in context with the activating electrolytes in flotation. This necessarily requires the description of electric double layers with inorganic electrolytes. The following sections are intended to briefly review the structure of electric double layers and to define the role of charge determining-, indifferent- and specifically adsorbed electrolytes. Furthermore, some information on overcharging and the necessary conditions for it to occur will be presented before proceeding with the experimental section where phase transfer under overcharging conditions will be experimentally investigated. The presentation will focus on the adsorption of the hydrolyzed species rather than on the adsorption of surfactants. This latter step in the adsorption process has been extensively studied by others (see Fuerstenau and Colic, 1999 for a review and many references) and we have little to add on this topic.

2. Short Overview on Electric Double Layers and Overcharging

2.1. Double Layer Structure With Simple Inorganic Electrolytes

Virtually all minerals acquire a surface charge when immersed in an aqueous electrolyte solution. The processes by which the surface charge is established may vary from system to system. Quite often the surface charge results from the ad-/desorption of charge determining ions, which are ions that have a particularly high affinity for the surface and become part of the adsorbent after adsorption (Lyklema, 1991). Which ions are charge determining depends on the system under consideration. For AgI, for instance, Ag⁺ and I⁻ have been identified as charge determining and for BaSO₄, Ba²⁺, and ${\text{SO}}_4^{2-}$ are charge determining. In the case of (hydr-) oxides and and many silicates H⁺ and OH⁻ are charge determining and therefore the surface charge density can be changed by pH control. Typical reactions at the surface can be formulated as ad-/desorption equilibria:

$\begin{array}{l}>\text{ROH }\leftrightarrow >{\text{RO}}^{-}+{\text{H}}^{+}\text{ and}\\ >\text{ROH}+{\text{H}}_{\text{2}}\text{O}\leftrightarrow >{\text{ROH}}_{\text{2}}^{\text{+}}+{\text{OH}}^{\text{-}}\end{array}$

In this notation >R denotes an atom of the solid. The surface charge density σ⁰ is defined as the difference between the surface excess of H⁺ and OH⁻, which can be determined experimentally by potentiometric titrations. Only by such methods can a point of zero charge be established.

Once a surface has acquired a charge, the surface charge density has to be compensated in equal and opposite amount on the solution side of the surface: an electric double layer will form, whose detailed structure varies from system to system. In the easiest case the surface charge density will be entirely compensated by indifferent electrolytes, which, by definition, experience purely Coulombic attraction/repulsion from the surface (Lyklema, 1991). When this is the case, the electrical double layer is said to be entirely diffuse and the variation of the electrical potential perpendicular to the surface follows Gouy-Chapman theory. The electroneutrality condition for such a double layer reads σ⁰ + σ^d = 0, in which σ^d is the charge density of the diffuse double layer. This parameter can be calculated via Gouy-Chapman theory if the diffuse layer potential is known. For a flat double layer in a symmetrical electrolyte diffuse layer charge density and potential are related by (Lyklema, 1995):

$\begin{array}{ll}{\sigma }^d=-\sqrt{8\epsilon {\epsilon }_{0}cRT}sinh(z{y}^d/2)& (1)\end{array}$

Here εε₀ is the dielectric constant of the solvent, R the ideal gas constant, T the temperature, c the concentration of the electrolyte, z the charge, and y^d = Fψ^d/RT. Note that the relationship between charge and potential of diffuse layer looks quite different when non-symmetrical electrolytes or electrolyte mixtures are considered.

In order to decide whether an electrolyte is truly indifferent or not, one has basically two options: (1) Measure either surface charge or diffuse layer charge density with electrolytes of the same charge but different nature and (2) measure the surface charge density and the diffuse layer charge density simultaneously. In the framework of option (1), an indifferent electrolyte would give the very same parameters for every electrolyte of the same charge. The more direct and quantitative option (2) allows testing of the electroneutrality condition. For an indifferent electrolyte this condition would always be fulfilled, implying that the point of zero charge (pH at which σ⁰ = 0) and the isoelectric point (pH at which σ^d = 0) coincide. Experimental evidence collected over the past decades shows that in many systems presumably indifferent electrolytes are not quite indifferent. Not only is this based on the shift of isoelectric points vs. points of zero charge, but violations of the simple electroneutrality condition have been observed as well (see for instance Lyklema, 1989, 1994). The basic tendency is |σ⁰| > |σ^d|, which implies that there has to be another location where charges can accumulate in order for the double layer to be electroneutral.

Such observations, together with experimental evidence from electrokinetic studies (see Dukhin and Derjaguin, 1974; Hunter, 1981; Delgado et al., 2007), make the introduction of a Stern layer necessary, a modification of the diffuse double layer structure suggested by Stern (1924). The resulting double layer configuration is schematically shown in Figure 1.

FIGURE 1

Figure 1. Schematic model of the electric double layer including a Stern- and a diffuse layer.

In this figure there is a negatively charged surface with charge density σ⁰ and associated surface potential ψ⁰. The region between the surface and the inner Helmholtz plane (iHp), where the electric potential is ψⁱ, is charge free. The iHp is the plane where specifically adsorbed ions reside (creating a charge density σⁱ) and its distance to the surface is often said to be determined by the size of the specifically adsorbed species. Note that specifically adsorbing ions experience, in addition to the purely electrostatic attraction, additional attraction to the surface. Due to the additional force(s) operating at the iHp equations like Eq. 1 that only consider an electrical attraction/repulsion no longer hold in this region of the double layer. For the charge density σⁱ one has to formulate an adsorption isotherm. Among the many options to do so, we quote Hunter and Wright (1971):

$\begin{array}{ll}{\sigma }^i=z_{i}e{N}_s{e}^{-(z_{i}e{\psi }^i+\Delta G_{ne})/kT}& (2)\end{array}$

Here e is the elementary charge, ψⁱ the electric potential at the iHp, k Boltzmann's constant, ΔG_ne a specific adsorption free energy and N_s the site density available for specific adsorption, which is not necessarily the same as the total number of surface sites. The specific adsorption free energy simply reflects the additional work terms that are needed to bring an ion from the free solution to the iHp and is of a non-electric nature. Examples include solvent structure mediated interactions, complex formation or hydrophobic bonding.

Going further to the solution side of the double layer, there is again a charge free region up to the outer Helmholtz plane (oHp). In Figure 1 we have not made a distinction between the oHp and the slip plane. Consequently the electrical potentials ψ^d and ζ are approximated to be equal. For a discussion on the positioning of the slip plane relative to the oHp and the distinctions between ψ^d and ζ we refer to Lyklema (2011) and Hunter (1981). The oHp, no matter if equated to the slip plane or not, marks the start of the diffuse part of the double layer, where the Gouy-Chapman theory applies. The electroneutrality condition for such a double layer reads σ⁰ + σⁱ + σ^d=0.

This picture of the double layer, although physically not the most precise, is sufficiently simple and able to account for many experimental results.

2.2. Overcharging

The phenomenon of overcharging describes a situation in which the addition of an electrolyte containing multivalent counterions can lead to a sign reversal of the ζ-potential, which is not induced by pH changes. Note that overcharging is also called charge reversal, electrokinetic charge inversion and superequivalent adsorption. There are two popular explanations that may account for this: ion-ion correlations and a drastic specific adsorption of certain species within the Stern layer. Both of these options are discussed in Jiménez et al. (2012) and Lyklema (2009) where many references can be found. Briefly one may state that ion correlation theories require simultaneously high surface charge densities and high concentrations of multivalent counterions. Experimentally such situations have been observed in surface force studies (e.g., Kekicheff et al., 1993).

With respect to specific adsorption, the observation is that multivalent electrolytes that tend to form hydrolysis species can reverse the sign of the ζ-potential at rather low concentrations and often at quite low surface charge densities¹ (e.g., Matijević et al., 1962, 1964, 1971; James and Healy, 1972; James et al., 1977; Lyklema and Golub, 2007; Jiménez et al., 2012). The usual reasoning is that such hydrolysis products appear to have a rather high affinity for specific adsorption at the iHp. This statement derives from the fact that the effect is usually only observed in a limited pH window for a given electrolyte.

As an example one may consider the speciation in an AlCl₃ solution as a function of pH (Figure 2). The calculations have been performed with ChemEQL (Mueller, 1996) assuming that all the available Al can be precipitated as amorphous Al(OH)₃. Immaterial of this assumption one can see that at acidic pH values hydrolyzed species are present and that not all the Al in the system is trivalent. At about pH = 5 the precipitation of Al(OH)₃ sets in and in the alkalic range the dominant species in ${\text{Al(OH)}}_4^{-}$.

FIGURE 2

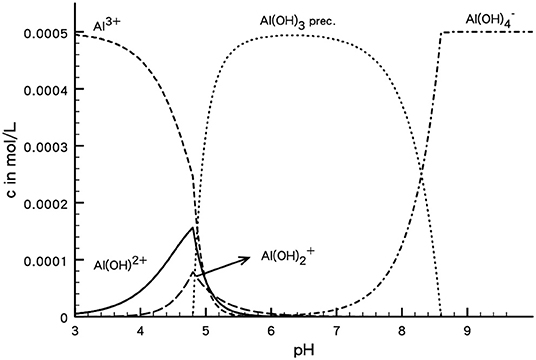
Figure 2. Speciation of Al in 0.5 mM AlCl₃ solution, assuming that all Al available can be precipitated into amorphous Al(OH)₃. Only dominant species are shown.

For aluminum chloride and nitrate solutions it was indeed observed that overcharging will only occur in the acidic range, being most effective around pH = 4–5. Such reasoning is of course applicable to many other electrolytes that form hydrolyzed species in other pH ranges and was observed for many different solids. This suggests that the phenomenon as such is quite generic. A further discussion of overcharging will be given at the end of the article.

An important point to make is, that the effect does not mean that the sign of the surface charge density changes, it is the diffuse layer charge density that changes sign (see Lyklema and Golub, 2007 for comprehensive experimental evidence). At a given concentration of electrolyte the surface charge density is determined by the pH in the case of oxides. If there is more specific adsorption at the iHp than is needed to compensate the surface charge, electroneutrality dictates that the diffuse layer charge density has to change sign, which is experimentally observed as a change in sign of the ζ-potential.

To promote overcharging, one has to look for multivalent electrolytes that form hydrolyzed species in aqueous solution. Popular candidates include Al(III), La(III), Fe(III), and Zn(II) chlorides and nitrates. Typically, there will be certain pH windows where hydrolyzed species are stable and these are precisely the pH ranges one wishes to investigate for overcharging.

3. Materials and Methods

The experiments reported in here have been conducted with a commercial spherical silica (SFP-30M from Denka, Japan). According to the manufacturer, the particle size is in the range between 0.1 and 2 μm with a median diameter of 0.6 μm and the specific surface area of the sample is 5.6 m²/g.

The chemicals used in the experiments have been used without further purification. The purity of the metal chlorides was at least 99% [CAS Numbers: 7784-13-6 (AlCl₃), 7646-85-7 (ZnCl₂)], n-Hexane (CAS Number: 110-54-3) was obtained from Merck as chromatographic grade and SDS was also obtained from Merck with a quoted homologue C₁₂ purity of ≥ 98% (CAS Number: 151-21-3).

Electrophoretic mobilities were measured with a Malvern Zetasizer Nano in folded capillary cells. The suspension has been stirred in a double-walled glass vessel that was connected to a water thermostad. Measurements have been carried out at 25°C with a drive voltage of max. 40 V. For each point 3 measurements have been made, each consisting of 50–100 sub runs.

Phase transfer experiments have been conducted in the following manner: An aqueous stock suspension was prepared with the desired concentration of a given metal salt, after which 2g/L silica were immersed in the solution. This suspension was then sonicated for ≈ 2 min in order to properly disperse the particles. The desired amount SDS was added to this suspension in dry form. Different pH values were then adjusted by the addition of HCl or NaOH. For each tube 20 mL of aqueous suspension were withdrawn and 5 mL n-Hexane were added. These tubes were then shaken in order to observe whether a successful phase transfer is accomplished.

The transmittance (relative to pure water) of the aqueous phase was measured with an Agilent Technologie Cary 60 UV-Vis spectrometer at 800 nm in order to obtain a qualitative indication of the efficiency of the phase transfer.

4. Results and Interpretation

The electrophoretic mobilities (μ_e) measured in different electrolyte solutions and in pure water are shown in Figure 3. Absolute electrophoretic mobilities will be used in discussing trends of this quantity.

FIGURE 3

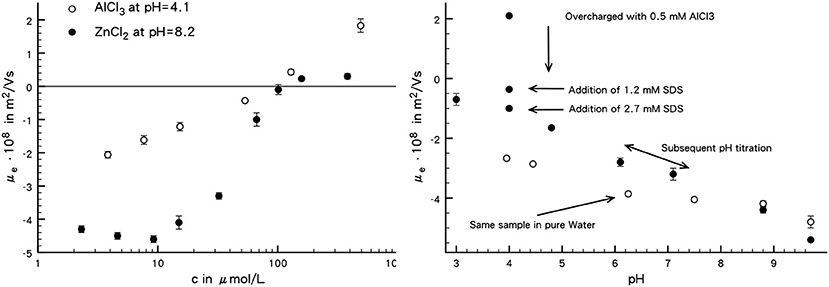
Figure 3. (Left) electrophoretic mobility of SFP-30M as a function of AlCl₃ at pH = 4.1 and ZnCl₂ at pH = 8.2. (Right) electrophoretic mobility of SFP-30M in pure water (open circles) and of the same sample at pH = 4 (full circles), overcharged with 0.5 mM AlCl₃. To this sample SDS was added with a subsequent pH titration. See text for detailed explanation. The error bars represent the standard deviation from three measurements.

First of all it is noted that the electrophoretic mobility in pure water is negative in the entire pH range studied. This is usual for silica and crystalline SiO₂ phases. Although the surface charge density is not at our disposal for this specific sample, it seems reasonably safe to say that the point of zero charge is not reached for the sample since there is rather good agreement in the literature that silicas have points of zero charge below pH = 3 if one is found at all (see Lyklema, 1995).

Based on the speciation of AlCl₃ and ZnCl₂ pH ranges were selected where overcharging can be suspected to occur. For aluminum chloride this is in the acidic range (roughly pH = 4–5) and for zinc chloride this is in the alkalic range (roughly pH = 8–9). Suspension were prepared with the desired pH and a titration with the corresponding electrolyte was conducted (see Figure 3, left). For aluminum chloride a steady increase of the electrophoretic mobility is observed and a change in its sign occurs at ≈ 0.1 mM. Upon further addition of electrolyte the mobility increases further, which indicates that the adsorption in the Stern layer is not completed after the change of sign.

The mobilities of zinc chloride suspensions are somewhat more complicated. At rather low concentration a decrease in mobility is noted. This is a definitive hint for Stern layer adsorption in conjunction with mobile ionic species in this part of the double layer. Such mobility maxima are observed on a standard basis in electrokinetic studies and can be traced back to surface conductance in the Stern layer (Delgado et al., 2007). Upon further addition of electrolyte, the mobility starts to increase rapidly and eventually changes sign at about 0.1 mM. Further addition of electrolyte does not change the mobility markedly anymore which can be taken as a sign that Stern layer adsorption of this species is completed.

Now that the solution compositions for overcharging are established, SDS was added to a suspension overcharged with 0.5 mM AlCl₃ at pH = 4 was measured (see Figure 3, right). The first addition of 1.2 mM SDS decreases the mobility from initially 2·10⁻⁸ m²/Vs to about −0.5 ·10⁻⁸ m²/Vs. Further addition of SDS (equivalent to 2.7 mM) decreases the mobility further to ≈ −1 ·10⁻⁸ m²/Vs. This can be taken as an indication that the adsorbed aluminum species act as adsorption sites for the negative part of the SDS. In order to investigate the stability of these Stern layer species, a pH titration was carried out after the addition of 2.7 mM SDS. The general shape of the mobility vs. pH curve is quite similar to the one recorded in pure water. Up to pH ≈ 9 the absolute mobilities in the SDS system are lower that those of pure water and in the alkalic range they do not differ too much from each other. Furthermore, it is interesting to note that the pH titration is reversible.

Figure 4 shows the results of the qualitative phase transfer experiments. The lower phase is the aqueous phase and the upper one is n-Hexane. It can immediately be concluded that the success of the phase transfer depends on the type and concentration of the electrolyte and the pH.

FIGURE 4

Figure 4. Pictures of the phase transfer experiments. (A) 0.5 mM AlCl₃ with 2 mM SDS, (B) ZnCl₂ with 2 mM SDS, (C) 0.5 mM CaCl₂ with 2 mM SDS and (D) 11 μmol AlCl₃ at pH = 4.6 with different SDS concentrations. pH values in (A–C) are indicated and the SDS concentration in (D) is given in mM.

The transmittance measurements of the aqueous parts of these systems are presented in Figure 5. Note that these measurements should be interpreted qualitatively, because in AlCl₃ - SDS systems precipitation of a Al-SDS phase occurs which will be discussed later.

FIGURE 5

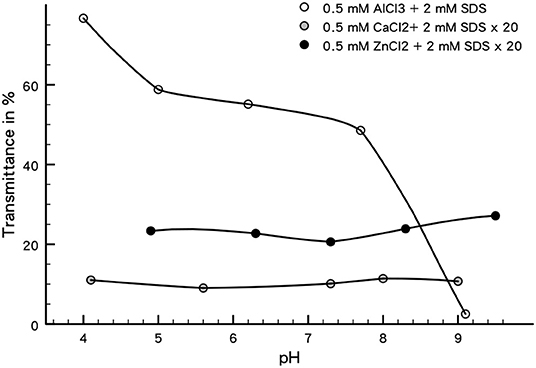
Figure 5. Transmittance (at 800 nm) of the aqueous phase of the phase transfer experiments shown in Figure 4. Note that the data for 0.5 mM CaCl₂ and ZnCl₂ have both been multiplied by a factor of 20 in order to make them visible with respect to the AlCl₃ system.

Even without a detailed mechanistic explanation one can conclude from Figures 4, 5 that the phase transfer in the system containing 0.5 mM AlCl₃ with 2mM SDS is most effective. Within this system there is a pronounced pH dependency of the transfer efficiency as indicated by the transmission measurements. At low pH, where overcharging is most pronounced, the phase transfer is almost complete, decreasing toward the alkalic range where a quite low amount of particles is transferred. Considering the system with 11 μmol/L AlCl₃ at pH = 4.6, where the Al concentration is too low to overcharge the silica, one cannot observe a phase transfer at all, immaterial of the SDS concentration. In the ZnCl₂ system one observes a partial, but pH independent phase transfer. As a comparison to this system, we have conducted the same experiment with CaCl₂, which does not hydrolyze significantly in the studied pH range and does not cause overcharging. No phase transfer at all is observed in this system. All these observations, although largely qualitative, show that overcharging is a necessary condition for a successful phase transfer in our system. The following section is intended to provide a more detailed explanation for these observations.

5. Discussion

Before discussing the details of overcharging and the subsequent adsorption of DS⁻, it is necessary to point out that we have observed the formation of a precipitate in solutions of AlCl₃ and SDS. Visually this can be observed at a ratio of SDS/AlCl₃ ≈1. Upon further addition of SDS the precipitation proceeds until a ratio of SDS/AlCl₃ ≈12 is attained, where the solution is entirely transparent again. This effect is known for AlCl₃ sulfonate systems (Somasundaran et al., 1988) and goes by the name precipitation-redissolution phenomena. In the Al(NO₃)₃-dodecylsulfate system similar observations have been made (Pereira et al., 2009). Regardless of the specific details of these processes, it must be noted that our AlCl₃ experiments have been conducted in a concentration range (SDS/AlCl₃ = 4) where precipitation occurs. It is therefore logical to question whether the successful phase transfer is due to the presence of the precipitate or due to the effect of overcharging with concomitant adsorption of DS⁻. It is for this reason that we have conducted the same experiments with a lower concentration of AlCl₃, where overcharging does not occur. In these experiments the SDS concentration was varied to cover a range of SDS/AlCl₃ = 4–178, where both precipitation and redissolution occur.

As mentioned in the previous section, no phase transfer was observed in these experiments. This suggests that overcharging is the dominating mechanism leading to the adsorption of DS⁻. To see this point, consider the experiments with ZnCl₂ and CaCl₂. Here we observe no phase transfer for CaCl₂, but observe a partial one for ZnCl₂. This is due to the ability of Zn to overcharge the silica at alkalic pH, whereas Ca is not able to do so at such low concentration. Furthermore, we have not observed (visually) a precipitation of ZnCl₂ + SDS solutions.

The experimental data presented in here and the numerous experimental observations cited in conjunction with the overcharging phenomenon demonstrate that the sign reversal of the electrophoretic mobility is at least in part due to the specific adsorption of hydrolyzed species. One may now wonder why such hydrolyzed species, which have a lower charge than the unhydrolyzed metal cation, adsorb so effectively.

In addition to the electrostatic adsorption energy at the iHp, which is ΔG_el=zeψⁱ, one may quite generally add a solvation term (see for instance James and Healy, 1972). The free energy change associated with ion solvation describes the process of transferring an ion from a region of high dielectric constant to a region of lower dielectric constant. These authors derived a relationship for the solvation work required to bring an ion from the free solution to the iHp:

$\begin{array}{l}\Delta G_{solv}=\left(\frac{z_i^2{e}^2}{16\pi {\epsilon }_0}\right)\left(\frac{1}{r_i+2r_w}-\frac{r_i}{2{(r_i+2r_w)}^2}\right)\left(\frac{1}{{\epsilon }_{iHp}}-\frac{1}{{\epsilon }_w}\right)\\ +\left(\frac{z_i^2{e}^2}{32\pi {\epsilon }_0}\right)\left(\frac{1}{r_i+2r_w}\right)\left(\frac{1}{{\epsilon }_s}-\frac{1}{{\epsilon }_{iHp}}\right)& (3)\end{array}$

In this relation z_i is the charge of the ions, e the elementary charge, ε₀ the permitivitty of free space, ε_w the relative dielectric constant of water, ε_s the one of the solid, ε_iHp the effective relative dielectric constant at the iHp, r_i the radius of the ion and 2r_w the diameter of a water molecule. Note that James and Healy (1972) place the iHp at a distance 2r_w + r_i away from the surface. The difficult point is to define and calculate reasonable values for the dielectric constant at the iHp, since at such small length scales a definition of a macroscopic quantity becomes somewhat ambiguous. James and Healy (1972) chose to relate this dielectric constant to the field strength in the double layer. This step, however, is somewhat inconsistent, because diffuse double layer theory is applied up to the iHp in order to obtain the required relationship. Moreover, the change of dielectric constant close to a solid surface is a general property of structurable solvents. This is why we choose a relationship suggested by Podgornik et al. (1987) to construct the dielectric profile:

$\begin{array}{ll}{\epsilon }_w(x)=\frac{{\epsilon }_w}{1+({\epsilon }_w/{\epsilon }_s-1)e^{-x/l}}& (4)\end{array}$

where x is the distance to the solid surface and l the correlation length of water. Last but not least, James and Healy (1972) added a chemical contribution to the adsorption free energy. This chemical contribution embraces all specific interactions that may occur in the system and, just like the electrical contribution, it is a favorable energy change. It is furthermore assumed that this term is constant and applies to all species present. Within this simple model the total adsorption free energy at the iHp is written as the sum of the discussed contributions: Δ_adsG=ΔG_el + ΔG_solv + ΔG_chem. An example calculation along these lines is shown in Figure 6. The parameters chosen for the calculation are as follows: As already mentioned above, the position of the iHp is fixed as 2r_w + r_i, where 2r_w = 0.284 nm and r_i=0.05 nm (Al^{3 +} ) (Marcus, 1988). The dielectric constant of SiO₂ has be taken as ε_s = 4 (Hunter, 2000) and the correlation length of water has been set to 2r_w = 0.284 nm. With these values the dielectric constant at 2r_w + r_i=0.33 nm is ε_iHp=10. Finally the electric potential at the iHp has ben set ψⁱ = −0.15 V and the chemical part of the adsorption free energy has been chosen as ΔG_chem = −25 kJ/mol (an intermediate value from James and Healy, 1972).

FIGURE 6

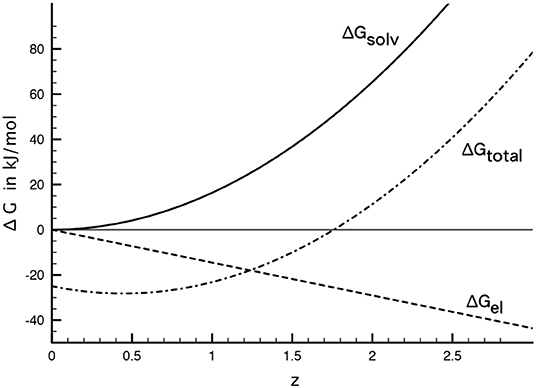
Figure 6. Solvation and electrostatic contribution to total free energy of adsorption in the Stern layer. For parameters see text. The chemical contribution of ΔG_chem = −25 kJ/mol (not shown) is added to the total adsorption free energy.

It can be seen that the electrical and chemical contributions represent a favorable energy change, i.e., they promote adsorption. While the chemical part has, as usual, been assumed constant, the electrical part increases lineraly with z. The energy penalty represented by the solvation term, however, scales with z². It thus represents an energy barrier for the adsorption of higher-valence ions. In the example presented here, the adsorption would be favorable for species with z 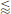2.

Due to the quite large number of unknown parameters such calculations should not be taken as quantitative unless more experimental data is available. They do, however, highlight the decisive role of solvation in the adsorption of hydrolyzed species. James and Healy (1972) used a similar approach to fit adsorption isotherms in such systems and were able to describe their experimental results with reasonable parameter choices. The difference being that they related the dielectric constant to the field strength in the double layer (see above). The simple treatment of the dielectric constant profile presented above is somewhat more attractive in that it does not involve the application of Gouy-Chapman theory in the inner part of the double layer and that it is applicable to structurable solvents in general.

The pH titration of overcharged SiO₂ in the presence of 2.7 mM SDS shown in Figure 3 is reversible with respect to pH changes. This is an important observation, because it shows that the Al-DS⁻ complexes are adsorbed quite strongly in the Stern layer. When SDS is added to the overcharged silica, part of the SDS adsorbs to the positive Al sites in the Stern layer. The amount of SDS added in our system is high enough to reverse the overcharging, meaning that |σ⁰| > |σⁱ|, which is indicated by the electrophoretic mobility going to negative values again. The fact that at pH = 4 the mobility remains well above the mobility of the sample in water suggests that there is still a finite charge density located in the Stern layer when AlCl₃ and SDS are added. If this charge density is more or less pH-independent, a titration to high pH will increase the surface charge density σ⁰ while σⁱ remains more or less constant. At alkalic pH σ⁰ becomes eventually so large that that the contribution of σⁱ becomes less notable and similar diffuse layer charge densities are obtained again (with respect to the pure water case). This is precisely what can be observed from the electrophoretic mobilities.

Moreover it was observed that the phase transfer as such is reversible. In the presence of 0.5 mM AlCl₃ + 2mM SDS at pH = 4, a rather effective phase transfer is observed (see Figures 4, 5). When NaOH is added to the aqueous phase and the tube is shaken again, most of the particles are transferred to the aqueous phase again. This is a remarkable observation, for which we do not have a definitive explanation up to now.

Apart from the energetic changes occurring at the aqueous-solid interface it is also permissible that the interface tension of the aqueous-Hexane interface is influenced by the precipitates in the AlCl₃-SDS system. Preliminary measurements indicate that at acidic pH the interface tension is lower at acidic pH than at alkalic pH, which can also contribute to the efficiency of the phase transfer. Altogether these results show that the systems studied here are quite complicated ones and that multiple adsorption processes at different interfaces as well as the liquid chemistry as such deserve further attention.

6. Conclusion

Using electrophoresis measurements and phase transfer experiments it was shown that overcharging by hydrolyzed metal species is responsible for the adsorption of an anionic collector (SDS) to a negatively charged surface. The phase transfer, and thus the hydrophobization of particles, was found to be most effective when overcharging is most pronounced. The complicated interactions between SDS and multivalent cations, however, hamper an in-depth understanding of the multiple adsorption phenomena at the different interfaces.

What appears to be established is that overcharging by hydrolyzed species is a necessary condition for a phase transfer in our systems. The processes leading to overcharging by inorganic ions were discussed an it was emphasized that ion solvation can play a decisive role by creating an energetic barrier for the adsorption of multivalent ions.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

CW designed, conducted, and interpreted the experiments. UP designed experiments and critically examined the results.

Funding

CW appreciates funding by the DFG (SPP2045, 313858373).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

CW acknowledges insightful discussions with Dr. Martin Rudolph and Edgar Schach (Helmholtz-Zentrum Dresden-Rossendorf). Paul Knüpfer and Klaus Graebe are thanked for experimental assistance and B. von Klitzing from Denka for supply of the silica.

Footnotes

1. ^Depending on the system just some 10–100 μmol/L and charge densities ${O}$(10⁰) μC/cm² are sufficient.

References

Delgado, A. V., Gonzalez-Caballero, F., Hunter, R., Koopal, L. K., and Lyklema, J. (2007). Measurement and interpretation of electrokinetic phenomena. J. Colloid Interface Sci. 209, 194–224. doi: 10.1016/j.jcis.2006.12.075

CrossRef Full Text | Google Scholar

Dukhin, S. S., and Derjaguin, B. V. (1974). “Chapter 2: Electrokinetic phenomena,” in Surface and Colloid Science, ed V. Matijević (New York, NY: John Wiley and Sons), 356.

Google Scholar

Fuerstenau, D. W., and Colic, M. (1999). Self-association and reverse hemimicelle formation at solid-water interfaces in dilute surfactant solutions. Colloids Surfaces A Physicochem. Eng. Aspects 146, 33–47. doi: 10.1016/S0927-7757(98)00795-X

CrossRef Full Text | Google Scholar

Furstenau, D. W., and Pradip (2005). Zeta potentials in the flotation of oxide and silicate minerals. Adv. Colloid Interface Sci. 9-26, 114–115. doi: 10.1016/j.cis.2004.08.006

CrossRef Full Text | Google Scholar

Furstenau, M. C., Rice, D. A., Somasundaran, P., and Furstenau, D. W. (1965). Metal ion hydrolysis and surface charge in beryl flotation. Trans. Am. Inst. Mining Metallur. Eng. 74, 381–391.

Google Scholar

Hunter, R. (1981). “Zeta potential in colloid science - Principles and applications,” in Colloid Science: A Series of Monographs, eds R. H. Ottewill and R. L. Rowell (London: Academic Press), 386.

Google Scholar

Hunter, R. (2000). Foundations of Colloid Science, 2nd Edn. New York, NY: Oxford University Press Press

Google Scholar

Hunter, R., and Wright, H. J. L. (1971). The dependence of electrokinetic potential on concentration of electrolyte. J. Colloid Interface Sci. 37, 564–580. doi: 10.1016/0021-9797(71)90334-1

CrossRef Full Text | Google Scholar

James, R. O., and Healy, T.W. (1972). Adsorption of hydrolyzable metal ions at the oxide-water interface iii. a thermodynamic model of adsorption. J. Colloid Interface Sci. 40, 65–81. doi: 10.1016/0021-9797(72)90174-9

CrossRef Full Text | Google Scholar

James, R. O., Wiese, G. R., and Healy, T.W. (1977). Charge reversal coagulation of colloidal dispersions by hydrolysable metal ions. J. Colloid Interface Sci. 59, 381–385. doi: 10.1016/0021-9797(77)90023-6

CrossRef Full Text | Google Scholar

Jiménez, M. L., Delgado, A. V., and Lyklema, J. (2012). Hydrolysis versus ion correlation models in electrokinetic charge inversion: establishing application ranges. Langmuir 28, 6786–6793. doi: 10.1021/la3010773

PubMed Abstract | CrossRef Full Text | Google Scholar

Kekicheff, P., Marcelja, S., Senden, T. J., and Shubin, V. E. (1993). Charge reversal seen in electrical double layer interaction of surfaces immersed in 2:1 calcium chloride solutions. J. Chem. Phys. 99, 6098–6113.

Google Scholar

Leistner, T., Müller, M., Erler, J. V., Rudolph, M., and Peuker, U. A. (2014). Selektive trennung sehr feiner partikelsysteme mittels flüssig/flüssig-flotation. Chem. Ingenieur Technik 86, 831–839. doi: 10.1002/cite.201400011

CrossRef Full Text | Google Scholar

Leistner, T., Türk, M., Weber, A., Weber, C., and Peuker, U. A. (2019). Selective separation using fluid-liquid interfaces. Mater. Sci. Forum 959, 113–124. doi: 10.4028/www.scientific.net/MSF.959.113

CrossRef Full Text | Google Scholar

Lyklema, J. (1989). Discrimination between physical and chemical adsorption of ions on oxides. Colloids Surfaces 37, 197–204. doi: 10.1016/0166-6622(89)80118-0

CrossRef Full Text | Google Scholar

Lyklema, J. (1991). Electrified interfaces in aqueous dispersions of solids. Pure Appl. Chem. 61, 895–906.

Google Scholar

Lyklema, J. (1994). On the slip process in electrokinetics. Colloids Surfaces A Phys. Eng. Aspects 92, 41–49. doi: 10.1016/0927-7757(94)02727-7

CrossRef Full Text | Google Scholar

Lyklema, J. (1995). Fundamentals of Interface and Colloid Science - Volume II: Solid-Liquid Interfaces. London: Academic Press.

Google Scholar

Lyklema, J. (2006). Overcharging, charge reversal: chemistry or physics. Colloids Surfaces A Phys. Eng. Aspects 291, 3–12. doi: 10.1016/j.colsurfa.2006.06.043

CrossRef Full Text | Google Scholar

Lyklema, J. (2009). Quest for ion-ion correlations in electric double layers and overcharging phenomena. Adv. Colloid Interface Sci. 147-148, 205–213. doi: 10.1016/j.cis.2008.12.002

CrossRef Full Text | Google Scholar

Lyklema, J. (2011). Surface charges and electrokinetic charges: Distinctions and juxtapositionings. Colloids Surfaces A Phys. Eng. Aspects 376, 2–8. doi: 10.1021/jp057096

CrossRef Full Text | Google Scholar

Lyklema, J. (2013). Coagulation by multivalent counterions and the schulze-hardy rule. J. Colloid Interface Sci. 392, 102–104. doi: 10.1016/j.jcis.2012.09.066

PubMed Abstract | CrossRef Full Text | Google Scholar

Lyklema, J., and Golub, T. (2007). Electrical double layer on silver iodide and overcharging in the presence of hydrolyzable cations. Croatica Chem. Acta 80, 303–311.

Google Scholar

Machunsky, S., Grimm, P., Schmid, H. J., and Peuker, U. A. (2009). Liquid-liquid phase transfer of magnetite nanoparticles. Colloids Surfaces A Phys. Eng. Aspects 348, 186–190. doi: 10.1016/j.colsurfa.2009.07.014

CrossRef Full Text | Google Scholar

Marcus, Y. (1988). Ionic radii in aqueous solution. Chem. Rev. 88, 1475–1498. doi: 10.1021/cr00090a003

CrossRef Full Text | Google Scholar

Matijević, E., Janauer, G. E., and Kerker, M. (1964). Reversal of charge of lyophobic colloids by hydrolyzed metal ions i. aluminum nitrate. J. Colloid Interface Sci. 19, 333–346. doi: 10.1016/0095-8522(64)90035-2

CrossRef Full Text | Google Scholar

Matijević, E., Mangravite, F. J., and Cassell, E. A. (1971). Stability of colloidal silica iv. the silica-alumina system. J. Colloid Interface Sci. 35, 560–568. doi: 10.1016/0021-9797(71)90214-1

CrossRef Full Text | Google Scholar

Matijević, E., Mathai, K. G., and Kerker, M. (1962). Detection of metal ion hydrolysis by coagulation v. zirconium. J. Phys. Chem. 66, 1799–1803. doi: 10.1021/j100816a006

CrossRef Full Text | Google Scholar

Mueller, B. (1996). ChemEQL. A Program to Calculate Chemical Speciation and Chemical Equilibria. Eidgenössische Anstalt für Wasserversorgung.

Google Scholar

Pereira, R. F. P., Valente, A. J. M., Burrows, H. D., Ramos, M. L., Ribeiro, C. F., and Lobo, V. M. M. (2009). Flocculation and micellization of sodium dodecyl sulfate solutions in the presemce of aluminum nitrate: effect of concentration and temperature. Acta Chim. Slovenica 56, 45–52.

Google Scholar

Podgornik, R., Cevc, G., and Zeks, B. (1987). Solvent structure effects in the macroscopic theory of van der waals forces. J. Chem. Phys. 87, 5957–5967. doi: 10.1063/1.453519

CrossRef Full Text | Google Scholar

Schubert, H. (1996). Aufbereitung Fetster Stoffe Band II: Sortierprozesse. Stuttgart: Deutscher Verlag für Grundstoffindustrie Stuttgart.

Google Scholar

Somasundaran, P., Ananthapadmanabhan, K. P., and Celik, M. S. (1988). Precipitation-redissolution phenomena in sulfonate-alcl₃ solutions. Langmuir 4, 1061–1063.

Google Scholar

Stern, O. (1924). Zur theorie der elektrolytischen doppelschicht. Zeitschrift für Elektrochemie und Angewandte Physikalische Chemie 30, 508–516.

Google Scholar