Dynamic Mechanical Hysteresis of Magnetorheological Elastomers Subjected to the Cyclic Loading and Periodic Magnetic Field

Magnetorheological elastomer (MRE) is one of the most promising smart materials with excellent magnetic-control mechanical properties. This work focuses on the study of the dynamic mechanical properties of MRE under cyclic loadings and periodic magnetic field. The influences of matrix, particle distribution, magnetic field on the dynamic mechanical hysteresis are systematically investigated. It is found that all the normal force, magnetic fields and shear strain would cause a hysteresis in the dynamic mechanical responses of MRE. The continuous cycle tests reveal the hysteresis tended to be saturated after several initial cycles. The hysteresis of MRE under the constant magnetic field can be attributed to the rearrangement of particles, which causes a hardening effect of MRE under the continuous dynamic tests. The periodic magnetic field causes a hysteresis in the dynamic modulus which could be attributed to the irreversible movement of the particles. Among them, the polymer matrix of MRE plays an important role in the dynamic mechanical hysteresis, which suggests more stable molecular chain structures in the matrix reducing the magnitude of hysteresis and improving its stability. Besides, the saturation of the mechanical hysteresis had also been studied, and then relevant physical mechanism was proposed for the qualitative explanation.

Introduction

The fiber-rubber composites exhibit an appreciable change in their mechanical response resulting from the previous maximum loading. This mechanical hysteresis, also known as Mullins effect, has been recognized in polymer science and engineering (Ogden and Roxburgh, 1999; Hanson et al., 2005; Qi and Boyce, 2005; Webber et al., 2007). The stress-strain curve demonstrates a marked hysteretic response during the loading-unloading cycle, in which the stress under unloading is significantly less than that under loading at the same strain (Dorfmann and Ogden, 2005). The magnitude of the hysteresis can be represented by the area between the tension and relaxation curves. Plenty of explanations and phenomenological models were reported for Mullins effect, and these were mainly based on the concepts of slippage and disentanglement of polymer molecules, bond rupture between particle fillers and polymer matrix, and breakdown of particle aggregation (Diani et al., 2009). Apart from the Mullins effect, the mechanical properties of fiber-rubber composites under the cyclic loading can be used to evaluate the stability of materials, which is a crucial performance index for the engineering application. Consequently, improving the stability of polymer composites is an urgent requirement, and the mechanism study of mechanical hysteresis has continuously been a research focus (Merabia et al., 2008; Drozdov, 2009; Machado et al., 2012; Chai et al., 2013).

Magnetorheological elastomer (MRE) belongs to the group of smart materials, which is stimulated to change its mechanical behavior by an external magnetic field. The MRE consists of micronized magnetic particles dispersed in a nonmagnetic elastic matrix, such as polyurethane (PU), natural rubber and silicone rubber (Gong et al., 2005; Stepanov et al., 2007; Li and Nakano, 2013; Wang et al., 2014; Jung et al., 2016; Qi et al., 2018b). As an intelligent engineering material, the MRE exhibits excellent magnetic-control properties as well as potentials for applications in the fields of noise reduction, vibration attenuation, smart sensing, electromagnetic shielding, etc. (Kashima et al., 2012; Hoang et al., 2013; Xing et al., 2015, 2016; Fu et al., 2016; Wang et al., 2016; Yu M. et al., 2016; Qi et al., 2018a). For the magnetorheological (MR) materials, the magnetic particles are inclined toward columns paralleled to the magnetic orientation. When the magnetic field is removed, the magnetic particle cannot return to its original position immediately. It will cause the hysteresis in the viscoelastic properties of MR materials, especially in the viscous matrix rather than in the elastic matrix. The hysteresis behaviors of devices based on MR materials have attracted the attention of many researchers (An and Kwon, 2003; Dominguez et al., 2004; Yu Y. et al., 2016; Chen et al., 2018; Xian-Xu et al., 2019). For the MRE, Gundermann et al. have investigated the motion of particles in MREs by X-ray micro-computed tomography (X-μCT) (Gundermann and Odenbach, 2014). They found that the process of particle motion was not reversible. It reveals the possibility of mechanical hysteresis behavior caused by the magnetic field in the MRE, which have been ignored in most literatures. However, in the area of polymer science and engineering, relevant researches on the dynamic mechanical behavior of MRE under the repeated cyclic loading or periodic magnetic field are comparatively rare.

The MR effect computed by the ratio of the magnetic-induced modulus to the initial modulus is the most considerable evaluation index of MREs. Generally, in order to improve the MR effect, the researchers enhanced the magnetic-induced modulus by increasing the concentration of magnetic particles, interface modification, incorporating additive, etc. (Li and Sun, 2011; Qiao et al., 2012; Yang et al., 2013; Aziz et al., 2016). The other defective method is decreasing the initial modulus by adding vast plasticizer or reducing the crosslinking density of MRE, which weakens the mechanical strength of MRE. These viscous matrices are able to make the mechanical hysteresis more serious in the MRE. As an engineering material, the MRE has to suffer different cyclical loadings and magnetic fields when under variable application conditions. The cyclic loadings and the variable magnetic field will change the mechanical performance of MRE, which leads the instability of the MRE-based device. Therefore, it is necessary to study the mechanism of the mechanical hysteresis, and improve the stability of MRE for the engineering application.

Previously, An et al. (2012) found a stress hardening phenomenon for the MR gel in the presence of stable magnetic field under the cyclic loading. They also deduced this phenomenon, which was opposite to the Mullins effect of the conventional particle-filled polymer composite, was caused by the rearrangement of particles under the external magnetic field. Xu et al. (2016) have also proposed a magneto-induced hardening mechanism to explain the transition from stress softening to stress hardening under cyclic loadings. For the elastomer reinforced by the magnetic particles, the hysteresis in the dynamic mechanical responses was first reported in the elastomer that contains hard magnetic particles, in which the magnetic remanence of hard magnetic particles was the priority consideration (Stepanov et al., 2012; Kramarenko et al., 2015; Yu et al., 2015c). Sorokin et al. (2015) have studied the hysteresis in dynamic modulus, loss factor and normal forces with regard to the MRE. The influences of particle size and composition have been studied, and they also discussed the possible mechanism for the mechanical hysteresis. In addition, Sorokin et al. (2014) further studied the Payne effect in the MRE using synthetically cycling measurements; the Payne effect increased significantly in the presence of an external magnetic field and varied with the cyclic loading, which reached saturation after several cycles. Thus, far, the study on the mechanical hysteresis of MRE is not enough, and the deeper investigation about the saturation of the mechanical hysteresis is eagerly needed.

PU has better degradation stability than natural rubber and superior mechanical stability than silicone rubber (Wei et al., 2010), and it has been widely used to be the matrix of the MRE (Wu et al., 2010, 2012; Ge et al., 2015). In this paper, two kinds of MRE based on the PU matrix and PU/epoxy (EP) interpenetrating network (IPN) matrix were prepared, respectively. The material properties and the details of the process and principle of preparation could be obtained in our previous work (Yu et al., 2015a,b). Several cycling tests have been carried out to study the most critical influences on the mechanical hysteresis of MRE, including the matrix, particle distribution, magnetic field. The saturation of the mechanical hysteresis has also been studied, and then relevant physical mechanism is proposed to explain it qualitatively. This work turns out that the material properties of MRE should be characterized by the repeating test rather than merely single test. More effective evaluation tests of MRE are of benefit to the potential applications. In particular, the discussion on the influences of matrix will provide guidance for improvement of material preparation.

Experiment

Materials

The soft magnetic carbonyl iron powder (CIP) (Type: CN; size distribution: 1–8 μm) was provided by BASF in Germany. PU matrix (Castor oil purchased from Sinopharm Chemical Reagent Co., Ltd., China; MDI (MDI: 4,4-~50%, 2,4-~50%) purchased from Yantai Wanhua Polyurethanes Co., Ltd., China), Stannous octoate (Sinopharm Chemical Reagent Co. Ltd., China) was used as catalyst in the process of PU preparation. EP based on diglycidyl ether of bisphenol-A was purchased from Baling Petrochemical Co., Ltd., Hunan, China. The 2,4,6-Tri(dimethylaminomethyl)phenol (DMP-30) acting as the curing agent of EP was acquired from Wuhan Hongda Co., Ltd., China. The Di-butyl phthalate (DBP) used as a plasticizer was bought from Tianjin Bodi Chemical Holding Co., Ltd., China.

MRE Preparation

In order to study the influence of the matrix and particle distribution on the hysteresis properties, we prepared different kinds of MRE samples. The isotropic samples and anisotropic samples were fabricated in the absence and presence of magnetic field, respectively. The PU and IPN denote that the MRE samples were based on PU matrix and PU/EP IPN matrix, respectively. The detailed compositions of MRE samples are listed in Table 1. Here the prefix of “ani” and “iso” denote the isotropic and anisotropic sample, respectively. Details about the process and principle of reaction of PU/EP IPN and PU can be obtained from our previous works (Yu et al., 2015a; Yang et al., 2016). The incorporation of EP would improve the crosslink degree of PU, and the interpenetration and entanglement of molecular chains in the PU/EP IPN would improve the structural stability of the polymer. Therefore, it should be noticed that the PU-MRE has higher viscous component, and the IPN-MRE has higher elastic component.

TABLE 1

Table 1. Detailed formation of MRE samples with different proportions of EP.

Characterization

The morphologies of the particles in the MRE samples were characterized via scanning electron microscopy (SEM; MIRA3 TESCAN). The microphotographs of MRE samples were taken for the fractured surface, on which the gold powder was coated prior to testing.

The cycling tests of MRE samples were implemented under shear oscillation mode using an advanced commercial rheometer (Model: MCR301, Anton Paar). A parallel-plate rotor and magnetron device were installed in the rheometer. The testing magnetic field of magnetron devices was generated by an electromagnet. The magnetic flux density could be changed from 0 to ~1.2 T by varying the drive current in the coil of the electromagnet with a range of 0–5 A. The details about this rheometer could be obtained from our previous work (Yu et al., 2013). In this study, the samples were prepared in disc forms with 20 mm in diameter and 2 mm in thickness. During the testing process, the samples were secured between the lower stationary plate and the upper movable plate that was connected to a forced torsional oscillator.

Results and Discussion

This work focuses on the influences of mechanical pressure, magnetic fields and shear strain on the dynamic mechanical hysteresis of MRE. Initially, the normal force cycling tests in the absence and presence of magnetic field were carried out to study the influences of the mechanical pressure. Then the MRE samples were tested under a triangular (periodic increase and decrease) magnetic field, and the hysteresis in the dynamic modulus caused by the magnetic field has been studied. Finally, the analysis of the amplitude cycle tests at different magnetic field strengths is presented.

Normal Force Cycling Tests

Compressive stress is a common loading when the MRE-based device is working. In order to study the mechanical hysteresis behavior of MRE under changing compressive stress, we tested the dynamic modulus of MRE under a cyclic normal force in the range of 5–30 N. The strain amplitude of 0.1%, pre-compression force of 5 N and test frequency of 5 Hz were selected for these tests. Measurements were carried out in several consecutive stages. Initially, the dynamic mechanical properties were measured under an increasing normal force actuated from 5 to 30 N. After reaching the maximum value, the normal force was linearly reduced from 30 to 5 N. These tests were conducted in the absence and presence of magnetic field to study the influence of magnetic field, and the number of cycles was set 5 for each test.

Figure 1 illustrates the dependence of dynamic modulus of iso-IPN, ani-IPN, and ani-PU samples on the cycling normal force, respectively. The color change of curves indicates the process of the cyclic tests. As can be seen, the dynamic modulus of all samples increases with the increasing normal force. This phenomenon also has been reported by Feng et al. (2015). It is attributed to the enhancement of the particle–particle and particle–matrix interactions with the high normal force. After the normal force declined linearly, an apparent hysteresis has been observed in all curves, while the modulus tends to saturate after several cycles. It indicated that the possibility of the balance between destruction and reformation of the particle structures which caused by the coupling effect of the cyclic mechanical loading and magnetic field. It also can be seen that the storage modulus increases with the increasing test cycle. It means that the compressive loading in the initial cycle produces a hardening effect of the MRE sample. The hardening effect is more obvious when the samples under the magnetic field. Similar to the MR gel and MR plastomer, this hardening effect in the magnetic field can be attributed to the rearrangement of CIPs (An et al., 2012; Xu et al., 2016). The qualitative comparative analyses of the hysteresis were carried out in the following section.

FIGURE 1

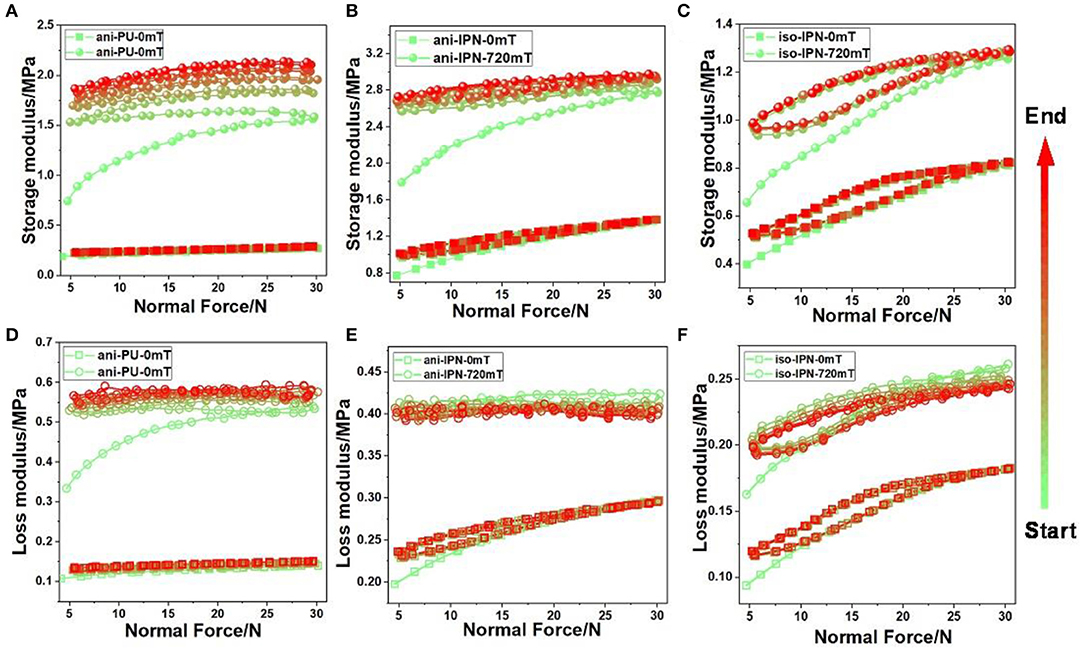
Figure 1. The influence of the normal force on the dynamic viscoelastic properties of MRE samples. Dependence of storage modulus of ani-PU sample (A), ani-IPN sample (B), and iso-IPN sample (C) on the normal force in the absence and presence of magnetic field. Dependence of loss modulus of ani-PU sample (D), ani-IPN sample (E), and iso-IPN sample (F) on the normal force in the absence and presence of magnetic field. The color scale indicates the progress of the cycle tests.

The magnitude of the hysteresis can be represented by the area between the ascending and descending curves. From the qualitative compare we can deduce that the hysteresis is more obvious in the presence of magnetic field than in the absence of magnetic field. The hysteresis of PU sample also greater than that of IPN sample, which indicated that the matrix played an important role in the destruction and reformation of the particle structures. To obtain a better understanding the influence of matrix, particle distribution and magnetic field on the hysteretic property, here we defined

$\begin{array}{ll}\lambda =({\text{G}}_{\text{n}}-{\text{G}}_1)/{\text{G}}_1& (1)\end{array}$

where G_n is the maximum value of dynamic modulus in the nth cyclic curve, and the G₁ is the maximum value of dynamic modulus in the initial cyclic curve. The parameter λ can commendably reflect the changes of dynamic modulus of MRE in the cycles, as Figure 2 shows. As can be seen the parameter λ of PU sample is significantly larger than that of IPN sample. In addition, the saturation of IPN sample is more apparent than that of PU sample, which indicates that the interpenetration and entanglement of molecular chains in IPN matrix would improve the stability of MRE. Comparing the curves in the absence and presence of magnetic field, we can deduce that the magnetic force between the magnetized CIPs intensifies the motion of CIPs when the MRE suffers compressive loading. The movement of CIPs and the enhancement of interaction forces between the CIPs and matrix are going to cause a larger hysteresis. Another phenomenon is that the parameter λ of ani-IPN is greater than that of iso-IPN, which can be attributed to the difference of the particle distribution. As can be seen from Figures 3a,b, it is observed that the CI particles are uniformly dispersed in the isotropic sample while they exhibited patterned chain-like structure in the anisotropic sample. The deformation and reagglomeration of the chain structure paralleled to the normal force will be enhanced by the compressive loading. In addition, the parameter λ of curves with magnetic field is greater than that of curves without magnetic field. It indicates that the magnetic field also causes a decrease in the stability of MRE when the MRE suffers the compressive loading. Since the magnetic field can enlarge the movement of particles in the process of reagglomeration, another phenomenon that the parameter λ of IPN samples has a slightly decrease in the presence of magnetic field can be seen in the Figure 2B. The decrease of the loss modulus can be attributed to the saturation of particle movement in the IPN matrix. It's contrary to the IPN sample, the loss modulus of PU sample increases with the cycle number because of the weaker restriction of the PU matrix. It revealed that the particle movement in PU sample is not saturated in these five cyclic tests.

FIGURE 2

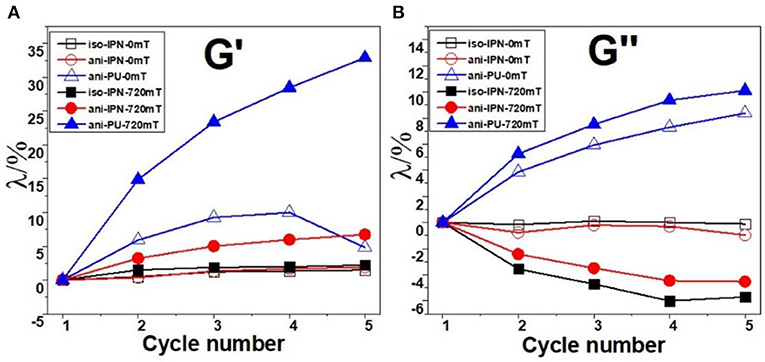
Figure 2. Dependence of the parameter λ (A: storage modulus G′; B: loss modulus G″). on cycle number for the samples under the ascending and descending normal force (The hollow symbol and solid symbol indicated the tests under 0 and 720 mT, respectively).

FIGURE 3

Figure 3. SEM images of iso-IPN (a) and ani-IPN (b). The red arrow indicates the direction of the pre-structure magnetic field.

Magnetic Field Cycling Test

The linear increasing magnetic field has been carried out by many researchers to study the MR effect of MR materials (Xu et al., 2011; Bica, 2012). In order to study the magneto-induced mechanical hysteresis of MRE under the triangular magnetic field, we tested the dynamic modulus of MRE under a cyclic triangular magnetic field in the range of 0–1,100 mT. The strain amplitude of 0.1%, pre-compression force of 5 N and test frequency of 10 Hz were selected for this test. Measurements were carried out in several consecutive stages. The dynamic mechanical properties were initially measured under the magnetic field increased from 0 to 1,100 mT. After reaching the maximum value, the magnetic field was linearly decreased from 1,100 to 0 mT, and the number of cycle also was 5 for each test.

Figure 4 shows the dynamic modulus as a function of the triangular magnetic field. The color change of curves indicates the direction of the cyclic test process. It can be seen that the dynamic modulus of all samples increases with the increasing magnetic field strength and decreases with the decreasing magnetic field strength. An apparent magneto-induced mechanical hysteresis has also been observed in these curves. As can be seen the descending curves are above the ascending curves, the similar phenomenon in MRE and electrorheological elastomer (ERE) has been reported by Sorokin and Niu, respectively (Niu et al., 2015; Sorokin et al., 2015). Mainly it is because the particles and the particle chains do not immediately revert to their original positions under the cyclical magnetic fields. Previously, Shen et al. (2004) proposed a mathematical model to estimate the magneto-induced storage modulus. According to their study, the magneto-induced modulus of MRE is determined by

$\begin{array}{ll}G=\frac{9\varphi C{m}^2\left(4-{\gamma }^2\right)}{8r_0^3{\pi }^2{a}^3{\mu }_0{\mu }_1{\left(1+{\gamma }^2\right)}^{7/2}}& (2)\end{array}$

where ϕ is the volume fraction of CIPs, a is the diameter of CIPs, μ₀ denotes the vacuum permeability, μ₁ is the permeability of MREs, r₀ is the initial spacing between two adjacent dipoles, γ is the shear strain, and m is the magnetic dipole moment. It can be deduced by Equation (2), due to the space between the magnetized particles r₀ in the descent stage is smaller than that in ascent stage, the larger magneto-induced modulus G causes a larger storage modulus in descent stage. It should be emphasized that the hysteresis of IPN samples tends to saturation after the initial cycle, and the storage modulus returns to its initial value on the elimination of magnetic field in later cycles. Due to the weaker restriction of PU matrix, the PU sample needs more cycles to achieve the saturation. In the engineering applications of MRE, due to the variable magnetic field and changing loads upon the MRE-based device, the material properties of MRE in the saturated region can make the device more effective.

FIGURE 4

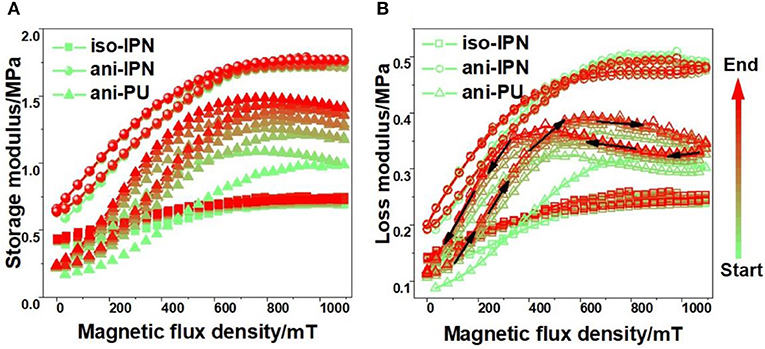
Figure 4. Dynamic modulus (A: storage modulus; B: loss modulus) as a function of the triangular magnetic field. The change of loss modulus is denoted by the direction of the black arrow in (B).

Unlike the curve shape of storage modulus, Figure 4B shows the loss modulus of descending curves is greater than that of ascending curves under the low magnetic field strength, but the contrary is under the high magnetic field strength. Since the loss modulus is based on the energy dissipation which is proportional to the relative movement of particles (Yang et al., 2012), this phenomenon can be explained by the state of particle motion. There is a critical magnetic field strength to keep the balance between magnetic interactions (between the magnetized particles) and elastic interactions (between the particles and matrix), and the critical magnetic field strength can be reflected by the intersection of loss modulus curves. Scheme 1 shows the advance and return movement of CIPs under the ascending and descending magnetic fields, and the cycle has been divided into ascent stage (stage A and stage B) and descent stage (stage C and stage D). Among them, the advance movement was caused by magnetic interactions at the ascent stage, and return movement was caused by elastic interactions at the descent stage. The energy dissipation of MRE mainly depended on the friction between the CIP and matrix (Li and Gong, 2008), and it could be expressed with the following equation (Yu et al., 2013):

$\begin{array}{ll}\text{ED}\propto F_{r}S& (3)\end{array}$

where F_r is the interfacial friction force between the CIP and the matrix; this force is decided with the magnetic flux density and elastic interactions. In addition, S represents the displacement of interfacial slipping between the CIP and the matrix. As can be seen from the Scheme 1, with the increase of distance between the particles and its initial positions, the particles become closer and the polymer molecular chain stretched longer. As a consequence, the F_r of MRE in stage B and stage C is greater than that of in stage A and stage D. When the magnetic field strength is lower than this critical value, the elastic interaction is dominated. The relative movement of CIPs has been restricted in the ascent stage (stage A) and accelerated in the descent stage (stage D). Correspondingly, when the magnetic field strength is higher than this critical value, the magnetic interaction is dominated. The relative movement of particles has been accelerated in the ascent stage (stage B) and restricted in the descent stage (stage C). Therefore, the displacement of interfacial slipping S in stage D is greater than that of in stage A, and S in stage B is greater than that of stage C. It leads to the descending curves of loss modulus is greater than that of ascending curves under the low magnetic field strength, and the contrary is under the high magnetic field strength. In addition, as can be seen from Figure 6B, the critical magnetic field of ani-PU is smaller than that of ani-IPN, which can be attributed to the weaker elastic interactions in the PU matrix.

SCHEME 1

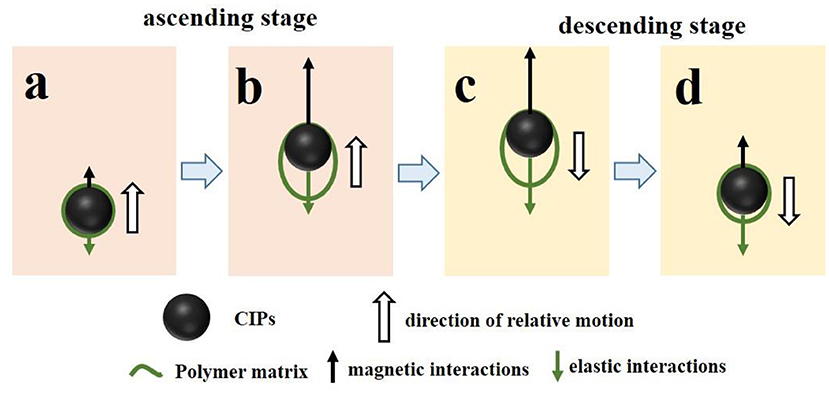
Scheme 1. The schematic of the movement of CIP under the ascending and descending magnetic field. (a) ascending stage with a smaller relative displacement; (b) ascending stage with a larger relative displacement; (c) descending stage with a larger relative displacement; (d) descending stage with a smaller relative displacement.

Correspondingly, the parameter λ calculated from Equation (1) has been plotted to study the stability of the magneto-induced mechanical hysteresis. Figure 5 shows the dependence of the parameter λ on the cycle number under the triangular magnetic field. Similarly, the parameter λ of PU sample is also significantly larger than that of IPN sample. This phenomenon occurred mainly because the displacement of interfacial slipping between the CIP and the matrix in PU sample is greater than that in IPN sample. The interpenetration and entanglement of molecular chains in IPN matrix would improve the elastic interactions, which can accelerate the particles revert to their original positions. In addition, the parameter λ of the iso-IPN is greater than that of the ani-IPN. It is mainly because the particles have formed the chain structure in the anisotropic sample, while the particles are distributed randomly in the isotropic sample, as shown in Figure 5. As the particles tend to form a columnar paralleled to the magnetic field, the movement of the particle in the isotropic sample is greater than that in the anisotropic sample, which causes a greater variation of the parameter λ.

FIGURE 5

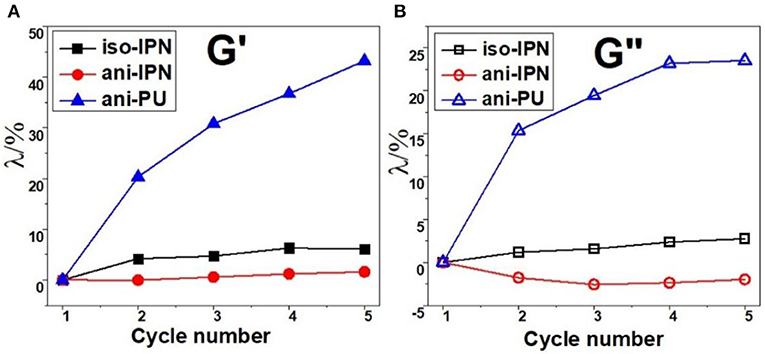
Figure 5. Dependence of the parameter λ (A: storage modulus; B: loss modulus) on cycle number for the samples under the triangular magnetic field.

Amplitude Cycling Tests

Decreasing in storage modulus G′ with the increasing strain amplitude, termed as Payne effect (Payne, 1962, 1967), has been recognized in polymer science and engineering (Meera et al., 2009; Papon et al., 2012; Ponnamma et al., 2013; Gan et al., 2016). The Payne effect of MRE has been studied by many researches, but the mechanical hysteresis caused by the shear strain has been rarely studied (Sorokin et al., 2014, 2015). In order to study the mechanical hysteresis of MRE under the ascending and descending strain, we tested the Payne effect of MRE under the cyclical amplitude in the absence and presence of magnetic field. The strain amplitude ranges of 0.01–20%, pre-compression forces of 10 N and test frequency of 5 Hz were selected for this test. Measurements were also carried out in several consecutive stages. The dynamic mechanical properties were initially measured under the changing strain that increased from 0.01 to 20%. After reaching the maximum value, the amplitude of strain was decreased from 20 to 0.01%. Five consecutive cycles were held for each sample in the absence and presence of magnetic field.

Figure 6 shows that the dynamic modulus as the functions of strain amplitude for iso-IPN, ani-IPN, and ani-PU samples is measured in the absence and presence of magnetic field, respectively. It can be seen that all samples demonstrate the Payne effect: the storage modulus decreases with the increasing strain (Payne, 1962, 1967). The loss modulus increased with the increasing strain initially, and then decreased with the increasing strain when it reaches its maximum. An apparent hysteresis has been observed in all curves, and the MRE samples show a strain hardening effect. The hysteresis is more obvious in the presence of magnetic field than in the absence of magnetic field, and the hysteresis of PU sample also greater than that of IPN sample. It can be seen that the modulus increased with the increasing test cycle, and the modulus tends to saturation after the several cycles. A significant change can be observed within the first cycle while only minor changes in the following cycles, which also has been reported by Sorokin et al. (2014, 2015). In particular, under the magnetic field, the Payne effect becomes much more pronounced, particularly for the anisotropic MRE samples. The quantitative comparison of Payne effect among these samples is discussed later using a phenomenological model.

FIGURE 6

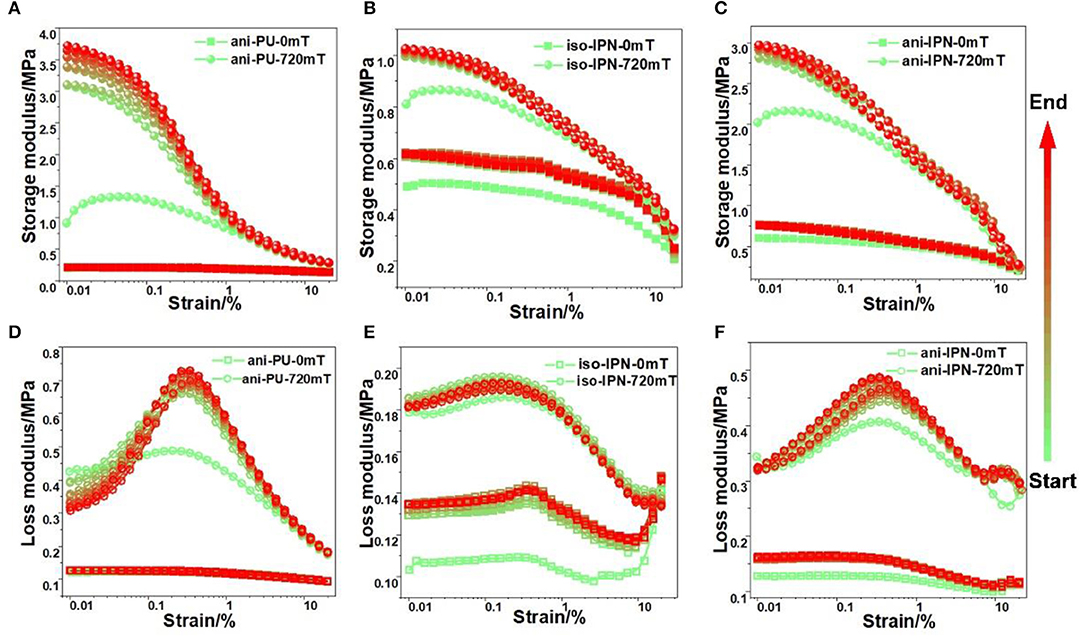
Figure 6. The influence of the shear strain on the dynamic viscoelastic properties of MRE samples. Dependence of storage modulus of ani-PU sample (A), ani-IPN sample (B), and iso-IPN sample (C) on the shear strain in the absence and presence of magnetic field. Dependence of loss modulus of ani-PU sample (D), ani-IPN sample (E), and iso-IPN sample (F) on the shear strain in the absence and presence of magnetic field. The color scale indicates the progress of the cycle tests.

There have been many explanations and phenomenological models are well reported for Payne effect, and they are mainly based on the concepts of change in the microstructure of the composites. Kraus model is based on the concepts of change in particle–particle interactions, and the strain hardening effect of MRE under the cycling strain tests is mainly caused by the particle reagglomeration. Therefore, for the better understanding of the hysteresis of Payne effect of MRE, Kraus model is adopted to determine the influence mechanism of Payne effect. The Kraus model is the first phenomenological model to represent and explicate the Payne effect, which provides the relations for the dynamic modulus and strain amplitude in Equation (3) (Kraus, 1984),

$\begin{array}{ll}\frac{{\text{G}}_{\mathrm{ \gamma }}^{\prime }-{\text{G}}_{\mathrm{ \infty }}^{\prime }}{{\text{G}}_{\mathrm{ 0}}^{\prime }-{\text{G}}_{\mathrm{ \infty }}^{\prime }}=\frac{1}{1+{\left(\gamma /{\gamma }_c\right)}^{2\text{m}}}& (4)\end{array}$

where ${{\text{G}}^{\text{′}}}_{\infty }$ is the value of storage modulus at very large strain; ${{\text{G}}^{\text{′}}}_0$ is equal to the value of storage modulus at very small strain; where γ_c and m are the fitting parameters, and γ_c is the critical strain when ${{\text{G}}^{\text{′}}}_{\gamma }$ reaches the half value of ${{\text{G}}^{\text{′}}}_0-{{\text{G}}^{\text{′}}}_{\infty }$; m is the shear strain sensitivity of the mechanism of particle-particle contact breakage and defines the shape of the ${{\text{G}}^{\text{′}}}_{\gamma }$ curve (Qu et al., 2014). To obtain a better understanding of the influence of matrix, particle distribution and magnetic field on the Payne effect, we fitted the ${{\text{G}}^{\text{′}}}_{\gamma }$ curves with the increasing strain amplitude. The obtained values of ${{\text{G}}^{\text{′}}}_0$, ${{\text{G}}^{\text{′}}}_{\infty }$, γ_c, and m for all samples are shown in Tables 2–5, respectively. It can be seen that the Kruas model can be used to describe the Payne effect of MRE samples felicitously, as shown in Figure 7. For clarity, only the first curves of the samples are presented. The dependences of the fitting parameters on the cycle number are shown in Figures 8, 9. It can be seen from the Figure 8 that both ${{\text{G}}^{\text{′}}}_0$ and ${{\text{G}}^{\text{′}}}_{\infty }$slightly increase with the cycle number in the absence of magnetic field. It attributes to that the matrix becomes stiffer for the subsequent measurement (Sorokin et al., 2015). On the other hand, the ${{\text{G}}^{\text{′}}}_0$ and ${{\text{G}}^{\text{′}}}_{\infty }$ increase evidently after the first cycle and then tend to be saturated. The application of magnetic field and increasing strain amplitude helps magnetic particles to rearrange. The particles become closer to form stronger chains structures under the magnetic field. The enhancement of MR effect is caused by the increase of ${{\text{G}}^{\text{′}}}_0$ and ${{\text{G}}^{\text{′}}}_{\infty }$ in the subsequent cycles. In addition, the ${{\text{G}}^{\text{′}}}_0$ and ${{\text{G}}^{\text{′}}}_{\infty }$ of the sample in the presence of magnetic field are both larger than that in the absence of magnetic field. The increscent modulus is also caused by the magneto-induced modulus.

TABLE 2

Table 2. ${{\text{G}}^{\text{′}}}_0$ (MPa) of the samples in the different cycles.

TABLE 3

Table 3. ${G^{\prime }}_{\infty }$ (MPa) of the samples in the different cycles.

TABLE 4

Table 4. Fitting parameter γ_c (%) of the samples in the different cycles.

TABLE 5

Table 5. Fitting parameter m (a.u) of the samples in the different cycles.

FIGURE 7

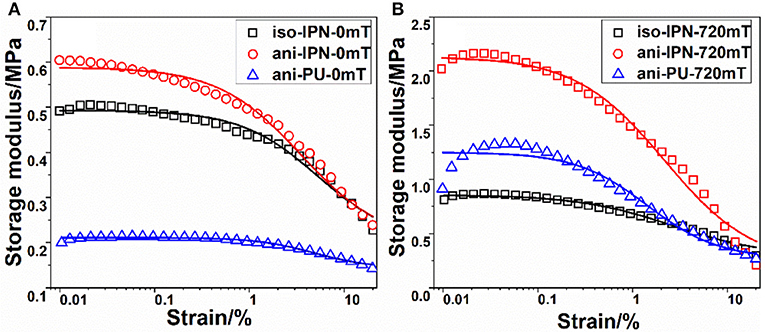
Figure 7. Fitting of the first ${{\text{G}}^{\text{′}}}_{\gamma }$ curve with the increasing strain amplitude obtained in the absence (A) and presence (B) of magnetic field. (Symbols are experimental date, and solid lines are the fitting curves).

FIGURE 8

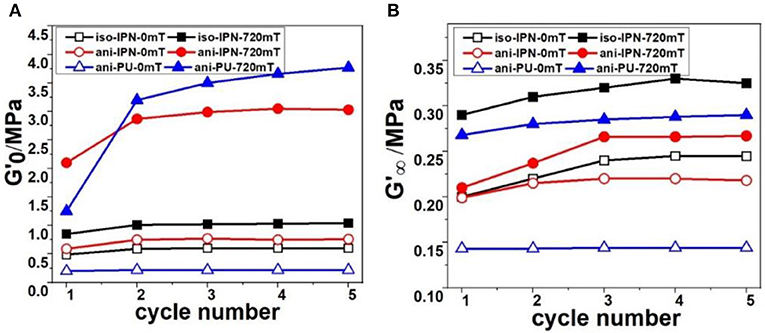
Figure 8. Cycle number dependence of the ${{\text{G}}^{\text{′}}}_0$ (A) and ${{\text{G}}^{\text{′}}}_{\infty }$ (B). The hollow symbol and solid symbol indicated the tests under 0 and 720 mT, respectively.

FIGURE 9

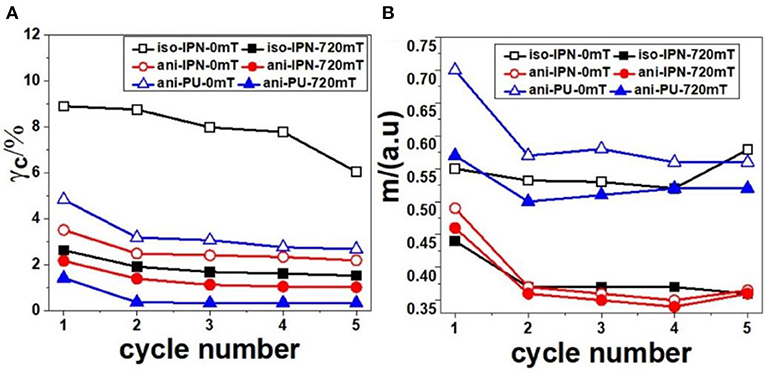
Figure 9. Cycle number dependence of the critical strain γ_c (A) and fitting parameter m (B). The hollow symbol and solid symbol indicated the tests under 0 and 720 mT, respectively.

Figure 9 shows the cycle number dependence of the critical strain γ_c and fitting parameter m. Similarly, the critical strain γ_c and fitting parameter m decrease after the first cycle and then tend to be saturated in the subsequent cycles.

The decrease of critical strain γ_c indicates that the particle networks can be destroyed easily after the first destruction. It also can be seen that the critical strain γ_c of samples in the absence of magnetic field is larger than that in the presence of magnetic field. The interaction force between the magnetized CIPs would enhance the strength of particle networks, which leads the decrease of γ_c. But the magneto-induced Payne effect caused by the breakdown of the magnetic particle network is more obvious. The decrease of γ_c caused by magneto-induced Payne effect is larger than the increase of γ_c caused by enhanced interaction force, thus the γ_c is smaller under the magnetic field. The fitting parameter m is related to the particle agglomerate structure (Heinrich and Kluppel, 2002). The decrease of m after the first cycle indicates the destruction of particle networks in high strain reduces the particle aggregates in the MRE. Besides, the m of the sample in the absence of magnetic field is larger than that in the presence of magnetic field. It's mainly because the particles tend to form a columnar paralleled to the direction of the magnetic field when imposes on the MRE. Some particles can overcome the restriction of matrix and begin to slip relatively to the elastomer matrix. Thus, the movement of particles leads to the increase in particle aggregates.

Conclusions

The dynamic mechanical hysteresis of MRE under the cyclic loading and periodic magnetic field is studied in this paper. The experimental results show that all the mechanical pressure, shear strain and periodic magnetic field would cause a hysteresis in the dynamic mechanical properties of MRE, and the hysteresis tends to be saturated after several cycles. The conclusions can be drawn as follows:

(1) The hysteresis in the dynamic mechanical properties of MRE is caused by the coupling effect of the cyclic mechanical loading and magnetic field. The saturation of the hysteresis indicates that there is a balance between destruction and reformation of the particle structures. In addition, the magnetic field can cause an obvious hardening effect of MRE under the mechanical pressure and high shear strain.

(2) The hysteresis of PU sample is greater than that of IPN sample, which indicates that the viscidity and elasticity of the matrix play important roles in the destruction and reformation of the particle structure. A stable molecular chain structure in the matrix would reduce the magnitude of the mechanical hysteresis and improve the stability of the hysteresis in the saturation stage.

(3) A significant increase of the storage modulus can be observed within the first cycle in each test, which means that the first dynamic oscillatory shear tests would destroy the unstable structure, making the matrix become stiffer.

(4) The periodic triangular magnetic field also caused the hysteresis in the dynamic modulus which can be attributed to the irreversible movement of the particles. The test result of loss modulus can be explained by the relative movement of CIPs. For the influence of the particle distribution, the hysteresis of the isotropic sample is greater than that of anisotropic sample in the presence of magnetic field, which can be attributed to the optimization of particle structure in the magnetic field.

This work turns out that the material properties of MRE should be characterized by the repeating tests rather than merely single test. More effective evaluation tests of MRE are of benefit to the potential applications. The hysteresis caused by mechanical loading and magnetic field is an intrinsic property of MRE and should be taken into account in future studies. In future work, we should not only explore the material preparation methods that reduce the hysteresis characteristics of MRE, but also carry out in-depth mechanism modeling research. The results achieved are important for fundamental understanding of material behavior of MRE, which would provide a guidance for the improvement of material preparation and the development of MRE devices.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

YZ, FF, and MY proposed and designed the research. YZ and SQ performed all experiments. The experimental data were analyzed by YZ, WH, and YC. All authors wrote the paper and participated in discussions.

Funding

This research was supported by the Science Challenge Project (No. TZ2016006-0504-01), High-end CNC Machine Tools and Basic Manufacturing Equipment Major National Science and Technology Project, China (2017ZX04022001), and National Key Research and Development Program of China (Grant No. 2017YFA0701200). Funding Support by Laboratory of Precision Manufacturing Technology, CAEP, China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

An, H. N., Picken, S. J., and Mendes, E. (2012). Direct observation of particle rearrangement during cyclic stress hardening of magnetorheological gels. Soft Matter 8, 11995–12001. doi: 10.1039/c2sm26587g

CrossRef Full Text | Google Scholar

An, J., and Kwon, D.-S. (2003). Modeling of a magnetorheological actuator including magnetic hysteresis. J. Intell. Mater. Syst. Struct. 14, 541–550. doi: 10.1177/104538903036506

CrossRef Full Text | Google Scholar

Aziz, S. A. A., Mazlan, S. A., Ismail, N. I. N., Ubaidillah, U., Choi, S. B., Khairi, M. H. A., et al. (2016). Effects of multiwall carbon nanotubes on viscoelastic properties of magnetorheological elastomers. Smart Mater. Struct. 25:077001. doi: 10.1088/0964-1726/25/7/077001

CrossRef Full Text | Google Scholar

Bica, I. (2012). The influence of the magnetic field on the elastic properties of anisotropic magnetorheological elastomers. J. Ind. Eng. Chem. 18, 1666–1669. doi: 10.1016/j.jiec.2012.03.006

CrossRef Full Text | Google Scholar

Chai, A. B., Verron, E., Andriyana, A., and Johan, M. R. (2013). Mullins effect in swollen rubber: experimental investigation and constitutive modelling. Polym. Test 32, 748–759. doi: 10.1016/j.polymertesting.2013.03.006

CrossRef Full Text | Google Scholar

Chen, P., Bai, X. X., Qian, L. J., and Choi, S. B. (2018). An approach for hysteresis modeling based on shape function and memory mechanism. IEEE/ASME Trans. Mechatronics 23, 1270–1278. doi: 10.1109/TMECH.2018.2833459

CrossRef Full Text | Google Scholar

Diani, J., Fayolle, B., and Gilormini, P. (2009). A review on the Mullins effect. Eur. Polym. J. 45, 601–612. doi: 10.1016/j.eurpolymj.2008.11.017

CrossRef Full Text | Google Scholar

Dominguez, A., Sedaghati, R., and Stiharu, I. (2004). Modelling the hysteresis phenomenon of magnetorheological dampers. Smart Mater. Struct. 13:1351. doi: 10.1088/0964-1726/13/6/008

CrossRef Full Text | Google Scholar

Dorfmann, A., and Ogden, R. W. (2005). A constitutive model for the Mullins effect with permanent set in a particle-reinforced rubber. Int. J. Solids Struct. 42, 4909–4910. doi: 10.1016/j.ijsolstr.2004.12.001

CrossRef Full Text | Google Scholar

Drozdov, A. D. (2009). Mullins' effect in semicrystalline polymers. Int. J. Solids Struct. 46, 3336–3345. doi: 10.1016/j.ijsolstr.2009.05.001

CrossRef Full Text | Google Scholar

Feng, J. B., Xuan, S. H., Liu, T. X., Ge, L., Yan, L. X., Zhou, H., et al. (2015). The prestress-dependent mechanical response of magnetorheological elastomers. Smart Mater. Struct. 24:085032. doi: 10.1088/0964-1726/24/8/085032

CrossRef Full Text | Google Scholar

Fu, J., Li, P. D., Wang, Y., Liao, G. Y., and Yu, M. (2016). Model-free fuzzy control of a magnetorheological elastomer vibration isolation system: analysis and experimental evaluation. Smart Mater. Struct. 25:035030. doi: 10.1088/0964-1726/25/3/035030

CrossRef Full Text | Google Scholar

Gan, S. C., Wu, Z. L., Xu, H. L., Song, Y. H., and Zheng, Q. (2016). Viscoelastic behaviors of carbon black gel extracted from highly filled natural rubber compounds: insights into the Payne effect. Macromolecules 49, 1454–1463. doi: 10.1021/acs.macromol.5b02701

CrossRef Full Text | Google Scholar

Ge, L., Xuan, S. H., Liao, G. J., Yin, T. T., and Gong, X. L. (2015). Stretchable polyurethane sponge reinforced magnetorheological material with enhanced mechanical properties. Smart Mater. Struct. 24:037001. doi: 10.1088/0964-1726/24/3/037001

CrossRef Full Text | Google Scholar

Gong, X. L., Zhang, X. Z., and Zhang, P. Q. (2005). Fabrication and characterization of isotropic magnetorheological elastomers. Polym. Test 24, 669–676. doi: 10.1016/j.polymertesting.2005.03.015

CrossRef Full Text | Google Scholar

Gundermann, T., and Odenbach, S. (2014). Investigation of the motion of particles in magnetorheological elastomers by X-mu CT. Smart Mater. Struct. 23:105013. doi: 10.1088/0964-1726/23/10/105013

CrossRef Full Text | Google Scholar

Hanson, D. E., Hawley, M., Houlton, R., Chitanvis, K., Rae, P., Orler, E. B., et al. (2005). Stress softening experiments in silica-filled polydimethylsiloxane provide insight into a mechanism for the Mullins effect. Polymer 46, 10989–10995. doi: 10.1016/j.polymer.2005.09.039

CrossRef Full Text | Google Scholar

Heinrich, G., and Kluppel, M. (2002). Recent advances in the theory of filler networking in elastomers. Filled Elastomers Drug Deliv. Syst. 160, 1–44. doi: 10.1007/3-540-45362-8_1

CrossRef Full Text | Google Scholar

Hoang, N., Zhang, N., Li, W. H., and Du, H. (2013). Development of a torsional dynamic absorber using a magnetorheological elastomer for vibration reduction of a powertrain test rig. J. Intell. Mater. Syst. Struct. 24, 2036–2044. doi: 10.1177/1045389X13489361

CrossRef Full Text | Google Scholar

Jung, H. S., Kwon, S. H., Choi, H. J., Jung, J. H., and Kim, Y. G. (2016). Magnetic carbonyl iron/natural rubber composite elastomer and its magnetorheology. Compos. Struct. 136, 106–112. doi: 10.1016/j.compstruct.2015.10.008

CrossRef Full Text | Google Scholar

Kashima, S., Miyasaka, F., and Hirata, K. (2012). Novel soft actuator using magnetorheological elastomer. IEEE Trans. Magn. 48, 1649–1652. doi: 10.1109/TMAG.2011.2173669

CrossRef Full Text | Google Scholar

Kramarenko, E. Y., Chertovich, A. V., Stepanov, G. V., Semisalova, A. S., Makarova, L. A., Perov, N. S., et al. (2015). Magnetic and viscoelastic response of elastomers with hard magnetic filler. Smart Mater. Struct. 24:035002. doi: 10.1088/0964-1726/24/3/035002

CrossRef Full Text | Google Scholar

Kraus, G. (1984). Mechanical losses in carbon-black-filled rubbers. Appl. Polym. Symp. 39, 75–92.

Google Scholar

Li, J. F., and Gong, X. L. (2008). Dynamic damping property of magnetorheological elastomer. J. Cent. South Univ. Technol. 15, 261–265. doi: 10.1007/s11771-008-0359-2

CrossRef Full Text | Google Scholar

Li, R., and Sun, L. Z. (2011). Dynamic mechanical behavior of magnetorheological nanocomposites filled with carbon nanotubes. Appl. Phys. Lett. 99:131912. doi: 10.1063/1.3645627

CrossRef Full Text | Google Scholar

Li, W. H., and Nakano, M. (2013). Fabrication and characterization of PDMS based magnetorheological elastomers. Smart Mater. Struct. 22:055035. doi: 10.1088/0964-1726/22/5/055035

CrossRef Full Text | Google Scholar

Machado, G., Chagnon, G., and Favier, D. (2012). Induced anisotropy by the Mullins effect in filled silicone rubber. Mech. Mater. 50, 70–80. doi: 10.1016/j.mechmat.2012.03.006

CrossRef Full Text | Google Scholar

Meera, A. P., Said, S., Grohens, Y., and Thomas, S. (2009). Nonlinear viscoelastic behavior of silica-filled natural rubber nanocomposites. J. Phys. Chem. C 113, 17997–18002. doi: 10.1021/jp9020118

CrossRef Full Text | Google Scholar

Merabia, S., Sotta, P., and Long, D. R. (2008). A microscopic model for the reinforcement and the nonlinear behavior of filled elastomers and thermoplastic elastomers (Payne and Mullins effects). Macromolecules 41, 8252–8266. doi: 10.1021/ma8014728

CrossRef Full Text | Google Scholar

Niu, C. G., Dong, X. F., and Qi, M. (2015). Enhanced electrorheological properties of elastomers containing TiO₂/urea core-shell particles. ACS Appl. Mater. Interfaces 7, 24855–24863. doi: 10.1021/acsami.5b08127

CrossRef Full Text | Google Scholar

Ogden, R. W., and Roxburgh, D. G. (1999). A pseudo-elastic model for the Mullins effect in filled rubber. Proc. R. Soc. A Math. Phys. Eng. Sci. 455, 2861–2877. doi: 10.1098/rspa.1999.0431

CrossRef Full Text | Google Scholar

Papon, A., Merabia, S., Guy, L., Lequeux, F., Montes, H., Sotta, P., et al. (2012). Unique nonlinear behavior of nano-filled elastomers: from the onset of strain softening to large amplitude shear deformations. Macromolecules 45, 2891–2904. doi: 10.1021/ma202278e

CrossRef Full Text | Google Scholar

Payne, A. R. (1962). The dynamic properties of carbon black-loaded natural rubber vulcanizates. Part I. J. Appl. Polym. Sci. 6, 57–64. doi: 10.1002/app.1962.070061906

CrossRef Full Text | Google Scholar

Payne, A. R. (1967). Dynamic properties of PBNA-natural rubber vulcanizates. J. Appl. Polym. Sci 11, 383–388. doi: 10.1002/app.1967.070110306

CrossRef Full Text | Google Scholar

Ponnamma, D., Sadasivuni, K. K., Strankowski, M., Moldenaers, P., Thomas, S., and Grohens, Y. (2013). Interrelated shape memory and Payne effect in polyurethane/graphene oxide nanocomposites. RSC Adv. 3, 16068–16079. doi: 10.1039/c3ra41395k

CrossRef Full Text | Google Scholar

Qi, H. J., and Boyce, M. C. (2005). Stress-strain behavior of thermoplastic polyurethanes. Mech. Mater. 37, 817–839. doi: 10.1016/j.mechmat.2004.08.001

CrossRef Full Text | Google Scholar

Qi, S., Guo, H. Y., Chen, J., Fu, J., Hu, C. G., Yu, M., et al. (2018a). Magnetorheological elastomers enabled high-sensitive self-powered tribo-sensor for magnetic field detection. Nanoscale 10, 4745–4752. doi: 10.1039/C7NR09129J

PubMed Abstract | CrossRef Full Text | Google Scholar

Qi, S., Yu, M., Fu, J., Zhu, M., Xie, Y. P., and Li, W. (2018b). An EPDM/MVQ polymer blend based magnetorheological elastomer with good thermostability and mechanical performance. Soft Matter. 14, 8521–8528. doi: 10.1039/C8SM01712C

PubMed Abstract | CrossRef Full Text | Google Scholar

Qiao, X. Y., Lu, X. S., Li, W. H., Chen, J., Gong, X. L., Yang, T., et al. (2012). Microstructure and magnetorheological properties of the thermoplastic magnetorheological elastomer composites containing modified carbonyl iron particles and poly(styrene-b-ethylene-ethylenepropylene-b-styrene) matrix. Smart Mater. Struct. 21:115028. doi: 10.1088/0964-1726/21/11/115028

CrossRef Full Text | Google Scholar

Qu, L. L., Wang, L. J., Xie, X. M., Yu, G. Z., and Bu, S. H. (2014). Contribution of silica-rubber interactions on the viscoelastic behaviors of modified solution polymerized styrene butadiene rubbers (M-S-SBRs) filled with silica. RSC Adv. 4, 64354–64363. doi: 10.1039/C4RA09492A

CrossRef Full Text | Google Scholar

Shen, Y., Golnaraghi, M. F., and Heppler, G. R. (2004). Experimental research and modeling of magnetorheological elastomers. J. Intell. Mater. Syst. Struct. 15, 27–35. doi: 10.1177/1045389X04039264

CrossRef Full Text | Google Scholar

Sorokin, V. V., Ecker, E., Stepanov, G. V., Shamonin, M., Monkman, G. J., Kramarenko, E. Y., et al. (2014). Experimental study of the magnetic field enhanced Payne effect in magnetorheological elastomers. Soft Matter. 10, 8765–8776. doi: 10.1039/C4SM01738B

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorokin, V. V., Stepanov, G. V., Shamonin, M., Monkman, G. J., Khokhlov, A. R., and Kramarenko, E. Y. (2015). Hysteresis of the viscoelastic properties and the normal force in magnetically and mechanically soft magnetoactive elastomers: effects of filler composition. strain amplitude and magnetic field. Polymer 76, 191–202. doi: 10.1016/j.polymer.2015.08.040

CrossRef Full Text | Google Scholar

Stepanov, G. V., Abramchuk, S. S., Grishin, D. A., Nikitin, L. V., Kramarenko, E. Y., and Khokhlov, A. R. (2007). Effect of a homogeneous magnetic field on the viscoelastic behavior of magnetic elastomers. Polymer 48, 488–495. doi: 10.1016/j.polymer.2006.11.044

CrossRef Full Text | Google Scholar

Stepanov, G. V., Chertovich, A. V., and Kramarenko, E. Y. (2012). Magnetorheological and deformation properties of magnetically controlled elastomers with hard magnetic filler. J. Magn. Magn. Mater. 324, 3448–3451. doi: 10.1016/j.jmmm.2012.02.062

CrossRef Full Text | Google Scholar

Wang, Y., Gong, X. L., Yang, J., and Xuan, S. H. (2014). Improving the dynamic properties of MRE under cyclic loading by incorporating silicon carbide nanoparticles. Ind. Eng. Chem. Res. 53, 3065–3072. doi: 10.1021/ie402395e

CrossRef Full Text | Google Scholar

Wang, Y., Xuan, S. H., Dong, B., Xu, F., and Gong, X. L. (2016). Stimuli dependent impedance of conductive magnetorheological elastomers. Smart Mater. Struct. 25:025003. doi: 10.1088/0964-1726/25/2/025003

CrossRef Full Text | Google Scholar

Webber, R. E., Creton, C., Brown, H. R., and Gong, J. P. (2007). Large strain hysteresis and mullins effect of tough double-network hydrogels. Macromolecules 40, 2919–2927. doi: 10.1021/ma062924y

CrossRef Full Text | Google Scholar

Wei, B., Gong, X. L., and Jiang, W. Q. (2010). Influence of polyurethane properties on mechanical performances of magnetorheological elastomers. J. Appl. Polym. Sci. 116, 771–778. doi: 10.1002/app.31474

CrossRef Full Text | Google Scholar

Wu, J. K., Gong, X. L., Fan, Y. C., and Xia, H. S. (2010). Anisotropic polyurethane magnetorheological elastomer prepared through in situ polycondensation under a magnetic field. Smart Mater. Struct. 19:105007. doi: 10.1088/0964-1726/19/10/105007

CrossRef Full Text | Google Scholar

Wu, J. K., Gong, X. L., Fan, Y. C., and Xia, H. S. (2012). Improving the magnetorheological properties of polyurethane magnetorheological elastomer through plasticization. J. Appl. Polym. Sci. 123, 2476–2484. doi: 10.1002/app.34808

CrossRef Full Text | Google Scholar

Xian-Xu, B., Fei-Long, C., and Peng, C. (2019). Resistor-capacitor (RC) operator-based hysteresis model for magnetorheological (MR) dampers. Mech. Syst. Signal. Process. 117C, 157–169. doi: 10.1016/j.ymssp.2018.07.050

CrossRef Full Text | Google Scholar

Xing, Z. W., Yu, M., Fu, J., Wang, Y., and Zhao, L. J. (2015). A laminated magnetorheological elastomer bearing prototype for seismic mitigation of bridge superstructures. J. Intell. Mater. Syst. Struct. 26, 1818–1825. doi: 10.1177/1045389X15577654

CrossRef Full Text | Google Scholar

Xing, Z. W., Yu, M., Sun, S. S., Fu, J., and Li, W. H. (2016). A hybrid magnetorheological elastomer-fluid (MRE-F) isolation mount: development and experimental validation. Smart Mater. Struct. 25:015026. doi: 10.1088/0964-1726/25/1/015026

CrossRef Full Text | Google Scholar

Xu, Y. G., Gong, X. L., Xuan, S. H., Zhang, W., and Fan, Y. C. (2011). A high-performance magnetorheological material: preparation, characterization and magnetic-mechanic coupling properties. Soft Matter 7, 5246–5254. doi: 10.1039/c1sm05301a

CrossRef Full Text | Google Scholar

Xu, Y. G., Liao, G. J., Zhang, C. Y., Wan, Q., and Liu, T. X. (2016). The transition from stress softening to stress hardening under cyclic loading induced by magnetic field for magneto-sensitive polymer gels. Appl. Phys. Lett. 108:161902. doi: 10.1063/1.4947131

CrossRef Full Text | Google Scholar

Yang, J., Gong, X. L., Deng, H. X., Qin, L. J., and Xuan, S. H. (2012). Investigation on the mechanism of damping behavior of magnetorheological elastomers. Smart Mater. Struct. 21:125015. doi: 10.1088/0964-1726/21/12/125015

CrossRef Full Text | Google Scholar

Yang, J., Gong, X. L., Zong, L. H., Peng, C., and Xuan, S. H. (2013). Silicon carbide-strengthened magnetorheological elastomer: preparation and mechanical property. Polym. Eng. Sci. 53, 2615–2623. doi: 10.1002/pen.23529

CrossRef Full Text | Google Scholar

Yang, P. G., Yu, M., and Fu, J. (2016). Ni-coated multi-walled carbon nanotubes enhanced the magnetorheological performance of magnetorheological gel. J. Nanopart. Res. 18:61. doi: 10.1007/s11051-016-3370-9

CrossRef Full Text | Google Scholar

Yu, M., Fu, J., Ju, B. X., Zheng, X., and Choi, S. B. (2013). Influence of x-ray radiation on the properties of magnetorheological elastomers. Smart Mater. Struct. 22:125010. doi: 10.1088/0964-1726/22/12/125010

CrossRef Full Text | Google Scholar

Yu, M., Qi, S., Fu, J., Yang, P. A., and Zhu, M. (2015a). Preparation and characterization of a novel magnetorheological elastomer based on polyurethane/epoxy resin IPNs matrix. Smart Mater. Struct. 24:045009. doi: 10.1088/0964-1726/24/4/045009

CrossRef Full Text | Google Scholar

Yu, M., Qi, S., Fu, J., and Zhu, M. (2015c). A high-damping magnetorheological elastomer with bi-directional magnetic-control modulus for potential application in seismology. Appl. Phys. Lett. 107:111901. doi: 10.1063/1.4931127

CrossRef Full Text | Google Scholar

Yu, M., Yang, P., Fu, J., Liu, S., and Qi, S. (2016). Study on the characteristics of magneto-sensitive electromagnetic wave-absorbing properties of magnetorheological elastomers. Smart Mater. Struct. 25:085046. doi: 10.1088/0964-1726/25/8/085046

CrossRef Full Text | Google Scholar

Yu, M., Zhu, M., Fu, J., Yang, P. A., and Qi, S. (2015b). A dimorphic magnetorheological elastomer incorporated with Fe nano-flakes modified carbonyl iron particles: preparation and characterization. Smart Mater. Struct. 24:115021. doi: 10.1088/0964-1726/24/11/115021

CrossRef Full Text | Google Scholar

Yu, Y., Li, Y., Li, J., and Gu, X. (2016). A hysteresis model for dynamic behaviour of magnetorheological elastomer base isolator. Smart Mater. Struct. 25:055029. doi: 10.1088/0964-1726/25/5/055029

CrossRef Full Text | Google Scholar