Nucleation and Grain Boundary Evolution in Dynamic Recrystallization of 316LN Steel During Hot Deformation

In this work, dynamic recrystallization (DRX) behavior of 316LN austenitic stainless steel was studied by hot compression experiments at temperature range of 900–1200°C and strain rate range of 0. 005–0.5 s⁻¹. The Arrhenius hyperbolic sine function was given to fit well with the hot deformation flow behavior of 316LN steel and the average activation energy (Q) was obtained. The variation of DRX fraction and average grain size was studied and modeled. Microstructural evolution of 316LN steel during hot deformation in condition of 1,100°C and 0.05 s⁻¹ was studied by EBSD analysis. It was found that twining plays a significant role in nucleation and growth of DRX during hot deformation. The nucleation of DRX in 316LN steel was characterized by bulging of serrated grain boundaries. Twining took place near the serrated grain boundary in large amount, accelerating the separation of bulging from deformed parent grains to form DRX nucleus. At the steady state strain, uniformly refined DRX grains almost took charge of the microstructure of 316LN steel.

Introduction

316LN austenitic stainless steel has been chosen to manufacture heavy key structural components in nuclear power plant owing to its excellent corrosion resistance, high temperature mechanical properties, and adequate weldability (Jones, 1996; Zhang et al., 2014). In recent years, the research of 316LN steel mainly focuses on two aspects: performance and hot deformation (Anita et al., 2006; Kim et al., 2009; Schwartz et al., 2010; Kim, 2012; Mathew et al., 2012; Samantaraya et al., 2012; Duan and Liu, 2013; Zhang et al., 2013; Chen et al., 2014; Samantaray et al., 2014; Sun et al., 2016). In terms of performance, researchers mainly studied creep and fatigue behavior (Schwartz et al., 2010; Mathew et al., 2012), stress corrosion crack (Anita et al., 2006), mechanical properties (Kim, 2012) and welding characteristics (Kim et al., 2009). In terms of hot deformation, Duan and Liu (2013) and Zhang et al. (2013) conducted researches on cracking issue of 316LN steel during hot deformation, and presented prediction models for cracking, respectively; Chen et al. (2014) predicted the microstructural evolution of 316LN steel using cellular automaton method; Hot processing map of 316LN steel was built by Sun et al. (2016) who discussed the hot workability of 316LN steel; Samantaraya et al. (2012); Samantaray et al. (2014) revealed the unbalance phenomenon between energy input and energy dissipation during hot deformation of 316LN steel.

As phase transition does not occur in 316LN steel and heat treatment does not contribute to grain refinement, dynamic recrystallization (DRX) is the most important grain refinement mechanism during hot deformation of austenitic stainless steel affecting the final microstructure and, hence, the mechanical properties. Grain refinement during primary deformation processing route is a challenge for manufacturing these heavy key structural components.

Electron backscattered diffraction (EBSD) technology can provide orientation data on microstructure of alloys. It cannot only distinguish different types of grain boundaries, but also provide statistical information of the material. Therefore, EBSD technology provides a powerful approach to study microstructural evolution during hot deformation. This paper mainly focused on study of DRX mechanism for 316LN austenitic stainless steel, in which grain boundary characteristics and the role of twinning were analyzed via EBSD. Meanwhile, the constitutive model and DRX kinetics model of 316LN steel during hot deformation were built.

It is known that a uniform and complete grain refinement of 316LN could be achieved in deformation condition of high temperature and low strain rate. However, for cracking nucleation and development concern, deformation condition of low temperature and high strain rate is preferred (Duan and Liu, 2013). In sum, the hot deformation condition for researching on microstructure evolution was chosen at medium high temperature and high strain rate −1100°C and 0.05 s⁻¹.

This research is helpful to understand the mechanism of grain refinement and grain boundary evolution in deformation condition of medium high temperature and high strain rate, which provides supportive information on microstructural evolution of 316LN steel to manufacture key structural components meeting high-quality requirements.

Materials and Methods

Chemical composition of 316LN austenitic stainless steel used in research is shown in Table 1. Cylindrical specimens with 10 mm in height and 8 mm in diameter were prepared for hot compression. The microstructure of original specimens after annealing has wrought equiaxed grains with annealing twins, as shown in Figure 1.

TABLE 1

Table 1. Chemical composition of 316LN austenitic stainless steel (wt%).

FIGURE 1

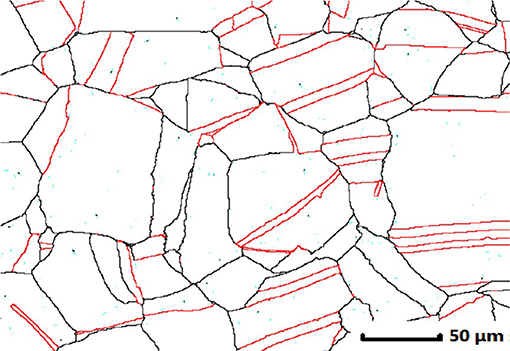
Figure 1. Microstructure of annealed specimen. The high angle and Σ-twin boundaries are shown as black and red lines, respectively.

Hot Compression

A Gleeble-1500D thermo-mechanical simulator was used for hot compression. The specimens were heated up to 1,200°C and hold for 5 min for homogenizing, then cooled down to the deformation temperature (900–1,200°C) and hold for 1 min for hot compression. Two groups of hot compression experiments were conducted. The test specimens of Group 1 were compressed to a constant strain of 0.69 at temperature range of 900–1,200°C and strain rate range of 0.005–0.5 s⁻¹. Moreover, the test specimens of Group 2 were compressed up to different true strains in the range of 0.11–0.92 at temperature of 1,100°C and strain rate of 0.05 s⁻¹. All the experiments were conducted in vacuum condition. After hot deformation, specimens were immediately quenched in water to freeze the microstructure.

Microstructural Studies

For Group 2, specimens were cut into thin slices with 1 mm in thickness. Whereafter, they were grinded and electropolished in 5% perchloric acid-ethanol solution before EBSD analysis.

A field emission gun scanning electron microscope (FEG-SEM) equipped with an EBSD detector provided by HKL Technology was used for EBSD test. Step sizes of 0.6 and 1 μm were used to scan cross-section of specimens. After scanning, the Channel 5 software was used to display and analyze the data. Afterwards, orientation imaging microscopy (OIM) maps were generated, which show high angle boundaries (misorientation > 15°) with black lines and low angle boundaries (misorientation < 15°) with white lines. One exception is that, in Figure 4, light blue lines illustrate low angle boundaries. Similarly, lines in different colors were used for high angle boundaries with a coincidence site lattice (CSL) relationship. In other words, only ordinary high angle boundaries were shown in black lines. Σ3 twin boundaries (misorientation of 60° about a (1,1,1) axis) was shown as red line. CSL boundaries, Σ5, Σ7, Σ9, and Σ11, were shown as green, blue, pink and yellow lines, respectively, as shown in Figure 10.

Results and Calculations

Flow Behavior and Kinetic Analysis

Figure 2 shows stress-strain curves of hot compression tests of 316LN steel in partial deformation conditions. During hot compression tests, several phenomena such as work hardening (WH), dynamic recovery (DRV) and dynamic recrystallization (DRX) occur simultaneously depending on thermo-mechanical parameters (temperature, strain rate and strain). High temperature and low strain rate facilitate nucleation of DRX. DRX restoration mechanism has been observed over a wide range of temperature and strain rate, the corresponding stress-strain curves exhibit flow softening with single peak before the flow stress reaches a steady state. The peak stress (σ_p) increases with increasing strain rate and decreasing temperature, which can be expressed by Arrhenius hyperbolic sine relationship shown in Equation (1). Zener-Holloman parameter shown in Equation (2) often is chosen to represent the comprehensive effect of temperature and strain rate on deformation behavior. Hence, the peak stress increases with increasing Zener-Holloman parameter (Z).

$\begin{array}{ll}\dot{\epsilon }=A{[\text{sinh}(\alpha {\sigma }_p)]}^n\text{ exp}(-\frac{Q}{RT})& (1)\end{array}$

$\begin{array}{ll}Z=\dot{\epsilon }\text{ exp}(\frac{Q}{RT})& (2)\end{array}$

where $\dot{\epsilon }$ is strain rate (s⁻¹), Q is activation energy (kJ mol⁻¹), T is absolute temperature (K), R is universal gas constant (8.31 J mol⁻¹K⁻¹), σ_p is peak stress (Pa), A, α and n are constants, and Z is Zener-Holloman parameter.

FIGURE 2

Figure 2. Stress-strain curves 316LN steel in several deformation conditions.

The activation energy for hot deformation can be calculated based on peak stress data at different temperatures and strain rates by taking logarithm on both sides of Equation (1). Therefore, the average Q for tested hot deformation conditions of 316LN steel was calculated as to be 494 kJ mol⁻¹, which is a little higher than the previous work of the same steel (433 kJ mol⁻¹) (Samantaray et al., 2014). The variation of Q for 316LN steel might be due to different element contents. But these values are much higher than the reported Q of 304 steel (400 kJ mol⁻¹) and lower than the reported Q of Nb-containing 316LN steel (536 kJ mol⁻¹) (Dehghan-Manshadi et al., 2008; Zhang et al., 2011).

Figure 3 shows that the hyperbolic sine function was found to fit well with the data in tested hot deformation conditions (correlation coefficient is 0.99). Some calculated values in Equation (1) are also presented in Figure 3.

FIGURE 3

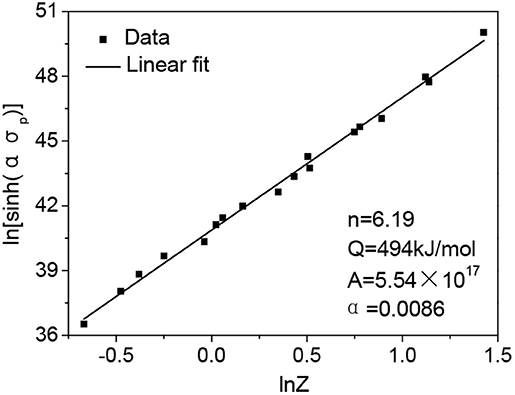
Figure 3. The relationship between σ_p and Z and the fitting curve with correlation coefficient of 0.99.

The true stress-strain curves obtained at different strains are shown in Figure 4. All curves show an accordant flow behavior, which is in a good agreement to represent the same deformation condition at 1,100°C and 0.05 s⁻¹. The complete flow curve exhibits typical DRX behavior. It shows a single peak stress followed by a gradually decrease of flow stress. Finally, the flow stress reaches to a steady state at high strain. Figure 4 also shows OIM microstructures at three characteristic strains during hot deformation. Before hot deformation, the microstructure of annealed 316LN sample contains equiaxed grains with annealing twins. During hot compression, due to work hardening, flow stress increases sharply. As strain increases, softening mechanism, such as dynamic recovery and recrystallization, arise to balance work hardening. As a result, slop of flow stress curve gradually decreases. At the strain of 0.11, the grain boundaries are serrated or corrugated, some bulges and new fine grains can also be observed. In the peak strain of 0.22, parent grains are deformed and elongated. Moreover, a high fraction of low angle grain boundaries can be observed inside the parent grains. Besides, dynamically recrystallized grains with twins are observed in a large number near grain boundaries of the parent grains. Hence, softening mechanism dominates over work hardening as the flow stress begins to decrease. Eventually, flow stress curve is flattened from steady state strain of 0.69, the elongated parent grains have been almost diminished and new recrystallized grains dominate.

FIGURE 4

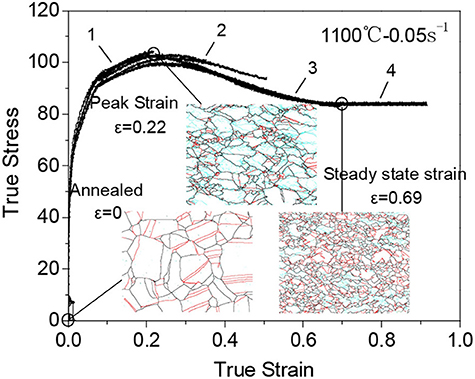
Figure 4. Typical strains and grain boundary evolution during DRX of 316LN steel. 1, Stress-strain curve to the strain of 0.22; 2, strain of 0.51; 3, strain of 0.69; 4, strain of 0.69. Small angle boundaries are shown as light blue lines.

The work hardening rate—true stress (θ-σ) curve was analyzed to find the critical stress, which revealed the initiation of dynamic recrystallization (DRX), as shown in Figure 5. The critical stress was obtained at inflection point of the curve (Poliak and Jonas, 1996). Peak stress (σ_p) is also found in θ-σ curve. The values of σ_c, σ_p, ε_c, and ε_p were determined as 99.4 MPa, 103.0 MPa, 0.11 and 0.22, respectively. Therefore, the normalized critical stress and strain can be expressed as σ_c/σ_p = 0.96 and ε_c/ε_p = 0.5, respectively. The value of normalized critical strain is within the range of 0.3 to 0.9 reported for steels (Poliak and Jonas, 1996, 2003; Mirzadeh and Najafizadeh, 2010).

FIGURE 5

Figure 5. Work hardening rate-true stress curve and method to find characteristic points.

Microstructural Evolution

Before hot deformation, the microstructure of annealed 316LN sample contains equiaxed grains with annealing twins in an average size of 57.3 μm, shown in Figure 1. Figure 6 shows the orientation imaging microscopy (OIM) band contrast maps and their misorientation distribution histograms in tested deformation condition (1,100°C and 0.05 s⁻¹) at different strains. In the annealed sample, most of the boundaries are in high angle types and many of them have Σ3 twin relationship. In contrast, the fraction of low angle boundaries is very small. However, a large fraction of boundaries in 0.22 true strain (ε_p) are sub-boundaries (Figure 6B), which is a result of dislocation generation and formation of cell walls during deformation and dynamic recovery (DRV) (McQueen, 2004; Mirzadeh and Najafizadeh, 2010). These changes are clearly displayed in histogram of Figure 6G. It is seen that the frequency of twins and other high angle boundaries decrease sharply. In the meantime, a very strong increase in low angle fraction is developed. Besides, many twin boundaries have lost their twin characteristics in deformed parent grains due to effects of deformation and grain rotation (Beladi et al., 2009). Conversely, as strain gradually increases (Figures 6C–F), the formation of new DRX grains starts to consume the deformed substructures which decrease the fraction of low angle boundaries and increase the fraction of high angle boundaries. At the same time, after the formation of DRX, a large fraction of newly formed boundaries has Σ3 twin relationship. This interesting discovery will be discussed in the following section.

FIGURE 6

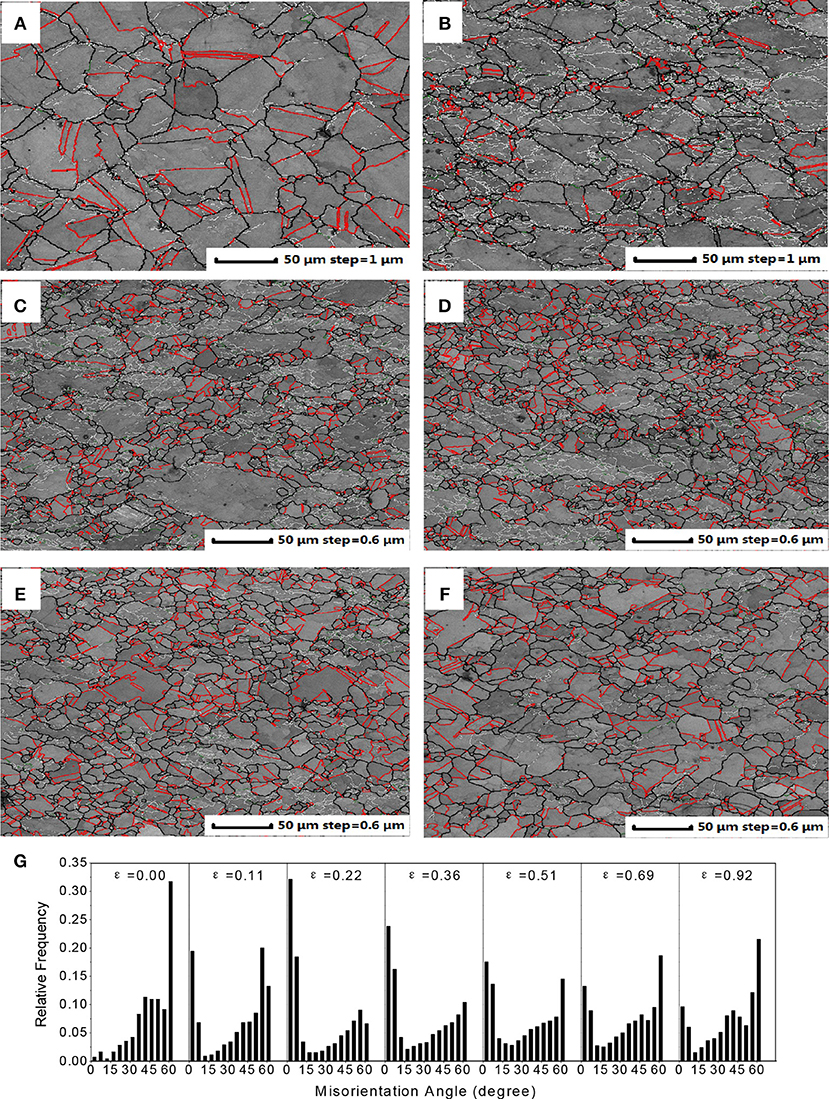
Figure 6. The OIM band contrast maps for deformed samples at strain of 0.11 (A), 0.22 (B), 0.36 (C), 0.51 (D), 0.69 (E), and 0.92 (F). Their misorientation distribution histograms containing grain boundaries with different orientations are also displayed (G). In OIM maps, the high and low angle boundaries are shown as black and white lines, respectively. Σ3 twin boundaries are shown as red lines.

DRX Kinetics

The typical method to measure the DRX fraction (X_d) is based on true tress-strain curve of hot compression test (Kim and Yoo, 2001). The equation is given in Equation (3):

$\begin{array}{ll}{X}_d=\frac{{\sigma }^{de}-{\sigma }^{dx}}{{{\sigma }_s}^{de}-{{\sigma }_s}^{dx}}& (3)\end{array}$

where σ^de is actual dynamic recovery (DRV) flow stress (Pa), σ^dx is actual dynamic recrystallization (DRX) flow stress (Pa), ${\sigma }_{\text{s}}^{\text{de}}$ is DRV stable flow stress (Pa), ${\sigma }_{\text{s}}^{\text{dx}}$ is DRX stable flow stress (Pa). σ^dx and ${\sigma }_{\text{s}}^{\text{dx}}$ can be acquired directly from tested stress-strain curve. σ^de and ${\sigma }_{\text{s}}^{\text{de}}$ can be obtained from DRV extension curve which stems from ε<ε_c segment of tested stress-strain curve.

Figure 7 shows plots of DRX fraction (X_d) vs. true strain at 1,100°C and 0.05 s⁻¹ obtained by both EBSD analysis and conventional method by Equation (3). Two curves are very close. DRX fraction (X_d) of 316LN steel increases with increasing strain and reaches to almost a constant at steady state strain of 0.69.

FIGURE 7

Figure 7. DRX fraction vs. true strain by different methods.

DRX kinetics model is a key model for hot deformation behavior and microstructural evolution characteristics of 316LN steel. It is calculated by linear regression fitting method by Equation (3) via DRX fraction data compressed at temperature range of 900–1,200°C and strain rate range of 0.005~0.5 s⁻¹. DRX kinetics model is obtained in Equation (4):

$\begin{array}{ll}{X}_d=1-\text{exp}\{-1.778{[(\epsilon -0.668{\epsilon }_p)/{\epsilon }_{0.5}]}^{0.989}\}& (4)\end{array}$

where X_d is DRX fraction, ε is true strain, ε_p is peak strain, ε_0.5 is the strain to achieve 50% softening fraction. Inflection point strain is always used as strain of 50% softening fraction.

Average grain size during DRX

Figure 8 shows plot of average grain size vs. strain at 1,100°C and 0.05 s⁻¹ obtained by EBSD analysis. It is revealed that the average grain size decreases with increasing strain during hot deformation. The original grain size (D₀) is 57.3 μm (Figure 1). While after hot deformation, the average grain size is 22.1 μm at the steady state strain of 0.69. The relevant evidence can also be found in flat part of true stress-strain curve in Figure 4. Furthermore, with the occurrence of DRX, not only finer grains have been achieved, but also high fraction of Σ3 twin boundaries has been developed.

FIGURE 8

Figure 8. Average grain size vs. strain.

Discussion

The Role of Twin Boundary Transformation During DRX

Figure 9 exhibits the misorientation distribution of deformed samples with strain of 0.11, 0.22, 0.36, and 0.92. It is observed that the frequency of twin peak decreases abruptly and is a little broadened at strain of 0.22, which indicates that the twin boundary in deformed grains lost its ideal orientation (Jorge-Badiola et al., 2005). However, at a little higher strain of 0.36, the frequency of twin peak is increased and narrowed, which is the evidence of twin boundary formation in newly formed DRX grains. The transformation of twin boundary during hot deformation can be explained. It has been reported that twinning plays an important role in nucleation and growth of DRX grains in materials with low stacking fault energy (Kim and Yoo, 2001; Li et al., 2011), 316LN steel for instance. As grain boundary mobility is high in materials with low stacking fault energy, twinning is easy to occur in newly formed DRX grains.

FIGURE 9

Figure 9. The misorientation distribution of annealed sample and deformed samples.

At experiment condition (high temperature and low strain rate), bulging is easy to occur. Moreover, dislocation sub-boundaries or twin boundaries induced by strain are formed. They separate the bulged parts from serrated parent grains (Wusatowska-Sarnek et al., 2002; Beladi et al., 2009). The evidence can be found during the nucleation of DRX grains on OIM maps in Figure 6. Furthermore, Figure 10 clearly shows the role of twinning in separation of bulged part and nucleation of DRX. The phenomenon illustrates that other coincidence site lattice (CSL) boundaries also take part in formation of new boundaries to separate grains. Some CSL boundaries, Σ5, Σ7, Σ9, Σ11 boundaries, were shown as green, blue, pink and yellow lines, respectively.

FIGURE 10

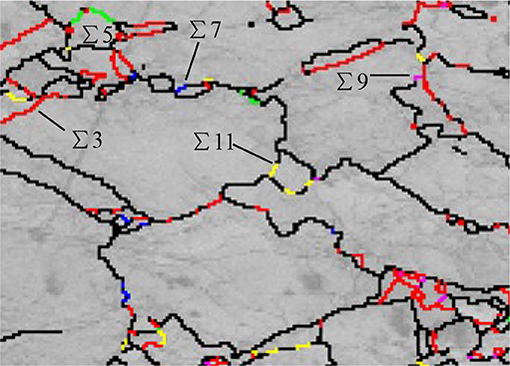
Figure 10. CSL boundaries in OIM map for deformed sample at critical strain (0.22). The high angle and Σ3 twin boundaries are shown as black and red lines, respectively.

It is found in Figure 10 that a large amount of twin boundaries (60° about a (1,1,1) axis) are generated during the growth of DRX grains. This phenomenon can be better explained that the dislocation sub-boundaries behind the bulged parts are free of twins at primary stage in dynamic recrystallization (DRX). As is known, twins can be found in statically recrystallized grains. However, recent study and other relevant works reveal that twinning is also a symbol of DRX (Wusatowska-Sarnek et al., 2002). In DRX, the privilege of twinning is to help decreasing the boundary energy of a growing grain and increasing the mobility of its moving boundary. As a result, DRX process can be speeding up.

Mechanism of DRX

The nucleation of DRX in 316LN steel is characterized by bulging of serrated grain boundaries, as shown in Figures 6A,B. The mechanism is related to grain boundary migration induced by strain. Grain rotation occurs under plastic deformation accompanied by shearing, contributing to local orientation and strain gradient. Bulging takes place to support nucleation of DRX. As long as partial grain boundary shearing occurs in serrated region, sub-grain or twining take place near the serrated grain boundary, accelerating the separation of bulging from deformed parent grains to form DRX nucleus. In studied condition, large amount of twin boundary occurs to separate the bulged parts from parent grains (Humphreys and Hatherly, 2004), as shown in Figure 11. Twin boundaries, combining DRX grains, might be able to transform into high-angle grain boundaries. Newly formed grains grow rapidly, consuming high dislocation density zone. Moreover, twining also takes place in the newly formed grains to decrease overall energy (Qin et al., 2017). Hence, many fine equiaxed grains are formed surrounding the elongated parent grains with increasing strain, as shown in Figures 6C,D. Necklace mechanism takes place layer by layer to consume deformed parent grains (Jafari and Najafizadeh, 2009). At steady state strain of 0.69, uniformly refined DRX grains almost take charge of the microstructure of 316LN steel.

FIGURE 11

Figure 11. Separation of twin boundary from parent grains. The high, low angle and Σ3 twin boundaries are shown as black, white and red lines, respectively.

Figure 12 shows the variation of fraction for different kinds of boundaries vs. true strain. It can be seen that the fraction of low angle boundaries (<10°) increases sharply and reaches to the top at peak strain of 0.22, but decreases continuously during development of DRX. The converse phenomenon occurs in high angle grain boundaries and Σ3 twin boundaries. However, the fraction of 10–15° low angle boundaries remains very low (lower than 5% of all boundaries) during hot deformation. Hence, sub-boundary separation mechanism promoted by dislocation slip and climb is not the main nucleation mechanism in 316LN steel in studied condition. In summary, twinning is an indispensable process during DRX nucleation and growth, which greatly accelerates the progress of DRX.

FIGURE 12

Figure 12. The variation of fraction for different kinds of boundaries vs. true strain.

Conclusions

(1) The Arrhenius hyperbolic sine function was given to fit well with the hot deformation flow behavior of 316LN steel. The average activation energy (Q) of 316LN steel was calculated to be 494 kJ/mol. The peak stress increased with increasing Zener-Holloman parameter (Z).

(2) Microstructural evolution of 316LN steel during hot deformation was studied by EBSD analysis. In deformation condition of 1,100°C and 0.05 s⁻¹, low angle boundaries were accumulated to the highest level at peak strain. Conversely, as strain gradually increased, newly formed DRX grains started to consume the deformed substructures which resulted in decreasing the fraction of low angle boundaries and increasing the fraction of high angle boundaries. Interestingly, a large fraction of newly formed boundaries in DRX grains was twin boundaries and twining played a significant role in nucleation and growth of DRX during hot deformation of 316LN steel.

(3) The nucleation of DRX in 316LN steel was characterized by bulging of serrated grain boundaries. Twining took place near the serrated grain boundary in large amount, accelerating the separation of bulging from deformed parent grains to form DRX nucleus. At steady state strain of 0.69, uniformly refined DRX grains almost took charge of the microstructure of 316LN steel. Twinning is an indispensable process during DRX nucleation and growth, which greatly accelerates DRX progress.

(4) The variation of DRX fraction (X_d) and average grain size was studied by EBSD analysis. DRX fraction model was built. With the progress of DRX, not only finer grains have been achieved, but also high fraction of Σ3 twin boundaries has been developed.

Data Availability

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

JL did all the experiments and analyzing work and wrote down the research article. HC designed the research idea and advised the research work.

Funding

This work was financially supported by the National Natural Science Foundation of China (No. 51575372). HC was the leader of the funding. I declare that open access publication fees was funded by our University—Taiyuan University of Science and Technology.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anita, T., Pujar, M. G., Shaikh, H., Dayal, R. K., and Khatak, H. S. (2006). Assessment of stress corrosion crack initiation and propagation in AISI type 316 stainless steel by electrochemical noise technique. Corros. Sci. 48, 2689–2710. doi: 10.1016/j.corsci.2005.09.007

CrossRef Full Text | Google Scholar

Beladi, H., Cizek, P., and Hodgson, P. D. (2009). Dynamic recrystallization of austenite in Ni-30 Pct Fe model alloy: microstructure and texture evolution. Metall. Mater. Trans. A. 40, 1175-1189. doi: 10.1007/s11661-009-9799-z

CrossRef Full Text | Google Scholar

Chen, F., Qi, K., Cui, Z., and Lai, X. (2014). Modeling the dynamic recrystallization in austenitic stainless steel using cellular automaton method. Comp. Mater. Sci. 83, 331–340. doi: 10.1016/j.commatsci.2013.11.029

CrossRef Full Text | Google Scholar

Dehghan-Manshadi, A., Barnett, M. R., and Hodgson, P. D. (2008). Hot deformation and recrystallization of austenitic stainless steel part I. dynamic recrystallization. Metall. Mater. Trans. A. 39, 1359–1370. doi: 10.1007/s11661-008-9512-7

CrossRef Full Text | Google Scholar

Duan, X. W., and Liu, J.S. (2013). Research on damage evolution and damage model of 316LN steel during forging. Mater. Sci. Eng. A. 588, 265–271. doi: 10.1016/j.msea.2013.08.078

CrossRef Full Text | Google Scholar

Humphreys, F. J., and Hatherly, M. (2004). Recrystallization and Related Annealing Phenomena. Oxford: Pregamon Press. doi: 10.1016/B978-008044164-1/50016-5

CrossRef Full Text | Google Scholar

Jafari, M., and Najafizadeh, A. (2009). Correlation between Zener-Hollomon parameter and necklace DRX during hot deformation of 316 stainless steel. Mater. Sci. Eng. A. 501, 16–25. doi: 10.1016/j.msea.2008.09.073

CrossRef Full Text | Google Scholar

Jones, R. (1996). Some critical corrosion issues and mitigation strategies affecting light water reactors. Mater. Perform. 357, 63–67.

Google Scholar

Jorge-Badiola., D., Iza-Mendia., A, and Gutiérrez, I. (2005). Study by EBSD of the development of the substructure in a hot deformed 304 stainless steel. Mater. Sci. Eng. A. 394, 445–454. doi: 10.1016/j.msea.2004.11.049

CrossRef Full Text | Google Scholar

Kim, D. W. (2012). Influence of nitrogen-induced grain refinement on mechanical properties of nitrogen alloyed type 316LN stainless steel. J. Nucl. Mater. 420, 473–478. doi: 10.1016/j.jnucmat.2011.11.001

CrossRef Full Text | Google Scholar

Kim, H. C., Kim, K., Lee, Y. S., Cho, S. Y., and Nakajima, H. (2009). Study on the weld characteristics of 316LN by magnetization measurement. J. Nucl. Mater. 386-388, 650–653. doi: 10.1016/j.jnucmat.2008.12.307

CrossRef Full Text | Google Scholar

Kim, S., and Yoo, Y. (2001). Dynamic recrystallization behavior of AISI 304 stainless steel. Mater. Sci. Eng. A. 311, 108–113. doi: 10.1016/S0921-5093(01)00917-0

CrossRef Full Text | Google Scholar

Li, D. F., Guo, Q. M., Guo, S.L., Peng, H.J., and Wu, Z.G. (2011). The microstructure evolution and nucleation mechanisms of dynamic recrystallization in hot-deformed Inconel 625 superalloy. Mater. Design 32, 696–705. doi: 10.1016/j.matdes.2010.07.040

CrossRef Full Text | Google Scholar

Mathew, M. D., Laha, K., and Ganesan, V. (2012). Improving creep strength of 316L stainless steel by alloying with nitrogen. Mater. Sci. Eng. A. 535, 76–83. doi: 10.1016/j.msea.2011.12.044

CrossRef Full Text | Google Scholar

McQueen, H. J. (2004). Development of dynamic recrystallization theory. Mater. Sci. Eng. A. 387–389, 203–208. doi: 10.1016/j.msea.2004.01.064

CrossRef Full Text | Google Scholar

Mirzadeh, H., and Najafizadeh, A. (2010). Prediction of the critical conditions for initiation of dynamic recrystallization. Mater.Design 31, 1174–1179. doi: 10.1016/j.matdes.2009.09.038

CrossRef Full Text | Google Scholar

Poliak, E. I., and Jonas, J. J. (1996). A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization. Acta. Mater. 44, 127–136. doi: 10.1016/1359-6454(95)00146-7

CrossRef Full Text | Google Scholar

Poliak, E. I., and Jonas, J. J. (2003). Initiation of dynamic recrystallization in constant strain rate hot deformation. ISIJ. Int. 43, 684–691. doi: 10.2355/isijinternational.43.684

CrossRef Full Text | Google Scholar

Qin, F., Zhu, H., Wang, Z., Zhao, X., He, W., and Chen, H. (2017). Dislocation and twinning mechanisms for dynamic recrystallization of ascast Mn18Cr18N steel. Mater. Sci. Eng. A. 684, 634-644. doi: 10.1016/j.msea.2016.12.095

CrossRef Full Text | Google Scholar

Samantaray, D., Mandal, S., Jayalakshmi, M., Athreya, C. N., and Bhaduri, A. K. (2014). New insights into the relationship between dynamic softening phenomena and efficiency of hot working domains of a nitrogen enhanced 316L(N) stainless steel. Mater. Sci. Eng. A. 598, 368–375. doi: 10.1016/j.msea.2013.12.105

CrossRef Full Text | Google Scholar

Samantaraya, D., Mandala, S., Kumar, V., and Albert, S. K. (2012). Optimization of processing parameters based on high temperature flow behavior and microstructural evolution of a nitrogen enhanced 316L(N) stainless steel. Mater. Sci. Eng. A. 552, 236–244. doi: 10.1016/j.msea.2012.05.036

CrossRef Full Text | Google Scholar

Schwartz, J., Fandeur, O., and Reya, C. (2010). Fatigue crack initiation modeling of 316LN steel based on non local plasticity theory. Proc. Eng. 2, 1353–1362. doi: 10.1016/j.proeng.2010.03.147

CrossRef Full Text | Google Scholar

Sun, C., Xiang, Y., Zhou, Q., and Politis, D. J. (2016). Dynamic recrystallization and hot workability of 316LN stainless steel. Metals. 152, 1–13. doi: 10.3390/met6070152

CrossRef Full Text | Google Scholar

Wusatowska-Sarnek, A. M., Miura, H., and Sakai, T. (2002). Nucleation and microtexture development under dynamic recrystallization of copper. Mater. Sci. Eng. A. 323, 177–186. doi: 10.1016/S0921-5093(01)01336-3

CrossRef Full Text | Google Scholar

Zhang, L., Feng, X., Wang, X., and Liu, C. (2014). On the constitutive model of nitrogen-containing austenitic stainless steel 316LN at elevated temperature. PLoS ONE. 911:e102687. doi: 10.1371/journal.pone.0102687

CrossRef Full Text | Google Scholar

Zhang, W., Sun, H., Zhao, D., Wang, B., Wang, Z., and Wantang, F. (2011). Hot deformation behavior of a Nb-containing 316LN stainless steel. Mater. Design. 32, 4173–4179. doi: 10.1016/j.matdes.2011.04.043

CrossRef Full Text | Google Scholar

Zhang, X., Zhang., Y., Li., Y., and Liu, J. (2013). Cracking initiation mechanism of 316LN stainless steel in the process of the hot deformation. Mater.Sci. Eng. A. 559, 301–306. doi: 10.1016/j.msea.2012.08.102

CrossRef Full Text | Google Scholar