Relative Influence of Topology, Dimensionality and Stoichiometry Toward the Properties of Covalent Network Glasses

Trends in density and fragility are analyzed in the Ge-As-Se, As-Se, and Ge-Se systems for the purpose of identifying correlations with structural characteristics related to topology, stoichiometry, and dimensionality. The Ge-As-Se system provides the most revealing testbed as it permits to isolate individual effects. The fragility of Ge-As-Se glasses is clearly controlled by stoichiometric factors while the topological transition at <r> = 2.4 is not observed in this system. The density of Ge-As-Se glasses broadly increases with average coordination but show two anomalies centered near <r> = 2.4 and 2.67. These anomalies merge into a single extremum corresponding to stoichiometric compositions when plotted against excess/deficiency in Se, thereby revealing their common link to stoichiometric factors. Nevertheless, when stoichiometric factors are fixed, dimensional effects are revealed in the form of a linear dependence upon content of tetrahedral Ge. Similarly, a diffuse maximum at the topological transition of <r> = 2.4 is observed when only Se-excess compositions are considered. For the As-Se system, a local maximum in fragility is observed at the two dimensional composition As₂Se₃ contrary to predictions from topological or stoichiometric factors, thereby indicating that dimensional effect control the fragile behavior. Finally, in the Ge-Se system, a topological transition associated with balance of constraints and degrees of freedom is found at <r> = 2.4 when contributions from stoichiometry, and dimensionality are absent. In all systems, no case is found where topological effects dominate either stoichiometric or dimensional effects, hence it can be concluded that it is the least predominant contribution while stoichiometry is found to be the prevailing effect.

Introduction

Chalcogenide glasses have numerous technological applications due to their excellent transparency in the mid-infrared range (Eggleton et al., 2011; Lucas et al., 2013) but they have also been the subject of much interest for investigating structure-property relationships due to the well-defined nature of their covalent networks. In these glassy networks, each atom generates a clear number of covalent bonds following Mott's 8-N rule (Mott and Davis, 1979) where Ge, As and Se are 4-, 3-, and 2-fold coordinated, respectively. This has led to the development of topological theories based on constraint counting arguments where the glass network properties are estimated from the balance between the number of constraints and degrees of freedom (Phillips, 1979; Thorpe, 1983). Within this conceptual framework, rigidity is expected to percolate through the structure when the average number of bonds per atom (average coordination) is <r> = 2.4. Some studies have shown trends in properties that are consistent with this prediction but they are usually limited to small sets of compositions (Tatsumisago et al., 1990; Senapati et al., 1997) and some show significant scattering (Wang et al., 2009). Other studies did not observe the predicted trends (Aitken, 2001; Yang et al., 2012). Nevertheless, topological principles have often remained the dominant theory for describing the physical properties of chalcogenide glasses (Boolchand et al., 2001; Gupta and Mauro, 2009; Zeidler et al., 2017).

Besides topology, other structural characteristics have been suggested to show correlations with trends in physical properties. Zallen first laid out a description of chalcogenide glasses in terms of network dimensionality where he emphasized the correlation between atomic coordination and the dimensionality of the resulting structure, i.e., 3D character for Ge, 2D for As and 1D for Se (Zallen, 1983). Based on these considerations Tanaka suggested that a transition observed at <r> = 2.67 in several chalcogenide systems may be dimensional in nature (Tanaka, 1989). Experimental observations of the effect of structural dimensionality have been reported in several systems (Wang et al., 2009; Yang et al., 2012). Another structural characteristic that appears to have a systematic contribution toward physical properties is the stoichiometry i.e., the relative excess or deficiency of selenium (or sulfur) relative to the metal atoms where stoichiometric compositions have exactly one Se(S) atom between each metal atom. Compositions with excess Se(S) link metal atoms with small chains while deficient compositions contain direct metal-metal bonds in large concentrations. These stoichiometric effects were found to be particularly prominent in ternary systems (Wang et al., 2011, 2014; Yang et al., 2015).

This paper collates a large body of data from the literature to assess the relative contribution of these three structural characteristics toward two fundamental physical properties: the density and the fragility. The present study is purposely limited to glassy systems containing only Ge, As, and Se due to the similarity in size and electronegativity of the three component atoms. This way, the relative effects of topology, stoichiometry and dimensionality can be investigated without interference from steric effects due to atomic radii mismatch, bonding effects due electronegativity mismatch, or density variations due to mismatch in molar mass. Indeed, density trends in systems containing heavier atoms such as Ge-As-Te or Ge-Sb-Se would be invariably dominated by the content of the large atoms and would mask other contributions so as to make interpretations ambiguous. Furthermore, chemical order is known to be largely preserved in the three systems under study (Sen and Aitken, 2002; Kaseman et al., 2013; Deschamps et al., 2015) with the unique exception of GeSe₂ (Petri et al., 2000). As a consequence, the effect of stoichiometry can be primarily associated with the presence of structural motives such as flexible Se-chains and rigid metal-metal bonds which are expected to influence the physical properties of the glassy network. In that respect the sulfide counterpart systems are also known to satisfy chemical order (Sen et al., 2001), hence it is expected that similar conclusions may apply to these systems as well. This is supported by the observation of identical stoichiometric trends in Ge-As-Se, and Ge-As-S systems (Wang et al., 2014; Yang et al., 2015). Conversely, systems that do not satisfy chemical order such as Ge-As-Te may not follow the same trends.

Accordingly, systems based on Ge, As, and Se provide the least ambiguous test beds for estimating the relative influence of topology, dimensionality, and stoichiometry. Overall it is found that stoichiometry is the dominant contribution followed by dimensionality and finally topology as a minor contribution.

Ge-As-Se System

Density

The Ge-As-Se system is often regarded as the ideal test bed for assessing structure-property relationship due to the similarity of the three component atoms (Tatsumisago et al., 1990). In the present work, density is chosen due to the wide availability of experimental data in the literature. While significant variability may be present due to differences in annealing conditions between studies, clear patterns can be observed. In order to minimize such variability only four large data sets were selected including over a 100 compositions and covering the full range of coordination and stoichiometry. Data set from Borissova (Borisova, 1981), Aitken (Aitken, 2001), Wang (Wang et al., 2009, 2011), and Wang (Wang et al., 2017) were used. All these samples were produced by mechanical melt-rocking which has been shown to yield fully homogeneous glasses (Lucas et al., 2019).

As shown in Figure 1A, the density of Ge-As-Se glasses generally increases with bond density (<r>) but also shows two anomalous extrema, one near 2.4, and one near 2.67. Tanaka (1989) previously suggested that the maximum near 2.4 is topological in nature and is associated with the balance of constraint and degrees of freedom while the minimum near 2.67 is associated with the dimensionality of the glass network. But contrary to previous observation by Tanaka made on a smaller set of compositions (Tanaka, 1989), the two extrema observed here are rather diffuse with significant scattering. This suggests that average coordination alone is too simple a parameter to predict the glass property over wide composition ranges. This in turn suggests that multiple effects may be in competition to determine the glass properties.

FIGURE 1

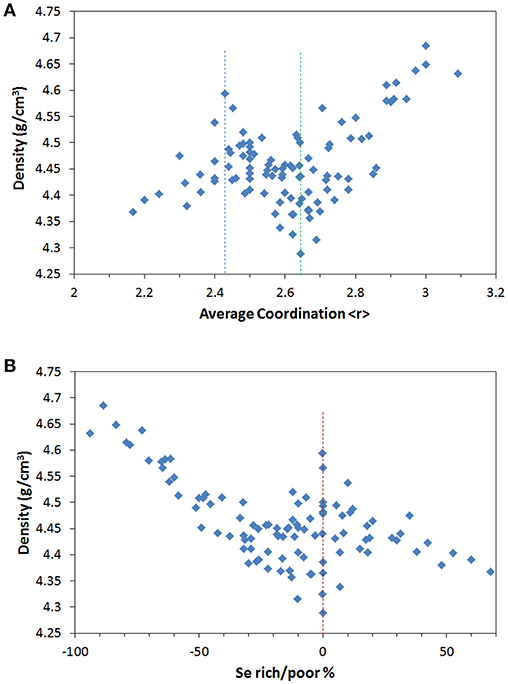
Figure 1. (A) Density of Ge-As-Se glasses as a function of the average coordination number <r>. The dashed line indicate the two extrema associated with topological effects near <r> = 2.4 and structural dimensionality near <r> = 2.67. (B) Density of Ge-As-Se glasses as a function of excess/deficiency of Se in the structure. The dashed line indicates the common extremum for stoichiometric composition. Data taken from Borisova (1981), Aitken (2001), Wang et al. (2009), Wang et al. (2011), Wang et al. (2017).

Instead, Figure 1B plots the density as a function of the stoichiometric contribution defined as the Se excess/deficiency in the glass [as quantified in (Wang et al., 2014)]. Interestingly it is found that the two extrema observed in Figure 1A now merge into one, thereby emphasizing the common origin of these anomalies. Indeed, the compositions showing extreme behaviors in Figure 1A are the same as in Figure 1B. The anomalous behavior can be clearly associated with the stoichiometric compositions where each metal atom is bridge by exactly one Se.

While the merging of the two extrema in Figure 1A suggest that Se% may be the most fundamental variable for describing structure-property relationship in Ge-As-Se glass, the non-monotonous evolution and the remaining scattering clearly indicate that multiple effects are at play in the relationship between structure and properties.

The relative contribution of each effect may be revealed if the contribution from other structural characteristics can be set to fixed values. For example, when the contribution from stoichiometry is neutralized by selecting only compositions at Se% = 0, the effect of network dimensionality can be clearly revealed as depicted in Figure 2. The density decreases linearly with Ge content as the network dimensionality increases, despite the concomitant increase in average coordination (Figure 2). This is opposite to the general trend observed in Figure 1A where density broadly increases with <r>. This seemingly inconsistent trend is the direct result of the dominant role of dimensionality effects where the 4-fold Ge atoms create a more open tetrahedral network despite the highest average coordination.

FIGURE 2

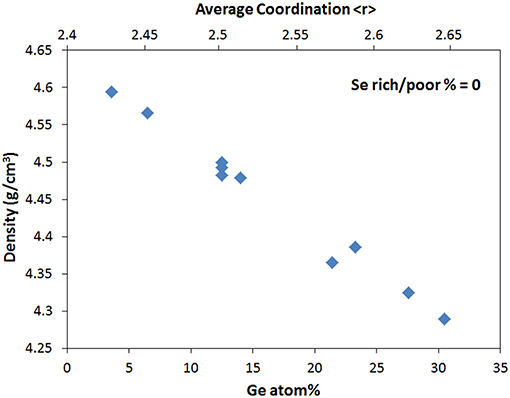
Figure 2. Density of Ge-As-Se glasses with stoichiometric composition (Se rich/poor = 0) as a function of percentage of Ge atoms and average coordination <r>. The density varies linearly with Ge% when the effect of stoichiometry is neutralized.

Similarly, if the network coordination if fixed at <r> = 2.5, the density shows a single maximum at the stoichiometric composition Se% = 0 (Figure 3) instead of the double extremum shown in Figure 1B. At this constant value of <r> the contributions of topology and dimensionality are fixed so that the individual contribution of stoichiometry can be revealed. This suggests that stoichiometry tends to maximize density when all other effects are kept constant.

FIGURE 3

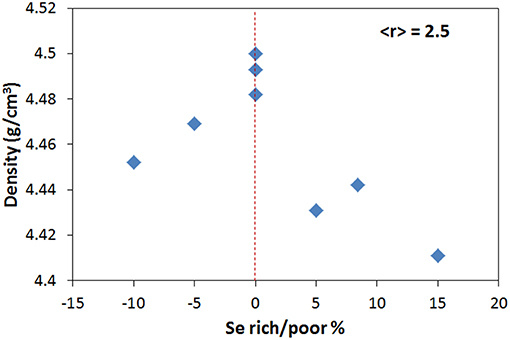
Figure 3. Density of Ge-As-Se glasses with fixed average coordination of <r> = 2.5 as a function of excess/deficiency of Se in the structure.

Finally, if the contribution of stoichiometry is minimized by selecting only Se-rich glasses with Se% > 0, the density shows a single maximum at <r> = 2.4, although significant scatter is still present as shown in Figure 4.

FIGURE 4

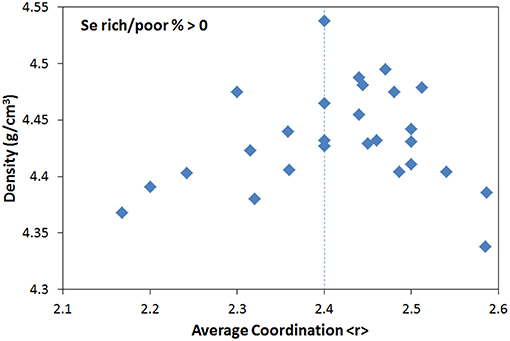
Figure 4. Density of Se-rich Ge-As-Se glasses (Se rich/poor % > 0) as a function of average coordination <r>.

Fragility

The calorimetric fragility of 34 glasses from the Ge-As-Se system was measured by differential scanning calorimetry (DSC) using the Moynihan cool rate method (Wang et al., 2014). The set of compositions cover the whole range of stoichiometry and average coordination. The variation of the fragility index m with stoichiometry and average coordination are shown in Figures 5A,B, respectively.

FIGURE 5

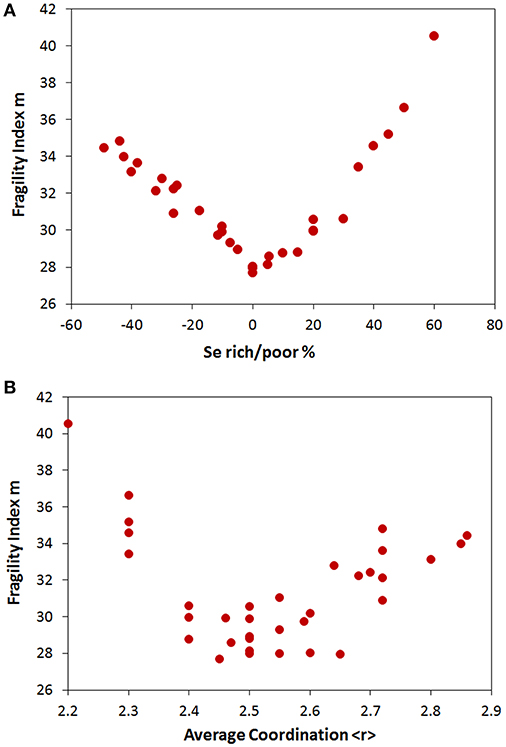
Figure 5. Fragility index m of Ge-As-Se glasses as a function of (A) excess/deficiency of Se in the structure. (B) average coordination <r>.

As in the case of density it clearly appears that stoichiometry is a more fundamental determinant of fragility than topological factors. A well-defined minimum in calorimetric fragility is observed at the stoichiometric compositions Se% = 0. In fact, five distinct compositions superimpose at the Se% = 0 with virtually the same value of fragility. Instead, no clear minimum can be observed as function of <r> expect a general basin centered around <r> = 2.5. This emphasizes that stoichiometry is clearly the dominant structural feature in controlling the fragile behavior of Ge-As-Se supercooled liquids.

As-Se System

Density

The structure of As-Se glasses can be described by the chain-crossing model where chains of selenium are increasingly cross-linked by the trivalent As atoms thereby increasing the dimensionality of the 1D chain structure into a reticulated network of higher dimension (~3D) (Yang et al., 2010; Deschamps et al., 2015). However, at the stoichiometric composition, the structure is composed entirely of AsSe₃ trigonal pyramids and forms a layer-like 2D structure reminiscent of the orpiment crystalline phase (Zallen, 1983; Yang et al., 2012). Upon further introduction of As, sharp Raman peaks indicate that As-rich molecular units are precipitating out of the network, reducing the overall reticulation and bringing back the backbone structure to a higher dimension (~3D). At even higher as concentrations, the network eventually collapses as the concentration of 0D molecular units dominates (Yang et al., 2010, 2012).

The contribution of the different structural characteristics is blurred in binary system because they tend to occur at the same composition. In the case of the As-Se system, the topological rigidity transition (<r> = 2.4) occurs at the same composition as the stoichiometry As₂Se₃ and as a minimum in dimensionality (2D). The density of As-Se glasses is shown in Figure 6 as a function of average coordination number <r>. A well-defined single minimum is observed at <r> = 2.4 which is consistent with the contributions from stoichiometry and topology observed in Figures 3, 4 for the Ge-As-Se system. The dimensionality varies non-monotonically and its contribution to the density appears to be non-dominant.

FIGURE 6

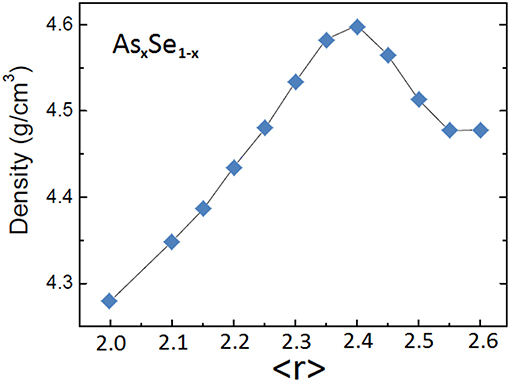
Figure 6. Density of As-Se glasses as a function of average coordination <r>. Data from Yang et al. (2010).

Fragility

The fragility of glasses from the As-Se system is shown in Figure 7. The fragility index is found to change non-monotonically with average coordination <r>. The same trend is observed whether the fragility is measured from viscosity, DSC, or modulated DSC (Musgraves et al., 2011; Yang et al., 2012). While the fragility appears to incline toward a minimum at the stoichiometric composition, consistent with Figure 5A, the fragility index actually shows a local maximum at the stoichiometry at <r> = 2.4. This non-monotonic pattern is not consistent with prediction from either stoichiometric or topological effects. However, it is fully consistent with the evolution of the structural dimensionality in this glass system. This anomaly was actually pointed out by Angell many years ago (Tatsumisago et al., 1990). Fragility is well-known to correlate to structural dimensionality with 3D networks such as silica being the strongest and 0D molecular glasses such as o-terphenyl being the most fragile (Angell, 1991). In the case of As₂Se₃ the sheet structure where layers are only bonded by weak Van der Wall interactions leads to faster collapse of the structure with temperature and a more fragile behavior. Hence, in the case of the As-Se system, dimensionality eventually dominates the fragility behavior.

FIGURE 7

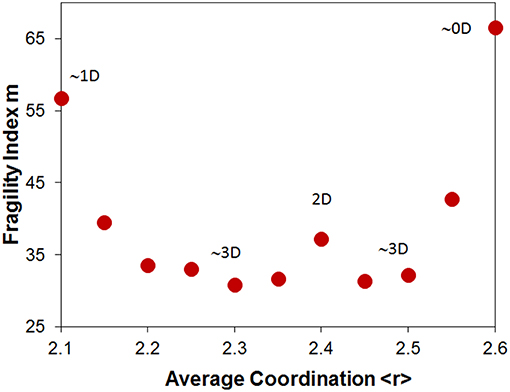
Figure 7. Fragility Index m of glasses from the As-Se system as a function of average coordination <r>. Labels identify the dimensionality character of the network. Data from Yang et al. (2012).

Ge-Se System

Density

Structural effects tend to overlap in the Ge-Se binary in the same way as for As-Se. In the case of Ge-Se, the stoichiometric composition GeSe₂ also corresponds to the 3D tetrahedral structure isomorphous of SiO₂. On the other end the topological transition at <r> = 2.4 does not overlap with other effects. The density trend shown in Figure 8 indeed exhibit a maximum near <r> = 2.4 which reveals the topological contribution. In the absence of other structural effects, the balance between constraints and degree of freedom can affect the trend in density. The density also shows a sharp minimum at the stoichiometric composition GeSe₂ (<r> 2.67). This trend is clearly dominated by structural dimensionality as the glassy network converts to an open tetrahedral framework. The effect of stoichiometry is only a minor contribution in this case.

FIGURE 8

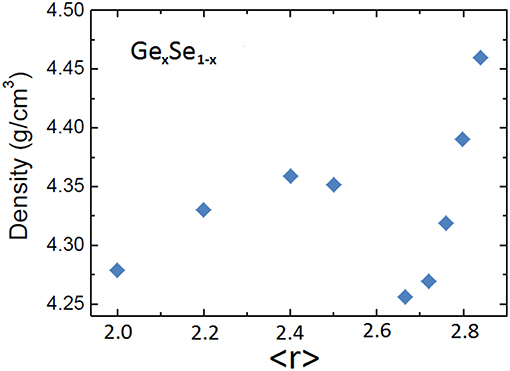
Figure 8. Density of Ge-Se glasses as a function of average coordination <r>. Data from Yang et al. (2013).

Fragility

Fragility data derived from viscosity are shown in Figure 9 for the Ge-Se system (Senapati and Varshneya, 1996). The fragility shows a broad minimum centered near <r> = 2.5, however the number of data points in this set is somewhat limited and broader data sets from the literature have been found to present a collective minimum near <r> = 2.45, although they show a considerable amount of scatter (Zeidler et al., 2017). Viscosity data for the stoichiometric composition cannot be obtained as GeSe₂ is a poor glass-former that readily crystallizes upon reheating. However, fragility values derived calorimetrically do not indicate any anomalous variation at that composition (Zeidler et al., 2017). Hence the fragility trend appears to be dominated by topological effects.

FIGURE 9

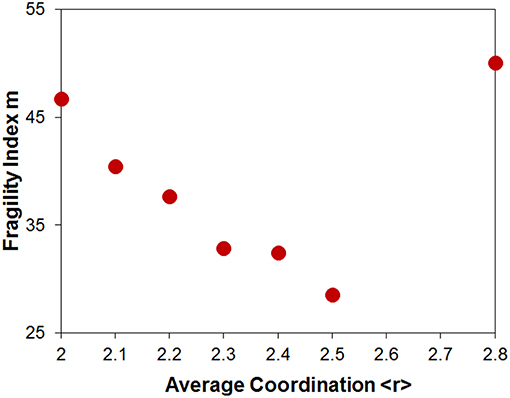
Figure 9. Fragility of Ge-Se glasses as a function of average coordination <r>. Data from Senapati and Varshneya (1996). Additional data sets such as that presented in Zeidler et al. (2017) show a collective broad minimum near <r> = 2.45.

One point of concern when describing structure-property relationship in the Ge-Se system is the considerable concentration of edge-sharing tetrahedra in the structure, up to ~35% (Petri et al., 2000; Lucas et al., 2009). This raises concern about the validity of the constraint counting procedure as constraints become interdependent for ring sizes smaller than 6 atoms (Thorpe, 1983). In the case of edge sharing tetrahedra, four member rings would lead to significant overestimates of the number of constraints, and in turn to the actual position of the rigidity transition. But more importantly, this structural segregation leads to very distinct dynamics of the different structural units upon reheating (Lucas et al., 2009; Gjersing et al., 2010) which should have a direct implication to the fragility behavior. This further complicates any structural interpretation of the supercooled liquid behavior in the Ge-Se system.

Conclusion

Experimental data for over a 100 glass compositions in the Ge-As-Se as well as As-Se and Ge-Se systems were analyzed to investigate correlations between trends in physical properties and the three structural characteristics: topology, dimensionality and stoichiometry. Two fundamental physical properties were selected for each system: the density for the glassy state and the fragility for the supercooled liquid state. Stoichiometry, i.e., the relative excess or deficiency of selenium relative to the metal atoms is found to be the most universal indicator of physical properties although structural dimensionality can also be a dominating factor. Topological effects based on constraint counting arguments are found to play a minor role and their contribution can only be observed in Se-rich composition when stoichiometric and dimensional effects are absent. This is the case in the Ge-Se system where the fragility exhibits a broad minimum near <r> = 2.45 (Zeidler et al., 2017). Sulfide systems that also satisfy chemical order are expected to follow the same trends, as suggested by a previous study (Yang et al., 2015). However, it is not clear that these trends will apply to systems known to violate chemical order such as Ge-As-Te.

Data Availability

This data can be found in the references provided in the manuscript.

Author Contributions

PL wrote this manuscript based on an original analysis of literature data.

Funding

PL acknowledge financial support from NSF-DMR under grant #: 1832817.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Aitken, B. G. (2001). “Structure-property relationships in Ge-As selenide and sulphide glasses,” in Proceedings of the International Congress on Glass, Vol. 1 (Edinburgh).

Google Scholar

Angell, C. A. (1991). Relaxation in liquids, polymers and plastic crystals - strong/fragile patterns and problems. J. Non Cryst. Solids. 131–133, 13–31. doi: 10.1016/0022-3093(91)90266-9

CrossRef Full Text | Google Scholar

Boolchand, P., Feng, X., and Bresser, W. J. (2001). Rigidity transitions in binary Ge-Se glasses and the intermediate phase. J. Non Cryst. Solids. 293–295, 348–356. doi: 10.1016/S0022-3093(01)00867-5

CrossRef Full Text | Google Scholar

Borisova, Z. U. (1981). Glassy Semiconductors. New York, NY: Plenum Press.

Google Scholar

Deschamps, M., Genevois, C., Cui, S., Roiland, C., LePolles, L., Furet, E., et al. (2015). Structure of arsenic selenide glasses studied by NMR: selenium chain length distributions and the flory model. J. Phys. Chem. C. 119, 11852–11857. doi: 10.1021/acs.jpcc.5b02423

CrossRef Full Text | Google Scholar

Eggleton, B. J., Luther-Davies, B., and Richardson, K. (2011). Chalcogenide photonics. Nat. Photonics. 5, 141–148. doi: 10.1038/nphoton.2011.309

CrossRef Full Text | Google Scholar

Gjersing, E. L., Sen, S., and Youngman, R. E. (2010). Mechanistic understanding of the effect of rigidity percolation on structural relaxation in supercooled germanium selenide liquids. Phys. Rev. B Condens. Matter Mater. Phys. 82:014203. doi: 10.1103/PhysRevB.82.014203

CrossRef Full Text | Google Scholar

Gupta, P. K., and Mauro, J. C. (2009). Composition dependence of glass transition temperature and fragility. i. a topological model incorporating temperature-dependent constraints. J. Chem. Phys. 130:094503. doi: 10.1063/1.3077168

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaseman, D. C., Hung, I., Gan, Z., and Sen, S. (2013). Observation of a continuous random network structure in Ge(x)Se(100-x) glasses: results from high-resolution 77Se MATPASS/CPMG NMR spectroscopy. J. Phys. Chem. B. 117, 949–954. doi: 10.1021/jp311320t

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucas, P., Coleman, G. J., Sen, S., Cui, S., Guimond, Y., Calvez, L., et al. (2019). Structural and chemical homogeneity of chalcogenide glass prepared by melt-rocking. J. Chem. Phys. 150:014505. doi: 10.1063/1.5054704

PubMed Abstract | CrossRef Full Text | Google Scholar

Lucas, P., King, E. A., Gulbiten, O., Yarger, J. L., Soignard, E., and Bureau, B. (2009). Bimodal phase percolation model for the structure of Ge-Se glasses and the existence of the intermediate phase. Phys. Rev. B: Condens. Matter 80:214114. doi: 10.1103/PhysRevB.80.214114

CrossRef Full Text | Google Scholar

Lucas, P., Yang, Z., Fah, M. K., Luo, T., Jiang, S., and Boussard-Pledel, C. (2013). Telluride glasses for far infrared photonic applications. Opt. Mater. Express. 3, 1049–1058. doi: 10.1364/OME.3.001049

CrossRef Full Text | Google Scholar

Mott, N. F., and Davis, E. A. (1979). Electronic Processes in Non-Crystalline Materials. Oxford: Clarendon Press.

Google Scholar

Musgraves, J. D., Wachtel, P., Novak, S., Wilkinson, J., and Richardson, K. (2011). Composition dependence of the viscosity and other physical properties in the arsenic selenide glass system. J. Appl. Phys. 110:063503. doi: 10.1063/1.3638122

CrossRef Full Text | Google Scholar

Petri, I., Salmon, P. S., and Fischer, H. E. (2000). Defects in a disordered world: the structure of glassy GeSe₂. Phys. Rev. Lett. 84, 2413–2416. doi: 10.1103/PhysRevLett.84.2413

PubMed Abstract | CrossRef Full Text | Google Scholar

Phillips, J. C. (1979). Topology of covalent non-crystalline solids. i. short-range order in chalcogenide alloys. J. Non Cryst. Solids. 34, 153–181. doi: 10.1016/0022-3093(79)90033-4

CrossRef Full Text | Google Scholar

Sen, S., and Aitken, B. G. (2002). Atomic structure and chemical order in Ge-As selenide and sulfoselenide glasses: an x-ray absorption fine structure spectroscopic study. Phys. Rev. B Condens. Matter 66:134204. doi: 10.1103/PhysRevB.66.134204

CrossRef Full Text | Google Scholar

Sen, S., Ponader, C., W., and Aitken, B. G. (2001). Ge and As x-ray absorption fine structure spectroscopic study of homopolar bonding, chemical order, and topology in Ge-As-S chalcogenide glasses. Phys. Rev. B. 64:104202. doi: 10.1103/PhysRevB.64.104202

CrossRef Full Text | Google Scholar

Senapati, U., Firstenberg, K., and Varshneya, A. K. (1997). Structure-property inter-relations in chalcogenide glasses and their practical implications. J. Non Cryst. Solids. 222, 153–159. doi: 10.1016/S0022-3093(97)00394-3

CrossRef Full Text | Google Scholar

Senapati, U., and Varshneya, A. K. (1996). Viscosity of chalcogenide glass-forming liquids: an anomaly in the ‘strong’ and ‘fragile’ classification. J. Non Cryst. Solids. 197, 210–218. doi: 10.1016/0022-3093(95)00628-1

CrossRef Full Text | Google Scholar

Tanaka, K. (1989). Structural phase transitions in chalcogenide glasses. Phys. Rev. B Condens. Matter. 39, 1270–1279. doi: 10.1103/PhysRevB.39.1270

PubMed Abstract | CrossRef Full Text | Google Scholar

Tatsumisago, M., Halfpap, B. L., Green, J. L., Lindsay, S. M., and Angell, C. A. (1990). Fragility of germanium-arsenic-selenium glass-forming liquids in relation to rigidity percolation, and the kauzmann paradox. Phys. Rev. Lett. 64, 1549–1552. doi: 10.1103/PhysRevLett.64.1549

CrossRef Full Text | Google Scholar

Thorpe, M. F. (1983). Continuous deformations in random networks. J. Non Cryst. Solids. 57, 355–370. doi: 10.1016/0022-3093(83)90424-6

CrossRef Full Text | Google Scholar

Wang, R. P., Bulla, D., Smith, A., Wang, T., and Luther-Davies, B. (2011). Structure and physical properties of GexAsySe1-x-y glasses with the same mean coordination number of 2.5. J. Appl. Phys. 109:023517. doi: 10.1063/1.3544309

CrossRef Full Text | Google Scholar

Wang, R. P., Smith, A., Luther-Davies, B., Kokkonen, H., and Jackson, I. (2009). Observation of two elastic thresholds in GexAsySe1-x-y glasses. J. Appl. Phys. 105:056109. doi: 10.1063/1.3079806

CrossRef Full Text | Google Scholar

Wang, T., Gulbiten, O., Wang, R., Yang, Z., Smith, A., Luther-Davies, B., et al. (2014). Relative contribution of stoichiometry and mean coordination to the fragility of Ge-As-Se glass forming liquids. J. Phys. Chem. B. 118, 1436–1442. doi: 10.1021/jp412226w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Qi, S., Yang, Z., Wang, R., Yang, A., and Lucas, P. (2017). Composition dependences of refractive index and thermo-optic coefficient in Ge-As-Se chalcogenide glasses. J. Non Cryst. Solids. 459, 88–93. doi: 10.1016/j.jnoncrysol.2017.01.004

CrossRef Full Text | Google Scholar

Yang, G., Bureau, B., Rouxel, T., Gueguen, Y., Gulbiten, O., Roiland, C. et al. (2010). Correlation between structure and physical properties of chalcogenide glasses in the AsxSe1-x system. Phys. Rev. B Condens. Matter. 82:195206. doi: 10.1103/PhysRevB.82.195206

CrossRef Full Text | Google Scholar

Yang, G., Gueguen, Y., Sangleboeuf, J.-C., Rouxel, T., Boussard-Pledel, C., Troles, J., et al. (2013). Physical properties of the GexSe1-x glasses in the 0 < x <0.42 range in correlation with their structure. J. Non Cryst. Solids. 377, 54–59. doi: 10.1016/j.jnoncrysol.2013.01.049

CrossRef Full Text | Google Scholar

Yang, G., Gulbiten, O., Gueguen, Y., Bureau, B., Sangleboeuf, J.-C., Roiland, C., et al. (2012). Fragile-strong behavior in the As_xSe_1−. glass forming system in relation to structural dimensionality. Phys Rev. B Condens. Matter 85:144107. doi: 10.1103/PhysRevB.85.144107

CrossRef Full Text | Google Scholar

Yang, Y., Zhang, B., Yang, A., Yang, Z., and Lucas, P. (2015). Structural origin of fragility in Ge-As-S glasses investigated by calorimetry and raman spectroscopy. J. Phys. Chem. B. 119, 5096–5101. doi: 10.1021/acs.jpcb.5b01768

PubMed Abstract | CrossRef Full Text | Google Scholar

Zallen, R. (1983). The Physics of Amorphous Solids. Weinheim: John Wiley and Sons.

Google Scholar

Zeidler, A., Salmon, P. S., Whittaker, D. A. J., Pizzey, K. J., and Hannon, A. C. (2017). Topological ordering and viscosity in the glass-forming Ge–Se system: the search for a structural or dynamical signature of the intermediate phase. Front. Mater. 4:32. doi: 10.3389/fmats.2017.00032

CrossRef Full Text | Google Scholar