Influence of the Various Deformation Modes on Rheology of High-Concentrated Magnetorheological Fluids of Complex Composition for Controlled Layered Structures

The results of an experimental study of the rheological behavior of highly concentrated magnetorheological fluids of complex composition containing the main magnetosensitive filler—carbonyl iron and additives—particles of aerosil, chromium dioxide, and bentonite clay are presented. The modes of continuous shear deformation, linear increase of shear stress, and harmonic shear oscillations are considered. The influence of the additive material on shear stress, yield stress, components of the complex shear modulus of magnetorheological fluids in a magnetic field is determined.

Introduction

In various industries (machine building and shipbuilding, aviation, rocket and space technology, etc.), flat thin-walled elements (beams, plates, and shells) of a layered structure are used in order to reduce material consumption while maintaining the required strength and rigidity of products. The most important requirement at the stage of development of such structures, which experience dynamic loads of a wide range of frequencies and strains, is to ensure their vibration protection while maintaining the rigidity of objects (Librescu and Hause, 2000).

Existing vibration protection methods divide into two groups (Chu et al., 2005; Fu et al., 2018). “Passive” methods are based on the use of inertial, elastic, and dissipative elements. They are implemented by introducing damping elements made of elastic or viscoelastic materials placed between the bounding layers into the object structure. Active or semi-active vibration damping systems use an external energy source to automatically adjust the dynamic characteristics of the structure (for example, hydropneumatic systems) (Song, 2009; Akhtar et al., 2015).

To solve the problems of semi-active and active damping of oscillations of flat elements, magnetosensitive materials which, in a controlled manner, change their elastic-viscous-plastic characteristics in external magnetic fields can be used as interlayers. The influence of the field causes a change in the structural state of the material from fluid to quasi-solid. It allows to create the necessary mode of material resistance to shear effects depending on the mechanical load. Outside the field, materials can be different consistencies and retain different degrees of fluidity, which are mainly determined by the concentration and physico-chemical characteristics of the particles of the dispersed phase. Such magnetosensitive quasi-solid materials as elastomers are known. They are a rubber-like matrix into which magnetic particles, for example iron, are introduced and oriented along the magnetic field strength vector (Zhou, 2003; Nayak et al., 2013; Tian et al., 2013; Li et al., 2014; Megha et al., 2016). It is shown that when exposed to an external magnetic field, the storage modulus G′ and the loss modulus G″ of such materials increase, and the resonant frequency of the vibrations of the layered structures changes. It is shown in previous studies (Megha et al., 2016) that due to the increase in the loss modulus, a decrease in the amplitude of forced and free oscillations is achieved both in a uniform and non-uniform magnetic field. However, it is established that the increase in the storage modulus in a magnetic field did not exceed two to three times, and the loss modulus did not exceed one and a half to two times. An increase in the concentration of magnetic filler leads to an increase in the rigidity of the object (storage modulus) and the value of the static yield stress. However, it was noted that this reduces the range of deformations, in which a linear relationship between shear stress and deformation (elastic zone) occurs, which complicates the implementation of controllability of these systems (Tian et al., 2013). A number of constructions of vibroprotective devices using magnetically sensitive elastomers have been developed (Li et al., 2014). A significant problem of their wide use is the poor adhesion of the elastomer to the surfaces of the limiting elements and the small range of regulation of the viscoelastic characteristics due to the initial high rigidity of the rubber-like matrix, as well as a slow structural response to the action of a magnetic field (Ahamed et al., 2018).

The use of magnetorheological fluid materials in flat thin-walled structural elements as controlled layers could solve these problems. Well-known studies (Dong et al., 2018) showed that increasing the concentration of the dispersed phase and using additives of ferrimagnetic particles can reduce unwanted separation and spreading of magnetorheological fluids. For example, the addition of 0.1 wt. % ferrimagnetic CoFe₂O₄ nanoparticles (about 100 nm in size) to a fluid with 50 wt. % carbonyl iron allowed to halve the sedimentation and increase the shear stress (up to three times in small fields) compared with the composition without nanoparticles. A significant increase in shear stress was also obtained when adding 1% of γ-Fe₂O₃ (Leong et al., 2016). The magnetorheological effect can be enhanced by several times with the use of magnetite additives (Ashtiani and Hashemabadi, 2015). A multiple increase in the components of the complex shear modulus and shear stress was also noted with the addition of non-magnetic particles of poly(methylmethacrylate) (Iglesias et al., 2015).

Previously, we studied the rheology of high-filled (mass concentration of carbonyl iron was 68.5% and of aerosil was 3%) composite fluid magnetorheological materials. Such materials that do not contain a rubber-like matrix (Korobko et al., 2014), have a significant yield stress in the absence of a magnetic field. An increase of almost two orders of value of the shear resistance of the MRF in a magnetic field was obtained. The optimal range of the magnetic field induction, in which the largest increase in the loss modulus takes place, is determined. The results obtained allowed to suggest that by using a higher concentration of the dispersed phase, as well as by adding both an ferrimagnetic component and non-magnetic additives of oxide particles, it is possible to achieve an increase in the growth of rheological parameters in the field and the necessary damping response in a given strain range.

In connection with the foregoing, the aim of this work is to establish the influence of different deformation modes on the change in the magnetic field of the rheological characteristics of the magnetorheological fluids of a complex composition containing magnetic and non-magnetic components.

Materials and Equipment

This paper presents the results of experimental studies of the developed compositions of highly concentrated magnetorheological composite fluids (MRF), which are high-filled pastes containing two types of particles as the dispersed phase.

The component of the composite dispersed phase of MRF, which has a high magnetorheological sensitivity, was particles of magnetically soft carbonyl iron (main diameter is about 3 μm). Samples containing 77 wt.% carbonyl iron and finely dispersed materials of a different nature to create a thixotropic matrix were investigated. Mobil synthetic oil was used as a dispersion medium. The compositions of the MRF samples and the values of the saturation magnetization of the magnetic components H_r are given in Table 1.

TABLE 1

Table 1. The content of the components in the MRF samples.

Aerosil particles (brand A-380) have a spherical shape and size of 5–15 nm, CrO₂ particles differ in a needle shape with a ratio of sizes of 15:1 and a length of 500 nm, and particles of bentonite clay have a plate shape and a size of 1–10 μm.

The rheological characteristics of the prepared MRF samples both without the influence of a magnetic field and under its influence in the magnetic induction range B 0–1 T are investigated. A Physica MCR 301 rheometer of Anton Paar with a measuring cell MRD 70/1T plate–plate type with a diameter of 20 mm (the gap between the plates is 0.7 mm) was used.

The measurements were carried out with the deformation of the MRF in three different modes. The first mode (1): tangential continuous shear of the upper plate with a constant shear rate in the range of change from 0.01 to 100 s⁻¹. The dependences of shear stress τ on shear rate γ (flow curves) are obtained. The second mode (2) is a linear increase of external shear stress τ. The value of τ increases linearly up to a given maximum value within 400 s. The dependences of τ on the strain ε and the static yield stress τ₀ were obtained. The third mode (3) is sinusoidal tangential oscillations of the upper plate with a constant frequency f = 10 Hz and strain amplitude ε_a in the range of changes in its values from 0.0001 to 1. The components of the complex shear modulus G^* = G′ + iG″ were measured (where G′ is the storage modulus (elastic modulus) and G″ is the loss modulus). All measurements were performed at a constant temperature 20°C.

Results and Discussion

Rheological Characteristics Without a Magnetic Field

Typical rheological parameters of the materials studied and obtained without a magnetic field, are presented in Table 2. It contains shear stress at γ = 100 s⁻¹ (τ₁₀₀), yield stress τ₀, G′ and G″ at ε_a = 0.01%. The measurement results show that the values of the rheological parameters of the MRF depend on the additive material used (Table 1). Among the studied compositions, the material MRF-1, containing 4 wt. % aerosil, the finest component, shows the highest values of the given rheological parameters. Replacement in the composition of the filler of 2 wt. % aerosil by 2% chromium oxide CrO₂ (MRF-2) leads to a decrease in τ₀ values by almost 6 times, τ₁₀₀ values by eight times, and G′ decreases by 15 times in comparison with the MRF-1 sample.

TABLE 2

Table 2. The values of the rheological parameters of MRF at B = 0.

For the composition of MRF-4, containing 10 wt. % of bentonite clay, as well as for the composition of MRF-3 with 8 wt. % of CrO₂, a greater decrease in the rheological characteristics in the plastic and viscoelastic states (τ₀, G′ and G″) is observed. In addition, an increase in shear stress in the fluid state (τ₁₀₀) compared with the data for MRF-2 is fixed.

This is due to the fact that aerosil matrix has greater strength at rest, even at lower particle concentrations than in the sample with bentonite clay MRF-4 and in the sample with CrO₂ MRF-3. However, it easily collapses when shear rates are of the order of 10 s⁻¹ (mode 1). With a further increase in γ, the shear stress remains almost unchanged. This is illustrated in Figure 1 (curve 1).

FIGURE 1

Figure 1. MRF flow curves in the absence of a magnetic field: 1—MRF-1; 2—MRF-2; 3—MRF-3; 4—MRF-4.

It can be seen that the MRF-4 sample with bentonite clay, unlike other samples, shows an increase in τ with an increase in shear rate (curve 4), but reaches a value much smaller than that of MRF-1. Other MRF compositions have τ₀ and τ₁₀₀ values even lower in the whole range of shear rates.

Rheological Characteristics in the Mode of Continuous Shear

Figure 2 shows the changes in τ(γ) with a change in the magnetic field induction B from 0 to 1000 mT in mode (1). It can be seen that as B increases the shear stress τ increases at all shear rates. The shear stress of the MRF-1, MRF-2, and MRF-3 samples does not change with increase of shear rate in the range of γ > 20 s⁻¹ at B < 300 mT. The flow curves (curves 1–4, Figures 2A–C) are almost parallel to the axis of shear rates, i.e. flow is viscoplastic. Only in the MRF-4 sample, an increase in τ was observed with an increase in the shear rate in the entire range of changes in the magnetic field induction (Figure 2D), which is characteristic of a pronounced viscoplastic flow. In this case, the shear stress is lower than that of the MRF-1.

FIGURE 2

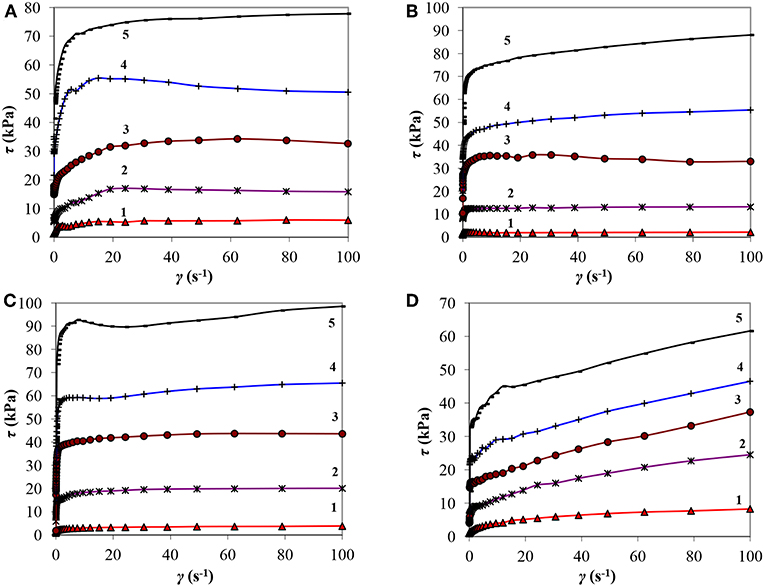
Figure 2. MRF flow curves in a magnetic field (A—MRF-1, B—MRF-2, C—MRF-3, D—MRF-4): 1-B = 100 mT, 2-300, 3-500, 4-700, 5-1,000.

This rheological behavior can be explained by the fact that, as in the absence of a magnetic field, the thixotropic matrix created by particles of bentonite clay (MRF-4) gradually collapses as the shear rate increases. The matrix of aerosil particles, as compared to bentonite one, is destroyed at lower shear rates. At the same time, the fine particles of aerosil do not prevent ferromagnetic particles from easily structuring in a magnetic field, unlike larger particles of bentonite clay, which prevent the interaction of particles, which reduces the magnetorheological effect. The thixotropic matrix of chromium dioxide particles in MRF-3 and MRF-2 also collapses at low shear rates. However, chromium dioxide particles have magnetic properties and are involved in the construction of bridge structures when influenced to a magnetic field, which leads to an increase in the shear resistance of the MRF-3 in a magnetic field compared to MRF-1 and MRF-4.

Rheological Characteristics in the Mode of Linear Increase of Shear Stress

Figure 3 shows the dependences of shear stress on strain τ(ε), obtained in mode (2) by the method of linear increase of shear stress, with the induction of a magnetic field B = 0 ÷ 1,000 mT.

FIGURE 3

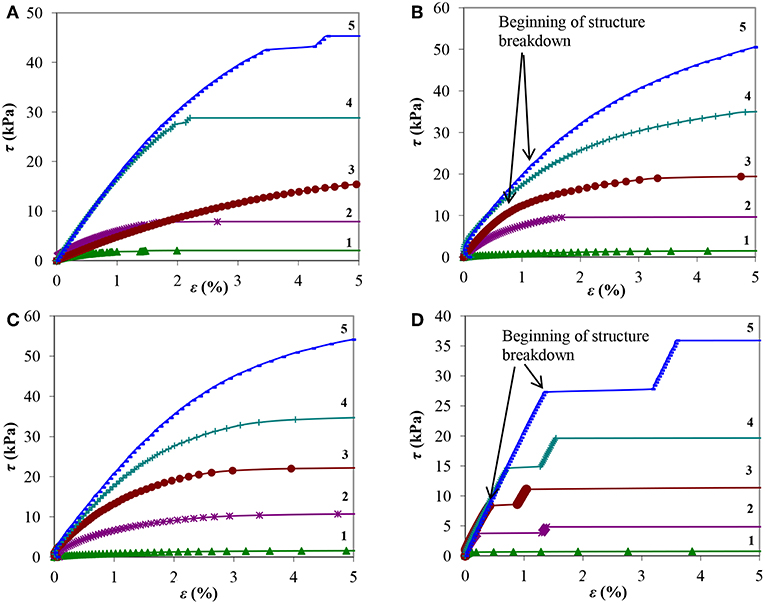
Figure 3. Dependences of the shear stress τ on strain ε of MRF at different magnetic field induction (A—MRF-1, B—MRF-2, C—MRF-3, D—MRF-4): 1-B = 100 mT, 2-300, 3-500, 4-700, 5-1,000.

From Figure 3D it can be seen that, prior to the beginning of the structure destruction, the composition of MRF-4 with bentonite clay is characterized by the presence of a significant region in the τ(ε) dependence, in which the shear stress and strain are proportional. For MRF compositions with aerosil and chromium dioxide (Figures 3A–C), the deviation of the dependence τ(ε) from linearity appears even at small strains. With increasing magnetic field induction, the transition limit to the non-linear dependence of shear stress on strain, corresponding to the onset of destruction of the MRF structure, shifts to the region of large strains. The destruction of the structure of the sample containing bentonite clay (MRF-4) in a magnetic field with induction B > 200 mT begins abruptly, the deformation increases with a jump when τ reaches the yield stress (Figure 3D). Probably, there is a rupture of the structure and sliding along a certain surface of the rupture. In this case, after a jump in the deformation due to particle rearrangement, the gap is eliminated and a slight increase in the structure strength is occurred. The resulting structure is again destroyed with further increase of τ (steps in Figure 3D, MRF-4). This sample shows the fragility of the structure in comparison with the sample containing as an additional component only aerosil (MRF-1), which collapses more smoothly with increasing deformation. The substitution of aerosol, partially with chromium dioxide (MRF-2) or completely (MRF-3), increases not only the zone of the linear dependence τ(ε), but also the value of τ₀ compared to the MRF-1 sample.

Figure 4 shows the dependences of the static yield stress τ₀ of MRF on magnetic field induction B, obtained in mode (2).

FIGURE 4

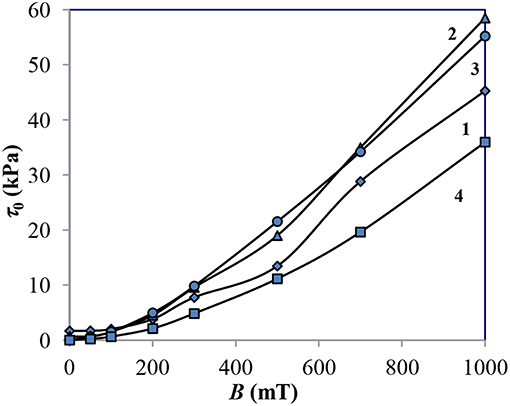
Figure 4. Dependences of yield stress τ₀ on magnetic induction B: 1—MRF-1; 2—MRF-2; 3—MRF-3; 4—MRF-4.

With the introduction of CrO₂ into MRF-3 and MRF-2, compared with MRF-1, τ₀ increases by 15–20%. The combination of 2% of aerosil and 2% of chromium dioxide provides the yield stress values that are the same with MRF-3, which uses 8% of chromium dioxide.

Rheological Characteristics in the Mode of Sinusoidal Shear Oscillations

Figure 5 shows the dependences of the components of the complex shear modulus on the amplitude of the deformation at the magnetic field induction B = 0 ÷ 1000 mT obtained in mode (3).

FIGURE 5

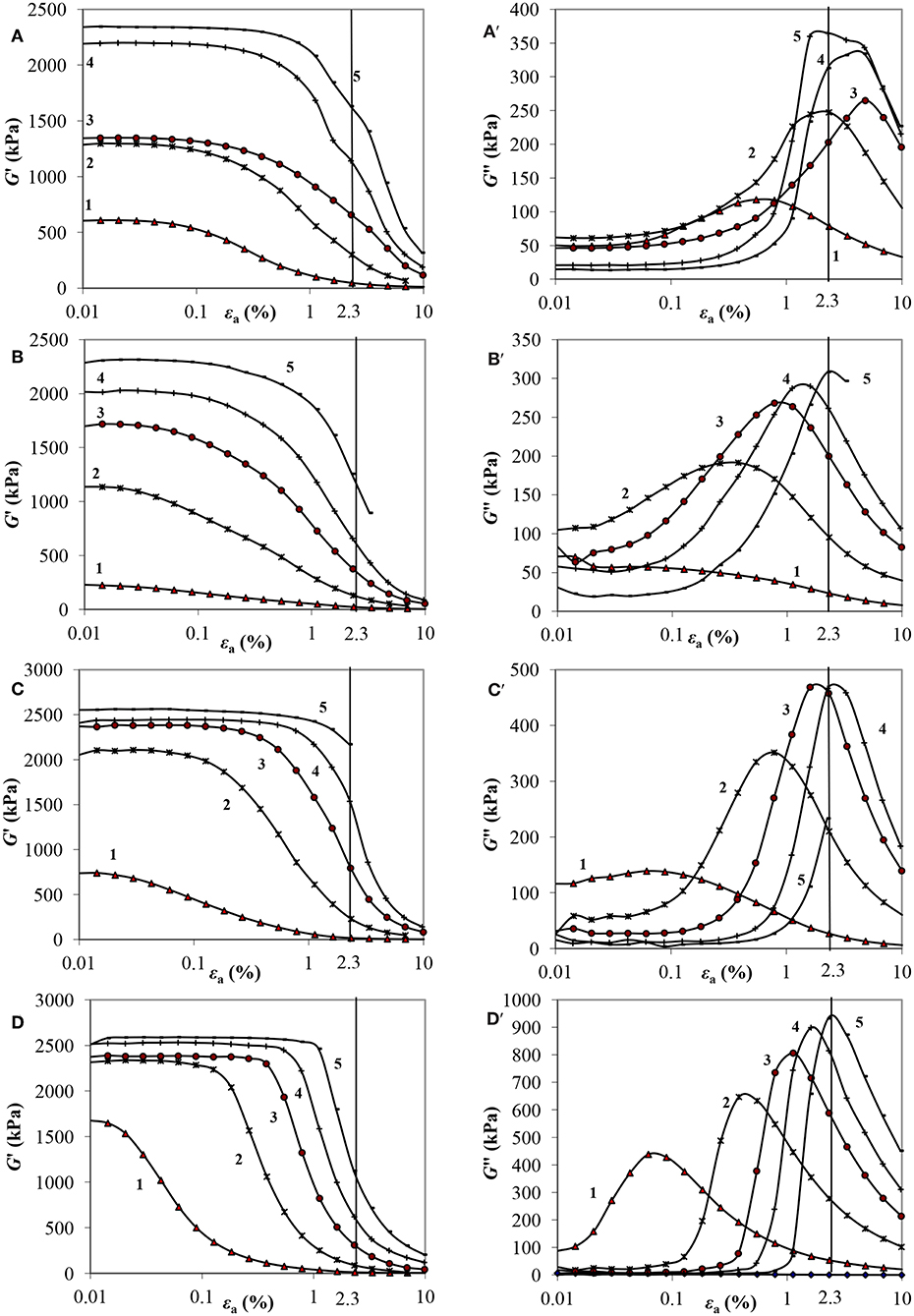
Figure 5. Dependences of the components of the complex shear modulus on the deformation amplitude at different magnetic field induction (A,A′—MRF-1; B,B′—MRF-2; C,C′—MRF-3; D,D′—MRF-4): 1-B = 100 mT, 2-300, 3-500, 4-700, 5-1,000.

At small strains (up to 1%), the storage modulus G′ does not change with an increase in the amplitude of the strain (linear range). In a magnetic field with an induction B = 1,000 mT, G′ is 2,000–2,300 kPa for all samples, increasing by 1–2 orders of magnitude compared with the values in the absence of a field. As the strain amplitude increases, the values of G′ fall sharply, decreasing by more than an order of magnitude. The MRF-1 has a less sharp fall. G″ with increasing of ε_a increases to the value of the deformation amplitude, at which the most rapid decrease in the value of G′ takes place. With increasing magnetic field induction, the values of the loss modulus G″ for all MRF samples increase by 1–2 orders of magnitude. The values of the maxima of G′′_max at that move in the region of large deformation amplitudes. The maximum values of the loss modulus G′′_max are characteristic for all samples at B = 1,000 mT and ε_a ≈ 3%. The smallest values of G′′_max ≈ 300–350 kPa for MRF-1 and MRF-2, containing aerosil, the highest (almost 1,000 kPa) are for MRF-4, containing bentonite clay.

Let us consider the dependences of the components of the complex shear modulus on the magnetic field induction at a certain constant amplitude of the shear strain. Figure 6 shows such a relationship with ε_a equal to 0.01%. The loss modulus (Figure 6B) has a maximum at some intermediate value B, then decreases. With increasing magnetic field induction, the size of the structured aggregates of particles of the dispersed phase increases and the viscous resistance to shear grows. With a further increase in B, almost all the aggregates are connected in solid structures, the MRF is in a solid-like state with a predominantly elastic shear resistance, which corresponds to an increase in G′ to maximum values for different B for each MRF.

FIGURE 6

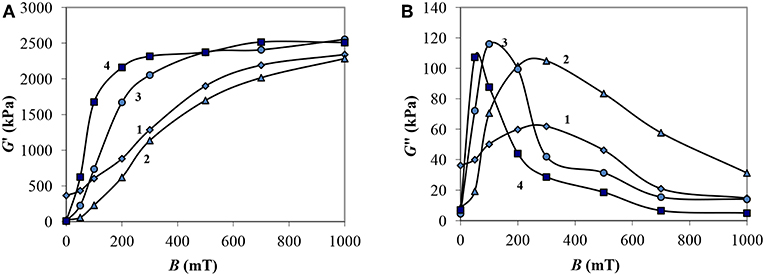
Figure 6. Dependencies of the storage modulus G′ (A) and loss modulus G″ (B) of MRF on the magnetic field induction at the strain amplitude ε_a = 0.01%: 1—MRF-1; 2—MRF-2; 3—MRF-3; 4—MRF-4.

With increasing magnetic field induction in the region of small deformations, an increase in the storage modulus of MRF-1 and MRF-2, containing aerosil particles, occurs in all range of B, unlike other samples, where G′ increases in the range up to 200 mT and at higher induction reaches its maximum. In this case, the loss modulus reaches a maximum at induction of 200–300 mT, greater than that of other samples (up to 100 mT), which is apparently caused by the resistance of the aerosil matrix to structuring magnetic particles, which is achieved only in strong fields, at B > 500 mT. So, with an increase in the magnetic field induction up to 200 mT, the values of G′ reach 2,000 kPa for MRF-4, for MRF-3 G″ ≈ 1,500 kPa, for MRF-1 G′ ≈ 880 kPa, for MRF-2 G″ ≈ 620 kPa.

In Figure 7 the dependence of the components of the complex shear modulus on the induction of the magnetic field at a strain amplitude of 2.3%, corresponding to the intensive destruction of the structure as a result of external influence is shown.

FIGURE 7

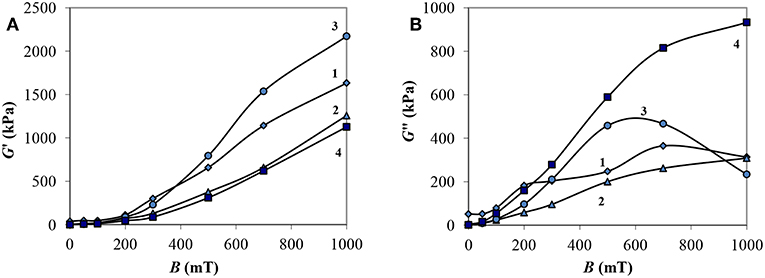
Figure 7. Dependencies of the storage modulus G′ (A) and loss modulus G″ (B) of MRF on the magnetic field induction at the strain amplitude ε_a = 2,3%: 1—MRF-1; 2—MRF-2; 3—MRF-3; 4—MRF-4.

It can be seen that the storage modulus increases smoothly with an increase in the intensity of the external field for all MRF compositions. The storage modulus reaches greatest value in MRF-3, containing chromium dioxide. The loss modulus of this material has a maximum at a value of B ~600–700 mT, with greater induction it decreases. In other MRF samples, an increase in G″ values was observed in the entire range of magnetic induction. The smallest values of G′ and the largest ones of G″ are in MRF-4 containing bentonite clay. At the same time, with small deformations, MRF-4, on the contrary, has the largest values of G′. The composition with bentonite clay has the strongest structure at rest, however, when subjected to shear deformations, it reveal a sharp destruction with the greatest energy losses among the materials studied. The presence of fine ferrimagnetic particles of chromium dioxide (MRF-3) prevents deformation fracture and increases the role of the elastic component of the material.

In Figure 8 the dependences of the strain amplitude ε_l, at which the loss moduli are maximal, that is, at this strain, the greatest viscous losses are recorded (Figure 5), on the magnetic field induction are shown.

FIGURE 8

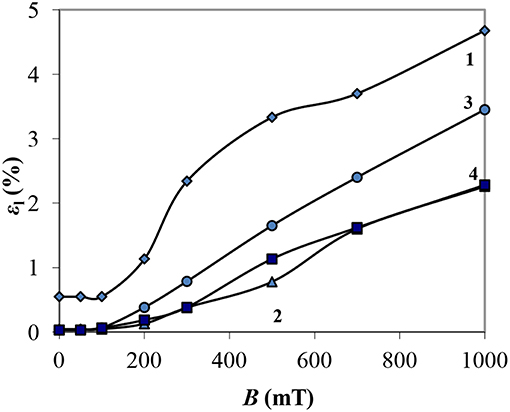
Figure 8. Dependences of the strain amplitude ε_l at the maximum value of the loss modulus from the magnetic field induction B: 1—MRF-1; 2—MRF-2; 3—MRF-3; 4—MRF-4.

It can be seen that with the induction of a magnetic field up to 100 mT, ε_l practically does not change, then grows with increasing B. MRF-1, containing aerosil, experiences intense structural destruction with large vibration amplitudes than other samples (curve 1) in the entire range B. Aerosil particles contribute to the formation of a more elastic structure capable of elastically deforming to large deformations.

Conclusion

For the purpose of application for controlled damping of layered structures with MRF in various shear modes, four compositions with additions of aerosil, chromium dioxide, and bentonite clay were investigated. The features of the rheological behavior of the MRF at continuous shear, linear increase of shear stress, sinusoidal tangential oscillations depending on the material of additives and magnetic field induction are established.

It has been established that in the continuous shear mode, the composition of MRF with bentonite clay shows a smooth increase in the shear stress with increasing shear rate, thus providing a greater range of its regulation.

In the mode of linear increase of shear stress when chromium dioxide is added to the carbonyl iron, the material shows greater structure strength compared to other compositions.

It is determined in the mode of shear oscillations that the optimal range of the magnetic field induction, in which the greatest change in the viscoelastic characteristics of the MRF takes place, is up to 300 mT. The use of bentonite clay in MR fluid provides the largest increase in loss modulus (from 1 to almost 1,000 kPa) in a magnetic field with strain amplitude in the non-linear region compared with other additives. This allows to recommend this composition for the creation of controlled damping of flat structural elements. The addition of chromium dioxide to the carbonyl iron into MRF allows one to achieve the greatest increase in the elasticity of the material in a magnetic field and, consequently, increase the rigidity of the structure with its use. MRF using bentonite clay in a linear zone of elasticity shows the values of the modulus of elasticity, close to the values for MRF with chromium dioxide.

The possibility of making a more targeted adjustment of the complex composition of the MRF by introducing additional particles of magnetic and non-magnetic nature makes it possible, for all the considered shear modes, to determine the features of their use in layered structural elements depending on the assigned tasks—increasing rigidity or damping, as well as yield stress.

Author Contributions

EK proposed the idea and supervised the work. MZ performed the experiments. They also wrote the manuscript. ZN prepared the MRF samples. All authors performed data analysis.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahamed, R., Choi, S.-B., and Ferdaus, M. M. (2018). A state of art on magneto-rheological materials and their potential applications. J. Intell. Mater. Syst. Struct. 29, 2051–2095. doi: 10.1177/1045389X18754350

CrossRef Full Text | Google Scholar

Akhtar, M., Alam, S., and Mohd, F. (2015). Fuzzy rules incorporated skyhook theory based vehicular suspension design for improving ride comfort. Int. J. Eng. Res. Appl. 5, 30–36.

Google Scholar

Ashtiani, M., and Hashemabadi, S. H. (2015). The effect of nano-silica and nano-magnetite on the magnetorheological fluid stabilization and magnetorheological effect. J. Intell. Mater. Syst. Struct. 26, 1887–1892. doi: 10.1177/1045389X15580659

CrossRef Full Text | Google Scholar

Chu, S. Y., Soong, T. T., and Reinhorn, A. M. (2005). Active, Hybrid and Semi-Active Structural Control. New York, NY: John Wiley and Sons.

Google Scholar

Dong, Y. Z., Hao, P. S., Zhang, K., and Choi, H. J. (2018). Effect of CoFe₂O₄ nanoparticles on a carbonyl iron based magnetorheological suspension. Colloids Surf. A 537, 102–108. doi: 10.1016/j.colsurfa.2017.10.017

CrossRef Full Text | Google Scholar

Fu, J., Li, P., Liao, G., Lai, J., and Yu, M. (2018). Active/semi-active hybrid isolation system with fuzzy switching controller. J. Intell. Mater. Syst. Struct. 29, 101–115. doi: 10.1177/1045389X17733054

CrossRef Full Text | Google Scholar

Iglesias, G. R., Roldán, A., Reyes, L., Rodríguez-Arco, L., and Durán, J. D. G. (2015). Stability behavior of composite magnetorheological fluids by an induction method. J. Intell. Mater. Syst. Struct. 26, 1836–1843. doi: 10.1177/1045389X15577656

CrossRef Full Text | Google Scholar

Korobko, E., Novikova, Z., Zhurauski, M., Kazak, H., and Dragašius, E. (2014). Investigation of elasticity of magnetosensitive adaptive materials for laminated composite structures. Mechanika 20, 466–470. doi: 10.5755/j01.mech.20.5.7080

CrossRef Full Text | Google Scholar

Leong, S. A. N., Samin, P. M., Idris, A., Mazlan, S. A., and Rahman, A. H. A. (2016). Synthesis, characterization and magnetorheological properties of carbonyl iron suspension with superparamagnetic nanoparticles as an additive. Smart Mater. Struct. 23:123001. doi: 10.1088/0964-1726/25/2/025025

CrossRef Full Text | Google Scholar

Li, Y., Li, J., Li, W., and Du, H. (2014). A state-of-the-art review on magnetorheological elastomer devices. Smart Mater. Struct. 23:123001. doi: 10.1088/0964-1726/23/12/123001

CrossRef Full Text | Google Scholar

Librescu, L., and Hause, T. (2000). Recent developments in the modeling and behavior of advanced sandwich constructions: a survey. Composite Struct. 48, 1–17. doi: 10.1016/S0263-8223(99)00068-9

CrossRef Full Text | Google Scholar

Megha, S., Kumar, S., and D'Silva, R. (2016). Vibration analysis of magnetorheological elastomer sandwich beam under different magnetic fields. J. Mech. Eng. Autom. 6, 75–80. doi: 10.5923/c.jmea.201601.14

CrossRef Full Text | Google Scholar

Nayak, B., Dwivedy, S. K., and Murthy, K. S. R. K. (2013). Vibration analysis of a three-layer magnetorheological elastomer embedded sandwich beam with conductive skins using finite element method. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 227, 714–729. doi: 10.1177/0954406212451812

CrossRef Full Text | Google Scholar

Song, S. (2009). Cost-effective skyhook control for semiactive vehicle suspension applications. Open Mech. Eng. J. 3, 17–25. doi: 10.2174/1874155X00903010017

CrossRef Full Text | Google Scholar

Tian, T. F., Zhang, X. Z., Li, W. H., Alici, G., and Ding, G. (2013). Study of PDMS based magnetorheological elastomers. J. Phys. Conf. Ser. 412:012038. doi: 10.1088/1742-6596/412/1/012038

CrossRef Full Text | Google Scholar

Zhou, G. Y. (2003). Shear properties of a magnetorheological elastomer. Smart Mater. Struct. 12, 139–146. doi: 10.1088/0964-1726/12/1/316

CrossRef Full Text | Google Scholar