On the Interrelationship Between Static and Vibration Mitigation Properties of Architected Metastructures

Continuous demand for improvement of material performance in structural applications pushes the need for materials that are able to fulfill multiple functions. Extensive work on effective static properties of different architected materials have shown their ability to push the modulus-density design space, in terms of high effective moduli at low relative density. On the other hand, variations in geometry allow for these materials to manipulate mechanical wave propagation, producing band gaps at certain frequency ranges. The enhanced static and vibration properties of architected metamaterials make them ideal candidates for multi-functional purposes. In this paper, we take inspiration from the mass-efficient static behavior of different lattice geometries to fully explore the capabilities of a periodic and locally resonant metastructure design platform. We numerically study the influence of four different lattice topologies on the dynamic and static behavior of metastructures that combine a periodic lattice geometry with locally resonant inclusions. We analyze the influence of lattice geometry on band gap frequencies in terms of the lattice effective static properties. We show that vibration mitigation over a wide range of frequencies is achieved by tailoring the lattice geometry for constant unit cell mass and size. Specifically, by selectively placing material inside the unit cell, we achieve up to a 6-fold change of lower edge band gap frequency and up to an 8-fold change of normalized band gap width, for metastructures with low-density lattices. We introduce multi-functional performance parameters to evaluate the metastructures in terms of their effective static stiffness and band gap properties. These parameters can inform the design of tailored materials that have desired mechanical and dynamic properties for applications in e.g., aerospace and automotive components, and energy infrastructure.

Introduction

Modern engineering continuously pushes the need for higher levels of mass efficiency. Light, load bearing materials on aerospace, aircraft, and automotive components are fundamental for the pursuit of higher performing systems. In addition, vibration propagation control is not only crucial for customer satisfaction, especially in aircraft, and automotive systems, but also for the safety of the components such us protecting satellites or electronic equipment from their dynamic environment during satellite launch. In many cases, suppressing vibrations typically require additional damping material or active control mechanisms. A stiff, mass efficient material that additionally includes vibration control capabilities can avoid the need to add alternative vibration attenuation mechanisms.

Architected materials have shown enhanced static properties as well as the ability to control elastic wave propagation, making them ideal for multifunctional applications. On one hand, they have opened up new areas of the material property space. This, in addition to evolving 3D printing techniques that enable their manufacturing, have motivated researchers to explore a variety of architectures (Schaedler and Carter, 2016) ranging from lattice topologies (Gibson and Ashby, 1997; Deshpande et al., 2001b; Luxner et al., 2004; Moongkhamklang et al., 2010; Vigliotti and Pasini, 2012; Zheng et al., 2014), foam-like metamaterials (Berger et al., 2017) triply periodic minimal surface geometries (Wang et al., 2011; Dalaq et al., 2016), hierarchical structures (Doty et al., 2012; Meza et al., 2015), honeycomb structures (Gibson and Ashby, 1997; Wadley, 2006; Fleck et al., 2010), and woven topologies (Erdeniz et al., 2015; Ryan et al., 2015; Zhang et al., 2015).

On the other hand, through Bragg scattering and local resonance phenomena, architected materials have shown to support band gap formation (Deymier, 2013; Hussein et al., 2014 and references therein; Bayat and Gaitanaros, 2018). Particularly, recent efforts have been made targeting low and broadband band gaps. Wang et al. (2015) demonstrated that locally resonant band gaps can be achieved in 2D periodic lattices by tuning their connectivity; D'Alessandro et al. (2016) and D'Alessandro et al. (2018) developed a 3D single-phase phononic crystal that shows ultra-wide complete band gaps. Taniker and Yilmaz (2015) use inertial amplification mechanisms to obtain wide and low frequency band gaps in an octahedron lattice.

These enhanced dynamic and static properties make architected materials promising for multifunctional applications. For example, previous investigations have explored architected materials with static, thermo-mechanical and energy absorption properties (Evans et al., 1998, 2001; Wadley, 2006; Valdevit et al., 2011; Wang et al., 2011, 2017; Dou et al., 2018), tunable Poisson's ratio and vibration mitigation (Chen et al., 2017), and honeycomb sandwich panel structures that are stiff and can attenuate noise (Han et al., 2017; Tang et al., 2017). The relationship between static and band gap properties of architected materials has also been studied in the literature (Phani et al., 2006; Nemat-Nasser et al., 2011).

Here we build on this prior work, and we present a systematic comparison of static elastic properties to band gap properties in metastructures, and a way to interpret the band gap frequencies in terms of local static effective properties of their constituents. To do this, we expand the design space of metastructures that combine geometric lattices with embedded resonators, originally introduced in Matlack et al. (2016). We study this metastructure design because it has numerically and experimentally shown to support tailorable band gaps through small manipulations of its lattice geometry. Band gaps in these metastructures are bounded between acoustic modes and optical modes, which makes them particularly suitable for achieving low frequency band gaps. Further, it is a 3D structure so it could conceivably be incorporated into structural components, and a straightforward manufacturing procedure was previously introduced to fabricate these metastructures (Matlack et al., 2016). The main objectives of this paper are to show how this metastructure design platform can achieve band gaps across different frequency ranges, to understand why different metastructures have different band gaps, and to understand the trade-offs between their band gap frequencies and widths and their static stiffness.

In this article, we analyze four different lattice-resonator metastructures with different lattice topologies: cubic, Kelvin, octet and idealized foam. We use finite element methods (FEM) to numerically analyze their static and dynamic behaviors. We analyze the effective static properties of both the individual lattices and the metastructures, for lattice relative densities ranging from 1% to 28%. We analyze wave propagation through metastructures with 1D periodicity, to understand the influences of lattice geometry and relative density on their band gaps. Modal analysis is used to qualitatively explain the differences in the dispersion curves in terms of the interaction between the lattice and resonators, as well as lattice effective properties. We calculate vibration transmission through finite metastructures to study the efficiency of wave mitigation. Finally, we compare the metastructure's dynamic performance in terms of their broadband and low-frequency band gap characteristics and introduce multifunctional performance parameters that evaluate the metastructures in terms of their vibration mitigation behavior and static stiffness.

Metastructure Geometries

The metastructures studied combine a periodic lattice geometry with embedded local resonators, introduced previously (Matlack et al., 2016). These metastructure unit cells (Figure 1B) are composed of an array of lattice unit cells modeled as polycarbonate (Figure 1A) with an embedded solid steel cube resonator. Four different lattice unit cells are studied: idealized foam (Gibson and Ashby, 1982), Kelvin or tetrakaidekahedron, cubic, and octet (Figure 1A). The metastructure unit cells studied contain a 5L x 5L x 6L array of the lattice (Figure 1B). Note the 6L dimension along the length is to accommodate the idealized foam geometry configuration.

FIGURE 1

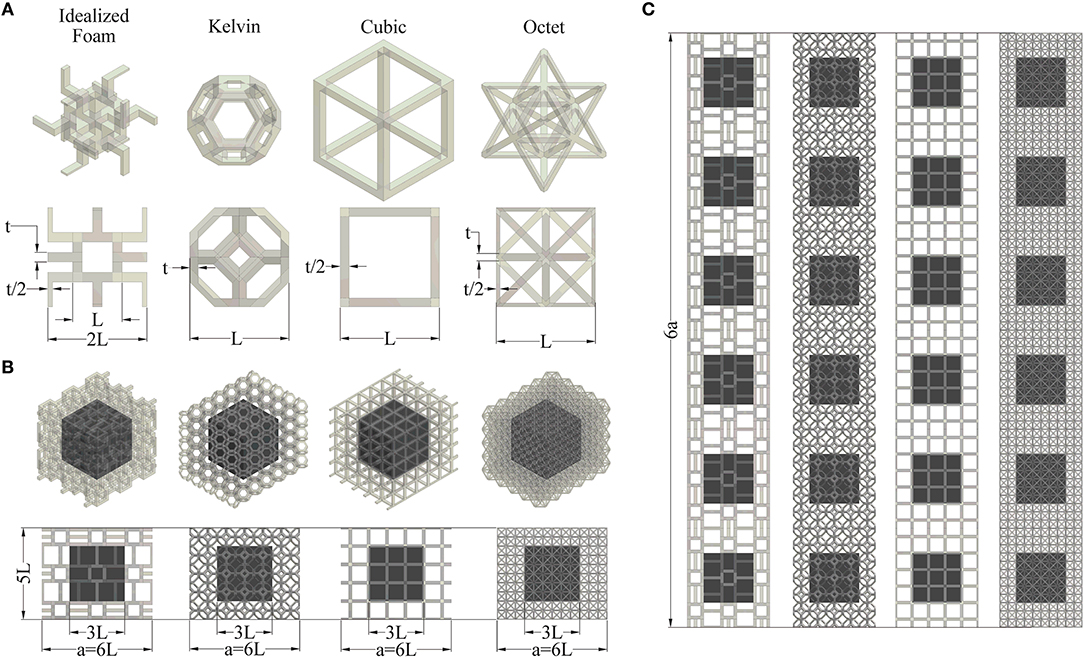
Figure 1. Metastructure geometries. (A) Lattice unit cells. (B) Metastructure unit cells. (C) Finite metastructures.

The idealized foam lattice is based on the geometry originally proposed by Gibson and Ashby (Gibson and Ashby, 1982). It is designed to contain 3 struts at each node in order to introduce bending deformations in a cubic unit cell, which results in a modified cubic unit cell of 2L to maintain a cube side length of L. All other lattices geometries contain a unit cell length of L. Finite metastructures explored in the multifunctional analysis are configured as 6 metastructure unit cells in length (Figure 1C) since it has been shown that this is enough to approximate band gaps of an infinitely periodic medium (Matlack et al., 2016).

The static properties of the lattice geometries and the static and dynamic properties of the metastructures are evaluated in terms of the relative density of their lattice unit cells (ρ_rel). We hold the lattice unit cell length (L) constant and vary the thickness (t) to achieve lattice relative densities from 1% to 28% without changing the metastructure periodicity constant (a). Geometry dimensions of the lattices are given in Table 1.

TABLE 1

Table 1. Dimensions of the metastructures studied.

We must explicitly point out that ρ_rel does not include the resonator, whose mass and size remains constant across all metastructures presented here. Including the resonator, the metastructure relative densities studied here range from 61% to 72%, where 100% relative density represents the steel resonator embedded in bulk polycarbonate. We present results in terms of lattice relative density to highlight the differences in band gaps that can be achieve due only to differences in geometry, while keeping the total mass constant. This treatment also allows us to confirm the lattice unit cell static results to those in the literature (e.g., Gibson and Ashby, 1982; Deshpande et al., 2001b; Luxner et al., 2004; Zheng et al., 2014), and to interpret band gaps of the metastructures in terms of the lattice unit cell properties. However, a fair comparison with other vibration mitigation materials should be done in terms of the metastructure relative density, and not the lattice relative density. To address this, we include metastructure relative density as a reference in figures related to metastructure properties.

Static Property Results

Lattice Static Properties

Prior work has shown the ability to open new areas of the stiffness-relative density space through lattice materials, e.g., (Gibson and Ashby, 1982; Deshpande et al., 2001b; Luxner et al., 2004; Zheng et al., 2014). Furthermore, at low relative densities where the strut cross section is small compared to its length and the effects of vertex stiffness do not play a major role, the scaling laws of static effective properties of the lattice material can be described by the following power-law approximations (Gibson and Ashby, 1997):

$\begin{array}{cc}\frac{E_{lattice}}{E_s}=C{\rho }_{rel}{}^n& (1)\end{array}$

$\begin{array}{cc}\frac{G_{lattice}}{E_s}=D{\rho }_{rel}{}^r& (2)\end{array}$

where ρ_rel is the lattice relative density, C, D, n, and r are proportionality constants and scaling exponents that depend on the lattice geometry, E_s is the Young's modulus of the bulk material and E_lattice and G_lattice are the lattice effective Young's and shear moduli, respectively. Lattice materials can be further classified into bend- and stretch-dominated structures, depending on the predominant deformation of their struts when exposed to external loading (Deshpande et al., 2001a). Effective moduli of bend-dominated lattices have a quadratic dependence on relative density (n = 2, r = 2) while effective moduli of stretch-dominated lattices have a linear dependence (n = 1, r = 1).

Here, we characterize the effective moduli of the four lattice geometries (without an embedded resonator) presented in Figure 1A. We will use these lattice properties to understand the static and dynamic behavior of the metastructures. Results are plotted in double logarithmic scale in Figure 2 and calculated scaling exponents n and r and proportionality constants C and D are presented in Table 2.

FIGURE 2

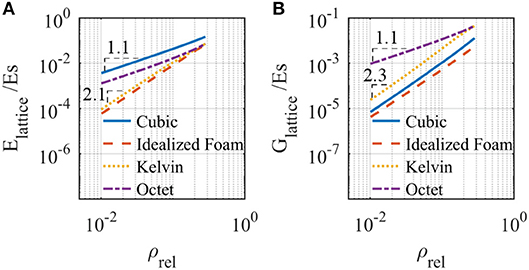
Figure 2. Lattice effective mechanical properties in terms of lattice relative density. Effective (A) Young's modulus and (B) shear modulus.

TABLE 2

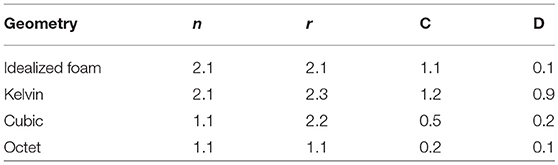
Table 2. Scaling exponents and proportionality constants for power-law approximations of E_lattice and G_lattice for the four lattice geometries.

We observe a stretch-dominated behavior of the octet lattice and bend-dominated behaviors of Kelvin and idealized foam lattices, consistent with many prior works (Gibson and Ashby, 1982; Deshpande et al., 2001b; Luxner et al., 2004; Zheng et al., 2014). The cubic lattice exhibits a mixed behavior. Under tension or compression, its behavior is stretch-dominated since the struts parallel to the applied force compress while the perpendicular ones have a negligible deformation. However, under shear deformation, struts perpendicular to the load direction bend, and struts parallel to the load direction have negligible deformation, thus its behavior is bend-dominated.

This behavior applies to the low relative density range (up to about 15%). At larger lattice relative densities, the rigidity of the vertex has a larger influence, i.e., bending deformation in stretch-dominated structures and axial deformation in bend-dominated structures cease to be negligible. The moduli at higher relative densities gradually deviate from the presented approximations.

Metastructure Static Properties

We calculate the static stiffness, K_static, of finite metastructures shown in Figure 1C. The finite metastructures have a beam like geometry, thus we can numerically calculate effective axial (K_axial), bending (K_bend) and torsional (K_tors) stiffnesses using the force-displacement relations that define static stiffness of a conventional cantilever beam (see section Finite Metastructure Static Stiffness). We characterize K_static for metastructures to (1) understand the influence of E_lattice and G_lattice (lattice static properties) on K_static (metastructure static properties), and (2) to characterize the multifunctional properties of finite metastructures in terms of their static and dynamic (band gap) properties. We focus on stiffness properties of metastructures (as opposed to modulus values) because due to their beam-like geometry, we can characterize the metastructure static behavior in terms of well-known concepts of beam axial, bending and torsional stiffness.

The calculated K_static of the metastructures as a function of lattice relative density (Figure 3) follow the power-law approximation in Equation 1 for lattice effective properties. We observe that the scaling exponents of K_axial (Table 3) agree with those of E_lattice (Table 2). Thus, we infer that K_axial ∝ E_lattice. In the same way, agreement of scaling exponents of K_tors (Table 3) with those of G_lattice (Table 2) suggest that K_tors ∝ G_lattice. For K_bend, both E_lattice and G_lattice seem to be involved. The transition in slope in the double logarithmic scale of the cubic metastructure (Figure 3B) from 1.6 to 1.3 suggests a stronger dependence on E_lattice with increasing lattice relative density. This is consistent with shear deformations observed at lower lattice relative density (Figure 3D) that decrease in magnitude at higher lattice relative density values (Figure 3E). Note the transition is not present in other lattices due to the similar scaling exponents of their E_lattice and G_lattice.

FIGURE 3

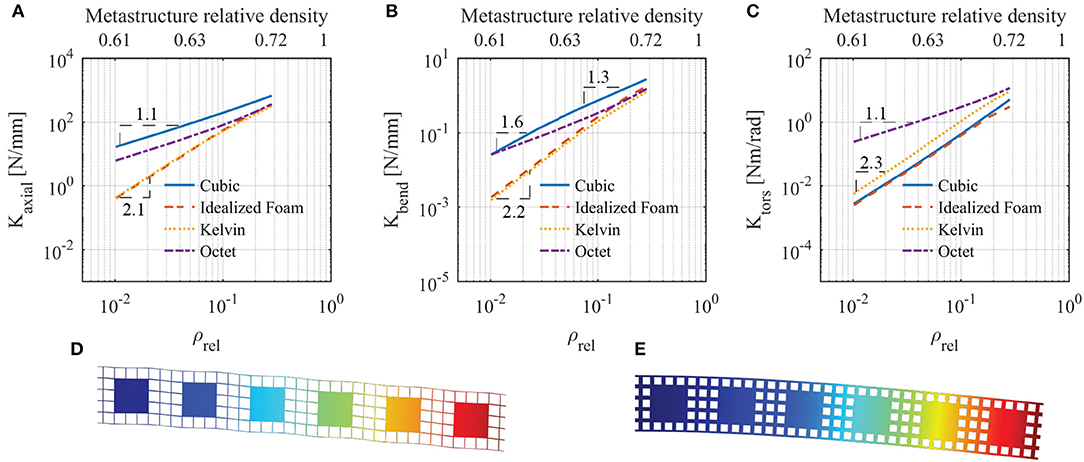
Figure 3. Finite metastructures mechanical properties. (A) K_axial (B) K_bend (C) K_tors (D) Deformation of cubic finite metastructure with 1% relative density under bending. (E) Deformation of cubic finite metastructure with 28% relative density under bending. Metastructure relative densities are shown for comparison.

TABLE 3

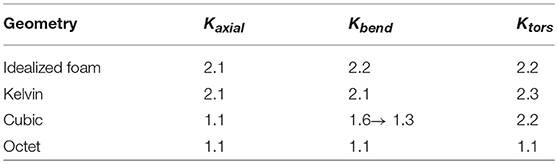
Table 3. Scaling exponents for power-law approximations of axial, bending, and torsional stiffness of finite metastructures.

While we keep the resonator size constant throughout all static analyses of finite metastructures in this work, it should be noted that the size of the resonator changes K_static. The resonator stiffens the lattice within the metastructure at the lattice-resonator interface, resulting in an overall increase in K_static. An increase in resonator surface area increases K_static, and an increase in resonator volume also increases K_static since the resonator material is significantly stiffer than that of the lattice. As we decrease resonator size, K_static asymptotically approaches values of K_static for a metastructure made purely of lattice material without a resonator.

Wave Propagation in Metastructures

Band Gaps

The dispersion relations and modal displacements of the four different metastructures for a lattice relative density of 8.3% are presented in Figure 4. In order to achieve the same lattice relative density and constant unit cell size across all geometries, we use different lattice thicknesses for the different metastructures. Dispersion curves show that the selective placement of the material inside the lattice unit cell space results in considerable differences in band gaps of the metastructures. The lower edge of the band gap ranges from 1,099 Hz in the idealized foam metastructure to 2579Hz in the octet metastructure. This is about a 2-fold difference without any change in total mass. In the same manner, normalized band gap widths range from 101% in the octet metastructure to 37% in the cubic metastructure (about a 3-fold change in normalized band gap width). These metastructures show a large range of their band gap properties while keeping the total mass constant, solely due to the difference in lattice geometry.

FIGURE 4

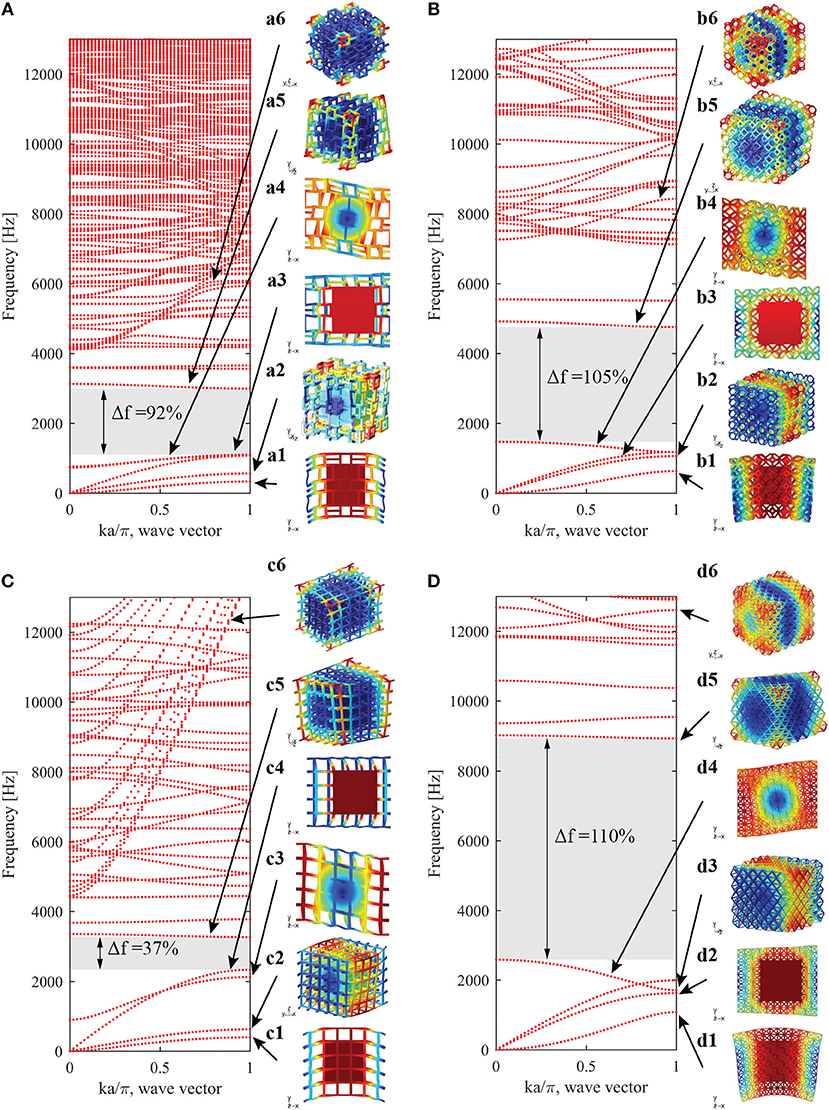
Figure 4. Dispersion relations and modal displacement for the different metastructures with lattice relative density equal to 8.3%. (A) Idealized foam. (B) Kelvin. (C) Cubic (D) Octet. (Modal displacements are taken at ka/π = 1).

Analyzing Band Gaps in Terms of Lattice Static Properties

Analysis of the modal displacements presented in Figure 4 shows that the band gaps are generated between lower frequency resonator modes, where most of the modal mass is concentrated in the resonator, and higher frequency lattice modes, where modal mass is concentrated in the lattice. We observe four low-frequency resonator modes: two bending modes, one torsional mode, and one axial mode. As an example, we analyze these modes and their dependence on lattice static properties through the example of the octet metastructure (Figure 5). However, this analysis can be extended to other metastructure geometries since, as we observe in Figure 4, they show analogous modal displacements to that of the octet.

FIGURE 5

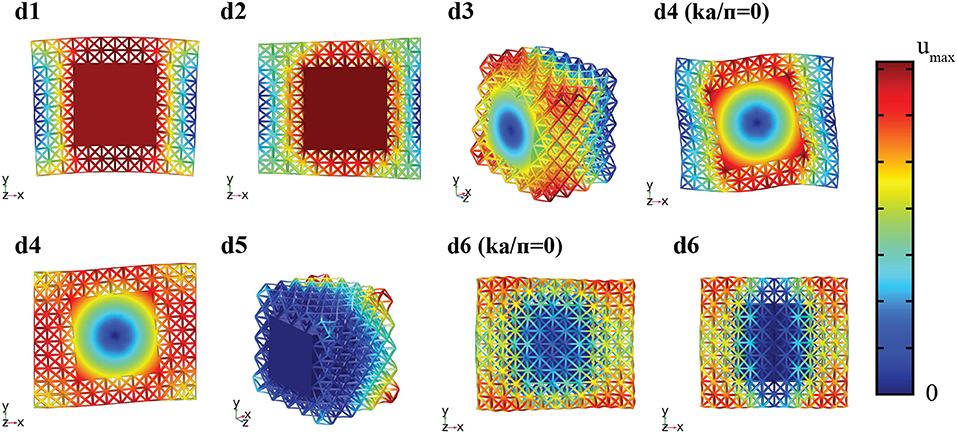
Figure 5. Detailed view of octet modal displacements, according to Figure 4. Geometries are cross-sectioned for a better description of motion. Modal displacements are taken at ka/π = 1 unless specified.

Resonator Modes

The first bending resonator mode (Figures 4a1,b1,c1,d1) is characterized by a translation of the resonator perpendicular to the axis of wave propagation. In this dispersion branch, there are actually two degenerate bending modes due to symmetry and material isotropy. The modal displacements reveal that the transverse motion of the resonator produces shearing of the lattice units to the left and right of the resonator (Figure 5d1). From this observation, we infer that the modal stiffness of this mode will be proportional to G_lattice. This is consistent with the fact that the frequency at the band edge increases with increasing G_lattice (in ascending order: idealized foam, cubic, Kelvin, octet).

The second resonator bending mode (Figures 4 a4,b4,c3,d4) is characterized by a rotation of the resonator about an axis perpendicular to the axis of wave propagation. Like the first bending mode, there are two of these modes (rotation about the y and z-axis), which are degenerate. Because of its higher order nature, this mode does not start from the origin of the dispersion diagram, thus it is interesting to inspect its evolution along the wavenumber spectrum. At ka/π = 0 (long wavelength regime) the Floquet boundary conditions (see section Dispersion Relations) impose equal displacement fields on the two faces of periodicity. As a result, the rotation of the resonator generates shearing of the lattice units that surround it (Figure 5d4 (ka/π = 0)). The deformation of the unit cells suggest that the modal stiffness of this mode is dominated by G_lattice. At ka/π = 1, the Floquet boundary condition impose displacement fields of the periodic faces to be equal in magnitude and opposite in sign. Here, we observe relative displacement in the y-direction (or z for the analogous mode) between lattice units in front of and behind the resonator as it rotates. These units now stretch or compress (depending on their location) and the shear deformation of top and bottom lattice units seems to be reduced (Figure 5d4). From analyzing the mode shapes, we predict that modal stiffness will transition from being proportional to G_lattice to being proportional to E_lattice, as wavenumber increases. We observe that as G_lattice increases so do the frequencies of this mode at the long wavelength edge (idealized foam, cubic, Kelvin, octet in ascending order). Frequencies at the low wavelength edge increase with E_lattice (idealized foam, Kelvin, octet, cubic in ascending order). Cubic and idealized foam metastructures exhibit a positive slope of this mode whereas octet and Kelvin metastructures have a negative slope. The relationship between E_lattice and G_lattice of individual lattices does not solely explain why the sign of the slope of this mode varies among metastructures, so there must be additional influences related to how strongly the lattice properties contribute to modal stiffness and differences in modal mass at ka/π = 0 compared to ka/π = 1.

The torsional resonator mode (Figures 4a2,b2,c2,d3) consists of the rotation of the resonator about the axis of wave propagation. This mode involves shear deformation of the lattice unit cells (Figure 5d3). The modal displacement increases with x-distance from the resonator, and the lattice units immediately surrounding the resonator simply rotate without any deformation. We look once more at the dispersion diagram and confirm that the frequency of this mode increases with G_lattice (in ascending order: idealized foam, cubic, Kelvin, octet).

In the axial resonator mode (Figures 4a3,b3,c4,d2) the resonator translates in the direction of wave propagation. The lattice deforms under both shear and compression/tension depending on their location (Figure 5d2). While lattice unit cells to the left and right of the resonator compress and stretch, unit cells located at the top and bottom of the resonator shear. The modal stiffness of this mode is thus dictated by both E_lattice and G_lattice. We inspect the dispersion relations and observe that frequencies of this mode increase with E_lattice + G_lattice (in ascending order: idealized foam, Kelvin, octet, and cubic). Note this mode was used in prior work to change the number of beams undergoing stretch, to preferentially lower the band gap (Matlack et al., 2016).

We gather further supporting evidence of the effects of lattice effective properties on the metastructure band gaps by observing how modal stiffness of each mode evolves with lattice relative density. Following the form of lattice and metastructure static properties, we predict that the modal stiffness will follow a power-law behavior with respect to the lattice relative density. We calculate the scaling exponents of the best-fit curve of modal stiffness vs. lattice relative density and present them in Table 4. We observe that scaling exponents of the 1st bending mode agree quite well with those of G_lattice (Table 2) for all metastructures. Thus, the modal stiffness 1st bending mode is proportional to G_lattice. Similarly, we find agreement between scaling exponents of 2nd bending (ka/π = 0) modal stiffness and E_lattice, 2nd bending (ka/π = 1) modal stiffness and G_lattice, 1st torsional modal stiffness and G_lattice. The 1st axial modal stiffness depends on both E_lattice and G_lattice and so it requires special attention. For all lattices except the cubic, their scaling exponents are the same for both E_lattice and G_lattice and they agree with that of 1st axial modal stiffness. In the cubic case, we observe agreement between cubic E_lattice and 1st axial modal stiffness scaling exponent. This is because the cubic E_lattice is large compared to its G_lattice and the effects of G_lattice become negligible.

TABLE 4

Table 4. Scaling exponents for power-law approximations of modal stiffness vs. relative density.

By analyzing the mode shapes, we conclude that the modal stiffness of the resonator modes depends strongly on the effective properties of the lattice. The first bending modes are dominated by the G_lattice, the second bending modes transition from being dominated by G_lattice to being dominated by E_lattice, the axial mode is dominated by a combination of E_lattice and G_lattice and the torsional mode is dominated by the G_lattice. Since the lower edge of the band gap in these metastructures are generally dominated by the resonator modes, this gives us a way to estimate the lower edge frequency range or inform the design of the metastructure to tune the lower edge of the band gap to the desired frequency range.

Lattice Modes

In the metastructure's high frequency range, the resonator's displacement is negligible, and the modal displacement is isolated in the lattice units (Figures 4a5-6,b5-6,c5-6,d5-6). Since the modal mass is much smaller than that of the resonator modes, these modes are generated at higher frequencies. As observed in Figure 4 there are numerous upper lattice modes. Since we are interested in low frequency band gaps, we will only analyze those that define the upper edge of the first full and polarized band gaps (see section Performance Parameters for polarized band gap definition).

Torsional and full band gaps upper edge is defined by the second torsional mode (Figures 4a5,b5,c5,d5). Taking a closer look at the modal displacements it can be observed that since the resonator has small movement so do the faces of the lattice units attached to it (Figure 5d5). The displacement of the rest of the unit cell is parallel to the resonator's face and increases further away from it. The displacement visually approximates shearing of the lattice unit cells, so we hypothesize that this upper mode modal stiffness should primarily depend on G_lattice. We inspect the dispersion diagrams and find that the upper mode frequencies increase with G_lattice (idealized, cubic, Kelvin, octet in ascending order). This is further supported by the good agreement, for all topologies, between scaling exponents of the modal stiffness of the 2nd torsional mode (Table 4) and G_lattice (Table 2).

Upper edge of the axial band gaps is defined by the second axial mode in the long wavelength region (Figures 4a6, b6, c6,d6). As in the second torsional mode, we observe shearing of the units that surround the resonator (Figure 5d6 (ka/π = 0)). Thus, we predict that the modal stiffness of this mode at small wavenumber will depend on G_lattice. We inspect the dispersion curves and observe that the frequencies increase with G_lattice (in ascending order: idealized, cubic, Kelvin, octet). We gain further evidence from the good agreement in scaling exponents of 2nd axial mode (ka/π = 0) modal stiffness (Table 4) and G_lattice (Table 2) for cubic, idealized foam, and Kelvin metastructures. In the octet metastructure, a slight difference between scaling exponents is observed (about 16%). This may be due to the higher frequency nature of this mode. Dynamic effects seem to introduce bending deformation of the lattice struts, raising the scaling exponent. Like the 2nd bending mode, we observe a transition on lattice property dependence of the 2nd axial mode as wavenumber increases. In the long wavelength region, the modal stiffness seems to depend on a combination of E_lattice and G_lattice. However, since this side of the k-space does not define any of the band gaps of interest, we will not go into further detail.

It is important to mention that at densities lower than about 3%, the octet metastructure upper modes deviate from the power-law approximation. At these lower densities, bending stiffness of the lattice struts of this metastructure is low compared to the G_lattice (due to increasing slenderness ratio of the struts with decrease in relative density). Thus, waves propagate through the outermost struts and no shear like deformation is observed on the unit cells surrounding the resonator.

It is not straightforward to realize a quantitative model that predicts the modal frequencies based on lattice effective properties presented in section Lattice Static Properties, however we present a general form to represent these frequencies in section Dynamic Performance Parameters. This is because in the effective properties calculations, the lattice unit is assumed to be periodic in all three dimensions, but the local boundary conditions of each lattice unit inside the metastructure depends on its location, i.e., some lattice unit cells have one face attached to the resonator, some lattice unit cells have one face that is traction free, while other lattice unit cells are connected to the surrounding lattice. The difference in boundary conditions changes the behavior of the lattice units inside the metastructure. Furthermore, because of the difference in geometry of the lattices, the effects of boundary conditions may be different for the different geometries. Predicting modal frequencies from static properties becomes even more challenging for lattice modes due to their higher frequency. It has been shown that a frequency-dependent elasticity is necessary to fully capture the dynamic behavior at the high frequency range (Nemat-Nasser et al., 2011; Srivastava, 2015). Instead, here we present a qualitative understanding of the physical differences among dispersion curves of different metastructures. These results motivate exploring more deeply the lattice-resonator metastructure framework due to its rich variety of wave propagation behaviors.

Influence of Resonator Size

To understand the influence of resonator size on band gaps, we calculate dispersion relations for the Kelvin metastructure for three different resonator sizes, at 8.3% lattice relative density (Figure 6). We observe differences in the dispersion relations for both resonator and lattice modes. A decrease in the resonator's side length, L_reso, causes two competing effects on the lower resonator modes. One is that the stiffness of the lattice and thus the modal stiffness decreases with decreasing L_reso, due to an increase in distance between the resonator and the metastructure outer surface. Note that we refer here to the stiffness of the lattice (dependent on length), as opposed to the modulus of the lattice (independent of length) discussed in earlier sections. The second effect is that the modal mass decreases, causing an increase in frequency of lower resonator modes: this effect dominates, since overall the resonator mode frequencies increase with a decrease in resonator size (Figure 6).

FIGURE 6

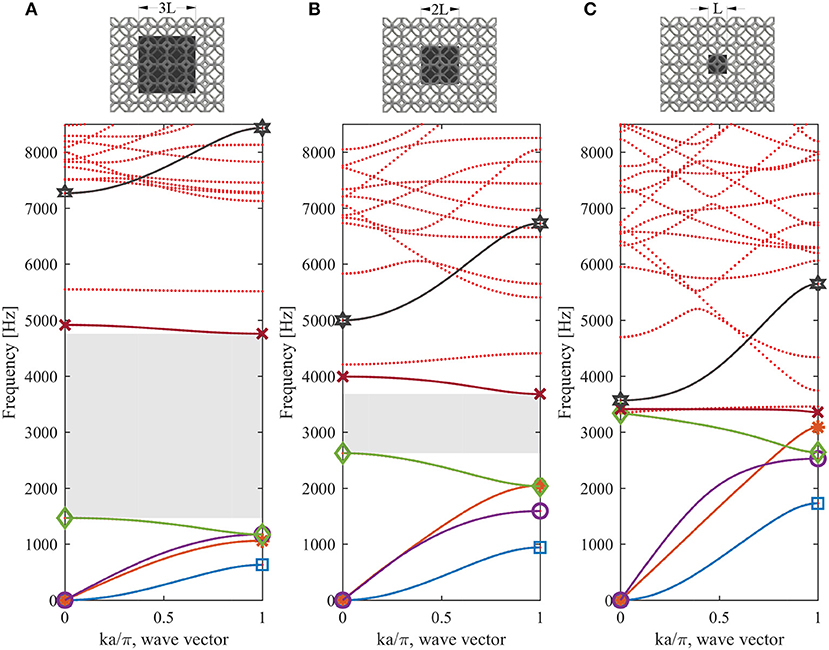
Figure 6. Dispersion relations for the Kelvin metastructure with lattice relative density of 8.3% and resonator side length equal to (A) 3L, (B) 2L, and (C) L. The lowest band gaps are indicated by gray boxes. Markers indicate the edge frequencies of modes of interest: 1st bending resonator mode (blue-square), torsional resonator mode (orange-asterisk), axial resonator mode (purple-circle), 2nd bending resonator mode (green-diamond), torsional lattice mode (red-cross), and axial lattice mode (gray-star).

The quantitative effect of resonator size on resonator mode frequency depends on the mode shape. In the limit where the lattice has a negligible contribution to modal mass, the modal mass of resonator modes that involve translation of the resonator, M_t (1st bending resonator mode and axial resonator mode) is proportional to the resonator's mass, m_reso, and thus volume of the cube resonator, such that $M_t\propto L_{reso}^3$. The modal mass of resonator modes that involve rotation of the resonator, M_r (2nd bending resonator mode and torsional resonator mode) is proportional to the resonator's moment of inertia about its center of mass, $I_{reso}=\frac{1}{6}{m}_{reso}{L}_{reso}^2$, such that $M_r\propto L_{reso}^5$. This explains why the 2nd bending resonator mode and torsional resonator mode frequencies increase at a faster rate with a decrease in resonator size, compared to the 1st bending resonator mode and axial resonator mode frequencies. This is evident in the comparison of mode edge frequencies indicated with markers in Figures 6A,B. Note that when the resonator size decreases so much so that the lattice contribution to modal mass is non-negligible, e.g., Figure 6C, these relationships must include an additional term that accounts for the lattice modal mass.

Upper lattice mode frequencies decrease with a decrease in the resonator side length: lattice length between the resonator and exterior surface of the metastructure increases, decreasing the modal stiffness. In addition, the total lattice mass increases, increasing the modal mass of the lattice modes. Both of these effects result in an overall decrease in upper lattice mode frequencies.

Overall, a decrease in resonator size increases the frequencies of resonator modes and decreases the frequencies of lattice modes. This decreases the band gap width, and eventually the band gap closes (Figure 6C).

Finite Metastructure Transmission Analysis

To understand the attenuation efficiency of the proposed metastructures, we simulated the frequency-dependent transmission for a harmonic axial excitation through 6-unit cell finite metastructures at the same relative density as the presented dispersion curves in Figure 4. Results (Figure 7A) show that the efficiency strongly depends on the metastructure's geometry. In general, wider band gaps result in stronger attenuation. Interesting comparisons arise when the transmission is normalized on the frequency axis by the frequency of the lower edge of the band gap (Figure 7B). The structural peaks (lattice-resonator “acoustic” modes) at low frequency almost align, and the initial slope of the transmission into the band gap is the same for all metastructures. This highlights that in the low frequency range of the resonator modes, all metastructures behave similarly, and are simply scaled with their lattice effective properties. Beyond the band gap lower edge frequency, all metastructures have very different frequency-dependent behaviors, indicating that the dynamics of the lattice geometries dominate. The Kelvin metastructure has a sharp, deep attenuation dip, though it does not have the widest band gap. The octet metastructure has the widest band gap with a large range of deep attenuation. Localized modes appear in the band gap of the octet and Kelvin metastructures. In all cases, the attenuation regions in the transmission curves correspond well to the axially-polarized band gap frequencies (see section Performance Parameters). We expect similar behavior in the other polarizations, as seen in prior work (Matlack et al., 2016).

FIGURE 7

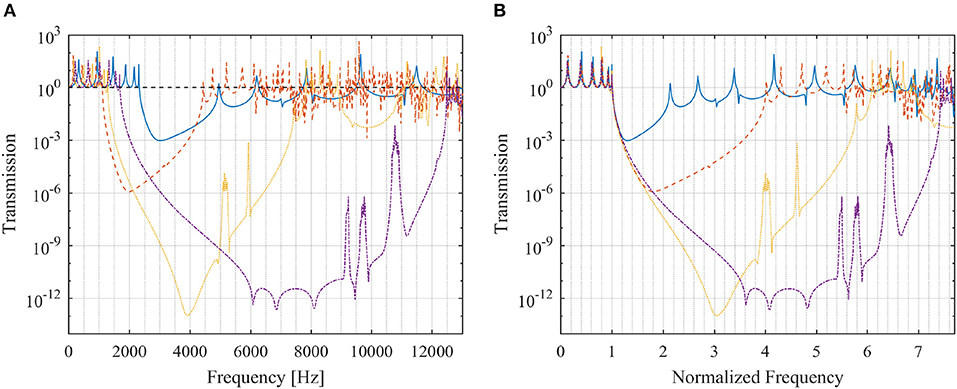
Figure 7. Frequency-dependent transmission for the cubic (blue solid), idealized foam (red dashed), Kelvin (yellow dotted) and octet (purple dashed-dotted) metastructures with lattice relative density equal to 8.3%. (A) Transmission vs. frequency. (B) Transmission vs. normalized frequency.

Performance Parameters

It is our final objective to evaluate the metastructures in terms of their static and dynamic properties. Here, we analyze standard band gap properties and introduce multifunctional (dynamic and static) performance parameters to compare the different metastructures over the range of lattice relative densities. We use the concept of polarized band gaps (Matlack et al., 2016) meaning band gaps bounded by modes of a specific polarization, i.e., axial, bending, and torsional modes. The metastructure's modal displacements reveal the mode's polarization, which we use to determine the axial, bending, and torsional polarized band gaps. We use polarized band gaps because it clarifies to which static stiffness we should compare the band gaps. Further, in most structural applications, it is typical to treat stiffness requirements in terms of the deflection direction, such that requirements are imposed on well-studied concepts of axial, bending and torsional stiffness. The mode of vibration that propagates through the component is typically the same as the static stiffness requirement. This approach allows us to systematically compare the band gaps to the static behavior of the metastructures, by comparing the polarized band gaps to the corresponding K_axial, K_bend, and K_tors (section Metastructure Static Properties). It can also aid in the selection of architected materials for structural components that must comply with a minimum static stiffness while providing vibration mitigation in the corresponding polarization.

For complex load conditions and cases where mode conversion occurs, the corresponding band gaps occur in the overlapping region of the polarized band gaps involved, and the relevant static properties would depend on the specific application. The full band gap of these metastructures (Figure 4) is simply the overlap of all the polarized band gaps.

It is important to highlight that since the major interest lies in achieving low band gap frequencies, we analyze only the first band gap of each metastructure for each polarization. Our objective with the performance parameters is to evaluate for low frequency and wide bands gaps, and high static stiffness, all of which are highly relevant for most structural applications. Further, it should be noted that the load carrying capabilities of metastructures at low relative densities has not been considered here, which is beyond the scope of the paper but crucial in applications. However, stress analysis of metastructure unit cells at the lowest lattice relative density shows a maximum von Mises stress of about 5 MPa due to weight of the resonator, which is well-below the ultimate strength of 3D printable stiff polycarbonate materials.

Dynamic Performance Parameters

We evaluate the metastructures in terms of two standard dynamic performance parameters: lower edge band gap frequency (f_low) and normalized band gap width (Δf), defined as:

$\begin{array}{cc}\Delta f=\frac{2(f_{high}-f_{low})}{f_{high}+f_{low}}& (3)\end{array}$

where f_high is the upper edge band gap frequency. Since we want to achieve low frequency and broadband mitigation, metastructures with lower f_low and higher Δf are considered more efficient.

We present these parameters in terms of lattice relative density for full, axial, bending, and torsional polarizations in Figure 8. The results show a large variation in band gap parameters that strongly depends on geometry and lattice relative density. At lower relative densities, we achieve a 6-fold change in full f_low and up to an 8-fold change in full Δf, only by changing the lattice geometry and keeping mass constant. As density increases, the difference in dynamic behavior of the metastructures decreases. This is expected since as we increase the relative density, we approach the bulk material.

FIGURE 8

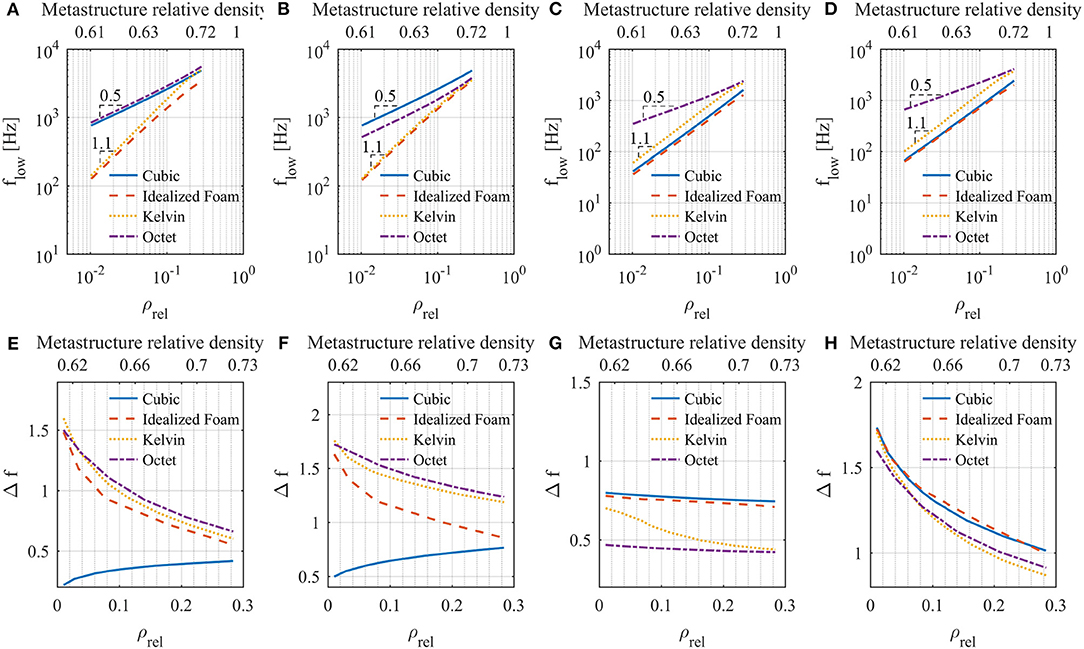
Figure 8. Dynamic performance parameters for all polarizations. (A) Full f_low. (B) Axial f_low. (C) Bending f_low. (D) Torsional f_low. (E) Full Δf. (F) Axial Δf. (G) Bending Δf. (H) Torsional Δf. Metastructure relative densities are shown for comparison.

We observe that Kelvin and idealized foam metastructures are the “best performing” in terms of full dynamic parameters since they support the lowest and close to the widest band gaps. For axial polarization, the idealized foam and Kelvin metastructures have the lowest band gaps and the octet and the Kelvin metastructures have the widest band gaps, and for bending and torsional polarizations, the cubic and idealized foam metastructures have the lowest and widest band gaps.

Full band gaps are defined between mode numbers 4 and 5 (see Figure 4) for most relative densities studied. This only changes for the idealized foam geometry at relative densities above 25% where mode a3 becomes stiffer than mode a4 redefining the lower band gap edge. The lower edge modes of the full band gaps are resonator modes (see d1–d4 in Figure 5). Thus, the change in lattice relative density has a negligible effect on modal mass. We can thus approximate f_low as proportional to the square root of the static effective properties of the lattices:

$\begin{array}{cc}{f}_{low}\propto \sqrt{a{E}_{lattice}+b{G}_{lattice}}& (4)\end{array}$

where a and b are participation factors that account for the dependence of the modal stiffness of the mode that defines f_low on lattice static properties (section Analyzing Band Gaps in Terms of Lattice Static Properties).

The polarization of the full band gap lower edge mode is different for each metastructure. For Kelvin and octet metastructures, the lower edge is defined by the second bending mode in the long wavelength region. The stiffness of this mode is proportional to G_lattice and Equation 4 is reduced to:

$\begin{array}{cc}{f}_{low}\propto \sqrt{b{G}_{lattice}}\approx \sqrt{(b{E}_{s}D)}{{\rho }_{rel}}^{r/2}& (5)\end{array}$

For the idealized foam metastructure, the mode defining the lower edge is the second bending mode at high wave number, where modal stiffness is proportional to E_lattice. We can then express f_low as:

$\begin{array}{cc}{f}_{low}\propto \sqrt{a{E}_{lattice}}\approx \sqrt{(a{E}_{s}C)}{{\rho }_{rel}}^{n/2}& (6)\end{array}$

The cubic metastructure lower edge mode is an axial mode that depends on both G_lattice and E_lattice. However, as mentioned before, the cubic lattice has a large E_lattice compared to G_lattice, so we neglect the G_lattice dependence and assume its behavior can be represented by Equation 6. Lower edge frequencies for full band gaps are plotted in double logarithmic scale in Figure 8A. There is good agreement between these results and Equations 4–6, especially in the low relative density range. As lattice relative density increases, we observe a slight decrease in slope because of increasing significance of lattice mass on total modal mass of the metastructure.

The upper edge mode of the full band gaps is defined by the 2nd torsional mode (Figure 5d5). Coming up with a simple power expression that describes the behavior of the frequencies of this mode is far more challenging than for the lower modes and escapes the scope of this article. However, the modal mass of this mode increases with increase in lattice relative density (since displacement is mostly concentrated in the lattice) while modal mass of lower modes remains approximately constant (since most modal mass is in the resonator). An increase in modal mass causes a decrease in modal frequency; thus, f_high grows at a slower rate than f_low. This is why, for most metastructures we observe a decrease in Δf (Figure 8E) with increasing lattice relative density. The cubic metastructure is an exception to this trend. The reason behind this is the mixed nature (in terms of stretch and bend dominated behavior) of this lattice geometry. As mentioned in section Wave Propagation in Metastructures, the modal stiffness of the 2nd torsional mode is proportional to G_lattice, where G_lattice ∝ ${\rho }_{rel}^2$ for the cubic lattice, while the cubic metastructure lower edge mode is dominated by E_lattice (Equation 6), where E_lattice ∝ ρ_rel for the cubic lattice. The larger scaling exponent of G_lattice seems to prevail over the increase in modal mass. The result is that f_high grows at a faster rate than f_low, causing an increase in Δf with increasing lattice relative density.

In contrast to the other polarizations, the bending band gaps are generated between two resonator modes (Figures 4a1,a4,b1,b4,c1,c3,d1,d4). Thus, we expect the general form presented in Equation 4 to hold for both upper and lower edge modes. The lower edge modal stiffness was shown to be proportional to G_lattice, so Equation 5 can be applied. However, the upper edge mode is more complex, since the location in wavenumber spectrum that bounds the band gap varies with geometry. For cubic and idealized foam metastructures, f_high is bounded at ka/π = 0, where modal stiffness is proportional to G_lattice (Equation 5). However, for octet and Kelvin metastructures, f_high is bounded at ka/π = 1, where modal stiffness is proportional to E_lattice (Equation 6). The scaling exponents of the lattice properties that dominate the lower edge modes are equal to the ones that dominate the upper edge modes for the cubic, octet, and idealized foam metastructures. Thus, we predict a relatively small change in Δf across the relative density range. This is confirmed by results presented in Figure 8G. The Kelvin lattice has a slightly higher G_lattice scaling exponent compared to its E_lattice, which supports the fact that Δf decreases with relative density.

A similar analysis can be done for both axial and torsional dynamic parameters (Figures 8B,D,F,H). In both cases, the lower edge is defined by a resonator mode and the upper edge by a lattice mode. Similar to the full band gaps, the axial parameters show the mixed behavior of the cubic lattice produces an increase in Δf with relative density. This does not occur in the torsional polarization since both lower and upper edge modes are dominated by G_lattice.

Multifunctional Performance Parameters

Here, we evaluate the metastructures in terms of their multifunctional properties of static deformation and band gap properties. We analyze three different static stiffnesses: K_axial, K_bend, and K_tors, which we can compare to the axial, bending, and torsional polarized band gaps. We define two multifunctional parameters that relate these properties:

$\begin{array}{cc}{\eta }_{lower edge}=\frac{K_{static}}{f_{low}}& (7)\end{array}$

$\begin{array}{cc}{\eta }_{bandgapwidth}=K_{static}\Delta f& (8)\end{array}$

where values of K_static are presented in section Metastructure Static Properties and values of f_low and Δf are presented in the section Dynamic Performance Parameters. For simplicity, we choose to weight stiffness and frequency parameters equal in our evaluation. We evaluate the metastructures in terms of these performance metrics compared to lattice and metastructure relative densities in Figure 9.

FIGURE 9

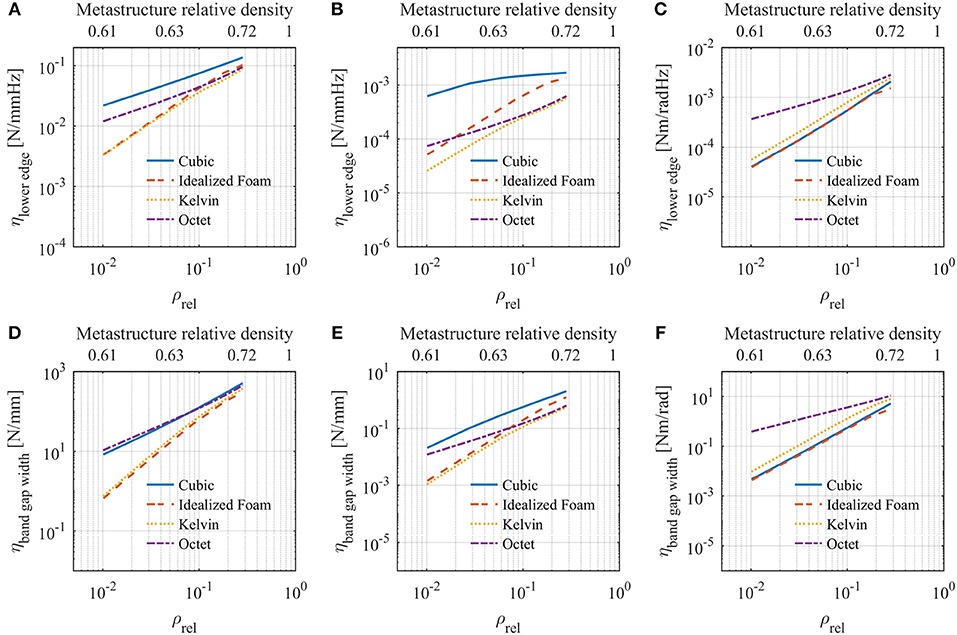
Figure 9. Multifunctional performance parameters for all polarizations. (A) Axial η_{lower edge}. (B) Bending η_{lower edge}. (C) Torsional η_{lower edge}. (D) Axial η_{band gap width}. (E) Bending η_{band gap width}. (F) Torsional η_{band gap width}.Metastructure relative densities are shown for comparison.

Incorporating static properties into performance metrics changes the way the metastructures are evaluated. For example, for axial deformations, the cubic metastructure has the lowest performance in terms of f_low. This changes completely in the multifunctional analysis. The cubic metastructure axial η_{lower edge} is the highest for all relative densities. Similarly, the octet metastructure has a poor torsional f_low but the highest torsional η_{lower edge}. In bending, the cubic metastructure is the “best performing” for both dynamic and multifunctional parameters.

“Best performing” metastructures in terms of η_{band gap width} are also different than those of Δf for axial and torsional polarization. For axial η_{band gap width}, the highest values of performance are achieved by the octet metastructure at low lattice densities and the cubic metastructure at higher ones. The octet metastructure has the highest torsional η_{band gap width}. In bending, the cubic metastructure shows the highest values similar to the dynamic analysis.

The differences in the outcome of the dynamic and multifunctional performance metrics show the importance of a multifunctional analysis. The stiffness or frequency parameters could be weighted differently if the specific application requires better performance of one parameter compared to another. One could redefine these parameters to include other mechanical properties such as energy absorption, heat transfer, or yield strength to fit certain criteria. Defining multifunctional metrics, can aid the design process, and achieve higher levels of performance of multifunctional architected materials.

Static Stiffness vs. Lower Band Gap Edge Frequency

As another metric of performance, we directly compare K_static of the metastructures with their f_low for axial, bending and torsional polarizations (Figure 10). The idealized foam metastructure shows slightly higher values of K_axial relative to f_low for axial polarizations (Figure 10A), and the idealized foam and cubic metastructures show slightly higher K_tors relative to f_low for torsional polarization (Figure 10C). However, overall there is not much difference in the metastructure's axial and torsional behavior, mainly because in these polarizations, the metastructure's K_static and the modal stiffness associated with f_low are proportional to the same lattice effective property.

FIGURE 10

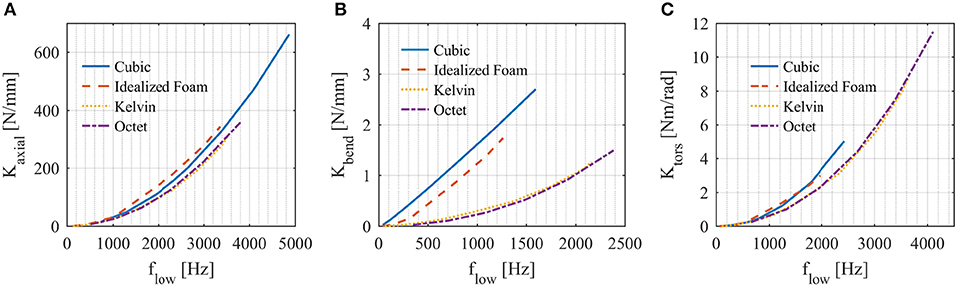
Figure 10. K_static vs. f_low. (A) Axial polarization. (B) Bending polarization (C) Torsional polarization.

More significant differences between metastructure geometries are observed for K_bend vs. f_low for bending (Figure 10B). This is because K_bend is proportional to both E_lattice and G_lattice, while the modal stiffness associated with f_low (1st bending mode) is proportional to only G_lattice. Higher ratios of E_lattice to G_lattice for the cubic and idealized foam lattices compared to that of the octet and Kelvin lattices (Figure 2) explain the significantly higher values of K_bend that can be achieved at a given f_low with the cubic and idealized foam metastructures. Furthermore, the mixed behavior of the cubic lattice allows us to break the typical quadratic relationship between K_static and f_low for the bending polarization. While all other stiffness-frequency curves follow the well-established quadratic relationship between stiffness and frequency, this relationship is instead approximately linear for the cubic metastructure under bending. This is due to the mixed behavior of the cubic lattice (section Lattice Static Properties), i.e., it has different scaling exponents of E_lattice and G_lattice (Table 2). In general, K_bend is proportional to both E_lattice and G_lattice such that for the cubic metastructure K_bend ∝ ${\rho }_{rel}^{1.}$⁴⁵ (on average, see Table 3), and f_low ∝ √G_lattice ∝ ρ_rel^1.1 (Figure 8C), which results in an approximately linear relationship between K_bend and f_low for bending.

Conclusion

In this article, we studied static properties and vibration mitigation behavior of metastructures that consist of different lattice geometries with embedded resonators. Through calculations of the static stiffness of finite metastructures, we show that metastructure stiffness is closely related to the effective static moduli of the lattice materials that compose them. The band gaps of these metastructures with iso-density lattices show that we can achieve large differences in band gaps by selectively placing the mass inside the lattice unit cell. By inspecting the modal displacements and the dispersion curves, we developed a qualitative understanding of the differences in band gap parameters in terms of the effective static properties of the lattices. We compared the exponential dependence on relative density of the modal stiffnesses of each metastructure mode, in the vicinity of the lowest band gap, to the static effective properties of the lattices to further support this point. We analyzed the transmission of the metastructures and found that the attenuation efficiency strongly depends on lattice topology. Our results show that the lattice effective properties drive the band gap frequencies, which is interesting since the lattice is extremely finite with various boundary conditions: there are only a few lattice unit cells in between each resonator, and only a few lattice unit cells in the other dimensions.

We evaluated the metastructures over a range of lattice relative densities from 1% to 28% (corresponding to metastructure relative densities from 61% to 72%). Dynamic parameters of lower edge band gap frequency and band gap width show the ability to tailor the band gap to a wide range of frequencies, especially at lower relative density values. We introduce multifunctional performance metrics to evaluate the metastructures in terms of their band gap properties and static stiffness, for general structural application considerations. In both cases, performance of the metastructure strongly depends on the polarization considered, and on whether only dynamic or both static and dynamic properties are considered. This type of evaluation can be used to formulate performance metrics that more accurately describe certain applications and could be modified to preferentially weight certain parameters more than others. Finally, we directly compare metastructure static stiffness to polarized lower band gap edge frequency. A particularly interesting behavior is observed in the bending polarization for the cubic metastructure, where the relationship between static stiffness and lower edge frequency approaches a linear behavior. This is primarily due to the mixed behavior of the cubic lattice unit cell under shear and compression.

While these metastructures may have application-specific drawbacks of additional resonator mass, we show that this metastructure design can be used to obtain a wide range of static and band gap properties by simply changing the lattice geometry. Further, our presented approach of understanding the dynamic properties of metastructures in terms of the effective properties of the lattice could be used to evaluate and interpret other designs, where optimal performance may be obtained.

Materials and Methods

Dispersion Relations

We obtain the dispersion relations by 3D Finite Element simulations in COMSOL Multiphysics V5.3 software. We model a single metastructure unit (Figure 1B) and use 10-node tetrahedral elements. Mesh size was chosen to ensure convergence of results. We impose Floquet boundary conditions in the external faces perpendicular to the x-direction to account for x-axis periodicity. The wave number, k, is swept in the first irreducible Brillouin zone and the eigenfrequency problem is solved to obtain the dispersion relations. The relative density of the lattice unit cells is varied by keeping unit length constant and sweeping the thickness of the struts that compose it. We calculate modal stiffness as:

$\begin{array}{cc}{K}^{(i)}=u^{{(i)}^T}[K]u^{(i)}& (9)\end{array}$

where K⁽ⁱ⁾ is the modal stiffness of mode i, u⁽ⁱ⁾ is the vector containing the modal displacements of mode i and [K] is the stiffness matrix.

Finite Metastructure Transmission Analysis

We obtain the transmission curves by 3D Finite Element simulations in COMSOL Multiphysics V5.3 software. We model a six-unit one-dimensional finite metastructure (Figure 1C) and use 10-node tetrahedral elements. Mesh size was chosen to ensure convergence of results. We fix one end of the metastructure and we apply a harmonic displacement (δ_x) parallel to the direction of periodicity to the opposite end. We perform a frequency sweep analysis over a range of frequencies from 0 to 13,000 Hz. We define transmission as the ratio of output to input force amplitudes.

Lattice Effective Properties

We calculate lattice effective properties (E_lattice and G_lattice) using 3D Finite Element simulations in COMSOL Multiphysics V5.3 software. We model a single lattice unit cell (Figure 1A) and use 10-node tetrahedral elements. Mesh size was chosen to ensure convergence of results. We perform a series of static linear analysis where appropriate displacement boundary conditions and periodic boundary conditions (Wallach and Gibson, 2001; Dalaq et al., 2016) are imposed to calculate the effective stiffness matrix considering the cubic symmetry of the lattice unit cells. We then calculate effective Young's modulus and effective shear modulus from the effective stiffness matrix. We vary the relative density of the lattice cells by keeping unit length constant and sweeping the thickness of the struts that compose it.

Finite Metastructure Static Stiffness

We obtain finite metastructure static stiffness (K_static) properties from 3D Finite Element simulations in COMSOL Multiphysics V5.3. We model a six-unit one-dimensional finite metastructure (Figure 1C) and use 10-node tetrahedral elements. Mesh size was chosen to ensure convergence of results. We numerically calculate the force and displacement profiles of the finite metastructure under static loading, and then use force-displacement relations of a conventional cantilever beam to calculate the axial, bending, and torsional stiffnesses of the metastructures. For axial stiffness (K_axial), we fix one end of the metastructure and we apply a displacement (δ_x) parallel to the direction of periodicity to the opposite end. We calculate K_axial as:

$\begin{array}{cc}{K}_{axial}=\frac{F_x}{{\delta }_x}& (10)\end{array}$

where F_x is the total reaction force at the fixed end parallel to the direction of periodicity. For bending stiffness (K_bend), we fix one end of the metastructure and we apply a displacement (δ_y) perpendicular to the direction of periodicity to the opposite end. We calculate K_bend as:

$\begin{array}{cc}{K}_{bend}=\frac{F_y}{{\delta }_y}& (11)\end{array}$

where F_yis the total reaction force at the fixed end perpendicular to the direction of periodicity. For torsional stiffness (K_tors), we fix one end of the metastructure and we apply a rigid connector to the opposite end. We apply an angular displacement (θ_x) about the direction of periodicity to this face. We calculate K_tors as:

$\begin{array}{cc}{K}_{tors}=\frac{M_x}{{\theta }_x}& (12)\end{array}$

where M_xis the total reaction moment at the fixed end about to the direction of periodicity. The relative density of the lattice cells is varied by keeping unit length constant and sweeping the thickness of the struts that compose it.

Material Properties

For all simulations, materials are based on prior 3D printed metastructures (Matlack et al., 2016) but chosen to be isotropic. Even though 3D printing methods do not achieve isotropy due to the material properties dependence on printing direction, it is the main objective of the paper to identify effects due to geometry changes and not due to material anisotropy. We use a linear elastic material model with no damping. Material properties used in all models are given in Table 5.

TABLE 5

Table 5. Material properties used for finite element simulations.

Author Contributions

IA performed the research, analyzed the data, developed the performance parameters, and wrote the paper. KM designed the research, analyzed the data, developed the performance parameters, and wrote the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partially supported by a University Research Program from Ford Motor Company.

References

Bayat, A., and Gaitanaros, S. (2018). Wave directionality in three-dimensional periodic lattices. J. Appl. Mech. 85:011004. doi: 10.1115/1.4038287

CrossRef Full Text | Google Scholar

Berger, J. B., Wadley, H. N. G., and McMeeking, R. M. (2017). Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 543, 533–537. doi: 10.1038/nature21075

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Li, T., Scarpa, F., and Wang, L. (2017). Lattice metamaterials with mechanically tunable poisson's ratio for vibration control. Phys. Rev. Appl. 7:024012. doi: 10.1103/PhysRevApplied.7.024012

CrossRef Full Text | Google Scholar

Dalaq, A. S., Abueidda, D. W., Abu Al-Rub, R. K., and Jasiuk, I. M. (2016). Finite element prediction of effective elastic properties of interpenetrating phase composites with architectured 3D sheet reinforcements. Int. J. Solids Struct. 83, 169–182. doi: 10.1016/j.ijsolstr.2016.01.011

CrossRef Full Text | Google Scholar

D'Alessandro, L., Belloni, E., Ardito, R., Corigliano, A., and Braghin, F. (2016). Modeling and experimental verification of an ultra-wide bandgap in 3D phononic crystal. Appl. Phys. Lett. 109:221907. doi: 10.1063/1.4971290

CrossRef Full Text | Google Scholar

D'Alessandro, L., Zega, V., Ardito, R., and Corigliano, A. (2018). 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep. 8:2262. doi: 10.1038/s41598-018-19963-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Deshpande, V. S., Ashby, M. F., and Fleck, N. A. (2001a). Foam topology: bending versus stretching dominated architectures. Acta Mater. 49, 1035–1040. doi: 10.1016/S1359-6454(00)00379-7

CrossRef Full Text | Google Scholar

Deshpande, V. S., Fleck, N. A., and Ashby, M. F. (2001b). Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 49, 1747–1769. doi: 10.1016/S0022-5096(01)00010-2

CrossRef Full Text | Google Scholar

Deymier, P. A. (ed.). (2013). Acoustic Metamaterials and Phononic Crystals. Berlin; Heidelberg: Springe

Google Scholar

Doty, R. E., Kolodziejska, J. A., and Jacobsen, A. J. (2012). Hierarchical polymer microlattice structures. Adv. Eng. Mater. 14, 503–507. doi: 10.1002/adem.201200007

CrossRef Full Text | Google Scholar

Dou, N. G., Jagt, R. A., Portela, C. M., Greer, J. R., and Minnich, A. J. (2018). Ultralow thermal conductivity and mechanical resilience of architected nanolattices. Nano Lett. 18, 4755–4761. doi: 10.1021/acs.nanolett.8b01191

PubMed Abstract | CrossRef Full Text | Google Scholar

Erdeniz, D., Levinson, A. J., Sharp, K. W., Rowenhorst, D. J., Fonda, R. W., and Dunand, D. C. (2015). Pack aluminization synthesis of superalloy 3D woven and 3D braided structures. Metall. Mater. Trans. A 46, 426–438. doi: 10.1007/s11661-014-2602-9

CrossRef Full Text | Google Scholar

Evans, A. G., Hutchinson, J. W., and Ashby, M. F. (1998). Multifunctionality of cellular metal systems. Prog. Mater. Sci. 43, 171–221. doi: 10.1016/S0079-6425(98)00004-8

CrossRef Full Text | Google Scholar

Evans, A. G., Hutchinson, J. W., Fleck, N. A., Ashby, M. F., and Wadley, H. N. G. (2001). The topological design of multifunctional cellular metals. Prog. Mater. Sci. 46, 309–327. doi: 10.1016/S0079-6425(00)00016-5

CrossRef Full Text | Google Scholar

Fleck, N. A., Deshpande, V. S., and Ashby, M. F. (2010). Micro-architectured materials: past, present and future. Proc. R. Soc. A Math. Phys. Eng. Sci. 466, 2495–2516. doi: 10.1098/rspa.2010.0215

CrossRef Full Text | Google Scholar

Gibson, L. J., and Ashby, M. F. (1982). The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A. Math. Phys. Sci. 382, 43–59. doi: 10.1098/rspa.1982.0088

CrossRef Full Text | Google Scholar

Gibson, L. J., and Ashby, M. F. (1997). Cellular Solids: Structure and Properties, 2nd Edn. Cambridge, UK: Cambridge University Press.

Google Scholar

Han, B., Zhang, Z.-J., Zhang, Q.-C., Zhang, Q., Lu, T. J., and Lu, B.-H. (2017). Recent advances in hybrid lattice-cored sandwiches for enhanced multifunctional performance. Extrem. Mech. Lett. 10, 58–69. doi: 10.1016/j.eml.2016.11.009

CrossRef Full Text | Google Scholar

Hussein, M. I., Leamy, M. J., and Ruzzene, M. (2014). Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66:040802. doi: 10.1115/1.4026911

CrossRef Full Text | Google Scholar

Luxner, M. H., Stampfl, J., and Pettermann, H. E. (2004). “Linear and nonlinear numerical investigations of regular open cell structures” in Proceedings of ASME 2004 International Mechanical Engineering Congress and Exposition (Anaheim, CA: ASME), 469–475. doi: 10.1115/IMECE2004-62545

CrossRef Full Text | Google Scholar

Matlack, K. H., Bauhofer, A., Krödel, S., Palermo, A., and Daraio, C. (2016). Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc. Natl. Acad. Sci.U.S.A. 113, 8386–8390. doi: 10.1073/pnas.1600171113

PubMed Abstract | CrossRef Full Text | Google Scholar

Meza, L. R., Zelhofer, A. J., Clarke, N., Mateos, A. J., Kochmann, D. M., and Greer, J. R. (2015). Resilient 3D hierarchical architected metamaterials. Proc. Natl. Acad. Sci. U.S.A. 112, 11502–11507. doi: 10.1073/pnas.1509120112

PubMed Abstract | CrossRef Full Text | Google Scholar

Moongkhamklang, P., Deshpande, V. S., and Wadley, H. N. G. (2010). The compressive and shear response of titanium matrix composite lattice structures. Acta Mater. 58, 2822–2835. doi: 10.1016/j.actamat.2010.01.004

CrossRef Full Text | Google Scholar

Nemat-Nasser, S., Willis, J. R., Srivastava, A., and Amirkhizi, A.V. (2011). Homogenization of periodic elastic composites and locally resonant sonic materials. Phys. Rev. B 83:104103. doi: 10.1103/PhysRevB.83.104103

CrossRef Full Text | Google Scholar

Phani, A. S., Woodhouse, J., and Fleck, N. A. (2006). Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 119, 1995–2005. doi: 10.1121/1.2179748

PubMed Abstract | CrossRef Full Text | Google Scholar

Ryan, S. M., Szyniszewski, S., Ha, S., Xiao, R., Nguyen, T. D., Sharp, K. W., et al. (2015). Damping behavior of 3D woven metallic lattice materials. Scr. Mater. 106, 1–4. doi: 10.1016/j.scriptamat.2015.03.010

CrossRef Full Text | Google Scholar

Schaedler, T. A., and Carter, W. B. (2016). Architected cellular materials. Annu. Rev. Mater. Res. 46, 187–210. doi: 10.1146/annurev-matsci-070115-031624

CrossRef Full Text | Google Scholar

Srivastava, A. (2015). Elastic metamaterials and dynamic homogenization: a review. Int. J. Smart Nano Mater. 6, 41–60. doi: 10.1080/19475411.2015.1017779

CrossRef Full Text | Google Scholar

Tang, Y., Ren, S., Meng, H., Xin, F., Huang, L., Chen, T., et al. (2017). Hybrid acoustic metamaterial as super absorber for broadband low-frequency sound. Sci. Rep. 7:43340. doi: 10.1038/srep43340

CrossRef Full Text | Google Scholar

Taniker, S., and Yilmaz, C. (2015). Design, analysis and experimental investigation of three-dimensional structures with inertial amplification induced vibration stop bands. Int. J. Solids Struct. 72, 88–97. doi: 10.1016/j.ijsolstr.2015.07.013

CrossRef Full Text | Google Scholar

Valdevit, L., Jacobsen, A. J., Greer, J. R., and Carter, W. B. (2011). Protocols for the optimal design of multi-functional cellular structures: from hypersonics to micro-architected materials. J. Am. Ceram. Soc. 94, s15–s34. doi: 10.1111/j.1551-2916.2011.04599.x

CrossRef Full Text | Google Scholar

Vigliotti, A., and Pasini, D. (2012). Stiffness and strength of tridimensional periodic lattices. Comput. Methods Appl. Mech. Eng. 229–232, 27–43. doi: 10.1016/j.cma.2012.03.018

CrossRef Full Text | Google Scholar

Wadley, H. N. G. (2006). Multifunctional periodic cellular metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 364, 31–68. doi: 10.1098/rsta.2005.1697

PubMed Abstract | CrossRef Full Text | Google Scholar

Wallach, J. C., and Gibson, L. J. (2001). Mechanical behavior of a three-dimensional truss material. Int. J. Solids Struct. 38, 7181–7196. doi: 10.1016/S0020-7683(00)00400-5

CrossRef Full Text | Google Scholar

Wang, L., Lau, J., Thomas, E. L., and Boyce, M. C. (2011). Co-continuous composite materials for stiffness, strength, and energy dissipation. Adv. Mater. 23, 1524–1529. doi: 10.1002/adma.201003956

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, P., Casadei, F., Kang, S. H., and Bertoldi, K. (2015). Locally resonant band gaps in periodic beam lattices by tuning connectivity. Phys. Rev. B 91:020103. doi: 10.1103/PhysRevB.91.020103

CrossRef Full Text | Google Scholar

Wang, Y., Gao, J., Luo, Z., Brown, T., and Zhang, N. (2017). Level-set topology optimization for multimaterial and multifunctional mechanical metamaterials. Eng. Optim. 49, 22–42. doi: 10.1080/0305215X.2016.1164853

CrossRef Full Text | Google Scholar

Zhang, Y., Ha, S., Sharp, K., Guest, J. K., Weihs, T. P., and Hemker, K. J. (2015). Fabrication and mechanical characterization of 3D woven Cu lattice materials. Mater. 85, 743–751. doi: 10.1016/j.matdes.2015.06.131

CrossRef Full Text | Google Scholar

Zheng, X., Lee, H., Weisgraber, T. H., Shusteff, M., DeOtte, J., Duoss, E. B., et al. (2014). Ultralight, ultrastiff mechanical metamaterials. Science 344, 1373–1377. doi: 10.1126/science.1252291

PubMed Abstract | CrossRef Full Text | Google Scholar