Combining Digital Image Correlation and Acoustic Emission for Monitoring of the Strain Distribution until Yielding during Compression of Bovine Cancellous Bone

In this work, the surface heterogeneity in mechanical compressive strain of cancellous bone was investigated with digital image correlation (DIC). Moreover, the onset and progression of failure was studied by acoustic emission (AE). Cubic cancellous bone specimens, with side of 15 mm, were obtained from bovine femur and kept frozen at −20°C until testing. Specimen strain was analyzed by measuring the change of distance between the platens (crosshead) and via an optical method, by following the strain evolution with a camera. Simultaneously, AE monitoring was performed. The experiments showed that compressive Young’s modulus determined by crosshead strain is underestimated at 23% in comparison to optically determined strain. However, surface strain fields defined by DIC displayed steep strain gradients, which can be attributed to cancellous bone porosity and inhomogeneity. The cumulative number of events for the total AE activity recorded from the sensors showed that the activity started at a mean load level of 36% of the maximum load and indicated the initiation of micro-cracking phenomena. Further experiments, determining 3D strain with μCT apart from surface strain, are necessary to clarify the issue of strain inhomogeneity in cancellous bone.

Introduction

The determination of trabecular bone tissue elastic and failure properties is important from both biological and clinical aspect, as they influence significantly the pathophysiology of aging, disease, and its treatment. Much research has been also performed in predicting bone fractures with the purpose of optimal design of orthopedic implants (Maurer-Ertl et al., 2015). The mechanical properties are typically obtained from experimental testing (Carter and Hayes, 1977) of excised specimens of trabecular bone. The measured mechanical properties underestimate the in vivo behavior of cancellous bone. Measurements of strain with extensometers include the “side-artifact,” as there is loss of connectivity at the outer surface of the machined specimen because of the interruption of the trabecular network during preparation (Un et al., 2006), which mechanistically depends on trabecular spacing (Onck et al., 2001; Un et al., 2006). This artifact can underestimate the elastic modulus up to 50% in human vertebral bone (Un et al., 2006). The accuracy of compressive strain measurements derived from the relative displacement of the platens is restricted by artifacts due to loss of connectivity at the specimen ends and friction at the specimen–platens interface (Linde and Hvid, 1987, 1989; Odgaard et al., 1989; Odgaard and Linde, 1991; Linde et al., 1992a,b).

For this reason, different techniques, most of them non-contact, have emerged to overcome the aforementioned measurement inaccuracies. Strain mapping techniques have been applied to monitor local damage and measure local displacements during deformation. Optical technique allow contactless measurements that permit the determination of strain without intervention at the local structure and response of the material. Among optical non-destructive techniques, used for monitoring crack initiation and progress, are the electronic speckle pattern interferometry and the digital image correlation (DIC) (Hoult et al., 2013; Lionello and Cristofolini, 2014), which give two-dimensional (2D) strain mapping. Optical methods have also recently included measurements of strain of the 3D space (Roberts et al., 2014; Palanca et al., 2015). DIC is a promising optical technique, which depicts clearly and accurately the surface strain field, as well as the transient changes originated from stress redistribution after local fracture events occurrence (Sutton et al., 1983, 2009; Freddi et al., 2015).

The amount of tissue damage at the microscopic level in bone tissue is a determinant of bone quality, contributing to whole bone fragility. Activities of daily living or overloading events can cause microdamage in bone tissue of normal individuals. Accumulation of microdamage is considered a mechanism in the development of fatigue fractures, insufficiency, and atypical fractures (Hernandez et al., 2014). The development of bone local yielding or fracturing as a consequence of mechanical loading, is difficult to quantify, which limits the ability to define injury and develop injury criteria. Tissue material toughness and resistance to the formation of tissue microdamage play the main role in understanding failure mechanisms in bone (Goff et al., 2015). Very low amounts of microdamage, which occupy less than 2% of the tissue, result in much higher decreases in stiffness, strength, and fatigue of cancellous bone (Lambers et al., 2013; Hernandez et al., 2014), displaying that tissue microdamage can have significant influence to clinical fractures.

Acoustic emission (AE) by materials is sonic and ultrasonic wave generation during their deformation when fracture or microcracking processes start. AE technique permits determination of structural health non-destructively and with high sensitivity and is widely used throughout civil and mechanical engineering. AE is a well-established method for real-time damage monitoring and has found wide use to detect effects in different mechanical structures. Its application within the field of orthopedic surgery is of particular interest. The use of AE technology in orthopedics is wide ranging and is implemented in the study of the mechanical behavior of bone (Cardoso et al., 2003), especially in fracture behavior, aiming in determining failure mechanisms, which are connected with bone overloading or cemented implants, aiming in improving prosthetic design. The last years, its analysis has been applied to discern microcracks initiated with yield in bone and continued in the post-yield region until failure (Wright et al., 1981). The nature of AE signals from bone has been already suggested as a tool for measuring its quality. AE has been monitored from whole bones subject to torque (Jonsson et al., 1984) and bending (Hanagud et al., 1973) and has been proposed as a tool for monitoring the bone fracture healing process (Shrivastava and Prakash, 2009, 2011).

In this work, the macroscopic strain and the surface strain field, at which crack formation initiated and propagated until fracture, were investigated. For this reason, DIC and AE were simultaneously performed. These results provide new insights into the process of failure and a new level of detail in fracture characterization.

Materials and Methods

Sample Preparation

Trabecular bone specimens were prepared from bovine femur resulting in n = 20 samples. All femurs were obtained from local butcheries. The specimens were cut along the longitudinal axis of the femur to produce 15 mm × 15 mm × 15 mm cubic specimens. They were kept frozen at a temperature of −20°C until testing. All tests were performed at room temperature. The cubic specimens were machined with a Struers Minitom Low-Speed Diamond Saw. Specimen dimensions were obtained with a micrometer before mechanical testing.

Strain Measurement

Specimens were loaded in compression, placed between two parallel steel platens, at a constant strain rate of 1/60 s⁻¹ in a Monsanto tensometer testing machine (Figure 1). Each specimen was compressed along its axis. There were performed two independent measurements of deformation: a measurement by the conventional extensometer fixed to the platens as close to the specimen as possible, and an optical deformation measurement, described below in detail.

FIGURE 1

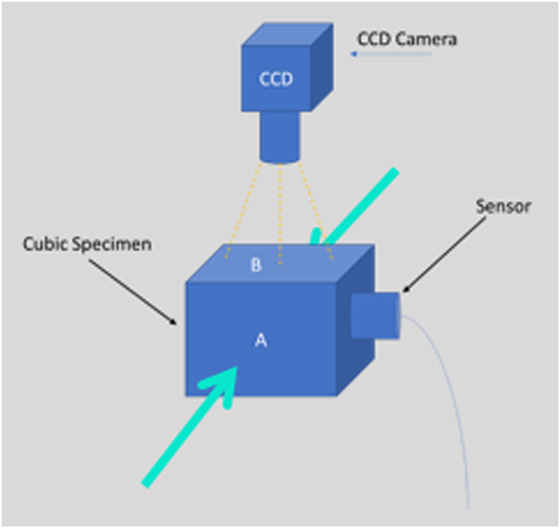
Figure 1. CCD camera used to monitor the whole experiment and acoustic emission sensor detects the acoustic events. The green arrows indicate the loading direction (compression mode) of the specimen.

The optically measured strain was determined between two points lying one in each of two pairs of transverse planes, which divide the length of the specimen in three equal parts. The pairs of planes created on the specimen’s surface two areas for strain measurement, the small and the large one (Figure 2). The small is the central part of the specimen, where usually macroscopic fractures occur. The large area represents the whole length of the specimen, with a certain length—approximately 1 mm from the platens—excluded. Thus, the surface strain was measured at a middle area of the specimen and simultaneously at a the whole length in order to examine the inhomogeneity of the strain along the length of the specimen. The strain in each of these areas was considered as homogeneous. The DIC set-up for measuring the displacement and strain at the frontal surface of the specimens was as the following: the specimen’s surface was painted white and black landmarks were created along the transverse planes in order to make contrast. These landmarks were followed by a CCD video camera (Sony Exmor R) throughout the test (Resolution of Images 1,280 × 720) (Figure 1), which recorded the whole experiment. The system captures pictures every 10 N. By using an algorithm via MATLAB Image Analysis, the strain distribution at the surface was determined by depicting the exact position of the pixel corresponding to a specific landmark/speckle dot at each image. Each speckle dot has been displaced a few pixels at every image as the specimen was compressed and deformed. The exact position of each dot was recorded in a Matlab array for every image. When all the images were processed, the displacement between two dots was calculated and consequently the strain, since the original distance (undeformed image) between two dots was known. With the optically calculated strain and the strain measured by the extensometer, two kinds of elastic moduli were determined and compared. Conventional elastic modulus was obtained as the maximum slope of the stress–strain curves by a best-fit linear (R² = 0.99) straight line over a range of approximately 0.02 strain with varying origin.

FIGURE 2

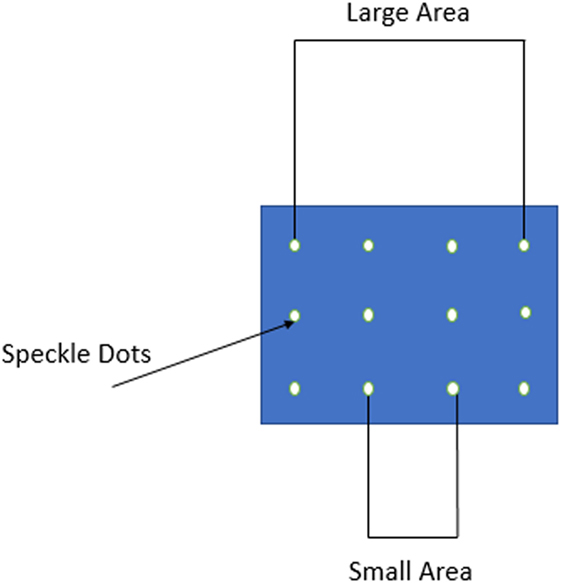
Figure 2. The formed speckle dots on the front surface of the specimen. “Large” and “small” areas are shown in the figure.

Ncorr DIC Algorithm

Ncorr is a well-documented flexible code that can be adapted to suit each user’s needs (http://www.ncorr.com/index.php). It is a freely available 2D subset-based DIC software package. The work flow of Ncorr is the following: 1-Set Reference Image; 2-Set Current Images; 3-Set Region of Interest (ROI); 4-Set DIC Parameters; 5-DIC Analysis; 6-Format Displacements; 7-Calculate Strains.

For the data analysis, the following elements were used: a group of neighboring pixels, which was compared in the reference and loaded images, consisting of 29 pixels (called subset size), a step size/subset spacing (the number of pixels the center point of this subset was moved in order to calculate the full displacement field) of 2 pixels, and a Strain Radius (suitable for the calculation of strains) of 29 pixels (equal to the number of the subset size). Additionally, the ROI was either a rectangle or an ellipse according to the geometry of the specimen and the needs of each experiment. The values of the above parameters were chosen as to minimize the computational cost without losing in the accuracy of the results.

Acoustic Emission

Acoustic signals emitted from the specimen during compression were monitored using a broadband sensor (R-15, Physical Acoustic Corporation) placed at the axis normal to the main compression direction (see Figure 1). The position of the sensor was chosen because the above surface of the specimen was monitored by the camera for the DIC method. One transducer was used for all the experiments. The specific sensor was selected due to their response because its diameter was suitable for the length (15 mm) of our specimens. Thus, its placement on the surface was easy. Furthermore, acoustic coupling was improved using sonic gel between the sensor and the contact point of it on the surface and tape was used to ensure the stability of the sensor during the experiment.

The signals were amplified at 35 dB and were continuously recorded using a two-channel acquisition system (Mistras micro-II board). A sampling rate of 10 MHz was implemented. The characteristics of the signal, which were recorded, were: AE amplitude (magnitude of the signal at the peak), AE energy, duration (time interval between the first and the last threshold crossing), and rise time (RT) (see Figure 3). The threshold was set at 35 dB (or 0.2 mV), while Gain and Pre-Ampl. was set at 0 dB. The peak and hit definition times (PDT and HDT) were 50 and 200 µs, respectively, whereas the hit lockout time was 500 µs.

FIGURE 3

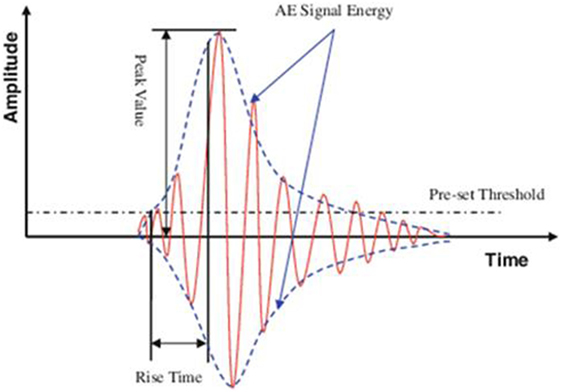
Figure 3. Amplitude, acoustic emission (AE) signal energy, rise time, and threshold of the AE activity.

Amplitude shows the intensity of the fracture incident. AE signal energy is determined by the area under the rectified waveform. Moreover, RT is the delay between the first threshold crossing and the peak amplitude (peak value). Another important parameter is the RT over amplitude (RA value). It is defined as RT divided by the amplitude and its unit is microseconds per volts. The average frequency equals the number of threshold crossings over the whole duration of the signal and represents the frequency content of the waveform.

Results

The experiments showed that compressive Young’s modulus (E) determined by platens relative displacement is underestimated at 23% in comparison to optically determined surface strain at the “small” middle area (Figure 4). Statistically significant difference (p < 0.001) between the values of E determined in the middle area of the specimen and in the “large” area was also observed (Figure 4). The optical measurements of strain show that trabecular bone exhibits linear elastic behavior, without initial concave part, and yields at low strains (less than 1.8%).

FIGURE 4

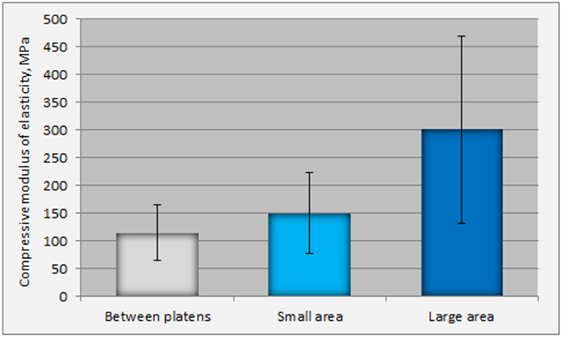
Figure 4. Differences in the values of Young’s Moduli as determined by platens displacements and by the optically calculated strain (in the small and large areas).

Figure 5 depicts the longitudinal surface strain field (e_xx) evolution during compression of the specimen until yielding. In any level of loading, there was not observed increased strain at the periphery of the specimen or at the plane end surfaces. Increased strain occurs only in areas where the bone is weaker and consequently more compliant.

FIGURE 5

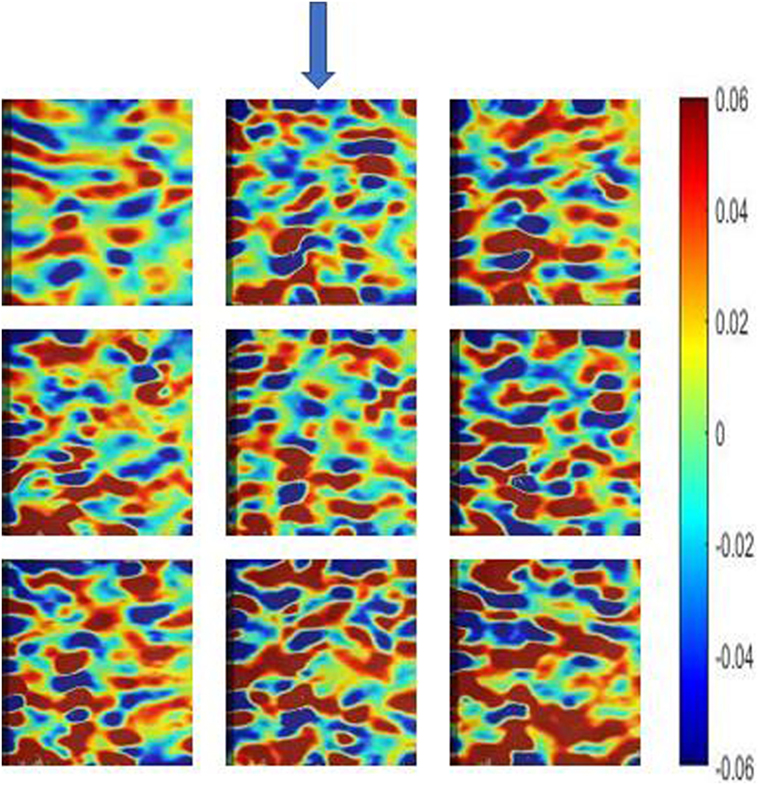
Figure 5. Longitudinal surface strain field (e_xx) evolution during compression of a specimen at nine time points until yielding, as measured by digital image correlation (Ncorr algorithm). The sequence of the images is from left to right starting from the upper left image. The arrow indicates the compression direction.

Figure 6A shows the load history and the cumulative AE activity for a specimen, which is typical for all specimens. Figure 6B focuses on cumulative AE activity at low loads. Acoustic signals start emitting before the peak of loading at a slow rate. The cumulative number of hits for the total AE activity recorded from the sensor showed that the activity started at a mean level of 36.6% of the maximum load. The time or the strain of the first initiation of the AE activity is the moment when micro-cracking phenomena were initiated within the specimens. Although there are differences among specimens and inhomogeneity is present, most of them exhibited the start of micro-cracking between 30 and 40% of the maximum load, and only a few exceptions were present.

FIGURE 6

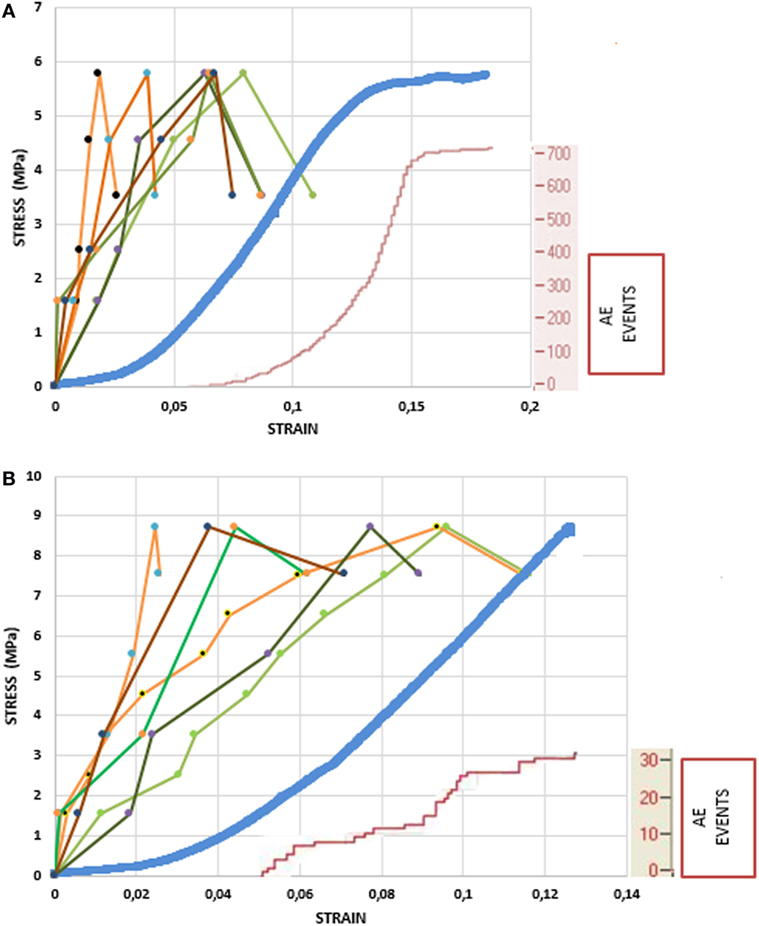
Figure 6. Load history and cumulative acoustic emission (AE) activity for two different specimens (small area is shown with tints of green color, large area with tints of orange color, platens displacement with blue color, and AE events are shown with red color). (A) Loading until fracture. (B) Focus on the stress–strain curve at the low loads.

The number of AEs released from the samples did not vary widely. The range of emissions was 200–700 events until macroscopic yielding. In the initial concave upwards part of the stress–strain curve, there are no AE events, which means that the trabeculae may buckle, deform under low loads, but not fracture. The strain at which AE activity initiates ranges between 3.5 and 5% (time 2.2–4.5 s), meaning that AE activity appears in the linear part of the σ–ε curve (Figure 6). The latency of the sharp change in strain relative to the onset of the AE was consistent across all experiments.

Amplitude, RT, and signal power were not correlated with any tissue material property. This result was attributed to the fact that some tests were destructive, while others were not and the number of AE events is very low. Steep strain gradients were observed when strain fields were calculated by DIC. They were attributed to bone inhomogeneity resulting in inhomogeneous strain distribution (Figure 5).

Discussion

It has been stated that structural phenomena at the interface result in an underestimation of Young’s modulus. On the other hand, the presence of frictional effects on the upper and bottom surfaces of the specimen, which contact the compression platens, may counteract this effect by increasing stiffness due to stress field altering by friction. The hypothesis that initiated the current experiments was whether the conventional compression test gives an accurate value of the compressive Young’s modulus after the compromise between friction and loss of connectivity, by comparing it with the optically determined one.

The mechanical testing of cancellous bone and the results interpretation are generally difficult due to its porosity. The loss of connectivity during preparation of cored samples results in a greater compliance at the cut surfaces than in in situ areas. If the compliance increases at the upper and bottom ends of the specimen, the consequence is an underestimation of the whole sample’s elastic modulus and strength (end effect). The trabeculae around the circumference of a sample loose also their connectivity during specimen preparation, resulting in reduced compliance (side artifact). In this way, the measured mechanical properties underestimate the in vivo behavior of cancellous bone, with intact trabecular network. Several published works confront this issue by correcting for side effects (Un et al., 2006). The hypothesis also tested in this work was whether surface strain, determined by DIC, was homogeneous throughout the surface of the specimen, or increased at the periphery, justifying underestimation of compressive Young’s modulus. Moreover, the macroscopic strain and the surface strain field, at which first yielding phenomena appeared with crack formation initiation, were investigated. For this reason, DIC and AE were simultaneously performed.

The specimens, in this work, were not confined by endcaps, as it has been found by three-dimensional finite element models that confining leads to overestimation of modulus for specimens shorter than 10 mm (Lievers et al., 2010).

The specimens were not preconditioned, as preconditioning has controversial effects on stiffness measurements. Decrease of tensile and compressive moduli by preconditioning suggested that initial yielding involves microstructural damage of a number of trabeculae and indicated that the tensile and compressive yield strain of trabecular bone from bovine tibiae is less than 0.5% (Keaveny et al., 1994). However, the compressive modulus was decreased by preconditioning at 5.3% (p < 0.01). The decrease in tensile modulus was even larger (on average 8.83%, p < 0.01). These results support the hypotheses that local microfractures of osteopenic vertebral bodies are created, start propagating, and accumulate at lower strains than those of normal vertebrae.

The measurements of the current research displayed a large difference between the values of Young’s modulus calculated in the “small” and “large” areas. This difference can be attributed to the fact that most specimens failed in the middle area, resulting in larger deformation of this specific area. In terms of strain, because the length of the middle area is smaller that that of the “large,” the strain in this area is higher, resulting in is lower modulus of elasticity in the middle area. It was difficult to interpret the onset of very high values of SD in the “large” area: the high spreading of values of modulus of elasticity (66–536 MPa) could be attributed to the higher length f examination, which increased the possibility of inclusion in the calculation of areas with large variation in architecture. Data (not shown) from cylindrical trabecular bone specimens have shown no underestimation of Young’s Modulus determined by platens relative displacement. Geometry of the specimen plays a significant role in mechanical properties of trabecular bone, as it has been recognized by several investigators (Linde et al., 1992a,b).

In the literature, average elastic modulus underestimation ranged from 22% for the human proximal tibia up to 38% for the bovine proximal humerus (Odgaard and Linde, 1991; Keaveny et al., 1993). Our values of underestimation were comparable to those found in the literature using cubic specimens and measuring strain in the central area. Experimental and numerical results have shown that side effects can be ignored if tested specimens have a suitably large diameter, whose minimum dimension depends on the cancellous architecture. This is justified by the fact that a cancellous bone specimen has a “damaged” region of lost connectivity around its periphery, with a characteristic thickness, t, depending upon the underlying architecture. In a cylinder with diameter D, when D increases, there is a decrease of the relative volume of this outer region in the periphery in relation to the total volume V of the cylinder. Therefore, if the specimen has an adequately large diameter, the magnitude of the side artifacts can become negligible, and there exists some minimum diameter above which the side effects can be ignored (Lievers et al., 2010). However, this logical result is not supported by our data. Because of the heterogeneous nature of cancellous bone, there are areas with a different microarchitecture (Perilli et al., 2008). The depiction of the longitudinal surface strain field evolution during compression reflected the presence of stiffer or more compliant areas of trabecular bone throughout the specimen surface. The strain was not increased in a systematic way at the periphery of the specimen. Thus, the hypothesis of reduced compliance due to loss of connectivity of the trabeculae at the periphery of a sample was not supported by these experiments.

Acoustic emission in cancellous bone during compression loading to confirm the microdamage initiation and accumulation (Hasegawa et al., 1993) was measured in this study. A microdamage event, either bone microfracture or microcrack propagation, releases energy. Some of this energy is in the form of acoustic waves. Using optical measurements, it has been found that trabecular bone exhibits fully linear elastic behavior and yields at low strains (less than 1.8%). It has been also suggested in the literature that minor structural changes may occur at a strain level as low as 0.8% (Linde et al., 1988; Madsen et al., 1988). AE activity revealed that microdamage initiated at about one-third of the maximum compressive strength. The surface yield strain in bone correlated with AE activity as in most homogeneous and non-porous materials (Alam and Loukili, 2010). On the contrary, initiation of AE activity occurred much earlier than the initiation of macroscopic yielding. The first detected microcracking probably concerned the thinner and most compliant trabeculae, which influenced the macroscopic stiffness in a smaller scale. The accumulation of these tiny microcracks led to macroscopic yielding, as it was revealed in the conventional stress–strain diagrams.

The number of AEs released from the trabecular bone samples did not vary widely. This behavior is totally different from that of compact bone where it has been noticed that a number of samples gave less than a dozen emissions until failure, whereas other samples generated hundreds of emissions (Agcaoglu and Akkus, 2013). These emission results imply that there are different patterns of compact bone failure: some samples failed with generation of few but large cracks whereas others failed by incremental growth of many small cracks. In trabecular bone, the failure mode is totally different. Fracture occurs after a sufficient number of trabeculae have been damaged. Moreover, the initiation of AEs of compact bone samples occurred at the time of the nonlinear increase in sample compliance and the cumulative number of AE events increased asymptotically in the prefailure period, whereas in cancellous bone AE events initiate in the macroscopic linear part of the σ–ε curve.

The detection of first AE of a significant amplitude would signal the initiation of failure. Thus, it is important to determine the time to failure at the first AE event. When these emissions are detected, they may provide an early warning in order to interrupt loading and prevent stress fracture, if AE is applied in vivo (Agcaoglu and Akkus, 2013). The AE is a function of bone material properties and the behavior of the bone microstructure during loading and failure procedure. More experiments are necessary to correlate the time of AE activity initiation with material properties in order to predict failure timely.

The measurement of the surface strain fields by DIC techniques have high resolution, enabling the determination of crack openings of microcracks present on the surface. However, this method is only limited to the surface of the specimen and cannot predict presence of cracks inside the specimen and inaccessible areas. Further experiments, determining 3D strain with digital volume correlation (DVC) apart from surface strain, are necessary to clarify the issue of strain inhomogeneity in cancellous bone (Gillard et al., 2014). Knowledge of the three-dimensional stress and strain distribution within bone tissue, MicroCT-imaging to assess the morphometric parameters and visualization of the failure region along with AE monitoring of released strain energy during bone mechanical testing will permit to understand the mechanism of bone failure, and may lead to an improved understanding of mechanisms of certain diseases’ initiation, prevention, and treatment (Leichter et al., 1990).

Conclusion

In conclusion, compressive Young’s modulus determined by platens relative displacement was underestimated in comparison to optically determined surface strain. There is also significant inhomogeneity in the strain distribution, resulting in large differences in the modulus, depending on the area over which it is calculated. Optical measurement of strain showed that compressive yielding occurs at low strains (less than 1.8%).

Strain at which microcracking initiates in cancellous bone and its relation to macroscopic yield strain has not been determined until now. Piezoelectric sensors on the specimens’ surface monitor AE activity, which indicates the initiation of local fracturing, which occurs much earlier than macroscopic yielding and fracture. AE activity recorded simultaneously with strain field measurements can clarify issues relating to understanding of the macroscopic strain at which crack formation initiate and propagates until fracture, inhomogeneity of bone tissue mechanical behavior and mechanisms of bone failure for improved understanding of certain diseases’ initiation, prevention, and treatment. Determination of 3D strain with DVC is necessary to clarify further the above issues.

Author Contributions

DD, University of Patras, contributed to overall design of the experiments, results interpretation, and manuscript writing. AT contributed to performance of experiments, results interpretation, and manuscript writing.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

Funding was provided from General Secretariat for Research and Technology (GSRT) and Hellenic Foundation for Research and Innovation (HFRI).

References

Agcaoglu, S., and Akkus, O. (2013). Acoustic emission based monitoring of the microdamage evolution during fatigue of human cortical bone. J. Biomech. 135, 81005–81008. doi: 10.1115/1.4024134

PubMed Abstract | CrossRef Full Text | Google Scholar

Alam, S. Y., and Loukili, A. (2010). “Application of digital image correlation to size effect tests of concrete,” in 7th International Conference on Fracture Mechanics of Concrete and Concrete Structures, North Korea, 91–97.

Google Scholar

Cardoso, L., Teboul, F., Sedel, L., Oddou, C., and Meunier, A. (2003). In vitro acoustic waves propagation in human and bovine cancellous bone. J. Bone Miner. Res. 18, 1803–1812. doi:10.1359/jbmr.2003.18.10.1803

PubMed Abstract | CrossRef Full Text | Google Scholar

Carter, D. R., and Hayes, W. C. (1977). The compressive behavior of bone as a two-phase porous structure. J. Bone Joint Surg. 59, 954–962. doi:10.2106/00004623-197759070-00021

PubMed Abstract | CrossRef Full Text | Google Scholar

Freddi, A., Olmi, G., and Cristofolini, L. (2015). Experimental Stress Analysis for Materials and Structures: Stress Analysis Models for Developing Design Methodologies. Cham: Springer.

Google Scholar

Gillard, F., Boardman, R., Mavrogordato, M., Hollis, D., Sinclair, I., Pierron, F., et al. (2014). The application of digital volume correlation (DVC) to study the microstructural behaviour of trabecular bone during compression. J. Mech. Beh. Biomed. Mater. 29, 480–499. doi:10.1016/j.jmbbm.2013.09.014

CrossRef Full Text | Google Scholar

Goff, M. G., Lambers, F. M., Sorna, R. M., Keaveny, T. M., and Hernandez, C. J. (2015). Finite element models predict the location of microdamage in cancellous bone following uniaxial loading. J. Biomech. 48, 4142–4148. doi:10.1016/j.jbiomech.2015.10.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Hanagud, S., Clinton, R. G., and Lopez, J. P. (1973). “Acoustic emission in bone substance,” in Proceedings of the ASME Symposium on Biomechanics, New York, 79–81.

Google Scholar

Hasegawa, K., Takahashi, H. E., Koga, Y., Kawashima, T., Hara, T., Tanabe, Y., et al. (1993). Mechanical properties of osteopenic vertebral bodies monitored by acoustic emission. Bone 14, 737–743. doi:10.1016/8756-3282(93)90205-O

PubMed Abstract | CrossRef Full Text | Google Scholar

Hernandez, C. J., Lambers, F. M., Widjaja, J., Chapa, C., and Rimnac, C. M. (2014). Quantitative relationships between microdamage and cancellous bone strength and stiffness. Bone 66, 205–213. doi:10.1016/j.bone.2014.05.023

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoult, N., Take, A., Lee, C., and Dutton, M. (2013). Experimental accuracy of two-dimensional strain measurements using digital image correlation. Eng. Struct. 46, 718–726. doi:10.1016/j.engstruct.2012.08.018

CrossRef Full Text | Google Scholar

Jonsson, U., and Eriksson, K. (1984). Microcracking in dog bone under load. A biomechanical study of bone visco-elasticity. Acta Orthop. Scand. 55, 441–445. doi:10.3109/17453678408992391

CrossRef Full Text | Google Scholar

Keaveny, T. M., Borchers, R. E., Gibson, L. J., and Hayes, W. C. (1993). Theoretical analysis of the experimental artifact in trabecular bone compressive modulus. J. Biomech. 26, 599–607. doi:10.1016/0021-9290(93)90021-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Keaveny, T. M., Guo, X., Wachtel, E., McMahon, T., and Hayes, W. (1994). Trabecular bone exhibits fully linear elastic behavior and yields at low strains. J. Biomech. 27, 1127–1136. doi:10.1016/0021-9290(94)90053-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambers, F. M., Bouman, A. R., Rimnac, A. C., and Hernandez, C. J. (2013). Microdamage caused by fatique loading in human cancellous bone: relationship to reductions in bone biomechanical performance. PLoS ONE 8, e1562. doi:10.1371/journal.pone.0083662

CrossRef Full Text | Google Scholar

Leichter, I., Bivas, A., Margulies, J. Y., Roman, I., and Simkin, A. (1990). Acoustic emission from trabecular bone during mechanical testing: the effect of osteoporosis and osteoarthritis. Proc. Inst. Mech. Eng. H 204, 123–127. doi:10.1243/PIME_PROC_1990_204_241_02

PubMed Abstract | CrossRef Full Text | Google Scholar

Lievers, W. B., Petryshyn, A. C., Poljsak, A. S., Waldman, S. D., and Pilkey, A. K. (2010). Specimen diameter and “side artifacts” in cancellous bone evaluated using end-constrained elastic tension. Bone 47, 371–377. doi:10.1016/j.bone.2010.03.024

CrossRef Full Text | Google Scholar

Linde, F., and Hvid, I. (1987). Stiffness behaviour of trabecular bone specimens. J. Biomech. 20, 83–89. doi:10.1016/0021-9290(87)90270-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Linde, F., Gothgen, C. B., Hvid, I., and Pongsoipetch, B. (1988). Mechanical properties of trabecular bone by a non-destructive testing approach. Eng. Med. 17, 23–29. doi:10.1243/EMED_JOUR_198017_008_02

CrossRef Full Text | Google Scholar

Linde, F., and Hvid, I. (1989). The effect of constraint on the mechanical behaviour of trabecular bone specimens. J. Biomech. 22, 485–490. doi:10.1016/0021-9290(89)90209-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Linde, F., Hvid, I., and Madsen, F. (1992a). The effect of specimen geometry on the mechanical behaviour of trabecular bone specimens. J. Biomech. 25, 359–368. doi:10.1016/0021-9290(92)90255-Y

PubMed Abstract | CrossRef Full Text | Google Scholar

Linde, F., Hvid, I., and Madsen, F. (1992b). The effect of specimen size and geometry on the mechanical behaviour of trabecular bone specimens. J. Biomech. 24, 454. doi:10.1016/0021-9290(91)90046-P

CrossRef Full Text | Google Scholar

Lionello, G., and Cristofolini, L. (2014). A practical approach to optimizing the preparation of speckle patterns for digital-image correlation. Meas. Sci. Technol. 25, 1–9. doi:10.1088/0957-0233/25/10/107001

CrossRef Full Text | Google Scholar

Madsen, F., Odgaard, A., and Linde, F. (1988). “The consequences of compression strain level on energy absorption in trabecular bone specimens performance,” in Proc 6th Mtg (London: ESB London).

Google Scholar

Maurer-Ertl, W., Friesenbichler, J., Svehlik, M., Holzer, L., Sadoghi, P., Ogris, K., et al. (2015). The effects of the surgical approach on the postoperative gait mechanics following total hip arthroplasty. Ann. Orthop. Rheumatol. 3, 1056.

Google Scholar

Odgaard, A., Hvid, I., and Linde, F. (1989). Strain distributions in cancellous bone specimens. J. Biomech. 23, 367. doi:10.1016/0021-9290(90)90078-H

CrossRef Full Text | Google Scholar

Odgaard, A., and Linde, F. (1991). The underestimation of Young’s Modulus in compressive testing of cancellous bone specimens. J. Biomech. 24, 691–698. doi:10.1016/0021-9290(91)90333-I

CrossRef Full Text | Google Scholar

Onck, P. R., Andrews, E., and Gibson, L. J. (2001). Size effects in ductile cellular solids. Part I: modeling. Int. J. Mech. Sci. 43, 681–699. doi:10.1016/S0020-7403(00)00042-4

CrossRef Full Text | Google Scholar

Palanca, M., Tozzi, G., and Cristofolini, L. (2015). The use of digital image correlation in the biomechanical area: a review. Int. Biomech. 3, 1–21. doi:10.1080/23335432.2015.1117395

CrossRef Full Text | Google Scholar

Perilli, E., Baleani, M., Ohman, C., Fognani, R., Baruffaldi, F., and Viceconti, M. (2008). Dependence of mechanical compressive strength on local variations in microarchitecture in cancellous bone of proximal human femur. J. Biomech. 41, 438–446. doi:10.1016/j.jbiomech.2007.08.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Roberts, B., Perilli, E., and Reynolds, K. (2014). Application of the digital volume correlation technique for the measurement of displacement and strain fields in bone: a literature review. J. Biomech. 47, 923–934. doi:10.1016/j.jbiomech.2014.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Shrivastava, S., and Prakash, R. (2009). Assessment of bone condition by acoustic emission technique: a review. J. Biomed. Sci. Eng. 2, 144–154. doi:10.4236/jbise.2009.23025

CrossRef Full Text | Google Scholar

Shrivastava, S., and Prakash, R. (2011). In vitro study of bone condition using acousto-ultrasonic technique. Int. J. Healthcare Manage. 12, 168–178. doi:10.1504/IJHTM.2011.039627

CrossRef Full Text | Google Scholar

Sutton, M., Wolters, W. J., Peters, W. H., Ranson, W. F., and McNeill, S. R. (1983). Determination of displacements using an improved digital correlation method. Image Vis. Comput. 1, 133–139. doi:10.1016/0262-8856(83)90064-1

CrossRef Full Text | Google Scholar

Sutton, M. A., Orteu, J. J., and Schreier, H. W. (2009). Image Correlation for Shape, Motion and Deformation Measurements. New York: Springer Science.

Google Scholar

Un, K., Bevill, G., and Keaveny, T. M. (2006). The effects of side-artifacts on the elastic modulus of trabecular bone. J. Biomech. 36, 1955–1963. doi:10.1016/j.jbiomech.2006.05.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Wright, T. M., Vosburgh, F., and Burstein, A. H. (1981). Permanent deformation of compact bone monitored by acoustic emission. J. Biomech. 14, 405–409. doi:10.1016/0021-9290(81)90058-0

CrossRef Full Text | Google Scholar