- Department of Mechanical Engineering, University of New Mexico, Albuquerque, NM, United States
We report an exploratory investigation into the cause of shear band formation in multilayer thin films subject to nanoindentation. The material system considered here is composed of alternating aluminum (Al) and silicon carbide (SiC) nanolayers, atop a silicon (Si) substrate. Finite element models are developed in an attempt to reproduce the shear banding phenomenon observed experimentally. By introducing strain softening into the material model for the hard SiC layers, shear bands can be seen to emerge from the indentation site in the finite element analysis. Broad implications, along with possible directions for future work, are discussed.
Introduction
Multilayer thin-film coatings offer mechanical property benefits beyond what single material films can provide. Alternating metal and ceramic nanolayers to create a multilayer structure lends increased strength and toughness, better wear and fatigue resistance, and favorable damage tolerance. Quantitatively characterizing the mechanical properties of these multilayer thin-films is of interest, with an eye toward applications from tooling to electronics (Romero et al., 2003; Deng et al., 2005a,b; Tang et al., 2008; Wieciński et al., 2014; Jamison and Shen, 2016).
To date, much of this characterization relies on nanoindentation to derive Young’s Modulus and hardness (Schuh, 2006). However, these methods were developed with homogeneous materials in mind, including the assumption that elastic recovery occurs during the indentation unloading phase (Tang et al., 2010). Multilayered configurations introduce complex internal stress and strain behaviors, which may affect the derived mechanical property values in ways not yet understood (Bhattacharyya et al., 2011; Jamison and Shen, 2016). Prior work in this area has investigated elastic modulus, hardness, plastic deformation during unloading, imperfect layer geometry, and delamination (Chawla et al., 2008; Tang et al., 2008, 2010; Wang et al., 2012; Jamison and Shen, 2016).
Figure 1 reveals the formation of shear bands within the structure of nanoindented and sectioned aluminum (Al) and silicon carbide (SiC) multilayers (Tang et al., 2010). The shear bands appear to initiate near the tip of the indentation. The localization of deformation can be strong enough to sever the hard ceramic layers. Similar observations were made in other metal–ceramic nanolayered materials (Wang et al., 2015). This phenomenon has not surfaced in the previous finite element models associated with elastic-perfect-plasticity. However, from the micro-tension tests of Deng et al. (2005a), it is inferred that the SiC film actually exhibits strain softening after yielding. The present exploratory work thus focuses on attempting shear band initiation in finite element models by incorporating strain softening of the SiC layers.

Figure 1. Cross-section scanning electron micrograph showing shear bands (highlighted by arrows) in Al/SiC thin-film multilayers after nanoindentation (Tang et al., 2010).
Numerical Model
A finite element model of the nanoindentation process was created and performed using ABAQUS (Version 6.14, Dassault Systemes Simulia Corp., Providence, RI, USA). See Figure 2A for a schematic of the model configuration. A conical diamond indenter was modeled in order to allow a two-dimensional, axisymmetric representation of the setup. The same projected contact area as the Berkovich nanoindenter, used in the experimental setup (Tang et al., 2009), was achieved with a semi-angle of 70.3°. In accordance with the experimental configuration, the model shown in Figure 2A also contained 41 total alternating layers of Al and SiC, with aluminum being the topmost layer. Each layer was 50 nm thick, with the multilayer film residing on a silicon (Si) substrate. The structure (Al/SiC film and Si substrate) had a radius of 40 µm and an overall height of 43 µm. No initial defects were included in the model.
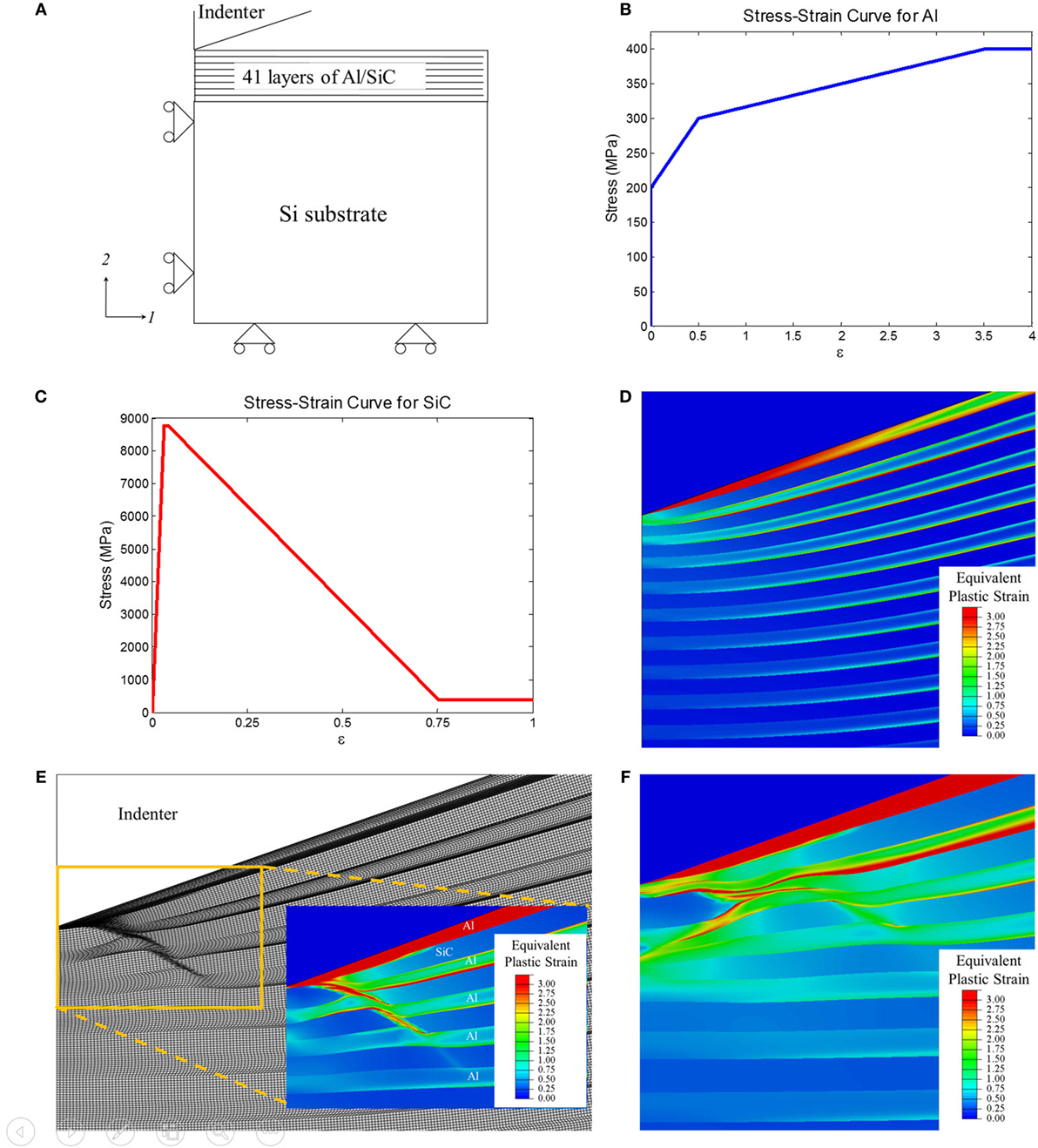
Figure 2. (A) Schematic of axisymmetric model setup, with symmetry axis and boundary conditions shown for the 41 alternating Al/SiC laminates on a Si substrate. (B) Stress–strain input curve for Al material model. (C) Stress–strain input curve for strain softened SiC material model. (D) Contour plot of equivalent plastic strain in the baseline Al/SiC film model (no strain softening of SiC), when the indentation depth is at 0.5 µm. (E) Deformed configuration and equivalent plastic strain in the multilayer Al/SiC model, with strain softening of SiC, when the indentation depth reaches 0.59 µm. (F) Shear bands resulting from a multilayer Al/SiC model with a slightly modified strain softening response of SiC, after indentation to 0.75 µm.
The left edge of the model was the axis of symmetry and was constrained such that it had freedom of displacement only in the 2-direction. The bottom edge of the model was constrained to only allow displacement along the 1-direction. The other two edges were free in either direction. Upon contact of the indenter with the top layer of aluminum, frictional contact was assumed, with the coefficient of friction being 0.1 (Lide, 1995; Bucaille et al., 2004).
Material parameters were garnered from previous work (Chawla et al., 2008; Tang et al., 2008, 2009, 2010; Jamison and Shen, 2016), taking into account the different properties of materials in the thin-film form compared to their bulk counterpart. The stress–strain curves extracted from micro-tensile experiments of Al and Al/SiC multilayer films show that, while independent Al layers experience an expected work hardening leading to perfect plasticity, the Al/SiC multilayer film as a whole exhibits work softening (Deng et al., 2005a). This implies that the SiC layers themselves have a strain softening behavior. The focus of the present study considers the impact of modifying the SiC model’s stress–strain input profile to include a gradual softening of the material after yield, with the yield strength of 8,770 MPa estimated from the actual hardness measurement of a single-layer SiC (Tang et al., 2010). Figures 2B,C detail the stress–strain input curves for the Al and SiC material models, respectively. The quantitative softening of SiC was chosen arbitrarily for the model’s computational purposes, while trying to preserve some of the qualitative aspects inferred from experimental measurements. For simplicity, the softening portion of the stress–strain profile is taken as linear until the plastic flow stress reaches 400 MPa, the same flow stress carried by the Al layers. More detailed considerations of the softening parameters are left as future work.
Simulations and Results
A control simulation for the multilayer indentation was run, which did not include any strain softening in the SiC material properties, keeping it elastic perfectly plastic. The result of this simulation is shown in Figure 2D, in the form of an equivalent plastic strain contour plot near the indentation tip, when the indentation depth is 0.5 µm. Due to the strain contrast, the individual Al and SiC layers are readily discernible. This is identical to the simulation result obtained previously, with no evidence of shear band formation (Tang et al., 2010; Jamison and Shen, 2016).
Implementing the Figure 2C strain softening curve for SiC yielded promising results. The initiation of a shear band was observed near the interface with the indenter tip in the early stages of the indentation. The band grew in a direction toward the lower right of the material model as the indentation depth increased. Figure 2E shows the deformed mesh and contour plot of equivalent plastic strain at an indentation of 0.59 µm; a prominent shear band with significantly higher plastic strains than its surrounding is evident.
It is thought that the strain softening, alone or in part, is responsible for shear band formation, as it is the only difference between the models producing Figures 2D,E. The fact that no initial defects were placed in the model further supports this assertion, as there were no obvious stress concentration areas other than the indenter tip to encourage deformation paths.
Multiple indentation depths between 0.1 and 0.6 µm were simulated for the two cases (with and without softening) in order to compare hardness and Young’s modulus calculations. At small indentation depths, the hardness values agreed well. At indentation depths above approximately 0.35 µm, the softened model hardness values consistently dip below the unsoftened baseline model’s, albeit slightly (less than 5%). Strain softening and shear bands, therefore, may slightly degrade calculated hardness, although more thorough study is needed. Regarding Young’s modulus, derived from the unloading load–displacement response, the two cases track well with each other through the majority of the displacement range. Although the hardness and modulus were not significantly affected during the early stages of shear banding, in actual materials, the intense shear may lead to internal damage, which impacts the indentation-measured properties.
In the multilayers, the much more ductile Al is attempting to flow away from the indentation, all while being constrained by the more brittle adjacent SiC layers. The mismatch between the stress–strain curves of each material, in conjunction with the softening tendency in SiC once the peak stress is reached, appear to be critical in triggering the localization of deformation. Once getting over the hurdle of formation itself, the softening curve and relative material properties can also have great effects in the shape and prominence of the shear bands. Figure 2F illustrates this point, as it reflects only one minor change to the Figure 2C input curve used in the Figure 2E simulation: the SiC plastic flow stress was doubled to 800 MPa, resulting in a marginally shallower softening slope. This change was enough to redirect the shear band from one prominent arm into a less well-defined band that split into two branches. One branch continued in the direction of the parent, only less aggressive, and the other split off in a mirrored fashion.
For comparison, separate homogeneous film models were also considered, with the 41 layers treated as either all Al or all SiC. Both materials were explored with and without the inclusion of strain softening. For the Al case, neither the standard nor the softening model produced any hint of shear band formation. As for the SiC, there was also no evidence of shear banding in the model without any strain softening. On the other hand, the inclusion of softening in the SiC model did trigger the initiation of a shear band, although it was significantly weaker than anything observed in the multilayer configurations. The internal deformation constraint unique to the multilayer structure is thus shown to play a prominent role in the development of shear bands.
Concluding Remarks
We have demonstrated that strain softening of the hard layer after yielding is a key factor in shear band formation in thin-film multilayers. The shape and prominence of shear banding are dependent on the relative stress–strain curves of each material in the structure. Sensitivity was observed to relatively small changes in the softening characteristics. Future work should include a detailed examination of the relative yield strengths of the hard/soft constituents, as well as the influence of the actual strain softening curve. The effect of layer thickness also warrants further investigation, as this study was done at a fixed bilayer period with equal thicknesses for Al and SiC. Variations on both the relative thicknesses of the hard/soft layers and the overall bilayer period thickness are left as future work. Furthermore, the question of imperfect geometry arises, such as the effect of undulating layers caused by fabrication of the nanoscale thin films. The importance of layer order is also unknown, and additional study is recommended. The present study serves as a basis, from the continuum-based modeling standpoint, for continued investigations of localized deformation phenomena caused by nanoindentation in multilayer thin-film material systems.
Author Contributions
SB performed the simulation and data analysis. Y-LS provided direction and resources for the study. Both authors contributed to the writing of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bhattacharyya, D., Mara, N. A., Dickerson, P., Hoagland, R. G., and Misra, A. (2011). Compressive flow behavior of Al-TiN multilayers at nanometer scale layer thickness. Acta Mater. 59, 3804–3816. doi: 10.1016/j.actamat.2011.02.036
Bucaille, J.-L., Stauss, S., Schwaller, P., and Michler, J. (2004). A new technique to determine the elastoplastic properties of thin metallic films using sharp indenters. Thin Solid Films 447-448, 239–245. doi:10.1016/S0040-6090(03)01100-3
Chawla, N., Singh, D. R. P., Shen, Y.-L., Tang, G., and Chawla, K. K. (2008). Indentation mechanics and fracture behavior of metal/ceramic nanolaminate composites. J. Sci. Mater. 43, 4383–4390. doi:10.1007/s10853-008-2450-3
Deng, X., Chawla, N., Chawla, K. K., Koopman, M., and Chu, J. P. (2005a). Mechanical behavior of multilayered nanoscale metal-ceramic composites. Adv. Eng. Mater. 7, 1099–1108. doi:10.1002/adem.200500161
Deng, X., Cleveland, C., Chawla, N., Karcher, T., Koopman, M., and Chawla, K. K. (2005b). Nanoindentation behavior of nanolayered metal-ceramic composites. J. Mater. Eng. Perform. 14, 417–423. doi:10.1361/105994905X56115
Jamison, R. D., and Shen, Y.-L. (2016). Indentation and overall compression behavior of multilayered thin-film composites: effect of undulating layer geometry. J. Compos. Mater. 50, 507–521. doi:10.1177/0021998315576768
Romero, J., Lousa, A., Martínez, E., and Esteve, J. (2003). Nanometric chromium/chromium carbide multilayers for tribological applications. Surf. Coat. Technol. 163, 392–397. doi:10.1016/S0257-8972(02)00634-5
Schuh, C. A. (2006). Nanoindentation studies of materials. Mater. Today 9, 32–40. doi:10.1016/S1369-7021(06)71495-X
Tang, G., Shen, Y.-L., Singh, D. R. P., and Chawla, N. (2008). Analysis of indentation-derived effective elastic modulus of metal-ceramic multilayers. Int. J. Mech. Mater. Des. 4, 391–398. doi:10.1007/s10999-008-9063-5
Tang, G., Shen, Y.-L., Singh, D. R. P., and Chawla, N. (2010). Indentation behavior of metal-ceramic multilayers at the nanoscale: numerical analysis and experimental verification. Acta Mater. 58, 2033–2044. doi:10.1016/j.actamat.2009.11.046
Tang, G., Singh, D. R. P., Shen, Y.-L., and Chawla, N. (2009). Elastic properties of metal-ceramic nanolaminates measured by nanoindentation. Mater. Sci. Eng. A 502, 79–84. doi:10.1016/j.msea.2008.11.013
Wang, D., Kups, T., Schawohl, J., and Schaaf, P. (2012). Deformation behavior of Au/Ti multilayers under indentation. J. Mater. Sci. Mater. Electron. 23, 1077–1082. doi:10.1007/s10854-011-0550-3
Wang, M., Wang, D., Kups, T., and Schaaf, P. (2015). Size effect on mechanical behavior of Al/Si3N4 multilayers by nanoindentation. Mater. Sci. Eng. A 644, 275–283. doi:10.1016/j.msea.2015.07.071
Keywords: shear band, multilayer, thin-film, nanoindentation, nanocomposites, nanolayers
Citation: Bigelow S and Shen Y-L (2017) Indentation-Induced Shear Band Formation in Thin-Film Multilayers. Front. Mater. 4:25. doi: 10.3389/fmats.2017.00025
Received: 29 January 2017; Accepted: 31 July 2017;
Published: 18 August 2017
Edited by:
Cher Ming Tan, Chang Gung University, TaiwanReviewed by:
Gregory Abadias, Institut Pprime, FranceKwadwo Mensah-Darkwa, Kwame Nkrumah University of Science and Technology, Ghana
Copyright: © 2017 Bigelow and Shen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yu-Lin Shen, c2hlbnlsQHVubS5lZHU=
 Shannon Bigelow
Shannon Bigelow Yu-Lin Shen
Yu-Lin Shen