Micromechanical Analysis of Soft Tactile Sensors

Today, soft materials (e.g., elastomers, polymers, fabrics, etc.), with compliances and extensibilities not allowed by rigid components, are investigated in order to develop artificial tactile sensors that can emulate the adaptability of the natural tissues to objects and environment in general. This research is fueled by the increasing demand for conformable, yet functional and robust, systems in many fields from soft robotics to wearable systems and biomedical devices (Kim et al., 2013).

In the past decades, remarkable results were obtained in the design and fabrication of tactile sensors and, more in general, of electronic skins (e-skins) (Someya et al., 2004; Sekitani et al., 2008; Kim et al., 2011; Park et al., 2014; Xu et al., 2014; Zhang et al., 2015). These achievements were fundamental for a plethora of new applications, such as human–machine interfaces, body-integrated electronics, and medical/health-monitoring devices. Also, they offered very advanced technological solutions for robotics and wearable systems. From a mechanical point of view, flexible and stretchable substrates were chosen, while the integrated components went from rigid (Yang et al., 2010; Kim et al., 2011; Xu et al., 2014) to semi-rigid (Engel et al., 2005; Yang et al., 2008) and finally to flexible (Tien et al., 2014; Park et al., 2015; Zhang et al., 2015) and stretchable (Someya et al., 2004; Sekitani et al., 2008; Park et al., 2014; Chou et al., 2015) devices.

In particular, pressure sensors are widely applied in classical robotics, i.e., where the materials of the robot body are rigid. Thus, when positioning the sensors on the hosting structures, the sensors’ functionality is not affected by the mechanical characteristics of the robot itself, since the rigid and elastic materials do not store any mechanical energy. Hence, tactile sensors were developed and characterized as independent components that were integrated in the robot at a later stage. On the other hand, especially for integrating pressure sensors in a soft robot or in a wearable system, this approach would not give the desired results. Indeed, the mechanical characteristics of the soft robots or the natural skin, which act as hosting substrates, could reduce or even totally impair the correct functionality of such mechanical sensors. In particular, due to the substrate softness, the largest compression can occur in the substrate rather than in the sensing device. The abovementioned weaknesses can be overcome with an integrated approach (i.e., considering the mechanical characteristics of both sensing device and substrate) in the modeling, fabrication, and characterization of such systems. For instance, in the case of wearable systems, the properties of human skin, and underlying tissues and bones, should be taken into account; whereas in soft robotics, the materials used for fabricating them [e.g., mainly elastomers such as polydimethylsiloxane (PDMS) and Ecoflex^® (Shepherd et al., 2011; Morin et al., 2012)] must be included as part of the working system. From the mechanical point of view, human skin can be approximated as a bilayer tissue standing on a soft substrate, with non-linear and viscoelastic properties (Hendriks et al., 2003) depending on several factors, such as the age, the sex, or the body region (Escoffier et al., 1989). The lower layer (hypodermis) has an average thickness around 0.8 mm, with a Young’s modulus around 2 kPa. Otherwise, the upper (dermis) has a thickness between 1.2 and 1.5 mm, with a Young’s modulus around 35 kPa, while the most superficial layer (epidermis) can be neglected from a mechanical point of view, due to its very low thickness (around 80 µm). Finally, the subcutaneous tissue (muscle) has an average Young’s modulus of 80 kPa (Pailler-Mattei et al., 2008). Looking at the soft robotics side, PDMS and Ecoflex^® present non-linear and viscoelastic behaviors for high strain rates, while the stress–strain relationships are almost linear for strain under 40% (Case et al., 2015). In particular, PDMS is a transparent silicone with a Young’s modulus varying from 100 kPa to 4 MPa, mainly due to its curing temperature and to the mix ratio of prepolymers. Also, Ecoflex^® has a Young’s modulus around 30–40 kPa (Case et al., 2015), and it is one of the very few materials available for mimicking the human skin mechanical behavior (Amjadi et al., 2015).

Hence, modeling the behavior of a soft pressure sensor on a multilayer soft substrate can be not trivial. In our opinion, analyzing the correlation between the mechanical and functional (e.g., electrical) behavior of sensors made of soft materials is mandatory. In particular, it is important to understand how the mechanical properties of the constituent materials of sensors affect the electrical response and to evaluate the influence of the soft structures and substrates in which they will be embedded. Then, these characteristics can be exploited to encode tactile cues more efficiently and with simpler designs. This requires the development of non-linear mechanical models, also considering the way the mechanical response of such materials is typically described in literature, i.e., with hyperelastic models like the Mooney–Rivlin, Ogden, or Fung (Fung, 1993; Holzapfel, 2000).

In the overall vision of designing innovative smart devices for soft robotics and wearable applications in the near future, here we present a case study evaluating the behavior of a skin-like soft pressure sensor when stimulated by external loads quasi-statically (i.e., the indentation velocity is low). This way, some theoretical insights can be given for future analyses of more complex stimuli. The sensor, shown in Figure 1A, is made of different soft layers. It is highly sensitive and can detect normal forces in the 20 N range. Since the sensor area is 8 mm × 8 mm, the pressure range is around 300 kPa. The device structure, sketched in Figure 1B, is built by integrating in between them two non-stretchable conductive textile electrodes (Zelt fabric, Mindsets Ltd., Whaltam Abbey, UK) and a thin film of Ecoflex^®. It is a super soft silicone elastomer (Smooth-On 0010, USA), which acts as a deformable dielectric layer. The whole structure is embedded between two PDMS (Sylgard 184, Dow Corning, Midland, TX, USA) layers that insulate the textile electrodes while providing a soft and compliant surface to outer stimuli. In our case, we used a 1:10 mix ratio, with the films cured at room temperature for at least 24 h before the use. Regarding elastomeric layers, the corresponding Young’s modulus is around 3 MPa for PDMS and 30 kPa for Ecoflex. Both values have been measured by means of indentation tests. Moreover, a particular aspect that affects sensor response is given by the textile electrodes: they consist of copper/tin-coated woven fabric. The architecture of a woven fabric is such that small air volumes (i.e., sheds) are embedded among the warp and weft that confer unique properties to the tactile sensor. Indeed, a microporous structure is obtained in the active region of the device. When a pressure is applied, together with the compression of elastomeric layers, the sheds’ volume in the stimulated area is reduced relevantly, thereby resulting in an enhanced sensor response for a wider pressure range (Viry et al., 2014).

FIGURE 1

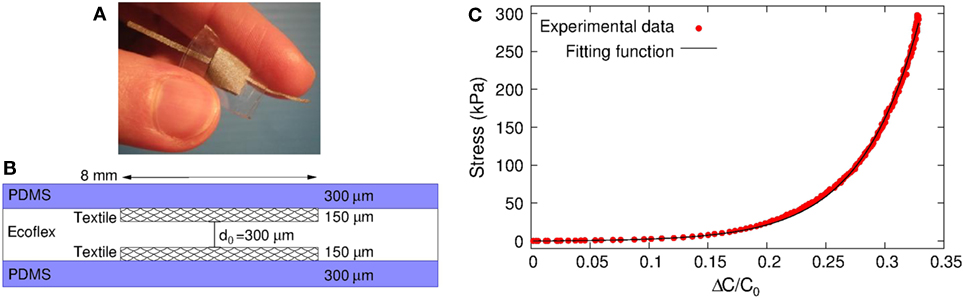
Figure 1. Picture (A) and schematic structure (B) of the soft capacitive pressure sensor based on conductive textile electrodes and silicone elastomers. (C) Stress vs. ΔC/C₀ experimental data (red circles), compared to the fitting curve (black solid line) considering the Ecoflex dielectric layer as a Fung non-linear material.

A pressure applied on the sensor surface causes the variation of the dielectric layer thickness d, with respect to d₀ = 300 μm, giving

$\frac{\mathrm{\Delta }C}{C_0}=\frac{d_0-d}{d}=\frac{{\mathrm{\epsilon }}_c}{1-{\mathrm{\epsilon }}_c},$ (1)

being C₀ = kA₀/d₀ the capacitance for null pressure, k and A₀ the permittivity and the sensor area, respectively, and ε_c = (d₀ − d)/d₀ the compressive strain of the dielectric layer. The best fitting of the compressive stress (σ_c)–strain (ε_c) experimental curve of the multilayer film is given by the Fung model, with an exponential stress–strain constitutive equation (Fung, 1993), valid for uniaxial response

${\mathrm{\sigma }}_c=c_1\left(e^{c_2{\mathrm{\epsilon }}_c}-1\right),$ (2)

with c₁ and c₂ two material constants.

Then, combining Eqs 1 and 2, we obtain

${\mathrm{\sigma }}_c=c_1\left(e^{c_2\frac{x}{1+x}}-1\right),$ (3)

where x = ΔC/C₀.

Equation 3 is exploited for the evaluation of experimental data obtained by indentation tests. In particular, a flat Delrin 8 mm × 8 mm probe was connected to a 6-axis load cell (ATI Nano 17, ATI Industrial Automation Inc., Apex, NC, USA), which acquired force data during the tests. The indentations were made at constant low velocity (10 µm/s) by means of a servo-controlled micrometric translation stage (M111.DG, Physik Instruments, Karlsruhe, Germany), while the capacitive output signals were acquired simultaneously with a custom made printed circuit board based on 24-bits resolution capacitance-to-digital converter (CDC) (AD7747, Analog Devices Inc., Nordwood, MA, USA) and PIC32 microcontroller that sends data to a control PC via USB interface. The CDC resolution is 1 fF, while the RMS noise is reduced to around 2 fF by implementing a differential capacitance reading strategy and using coaxial cables. Thus, the minimum detectable signal is around 6 fF (three times the RMS noise), which allows a readout force resolution at the millinewton scale.

In Figure 1C, the σ_c − ΔC/C₀ curve, averaged over 12 tests, is fitted using Eq. 3, showing a very good agreement. We obtain c₁ = 0.0660 and c₂ = 33.847 kPa.

To study the influence of each different layer, a first approach could be to limit the analysis to small deformations. In this case, linearizing Eq. 2, ${\mathrm{\sigma }}_c\simeq c_1{c}_2{\mathrm{\epsilon }}_c=E{\mathrm{\epsilon }}_c$, and the product c₁c₂ represents the Young’s modulus for small deformations. Then, for small strain, the apparent Young’s modulus of the whole structure is E_a = c₁c₂ = 2.24 kPa, well below the nominal value of Ecoflex E₀ = 30–40 kPa. A direct measurement of the Young modulus of textile by means of indentation tests is not trivial, since the experimental errors can affect the results considerably. Thus, we made tests on a multilayer composed of Ecoflex embedded between two textile films (which correspond to the active region of the sensor), obtaining a multilayer modulus E_m = 4 kPa. Finally, comparing the stiffness of the whole structure to the series of three layers, the Young’s modulus E_t of the textile electrodes can be estimated. Indeed, considering

$\frac{d_0+2d_t}{E_m}=\frac{d_0}{E_0}+\frac{2d_t}{E_t},$ (4)

where d_t = 150 μm is the textile thickness, we obtain E_t = 2.22 kPa, almost equal to E_a. This demonstrates the relevance of the textile material in the mechanical behavior of the sensor. Also, as already shown in Viry et al. (2014), the air sheds enhance the sensor response at low pressure ranges and considerably enlarge its operating range. Moreover, it is noteworthy to mention that, even if during compression all different layers are subjected to deformation, the capacitance variation is due mainly to the thickness variation of the central sensor region. Therefore, due to the strong non-linear behavior of the whole structure, it is not possible to relate directly the total compressive strain to the measured capacitance. Indeed, the output signal is due to the compression of the central region only. By contrast, this example suggests that such electrical measurements could also be exploited as a tool to evaluate the effective deformation of a single layer embedded in a composite structure, even in the presence of several non-linear materials.

In conclusion, we provided some insight about the kind of complexity introduced by the presence of soft materials in modeling and designing a tactile sensor. Starting from this analysis, future work will be dedicated to quantitatively describe the effect of mechanical behavior of the constituent materials (especially textile) on the sensor response, by using stimuli with different stiffness and shape. In addition, the effect of the soft substrates, such as human skin for wearable systems or elastomers (i.e., PDMS, Ecoflex^®) for soft robotic applications, should be included, as mentioned above. In this way, it will be possible to better understand how to encode different tactile features, thus not only force but also, e.g., shape and hardness, with improved but simple sensor designs.

Author Contributions

MT, NP, and LB developed and discussed the model. MT performed experiments. LB supervised the work. All the authors discussed the results and wrote the manuscript preparation.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a past coauthorship with one of the authors (NP) and states that the process nevertheless met the standards of a fair and objective review.

Acknowledgments

NP is supported by the European Research Council PoC 2015 “Silkene” No. 693670 and by the European Commission H2020 under the Graphene Flagship Core 1 No. 696656 (WP14 “Polymer Nanocomposites”) and under the FET Proactive “Neurofibres” No. 732344.

References

Amjadi, M., Yoon, Y. J., and Park, I. (2015). Ultra-stretchable and skin-mountable strain sensors using carbon nanotubes–Ecoflex nanocomposites. Nanotechnology 26, 375501. doi:10.1088/0957-4484/26/37/375501

CrossRef Full Text | Google Scholar

Case, J. C., White, E. L., and Kramer, R. K. (2015). Soft material characterization for robotic applications. Soft Rob. 2, 80–87. doi:10.1089/soro.2015.0002

CrossRef Full Text | Google Scholar

Chou, H.-H., Nguyen, A., Chortos, A., To, J. W. F., Lu, C., Mei, J., et al. (2015). A chameleon-inspired stretchable electronic skin with interactive colour changing controlled by tactile sensing. Nat. Commun. 6, 8011. doi:10.1038/ncomms9011

PubMed Abstract | CrossRef Full Text | Google Scholar

Engel, J., Chen, J., Fan, Z. F., and Chang, L. (2005). Polymer micromachined multimodal tactile sensors. Sens. Actuators Phys. 117, 50–61. doi:10.1016/j.sna.2004.05.037

CrossRef Full Text | Google Scholar

Escoffier, C., de Rigal, J., Rochefort, A., Vasselet, R., Leveque, J.-L., and Agache, P. G. (1989). Age-related mechanical properties of human skin: an in vivo study. J. Invest. Dermatol. 93, 353–357. doi:10.1111/1523-1747.ep12280259

PubMed Abstract | CrossRef Full Text | Google Scholar

Fung, Y. (1993). Biomechanics: Material Properties of Living Tissues. New York: Springer.

Google Scholar

Hendriks, F. M., Brokken, D., Van Eemeren, J. T. W. M., Oomens, C. W. J., Baaijens, F. P. T., and Horsten, J. B. A. M. (2003). A numerical-experimental method to characterize the non-linear mechanical behaviour of human skin. Skin Res. Technol. 9, 274–283. doi:10.1034/j.1600-0846.2003.00019.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzapfel, G. A. (2000). Nonlinear Solid Mechanics. Chichester: John Wiley & Sons.

Google Scholar

Kim, D.-H., Lu, N., Ma, R., Kim, Y.-S., Kim, R.-H., Wang, S., et al. (2011). Epidermal electronics. Science 333, 838–843. doi:10.1126/science.1206157

CrossRef Full Text | Google Scholar

Kim, S., Laschi, C., and Trimmer, B. (2013). Soft robotics: a bioinspired evolution in robotics. Trends Biotechnol. 31, 23–30. doi:10.1016/j.tibtech.2013.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Morin, S. A., Shepherd, R. F., Kwok, S. W., Stokes, A. A., Nemiroski, A., and Whitesides, G. M. (2012). Camouflage and display for soft machines. Science 337, 828–832. doi:10.1126/science.1222149

PubMed Abstract | CrossRef Full Text | Google Scholar

Pailler-Mattei, C., Bec, S., and Zahouani, H. (2008). In vivo measurements of the elastic mechanical properties of human skin by indentation tests. Med. Eng. Phys. 30, 599–606. doi:10.1016/j.medengphy.2007.06.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Park, J., Kim, M., Lee, Y., Lee, H. S., and Ko, H. (2015). Fingertip skin–inspired microstructured ferroelectric skins discriminate static/dynamic pressure and temperature stimuli. Sci. Adv. 1, e1500661. doi:10.1126/sciadv.1500661

CrossRef Full Text | Google Scholar

Park, S., Kim, H., Vosgueritchian, M., Cheon, S., Kim, H., Koo, J. H., et al. (2014). Stretchable energy-harvesting tactile electronic skin capable of differentiating multiple mechanical stimuli modes. Adv. Mater. Weinheim 26, 7324–7332. doi:10.1002/adma.201402574

PubMed Abstract | CrossRef Full Text | Google Scholar

Sekitani, T., Noguchi, Y., Hata, K., Fukushima, T., Aida, T., and Someya, T. (2008). A rubberlike stretchable active matrix using elastic conductors. Science 321, 1468–1472. doi:10.1126/science.1160309

PubMed Abstract | CrossRef Full Text | Google Scholar

Shepherd, R. F., Ilievski, F., Choi, W., Morin, S. A., Stokes, A. A., Mazzeo, A. D., et al. (2011). Multigait soft robot. Proc. Natl. Acad. Sci. U.S.A. 108, 20400–20403. doi:10.1073/pnas.1116564108

PubMed Abstract | CrossRef Full Text | Google Scholar

Someya, T., Sekitani, T., Iba, S., Kato, Y., Kawaguchi, H., and Sakurai, T. (2004). A large-area, flexible pressure sensor matrix with organic field-effect transistors for artificial skin applications. Proc. Natl. Acad. Sci. U.S.A. 101, 9966–9970. doi:10.1073/pnas.0401918101

PubMed Abstract | CrossRef Full Text | Google Scholar

Tien, N. T., Jeon, S., Kim, D.-I., Trung, T. Q., Jang, M., Hwang, B.-U., et al. (2014). A flexible bimodal sensor array for simultaneous sensing of pressure and temperature. Adv. Mater. Weinheim 26, 796–804. doi:10.1002/adma.201302869

PubMed Abstract | CrossRef Full Text | Google Scholar

Viry, L., Levi, A., Totaro, M., Mondini, A., Mattoli, V., Mazzolai, B., et al. (2014). Flexible three-axial force sensor for soft and highly sensitive artificial touch. Adv. Mater. Weinheim 26, 2659–2664. doi:10.1002/adma.201305064

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, S., Zhang, Y. H., Jia, L., Mathewson, K. E., Jang, K. I., Kim, J., et al. (2014). Soft microfluidic assemblies of sensors, circuits, and radios for the skin. Science 344, 70–74. doi:10.1126/science.1250169

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, Y. J., Cheng, M. Y., Chang, W. Y., Tsao, L. C., Yang, S. A., Shih, W. P., et al. (2008). An integrated flexible temperature and tactile sensing array using PI-copper films. Sens. Actuators Phys. 143, 143–153. doi:10.1016/j.sna.2007.10.077

CrossRef Full Text | Google Scholar

Yang, Y. J., Cheng, M. Y., Shih, S. C., Huang, X. H., Tsao, C. M., Chang, F. Y., et al. (2010). A 32 × 32 temperature and tactile sensing array using PI-copper films. Int. J. Adv. Manuf. Technol. 46, 945–956. doi:10.1007/s00170-009-1940-z

CrossRef Full Text | Google Scholar

Zhang, F. J., Zang, Y. P., Huang, D. Z., Di, C. A., and Zhu, D. B. (2015). Flexible and self-powered temperature-pressure dual-parameter sensors using microstructure-frame-supported organic thermoelectric materials. Nat. Commun. 6, 8356. doi:10.1038/Ncomms9356

PubMed Abstract | CrossRef Full Text | Google Scholar