The interaction of C60 on Si(111) 7 × 7 studied by supersonic molecular beams: interplay between precursor kinetic energy and substrate temperature in surface activated processes

Buckminsterfullerene (C₆₀) is a molecule fully formed of carbon that can be used, owing to its electronic and mechanical properties, as “clean” precursor for the growth of carbon-based materials, ranging from π-conjugated systems (graphenes) to synthesized species, e.g., carbides such as silicon carbide (SiC). To this goal, C₆₀ cage rupture is the main physical process that triggers material growth. Cage breaking can be obtained either thermally by heating up the substrate to high temperatures (630°C), after C₆₀ physisorption, or kinetically by using supersonic molecular beam epitaxy techniques. In this work, aiming at demonstrating the growth of SiC thin films by C₆₀ supersonic beams, we present the experimental investigation of C₆₀ impacts on Si(111) 7 × 7 kept at 500°C for translational kinetic energies (KEs) ranging from 18 to 30 eV. The attained kinetically activated synthesis of SiC submonolayer films is probed by in situ surface electron spectroscopies (X-ray photoelectron spectroscopy and ultraviolet photoelectron spectroscopy). Furthermore, in these experimental conditions, the C₆₀-Si(111) 7 × 7 collision has been studied by computer simulations based on a tight-binding approximation to density-functional theory. Our theoretical and experimental findings point toward a kinetically driven growth of SiC on Si, where C₆₀ precursor KE plays a crucial role, while temperature is relevant only after cage rupture to enhance Si and carbon reactivity. In particular, we observe a counterintuitive effect in which for low KE (below 22 eV), C₆₀ bounces back without breaking more effectively at high temperature due to energy transfer from excited phonons. At higher KE (22 < K < 30 eV), for which cage rupture occurs, temperature enhances reactivity without playing a major role in the cage break. These results are in good agreement with ab initio molecular dynamics simulations. Supersonic molecular beam epitaxy is thus a technique able to drive material growth at low-temperature regime.

Introduction

The synthesis of carbon-based thin films and nanostructured compounds, such as carbides and graphene, on top of semiconductor or metal surfaces represents a serious challenge to the production of electronic devices and materials coating. Several methods, mainly based on the chemical vapor deposition (CVD) of organic molecules or molecular beam epitaxy (MBE), have been successfully developed to obtain large area carbon-based materials with the common feature of working at very high temperatures. For example, the low energy deposition of fullerene on silicon has been deeply studied with experimental approaches, mainly using standard techniques (Sakamoto et al., 1999; De Seta et al., 2000; Sanvitto et al., 2000; Balooch and Hamza, 1993). MBE, in particular, has shown to be a viable approach to silicon carbide (3C–SiC) synthesis at about 800°C, using fullerene (C₆₀) as carbon precursor and silicon as a growth substrate (Sanvitto et al., 2000; De Seta et al., 2000). The required high temperature, however, leads to structural defects at the nano- and micro-scale, mainly due to high lattice mismatch between SiC and Si and due to increasing thermal diffusion through the SiC film. Moreover, only amorphous Si films can be achieved at 800°C, and postdeposition thermal treatments at higher temperatures are necessary to improve crystallinity.

At room temperature, the most common process at the fullerene–surface interface, be it metallic or semiconductor, is represented by physisorption. Chemisorption is a viable way only on reconstructed silicon surfaces (both Si(111) 7 × 7 and Si(100) 2 × 1) due to the presence of several dangling bonds on the surface, the most reactive for fullerenes being the 7 × 7 reconstruction of Si(111). Furthermore, to induce cage breaking on the top of the surface, one needs to increase the substrate temperature. Finally, subsequent to rupture, the most common outcome on Si(111) 7 × 7 surfaces results in the formation of several new Si–C bonds up to the synthesis of silicon carbide (SiC) at 800°C.

To overcome the temperature issues, in a previous work (Verucchi et al., 2012), we reported the room temperature (about 20°C) synthesis of nanocrystalline 3C–SiC with fullerene on Si(111) 7 × 7 surface by the so-called supersonic molecular beam epitaxy (SuMBE) technique. Using this approach, the C₆₀ translational kinetic energy (KE) can reach values up to 30–35 eV by aerodynamic acceleration due to isoentropic expansion in vacuum. We demonstrated that the cage rupture after impact with the silicon surface is driven by charge excitations to the excited levels of the system and the 3C–SiC synthesis is activated by the extra precursor KE content for both high and low (room T) substrate temperatures (Verucchi et al., 2002; Verucchi et al., 2012). At room temperature, where thermal contribution to observed processes is negligible, out-of-thermal-equilibrium conditions achieved by SuMBE induce chemical processes at the silicon surfaces, overcoming activation barriers toward the synthesis of ordered SiC. Moreover, by using C₆₀ supersonic beams at 20 eV, we have shown that a polycrystalline 3C–SiC thick layer can be grown on Si(111) 7 × 7 at 750°C (Verucchi et al., 2002). This is due to the unquestionable ability of the high fullerene KE to induce cage breaking, synthesis of carbide as well as implement film structural order also in conditions where influence of temperature (and thus thermal equilibrium conditions) is significant.

In order to better identify the role played by temperature on SiC growth on Si by SuMBE, in this work, we present the experimental and ab initio investigations of supersonic C₆₀ impacts on Si(111) 7 × 7 at temperature of 500°C, where MBE approach is not able to induce SiC formation (De Seta et al., 2000). This regime is intermediate between the room temperature experiments, which gave evidence of nanocrystalline SiC island formation, and the full synthesis regime at 750–800°C, where all the carbon precursors were transformed into an ordered uniform layer. Synthesis of SiC by SuMBE is thus expected also at 500°C, but interplay between fullerene KE and substrate temperature can be better addressed.

Using photoelectron spectroscopy and low-energy electron diffraction (LEED), we explore the chemical, structural, and electronic changes induced by varying the supersonic C₆₀ beam KE at fixed substrate temperature. Experimental results point toward a SiC growth model driven by fullerene KE and where, surprisingly, temperature effects do not affect critically the cage rupture. Furthermore, aiming at modeling the interaction between C₆₀ and Si surface for several initial KEs and different temperatures, in this work, we also show first-principle simulations based on the density-functional tight-binding (DFTB) method (Matthew et al., 1989; Elstner et al., 1998;Frauenheim et al., 2002) within the Born-Oppenheimer approximation. Classical molecular dynamics simulations of C₆₀ impacts on Si have been already carried out by Averback (Hu et al., 2000) using a lower accuracy description of the atomic interaction through a Tersoff potential (Tersoff, 1988). However, classical molecular dynamics is not suitable for reactive problems out of thermal equilibrium, where bonds break and form as in our case. At variance, a DFTB-based approach has been recently applied to study high KE impact dynamics of fullerenes on graphite (Galli and Mauri, 1994) and room temperature growth of SiC (Taioli et al., 2013), displaying an accuracy comparable to density-functional theory (DFT).

Gaining insights on the chemical–physical mechanisms involved in SiC epitaxy by SuMBE and understanding their dependence on externally tunable parameters, such as the C₆₀ beam KE and the substrate temperature, is at the basis to control and improve SiC synthesis even at room temperature and to transfer this technique to produce other materials (Taioli, 2014). Indeed, the study of the C₆₀ cage breaking dynamics on metallic or semiconductor surfaces can reveal new paths toward the epitaxial growth of materials by our SuMBE approach directly on substrates already employed in the electronic device production, thus suitable for very large scale integration production.

Materials and Methods

Experiments have been performed at the IMEM-CNR laboratory in Trento in a tailored deposition in situ characterization facility operating in ultra-high vacuum (UHV). A detailed description of the SuMBE deposition technique can be found in the study by Milani and Iannotta (1999). On the computational side, DFTB calculations have been performed using the DFTB + code (Aradi et al., 2007; Elstner et al., 1998) within the self-consistent charge framework that leads to an improved description of the Coulomb interaction between atomic partial charges.

Surface and Structural Characterization

Chemical and electronic surface properties have been probed by means of X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS). The UHV chamber is equipped with a CLAM2 Electron Hemisperical Analyzer, an MgKα X-ray source, and a helium discharge lamp, thus the excitation photon for XPS is at 1253.6 eV and for UPS the HeI at 21.22 eV. The total resolution allowed by the analyzer is 0.95 eV for XPS and 0.1 eV for UPS. Spectra were acquired at normal electron acceptance geometry. Core-level binding energies (BEs) have been calculated using as a reference the Au surface after sputter cleaning, i.e., the 4f 7/2 Au level at 84.0 eV, while in UPS the spectra are referred to the Fermi level of a gold foil in electric contact with the sample. Core levels have been analyzed by Voigt lineshape deconvolution after background subtraction by a Shirley function (Hüfner, 1995). The typical precision for peak energy positioning is ±0.05 eV, uncertainty for full width at half maximum (FWHM) is less than 5% and for area evaluation is about 2.5%. Surface structural characterization has been performed by LEED operated at 50 eV.

Thin Film Deposition

Substrates for C₆₀ deposition were obtained from a Si(111) wafer (resistivity 1.20 × 10^-4 Ωm) cleaned by a modified Shiraki procedure (Verucchi et al., 2002). The silicon oxide film was then removed in vacuum by several annealing cycles, until a complete Si(111) 7 × 7 surface reconstruction. The entire procedure was checked by analyzing LEED images, and no traces of oxygen and carbon were detected from XPS analysis. Submonolayer (sub-ML) C₆₀ films were deposited on clean and reconstructed Si(111) 7 × 7 surfaces kept at 500°C, using different precursor KE ranging from 18 to 30 eV. The deposition times were adjusted in order to reach a similar thickness for all the films for ease of comparison, with an average coverage of 0.5 ML (± 0.1 ML). The C₆₀ supersonic source is made of two coaxial quartz capillary tubes, resistively heated by a tantalum foil. The experiments were carried out using a free-jet expansions of H₂ in which the seeded fullerene particles are highly diluted (about 10⁻³ in concentration) and can reach a KE up to 30 eV, with an average growth rate on silicon of about 0.1 Å/min having the supersonic beam perpendicular to the substrate. Fullerene KEs of about 18, 22, 25, and 30 eV have been employed, as measured from time of flight analysis (Verucchi et al., 2002).

Theory

DFTB is based on a second-order expansion of the density appearing in the full DFT approach to electronic structure calculations. In this approach, the energy of a system of atoms is expressed as a sum of tight-binding-like matrix elements, a Coulomb interaction, and a repulsive pair-potential. The parameters appearing in the formulae expressing these contributions are evaluated using high-level electronic structure methods and are highly transferable to different physical and chemical environments (Slater–Koster parameters).

The advantage of using DFTB with respect to other ab initio methods, such as DFT, is due to the computational cost of this approach to electronic structure that is about two orders of magnitude cheaper than the corresponding full DFT calculation (Garberoglio and Taioli, 2012). As a result of this substantial speed gain, DFTB may be used (i) to investigate much larger systems than those accessible by DFT, (ii) to follow their dynamics for much longer timescales, and (iii) makes it possible to perform several tests by tuning the main parameters affecting the impact at an affordable computational cost.

In our simulations, the Si substrate is represented by eight silicon bilayers cleaved along the (111) direction.

According to the dimer adatom stacking fault model (DAS) (Takayanagi et al., 1985), only the first silicon bilayer participates into the superficial reconstruction, resulting in a 7 × 7 reconstructed surface. This reconstructed surface, represented in Figure 1, turns out to be optimal for our applications, showing high reactivity due to the presence of 19 dangling bonds on the surface (12 adatoms, six rest atoms, and one atom at the center of the hole in the unitary cell) and to its metallic character (Cepek et al., 1999). The computational supercell used in the impact calculations is hexagonal and, after optimization of both atomic positions and lattice vectors, measures 23.21 Å along the short diagonal and 26.79 Å along the large one. Fullerene was separately optimized and initially placed at 5 Å distance on the top of the silicon substrate and the cell size along the collision direction, perpendicular to the surface plane, was set to 50 Å to avoid spurious interaction among periodic images. The Brillouin zone was sampled at the ⌈-point only, due to the large number of atoms in the unitary cell (848). Atomic interactions between chemical species were treated by the semirelativistic, self-consistent charge Slater–Koster parameter set “matsci-0-3” (Frenzel et al., 2009). To help and enhance convergence of band structure calculations, we employed a room temperature Fermi smearing of the electronic density. Molecular dynamics simulations were performed in the micro-canonical ensemble (NVE), setting the time step to 1 fs to enforce total energy conservation and each simulation lasted 2 ps. Finally, the last silicon bilayer was kept fixed during the dynamic evolution to simulate the presence of a silicon bulk.

FIGURE 1

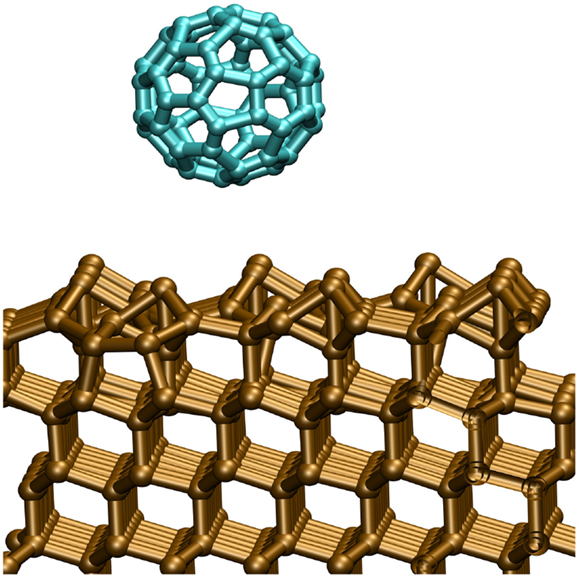
Figure 1. Calculation supercell showing the reconstructed Si(111) 7 × 7 surface. At some distance from the surface, we report the incoming C₆₀ molecule.

As a second step of our analysis, we increased the substrate temperature up to 500°C to gain some insight on the role of temperature on SiC growth obtained via SuMBE. In particular, our goal was to find out the temperature effect on C₆₀ cage mechanical stability.

Results

Photoemission

High-resolution C1s core levels for thin films deposited at increasing beam KE’s are shown in Figure 2. They are all characterized by the presence of a main peak that is not fully symmetric but has a weak shoulder at lower BEs whose intensity increases significantly with beam KE. The lineshape analysis of core levels has been carried out by introducing the main component at 285.2 eV (FWHM of 1.1 eV) and up to two more features at low BE (with fixed FWHM of 1.0 and 0.9 eV), in particular at 284.1 and 283.2 eV. Peak positions do not change as the fullerene KE increases. Previous experiments (Verucchi et al., 2012; Taioli et al., 2013) on the impact of supersonic fullerene on silicon at room and higher temperatures have shown that the molecule can undergo different paths, going from physisorption with intact cages to chemisorption, cage rupture and formation of new compounds, such as SiC, whose intensity increases with the precursor KE. The main peak at higher BE, P1, reflects the presence of unperturbed and physisorbed fullerenes, while the peaks at 284.1 and 283.2 eV can be identified as related, respectively, to chemisorbed species and to the formation of SiC occurring after cage breaking. The higher is the C₆₀ KE, the more intense is the contribution from “totally reacted” molecules (see Table 1), i.e., the fraction of fullerenes leading to new species on the surface. The contribution from physisorbed molecules is always the main one. This is quite surprising, since the 30 eV precursor KE is the same as used in SuMBE room temperature experiments (Verucchi et al., 2012), where physisorbed species are <30 and 50% of the total C1s area at coverages of 0.30 and 0.65 ML.

FIGURE 2

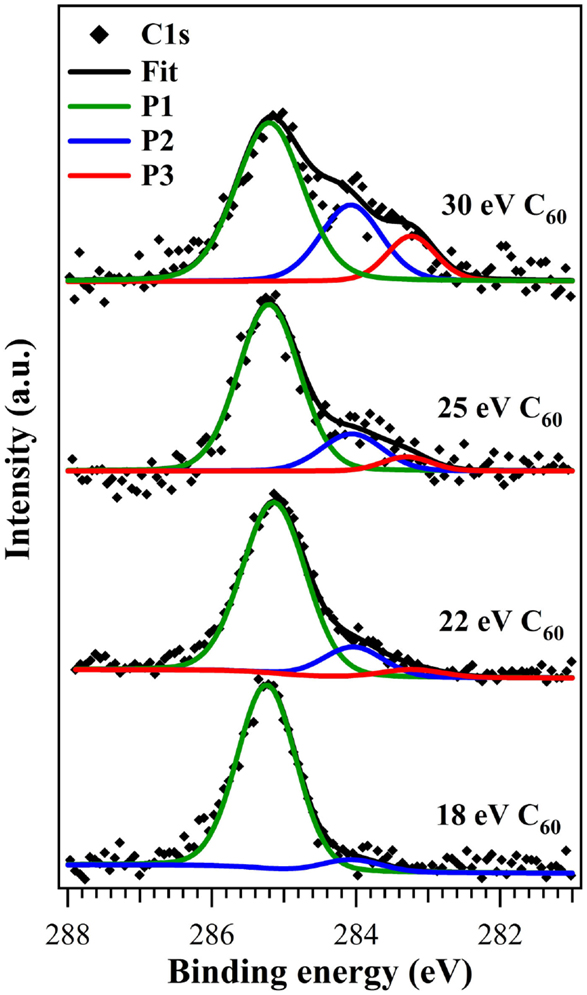
Figure 2. C1s core level spectra (normalized in height) of submonolayer films grown at C₆₀ kinetic energies of 18, 22, 25, and 30 eV. Green component corresponds to physisorbed fullerenes, blue component to chemisorbed cages, and red component to broken fullerenes and formation of silicon carbides.

TABLE 1

Table 1. Peak area% (±3) on total C1s emission.

Chemisorbed fullerenes (peak at 284.1 eV) are present for all films and increase with precursor KE, while SiC-related species (peak at 283.2 eV) are present only from the C₆₀ KE of 22 eV and significantly increases only at 30 eV. The peak at 283.2 eV has a BE between that of 3C–SiC (Sakamoto et al., 1999; Mélinon et al., 1998) and non-stoichiometric SiC (Liu et al., 1995), thus it can be attributed to SiCs showing low structural order. The impossibility to achieve reliable results from the analysis of the Si2p core level (due to the prevailing and masking contribution coming from the bulk silicon on all surface components) makes any comment on the carbide stoichiometry purely speculative.

The valence band photoemission is reported in Figure 3, together with reference spectra for comparison from a clean silicon surface, a thick fullerene film and a completely synthesized SiC film by means of SuMBE at higher substrate temperatures. Si(111) 7 × 7 valence band is characterized by weak and broad structures, the one at about 0.9 eV related to the surface states, and a metallic character evidenced by the presence of signal at about 0 eV. C₆₀ thick film shows intense and different bands, representing the different π and σ molecular orbitals. In particular, we found at about 2.0 eV the highest occupied molecular orbital (HOMO). At low beam KE, the features related to the clean silicon surface completely disappear, while the HOMO and the other molecular C₆₀ bands are clearly visible. This is expected since the π and σ bands are reported to be fully developed (Ohno et al., 1991) also at this low coverage (less than 1 ML). There are, however, significant discrepancies between data found in literature, in particular with the work of Sakamoto et al. (1999). HOMO and HOMO-1 molecular levels (at 2.2 and 3.5 eV) are not fully developed and slightly shifted toward higher BEs with respect to the bulk organic film (2.0 and 3.3 eV). Moreover, the σ bands in the 5–8 eV energy region loose some of their distinctive characteristics, most notably the shoulder at 5.2 eV disappears and the bands at 6.9 and 8.1 eV are no longer clearly resolved. For precursor KEs of 22 and 25 eV, a new peak appears in the UPS spectra between the HOMO and HOMO-1 structures (see arrow in Figure 3), probably is present also in film at 18 eV but very weak. A similar peak has been actually observed and identified as related to the strong chemical interaction with the surface (Sakamoto et al., 1999; De Seta et al., 2000). In the highest KE case, the valence band structure changes strongly and only a small residual of the original molecular π structure can be found in the 0–5 eV energy range. At BE of about 6–8 eV, the σ-bands disappear and a broad structure is formed, reminding of the analogous structure of not-crystalline SiC (Aversa et al., 2003) in which the mixed C2p-Si3s orbitals (“sp-like” band in cubic SiC) are predominant with respect to the p-like C and Si orbitals at about 3 eV (Mélinon et al., 1998). This suggests that SiC synthesis is clearly achieved at 30 eV C₆₀ KE, even if we are dealing with a partially formed carbide, as demonstrated by the differences with the SiC valence band in Figure 3 (top curve).

FIGURE 3

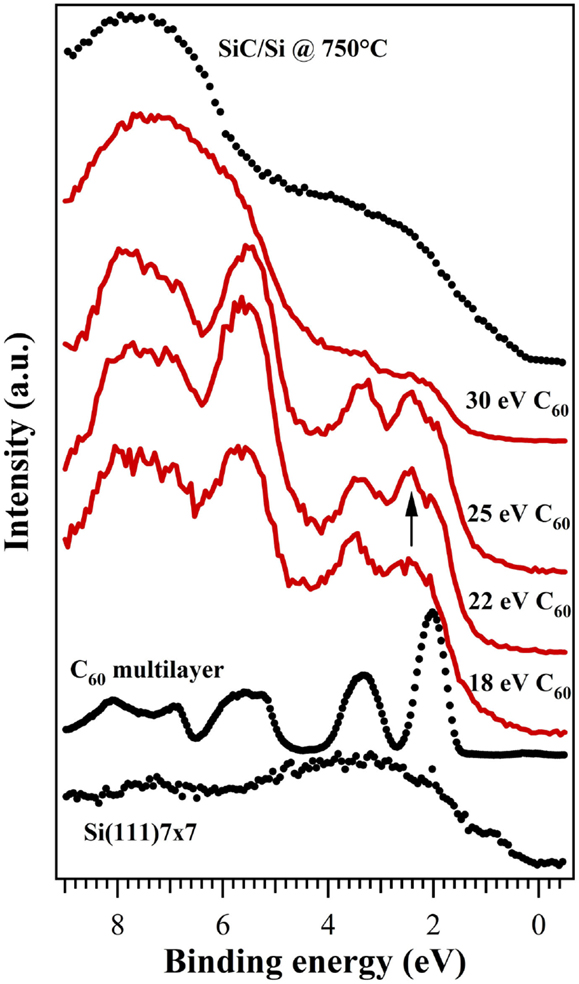
Figure 3. VB spectra of submonolayer films of C₆₀ at different kinetic energies (18, 22, 25, and 30 eV) and at a process temperature of 500°C. For reference, VB spectra from a 3C–SiC film, the clean Si substrate, and a C₆₀ multilayer are also reported. Spectra are plotted with a vertical shift to better compare them.

There is a fair agreement between XPS and UPS data, suggesting that a C₆₀ KE of 22 eV highly improves chemisorption processes, while the cage rupture and SiC synthesis is at least partially achieved at 30 eV, where formation of defected carbides probably occurs.

LEED

From a structural standpoint, the interaction of C₆₀ with silicon surface at 500°C leads to quite a few changes, but not to the appearance of new extraspots related to the formation of ordered compounds. Figure 4 shows the LEED patterns of Si(111) clean surface and of the system after C₆₀ impact at the lowest and highest KE, respectively, taken for a primary electron energy of 50 eV. The clean surface is characterized by the well-known 7 × 7 reconstruction pattern of Si(111) (Figure 4A), with bright spots within a high contrast background, typical of a clean and ordered surface. Upon low KE impact of fullerene, the reconstruction pattern disappears and only the 1 × 1 hexagonal pattern is visible (Figure 4B), with spots having lower brightness and sharpness. At highest energy impacts, the LEED pattern undergoes further modifications, with hexagonal pattern losing spots and becoming more similar to a triangular one. The extra spots (Verucchi et al., 2002) related to the formation of ordered 3C–SiC islands do not appear, a result that is in complete agreement with both XPS and UPS results, where formation of a not fully developed and defected carbide is clearly detectable.

FIGURE 4

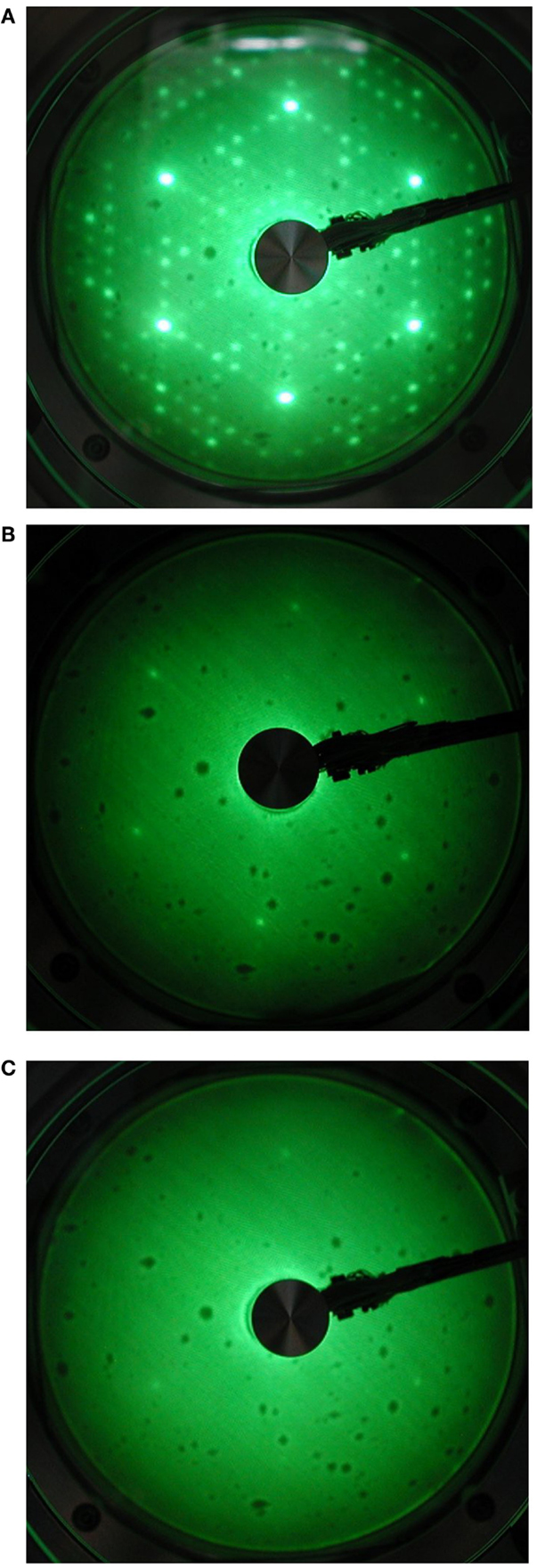
Figure 4. LEED patterns (at 50 eV) of (A) a clean Si(111) 7 × 7 surface, (B) a submonolayer film of C₆₀ at KE of 18 eV, and (C) a submonolayer film of C₆₀ at KE of 30 eV.

Theory

The first step of our computational analysis is the simulation of the impacts with the silicon surface kept at room temperature. Depending on the initial KE (K_C60), we were able to identify three regimes: (i) for K_C60 < 75 eV surface penetration does not occur with the cage undergoing simple distortion; (ii) between 100 and 150 eV, we found strong C₆₀ cage distortion and surface penetration; (iii) above 175 eV, the cage starts to break up and Si–C bond formation occurs with small surface damaging.

Thus, by using DFTB to describe interatomic forces in the C₆₀-silicon surface collision, the minimum impact KE to obtain heavy damage of the silicon surface and fragmentation of the C₆₀ cage is predicted to be well above 200 eV, slightly below Averback’s findings. Movies of the full trajectory for 50 and 175 eV initial KE can be found in the Videos S1 and S2 in Supplementary Material.

We point out that there is an important discrepancy between simulations and experiments in the assessment of the precursor KE inducing cage break. In this regard, it is clear that DFTB is missing a comprehensive explanation of the cage break. The reason of this discrepancy was already identified and thoroughly discussed in Taioli et al. (2013). In that analysis, non-adiabatic effects and, specifically, the failure of the Born–Oppenheimer approximation was found responsible for this important discrepancy between simulation and experiments to determine cage rupture KE threshold. In this regard, due to very fast collisional times for the KE under investigations, electronic and nuclear motion do not decouple, as assumed within the framework of the Born–Oppenheimer approximation, as electrons do not relax fast enough to the ground state of the instantaneous positions of the nuclei. Thus, electronic and nuclear dynamics should be treated on an equal quantum mechanical footing.

However, in this work, our goal is primarily to investigate the role that temperature might play in the SiC growth by SuMBE. While we underline that a proper non-adiabatic quantum treatment of the collision processes, intertwining electronic and nuclear motion, should be used, in this analysis of temperature effects on growth this approach can be ruled out by two factors, namely physics and computational cost. First, the effect of temperature on the electrons is provided by the Fermi–Dirac distribution. In this statistics, temperature appears in the exponential factor at denominator and plays the role of “smearing” or increasing the electronic population in the excited states of the system. However, a temperature enhancement of 800 K corresponds to about 0.06 eV. The energetic distance between electronic orbitals close to the Fermi level in fullerene is much higher (of the order of 1 eV, corresponding to about 12000 K). Thus, the effect of a small temperature increase, such as that investigated in our work, on the electronic motion can be safely neglected, while nuclear motion is quite sensitive to temperature effects. Second, the computational cost associated with non-adiabatic simulations, at least two orders of magnitude larger than using DFTB, is unaffordable for screening the C₆₀-silicon impact for several KEs and different temperatures. Thus, the use of DFTB is totally justified to investigate temperature effects in the case of high KE fullerene impacts on a silicon surface.

MD simulations (Zhang et al., 1993; Kim and Tománek, 1994) indeed show that a break may occur if the total internal energy stored in the C₆₀ cage is between 30 and 40 eV. The internal energy is defined as the total KE of the fullerene bouncing back after the impact minus the center of mass KE. A temperature increase may help to destabilize fullerene by exciting substrate phonons, which can transfer energy to C₆₀, eventually resulting in a lower cage breaking KE.

Thus, we performed a temperature dependent investigation of the internal KE after the impact, when fullerene bounces and leaves the silicon surface, in the same range of initial KEs previously examined at a temperature of 500°C. The system was thermostated to this temperature by a Nose–Hoover thermostat for 1 ps to reach thermal equilibrium and then NVE ensemble with a Fermi smearing corresponding to 500°C was adopted during the impact molecular dynamics run.

Surprisingly, the results point toward a not significant effect of temperature on the internal KE for all the impinging KEs.

The results are reported in Figure 5 and demonstrate that the fullerene internal energy for the impinging KEs under investigation (from 25 to 175 eV) at room temperature conditions ranges from 13 to 28 eV (blue diamonds). For the assessment of the internal KE, we chose a molecular dynamics step corresponding to a maximum of the oscillating total KE immediately after the collision. A substrate temperature increase to 500°C (red diamonds) of course results into a higher final internal KE with respect to the room temperature case (blue diamonds) due to enhanced thermal fluctuations. However, this increase is not such to cause the rupture in the 25–175 eV energy range as much of the energy is spent by fullerene to increase its translational KE for leaving the surface, as shown by the evolution of the center of mass KE of C₆₀ after impact (see blue and red circles in Figure 5).

FIGURE 5

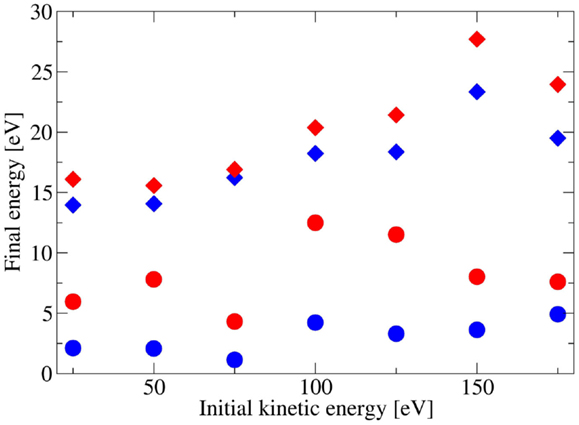
Figure 5. Fullerene total internal kinetic energies after bouncing back from the Si(111) 7 × 7 surface at room temperature (blue diamonds) and 500°C (red diamonds) as a function of the initial C₆₀ kinetic energy. Furthermore, we show the center of mass kinetic energies for both 20°C (blue circles) and 500°C (red circles) substrate temperatures.

We point out that the interaction potential energy of C₆₀ as a function of the distance from the silicon surface is not a quantity at our disposal (just the total interaction potential energy is, as shown below). This analysis could be in principle performed using classical molecular mechanics, where all the interactions terms are analytically known and are singly computable within the reach of this theory. However, in the conditions at which C₆₀–Si collision occurs, we are abundantly out of thermodynamic equilibrium with bonds breaking and forming. Thus, we are forced to use a “first-principles” technique, explicitly including electronic motion in a self-consistent way, to have a reliable description of the high KE impact. In DFTB, single terms of the potential energies are not a direct output, particularly as a function of the distance between C₆₀ and the silicon surface. In principle, one could perform a very expensive analysis to obtain this quantity, consisting in repeating all calculations at different KEs and temperatures as follows. Indeed, one could calculate separately the interaction potential energy of the isolated C₆₀ and silicon slab at each position, keeping fixed the atomic coordinates as by simulations of C₆₀ approaching the surface. Finally, one could subtract the sum of these two separate contributions from the total interaction potential energy of the real interacting system at all distances, thus obtaining the C₆₀–silicon slab interaction potential energy as a function of the distance. Such a calculation is of course unfeasible due to the computational scaling of our approach.

The plot in Figure 6 represents the total interaction potential energy, a quantity computable by DFTB, for three different KEs and two different temperatures as a function of computing time, which is somehow proportional to the distance of C₆₀ from the silicon surface (see Figure 1). In this plot, the potential energy curves for 800 K are shifted up in energy by 600 eV for the sake of visibility. From Figure 6 one can clearly see that, at the point where C₆₀ starts experiencing the interaction with the silicon surface (below 100 fs), the total interaction potential energy changes abruptly only in the case of high KE (350 eV, orange and cyan lines for the cases of ambient temperature and 800 K, respectively). For this KE, C₆₀ is completely fragmented. Furthermore, in this high KE regime, the difference between the total interaction potential energy at ambient temperature and 800 K is clearly visible at all times. At variance, for low KE (25 eV, green and violet curve for the cases of ambient temperature and 800 K, respectively), where C₆₀ is just physisorbed on the silicon surface, the total interaction potential energy shows little change with time and is almost independently of temperature. Finally, at intermediate regimes (175 eV, red and black curve for the cases of ambient temperature and 800 K, respectively), where C₆₀ is partially fragmented, the change of the total interaction potential energy again seems to be due more to kinetic effects than to temperature, however showing larger fluctuations with increasing temperatures with respect to the ambient temperature impact.

FIGURE 6

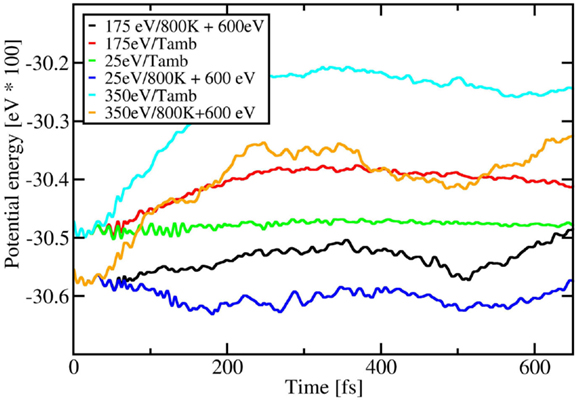
Figure 6. Total interaction potential energy (eV*100) as a function of time (fs) for different kinetic energies (eV) and temperatures (K). The potential energy curves for 800 K are shifted up in energy by 600 eV for the sake of visibility.

To further enrich our discussion about temperature effects on SiC growth by SuMBE, we performed the calculation of the mean squared displacement (MSD) as a function of impinging C₆₀ KE and time for different temperatures. This quantity provides of course a measure of the dispersion or diffusion of carbon atoms of the C₆₀ molecule. These results are sketched in Figures 7A,B. In Figure 7A, we report, in particular, the behavior of the MSD of C₆₀ carbon atoms at ambient (black curve) and 800 K (red curve). From this figure, one safely concludes that temperature effects are relevant only at high KE regimes, when the cage is fragmented (350 eV) or partially broken (175 and 260 eV).

FIGURE 7

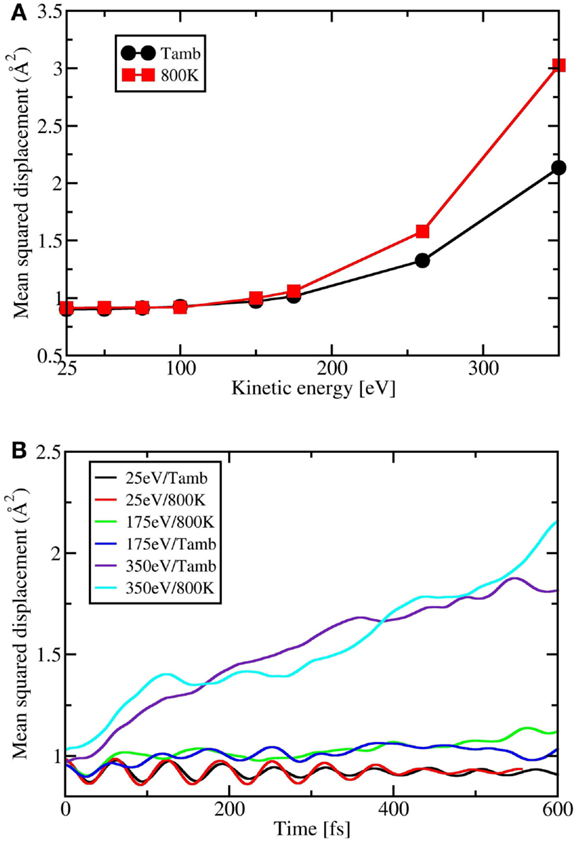
Figure 7. (A) Mean square displacement (Ų) of C₆₀ carbon atoms as a function of impinging C₆₀ kinetic energy (eV) for two different temperatures (K). (B) Mean squared displacement (Ų) of C₆₀ carbon atoms as a function of time (fs) parameterized as a function of the impinging C₆₀ kinetic energy (eV).

In Figure 7B, MSD is sketched as a function of time (or, which is the same, of C₆₀ approaching the silicon surface). Again, MSD is almost constant or slightly increasing at low KE regimes (25 and 175 eV) while is divergent at 350 eV, meaning that C₆₀ is completely fragmented. Furthermore, MSD is larger at higher temperature with a sharp increase at long times. This analysis clearly points toward a cage break model that is almost independent on temperature with kinetic effects playing a major role. Temperature effects become important only after cage rupture.

Discussion

Experimental results of C₆₀ supersonic impact on Si(111) 7 × 7 at 500°C show a picture completely different from what was observed using the same deposition technique at higher and lower substrate temperatures, evidencing an unexpected mechanism of interaction between the precursors and the surface. From previous experiments (Verucchi et al., 2002, 2012), as well as theoretical calculations (Taioli et al., 2013), one finds a clear indication of a kinetically driven growth mechanism leading to sub- or thick SiC layer formation already at room temperature, with temperature factor not playing a major role. Raising the silicon substrate temperature to 500°C should generally result in a higher silicon–carbon reactivity, with increasing carbide percentage over physisorbed fullerene. Core level and valence band analysis (Figure 2) point toward a completely different situation with respect to our expectations. Indeed, the great majority of species present on the surface after impact are unperturbed C₆₀ up to high KE, whereby a reactivity increase is found in terms of percentage of chemisorbed fullerene and carbide formation. Valence band spectra suggest the same behavior, with molecular bands having characteristics more similar to physisorbed fullerene with C₆₀ cage breaking and carbide synthesis clearly evident only for the 30 eV KE case. Nevertheless, we achieve formation of defected SiC and not ordered cubic 3C–SiC, as observed in previous experiments at 750–800°C (Verucchi et al., 2002) and room temperature (Verucchi et al., 2012).

At 500°C, C₆₀ KE is crucial, with a threshold for SiC synthesis and cage breaking identified at about 30 eV. However, it is clear that chemical reactivity is different from both 750°C and room temperature cases. This may represent a surprising result, assuming that the higher the substrate temperature the easier should be the cage breaking. Indeed our calculations clearly indicate that the internal energy for a fixed value of the C₆₀ initial KE is slightly higher if temperature is raised up to 500°C (see Figure 5). This trend is confirmed for all KEs investigated. However, our computational analysis shows that a major part of both the increasing KE and temperature is spent to eject more effectively the fullerene at the expense of an enhanced reactivity. This can be clearly seen in the low and intermediate (below 150 eV) KE regimes, where increasing the temperature corresponds to enhance proportionally the center of mass KE of the C₆₀ bouncing back from the surface instead of the internal energy of the system, responsible for the cage break. A similar effect was observed in the collision of SF₆ from GaSe surface where an uptake of energy was identified (Boschetti et al., 1992). Additionally, at high KEs, when fullerene gets trapped within the silicon substrate and thus do not bounce back, temperature effects start to be more effective in transferring energy from silicon to fullerene vibrational modes, as reported in Figure 5, in perfect agreement with our experimental results. However, this is not enough to justify cage opening. Thus, both calculations and experimental results clearly point toward a kinetically driven fullerene cage breaking and SiC synthesis, with a KE threshold not critically affected by temperature below the well-known value of 750°C (Verucchi et al., 2002).

In conclusion, we have analyzed in details the impacts of energetic supersonic C₆₀ on the reconstructed Si(111) 7 × 7 surface at 500°C by means of experiments and ab initio simulations. Surface chemical and structural characterization carried out at increasing fullerene KE (18 eV to 30 eV) has shown the presence of physisorbed, chemisorbed, and reacted molecules, the latter leading by the formation of SiC, probably defected cubic carbide or non-stoichiometric species. Compared to previous experiments with substrate kept at room temperature, we do not find an enhancement in reactivity with increasing temperature. DFTB calculations reveal that the excess of initial KE is spent more effectively to increase the translational KE (center of mass KE) and substrate temperature helps this process via phonon transfer, at least in the low and intermediate KE regime. Only for higher KE, when cage rupture occurs, the reactivity starts to be relevant, as shown in our MSD analysis, demonstrating that this process is kinetically driven. While our discussion has been limited to the case of SiC growth, we believe that SuMBE may represent a more general approach to grow materials in the low-temperature regime even on metals, notably nickel and copper, in which carbide formation may compete energetically with π-conjugate structures, such as graphene (Batzill, 2012; Lu et al., 2011).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The research leading to these results has received funding from the European Union Seventh Framework Programme under grant agreement no. 604391 Graphene Flagship and from project SuperCar (CMM-FBK, Fondazione Bruno Kessler). ST acknowledges support from the Istituto Nazionale di Fisica Nucleare through the “Supercalcolo” agreement with Fondazione Bruno Kessler, from the European Science Foundation under the INTELBIOMAT Exchange Grant “Interdisciplinary Approaches to Functional Electronic and Biological Materials” and the Bruno Kessler Foundation for providing economical support through the “research mobility scheme” under which this work has been accomplished. Finally, ST gratefully acknowledges the Institute of Advanced Studies in Bologna for the support given under his ISA research fellowship, and the high-performance computing service Archer in UK where impact calculations were performed.

Supplementary Material

The Supplementary Material for this article can be found online at http://journal.frontiersin.org/article/10.3389/fmats.2015.00046/abstract

References

Aradi, B., Hourahine, B., and Frauenheim, T. (2007). DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 111, 5678–5684. doi: 10.1021/jp070186p

PubMed Abstract | CrossRef Full Text | Google Scholar

Aversa, L., Verucchi, R., Boschetti, A., Podesta, A., Milani, P., and Iannotta, S. (2003). Fullerene freejets-based synthesis of silicon carbide. Mater. Sci. Eng. B 101, 169–173. doi:10.1016/S0921-5107(02)00703-1

CrossRef Full Text | Google Scholar

Balooch, M., and Hamza, A. V. (1993). Observation of C₆₀ cage opening on Si(111) 7x7. Appl. Phys. Lett. 63, 150–152. doi:10.1063/1.110382

CrossRef Full Text | Google Scholar

Batzill, M. (2012). The surface science of graphene. Surf. Sci. Rep. 67, 83–115. doi:10.1016/j.surfrep.2011.12.001

CrossRef Full Text | Google Scholar

Boschetti, A., Cagol, A., Corradi, C., Jacobs, R., Mazzola, M., and Iannotta, S. (1992). Energy transfer processes and molecular degrees of freedom in the collision of SF₆ molecules with the GaSe(001) surface. Chem. Phys. 163, 179–191. doi:10.1016/0301-0104(92)87102-F

CrossRef Full Text | Google Scholar

Cepek, C., Schiavuta, P., Sancrotti, M., and Pedio, M. (1999). Photoemission study of C₆₀/Si(111) adsorption as a function of coverage and annealing temperature. Phys. Rev. B 60, 2068–2073. doi:10.1103/PhysRevB.60.2068

CrossRef Full Text | Google Scholar

De Seta, M., Tomozeiu, N., Sanvitto, D., and Evangelisti, F. (2000). SiC formation on Si(100) via C₆₀ precursors. Surf. Sci. 460, 203–213. doi:10.1016/S0039-6028(00)00533-1

CrossRef Full Text | Google Scholar

Elstner, M., Porezag, D., Jungnickel, G., Elsner, J., Haugk, M., Frauenheim, T., et al. (1998). Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 58, 7260–7268. doi:10.1103/PhysRevB.58.7260

CrossRef Full Text | Google Scholar

Frauenheim, T., Seifert, G., Elstner, M., Niehaus, T., Köhler, C., Amkreutz, M., et al. (2002). Atomistic simulations of complex materials: ground-state and excited-state properties. J. Phys. Condens. Mater. 14, 3015–3047. doi:10.1088/0953-8984/14/11/313

CrossRef Full Text | Google Scholar

Frenzel, J., Oliveira, A. F., Jardillier, N., Heine, T., and Seifert, G. (2009). Semi-Relativistic, Self-Consistent Charge Slater-Koster Tables for Density-Functional Based Tight-Binding (DFTB) for Materials Science Simulations. TU-Dresden 2004-2009.

Google Scholar

Galli, G., and Mauri, F. (1994). Large scale quantum simulations: C₆₀ impacts on a semiconducting surface. Phys. Rev. Lett. 73, 3471–3474.

Google Scholar

Garberoglio, G., and Taioli, S. (2012). Modeling flexibility in metal – organic frameworks: comparison between density-functional tight-binding and universal force field approaches for bonded interactions. Microporous Mesoporous Mater. 163, 215–220. doi:10.1016/j.micromeso.2012.07.026

CrossRef Full Text | Google Scholar

Hu, X., Albe, K., and Averback, R. S. (2000). Molecular-dynamics simulations of energetic C₆₀ impacts on (2×1)-(100) silicon. J. Appl. Phys. 88, 49–54. doi:10.1063/1.373622

CrossRef Full Text | Google Scholar

Hüfner, S. (1995). Photoelectron Spectroscopy. Berlin: Springer-Verlag.

Google Scholar

Kim, S. G., and Tománek, D. (1994). Melting the fullerenes: a molecular dynamics study. Phys. Rev. Lett. 72, 2418–2421. doi:10.1103/PhysRevLett.72.2418

CrossRef Full Text | Google Scholar

Liu, C. C., Lee, C., Cheng, K. L., Cheng, H. C., and Yew, T. R. (1995). Effect of SiH₄/CH₄ flow ratio on the growth of β-SiC on Si by electron cyclotron resonance chemical vapor deposition at 500°C. Appl. Phys. Lett. 66, 168–170. doi:10.1063/1.113552

CrossRef Full Text | Google Scholar

Lu, J., Yeo, P. S. E., Gan, C. K., Wu, P., and Loh, K. P. (2011). Transforming C₆₀ molecules into graphene quantum dots. Nat. Nanotechnol. 6, 247. doi:10.1038/NNANO.2011.30

PubMed Abstract | CrossRef Full Text | Google Scholar

Matthew, W., Foulkes, C., and Haydock, R. (1989). Tight-binding models and density-functional theory. Phys. Rev. B 39, 12520–12536.

Google Scholar

Mélinon, P., Kéghélian, P., Perez, A., Ray, C., Lermé, J., Pellarin, M., et al. (1998). Nanostructured SiC films obtained by neutral-cluster depositions. Phys. Rev. B 58, 16481–16490. doi:10.1103/PhysRevB.58.16481

CrossRef Full Text | Google Scholar

Milani, P., and Iannotta, S. (1999). Cluster Beam Synthesis of Nano-Structured Materials. Berlin: Springer-Verlag.

Google Scholar

Ohno, T. R., Chen, Y., Harvey, S. E., Kroll, G. H., Weaver, J. H., Haufler, R. E., et al. (1991). C₆₀ bonding and energy-level alignment on metal and semiconductor surfaces. Phys. Rev. B 44, 13747–13755. doi:10.1103/PhysRevB.44.13747

CrossRef Full Text | Google Scholar

Sakamoto, K., Kondo, D., Ushimi, Y., Harada, M., Kimura, A., Kakizaki, A., et al. (1999). Temperature dependence of the electronic structure of C₆₀ films adsorbed on Si(001)-(2x1) and Si(111)-(7x7) surfaces. Phys. Rev. B 60, 2579–2591. doi:10.1103/PhysRevB.60.2579

CrossRef Full Text | Google Scholar

Sanvitto, D., De Seta, M., and Evangelisti, F. (2000). Growth of thin C₆₀ films on hydrogenated Si(100) surfaces. Surf. Sci. 452, 191–197. doi:10.1016/S0039-6028(00)00321-6

CrossRef Full Text | Google Scholar

Taioli, S. (2014). Computational study of graphene growth on copper by first-principles and kinetic Monte Carlo calculations. J. Mol. Model 20, 2260. doi:10.1007/s00894-014-2260-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Taioli, S., Garberoglio, G., Simonucci, S., a Beccara, S., Aversa, L., Nardi, M. V., et al. (2013). Non-adiabatic ab initio molecular dynamics of supersonic beam epitaxy of silicon carbide at room temperature. J. Chem. Phys. 138, 044701. doi:10.1063/1.4774376

PubMed Abstract | CrossRef Full Text | Google Scholar

Takayanagi, K., Tanishiro, Y., Takahashi, M., and Takahashi, S. (1985). Structural analysis of Si(111)-7×7 by UHV-transmission electron diffraction and microscopy. J. Vac. Sci. Technol. A 3, 1502–1506. doi:10.1016/j.ultramic.2013.04.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Tersoff, J. (1988). New empirical approach for the structure and energy of covalent systems. Phys. Rev. B. 37, 6991–7000. doi:10.1103/PhysRevB.37.6991

CrossRef Full Text | Google Scholar

Verucchi, R., Aversa, L., Ciullo, G., Podesta’, A., Milani, P., and Iannotta, S. (2002). SiC film growth on Si(111) by supersonic beams of C₆₀. Eur. Phys. J. B 26, 509–514. doi:10.1140/epjb/e20020120

CrossRef Full Text | Google Scholar

Verucchi, R., Aversa, L., Nardi, M. V., Taioli, S., a Beccara, S., Alfè, D., et al. (2012). Epitaxy of nanocrystalline silicon carbide on Si(111) at room temperature. J. Am. Chem. Soc. 134, 17400–17403. doi:10.1021/ja307804v

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, B. L., Wang, C. Z., Chan, C. T., and Ho, K. M. (1993). Thermal disintegration of carbon fullerenes. Phys. Rev. B 48, 11381–11384.

Google Scholar