Covalently Linked Organic Networks

Addicoat, Matthew A.; Tsotsalas, Manuel

doi:10.3389/fmats.2015.00007

MINI REVIEW article

Front. Mater., 04 February 2015

Sec. Computational Materials Science

Volume 2 - 2015 | https://doi.org/10.3389/fmats.2015.00007

Covalently linked organic networks

$\r\n Matthew A. Addicoat*$ Matthew A. Addicoat¹*

Manuel Tsotsalas²*

¹Engineering and Science, Jacobs University Bremen, Bremen, Germany
²Institute of Functional Interfaces (IFG), Karlsruhe Institute of Technology (KIT), Eggenstein-Leopoldshafen, Germany

In this review, we intend to give an overview of the synthesis of well-defined covalently bound organic network materials such as covalent organic frameworks, conjugated microporous frameworks, and other “ideal polymer networks” and discuss the different approaches in their synthesis and their potential applications. In addition we will describe the common computational approaches and highlight recent achievements in the computational study of their structure and properties. For further information, the interested reader is referred to several excellent and more detailed reviews dealing with the synthesis (Dawson et al., 2012; Ding and Wang, 2013; Feng et al., 2012) and computational aspects (Han et al., 2009; Colón and Snurr, 2014) of the materials presented here.

Introduction

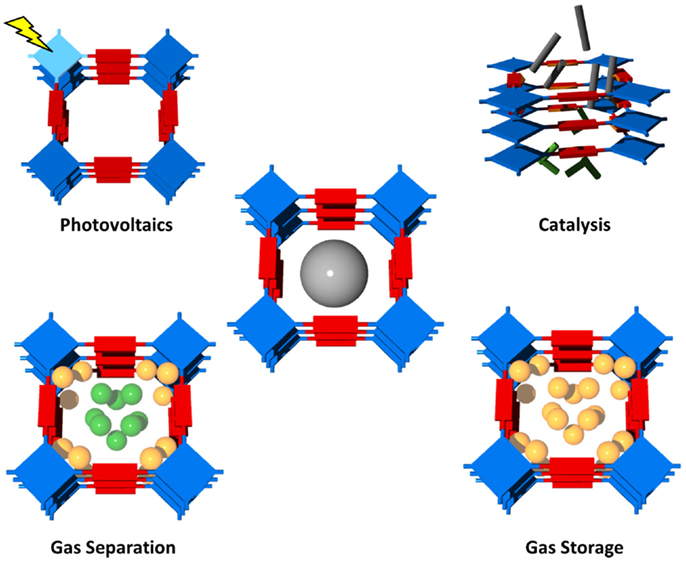
Polymeric networks, with well-defined structures, can accommodate, interact with, and discriminate molecules, thereby leading to prominent applications. Indeed, due to the porous and robust nature of the frameworks as well as the chemical properties of the wall components, many of the materials have shown notable abilities for gas storage, gas separation, drug delivery, sensing, catalytic, and photovoltaic (Wan et al., 2008) applications (see Figure 1 for possible applications of organic polymer networks) (McKeown and Budd, 2010; Xiang and Cao, 2013).

FIGURE 1

Figure 1. Summary of applications for covalently linked organic networks.

The high potential of covalently linked organic networks for these selected applications originates from the combination of large surface are, the high variability in the design of the organic building blocks and the tunable pore sizes. Another important feature of most covalent organic networks is their high physicochemical stability, which enables their application even at high temperatures and under humid conditions. In the following paragraphs, we will highlight the specific features for the different applications and refer to selected example from the literature.

Catalysis: the incorporation of catalytic sites within covalently linked organic frameworks showed to be comparable with the activities of the corresponding homogeneous catalysts, with the added potential of size selectivity, recyclability, and chirality (Kaur et al., 2011).

Gas separation: in gas separation vapors, gases, or liquids can be separated depending on their size (molecular sieving) and/or their affinity to the pore surface (selective adsorption). The organic networks can be either synthesized as freestanding membranes (Lindemann et al., 2014) or be used in pressure swing adsorption (Chang et al., 2013).

Gas storage: the main advantages of covalently linked organic networks for gas separation are their high surface area/low density due to their construction by lightweight elements in combination with their high versatility in terms of incorporation of functional groups (either within the building blocks or via post-synthetic functionalization). The high variability allows the storage of large amounts of gases with tailorable heat of adsorption within the covalent networks (Liebl and Senker, 2013; Arab et al., 2014).

Photovoltaics: in organic photovoltaics, the possibility to include functional building blocks into the organic networks and their organization in well-defined geometries promises large potential in order to optimize material properties toward high absorbance, efficient charge separation, and transfer at the donor–acceptor interface, fast diffusion of excitons, and efficient charge collection (Chen et al., 2010; Dogru and Bein, 2014).

To take full advantage of the possibilities of organic networks for applications is their macroscopic shaping in order to be able to incorporate the materials within functional devices. Recent examples include the interfacial synthesis (Colson and Dichtel, 2013) the layer-by-layer synthesis and the mechanochemical synthesis in order to create thin layers, freestanding membranes (Lindemann et al., 2014), or exfoliated layers (Biswal et al., 2013).

Synthesis of Covalently Linked Organic Networks

Control over network topology and specific surface area of covalently linked organic materials can be achieved via three different methods: (i) The first method is to use rigid, sterically demanding molecular building blocks hold together via irreversible, but high yielding reactions, to create networks with large free volumes. (ii) The second method is to use reversible covalent reactions enabling self-assembly of the building block into networks of long-range order and crystallinity. (iii) The third method is to use a pre-synthesized template, which guides the structure and connectivity. Figure 1 shows the three different approaches to create covalently linked organic networks with control over topology and degree of order – ranging to highly crystalline to amorphous – and with a wide range of mechanical properties – from soft gel-like to highly rigid (see Figure 2A for the three different synthesis methods to create organic polymer networks).

FIGURE 2

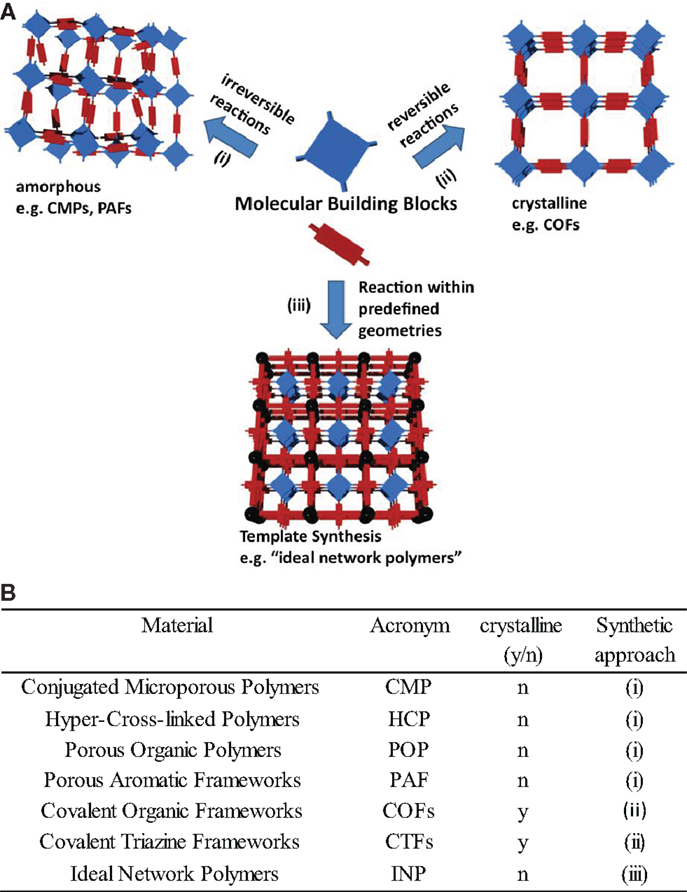
Figure 2. (A) Synthesis approaches to create organic polymer networks via (i) intrinsic porosity of rigid building blocks, (ii) self-assembly of reversibly connected building blocks, and (iii) template synthesis. We classified the covalently linked organic networks according to the three above mentioned synthesis approaches to control the network topology followed by an introduction to the possibilities to simulate the network structures and properties computationally. (B) Summary of commonly used acronyms for covalently linked organic networks, their synthetic approach, and properties.

Covalent Networks Synthesized via Irreversible Reactions of Sterically Demanding Highly Rigid Molecular Building Blocks

Several different classes of organic polymer networks synthesized via high yielding reactions between rigid and sterically demanding molecular building blocks have been reported. The rigid organic building blocks are mostly based on aromatic subunits and the chemical reactions employed to connect them are mostly coupling reactions such as Ullmann, Yamamoto, or Click-Chemistry. Their common feature is permanent porosity upon removal of the solvent used in the synthesis and high physical and chemical stability. They typically lack long-range order and hence crystallinity, nevertheless often show narrow pore size distribution (PSD).

Naming of these compounds is somewhat arbitrary. Examples of such materials are conjugated microporous polymers (CMP), (Jiang et al., 2007) hyper-cross-linked polymers (HCP), (Tsyurupa and Davankov, 2002) porous organic polymers (POP), (Farha et al., 2009), and porous aromatic frameworks (PAF) (Ben et al., 2009). However, since a common feature of this class of materials is intrinsic porosity they can be regarded as a highly cross-linked sub-class of polymers of intrinsic microporosity (PIM).

The first reported porous poly(aryleneethynylene) CMPs networks are composed of aromatic halides and aromatic alkynes, which are connected using palladium-catalyzed Sonogashira–Hagihara cross-coupling reactions.

Porous Polymers Synthesized via Reversible Covalent Reactions

This class of materials is known as covalent organic frameworks (COFs). COFs are composed of covalent building blocks made of boron, carbon, oxygen, and hydrogen, in many cases also including nitrogen or silicon, stitched together by organic subunits. The atoms are held together by strong covalent bonds. Depending on the selection of building blocks, the COFs may form 2D or 3D networks. Planar building blocks are the constituents of 2D COFs, whereas for the formation of 3D COFs, typically tetragonal building blocks are involved. High symmetric covalent linking, as it is perceived in reticular chemistry, was confirmed for the products.

Reversible reactions in the synthesis of COFs are usually condensation reactions where the reversability originates from the hydrolysis back reaction. Most COFs are synthesized either by boronic acid condensation forming boronic anhydrite or by boronic acid condensation with catechol (El-Kaderi et al., 2007). Other condensation reactions include imine (Uribe-Romo et al., 2009) or hydrozone (Uribe-Romo et al., 2011) formation through condensation of aldehyde and amine or aldehyde and hydrazide. Two reaction mechanism not based on condensation reaction have been reported to create crystalline frameworks. Covalent triazine frameworks (CTFs) produced by trimerization of dicyano compounds, however to generate reversibility the reaction has to be carried out under much harsher conditions (Kuhn et al., 2008). A recently reported reaction mechanism for the synthesis of crystalline, covalently connected organic networks is the dimerization of nitroso compound to azodioxides (Beaudoin et al., 2013). These compounds show excellent crystallinity and even enabled the first single crystal COF structures. However, due to the low stability, no permanent porosity could be achieved and upon removal of the solvent molecules the crystallinity was lost.

The first example of COFs (named COF-1) was prepared by self-condensation of benzene-1,4-diboronic acid, via the elimination of water (Côté et al., 2005).

Template Synthesis of Covalent Organic Polymer Networks

The synthesis of this class of materials is also based on irreversible covalent reactions; however, the synthesis is directed by a template. The template is usually formed via self-assembly using non-covalent interactions of the building blocks. In this class of materials, the network topology and overall morphology arises from the template, which is formed by self-assembly of molecular building blocks connected either via coordination bonds (e.g., a metal-organic framework or porous coordination polymer) or self-assembled via hydrogen bonding or van der Waals interactions.

These structures are, in a subsequent step, covalently cross-linked to enhance the thermal and mechanical stability. The templates employed for this process can be divided in completely preserved templates and sacrificial or semi-sacrificial templates.

The complete conversion of a template into a cross-linked structure involves the crystallization of a specifically designed photoreactive monomer into a layered structure and a photo-polymerization step within the crystal (Kissel et al., 2012).

The (semi-)sacrificial conversion of a template structure was achieved by the use of metal-organic frameworks as template. In this approach, “ideal polymer networks” were created by covalent cross-linking of the organic linkers in the MOF structure followed by removal of the metal ions. The transformation of templates consisting of well-defined three-dimensional nanoporous network such as MOFs represents one of the most promising routes for creation of polymer networks with well-defined repeating units in the network structure, i.e., “ideal network polymers” (Ishiwata et al., 2013; Tsotsalas et al., 2014).

Figure 2B lists the commonly used acronyms for covalently linked networks of paragraphs 1.1–1.3 and their properties.

Molecular Modeling of Covalent Networks

Covalent network chemistry is an area where experimentally and computationally available information is quite complementary and most studies contain some component of modeling. Typically, comparison of the refined experimental and calculated PXRD patterns is used to assign the structure, particularly in the case of 2D COFs, where it has not been possible to grow a single crystal suitable for XRD. Structural calculations generally employ either force field methods or Density Functional Tight Binding (DFTB), both of which are capable of calculating periodic unit cells containing hundreds or even thousands of atoms relatively cheaply and yield lattice parameters typically within a few percent of the experimental parameters (Addicoat et al., 2014b; Guo et al., 2013). Both force field and DFTB methods suffer from a limitation of scope. Parameterized force fields can readily compute cells with tens of thousands of atoms, but will generally produce poor results if applied to systems that differ too strongly from those used in the parameterization. DFTB can be used for systems containing hundreds of atoms but is limited by the availability of parameters, which are needed for every pair of atoms, X-Y, present in the system. Parameters for all combinations of H, C, N, O, S, and P are readily available, facilitating DFTB calculations of a majority of COFs, however, metal-doped or functionalized COFs often have no appropriate parameters available.

Calculations are often able to provide more detail than is available experimentally, in particular for the interlayer geometry of 2D networks. The experimentally measured PXRD of 2D COFs readily differentiate between eclipsed and staggered stacking (e.g., AA and AB stacking) but are unable to resolve the difference between fully eclipsed and slightly offset stackings. Computational studies on a variety of square and hexagonal 2D frameworks by Lukose et al. (2011), Spitler et al. (2011), and Zhou et al. (2010) all showed that slightly offset stackings were significantly lower in energy than the fully eclipsed structures, with only small effects on the PXRD pattern, and that this effect is primarily due to minimizing repulsive interactions between layers. Calculations are also able to elucidate the effects of framework flexibility. A straightforward approach may simply calculate several different framework structures, for example, rotating linkers. An elegant approach, developed recently for MOFs but which applies also to covalent frameworks, identifies the key flexible bonds and structural units in the framework as analogous to hinges and trusses, thus yielding an understanding of the mechanical flexibility of the framework (Sarkisov et al., 2014).

Beyond simply the determination of structural information, calculations are a means to access more detailed properties of the material. Of particular interest for the eventual application of these materials in gas storage and separation, are the surface area and void volume. Calculating these parameters may be done by a number of methods, including Voronoi decomposition and Delaunay tessellation. Both of these are geometric methods that work by partitioning the pore space into suitably small units. Another method, is to computationally mimic the experimental measurement by using a spherical probe, chosen as either an infinitely small point or given the radius of either the He atom or N2 molecule, and repeatedly inserting it into the structure at random locations. If the probe does not overlap with any framework atoms, then it must be in a void. Pore geometry, including the largest free sphere (which defines the Pore Limiting Diameter), the largest included sphere (which defines the Largest Cavity Diameter, i.e., the pore “size”), and pore connectivity (whether pores are connected in one, two, or three dimensions) can also be calculated similarly. Recording the largest probe that can fit at a given point, without overlapping any framework atoms yields the PSD, which shows how much of the void volume corresponds to particular pore sizes. The surface area accessible to a probe of a given size may be computed by effectively rolling the probe over the surface.

Moving beyond a static picture of a framework structure, calculations can also be used to describe and predict gas absorption properties. Molecular Dynamics (MD) calculations can be used to calculate the diffusion coefficients and transport properties of gas molecules through a framework. Grand Canonical Monte Carlo (CGMC) simulations yield enthalpies of absorption, absorption isotherms, and where a mixture of gases is simulated, selectivities. If the framework is quite rigid, the framework atoms may be fixed at their original (simulated or crystallographic) positions, however, in flexible frameworks or when interpenetrated frameworks may shift relative to each other, the motion of these atoms must be included in the simulation. Due to the expense of simulating large unit cells over a long time period, these calculations are usually based on classical mechanics, though several recent studies use quantum mechanical calculations to parametrize force fields, which are then used in the MD or GCMC simulations (Bureekaew et al., 2013).

Quantum mechanical, most often Density Functional Theory (DFT) calculations have had some use in directly investigating various periodic covalent network structures (Srepusharawoot et al., 2009). However, as mentioned above, this is prohibitively expensive and many studies, particularly those investigating binding of small molecules within framework structures, employ a co-called cluster model, whereby a section of the periodic structure is cut from the bulk. After saturating the excised bonds (e.g., with H atoms), the calculation may then proceed as a straightforward gas-phase calculation. Care must be taken that the size of the model is appropriate in order to avoid spurious results arising from interaction with the cut edges, and such studies may neglect spatial and electronic effects from neighboring framework atoms either through-bond or through-space. Despite these concerns, this approach has been extraordinarily fruitful (Klontzas et al., 2008; Assfour and Seifert, 2010; Choi et al., 2011).

The most significant recent development in the computational study of framework materials is in the high-throughput computational prediction of new covalent network structures. Several software packages capable of generating arbitrary network structures given a topology and the required building blocks were released (Martin and Haranczyk, 2014; Addicoat et al., 2014a; Gomez-Gualdron et al., 2014). In all cases, the topologies themselves are sourced from the Reticular Chemistry Structure Resource (RCSR) developed by O’Keeffe et al. (2008). For 3D covalent frameworks, the most common topologies are dia, ctn, bor, pto, and tbo (Bureekaew and Schmid, 2013). 2D frameworks are typically either hexagonal (layer symbol hca, hcb) or square planar (sql). This new software is now being employed in predictive high-throughput computational studies, such as the work of Martin et al. who generated an impressive 18,000 synthetically accessible covalent networks with diamond-like topology (RCSR symbol dia) (Martin et al., 2014) and identified promising candidates for methane storage. The predictive capability (pre-synthesis) offered by such software is fundamental to the development of frameworks with specific properties and represents a new way forward in the development of materials targeted to specific applications.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Matthew A. Addicoat gratefully acknowledges a Marie Curie Actions (MC-IIF: GA-MOF, Grant Agreement 327758) fellowship. We acknowledge support by Deutsche Forschungsgemeinschaft and Open Access Publishing Fund of Karlsruhe Institute of Technology.

References

Addicoat, M. A., Coupry, D. E., and Heine, T. (2014a). AuToGraFS: automatic topological generator for framework structures. J. Phys. Chem. A 118, 9607–9614. doi: 10.1021/jp507643v

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Addicoat, M. A., Vankova, N., Akter, I. F., and Heine, T. (2014b). Extension of the universal force field to metal-organic frameworks. J. Chem. Theory Comput. 10, 880–891. doi:10.1021/ct400952t