Improved deep learning method and high-resolution reanalysis model-based intelligent marine navigation

Large-scale weather forecasting is critical for ensuring maritime safety and optimizing transoceanic voyages. However, sparse meteorological data, incomplete forecasts, and unreliable communication hinder accurate, high-resolution wind system predictions. This study addresses these challenges to enhance dynamic voyage planning and intelligent ship navigation. We propose IPCA-MHA-DSRU-Net, a novel deep learning model integrating incremental principal component analysis (IPCA) with a spatial-temporal depthwise separable U-Net. Key components include: (1) IPCA preprocessing to reduce dimensionality and noise in 2D wind field data; (2) depthwise-separable convolution (DSC) blocks to minimize parameters and computational costs; (3) multi-head attention (MHA) and residual mechanisms to improve spatial-temporal feature extraction and prediction accuracy. The framework is optimized for real-time onboard deployment under communication constraints. The model achieves high accuracy in high-resolution wind predictions, validated through reanalysis datasets. Experiments demonstrated enhanced path planning efficiency and robustness in dynamic oceanic conditions. The IPCA-MHA-DSRU-Net balances computational efficiency and accuracy, making it viable for resource-limited ships. This novel IPCA application provides a promising alternative for preprocessing large-scale meteorological data.

1 Introduction

Marine transportation has been recognized as one of the indispensable transport models for developing a global logistics network. In recent years, with the rapid development of global trade and the vast expansion of the supply chain network, the demand for reliable and efficient marine transport has increased sharply (Koukaki and Tei, 2020). Yet, potential challenges and risks arise for sea-going vessels when it comes to long-distance path planning due to the instability and unpredictability of the meteorological environment resulting in too much uncertainty (Lau et al., 2024). This is especially so when encountering adverse sea conditions, such as extreme wind and wave scenarios, that can significantly impede ship navigation, thus, requiring timely speed reduction and route deviation so as to ensure safety (Rawson et al., 2021). Ocean state conditions can significantly impact the safety and decision-making of marine vehicles. Although shipping route recommendations could be obtained from weather routing companies (Szlapczynski et al., 2023), real-time access to weather forecasts is becoming more crucial for underway ships. Accurate and timely weather forecasting can support the captain in designing and determining the ship’s path in advance and further ensure the safety of mariners and ships. More importantly, efficient and handy onboard weather predictions can provide invaluable marine environment references for intelligent navigation (He et al., 2022). Accurate and fine-grid weather predictions are essential for the seaworthiness and safety of sea-going ships, especially during long transoceanic voyages, where vessels are exposed to the open ocean’s full range of meteorological and oceanographic phenomena. These voyages can last days or weeks, during which weather and sea states can change rapidly and drastically, impacting both the physical safety of the vessel and the efficiency of its journey. Fine-scale weather predictions play a critical role in enhancing situational awareness for shipping operations, enabling them to anticipate and mitigate risks associated with severe sea conditions, such as strong winds, and intense storms. For instance, accurate, high-resolution weather forecasts enable route planning to avoid severe weather, which reduces fuel consumption, lowers operational costs, and minimizes emissions. Given the substantial size and fuel requirements of ocean-going vessels, even minor deviations from optimal weather conditions can result in significant additional fuel consumption, which contributes to both increased costs and environmental impact. Fine-grid predictions allow for precise navigational adjustments that align with favorable weather patterns, helping ships follow safer and more efficient routes. Moreover, a precise forecast of extreme wind on a fine grid can give shipping operators and crew sufficient warning to take preventive measures, such as adjusting speed, changing course, or securing loose cargo. For crews, these predictions mean better preparation and safety measures, reducing the likelihood of accidents or fatalities. As a consequence, providing accurate and efficient meteorological prediction is crucial for achieving intelligent, safe, and green ship path planning (Zis et al., 2020).

Classical ocean and meteorology forecasting relies on the numerical weather prediction model (NWP). It uses the collected meteorological parameters, geographical boundaries, and initial conditions to predict weather variability based on a physical conservation equation (Cheng et al., 2013; Hur, 2021). Nevertheless, the inherent instability and stochasticity characteristics of earth system evolution make it challenging to forecast global weather using deterministic weather forecast models. In addition, with the increasing complexity, higher uncertainty, and variability of earth systems due to global climate changes, traditional numerical forecasting models tend to fail to capture abrupt and intricate spatial-temporal disturbances and dependencies inherited in earth-evolving systems (Ouyang et al., 2017; Wu et al., 2023). The computational cost of a physical model-based numerical method is very high. These intricate numerical models pose significant challenges in development and maintenance, yet, are quite rigid for real-time applications (Cai et al., 2020; Yan et al., 2023). Moreover, the spatial-temporal resolution of a numerical model would have a significant impact on prediction accuracy, such as the grid and temporal interval resolution. Improving the grid resolution will achieve longer processing times and higher computational requirements. Most weather forecast and weather observation systems mainly provide sparse low-resolution data samples. For instance, as illustrated in Figure 1, there is missing wind forecasting or observational data in different large regions, and as marine meteorology is vast and complex, the observational and monitoring costs of the marine environment are much higher than those of the continents. Only certain parts of the ocean region where data samples are available can be validated.

Figure 1

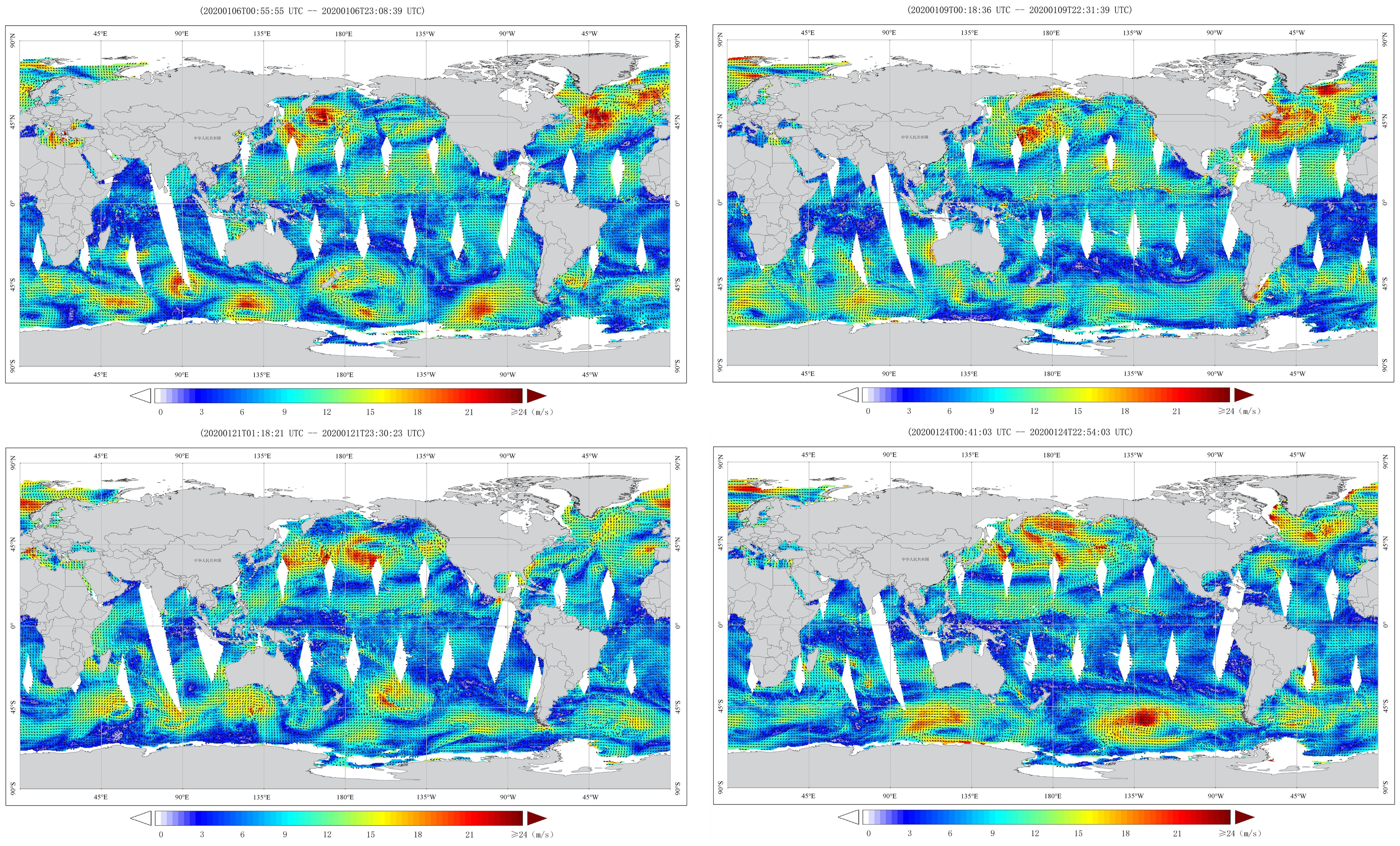
Figure 1. Global sea surface wind from National Satellite Ocean Application Service (http://www.nsoas.org.cn/eng/column/141.html).

Tremendous efforts have been implemented to explore ship path planning and optimization based on ocean forecasts, such as dynamic programming, A-star algorithm, and genetic algorithm (Chen et al., 2021b; Khan et al., 2022). For example, a new stability-related, dynamic route constraint was proposed for path optimization (Krata and Szlapczynska, 2018). Du (2022) developed an improved 3D dynamic programming algorithm for ship path planning, which takes the meteorological conditions, constraints of engine power, and safety into consideration. Yet, many previous ship path planning approaches primarily focused on realizing the shortest navigation time. Those optimization methods usually neglected the comprehensive energy consumption and motion response factors, especially when encountering severe sea states. Currently, the marine industry is paying more and more attention to shipping energy efficiency, thus, more comprehensive factors, including fuel consumption, the safety of mariners and vessels, reduction of greenhouse gas emissions, and so on, have to be taken into account to achieve greener route planning (Moradi et al., 2022; Chen and Mao, 2024). For example, a multi-objective route optimization methodology was proposed (Vettor and Soares, 2016) by employing the genetic evolution algorithm while realizing route and speed optimization simultaneously. Ma et al. (2021) established a ship routing and speed multi-objective optimization framework for minimizing greenhouse gas emissions by selecting appropriate plans. A genetic algorithm is employed to derive the optimal route based on a ship heading or on both heading and propulsion power information. Yet, a low-resolution sea state dataset was integrated into this study and their main focus was to achieve fuel savings (Kytariolou and Themelis, 2022). Important weather and sea state information is often absent for the ship sensors, thus, a hybrid data fusion and machine learning model was proposed to evaluate the relationship between fuel consumption rate and the voyage’s weather situation. This study attempted to aggregate meteorological data and sensor information for the purpose of enhancing the accuracy of machine learning (ML) models, and they focused on quantifying ship fuel consumption based on weather conditions, sailing speed, and sea conditions (Du et al., 2022). A novel study established a hybrid genetic algorithm to optimize ship path planning for safe transoceanic navigation with complicated sea conditions. They mainly focused on the voyage time and fuel consumption as the optimization criteria, yet overlooked the issue of the ship’s own structure’s resistance to wind and waves and the workload of personnel during high wind and wave weather (Zhou et al., 2023). An improved A* algorithm was proposed for ship collision avoidance path planning by integrating the multi-target point artificial potential field method (MPAPF). They analyzed the static environment and ship navigating situation, thus, the dynamic weather information may be lost (Huang et al., 2024). The Non-Dominated Sorting Genetic Algorithm III (NSGA-III) model was employed to realize ship weather routing tasks by integrating ship heading angle and speed. The main aim was to optimize operational costs and CO₂ emissions (Ma et al., 2024). A constrained policy optimization (CPO) perspective was proposed for a multi-objective path planning model to investigate Pareto-optimal paths, and the results demonstrated that adapting the potential policy factors into the ship path planning model could achieve an advantageous result in complex environments (Zhu et al., 2025a). In order to reduce fuel consumption during a ship voyage, a route planning model that is able to identify energy-efficient routes in complicated sea conditions was proposed by combining ocean currents into the traditional level set method. They proved that ocean environmental factors, such as ocean currents, were very useful for energy-efficient ship voyage planning (Zhu et al., 2025b).

The above studies focused on ship path planning from different perspectives. Nevertheless, most of these approaches employed meteorological forecasts with very low spatial-temporal resolution. It has been emphasized that low spatial and temporal resolution weather forecasting data usually result in inaccuracy in shipping path optimization (Wu et al., 2023). In addition, high-resolution ocean weather prediction plays a major role in ensuring the safe navigation of intelligent autonomous marine vehicles (Chen et al., 2021a; Qiao et al., 2023).

Deep learning methods have been demonstrated to show promise in mitigating the gaps in numerical weather forecasting models and marine environment monitoring systems (Kochkov et al., 2024; Zhao et al., 2024). A deep learning-based weather prediction model has exhibited great potential in uncovering underlying climatic patterns from historical records, enabling the acquisition of high-resolution forecasting data, which provides a new perspective for improving the reliability of highly efficient and intelligent ship path planning. Many researchers have been attempting to explore different kinds of ML methods for obtaining accurate natural wind estimations (Wang et al., 2021). However, the intricate non-linear spatiotemporal properties of large-scale spatial-temporal weather systems represent great challenges for traditional machine learning which attempts to extract sequential evolutionary trends from past records (Khodayar and Wang, 2018).

For the purpose of alleviating the above-mentioned limitations and research gaps, an incremental principal component analysis (IPCA) based on a spatial-temporal depthwise separable U-Net model by aggregating an attention and residual learning scheme, the IPCA-MHA-DSRU-Net, was developed for fine-grid large-scale extreme wind speed field system predictions. Specifically, the depthwise-separable convolution (DSC) blocks first introduced into this proposed method can provide an effective way to improve forecasting efficiency and performance while reducing their computational and memory requirements. The depthwise separable blocks greatly reduce the number of parameters and computation requirements compared to traditional convolutions. They can allow for better feature extraction and aggregation by separating the spatial and channel-wise information in the input data (Zhou et al., 2024; Xu et al., 2024). Incremental principal component analysis (IPCA) is also employed for 2D wind field preprocessing, which can effectively filter the feature space of data samples by reducing dimensionality and redundant noise effects. IPCA is an adaptive version of principal component analysis (PCA) designed for large or streaming datasets. Instead of processing the entire dataset at once, IPCA updates the principal components incrementally as new data arrives, making it memory-efficient and suitable for real-time or large-scale applications. Moreover, a sequential sliding-data window scheme (Yin et al., 2023), obeying a strictly chronological order, was mixed into the tensor-preparation phase, which would enable the accurate preservation of wind temporal-dependent variabilities within consecutive spatial patterns. The framework of the developed wind system forecast model is displayed in Figure 2.

Figure 2

Figure 2. The diagram of the proposed wind forecast model.

As can be seen in Figure 2, the wind system forecast model demonstrates the structure and workflow of the IPCA-based spatial-temporal depthwise separable U-Net model. U-Net is a convolutional neural network (CNN) architecture designed for computer vision tasks. It features a symmetric U-shaped structure with an encoder-decoder pathway: the encoder captures contextual information by downsampling the input, while the decoder reconstructs precise localization by upsampling. Skip connections between corresponding encoder and decoder layers help preserve spatial details, making U-Net highly effective for tasks like 2D image processing and object detection. This developed forecasting model utilizes modular IPCA preprocessing to effectively reduce the dimensionality of the input data while preserving key spatial-temporal patterns, which are essential for forecasting wind systems. By incorporating depthwise separable convolutions, the model achieves computational efficiency, allowing the processing of large-scale spatial-temporal datasets with reduced complexity. The attention mechanism selectively focuses on the most critical regions in the input data, enhancing the model’s ability to capture significant features that influence wind predictions. Meanwhile, the residual learning scheme aids in preserving finer details and mitigates the vanishing gradient problem, allowing deeper layers to learn more nuanced patterns in the data.

First, the reanalysis dataset, which assimilates real observations with numerical simulation, is employed as the input, and then the input data sample is preprocessed by the employed IPCA method to filter noise and retain principle components of wind variability. Next, the processed wind dataset is fed into the proposed forecasting hybrid U-Net model. The last step is to aggregate the forecasting output from the hybrid U-Net model and analyze the forecasting performance. The figure provides a step-by-step visual representation of the data flow, making it easier to understand the contributions of each component in achieving accurate and efficient wind forecasting. This comprehensive architecture, with its innovative use of IPCA, depthwise separable convolutions, attention, and residual connections, demonstrates a balanced approach to handling complex spatial-temporal wind data for forecasting applications.

Our study developed a novel deep learning model for onboard weather prediction during large-scale ocean voyages. It provided us with a fully complete large-scale sea surface wind field forecasting with very high resolution and accuracy, which is very important and valuable for voyage scheduling to avoid severe sea states and ensure the safety of seafarers and ship transoceanic navigation. In addition, the transferability of the proposed model is also verified by utilizing two different geospatial regions with various weather characteristics. By mapping weather observational gaps into a fine-grid and complete spatial perspective, the proposed approach, implemented on a single laptop, aims to enhance the timeliness and accuracy of onboard ship routing, thereby enhancing ship navigation safety. The main aim and focus of this study is to provide ships undertaking transoceanic ship voyages with a highly accurate and high-resolution sea state forecasting model onboard while taking the factors of ship structure safety and seafarer workload into consideration. Finally, the model provides instantaneous extreme wind system pattern mapping, helping achieve adaptive and intelligent path planning for marine vehicles, especially for sea-going navigations in large-scale oceans.

The main contributions of this study can be summarized as follows:

1. A novel intelligent neural-learning model was developed by aggregating a depthwise-separable convolution-based U-Net framework with attention and residual learning blocks.

2. Incremental principal component analysis was first introduced to preprocess a fine-grid wind dataset, filter Empirical Orthogonal Function (EOF) models, and retain principal wind evolution information.

3. The DSC-based methodology was developed to achieve fine-grid spatial-temporal extreme wind field forecasting on a large scale.

4. The fine-grid wind prediction model can enhance the navigation safety of sea-going vessels.

5. A sequential sliding-data window is adopted for the aggregation of input-target tensor pairs to better preserve the temporal wind evolution information.

6. A sensitivity trial was implemented to explore wind forecasting model parameter adjustment and optimization.

7. The transferability of the intelligent neural learning model was validated by employing two geographic regions with different wind patterns.

The remainder of this article is arranged as follows. Section 2 introduces the developed spatial-temporal wind prediction approach. The targeted experimental case is presented in Section 3 with the quantitative forecasting analysis, and Section 4 validates the model transferability. Finally, Section 5 summarizes the work and outlines future directions.

2 Methodology

The novel hybrid wind systems forecasting model, IPCA-MHA-DSRU-Net, integrates IPCA with a spatial-temporal depthwise separable U-Net architecture, enhanced by attention and residual learning mechanisms. This model aims to achieve fine-grid, large-scale wind system predictions, improving voyage planning and navigation safety. The use of DSC blocks significantly reduces model parameters and computational complexity. By leveraging the strengths of modular IPCA preprocessing, residual learning, multi-head attention, and the depthwise separable CNN-based U-Net architecture, this hybrid framework is optimized to predict complex, spatial-temporal variations in extreme wind signals. Detailed explanations for each component of the proposed model are as follows.

2.1 Incremental principal component analysis

The basic theory of PCA is to generate a set of independent composite indicators by recombining the raw variables, thereby reducing the dimensionality of the original data samples while retaining most of the original/principal information features. Specifically, PCA performs data transformation on the original data and projects it onto a new coordinate system, resulting in the projected data having the largest variance. The main merits of PCA include reducing data dimensionality, decreasing computational complexity and model complexity, reducing the impact of noise, improving the signal-to-noise ratio of data, identifying the most important features in data samples through dimensionality reduction, and removing some redundant features, thereby reducing the risk of overfitting and improving the model’s generalization ability (Xu et al., 2023a; Xiao et al., 2023; Zhang et al., 2024b).

Provided that the targeted data-sample size is m x n, the data sample matrix is represented in the Equation 1 as follows:

$\begin{array}{ll}P=\left[\begin{array}{c}{p}_{11} p_{12} \cdots p_{1n}\\ p_{21} p_{22} \cdots p_{2n}\\ \cdots \cdots \cdots \cdots \\ p_{m1} p_{m2} \cdots p_{mn}\end{array}\right]& (1)\end{array}$

subtract the average value of each column in the Equation 2:

$\begin{array}{ll}P=\left[\begin{array}{c}{p}_{11}-b_1 p_{12}-b_1 \cdots p_{1n}-b_1\\ p_{21}-b_1 p_{22}-b_1 \cdots p_{2n}-b_1\\ \cdots \cdots \cdots \cdots \\ p_{m1}-b_1 p_{m2}-b_1 \cdots p_{mn}-b_1\end{array}\right]& (2)\end{array}$

where bi is the average of each column in the Equation 3:

$\begin{array}{ll}{b}_i=\frac{1}{m}{\displaystyle \sum _{i=1}^m{p}_{ji}}& (3)\end{array}$

The covariance CM is an m × m matrix, and the CM_ij of the covariance matrix indicates the covariance value of the targeted variables p_i and p_j. Next, the eigenvalues of the covariance CM are derived and the computed eigenvalues are filtered in descending order. The eigenvectors related to the first k eigenvalues are employed to aggregate a new feature matrix. Finally, after the dimensionality reduction operation, the projection of P on the new eigenvector matrix is computed to represent the eigenvectors.

IPCA decomposes a large-scale sample into multiple small-batch datasets through gradual iterations and performs principal component analysis on each small-batch dataset. This avoids the memory and computing resource consumption caused by processing the entire dataset at once. After conducting principal component analysis on each small-batch dataset, the obtained principal components are merged so as to obtain the principal components of the entire dataset. Compared to traditional PCA algorithms, IPCA has lower computational complexity and can obtain principal components with greater efficiency. It can also perform incremental updates when new data arrives without recalculating the principal components of the entire dataset, thus achieving real-time data processing. IPCA employs singular value decomposition to perform linear dimensionality reduction on target data samples, retaining only the most important singular vectors, and then processing/projecting the data samples into a lower dimensional feature space. It finds principal components by calculating singular value decomposition, processing only one batch of samples in one iteration to reduce memory consumption (Greenacre et al., 2022; Weng et al., 2003). The principal component is calculated by the Equations 4 and 5:

$\begin{array}{ll}{\widetilde{PC}}_i(n)=P{C}_i(n-1)+{\alpha }_i(n)u(n)u^T(n)P{C}_i(n-1)& (4)\end{array}$

$\begin{array}{ll}\begin{array}{l}P{C}_i(n)=orthonormalize{\widetilde{PC}}_i(n) with respect to P{C}_i(n),\\ j=1,2,\dots ,i-1\end{array}& (5)\end{array}$

where the PC_i(n) denotes the projection of the ith dominant eigenvector for the derived sample covariance matrix CM = E{u(n)u^T(n)}. The a_i indicates a stochastic approximation gain. The u_n is a m-dimensional vector.

The full wind speed field can be reconstructed by the linear combination of the leading principal components (PCs) and their corresponding EOFs after filtering redundant features and noise signals. The EOF analysis is a statistical technique used to identify dominant patterns or structures in spatial-temporal datasets, such as climate or geophysical data. It decomposes the data into EOFs that capture the maximum variance, with associated time coefficients describing their temporal evolution. A given wind field Wind_t, at time step t can be calculated as follows in the Equation 6:

$\begin{array}{ll}Win{d}_{m,t}={\displaystyle \sum _{n=1}^{k}P{C}_{n,t}EO{F}_{m,n}}& (6)\end{array}$

where m denotes the grid index of the wind field, t indicates the time index, and k is the total number of retained PCs.

IPCA is an adaptation of PCA that allows for processing data in an incremental manner, rather than requiring the entire dataset to be available in memory at once. Thus, instead of computing the covariance matrix from the entire dataset at once, the algorithm updates the principal components incrementally as new data arrives. The key idea is that there is no requirement to store the whole dataset, but data is processed in small batches (minibatches) and the principal components are updated as new data is fed into the model.

The application of IPCA in 2D extreme wind field preprocessing offers a strategic approach to handle data dimensionality and mitigate noise interference. It is very crucial for improving prediction accuracy in wind field forecasting models. Here is a detailed explanation of IPCA’s principles, and how they rationalize its application in this context. Since wind field data are typically represented as large 2D grids, with each cell corresponding to specific wind metrics (e.g., speed and direction) at that spatial point. Processing such high-dimensional input directly in deep learning models would lead to high computational costs and increase the risk of overfitting, especially with limited training data. The IPCA reduces the spatial dimensions, retaining only essential components that reflect the primary spatial patterns in wind fields, making the data manageable without significant information loss. By focusing on principal components, the IPCA naturally discards lower-variance components, which are likely to be noise. This selective filtering of information means that the data entering the forecasting model is “cleaner,” which supports better model training and more accurate predictions. In addition, as a ship navigates through different ocean regions, wind patterns will vary significantly. The IPCA’s incremental nature allows it to adapt to these changes by updating principal components with incoming data. This ongoing adaptation ensures that the data fed into the forecasting model always reflects current environmental conditions, enhancing prediction accuracy, which allows forecasting models to focus on essential features without the burden of excessive, redundant information. This burden reduction lowers computational demands, allowing models to train faster and reducing the risk of overfitting. Additionally, because the model is working with a cleaner, lower-dimensional dataset, prediction accuracy tends to improve.

In summary, the choice of IPCA in 2D wind field preprocessing is rational due to its ability to reduce dimensionality, handle real-time data, and filter out noise, all while requiring limited resources. This pre-processing step enhances the predictive model’s accuracy and efficiency by supplying a refined, lower-dimensional input that captures the most relevant spatial patterns in the wind field data. As a result, IPCA-based preprocessing is a practical and effective solution to prepare 2D wind data for deep learning models in a constrained, dynamic environment like that on a ship.

2.2 Depthwise separable convolution

In general, the basic U-Net framework is prone to overfitting and is computationally heavy with traditional convolution operations. In this study, we introduced the DSC block to reduce the basic U-Net model size and trainable parameters (Chollet, 2017). The DSC block separates a complete convolution operation into two steps: pointwise convolution (PTC) and depthwise convolution (DC). The operation of PTC is similar to classical convolution, and its convolution kernel has a size of 1 × 1. Unlike the classical convolution computing process, a kernel of DSC is responsible for one channel. Therefore, the entire model parameters are greatly reduced. Each input channel was applied by a single convolutional kernel in the depthwise convolution and outputs the respective feature maps.

In a standard 2D convolutional operation, a kernel spans all input channels (or depth) and slides over the spatial dimensions (height and width) of the input, creating output channels by combining information from all input channels. However, in depthwise convolution, each input channel has its own independent kernel. Specifically, instead of applying a single kernel across all input channels, the depthwise convolution applies one filter per implementation independently. This process captures spatial information within each channel but does not combine information across different channels, which limits its expressive power. Thus, the next step, pointwise convolution, is introduced to address this issue. The pointwise convolution can adjust the number of output channels and helps to combine the channel-wise information produced by the depthwise convolution. By performing these two operations sequentially, the depthwise-separable convolution emulates the effect of a standard convolution while significantly reducing the computational cost.

Considering the input feature map I is (D_I, D_I, M), the target-output O is (D_O, D_O, N); and the standard convolutional operation kernel K indicates (D_K, D_K, M, N), of which M and N represent the number of inputs and target channels, correspondingly. D denotes the size of convolved high-dimensional feature maps. Specifically, the kernel K is divided into two convolutional modulations: the depthwise (D_K, D_K, 1, N) and pointwise convolution (1, 1, M, N). In addition, the classical 1 x 1 convolutional kernel is employed in the pointwise convolution modulation, and the channel features derived by depthwise convolution operation are then projected onto the deeper and higher channel space. The pointwise convolution was applied after the depthwise operation, using N convolutional kernels with 1 x 1 x M size for the purpose of representing the M D_K x D_K feature maps. The weighted combination operation is then performed in the depth direction in order to generate the N D_K, D_K x 1 feature maps O (D_O, D_O, N). The two convolutional modulations are illustrated in Figure 3.

Figure 3

Figure 3. The Schematic illustration of depthwise separable CNN.

The formula of standard convolution is expressed in the Equation 7:

$\begin{array}{ll}{O}_{k,l,n}=\sum _{i,j,m}{K}_{i.j,m,n} . I_{k+i-1,l+j-1,m}& (7)\end{array}$

and the formula of depthwise separable convolution is shown in in the Equation 8:

$\begin{array}{ll}{\widehat{O}}_{k,l,m}=\sum _{i,j}{\widehat{K}}_{i,j,m} . I_{k+i-1,l+j-1,m}& (8)\end{array}$

2.3 Multi-head attention

The attention strategy in deep learning is widely used in image, natural language processing, speech recognition, and so on. The core task of the attention mechanism is to optimally extract critical information from mass data samples quickly and accurately. Compared with the standard convolution mechanism, the attention strategy is characterized by fewer parameters, high accuracy, and lower computational cost. The basic scaled dot-production attention block consists of multi-head attention modulation. It has been demonstrated that multi-head attention is able to better catch and preserve underlying high-dimensional features (Xu et al., 2023b, 2024). In particular, the attention mechanism has been proven to be helpful for spatial-temporal wind speed forecasting (Yu et al., 2023), and more non-linear dynamics could potentially be reproduced, especially for the dynamic fluid field (Niu et al., 2021; Che et al., 2022) based on the multi-head strategy. The attention can be understood as a key-value query, which maps queries and key values to the target output. The essence of the attention is the processing of weighted summation for values based on keys and queries, together with the weight redistribution.

The multi-head attention strategy exhibits lower complexity compared to the scaled dot-product attention, allowing the forecasting model to deeply map different high-dimensional representations while avoiding the loss of small targets. In this study, the query matrices were linearly projected three times on the sequential wind-speed tensors. Then, the projected weight matrices were concatenated to generate the refinement forecasting outputs.

In wind field forecasting, multi-head attention enhances the model’s ability to interpret the spatial and temporal relationships within the wind data. By simultaneously attending to multiple areas of the input grid, the model captures subtle, location-specific patterns (e.g., shifts in wind intensity across regions and changes over time) that a standard convolutional layer may miss. Moreover, traditional convolutional layers have a fixed receptive field and struggle with long-range dependencies, particularly in spatial-temporal data. Multi-head attention addresses this limitation by dynamically focusing on relevant areas across both spatial and temporal dimensions. In the U-Net model, this allows the encoder-decoder structure to more effectively aggregate spatial-temporal information, which is crucial for fine-grid forecasting of fluctuating wind conditions. More importantly, for real-time applications on ships, balancing latency with model accuracy is essential. Multi-head attention, while enhancing predictive accuracy through improved feature attention, may introduce latency due to the processing load. Efficient implementation techniques, such as attention approximation methods (e.g., sparse or low-rank approximations), can be considered to reduce the burden of multi-head attention.

H and W are the height and width of the 2D input matrix and the C indicates the feature number for the input-sequential tensors. Providing that the sequential series represent $\mathit{W}\mathit{i}\mathit{n}\mathit{d}=[{\mathit{x}}_{1,\dots },{\mathit{x}}_N]\in {ℝ}^{\text{HxWxC}}$, the dot-product will aggregate and derive the K and the Q together with the V query terms using three projected matrices W_k $\in {ℝ}^{D_x\text{x}{D}_k}$, W_q $\in {ℝ}^{D_x\text{x}{D}_q}$, and W_v $\in {ℝ}^{D_x\text{x}{D}_v}$ in the Equation 9:

$\begin{array}{ll}\begin{array}{l}\mathit{K}=\mathit{W}\mathit{i}\mathit{n}\mathit{s}{\mathit{W}}_{\mathit{k}}\in {ℝ}^{H\text{x}W\text{x}{D}_k}\\ \mathit{Q}=\mathit{W}\mathit{i}\mathit{n}\mathit{d}{\mathit{W}}_{\mathit{q}}\in {ℝ}^{H\text{x}W\text{x}{D}_k}\\ \mathit{V}=\mathit{W}\mathit{i}\mathit{n}\mathit{d}{\mathit{W}}_{\mathit{v}}\in {ℝ}^{H\text{x}W\text{x}{D}_k}\end{array}& (9)\end{array}$

In the attention-based data-processing stage, a specific normalization term ξ(${\mathit{q}}_i^T{\mathit{k}}_j$) $\in {ℝ}^1$ will be introduced to calculate the similarity between the ith query ${\mathit{q}}_i^T\in {ℝ}^{D_k}$ and the jth key ${\mathit{k}}_j\in {ℝ}^{D_k}$. Then at a designated position i, the attention weight is derived by the Equation 10

$\begin{array}{ll}\mathit{\vartheta }(\mathit{Q},\mathit{K},\mathit{V})=\text{ξ}(\frac{\mathit{Q}{\mathit{K}}^T}{\sqrt{d_k}})\mathit{V}& (10)\end{array}$

Larger d_k derived from the input sequential tensors with higher dimensions will then lead to the softmax-normalization trapped into local optima with extremely small gradients. The scaled term $\frac{1}{\sqrt{d_k}}$, laterally aggregated into the weighted summation, will alleviate this traditional vanishing gradient issue.

The ith row weights can be derived as the Equation 11

$\begin{array}{ll}\mathit{\vartheta }{(Q,K,V)}_i=\frac{{\displaystyle {\sum }_{j=1}^N{e}^{{\mathit{q}}_i^T{\mathit{k}}_j}{\mathit{v}}_j}}{\sqrt{d_k}{\displaystyle {\sum }_{j=1}^N{e}^{{\mathit{q}}_i^T{\mathit{k}}_j}}}& (11)\end{array}$

sequentially, it can be simplified as

$\begin{array}{ll}\mathit{\vartheta }{(Q,K,V)}_i=\frac{{\Psi ({\mathit{q}}_i)}^T{\displaystyle {\sum }_{j=1}^N\rho (k_j){\mathit{v}}_j^T}}{\sqrt{d_k}\Psi {({\mathit{q}}_i)}^T{\displaystyle {\sum }_{j=1}^N\rho (k_j)}}& (12)\end{array}$

The Equation 12 can, then, be illustrated when different types of normalization functions $\varphi$() were aggregated

$\begin{array}{ll}\mathit{\vartheta }{(Q,K,V)}_i=\frac{{\displaystyle {\sum }_{j=1}^N\varphi ({\mathit{q}}_i,{\mathit{k}}_i){\mathit{v}}_i}}{{\displaystyle {\sum }_{j=1}^N\varphi ({\mathit{q}}_i,{\mathit{k}}_i)}}& (13)\end{array}$

$\varphi$(q_i, k_j) function will calculate the correlated similarities between q_i and k_j.

A constraint term can be illustrated as the ker(x, y) ${ℝ}^{2\text{x}F}\to {ℝ}_{+}$, which would ensure that the specific attention blocks are non-negative. The Equation 13 can be expressed as

$\begin{array}{ll}\mathit{\vartheta }(Q,K,V)=\frac{{\displaystyle {\sum }_{j=1}^N\varsigma {({\mathit{q}}_i)}^T\varsigma ({\mathit{k}}_i){\mathit{v}}_i}}{{\displaystyle {\sum }_{j=1}^N{\varsigma ({\mathit{q}}_i)}^T\varsigma ({\mathit{k}}_i)}}& (14)\end{array}$

The associative property of the matrix multiplication was used to rewrite Equation 14

$\begin{array}{ll}\mathit{\vartheta }(Q,K,V)=V^{\prime }=\frac{\varsigma {({\mathit{q}}_i)}^T{\displaystyle {\sum }_{j=1}^N\varsigma ({\mathit{k}}_i){\mathit{v}}_i^T}}{\varsigma {({\mathit{q}}_i)}^T{\displaystyle {\sum }_{j=1}^N\varsigma ({\mathit{k}}_i)}}& (15)\end{array}$

Equation 15 can, subsequently, be simplified when the numerator is in the vector form as the Equation 16:

$\begin{array}{ll}(\varsigma (\mathit{Q})\varsigma {(\mathit{K})}^T)\mathit{V}=\varsigma (\mathit{Q})(\varsigma {(\mathit{K})}^T\mathit{V})& (16)\end{array}$

2.4 Spatial-temporal forecasting network

The underlying spatial-temporal features inherited in the sequential wind speed systems with low-level nonlinearities are mapped by the encoder module of the U-Net backbone, and high-level semantic representations will then be extracted into the decoder modulation (Ronneberger et al., 2015). Yet, the ordinary skip-connection operations would usually lead to insufficient exploration of potential semantic and contextual features, especially for fine-grid 2D wind speed system mapping tasks. Thus, in this study, two additional multi-head attention blocks together with deep residual learning (Manucharyan et al., 2021) are introduced together with depthwise separable convolutional modulation to mitigate these issues. The residual learning block mitigates the vanishing gradient problems that would usually occur in very deep networks. It enables the constructed wind mapping network to be deep enough. In addition, in the context of wind field forecasting, residual learning allows the model to refine spatial-temporal representations by focusing on differences in wind patterns across time and space. This focus is especially important for forecasting applications where subtle changes in wind conditions need to be captured accurately. Residual learning supports the model’s ability to detect and propagate important spatial-temporal features throughout the network, improving forecasting accuracy. The IPCA-based dimensionality reduction further enhances residual learning by streamlining the data. With IPCA pre-compressing high-dimensional inputs, residual layers can focus on fine-tuning only the most critical components of the compressed data, which reduces both computation and memory usage without compromising model performance. Finally, residual learning enables the model to adapt to rapidly changing wind conditions by emphasizing residuals, or deviations, in the wind field data. This adaptability is particularly valuable in marine environments where weather and wind conditions can shift quickly. With residual learning, the model becomes better equipped to capture these subtle changes, leading to more accurate and timely forecasts.

The diagram of the wind system mapping based U-Net model combination is illustrated in Figure 4.

Figure 4

Figure 4. The wind system forecasting network.

The residual block was only integrated into two layers of the Decoder part, which would alleviate the total computational burden. Specifically, one block was incorporated into the last layer of the decoder, and the other one was located in the first layer of decoder modulation. The attention block in between the Bottleneck layer and 2D depthwise separable CNN layers can query and reproduce more embedded spatial wind system features with refinement operations. The second one further augments original feature maps aggregated by skip-connections, deeper refinement, and feature augmentation realized by the attention operations can improve the final forecasting performance (Vaswani et al., 2017). These newly introduced modifications, including DSC modulation, attention blocks, and residual learning strategy, for the raw U-Net-backbone, can enhance the reproduction performance of underlying fine-grid 2D wind spatial variabilities. In addition, dropout layers were retained in the forecasting operations due to the dropout being a potential Bayesian approximation that could mitigate the predictive uncertainty for deep learning regression tasks (Gal and Ghahramani, 2016).

The core architecture of this hybrid model is a depthwise separable CNN-based U-Net-like structure, as illustrated in Figure 4. The model adopts a U-Net-like architecture, which is characterized by an encoder-decoder structure with skip connections. This design is particularly effective for capturing multi-scale features, making it suitable for spatiotemporal data such as wind fields, and the 2D DSC layers employed in the U-Net framework can process spatial data (e.g., wind speed maps) across time steps, enabling it to learn spatial patterns and temporal dynamics simultaneously. One of the major innovation points of this proposed model is that the depthwise separable convolutions are employed as the main CNN block, as shown in Figure 3, which could reduce computational complexity and the number of trainable parameters. This convolution operation separates spatial filtering (depthwise convolution) from channel-wise feature combinations (pointwise convolution), making the model more efficient. This depthwise separable CNN block enhances the model’s ability to extract localized spatial features from extreme wind data samples, which is critical for capturing fine-grained patterns in wind fields. The other innovation of this model is that multi-head attention is integrated into the proposed network to capture long-range dependencies and interactions across both spatial and temporal dimensions. This mechanism allows the model to focus on the most relevant regions of the input data at different scales. By computing attention scores across multiple heads, the model can dynamically weight the importance of different spatial and temporal features, improving its ability to model complex wind dynamics. In addition, the residual connections are also incorporated to facilitate gradient flow during training, mitigating issues such as vanishing gradients and enabling the training of deeper networks. These connections allow the model to reuse features from earlier layers, enhancing its ability to learn hierarchical representations of wind field data. As can be seen in Figures 2, 4, a reanalysis of the extreme wind field dataset, which combines the real observation and numerical model simulations using the data assimilation method, was aggregated from the ERA5 model, and we then implemented z-score normalization in the raw extreme wind dataset and transformed the dataset into a standard form with a mean of 0 and a standard deviation of 1. Then, the IPCA approach was employed for 2D wind field decomposition, which can effectively filter the feature space of data samples by reducing dimensionality and redundant noise effects. The autocorrelation analysis, as outlined in section 3.1, is employed to obtain a comprehensive perspective on the temporal dependency of the overall extreme wind speed field sequential lagging. The sequential wind field time lag is determined as 12 time steps, and the target wind field is a one-time step. We then split the dataset into 70% training and 30% testing parts. Afterward, several batch-size wind map data samples with the aggregated wind tensors were fed into the developed forecasting network for parameter training and optimization, and the rest 30% testing data sample was used to test the model performance compared to the reanalysis target.

A novel architecture was designed specifically for spatiotemporal significant extreme wind signal prediction in a large-scale perspective, which leverages the strengths of U-Net framework for precise feature extraction. The IPCA approach was employed for 2D wind field decomposition, which can effectively filter the feature space of data samples by reducing dimensionality and redundant noise effects. The depthwise separable convolution block was incorporated to reduce computational complexity and improve model efficiency without sacrificing performance. In addition, the multi-head attention mechanism was introduced to enhance the model’s ability to capture complex spatiotemporal dependencies in wind data. Finally, the residual learning block was also aggregated into the new framework to address potential vanishing gradient issues in deep networks, ensuring stable training and improved feature representation.

3 Experimental results and discussion

3.1 Case study

This study utilized a Linux platform as the simulation environment based on the Tensorflow framework by employing a single NVIDIA-A100 GPU. The forecasting experiment covers the Asia-Pacific region within a longitude of 96.5-160°E and a latitude of 6-69.5°N, and 2 years of hourly wind data samples spanning from 2016 to 2017 with fine-grid 256 x 256 spatial resolution were selected. One year of hourly samples from 2016 were utilized to train the forecasting model, and the independent validation dataset covers 3 months of data samples from January to March in 2017 (UTC). The weather forecast ERA5 data was provided by the European Centre for Medium-Range Weather Forecasts (ECMWF), while the weather observation data was provided by the National Satellite Ocean Application Service (IMOS). The spatial resolution of the hourly weather forecast was 0.25° × 0.25°. The reanalysis data had global horizontal coverage. The temporal coverage was from 1940 to the present. The dataset size utilized in this research was approximately 9Gb, covering a time period from 2016 to 2017 with 256x256 spatial resolution (the pixel size is 256x256 for each hourly wind field snapshot).

3.2 Wind field decomposition

The dominant variability of spatial-temporal wind speed patterns could be decomposed into a certain number of principal EOF models, and the derived EOF time series is able to represent wind spatial variation patterns associated with its corresponding temporal PC time series. Based on the IPCA data-preprocessing approach, the reconstruction of the wind speed pattern, after cleaning redundant wind features and noise signal, is calculated by multiplying the decomposed PCs with retained EOFs models (Zhang et al., 2022):

$\begin{array}{ll}Win{d}_{recon}={\widetilde{PC}}_{i}EO{F}_i& (17)\end{array}$

As can be seen from Figure 5, far more than 1,000 principal wind variability components were decomposed from the original raw wind data samples in Panel (a), which explained most of the wind evolutional variance, yet, a certain portion of noise signals and irrelevant features have already been coupled and embedded within the original data samples due to the stochasticity and non-linearity of the evolved earth system. Panel (b) clearly illustrates that the first 25 PC models would be capable of explaining almost 70% of the total wind evolutional variance. In order to save computational resources, reduce time consumption, and further clean up the additional redundant noise signals with potentially irrelevant features, the first 25 EOFs (as displayed in Figure 6) were selected as the primary evolutional variability model of wind speed patterns. Finally, the cleaned input wind data samples were reconstructed by employing the 25 principal EOF models with their corresponding PC time series based on Equation 17.

Figure 5

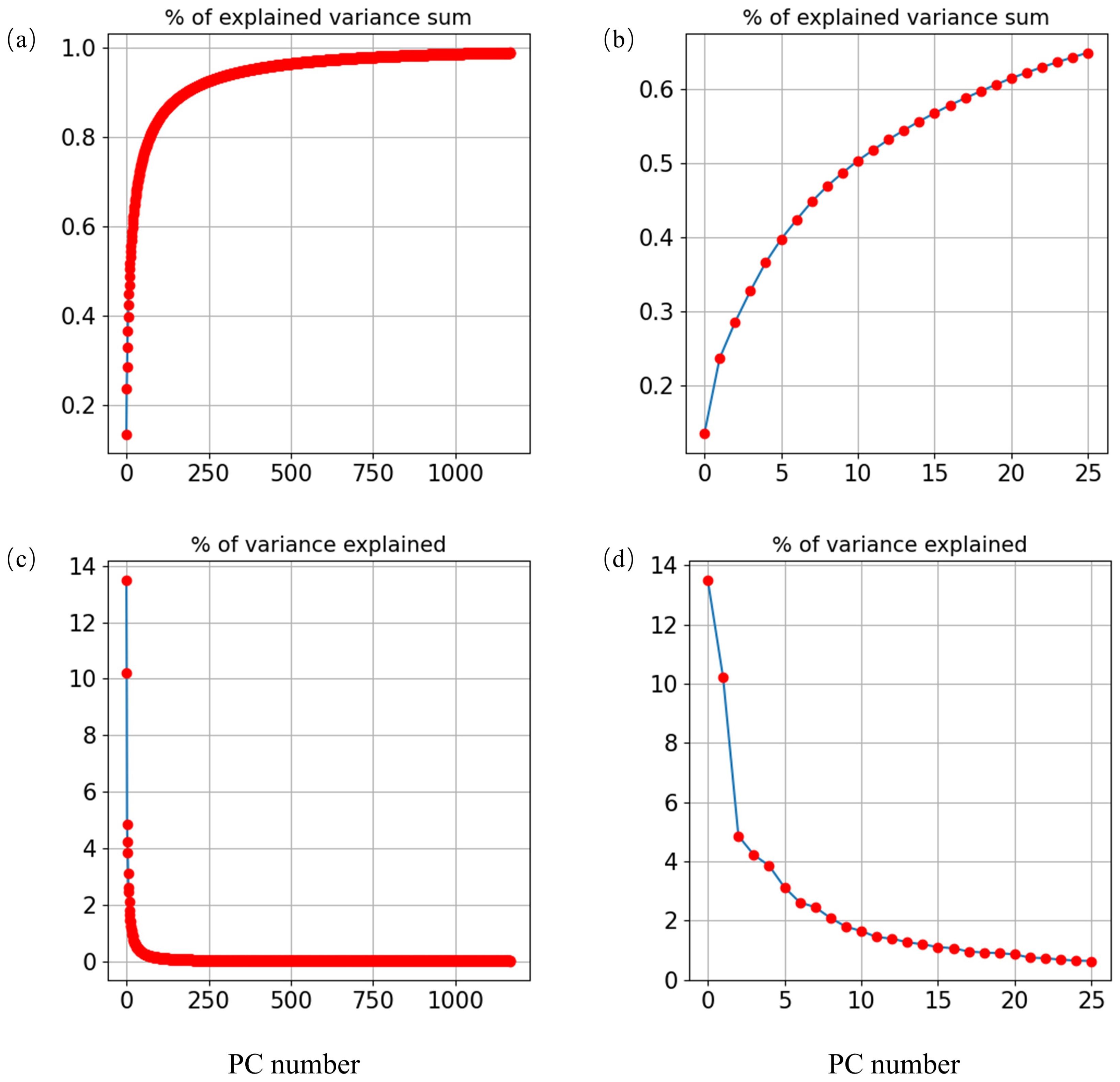
Figure 5. The variance explained based on the decomposed spatial wind patterns. Panels (a, c) indicate the complete explained wind evolutional variance, panels (b, d) represent 70% explained wind variance.

Figure 6

Figure 6. The first 25 decomposed EOF models of raw wind pattern.

3.3 The sliding-data window method

The autocorrelation analysis was employed to obtain a comprehensive perspective on the temporal dependency of the overall wind field sequential-lagging, which can usually explore the relatively optimal historical time lags, coupled with the most inter-correlated sequential information, for the aggregated wind samples by showing time-series correlation maps of both regionally averaged and randomly selected grid-cell based wind series. In Figure 7, the bounds of the derived 95% confidential interval are represented as the shadow blue band.

Figure 7

Figure 7. The Autocorrelation analysis of wind component pattern variability with field-mean time series panels (a, b), the random selected grid-point time series panels (c, d).

Given a time series for correlation analysis with its delayed values, the formula of correlation can be calculated based on the following Equations 18, 19 and 20:

$\begin{array}{ll}corr(X,Y)=\frac{cov(X,Y)}{{\sigma }_X{\sigma }_Y}& (18)\end{array}$

$\begin{array}{ll}corr(X,Y)=\frac{E[(X-{\mu }_X)(Y-{\mu }_Y)]}{{\sigma }_X{\sigma }_Y}& (19)\end{array}$

$\begin{array}{ll}corr(X,Y)=\frac{E[X,Y]-E[X]E[Y]}{\sqrt{E[X^2]-E{[X]}^2}\sqrt{E[Y^2]-E{[Y]}^2}}& (20)\end{array}$

for wind time-series G in time t step, X = G_t+1 and Y = G_t.

The partial autocorrelation function (PACF) also employs the same correlation formula to derive the autocorrelation in between time lags, yet the PACF disregards the indirect correlations between Gt+1 and Gt. The Equation 21 is as follows given k≥ 2:

$\begin{array}{ll}PACF(k)=corr(G_{t-k}-P_{t,k}(G_{t+k}),W_t-P_{t,k}(G_t))& (21)\end{array}$

where P_t,k (x) indicates the subjective operator of the orthogonal projection for x onto the linear subspace of Hilbert spanned by G_t+1,…,G_t+k.

As shown in Figure 7, the PACF within the shadow blue band occurred at lag step 12 and lag step 7, correspondingly. Note that the correlation values distributed within the shadow blue band indicate these time lags were not significant. Thus, in this study, the wind time series ranging from historical time-lag t-1 to t-7 was finally filtered to aggregate the input-tensor depth. In this study, the wind pattern time series consists of 256 x 256 (Width × Height) grids. Based on the optimal correlated time lags, the sequential sliding data window with a fixed window size of 7 was set. Each pair of the training and validation sample contains seven wind field snapshots with strict chronological order as SSW_t = (Wind_t-10, …, Wind_t-2, Wind_t-1), combining one or more output-wind speed maps with a specific given leading time-steps. Specifically, the prepared modeling data sample was normalized into the value range [-1,1] to speed up convergence efficiency. In addition, the scale consistency will be eliminated between data samples by implementing normalization pre-processing. The learning rate of the selected Adam optimizer in the wind-forecasting model was set to 1e-4, the batch size was set as 200, and the loss function employed Huber loss, which was minimized by using the gradient descent approach. An early-stopping criterion that the training iteration will be terminated if the loss metric has stopped improving after consecutive 12-iterations was further employed. The Huber loss Equation 22 is as follows:

$\begin{array}{ll}{L}_{\varsigma }(O,\mathit{\vartheta }(X))=\{\begin{array}{c}\frac{1}{2}{(O-\mathit{\vartheta }(X))}^2\\ \varsigma |0-\mathit{\vartheta }(X)|\frac{1}{2}{\varsigma }^2\end{array}& (22)\end{array}$

where O is the reanalysis model and ϑ denotes the deep neural learning model. In this study, the ς was tested and set as 1.0. The Huber loss is usually less sensitive to outliers, since it can approach an L2 loss if the ς approximate to 0, and approaches L1 when the ς is positive infinity. The flowchart of the established wind pattern forecasting network is presented in Figure 8, so as to provide an clear model operation process.

Figure 8

Figure 8. The flowchart of the established wind pattern forecasting network.

3.4 Model sensitivity analysis

The rationale concerning how to determine the model hyperparameter settings is very important to evaluate its robustness and uncertainty. In this study, we tested a range of hyperparameters, consisting of the batch size, activation function, learning rates, and loss function, to assess the model’s robustness based on forecasting performance.

The statistics forecasting skills for wind pattern prediction are illustrated in the Appendix (Supplementary Table S1–S4), employing the varied hyperparameters. Note that we implemented forecasting experiments using different parameter settings, yet, for the optimization algorithm, the reasonable parameter range settings are also determined by preliminary experiments and domain knowledge (Parri and Teeparthi, 2024). Also, it has been emphasized that optimizing hyperparameters of machine learning models is a laborious process (Zhang et al., 2024a). Moreover, one can better monitor the comprehensive model performance and robustness by applying model sensitivity experiments in which varied model parameter settings are explored, which can provide us with a deeper insight into a better understanding of which hyperparameters might have a potential impact on the predictive capability. More importantly, it has been illustrated that a sensitivity trial can provide a basis for model parameter adjustment and optimization, and further enable quantification of the potential model uncertainties (Asheghi et al., 2020). The uncertainty of the specific model settings can be quantified by exploring the underlying impact of these hyperparameters on predictive performance. Thus, potential model uncertainties together with its robustness derived from varied parameter settings could furnish us with a valuable reference concerning optimization and adjustment of the developed framework, and better show the confidence interval of the model settings (Abbaszadeh et al., 2022).

3.5 Wind system prediction

In order to evaluate the prediction errors, several methods including recurrent neural network (RNN), Long-short term memory network (LSTM), CNN-LSTM, Encoder-decoder, ResU-Net, and MHA-ResU-Net were used for a comparison with the proposed approach. For the prediction experiments, the mean absolute error (MAE) derived using Equation 23 and the root mean square error (RMSE) derived using Equation 24 were employed as model-evaluation metrics to reveal the performance.

$\begin{array}{ll}MAE= \frac{1}{n}{\displaystyle \sum _{i=1}^n\left|X_{prediction,i}-Y_{observation,i}\right|}& (23)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}{{\displaystyle {\sum }_{i=1}^n(X_{prediction,i}-Y_{observation,i})}}^2}& (24)\end{array}$

where the Y_{observation,i} denotes the reanalysis 2D wind map and the X_prediction,i indicates the predicted snapshot.

The forecasting metrics are illustrated in Figure 9. The lowest forecasting errors were obtained by the proposed prediction model amongst all individual experiments, which verified that the proposed deep neural learning model outperforms the rest of the models, especially in fine-grid spatial-temporal 2D wind system mapping. The derived area-mean RMSEs for 1-hour-ahead and 12-hour-ahead predictions were less than 0.15 m/s and 0.53 m/s, respectively.

Figure 9

Figure 9. Wind pattern forecasting error analysis.

The spatial-resolved wind gust speed predictions were derived and are shown in Figure 10, to further explore the model performance in a fine-grid spatial perspective. Pre indicates model forecasting, ob represents the reanalysis samples. As displayed in Figure 10, the proposed neural-learning method can preserve the spatial-temporal sequential wind system variabilities, which shows that the spatial-temporal wind evolution patterns were well reproduced for each single wind field snapshot. In addition, extreme wind signals were also well captured continually within the sequential wind evolving trend. Longer leading-step predictions with corresponding deviation maps are shown in Figure 11.

Figure 10

Figure 10. Snapshots of spatial-resolved wind speed patterns forecasting.

Figure 11

Figure 11. Longer surface extreme wind forecasting.

In order to explore the effectiveness of deep-learning-based weather prediction for ship path planning, two types of weather predictions were employed to evaluate an empirical shipping route. It has been proven that if the raw numerical model forecasting data with sparse-grid resolution and with 24-h intervals are utilized to schedule the voyage path, the extreme wind field could not be identified by the ship route optimization software (Yuan et al., 2022; Wu et al., 2023). On the contrary, the developed spatial-temporal deep learning model is able to provide continuous weather forecasting with a very high spatial resolution of 0.25° × 0.25° and an hourly time scale, which will help the path optimization software to identify dangerous navigation regions with accurate area boundaries where severe sea states exist, as displayed in Figure 12. More importantly, the proposed model is able to offer continuous weather forecasting updates, even on a single laptop. This means that the proposed framework combined with reanalysis data samples is very convenient and practical for adaptive path planning of marine vehicles, especially for sea-going navigation in large-scale oceans.

Figure 12

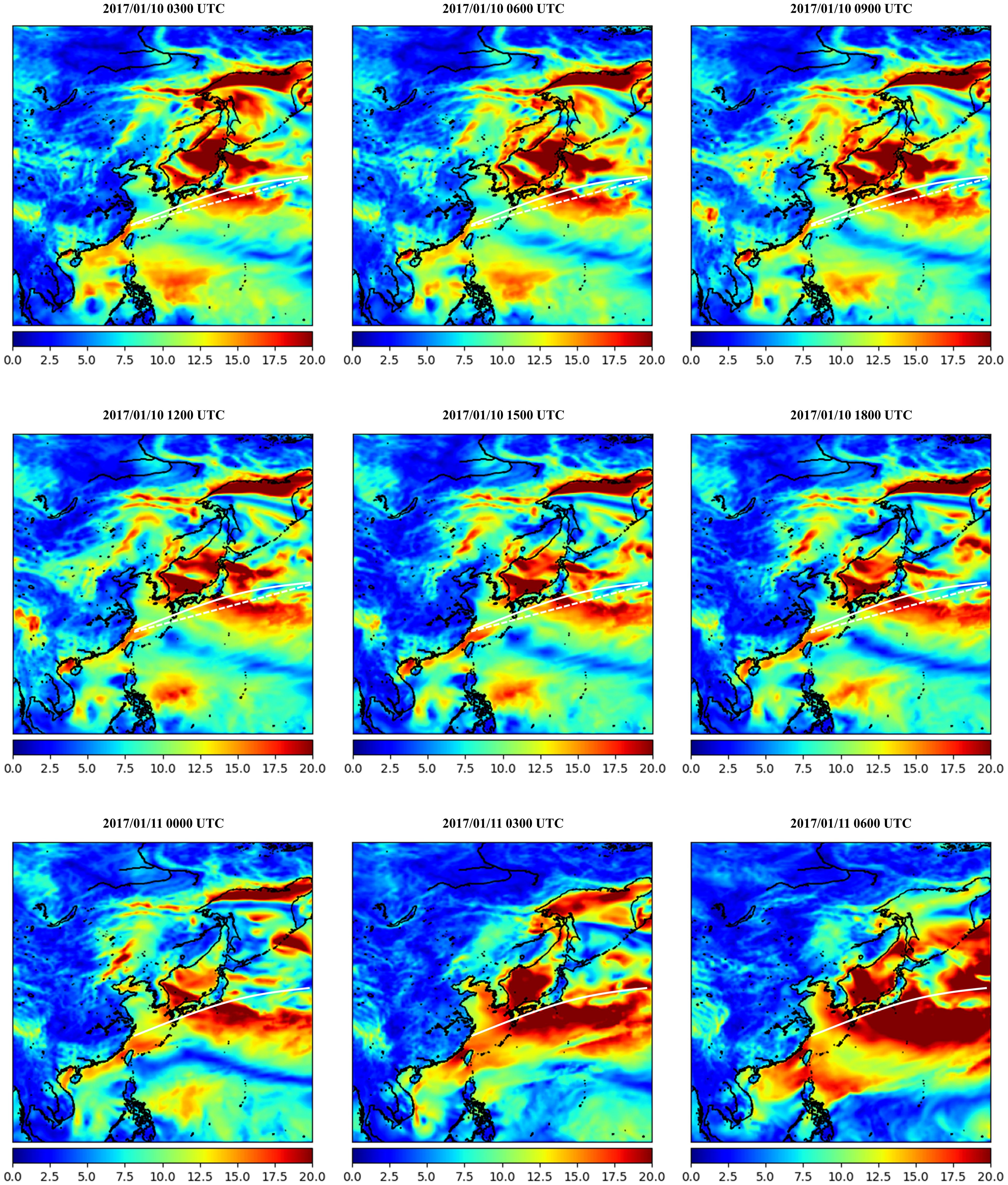
Figure 12. Ship path planning based on the wind field forecasting, the white dash-line indicates adaptive path and white line is experimental route.

Moreover, a shipping path application was evaluated based on the deep learning-based wind forecast for the sake of better illustrating its effectiveness for efficient and intelligent route planning. Generally speaking, the major part of the experimental shipping route would directly pass through the high sea-state region, if the sparse weather forecasting and weather observation system could not recognize the severe sea state. However, the adaptive ship route based on the proposed continuous fine-grid wind forecasting model would accurately avoid adverse weather conditions as much as possible, since the variability of the sea state would be perceived based on weather routing software (Vettor and Soares, 2016; Wu et al., 2023). In addition, it can be seen in Figure 12 that the fine-grid sea-state region detection can help to adjust the experimental path planning accurately using 1-day weather forecasting, and from a sea-going navigation practical perspective, a longer prediction time-span that exceeds 1 day would provide a timely reference for future voyage adjustment. Moreover, with the efficient and intelligent identification of severe weather conditions, autonomous marine vehicles would be able to achieve active obstacle avoidance and intelligent route adjustment, which will lay a solid foundation for intelligent ocean environment perception and the development of smart ships.

4 Model transferability

Deep learning model transferability is a strategy that involves transferring knowledge obtained from the source domain to solve the tasks in a related target domain (Pan and Yang, 2009; Hu et al., 2016). This study provides a machine learning approach that can be employed to transfer the weather forecasting model knowledge gained for available trained jobs from one specific geospatial region to another region’s field and time span. It provides an opportunity to transfer information between different datasets and different geospatial regions. Model transferability, including the model hyperparameters and model weights relocation, demonstrates whether a newly developed machine learning method can be transferred directly to an unknown region to realize specific weather forecasting-based ship path planning tasks. A square area covering the North Atlantic Ocean within 6.25 - 70°N, -53.75 - 10°E was selected as the modeling region to realize the same model-hyperparameter transferability-based wind field forecasting directly.

It is illustrated in Figure 13 that the developed neural-learning approach reproduced the spatial-temporal sequential wind system variabilities again. This indicates that the spatial-temporal wind distribution patterns located in different geospatial regions were well preserved for each single field snapshot. The extreme wind signals were also continually captured within the sequential wind-evolving trend. The corresponding longer leading-step forecasting with its deviation fields is displayed in Figure 14.

Figure 13

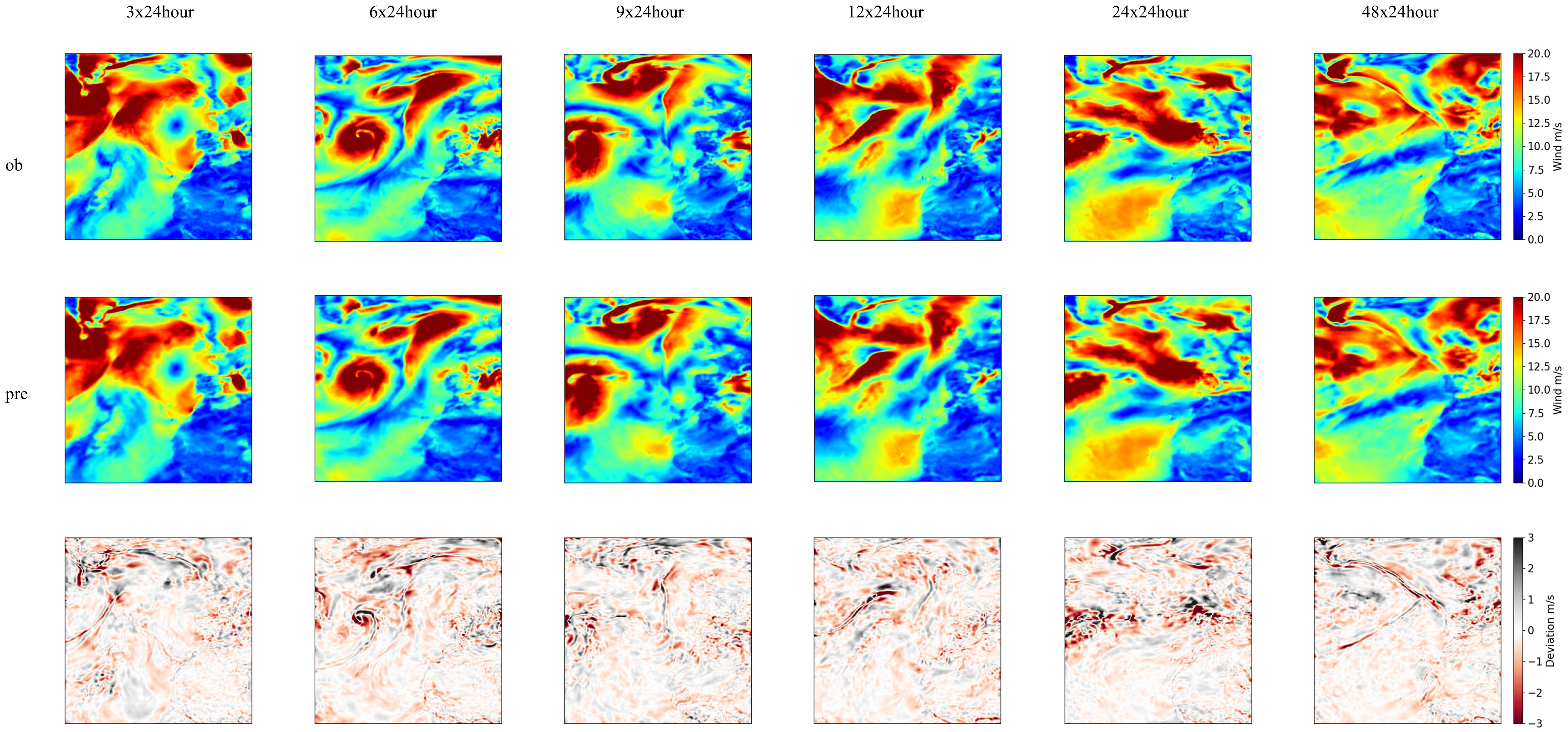
Figure 13. Snapshots of spatial-resolved wind speed patterns forecasting as Figure 10, but for the North Atlantic Ocean region.

Figure 14

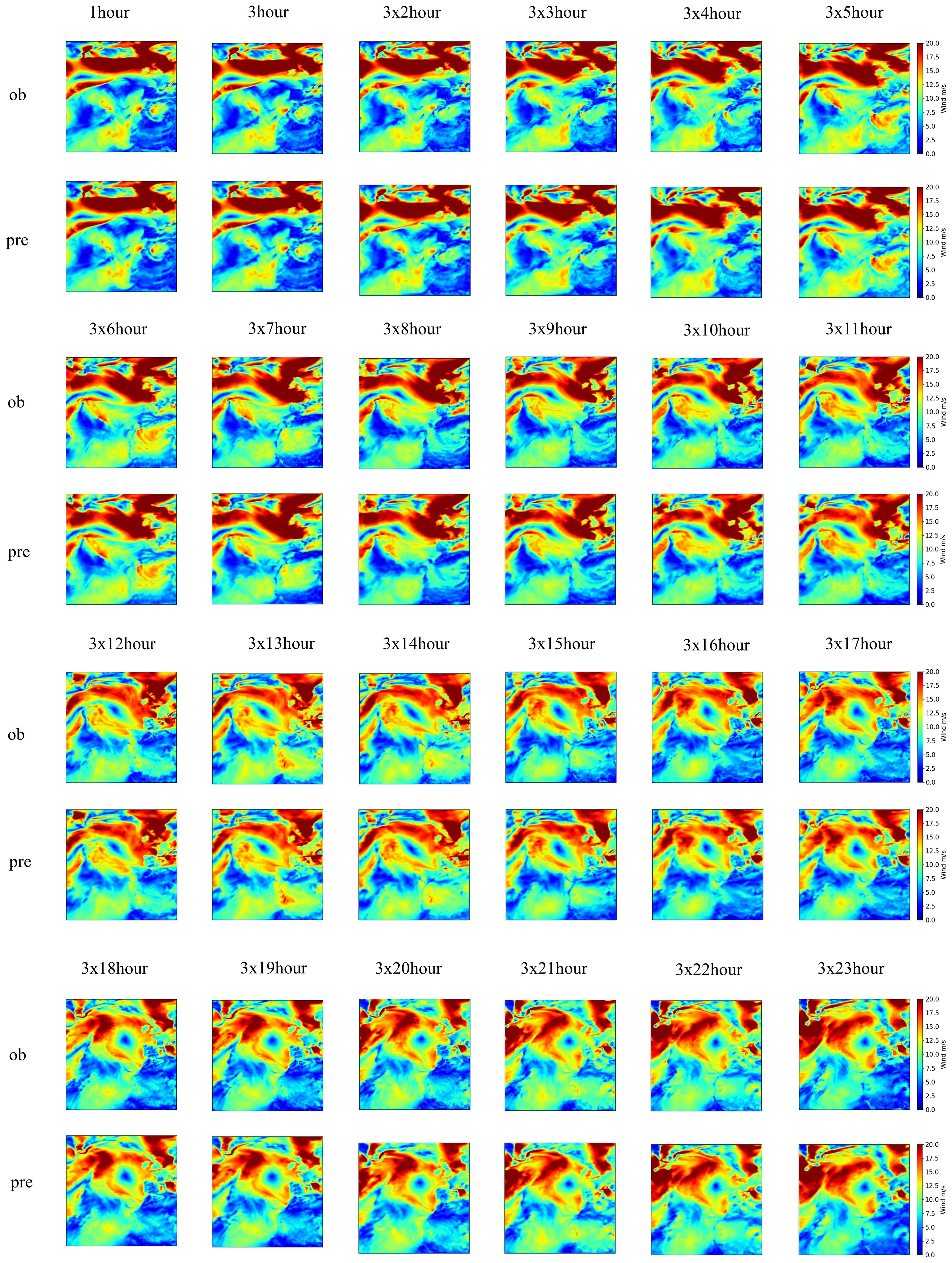
Figure 14. The same as Figure 11, but for the North Atlantic Ocean.

A new shipping path was evaluated using the deep learning-based wind forecast for the sake of better illustrating its effectiveness on the route plan in the North Atlantic Ocean. It can be seen that the major part of the experimental shipping route directly passes through the high sea state region in Figure 15. However, the adaptive ship route based on the proposed continuous fine-grid wind forecasting model was able to avoid adverse weather conditions as accurately as possible. This can not only ensure the safety of marine vehicles and navigators but also provide voyage planning with timely or real-time path adjustment. The smart shipping industry will greatly benefit from the efficient and intelligent detection of severe large-scale sea states using the proposed wind forecasting model.

Figure 15

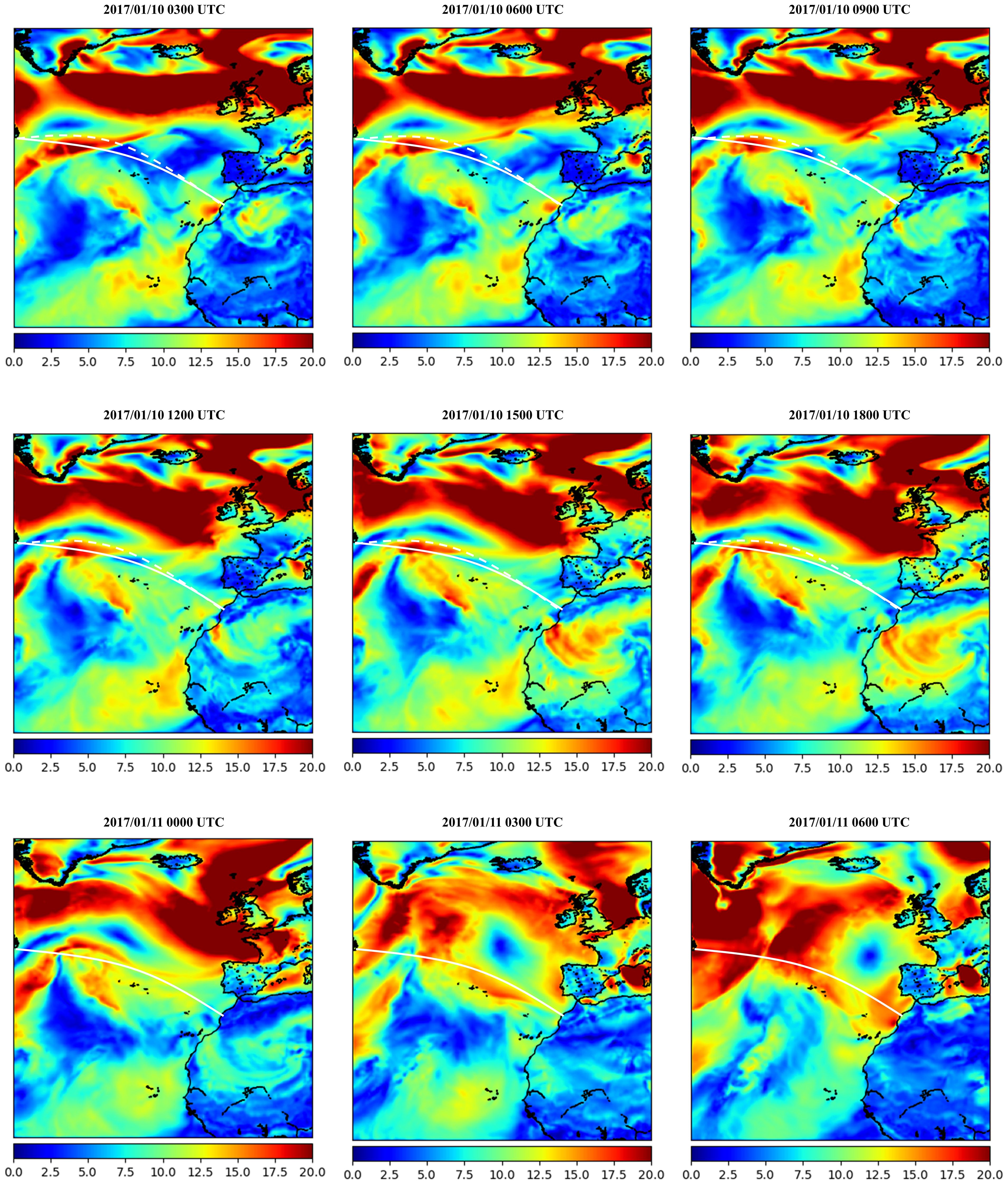
Figure 15. The same as Figure 12, but for ship path planning at the North Atlantic Ocean.

5 Discussion and conclusion

5.1 Discussion of the model’s potential applications and limitations

A depthwise separable U-Net with spatial-temporal attention layers typically has a lower parameter count than standard convolutional U-Nets. Yet, the model is still complex and requires significant computing power for real-time inference. Wind field forecasting involves large volumes of spatial-temporal data, often requiring high-resolution inputs over a continuous time frame. Real-time processing is necessary for effective forecasting, meaning the model must handle frequent data updates without lag. IPCA facilitates dimensionality reduction, which helps manage data size, but there is still a need for fast data preprocessing pipelines to feed into the model without creating bottlenecks. The IPCA-based model necessitates sufficient memory to handle large input matrices (spatial-temporal wind data), intermediate activations, and model weights. The memory requirement can be reduced by applying IPCA to pre-process and compress the input data, but this is still contingent on having enough capacity to maintain intermediate data during real-time inference.

Most ships are limited in terms of the onboard processing power available, typically having less powerful central processing units (CPUs) and possibly limited or no GPUs. While some larger vessels may have limited GPU capacity, deploying such a GPU-based model requires specialized hardware, such as embedded systems with tensor-processing units (TPUs) or compact GPUs. Alternatively, high-performance CPUs capable of supporting multithreading and parallel processing may also be viable, though potentially slower. In addition, other constraints are critical on ships where energy resources are shared among navigation, communication, and other systems. Depthwise separable U-Nets help in reducing computation costs by focusing only on the most relevant filters in the spatial-temporal data. Additionally, IPCA can reduce the data dimensions, resulting in lower power consumption. Nevertheless, the system should be designed to operate within the ship’s power constraints, often requiring energy-efficient processors. IPCA provides an advantage by enabling incremental updates, essential for real-time processing on ships, where data is generated continuously and model re-training is impractical. IPCA reduces data dimensions iteratively, which is efficient, but still requires sufficient processing power to perform real-time updates. A balance is necessary between the model’s forecasting accuracy and the latency in delivering these forecasts. The depthwise separable U-Net offers computational efficiency, but the real-time application might still necessitate simplifying the model further or accepting coarser forecasting to ensure timely output.

In summary, implementing an IPCA-based spatial-temporal depthwise separable U-Net model on ships requires hardware capable of efficient parallel processing, compact design, and low power consumption. Compact GPUs or embedded TPUs are ideal but may not always be feasible, especially on smaller vessels. CPU-based implementations are possible but might face latency issues. Reducing model complexity and utilizing IPCA for dimensionality reduction can mitigate some hardware limitations, but ongoing trade-offs between computational power, accuracy, and latency will be required to make this model operational on actual ships. For stakeholders, understanding these constraints is crucial for planning resource allocation, assessing deployment feasibility, and selecting suitable hardware for maritime forecasting applications.

Concerning the model’s limitations, in marine environments, wind patterns are highly variable and can be influenced by various factors such as ship movements and surrounding weather systems. The IPCA’s incremental learning approach may not fully capture this complexity, as it assumes incremental changes to the learned principal components, which may not adapt quickly enough to abrupt shifts or highly dynamic wind fields. Furthermore, incremental updates in IPCA rely on frequent model retraining with new data. This approach risks underperforming if updates are too infrequent or if older components fail to capture emerging patterns. This can lead to model drift, where the U-Net model’s depthwise separable convolutions become misaligned with the shifting data distributions. Moreover, onboard computing systems may be limited in memory and processing power, restricting the model’s ability to perform complex IPCA transformations alongside the spatial-temporal depthwise separable U-Net operations. This constraint could necessitate simplifying the model at the cost of predictive accuracy.

While depthwise separable convolutions reduce computation by splitting spatial and channel-wise filtering, combining them with IPCA can lead to a loss in detail, particularly in fine-grid scenarios where capturing spatial intricacies is critical. Depthwise operations, while efficient, may not fully exploit the principal components’ spatial relationships, leading to potential oversimplification. Depthwise separable convolutions, when paired with IPCA, might over-rely on a limited number of components, as selecting too many can offset efficiency gains. Choosing an appropriate number of components becomes crucial but challenging in achieving a balance between spatial detail and computational feasibility. In addition, ships’ routes, speeds, and maneuvers might introduce unique challenges in wind field predictions. These unpredictable movements can make it difficult for an IPCA-based U-Net model to maintain consistent predictive accuracy, as rapid course or speed changes could invalidate previously learned components or spatial patterns. Addressing these limitations would involve strategies such as incorporating more adaptive or hierarchical components within the IPCA process, leveraging advanced real-time data filtering, or incorporating more sophisticated recurrent mechanisms within the U-Net architecture in the future steps to handle temporal dynamics better.

5.2 Conclusions

In order to provide instantaneous extreme wind system pattern mapping tasks, and provide adaptive and intelligent path planning for marine vehicles, especially for sea-going navigations in large-scale oceans, a spatial-temporal 2D depthwise separable convolutional based neural-learning model was developed by integrating the multi-head feature-concentrated attention scheme. Specifically, incremental principal component analysis was first employed to filter the feature space of 2D wind data samples by reducing dimensionality and redundant features. The proposed wind forecasting network was employed to capture and preserve the intermittence and non-linearity of spatial-temporal wind system evolutions between the future wind pattern distributions and the historical wind time-series snapshots. The historical wind time lags with a strict chronological order were determined by further introducing a sequential sliding-data window approach and the established spatial-temporal feature mapping methodology was then able to capture the underlying temporal dependencies and variabilities from the consecutive wind maps. In addition, the transferability of the proposed model was verified by employing two geospatial regions with different weather characteristics. By mapping weather observational gaps into a fine-grid and complete spatial format, the proposed approach, implemented in a single laptop, aimed to improve the timeliness and accuracy of onboard ship routing, thereby enhancing ship navigation safety. Based on the efficient and intelligent identification of severe weather conditions, autonomous marine vehicles will be able to achieve active obstacle avoidance and intelligent route adjustment, which will lay a solid foundation for intelligent ocean environment perception for the development of smart shipping.

The experimental findings in this study demonstrate that the developed deep learning-based methodology can accurately and effectively detect severe wind fields. Yet, some limitations remain. For example, other meteorological factors such as atmosphere pressure and wave height conditions were not fully taken into account. Furthermore, issues such as fuel consumption were not considered, which could impact intelligent weather routing-based predictions and ship navigation safety, thus, future research is required to better consider ship navigation performance and its efficiency index and realize a more reliable smart ship path planning task.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5.

Author contributions

ZZ: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft. LC: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft. JY: Conceptualization, Funding acquisition, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the National Natural Science Foundation of China under Grants 52271361 and 52231014, the Special Projects of Key Areas for Colleges and Universities in Guangdong Province under Grant 2021ZDZX1008, the Natural Science Foundation of Guangdong Province of China under Grant 2023A1515010684.

Acknowledgments

We would like to acknowledge the organizations that provided the sources of the data used in this work, namely, the European Centre for Medium-Range Weather Forecasts.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2025.1495822/full#supplementary-material

References

Abbaszadeh S., Shan C., Larsson S. (2022). A novel approach to uncertainty quantification in groundwater table modeling by automated predictive deep learning. Nat. Resour. 31, 1351–1373. doi: 10.1007/s11053-022-10051-w

Crossref Full Text | Google Scholar

Asheghi R., Hosseini S. A., Saneie M., Shahri A. A. (2020). Updating the neural network sediment load models using different sensitivity analysis methods: a regional application. J. HYDROINFORM. 22, 562–577. doi: 10.2166/hydro.2020.098

Crossref Full Text | Google Scholar

Cai H., Jia X., Feng J., Li W., Hsu Y. M., Lee J. (2020). Gaussian process regression for numerical wind speed prediction enhancement. Renew Energ. 146, 2112–2123. doi: 10.1016/j.renene.2019.08.018

Crossref Full Text | Google Scholar

Che H., Niu D., Zang Z., Cao Y., Chen X. (2022). ED-DRAP: Encoder–decoder deep residual attention prediction network for radar echoes. IEEE GEOSCI Remote S, 1–5. doi: 10.1109/LGRS.2022.3141498

Crossref Full Text | Google Scholar

Chen C., Sasa K., Prpić-Oršić J., Mizojiri T. (2021a). Statistical analysis of waves’ effects on ship navigation using high-resolution numerical wave simulation and shipboard measurements. Ocean eng. 229, 108757. doi: 10.1016/j.oceaneng.2021.108757

Crossref Full Text | Google Scholar

Chen G., Wu T., Zhou Z. (2021b). Research on ship meteorological route based on A-star algorithm. MATH PROBL ENG. 2021, 1–8. doi: 10.1155/2021/9989731

Crossref Full Text | Google Scholar

Chen Y., Mao W. (2024). An isochrone-based predictive optimization for efficient ship voyage planning and execution. IEEE Trans. Intell Transp. Syst. 25, 18078–18092 doi: 10.1109/TITS.2024.3416349

Crossref Full Text | Google Scholar

Cheng W. Y., Liu Y., Liu Y., Zhang Y., Mahoney W. P., Warner T. T. (2013). The impact of model physics on numerical wind forecasts. Renew. Energ. 55, 347–356. doi: 10.1016/j.renene.2012.12.041

Crossref Full Text | Google Scholar

Chollet F. (2017). “Xception: Deep learning with depthwise separable convolutions,” in Proceedings of the IEEE conference on computer vision and pattern recognition (CVPR, Honolulu, HI, USA), 1251–1258.

Google Scholar

Du Y., Chen Y., Li X., Schönborn A., Sun Z. (2022). Data fusion and machine learning for ship fuel efficiency modeling: Part III–Sensor data and meteorological data. Commun. Transport Res. 2, 100072. doi: 10.1016/j.commtr.2022.100072

Crossref Full Text | Google Scholar

Gal Y., Ghahramani Z. (2016). “Dropout as a bayesian approximation: Representing model uncertainty in deep learning,” in ICML’16: proceedings of the 33rd international conference on international conference on machine learning (New York, NY, USA: ICML), 1050–1059.

Google Scholar

Greenacre M., Groenen P. J., Hastie T., d’Enza A. I., Markos A., Tuzhilina E. (2022). Principal component analysis. Nat. Rev. Methods Primers. 2, 100. doi: 10.1038/s43586-022-00184-w

Crossref Full Text | Google Scholar

He Y., Liu X., Zhang K., Mou J., Liang Y., Zhao X., et al. (2022). Dynamic adaptive intelligent navigation decision making method for multi-object situation in open water. Ocean Eng. 253, 111238. doi: 10.1016/j.oceaneng.2022.111238

Crossref Full Text | Google Scholar

Hu Q., Zhang R., Zhou Y. (2016). Transfer learning for short-term wind speed prediction with deep neural networks. Renew Energ. 85, 83–95. doi: 10.1016/j.renene.2015.06.034

Crossref Full Text | Google Scholar

Huang Y., Zhao S., Zhao S. (2024). Ship trajectory planning and optimization via ensemble hybrid A* and multi-target point artificial potential field model. J. Mar. Sci. Eng. 12, 1372. doi: 10.3390/jmse12081372

Crossref Full Text | Google Scholar

Hur S. H. (2021). Short-term wind speed prediction using Extended Kalman filter and machine learning. Energy Rep. 7, 1046–1054. doi: 10.1016/j.egyr.2020.12.020

Crossref Full Text | Google Scholar

Khan S., Grudniewski P., Muhammad Y. S., Sobey A. J. (2022). The benefits of co-evolutionary Genetic Algorithms in voyage optimisation. Ocean Eng. 245, 110261. doi: 10.1016/j.oceaneng.2021.110261

Crossref Full Text | Google Scholar

Khodayar M., Wang J. (2018). Spatio-temporal graph deep neural network for short-term wind speed forecasting. IEEE T SUSTAIN ENERG 10, 670–681. doi: 10.1109/TSTE.2018.2844102

Crossref Full Text | Google Scholar

Kochkov D., Yuval J., Langmore I., Norgaard P., Smith J., Mooers G., et al. (2024). Neural general circulation models for weather and climate. Nature 632, 1060–1066. doi: 10.1038/s41586-024-07744-y

PubMed Abstract | Crossref Full Text | Google Scholar

Koukaki T., Tei A. (2020). Innovation and maritime transport: A systematic review. Case Stud. Transp. Policy. 8, 700–710. doi: 10.1016/j.cstp.2020.07.009

Crossref Full Text | Google Scholar

Krata P., Szlapczynska J. (2018). Ship weather routing optimization with dynamic constraints based on reliable synchronous roll prediction. Ocean Eng. 150, 124–137. doi: 10.1016/j.oceaneng.2017.12.049

Crossref Full Text | Google Scholar

Kytariolou A., Themelis N. (2022). Ship routing optimisation based on forecasted weather data and considering safety criteria. J. Navig. 75, .1310–.1331. doi: 10.1017/S0373463322000613

Crossref Full Text | Google Scholar

Lau Y., Chen Q., Poo M. C. P., Ng A. K., Ying C. (2024). Maritime transport resilience: A systematic literature review on the current state of the art, research agenda and future research directions. Ocean Coast. Manage. 251, 107086. doi: 10.1016/j.ocecoaman.2024.107086

Crossref Full Text | Google Scholar

Ma W., Ma D., Ma Y., Zhang J., Wang D. (2021). Green maritime: A routing and speed multi-objective optimization strategy. J. Clean Prod. 305, 127179. doi: 10.1016/j.jclepro.2021.127179

Crossref Full Text | Google Scholar

Ma D., Zhou S., Han Y., Ma W., Huang H. (2024). Multi-objective ship weather routing method based on the improved NSGA-III algorithm. J. Ind. Inf. Integr. 38, 100570. doi: 10.1016/j.jii.2024.100570

Crossref Full Text | Google Scholar

Manucharyan G. E., Siegelman L., Klein P. (2021). A deep learning approach to spatiotemporal sea surface height interpolation and estimation of deep currents in geostrophic ocean turbulence. J. Adv. Model. Earth Sy 13, e2019MS001965. doi: 10.1029/2019MS001965

Crossref Full Text | Google Scholar

Moradi M. H., Brutsche M., Wenig M., Wagner U., Koch T. (2022). Marine route optimization using reinforcement learning approach to reduce fuel consumption and consequently minimize CO2 emissions. Ocean Eng. 259, 111882. doi: 10.1016/j.oceaneng.2022.111882

Crossref Full Text | Google Scholar

Niu Z., Zhong G., Yu H. (2021). A review on the attention mechanism of deep learning. Neurocomputing 452, 48–62. doi: 10.1016/j.neucom.2021.03.091

Crossref Full Text | Google Scholar

Ouyang T., Zha X., Qin L. (2017). A combined multivariate model for wind power prediction. Energ Convers Manage. 144, 361–373. doi: 10.1016/j.enconman.2017.04.077

Crossref Full Text | Google Scholar

Pan S. J., Yang Q. (2009). A survey on transfer learning. IEEE Trans. Knowl. 22, 1345–1359. doi: 10.1109/TKDE.2009.191

Crossref Full Text | Google Scholar

Parri S., Teeparthi K. (2024). SVMD-TF-QS: An efficient and novel hybrid methodology for the wind speed prediction. Expert Syst. Appl. 249, 123516. doi: 10.1016/j.eswa.2024.123516

Crossref Full Text | Google Scholar

Qiao Y., Yin J., Wang W., Duarte F., Yang J., Ratti C. (2023). Survey of deep learning for autonomous surface vehicles in marine environments. IEEE Trans. Intell. Transp. Syst. 24, 3678–3701. doi: 10.1109/TITS.2023.3235911

Crossref Full Text | Google Scholar

Rawson A., Brito M., Sabeur Z., Tran-Thanh L. (2021). A machine learning approach for monitoring ship safety in extreme weather events. Saf. Sci. 141, 105336. doi: 10.1016/j.ssci.2021.105336

Crossref Full Text | Google Scholar

Ronneberger O., Fischer P., Brox T. (2015). “U-net: Convolutional networks for biomedical image segmentation,” in Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference (Springer International Publishing, Munich, Germany), 234–241.

Google Scholar

Szlapczynski R., Szlapczynska J., Vettor R. (2023). Ship weather routing featuring w-MOEA/D and uncertainty handling. Appl. Soft Comput. 138, 110142. doi: 10.1016/j.asoc.2023.110142

Crossref Full Text | Google Scholar

Vaswani A., Shazeer N., Parmar N., Uszkoreit J., Jones L., Gomez A. N., et al (2017). Attention is all you need. Adv. Neural Inf. Process. Syst. 30, 5998–6008. doi: 10.48550/arXiv.1706.03762

Crossref Full Text | Google Scholar

Vettor R., Soares C. G. (2016). Development of a ship weather routing system. Ocean Eng. 123, 1–14. doi: 10.1016/j.oceaneng.2016.06.035

Crossref Full Text | Google Scholar

Wang Y., Zou R., Liu F., Zhang L., Liu Q. (2021). A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy. 304, 117766. doi: 10.1016/j.apenergy.2021.117766

Crossref Full Text | Google Scholar

Weng J., Zhang Y., Hwang W. S. (2003). Candid covariance-free incremental principal component analysis. IEEE Trans. Pattern Anal. Mach. Intell. 25, 1034–1040. doi: 10.1109/TPAMI.2003.1217609

Crossref Full Text | Google Scholar

Wu Z., Wang S., Yuan Q., Lou N., Qiu S., Bo L., et al. (2023). Application of a deep learning-based discrete weather data continuousization model in ship route optimization. Ocean Eng. 285, 115435. doi: 10.1016/j.oceaneng.2023.115435

Crossref Full Text | Google Scholar

Xiao Y., Zou C., Chi H., Fang R. (2023). Boosted GRU model for short-term forecasting of wind power with feature-weighted principal component analysis. Energy. 267, 126503. doi: 10.1016/j.energy.2022.126503

Crossref Full Text | Google Scholar

Xu H., Hu F., Liang X., Zhao G., Abugunmi M. (2024). A framework for electricity load forecasting based on attention mechanism time series depthwise separable convolutional neural network. Energy 299, 131258. doi: 10.1016/j.energy.2024.131258

Crossref Full Text | Google Scholar

Xu X., Hu S., Shi P., Shao H., Li R., Li Z. (2023a). Natural phase space reconstruction-based broad learning system for short-term wind speed prediction: Case studies of an offshore wind farm. Energy 262, 125342. doi: 10.1016/j.energy.2022.125342

Crossref Full Text | Google Scholar

Xu L., Ou Y., Cai J., Wang J., Fu Y., Bian X. (2023b). Offshore wind speed assessment with statistical and attention-based neural network methods based on STL decomposition. Renew Energ. 216, 119097. doi: 10.1016/j.renene.2023.119097

Crossref Full Text | Google Scholar

Yan B., Shen R., Li K., Wang Z., Yang Q., Zhou X., et al. (2023). Spatio-temporal correlation for simultaneous ultra-short-term wind speed prediction at multiple locations. Energy 284, 128418. doi: 10.1016/j.energy.2023.128418

Crossref Full Text | Google Scholar

Yin J., Wang H., Wang N., Wang X. (2023). An adaptive real-time modular tidal level prediction mechanism based on EMD and Lipschitz quotients method. Ocean Eng. 289, 116297. doi: 10.1016/j.oceaneng.2023.116297

Crossref Full Text | Google Scholar

Yu C., Yan G., Yu C., Mi X. (2023). Attention mechanism is useful in spatio-temporal wind speed prediction: Evidence from China. Appl. Soft Comput. 148, 110864. doi: 10.1016/j.asoc.2023.110864

Crossref Full Text | Google Scholar

Yuan Q., Wang S., Zhao J., Hsieh T. H., Sun Z., Liu B. (2022). Uncertainty-informed ship voyage optimization approach for exploiting safety, energy saving and low carbon routes. Ocean Eng. 266, 112887. doi: 10.1016/j.oceaneng.2022.112887

Crossref Full Text | Google Scholar

Zhang Z., Lin L., Gao S., Wang J., Zhao H. (2024a). Wind speed prediction in China with fully-convolutional deep neural network. RENEW SUST ENERG Rev. 201, 114623. doi: 10.1016/j.rser.2024.114623

Crossref Full Text | Google Scholar

Zhang C., Tao Z., Xiong J., Qian S., Fu Y., Ji J., et al. (2024b). Research and application of a novel weight-based evolutionary ensemble model using principal component analysis for wind power prediction. Renew Energ. 232, 121085. doi: 10.1016/j.renene.2024.121085

Crossref Full Text | Google Scholar

Zhang Z., Wagner S., Klockmann M., Zorita E. (2022). Evaluation of statistical climate reconstruction methods based on pseudoproxy experiments using linear and machine-learning methods. Clim Past. 18, 2643–2668. doi: 10.5194/cp-18-2643-2022

Crossref Full Text | Google Scholar

Zhao Q., Peng S., Wang J., Li S., Hou Z., Zhong G. (2024). Applications of deep learning in physical oceanography: a comprehensive review. Front. Mar. Sci. 11. doi: 10.3389/fmars.2024.1396322

Crossref Full Text | Google Scholar

Zhou Y., Kang X., Ren F., Lu H., Nakagawa S., Shan X. (2024). A multi-attention and depthwise separable convolution network for medical image segmentation. Neurocomputing 564, 126970. doi: 10.1016/j.neucom.2023.126970

Crossref Full Text | Google Scholar

Zhou P., Zhou Z., Wang Y., Wang H. (2023). Ship weather routing based on hybrid genetic algorithm under complicated sea conditions. J. Ocean Univ. China 22, 28–42. doi: 10.1007/s11802-023-5002-1

Crossref Full Text | Google Scholar

Zhu M., Kong M., Wen Y., Gu S., Xue B., Huang T. (2025a). A multi-objective path planning method for ships based on constrained policy optimization. Ocean Eng. 319, 120165. doi: 10.1016/j.oceaneng.2024.120165

Crossref Full Text | Google Scholar

Zhu J., Shen H., Tang Q., Qin Z., Yu Y. (2025b). Energy-efficient route planning method for ships based on level set. Sensors. 25, 381. doi: 10.3390/s25020381

PubMed Abstract | Crossref Full Text | Google Scholar

Zis T. P., Psaraftis H. N., Ding L. (2020). Ship weather routing: A taxonomy and survey. Ocean Eng. 213, 107697. doi: 10.1016/j.oceaneng.2020.107697

Crossref Full Text | Google Scholar