Research on ocean buoy attitude prediction model based on multi-dimensional feature fusion

Buoys, serving as crucial platforms for ocean observation, require precise predictions of their motion states, which are essential for buoy structure design, testing, and directly related to the stability and reliability of data collection. Leveraging data-driven methods instead of traditional software modeling analysis enables efficient analysis of the ocean environment’s impact on buoys. However, the coupling mechanisms between the ocean and the atmosphere complicate the pre-diction of buoy attitudes. In response to these challenges, this paper systematically analyzes the key ocean surface elements that affect buoy attitudes and innovatively applies the Pearson correlation coefficient to quantify the potential coupling relationships between these elements. The Recursive Feature Elimination with Cross-Validation (RFECV) algorithm is employed to select the optimal feature subset from a large number of raw features. Based on this, a Convolutional Neural Networks-Bidirectional Gated Recurrent Unit (CNN-BiGRU) buoy attitude prediction model is constructed. Experimental results demonstrate that the optimized prediction model, when combined with the feature selection algorithm, achieves a minimum prediction accuracy of 95.7%. This model not only reduces the dimensionality of the original data but also precisely captures the dynamics of ocean elements and their effects on buoy attitudes, leveraging the powerful feature extraction and fusion capabilities of CNN.

1 Introduction

With the continuous development of global ocean observation technologies, real-time monitoring data of sea surface elements (such as wind fields, sea waves, and ocean currents) have become increasingly abundant. These data are of great significance for understanding ocean environmental dynamics, predicting meteorological changes, ensuring maritime safety, and promoting the sustainable utilization of marine resources (Wang et al., 2016; Li and Wang, 2023). As a key platform in the ocean observation system, buoys are undeniably important. However, given that buoys are located at the complex interface of ocean-atmosphere interaction, their motion attitudes are deeply influenced by the coupling effects of oceanic and atmospheric dynamic processes, exhibiting a high degree of complexity, dynamics, and irregularity. Therefore, an in-depth exploration of the mechanism by which ocean environmental parameters influence buoy motion response has become an urgent need to enhance the understanding of ocean dynamic processes, optimize ocean observation strategies, strengthen meteorological forecasting capabilities, ensure the safety of marine engineering, and promote environmental protection (Xu et al., 2019; Jin et al., 2022). This exploration can also help us scientifically plan the layout of ocean observation stations, optimize the design and data collection strategies of buoys, and thereby improve the accuracy and efficiency of ocean observation, laying a solid foundation for marine scientific research.

In existing research, the methods for buoy attitude prediction can be mainly categorized into: (a) physics-based modeling approaches (Le Cunff et al., 2007; Ma et al., 2016; Zhu and Yoo, 2016; Yang et al., 2020; Chen et al., 2022; Zheng et al., 2024) and (b) data-driven methods (Li and Bian, 2021; Deng et al., 2022). The physics-based modeling approaches primarily utilize tools such as ANSYS (Wang et al., 2024), STARCCM+ (Li et al., 2023), and OpenFOAM (Jiang et al., 2021) to construct physical models of buoys, encompassing geometry, materials, boundary conditions (e.g., external forces like currents, waves, wind), and possible constraints to simulate the dynamic behavior of buoys in marine environments. However, for equipment situated in harsh and variable environments, it is often challenging to establish relatively accurate model systems, facing issues such as model simplification, complex mesh generation, high professional requirements, significant computational demands, and data sensitivity. In contrast, data-driven prediction methods focus on utilizing actual operational historical data of buoys to establish prediction models through data analysis, machine learning, or deep learning techniques to forecast future buoy attitudes (e.g., pitch, roll, heave). These methods do not require a deep understanding of the complex physical mechanisms within buoys but instead construct prediction models based on correlations and statistical laws among data, offering high flexibility and adaptability, minimal reliance on experience, and strong capabilities in handling nonlinear relationships. Among them, the Least Squares Support Vector Regression (LSSVR) model proposed by Li et al. (Li and Bian, 2021) provides a new perspective for predicting buoy motion characteristics. This model captures buoy motion characteristics under different conditions, providing crucial information for marine environmental monitoring and early warning. Furthermore, Deng et al. (Deng et al., 2022) utilized transfer learning to integrate in-formation data under different conditions, enhancing the prediction performance of marine buoy motion characteristics and offering a new perspective for marine scientific re-search. Therefore, a data-driven buoy attitude prediction method is undoubtedly a better choice.

However, current prediction methods for buoy attitudes have not analyzed the coupling relationship between buoy attitudes and various marine environmental factors. The motion characteristics of buoys are primarily influenced by multiple marine environmental factors such as wind speed, waves, and ocean currents. Generally speaking, utilizing multiple marine observation parameters as inputs ensures data diversity, which helps improve prediction accuracy. However, these parameters may contain redundancies or have low correlation with buoy attitudes. If they are directly used as inputs for the prediction model, it will not only increase the number of parameters in the prediction algorithm, affecting calculation speed, but may also reduce prediction accuracy. Therefore, in the face of multiple ocean surface parameter data, feature selection becomes crucial for enhancing prediction accuracy.

Feature selection is a data preprocessing method to eliminate irrelevant subsets (Jović et al., 2015), which is generally divided into four types: filter methods, wrapper methods, embedded methods, and hybrid methods (Chandrashekar and Sahin, 2014). Filter methods (Sánchez-Maroño et al., 2007) are based on the statistical proper-ties or information theory indicators of the data itself, such as Pearson correlation coefficient, chi-square test, mutual information, etc., to evaluate the correlation or importance between features and target variables, and quickly screen features. However, it may ignore the relationship between features, leading to the selection of redundant features. Wrapper methods (El Aboudi and Benhlima, 2016) evaluate the contribution of feature subsets to model performance through optimization algorithms (such as recursive feature elimination (Liang et al., 2023), genetic algorithm ( (Oh et al., 2004), etc.) to select the optimal feature subset. It considers the interaction between features and has high accuracy but complex calculations. It is suitable for scenarios with high requirements for model performance, such as buoy attitude prediction. Embedded methods (Boroujeni et al., 2017) integrate feature selection with model training and simultaneously select features and train models through the objective function of optimization algorithms, such as L1 regularization, decision trees, and random forests (Genuer et al., 2010). They have high computational efficiency but may contain features that are less correlated with target variables but have an indirect impact on model performance. It can be seen that the wrapper method and the filter method complement each other. The filter-based method can efficiently and quickly search the feature space, but the evaluation bias of subsequent learning tasks is large; while the wrapper-based method has better accuracy but slower search speed. Therefore, the hybrid method of the filter method and the wrapper method (Chen et al., 2020; Hu et al., 2020; Mandal et al., 2021) is widely used to ensure accuracy and reduce computational complexity. Given that buoy attitudes are affected by various complex marine environmental factors, this paper adopts a fused feature selection method.

In summary, data-driven prediction methods, especially those combined with feature selection algorithms (Farhangi et al., 2023; Wei et al., 2023; Liu et al., 2024), can fully utilize the implicit information in ocean surface parameter data. However, there can also be coupling effects among various marine environments. Therefore, the prediction model first needs to integrate multiple marine observation parameters and extract their coupling effects on buoy attitudes. The CNN-BiGRU network model, as an integrated architecture that combines Convolutional Neural Networks (CNN) and Bidirectional Gated Recurrent Units (BiGRU) (Liu et al., 2022), can effectively capture complex nonlinear relationships in both spatial and temporal dimensions. Through the powerful feature extraction capabilities of CNN, high-level spatial features can be identified, while BiGRU excels in processing time series data, capable of deeply mining dynamic patterns in the temporal dimension.

In view of this, this article aims to use feature selection algorithms to deeply analyze the coupling characteristics of sea surface elements to improve the accuracy and efficiency of buoy attitude prediction. Specifically, this paper first builds an experimental platform to collect and process various sea surface elements and buoy attitude data, and then uses advanced feature selection algorithms to screen out the feature subsets that have the greatest impact on buoy attitude prediction. On this basis, the interaction relationship between these features is further analyzed, and a buoy attitude prediction model based on feature selection algorithm is constructed. Finally, the prediction performance of the model is verified through experiments.

The rest of the article is structured as follows. Section 2 introduces the principles of the model and its algorithm implementation in detail. Section 3 presents the experimental data. In addition, the data characteristics are discussed to determine the appropriate modeling method. Section 4 applies Pearson correlation coefficient and RFECV to analyze the correlation of features and select the optimal feature subset. CNN-BiGRU is used to predict buoy motion characteristics. The prediction results are compared with existing prediction models, demonstrating the advantages of the proposed model in this paper. Finally, Section 5 summarizes related work.

2 Methods

2.1 Feature selection

To enhance the accuracy of buoy attitude information prediction, it is first necessary to employ feature selection methods to deeply analyze the interaction between sea surface environmental parameters and buoy attitude. In this study, we initially utilize the Pearson correlation coefficient to conduct a preliminary analysis of the correlations among environmental parameters, with the aim of eliminating some irrelevant or weakly correlated features. Subsequently, the RFECV method of random forest (RF) is adopted to further optimize the feature set. By constructing a random forest model, a mapping relationship between environmental features and buoy attitude targets is established. The model is repeatedly trained to evaluate the importance of each feature, and those with lesser contributions to prediction are recursively eliminated.

2.1.1 Pearson correlation coefficient

The Pearson correlation coefficient (Liu et al., 2020) is a widely used statistical method for accurately measuring the degree of linear correlation between two variables. Its value ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no linear relationship between the two variables. The closer the absolute value of the Pearson Correlation Coefficient is to 1, the stronger the linear relationship between the two variables. Its calculation principle is based on covariance and standard deviation, with the specific formula as Equation 1:

$\begin{array}{ll}r=\frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_{i=1}^n{(X_i-\overline{X})}^2{(Y_i-\overline{Y})}^2}}& (1)\end{array}$

In the formula: r represents the correlation coefficient, X represents the main index, and Y represents the characteristic value.

2.1.2 Recursive feature elimination with cross-validation

The RFECV algorithm (Liang et al., 2023) is an automated feature selection technique that integrates the advantages of Recursive Feature Elimination (RFE) and Cross-Validation (CV). The algorithm first initiates the RFE process, which gradually optimizes the feature set by con-structing a model, evaluating feature importance, and iteratively removing the least important features until a predetermined performance peak is reached or a specific stopping condition is met. Subsequently, RFECV utilizes a cross-validation strategy to comprehensively evaluate each feature subset ranked by RFE, ensuring that the selected feature subset maintains stable predictive performance across different data subsets. In each fold of cross-validation, RFECV employs a Random Forest model as the base learner to fit the currently considered feature subset and calculate the cross-validation score of the model on that fold of data. By synthesizing the scores from all folds, RFECV is able to identify the optimal feature subset that performs best across the entire dataset. This process is illustrated in Figure 1, which briefly depicts the complete flow from the full feature set, through RFE ranking and cross-validation screening, to the final determination of the optimal feature subset. Starting with all features, in each iteration, the least important feature is removed based on the performance of the estimator (Random Forest, RF) on the cross-validation set. After each step of feature selection, cross-validation (cv=5, indicating 5-fold cross-validation) is employed to evaluate the performance of the current feature subset. Here, Mean Squared Error (MSE) is used as the performance criterion, meaning that the goal is to maximize the negative of the mean squared error (i.e., to minimize the mean squared error). RFECV continues to remove features until a stopping criterion is met. For RFECV, this stopping criterion is based on cross-validation scores. Specifically, it selects the feature subset with the highest average score during the cross-validation process. Once a feature subset fails to improve the average cross-validation score in subsequent feature removals, RFECV stops further feature removal and returns this optimal feature subset.

Figure 1

Figure 1. Flowchart of RFECV feature selection.

2.2 Convolutional neural networks- bidirectional gated recurrent unit

In this paper, a 1D- CNN is employed to extract the overall characteristics of the input features. The BiGRU method is adopted to extract the correlations among the input features. The overall structure of the proposed hybrid model network is shown in Figure 2, and the model parameter design is presented in Table 1 (the parameter settings were selected based on optimal values obtained through multiple experimental comparisons). Firstly, the feature subset after feature selection is used as input, and the CNN is utilized to extract the correlations among features, fusing multiple features to better learn the coupling characteristics among them. Then, the extracted features are input into the BiGRU to extract sequential features, thereby enhancing the effect of regression prediction. Finally, the forward and backward outputs are merged and outputted. CNN-BiGRU (Song et al., 2024) can effectively extract both local and global feature information.

Figure 2

Figure 2. The architecture of CNN-BiGRU model.

Table 1

Table 1. Model parameter setting.

The primary objective of CNN is to extract salient features from input data. A typical CNN architecture comprises several layers, namely convolutional, pooling, and fully connected layers. Convolutional layers play a vital role in feature extraction, where convolutional kernels capture relevant features from the input data. The level of abstraction of the extracted features increases with the number of convolutional kernels used. The fully connected layers flatten the pooled neurons into a one-dimensional vector form, facilitating more manageable data processing. However, CNNs are ineffective in capturing the temporal dependencies of time-series data for predictive tasks. Therefore, it is essential to integrate recurrent neural network techniques and combine CNNs with BiGRU networks to enhance performance.

GRU (Busari and Lim, 2021) is a type of recurrent neural network model commonly used for processing sequential data, which can better address long-term dependency issues. Compared to traditional recurrent neural networks, GRU introduces a gating mechanism that enables it to learn effectively to retain or forget information in the sequence. GRU incorporates two gating mechanisms: the update gate and the reset gate. The update gate controls how much past information to retain, thereby addressing the issue of gradient vanishing; the reset gate helps the network determine how much past information to ignore, facilitating the processing of short-term dependencies. The computational formulas for each GRU gating unit are shown in (Equations 2–5):

$\begin{array}{ll}{r}_t=\sigma (W_r{x}_t+U_r{h}_{t-1})& (2)\end{array}$

$\begin{array}{ll}{z}_t=\sigma (W_z{x}_t+U_z{h}_{t-1})& (3)\end{array}$

$\begin{array}{ll}{\tilde{h}}_t=tanh(W_h{x}_t+U_h(r_t\odot h_{t-1}))& (4)\end{array}$

$\begin{array}{ll}{h}_t=z_t\odot {\tilde{h}}_t+(1-z_t)\odot h_{t-1}& (5)\end{array}$

In the above equations, $x_t$ represents the input to the hidden layer at time $t$; $h_t$ is the output of the current layer at time $t$; $r_t$ and $z_t$ represent the reset gate and update gate, respectively; ${\tilde{h}}_t$ is the candidate memory unit at time $t$; $W_r$ and $U_r$ are the weight coefficients for the update gate; $W_z$ and $U_r$ are the weight coefficients for the reset gate; $\sigma$ refers to both the sigmoid activation function and the hyperbolic tangent function. As a unidirectional recurrent neural network structure, GRU typically propagates states in a forward direction. However, BiGRU consists of two GRU models with opposite directions, enabling it to more comprehensively capture global information and long-term dependencies within the time series.

2.3 The prediction process of buoy attitude

This study has constructed a systematic and comprehensive methodological frame-work, which covers four core links. It aims to deeply explore the complex relationship between sea surface elements and buoy attitude, and design an ap-propriate buoy attitude prediction model based on the coupling relationship between the two. The specific research process and methodology system are described as follows:

1. Data collection and preprocessing stage. This stage focuses on the construction of a high-quality dataset. Firstly, diversified sea surface element data were comprehensively collected from the buoy system, including but not limited to key parameters such as wind speed, wind direction, wave height, wave direction, sea water temperature, and ocean current speed. To ensure the validity of the data, a strict data synchronization strategy was implemented to ensure precise matching between buoy attitude data and sea surface element data in terms of time and space dimensions, laying a solid foundation for subsequent analysis. Subsequently, through a meticulous data cleaning process, outliers and missing values were effectively eliminated, and scientific interpolation methods were used to fill data gaps, ensuring the completeness and accuracy of the dataset. In addition, according to research needs, the original data was further converted and derived, extracting new features and statis-tics, enriching the dimensions and depth of the dataset.

2. The design and application stage of feature selection algorithms. To extract the most critical subset of features from massive data for predicting buoy attitude, an efficient feature selection algorithm was designed. Firstly, Pearson correlation coefficient was used to conduct a correlation analysis, initially screening out sea surface element features that are highly correlated with buoy attitude. Then, the RFECV method based on RF was employed to deeply quantify the impact of each feature on the performance of the prediction model, further refining the optimal feature combination. Additionally, feature redundancy analysis was performed to effectively avoid the problem of model overfitting caused by high correlations between features.

3. Coupling characteristic analysis and modeling stage. After identifying the key features, the focus shifts to the coupling mechanisms between sea surface elements and their combined influence on buoy attitude. Through data-driven methods, the interaction relationships between various elements are deeply analyzed, revealing the com-plex pathways through which they jointly affect buoy attitude. Based on these in-sights, a machine learning model that can accurately reflect the coupling characteristics of sea surface elements is constructed, providing a powerful tool for precise pre-diction of buoy attitude.

4. Experimental design and result analysis stage. To ensure a comprehensive evaluation of model performance, an elaborate experimental scheme was designed. The predictive capability of the model was systematically tested through reasonable partitioning of training and testing sets, implementation of cross-validation strategies, and arrangement of comparative experiments. During the evaluation process, several widely recognized performance metrics, such as Root Mean Square Error (RMSE) and Mean Absolute Error (MAE), were selected to quantify the prediction accuracy and generalization ability of the model in multiple dimensions. Ultimately, through in-depth analysis of the experimental results, not only the specific contribution of different features to the prediction outcomes was revealed, but also valuable insights were provided for subsequent model optimization and application promotion. The equations should be inserted in editable format from the equation editor.

2.4 Evaluation criteria

This paper uses three of the most commonly used metrics to evaluate the performance of the model: MAE, RMSE, and Coefficient of Determination (R²). The specific calculation formulas for these metrics are shown in (Equations 6-8):

$\begin{array}{ll}MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\widehat{y}}_i| & (6)\end{array}$

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}\sum _{i=1}^n\mid y_i-{\widehat{y}}_i{\mid }^2}& (7)\end{array}$

$\begin{array}{ll}{R}^2=1-\frac{{\sum }_{i=0}^n{(y_i-{\widehat{y}}_i)}^2}{{\sum }_{i=0}^n{(y_i-{\overline{y}}_i)}^2}& (8)\end{array}$

Where, n is the total number of samples; $y_i$ is the actual value at sample point $i$; and ${\widehat{y}}_i$ is the predicted value at sample point $i$.

3 Experimental data description and analysis

Based on the “Bailong” buoy (Yuan et al., 2023), this study designed a buoy system equipped with a data acquisition device to collect real-time parameters related to the buoy’s in-situ operation. The buoy body is made of foam with a diameter of 2.3m, weighing 750kg, has a submergence depth of 0.56m, and a tower height of 2.3m. The buoy employs an r-type mooring system and is equipped with meteorological sensors, current meters, wave sensors (Zhou et al., 2022), attitude sensors, and a data acquisition controller. The sampling period for the wave sensor is 10 minutes, the sampling frequency for the attitude sensor is 4Hz, and the sampling frequency for all other sensors is 1Hz. Powered by solar panels and lead-acid batteries, the data is transmitted via 4G and periodically returned to the data receiving center for storage, analysis, display, and upload. The experimental buoys is illustrated in Figure 3. Figure 3A shows the deployment process of the buoy and the scene after deployment. Figure 3B displays the structural layout of the buoy, as well as the relative positions and installation heights of the load sensors, and provides the model of each sensor.

Figure 3

Figure 3. Experimental buoys (A) Deployment scenarios, (B) Mounted equipment.

The buoy’s measured working dataset used in this paper was collected from the National Deep-Sea Base Management Center from 16:30, November 10, 2023 to 07:10, November 21, 2023, and from 00:30, November 22, 2023 to 09:40, December 12, 2023. Given that the sampling frequency of wave data is 10 minutes, the overall feature data was grouped and processed accordingly to this time interval, i.e., the data from every 10 minutes was considered as an independent unit. After statistical analysis of these grouped data, a total of 4321 sets of valid data were screened out. After the data collection was completed, 30 key environmental information features were identified and recorded, and their corresponding abbreviations are detailed in Table 2.

Table 2

Table 2. Environmental parameter characteristics and abbreviations.

During the data preprocessing stage, the first step involved checking the data for errors, missing or abnormal values, and deleting incomplete or corrupted data. Interpolation methods were used to estimate missing values. Secondly, to eliminate the dimensional differences among various feature variables, all features were normalized. In particular, given the high symmetry of the buoy structure, this study focuses on predicting the pitch, roll, and heave characteristics of the buoy. Furthermore, due to the high symmetry exhibited by the pitch, roll, and heave characteristics of the buoy at troughs and peaks (as shown in Figure 4), the mean absolute value and trough mean of each set of attitude data were calculated as target features (refer to Equations 9, 10 for specifics). The statistical values of the overall data after processing are presented in Table 3.

Figure 4

Figure 4. Diagram of symmetry in Pitch feature valleys and peaks.

Table 3

Table 3. Dataset statistical information.

$\begin{array}{ll}valleymean=\frac{{\sum }_{i=1}^{n}valle{y}_i}{n}& (9)\end{array}$

$\begin{array}{ll}absmean=\frac{{\sum }_{i=1}^n\left|ab{s}_i\right|}{n}& (10)\end{array}$

In the above formula, $n$ refers to the total number of samples in 10-minute data.

4 Results and discussion

4.1 The result of feature selection

This study first adopts the Pearson correlation coefficient as a quantitative indicator to analyze the influence of sea surface environmental factors on the motion attitude of buoys. As one of the most direct forces, waves directly lead to periodic vertical lifting, horizontal shaking, and even rotational motion of buoys due to changes in their frequency and intensity. This not only tests the stability of the buoy but also directly affects the accuracy of the observed data. Figure 5 shows the correlation analysis results between wave parameters and buoy attitudes. The analysis results show that there is a significant linear correlation between wave period, wave height, D_mean, and attitude characteristics. However, the linear correlation between D_main, D_p, MaxDirSpec, and attitude parameters is very small. Moreover, the correlation coefficients between H_max, H_avr, H_1/3, H_m0, H_{avr_s}, and the six attitude characteristics are basically the same, and they are positively correlated with Abs_Pitch, Abs_Roll, Abs_Heave, and negatively correlated with Valley_Pitch, Valley_Roll, Valley_Heave. The correlation coefficients between T_max, T_avr, T_1/3, T_P, T_{avr_s}, and the six attitude characteristics are also basically the same, and they are negatively correlated with Abs_Pitch, Abs_Roll, Abs_Heave, and positively correlated with Valley_Pitch, Valley_Roll, Valley_Heave. In other words, the larger the wave height, the greater the amplitude of the attitude characteristics; the larger the wave period, the smaller the attitude amplitude. F_p also shows a moderate correlation with attitude parameters. Considering that there is a strong correlation among H_max, H_avr, H_1/3, H_m0, and H_{avr_s}, to eliminate feature redundancy and reduce the dimension of input features, only one of these five features needs to be selected. Similarly, only one feature needs to be selected from T_max, T_avr, T_1/3, T_P, and T_{avr_s}. Based on the above analysis, D_mean, F_p, wave height, and wave period are selected as the four features among the various wave parameters.

Figure 5

Figure 5. Pearson correlation analysis between wave parameters and buoy attitudes.

Meanwhile, ocean currents, with their continuous pushing or dragging, subtly alter the horizontal position of buoys, especially in strong current areas, potentially exacerbating their attitude instability and increasing the difficulty of observation. The impact of changes in wind speed and direction on buoys cannot be overlooked. Strong winds not only increase the aerodynamic load above the buoy, causing it to tilt or deviate, but they may also indirectly affect the water flow conditions below the buoy through wind shear and turbulence, further complicating its dynamic response. Changes in wind direction may also affect the relative angle between the buoy and the mooring system, increasing the tension variation in the mooring lines. Additionally, changes in rainfall, long and short-wave radiation, sea surface temperature, and atmospheric pressure can also indirectly affect the attitude of the buoy. Therefore, this study utilizes the Pearson correlation coefficient to analyze the correlation between hydrological and meteorological characteristics and buoy attitude parameters. As shown in Figure 6, which depicts the correlation analysis results between hydrological and meteorological data and buoy attitudes, features with a correlation coefficient greater than 0.2 are selected for the study. Among them, CD, WS, R, and SST exhibit low correlation, WD, AT, AP, and LR show moderate correlation, WP demonstrates strong correlation, and CV displays an extremely strong correlation.

Figure 6

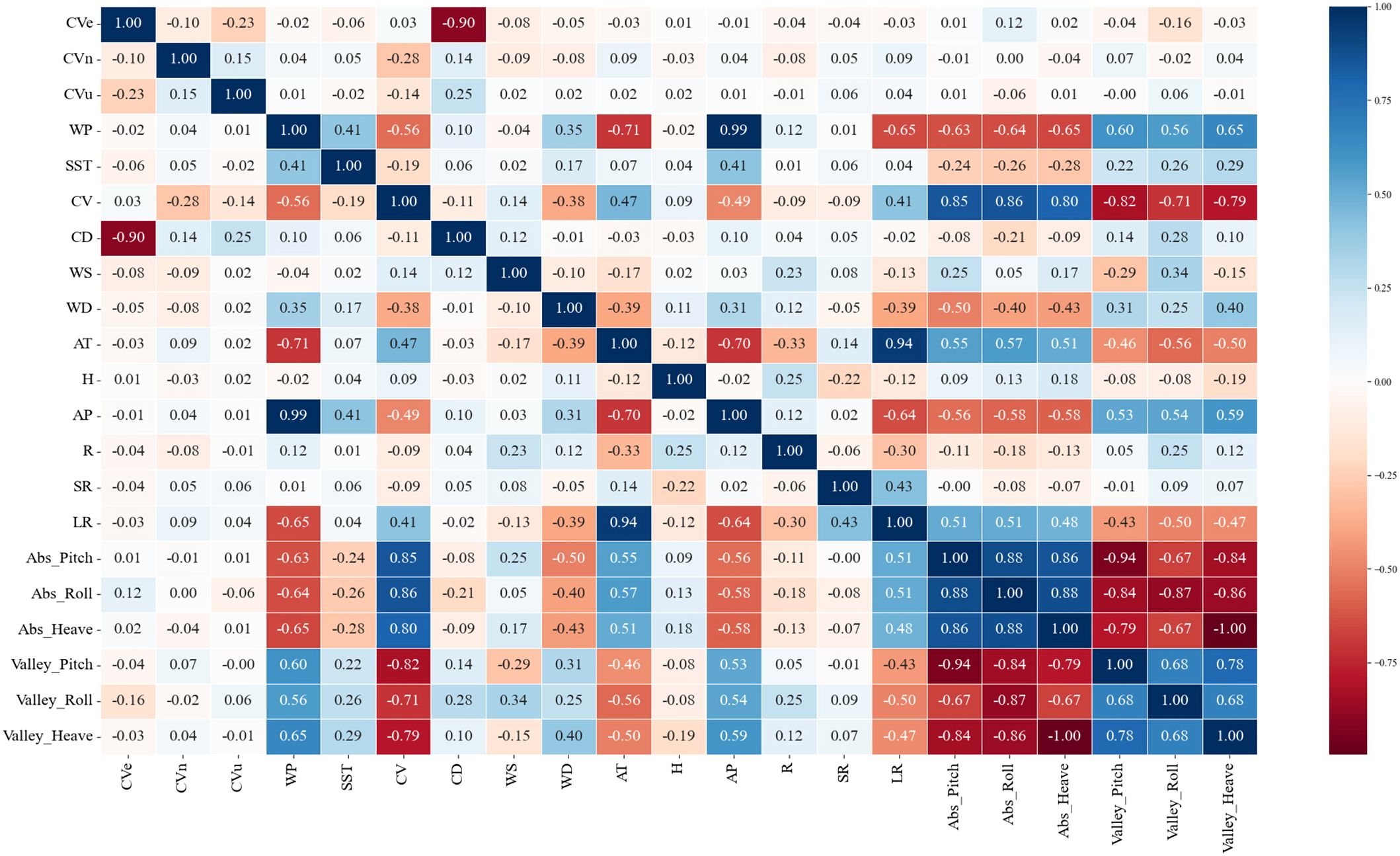
Figure 6. Pearson correlation analysis between hydrological and meteorological parameters and buoy attitudes.

In summary, the initial screening using the Pearson correlation coefficient reduced the number of features from 30 to 14, specifically: D_mean, F_p, wave height, wave period, CD, WS, R, SST, WD, AT, AP, LR, WP, and CV.

After the initial assessment of feature relevance using the Pearson correlation coefficient, the RFECV method with RF as the underlying estimator was further employed to refine the feature selection. By inputting environmental parameters and predicting attitude parameters, the optimal feature subset was identified through multiple iterative experiments based on the average frequency of feature occurrence across experiments, resulting in a selection of 14 features. As depicted in Figure 7, the scores of these features reflect their importance. Notably, the selection of wave parameters H_{avr_s} and T_{avr_s} is highly consistent with the previous filter-based feature selection results, demonstrating the complementarity of these two methods in identifying key wave characteristics. However, unlike the filter-based approach, RFECV, as a wrapper feature selection method, additionally selected CV_n and CV_e, which showed lower correlation with attitude features in the initial correlation analysis. To delve into the actual contributions of these two features, two sets of comparative experiments were designed: one using 12 features excluding CV_n and CV_e, and the other utilizing all 14 features selected by RFECV. Both sets were employed for attitude prediction through the CNN-BiGRU model. The experimental results, as presented in Table 4, clearly indicate that the model with 14 features, including CV_n and CV_e, significantly outperforms the model using only 12 features, strongly justifying the necessity of CV_n and CV_e in enhancing the predictive capability of the model. In summary, the final set of features selected for this study is: CV, WS, WD, R, CD, H_{avr_s}, SST, WP, LR, T_{avr_s}, AT, CV_n, CV_e, and AP. This feature set provides comprehensive and effective input for the subsequent attitude prediction model.

Figure 7

Figure 7. Scores of selected features.

Table 4

Table 4. Analysis table of the impact of CVn and CVe features.

4.2 Ablation experiment

In this section, an initial evaluation of the model’s effectiveness is conducted, comparing the performance of GRU, BiGRU, and CNN-BiGRU through ablation experiments. As shown in Table 5, the ablation experiment results clearly demonstrate the significant advantages of CNN-BiGRU. The specific data are as follows: compared to the GRU and BiGRU models, the CNN-BiGRU model achieves significant error reductions across multiple key evaluation metrics. Specifically, in terms of the RMSE evaluation for Abs_Heave, CNN-BiGRU reduces errors by 4.65% and 2.38% respectively compared to GRU and BiGRU. For Abs_Pitch, the RMSE reduction is even more pronounced, achieving reductions of 16.44% and 12.84% respectively. Similarly, the RMSE for Abs_Roll also experiences a noticeable decrease, with reductions of 14.54% and 19.51% respectively. In the Valley series of metrics, CNN-BiGRU also performs exceptionally well. For example, the RMSE for Valley_Heave is reduced by 9.68% and 6.67% compared to GRU and BiGRU, respectively. Similarly, significant reductions are also observed in the RMSE of Valley_Pitch and Valley_Roll, with decreases of 9.89%, 5.88%, 15.84%, and 21.46% respectively.

Table 5

Table 5. Ablation experiment results.

Upon further examination of the MAE metrics, the CNN-BiGRU model continues to demonstrate its superiority. In terms of the MAE for Abs_Heave, compared to GRU and BiGRU, the reduction percentages are 3.7% and 0% respectively (remaining at par with BiGRU without any regression). For Abs_Pitch and Abs_Roll, the MAE reductions are even more significant, with decreases of 14.08%, 10.2%, 17.99%, and 23.51% respectively. In the Valley series, CNN-BiGRU also achieves notable reductions in MAE. Specifically, the MAE for Valley_Heave, Valley_Pitch, and Valley_Roll decreases by 10.26%, 5.4%, 7.5%, 4.48%, 18.28%, and 26.41% respectively.

The results presented above showcase the unique advantages of CNN-BiGRU, which are primarily attributed to the integration of the dual strengths of CNN and BiGRU. The CNN layer, with its exceptional ability in local feature extraction, effectively mines and enhances key information from the input data, providing a richer and more meaningful data foundation for the subsequent BiGRU layer. The BiGRU layer, on the other hand, leverages its unique bidirectional structure to not only capture the forward dependencies within the sequence but also incorporate backward information, enabling a comprehensive understanding of the contextual relationships within the sequence. This deeply integrated design allows the CNN-BiGRU model to more accurately capture key information when processing complex sequential data, thereby demonstrating superior performance in tasks such as prediction and classification.

4.3 Comparison of different prediction models

To further validate the predictive performance of the CNN-BiGRU model, a comparative analysis was conducted using models such as LSSVR, ELM, Bagging, XGBoost, BiLSTM, and CNN-BiLSTM. The training and testing sets remained consistent with those used for the CNN-BiGRU model, and the evaluation metrics for the prediction results of each model were compared to assess their accuracy. As shown in Table 6, which summarizes the prediction accuracy of the different models, CNN-BiGRU exhibits the best performance in the prediction task. Compared to LSSVR, ELM, Bagging, XGBoost, BiLSTM, and CNN-BiLSTM, the CNN-BiGRU model achieves the following RMSE reductions for Abs_Heave: 31.67%, 19.61%, 8.89%, 4.65%, 4.65%, and 0% respectively. For Abs_Pitch, the RMSE reductions are 48.97%, 48.87%, 18.12%, 9.61%, 11.36%, and 3.44% respectively. Similarly, for Abs_Roll, the RMSE reductions are 46.7%, 41.44%, 18.37%, 12.95%, 11.11%, and 1.76% respectively. In terms of Valley_Heave, the RMSE reductions are 31.71%, 23.29%, 13.85%, 12.5%, 11.11%, and 6.67% respectively. For Valley_Pitch, the RMSE reductions are 43.73%, 39.56%, 16.74%, 10.43%, 7.04%, and 5.79% respectively. Lastly, for Valley_Roll, the RMSE reductions are 47.08%, 43.66%, 21.8%, 16.07%, 16.59%, and 7.28% respectively. These results indicate that the CNN-BiGRU model significantly outperforms the other comparison models in terms of accuracy and prediction performance, demonstrating its strong capability in handling complex time series prediction tasks. This validates that the CNN-BiGRU model successfully extracts the high-dimensional nonlinear mapping relationships between buoy attitude parameters and environmental parameters.

Table 6

Table 6. Prediction accuracy of different models.

Taking Abs_Roll and Valley_Roll as examples, Figures 8A, B respectively display the scatter plots of prediction results and the fitting equations between predicted and actual values for the various algorithms applied to Abs_Roll and Valley_Roll features. Figure 9 illustrates the comparison curve between the predicted values and the actual values obtained from the CNN-BiGRU model. Combining the error table and the comparison graphs of prediction effects, it becomes clearer that the prediction curve of CNN-BiGRU exhibits a high degree of fitting with the actual characteristic curve, demonstrating a significantly better prediction performance than other models. This observation further validates the superior performance of the CNN-BiGRU model in the field of buoy platform motion attitude prediction.

Figure 8

Figure 8. Fitting conditions of different models (A) Abs_Roll, (B) Valley_Roll.

Figure 9

Figure 9. Comparison of CNN-BiGRU prediction results with actual values.

5 Conclusions

This paper innovatively constructs a buoy attitude variation prediction model based on CNN-BiGRU through an in-depth study of the complex coupling characteristics between ocean environmental factors and moored buoy attitude, using a hybrid strategy of filter-based and wrapper-based feature selection. Firstly, the Pearson coefficient is used to conduct an initial feature correlation analysis, and RFECV is employed to select the optimal feature subset, which serves as the final input feature subset. Subsequently, CNN-BiGRU is leveraged to deeply mine the potential information within these feature parameters, enabling the prediction of moored buoy attitude parameters. The research results demonstrate that the feature selection algorithm plays a pivotal role in optimizing data input and enhancing model prediction accuracy. By screening out the feature subset with the most significant impact on buoy attitude prediction, not only is the consumption of computational resources reduced, but the generalization ability and interpretability of the model are also significantly improved. Furthermore, based on these optimized features, the CNN-BiGRU model constructed using them exhibits higher accuracy and stability in comparative experiments. Specifically, the prediction accuracy for Abs_Heave, Abs_Pitch, Abs_Roll, Valley_Heave, Valley_Pitch, and Valley_Roll reaches 98.67%, 97.87%, 97.45%, 98.59%, 96.67%, and 95.70% respectively, fully validating the core value of feature selection in complex signal prediction tasks and opening up new avenues and methodologies for buoy attitude prediction. Additionally, this paper reveals the intricate coupling relationships among sea surface elements, which are vital for understanding the dynamic impact of the ocean environment on buoy attitude. Through in-depth analysis of these coupling characteristics, valuable reference information is provided for marine scientific research, ocean engineering design, and offshore operation safety.

It should be noted that the current research is limited by the difficulty in obtaining remote ocean environmental parameters and attitude data, and the data volume is relatively limited. Therefore, in future work, we will focus on collecting more diverse and higher-precision ocean data to further enhance the prediction ability of the model under different sea conditions and environmental conditions, and continuously improve the accuracy and reliability of buoy data.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

YL: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft. CN: Conceptualization, Data curation, Formal analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing – original draft, Writing – review & editing. QZ: Methodology, Writing – review & editing. GY: Data curation, Resources, Writing – original draft, Writing – review & editing. CL: Data curation, Resources, Supervision, Writing – original draft.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the National Key Research and Development Program of China (Grant number 2022YFC3104301); Financially supported by Laoshan Laboratory (Grant number LSKJ202201601).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Boroujeni F. R., Stantic B., Wang S. (2017). “An embedded feature selection framework for hybrid data,” in Databases Theory and Applications: 28th Australasian Database Conference, ADC 2017. (Brisbane, Australia: Springer). 138–150. doi: 10.1007/978-3-319-68155-9_11

Crossref Full Text | Google Scholar

Busari G. A., Lim D. H. (2021). Crude oil price prediction: A comparison between AdaBoost-LSTM and AdaBoost-GRU for improving forecasting performance. Comput. Chem. Engineering. 155, 107513. doi: 10.1016/j.compchemeng.2021.107513

Crossref Full Text | Google Scholar

Chandrashekar G., Sahin F. (2014). A survey on feature selection methods. Comput. electrical engineering. 40, 16–28. doi: 10.1016/j.compeleceng.2013.11.024

Crossref Full Text | Google Scholar

Chen C. W., Tsai Y. H., Chang F. R., Lin W. C. (2020). Ensemble feature selection in medical datasets: Combining filter, wrapper, and embedded feature selection results. Expert Systems. 37, e12553. doi: 10.1111/exsy.12553

Crossref Full Text | Google Scholar

Chen X., Liu B., Le G. (2022). Numerical simulation research on the anchor last deployment of marine submersible buoy system based on VOF method. J. Mar. Sci. Eng. 10, 1681. doi: 10.3390/jmse10111681

Crossref Full Text | Google Scholar

Deng H., Li X., Zhu J., Liu Y. (2022). Transfer learning for modeling and prediction of marine buoy motion characteristics. Ocean. Eng. 266, 113158. doi: 10.1016/j.oceaneng.2022.113158

Crossref Full Text | Google Scholar

El Aboudi N., Benhlima L. (2016). “Review on wrapper feature selection approaches,” in 2016 international conference on engineering & MIS (ICEMIS). (Agadir, Morocco: IEEE). 1–5. doi: 10.1109/ICEMIS.2016.7745366

Crossref Full Text | Google Scholar

Farhangi F., Sadeghi-Niaraki A., Safari Bazargani J., Razavi-Termeh S. V., Hussain D., Choi S. M. (2023). Time-series hourly sea surface temperature prediction using deep neural network models. J. Mar. Sci. Eng. 11, 1136. doi: 10.3390/jmse11061136

Crossref Full Text | Google Scholar

Genuer R., Poggi J. M., Tuleau-Malot C. (2010). Variable selection using random forests. Pattern recognition letters. 31, 2225–2236. doi: 10.1007/3-540-35978-8_30

Crossref Full Text | Google Scholar

Hu X., Che Y., Lin X., Onori S. (2020). Battery health prediction using fusion-based feature selection and machine learning. IEEE Trans. Transportation Electrification. 7, 382–398. doi: 10.1109/TTE.2020.3017090

Crossref Full Text | Google Scholar

Jiang C., el Moctar O., Schellin T. E. (2021). Mooring-configurations induced decay motions of a buoy. J. Mar. Sci. Eng. 9, 350. doi: 10.3390/jmse9030350

Crossref Full Text | Google Scholar

Jin Y., Xie K., Liu G., Peng Y., Wan B. (2022). Nonlinear dynamics modeling and analysis of a marine buoy single-point mooring system. Ocean. Eng. 262, 112031. doi: 10.1016/j.oceaneng.2022.112031

Crossref Full Text | Google Scholar

Jović A., Brkić K., Bogunović N. (2015). “A review of feature selection methods with applications,” in 2015 38th international convention on information and communication technology, electronics and microelectronics (MIPRO). (Opatija, Croatia: IEEE). 1200–1205. doi: 10.1109/MIPRO.2015.7160458

Crossref Full Text | Google Scholar

Le Cunff C., Ryu S., Duggal A., Ricbourg C., Heurtier J. M., Heyl C., et al. (2007). “Derivation of CALM buoy coupled motion RAOs in frequency domain and experimental validation,” in ISOPE International Ocean and Polar Engineering Conference, (Lisbon, Portugal: ISOPE). 07–402.

Google Scholar

Li X., Bian Y. (2021). Modeling and prediction for the Buoy motion characteristics. Ocean. Eng. 239, 109880. doi: 10.1016/j.oceaneng.2021.109880

Crossref Full Text | Google Scholar

Li Y., Wang J. (2023). Technical development of operational in-situ marine monitoring and research on its key generic technologies in China. Acta Oceanol. Sin. 42, 117–126. doi: 10.1007/s13131-023-2207-5

Crossref Full Text | Google Scholar

Li Y., Yang F., Li S., Tang X., Sun X., Qi S., et al. (2023). Influence of six-degree-of-freedom motion of a large marine data buoy on wind speed monitoring accuracy. J. Mar. Sci. Eng. 11, 1985. doi: 10.3390/jmse11101985

Crossref Full Text | Google Scholar

Liang H., Wu J., Zhang H., Yang J. (2023). Two-stage short-term power load forecasting based on RFECV feature selection algorithm and a TCN–ECA–LSTM neural network. Energies 16, 1925. doi: 10.3390/en16041925

Crossref Full Text | Google Scholar

Liu B., Gan H., Chen D., Shu Z. (2022). Research on fault early warning of marine diesel engine based on CNN-BiGRU. J. Mar. Sci. Eng. 11, 56. doi: 10.3390/jmse11010056

Crossref Full Text | Google Scholar

Liu Y., Mu Y., Chen K., Li Y., Guo J. (2020). Daily activity feature selection in smart homes based on pearson correlation coefficient. Neural Process. letters. 51, 1771–1787. doi: 10.1007/s11063-019-10185-8

Crossref Full Text | Google Scholar

Liu Y., Wang K., Lu Y., Zhang Y., Li Z., Ma R., et al. (2024). A ship energy consumption prediction method based on TGMA model and feature selection. J. Mar. Sci. Eng. 12, 1098. doi: 10.3390/jmse12071098

Crossref Full Text | Google Scholar

Ma C., Iijima K., Nihei Y., Fujikubo M. (2016). Theoretical, experimental and numerical investigations into nonlinear motion of a tethered-buoy system. J. Mar. Sci. Technol. 21, 396–415. doi: 10.1007/s00773-015-0362-x

Crossref Full Text | Google Scholar

Mandal M., Singh P. K., Ijaz M. F., Shafi J., Sarkar R. (2021). A tri-stage wrapper-filter feature selection framework for disease classification. Sensors 21, 5571. doi: 10.3390/s21165571

PubMed Abstract | Crossref Full Text | Google Scholar

Oh I. S., Lee J. S., Moon B. R. (2004). Hybrid genetic algorithms for feature selection. IEEE Trans. Pattern Anal. Mach. intelligence. 26, 1424–1437. doi: 10.1109/TPAMI.2004.105

PubMed Abstract | Crossref Full Text | Google Scholar

Sánchez-Maroño N., Alonso-Betanzos A., Tombilla-Sanromán M. (2007). “Filter methods for feature selection–a comparative study,” in International Conference on Intelligent Data Engineering and Automated Learning. (Berlin, Heidelberg: Springer). 178–187. doi: 10.1007/978-3-540-77226-2_19

Crossref Full Text | Google Scholar

Song M., Hu W., Liu S., Chen S., Fu X., Zhang J., et al. (2024). Developing an artificial intelligence-based method for predicting the trajectory of surface drifting buoys using a hybrid multi-layer neural network model. J. Mar. Sci. Eng. 12, 958. doi: 10.3390/jmse12060958

Crossref Full Text | Google Scholar

Wang H., Chen J., Feng Z., Du G., Li Y., Tang C., et al. (2024). Development of a mobile buoy with controllable wings: design, dynamics analysis and experiments. J. Mar. Sci. Eng. 12, 150. doi: 10.3390/jmse12010150

Crossref Full Text | Google Scholar

Wang J., Wang Z., Wang Y., Liu S., Li Y. (2016). Current situation and trend of marine data buoy and monitoring network technology of China. Acta Oceanol. Sin. 35, 1–10. doi: 10.1007/s13131-016-0815-z

Crossref Full Text | Google Scholar

Wei Y., Chen Z., Zhao C., Chen X., He J., Zhang C. (2023). A time-varying ensemble model for ship motion prediction based on feature selection and clustering methods. Ocean. Eng. 270, 113659. doi: 10.1016/j.oceaneng.2023.113659

Crossref Full Text | Google Scholar

Xu G., Shi Y., Sun X., Shen W. (2019). Internet of things in marine environment monitoring: A review. Sensors 19, 1711. doi: 10.3390/s19071711

PubMed Abstract | Crossref Full Text | Google Scholar

Yang J., Teng B., Gou Y., Chen L., Jin R. (2020). Half-wave frequency response phenomenon of a tightly moored submerged sphere under monochromatic wave action simulated by using the body-exact approach. Appl. Ocean Res. 103, 102317. doi: 10.1016/j.apor.2020.102317

Crossref Full Text | Google Scholar

Yuan G., Ning C., Liu L., Li C., Liu Y., Sangmanee C., et al. (2023). An automatic internal wave recognition algorithm based on CNN applicable to an ocean data buoy system. J. Mar. Sci. Eng. 11, 2110. doi: 10.3390/jmse11112110

Crossref Full Text | Google Scholar

Zheng H., Chen Y., Liu Q., Zhang Z., Li Y., Li M. (2024). Theoretical and numerical analysis of ocean buoy stability using simplified stability parameters. J. Mar. Sci. Eng. 12, 966. doi: 10.3390/jmse12060966

Crossref Full Text | Google Scholar

Zhou F., Zhang R., Zhang S. (2022). Measurement principle and technology of miniaturized strapdown inertial wave sensor. Front. Mar. Sci. 9. doi: 10.3389/fmars.2022.991996

Crossref Full Text | Google Scholar

Zhu X., Yoo W. S. (2016). Dynamic analysis of a floating spherical buoy fastened by mooring cables. Ocean. Eng. 121, 462–471. doi: 10.1016/j.oceaneng.2016.06.009

Crossref Full Text | Google Scholar