- 1Frontier Science Center for Deep Ocean Multispheres and Earth System (FDOMES), and Key Laboratory of Physical Oceanography, Ministry of Education, Ocean University of China, Qingdao, China
- 2College of Oceanic and Atmospheric Sciences, Ocean University of China, Qingdao, China
- 3College of Marine Geosciences, Ocean University of China, Qingdao, China
- 4The First Exploration Team of Shandong Coalfield Geologic Bureau, Qingdao, China
- 5Laoshan Laboratory, Qingdao, China
- 6Key Laboratory of Ocean Space Resource Management Technology, MNR, Hangzhou, China
- 7Qingdao Meteorological Bureau, Qingdao, China
Stricter controls on destructive human activities in recent years have improved the protection and management of sandy coasts in China. Marine-driven geomorphic changes have become the predominant process influencing future beach evolution. However, in the complex geomorphic conditions of mixed artificial and natural coastlines, the mechanisms and contributions of various marine-driven factors to beach changes remain unclear. Using methods of field observations and numerical simulations by FVCOM model, this study reveals the sedimentary dynamic mechanism of straight sandy beach in the southern Shandong Peninsula (Wanpingkou beach, WPK beach). From 2005 to 2016, the northern section of WPK Beach eroded at a rate of approximately 2-3 m/year, the middle section at about 0.5-1.5 m/year, and the southern section accrued at an average rate of about 1-2 m/year, demonstrating an overall pattern of “northern erosion and southern accretion.” During winter, the average grain size of beach sediments is about 0.5 mm with minimal variations, indicating an onshore transport trend; in summer, the average grain size is about 0.7 mm with larger variations, indicating an offshore transport trend. Offshore sediment transport correlates mainly with seasonal changes in wind direction, while alongshore sediment transport is influenced by tidal currents, wind-induced currents, and wave-induced currents. Wave-induced currents are the primary force in alongshore sediment transport with a velocity of 0.1-0.3 m/s toward southwest. Followed by tidal currents with a velocity of 0.05-0.1 m/s, and wind-induced currents with a velocity of 0-0.1 m/s, which have a relatively minor impact. Therefore, seasonal changes in beach morphology are primarily controlled by waves, while interannual variations is mainly influenced by a combination of wave-induced currents and tidal currents. With increasing efforts in beach maintenance and coastal ecological restoration in recent years, understanding the sedimentary dynamics of beaches remains of vital theoretical and practical value.
1 Introduction
Since the 20th century, the intensification of erosion along sandy coasts has emerged as a significant global issue. This erosion not only leads to the direct loss of land in coastal areas but also indirectly contributes to increased occurrences of marine dynamic disasters, ecological degradation, and socio-economic damages. In the United States, erosion affects at least 80% of sandy coasts, while in China, the figure stands at approximately 70%. In Europe, annual losses of coastal zones have been quantified at 1.5 km2 (Cai et al., 2009; Houston and Dean, 2014). Governments worldwide are thus compelled to allocate substantial financial and material resources to address this challenge. The erosion of these coastal zones has had profound adverse effects on both the natural environments and the socio-economic development of these areas (Van-Rijn, 2011). As a result, there is a growing consensus among stakeholders regarding the necessity to enhance our understanding, research, and responses to coastal erosion and to elucidate its dynamic mechanisms.
From an interannual perspective, the transportation of sediment along the coast is widely acknowledged as the primary driver of erosion on straight sandy beaches, which typically feature slopes ranging from 1/20 to 1/50. Waves arriving obliquely at the shore induce wave breaking in the nearshore zone, leading to the formation of alongshore wave-induced currents and sediment transport (Karambas and Karathanassi, 2004). As waves transition from deeper to shallower waters, variations in water depth, topography, and wave energy dissipation facilitate wave transformation, ultimately resulting in wave breaking and the generation of wave-induced longshore currents (Beach and Sternberg, 1992). Wave-induced currents are primarily present in shallow coastal waters and attenuate rapidly as water depth increases, whereas wind-induced currents exhibit higher velocities in open waters far from the coast but are reduced in nearshore areas due to the influence of complex topography, which shortens the effective wind fetch (Kato and Yamashita, 2001; Xie et al., 2001). The movement of sediment along the coast is driven by the cumulative effects of wave action and longshore currents. On straight sandy coasts, this process predominantly occurs within the surf zone, where sediment is transported in suspension (Li et al., 2015). Therefore, both alongshore and cross-shore sediment transport under wave action are critical factors influencing the evolution of sandy coastlines and beaches (Xie, 2011; Tang et al., 2016). On these coastlines, the dynamics of sediment are largely dictated by changes in coastal sediment transport, while the processes of erosion and accretion are primarily dependent on fluctuations in net sediment transport along the coast, with offshore transport playing a minimal role (Li et al., 2015; Nair et al., 2015).
From a seasonal perspective, sediment transport on straight beaches is subject to seasonal variations in ocean dynamics, including storm events. Alterations in seasonal wave intensity, direction, and height result in significant changes in alongshore sediment transport conditions. During storm events, strong winds and large waves resuspend sea floor sediments, and rapid alterations in wave direction and currents modify sediment transport pathways. These meteorological variations in alongshore sediment transport can swiftly induce substantial changes in coastal morphology, profoundly affecting the shape of the coastline. Offshore, seasonal sediment transport generally occurs within the closure depth, transitioning between underwater sandbars and the shoreface (Hallermeier, 1978). However, continual imbalances in sediment transport lead to shoreline adjustments towards a new equilibrium state, perpetuating the erosion of the backshore and heightening the coast’s vulnerability to storm events, thus manifesting an accelerating trend of episodic erosion (Dean, 1991). Previous research has suggested that sediment transport during storm events is influenced by the interactions among wind, waves, and tidal currents (Bartholomä et al., 2009), but most studies have focused on the influence of wave-induced currents, while studies on wind-induced currents are largely concentrated in open waters. There is relatively little research on wind-induced currents within the closure depth. As a result, the dominant factors controlling coastal sediment transport remain uncertain, and the contributions of tidal currents, wind-induced currents, and wave-induced currents to coastal transport at different temporal scales are still unclear. Therefore, further numerical simulations are needed to explore these processes.
The Shandong Peninsula, a prominent region in northern China, is distinguished by its expansive sandy coastlines, encompassing 123 coastal beaches that collectively stretch approximately 365 kilometers. Geographically, it is segmented into three distinct areas: the northern part (Yantai), the eastern part (Weihai), and the southern part (Qingdao and Rizhao) (Yin et al., 2018). The diverse beach types found in this region include straight beaches, bay beaches, and barrier-lagoon beaches (Cai et al., 2007). Historically, the beaches of the Shandong Peninsula were rich in natural resources, characterized by well-developed depositional landforms, vast sandy expanses, and extensive straight and barrier-lagoon beaches across its three regions. Notably, in the Rizhao area, several beaches supported the development of sand dunes several meters high, with some areas experiencing wind and sand disasters, necessitating extensive planting of Pinus thunbergii for protection (Zhuang et al., 1989). However, rapid social development has led to human activities becoming the predominant factors driving coastal erosion. By the 1980s, erosion rates on the sandy coasts of southern Shandong had escalated to 2-3 meters per year (Yin et al., 2018). During this period, and subsequently, the primary contributors to beach erosion included sand mining on the beach surface, modifications to coastal structures affecting the erosion and siltation environment, and a decrease in sediment supply from runoff (Zhuang et al., 2000). By 2010, over 80% of the sandy coasts of the Shandong Peninsula continued to experience erosion, with rates reaching up to 15 meters per year on some smaller beaches, leading to their gradual disappearance. The sand dune landforms of large beaches vanished, and the beach shoulders became narrower (Li et al., 2013). In recent years, strengthened coastal zone management has led to stringent controls over human activities such as beach or underwater sand mining and coastal construction. Large beaches have also been developed and preserved as seaside resorts, gradually undergoing restoration under the guidance and support of national marine ecological conservation and restoration projects (Yu and Yu, 2020). With over a decade of strict regulation, these beaches, previously eroded primarily due to human activities, have seen a cessation of destructive practices. Although the supply of sediment from runoff has not fully recovered, the main driving force for current and future changes in these beaches has shifted from human activities to natural forces. In coastal zones where artificial and natural shorelines coexist, understanding the dynamics of sediment and the respective driving factors of natural forces on beaches remains crucial for predicting future beach changes and guiding restoration efforts.
This study focuses on Wanpingkou Beach (WPK beach) in the southern part of the Shandong Peninsula as a representative example of a typical straight beach. Utilizing methods such as repeated topographic measurements, sediment grain size analysis, and numerical simulations, it explores the potential impact mechanisms and contributions of ocean dynamic elements like tidal currents, wind-induced currents, waves, and wave-induced currents on beach changes at different time scales, elucidating the dynamic processes of recent beach evolution. The paper is structured as follows: Section 2 provides an introduction to the study area, followed by a description of the observed data and methodology in Section 3. The analysis of the observed results is presented in Section 4. Finally, Section 5 discusses the hydrodynamic mechanisms of sandy beach change at different time scales in WPK beach.
2 Study areas
WPK beach is situated on the southwest coast of the Shandong Peninsula and exemplifies the sandy coast in southern Shandong. The coastline here extends northeast to southwest and features a low elevation (Figure 1A).
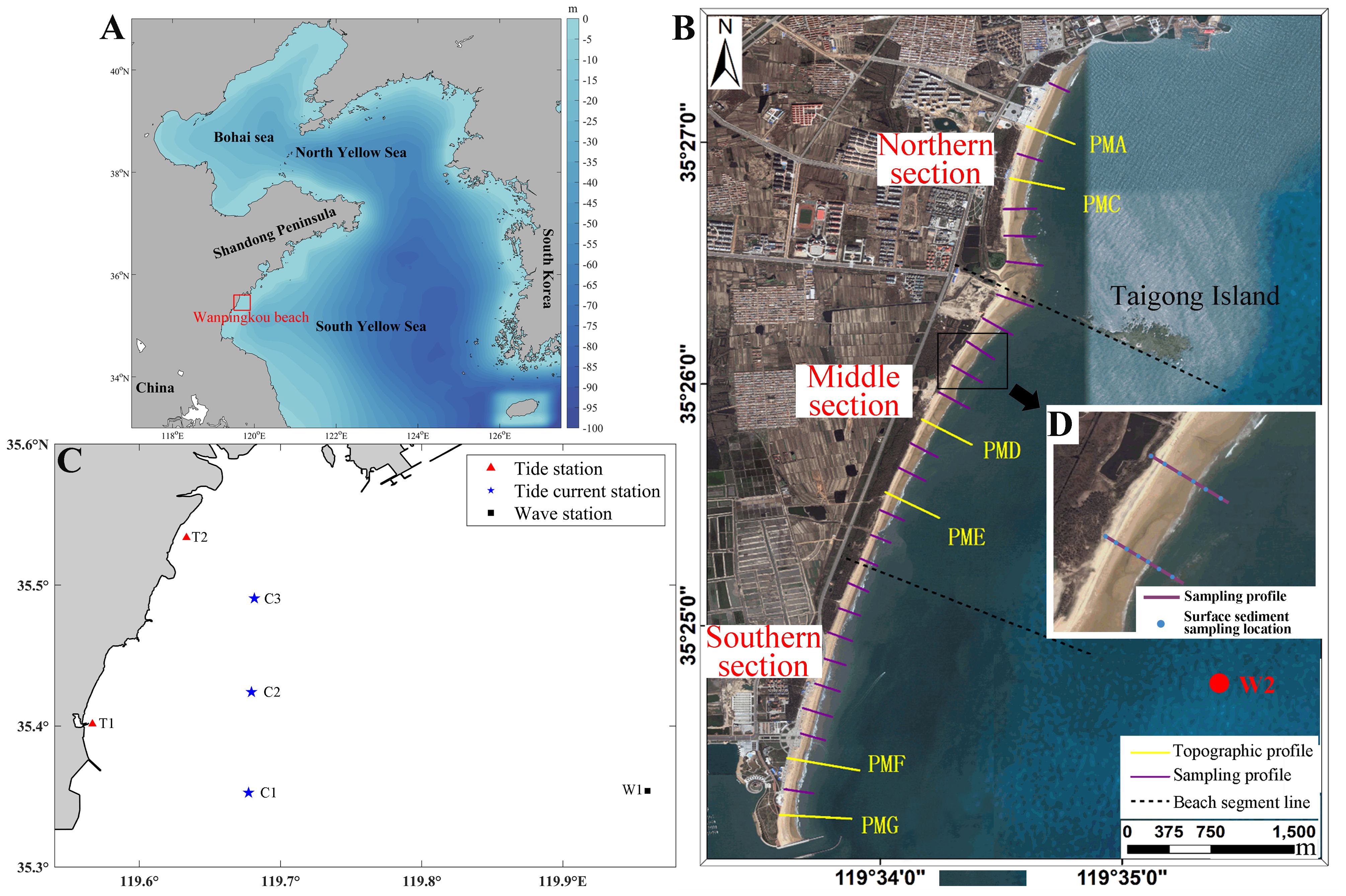
Figure 1. (A) The red box indicates the location of WPK beach in the Yellow Sea. (B) Beach segmentation and survey line location at WPK beach. The survey line indicates direction rather than measurement length. The red point (W2) is the wave sampling point in the model. (C) Station positions are marked with a red triangle for tidal observation stations (T1 and T2), blue pentagrams for synchronous tidal current observation stations (C1-C3), and black squares for wave measurement stations (W1). (D) Surface sediment sampling points along the two profiles marked by the red box in (B), with blue points representing sampling locations, where 6-7 samples were collected along each profile.
Several short mountain streams traverse the region, carrying significant amounts of sand during summer floods, which enrich the sediment supply to the coast. However, from the 1960s to the 1980s, the construction of approximately 10 large and 50 medium-sized reservoirs on the Shandong Peninsula led to a substantial reduction in sediment discharge, from nearly 12 million tons to about 40,000 tons annually. Consequently, the annual sediment supply from land in the study area plummeted from nearly 500,000 tons to around 10,000 tons (Zhuang et al., 1989, 2000).
WPK beach stretches 6.39 km in length, with widths ranging from a maximum of about 50 m to a minimum of about 10 m. The beach covers approximately 19.6 km², with a thickness exceeding 2 m from the beach shoulder to the surface. The shoreline is wide and straight, sloping gently at an angle between 0.03 and 0.06.
The tidal regime in the study area is influenced by the semi-diurnal tidal wave system of the South Yellow Sea, characterized by a regular semi-diurnal tide with an average tidal range of about 3.0 m. Tides reach their peak earlier in the north and later in the south. The region is under the influence of the East Asian monsoon, with prevailing waves from the south-southeast, averaging 0.6 m in height and a period of 3.8 s. Taigong Island, located within the WPK beach area, serves as a natural breakwater, dividing the beach into two distinct zones.
3 Data and methods
3.1 Data
This study primarily relies on satellite-extracted shorelines, topographic profiles, interannual and seasonal variations in surface sediments, and the beach layering structure to analyze data and discuss the recent sedimentary geomorphic evolution of WPK beach.
3.1.1 Topography
WPK beach is divided into three sections from north to south: north, central, and south, with six monitoring profiles designated as A to G (Figure 1B). From 2011 to 2017, four monitoring campaigns were conducted in October 2011, August 2016 (summer half-year), April 2011, and January 2017 (winter half-year). The topographic monitoring encompasses the supratidal, intertidal, and subtidal zones, with a horizontal resolution of approximately 5 meters along the profiles.
3.1.2 Surface Sediments
In addition to the six topographic cross-sections, 23 parallel surface sediment sampling profiles were established (Figure 1B), spaced approximately 200 meters apart. In areas of significant variation in surface sediments, such as the backshore, foreshore, nearshore, and low tide line, 6-7 surface sediment samples were collected along each profile, totaling 181 samples, for grain size analysis in the laboratory using the sieving method. Sampling was conducted concurrently with the topographic surveys in 2016 and 2017.
3.1.3 Remote Sensing Images
Satellite remote sensing images were used to extract shorelines for spatial shoreline change analysis. Historical shorelines from the northern, central, and southern sections of WPK beach were compared. The 2005 shorelines were extracted from Quickbird satellite imagery with a resolution of 0.6 m, while the 2009 and 2016 shorelines were obtained from Worldview satellite imagery with a resolution of 0.4 m. The remote sensing images for WPK beach in 2009 and 2016 were calibrated on-site using RTK technology.
The high tide line was chosen as the defining boundary for the shoreline in this study. Initially, the high tide line visible in high-resolution remote sensing images was extracted. Subsequent comparisons and calibrations were based on the high tide marks observed on the beach profiles in 2009 and 2016, and were then verified against the elevation data from high tide levels recorded in tide observations. The resulting high tide line is used as the shoreline for calculating changes in the beach shoreline.
3.1.4 Tide Level
Tide level data for this study were collected from two tide gauge stations (T1 and T2) deployed in the research area in June 2016, over a monitoring period of one month, with a sampling interval of 10 minutes.
3.1.5 Tidal Current
Tidal current data for this study were obtained using a Nortek 600 kHz ship fixed (downward looking) continuous logging Acoustic Doppler Current Profiler (ADCP) from three tidal current stations (C1-C3) deployed in the research area in July 2016. Considering the observation blanking area of ADCP, the surface current is measured synchronously using a Seaguard RCM current meter. Observations were carried out simultaneously at the three stations on July 4-5 during the spring tide period and July 9-10 during the neap tide period, with continuous monitoring for 26 hours each and a sampling interval of 1 hour.
3.1.6 Waves
Wave data for this study were derived from buoy observations at station W1, using an Acoustic Wave and Current Meter (AWAC), conducted from November 19 to December 19, 2016. The monitoring period lasted one month, with data collected every 10 minutes.
3.1.7 Wind Field
The surface wind field model utilizes 10m wind speed data from the Climate Forecast System Reanalysis (CFSR) provided by the National Centers for Environmental Prediction (NCEP) in the United States. The data covers the period from July 2015 to July 2017, with a spatial resolution of 1/4° and a temporal resolution of one hour. (https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.html)
3.2 Numerical modelling
3.2.1 Model description
This study employs the Finite Volume Coastal Ocean Model (FVCOM) with an unstructured grid (Smagorinsky, 1963; Mellor and Yamada, 1982; Chen et al., 2003). The model uses a sigma coordinate system in the vertical direction, a triangular unstructured grid in the horizontal direction and a wetting-drying grid method in the intertidal zone, enhancing the representation of complex coastlines and seafloor topography. The numerical method is based on the finite volume method, and the FVCOM has been widely applied by other scholars in studies of the East China Sea (Song et al., 2011, 2013; Ding et al., 2018, 2019; Zhang et al., 2019).
Furthermore, the Mellor-Donelan-Oey (MDO) wave proposed by Mellor et al. (2008) is employed in this study and coupled with FVCOM. The coupled model has been successfully applied to the study of wave-induced currents by Gao et al. (2018) and Song et al. (2021). For more details on the model description, please refer to the appendix (Appendix: Model description).
3.2.2 Model setup
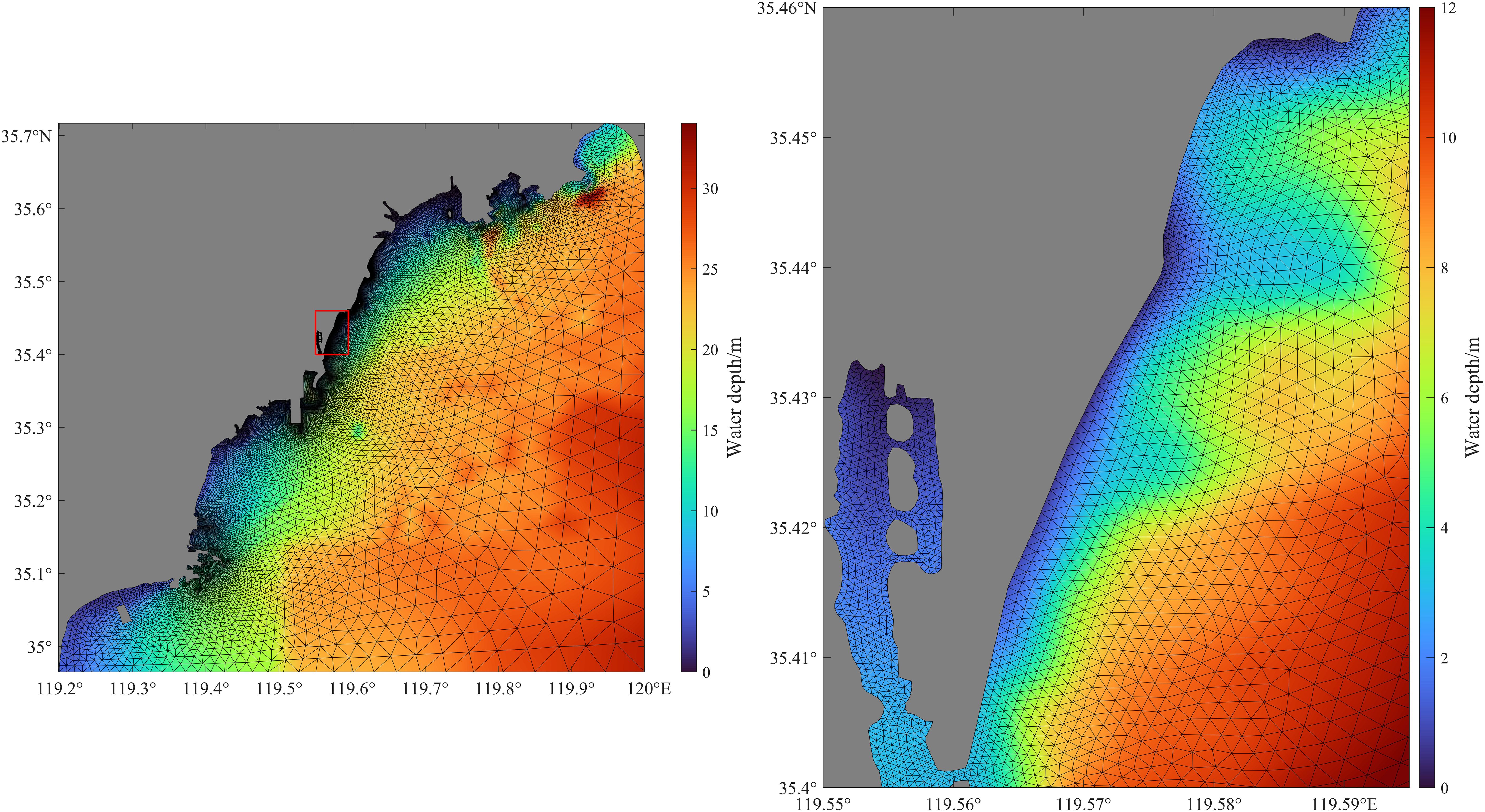
The model domain spans from 119.19°E to 120.31°E and from 34.80°N to 36.00°N. Within this domain, a hydrodynamic and wave model for the WPK beach is established, incorporating wave-current interaction processes (Gao et al., 2018). The grid near the WPK beach is refined to a minimum resolution of approximately 20m. The model grid comprises 43,580 nodes and 83,136 cells, utilizing a vertical σ-coordinate system divided into 10 layers (Figure 2).
The hydrodynamic model boundary is influenced by eight major astronomical tides (M2, S2, N2, K2, K1, O1, P1, Q1). Tidal elevation data is interpolated from the TOPEX/POSEIDON global tidal model (TPXO9) (TPXO9 Atlas) to derive the open boundary tidal harmonic constants. Subsequently, the t-tide toolbox is utilized for water level forecasting to establish the open boundary water level driver (Pawlowicz et al., 2002). The model does not account for the influence of freshwater runoff. The wave model boundary, connected to the open sea, primarily considers the impact of wind fields on waves, while also accounting for the bidirectional coupling effect between waves and currents. The model is a three-dimensional hydrostatic model that does not consider variations in temperature and salinity, with fixed values of 25°C for temperature and 30 PSU for salinity. It calculates results for the entire year of 2016, starting with a cold initialization and achieving stability after 30 days of operation before the results are analyzed.
3.2.3 Model verification
3.2.3.1 Water level validation
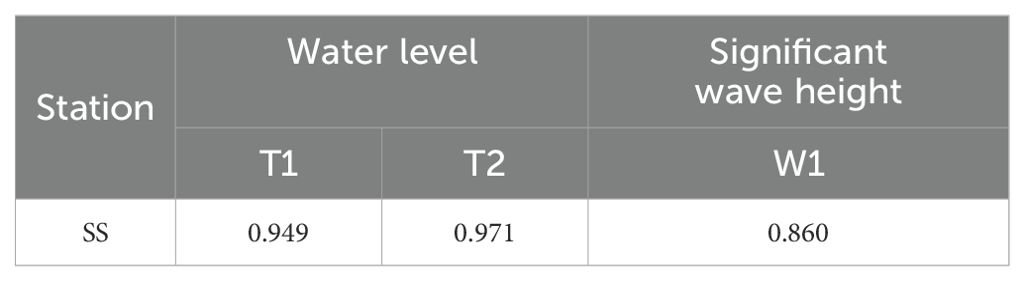
Based on data from stations T1 and T2, and corresponding model results (Figures 3A, B), there is a high degree of agreement. The skill score (SS) values (Allen et al., 2007) for the two stations are 0.949 and 0.971 (Table 1), respectively, indicating excellent performance of the model in simulating water levels in the study area.
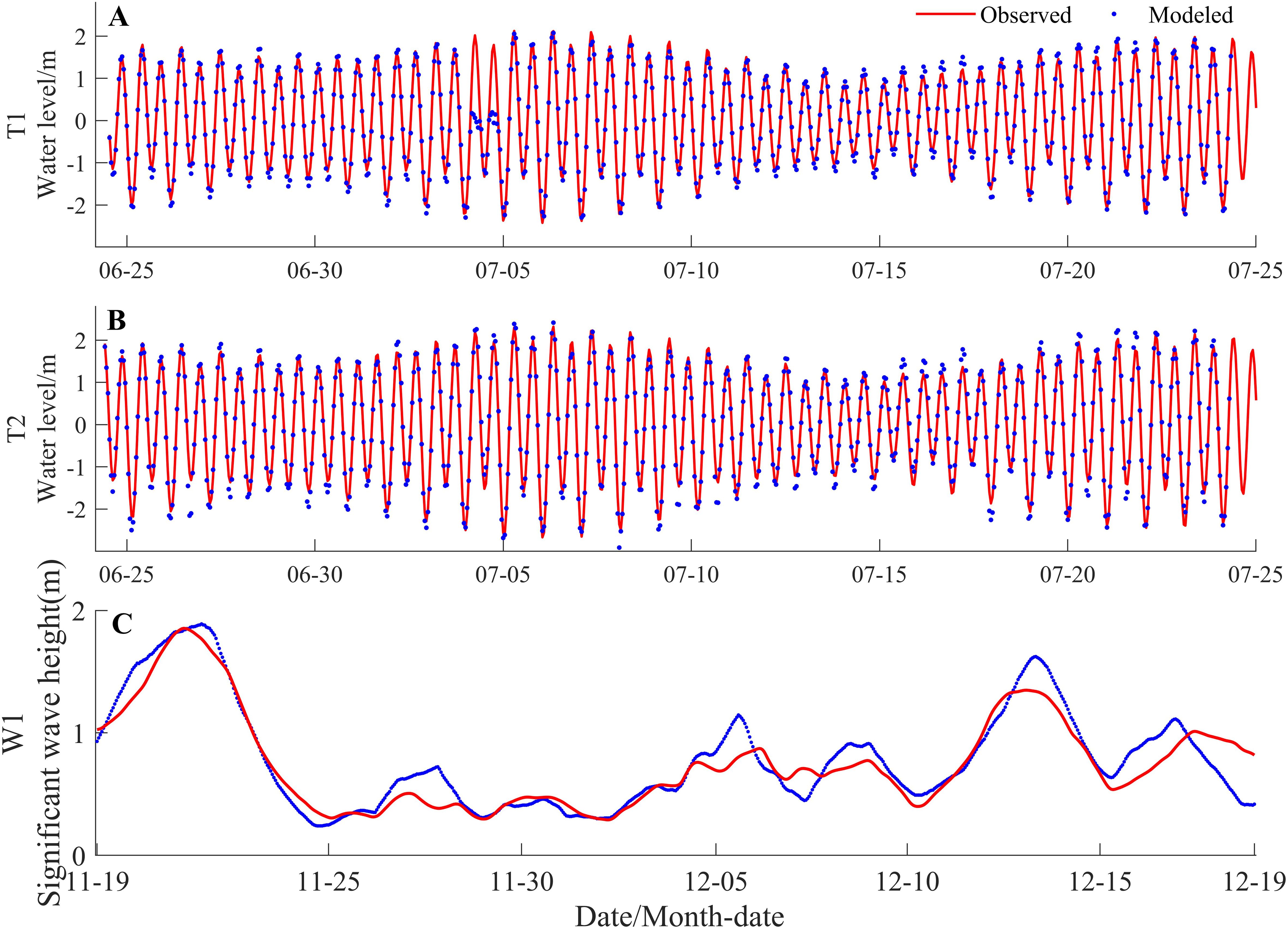
Figure 3. Water level verification at stations T1 (A) and T2 (B) and significant wave height verification at stations W1 (C).
3.2.3.2 Wave verification
The validation of significant wave height at station W1 is shown in Figure 3C. The results demonstrate excellent agreement with the simulation, with an SS of 0.896 (Table 1), accurately reflecting the real wave processes.
3.2.3.3 Current validation
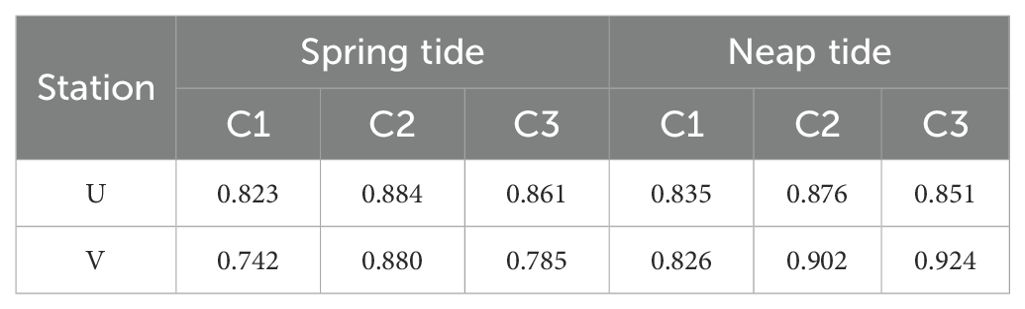
The current validation results are presented in Figure 4. Overall, the simulated current velocities align well with the measured data, and the SS results are excellent (Table 2), confirming the reliability of the model’s simulation of tidal currents.
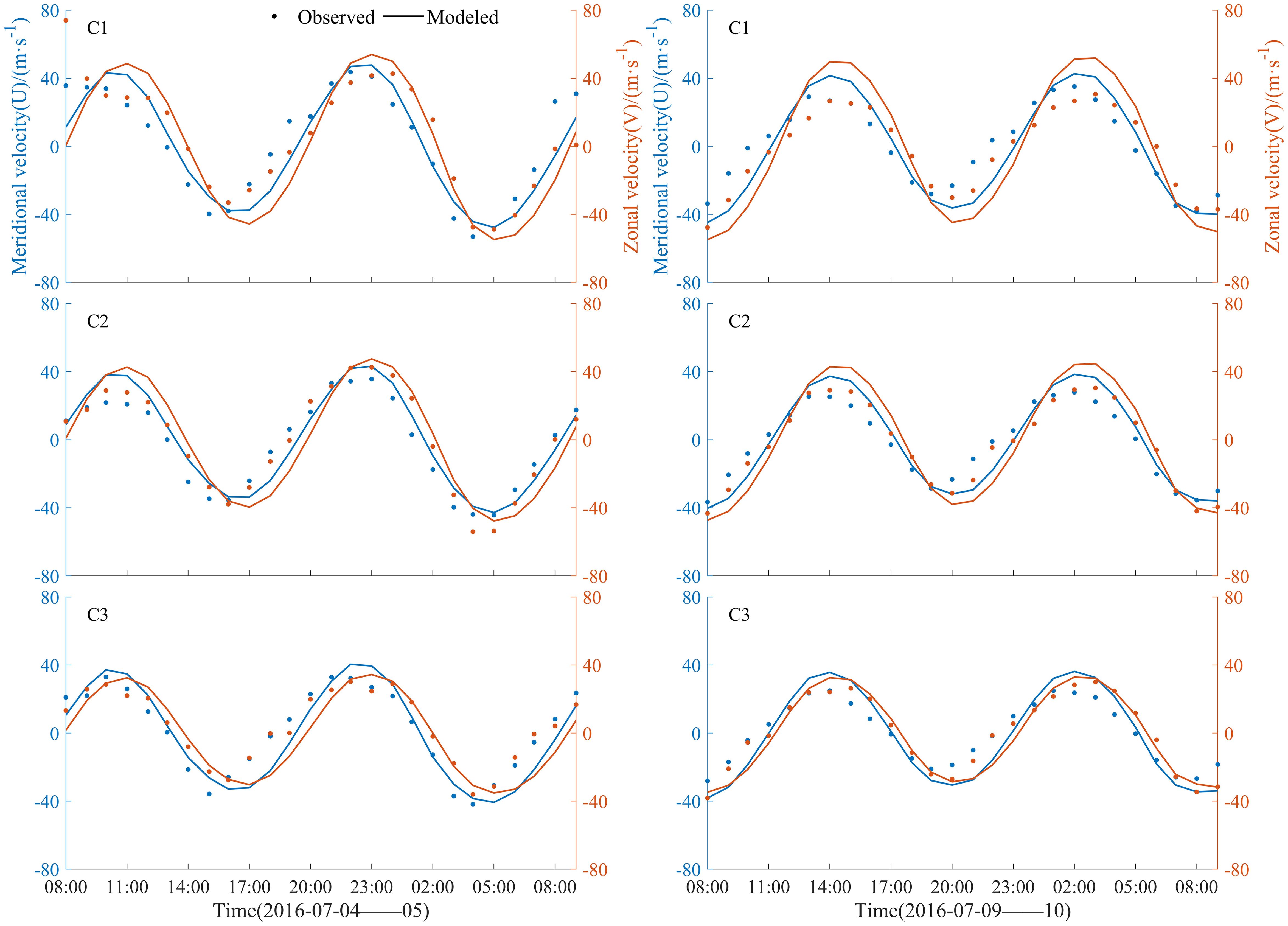
Figure 4. Current velocity verification during a spring tide on July 24-25, 2016 and a neap tide on July 9-10, 2016.
3.2.4 Numerical experiments
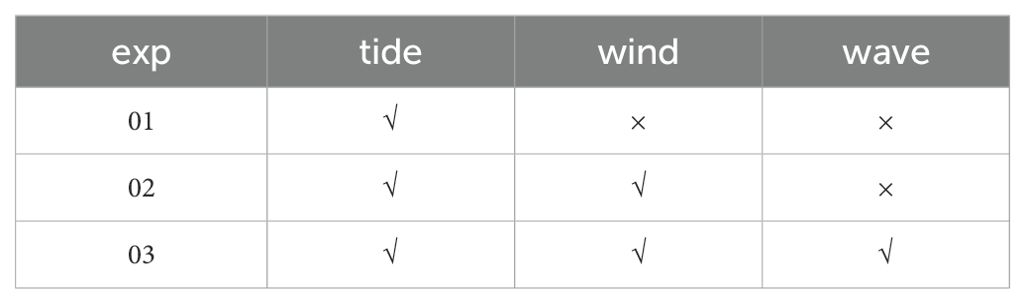
In this study, three numerical simulation experiments were designed to investigate the effects of dynamic factors such as tidal currents, wind-induced currents, waves, and wave-induced currents on coastal sediment transport (Table 3). Experiment 01 considered only the astronomical tide; Experiment 02 added wind field, using 10m wind speed data from CFSR, and circulation in the model’s open boundary input to Experiment 01; Experiment 03 introduced wave-current coupling on top of Experiment 02.
Tidal currents are represented by the flow field results of Experiment 01. Wind-induced currents in the study area are derived by subtracting the results of Experiment 01 from those of Experiment 02, and similarly, wave-induced currents are obtained by subtracting the results of Experiment 02 from those of Experiment 03. Seasonal, event, and inter-annual residual currents were calculated as the average flow field over three months, one day, and one year, respectively.
4 Results
4.1 Seasonal and interannual variations in topographic profiles
Owing to spatial limitations, this study focused on representative profiles C, D, and G (PMC, PMD, PMG) to analyze topographic changes in the northern, central, and southern sections of WPK Beach.
4.1.1 Northern Section of WPK beach
Analysis of Profile C during the summers of 2011 and 2016 revealed significant retreat and erosion at both the beach shoulder and the intertidal zone (Figure 5A). These findings demonstrate a marked trend of interannual erosion in the northern section.

Figure 5. Topographic comparison of Profile C (A), Profile D (B) and Profile G (C) in WPK beach. Taigong Island reef area (near Profile D) in the middle section of WPK beach (D).
Seasonal fluctuations primarily occurred above the high tide line and near mean sea level at the lower edge of the beach shoulder and within the intertidal zone. From summer to winter (2016.08–2017.01), there was a slight accumulation at the upper edge of the beach shoulder, whereas the lower edge experienced minor erosion. Near the low tide line within the intertidal zone, slight accumulation was noted, with sediment displacement towards both the upper and lower areas near mean sea level, resulting in an overall erosional state across the profile. From winter to summer (2011.04–2011.10), more pronounced erosion was observed from the beach shoulder to the intertidal zone beach surface (Figure 5A), indicating a loss of seasonal sediment stability and a state of continuous erosion. This section is the most severely eroded area of WPK Beach, with an average erosion rate of approximately 3 meters per year over six years under natural conditions.
4.1.2 The middle section of WPK beach
The middle section of WPK Beach, represented by Profile D, exhibited minor erosion and accretion changes from 2011 to 2017 (Figure 5B), maintaining a relatively stable profile. Over the past six years, this section has experienced slight erosion. A notable reflective steep slope has formed above mean sea level in this area, with the average high tide line nearing the windbreak forest or the base of the sand dunes. During high tide, the beach surface is narrow, displaying distinct erosion scarps (Figure 5B). From summer to winter (2016.08–2017.01), Profile D primarily experienced erosion near the average high tide line. From winter to summer (2011.04–2011.10), some accretion was noted.
Over the six-year period, the middle section of the beach has undergone slow erosion, reaching the base of the backshore sand dunes and forming a permanent erosional scarp. The backshore sand dunes and the wave dissipation effect of Taigong Island have impeded further erosion. The rocky reefs of Taigong Island act as a large underwater submerged breakwater, influencing the local hydrodynamic environment and contributing to wave dissipation and sand stabilization, thus partially mitigating beach erosion. The reduction in hydrodynamic force has led to finer sediment deposition in this area (Figure 5D).
Given the protection offered by the rocky reefs, backshore sand dunes, and artificial defenses, the middle section of the beach might continue to experience slow erosion or remain relatively stable in the future. Nevertheless, the passage of typhoons could disrupt this stability, potentially eroding the sand dunes and causing further shoreline retreat. The stepped seawall built in the southern part of the middle section is likely to cause downward erosion of the beach surface, resulting in continued loss of beach sand.
4.1.3 Southern section of WPK beach
In recent years, the southern section of the beach has demonstrated an overall trend of accretion (Figure 5C). The beach shoulder in Profile G has been gradually expanding seawards, and similar accretion is observable on the intertidal and subtidal beach surfaces. This interannual variation is linked to the construction of a sand trap at the southern end of WPK beach, which captures sediment moving southward along the coast, resulting in accumulation at this site.
From summer to winter (2016.08–2017.01), Profile G underwent slight erosion at the backshore, accompanied by accretion near the average high tide line. This was followed by erosion at the lower edge of the beach shoulder, transitioning to accretion near the low tide line on the foreshore, indicating an overall state of accretion. Conversely, from winter to summer (2011.04–2011.10), the beach was in a state of erosion. Despite these changes, the sediment transport and topography in the southern section remain relatively stable with slight accretion over the years. This stability, along with a consistently available sediment supply due to the sand trap, has resulted in relatively stable depositional landform characteristics.
Considering the overall changes in the topography of WPK beach from 2011 to 2017, the beach has exhibited a pattern of “northern erosion and southern accretion” over these six years. There is pronounced erosion in the northern part, relatively slow erosion in the central part, and slight accretion in the southern part, showing a sediment transport trend from north to south. Seasonal variations in the beach topography profiles indicate that during the summer half-year, the natural state of WPK beach’s topography profiles is closer to wind-wave profiles, with sediment transport towards the foreshore and subaqueous areas, indicating erosion near the beach shoulder. This erosion is associated with stronger onshore waves driven by southerly winds in the nearby sea during summer and autumn. In contrast, during the winter half-year, the topography profiles resemble swell profiles, with sediment transport moving towards the beach shoulder from the foreshore and subaqueous areas, indicating accretion near the beach shoulder. This accretion is related to northerly winds and offshore waves during winter and spring in the nearby sea. When distinct erosion scarps or reflective steep slopes form, seasonal variations in topography profiles largely disappear.
4.2 Seasonal variations in characteristics of surface sediments
The characteristics of surface sediments on the beach reflect not only the natural conditions of the coastal bathing area but also signal changes in the hydrodynamics and erosion-sedimentation trends along the shoreline (Noujas, 2016). From 2016 to 2017, the average grain size of the sand at WPK beach was approximately 0.6 mm, predominantly consisting of coarse and medium-coarse sand.
Based on the spatial distribution of average grain size (Figure 6), the variation in grain size across the beach is not uniform. In summer, the overall average grain size is around 0.7 mm, coarser than the 0.5 mm observed in winter. This is consistent with the erosion observed in the summer topographic profile and the sedimentation in the winter profile. Both the northern and central sections of the beach exhibit a trend where the average grain size increases from the foredune to the backdune in both summer and winter, with the maximum average grain size being near Taigong Island. This increase is related to the stronger southeastward wave erosion of the rocks during summer.
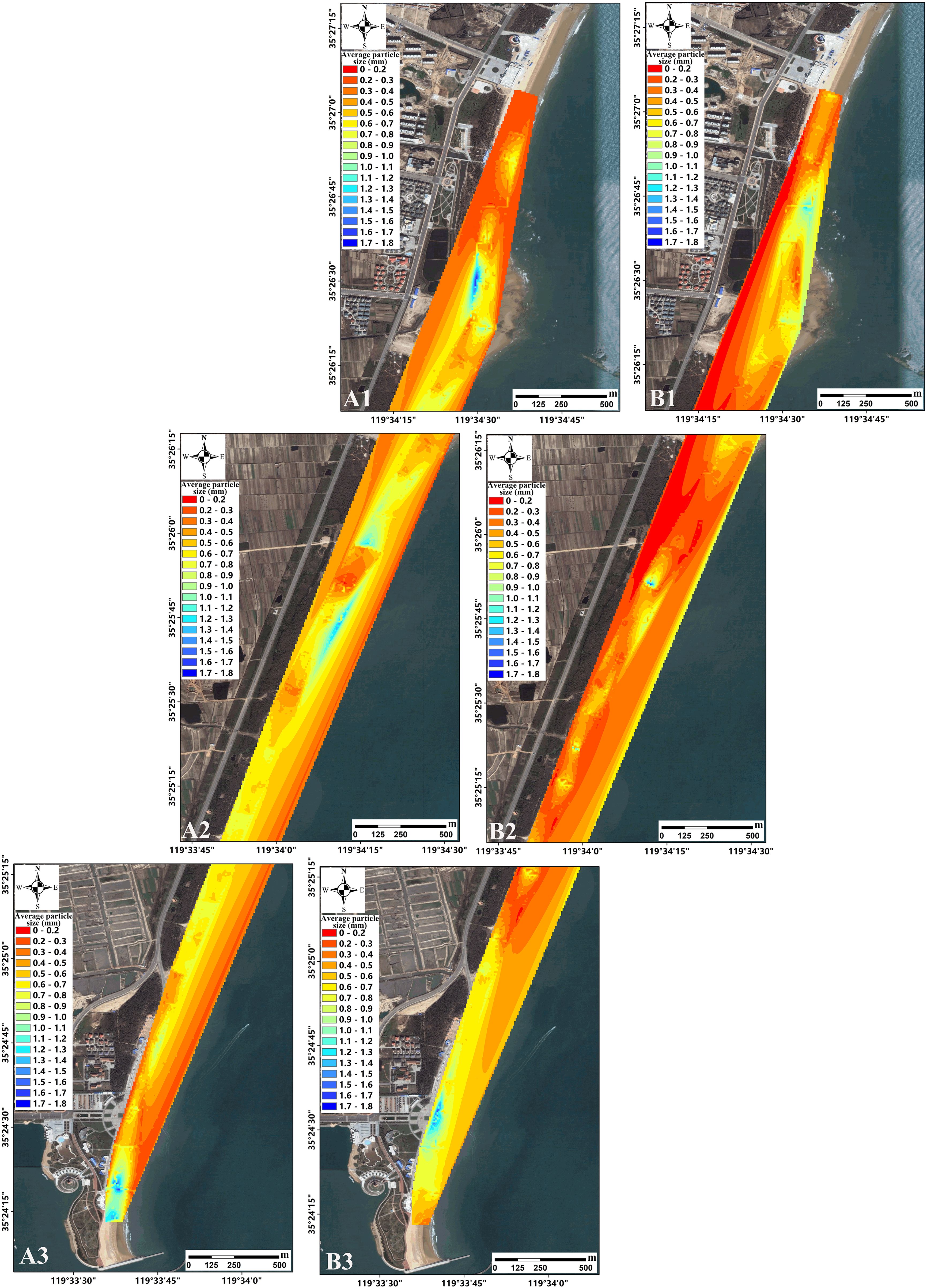
Figure 6. Spatial distribution of average particle size of surface sediment in WPK beach in summer (A) and winter (B), of which the a1-a3 are average particle size distribution in the north, middle, and south section of the beach, respectively, in Aug, 2016, and b1-b3 are in Jan, 2017.
The spatial distribution characteristics of average grain size in the southern section of the beach differ slightly from those in the northern and central sections. In summer, this section experiences a wide range of grain size variations with a relatively even distribution, displaying a pattern of coarser grains in the backdune and finer grains in the foredune. This indicates a regular response to strong marine dynamics during summer, with relatively stable sedimentary dynamics along the beach profile. In winter, the range of grain size variations is smaller and less regular, suggesting a smaller impact of marine dynamics on grain size distribution, likely due to weaker winter marine dynamics. Additionally, the southern section serves as the main swimming and tourist area of WPK beach, where the presence of irregular coarse grains may result from local disturbances due to human activities.
4.3 Interannual variations in shoreline changes
A comparison of shorelines reveals that the northern section of WPK beach is experiencing annual erosion, which is relatively severe (Figure 7A). From 2005 to 2016, the northern shoreline retreated an average of 25 meters, with an erosion rate of about 2.3 meters per year. Considering the erosion rates at specific points in section C of the northern segment from 2011 to 2016 (3 meters per year), the average erosion rate over the past decade in the northern section is estimated to be between 2 and 3 meters per year (Figure 7A).
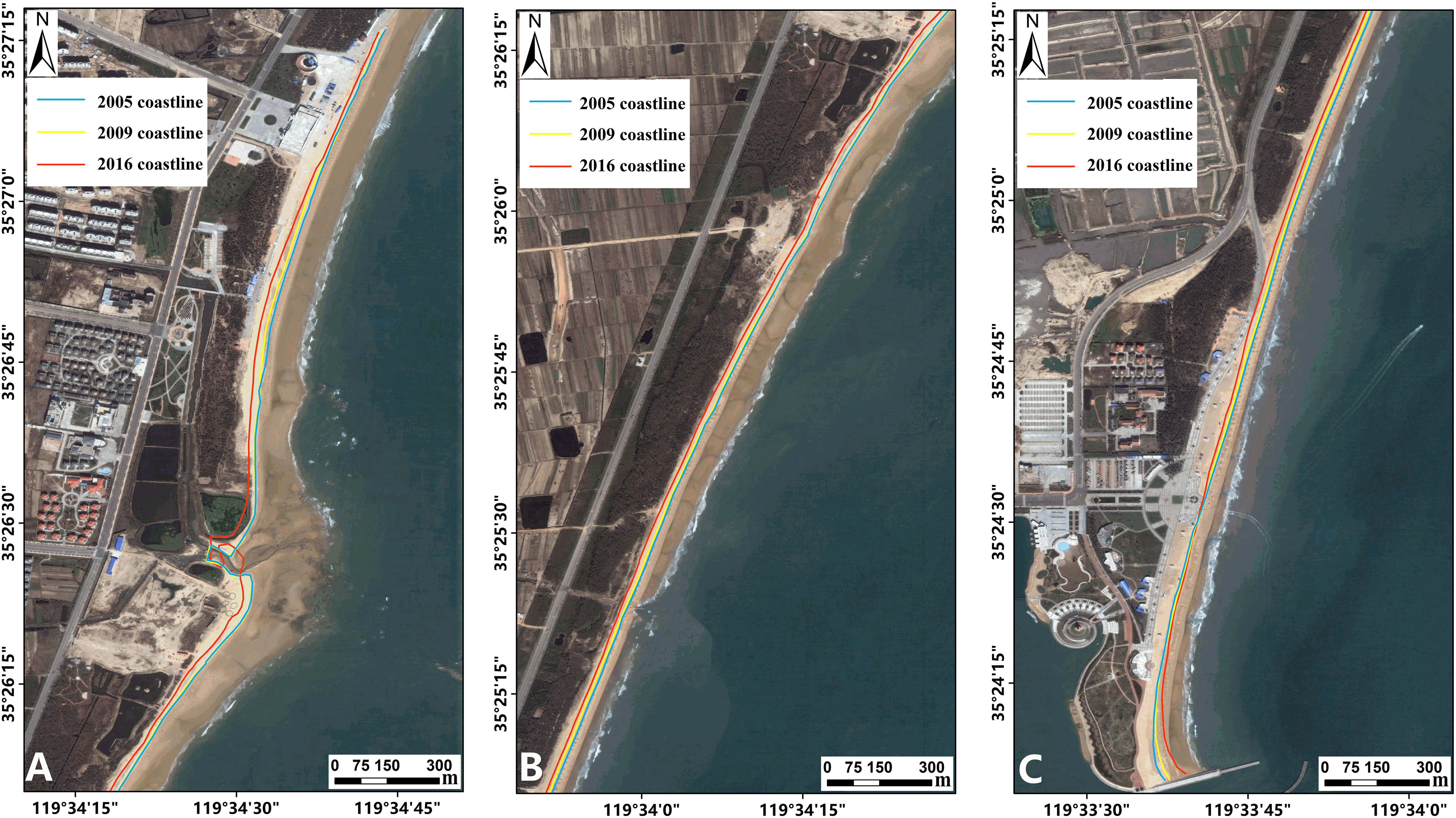
Figure 7. Comparison of shoreline changes in north section (A), middle section (B), and south section (C) of WPK beach in 2005, 2009, and 2016 (The base map is from remote sensing images in 2009).
In the central section of WPK beach, shoreline changes over the past decade have been relatively minor compared to the northern section, yet still indicate an erosion trend. From 2005 to 2016, the average retreat of the shoreline was about 8 meters, with an average erosion rate of approximately 0.8 meters per year. Compared to the northern section, the erosion rates at various points in the central section have shown smaller variations. Considering the erosion rates at shoreline points in profiles D and E of the central section from 2011 to 2016 (1.0 meter per year), the average erosion rate over the past decade in the central section is estimated to be around 0.5 to 1.5 meters per year (Figure 7B).
Between 2005 and 2009, shoreline changes in the southern section of WPK beach were relatively minor, with slight erosion in the northern part similar to the central section, while the central-southern part exhibited a clear state of accretion. The average accretion distance in the central-southern part exceeded 20 meters, with an accretion rate of about 2 meters per year. Considering the accretion rates at shoreline points in profiles F and G of the southern section from 2011 to 2016 (2 meters per year), the average accretion rate over the past decade in the southern section is estimated to be around 1 to 2 meters per year (Figure 7C).
4.4 Mean annual flow field in the study area
According to the model results for the flow field, the residual tidal currents in 2016 exhibited higher velocities near coastal headlands, reaching up to 0.3 m/s (Figure 8A). In contrast, velocities along gentle nearshore coastlines and in offshore areas were lower, typically below 0.01 m/s. Wind-induced currents demonstrated lower velocities near the coast, usually remaining below 0.01 m/s, primarily due to the variable coastline and the shorter wind fetch in coastal areas. However, in the western region of the Yellow Sea, more than 20 kilometers from the coast, the velocities of wind-induced currents in the open sea could exceed 0.1 m/s (Figure 8B).
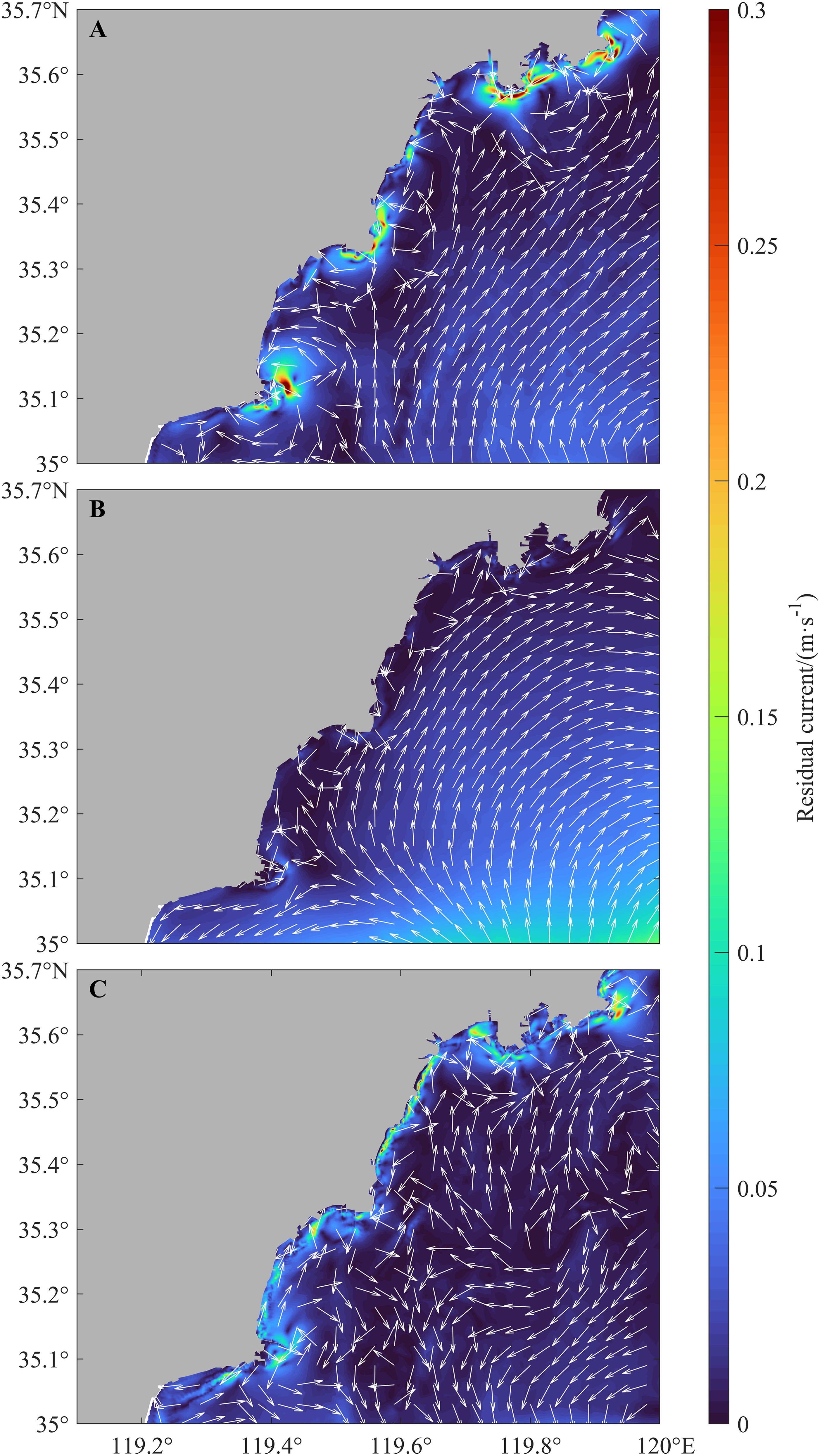
Figure 8. In the study area in 2016, residual currents were classified as follows: tidal residual currents (A), wind-induced residual currents (B), and wave-induced residual currents (C).
Unlike wind-induced currents, wave-induced currents generally exhibited higher velocities throughout the coastal sea area, ranging between 0.1 m/s and 0.3 m/s (Figure 8C). Their influence in offshore areas, however, could be negligible. Therefore, when studying coastal transport issues, it is important to focus on the effects of astronomical tides and wave-induced currents, with wind-induced currents playing a relatively minor role.
5 Discussion
5.1 Dynamic mechanisms of seasonal changes on beaches
Observations of the topography at WPK beach reveal that during the summer, sediments from the beach shoulder migrate toward the foreshore and underwater, leading to erosion at the beach shoulder. Conversely, in the winter, sediments from the foreshore and underwater move toward the beach shoulder, resulting in accumulation there. In some sections of the coast where distinct erosion cliffs or steep slopes have formed, the seasonal variations in the topographic profile are not pronounced. The dynamic mechanism behind these seasonal changes in beach profiles is primarily associated with seasonal waves and currents driven by the monsoon. This includes tidal currents, wind-induced currents, waves, and wave-induced currents. However, due to the low velocity of the coastal wind-induced currents at WPK beach, their effect is not considered significant in this analysis.
5.1.1 Seasonal variation of residual flow field
5.1.1.1 Tidal residual flow
The seasonal variation in tidal currents is minimal, serving as the background flow field for the beach (Figures 9A1, A2). The velocity of the tidal residual flow ranges from approximately 0.04 to 0.06 m/s. In the northern section, the flow generally moves from the bay head outward toward both sides, while in the middle and southern sections, it flows southwestward. The presence of Taigong Island roughly divides WPK beach into a cape bay-type beach in the northern section, and a straight-type beach in the middle and southern sections. Despite this division, Taigong Island does not entirely prevent the transport of coastal material; suspended sediments from the northern section can gradually move southward and are eventually intercepted by the sand trapping dam at the southern end of the beach.

Figure 9. Distribution of residual currents at WPK beach during the summer and winter seasons. (A1) represents summer tidal residual currents, (A2) represents winter tidal residual currents; (B1) represents summer wave-induced currents, and (B2) represents winter wave-induced currents.
5.1.1.2 Wave-induced currents
Wave-induced currents are net coastal currents generated after waves break near the shore (Figures 9B1, B2). In the summer, southerly wind waves refract near the coast due to the shallowing topography and approach the vertical coastline. Due to the long fetch of the wind region, wind waves are relatively large, resulting in faster wave-induced currents, approximately 0.1 to 0.3 m/s. The overall flow direction is similar to that of the tidal residual flow, with the northern section flowing from the bay head toward both sides, and the middle and southern sections flowing southwestward. However, three adjacent eddies form outside the PME section in the middle section, promoting the formation of shear flow near this area. In the winter, the wind region of northerly winds is shorter, leading to relatively smaller wind waves and wave-induced currents, with velocities of about 0.05 to 0.2 m/s, predominantly flowing southwestward. Because wave-induced currents have relatively higher velocities, they have the most significant impact on the coastal transport of suspended sediments along the beach.
In summary, the long-term north-to-south sediment transport process at WPK beach, as indicated by topographic cross-section observations, is primarily influenced by wave-induced currents and tidal currents, with both currents having similar flow directions. Consequently, the seasonal variations in beach flow patterns and sediment transport are minimal. This observation also serves as the driving mechanism for the formation of the sandbar-lagoon system at the southern end of the beach.
5.1.2 Seasonal variations in waves
Simulation results from W2 (Figure 1B) indicate that the predominant wave direction throughout the year is ESE, with SE being the secondary predominant direction (Figures 10A1-A4). The seasonal average effective wave height field within a 2 km range near the beach is approximately perpendicular to the coastline. This alignment suggests significant wave refraction as waves approach the beach and encounter shallower water. In the summer, influenced by the southeast monsoon, wind waves intensify over the open sea, and the average effective wave height near the coast peaks at about 1 m. These stronger waves can mobilize larger sediment particles, leading to a coarser average grain size on the summer beach. Regions on the beachfront with higher wave heights also exhibit coarser grain size distributions (Figures 10B2, 6A). In contrast, the winter season is shaped by the East Asian winter monsoon. Despite frequent strong winds, the shorter fetch in the coastal wind zone results in smaller wind waves, with maximum average effective wave heights near the beach reaching about 0.5 m. The reduced wave energy in winter leads to a finer overall grain size of surface sediments compared to summer. Additionally, the frequent strong winds in winter influence the grain size distribution of surface sediments, potentially transporting finer particles towards the backshore. In summer, although the waves are stronger, the weaker winds and less frequent strong wind events result in a finer grain size distribution in the backshore and coarser in the foreshore (Figures 10B1, 6B).
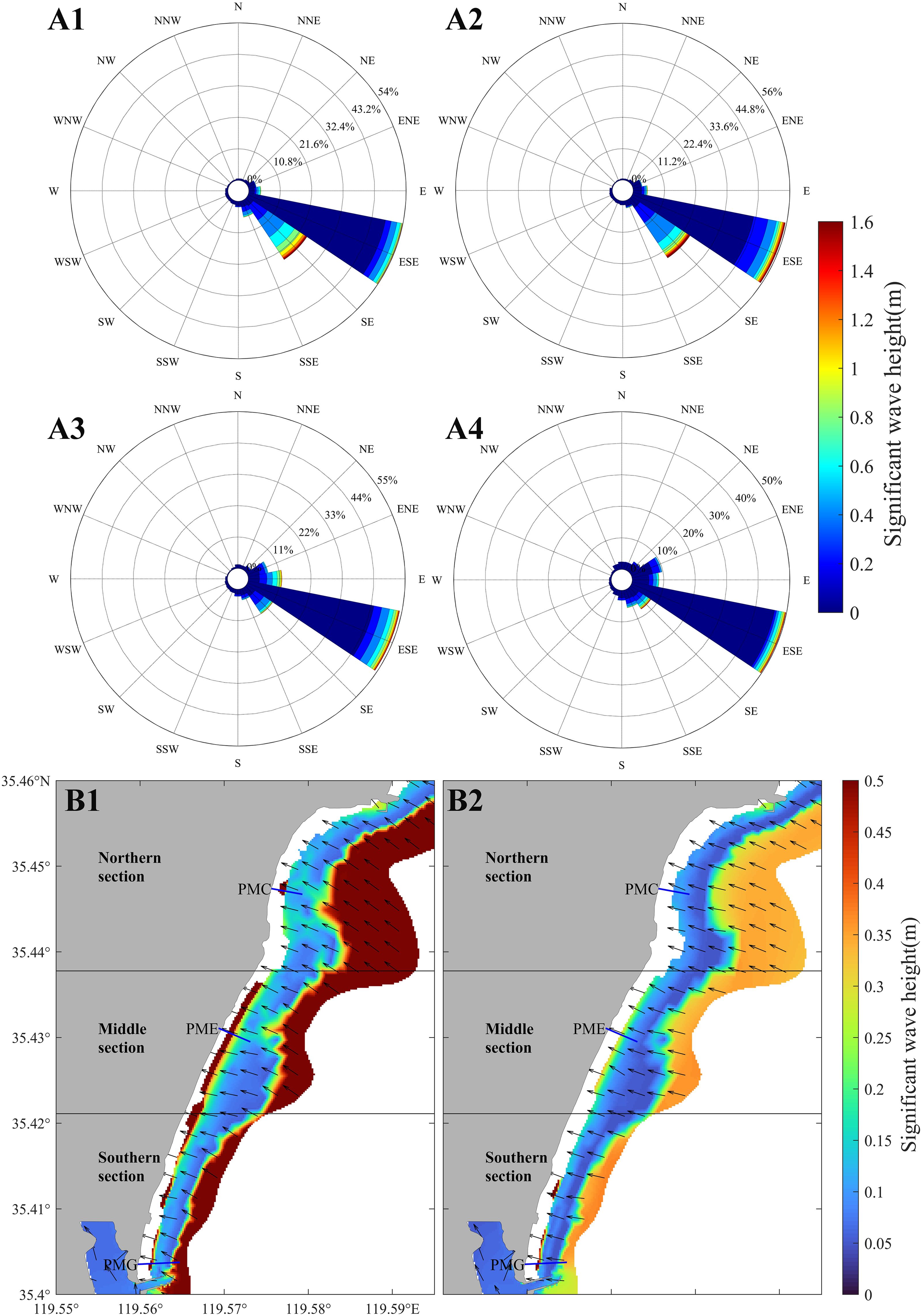
Figure 10. Wave distribution map of WPK beach. (A1–A4) show the wave rose diagrams for the study area at W2 in spring, summer, autumn, and winter respectively; (B1, B2) depict the average waves for the summer and winter seasons.
In summary, the waves at WPK beach are influenced by coastal topography and seasonal monsoons, exhibiting stronger waves in summer and weaker waves in winter. Seasonal wind-induced currents on the beach are weak, resulting in negligible seasonal changes in surface sediment grain size. Thus, the driving factors behind the seasonal changes in surface sediment on the beach are primarily the variations in wave energy and wind speed.
5.2 Mechanisms of event-induced changes in beach dynamics
Episodic weather events significantly contribute to the seasonal variations in beach dynamics. In summer, not only is the significant wave height greater than in winter, but the frequency of large waves is also higher (Figures 11A1, A2). For instance, at the mid-section PME profile of the beach, the number of large waves exceeding 0.6 m in summer is around ten times greater than in winter.
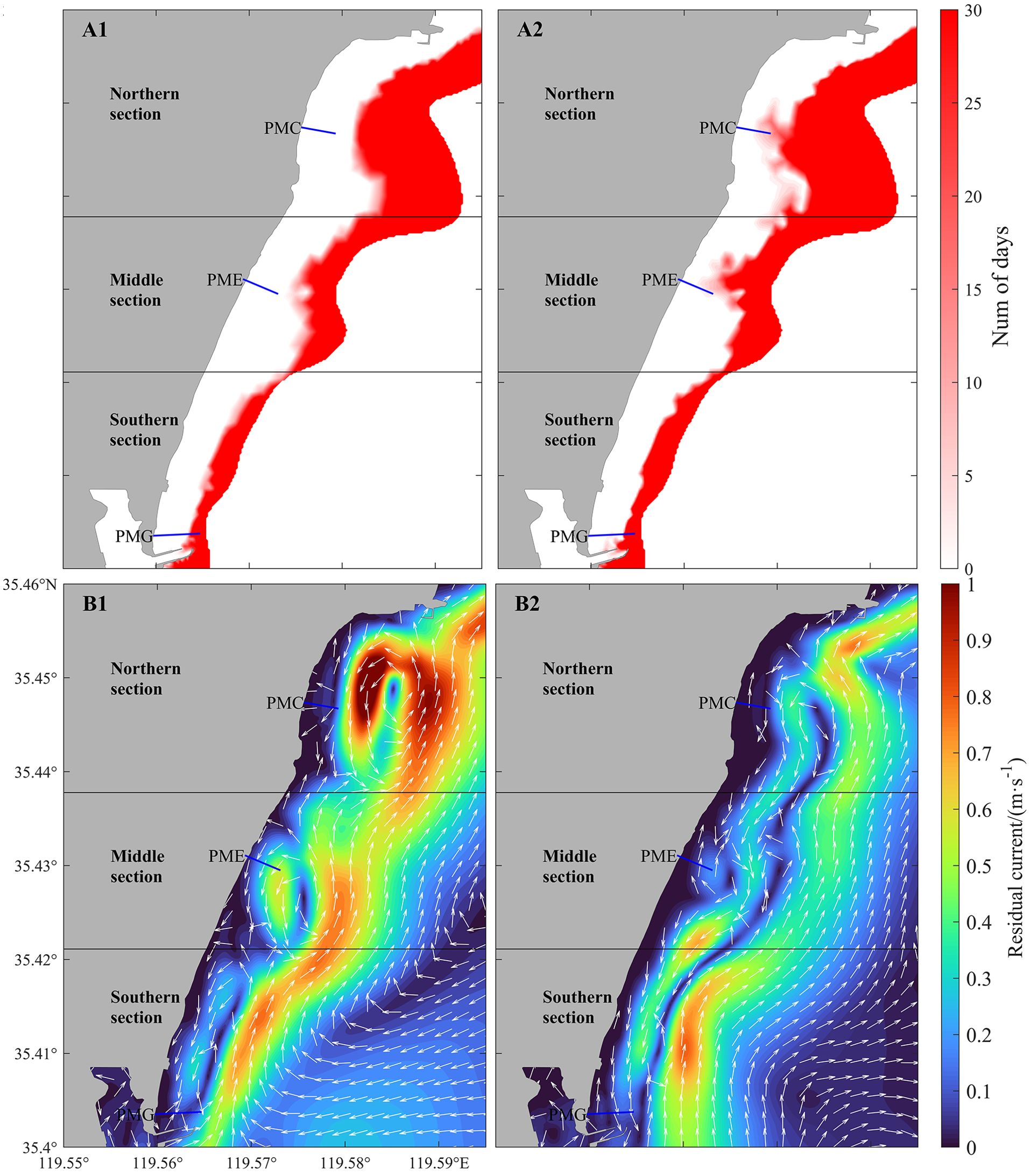
Figure 11. (A1, A2) display the number of days with significant wave heights exceeding 0.5m during the summer and winter seasons, respectively; (B1, B2) illustrate the daily average wave-induced flow for typical large wave conditions in the summer and winter seasons.
Analysis of wave processes on a typical winter day and a summer day (with significant wave heights reaching 1m 1 km from the shore) reveals the characteristics of the nearshore flow field under large wave conditions (Figures 11B1, B2). In winter, the structure of the wave-induced flow field under large wave conditions exhibits a nearshore flow from north to south and an opposing offshore flow, with a distinct frontal boundary between them. Throughout these large wave events, sediment suspended by the waves is transported from north to south along the beach, leading to sediment loss in the mid and northern sections. The wave-induced flow in summer mirrors the average summer wave-induced flow distribution but reaches higher velocities of up to 0.8 m/s. Therefore, the episodic dynamic mechanisms of beach changes are similar to the seasonal mechanisms but with increased intensity, making them a major component of seasonal beach variations. Among the driving factors, wave action initiating sediment movement and wave-induced sediment transport remain the primary mechanisms for coastal sediment transport.
5.3 Interannual variation mechanism of beach residual currents
The interannual variation in oceanic dynamic factors is primarily attributed to annual average changes in wind and wave conditions. The characteristics of tidal residual currents on an annual basis generally align with those observed during average tidal cycles (Figures 9A1, A2, 12A). Simulation results indicate that wind-induced currents typically flow from north to south; however, their speeds average below 0.01 m/s annually, rendering their impact on material transport negligible (Figure 12B). Conversely, the inclusion of wave-induced currents significantly augments the flow field within the sea area. In the northern section, currents flow from the bay top toward the sides, while in the central and southern sections, besides a clockwise eddy in the PME section, the predominant flow direction is southwest (Figure 12C). Wave-induced currents serve as the primary driver of the net annual flow of coastal waters along the beach, moving southwest at speeds approximately between 0.15 and 0.2 m/s. These currents are more than five times faster than regional tidal currents and over twenty times faster than wind-induced currents. Therefore, wave-induced currents are the dominant force in transporting beach sediments along the coast, resulting in a pattern of “northern erosion and southern accretion.”
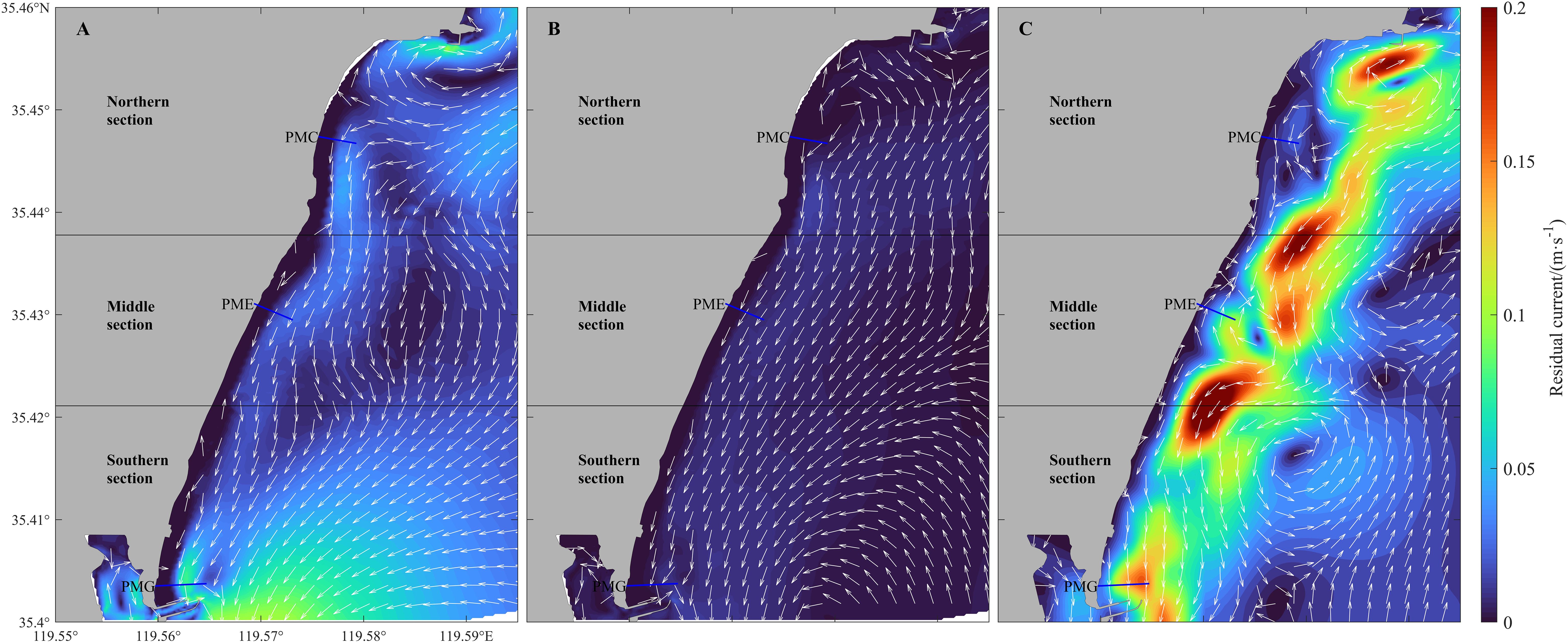
Figure 12. Distribution of annual residual currents at WPK beach. (A) represents annual average tidal currents, (B) displays annual average wind-induced currents, and (C) presents annual average wave-induced currents.
5.4 Limitation
This study only adopted a one-year timescale to analyze inter-annual variations, while the impact of sea level rise on the beach generally requires a timescale of several decades. Therefore, the impact of sea level changes on the beach was not considered in this study.
Sediment transport and topographic changes were not modeled in this study due to the lack of time-series observation data of sediment transport. Although the simulation analysis of hydrodynamic mechanism has been able to explain the sediment transport and shoreline change, the sediment simulation can show the material transport results of hydrodynamic mechanism more intuitively. In the next study, the collection or observation of sediment data will continue to be carried out to further improve the beach sediment transport simulation.
This study focuses on the dynamic mechanism of shoreline evolution of long straight beaches, where shoreline change is mainly characterized by alongshore sediment loss. The contribution of sediment loss in the offshore direction to the shoreline evolution is usually relatively small, so it is not considered in this study, and will continue to be investigated using other cross-sectional two-dimensional sediment transport model in the next study on the beach profile evolution.
6 Conclusion
In China, direct human activities harmful to beaches are strictly prohibited, which has led to emerging trends in how beaches adapt to ocean dynamics within complex shoreline configurations. To explore the hydrodynamic mechanisms behind beach changes across different timescales, extensive observations and numerical simulations were conducted at WPK beach, located in the southern part of the Shandong Peninsula. The findings reveal that WPK beach generally exhibits a pattern of “northern erosion and southern accretion.” The northern section undergoes significant erosion at a rate of approximately 2-3 m/a, the central section erodes more gradually at about 0.5-1.5 m/a, and the southern section experiences accretion at an average rate of about 1-2 m/a.
WPK beach demonstrates substantial seasonal variations. Offshore, during the winter, the region experiences brief northwesterly winds that generate relatively small wind waves with an average maximum significant wave height of about 0.5 m. The beach’s surface sediment is characterized by a relatively small average grain size with limited variability. Nevertheless, strong winds transport fine-grained sediments to the beach. In the summer, southerly winds dominate, leading to longer fetch areas and larger wind waves with an average maximum significant wave height of about 1 m. During this season, the beach’s surface sediment features a larger average grain size and greater variability, with a prevailing trend of sediment transport seaward. Alongshore, the primary forces driving sediment transport are wave-induced and tidal currents, both flowing southwestward. Wave-induced currents, with velocities ranging from 0.1 to 0.3 m/s, are significantly faster than tidal currents. Seasonal changes in beach processes are largely driven by episodic weather events, with wave-induced currents remaining the predominant force. In the summer, large wave events are more frequent, and daily wave-induced current velocities can peak at up to 0.8 m/s. Wave action initiates sediment movement, with wave-induced currents serving as the primary mechanisms for transporting sediment along the coast.
In the absence of terrestrial sediment supply, the long, straight beach exemplified by WPK beach undergoes long-term changes primarily due to alongshore sediment transport. Ocean dynamics, including wave-induced currents, tidal currents, and wind-induced currents, are the main factors influencing sediment transport along the coast. Among these, wave action is the most significant oceanic driving force. In different regions around the world, the strength of tidal and wind-induced currents will inevitably exhibit local variations due to factors such as tidal range and topography, necessitating specific analyses.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
KL: Writing – original draft, Software, Writing – review & editing, Formal analysis, Validation, Visualization. YH: Writing – review & editing, Formal analysis, Investigation, Data curation. NW: Writing – review & editing, Data curation, Validation, Conceptualization, Investigation, Methodology, Supervision, Writing – original draft. YF: Formal analysis, Investigation, Writing – review & editing, Funding acquisition, Resources. DS: Writing – review & editing, Conceptualization, Methodology, Software. YC: Data curation, Software, Writing – review & editing. HZ: Formal analysis, Investigation, Writing – review & editing, Data curation. ZR: Writing – review & editing, Data curation, Resources. XB: Writing – review & editing, Funding acquisition, Project administration, Resources, Supervision.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This study was financially supported by the National Natural Science Foundation of China (42076010, U1706215, 41876088), and the Taishan Scholar Foundation of Shandong Province, China (tsqn202211056).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allen J. I., Somerfield P. J., Gilbert F. J. (2007). Quantifying uncertainty in high-resolution coupled hydrodynamic-ecosystem models. J. Mar. Syst. 64, 3–14. doi: 10.1016/j.jmarsys.2006.02.010
Bartholomä A., Kubicki A., Badewien T. H., Flemming B. W. (2009). Suspended sediment transport in the German Wadden Sea—seasonal variations and extreme events. Ocean Dynam. 59, 213–225. doi: 10.1007/s10236-009-0193-6
Beach R. A., Sternberg R. W. (1992). Suspended sediment transport in the surf zone: Response to incident wave and longshore current interaction. Mar. Geol. 108, 275–294. doi: 10.1016/0025-3227(92)90201-R
Cai F., Cao H. M., Su X. Z., Xia D. X. (2007). Analysis on morphodynamics of sandy beaches in South China. J. Coast. Res. 23, 236–246. doi: 10.2112/04-0197.1
Cai F., Su X. Z., Liu J. B., Li B., Lei G. (2009). Coastal erosion in China under the condition of global climate change and measures for its prevention. Prog. Natural Sci. 19, 415–426. doi: 10.1016/j.pnsc.2008.05.034
Chen C., Liu H., Beardsley R. (2003). An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries. J. Atmos. Ocean. Technol. 20, 159–186. doi: 10.1175/1520-0426;2
Ding Y., Bao X., Yao Z., Bi C., Wan K., Bao M., et al. (2019). Observational and model studies of synoptic current fluctuations in the Bohai Strait on the Chinese continental shelf. Ocean Dynam. 69, 323–351. doi: 10.1007/s10236-019-01247-5
Ding Y., Bao X., Yao Z., Song D., Song J., Gao J., et al. (2018). Effect of coastal-trapped waves on the synoptic variations of the Yellow Sea Warm Current during winter. Continent. Shelf Res. 167, 14–31. doi: 10.1016/j.csr.2018.08.003
Gao G., Wang X., Song D., Bao X., Yin B., Yang D., et al. (2018). Effects of wave-current interactions on suspended-sediment dynamics during strong wave events in Jiaozhou Bay, Qingdao, China. J. Phys. Oceanogr. 48, 1053–1078. doi: 10.1175/jpo-d-17-0259.1
Hallermeier R. J. (1978). Uses for a calculated limit depth to beach erosion. Coast. Eng. Proc. 1, 88. doi: 10.1061/9780872621909.090
Houston J. R., Dean R. G. (2014). Shoreline change on the east coast of Florida. J. Coast. Res. 296, 647–660. doi: 10.2112/JCOASTRES-D-14-00028.1
Karambas T. V., Karathanassi E. K. (2004). Longshore sediment transport by nonlinear waves and currents. J. waterway port coastal ocean Eng. 130, 277–286. doi: 10.1061/(ASCE)0733-950X(2004)130:6(277
Kato S., Yamashita T. (2001). A three-dimensional model for wind and wave-induced coastal currents, and its verification by ADCP observations in the nearshore zone. Coast. Eng. 2000. 1, 3777–3790. doi: 10.1061/40549(276)295
Li G. X., Gong L. X., Yang J. C., Ding D., Li B., Cao L. H., et al. (2013). Beach erosion along the coast of Shandong Province and protection countermeasures. Mar. geol. Quater. geol. 33, 35–46. doi: 10.3724/SP.J.1140.2013.05035
Li L., Walstra D. J. R., Storms J. E. (2015). The impact of wave-induced longshore transport on a delta–shoreface system. J. Sediment. Res. 85, 6–20. doi: 10.2110/jsr.2014.95
Mellor G. L., Donelan M. A., Oey L. Y. (2008). A surface wave model for coupling with numerical ocean circulation models. J. Atmos. Ocean. Technol. 25 (10), 1785–1807. doi: 10.1175/2008JTECHO573.1
Mellor G. L., Yamada T. (1982). Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys. 20, 851–875. doi: 10.1029/RG020i004p00851
Nair L. S., Sundar V., Kurian N. P. (2015). Longshore sediment transport along the coast of Kerala in southwest India. Proc. Eng. 116, 40–46. doi: 10.1016/j.proeng.2015.08.262
Noujas V. (2016). Coastal hydrodynamics and sediment transport regime of the Central Kerala coast in comparison to Southern Kerala.
Pawlowicz R., Beardsley B., Lentz S. (2002). Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Comput. Geosci. 28, 929–937. doi: 10.1016/s0098-3004(02)00013-4
Smagorinsky J. (1963). General circulation experiments with the primitive equations, I. The basic experiment. Month. Weather Rev. 91, 99–164. doi: 10.1175/1520-0493(1963)091x0003C;0099:gcewtp>2.3.co;2
Song D., Wang X. H., Kiss A. E., Bao X. (2011). The contribution to tidal asymmetry by different combinations of tidal constituents. J. Geophys. Res. 116, C12007. doi: 10.1029/2011JC007270
Song D., Wang X. H., Zhu X., Bao X. (2013). Modeling studies of the far-field effects of tidal flat reclamation on tidal dynamics in the East China Seas. Estuar. Coast. Shelf Sci. 133, 147–160. doi: 10.1016/j.ecss.2013.08.023
Song D., Wu W., Li Q. (2021). Effects of wave-current interactions on bay-shelf exchange. J. Phys. Oceanogr. 51, 1637–1654. doi: 10.1175/JPO-D-20-0222.1
Tang J., Lyu Y., Shen Y. (2016). Numerical simulation of sediment transport in coastal waves and wave-induced currents. Acta Oceanol. Sin. 35, 111–116. doi: 10.1007/s13131-016-0932-8
Van-Rijn L. C. (2011). Coastal erosion and control. Ocean Coast. Manage. 54, 867–887. doi: 10.1016/j.ocecoaman.2011.05.004
Xie L., Wu K., Pietrafesa L., Zhang C. (2001). A numerical study of wave-current interaction through surface and bottom stresses: Wind-driven circulation in the South Atlantic Bight under uniform winds. J. Geophys. Res.: Oceans 106, 16841–16855. doi: 10.1029/2000JC000292
Xie M. (2011). Establishment, validation and discussions of a three dimensional wave-induced current model. Ocean Model. 38, 230–243. doi: 10.1016/j.ocemod.2011.03.006
Yin P., Duan X., Gao F., Li M., Lü S., Qiu J., et al. (2018). Coastal erosion in Shandong of China: status and protection challenges. China Geol. 1, 512–521. doi: 10.31035/cg2018073
Yu X. Q., Yu J. (2020). Policy development, current problems and recommendations for coastal ecological restoration in China. Chin. Fish. Econ. 38, 8–16. doi: 10.3969/j.issn.1009-590X.2020.05.002
Zhang J., Song D., Wu W., Bao X. (2019). Impacts of human activities on tidal dynamics in a sexta-diurnal tidal resonant bay. Anthropocene Coasts 2, 126–144. doi: 10.1139/anc-2018-0011
Zhuang Z. Y., Chen W. M., Xu W. D., Shen C. L. (1989). Retrogression of straight sandy beaches in the Shandong Peninsula and its results. J. Ocean Univ. Qingdao 19, 90–98. doi: 10.16441/j.cnki.hdxb.1989.01.009
Zhuang Z. Y., Yin P., Wu J. Z., Zhuang L. H. (2000). Coastal erosion and its influence on southern Shandong sandy coast. Mar. Geol. Quater. Geol. 20, 15–21. doi: 10.16562/j.cnki.0256-1492.2000.03.003
Appendix: model description
A.1 Wetting-drying grid
For the intertidal zone, FVCOM incorporates a wetting-drying grid technique into the three-dimensional unstructured grid model. A viscous boundary layer thickness is added to the bottom layer in the σ coordinate, and the wetting/drying criteria are defined as follows:
For grid points: is considered a wet point; is considered a dry point.
For triangular grids: is considered a wet grid; is considered a dry grid.
Where D represents the water depth, H is the reference water depth, is the water surface elevation, is the shoreline height, and are the indices of the three vertices of the triangular grid.
When a triangular grid becomes a dry grid, the flow velocity within that grid is defined as zero, and there is no flow at the grid’s boundary. This triangular grid is removed from flow calculations. Only the flow in wet grids is considered during flow computations, ensuring conservation of fluid volume (Chen et al., 2003).
A.2 Governing equations of the model
(1) Governing Equation
In the vertical direction, the model uses a σ coordinate transformation, defined as:
Under the σ coordinate transformation, the system of control equations for the model includes:
The horizontal diffusion term is formulated into:
In the equation, and represent the horizontal eddy viscosity coefficient and diffusion coefficient, respectively; ; f denotes the Coriolis parameter; and indicate the vertical turbulent viscosity coefficient and vertical diffusion coefficient, respectively; expresses the vertically transformed velocity component.
The determination of and is based on the Mellor-Yamada 2.5-order closure model (Mellor and Yamada, 1982; Chen et al., 2003) and the Smagorinsky closure model (Smagorinsky, 1963; Chen et al., 2003), ensuring the mathematical closure of the model equations.
(2) Boundary conditions (Chen et al., 2003)
1) Free surface boundary condition :
For pure astronomical tides, the wind stress satisfies ;
2) Boundary condition near the seabed :
Where and , represents the Karman constant, indicates the seabed roughness, and is the distance from the nearest grid to the seabed.
3) Shoreline boundary conditions:
Here, represents the direction of the normal vector outward from the coastline.
4) Boundary conditions:
(3) Wave model (Gao et al., 2018)
The FVCOM-MDOWAVE employs the frequency-averaged wave energy equation:
The horizontal coordinates are represented as and ; the vertical coordinate in sigma coordinates is denoted as to avoid confusion with the wave frequency , where indicates the water depth, and represents the total water depth, with H denoting the mean water depth; z is the vertical upward coordinate, with located at mean sea level.
The first term on the left side of the equation, , represents the average wave energy spectrum,
where represents the kinetic energy of the wave spectrum when the seawater density is not considered. The overline in the second term on the left side represents the average value of the wave spectrum.
The above two factors determine the propagation of wave energy in both temporal and horizontal spatial dimensions. The third factor is the refraction term, which is related to the change in the direction of wave energy propagation. represents the Doppler velocity; represents the refraction velocity. and are specifically defined as:
The last term on the left side of the equation represents the energy exchange in the average velocity energy equation. represents the wave radiation stress term; is the ocean current and Stokes drift term, with , where is the total wave energy, c indicates the phase velocity, , and is the wave number vector. represents the dominant wave direction, which is calculated through .
All terms in Equation 12 are functions of the wave spectrum, θ. On the right side of the equation, represents the source term for wave energy, determined by the wind; and are wave dissipation terms, determined by the processes of waves at the sea surface and seabed, respectively. All terms are in kinematic units (i.e., energy terms are divided by seawater density), thereby representing the atmospheric action on seawater as .
The frequency is determined by θ, as shown in the following equation:
Where , with . near the θ, and waves are driven by the wind, with as an additional source term.
Here, represents the peak frequency, while the propagation equation is formulated into .
Keywords: sandy coast, Wanpingkou beach, sedimentary dynamics, FVCOM, geomorphology evolution
Citation: Li K, Hao Y, Wang N, Feng Y, Song D, Chen Y, Zhang H, Ren Z and Bao X (2024) Hydrodynamic mechanisms of topographic evolution in straight sandy beach: a case study of Wanpingkou beach, China. Front. Mar. Sci. 11:1488610. doi: 10.3389/fmars.2024.1488610
Received: 30 August 2024; Accepted: 21 October 2024;
Published: 12 November 2024.
Edited by:
Li Li, Zhejiang University, ChinaCopyright © 2024 Li, Hao, Wang, Feng, Song, Chen, Zhang, Ren and Bao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Wang, d2FuZ25hbjA1MTVAb3VjLmVkdS5jbg==
 Kang Li1,2
Kang Li1,2 Yi Hao
Yi Hao Nan Wang
Nan Wang Dehai Song
Dehai Song