South Atlantic meridional overturning circulation and its respective heat and freshwater transports from sustained observations near 34.5°S

The Atlantic Meridional Overturning Circulation (AMOC) drives northward Meridional Heat Transport (MHT) and affects climate and weather patterns, regional sea levels, and ecosystems. This study uses a methodology recently applied in 22.5°S to estimate the strength and structure of the AMOC, MHT and freshwater (FWT) transports at 34.5°S since 2005. For this, temperature and salinity profiles from sustained observations were used in conjunction with satellite and reanalysis data under two mapping methodologies: (i) an optimized mapping and (ii) a two-layer feed-forward neural network approach. There is strong agreement between both methods for AMOC, MHT and FWT estimates, thus showing the mapping methodologies are robust. In addition, the AMOC variability estimate is significantly correlated with the monthly SAMBA array data (correlation of 0.41). The mean AMOC transport of 17.0 ± 1.6 Sv, a MHT of 0.6 ± 0.1 PW, and a FWT of -0.02 ± 0.01 Sv are estimated between January 2005 and May 2023 at 34.5°S. The MHT and FWT are analyzed in terms of their horizontal (Hhor and Fhor) and overturning contributions (Hov and Fov), and vertical structures. The MHT is dominated by the overturning contribution (correlation of 0.92), while the FWT is controlled by the overturning contribution driven by the wind via Ekman transport at seasonal timescale, and by horizontal contribution at longer timescales. Both horizontal heat (Hhor) and freshwater (Fhor) components are mostly confined to the upper 500 m, with the geostrophic Fov and Fhor offsetting each other between 50 m and 500 m, and the Ekman Fov in the upper 50 m determining the negative FWT. Finally, the estimated mean Fov of -0.15 Sv agrees with previous estimates that the AMOC exports freshwater in the South Atlantic, and suggests that the AMOC is unstable. Although a long-term trend in the Fov was not detected in the past 20 years, there is a salinification trend (0.05 ± 0.01 PSU/decade) in the upper 300 m near 34.5°S since 2005.

1 Introduction

The Atlantic Meridional Overturning Circulation (AMOC) represents one of the key components of the Earth's climate system, influencing heat and freshwater distribution across the Atlantic Ocean (Collins et al., 2019; Todd et al., 2019). Its role in regulating climate, sea level, and the redistribution of heat, freshwater, carbon and nutrients makes understanding its behavior essential for climate predictions (Zhang and Delworth, 2006; Chang et al., 2008; Lopez et al., 2016; Johns et al., 2023; Volkov et al., 2023). However, despite its significance, numerous challenges persist in accurately modeling, observing and quantifying the AMOC, and its derived quantities such as heat (MHT) and freshwater (FWT) transports (Chidichimo et al., 2023; Jackson et al., 2023).

The International Panel on Climate Change (IPCC) states that a weakening of the AMOC by the end of the 21^st century is very likely (Collins et al., 2019; Fox-Kemper et al., 2021; Lee et al., 2021). Recent studies using AMOC proxies and fingerprints suggest that a decrease in the AMOC is underway (Caesar et al., 2018, 2021; Zhu and Liu, 2020; Zhu et al., 2023). Observations from various sources show that the deep and abyssal transports may be slowing down and becoming more buoyant with a warming trend (Campos et al., 2021; Biló et al., 2024), which points to a possible weakening of the water mass formations at convection zones, one of the engines of the AMOC. Currently, the only AMOC observing system that shows an AMOC weakening is the RAPID array at 26.5°N (Johns et al., 2023). However, the inherent complexities of AMOC, due to the multiplicity of periodicities and latitudinal inhomogeneities, combined with the short duration of the direct measurements from RAPID and other mooring arrays, pose challenges in inferring decadal to centennial AMOC changes. Additionally, the instability of the AMOC fingerprints and their sensitivity to other physical processes, as well as the inadequacy of some localized paleo proxies to infer basin-scale ocean circulations, can induce a large uncertainty in these estimates on long-term inferences of the AMOC behavior (Kilbourne et al., 2022).

The FWT can be separated in overturning (Fov) and horizontal (Fhor) contributions, and its overturning contribution in the South Atlantic has been used as an indicator for AMOC stability (Drijfhout et al., 2011; Weijer et al., 2020; Chidichimo et al., 2023). A positive (northward) Fov generally suggests a stable AMOC, whereas a negative (southward) Fov implies an unstable AMOC. This relationship stems from the salt-advection in the Atlantic basin, which can operate under two scenarios (Rahmstorf, 1996): i) when Fov is positive, freshwater imports into the Atlantic basin could lessen in a potential AMOC weakening, resulting in a saltier basin and an AMOC strengthening (stable AMOC case); ii) when Fov is negative, the Atlantic basin exports freshwater, but reduced freshwater exports during an AMOC weakening event would lead to a freshwater basin, which would promote further weakening of the AMOC (unstable AMOC case). While climate models tend to classify the AMOC as stable, observations and ocean reanalysis tend to categorize the AMOC as unstable (Liu et al., 2017).

Long-term trends in South Atlantic FWT could be a useful tool for early detection of a possible AMOC shutdown (van Westen et al., 2024). The Coupled Model Intercomparison Project Phase 6 (CMIP6) ensemble predicts an AMOC decrease of 34-45% until 2100 (Weijer et al., 2020). Earlier studies have focused on these early signals for a possible AMOC weakening using FWT or salt content anomalies (e.g., Zhu and Liu, 2020; Zhu et al., 2023). Zhu and Liu (2020) suggested that anthropogenic warming could lead to an increase in the South Atlantic salinity due to reduced basin-wide salinity divergence caused by AMOC weakening, since results show the reduction in salinity transport north of 34.5°S would be greater than south of 34.5°S. On the other hand, other studies suggest that the Fhor is the main driver at interannual FWT, rather than the overturning component at 34.5°S (Mignac et al., 2019; Liu et al., 2023). Mignac et al. (2019) used free-running models and ocean reanalysis to demonstrate that in the South Atlantic, the AMOC is not strongly associated with FWT due to the presence of Antarctic Intermediate Water, which reduces salinity differences between the AMOC branches. Their findings indicate that the primary control over South Atlantic FWT is governed by zonal salinity differences in the upper 300 m, which significantly affect Fhor. Given their importance, more observational-based FWT estimates are encouraged (Chidichimo et al., 2023). Therefore, the necessity for continuous and accurate observations is evident to capture the full spectrum of the AMOC's dynamics.

An optimal approach for expanding the observation system remains undetermined (Frajka-Williams et al., 2023; Srokosz et al., 2023), and several efforts are in place to fill the gaps of the AMOC observing system, including in the South Atlantic. The longest AMOC observing system in the South Atlantic is the South Atlantic Meridional Overturning Circulation Basin-wide Array (SAMBA) at 34.5°S, which is based on Pressure Inverted Echo Sounders (PIES) on both sides of the basin, and its most updated time series ranges from 2009 to 2017, with some gaps between 2010 and 2014. The SAMBA array has evolved to include more than 20 moorings across the basin, which has also increased the estimated AMOC variability at that latitude (Kersalé et al., 2021; Frajka-Williams et al., 2023) compared to previous estimate (Meinen et al., 2018). Nonetheless, AMOC variability from the SAMBA array estimates tends to be greater than the estimates based on synthetic methods, inverse models, and eXpendable BathyThermograph (XBT) measurements (Garzoli et al., 2013; Dong et al., 2015; Goes et al., 2015; Majumder et al., 2016; Kersalé et al., 2020, 2021; Caínzos et al., 2022; Baker et al., 2023; Arumí-Planas et al., 2024). The SAMBA array estimates a monthly-mean standard deviation for the AMOC of 11.35 Sv (Baker et al., 2023), while other estimates are not higher than 3.48 Sv (Dong et al., 2015; Majumder et al., 2016; Caínzos et al., 2022; Arumí-Planas et al., 2024). AMOC estimates from the SAMBA array have geostrophic and Ekman components in phase (i.e., increasing total AMOC variability) while synthetic estimates perceive both AMOC components out of phase, leading to a decrease in variability on the monthly-mean, interannual and seasonal signals (Dong et al., 2021; Baker et al., 2023). Those differences are mainly observed on the geostrophic component, where both barotropic and baroclinic components have similar phase in SAMBA and are out of phase in other products. Baker et al. (2023) suggest that those differences could be partially explained by different methods of estimating the barotropic velocity at the reference level.

The typical processing delay in generating AMOC time series from mooring-based observational array systems can extend up to 18 months post-recovery of instruments, which prevents the monitoring and analysis of the AMOC in near-real timescales (Srokosz et al., 2023), and can be subject to instrument density changes due to operational costs. To fill gaps, expand in time, and obtain a faster time series update, methods have been developed that are based on statistical relationships between satellite altimetry sea level and sustained hydrographic data to reconstruct the AMOC in several latitudes (Willis, 2010; Dong et al., 2015; Majumder et al., 2016). In a recent paper, Pita et al. (2024) developed a methodology that instead used altimetry-derived sea level to optimize the mapping of ocean profiles along a nominal transect across the South Atlantic basin, which for the first time provided an AMOC time series at 22.5°S from 2007 to 2023. This was possible due to the high-resolution XBT data sampling at the western boundary, and the Argo float data across the basin. The high-resolution XBT measurements, Argo data, and trans-basin conductivity-temperature-depth (CTD) section at 34.5°S make it another candidate to use this low-cost observational method, which, if validated, can complement the observations from the SAMBA array at that latitude.

In this study, we estimate the AMOC, heat and freshwater transports at 34.5°S using sustained observations calibrated with satellite altimetry measurements. We compare the results with the SAMBA array, and with another method based on machine learning to shed light on the effect of mapping choices on the AMOC estimates. These estimates allow us to understand the vertical and zonal structure of the heat and freshwater transports into the Atlantic Ocean, which has critical impacts on the stability and prediction of AMOC variability.

2 Data and methods

2.1 In-situ profile data

Observational data from three high-density XBT transects: AX08 (Cape Town-New York), AX18 (Cape Town-Buenos Aires) and AX25 (Cape Town-Antarctica), as well as Argo profiling floats and CTD stations collected from 2005 to 2023 between 27.5°S and 40°S, are used to build a trans-basin transect at 34.5°S (Figure 1). The XBT probes measure temperature (T) from the surface to depths of about 800 m, the standard Argo floats measure T and salinity (S) down to 2000 m, and CTD stations measure T and S for the entire water column. The southern boundary (40°S) is selected to avoid the signal from the subtropical front, which is known to be the limit between the subtropical domain and the subantarctic region (Chen et al., 2022).

Figure 1

Figure 1. Data distribution of Argo, XBT and CTD profiles between 2005 and 2023 for the South Atlantic Ocean (27.5°S and 40°S). The number of profiles located in a 1° x 1° box centered at a specific coordinate along the reference transect (A). Histograms of data density in time (B) and space (C) as well as profile location (D) are shown. Argo, XBT and CTD datasets are represented by colors blue, red and yellow, respectively.

The average temporal sampling frequency of the AX08 and AX18 transects is 4 repetitions per year, while AX25 has 2 to 3 repetitions per year during austral summer months. The average horizontal sampling ranges from 18 to 27 km. XBT data are obtained from the NOAA/AOML database (XBT Network, 2024), and the salinity profile corresponding to each XBT temperature profile is derived using a seasonal regression method developed by Goes et al. (2018). The delayed-mode Argo profile data (Argo, 2024) used in this study are from the Global Argo Data Repository of the National Centers for Environmental Information (NCEI). Only adjusted Argo T-S profiles flagged as good or probably good are used. The disparity found in some profiles, for which the available S data were fewer than the T data, was circumvented by applying the seasonal regression method (Goes et al., 2018) to estimate S from the Argo-measured T profiles.

To complete the profiles for the full water column, i.e., below 800 m for XBT data and below 2000 m for Argo data, T-S climatology from NCEI World Ocean Atlas 2018 (WOA18) at 0.25° horizontal resolution is used, which is at monthly averages between 800 and 1500 m, and seasonal averages below 1500 m (Locarnini et al., 2019; Zweng et al., 2019; Garcia et al., 2019). Monthly WOA18 data have 57 vertical levels from 0 to 1500 m, and seasonal data have 112 vertical levels from 0 to 5500 m.

2.2 Auxiliary data

Daily sea level anomaly (SLA) data on a ¼° grid from a multi-satellite altimetry mission, processed and distributed by the Copernicus Marine and Environment Monitoring Service (CMEMS; Pujol et al., 2023), and ¼° gridded Daily Optimum Interpolation Sea Surface Temperature (DOISST; Huang et al., 2020) were interpolated to the location of the in-situ T-S profiles and used as inputs for machine learning algorithms described below.

We use monthly SLA data from January 1993 to June 2023 from CMEMS (Pujol et al., 2016, 2023) for calibration of the optimal interpolation parameters of the mapping method for the scattered observations as well as for training and validating neural networks. The 20-year mean dynamic topography (Mulet et al., 2021) is added to SLA to obtain the sea surface height fields. To avoid time-varying biases during the mapping optimization phase, linear trends are removed from the fields at each longitude of the reference transect.

Monthly zonal wind stress data from the ERA5 atmospheric reanalysis (Hersbach et al., 2020) are used to estimate the Ekman component of the AMOC. ERA5 wind stress surface data are available at a 0.25° horizontal grid since 1979 and are linearly interpolated to the 34.5°S reference section for the period January 2005 to May 2023.

A comparison with the T and S data from the Met Office Hadley Centre “ENACT/ENSEMBLES” series version 4 (EN4, Good et al., 2013) and the Ocean Reanalysis System 5 (ORAS5, Zuo et al., 2019) from the European Centre for Medium-range Weather Forecast (ECMWF) is performed along the reference transect. This comparison allows us to understand how products with different spatial resolutions, including AXMOC, observe upper ocean T and S dynamics. Monthly T and S EN4 (ORAS5) products are provided on 1° (1/4°) horizontal resolution and 42 (75) vertical levels from January 2000 to December 2023 (January 2002 to December 2022).

The synthetic monthly AMOC and MHT time series from Dong et al. (2021) are compared against optimal mapping and neural network approaches (see section 2.3). In their methodology, Dong et al. (2021) establish a linear relationship between isotherm depths from in-situ temperature profiles and SLA from satellite altimetry for T ranging between 3°C and 28°C. These linear relationships are used to generate synthetic T profiles by enforcing SLA at each longitude along the 34.5°S section. SST for each synthetic profile is obtained from DOISST, and the corresponding salinity profiles are inferred using the T/S relationship from Goes et al. (2018). Geostrophic AMOC transport is calculated with a reference level of 1000 m, based on Argo-derived velocities (Lebedev et al., 2007). The Ekman component of the AMOC is estimated using monthly mean wind stress data from ERA5. To ensure zero net mass transport across the section, a uniform velocity correction is applied across the section.

2.3 High-resolution T/S reference section mapping methods

To reconstruct the AMOC at 34.5°S, we define a reference section (AXMOC), crossing the basin from 60°W to 20°E. Along the reference section, monthly gridded T-S profiles are produced with 1/4° spatial resolution from January 2005 to May 2023, on 140 depth levels (10 m intervals between 5-745 m, 50 m intervals between 745-2000 m, and 100 m intervals between 2000-6000 m). We developed two methods to map the observed data onto the reference section: i) an optimal mapping (OM), which uses weighted averages of the profiles given a temporal and a spatial parameter (Δt and ΔR; respectively), optimized to minimize the root mean square error (RMSE) between in-situ dynamic height and sea surface height derived from satellite altimetry; and ii) a machine learning algorithm, trained, evaluated and applied to ocean profiles using additional predictor variables. Further details on the two methodologies are given below.

2.3.1 Optimal mapping

The mapping method used to reconstruct T and S profiles along the reference section consists of weighted averages (Goes et al., 2010, 2020; Pita et al., 2024) using a normalized separable exponential function in space (ΔR) and time (Δt). Pre-defined values for ΔR (0.25°, 0.50°, 1°, 3° and 5° radius) and Δt (30, 60, 90 and 180 days) were used, following the method of Pita et al. (2024).

The optimal T-S section was obtained by selecting the mapping parameters ΔR and Δt locally that minimize the RMSE (used as a cost function) between the absolute dynamic height and the sea surface height data interpolated to the reference section (Figure 1D). The absolute dynamic height of each parameter subset was referenced to 1000 m, and the absolute geopotential field from a blended Argo/altimetry climatology product was added at this level, following a similar methodology for absolute dynamic height calculation described by Goes et al. (2019), though using a different reference level. During calibration, both datasets (Altimetry and AXMOC) were detrended in time to avoid misfits due to the mass and barotropic components of the variability in altimetry data. For more information on OM, see Supplementary Material (Supplementary Text S1).

2.3.2 Neural network

Two machine learning algorithms based on feed-forward neural networks (NN; Beale et al., 2024) were created: one for the T field (NN_T) and the other for the S field (NN_S). Both NN_T and NN_S were constructed using the “feedforwardnet” function and trained using the “train” function from Version 14.4 of the Deep Learning Toolbox for MATLAB (R2022a). Each NN had two hidden layers, with 20 neurons in the first layer and 10 neurons in the second layer. The NN structure was chosen after some trials to balance computational cost and algorithm performance. A similar NN structure was used for global oxygen mapping (Sharp et al., 2023). The NNs were fed with normalized profile position data (e.g., latitude, longitude, depth, year, day of the year) as well as surface satellite data (SLA and SST, interpolated to the profile position).

Considering the number of inputs (N₀ = 8), the number of nodes in both hidden layers (N₁ = 20 and N₂ = 10) and the number of outputs for each NN (N₃ = 1), according to Equation 1, the total trainable parameters (P) of each NN is 401 (370 weights, and 31 bias components).

$\begin{array}{ll}\mathit{P}={\mathit{N}}_{\mathbf{0}}{\mathit{N}}_{\mathbf{1}}\mathbf{+}{\mathit{N}}_{\mathbf{1}}{\mathit{N}}_{\mathbf{2}}\mathbf{+}{\mathit{N}}_{\mathbf{2}}{\mathit{N}}_{\mathbf{3}}\mathbf{+}({\mathit{N}}_{\mathbf{1}}\mathbf{+}{\mathit{N}}_{\mathbf{2}}\mathbf{+}{\mathit{N}}_{\mathbf{3}})& (1)\end{array}$

Both NNs were trained using a Levenberg-Marquardt algorithm and 80% of the available T and S profiles. During the training phase, 15% of the training data was reserved for testing the NN during training epochs and the number of epochs available for training was set to 2000. The same T and S profiles were used in the training phase for both NNs.

The effectiveness of the machine learning algorithm used to estimate T and S sections was tested by comparing the output of the NN (NN_Eval) to the in-situ T and S data (Target) using the subset of the remaining 20% of profiles (see Supplementary Figure S1). This exercise was intended to evaluate the ability of the machine learning scheme to reproduce measured data that was not included in algorithm training. The RMSE between NN_Eval and Target are 0.51°C and 0.07 PSU for T and S, respectively.

2.4 AMOC, MHT and FWT time series

The AMOC and MHT across the reference section are calculated following published methodologies for the South Atlantic (e.g., Dong et al., 2015, 2021; Goes et al., 2015, 2020; Pita et al., 2024). The AMOC is defined as:

$\begin{array}{ll}{\mathbf{\text{Ψ}}}_{\mathbf{\text{y}}}\mathbf{(}\mathit{z}\mathbf{)}\mathbf{=}\underset{{\mathit{x}}_{\mathit{E}}}{\overset{{\mathit{x}}_{\mathit{W}}}{{\displaystyle \int }}}\underset{-\mathit{H}}{\overset{\mathit{z}}{{\displaystyle \int }}}\mathit{v}\mathbf{(}\mathit{x},\mathit{z}\mathbf{)}\mathit{d}\mathit{x} \mathit{d}\mathit{z}& (2)\end{array}$

where the AMOC streamfunction across a zonal section (${\Psi }_y$) is the integral of the meridional velocity ($v$; adjusted to ensure zero net volume transport across the section) from the bottom ($H$) to depth ($z$) and between the western ($x_W$) and eastern ($x_E$) boundaries. $v$ consists of the sum of the meridional components of the absolute geostrophic velocity and the Ekman velocity. The AMOC intensity at any given time is defined at the streamfunction maximum, and is generally located around 1000 m.

The MHT is defined as:

$\begin{array}{ll}\mathit{M}\mathit{H}\mathit{T}={\mathbf{\text{ρ}}}_{\mathbf{0}}{\mathit{c}}_{\mathit{p}}\underset{{\mathit{x}}_{\mathit{E}}}{\overset{{\mathit{x}}_{\mathit{W}}}{{\displaystyle \int }}}\underset{-\mathit{H}}{\overset{\mathbf{0}}{{\displaystyle \int }}}\mathit{v}(\mathit{x},\mathit{z})\mathit{\theta }(\mathit{x},\mathit{z})\mathit{d}\mathit{x} \mathit{d}\mathit{z}& (3)\end{array}$

where ${\rho }_0$ is the mean water density ($1025 kg m^{-3}$), $c_p$ is the specific heat of the seawater ($4187J{k}^{-1}{K}^{-1}$), and $\theta$ is the potential temperature along the section. Since the mass balance is enforced across the section, the heat transport calculation is independent of the reference temperature (Jayne and Marotzke, 2001) or can otherwise be assumed to be 0°C (Johns et al., 2011, 2023; Dong et al., 2015; 2021; Majumder et al., 2016; Kersalé et al., 2021).

The FWT is defined as:

$\begin{array}{ll}\mathit{F}\mathit{W}\mathit{T}=-\frac{\mathbf{1}}{{\mathit{S}}_{\mathbf{0}}}\underset{{\mathit{x}}_{\mathit{E}}}{\overset{{\mathit{x}}_{\mathit{W}}}{{\displaystyle \int }}}\underset{-\mathit{H}}{\overset{\mathbf{0}}{{\displaystyle \int }}}\mathit{v}(\mathit{x},\mathit{z})(\mathit{S}-{\mathit{S}}_{\mathbf{0}})\mathit{d}\mathit{x} \mathit{d}\mathit{z}& (4)\end{array}$

where the reference salinity $S_0$ is the mean section salinity varying in time (mean of 34.76 ± 0.001 PSU). By definition, the freshwater transport is dependent on a reference salinity S₀. Talley (2008) selected S₀ based on the average salinity of multiple sections analyzed. When multiple sections are used, the values for reference salinity typically range from 34.7 to 35 (Rahmstorf, 1996; Weber et al., 2007; Talley, 2008, Arumí-Planas et al., 2023).

The AMOC, MHT, and FWT are composed of geostrophic and Ekman components. The geostrophic velocity field is computed from the thermal wind equation, using the OM and NN T-S data. Sensitivity experiments were performed for 4 different constraints. We tested two levels of no-motion references at 1000 m and 3700 m, and two Argo-based parking velocity products as references at 1000 m from Schmid (2014) and Lebedev et al. (2007); Supplementary Figure S2). All methods produce similar variability but different mean AMOC states. This difference arises mainly from the western boundary, where the barotropic component is more intense (Baringer and Garzoli, 2007). Using Schmid (2014) product, the velocity at the western boundary reaches up to -0.08 m/s, while using Lebedev et al. (2007) product, the velocity reaches up to -0.02 m/s. Mean southward bottom velocity west of 45°W reaches values up to -0.06 m/s, -0.02 m/s, -0.01 m/s and -0.00 m/s using Schmid (2014); Lebedev et al. (2007), 1000 m and 3700 m as reference, respectively. Here, we adopted a temporally constant and zonally varying Argo-based parking velocity product (Schmid, 2014) as a reference level at 1000 m to represent the barotropic velocity, since it produces mean AMOC strength similar to values published at 34.5°S (Dong et al., 2015; 2021; Meinen et al., 2018; Kersalé et al., 2020). Similar reference level was also adopted by previous studies (e.g., Dong et al., 2015; 2021; Garzoli et al., 2015; Majumder et al., 2016; Vilela-Silva et al., 2023). A zero net volume transport constraint is applied to the section at each month by adjusting the velocity field with a constant, calculated from the integrated transport across the section divided by the area of the section. This method is a classical approach to estimate the AMOC and MHT (e.g., Dong et al., 2015, 2021; Goes et al., 2015, 2020; Pita et al., 2024). The geostrophic AMOC streamfunction is estimated from the adjusted velocities ($v$, Equation 2), and its strength is defined as the maximum value of ${\Psi }_y$ at each timestep. The Ekman component, estimated using the 1/4° monthly ERA5 reanalysis zonal mean surface wind stress data (Hersbach et al., 2020), is integrated to the depth of the Ekman layer, which is considered to be 50 m deep. The meridional Ekman velocity was considered as its zonal average across 34.5°S. The Ekman transport is compensated barotropically below 50 m by ensuring the mass balance of the section. The AMOC, MHT, and FWT represent the sum of Ekman and geostrophic components. The time series of the AMOC, MHT, and FWT span from January 2005 to May 2023.

The MHT and FWT can be separated into two components: the meridional overturning component (Hov and Fov, respectively) and the horizontal component (Hhor and Fhor, respectively). For FWT the components are calculated as:

$\begin{array}{ll}\mathit{F}\mathit{o}\mathit{v}=-\frac{1}{S_0}\underset{-\mathit{H}}{\overset{\mathbf{0}}{{\displaystyle \int }}}\overline{v}(z)[\langle S(z)\rangle -S_0] dz& (5)\end{array}$

$\begin{array}{ll}\mathit{F}\mathit{h}\mathit{o}\mathit{r}=-\frac{1}{S_0}\underset{-\mathit{H}}{\overset{\mathbf{0}}{{\displaystyle \int }}}\overline{v^{\prime }(z)S\text{'}(z)} dz& (6)\end{array}$

where the overbar and the brackets< > denote zonal integration and zonal averaging, respectively, and $v\text{'}$ and $S$ ’ are deviations from zonal means (Weber et al., 2007). For MHT the decomposition is calculated similarly (Johns et al., 2011). The overturning components of MHT and FWT are further divided into geostrophic (Hov_g and Fov_g, respectively) and Ekman contributions (Hov_E and Fov_E, respectively) by using the meridional components of the geostrophic velocity and Ekman velocities instead of the total meridional velocity on Equations 5, 6, therefore:

$\begin{array}{ll}MHT = Hov + Hhor = Ho{v}_g + Ho{v}_E + Hhor & (7)\end{array}$

$\begin{array}{ll}FWT = Fov + Fhor = Fo{v}_g + Fo{v}_E + Fhor & (8)\end{array}$

The time series analyzed here are smoothed on a 3-month temporal scale. The seasonal cycle is considered the monthly averages of nearly two decades worth of data. The interannual signals are obtained by applying a low-pass filter (13-month gaussian filter) on the anomaly time series (without seasonal cycle).

3 Results and discussion

Our results are structured into three subsections: an initial comparison of the methods (OM and NN) and the analysis of AXMOC-derived time series for AMOC, MHT and FWT [AXMOC data is compared against SAMBA array and synthetic estimates (D35S; Dong et al., 2021) at 34.5°S]; the decomposition of MHT and FWT into geostrophic and Ekman, and into overturning and horizontal components and their distribution across the water column; and finally an examination of potential long-term trends, leveraging nearly two decades of data in our time series.

3.1 Method comparison and AMOC, MHT and FWT estimates

Both OM and NN mapping methods yield similar AMOC, MHT and FWT values (Figure 2). The correlation coefficients between OM and NN are 0.72 for AMOC, 0.85 for MHT and 0.92 for FWT, with scatter plots closely aligning along the identity line (x=y), indicative of the robustness and reliability of both methods (Figures 2B, D, F). The AMOC variability (using standard deviation as a proxy) is similar for both methods (4.28 Sv for OM and 4.21 Sv for NN) and for the MHT (0.20 PW for OM and 0.19 PW for NN), and the same for the FWT (0.09 Sv for both OM and NN) estimates. Given the similarity of the results presented by both methods, the OM method will be used onwards to compare to other estimates.

Figure 2

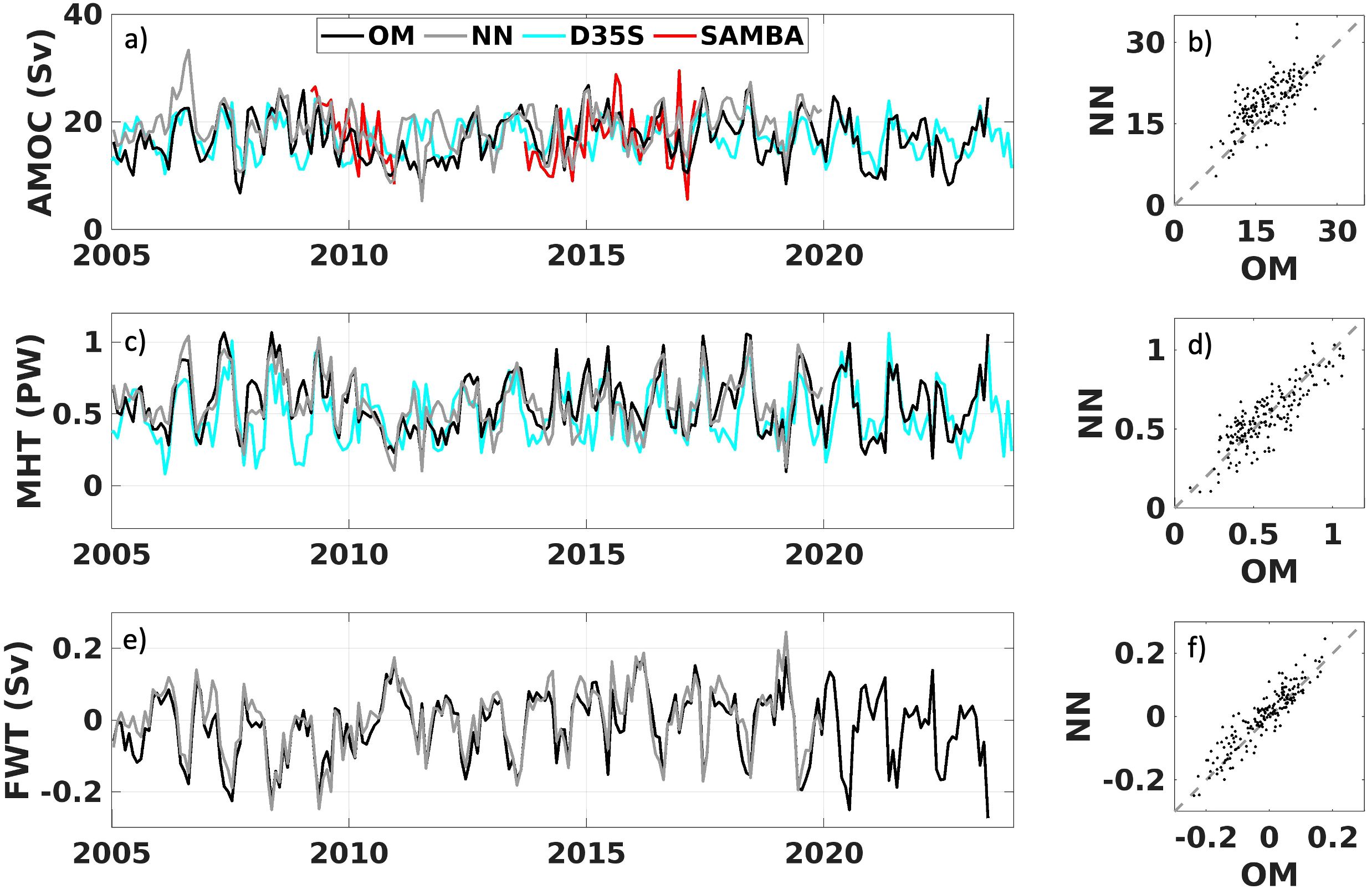
Figure 2. Differences from optimal mapping (OM) and neural network (NN) methods. AMOC (Sv - A), MHT (PW - C) and FWT (Sv - E) time series at 34.5°S for both methods and respective regression plots (B, D, F respectively) are presented. Black (gray) lines represent OM (NN). SAMBA (red line) AMOC and D35S (blue lines) AMOC and MHT time series are shown (A, C). The correlation coefficients between OM and NN are 0.72 for AMOC (B), 0.85 for MHT (D) and 0.92 for FWT (F).

The mean (standard deviation) transport values derived from AXMOC are 17.0 (4.3) Sv for AMOC, 0.6 (0.2) PW for MHT and -0.02 (0.09) Sv for FWT between January 2005 and May 2023 (Figure 2; Table 1). The mapping uncertainty for the AMOC was estimated as the standard error of the AMOC time series among all the 20 hyperparameter subsets (i.e. varying Δt and ΔR). The uncertainty for MHT and FWT was estimated the same way. These uncertainties of the AMOC, MHT and FWT are ±1.6 Sv, ± 0.1 PW and ±0.01 Sv, respectively. Several factors contribute to uncertainties in the final AMOC, MHT, and FWT estimates, beyond mapping errors. These include instrument error, data padding, use of monthly averages, choice of reference level, and the atmospheric data used in Ekman transport calculations. Instrument errors are as follows: XBT probes have an error of ±0.2°C, while Argo floats have errors of ±0.002°C for temperature and ±0.01 PSU for salinity. At 34.5°S, WOA18 T and S estimates below 2000 m have standard errors of ±0.08°C and ±0.01 PSU, respectively. These uncertainties in T and S profiles translate to potential errors of ±0.7 Sv in AMOC, ± 0.01 PW in MHT, and ±0.003 Sv in FWT estimates. Previous studies highlight the importance of selecting an appropriate reference level, as it is one of the main sources of uncertainty for AMOC and MHT estimates (Baringer and Garzoli, 2007; Goes et al., 2015, 2018), and consequently for FWT estimates. In Section 2.4, we show that different choices of reference level and velocity products yield similar variability, but the chosen approach aligns more closely with previous AMOC intensity estimates, whereas the others underestimate the mean circulation. Baringer and Garzoli (2007) also quantified uncertainties in MHT from hydrographic lines, attributing ±0.05 PW to reference level selection, ± 0.04 PW to Ekman transport, and ±0.01 PW to unresolved shelf transport.

Table 1

Table 1. Mean and standard deviation (Std) values for Atlantic Meridional Overturning Circulation (AMOC), and its respective heat (MHT) and freshwater (FWT) transports at 34.5°S.

There is a strong agreement between the AXMOC with SAMBA and Dong et al. (2021) estimates at 34.5°S (D35S; Figure 2A). The mean (standard deviation) AMOC for the SAMBA array estimate is 17.3 (5.4) Sv. For the period covered by the SAMBA observations, the mean (standard deviation) AMOC of the AXMOC and D35S are 17.0 (4.0) Sv and 17.0 (3.1) Sv, respectively (Table 1). Both SAMBA and D35S estimates present mean AMOC values similar to that from the AXMOC (within the estimated mapping uncertainty of ±1.6 Sv). The RMSE between AXMOC and SAMBA is 5.0 Sv and the correlation is 0.41. Additionally, the RMSE between AXMOC and D35S is 3.9 Sv and the correlation is 0.45. Between SAMBA and D35S, the RMSE is 4.7 Sv and the correlation is 0.42. For the entire study period between January 2005 and May 2023, the D35S AMOC mean value (standard deviation) is 17.3 (3.2) Sv, which is similar to the one derived from AXMOC; however, its variability is weaker accounting for approximately 70 to 80% of the AMOC variability (using standard deviation as a proxy) observed by the AXMOC dataset.

Previous studies have shown that between 20°S and 25°S, the Ekman component of the AMOC is southward, opposite to the geostrophic component (Dong et al., 2015, 2021; Pita et al., 2024). At 34.5°S, however, both the Ekman and geostrophic AMOC components are positive, i.e. northward (Figure 3A). This difference in the Ekman transport direction is due to the influence of the easterly trade winds near 22°S, and the influence of the westerlies south of 30°S (Supplementary Figure S3). MHT and AMOC are highly correlated (see Supplementary Figure S4 - correlation of 0.91 on the interannual signal), as observed in the previous studies for the South Atlantic (Dong et al., 2015; Majumder et al., 2016; Pita et al., 2024). Notably, an AMOC weakening between 2008 and 2011 in the AXMOC is also observed in SAMBA (Figure 2A). This weakening is driven by anomalies in the geostrophic component (Figure 3A). The interannual AMOC variability is dominated by the geostrophic component, (correlation of 0.92), while the Ekman component plays a minor role (correlation of 0.25). Similar results are also observed for the MHT (FWT), where the correlation of total transport with the geostrophic signal is 0.83 (0.75) and 0.44 (0.64) with the Ekman component (see Supplementary Figures S4, S5). The correlation between the total MHT/FWT and their respective Ekman components is greater than for the AMOC components, possibly because non-linearities in the product between the velocity and T/S, which are more significant in the upper ocean and within the surface Ekman layer. For the seasonal cycle, the AMOC, MHT and FWT align closely with the Ekman component, and the geostrophic component appears out-of-phase, particularly in the first half of the year (Figure 3). This is consistent with patterns noted in synthetic MHT estimates (Dong et al., 2021) but different to the SAMBA estimates (Baker et al., 2023). However, the SAMBA array has yet to incorporate recently acquired data, with its last updated AMOC time series dating back to 2017 (Baker et al., 2023) and the limited temporal range for the SAMBA could lead to significant uncertainties, especially on the seasonal cycle (Goes et al., 2015; Chidichimo et al., 2023).

Figure 3

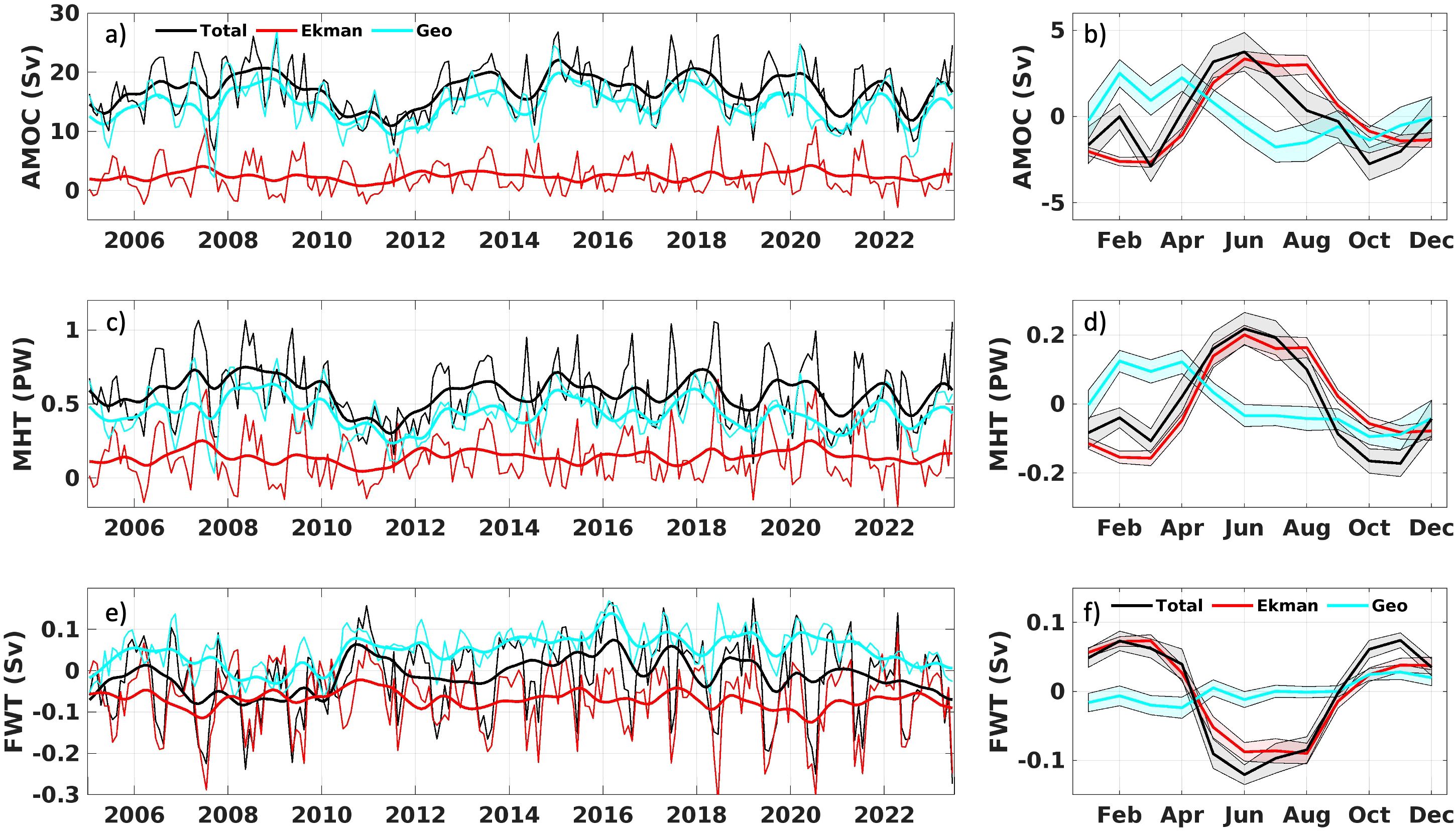
Figure 3. AMOC (Sv - A, B), MHT (PW - C, D) and FWT (Sv - E, F) interannual signal (left) and associated seasonal cycles for 34.5°S (right) using the OM method. Thin (thicker) lines represent 3-month smoothed (interannual) signals. Total (black), Ekman (red) and geostrophic (cyan) components are presented. Shaded areas represent the standard error interval for each estimate.

For the FWT, the predominance of wind-driven forcing on the seasonal variability is also observed (Figure 3F). The geostrophic component represents only 27% of the peak-to-trough amplitude of FWT, which is weak compared to 64% and 56% for AMOC and MHT, respectively. This difference may be due to the fact that, for FWT, seasonal signals of the geostrophic overturning and horizontal components are of similar intensity but opposite in phase, effectively reducing the seasonal peak-to-trough amplitude. In contrast, for the MHT, the geostrophic overturning component is much stronger than the horizontal component, leading to a more pronounced seasonal variation (not shown, more details in Section 3.2).

3.2 MHT and FWT decompositions

Both MHT and FWT are further decomposed into horizontal (Hhor and Fhor, respectively) and overturning (Hov and Fov, respectively) components (Figure 4). The Hov and Hhor components of the MHT have mean values with opposing signs, averaging 0.7 PW ( standard deviation of 0.2 PW) and -0.1 PW (standard deviation of 0.1 PW), respectively (Table 1). These values are similar to the ones reported by Dong et al. (2021). The MHT is driven by the Hov component (correlation of 0.92, see Supplementary Figure S4). While the seasonal MHT signal is largely driven by the Ekman contribution to the overturning component (Hov_E, Figure 4C), the interannual MHT variability is dominated by the geostrophic contribution to the overturning component (Hov_g) (correlation of 0.75; Figure 4B and Supplementary Figure S4), followed by the wind-driven contribution (correlation of 0.44). The Hhor component is not significantly correlated with the MHT in either seasonal or interannual timescales (Figure 4A, B).

Figure 4

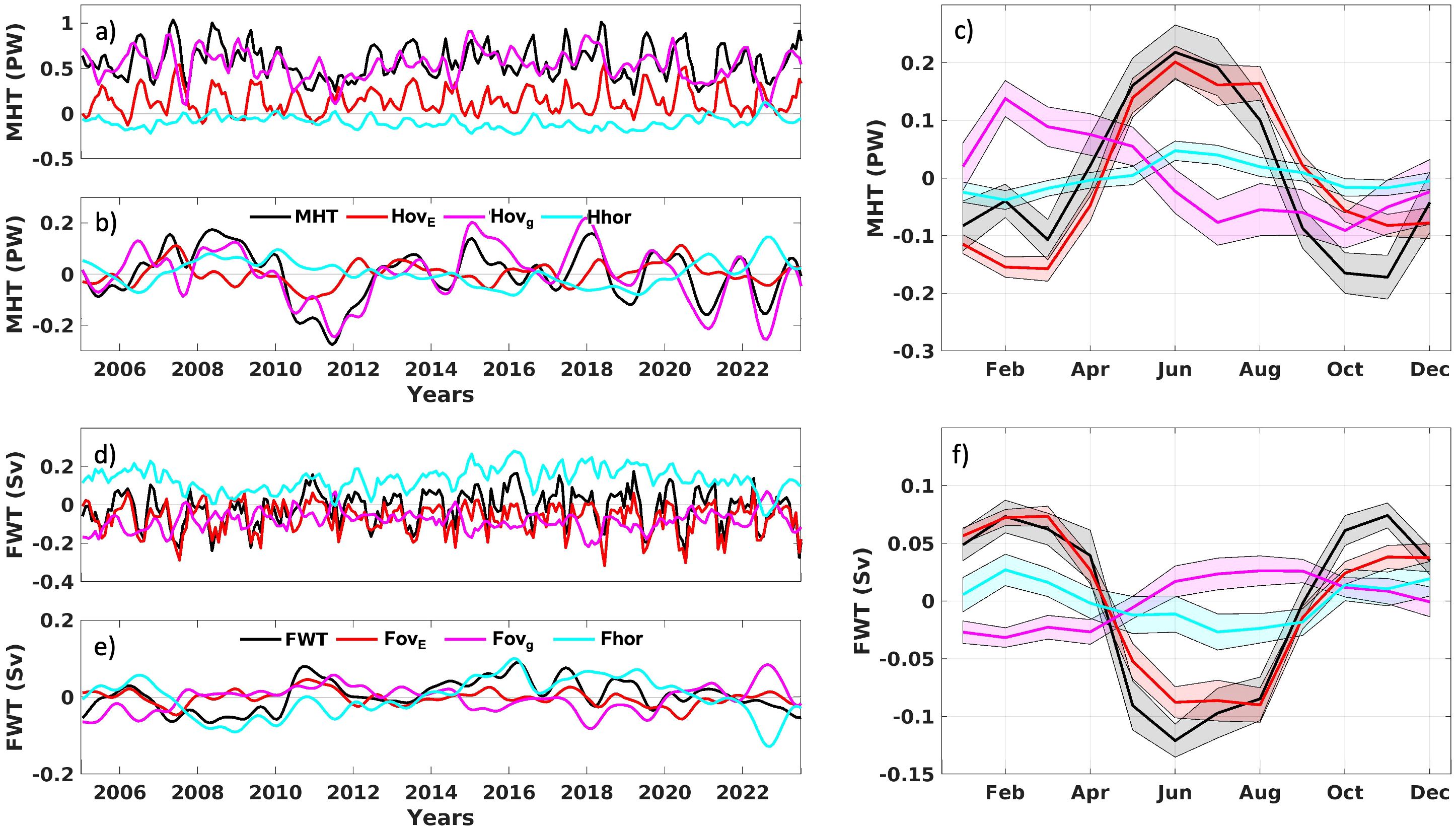
Figure 4. Meridional heat transport and freshwater transport decompositions at 34.5°S (A, D, respectively) and their respective interannual (B, E) and seasonal components (C, F). Meridional heat and freshwater transports (MHT and FWT; black), horizontal component (Hhor and Fhor; cyan), and both Ekman (_E; red) and geostrophic (_g; magenta) contributions for the overturning component (Hov and Fov) are presented.

The Fov and Fhor components of the FWT also have mean values with opposing signs, averaging -0.15 Sv (standard deviation of 0.08 Sv) and 0.13 Sv (standard deviation of 0.06 Sv), respectively (Table 1). Previous studies indicate that the interannual FWT variability is dominated by the horizontal component instead of the overturning component at 34.5°S (Mignac et al., 2019; Liu et al., 2023). Our results indicate that the relative dominance of the horizontal (Fhor) and overturning (Fov) components in freshwater transport (FWT) depends on the frequency of the signal analyzed. In addition, the decomposition of Fov into geostrophic (Fov_g) and Ekman (Fov_E) contributions elucidates the impact of the overturning component on the FWT (Figures 4D–F; Supplementary Figure S5). On seasonal timescales, FWT is predominantly controlled by Fov, particularly through its Ekman contribution (Fov_E), which is especially active from May to August (Figure 4F). Fov_g is out-of-phase with Fov_E, and its small seasonal variance is generally offset by Fhor, contributing to the reduced amplitude of the seasonal signal in the FWT geostrophic component (Figure 3F). On interannual timescales, FWT is strongly correlated with Fov_E (0.64) and Fhor (0.59), and has no correlation with Fovg (<0.05). Notably, the opposing signals of Fhor and the Fov_g at these timescales, with an anticorrelation of -0.72, likely dampen the overall FWT variability. Over longer periods, Fhor becomes the primary driver of FWT anomalies, explaining significant events such as the FWT minimum in 2008-2009 and the maximum in 2016-2017 (Figure 4E). Thus, our findings suggest that Fov, driven by Ekman dynamics, is central to seasonal FWT variability, while Fhor governs interannual to decadal timescale FWT anomalies.

Furthermore, a more detailed vertical structure of the MHT and FWT and the contributions from horizontal and overturning components is presented in Figure 5. This was possible by integrating the MHT and FWT components (Equations 3-6) at 100 m depth intervals, rather than integrating over the entire water column. The following analyses are valid only when adopting a potential temperature reference of 0°C and S₀ of 34.76 ± 0.001 at 34.5°S. The overturning circulation influence on the MHT is depth-dependent (Figure 5C; Supplementary Figure S6A). The Hhor component is limited to the upper 500 m. For the MHT, the geostrophic heat transport contributes to both overturning (Hov_g) and horizontal (Hhor) components, while Ekman heat transport (MHT_E) solely contributes to the overturning component (Supplementary Figure S6C), since the horizontal component is based on deviations from the mean field and we defined the Ekman meridional velocity as a zonal mean across the section. MHT_g influences the upper 750 m, while MHT_E is confined at the Ekman layer (50 m), which is compensated by a small constant barotropic flow over depth (Figure 5E; Supplementary Figure S6C).

Figure 5

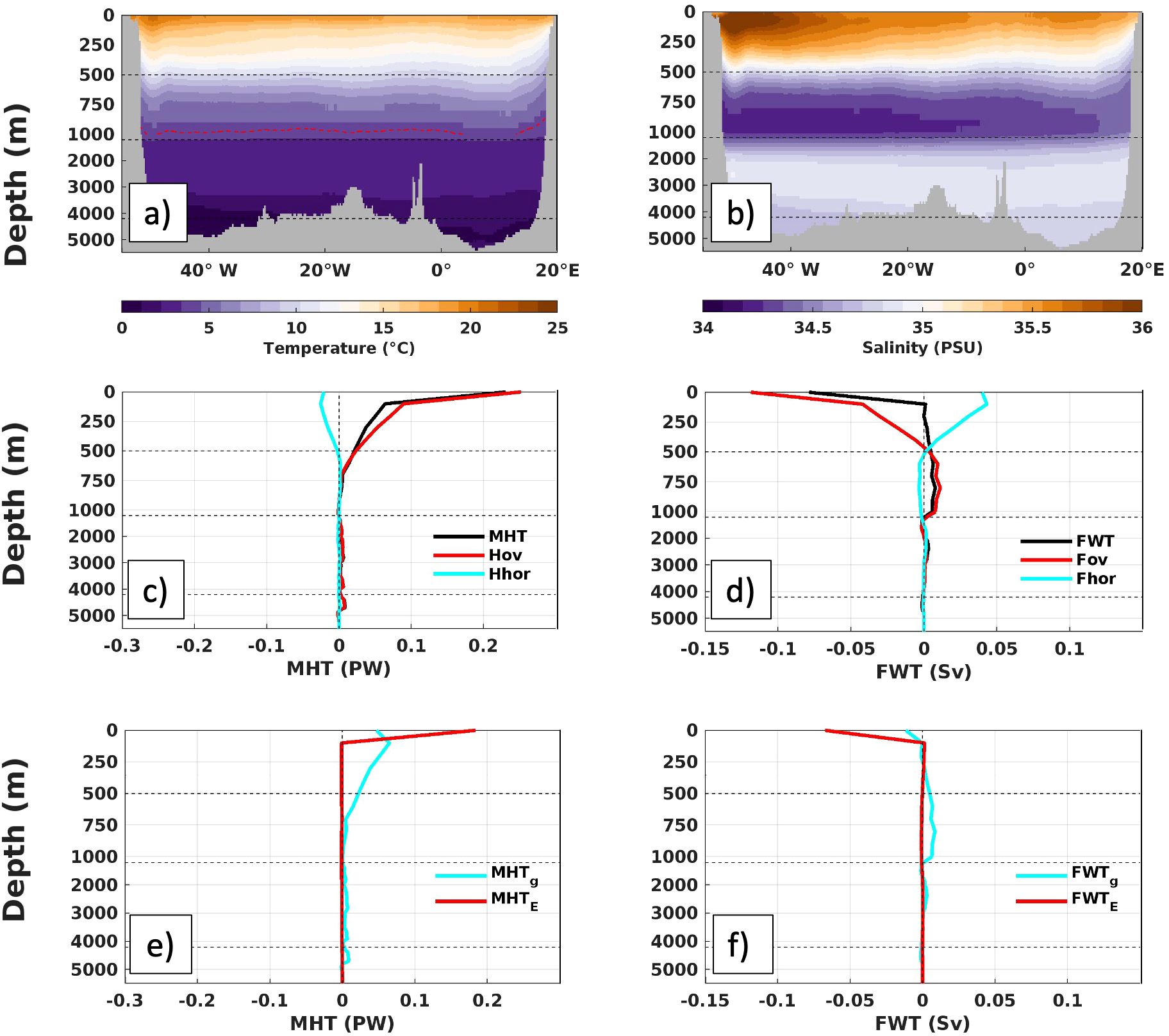
Figure 5. Time-averaged (2005-2023) Temperature (A) and Salinity (B) fields at 34.5°S. Decomposition of MHT and FWT in overturning and horizontal contributions (C, D, respectively) as well as Ekman and geostrophic components (E, F, respectively) are represented in z levels (values integrated in 100 m intervals). Freshwater and heat transports are decomposed in overturning (Fov and Hov, respectively) and horizontal (Fhor and Hhor, respectively) contributions. Note the change on the vertical axis to highlight upper ocean changes (0 - 1000 m). Integrals (cumulative transport) of (C, F) are shown in Supplementary Figure S5.

The overturning component of the FWT (Fov) is negative in the upper 500 m with a value of about -0.12 Sv at the surface, positive between 500 m and 1000 m with a value of about 0.01 Sv, and it becomes close to zero below 1200 m (Figure 5D). The horizontal component (Fhor) is restricted to the upper 500 m with positive values. Fov and Fhor tend to partially compensate each other in the first 500 m, mostly in the geostrophic contributions, and the addition of the Ekman contribution to Fov in the upper 50 m, breaks this balance and drives the FWT southward (Figures 5D, F; Supplementary Figure S6D). Below 500 m, where the Fhor component and the Ekman contribution to the FWT are negligible, the FWT is controlled by the Fov_g. The magnitude of this flow below 500 m to the total FWT is small, which results in a small correlation between Fov_g and FWT (see Supplementary Figure S5).

Even though there is a weak correlation between FWT and the AMOC (correlation of -0.2) at interannual timescales (see Supplementary Figure S5), which suggests that circulation is not driving the variability of FWT, there is a significant correlation (-0.56) between AMOC and Fov, which is mostly driven by the geostrophic component. The lack of correlation between the AMOC and FWT is because the Fov and Fhor components are anti-correlated (see Supplementary Figure S5), and because the freshwater transport is not only influenced by changes in circulation but also by changes in overall salinity carried by the currents across 34.5°S. Indeed, different products show basin-wide changes in both T and S (Figure 6). The anomalies of the averaged upper 300 m T and S (T300 and S300, respectively) show westward propagations across the basin, which are more pronounced in the AXMOC and ORAS5 products (Figures 6A, B, D, E). In contrast, EN4 is much smoother and also does not show clear propagation (Figures 6G, H), a feature that is also found in other observational products that do not use optimal mapping parameters (Pita et al., 2024). Underlying this propagation, a low-frequency basin-wide pattern is observed in both T and S, first with a positive phase from 2005-2007, followed by a negative phase until 2016, and strongly positive after that. The structure of this anomaly is more clearly observed in the zonally averaged S and T anomalies across all products (Figures 6C, F, I; T plots are not shown), which are largely confined to the top 1,000 m of the water column. Between 2005 and 2010, there was a notable peak in freshening and cooling anomalies in the upper 1,000 m, with rates of -0.02 ± 0.01 PSU/year and -0.16 ± 0.06°C/year, respectively. Since 2010, however, salinification and warming trends have emerged in this layer, reversing the earlier anomalies and leading to strong positive salinity and temperature anomalies from 2017 onward, with rates of 0.01 ± 0.04 PSU/year and 0.03 ± 0.03°C/year, respectively.

Figure 6

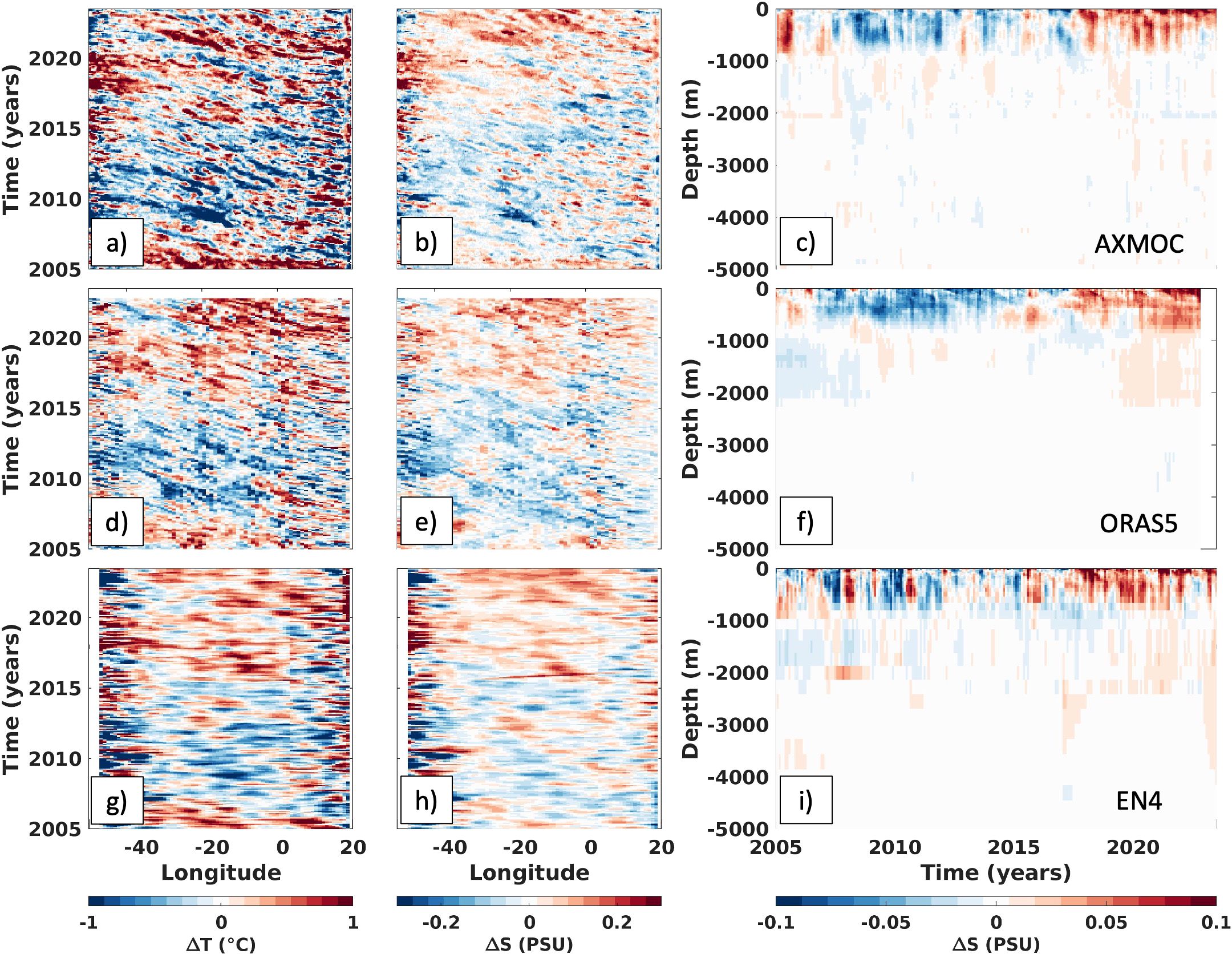
Figure 6. Anomalies of temperature and salinity averaged in the upper 300 m from AXMOC (A, B), ORAS5 (D, E) and EN4 (G–H) products are presented as well as the AXMOC zonally averaged salinity for AXMOC, ORAS5 and EN4 (C, F and I, respectively).

Overall, our results indicate a significant positive salinity and temperature trends in the upper 300 m at 34.5°S at a rate of 0.05 ± 0.01 PSU/decade and 0.13 ± 0.06°C/decade, similar to the trend observed from ORAS5 (0.05 ± 0.01 PSU/decade and 0.17 ± 0.04°C/decade) and EN4 data (0.06 ± 0.02 PSU/decade and 0.10 ± 0.04°C/decade; Figures 6C, F, I), calculated for the period between January 2005 and December 2023 (January 2005 and December 2022 for ORAS5). The data presented here do not allow the identification of the drivers of this large-scale T/S feature, which could be associated with a natural oscillation or recent trend driven by factors such as Agulhas leakage anomalies (de Ruijter et al., 1999; Lübbecke et al., 2015).

4 Conclusion

AMOC, MHT and FWT estimates are obtained by leveraging Argo, XBT and CTD data at 34.5°S. The method presented in Pita et al. (2024) was applied to 34.5°S and compared with a machine learning neural network approach, which produced similar results, as well as the AMOC observational array (SAMBA). Both optimal mapping (used on AXMOC estimates) and neural network proved to be robust mapping methods and presented similar AMOC, MHT and FWT variabilities and mean states (Figure 2). The AXMOC mapping errors were smaller than the standard deviation of each estimate. The mean (standard deviation) calculated for the AMOC between January 2005 and May 2023 was 17.0 ± 1.6 Sv (4.3 Sv), 0.6 ± 0.1 PW (0.2 PW) for the MHT, and -0.02 ± 0.01 Sv (0.09 Sv) for the FWT (Table 1). The mean value of the AMOC strength is critically dependent on the reference velocity applied to the section, but the AMOC variability remains consistent across different reference velocities (Supplementary Figure S2). Notably, our analysis identified a pronounced weakening of the AMOC between 2008 and 2011, driven primarily by geostrophic anomalies. This period of weakening partly aligns with observations from the SAMBA array, highlighting the critical role of geostrophic flows in modulating AMOC variability (Figures 2 and 3). The AMOC variability estimated by the SAMBA array (Baker et al., 2023) is notably higher than that of synthetic estimates (Dong et al., 2015, 2021; Majumder et al., 2016). In this study, we compared the AXMOC data with a synthetic estimate (D35S) and found that AMOC variability from AXMOC estimates was 35% greater than that of D35S during the period from January 2005 to May 2023 (Table 1). Since our approach reconstructs T and S profiles across the entire basin and the variability of our derived transports align well with those from the SAMBA array, these results suggest that AXMOC data could complement the SAMBA array by reducing temporal and spatial gaps and enhancing its estimates. In addition, the mapping procedure adopted here minimizes the latitudinal variability in the XBT AX18 transect caused by changes in ship line routes.

The estimated overturning and horizontal components of MHT are in opposite directions, northward for the overturning (0.68 ± 0.21 PW) and southward for the horizontal (-0.10 ± 0.07 PW) contribution (Figure 4). In addition, the dominance of the overturning over the horizontal contribution for the total MHT was observed on seasonal and interannual timescales. The overturning contribution can be further decomposed into the wind-driven (Ekman) and geostrophic contributions. We find the Ekman contribution dominates the seasonal cycle, whereas the geostrophic contribution drives the interannual variability. In addition, the overturning component of the MHT is more intense than its horizontal component and largely determines the MHT structure throughout most of the water column when considering the potential temperature reference of 0°C (Figure 5C).

There is an ongoing debate about the influence of AMOC on the FWT anomalies. Mignac et al. (2019) suggest the AMOC stability is driven by indirect Fhor feedbacks or Fov in the North Atlantic, instead of the Fov at 34.5°S. We agree partially with some studies (e.g., Mignac et al., 2019; Liu et al., 2023) based on ocean reanalysis and free-running models, which suggest that the FWT is driven by the horizontal component instead of the overturning circulation in the historical period. However, when decomposing the overturning component of the FWT into Ekman and geostrophic contributions, it is observed that the FWT anomalies are mostly driven by the Ekman-induced overturning (Fov_E) and horizontal (Fhor) variability on seasonal and interannual-to-decadal timescales, respectively, while the geostrophic contribution to the overturning component (Fov_g) plays a minor role in FWT in the period analyzed (Figures 4D-F). The FWT overturning component (Fov) is southward (-0.15 Sv) with a standard deviation of 0.08 Sv. The mean Fov indicates an unstable AMOC, agreeing with previous observational studies (Garzoli et al., 2013; Caínzos et al., 2022; Arumí-Planas et al., 2024). In terms of the vertical structure of the FWT components, Fhor is mostly confined to the upper 500 m, with Fov_g and Fhor offsetting each other between 50 m and 500 m, and the Fov_E in the upper 50 m determining the negative FWT. A caveat of this analysis is that the freshwater transport and its structure is dependent on the reference salinity value S₀. This value is not widely agreed upon and may change over time. We use in our definition of S₀ the salinity of the bounding section instead of a regional or global value, which is a better choice consistent with previous studies that address this issue (e.g., Treguier et al., 2014; Tsubouchi et al., 2012). Consequently, the vertical structures of MHT and FWT differ in part because of the different choices of reference.

When analyzing upper ocean T and S dynamics, all three products analyzed here, AXMOC, ORAS5 and EN4, show zonally averaged upper 300 m salty and warm anomalies at 34.5°S starting in 2017 (Figure 6), however, the westward wave propagations are observed only by AXMOC and ORAS5 reanalysis, and it is not visible in the EN4 gridded product. This highlights the need for optimal mapping tools constrained by ocean dynamics in observational products to resolve these features.

In the future, the South Atlantic could become saltier due to a reduced salinity divergence caused by a weakening AMOC under anthropogenic warming (Zhu and Liu, 2020). Studies have focused on these early signals for AMOC anomalies using FWT or salt content anomalies (e.g., Zhu and Liu, 2020; Zhu et al., 2023). Long-term trends in the South Atlantic FWT are a useful tool for early detection of a possible AMOC weakening (van Westen et al., 2024), as the northward salinity transports would decrease in an AMOC weakening scenario, leading to a salinity increase in the South Atlantic (Zhu et al., 2023). Salinity trends are also recognized as a proxy for an intensifying global water cycle under climate change (Durack and Wijffels, 2010; Durack et al., 2012). The salinification of the basin could disrupt ocean stratification, promoting vertical mixing that could promote water mass changes in the basin. Additionally, this change could result in a negative halosteric sea level trend, partially offsetting sea level rise (Llovel et al., 2019). However, given that our time series are not long enough to analyze centennial trends, it is challenging to separate the effects of anthropogenic influence on the salinification and warming of the South Atlantic from those driven by atmospheric and circulation changes. In the context of climate change, long-term salinity trends in the subtropical Atlantic Ocean may be influenced by a combination of atmospheric factors, circulation changes, heaving of isopycnals and anthropogenic factors (Sathyanarayanan et al., 2021).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

IP: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Visualization, Writing – original draft, Writing – review & editing. MG: Investigation, Methodology, Supervision, Writing – review & editing. DV: Writing – review & editing. SD: Data curation, Writing – review & editing. CS: Data curation, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was carried out in part under the auspices of the Cooperative Institute for Marine and Atmospheric Studies, a cooperative institute of the University of Miami and the National Oceanic and Atmospheric Administration (NOAA), cooperative agreement NA20OAR4320472, and was supported by NOAA's Atlantic Oceanographic and Meteorological Laboratory (AOML). MG and DLV were also supported by the National Oceanic and Atmospheric Administration (NOAA) Climate Variability and Predictability program (Grant NA20OAR4310407).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmars.2024.1474133/full#supplementary-material

References

Argo (2024). Argo float data and metadata from global data assembly center (Argo GDAC) (Brest, France: SEANOE). doi: 10.17882/42182

PubMed Abstract | Crossref Full Text | Google Scholar

Arumí-Planas C., Dong S., Perez R., Harrison M. J., Farneti R., Hernandez-Guerra A. (2024). A multi-data set analysis of the freshwater transport by the Atlantic meridional overturning circulation at nominally 34.5°S. J. Geophysical Res.: Oceans 129, e2023JC020558. doi: 10.1029/2023JC020558

Crossref Full Text | Google Scholar

Arumí-Planas C., Pérez-Hernández M. D., Pelegrí J. L., Vélez-Belchí P., Emelianov M., Caínzos V., et al. (2023). The South Atlantic circulation between 34.5 S, 24 S and above the mid-Atlantic ridge from an inverse box model. J. Geophysical Res.: Oceans 128, e2022JC019614. doi: 10.1029/2022JC019614

Crossref Full Text | Google Scholar

Baker J. A., Renshaw R., Jackson L. C., Dubois C., Iovino D., Zuo H., et al. (2023). South Atlantic overturning and heat transport variations in ocean reanalyses and observation-based estimates. State of the Planet 1, 1–15. doi: 10.5194/sp-1-osr7-4-2023

Crossref Full Text | Google Scholar

Baringer M. O., Garzoli S. L. (2007). Meridional heat transport determined with expendable bathythermographs—Part I: Error estimates from model and hydrographic data. Deep Sea Res. Part I: Oceanographic Res. Papers 54, 1390–1401. doi: 10.1016/j.dsr.2007.03.011

Crossref Full Text | Google Scholar

Beale M., Hagan M., Demuth H. (2024). Deep learning toolbox user’s guide (Natick, MA: The MathWorks, Inc.). Available online at: https://www.mathworks.com/help/pdf_doc/deeplearning/nnet_ug.pdf (Accessed 21 April 2024).

Google Scholar

Biló T. C., Perez R. C., Dong S., Johns W., Kanzow T. (2024). Weakening of the Atlantic Meridional Overturning Circulation abyssal limb in the North Atlantic. Nat. Geosci. 17, 419–425. doi: 10.1038/s41561-024-01422-4

Crossref Full Text | Google Scholar

Caesar L., McCarthy G. D., Thornalley D. J. R., Cahill N., Rahmstorf S. (2021). Current Atlantic meridional overturning circulation weakest in last millennium. Nat. Geosci. 14, 118–120. doi: 10.1038/s41561-021-00699-z

Crossref Full Text | Google Scholar

Caesar L., Rahmstorf S., Robinson A., Feulner G., Saba V. (2018). Observed fingerprint of a weakening Atlantic Ocean overturning circulation. Nature 556, 191–196. doi: 10.1038/s41586-018-0006-5

PubMed Abstract | Crossref Full Text | Google Scholar

Caínzos V., Hernández-Guerra A., McCarthy G. D., McDonagh E. L., Cubas Armas M., Pérez-Hernández M. D. (2022). Thirty years of GOSHIP and WOCE data: Atlantic overturning of mass, heat, and freshwater transport. Geophysical Res. Lett. 49, e2021GL096527. doi: 10.1029/2021GL096527

Crossref Full Text | Google Scholar

Campos E. J., Van Caspel M. C., Zenk W., Morozov E. G., Frey D. I., Piola A. R., et al. (2021). Warming trend in Antarctic bottom water in the vema channel in the South Atlantic. Geophysical Res. Lett. 48, e2021GL094709. doi: 10.1029/2021GL094709

Crossref Full Text | Google Scholar

Chang P., Zhang R., Hazeleger W., Wen C., Wan X., Ji L., et al. (2008). Oceanic link between abrupt changes in the North Atlantic Ocean and the African monsoon. Nat. Geosci. 1, 444–448. doi: 10.1038/ngeo218

Crossref Full Text | Google Scholar

Chen Y., Speich S., Laxenaire R. (2022). Formation and transport of the South Atlantic subtropical mode water in eddy-permitting observations. J. Geophysical Res. Oceans 127, e2021JC017767. doi: 10.1029/2021JC017767

Crossref Full Text | Google Scholar

Chidichimo M. P., Perez R. C., Speich S., Kersalé M., Sprintall J., Dong S., et al. (2023). Energetic overturning flows, dynamic interocean exchanges, and ocean warming observed in the South Atlantic. Commun. Earth Environ. 4, 10. doi: 10.1038/s43247-022-00644-x

Crossref Full Text | Google Scholar

Collins M., Sutherland M., Bouwer L., Cheong S. M., Frölicher T., Jacot Des Combes H., et al. (2019). “Extremes, abrupt changes and managing risk,” in IPCC special report on the Ocean and cryosphere in a changing climate. Eds. Pörtner H. O., Roberts D. C., Masson-Delmotte V., Zhai P., Tignor M., Poloczanska E., et al (Cambridge, UK and New York, NY, USA: Cambridge University Press), 589–655. doi: 10.1017/9781009157964.008

Crossref Full Text | Google Scholar

de Ruijter W. D., Biastoch A., Drijfhout S. S., Lutjeharms J. R. E., Matano R. P., Pichevin T., et al. (1999). ). Indian-Atlantic interocean exchange: Dynamics, estimation and impact. J. Geophysical Res.: Oceans 104, 20885–20910. doi: 10.1029/1998JC900099

Crossref Full Text | Google Scholar

Dong S., Goni G., Bringas F. (2015). Temporal variability of the South Atlantic meridional overturning circulation between 20 S and 35 S. Geophysical Res. Lett. 42, 7655–7662. doi: 10.1002/2015GL065603

Crossref Full Text | Google Scholar

Dong S., Goni G., Domingues R., Bringas F., Goes M., Christophersen J., et al. (2021). Synergy of in situ and satellite ocean observations in determining meridional heat transport in the Atlantic Ocean. J. Geophysical Res.: Oceans 126, e2021JC017946. doi: 10.1029/2020JC017073

Crossref Full Text | Google Scholar

Drijfhout S. S., Weber S. L., van der Swaluw E. (2011). The stability of the MOC as diagnosed from model projections for pre-industrial, present and future climates. Climate Dynamics 37, 1575–1586. doi: 10.1007/s00382-010-0930-z

Crossref Full Text | Google Scholar

Durack P. J., Wijffels S. E. (2010). Fifty-year trends in global ocean salinities and their relationship to broad-scale warming. J. Climate 23, 4342–4362. doi: 10.1175/2010JCLI3377.1

Crossref Full Text | Google Scholar

Durack P. J., Wijffels S. E., Matear R. J. (2012). Ocean salinities reveal strong global water cycle intensification during 1950 to 2000. science 336, 455–458. doi: 10.1126/science.1212222

PubMed Abstract | Crossref Full Text | Google Scholar

Fox-Kemper B., Hewitt H. T., Xiao C., Aðalgeirsdóttir G., Drijfhout S. S., Edwards T. L., et al. (2021). “Ocean, cryosphere and sea level change,” in Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Eds. Masson-Delmotte V., Zhai P., Pirani A., Connors S. L., P.an C., Berger S., et al (Cambridge, UK: Cambridge University Press), 1211–1362. doi: 10.1017/9781009157896.011

Crossref Full Text | Google Scholar

Frajka-Williams E., Foukal N., Danabasoglu G. (2023). Should AMOC observations continue: how and why? Philos. Trans. R. Soc. A 381, 20220195. doi: 10.1098/rsta.2022.0195

PubMed Abstract | Crossref Full Text | Google Scholar

Garcia H. E., Boyer T. P., Baranova O. K., Locarnini R. A., Mishonov A. V., Grodsky A., et al. (2019). “World Ocean atlas 2018: Product documentation” in NOAA atlas NESDIS. Ed. Mishonov A.. (MG, USA: Silver Spring). Available at: https://www.ncei.noaa.gov/sites/default/files/2020-04/woa18documentation.pdf (accessed December 10, 2024).

Google Scholar

Garzoli S. L., Baringer M., Dong S., Perez R., Yao Q. (2013). South Atlantic meridional fluxes. Deep-Sea Res. Part A: Oceanographic Res. Papers I 71, 21–32. doi: 10.1016/j.dsr.2012.09.003

Crossref Full Text | Google Scholar

Garzoli S. L., Dong S., Fine R., Meinen C. S., Perez R. C., Schmid C., et al. (2015). The fate of the deep western boundary current in the South Atlantic. Deep Sea Res. Part I: Oceanographic Res. Papers 103, 125–136. doi: 10.1016/j.dsr.2015.05.008

Crossref Full Text | Google Scholar

Goes M., Christophersen J., Dong S., Goni G., Baringer M. O. (2018). ). An updated estimate of salinity for the Atlantic ocean sector using temperature–salinity relationships. J. Atmospheric Oceanic Technol. 35, 1771–1784. doi: 10.1175/JTECH-D-18-0029.1

Crossref Full Text | Google Scholar

Goes M., Cirano M., Mata M. M., Majumder S. (2019). Long-term monitoring of the Brazil current transport at 22°S from XBT and altimetry data: Seasonal, interannual, and extreme variability. J. Geophysical Res.: Oceans 124, 3645–3663. doi: 10.1029/2018JC014809

Crossref Full Text | Google Scholar

Goes M., Goni G., Dong S. (2015). An optimal XBT-based monitoring system for the South Atlantic meridional overturning circulation at 34°S. J. Geophysical Res.: Oceans 120, 161–181. doi: 10.1002/2014JC010202

Crossref Full Text | Google Scholar

Goes M., Goni G., Dong S., Boyer T., Baringer M. (2020). The complementary value of XBT and Argo observations to monitor ocean boundary currents and meridional heat and volume transports: A case study in the Atlantic Ocean. J. Atmospheric Oceanic Technol. 37, 2267–2282. doi: 10.1175/JTECH-D-20-0027.1

Crossref Full Text | Google Scholar

Goes M., Urban N. M., Tonkonojenkov R., Haran M., Schmittner A., Keller K. (2010). What is the skill of ocean tracers in reducing uncertainties about ocean diapycnal mixing and projections of the Atlantic Meridional Overturning Circulation? J. Geophysical Res. 115, 3213. doi: 10.1029/2010JC006407

Crossref Full Text | Google Scholar

Good S. A., Martin M. J., Rayner N. A. (2013). EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates. J. Geophysical Res.: Oceans 118, 6704–6716. doi: 10.1002/2013JC009067

Crossref Full Text | Google Scholar

Hersbach H., Bell B., Berrisford P., Hirahara S., Horanyi H., Munoz-Sabater J., et al. (2020). The ERA5 global reanalysis. Q. J. R. Meteorological Soc. 146, 1999–2049. doi: 10.1002/qj.3803

Crossref Full Text | Google Scholar

Huang B., Liu C., Banzon V., Freeman E., Graham G., Hankins B., et al. (2020). Improvements of the daily optimum interpolation sea surface temperature (DOISST) version 2.1. J. Climate 34, 2923–2939. doi: 10.1175/JCLI-D-20-0166.1

Crossref Full Text | Google Scholar

Jackson L. C., Hewitt H. T., Bruciaferri D., Calvert D., Graham T., Guiavarc’h C., et al. (2023). Challenges simulating the AMOC in climate models. Philos. Trans. R. Soc. A 381, 20220187. doi: 10.1098/rsta.2022.0187

PubMed Abstract | Crossref Full Text | Google Scholar

Jayne S. R., Marotzke J. (2001). The dynamics of ocean heat transport variability. Rev. Geophysics 39, 385–411. doi: 10.1029/2000RG000084

Crossref Full Text | Google Scholar

Johns W. E., Baringer M. O., Beal L. M., Cunningham S. A., Kanzow T., Bryden H. L., et al. (2011). Continuous, array-based estimates of Atlantic Ocean heat transport at 26.5 N. J. Climate 24, 2429–2449. doi: 10.1175/2010JCLI3997.1

Crossref Full Text | Google Scholar

Johns W. E., Elipot S., Smeed D. A., Moat B., King B., Volkov D. L., et al. (2023). Towards two decades of Atlantic Ocean mass and heat transports at 26.5 N. Philos. Trans. R. Soc. A 381, 20220188. doi: 10.1098/rsta.2022.0188

PubMed Abstract | Crossref Full Text | Google Scholar

Kersalé M., Meinen C. S., Perez R. C., Le Henaff M., Valla D., Lamont T., et al. (2020). Highly variable upper and abyssal overturning cells in the South Atlantic. Sci. Adv. 6, eaba7573. doi: 10.1126/sciadv.aba7573

PubMed Abstract | Crossref Full Text | Google Scholar

Kersalé M., Meinen C. S., Perez R. C., Piola A. R., Speich S., Campos E. J. D., et al. (2021). Multi-year estimates of daily heat transport by the Atlantic Meridional overturning circulation at 34.5 S. J. Geophysical Res.: Oceans 126, e2020JC016947. doi: 10.1029/2020JC016947

Crossref Full Text | Google Scholar

Kilbourne K. H., Wanamaker A. D., Moffa-Sanchez P., Reynolds D. J., Amrhein D. E., Butler P. G., et al. (2022). Atlantic circulation change still uncertain. Nat. Geosci. 15, 165–167. doi: 10.1038/s41561-022-00896-4

Crossref Full Text | Google Scholar

Lebedev K. V., Yoshinari H., Maximenko N. A., Hacker P. W. (2007). Velocity data assessed from trajectories of Argo floats at parking level and at sea surface. IPRC Tech. Note 4, 1–16. Available online at https://apdrc.soest.hawaii.edu/projects/yomaha/yomaha07/YoMaHa070612.pdf (accessed December 10, 2024).

Google Scholar

Lee J.-Y., Marotzke J., Bala G., Cao L., Corti S., Dunne J. P., et al. (2021). “Future global climate: Scenario-based projections and near-term information,” in Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Eds. Masson-Delmotte V., Zhai P., Pirani A., Connors S. L., P.an C., Berger S., et al (Cambridge, UK: Cambridge University Press), 553–672. doi: 10.1017/9781009157896.006

Crossref Full Text | Google Scholar

Liu X., Köhl A., Stammer D. (2023). Causes for Atlantic freshwater content variability in the GECCO3 ocean synthesis. J. Geophysical Res.: Oceans 128, e2022JC018796. doi: 10.1029/2022JC018796

Crossref Full Text | Google Scholar

Liu W., Xie S. P., Liu Z., Zhu J. (2017). Overlooked possibility of a collapsed Atlantic Meridional Overturning Circulation in warming climate. Sci. Adv. 3, e1601666. doi: 10.1126/sciadv.1601666

PubMed Abstract | Crossref Full Text | Google Scholar

Llovel W., Purkey S., Meyssignac B., Blazquez A., Kolodziejczyk N., Bamber J. (2019). Global ocean freshening, ocean mass increase and global mean sea level rise over 2005–2015. Sci. Rep. 9, 17717. doi: 10.1038/s41598-019-54239-2

PubMed Abstract | Crossref Full Text | Google Scholar

Locarnini M. M., Mishonov A. V., Baranova O. K., Boyer T. P., Zweng M. M., Garcia H. E., et al. (2019). “World ocean atlas 2018, volume 1: Temperature,” in NOAA atlas NESDIS, vol. 81 . Ed. Mishonov A.. (MG, USA: Silver Spring), 52. Available at: https://www.ncei.noaa.gov/sites/default/files/2020-04/woa18_vol1.pdf (accessed December 10, 2024).

Google Scholar

Lopez H., Dong S., Lee S.-K., Goni G. (2016). Decadal modulations of interhemispheric global atmospheric circulations and Monsoons by the South Atlantic meridional overturning circulation. J. Climate 29, 1831–1851. doi: 10.1175/JCLI-D-15-0491.1

Crossref Full Text | Google Scholar

Lübbecke J. F., Durgadoo J. V., Biastoch A. (2015). Contribution of increased Agulhas leakage to tropical Atlantic warming. J. Climate 28, 9697–9706. doi: 10.1175/JCLI-D-15-0258.1

Crossref Full Text | Google Scholar

Majumder S., Schmid C., Halliwell G. (2016). An observations and model-based analysis of meridional transports in the South Atlantic. J. Geophysical Res.: Oceans 121, 5622–5638. doi: 10.1002/2016JC011693

Crossref Full Text | Google Scholar

Meinen C. S., Speich S., Piola A. R., Ansorge I., Campos E., Kersalé. M., et al. (2018). Meridional overturning circulation transport variability at 34.5 S during 2009–2017: Baroclinic and barotropic flows and the dueling influence of the boundaries. Geophysical Res. Lett. 45, 4180–4188. doi: 10.1029/2018GL077408

Crossref Full Text | Google Scholar

Mignac D., Ferreira D., Haines K. (2019). Decoupled freshwater transport and meridional overturning in the South Atlantic. Geophysical Res. Lett. 46, 2178–2186. doi: 10.1029/2018GL081328

Crossref Full Text | Google Scholar

Mulet S., Rio M. H., Etienne H., Artana C., Cancet M., Dibarboure G., et al. (2021). The new CNES-CLS18 global mean dynamic topography. Ocean Sci. 17, 789–808. doi: 10.5194/os-17-789-2021

Crossref Full Text | Google Scholar

Pita I., Goes M., Volkov D. L., Dong S., Goni G., Cirano M. (2024). An ARGO and XBT observing system for the atlantic meridional overturning circulation and meridional heat transport (AXMOC) at 22.5° S. J. Geophysical Res.: Oceans 129, e2023JC020010. doi: 10.1029/2023JC020010

Crossref Full Text | Google Scholar

Pujol M. I., Faugère Y., Taburet G., Dupuy S., Pelloquin C., Ablain M., et al. (2016). DUACS DT2014: The new multi-mission altimeter data set reprocessed over 20 years. Ocean Sci. 12, 1067–1090. doi: 10.5194/os-12-1067-2016

Crossref Full Text | Google Scholar

Pujol M.-I., Taburet G., SL-TAC team (2023). Sea level TAC—DUACS products. Copernicus Mar. doi: 10.48670/moi-00148

Crossref Full Text | Google Scholar

Rahmstorf S. (1996). On the freshwater forcing and transport of the Atlantic thermohaline circulation. Climate Dynamics 12, 799–811. doi: 10.1007/s003820050144

Crossref Full Text | Google Scholar

Sathyanarayanan A., Köhl A., Stammer D. (2021). Ocean salinity changes in the global ocean under global warming conditions. Part I: Mechanisms in a strong warming scenario. J. Climate 34, 8219–8236. doi: 10.1175/JCLI-D-20-0865.1

Crossref Full Text | Google Scholar

Schmid C. (2014). Mean vertical and horizontal structure of the subtropical circulation in the South Atlantic from three-dimensional observed velocity fields. Deep Sea Res. Part I: Oceanographic Res. Papers 91, 50–71. doi: 10.1016/j.dsr.2014.04.015

Crossref Full Text | Google Scholar

Sharp J. D., Fassbender A. J., Carter B. R., Johnson G. C., Schultz C., Dunne J. P. (2023). GOBAI-O 2: temporally and spatially resolved fields of ocean interior dissolved oxygen over nearly two decades. Earth System Sci. Data 15, 4471–4518. doi: 10.5194/essd-15-4481-2023

Crossref Full Text | Google Scholar

Srokosz M. A., Holliday N. P., Bryden H. L. (2023). Atlantic overturning: new observations and challenges. Philos. Trans. R. Soc. A 381, 20220196. doi: 10.1098/rsta.2022.0196

PubMed Abstract | Crossref Full Text | Google Scholar

Talley L. D. (2008). Freshwater transport estimates and the global overturning circulation: Shallow, deep and throughflow components. Progress in Oceanography 78 (4), 257–303. doi: 10.1016/j.pocean.2008.05.001

Crossref Full Text | Google Scholar

Todd R. E., Chavez F. P., Clayton S., Cravatte S., Goes M., Graco M., et al. (2019). Global perspectives on observing ocean boundary current systems. Front. Mar. Sci. 6. doi: 10.3389/fmars.2019.00423

Crossref Full Text | Google Scholar

Treguier A. M., Deshayes J., Le Sommer J., Lique C., Madec G., Penduff T., et al. (2014). Meridional transport of salt in the global ocean from an eddy-resolving model. Ocean Sci. 10, 243–255. doi: 10.5194/os-10-243-2014

Crossref Full Text | Google Scholar

Tsubouchi T., Bacon S., Naveira Garabato A. C., Aksenov Y., Laxon S. W., Fahrbach E., et al. (2012). The Arctic Ocean in summer: A quasi-synoptic inverse estimate of boundary fluxes and water mass transformation. J. Geophysical Res.: Oceans 117, C01024. doi: 10.1029/2011JC007174

Crossref Full Text | Google Scholar

van Westen R. M., Kliphuis M., Dijkstra H. A. (2024). Physics-based early warning signal shows that AMOC is on tipping course. Sci. Adv. 10, eadk1189. doi: 10.1126/sciadv.adk1189

PubMed Abstract | Crossref Full Text | Google Scholar

Vilela-Silva F., Silveira I. C., Napolitano D. C., Souza-Neto P. W., Biló T. C., Gangopadhyay A. (2023). On the deep western boundary current separation and anticyclone genesis off northeast Brazil. J. Geophysical Res.: Oceans 128, e2022JC019168. doi: 10.1029/2022JC019168

Crossref Full Text | Google Scholar

Volkov D. L., Smeed D. A., Lankhorst M., Dong S., Moat I., Willis J., et al. (2023). “Meridional overturning circulation and heat transport in the Atlantic Ocean,” in State of the climate in 2022, vol. 104 . Eds. Blunden J., Boyer T., Bartow-Gillies E. (Boston, MA, USA: Bulletin of the American Meteorological Society), Si–S501. doi: 10.1175/2023BAMSStateoftheClimate.1

Crossref Full Text | Google Scholar

Weber S. L., Drijfhout S. S., Abe-Ouchi A., Crucifix M., Eby M., Ganopolski A., et al. (2007). The modern and glacial overturning circulation in the Atlantic ocean in PMIP coupled model simulations. Climate Past 3, 51–64. doi: 10.5194/cp-3-51-2007

Crossref Full Text | Google Scholar

Weijer W., Cheng W., GAruba O. A., Hu A., Nadiga B. T. (2020). CMIP6 models predict significant 21st century decline of the Atlantic Meridional Overturning Circulation. Geophysical Res. Lett. 47, e2019GL086075. doi: 10.1029/2019GL086075

Crossref Full Text | Google Scholar

Willis J. K. (2010). Can in situ floats and satellite altimeters detect long-term changes in Atlantic Ocean overturning? Geophys. Res. Lett. 37, L06602. doi: 10.1029/2010GL042372

Crossref Full Text | Google Scholar

XBT Network (2024). High density XBT transect data from physical Oceanography Division (PhOD), Atlantic Oceanographic and Meteorological Laboratory (AOML) (National Oceanic and Atmospheric Administration). Available at: http://www.aoml.noaa.gov/phod/hdenxbt/ (accessed December 10, 2024).

Google Scholar

Zhang R., Delworth T. L. (2006). Impact of Atlantic multidecadal oscillations on India/Sahel rainfall and Atlantic hurricanes. Geophysical Res. Lett. 33, L17712. doi: 10.1029/2006GL026267

Crossref Full Text | Google Scholar

Zhu C., Liu Z. (2020). Weakening Atlantic overturning circulation causes South Atlantic salinity pile-up. Nat. Climate Change 10, 998–1003. doi: 10.1038/s41558-020-0897-7

Crossref Full Text | Google Scholar

Zhu C., Liu Z., Zhang S., Wu L. (2023). Likely accelerated weakening of Atlantic overturning circulation emerges in optimal salinity fingerprint. Nat. Commun. 14, 1245. doi: 10.1038/s41467-023-36288-4

PubMed Abstract | Crossref Full Text | Google Scholar

Zuo H., Balmaseda M. A., Tietsche S., Mogensen K., Mayer M. (2019). The ECMWF operational ensemble reanalysis–analysis system for ocean and sea ice: a description of the system and assessment. Ocean Sci. 15, 779–808. doi: 10.5194/os-15-779-2019

Crossref Full Text | Google Scholar

Zweng M. M., Seidov D., Boyer T. P., Locarnini M., Garcia H. E., Mishonov A. V., et al. (2019). “World ocean atlas 2018, volume 2: Salinity,” in NOAA atlas NESDIS, vol. 82 . Ed. Mishonov A.. (MG, USA: Silver Spring), 50. Available at: https://www.ncei.noaa.gov/sites/default/files/2022-06/woa18_vol2.pdf (accessed December 10, 2024).

Google Scholar