Analysis of acoustic field characteristics of mesoscale eddies throughout their complete life cycle

Mesoscale eddies exert a profound influence on oceanic temperature and salinity structures, thereby altering the ecological environment and acoustic propagation characteristics. Prior research on acoustic propagation beneath mesoscale eddy effects has predominantly concentrated on fragmented, snapshot-style analyses. In contrast, this study employs a holistic approach by integrating multi-source data to elucidate oceanic temperature and salinity structures, ultimately impacting their ecological environment and acoustic propagation. While the existing paper, this study adopts a more comprehensive and successional methodology. Through the amalgamation of multi-source data, this research introduces an innovative mesoscale eddy tracking algorithm and an enhanced Gaussian eddy model. Utilizing the BELLHOP ray theory model, this investigation scrutinizes the acoustic field characteristics of a cyclonic eddy and a typical anticyclonic eddy (CE-AE) pair exhibiting complete life cycles in the Northwest Pacific. The results reveal that the complete life cycles of mesoscale eddies substantially impact the acoustic field environment. As a CE intensifies, the convergence zone (CZ) distance diminishes, the CZ width expands, and the direct wave (DW) distance shortens. Conversely, an intensifying AE increases the CZ distance, contracts the CZ width, and prolongs the DW distance. This paper presents a quantitative analysis to delineate the critical factors influencing eddy life cycles, indicating that both eddy intensity and deformation parameters significantly affect acoustic propagation characteristics, with eddy intensity exerting a more substantial influence. This research substantially contributes to the application of sea surface altimetry data for underwater acoustic studies and provides preliminary insights into the impacts of eddy parameters on underwater acoustic propagation within typical mesoscale eddy environments. Moreover, this research offers a foundation for future investigations into the intricate relationships between eddy dynamics and acoustic propagation in oceanic systems.

1 Introduction

Mesoscale eddies, ranging from tens to hundreds of kilometers in size and lasting from tens to hundreds of days, are a fundamental mesoscale phenomenon in ocean dynamics (Chelton et al., 2011). These eddies, prevalent throughout global oceans, profoundly affect the structure and function of the ocean system. They are classified as cyclonic eddies (CEs) or anticyclonic eddies (AEs), depending on their rotation. In the Northern Hemisphere, CEs rotate counterclockwise and AEs clockwise, with the opposite pattern occurring in the Southern Hemisphere. This rotation is crucial for understanding the dynamics and behavior of mesoscale eddies (Zhang et al., 2013). These eddies significantly influence the mixing and redistribution of water masses, creating marked differences in temperature and salinity between internal and external areas, thereby affecting spatial water distribution patterns and the overall structure of ocean circulation (Qiu and Chen, 2005a). Moreover, mesoscale eddies facilitate the exchange of materials and the transfer of energy in the ocean, crucial for the long-term evolution of the marine environment (Zhang et al., 2014). They mix water from various sources, enhancing material exchanges (Itoh and Yasuda, 2010), and transport energy from surface to deeper layers, impacting the structural integrity of the ocean (Dong et al., 2014). Additionally, changes in the trajectories and lifecycles of mesoscale eddies can reshape ocean circulation, influencing long-term changes in the marine environment (Oka and Qiu, 2012).

The extensive deployment of ocean observation satellites has yielded high-precision, long-term remote sensing data of the ocean, providing invaluable resources for the identification, detection, and quantitative analysis of mesoscale eddies. Various mesoscale eddy recognition algorithms have been developed and can be categorized into three main types: 1) physical parameter-dependent methods (Okubo, 1970; Weiss, 1991; Liu et al., 2016); 2) flow field geometry-based methods (Chaigneau et al., 2008; Nencioli et al., 2010; Chelton et al., 2011); and 3) machine vision techniques (Franz et al., 2018; Xu et al., 2019; Nian et al., 2021). These methods have greatly enhanced research into mesoscale eddies. Following the identification of these eddies, researchers have performed in-depth studies on their development and evolution. Zhang and Qiu (2018) assessed sub-mesoscale ageostrophic motions throughout the life cycles of marine mesoscale eddies using ocean surface drifter and satellite altimetry data, elucidating the impact of deformation strain rate on sub-mesoscale energy at different stages in the life cycles of these eddies, with implications for oceanic balance and climate modeling and forecasting. Morvan et al (2020) investigated the life cycles of mesoscale eddies in the Gulf of Aden by applying an eddy tracking algorithm and a regional mesoscale eddy equation model, concluding that wind stress, water depth, and the surrounding eddy field influence eddy dynamics. Czeschel et al (2018) explored the influence of mesoscale eddies on the flow field and water masses in the eastern tropical South Pacific using moored instruments, drifters, and satellite altimetry, noting significant transverse mixing between the seasonal temperature and salinity structures and the eddy core during the early stages of the eddy life cycle. Chen et al (2022) analyzed over two decades of daily sea surface altimetry data to discern patterns in the geographical distribution and longevity of ocean eddies, revealing asymmetrical growth and decay processes characterized by a single flat peak in their life cycle. Collectively, these investigations highlight the dynamic changes mesoscale eddies experience, marked by various measurable properties throughout their life cycles.

The pervasive presence of mesoscale eddies not only influences oceanic processes but also alters the structure of the acoustic field. These modifications arise from the distinctive temperature and salinity profiles of eddies and have considerable implications for human activities such as communication and detection in the ocean, as well as for the survival of marine organisms (Godø et al., 2012). In their study of a mesoscale eddy in the Northwest Pacific Ocean, Liu et al (2021) noted that the convergence zone (CZ) of acoustic propagation shifts toward and away from the acoustic source with changes in eddy polarity. Liu et al (2024) employed a finite element model to analyze the impact of environmental changes on the acoustic field within a mesoscale eddy, corroborating their findings with in-situ observational data. This model successfully predicted remote sensing data even in the absence of complete details of the underwater acoustic field. Additionally, a 2022 in-situ analysis in the Bering Sea region indicated that acoustic propagation is notably more pronounced along the direction of the eddy in a mesoscale eddy environment. Li et al (2012) used the MMPE model to simulate underwater acoustic propagation influenced by eddy currents and acoustic sources under various conditions. Their research indicates that AE shifts the CZ backward and broadens it, whereas CE narrows and shifts it forward. These findings suggest that the acoustic field structure significantly changes in response to the mesoscale eddy characteristics during its life cycle. Moreover, mesoscale eddies exhibit predictable regularities under stable conditions, including variations in temperature and salinity anomalies or sea surface height (SSH) sea surface level anomaly (SLA), and at the centers of eddies, eddy type (CE or AE), central position, and deformation. These characteristics evolve throughout the life cycles of the eddies. Therefore, analyzing the influence of mesoscale eddies on underwater acoustic propagation necessitates a comprehensive understanding of these attributes over the entire cycle. Previous studies typically focused on a single aspect of a mesoscale eddy at one time, leading to “pixelates” analyses that do not capture the acoustic field comprehensively under varying conditions. By contrast, this study uses SSH and SLA data and an enhanced Gaussian eddy model to analyze acoustic field characteristics throughout the full mesoscale eddy life cycle, enabling a continuous and quantitative analysis that clarifies the impact of mesoscale eddies on regional acoustic propagation from start to finish.

2 Data and method

2.1 Data

This paper uses daily data spanning from January 1, 2007, to December 31, 2020.

2.1.1 Argo data

The Argo program (Array for Real-time Geostrophic Oceanography) is a global network of underwater floats that provides observational data on the ocean. Initially implemented on a local scale in 1999, the network achieved global coverage by 2004. By 2007, the program had deployed 3,000 floats, solidifying its utility for oceanographic research (Qiu and Chen, 2005b; Roemmich et al., 2009; Johnson et al., 2022). As of December 2023, the active number of Argo floats has reached 3,840. Additionally, since 2015, the China Argo real-time data center has been offering data exchange services, facilitating access to Argo data for Chinese researchers.

2.1.2 AVISO data

Sea Level Anomaly (SLA) and geostrophic data, gridded products developed by the Archiving, Validation, and Interpretation of Satellite Oceanographic Data (AVISO) group at CNES, incorporate altimetry data from multiple satellites. This data is interpolated onto a quarter-degree grid using the Mercator projection. With a temporal resolution of seven days refined to one day, these datasets are extensively utilized in research on marine mesoscale phenomena (Ablain et al., 2015; Cazenave et al., 2018).

2.1.3 Ocean reanalysis data

JCOPE2M (Japan Coastal Ocean Predictability Experiment 2 Modified) dataset, referenced in the study (Miyazawa, 2003), is a high-resolution reanalysis produced by the Japan Marine Affairs Agency focusing on the Northwest Pacific Ocean. It features a daily temporal resolution and a spatial resolution of 1/12°, encompassing 46 vertical layers throughout the full depth. JCOPE2M incorporates the assimilation of sea surface temperature, SSH anomalies, and selected Argo observations. Owing to its high accuracy and reliability, JCOPE2M is extensively used in research concerning mesoscale eddies, analyzing temperature, salinity, and flow dynamics (Xu et al., 2024).

2.2 Methods

2.2.1 Mesoscale eddy recognition and tracking algorithm

The flow field geometry method analytically identifies mesoscale eddies based on geometric characteristics of the velocity vector field, specifically recognizing regions displaying rotational flow. An eddy is defined in this context if a minimum speed point is surrounded by symmetrically distributed velocity vectors rotating clockwise or counterclockwise. In contrast, the SLA closed curve method directly identifies a closed curve of SSH around a local extreme, relying solely on SLA data, which reduces the incidence of unclosed eddies common in the flow field geometry method. However, the SLA method requires setting a threshold for SSH differences to define eddy boundaries, making the identification susceptible to subjective bias. To optimize the balance between accurate eddy recognition and threshold sensitivity, a hybrid algorithm that integrates both methods is utilized (Ma et al., 2024).

This study employs two distinct identification methods, applied separately to the analysis of surface flow fields and SLA data. The objective is to integrate these methods to precisely detect mesoscale eddy pairs with maximal boundary overlap. Given that AE and CE pairs necessitate specific parameter adjustments for each method, we introduce a universal custom threshold criterion to meet this objective. The identification outcomes from both methods are deemed valid only if the intersection area of the two eddies exceeds 50% of the area of an individual eddy as defined by each method, and the distance between the centers of the eddies does not surpass 1/12 degree. Under these criteria, the eddy center identified by the flow field geometry method is prioritized as the actual center.

After obtaining the daily eddy detection data, this study introduces a hybrid threshold-matching eddy tracking algorithm. The algorithm employs the surface height information from the eddy profile to conduct a Hu invariant moment similarity test (with a threshold of 0.9) and a polygon collision detection technique. The steps involved in the eddy tracking algorithm are outlined in Algorithm 1. Hu moment invariants (Hu, 1962), widely used in image processing and computer vision for feature extraction, are applicable in object recognition and tracking. This method is robust against rotation, translation, and scaling transformations, offering a straightforward and cost-effective implementation.

Algorithm 1. Eddy-tracking.

However, it demonstrates limitations in characterizing noise and non-convex objects. Given that the eddies identified by the recognition algorithm in this study’s eddy tracking process have convex contours and are relatively free of significant noise, we employ Hu invariant moments as one of the criteria for eddy matching (Figure 1).

Figure 1

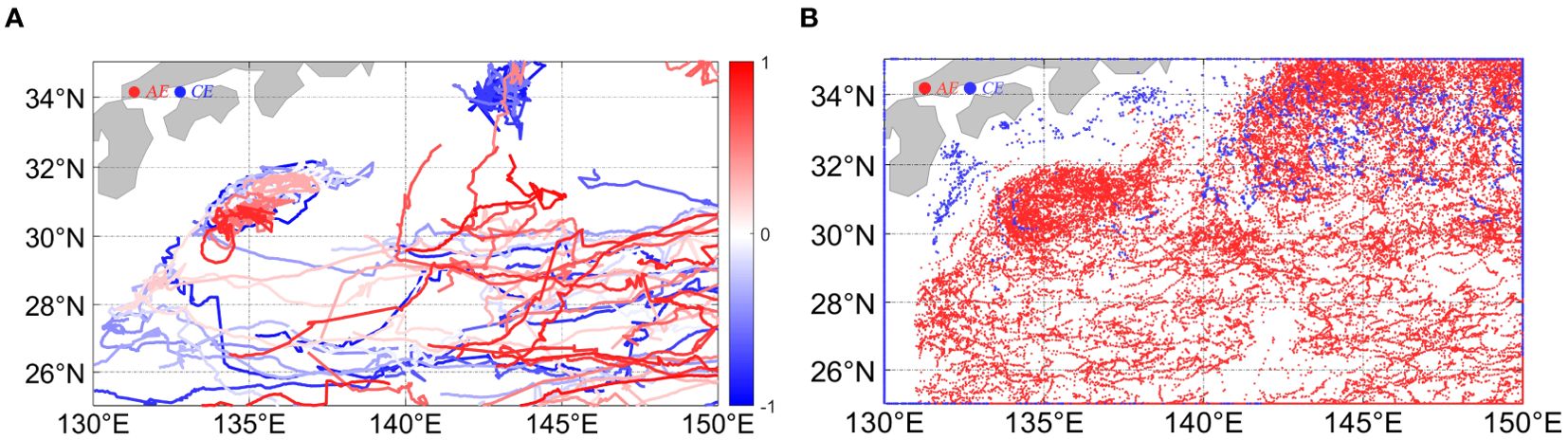
Figure 1. (A) General tracking map of mesoscale eddies in the Kuroshio extension area, filtered over 120 days from January 1, 2007, to December 31, 2020 (the color differences represent the mean sea level height of eddies during the tracking period, AE in red and CE in blue). (B) Distribution of all recognized eddy centers from January 1, 2007, to December 31, 2020 (AE in red and CE in blue).

2.2.2 Acoustic field calculation model and parameter setting

According to the Gaussian beam tracking algorithm (Porter and Bucker, 1987), BELLHOP computes the acoustic field in both homogeneous and heterogeneous environments. By mapping each acoustic ray to a corresponding inner ray within a Gaussian beam characterized by its Gaussian intensity, the model effectively simulates acoustic propagation in a manner that aligns closely with full-wave models. Consequently, BELLHOP is extensively employed in acoustic modeling (Gul et al., 2017; Shehwar et al., 2021; Sun et al., 2023). In this model, the evolution of the acoustic beam is controlled by the beam width, denoted as $p(s)$, and the beam curvature, denoted as $q(s)$. The ray equation in cylindrical coordinates is formulated as shown in Equation 1. The parameters p and q are determined by Equation 2:

$\begin{array}{ll}\frac{d}{ds}\left[\frac{1}{c(r,z)}\frac{dr}{ds}\right]=-\frac{1}{c^2(r,z)}\text{∇}c(r,z)& (1)\end{array}$

$\begin{array}{ll}\frac{dq}{ds}=c(s)p(s), \frac{dp}{ds}=\frac{c_{nn}}{c^2(s)}q(s)& (2)\end{array}$

Where s represents the acoustic ray, $c(·)$ denotes the speed of sound, and $c_{nn}$ indicates the second derivative of the path direction (subscript represents the direction of derivation), as follows: $r=r(s),z=z(s)$, and $[r(s),z(s)]$ are the coordinates of the arc length function. $c_{nn}$ can be calculated using Equations 3, 4:

$\begin{array}{ll}{c}_{nn}=c_{rr}{\left(\frac{dr}{dn}\right)}^2+2c_{rz}\left(\frac{dr}{dn}\right)\left(\frac{dz}{dn}\right)+c_{zz}{\left(\frac{dz}{dn}\right)}^2& (3)\end{array}$

$\begin{array}{ll}=c_{rr}{(N_{(r)})}^2+2c_{rz}(N_{(r)})(N_{(z)})+c_{zz}{(N_{(z)})}^2& (4)\end{array}$

Where $N_{(r)}$ $N_{(z)}$ represents the unit normal in both directions, which can be expressed as Equation 5:

$\begin{array}{ll}(N_{(r)})(N_{(z)})=\left(\frac{dz}{ds},-\frac{dr}{ds}\right)=c(s)[\zeta (s),-\rho (s)]& (5)\end{array}$

In summary, the beam can be defined as $u(s,n)$ as Equation 6:

$\begin{array}{ll}u(s,n)=A\sqrt{\frac{c(s)}{rq(s)}}{e}^{\left(-iw\left\{\tau (s)+0.5\left[\frac{p(s)}{q(s)}\right]n^2\right\}\right)}& (6)\end{array}$

Where A represents the constant determined by the properties of the acoustic source, n denotes the vertical distance of the acoustic line, and $\omega$ is the angular frequency of the acoustic source. $\tau (s)$ indicates the phase delay constrained by the limits: $\frac{d\tau }{ds}=1/c(s)$. Finally, the acoustic source beam is weighted as shown in Equation 7:

$\begin{array}{ll}A(s)=\delta \alpha \left(\frac{1}{c_0}\right)\sqrt{\frac{q(s)\omega \cos \alpha }{2\pi }}{e}^{\left(\frac{i\pi }{4}\right)}& (7)\end{array}$

Where $\delta \alpha$ represents the angle between the beams. In this paper, when applying the $Bellhop$ ray theory model, the main sedimentary layer in the study area is assumed to be deep-sea clay, with parameters listed in Table 1. The empirical formula for sound speed is given by the $Chen-Milero$ formula (Chen and Millero, 1977).

Table 1

Table 1. Acoustic parameters of the main types of sedimentary layers in the study area.

2.2.3 Acoustic propagation evaluation indicators

This paper employs two practical indicators of acoustic propagation: the action distance and width of the DW, and the initial distance and width of the CZ.

In underwater acoustics, the convergence zone (CZ) denotes the area where sound waves focus due to speed gradient variations. The CZ distance is the horizontal range from the source to the initial CZ formation, influenced by sound speed profiles. CZ width represents the lateral extent of high-intensity sound within the CZ, expanding with higher CZ sequence numbers. Direct wave distance is the straight-line propagation path from the source to the observation point.

In the context of ocean acoustic propagation, DWs represent the unimpeded transmission of sound waves directly from the source to the receiver, devoid of scattering or reflections. DWs are distinguished by their shortest propagation path and, as such, maintain high energy and phase stability; this study specifically considers a DW at a depth of 500 m. In contrast, sound waves interacting with the sea surface or seabed are subject to reflection, refraction, and scattering, leading to significant modifications in their propagation path and energy distribution. DWs, which travel perpendicularly or nearly so to the sea surface, circumvent these boundary interactions, thereby holding a unique significance in ocean acoustic studies.

The CZ is defined as a region where acoustic energy concentrates, occurring when the source is situated at or near the ocean surface. As acoustic waves propagate over substantial distances, their refraction leads them to reconverge near the sea surface, tens of kilometers from the source. This phenomenon notably decreases acoustic propagation loss within the zone compared to adjacent areas. Variations in the marine environment, especially those altering the acoustic speed profile, markedly affect acoustic propagation in the CZ.

Figure 2 utilizes a typical deep-sea Munk acoustic speed profile as the foundational model to elucidate the two index concepts more distinctly. The BELLHOP ray theory model calculates the acoustic propagation loss, highlighting the effects of the DW and the CZ. In this study, the boundaries of DW and CZ are defined by a propagation loss threshold of less than 90 dB at a depth of 200 m.

Figure 2

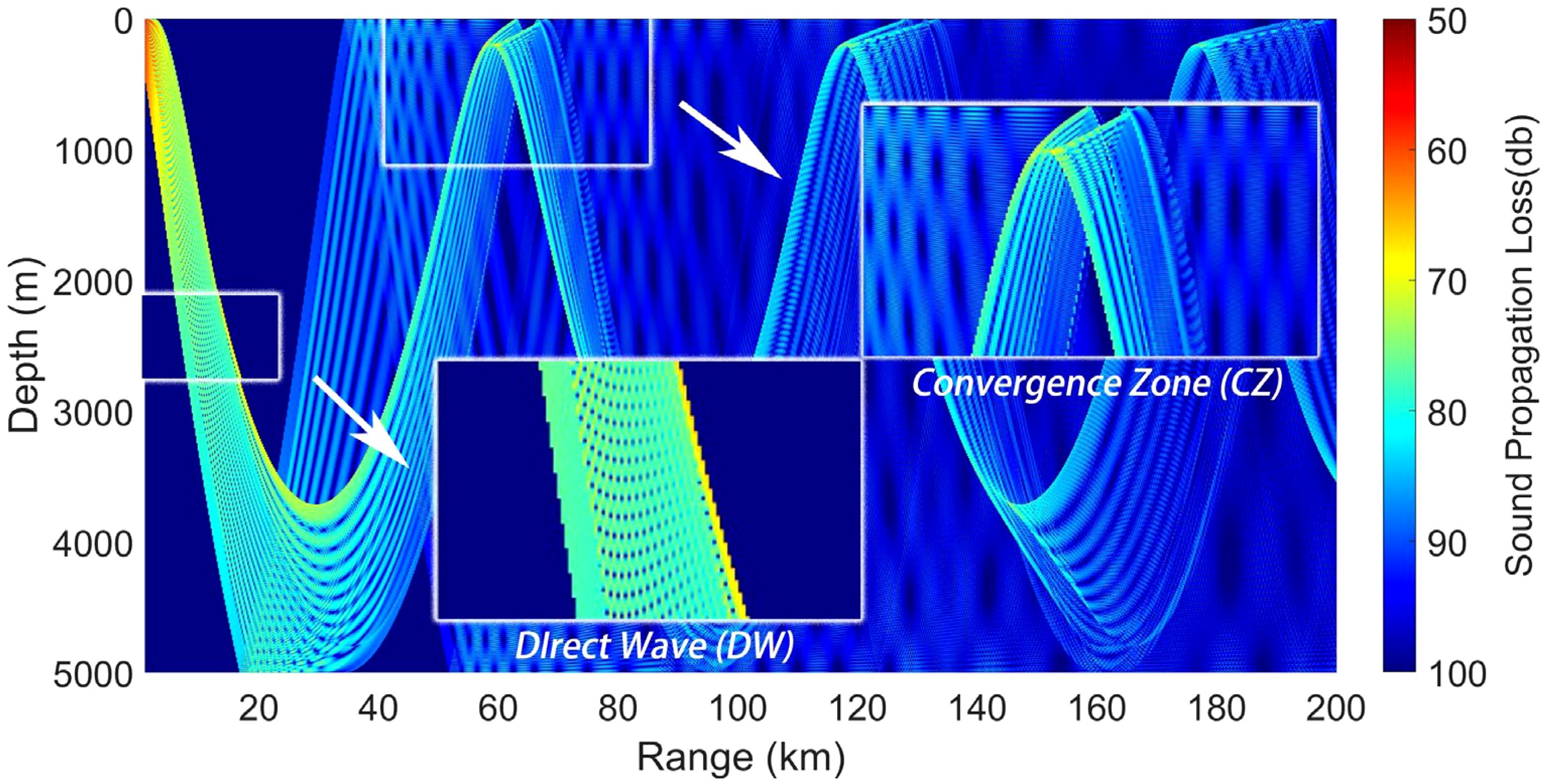
Figure 2. Diagram of CZ and DW effect under a typical deep-sea Munk acoustic speed profile (source depth: 10 meters, source incidence Angle: 0° to 45°, source frequency: 1000HZ).

2.2.4 Improved two-dimensional Gaussian eddy model

The two-dimensional, slowly varying Gaussian eddy model simulates the formation, evolution, and ultimate dissipation of eddies by representing them as Gaussian distributions within a two-dimensional framework. Each eddy is characterized by parameters such as central position, intensity, and rotational speed, among others, which evolve to describe effectively the dynamics of the eddy. Equations 8–10 provide a summary of acoustic speed:

$\begin{array}{ll}c(r,z)=c_0(z)+\delta c(r,z)& (8)\end{array}$

$\begin{array}{ll}{c}_0(z) = C_1\left\{1+0.00741[e^{-\eta }-(1-\eta )]\right\}& (9)\end{array}$

$\begin{array}{ll}{\delta }_c(r,z) = DC\times e^{-{(\frac{r-R_e}{DR})}^2-{(\frac{z-Z_e}{DZ})}^2}& (10)\end{array}$

Where r represents the horizontal distance from the eddy center, and z denotes the vertical distance from the eddy center. $C_0$ corresponds to the Munk profile model, $\eta =2(z-z_1)/1300$. $C_1$ denotes the acoustic speed along the channel axis, and $z_1$ is the depth of the channel axis. DC represents the eddy intensity, taking a negative (positive) value for CEs (AEs). DR signifies the horizontal radius of the eddy, DZ indicates the vertical radius of the eddy, Re denotes the horizontal position of the eddy center, and Ze represents the vertical position of the eddy center. The eddy intensity is derived from the SSH. The horizontal radius of the eddy corresponds to the radius of the individual eddy identified in Section 2.2.1. Finally, the vertical radius and vertical position of the eddy center are obtained from Argo data associated with the individual eddy center.

However, typical Gaussian eddies, which are seldom observed in the ocean due to the interaction between air-sea dynamics and eddy currents, present complexities in their characterization. The acoustic speed profile of these eddies, derived from sea surface data, often leads to misleading interpretations. This is because the visible center of the eddy at the surface may not align with its actual center, necessitating the use of a modified Gaussian eddy model. This improved model incorporates an additional parameter, the eddy center bias coefficient, which quantifies the displacement of the eddy center. This coefficient is calculated from the ratio of the distance between the two most distant points on the sea surface profile of the eddy to its radius. When deploying an Argo float within a stable eddy, it is possible to acquire vertical acoustic speed profiles throughout the lifespan of the eddy. Consequently, the conventional empirical Munk profile (Munk, 1950) used in earlier models is replaced with these directly measured profiles. Adjustments to the acoustic speed profile are encapsulated in Equations 11–13:

$\begin{array}{ll}C(r,z)=C_0(z)+{\delta }_C(r,z)& (11)\end{array}$

$\begin{array}{ll}{C}_0(z) = Argo& (12)\end{array}$

$\begin{array}{ll}{\delta }_C(r,z)=DC\times \{\begin{array}{cc}{e}^{-{(\frac{r-R_e}{2\alpha DR})}^2-{(\frac{z-Z_e}{DZ})}^2}& (r-R_e\le 2\alpha DR)\\ e^{-{(\frac{r-R_e}{2(1-\alpha )DR})}^2-{(\frac{z-Z_e}{DZ})}^2}& (r-R_e\ge 2\alpha DR)\end{array}& (13)\end{array}$

3 Analysis of acoustic field variation under the life cycle of a typical mesoscale eddy

3.1 Analysis of acoustic field change in improved Gaussian eddy environment

To analyze the changes in the acoustic field throughout the life cycle of a mesoscale eddy, it is essential to first compile a sequence of acoustic speed profiles spanning the eddy’s entire life cycle. However, due to the general inaccessibility of comprehensive oceanographic commissioning data for such durations, we adopt an alternative approach by correlating SSH data of mesoscale eddies with Argo float data. The procedure is as follows: We use mesoscale eddy identification and tracking information from Section 2.2.1 to locate corresponding Argo data points. A match is considered if the measurement of an Argo data point falls within one day before or after the observed lifespan of the eddy. Subsequently, verification is conducted to determine whether the geographical coordinates of the Argo data point are within the spatial contour of the eddy at the corresponding time. If this condition is met, the data point is deemed a match. For eddies with life cycles spanning multiple days, a sequence of matched data pairs between the eddy and corresponding Argo data is deemed viable if matches are present for each day and periods without matching data do not exceed one day.

To ensure the effectiveness of the data for the following acoustic field analysis, we implemented stringent criteria for selecting eddy-Argo data pairs:

1. The lifecycle of the eddy should span at least 30 days;

2. The eddy should encompass a minimum of three Argo floats daily, with at least one float situated within 1/5 of the radius from the eddy center.

Using the specified criteria, we analyzed data from the Pacific Northwest spanning January 1, 2007, to December 31, 2020. This analysis includes two distinct examples: one CE and one AE, each demonstrating unique characteristics and trajectories. The lifespans recorded for these eddies were 145 d (CE) and 249 d (AE). During their lifespans, both eddies consistently captured over three Argo floats daily, primarily concentrated near their centers. Figure 3 delineates the path of the CE, whereas Figure 4 displays variations in its multiple characteristics. It is pertinent to note that mesoscale eddies typically undergo a generative phase, a mature phase, and a decaying phase. Although the specific life cycle values of these eddies may vary, their developmental patterns are generally stable. This research focuses on the entire life cycle of mesoscale eddies. As such, we have carefully selected a pair of mesoscale eddies for a detailed examination. The attributes of this eddy pair closely represent the variations in the underwater acoustic fields associated with long-period eddies.

Figure 3

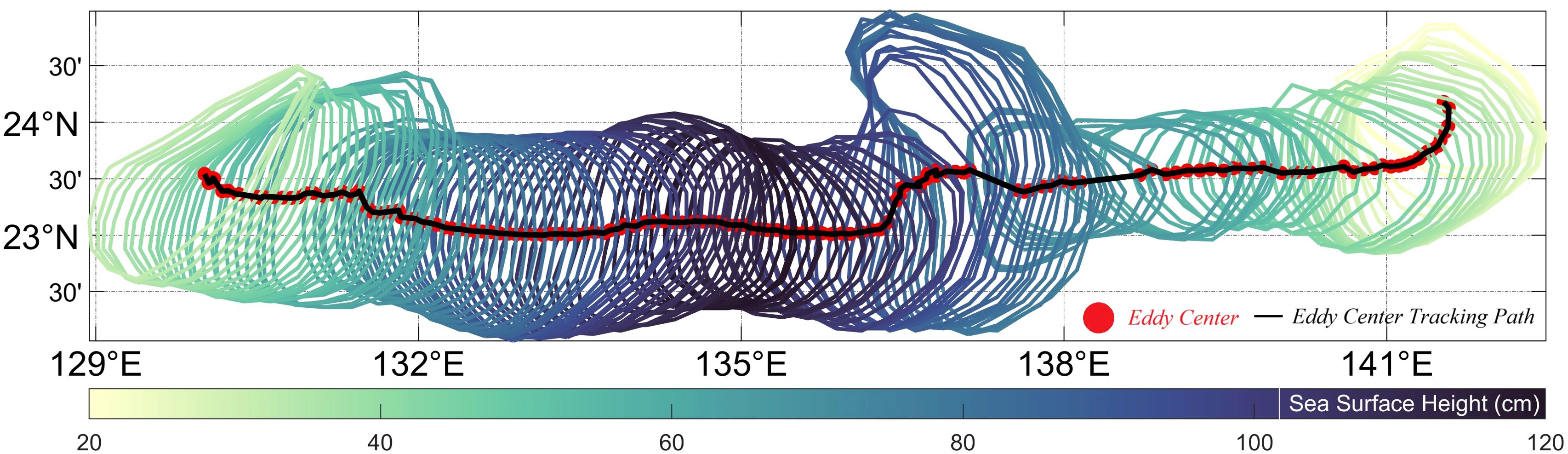
Figure 3. Diagram of the identification profile, eddy center, and tracking path of the mesoscale eddy over a full life cycle. The red circles indicate the daily positions of the eddy center. The color gradient of the eddy contour, from dark to light, represents the eddy center SSH, with darker colors indicating higher SSH. Eddies in the growth and dissipation phases exhibit lower SSH, while eddies in the flourishing phase show higher SSH.

Figure 4

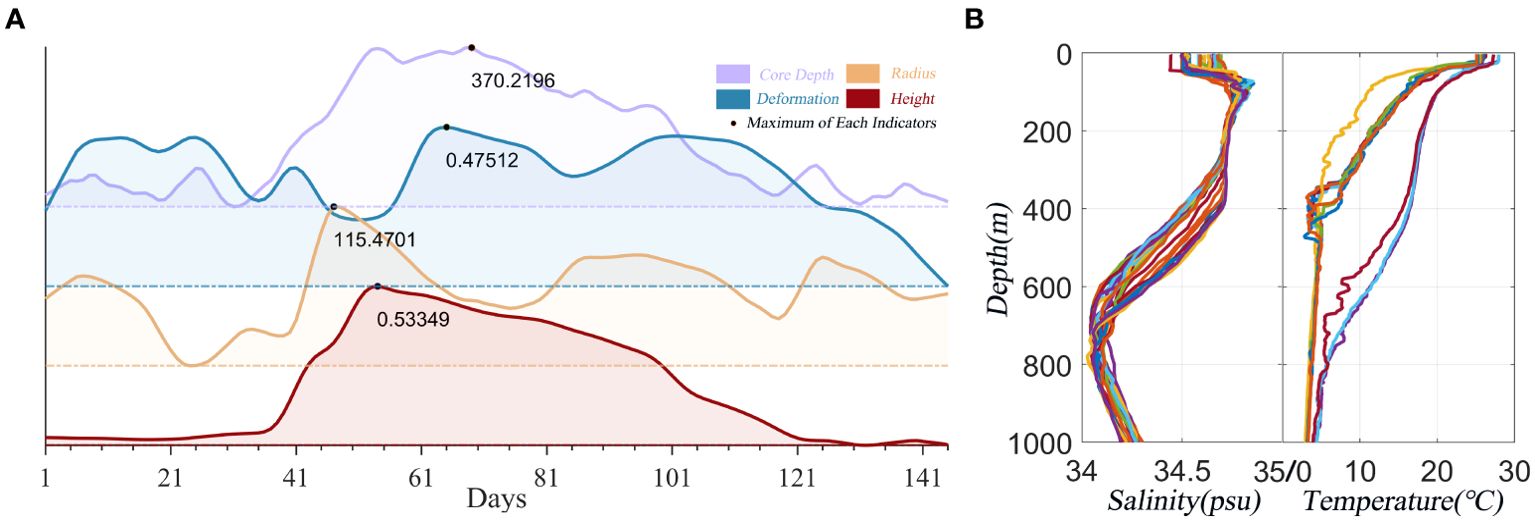
Figure 4. (A) Diagram of changes in eddy feature information in a mesoscale eddy environment. The height of the eddy center represents the SSH at the extreme point within the eddy profile (shown here for a CE, with negative values presented as absolute values). The eddy radius is defined as the equivalent eddy radius, α is as defined in Section 2.2.3, and the depth of the eddy center is calculated from the local extreme of the captured Argo acoustic speed profile and gradient elements (Chaigneau et al., 2011). (B) Multi-day temperature and salinity profiles measured by the Argo float within the eddy.

Figures 3, 4 depict the typical progression of development, intensification, and decay within a complete mesoscale eddy lifecycle, as evidenced by variations in eddy core depth and SSH. Notably, the coefficient and equivalent radius of the eddy does not follow a consistent trend throughout this sequence.

An eddy simulation was conducted using the enhanced Gaussian eddy model detailed in Section 2.2.4, applying parameters obtained from eddy characteristic analyses. The simulation produced sequences of two acoustic speed profiles over periods of 145 d (CE) and 249 d (AE). The BELLHOP ray theory model, as described in Section 2.2.2, was used to simulate the acoustic field. The acoustic source was positioned at the center of the eddy at a depth of 100 meters, emitting at 300 Hz. The analysis evaluated the distances to DW and the extent and width of the initial CZ as specified in Section 2.2.3. Figure 5 illustrates the temporal variations in the distance of the first CZ, the distance of DW, and the width over 145 d (249 d). The distance between DW and CZ was determined by the median of their respective boundary distances.

Figure 5

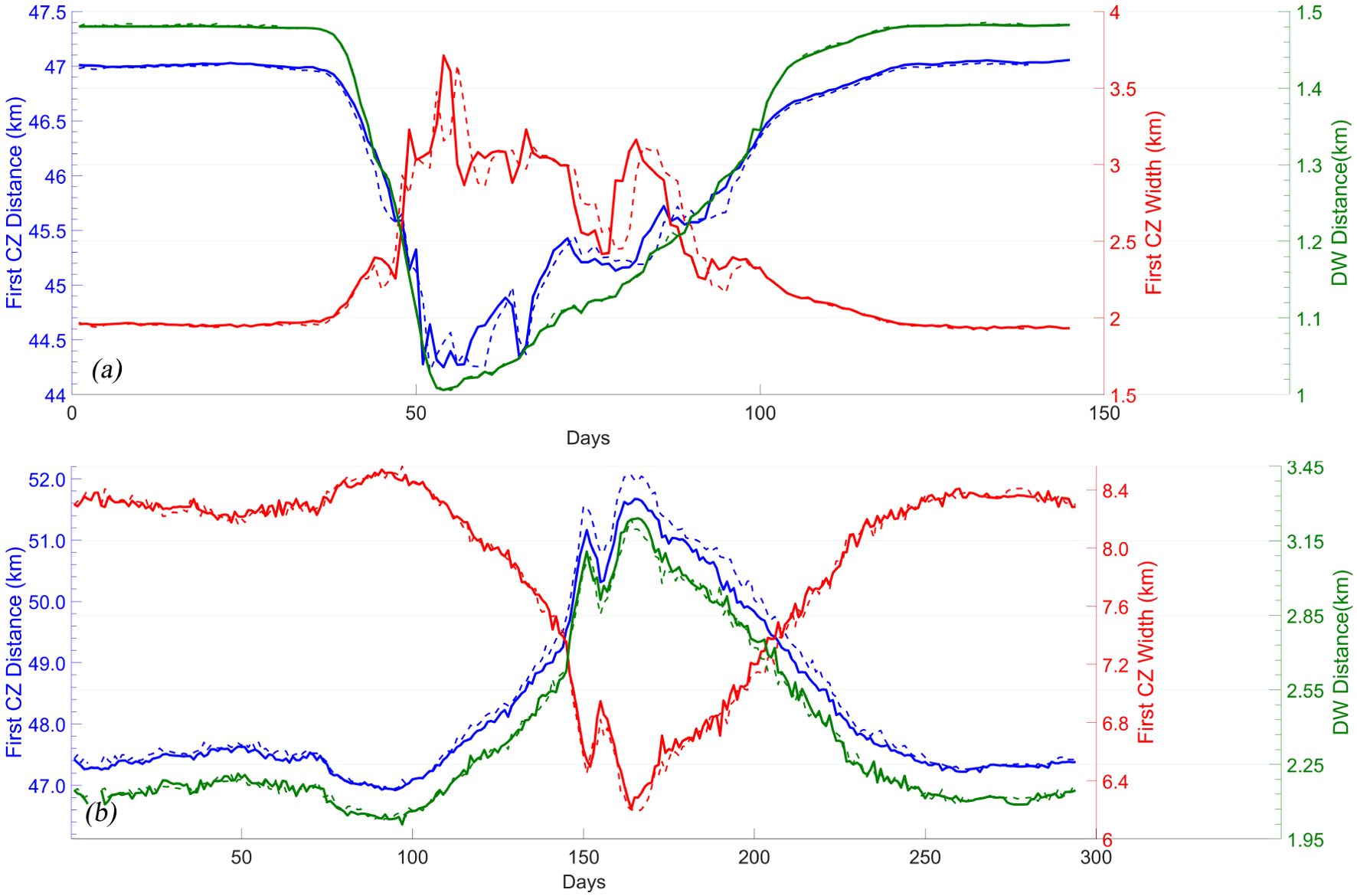
Figure 5. Curves of the first CZ of typical CE (A) and AE (B), along with the distance and width of DWs over 145 days (249 days) (the dashed and solid lines in this figure represent the simulation results of acoustic waves emitted from the eddy center to both sides along the Longitude direction, respectively).

Figure 5 demonstrates that AEs and CEs exert substantial yet contrary influences on the dimensions of the CZ and the position of the DW. Specifically, as the intensity of CEs increases, the CZ narrows and its width expands, while the DW approaches closer. Conversely, increasing intensity of AEs results in a broader CZ, a reduction in its width, and a further displacement of the DW. These observations align with the prior research reported by Zhu et al (2021) and Sun et al (Sun et al., 2023).

The influence of mesoscale eddies on the acoustic field primarily manifests during the transition from the growth and dissipation period to the mature stage. This is due to significant alterations in eddy characteristics during these phases. Changes in the ocean’s internal barocline, driven by air-sea interactions, eddy interactions, and baroclinic instability, result in continuous shifts in eddy intensity and core position. These dynamics critically impact the temperature and salinity profiles, thereby altering the acoustic characteristics as depicted in Figure 5. Further analysis is required to assess whether the sound field characteristics of the Gaussian eddy model employed in this study accurately reflect real-world conditions. Subsequent simulations and validations will utilize ocean reanalysis data.

3.2 Analysis of acoustic field variation in marine reanalysis data

To enhance the reliability and stability of the simulation results described in Section 3.1.1, we conducted additional experiments using reanalysis data. Initially, we extracted acoustic speed profiles from the JCOPE2M dataset, incorporating sea surface information from two typical AEs and CEs, outlined in Section 3.1.1. This process involved extending the profile extraction from the center of each identified eddy to 1.2 times its equivalent radius in the longitudinal direction. Subsequently, complete temperature and salinity profiles were obtained along the vertical axis. By applying the empirical formula detailed in Section 2.2.2, we transformed these temperature and salinity measurements into acoustic speed profiles.

After determining the acoustic speed profile structures for both AEs and CEs, we utilized the BELLHOP model to compute acoustic features. We placed the acoustic source at the center of the eddy at a depth of 150 m with a frequency of 300 Hz. Figure 6 illustrates the outcomes of these computations.

Figure 6

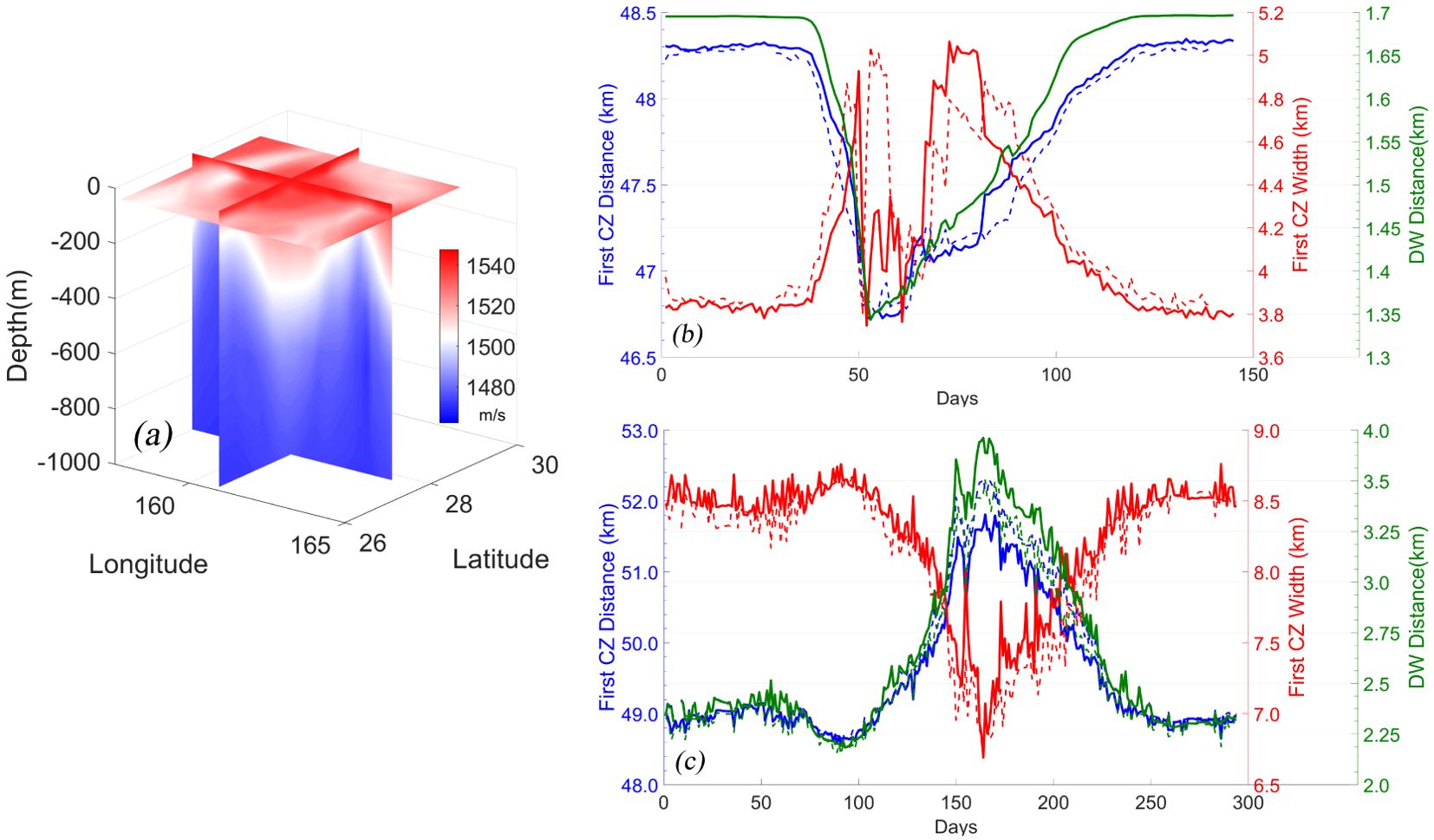
Figure 6. Diagram of (A) the AE speed profile based on JCOPE2M ocean reanalysis data, extracted using sea surface recognition eddy information (where the projection of the extracted profile on the sea surface is highlighted by the protruding part of the sea surface); BELLHOP model was used to simulate and calculate the variation curves of CE (B) and AE (C). Dashed and solid lines in this figure represent the simulation results of acoustic waves emitted from the eddy center along the longitude.

An analysis of feature changes depicted in Figure 6 indicates that the influence of mesoscale eddy on acoustic propagation, across the entire life cycle of ocean reanalysis data, is consistent with the observations reported in Section 3.1.1. Comparative analysis of the distance characteristics of the first CZ with the acoustic field properties under the enhanced Gaussian eddy model yields similar findings, confirming model appropriateness. However, while the enhanced Gaussian eddy model accurately represents the AE characteristics, it demonstrates notable discrepancies for the CE. Reanalysis data reveal the presence of a sub-surface acoustic channel, predominantly influenced by the mixed layer, within the JCOPE dataset at depths between 0 and 75 m. This condition creates an acoustic speed profile in this region that deviates substantially from predictions by the enhanced Gaussian eddy model. Consequently, the CZ calculation method employed in this study was found to be ineffective, resulting in anomalous outputs.

3.3 Analysis of influencing factors of mesoscale eddy acoustic field variation

In Section 3.1, we analyzed the temporal variations in various acoustic features throughout their entire life cycles. The changes in acoustic field characteristics arise from the interplay of multiple factors; thus, a comparative study is essential to identify the most influential factors. Consequently, this section details a study where a single factor was varied, holding others constant. Due to the limitations of ocean reanalysis data in controlling several major factors simultaneously, we employed the refined Gaussian eddy model to separately examine the AEs and CEs using parameters outlined in Section 3.1.1. Previous research has shown that various elements of the acoustic source markedly influence the propagation of the acoustic field in mesoscale eddies. However, this paper focuses on the changes in the acoustic field resulting from mesoscale eddies over their complete life cycles, emphasizing the alterations in eddy characteristics rather than acoustic source features. Accordingly, acoustic source parameters remained unchanged throughout this investigation, as indicated in Table 2.

Table 2

Table 2. Basic parameters of the acoustic source and receiver utilized in this section.

3.3.1 Analysis of eddy intensity

Simulations were performed using the BELLHOP model, with the eddy intensity (calculated by SLA at the eddy center) adjusted from 0.00 m to 1.00 m, while other parameters remained constant. The results, correlating eddy core intensity to SSH, are depicted in Figure 7. Details of the parameter settings are provided in Table 3. It is crucial to note the strong coupling between sea surface intensity and the subsurface structure, which changes throughout the lifecycle of the eddy, complicates a full depiction of the subsurface structure of the mesoscale eddy using a single Argo profile. Therefore, it is asserted that the alignment between the selected eddy and its corresponding Argo profile is maintained over the entire lifecycle of the eddy. This alignment enables sequential analysis despite a limited sample size.

Figure 7

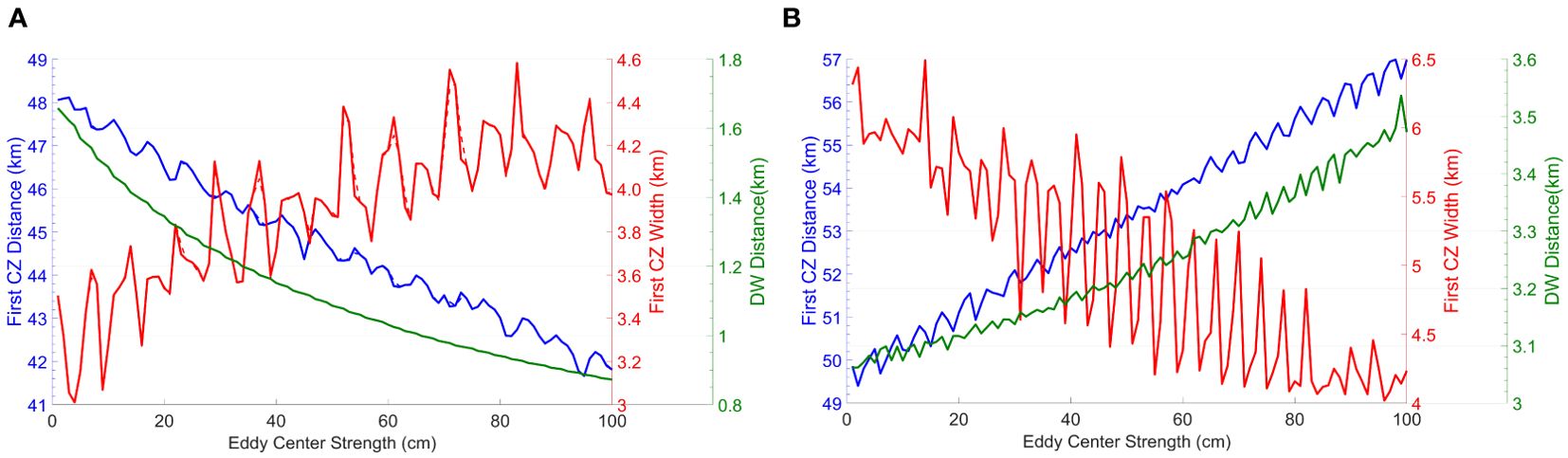
Figure 7. Typical CE (A) and AE (B) in 145 days (249 days) of the first CZ and DW distance and width change with time.

Table 3

Table 3. The value range and parameter setting of eddy intensity in this section.

The analysis in Figure 7 shows that the characteristics of acoustic propagation, specifically the CZ and the DW pathways, undergo notable changes in response to variations in eddy center intensity. Under CE conditions, increasing eddy intensity results in a significant reduction in the DW distance, decreasing from 1.62 km to 0.87 km, a 46.30% decrease. Concurrently, the distance to the first CZ decreases from 48.05 km to 42.10 km, a 12.38% reduction. In contrast, the width of the first CZ increases by 52.49%, from 3.01 km to 4.59 km. In AE scenarios, as eddy intensity increases, the DW distance extends from 3.08 km to 3.54 km, showing a 14.94% increase. Similarly, the distance to the first CZ increases from 49.64 km to 56.89 km, a 14.61% expansion. However, the width of the first CZ decreases from 6.47 km to 4.01 km, a 38.02% contraction.

Based on Figure 7 and previous data analysis, the propagation characteristics of the acoustic field in CE and AE are found to be significantly influenced by changes in eddy intensity. Specifically, in CEs, an increase in intensity shifts the DW and CZ toward the acoustic source and expands the CZ. In contrast, AEs exhibit the opposite response: the DW and CZ move away from the acoustic source and contract with increasing intensity. A comparative analysis of various indices influenced by intensity changes shows that the distance to the DW is more responsive in CEs, whereas the impacts on the distance to the first CZ are similar in both CE and AE. The width of the first CZ is equally affected in both types of eddies. These findings underscore the pronounced impact of eddy intensity on acoustic field propagation, with cold eddies demonstrating greater sensitivity to intensity variations.

3.3.2 Analysis of eddy deformation parameter

In this study, the eddy deformation parameter (α) is closely related to eddy variation and deformation. However, to maintain stability and fluid continuity within the water body, the α parameter for mesoscale eddies cannot be unbounded or infinitely small. Thus, characteristic information from 1 million randomly selected mesoscale eddies, identified using SSH data collected between January 1, 2007, and December 31, 2020, was analyzed. Statistical analysis of their respective α parameters (Figure 8) allowed for the determination of a generally reliable range for the deformation parameter α in mesoscale eddies with conventional morphology.

Figure 8

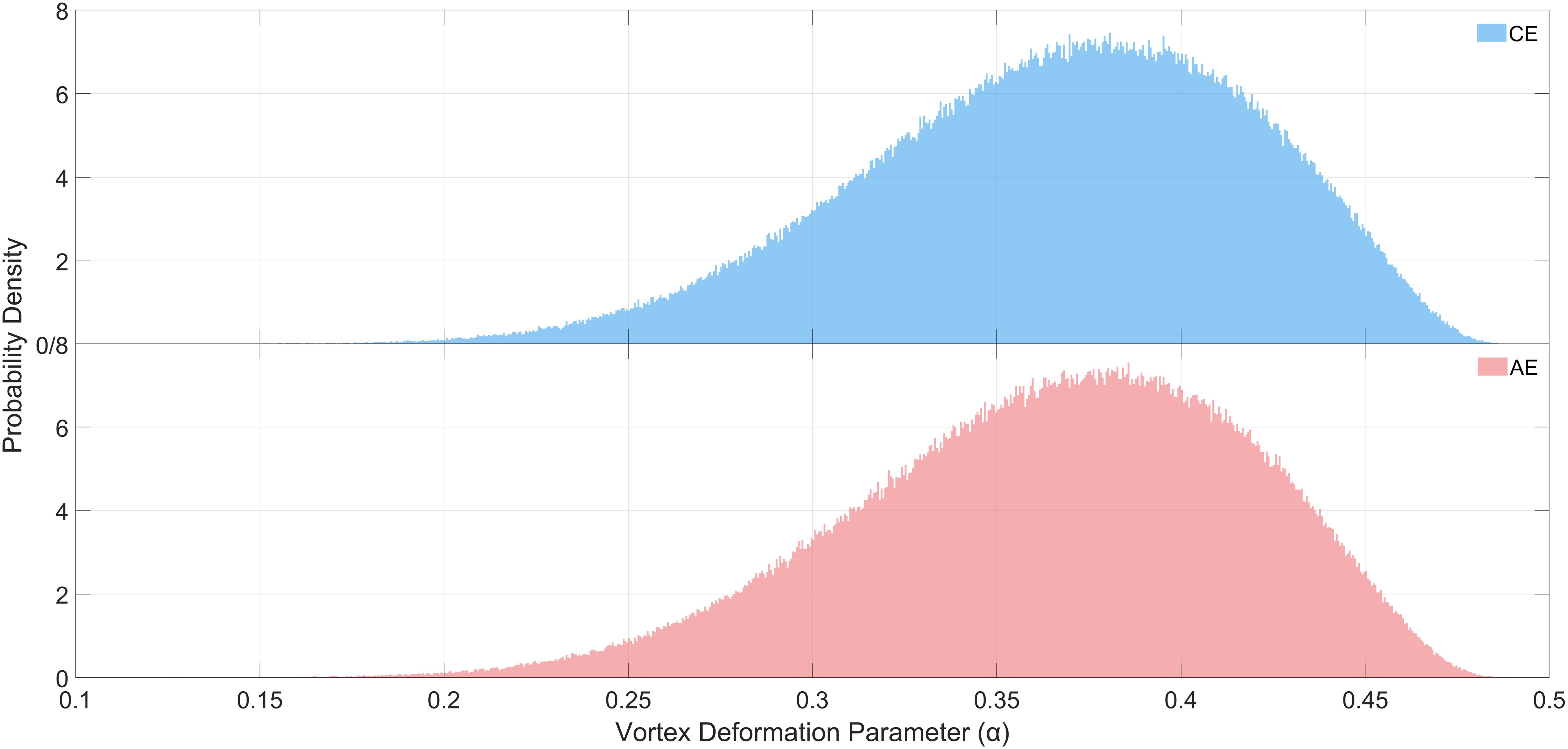
Figure 8. Histogram of the probability density distribution of α parameters calculated from 1 million CE and AE samples from January 1, 2007 to December 31, 2020.

The probability density distribution of the α parameter for both CE and AE, as shown in Figure 8, guided the selection of the value range used in this section, with values corresponding to probability densities greater than 0.5 being selected (Table 4).

Table 4

Table 4. Range and setting of α parameter value corresponding to probability density above 0.5.

An eddy intensity of 50cm was set, with the signal parameters for the acoustic source and receiver matching those in Table 2. Simulations were performed using the BELLHOP model, distinguishing between AEs and CEs, with the results presented in Figure 9.

Figure 9

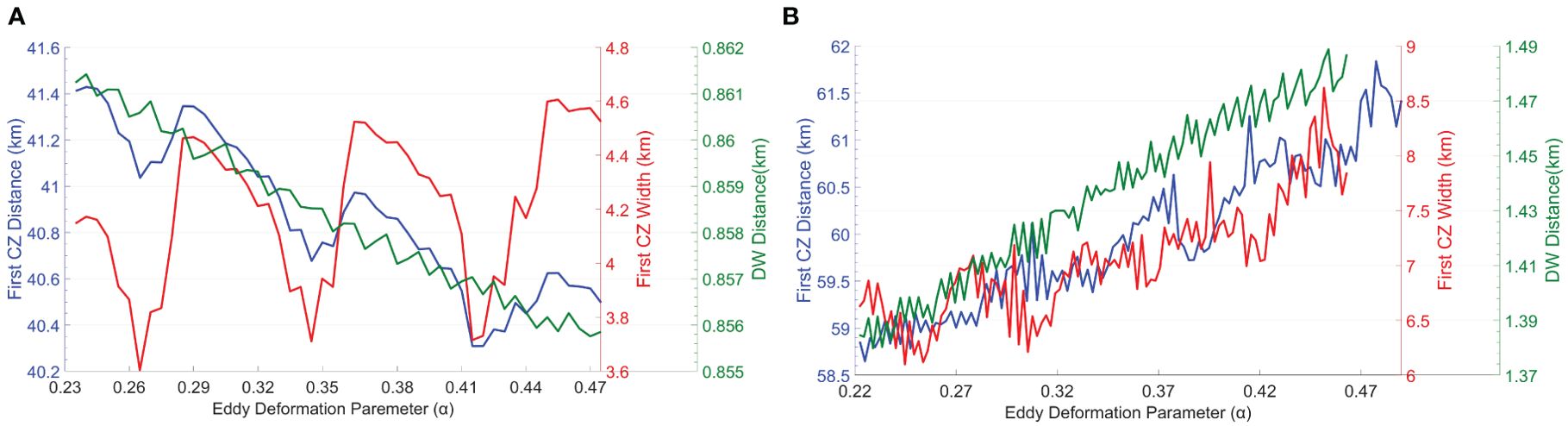
Figure 9. Change curve of acoustic field propagation under mesoscale eddy environment influenced by deformation parameter α [CE in (A), AE in (B)].

The simulation results in Figure 9 show a strong correlation between eddy deformation parameters and the underwater acoustic field in both AE and CE environments. In CE conditions, the DW distance decreases gradually with increasing eddy deformation parameter α, from 0.861 km to 0.856 km, representing a reduction of 0.581%. Meanwhile, the distance to the first CZ decreases from 41.41 km to 40.32 km, a 2.63% reduction, while the width of this zone increases from 4.15 km to 4.57 km, a 10.12% expansion. In AE conditions, the DW distance gradually increases with eddy intensity, rising from 1.394 km to 1.488 km, a 6.743% increase. The distance to the first CZ extends from 58.76 km to 61.66 km, a 4.93% increase and the width of the first CZ broadens from 6.15 km to 8.23 km, a 33.82% increase.

These results demonstrate that eddy deformation parameters have a notable impact on acoustic propagation characteristics within mesoscale eddy environments. As α increases, the CZ shifts closer to the acoustic source, with more pronounced fluctuations in its width, while the DW distance remains relatively unaffected. This discrepancy may stem from the minor influence of the increased eddy deformation parameter on the marine environment along the DW path, in contrast to its greater effect on acoustic propagation conditions further from the source, thereby exerting a stronger influence on the CZ distance. In the AE environment, a rise in α leads to a gradual expansion in both CZ distance and width, as well as DW distance, with a markedly greater range of increase than observed in the CE environment. In conclusion, eddy deformation parameters effectively alter acoustic propagation characteristics in mesoscale eddy environments, particularly under AE conditions; however, the overall impact remains less pronounced than changes induced by eddy intensity.

4 Summary and outlook

This paper provides a comprehensive analysis of using remote sensing data to study underwater acoustic propagation. The research investigates the influence of measured eddy parameters on acoustic propagation within a typical mesoscale eddy environment. Initially, a hybrid mesoscale eddy recognition algorithm, based on flow field geometry and the closed contour method, is employed to identify and extract features from multi-year SSH data, producing a dataset of mesoscale eddy characteristics (such as eddy radius, eddy center height, and eddy deformation parameters). Subsequently, these identified eddy features are correlated with concurrent Argo data. After rigorous quality control, matched eddy-Argo data pairs are established. Using these data pairs, the study introduces a novel mesoscale eddy tracking algorithm that utilizes pairing information and the Hu indefinite moment judgment method to achieve precise and consistent tracking results. The research focuses on eddies that maintain prolonged interaction with Argo floats, exhibit relatively complete lifecycles, and demonstrate stable movement patterns. From this selection, one AE and one CE are chosen as representative cases. These cases facilitate an in-depth analysis of the acoustic field environmental changes occurring throughout the full lifecycle of the mesoscale eddies.

After obtaining a representative pair of typical AEs and CEs, the acoustic field was constructed and analyzed as follows: Initially, an optimized two-dimensional, slowly varying Gaussian eddy model was introduced. This model incorporates a novel parameter: the eddy deformation parameter α, specifically designed to characterize the eddy center bias state influenced by geostrophic deflection forces and baroclinic instability. The simulation results generated from the BELLHOP model demonstrate consistency with the JCOPE2M ocean reanalysis data, confirming the model’s validity and robustness. Leveraging this foundation, characteristic information from two representative AEs and CEs with complete life cycles, identified and tracked, was integrated with observed Argo data. Using the enhanced Gaussian eddy model, we reconstructed the acoustic field profile sequence over a 145-day (249-day) period. Subsequently, the BELLHOP model was applied to calculate the acoustic field characteristics. Findings reveal that the life stages of typical AEs and CEs have significant, opposing effects on several key parameters: the distance to the CZ, the width of the CZ, and the DW distance. Specifically, with increasing CE intensity, the CZ distance progressively decreases, the width gradually expands, and the DW distance steadily shortens. Conversely, as AE intensity increases, the distance to the CZ progressively increases, the width contracts and the DW distance lengthens.

To identify key factors influencing acoustic field propagation characteristics over a multi-variable life cycle, we analyzed two primary factors independently: eddy intensity and eddy deformation parameters. Using the BELLHOP model and a control variable approach, we simulated the acoustic field. Results indicate that both factors significantly impact the acoustic field characteristics beneath the eddy, with eddy intensity exerting a more pronounced effect. As eddy intensity increases, the DW and CZ regions shift closer to the acoustic source, while the CZ width expands. Conversely, when eddy intensity decreases, the DW and CZ move away from the acoustic source, causing the CZ to narrow. The eddy deformation parameter also affects the acoustic field structure under the eddy. With an increase in the CE parameter α, the CZ shifts closer to the acoustic source and exhibits greater width fluctuation, suggesting that higher values of α have a limited effect on the marine environment along the DW path but alter acoustic propagation conditions further from the source, significantly impacting CZ distance. In the AE environment, as parameter α increases, CZ distance, width, and DW distance all show gradual expansion, with this growth range considerably exceeding that observed in the CE environment.

However, several considerations must be noted: First, while the enhanced Gaussian eddy model provides a more accurate representation of the ocean acoustic field influenced by eddies, it should be noted that this study relies solely on JCOPE2M ocean reanalysis data for validation. Although this dataset includes extensive observed information, its accuracy in representing the actual marine environment remains uncertain. Given the significant challenges in obtaining in situ data covering the full life cycle of a mesoscale eddy, this study employs reanalysis data as a substitute for direct validation. Second, the study focuses on a single mesoscale eddy pair over one complete life cycle, without broadening the dataset. This limitation requires further analysis to verify the generalizability of the model and the robustness of the conclusions. Third, mesoscale eddies, in their early stages, must reach a certain scale and intensity to be detectable. It is also worth mentioning that the two eddies analyzed in this study represent a significant portion but not the entirety of their life cycles. The acoustic field structure of mesoscale eddies, particularly in the formative phases, is likely affected by various other marine processes, which may cause their acoustic propagation characteristics to show instability and unpredictability. The eddy pair analyzed in this study was identified using the hybrid recognition algorithm only after a relatively stable structure had emerged. Thus, future research should emphasize assessing the acoustic propagation characteristics during the early stages of mesoscale eddy formation.

Data availability statement

Publicly available datasets were analyzed in this study. We gratefully acknowledge JCOPE2M JAMEST for offering data support (https://www.jamstec.go.jp/jcope/htdocs/distribution/index.html). We extend our gratitude to NCEI ETOPO for offering the water depth data (https://www.ncei.noaa.gov/products/etopo-global-relief-model). We also thank AVISO for the mesoscale eddy dataset (https://www.aviso.altimetry.fr/en/data/products/value-added-products/global-mesoscale-eddy-trajectory-product.html). We are grateful for the buoy data from the International Argo Program (https://argo.ucsd.edu/).

Author contributions

XM: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. LZ: Conceptualization, Investigation, Software, Writing – review & editing. WX: Data curation, Methodology, Supervision, Writing – review & editing. ML: Formal analysis, Project administration, Validation, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

We would like to thank other scholars and institutions who assisted in this research process.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ablain M., Larnicol G., Balmaseda M., Cipollini P., Faugère Y., Benveniste J. (2015). Improved sea level record over the satellite altimetry era (1993–2010) from the Climate Change Initiative project. Ocean Sci. 11, 67–82. doi: 10.5194/os-11-67-2015

Crossref Full Text | Google Scholar

Cazenave A., Palanisamy H., Ablain M. (2018). Contemporary sea level changes from satellite altimetry: What have we learned? What are the new challenges? Adv. Space Res. 62, 1639–1653. doi: 10.1016/j.asr.2018.07.017

Crossref Full Text | Google Scholar

Chaigneau A., Gizolme A., Grados C. (2008). Mesoscale eddies off Peru in altimeter records: Identification algorithms and eddy spatio-temporal patterns. Prog. Oceanography 79, 106–119. doi: 10.1016/j.pocean.2008.10.013

Crossref Full Text | Google Scholar

Chaigneau A., Le Texier M., Eldin G., Grados C., Pizarro O. (2011). Vertical structure of mesoscale eddies in the eastern South Pacific Ocean: A composite analysis from altimetry and Argo profiling floats. J. Geophys. Res.: Oceans 116 (C11).

Google Scholar

Chelton D., Schlax M. G., Samelson R. M. (2011). Global observations of nonlinear mesoscale eddies. Prog. Oceanography 91, 167–216. doi: 10.1016/j.pocean.2011.01.002

Crossref Full Text | Google Scholar

Chen C. T., Millero F. J. (1977). Speed of sound in seawater at high pressures. J. Acoustical Soc. America 62, 1129–1135. doi: 10.1121/1.381646

Crossref Full Text | Google Scholar

Chen W., Zhang Y., Liu Y., Wu Y., Zhang Y., Ren K. (2022). Observation of a mesoscale warm eddy impacts acoustic propagation in the slope of the South China Sea. Front. Mar. Sci. 9, 1086799. doi: 10.3389/fmars.2022.1086799

Crossref Full Text | Google Scholar

Czeschel R., Schütte F., Weller R. A., Stramma L. (2018). Transport, properties, and life cycles of mesoscale eddies in the eastern tropical South Pacific. Ocean Sci. 14, 731–750. doi: 10.5194/os-14-731-2018

Crossref Full Text | Google Scholar

Dong C., McWilliams J. C., Liu Y., Chen D. (2014). Global heat and salt transports by eddy movement. Nat. Commun. 5, 3294. doi: 10.1038/ncomms4294

PubMed Abstract | Crossref Full Text | Google Scholar

Franz K., Roscher R., Milioto A., Wenzel S., Kusche J. (2018). “Ocean eddy identification and tracking using neural networks,” in Igarss 2018-2018 IEEE international geoscience and remote sensing symposium (Valencia, Spain: IEEE). doi: 10.1109/IGARSS.2018.8519261

Crossref Full Text | Google Scholar

Godø O. R., Samuelsen A., Macaulay G. J., Patel R., Hjøllo S. S., Horne J., et al. (2012). Mesoscale eddies are oases for higher trophic marine life. PLoS One 7, e30161. doi: 10.1371/journal.pone.0030161

PubMed Abstract | Crossref Full Text | Google Scholar

Gul S., Zaidi S. S. H., Khan R., Wala A. B. (2017). “Underwater acoustic channel modeling using BELLHOP ray tracing method,” in 2017 14th International Bhurban Conference on Applied Sciences and Technology (IBCAST) (Islamabad, Pakistan: IEEE), 665-670. doi: 10.1109/IBCAST.2017.7868122

Crossref Full Text | Google Scholar

Hu M.-K. (1962). Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 8, 179–187. doi: 10.1109/TIT.1962.1057692

Crossref Full Text | Google Scholar

Itoh S., Yasuda I. (2010). Water mass structure of warm and cold anticyclonic eddies in the western boundary region of the subarctic north pacific. J. Phys. Oceanography 40, 2624–2642. doi: 10.1175/2010JPO4475.1

Crossref Full Text | Google Scholar

Johnson G. C., Hosoda S., Jayne S. R., Oke P. R., Riser S. C., Roemmich D., et al. (2022). Argo—Two decades: Global oceanography, revolutionized. Annu. Rev. Mar. Sci. 14, 379–403. doi: 10.1146/annurev-marine-022521-102008

PubMed Abstract | Crossref Full Text | Google Scholar

Jia-xun L. I., Ren Z., Chen-zhao L., Hong-jun F. (2012). Modeling of ocean mesoscale eddy and its application in the underwater acoustic propagation.

Google Scholar

Liu C., Wang Y., Yang Y., Duan Z.. (2016). New omega eddy identification method. Sci. China Physics Mechanics Astronomy 59, 1–9.

Google Scholar

Liu J., Piao S., Gong L., Zhang M., Guo Y., Zhang S (2021). The effect of mesoscale eddy on the characteristic of sound propagation. J. Mar. Sci. Eng. 9 (8), 787. doi: 10.3390/jmse9080787

Crossref Full Text | Google Scholar

Liu Y., Xu J., Jin K., Feng R., Xu L., Chen L., et al. (2024). A FEM flow impact acoustic model applied to rapid computation of ocean-acoustic remote sensing in mesoscale eddy seas. Remote Sens. 16 (2), 326. doi: 10.3390/rs16020326

Crossref Full Text | Google Scholar

Ma X., Zhang L., Xu W., Li M., Zhou X. (2024). A mesoscale eddy reconstruction method based on generative adversarial networks. Front. Mar. Sci. 11, 1411779. doi: 10.3389/fmars.2024.1411779

Crossref Full Text | Google Scholar

Miyazawa Y. (2003). The JCOPE ocean forecast system. (Tokyo, Japan: First ARGO Science Workshop).

Google Scholar

Morvan M., L'Hégaret P., de Marez C., Carton X., Corréard S., Baraille R. (2020). Life cycle of mesoscale eddies in the Gulf of Aden. Geophysical Astrophysical Fluid Dynamics 114 (4-5), 631–649. doi: 10.1080/03091929.2019.1708348

Crossref Full Text | Google Scholar

Munk W. H. (1950). On the wind-driven ocean circulation. J. Atmospheric Sci. 7 (2), 80–93. doi: 10.1175/1520-0469(1950)007<0080:OTWDOC>2.0.CO;2

Crossref Full Text | Google Scholar

Nencioli F., Dong C., Dickey T., Washburn L., McWilliams J. C. (2010). A vector geometry–based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. Atmospheric Oceanic Technol. 27 (3), 564–579. doi: 10.1175/2009JTECHO725.1

Crossref Full Text | Google Scholar

Nian R., Cai Y., Zhang Z., He H., Wu J., Yuan Q., et al. (2021). The identification and prediction of mesoscale eddy variation via memory in memory with scheduled sampling for sea level anomaly. Front. Mar. Sci. 8, 753942. doi: 10.3389/fmars.2021.753942

Crossref Full Text | Google Scholar

Oka E., Qiu B. (2012). Progress of North Pacific mode water research in the past decade. J. Oceanography 68, 5–20. doi: 10.1007/s10872-011-0032-5

Crossref Full Text | Google Scholar

Okubo A. (1970). “Horizontal dispersion of floatable particles in the vicinity of velocity singularities such as convergences,” in Deep sea research and oceanographic abstracts (Elsevier) 17 (3), 445-454. doi: 10.1016/0011-7471(70)90059-8

Crossref Full Text | Google Scholar

Porter M. B., Bucker H. P. (1987). Gaussian beam tracing for computing ocean acoustic fields. J. Acoustical Soc. America 82, 1349–1359. doi: 10.1121/1.395269

Crossref Full Text | Google Scholar

Qiu B., Chen S. (2005a). Variability of the Kuroshio Extension jet, recirculation gyre, and mesoscale eddies on decadal time scales. J. Phys. Oceanography 35, 2090–2103. doi: 10.1175/JPO2807.1

Crossref Full Text | Google Scholar

Qiu B., Chen S. (2005b). Eddy-induced heat transport in the subtropical north pacific from argo, TMI, and altimetry measurements. Gayana 68, 499–501.

Google Scholar

Roemmich D., et al. (2009). The Argo Program: Observing the global ocean with profiling floats. Oceanography 22, 34–43. doi: 10.5670/oceanog.2009.36

Crossref Full Text | Google Scholar

Shehwar D. E., Gul S., Zafar M. U., Shaukat U., Syed A. H., Zaidi S. S. H., et al. (2021). “Acoustic wave analysis in deep sea and shallow water using bellhop tool,” in 2021 OES China Ocean Acoustics (COA), Harbin, China, pp. 331-334. doi: 10.1109/COA50123.2021.9519944

Crossref Full Text | Google Scholar

Sun X., Zhang S., Nian X. (2023). Studying the influence of cold-core mesoscale ocean eddies on sound propagation based on the parabolic equation method. AIP Adv. doi: 10.1063/5.0173163

Crossref Full Text | Google Scholar

Weiss J. (1991). The dynamics of enstrophy transfer in two-dimensional hydrodynamics. Physica D: Nonlinear Phenomena 48, 273–294. doi: 10.1016/0167-2789(91)90088-Q

Crossref Full Text | Google Scholar

Xu G., Cheng C., Yang W., Xie W., Kong L., Hang R., et al. (2019). Oceanic eddy identification using an AI scheme. Remote Sens. 11 (11), 1349. doi: 10.3390/rs11111349

Crossref Full Text | Google Scholar

Xu W., Zhang L., Wang H. (2024). Machine learning–based feature prediction of convergence zones in ocean front environments. Front. Mar. Sci. doi: 10.3389/fmars.2024.1337234

Crossref Full Text | Google Scholar

Zhang Z., Qiu B. (2018). Evolution of submesoscale ageostrophic motions through the life cycle of oceanic mesoscale eddies. Geophysical Res. Lett. 45, 11,847–11,855. doi: 10.1029/2018GL080399

Crossref Full Text | Google Scholar

Zhang Z., Wang W., Qiu B. (2014). Oceanic mass transport by mesoscale eddies. Science 345, 322–324. doi: 10.1126/science.1252418

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang Z., Zhang Y., Wang W., Huang R. X. (2013). Universal structure of mesoscale eddies in the ocean. Geophysical Res. Lett. 40, 3677–3681. doi: 10.1002/grl.v40.14

Crossref Full Text | Google Scholar

Zhu F., Zhang H., Qu K. (2021). Influence of mesoscale warm eddies on sound propagation in the northeastern South China Sea. J. Harbin Eng. Univ. 42, 1496–1502.

Google Scholar